"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "skip"
},
"tags": [
"remove-cell"
]
},
"source": [
"## Preamble"
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"hideCode": false,
"hidePrompt": false,
"slideshow": {
"slide_type": "skip"
},
"tags": [
"remove-cell"
]
},
"outputs": [],
"source": [
"import pandas as pd\n",
"import numpy as np\n",
"import joypy\n",
"import matplotlib.pyplot as plt\n",
"from matplotlib.ticker import FuncFormatter\n",
"import seaborn as sns\n",
"import altair as alt\n",
"import networkx as nx\n",
"import cartopy.crs as ccrs\n",
"import cartopy.feature as cfeature\n",
"import wbdata as wb\n",
"import datetime\n",
"import warnings\n",
"import random\n",
"import imageio\n",
"# Suppress benign warnings\n",
"warnings.filterwarnings(\"ignore\")\n",
"\n",
"from IPython.display import Image, HTML, display\n",
"from sklearn.preprocessing import StandardScaler, MinMaxScaler, RobustScaler,power_transform\n",
"from sklearn.decomposition import PCA, FastICA\n",
"\n",
"%matplotlib inline\n",
"plt.rcParams['figure.figsize'] = (10, 6)"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"source": [
"# Trade mis-invoicing in Africa"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"Policy and media attention on illicit financial flows (IFF) has increased, with the recognition that Africa is a net creditor to the world."
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "-"
}
},
"source": [
"
\n",
"
\n",
"
\n",
"
\n",
"
\n",
"
\n",
"
New York Times (2013)
\n",
"
Guardian (2015)
\n",
"
\n",
"
\n",
"
\n",
"
\n",
"
\n",
"
Guardian (2017)
\n",
"
Economist (2019)
\n",
"
\n",
"
"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"**What is trade mis-invoicing?**\n",
"- The deliberate mis-statement of price or quantity of internationally traded goods in invoices presented to customs\n",
"- Can occur at import or export\n",
"- Can result in an inflow or outflow of money"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"**Motivations for trade mis-invoicing include:**\n",
"- Evading tariffs\n",
"- Exploiting subsidy regimes\n",
"- Subverting forex and capital controls\n",
"- Hiding transfers of wealth"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"**Mechanisms of mis-invoicing**"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"source": [
"From the reporting country’s perspective, trade mis-invoicing can result in an *inflow* or an *outflow* of capital, and this can be achieved by misreporting the value of both imports and exports. Money can be moved out of the country by over-invoicing imports, where that country pays too much money to buy goods from its partner; or by under-invoicing exports, where that country does not charge enough money for the goods that it sells to its partner. Conversely, money can be illicitly routed in to that country by under-invoicing imports, where the country pays too little money to buy goods from its partner; or by over-invoicing exports, where the country charges too much for the goods that it sells to its partner. The direction of trade mis-invoicing in addition to its mechanisms is represented in the diagram below."
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "-"
}
},
"source": [
"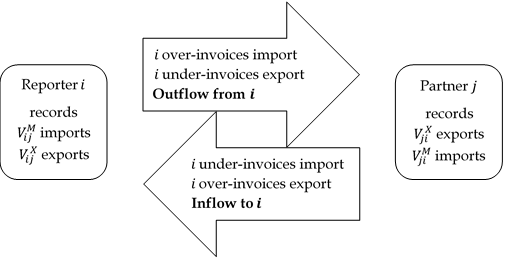"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"**Why does trade mis-invoicing matter?**\n",
"- Outflows undermine the fiscal base and public spending\n",
"- Financing gap needed to meet the Sustainable Development Goals (SDGs)\n",
"- Combating trade mis-invoicing is crucial for the mobilization of domestic resources in the continent, and can catalyze sustainable development"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "-"
}
},
"source": [
"
\n",
"
\n",
"
\n",
"
\n",
"
\n",
"
Governance loop (credit: William Davis)
\n",
"
\n",
"
"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"**Data source**\n",
"- Trade mis-invoicing data-set of the United Nations Economic Commission for Africa\n",
"- Panel with $n=6,248,254$ of mis-invoiced trade between 179 reporting jurisdictions and 179 partner countries for years 2000-2016 and disaggregated commodities\n",
"- Citation: Lépissier, Alice, Davis, William, & Ibrahim, Gamal. (2019). Trade Mis-Invoicing Dataset (Version 1). "
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"- The entire data-set `panel_results.Rdata` with ~6 million observations is available online.\n",
"- The unit of observation is a *reporter-partner-commodity-year* tuple, where the data represent the illicit flow embedded in a transaction between a reporter $i$ and a partner $j$ for a commodity $c$ in year $t$.\n",
"- The full panel is ~2GB. This notebook works with smaller summary data-sets generated from the full panel. The code to generate these summary data-sets is available on the repository by running the script file `Compute IFF Estimates.R`."
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"source": [
"Nota bene: the figures in this notebook that are not generated here can be reconstructed by running the `Data Visualization.R` script in that same repository."
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"**Methodology for calculating mis-invoiced trade**\n",
"- We locate mis-invoicing in the discrepancies between reported trade flows and their mirrored statistics\n",
"- But not all observed discrepancies are due to illicit motives!\n",
"- Imports tend to be recorded on the basis of Cost of Insurance and Freight (CIF), while exports are recorded Free On Board (FOB)"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"*Our approach*\n",
"1. Estimate the discrepancies between imports and mirror net exports as a function of both licit and illicit predictors\n",
"2. Perform a harmonization procedure in order to generate a reconciled value that represents our best estimate of what the legitimate value of the trade should be on a FOB basis\n",
"3. Calculate the IFF embedded in each transaction as the difference between the observed value and the reconciled value"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"source": [
"**What this data-set represents**\n",
"- The data-set presents estimates of mis-invoicing both in *imports* and *exports*. I will be working with the import data.\n",
"- There is a *low* and a *high* variant of mis-invoicing estimates. Discussion of how they vary is beyond the scope of this project, but note that we will be working with the *high* variant exclusively, as those are the official numbers of UNECA.\n",
"- A negative value represents an illicit *inflow*, while a positive value represents an illicit *outflow*."
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"- The panel can be aggregated over several dimensions, e.g. partner country, commodity, year. There are two methods to aggregate up the illicit flow:\n",
" - **Net** basis: simply add up all negative and positive values, so that inflows and outflows cancel each other out\n",
" - **Gross Excluding Reversals (GER)** basis: ignore all inflows, and sum up the positive values only across trading partners"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"source": [
"**Aggregation strategy**\n",
"\n",
"It is important to note that for a given country pair $i$ and $j$ in a given year $t$, the same trade flow can be associated with either an inflow or an outflow according to what commodity is traded. While it might seem unlikely that illicit funds might be traveling in both directions for the same trade flow, there could be a variety of different actors doing this for different reasons. For example, country $i$ might have export taxes on raw materials and export subsidies for manufacturing output, which would give an incentive to under-invoice exports of raw materials (resulting in an illicit outflow) and to over-invoice exports of manufactured goods (resulting in an illicit inflow). Alternatively, a criminal syndicate that has a legitimate front company may use re-invoicing to send money to an affiliate in another country to make an investment (e.g. hiring \"muscle\" to fight off a competitor) and then bring funds back using exports to the same country when the investment bears fruit."
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"source": [
"The object of analytical inquiry should guide the choice of aggregation strategy. For example, stakeholders interested in getting a picture of the total amount of funds departing a country on balance should favor a net aggregation basis. By contrast, stakeholders interested in better understanding the drivers and mechanisms of IFF should favor aggregation using GER in order to identify where money is flowing out or in."
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"source": [
"In this project, I will be using unsupervised machine learning to extract insights on analytically relevant dimensions of variation, so I will use summary data-sets that have been aggregated on a **Gross Excluding Reversals** basis. In other words, I am more interested in the direction and topology of the illicit flows, rather than their magnitude."
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"**Zoom in on Africa**\n",
"- During 2000-2016, the continent lost on average \\$83 billion a year in gross illicit outflows\n",
"- Net cumulative flows during that period were \\$362 billion"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "-"
}
},
"source": [
"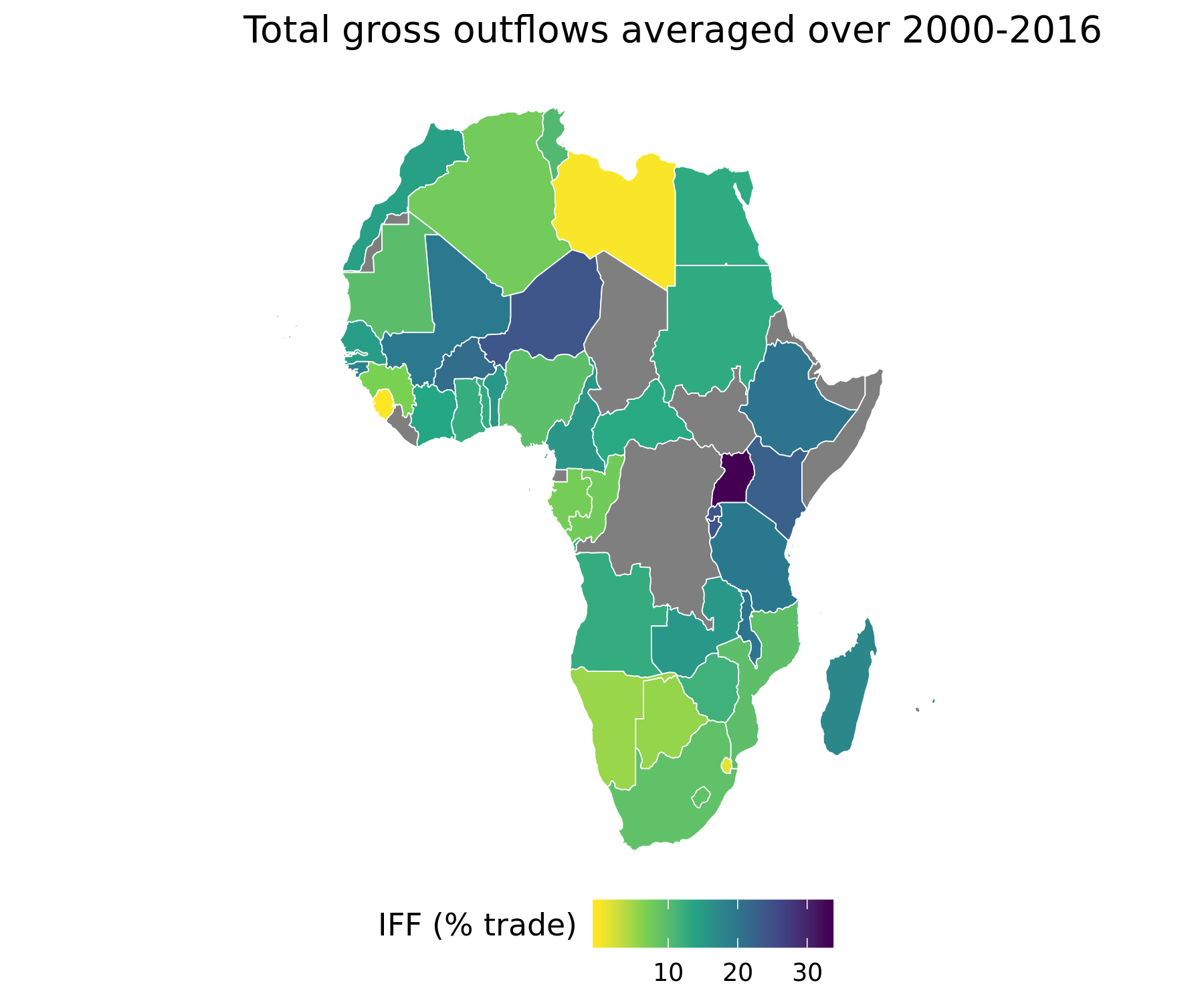\n",
"*Source*: generated by `Data Visualization.R` in "
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"## Goals"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"source": [
"While generating estimates of the dollar value of illicit trade has been helpful to shed light on the severity of the problem, the next step in the analysis is to further understand the nature of the illicit activity in terms of its origins, destinations, and sectors.\n",
"\n",
"Therefore, the goal of this project is to extract meaningful insights on illicit trade using unsupervised machine learning techniques. By doing so, I can identify analytically relevant categories and dimensions of variation, in order to generate hypotheses and guide further work."
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "-"
}
},
"source": [
"This project will apply the following techniques to the data:\n",
"1. Dimension reduction using Principal Components Analysis (PCA)\n",
"2. Clustering\n",
"3. Graph analysis"
]
},
{
"cell_type": "markdown",
"metadata": {
"hideCode": false,
"hidePrompt": false,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"## Data wrangling"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"source": [
"I will work with two summary forms of the full data-set `panel_results.Rdata`: one where the data is aggregated up to the reporter country, and one where the dyadic nature of the data is preserved."
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"source": [
"In the case where the data is aggregated up to the reporter country, there are two possible views of the feature space. On the one hand, the feature space can be spanned by the sectors of the different commodities ($p=21$). On the other hand, the feature space can be spanned by the reporter African countries ($p=46$)."
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"1. **Mis-invoiced trade for countries** (aggregated data)\n",
" - View 1: unit of observation = reporter-year; features = sectors\n",
" - View 2: unit of observation = sector-year; features = reporters\n",
"2. **Bilateral matrix of mis-invoiced trade** (dyadic data)\n",
" - Unit of observation = reporter-partner-year"
]
},
{
"cell_type": "markdown",
"metadata": {
"hideCode": false,
"hidePrompt": false,
"slideshow": {
"slide_type": "skip"
}
},
"source": [
"### Mis-invoiced trade data (for African reporting countries)"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"source": [
"Let's read in a summary data-set of the full panel which contains mis-invoicing estimates for reporter $i$ in commodity $c$ in year $t$ (aggregated over partner countries $j$ using the GER strategy)."
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"hideCode": false,
"hidePrompt": false,
"slideshow": {
"slide_type": "skip"
}
},
"outputs": [],
"source": [
"IFF_Sector = pd.read_csv('Data/GER_Orig_Sect_Year_Africa.csv')"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"source": [
"Let's also extract the relevant labels for the countries in the data-set."
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {
"slideshow": {
"slide_type": "skip"
},
"tags": [
"hide-input"
]
},
"outputs": [],
"source": [
"obs_info = IFF_Sector.reset_index().drop_duplicates(['reporter.ISO', 'year'])[['reporter.ISO', \n",
" 'year', \n",
" 'reporter', \n",
" 'rIncome', \n",
" 'rDev']]\n",
"obs_info = obs_info.replace({'LIC': 'Low income', \n",
" 'LMC': 'Lower-middle income',\n",
" 'UMC': 'Upper-middle income',\n",
" 'HIC': 'High income'})\n",
"obs_info = obs_info.rename(columns={'rIncome': 'Income group (World Bank)', \n",
" 'rDev': 'Country status (UN)'})"
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {
"hideCode": false,
"hidePrompt": false,
"slideshow": {
"slide_type": "skip"
},
"tags": [
"remove-cell"
]
},
"outputs": [],
"source": [
"# More data wrangling\n",
"IFF_Sector = IFF_Sector.fillna(0).drop(columns=['reporter', 'rIncome', 'rDev', 'section.code',\n",
" 'Imp_IFF_lo', 'Exp_IFF_lo']) \\\n",
" .set_index(['reporter.ISO', 'year'])"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {
"slideshow": {
"slide_type": "skip"
},
"tags": [
"remove-cell"
]
},
"outputs": [],
"source": [
"# Create a version of the data-set where mis-invoicing is averaged over years\n",
"IFF_Sector_mean = IFF_Sector.reset_index().groupby(['reporter.ISO', 'section']).mean(). \\\n",
" reset_index().set_index('reporter.ISO')"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"**Mis-invoiced trade for countries by sectors**"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"source": [
"The table below displays the raw data of mis-invoiced trade for 46 African countries in 21 different sectors during 2000-2016, aggregated over partner countries."
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {
"slideshow": {
"slide_type": "skip"
},
"tags": [
"remove-cell"
]
},
"outputs": [],
"source": [
"# Extract mis-invoicing in exports\n",
"IFF_Sector_Exp = IFF_Sector[['section', 'Exp_IFF_hi']]"
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {
"hideCode": false,
"hidePrompt": false,
"slideshow": {
"slide_type": "-"
},
"tags": [
"remove-input"
]
},
"outputs": [
{
"data": {
"text/html": [
"
\n",
"\n",
"
\n",
" \n",
"
\n",
"
\n",
"
\n",
"
section
\n",
"
Imp_IFF_hi
\n",
"
\n",
"
\n",
"
reporter.ISO
\n",
"
year
\n",
"
\n",
"
\n",
"
\n",
" \n",
" \n",
"
\n",
"
DZA
\n",
"
2001
\n",
"
Animal and Animal Products
\n",
"
1.914633e+08
\n",
"
\n",
"
\n",
"
2001
\n",
"
Pulp of Wood or of Other Fibrous Material
\n",
"
7.436143e+07
\n",
"
\n",
"
\n",
"
2001
\n",
"
Textiles
\n",
"
3.560644e+07
\n",
"
\n",
"
\n",
"
2001
\n",
"
Footwear and Headgear
\n",
"
1.146507e+06
\n",
"
\n",
"
\n",
"
2001
\n",
"
Stone, Glass, and Ceramics
\n",
"
2.935880e+07
\n",
"
\n",
"
\n",
"
...
\n",
"
...
\n",
"
...
\n",
"
...
\n",
"
\n",
"
\n",
"
ZWE
\n",
"
2007
\n",
"
Arms and Ammunition
\n",
"
0.000000e+00
\n",
"
\n",
"
\n",
"
2009
\n",
"
Works of Art
\n",
"
0.000000e+00
\n",
"
\n",
"
\n",
"
2013
\n",
"
Miscellaneous Manufactured Articles
\n",
"
0.000000e+00
\n",
"
\n",
"
\n",
"
2014
\n",
"
Miscellaneous Manufactured Articles
\n",
"
0.000000e+00
\n",
"
\n",
"
\n",
"
2014
\n",
"
Mineral Products
\n",
"
0.000000e+00
\n",
"
\n",
" \n",
"
\n",
"
11133 rows × 2 columns
\n",
"
"
],
"text/plain": [
" section Imp_IFF_hi\n",
"reporter.ISO year \n",
"DZA 2001 Animal and Animal Products 1.914633e+08\n",
" 2001 Pulp of Wood or of Other Fibrous Material 7.436143e+07\n",
" 2001 Textiles 3.560644e+07\n",
" 2001 Footwear and Headgear 1.146507e+06\n",
" 2001 Stone, Glass, and Ceramics 2.935880e+07\n",
"... ... ...\n",
"ZWE 2007 Arms and Ammunition 0.000000e+00\n",
" 2009 Works of Art 0.000000e+00\n",
" 2013 Miscellaneous Manufactured Articles 0.000000e+00\n",
" 2014 Miscellaneous Manufactured Articles 0.000000e+00\n",
" 2014 Mineral Products 0.000000e+00\n",
"\n",
"[11133 rows x 2 columns]"
]
},
"execution_count": 7,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# Extract mis-invoicing in imports\n",
"IFF_Sector_Imp = IFF_Sector[['section', 'Imp_IFF_hi']]\n",
"IFF_Sector_Imp"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"source": [
"### Mis-invoiced trade data (bilateral trade matrix)"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"source": [
"Now, let's read in another summary data-set of the full panel which contains mis-invoicing estimates for reporter $i$ with partner $j$ in year $t$ (aggregated over commodities $c$ using the GER strategy)."
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"outputs": [],
"source": [
"IFF_Dest = pd.read_csv('Data/GER_Orig_Dest_Year_Africa.csv')"
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {
"slideshow": {
"slide_type": "skip"
},
"tags": [
"remove-cell"
]
},
"outputs": [],
"source": [
"# More data wrangling\n",
"IFF_Dest = IFF_Dest.fillna(0).drop(columns=['reporter', 'rIncome', 'rDev', \n",
" 'partner', 'pRegion', 'pIncome', 'pDev',\n",
" 'Imp_IFF_lo', 'Exp_IFF_lo']) \\\n",
" .set_index(['reporter.ISO', 'year'])"
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {
"slideshow": {
"slide_type": "skip"
},
"tags": [
"remove-cell"
]
},
"outputs": [],
"source": [
"# Create a version of the data-set where mis-invoicing is averaged over years\n",
"IFF_Dest_mean = IFF_Dest.reset_index().groupby(['reporter.ISO', 'partner.ISO']).mean(). \\\n",
" reset_index().set_index('reporter.ISO')"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"**Mis-invoiced trade for dyads**"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"source": [
"The table below displays the raw data of mis-invoiced trade for 46 African countries with 167 partner countries during 2000-2016, aggregated over commodity sectors."
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {
"slideshow": {
"slide_type": "skip"
},
"tags": [
"remove-cell"
]
},
"outputs": [],
"source": [
"# Extract mis-invoicing in exports\n",
"IFF_Dest_Exp = IFF_Dest[['partner.ISO', 'Exp_IFF_hi']]"
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {
"slideshow": {
"slide_type": "-"
},
"tags": [
"remove-input"
]
},
"outputs": [
{
"data": {
"text/html": [
"
\n",
"\n",
"
\n",
" \n",
"
\n",
"
\n",
"
\n",
"
partner.ISO
\n",
"
Imp_IFF_hi
\n",
"
\n",
"
\n",
"
reporter.ISO
\n",
"
year
\n",
"
\n",
"
\n",
"
\n",
" \n",
" \n",
"
\n",
"
DZA
\n",
"
2001
\n",
"
AND
\n",
"
1.609561e+04
\n",
"
\n",
"
\n",
"
2001
\n",
"
ARG
\n",
"
4.717459e+07
\n",
"
\n",
"
\n",
"
2001
\n",
"
AUS
\n",
"
2.027641e+07
\n",
"
\n",
"
\n",
"
2001
\n",
"
AUT
\n",
"
7.641706e+07
\n",
"
\n",
"
\n",
"
2001
\n",
"
BEL
\n",
"
2.285729e+07
\n",
"
\n",
"
\n",
"
...
\n",
"
...
\n",
"
...
\n",
"
...
\n",
"
\n",
"
\n",
"
ZWE
\n",
"
2014
\n",
"
MDG
\n",
"
0.000000e+00
\n",
"
\n",
"
\n",
"
2014
\n",
"
SGP
\n",
"
0.000000e+00
\n",
"
\n",
"
\n",
"
2014
\n",
"
CHE
\n",
"
0.000000e+00
\n",
"
\n",
"
\n",
"
2014
\n",
"
ARE
\n",
"
0.000000e+00
\n",
"
\n",
"
\n",
"
2015
\n",
"
UGA
\n",
"
0.000000e+00
\n",
"
\n",
" \n",
"
\n",
"
34757 rows × 2 columns
\n",
"
"
],
"text/plain": [
" partner.ISO Imp_IFF_hi\n",
"reporter.ISO year \n",
"DZA 2001 AND 1.609561e+04\n",
" 2001 ARG 4.717459e+07\n",
" 2001 AUS 2.027641e+07\n",
" 2001 AUT 7.641706e+07\n",
" 2001 BEL 2.285729e+07\n",
"... ... ...\n",
"ZWE 2014 MDG 0.000000e+00\n",
" 2014 SGP 0.000000e+00\n",
" 2014 CHE 0.000000e+00\n",
" 2014 ARE 0.000000e+00\n",
" 2015 UGA 0.000000e+00\n",
"\n",
"[34757 rows x 2 columns]"
]
},
"execution_count": 12,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# Extract mis-invoicing in imports\n",
"IFF_Dest_Imp = IFF_Dest[['partner.ISO', 'Imp_IFF_hi']]\n",
"IFF_Dest_Imp"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"source": [
"### Crosswalk data"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"source": [
"Finally, let's import a table that contains labels for the countries, such as their ISO codes, geographic regions, and income groupings that they belong to."
]
},
{
"cell_type": "code",
"execution_count": 13,
"metadata": {
"slideshow": {
"slide_type": "skip"
},
"tags": [
"remove-cell"
]
},
"outputs": [],
"source": [
"# Uncomment this line to download the data\n",
"# Depending on the provider, this may not work in Binder\n",
"# ! wget -qO Data/crosswalk.xlsx https://github.com/walice/Codes-Masterlist/blob/master/Codes_Masterlist.xlsx?raw=true"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"**Metadata for countries**"
]
},
{
"cell_type": "code",
"execution_count": 14,
"metadata": {
"slideshow": {
"slide_type": "-"
}
},
"outputs": [
{
"data": {
"text/html": [
"
\n",
"\n",
"
\n",
" \n",
"
\n",
"
\n",
"
ISO3166.3
\n",
"
ISO3166.2
\n",
"
country
\n",
"
UN_Region
\n",
"
UN_Region_Code
\n",
"
UN_Sub-region
\n",
"
UN_Sub-region_Code
\n",
"
UN_Intermediate_Region
\n",
"
UN_Intermediate_Region_Code
\n",
"
UN_M49_Code
\n",
"
...
\n",
"
WB_Income_Group_Code
\n",
"
WB_Region
\n",
"
WB_Lending_Category
\n",
"
WB_Other
\n",
"
OECD
\n",
"
EU28
\n",
"
Arab League
\n",
"
Commonwealth
\n",
"
Longitude
\n",
"
Latitude
\n",
"
\n",
" \n",
" \n",
"
\n",
"
0
\n",
"
ABW
\n",
"
AW
\n",
"
Aruba
\n",
"
Americas
\n",
"
19.0
\n",
"
Latin America and the Caribbean
\n",
"
419.0
\n",
"
Caribbean
\n",
"
29.0
\n",
"
533.0
\n",
"
...
\n",
"
HIC
\n",
"
Latin America and Caribbean
\n",
"
..
\n",
"
NaN
\n",
"
0
\n",
"
0
\n",
"
0
\n",
"
0
\n",
"
-69.982677
\n",
"
12.520880
\n",
"
\n",
"
\n",
"
1
\n",
"
AFG
\n",
"
AF
\n",
"
Afghanistan
\n",
"
Asia
\n",
"
142.0
\n",
"
Southern Asia
\n",
"
34.0
\n",
"
NaN
\n",
"
NaN
\n",
"
4.0
\n",
"
...
\n",
"
LIC
\n",
"
South Asia
\n",
"
IDA
\n",
"
HIPC
\n",
"
0
\n",
"
0
\n",
"
0
\n",
"
0
\n",
"
66.004734
\n",
"
33.835231
\n",
"
\n",
"
\n",
"
2
\n",
"
AFG
\n",
"
AF
\n",
"
Afghanistan, Islamic Republic of
\n",
"
Asia
\n",
"
142.0
\n",
"
Southern Asia
\n",
"
34.0
\n",
"
NaN
\n",
"
NaN
\n",
"
4.0
\n",
"
...
\n",
"
LIC
\n",
"
South Asia
\n",
"
IDA
\n",
"
HIPC
\n",
"
0
\n",
"
0
\n",
"
0
\n",
"
0
\n",
"
66.004734
\n",
"
33.835231
\n",
"
\n",
"
\n",
"
3
\n",
"
AGO
\n",
"
AO
\n",
"
Angola
\n",
"
Africa
\n",
"
2.0
\n",
"
Sub-Saharan Africa
\n",
"
202.0
\n",
"
Middle Africa
\n",
"
17.0
\n",
"
24.0
\n",
"
...
\n",
"
LMC
\n",
"
Sub-Saharan Africa
\n",
"
IBRD
\n",
"
NaN
\n",
"
0
\n",
"
0
\n",
"
0
\n",
"
0
\n",
"
17.537368
\n",
"
-12.293361
\n",
"
\n",
"
\n",
"
4
\n",
"
AIA
\n",
"
AI
\n",
"
Anguila
\n",
"
Americas
\n",
"
19.0
\n",
"
Latin America and the Caribbean
\n",
"
419.0
\n",
"
Caribbean
\n",
"
29.0
\n",
"
660.0
\n",
"
...
\n",
"
NaN
\n",
"
NaN
\n",
"
NaN
\n",
"
NaN
\n",
"
0
\n",
"
0
\n",
"
0
\n",
"
0
\n",
"
-63.064989
\n",
"
18.223959
\n",
"
\n",
" \n",
"
\n",
"
5 rows × 25 columns
\n",
"
"
],
"text/plain": [
" ISO3166.3 ISO3166.2 country UN_Region \\\n",
"0 ABW AW Aruba Americas \n",
"1 AFG AF Afghanistan Asia \n",
"2 AFG AF Afghanistan, Islamic Republic of Asia \n",
"3 AGO AO Angola Africa \n",
"4 AIA AI Anguila Americas \n",
"\n",
" UN_Region_Code UN_Sub-region UN_Sub-region_Code \\\n",
"0 19.0 Latin America and the Caribbean 419.0 \n",
"1 142.0 Southern Asia 34.0 \n",
"2 142.0 Southern Asia 34.0 \n",
"3 2.0 Sub-Saharan Africa 202.0 \n",
"4 19.0 Latin America and the Caribbean 419.0 \n",
"\n",
" UN_Intermediate_Region UN_Intermediate_Region_Code UN_M49_Code ... \\\n",
"0 Caribbean 29.0 533.0 ... \n",
"1 NaN NaN 4.0 ... \n",
"2 NaN NaN 4.0 ... \n",
"3 Middle Africa 17.0 24.0 ... \n",
"4 Caribbean 29.0 660.0 ... \n",
"\n",
" WB_Income_Group_Code WB_Region WB_Lending_Category \\\n",
"0 HIC Latin America and Caribbean .. \n",
"1 LIC South Asia IDA \n",
"2 LIC South Asia IDA \n",
"3 LMC Sub-Saharan Africa IBRD \n",
"4 NaN NaN NaN \n",
"\n",
" WB_Other OECD EU28 Arab League Commonwealth Longitude Latitude \n",
"0 NaN 0 0 0 0 -69.982677 12.520880 \n",
"1 HIPC 0 0 0 0 66.004734 33.835231 \n",
"2 HIPC 0 0 0 0 66.004734 33.835231 \n",
"3 NaN 0 0 0 0 17.537368 -12.293361 \n",
"4 NaN 0 0 0 0 -63.064989 18.223959 \n",
"\n",
"[5 rows x 25 columns]"
]
},
"execution_count": 14,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"crosswalk = pd.read_excel(\"Data/crosswalk.xlsx\").rename(columns={'Country': 'country'})\n",
"crosswalk.head()"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"## Auxiliary functions"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"source": [
"I create three auxiliary functions to aid me in running Principal Component Analysis:\n",
"1. A function which creates the feature space for PCA from a data-set in a long format (which is the format of `IFF_Sector` and `IFF_Dest`)\n",
"2. A function which runs PCA and plots a biplot for two chosen principal components\n",
"3. A function which plots a cumulative scree plot"
]
},
{
"cell_type": "code",
"execution_count": 15,
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"outputs": [],
"source": [
"def create_features(data, values, features, obs):\n",
" \"\"\"\n",
" Convert data-set in long format to wide and preserve information on year.\n",
" \n",
" data: {IFF_Sector_Imp, IFF_Dest_Imp, IFF_Dest_AFR, ...}, as Pandas dataframe, \n",
" name of data-set from which to create feature space, must be in long format\n",
" values: {'Imp_IFF_hi', 'Exp_IFF_hi'}, as string, values that data-set will represent\n",
" features: {'reporter.ISO', 'section', 'partner.ISO'}, as string, \n",
" what to use as the feature space\n",
" obs: {'section', 'reporter.ISO'}, as string, what to use as the observation level\n",
" \"\"\"\n",
" features_data = data.pivot_table(values=values, \n",
" columns=features, \n",
" index=[obs, 'year'], \n",
" fill_value=0)\n",
" return features_data"
]
},
{
"cell_type": "code",
"execution_count": 16,
"metadata": {
"slideshow": {
"slide_type": "skip"
},
"tags": [
"hide-cell"
]
},
"outputs": [],
"source": [
"# Extra function to run the analysis on average mis-invoicing over the years\n",
"def create_features_mean(data, values, features, obs):\n",
" \"\"\"\n",
" Convert data-set in long format to wide.\n",
" \n",
" data: {IFF_Sector_mean, IFF_Dest_mean, ...}, as Pandas dataframe, \n",
" name of data-set from which to create feature space, must be in long format\n",
" values: {'Imp_IFF_hi', 'Exp_IFF_hi'}, as string, values that data-set will represent\n",
" features: {'reporter.ISO', 'section', 'partner.ISO'}, as string, \n",
" what to use as the feature space\n",
" obs: {'section', 'reporter.ISO'}, as string, what to use as the observation level\n",
" \"\"\"\n",
" features_data = data.pivot_table(values=values, \n",
" columns=features, \n",
" index=obs, \n",
" fill_value=0)\n",
" return features_data"
]
},
{
"cell_type": "code",
"execution_count": 17,
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"outputs": [],
"source": [
"def biplot_PCA(features_data, nPC=2, firstPC=1, secondPC=2, obs='reporter.ISO', show_loadings=False):\n",
" \"\"\"\n",
" Project the data in the 2-dimensional space spanned by 2 principal components\n",
" chosen by the user, along with a bi-plot of the top 3 loadings per PC, and color observations\n",
" by class label.\n",
"\n",
" Args:\n",
" features_data: as Pandas dataframe, data-set of features\n",
" nPC: number of principal components\n",
" firstPC: integer denoting first principal component to plot in bi-plot\n",
" secondPC: integer denoting second principal component to plot in bi-plot\n",
" obs: string denoting index of class labels (in features_data)\n",
" show_loadings: Boolean indicating whether PCA loadings should be displayed\n",
" Returns:\n",
" plot (interactive)\n",
" pca_loadings (if show_loadings=True)\n",
" \"\"\"\n",
" \n",
" # Run PCA (standardize data beforehand)\n",
" features_data_std = StandardScaler().fit_transform(features_data)\n",
" pca = PCA(n_components=nPC, random_state=234)\n",
" princ_comp = pca.fit_transform(features_data_std)\n",
"\n",
" # Extract PCA loadings\n",
" cols = ['PC' + str(c+1) for c in np.arange(nPC)]\n",
" pca_loadings = pd.DataFrame(pca.components_.T, \n",
" columns=cols,\n",
" index=list(features_data.columns))\n",
" \n",
" # Extract PCA scores\n",
" pca_scores = pd.DataFrame(princ_comp, \n",
" columns=cols)\n",
" pca_scores[obs] = features_data.reset_index()[obs].values.tolist()\n",
" pca_scores['year'] = features_data.reset_index()['year'].values.tolist()\n",
" \n",
" score_PC1 = princ_comp[:,firstPC-1]\n",
" score_PC2 = princ_comp[:,secondPC-1]\n",
" \n",
" # Generate plot data\n",
" if obs == 'reporter.ISO':\n",
" plot_data = pd.merge(pca_scores, obs_info, on=[obs, 'year'])\n",
" color_obs = 'reporter'\n",
" tooltip_obs = ['reporter', 'year', 'Income group (World Bank)', 'Country status (UN)']\n",
" else:\n",
" plot_data = pca_scores\n",
" color_obs = 'section'\n",
" tooltip_obs = ['section', 'year']\n",
"\n",
" # Return chosen PCs to plot\n",
" PC1 = 'PC'+str(firstPC)\n",
" PC2 = 'PC'+str(secondPC)\n",
"\n",
" # Extract top loadings (in absolute value)\n",
" # TO DO: use dict to iterate over\n",
" toploadings_PC1 = pca_loadings.apply(lambda x: abs(x)).sort_values(by=PC1).tail(3)[[PC1, PC2]]\n",
" toploadings_PC2 = pca_loadings.apply(lambda x: abs(x)).sort_values(by=PC2).tail(3)[[PC1, PC2]]\n",
"\n",
" originsPC1 = pd.DataFrame({'index':toploadings_PC1.index.tolist(), \n",
" PC1: np.zeros(3), \n",
" PC2: np.zeros(3)})\n",
" originsPC2 = pd.DataFrame({'index':toploadings_PC2.index.tolist(), \n",
" PC1: np.zeros(3), \n",
" PC2: np.zeros(3)})\n",
" \n",
" toploadings_PC1 = pd.concat([toploadings_PC1.reset_index(), originsPC1], axis=0)\n",
" toploadings_PC2 = pd.concat([toploadings_PC2.reset_index(), originsPC2], axis=0)\n",
"\n",
" toploadings_PC1[PC1] = toploadings_PC1[PC1]*max(score_PC1)*1.5\n",
" toploadings_PC1[PC2] = toploadings_PC1[PC2]*max(score_PC2)*1.5\n",
" toploadings_PC2[PC1] = toploadings_PC2[PC1]*max(score_PC1)*1.5\n",
" toploadings_PC2[PC2] = toploadings_PC2[PC2]*max(score_PC2)*1.5\n",
" \n",
" # Project top 3 loadings over the space spanned by 2 principal components\n",
" lines = alt.Chart().mark_line().encode()\n",
" for color, i, dataset in zip(['#440154FF', '#21908CFF'], [0,1], [toploadings_PC1, toploadings_PC2]):\n",
" lines[i] = alt.Chart(dataset).mark_line(color=color).encode(\n",
" x= PC1 +':Q',\n",
" y= PC2 +':Q',\n",
" detail='index'\n",
" ).properties(\n",
" width=400,\n",
" height=400\n",
" )\n",
" \n",
" # Add labels to the loadings\n",
" text=alt.Chart().mark_text().encode()\n",
" for color, i, dataset in zip(['#440154FF', '#21908CFF'], [0, 1], [toploadings_PC1[0:3], toploadings_PC2[0:3]]):\n",
" text[i] = alt.Chart(dataset).mark_text(\n",
" align='left',\n",
" baseline='bottom',\n",
" color=color\n",
" ).encode(\n",
" x= PC1 +':Q',\n",
" y= PC2 +':Q',\n",
" text='index'\n",
" )\n",
" \n",
" # Scatter plot colored by observation class label\n",
" points = alt.Chart(plot_data).mark_circle(size=60).encode(\n",
" x=alt.X(PC1, axis=alt.Axis(title='Principal Component ' + str(firstPC))),\n",
" y=alt.X(PC2, axis=alt.Axis(title='Principal Component ' + str(secondPC))),\n",
" color=alt.Color(color_obs, scale=alt.Scale(scheme='category20b'),\n",
" legend=alt.Legend(orient='right')),\n",
" tooltip=tooltip_obs\n",
" ).interactive()\n",
" \n",
" # Bind it all together\n",
" chart = (points + lines[0] + lines[1] + text[0] + text[1]) \n",
" chart.display()\n",
"\n",
" if show_loadings:\n",
" return pca_loadings"
]
},
{
"cell_type": "code",
"execution_count": 18,
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"outputs": [],
"source": [
"def scree_plot(features_data, show_explained_var=False):\n",
" \"\"\"\n",
" Create a cumulative scree splot and (optional) return the explained variance by each component.\n",
" \n",
" features_data: as Pandas dataframe, the data-set on which to run PCA\n",
" show_explained_var: as Boolean, flag for whether to return explained variance\n",
" \"\"\"\n",
" \n",
" features_data_std = StandardScaler().fit_transform(features_data)\n",
" pca = PCA(n_components=features_data_std.shape[1], random_state=234)\n",
" princ_comp = pca.fit_transform(features_data_std)\n",
" \n",
" explained_var = pd.DataFrame({'PC': np.arange(1,features_data_std.shape[1]+1),\n",
" 'var': pca.explained_variance_ratio_,\n",
" 'cumvar': np.cumsum(pca.explained_variance_ratio_)})\n",
"\n",
" # Adapted from https://altair-viz.github.io/gallery/multiline_tooltip.html\n",
" # Create a selection that chooses the nearest point & selects based on x-value\n",
" nearest = alt.selection(type='single', nearest=True, on='mouseover',\n",
" fields=['PC'], empty='none')\n",
"\n",
" # The basic line\n",
" line = alt.Chart(explained_var).mark_line(interpolate='basis', color='#FDE725FF').encode(\n",
" alt.X('PC:Q',\n",
" scale=alt.Scale(domain=(1, len(explained_var))),\n",
" axis=alt.Axis(title='Principal Component')\n",
" ),\n",
" alt.Y('cumvar:Q',\n",
" scale=alt.Scale(domain=(min(explained_var['cumvar']), 1)),\n",
" axis=alt.Axis(title='Cumulative Variance Explained')\n",
" ),\n",
" )\n",
"\n",
" # Transparent selectors across the chart. This is what tells us\n",
" # the x-value of the cursor\n",
" selectors = alt.Chart(explained_var).mark_point().encode(\n",
" x='PC:Q',\n",
" opacity=alt.value(0),\n",
" ).add_selection(\n",
" nearest\n",
" )\n",
"\n",
" # Draw points on the line, and highlight based on selection\n",
" points = line.mark_point().encode(\n",
" opacity=alt.condition(nearest, alt.value(1), alt.value(0))\n",
" )\n",
"\n",
" # Draw text labels near the points, and highlight based on selection\n",
" text = line.mark_text(align='left', dx=5, dy=-5).encode(\n",
" text=alt.condition(nearest, 'cumvar:Q', alt.value(' '))\n",
" )\n",
"\n",
" # Draw a rule at the location of the selection\n",
" rules = alt.Chart(explained_var).mark_rule(color='gray').encode(\n",
" x='PC:Q',\n",
" ).transform_filter(\n",
" nearest\n",
" )\n",
"\n",
" # Put the five layers into a chart and bind the data\n",
" out = alt.layer(\n",
" line, selectors, points, rules, text\n",
" ).properties(\n",
" title='Cumulative scree plot',\n",
" width=500, height=300\n",
" )\n",
" \n",
" out.display()\n",
" \n",
" if show_explained_var:\n",
" return explained_var[['PC', 'var']]"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"## PCA on feature space (for individual reporting countries)"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"source": [
"I now run PCA on the data-set `IFF_Sector` which includes mis-invoiced trade for a country $i$ in commodity $c$ in year $t$."
]
},
{
"cell_type": "markdown",
"metadata": {
"hideCode": false,
"hidePrompt": false,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"### Sector features"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"source": [
"One possible view of `IFF_Sector` is to view the sectors as the feature space where $p=21$. Therefore, I use the function `create_features()` to generate the data-set to be used in PCA analysis."
]
},
{
"cell_type": "code",
"execution_count": 19,
"metadata": {
"slideshow": {
"slide_type": "-"
}
},
"outputs": [
{
"data": {
"text/html": [
"
"
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"# Plot distribution of illicit flow in each feature (i.e. sector)\n",
"fig, axes = joypy.joyplot(sector_features, colormap=plt.cm.viridis, figsize=(8,8),\n",
" title='Distribution of mis-invoicing across sectors');"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"source": [
"I explore two possible transformations of the data: a (modified) log transformation and a Yeo–Johnson. The values of the data-set are all non-negative, with some values equal to 0. Therefore, the figure below displays the distribution of the data after taking $log(x+1)$."
]
},
{
"cell_type": "code",
"execution_count": 25,
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"outputs": [],
"source": [
"sector_features_log = sector_features.apply(lambda x: np.log(x+1) if np.issubdtype(x.dtype, np.number) else x, axis=0)"
]
},
{
"cell_type": "code",
"execution_count": 26,
"metadata": {
"slideshow": {
"slide_type": "skip"
},
"tags": [
"remove-input"
]
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAk8AAAI1CAYAAADPfh7JAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4yLjEsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy+j8jraAAAgAElEQVR4nOydd5wXxf3/n+9Pu8/1g7vjOHqvh1QREP1hSYJRQROjMRp7jCYxTb/GJCZiNIkmRo0lxcQokdgSTcBoFEkEK1KkIyD9gOvH9U/f9++P3YPjvApXuXnyWG4/u7Mz75md2Xnte2Z3RVUxGAwGg8FgMLQMV2cbYDAYDAaDwdCdMOLJYDAYDAaDoRUY8WQwGAwGg8HQCox4MhgMBoPBYGgFRjwZDAaDwWAwtAIjngwGg8FgMBhagRFPBkMbICJ/EJGftFFcg0SkSkTczu/lInJDW8TtxPcfEbm6reJrRbr3ikixiOS3QVw/EpE/H8dxV4jI0hNNvwXpVInIsGbCHHOeDd0TERknImvq/N4rIud2pk1tjdg8JSKHRWRVZ9tTHxE5Q0S2t0E8cSKyTUT6NBvWvOfJYGgaEdkLZAFRIAZsBf4KPKGq1nHEdYOqLmvFMcuBRap6PGJhATBCVa9s7bFtiYgMBHYAg1W1sDNtMZzcnEh7Oc70XgL+rqrPO7/30so23sJ0ltOB+aqX9hnAc8BoVa3u6PQbsEeBkaq6sx3ivh3IUtVbmwpnPE8GQ8u4UFWTgcHAfcAPgCfbOhER8bR1nF2EwUCJEU7di57mFXM8LC3uF0UkGzgL+Ff7WdViW9rz2jEY2Hs8wqkbXtOeBa4WkbgmQ6mqWcxiliYWYC9wbr1t0wELyHF+Pw3c66xnAP8GyoBS4B3sG5VnnGMCQBVwOzAEUOB6YD/wdp1tHie+5cAvgVVAObAY6O3smwMcaMheYC4QBiJOehvqxHeDs+4C7gT2AYXYHrVUZ1+tHVc7thUDP26inFKd44uc+O504j/XybPl2PF0A8fOAQ44ZVII5AEXAZ/H9liVAj+qE34B9l04gB9YBJQ4Zb4a+86xIRuvAd6t81uBm4BPgMPA44AAcU5cOXXCZjr56OP8/hqw07FtCdCvXrwjnPV44DdOmZQD7zrbGjrP9wDvAZXAUiCjTpxXOXGUAD+hgXpZJ+z5wDqgAsgFFtTbPxt438ljLnBNnXr8e+A1oNo5d2Md28qALcC8OvF8HtsTWwkcBG5rqg00YKcADznnvBzYyNE2FQc8gF33CoA/APF1jp0PrHfyuAu7vv8c2zscxK5rjzlhZzn1otz5O6tOPMud495zzu8I7Hqy28nXHuCKRsr5KmBZY9cLJw8PA4ec5WEgrk7Y27Hr+iHgBurUm3pxNpYvBb6JXX/3ONt+65zTCmAtcEa9dvMidjutdM7ntDr7f+Ccx0pgO3AO9rUp6KRfBdzdwvp/xC5a376nAx9g15884DHA5+x724m/2rHnMupdB2m6zj6N3c5fdfL5ITC8Xnl/Avy/JvuF9uhszGKWk2mhkU4K+6J+s7P+NEfF0y+xL/ReZzmDo0Pkx8TF0Q70r0AijXeqB4EcJ8xLHBUOx1w06qdBHZFRZ/9yjoqn65wL4DAgCXgZeKaebX9y7JoIhICxjZTTX7GFXbJz7A7g+sbsrHfsHOxh0Z86ZfY1bBH2rBPfeOwL+LD6+QK+DrwCJABuYCqQ0kg61/Bp8fRvIA0Y5KQ519n3F+DndcJ+E3jdWT8bW0xOwe4gHwXerhdvrXh63Cnz/o59s5xjGjrPu4BRTnkvB+5z9o3D7ihmAz5sURGhcfE0B5iALV5PwRYfFzn7BmF3Gpc7ZZ0OTKpTj8uB051jk5368SMn3bOdY0c74fNwOmegFzCluTZQz87PYXfwadhCaiyQ7ex7GLtT7u3Y8QrwS2ffdMfOzzh29gfG1K/fzu/e2ML4q4DHyfdhIL1O+P3YdcyDfRNQUSeP2cD4Rsr518DjTbS/nwErgT7Y4vt94B5n31wg30k3AfvmqkHx1FC+6tSzN508xjvbrnTOqQe41UnDX6fdBLFFi9s5TyudfaOxRVe/Ou1/eCPtpiX1/4hdtL59TwVmOHkYAnwMfLeh9lX/+uLE31SdfRpbrE134v8b8Hy9cl0CfLupfsEM2xkMx88h7ItDfSLYF9zBqhpR1XfUaZFNsEBVq1U10Mj+Z1R1s9pu858Al7bRkMoVwIOqultVq4AfAl+u52q/W1UDqroB2IAtoo7BseUy4IeqWqmqe7G9LV9thS0RbLESAZ7H9l781olvC/Yd5CmNHJeOfTGNqepaVa1oRbr3qWqZqu4H3gImOdufxe5oa/mKsw3scvuLqn6kqiHscpspIkPqRuwMAV0HfEdVDzr2ve8c0xBPqeoOpx68WMeWS4BXVPVdVQ1jd0KN1ilVXa6qm1TVUtWN2PNV/l8d25ep6nNO/SxR1fV1Dl+squ+pPZ9vEraovk9Vw6r6P2yxWVsuEWCciKSo6mFV/ajO9pa0gQh25zkGW1x9rKp5IiLYHez3VLVUVSuBXwBfdo67Hrv833TyeFBVtzVSHOcDn6jqM6oaVdXngG3AhXXCPK2qW1Q1it3JW0COiMSrap5T/xoiDbtjbowrgJ+paqGqFgF3c7RNXIp9vreoao2z73j4pVNGAQBVXeSc06iq/gZb3IyuE/5dVX1NVWPYgq22PcecsONExKuqe1V1VxP5aq7+H2MXrWjfThte6eRhL/BHjtbf5phB03UW4GVVXeWc779xtJ3VUol9bhvFiCeD4fjpj30HU59fY9/5LBWR3SJyRwviym3F/n3Yd1cZLbKyafo58dWN24M9Qb6Wuk/H1WBfmOqTgX2XVz+u/q2wpcS5oIM9fAK2x4Q62xpK+xngDeB5ETkkIr8SEa/zBE6VszTW+UHj+fsfEC8ip4nIYOwL7D+dfceUmyM8S/h0fjOwhxUb64Raaks/6tQBp7MtaSwSx+a3RKRIRMqxhyZr68vAZuypW9f6Abl67IMRdc/rF7G9GPtEZIWIzHS2t6gNOB3bY9jeuQIReUJEUrC9NAnAWhEpE5Ey4HVne0vyUJf6dbx+Ho7Js3ODchl2meWJyKsiMqaRuA9ji7+Wpr3P2Va7r25ZN3cNaIxjjhORW0XkYxEpd8otlWOvFfXrmF9EPGpPvv4utneqUESeF5F+NExL6n/9/LS4fYvIKBH5t4jki0gFtnBu6fWuuToLzV/TkrGH/BrFiCeD4TgQkVOxG+O79fc5d1K3quow7Lvb74vIObW7G4myOc/UwDrrg7Dv4oqxx/0T6tjl5mgH05J4D2FPBq0bd5RjL2otodixqX5cB1sZT6txPBt3q+o47CGxC4CrHG9HkrOMP454LWzvz+XYXqd/Ox4QqFduIpKI7f2qn99i7OGI4a1Nvx55wIA66cU76TXGs9hDDwNVNRV7CE2cfbnN2FO3zhwCBtabRH3kvKrqalWdjz0s9S/s8mquDRybmOojqjoVe+hmFPB/2OUWwB4uS3OWVFWt7eSaykP9Ol+/jh+Th4aOUdU3VPUz2N6zbdhD1w2x0bG5MRpqX4ec9WPOKce28YZo9trhPBX3A2yvVi9VTcMe3pRGjj02ItVnVXW2Y7MC9zcStCX1v7lrT1P8HrvcR6pqCvYQXIvyQDN1toWMxfayN4oRTwZDKxCRFBG5ANvtvEhVNzUQ5gIRGeEMPVRgu8Nr77gKsOcXtZYrnffJJGDPo/iHcxe3A/vO8XwR8WJP0q77lEgBMKSJJ4ieA74nIkNFJAn7Du8Fx53dYhxbXgR+LiLJjqfm+9gTudsVETlLRCY4wrECW8TFmjmspTyL7YW4gqNDdrXbrxWRSc5TOb8APnSGGI7gCLC/AA+KSD8RcYvIzGaf5Pk0/wAuFJFZIuLDHuJpqjNJBkpVNSgi07HFXy1/A84VkUtFxCMi6SJSf9iilg+xBfrtjjdvDrYYel5EfGK/NyvVGYqprevNtYEjiMipjpfM66QTBGJOuf0JeEicd+6ISH8R+Zxz6JPY5X+OiLicfbXeofpt7DVglIh8xcnvZdhzyP7dUIZFJEtE5jmCIIQ916yx+vQmMEVE/I3sfw64U0QyRSQDe7i1tk286ORhrNOuf9pIHLW05NqRjH3zUwR4ROSnQEozxwAgIqNF5GynbgaxxWtj+W5R/T8BkrHrTZVzXm+ut7+psmi0zrYkYRHpjz0dY2VT4Yx4MhhaxisiUol9x/tj4EHg2kbCjgSWYV90PwB+p6rLnX2/xL6YlonIba1I/xnsiY752MNA3wZQ1XLgG8Cfse+sqrGfaqnl787fEhH5iE/zFyfut7GfigkCt7TCrrrc4qS/G9sj96wTf3vTF1tcVGBPLF1BG4k2Va29EPcD/lNn+3+x5569hO1BGM7R+Tj1uQ3YhP2UVyn23Xyrrr3OnJBbsDuAPOw5GYXYnXtDfAP4mVNnf4rjEXLi2o891HarY896GpjH5oQNA/OA87C9Qb/D9urVzi/6KrDXGVq5CXuyMjTdBuqSgi2SDnP0ScIHnH0/wB76W+nEvwxn7o6qrsJufw9he1ZWcNQT8lvgErFf6PiIqpZgeyNvdeK/HbhAVYsbKTuXE/aQUz7/D7s8GyqfAuzh3fmNxHUvsAbbQ7UJ+MjZhqr+B3gEe57dTuxygsbP6TH5aiTMG9j1dAd2eQZp+XBgHPZrWIqxrzN9sD0+n6KV9f94uA1b8Fdi148X6u1fACx0rqOX1rOtuTrbHF8BFmrj8xIB85JMg8Fg6HY4XsIy7GGNPZ1tT09GRMYBC4HpjUyKb2k8Y4HN2K8yaJXn19A2OF60DcCZ2sw76Yx4MhgMhm6AiFwI/Bd7uO43wGnYrwYwF/FuiohcjP2+oURsAWap6kWda5WhJZhhO4PBYOgezOfoyxZHAl82wqnb83Xs+Um7sOcX1Z/bY+iiGM+TwWAwGAwGQyswnieDwWAwGAyGVmDEk8FgMBgMBkMr6G5fOzYYThbMeLnBYDC0DS19gWabYTxPBoPBYDAYDK3AiCeDwWAwGAyGVmDEk8FgMBgMBkMrMOLJYDAYDAaDoRUY8WQwGAwGg8HQCox4MhgMBoPBYGgFRjwZDAaDwWAwtAIjngwGg8FgMBhagRFPBoPBYDAYDK3AiCeDwWAwGAyGVmDEk8FgMBgMBkMrMOLJYDAYDAaDoRUY8WQwGAwGg8HQCox4MhgMBoPBYGgFns42wGAwGAyGjsCyLA4fPkxNTQ1erxe/309qaioi0tmmGboZRjwZDAaD4aSjpqaGFStWsGLFCjZs2MDGDRspKCwgFosdEy7eH0//fv2ZOGkis06fxRlnnMHUqVNxuczAjKFxRFU72waDoSdiGp7B0MYEg0FeeeUVFi5cyLJlywiFQrjETZIrhSRNJdGbRJz4cakbCwuLGEEC1MSqKIuWEKQGgPReGVz8hYu44Ws3MH36dOOZ6vp0+Aky4slg6BxMwzMY2oiioiIeeeQRfvf47yg9XEqiJ4lM7U8fTz8SQ2m4xd2ieEIapJRCSj35FEYPEiPG6OGj+b8f/h9XXXUVXq+3nXNiOE6MeDIYegim4RkMJ0hxcTH33nsvTzzxBMFAkCz3AAZ7R5IU7HXC3qKoRshnP4dce6iwysjK6MuCe+7i+uuvNyKq62HEk8HQQzANz2A4TkKhEI8++ij33nMvlZWV9HMNYah7LHGR+DZPS1UpIZ+9rm2UWSUM7DeIJ578I3Pnzm3ztAzHjRFPBkMPwTQ8g+E4ePfdd7n++uvZsWMHfTz9Ge2eSFw4od3TVVWKyeMT2UiNVnH2meew8G9PM2DAgHZP29AsRjwZDD0E0/AMhlZQWVnJD3/4Qx5//HGSfSmMdU0lJZTe4XZYGmM/n7CHj/F6vTz44IPc9M2bzKTyzsWIJ4Ohh2AansHQQj788EMuv/xy9u7dyxD3KIbExuGmZZPA24sarWKb6yNKrUJmTJ3Fy6/8g+zs7E61qQfT4eLJvMjCYDAYDF0Sy7K47777mD17NkUHS5gZ9xmGxyZ0unACSJAkJltnMJpJrFr7IaOGj+bVf7/a2WYZOgjjeTIYOgfT8AyGJigoKODKK69k2bJlZHsGM0Yn47a65nudq7SczbKKKi3nmzd+i4cffwiPp2vaepJihu0Mhh6CaXgGQyOsX7+eefPmkZ+XzxjXZPqEB3b5OUUxjbKdDRxiDxNGn8KbK5aSlZXV2Wb1FIx4Mhh6CKbhGQwN8PLLL/PVK7+KRN1Mdp+OP5TU2Sa1ijzdx8d8RHJiCq8ve40ZM2Z0tkk9ATPnyWAwGAw9D1Xl3nvv5Ytf/CJx4QRO1bO6nXACyJbBTGMO4ZoQs2edwRO/e6KzTTK0A8bzZDB0DqbhGQwOgUCA66+/nueee45+7iGMjk1u8SdVuiphDbFJVnJYi7j+qzfwh7/83syDaj/MsJ3B0EMwDc9gAA4dOsT8+fNZu2Yto7ynMCAyosvPb2opllrsYAMH2MX0STNYuvx1UlNTO9uskxEjngyGHoJpeIYez9q1a5k3bx5FBUVM9MwkLdyns01qFw7qbraxjr4Z/Vj+3v8YNWpUZ5t0smHmPBkMBoPh5Ofvf/87Z8w+g/LCSk7znHPSCieA/jKMKZxJcXExkyZM4o3Xl3a2SYYTxIgng8FgMHQYlmVx9913c+mllxIfTWaanoU/3P0mhreWXpLJqZyFO+LjvPPm8uCvH+pskwwngBm2Mxg6B9PwDD2OmpoarrnmGv7+978zwDOUUdFJuLr5xPDWEtUIW1yrKbIOcdVXrubPT/8Jr9fb2WZ1d8ycJ4Ohh2AanqFHceDAAebPn8+6desY7ZlE/8iwk2ZieGtRVXbKZvbpdqZPOY3/vPkavXv37myzujNGPBkMPQTT8Aw9hlWrVnHRRRdRWlTKKZ6ZpIYyOtukLsEh3cs2PqJvVjbL3nqTsWPHdrZJ3RUjngyGHoJpeIYewaJFi7jhhhuIw88k1+n4ggkdbkNUo4QIECWMorhw4SWOOOJxSedO/S3TYjayEnec8NI/X+K8887rVHu6KUY8GQw9BNPwDCc1sViMO+64gwceeIA+vmxymIEr0jHzmwJaTQn5lFJIBYcJUtNgOEFIIJk0MuhNHzLoi1s6/kWWAa1mk2sllVYZv/rVr7j1tlt77JDmcWLEk8HQQ+hWDS8/P59t27ZRUFBAUVERsVgMt9tNSkoKAwcOZPDgwQwdOtRc8A0AlJWVcfnll/P6668z2DuKEdEcpJ0f7o5qhHxyyWMv5ZQC4JdE0rxZJLl64Xcl4XX5cYkQ0xhhDRKIVVARLaEsWkCMCC7c9KE/AxlOqqS3q72ftj/Kx+41FMQOcMXlV/KXp5/E5/N1qA3dGCOeDIYeQpdueLt27eL111/njTfe4MMPP6SwsLDZY5ITk5k6dSqfnftZLrzwQsaPH2/EVA9k27ZtzJ8/n107dzHOM5WsyKB2TS+sIXL5hFx2ESVCoiuNfnGj6OMbTKI7tUV1UNXicDSfvNAu8sO7iGqEVMlgmI4lXbLa1f5j7VD2uD5mt7WVaZOm8drS18jMzOyw9LsxRjwZDD2ELtfwioqKeO6553jmmWdYs2YNAEmeFFKs3vT2ZRIfS8Qd8eIjDsGFYhElQpAAIXcNVe5ySiNFVGoZAAOyB/K1m27g2muvZeDAgZ2ZNUMH8eKLL3LDDTcQC1lMdM8iMdh+nyKJaZR97GAv27GI0cc7hCH+U0jz9jkh0R7VMAeC29kX3EzQqiJd+jJSJ5AkHfdZlXzdz1bWkpmRyZv/W8qECRM6LO1uihFPBkMPocs0vC1btvDggw+yaNEiwuEwaZ50+rkH0zuahd9KbHV8QQ1QIvkUuQ5SHMtHEM4561x+evdPmD17tvFGnYSEQiFuu+02HnvsMTLispjAabjD7TPkpKoUcIBP2EiIAFm+oQyPn0Kyp20f9bc0xv7gVnYF1hHTMENkLEN1dIe9l6pcS9koH4DH4rnnn+PiL1zcIel2U4x4Mhh6CJ3e8N5//33uueceXn/9dTxuL/0YzCD3SPyR1gumxghoNXmufRywdhEmRM6YCdzzy58xf/58I6JOEvbs2cOll17KmjVrGOoZw7DYeKSd+rKg1vAxaymhgGR3OmMSZtLbl90uadUStoJsq/6AvPBOEiWV8TqNFOnVrmnWEtQAm1wfUG6V8uM77uRnP78bl8t8GKQBjHgyGHoIndbw1q9fz5133smrr75KvDeBgYwgOzYEr7bf5NSYRjnEPnLlE2q0inGjxvPQow/ymc98xoioboqqsmjRIm655RZCNSHGu06lV7h95gepKofYyw42oMCohFMZ5B+HdOBrBorCuWypepuwBhklExmgHfOSz5hG+VjWkq+5zJg6k5dfeYns7PYVjN0QI54Mhh5Chze87du3c9ddd/HCCy8Q5/EzREbTPzoUFx33aLalFnnsY698TEBrmDpxGo/87rfMmjWrw2wwnDjFxcXcdNNNvPTSS2T4ssiR6XjCce2SVkTDbGE1xeTRy5PN+MQzSPR03PyjuoStIJuqllMcyaWPDGScTsEj7f9pFVXlILvZwUYS4hNY9OwzzL9ofrun240w4slg6CF0WMPLz89nwYIF/PnPf8aNm4EykoHWCDzaed/TsjTGAfawT7YR0iDnzjmXhx97mPHjx3eaTYaWsWTJEm688UaKi4oZ4Z7AgMjwdvPAVOhhNrGSIAFGJUxnsD+n0z2Vqsre4CY+qVlFgqQwUWeSIB3zYeNqrWCLazUV1mGu+srVPP7Hx0hKOvk/qtwCjHgyGHoI7d7wqqqqeOCBB3jggQcIBIIMdA1nqIzFE+06HyGNaZRc2cle3U6MKJd+6TLu//V9DB48uLNNM9QjNzeXW265hcWLF9PLl06O+zTi2vFt4fanS9bhlTgmJp9LL2/HvTKgJZRGDrG+chkAp+gMeknHvFLA0hg7ZTP79RMyemXy9DNPcf7553dI2l0YI54Mhh5CuzW8SCTCk08+yYIFCygoKKCfdzAjXRPwhv3tleQJE9YQ+1072G99gsvt4qabbuauBT8lI8N8A62zCYfDPProo9x1112EQxGGyTj6R4a122dNLI2xnQ0cZDe9PNmcknQ2fnfHf9KlJVTHyllX8QY1ViVjZQr9GNJhaZdpMdvkI6q0gvnnX8SfnnqiJ78Tyogng6GH0OYNT1VZvHgxd9xxB9u3byfD15fR7onEB5PbOql2I6g17HVv40BsD/F+Pz/4wQ+49bZbzdBEJ6CqvPjii/zoRz9i9+7dZHkHMNY1ud3mNoF9/jfyARUcZoj/FEYmnNrp355rjogVYkPlfymJHmS4K4ch1ugOG1q0NMZe2c4e3UZ8nJ+77l7Ad7/3nZ74ZnIjngyGHkKbNTxV5bXXXmPBggWsWbOGVF8vRrpOITWY0enzQ46XKq1gj3srBbED9Ertzc/uvZsbb7yxJ3YKHY6qsmzZMu68805WrVpFr7h0RsopJAd7t2t9KtUCNvEhFkpO0pn0jRvWbmm1NZZabK5aQV54JwNdIxllndKhba9KK9jl2kSRlUf/vgN45PHfcvHFF3fb9n8cGPFkMPQQTrjhqSpvvPEGd911F6tWrSI5LpWhjCEj1L/L3623lHItYZd7C6WxQvpl9ee+X/+Syy+/HI+n4z/eerJjWRaLFy/mF7/4BWvWrCHRl8wIGU9GqH+7dsKqyj62s5MtJLpSmZR8LkmejnmPUluiquyo+ZC9wU1kuQYx3praYS/UrKVY89np2kSVVc6YkWP5xf0/Z/78+T3h3VBGPBkMPYTjbnihUIjnn3+ehx56iA0bNpDsS2EIY8kMnzyiqS6qSgn57HZtpcI6TFZGFv93x/9x4403kpzcfYYkuyqHDx9m4cKF/OEPf2D79u2kxKUxWEeTGe7X7p1/VCNsYTVFHKKvbxjjk87skEf/25M9gQ3sqFlFb1dfTrFO6/D8WGqRz372ynZqtJIRQ0fykwV3cumll+L3d915jyeIEU8GQw+h1Q3vwIEDPPXUU/zud78jPz+ftLh0BjHipPI0NYWqUkweue6dlMYKSfAncN311/H1m75OTk5OZ5vXrYhGoyxfvpxFixbxwgsvEAwGSff2YbB7JGnBrA6pT1VazkY+IEA1oxJO6xKvIWgrDgZ3sKX6bZKlN5N0Fj5pv3lijWGpRQEH2CfbqdJyUpNTufHrN/KNb36DIUOGdLg97YwRTwZDD6FFDa+mpoYlS5bw1FNP8eabb6Kq9PH0Z6h3NEmBXidNZ9NayrWUg55d5EVzUSwm5kzk5m/dzCWXXEJ6enpnm9clCYVCvPvuu/zjH//gpZdeoqioCJ/bRxaDGOwdiT/Udp/laY7aD996xMfEpHPa/RMrnUFheB8bKv9LvCQxWU/HL53zxKCqUkoheZ695EcPAMqpU6dz9bVX8aUvfYk+ffp0il1tjBFPBkMPodGGV1xczKuvvsq//vUv3njjDQKBAEm+FPpag+jvGoI30nmud1UlQogwYTx4iCO+UwVcWEMUuHI5pHuo1HJcLhczT5vFZZdfyrx583r0+6JisRhbt27lrbfeYunSpSxfvpzq6mq8bi8ZZNM/bijJNb1xd+C8HEstPmEjuewkzZPFxKRz8Ls7TrR1NKWRPD6qeAOv+Jiss0mUzh1mDmoNBe5c8qz9VDntZdqUacy7aB5z585l8uTJ3XV+lBFPXRERuRh4GRirqttaEP7PwIOquvUE0x0C/FtV23RMorl4ReR7wC+BLFUtb0F8rwFfUdWyE7RrDnCbql7QwPbFwG7ADzyvqnefQDpVqtrqZ99FZBLQT1VfO96066DgfLPr0CFWrlzJihUrWL58OZs2bQIg0ZtMRqwv2b5BJAbTOlWkVGk5ueykiEOECR3Z7sFHumTRX4fSi8xOs1FVqaSMEk8++bFcqrUCgAH9BnDOuedw1tlnMXPmTEaMGNFdO4cmCYVCfPLJJ2zdupW1a9eyatUq1qxeQ1V1FQApvjTSoplkxfUnKZCGWzp+wn1QA2xiJeWUMDguh5EJ03G7OnZCdWdQES1mTcV/AJisp3fYR4Wbo0rLKfYcotDKo8IqBSAtJY1Zp8/i9NmnM3ldkUIAACAASURBVGPGDKZOnUpqaud8CqeVGPHUFRGRF4Fs4L+quqAD0x1C54inVUAIeFJVn27LtJuxaw6Ni6fbVPUCEUkE1gNfVtW1dcJ4VDXawnSOVzxdA0xT1W+19tj63Hbbbbp+/XrWr1tPSWkJAF63lzTJoLerD+mSRXwoudOH5cIaZAcbyWc/bvGQmTCctLhsfO4EolaI8lABhTU7iVhBerv6Mtqa2Ol31wDVWkmZu5DDUkxJtIAIYQDi/fHk5Exg2qlTGTVqFMOHD2fYsGEMHTqUhISu+SJGgEAgQFFREQcOHGD//v3k5uaSm5vLvn372PbxNnbt3kUsFgPAJW5SPb1IjvUiPa4PiaFU/Nq5eSvRAjazCosY4xLPoJ9/RKfa09FUx8pYU/EfIlaISczqsLeRt5SwBjkshZR5SiiNFFJN5ZF9fbP6kjMhh5ycHEaPHs2gQYOOLCkpKZ1o9TEY8dTVEJEkYDtwFrBEVcc42+cAC4BiIAdYC1ypqioiy7E7+zUiUgU8DpwLHAZ+BPwKGAR8V1WXOGLmGaDWf/0tVX2/MZHj2LQY6AV4gTtVdbET/j/Au8As4CAwX1UDIjIV+AtQ4+w/ryHxJCLDgVeAm4EfqernnO3XAPOABGA48E9Vvd3ZtxeYBiQBrzvxzwA2AE8BdwN9gCtUdZWITAceBuKBAHCtqm5viXhyfj+P7QkcB/QDhjjn4YdOHjOBIife/SIyFHgW8Dj2fU9VkxqI9zFgjao+LSKnAr91zkkI+AywybH5ILZnLt8JA7Yn6UxVPXrVaQKvx6dJkkqilUxvXwaJVioJ4ZQuNfG7TIvZyAdEiDA0dRqD06YR5/l0JxyzIuRWbGTn4fdRtRjLFPoysBMsbhhVpYpyqt3lVLsrKYuUUKllRIkcEy4lOYXMzEz69u1L3+y+ZGRkkJycTFJSEomJiSQlJZGUlER8fDxutxuPx4Pb7f7UumVZxGKxI0s0Gj1mPRqNEggEqKmpoaamhurq6iPrNTU1VFZWUlpaSklJCcVFxZSUlhIKBT+VL5/Lh18S8VuJpHrTSHanEReJxx9N6tChuKZQVfbwMbvZSqIrjYnJ55Ds6d3ZZnUKwVgVayr+Q8CqYAIzyJR+nW1So0Q0TDmlBH1VVGkFFZHDVFNBjNgx4ZISk8jK6ktGZjqZmZmkp6fTu3dvevfuTWJiIgkJCccsiYmJxMfH4/V68Xg8R9pN7Xrdxe1243K5EJEmF5fLhcvl6nDxZF6W0jwXAa+r6g4RKRWRKar6kbNvMjAeOAS8B5yOLRzqkggsV9UfiMg/gXuxO+JxwEJgCVAIfEZVgyIyEngOW4w0RhC4WFUrRCQDWCkiS5x9I4HLVfVrjsfsi8AibBFzi6quEJFfNxH35U767wCjRaSPqhY6+yY5eQ4B20XkUVXNrXf8COBLwI3AauArwGxs4fUjpzy3YQuNqIicC/zCsbNZRCQdW5jdg12GU4HZjkB8Bfirqi4UkeuAR5z0fgv8XlX/KiLfbEEaPuAF4DJVXS0iKdii86fU8Tw56X1TVd9zBO2ne7hGODN24VGhVDsK1oXmfh/SfXzMGuI9qUzLupQUf+PfFXO7vAxJm0pW0kg25P+bzaEPqXZXMyzWcW9abgoRIZk0kq00sOxtihIhTIAqAlQToJpQZZCqyhBbd+9gPZsIEyJGFKteh9EeuHDjxo0LNx48ePDhxYeXOPoyyFn3EUcCfuLxk2B/2Ln23jfiLNBl6lFYQ2xhFSUUkO0bztjE2XhdPfclp353EtNTL2RtxetsjH3AWJ1GP+mac/K84iODvsfUKVUlRIAgNQSdv6HqAFW7gxzevYetbCdCmAihT4ms9uZcuST7TevveR2ZphFPzXM5tpcE4Hnnd614WqWqBwBEZD22B6S+eApjezvA9lyEVDUiIpuc8GB7jx5z5tTEgFHN2CTAL0TkTOzuoD9Q27vtUdX1zvpaYIiIpAJpqrrC2f4McF4jcX8ZW5hZIvIythB63Nn339o5UCKyFRgM1BdPe1R1kxNmi3OM1stvKrDQEYrq5L85zhCRdU5+71PVLSLyJWxvYMAJMxP4Qp08/spZP52j4uwZ4P5m0hoN5KnqagBVewJNA0LgPeBBEfkb8HJtXWgJaRmphAKhLiEu6rM/soutodWk+wcyKWseXk98i46L96Qwvf9lbClcyp6qzWicxXjPpC6ZR4B4/KTw6WEHVfuFkVbUwopZtieJaJ0lhjr/OLJ29J+dW3H+uY6s1f1niyXPEcFUW0Yut30nLW6Xc9fdkSXSdpTEClgXfJ+QBhmXMJsB/jFdth50JD6Xn1NTP8+6ijfZGl0NXothvjGdbVaLicePPeBxLKqglt1eYjHb82oRO9Jeam9CatePbTFWk7+dFJr8H/gc8HS7ZbwBjHhqAsfLcTaQIyIKuAEVkdudIKE6wWM0XJ4RPTo2atUe44iT2vDfAwqAiYCL5j0YV2APTU11hNhe7InUDdkUjy22mh2fFZFTsD1XbzoXOh/2JO1a8dSS/NYNY9X5bdUJfw/wlqpe7Aw1Lm/ONuCd+sN5DtVNHKONrNcSxS7vWmrLsEXlpar3icirwOexvX/ntuSBAoCXiv7SkmAdzjPPPMPVV19NVvJwJmZeiKuVE4td4ianz1w87jj2ln/E3CvP5fd//m3zBxpOCsLhMHfddRf33/8sKf5eTE8+n/hYWmeb1aXwiI+pKXPZVP0WW0Nr+dxNc/jNw7824vLEeLqjE+w6Eyy6JpdgDwMNVtUhqjoQ2IM9DNWWpGJ7Oizgq9girbnwhY5wOgvbA9QozlNw5SJSa/cVjQS9HFjg5HWIqvYD+ou0uW85FXveEMA1bRjv+9ieM7DzWOsFfK/e9lr2AeNEJM7xzp3jbN8G9HPmPSEiyY7QrQSOzIYWkeGquklV7wfWAN3nFrIB3nrrLa677joyk4YwMXNeq4VTLSLCmPSz6J88nj88+Qh3/+QXbWypoSuybds2Zs6cyX333ceghLFMT7zICKdGcImbUxLPZoB/DA898huuuuJaLMvqbLMMrcCIp6a5HPhnvW0vYc/jaUt+B1wtIiuxh+ya8qYA/A2YJiJrsMVAS7wd1wKPi8gH2JO0G+LLfDq//+So8GgrfgX8UkTeo3mh2Bq+DVwrIhuxReh3nO3fAb4pIquxhRsAznytF4GN2GW6ztkeBi4DHhWRDcCb2F6pt7DF1noRuQz4rohsdsIEsCfrd0u2b9/OF7/4RRJ9vZiQcf4Jf5ZDRBif+VkyE4ax4N47efnvS5o/yNAticViPProo0yZMoVtW7Zzavp5jPGfjku7xqT1roqIi3EJsxkafwqLnlvIBZ+bRzgc7myzDC3EPG1nMHQOXabhVVVVMX78ePIPFjI9+3KS4truDd1RK8wHBxYR1SAbNq1n9JiRbRa3ofPZsmULN9xwAytXrqRvwhByks/EHe34T5F0d2q/h3fqpNNY+tbrpKUZj10r6fAxT+N5Mhh6KKrKq6++ytChQ9m/fz85mee1qXAC8Lh8TO47n2gsytSJM3js0ceIRCLNH2jo0oRCIe666y4mT57MxnWbmNL7XE7xn2uE03EyNH4i4xPPZM361YwblcP27ds72yRDMxjPk8HQOXRqw3v33Xe59dZbWbVqFQDD0k5jVPoZ7ZZeftUO1hcsIcmbQVpGAg/+9gEuueQSM0m2m6GqLFmyhFtvvZVdu3YxIHE0YxJn4I713FcQtCWlkTw2VC3D5RH+8dI/OP+Cz3e2Sd0F43kyGAztx65du/jSl77EGWecwaZ1W3Dhopd/ACN7n96u6fZNGsWglElURYqpKglz6aWXMmHcRFasWNH8wYYuwebNm/nsZz/LRRddRMmhcmZmXsh4/5lGOLUhvb3ZnJYyH68Vz4UXXsCCn/4M4+DomhjPk8HQOXRowysrK+Pee+/lkUceAUsYmjCR/Jo9BLSKWQOuJt7b/p9UiVkR3j/wDFErxNC4iewNbSQYq+KcOZ/h8T88yujRo9vdBkPr2bt3L/fccw8LFy7E6/YxIn4q2e7RXept+CcbUQ2zufptCkJ7OHPWHF5e8g/S09t2SP0kw3ieDAZD2xGJRHjssccYMXwED/7mQfp6h3NGr0uxokpFrJhxGed2iHAC+03kp2SdTzgW4LBVyOkplzAq4VRWrFjOuLHj+Nr1N1JUVNQhthia58CBA9x8882MGjWKvy58hkH+ccxO/RL9PWONcGpnPOJjYuI5jEmYybvvv82o4aN5++13OtssQx2M58lg6BzateGpKq+88gq3334727dvJzN+IOOSZuK3UqmIlrCy/F9kJY5kUt8L29OMBtl9+EN2lL5DTvJZ9PeNIGQF2BNax/6arfjj/Pz4zh/z/Vu/T3x8y95sbmhbNm3axEMPPcTf/vY3YtEYA+LHMCJpCp6ov/mDDW1OebSIjVX/IxCr5Bs3fYtfP3i/aRufxnwY2GDoIbRbw1u3bh233norb731Fmnx6YxOnEGqlY2IYGmMleX/IqRBTh94TYMf+m1vVC1WHXqRylAhs1K/SLw7CYCqWBm7gqvJD+4lK7Mvv/7Nr7jiiitwuYyXo72xLIs333yTBx98kKVLl+L1+OgfN4phiRPxxjq+jhiOJWqF2RH8kNzANgZkD+L5vz/L6ae37zzFboYRTwZDD6HNG97Bgwe58847WbhwIX5fAiPip9DXNeqYIZZPatawO7COyVnzyUrqvHcu1UTKeC93Iam+vkxL/NwxT92VRg6xI7CK8kgROeMm8OjjjzBnzpxOs/VkZv/+/Tz11FM89dRT7Nu3j8S4ZAbGjWNA3BjclpkI3tUoDh9ga807BGLVfPUrV/Gbh39NZmZmZ5vVFTDiyWDoIbRZwysoKOD+++/n97//PdFIlMHxOQyLn4TLOvZ7y+XRIj4sX0x20lhOyer8R6BzKzawpehNxiTPZrBv7DH7VJX88E52BNYQjFXx2XPn8ttHH2LMmG79BZwuQUlJCYsXL+b5559n2bJlqCp94gcxKHEMvawBJ/x2eUP7EtUwOwNr2R/YQrw/gQV338V3vvsdfL4eLXaNeDIYeggn3PAKCwt54IEHeOyxxwgGQwyIH8XIpKkNDrNYGuOD8n8SIcLpA67G5+n8OROqytr8lykN5DIr9WIS3Z9+q3JMo+wPb2F39TosYnzh4i/y0wU/YcKECZ1gcfclLy+PJUuW8NJLL/G///2PWCxGclwa2b4RDPCPxmuZobnuRlX0MDuCH1IUyiUrsy9337OAa6+9tqeKKCOeDIYewnE3vM2bN/Pwww+zaNEiwuEI/eNHMDJpGr5YYqPH7KhZzZ7Aeqb0/QJ9Eocdb9JtTjBaxbu5T5PoSWN60vmNPsUVsgLsC21gf+BjYhrl7Dnn8tMFd3LmmWeaF202QE1NDW+//TZvvvkmS5cuZfPmzQCk+HvTxzOYfgkj8EdTTdl1c1SV4sgBdofWURYuICszmzt+9AOuu+5aUlJSOtu8jsSIJ4Ohh9CqhhcIBFi8eDFPPvkky5Ytw+vx0c83gmFJE/HFkpo8tjxaxMryxfRPGseErPNOyOj2IK9yGxsK/83IxOkM809sMmzYCnIg/DH7ApsJW0GGDR7ON265mauvvpqMjIwOsrjrkZeXxwcffMAHH3zA+++/z5o1awiHw3jcHnr5ssn0DSTDOwC/lWIE00lIrYjaG1pPaTgff1w8V331Km7+5k1MnDixJ5xzI54Mhh5Csw0vEonwzjvv8OKLL/L8889TXl5OUlwqA+LGtHhCb1ccrmuI9fmvUFD9CTNSLyLF0/zLAGMaJS+0i0ORHRwO5+Nxezj7rHO4/IovM2/ePHr37t0BVnc8lmWxe/duNm7cyKZNm9i4cSNr137Evn17AXC7PKT5Mkn19CErfhCJsQzc4mkfWzRGZayUimgRldHDBK1KAlYVEQ0R0ygxjeISF268eFw+/K5E4l3JJLrTSPVkkuLJwCPe5hMytIryaBEHI9s4WPMJFjGGDRnO1ddexWWXXcaoUaNOViFlxFNLEZGLgZeBsaq6rQXh/ww8qKpbTzDdIcC/VTXnROJx4noa+EBV/1hn20XAjaraJjN6HXtnqeqzzYSbA9ymqhc0sG8vME1Vi1uY5nIgGwg4m+5V1X80Eva7wBOqWtOSuE8UEVkAVKnqAw3suxH4vvOzAvi+qr7r7DtSf1pbHo3QYMPLzc3l7bff5rXXXuO1116jrKwMj9tLlm8oQ5LHkhjNbNXF75Oa1ezugsN19QnHAryb+zQ+8TMzZX6rJi1XRkvJj+7kUGAXQasKl8vFjNNmMve8z3HWWWcxffr0bjUPRFUpLi5m586d7Ny5k127drFz50527NjBls1bqAnYTUUQkuN6kUAamQn9SPX0IT6W1m4TvlXtF6sWh3MpjhygPFqEYgHgkTjivSn4PSn43Am4xYNbPFgaI6ZRolaQQLSSQLSccKy2qQupnkwyvAPI8A4k1dO6um1omrAVpDCyh/zIbkpChwAY2H8g5194PnPnzmX27Nkn01vLjXhqKSLyInYH/V9VXdCB6Q7hOMWTiLhVNVbn9+eAO1T1rDrbngdeVdVn2sDcJkVRS8Mdp3i6TVXXtCBsq+I+URoTTyJyAXA38DlVLRaRKcC/gOmqmt8ONmthYSGbN29m8+bNrF69mnfeeYd9+/YBEO9NJN0zgP5Jw0mK9TmuO/Tap+v6ddHhuvoUVu/io/x/MjRhMqPip7X6+COdu7WPwsB+KqIlAMT54sjJmcC0U6cyefJkJkyYwLBhw8jKyurwzjoQCFBSUkJhYSGHDh3i4MGDHDx48Oj6gYPs2buHqqqqOkcJib5k/CST4k0nLT6TRE3Drynt5lWqRVWpjJWQF9pJXng3IasagBRfFr3jB5Eal0WaPxu/p+XDgeFYDeXBfMqChygO7KM8lAdAvDuFbN9w+sWNaPDhAcPxE4hVURzdT2nsEEXBXGIaBWDwoCHMOn0mp512GuPGjWPMmDEMGDCgO4pYI55agogkAduBs4AlqjrG2T4HWAAUAznAWuBKVdW6HbqIVAGPA+cCh4EfAb8CBgHfVdUljkh6BqidhfstVX2/MfEkdm37FXAetlfhXlV9wbHpLiAPmKSq4+oc4wYOAFNUNU9EEoD9wFBgFPAgkOTk5xonzKnAk0A18C5wnqrmOHHdB8wB4oDHVfWPIrISGAvsARYC/2wkX3OAnwElwGjgbeAbqmrVFQsiciXwbcAHfOiEOSIInXwdKes6234PnArEA/9Q1btE5NvAA865LHbOx5PANKcM/6KqD9WL+0LgTif9EuAKVS1wRNEgYJjz92FVfcQ55sfAVUAuUASsbUA8vQPcpar/q7PtHgBV/Um9+rPXsTEAvAgMANzAPar6Ai2gT58+WvdTJPHeRFJdWWQmDCDN3Yd4KxU5gU9gdJfhuvpsLnyDA5WbmZ5yIb28WScUV9gKcjiaR6UUUxYspCJSTETDR/b74/wMHDiIQYMGkpGZQUZGBunp6fTu3Ru/34/f7ycuLg6/34/P50NVicVixGIxLMsiFosRiUSorq6murqampqaI+vV1dWUl5dTUlJiL8UllJSWEgwGPmWnIMR7E4lzJeDVeBK9KSTH9SLenYInEk+CK7nDXx8QtoIcCu3gQGg71bEyBBcZCUPomzCK9MSh+D2NP5zQ6rRiNRRW7yavaislgf0A9Pb2Y7A/h0zvoC7XkasqUaceibi63dCjpTHKooVUUUxZpJDSUMERUQwQH5/AiOEjGDpsCAMGDKB///7079+f7OxsevXqRVpa2pHF6+0yee/wStK+ty3tx0XA66q6Q0RKRWSKqn7k7JsMjAcOAe8Bp2OLjLokAstV9Qci8k/gXuAzwDhsgbEEKAQ+o6pBERkJPIfdYTbGF4BJwEQgA1gtIm87+6YDOaq6p+4BqhoTkZeBS4HfAvOAt4Ag8CgwX1WLROQy4OfAdcBT2MN674vIfXWiux4oV9VTRSQOeE9ElgJ3UMej5Ai0xvI13SmDfcDrTp6ODLeJyFjgMuB0VY2IyO+AK4C/NlAefxOR2p7iHODHqlrqiLz/isgpqvqIiHwfOMsRZlOB/rXCVEQauv18F5jhCOIbgNuBW519Y7AFdTKw3RFspwBfxq4XHuAjbFFdn/ENbF8DXN1A2FrmAodU9XzH3tQmwh6Dr6IXYxKHk+TpTZKrFz6JP9pJKCd8KdhZs5aq2GGm9P1CtxFOAGMy5lAc2Mem6hXMSr34hDomn8tPlm8oWQwFr93pBa0qqmKHCWglgVgVFfsrWLt3E2ENEbGCRDR0QvYLLmfIyotHvHglDq/48bkSyXal403043M520jA70rE54pv+ClDC1uSdyAV0WL2B7eSF9qJRYy0uH6MSzuVrKSR7fY2ep87gQEpOQxIySEYreRg5RZyy9ezrnIp8e4Uhvhz6B83ut29bA1hqUVZtICSyEEqosVUxUoJWYEjw5UAbvHidyWR4k4n1dOHTN9AEtxd90k3l7jp7c2mN9kM8gIJELJqqI6VUR0rp9oqI2/7YfZ8nEvIqmmyTXhcPnweH26XB4/bay/OutvlwePyICKIuJy/ggsX1K6LC0GO7BNcR6590sBFUI7upO7Kml0r2q6AWkh3FU+XAw876887v2vF0ypVPQAgIuuBIXxaPIWxxQHAJiDkiIFNTngAL/CYiEwCYtieoKaYDTzneGEKRGQFtqelwrFpTyPHPQf8Gls8fRlbiIzG9py96XSobiDPERPJqvq+c+yzQO0w22eBU0TkEud3KjDSyWtdmsrXKlXdDSAizzl5qjtX6RxgKrYwBNuLVNhIvq6o53m6yZlT5MEebh0HbKx3zG5gmIg8CrwKLG0g3gHACyKSje19qluur6pqCAiJSCGQBZwB/LN2TpWILGnE3oYQmp7YvQl4QETux/ZGtvjLnTlJ/w9xSbvcVZeED7InuIEByRO69DynhvC44pjQZy6rD73IJ8E1jE9q209QJJJKIvU1rqKWLa4stYhqGIsYljoLMSy1jpwrwbngY3se3NhiyS2eYz1EgtMpOD+6KKpKcfgAu2o+4nAkH7d46Jc8nsEpk0j29+lQW/yeZIb3msHQtOkUVn/C3rK1fFz9PrsDGxiaMJFB8WM7RESVR4rYH9hKQWgvEQ0CQpI/k15Jw/B7k/F6EhDszx2FIlUEwocpqckjr2Yn22ogyZvOgLhR9ju0XHHtbu+JEu9OIt6bRAYDjm5UxbKUmEYJWtWErQARDRHVMBHL+es8HGBpDCsSIxaOESZK0GlDMY0BiqKgSu0/6q6pLUQVq87FtqHLrh67p87K3Iwbv/Z68RN/atNCaYZuJ55EJB04G8gREcUWFioitztB6srkGA3nMaJHxyut2mOcIara8N8DCrA9SS5sb1CTpjWxr7qJfe8B2SIyEZiFLaBGAltUdeYxCYj0aib9W1T1jXrHzKkXrql81a+x9X8LsFBVf9iEHZ82TGQocBtwqqoedibKf+oro86+icDngG9ie+SuqxfsUeyJ20vqDNPW0ti5b8nY9FZsYfi/OtumONsbxPF8TgU+D/xSRJaq6s9akBZ/WX0vVWVtP0e+rLyMeZedR2pCJuP6nN3m8XcE6fGDGJw6lX3la/nB3d/l3HPO6WyTTkpUlbfe/i+///NjbNyygcS4VMZnnU12wjg8rs79CLBLXPRNGk1W4ihKg7nsLvuAbVXvc4iPuflr3+DKy76Kz9e2okRVefu95Tz+p0fZsGkdHo+PPr3HkJ0+ltT4IXjcTaenqgTChykq30FB2Va2VX3AruBaLrrgEr5983fok9mxQrQzsSyLaDhGJBIlFokRi9rD3FbMwoopsZiFWvbNilqK2ioKVXtdVY9ctWu76ganGDle+kdv+9vLHZY5h24nnoBLgL+q6tdrNzhentltnE4qcMARVFfTvAP9beDrIrIQ6A2cCfwf9lBSozjDTy9iDxe+5gynbQcyRWSmqn4gIl5glKpuEZFKEZmhqiuxhVYtbwA3i8j/HC/aKOAgUIk9jNWSfE13hM4+7OG5J+qZ+19gsYg8pKqFItIb2xO2r5myScEWkOUikoU9L2y5s6/WvmIRyQDCqvqSiOwCnm4grlQnX9D0kFotbwNPO0OcHuBC4I8NhPsVcL+IzFXVEsczdw1wWmMRi0g/oFT1/7N33vFRVtn/f98pSSa990ZCCCWhI4KiYseOiisqCLr6212767rr6u7iNv2uulbQxYaCKAooWBELKE1AeiBACCEkpPdkkqnn98dMEDFAgCSTZJ736zWvefKUe8995jmZz5xzi8xz96Ob1g57AIjv0/H/SEWESZMeorKqknGpU9HRbfojnDT9ws+mqnk/f/rbQxy4PZ+wsOP9btA4GZxOJ4sXL+af//gnW7dtJdAvjKEJE4j2zUTngdTY8VBKEWFKJsKUTHXzQfLr1vJ/z/6Lt955k6ee/j9uuvmmDlk4+vvvv+eRRx5h9erVBAVEkNXnMqKDszDo2y8ilVL4+4aTEn0mKdFnUm8upbhqIwuXvMdHnyzkt7/9Hf/8198JCgo6cWEaJ8Xl086t6uo6e+Jy5ZNxdXo+kkXATR1czyzgVneH634cP3qE26ZtwFZc0YuHjx6ldRzexRUJeg9ARKy4ROL/KaW2AltwRaXA1bdptlJqLa5IUJ17/2u4oiSblFI7cAkEg9smu1Jqq1LqgRO0ay2uTuc7cKXDfnafxTXNw2PAl0qpbcByXCm44yIiW4HNQA7wBq5oWyuzgc+VUt8CCcAKd7p1DtBWhGsG8IG7g/cJR7u5+8ItwHUPFwFtptZEZKnbtjVKqVzgVVyDDUqOU3w2sN5t76O4+s55jNdee41FixaRGTkOP3r2PEd6nZHsqMtoNNdxzYQb2v7VqXFS2O123nnnHbIGZTFp0iTy9xQxPPEKxsZPI9ZvULcTDp0EQgAAIABJREFUTkcTbkpiRMwkRsZdj7nezpSpUxiQmcXy5ctPuczKykqmTZvGOeecw5ZNOxicdiWjM35DfNjIkxJObRHsH8uApCs4a+BdRIcO4IUXnyc1JZ0PPlioPc+9gB452s6bUUoFikije/tPQJyI3OdhszROng51vI0bN3L22WcT6pvA0MiJ3W6E0qmSV72GvJo1/O3P/2TGvx71tDk9EpvNxty5c3niiSfIy8sjxBRFRuRYIozppzWi05OICCWNu9hbs5pmWx1nnTmOl15+gaFDh7a7jPnz53PvvfdSU1NLWtxYUqPHdaqArG0qIvfgp9Sby7hg/CW89/48r54Vv4PRpirQOD7ukXeP4IoqHcA1hUHF8a/S6IZ0mONVVlYyYsQIaisbOTP+ZnTS/TuothcRJ5tKP6Sy+QCfffIFl152kadN6jFYLBbefPNNnnzySQ4cOECYfywZkWcRZkjtNeLa4bRTWL+F/Np12BwWrr3mep559j+kpqYe85q6ujruuusu3nnnHSJCkslKvRJffddMFukUBwfK1pFXsoLgwBDee/9dLr304i6pu5ejiScNDS+hQxzP4XBw6aWXsmLFSs5KuRkTve+XrM3RwrridxCdnZxd20ntk+Jpk7o1ZrOZ2bNn8/TTT1NcXExEQCIZkWMJ0Sf1GtF0NDZHC/vrNlBQ+yNKB7+58zfM+PvffhHZWbduHZMnT6awsJCMhPNIihx7zMWoO5N6cwk7DnxIY3MV9937IP999j8d0nfLi9HEk4aGl3Dajici3HPPPcycOZOh8ZcRaxp44ot6KI3WStYWzyc2Mp6cPVsICWn3lFpeQ319PTNnzuTZZ5+loqKCqKAUMiLHEqTie61oOpoWewP5tWsprNuOyc/Enx75Ew899Hv8/f353//+xz333IOfTzCD064lwHjC7pqdisNpI/fg5xRXbWHsmefy2RdLtOf61NHEk4aGl3DajvfUU0/x8MMPkx5xBhmh53SETd2aiqZ8NpV+xKDMIWzcuhZf396TnjwdqqqqeP7553nxxRepra0lNjidjMixBKjTm6G9J9NorSSvdjWlDXsJC41gUNYAVq1aRUxYP7JTJ6JT3ePZEREOVm5kd9EyoiPj+PrbZQwaNMjTZvVENPGkoeElnJbjzZ8/n5tvvpnE0IEMCp/gNZGF4oYctpd/znlnXcTyFZ9hMHTvEWKdyf79+3nhhRd49dVXaWpqIj4kk36RY/Gj1yz2etqUNe5lW8XnOJxWUmPGkhF/frfsJF/TeICt+xeilJOPPvqQSydc4mmTehqaeNLQ8BJO2fHef/99brrpJiL8kxgaPRFdV6/h4WH2125gd9VKzj/3Er5Y/nF3Wl+r0xERVq9ezbPPPstHH30EKOKD+tM3cgx+aIvpHkmjtZKNJYuwOVsYlHwlseEnvZZ7l9JsrWPzvncxt1Qx86VX+M3vfu1pk3oSmnjS0PASTsnxDgungESGxUxEOb0z8tIqoMaNGc/ybz/v9Sk8s9nMwoULefHFF9m4cSN+vgEkBmaTEjocI52z5lxPprr5IJtKP0KnMzA8fTLBAfGeNqld2OwtbN3/PtUNBTz80KM8+Z9/eE1U+TTRxJOGhpdw0o43a9Ys7rnnHiICkxjuxcKplQN1m9lV+TWD+g/hm5VfEh3d+5a/2Lp1K6+++irz5s2jrq6OEP8oUkOGE23qj/40Fk3uzZQ05LKt/HP8fcMYnj4Zk1/Pmp3e6bSz48BSSmt2cMP1tzD/vTno9d4VXT4FNPGkoeEltNvxHA4Hf/jDH3j22WeJD+lHVtRl6MS7hVMrJY257Cj/gpCQML786nNGjBjhaZNOm7KyMj744APmzp3L+vXr0esNxAX2IyV8GIEqVotEHAMRoaBuI7urVhIWkMzQtBswGntmVE5E2HvoawrK1nDBeRP4bNlH+Pj4eNqs7owmnjQ0vIR2OV5JSQlTp07lq6++Ii1iJBkh53TLDq+epM5SyubSJdiczTw+4+888ugfe9ycOTU1NSxevJh3332Xb7/9FqfTSah/DInB2cQGDMBA705Lni4iTnZVfkth/WZiQgeSlXI1en3Pj8ztL1vD3uKvGDFsLN+tWo6/f88Ug12AJp40NLyEEzreJ598wm233UZtbR2Doi4g1qQNYT4WFnsTO6u+oqxxL0OzR/DGW68ybNgwT5t1TESE3NxcPv30Uz799FNWrVqF3W4n2D+SGFM/EkIG4Kd6VrrJUzicNraWf0p5Ux4p0WPol3Bhr4rOFVVuYmfhp2T2zWLdhu8IDdUGBrSBJp40NLyEYzregQMHeOCBB/jwww8JC4xlaOyV+Io2ed6JEBGKG3LYU70Sq6OFmyffwt//OYO0tDRPmwZAaWkp3333HStXruSLL74gPz8fgLCAWCL8UokP6Y+JiF71xd/ZWB1mfiz5kDpLCf0TLyE5erSnTeoUSmt2sr3gQxLiUtjw42piY2M9bVJ3QxNPGhpewi8cr6SkhKeeeopXXnkFh91JetgYkoKGokPr33Qy2Bwt5Nf9QEHNj6Dgisuv5P4H7uXcc8/tso63NpuNnTt3smnTJtauXcvKlSvZs2cPAEaDL+F+icSFZBDum4qPCuwSm3obZlstG0sW0WJvIDt1IjFhAzxtUqdSVb+PLfnvExYayQ8bVnWbHwXdBE08aWh4CQKuaMkPP/zAa6+9xrx587DZbMQHDyQzchxGCfC0jT2aFnsjBxu2UFi7GZvTQkR4JJMmXc9FF1/EOeec0yEr2jscDg4cOMCePXvYs2fPYcG0bds2LBYLAD5GE2G+8UQGphBuSsSkItApbfTU6VDbUsKmksWIgmHpNxIamORpk7qE2saDbN73LiaTP9+vWsHgIdmeNqm7oIknDRdKqYnAYmCAiOR62p7joZRKBT4RkTZnoVNKPQA8AcSISF0XmnZMlFIjgakicq9S6jzAKiJr3Md+A5hF5O3Oqn/NmjWydOlSlixZQm5uLkaDD/GBA0iPPBMfCeqsar0Sh9NGhTmf8uY9lDXk4xAbAHGx8WQPzqZ//0xiY2OJjo4mIiICHx8fDAYDer2elpYWGhsbaWxspL6+ntLSUg4dOkRJSQkHDxZRULAfq9V6uC4fgx/BvjGE+MYQHhSPiQhM+lAtFdeBlDXlsbXsE3yNgQxPv4kAU+9bDPt4NDSXsSnvHXR6WL78S846e4ynTeoOaOJJw4VS6n0gDvhaRGa0cVwvIo4uN6wN2iGe1gMW4HURmdN1lrUPpdQMoFFEnu7COkWn0xMRkERC8AAifTMwKG0ocmfjFAd1llLqbSU0Wiupay7HbKvF7rSe+GJAr9Nj8gnGR+ePjy6AIFMEQb4RmPQh+BCMj95fE0qdyIG6Teyq/IZg/3iGpd2Ir49nU54Opw2bvRmlFDplwKD365LP32ypZlPeO9gcrslTr7r6ik6vs5ujiScNUEoFAruB8cBSEenv3n8e8DegBBgK/A54HChz/70Y2A7cB5iAa0Rkn1Jqkvs6B1AnIue0Ud8SIAwwAo+JyBK3KPocWAWMBYqBq0WkWSk1AngDMLuPT2hLPCml0oGPgd8CfxaRS9z7pwHXAHogC3gG8AGm4BJal4lItVJqBbAZGAFEAVOBR4BsYIGIPHa0eFNKPQQEisgM9/U/uO9lKHC7iHzvvpcPAXcD69z3pgK4B7gAt5hSSg0FXgH8gX3AbSJSc6xy2/g422R4/FUS7puCUe/X3ks0OhGH04bVYcbqbEHEieBExOn6QtQZ0SsfDDofDDpfTRx5ABFhd9VKCuo2EhXcj8F9rkWv79ofG3aHleqG/VQ37KfOfIimlgrsDsvPztHpjJh8Qgnxjyc0MJmokAx8jZ0j8Cy2BjblzaexpYLbpv+aiy+5AF9fX/z8/PD19cVgMKDT6dDr9eh0uuNut/59vGf7WMdOdn9HlwUQFxfX5U6p9UTtnlwDfCEie5RS1Uqp4SKyyX3sDCBLRPa7BcAQYABQDeQDr4nIGUqp+3AJgfuBvwKXiEixUqqtca4twEQRqVdKRQLrlFJL3ccygMkicoc7GnYdMA94E7hHRFYqpZ46TlsmA+8C3wOZSqloESl3H8sChgF+QB7wRxEZppR6FpdIes59nlVEznG3aQkuIVUN7HOfeyIM7ntyGS4ReWHrAREpUEq9whGRJ6XUBUdc+/YR7fy7+/r7T1TuiYjxz2zvqRpdgF5nxKQLwYQ2qrG74XDa2V7+GaVNe0iKHEn/xEtQuq7pMyYi1DQWUlT5I+W1uTjFjl7nQ2BgHDExQ/H1DcFoMAHgdNhosdRhbq6kon4vh6q3AoqwoBQSI4YTEzagQ/u6+RqDGNnvVrbse4/X35jNW2+9jd3R0mHl9yQuTX+o3+d5T+3pyjo18dQ9mcxPwuE999+t4mm9iOw/4twNIlICoJTaB3zp3r8dV1QEYDUwxy1+FrdRnwL+rZQ6B3ACCUCM+9h+Edni3v4RSFVKhQChIrLSvX8uMOEYbbkRlzBzKqUWA5OAme5j34pIA9CglKrDFaFqtX3wEWUsPWJ/zhHtzQeSgNpj1N1Ka5t/BFJPcO5h2mjnW8AHp1suQERMMJYWW9fHmjU0ehDN1gbW579PtfkQ/RIuJCV6TJdE/kSE8rrd7CtZSWNzGQa9H3FxI4iKHERoaCo63fG/OkWEpqYyyiu2U1a2le0Fi9lzKITU6DNJihyJroPEn1Hvx4i+t7Ct4EPKa3eREJxNQmAWggMRQXCCCIIArndXtqmtbWeH2IS7xFO5qs297SsqC9DEkzejlIoAzgeylFKCK60lSqmH3ac0HXXJkXFj5xF/O3F/viLyG6XUaOByYItSaqiIVB1x3c24UmIjRMSmlCrAFQ06unwHrnSgoh2TPCqlBuOKXC13/8PzwRUdaxVPJ7T9qPOcbVxjAOzAkVNKH50La73GQcc+86dc7rzVf+lAMzQ0eh8bNmzgmmuuodFezcjMGwkP6Ncl9dY0FpJbtIwGcwkmUwT9+00kJmbISaUJlVIEBsYSGBhLn9QLqKraTeHBVewuWkZhxXr6xp9PbOjADhGCOp2BIX2uI7doGQcrNjDs7L4s/mgBRmPPn2H9JGgrKNCp9Kw1DLyD64G3RSRFRFJFJAnYD5x9qgUqpdJF5AcR+StQiStacyQhQLlbOI0HUo5XnojUAnVKqVabbj7GqZOBGe52pIpIPJCglDpu+adAGRCtlIpQSvkCJ9t7sgH4xRA398jAGqXUOPeuKcDKo8/T0NDoWObNm8e4ceNorLcyZsDtXSKcrHYzOQc+ZsOeOVgdZgZkXsfoUfcTHz/qtPpXKaUjMnIAw4fdwZDB09AZfNi+fxGb8t+lxdoxg4+V0tE/8VL6xo3nk88+ZPSocdTU1HRI2Rpto0Weuh+TgSeP2rcIuAlYcIplPqWUysAVMfoa2HrU8XeAj5VSG4EtQHumRpgOvKGUMgPLjnHOjfwynfehe39ZO20/IW7R93dcHbj30z77j+RjYKFS6mpc/cSO5FbgFaWUP66o2fTTtVdDQ6Nt7HY7jzzyCE8//TTRYWkM6XM96heB5I6nom4POw4sxe5oITlxHKmp4zEYOr7eiPB+hIf1pah4Lfvyv2T1rlfol3ARiRHDTjsKpZQiLW4cfj7BbN32CQP6Z7Ni5Vf079+/g6zXOBJttJ2Ghmfo9o7ndDrJz88nJyeHnTt3UlxcTGVlJdXV1YgIBoMBPz8/YmNjSUhIIC0tjWHDhtGvX78um8lbo/dQVFTEjTfeyOrVq0mNPYOM+ItQdO5z5HDa2FP8FQcrNhAYEMvA/pMIDIrr1DpbaW6uJnf3Ympq84kJz2JQ0uUY9B2zAHRNYyFb8z9Ap4dFiz7gssuP1SW116BNVaCh4SV0S8fLz8/n448/ZsWKFaxc+R01NdWHj/kY/fEx+GPQuX6RO8WJU+xYbY1Y7ebD5/n5mjhj9GiuuOIyLr74YgYPHqwN79c4Lp9//jlTpkyhscHMoJQriAzq/KVWzC3VbMl/n8aWcpISziI97WJ0+q7tJyTi5EDhd+TvX47JL5whqdcT7B9z4gvbQbOlli37F9DYXMHfH/8Xjz72x97sh5p40tDwErqN4xUVFfHmm2+yePFitmxxDawM9I8gNCCZyNBU/Azh+PtEHvdXscNpx2ypoqG5FLO1jIqafBqaXTNSxMUlMmXKzUyZcgtZWW3Oo6rhpTQ3N/OXv/yFZ555hvCQBIakXY9Rdf50EZV1eWwrWIxSOgYOuIGIiK7pjH4samr3k7PzPRx2C9mpE4kO7ZipTOwOCzsOfER57W4uOP9SFi56l9DQtmar6fFo4klDw0vwuOOtW7eO5557joULF+J0OgkLSiYuYiARgRn4GU//H2yLtZ6qhn1U1OdSUbMPwUlmvwHcd/89TJkyhcBAbUFcb2b9+vXceuut5ObmkhJzBv0SLkR1cjdcEaGgbA17D31NYEAs2YNuxuQf0al1theLpZ5tO+bS0HCIjMQLSY06s0MiRSLCgfJ17C3+mqioWD77fCkjRozoAIu7FZp40tDwEjzieDabjYULF/Lss8+xYcN6fIwmEqOGkxQ5El9D5/3it9iaKKvdSUn1FuqaSjD5+TNlylTuf+BeBgzo/BSNRvfBYrHwj3/8gyeffBJ/vxAGpVxJsF9HD8D9JU6ng5wDSymp2U50VDYDMq9Fb+iYPkYdhcNhZVfuQsordhAfOYyBSZd12MSatY0H2VawCJvdzIwZf+eRPz/cm/omauJJQ8NL6FLHq6qqYvbs2bz44kuUlBwiwC+CtPgxRAVlYejCZS5EhLqmIoprNlFSuQOnOBh/3oX89W+Pcu655/bmPhkawLJly7j77rvJy8sjKXo4mYkXo6Pznz+7w8LW/A+oasgnLfVCUlLGd9tnTcTJ/oKvKTjwLZGh/RiSeh16Xcf0xbLazews/Jjy2t0MGTyCRYsXkJ6e3iFlexhNPGloeAld4ng5OTk8//zzvP32XCyWFiJD0kmNOZOwgDSPf3lYbU0UVW+isHw9VlsTAwdk85e//pnrr78eg0GbRaU3UVhYyIMPPsiiRYsICYpmQNKlBPuldkndFlsTm/bNp9FcRv/MicTF9YyUVVHxOvbs/ZiQoCSG9/nV4WVgThcR4VD1NnYXLUPphH/961888MB9Pd3nNPGkoeEldJrjOZ1OPv/8c5577jm++uor9HojCZFDSIwYRaBfVGdVe8o4nDZKqrdxoPwHmloqiY2J549//AN33HkHAQEBnjZP4zSorKzkiSeeYObMmTidQlrsOJIjz0R14Bpvx8NsqeHHvHew2BrIGngjkZE9K0VcXr6dnF3vE2CKZFjaTZh8fjGX7ynTYq1n18FPqKjLo296f+a89RpnnXVWh5XfxWjiSUPDS+hwx2tsbGTOnDm88PwL7M3bi79fCCkxZxATMgQfg39HV9fhiAgVdbsprFxHdX0hgQFB3HXXXTzw4P3ExHTM8G2NrqGmpoYXX3yRp59+msbGJhKjhpKRcC4G1XFf/iei3lzCprz5OHEyJHsqISGd36+qM6iuzmN7zjyMBn9GpN9CgF94h5UtIpTV7mJP8XJarHVcf92veOa//yE5ObnD6ugiNPGkoeEldJjj7d27l5dffpk33niDuro6woOT6BM3hjD/jA5dxb0rqW08SGHlOkqrczHoDUy89loeeuhBzjjjDE+bpnEcDh48yHPPPcfs2bNpbGwkLmIgmUkX4KML61I7qhr2s2XfAgxGE0OzpxEQ2LPFd319EVu3zUEpHcP73kywqWPbY3dYKShbRUHZWnQ6xe2338GMx/9KbGxsh9bTiWjiSUPDSzgtx3M4HHz22WfMnDmTZcuWodPpiQ0fSFrcGPyNPeYf3glpaqmiuHojRRVbsDssDM4exkN/eIAbbrgBX9/uNVLKW3E6nXzzzTe8+uqrLF68GKfTSXxENmnxZ+Gnj+xye0prcthe8CH+pkiGDJ6Gn1/vmNeoqamMzVvfwOm0Myx9MmEBiR1eR4u1jv3lqygq34zRaOS222/noYce7AmdyjXxpKHhJZyS4+Xl5TFv3jzeeustCgoKCPAPJSF8OEmRw9Drem//ILvDQknNNgorNtDUXElIcCi33HILt90+nWHDTn9dMI2TZ+/evSxYsIDXX3+dgoICTL4BxIYNJjX2TIy6rkvPHUlh+Xpyi74gJDiFwVlTMPp0/3T1ydDcXM2WrW9gtTYyJO0GIoPTOqUec0s1BRWrKK7cDji59JLLeOgPD3Leeeeh0+k6pc7TRBNPGhpeQrsdr6ysjMWLFzN37lzWrl2LUorIkDRSY0cRYkrvsam5U0FEqG7Ip6RmC6XVuTjFQUbfTH59x21ce+219O3b19Mm9lpEhJycHD788EMWLlzItm3bAIgKTSc5ZgShpr7odZ4ZsSUi5B36hv1lq4mMGMCgAb9Cb+i6KTi6Eoulni3b3sRsrmRwn+uICe28hX9brA0UV/9IYflGbHYzcbEJTL9tGtOm3UpGRkan1XsKaOJJQ8NLOKbjtX5JLV26lI8//pgffvgBESE0KI7YsCziwrMx6rTZuW32ZtfEmzXbqGk4CEBG30wm3XAdV199NSNGjOhNkwB6hKKiIr755hu++uorvvrqK0pKSgCIDE0lJnQAUSGZ+OiDO9UGu8OK2VKN3WEBBKPehJ9PCEbDT2ss7ir8hOKqLcTHjaJfxlXodL37c7fZzGzd9hb1DUUMSrmKhIghnVqfw2mjvDaX0trtVNTuA4TMfgO47vqJXHXVVYwaNcrTESlNPGn0PpRSDmA7rgfcAdwtIms6qa4ZwN+ADBHJc+97APgvMEpENh7n2vuB2SJiPtY57vNWAA8dr6x2cNjxnE4nOTk5fPfdd3z33Xd8//33h7+kwkMSiQzuR0xof/wMEVp66hiYLTVUNeylvHY31Q0HEHESGBDEuHHjuODC8zn33HMZPHgwPj69MxpxuogIZWVlbNu2jQ0bNrBhwwbWr19/+Dk0+QURGpBCTFhfQv374GPovLSc0+mgsn4vFXV7qWrYT4u1ts3z/HxDCQtIoam5gvrmQ6SmjKdP6oVe4yN2u4XtO+ZRU7uPzKRLSIka3SX1tljrKa/bSUXdHqobChFxEhwcwrhx4xg//jzGjRvH0KFDu9rXNPGk0ftQSjWKSKB7+xLgzyJybifVNQO4FnhfRP7p3rcaCAVuPYF4KgBGikjlCepYwWmKp//973+yZcsWtmzZwvZt22kyNwEQYAolxD+J6LB0Qv3T8DFoEaaTxWo3U9Wwj4bmIipq82lqqQLAYDDQP3MAI0eNYPjw4WRmZtK3b1+Sk5N7+gSB7cJms3Ho0CEKCws5ePAghYWF7N69m127drFrVy719XWHzw0OjCbQN5aIkCRC/JMxGSM7XZRY7WYOlK+juHIzVnsTeoMvoZEZBIYkYAqIxOjrD0phszTR0lRFQ+1BaivzcNgtGIz+JCWeTWL8aIzGjplMsifgdNrJ2fkeFZU7SYs7l/TYc7pUPNrszVTW51HXXEhl7X7MlmoA9HoDmf0yGTFyOEOGDKF///6kpaWRmpqKydQpn48mnjR6H0eJp0nAzSJyjVIqEFgChAFG4DERWaKUCgDeBxIBPfAPEVmglBqBK4IUCFQC00Sk5Ki6ZgA6YIKIjFJKpQEvAf64BY9S6mLgccAX2AdMB24DngZ2A5UiMl4p9TIwCjABC0Xkb+46VgAPAZuB14GRuCJJb4jIs+28J+JjNBHkH0OQKYbw4EQCfRPwNYR4zS/nrqLF2kBd00HMtjJqG0qoayrBam86fFyvN5CcnEyfPn2Ii4slNvanV2RkJMHBwQQHBxMUFHT43RNiS0Qwm800NTUdfjU2Nv5su7q6mqqqKiorK3/2XnKohNKyUo7+f+/vF4y/byT+vhGEBsUQ4BuJnyH6cEqsK3A4bRSUraGgbC0Op43wmP7EpZxJaHS/E6bfnA47NRV7OLR/NbUVezEYTfRJuYCE+NG9PnXXitPpIHf3YkrLNpMcPZrMhIs99j/EYmugtukgZms5dY0l1DWVYrE1/OycmOhYUlJTiI+PIzY2lpiYGGJiYoiKiiIkJOSwn7X6WmBgYHvS75p40uh9HJG28wPigPNF5EellAHwF5F6pVQksA7IwBU5ulRE7nBfHwKYgZXA1SJSoZT6FXCJiNx2VF0zgEZgLPBX4GqgCJdAeggoABbjEldNSqk/Ar4i8vejI09KqXARqVau6ZC/Bu4VkW1HiCcBnhSRi9znh4pI2zmGozgn6z7x89GEkicQESy2RsyWapqt1TRbatzb9VhtjVjsTTidtuOWodcZ0OsN6HR69DoDOp0BvV5/+G+ldG1+tof3SWveVhBx4nA6cLpfDqf98PbhlzhxOh3tbqNR74fR4I/RYMKoN+FjDMDkE4KfTwh+xmB8jcH4+QRj0Ht2uoeq+nx2Fn5Ks7WGiNgsUjIvJiDk1KbaaKw7xP6cT6itzCMgMI6B/ScRFNh7pu04HiJO9uZ9RlHxGuIjhjIw+Qp0qnuMirPazS7/stTQYq3FbKmh2VqLxdaE1d6Ezd7MicbP/ORjrpdBZ0CnN2DQG9HrDAxOnqJf9uPjzq5pkYveH6vW6A40i8hQAKXUGOBtpVQWrl8L/1ZKnQM4gQQgBpfQelop9X/AJyLyvfv8LGC5+wtID5T8sqrDvAfcCFwCXIBLPAGcCQwEVrvL8QHWHqOMG5RSd+Lykzj3dduOOJ4PpCmlXgQ+Bb5s3+0Ak69r7hlNPHU9SilMvsGYfIOB1COOCCIuceVwWrHYGrHZzdidVuwOCw6H5adtpxWRn0SNa9v1Eodrf3sQBIURvdJjUDp0Br1beOnRud+VUuiUHqX06HVG9Hof17vup3fXl4gPBr0Jo8H0sy9O1yPWvZ4zh9PO7oNfcLDyR0z+kWQPv5PQ6NMbKRkYEk/WmDuoKs2GX9VvAAAgAElEQVQhb+tiNm6aSVqfi0hOPBvVTYREZ6GUjoy+l2M0+LH/wDfYHS0M6XMdOg+NfjwSX2MAvsYAwgKTfra/NXDjFCc2exNWmxm70+L2NevhbbvDglPsLv9yOpAjtp0OOza7A+AfwKNd2S7P31kNr0JE1rqjTFHAZe73ESJic0d+/ERkjztFdxnwhFLqS+BDIEdExrSzqo+Bp4CN7shW634FLBeRyce7WCnVB1d0aZSI1Cil5uCKnB3Zlhql1BBcAu0u4AZc6b8TsnjFI7S0WNvZFA2N3kN+/j5u+/WtHKzcTnLGuST1uxid3tghZSuliIzLIjg8lbyti9m37wvq6g8yMPN6DIbePamqUoo+fS7EYDSxN+9Tag3f8sGCDwgM7P39Jm+69JnHu7pOTTxpdClKqf64okZVQAhQ7hZO44EU9znxQLWIzFNKNQLTgCeBKKXUGLcAMwL9RCSnrXpEpNmdkttz1KF1wEylVF8RyVNK+QOJIrIHaACCcPWnCgaagDqlVAwwAVhxVFsiAauILFJK7QPmtPc+BAT5ERDUdf1KNDS6A5999hmTJ0/GanUw9KxfExTRr1Pq8fENZMCoKRzKX0X+zk/ZaH6ZwVlT8DdFdEp93YmkxLMw6P3YsGExV1x5Od99/w1hYV27PE5Xs+zHx7v8l6gmnjS6ApNSaot7W+Ea9eZQSr0DfKyU2ghsAXLd52QDTymlnIAN+K2IWJVS1wMvuPtAGYDngDbFE4CIvNfGvgql1DTgXaVU60/Rx3CJrNnA50qpEneH8c3u8vOB1W1UkQC8qX7KCTzSrruhoeGFzJo1i3vuuYfgsESGjZ2CwSekU+tTSpGQPo6AkDh2bZjHj5v/x5DsWwkOSujUersDcXEj0Bt8ydm5gOHDzmDtuu970jp1PQKtw7iGhmfocY5ntVqpqqqipqYGp9OJwWDA19eX2NjYzhp+rNELcDgcPPzww/z3v/8lKn4Q/Ybd1GFpuvZibihnx7rXsFvNZGXdQkSYd8xEX12dx/acuYSHR7F69YruNit4R6KNttPQ8BK6reOJCHv37uW7775jw4YN7Ny5k127dlFVVXXMa4KDQ0hJSWXEiGEMGzaMsWPHMmzYMG2Gby/H4XAwffp05s6dS1LfcaQMuNxjnbctzXXsWPc6zU0VZA26maiIzlvWpDtRV1fIth1vo9crFi78gMsvn+BpkzoDTTxpaHgJ3crxmpubWb58OYsWLeKLL5ZRXl4GgK9vACZTFEGB0fj7h2M0+mPQ+yEonE4nInZstkYsljoaGyupqy/GZnPNoRQUFMz48eczceLVXHPNNYSG9o7V7TXax5HCKX3QBOLTx3vaJGxWMzvWvkZTfQlZWd4joJqbq9meM4+mpjIef/xfPPbYn3rbSF9NPGloeAkedzwRYc2aNcyaNYslS5bQ1NSEr28AYWEZREX2JSAgGZPfyS0JIyJYrQ3U1ObT0LCf8oo9WCx1GAxGzj//QqZPn8rEiRPx9e3dI5+8ne4onFqx25rZvuZVrxNQdruF3N2LKK/YwRVXXMt7771NQECAp83qKDTxpKHhJXjM8VpaWliwYAHPP/88mzdvxtfXn6jILOLiBhPgn9KhMzOLCPUNRVRWbae0dDsWSx3BwaFMnz6du+76bW/ug+G1OBwOpk2bxrx580jPuoz4tPM8bdIvOFJAZWffQmR4pqdN6hJEnBQcWMH+gq+Jj0/mk08+ZNiwYZ42qyPQxJOGhpfQ5Y5XXFzMK6+8wssvv0JVVSWBgTGkpp5NRFg2en3nL+Ip4qSmZh+lZRspK89BxMnYseP485//yIQJEzy9KrtGB9AThFMrLgE1G3NDGUOGTCcspI+nTeoyqmv2sSv3A+z2Zp588kl+//sHenoaTxNPGhpeQpc4noiwbt06XnjhBRYuXIjd7iA6agBJSWcRHJTquTWwLPWUlm2iqPgHLJY6kpP78Kc//YFbb70Vf39/j9ikcXo4HA5uvfVW3nnnnW4vnFqxWZrYunoW1pZ6hg25g+CgeE+b1GVYrY3k7llMZWUuY8acw7vvvk1KSoqnzTpVNPGkoeEldKrjWSwW3n//fV544QU2btyI0WgiMWEUcbFn4OcX3plVnxROp4Pyiu0UFa+mvr6YoKAQ7rrrLu677x5tXpoeRE8UTq1YmmvZumoWToeN4UP/HwH+kZ42qcsQEYoPrWNf/jL0eh1PPPEE999/b0+MAmviSUPDS+gUxyspKTmcmquoKCcwMJrU5LMIDx/crZenEBFq6wo4dGgNZeU7MRgM3HDDr/jjH//A4MGDPW2exnFwOBxMnTqV+fPn9zjh1Iq5sYJtq2ah0xkZPvROTH7eNTK0uaWGvXuXUFm1h6ysobz22iuMHj3a02adDJp40tDwEjrM8VpTcy+99BLvv/8+DoeDyMj+pCafTWCg51Jzp4rZXEnxobUUH9qI02lj9Oix/OEPD3L11VdjMGiLInQn7HY7t956K/Pnz6dv9uXE9TnX0yadMo11xWxb/Qo+vsEMH3IHvj69f024IxERSss2sy//C6zWRiZOvJ7nnnuG5ORkT5vWHjTxpKHhJZy24zU1NTF//nxmzZrFli1b8PU1ERszgqTEMfj49Py1rGw2M6VlP1JUtI7mlhpiouO49757uPPOO4iM9J7USnflZ8Ip63Li0nqucGqlrmo/O9a+in9gDMMH347B4H3rT9rtFgoPfkfhwe/R63VMn347f/nLn0lMTPS0acdDE08aGl7CKTmeiLB161befPNN5syZQ319PWGhCSTEjyYiIhu9vvum5k4VESeVVbkcKvmBqqq9GI0+XHXV1dx556+54IILtFnMPYDdbmfq1Km8++67vUY4tVJdtoud698iODSVoVm3ou/ipWS6Cy0ttRwo/IZDJZvQ6XTccstUHn749wwcONDTprWFJp40NLyEk3K8oqIi5s+fz9y5c9mxYwd6vYGY6GxSksfi5xff41Jzp0pjUxmlpRs4VLIZu72ZqKgYpk+fxtSpUxg4cKDX3AdP0puFUyvlRZvYvek9IqIGkD3gpg6d+6yn0dxSQ3HxKoqKN+B02hk9eiwPPHAvEydOxMen86c4aSeaeNLQ8BKO63giQm5uLkuXLmXp0qWsXbsWESEiPJXY2GFERAzCoPfeIf1Op53Kyl2UV2yhonI3Ik5SUvowadJ1XHvttYwePbonjhjq9tjtdm655RYWLFhAn4ETSOzbfWYO72gO7V/Nvu1LiIkbzsB+13psTb7ugtXaSFn5JoqK19PcXE1QYDATr72Wm2+ezPjx4zEaPRqh08SThoaX8AvHKy0tZeXKlaxcuZLly5eTl5cHQFhYEpERA4iJHoqPj3eNAmoPFksDVdW7qKzaSVVVHiJOQkPDGD9+PBdddCHjx48nMzNTi0qdIhUVFWzYsIF169bx6quvUlpaSnL/i0npd6GnTet0DuxeTuHu5SQmnUVG2mXaM4QrjV5dk0dl5XZKy3bgcFgICgrmwgsv5NJLL+Giiy6iT58un3BUE08djVIqFngOGAVYgALgfiAeeEhEruiEOteIyNhTuG4G0CgiT3e0TW3UdR7Hab9S6nngeiBJRJzufdOAkSJy95G2KqX+DnwnIl+1s+5U4BMRyWrP/hOUddim9l5zxLV/FpF/H+f4Z8BNIlJ7smWfiLq6OtmyZQubN29m8+bNrFu3jj179gBgNPoRGpJKbMxAQkP7YTQGd3T1vRabrZnqmt3U1e2jsjKPFksdAOHhEYwcOZJRo0YyYsQIhgwZQkpKitZfyo3dbqe0tJR9+/aRm5t7+JWTs5ODBwt/dm7qgAkkZfTeiNORiAj5O5ZyaP9q+qRdRJ9k72h3e3E4bFTX7KWmJpeKyj1YLPUAxMUlMGbMmYwefQZnnHEG2dnZREREdKYpXS6eevW4X+X6mfAh8JaI3OjeNxSI6cx6T0U4dSeUKz49ETgInAOsON75IvLXLjCrM/gz8Avx5H5ulIhc1lkVh4b+FEHyN4UQEBBP/8wrCAvtg69vtFf3sTgdjEYTMdFDiYkeSkZfobm5mrr6fBoai1izZivLly/H/VsAo9FISkoq/ftnkpGRQWJiInFxcYdfMTExBAcH96j0n4jQ0tJCc3Mzzc3N1NfXU1NTQ01NDdXV1Yffq6qqOHToEEVFRRQVFVFaWorT6TxcjsHgQ2BgNH6+EWT2G0RZ+U5qaw+QNuhKEtLHebCFXYtSirSsK7FbzezPX47RYCIx/kxPm9Vt0OuNREUOJCpyIBl9BbO5gtq6fOobDvD559+yePGiw+eGhYXTv39/Bg4cQFpaGgkJCSQmJpKYmEhCQgIBAQE9KrLXq8UTMB6wicgrrTtEZAscjrwEKqUWAlnAj8AtIiJKqRHAf4FAoBKYJiIlSqkVwGZgBBAFTAUeAbKBBSLymLvsRhEJdG8/DEwBnMDnIvInpdQdwJ2AD5AHTBER85GGK6XuBX4D2IGdreLviOOpwFygdVnsu0VkjbtdM9x2H92uS3FF4SqBTSe4bzuABcBkTiCelFJzcEWMFh7n3o0A3gDMwKrjlecucxpwFeAPpAMfisjD7mPTcd33EmAProjiz+xw/90oIoFKqTh3W4JxPfO/BS4HTEqpLUAO8CjwOfAtMAa4Rim1EldUq1IpdQtwL67P7Afgd25TXwdG4krDvSEiz56obQB90y8hNCQRP79ofHyC2nOJxkmilMLfPwJ//wjiGAW4fik3NZVibi7HYqmmoaGCFd9u4LPPluF02tosJyAgkODgYEJCQggNDSEoKAgfH5+fvYxG4+HtkxFbDocDu91++HX038fab7PZaG5uxmxuxmw209LSTHNzCy0tze2q12g04ecXjI8xGF/fONL6DMRkCsXXJxQfn3B8fYNRSofDYWNHznxqaw+Qnn0N8X169O/CU0IpHRnDbsBub2HPno8xGEzERg/xtFndDqUUAQHRBAREk4BLYFqtTTQ0FGOxVmI2V7Br1yF+/HEbVmvjL643Gn0IDQ0lLCyMiIhwwsPDCQ0NxWQy/eLl5+eHyWTC19cXHx8fJk+e3NXN7fXiqVU8HIthwCDgELAaOEsp9QPwInC1iFQopX4F/Au4zX2NVUTOUUrdByzBJaSqgX1KqWdFpKq1cKXUBOAaYLSImJVSretiLBaRV93n/BO43V3nkfwJ6CMiFqVUWx1dyoGLRKRFKZUBvIvrS/xY7doIvAqcj0uwLTjOfZnsLm8J8G+llFFE2v5mOQKllJFj37s3gXtEZKVS6qkTleVmqLstFmC3UupFXGLycVz3vQ6X2Nl8gnJuApaJyL+UUnrAX0S+V0rdLSJD3banApnAdBH5nXtfa7sGAL8CzhIRm1JqFnAzLtGV0JpmPMbn1CbJST1vhJLdbqGlpQaLpR4RBygdvj6B+PmFYzSaPG1eu9DrjQQHJxEcnPSz/SKC3d6C1VqPxdqA1dqI1dqI3d6Cw2HBbm+hqrKFsrJKHI5ixOnEKQ7EaXe/Ow6/y0kMpFRKd/wXbe1XKKVHpzOg0/uj14XgbzISFGh07dMZ0euN7ncfjAZ/jEYTBkPry69dkU273cL2nHeoqcmj7+BriUv13oiLTqen/8hb2LH2NXbt+gCDwY/I8EzA9ew0N1dRX3+QhsYSmpsrsVgbsTtaUCh0OgM+PkGY/EIJDIwnOCiRwMBYr+iA7uMTQEREP6Dfz/Y7HDYslnos1jrXu6Uem82M3d5MTU0zFeXl2OwHsNubcTrtOB0217vY26zntdkFV3z97SOfdEGTDtPbxdOJWC8iRQDuCEQqUItLdC13f3nqcUU4Wlnqft8O5IhIifv6fCAJqDri3AuBN1ujSiJS7d6f5RZNobgiNMvasG0b8I5S6iPgozaOG4GX3GlIBz9/OttqVyOwX0T2uvfPwxX9+hlKKR/gMuABEWlwi8mLgU/bsOFoMmnj3imlQoBQEVnpPm8uMKEd5X0tInVuu3YCKUAksEJEKtz7F3C0Z/6SDcAbbnH3UWv0sQ0OiMi6NvZfgEusbXC3y4RLvH4MpLlF3afAl+1oEwBx8aFYrfauT9SfBE5xUlmRR1HxVsor8qivLznmuf4BEURH9SUhLpvY2AE9dG6cIFwB5eMjAk4RxCmICE4RENeXaGsX0vb0JT0yReHaVLTu+km4u7fd78p9rLOzGy2WBr5f9Sa1tUX0G3oDMckjT3xRL0evNzJo9DS2r5nN9h3vMCT7GpqaKjlUsoOmpkoAdHoDfkFRGAKDMBldfXycDhstzfXUVR7EcWg9AL5+wcTHDSIleSRRkX17VLqq4zj2RL4CiFNwOAWnw4nT6fIzp8OB3W7DbrficNhwOO3gSsO3L+TagfR28ZSDq9PzsbAcse3AdT8ULlE05gTXOI+63skv76ei7SHpc4BrRGSrOz11XhvnXI6rv9FVwF+UUoNEfia7HwDKgCGADmg5Qbs4hi1HcykQAmx3O7Q/rlRbe8RTm/fOHZE5lZEJJ9sOO6570dpvyQdARL5TSp2D657OVUo9JSJvt3F90zHKVbj6zT3yiwNKDQEuAe4CbuCnCOVxmffOb9tzmkeorq7mlVdeYebMmRw6dAiD0ZfgsBTSk4fgHxiNTh+I0usRpxNrSz02Sw311QcoKt5GQcEPBAYGM23aNB5++CGSkpJOXKFGt6KgoICLL76YxsZSBo+dTnBEpqdN6jbo9T7EJI9k/87P2LJ1ITq9gZDYDBKGjscvLBXf4CjUMaJ6IoKlsZrG8nwaSndTWLSJ/fvXkpyazu8fvI8777gDPz/vm9G8g/i6qyvs7eLpG1xppzuOSJONwiUIjsVuIEopNUZE1rqjFf1EJOcU6v8S+KtSan5r2s4dfQrCFZEx4kr/FB95kbvDdpKIfKuUWoUr7RSIKyrWSghQJCJOpdStuKI8xyMX6KOUSheRfbhSc20xGfi1iLzrtiUA2K+Uas+kQse8d0qpOqXU2SKyyt3mU+UH4HmlVARQD0wCtrqPFeCKEL0PXI0rOodSKgUoFpFX3e0ZDrwN2NqZkvwaWOJOy5a7069BuMSWVUQWKaX24RLFPZba2lr+/e9/M3PmTMxmMxGx/Rky5iICwjLQG44/GV5cHxCng5rKPCqLNzFz5kvMmjWT6yf9imee/r/uvrSDhputW7cyYcIEamrrGXr2/8MvSBO/4Hq2y4o2cXDPN7SYqzCFxBCZfgaRaSMx+rVvDTylFH5BEfgFRRCZPopku5XqA1uozFvHfffey4zH/8FfHv0zd931u+40+aTGMejV4sndSXoi8JxS6k+4ojMFuKYqSDjGNVal1PXAC+50kwFXJ+uTFk8i8oU7rbZRKWUFPsM1wusvuETAAVzpv6N7DOuBee76FfBsG8PlZwGLlFKTcPX7OVbUpNWWFqXUncCnSqlKXJ22j54qwB9XFOX/HXFdk1vAXdmO9h7v3k3HlToz03aasl24O5/PANbiSqdu4ifh+CoukbMel+BpvSfnAX9QStlwpS+nuvfPBrYppTbh6jB+rDp3KqUeA750C1sbrkhTM/Cm+qnzwi8iUz0Bu93OrFmzePzxx6mpqSEmaRjZ/c7Hxz/6pMpROj3h0ZmER2eSnHkpJftXsfCD9/lw8SLuvfc+Zsz4C4GB3rXYak9iyZIl3HzzzaDzZei432H0O3EK0xuordzHvu1LMDeU4h+WQMao6YQmDjrtVJve4ENU+hlEpZ9BfWkeJTu+5MEHH+C/z73Aa6++wiUXX9xBLdDoDHr9PE8aGt2UbuF4O3bsYNq0afz4449ExPSjb/aV+Ph33EweLeYaCnO/oKxoMxGRMbzx+myuuuqqDitf4/QREf7zn//wyCOPEBaZwoBRU9EZNJFrtTSSv2MJFcVb8Q0II2n4VYQlZ3dq/6Taop0U/riEloZKLrnsSubOeZ2oKE3EtgNtkkwNDS/Bo45nt9t56qmnmDFjBjq9L/2GXktwZOetDVdfXUDetsU01Zdy2eXXMOfN2dqXQjegqamJ3/zmN8ybN4+45OH0HXI9qF6dkGgXlYe2s3fbYhx2C/GDzidu4Hh0xq5JpTkdNkpyVnBox3ICAoN4843Xuf66a7uk7h6MJp40NLwEjznezp07mTZtGhs2bCA6YQjpg6/BYAw48YWnidNp5+Debzm45xv8/QOYNeslpky5xUtHGnmenJwcJk2aRG5uLn0GXkp82nle/1nYrGb2bV9CRfFm/MMTSRtzI/5hcR6xxVxTwv6179JUXcx1N9zE22++ir+/965neQI08aSh4SV0ueM5HA6eeeYZ/vrXv4Iy0m/otYRGt3slnA6jqb6UvK0Lqa8p5MKLJjD37TeIjY3tcju8FRFhzpw53HXXXej0vmQOn0xAaJevRdbtaKg9yK6N87A21xGffSFxWRd6fKZ/p8NO8bZllOR8S3Kfvny17FMyMjI8alM3RRNPGhpeQpc6Xm5uLtOnT2fdunVEJ2STnj0Rg4/n+rWI00Fx/vccyP0Sk8mfl1+eyS233Oz1kY/OpqysjN/97ncsXryYyNh+9B8xGaXv/Khjd0ZEKD2wjn07lmL0C6LvuCkERqV62qyfUXsol/zV76BT8Pbbb/OrSdd52qTuhiaeNDS8hC5xPIfDwXPPPcejjz4KykDGkImERndup9eTwdxQTt7WD6irPsBFF0/grTmvExfnmTRJb0ZEWLBgAXfffTd1dfWk9r+Y2D7jvGKW6+PhsFvZu3URFcWbCYnvT9rYye2eeqCrsTRWs+/7t2msOsj9v/8j/33qiW7jx90ATTxpaHgJne54u3bt4rbbbnNHm7LoO/ha9Mbu98Ug4uRQ/ioKdn2Byd+fmS+9yNSpU7Qvhg4iNzeX+++/n2XLlhEelUrm8Bsw+EZ62iyP02KuIWf9HMz1pSQMvoT47Au6vZh0OmwUrF9E5b4NXHTplSz98H1tYk0XmnjS0PASOs3xjhxJpzf4kp51JaExQ7q9GDE3lpO3dSF1VQVceNElvDXnDeLj4z1tVo+ltraWf/7znzz//PMYDL4kZ15IdNKZx5wB25uorz7AzvVv4RQ76WdPITShv6dNajciQsnObyna/Cl9+2fz/bdfan0GNfGkoeE1dIrjbd68mV//+tds2rSJmKQhZAyeiNL3nBE6Ik5K9q9m/87PMZlMvPji80ybNq3bC7/uRH19Pc8//zzPPPMM9fX1xKeeQZ8BE1CGnvMcdCblRZvYs2UhPv4h9DvvdkyhHTevWVdSXbiN/NXzCQoJY8U3yxk6ZLCnTfIkmnjS0PASOtTxKisreeyxx5g9ezZ+piAyhkwkJGpQR1bRpTQ3VpC3bSG1lfs597wLeP21/5Genu5ps7o1paWlvPzyy7z00ktUV1cTnZBN2sCLMZp6pjjoaET+P3vnHR9Vlf7/95mWmfTeAyGhN6lSxAgWbBSxrLqKIpbdda27ut9d3VXX39bvuu7a1oJiw7KCIkVFkCJGeu8hgRQS0nuZTLvP748Z+CISSCCV3PfrdV/3zrn3nPPcm3lyP3PKczRyDyznSOYqgqJT6J12Z6cd39Rc6suPkLlmLoiHJUsWMfnyyzrapI5CF086Ot2EVnE8h8PB66+/ztNPP01NTS0JqePp0fcKDMauPw7C2wq1juz9y1Bo3HPvffz5T88SERHR0aZ1GkSEzZs38/LLL/Pxxx/jdruJjBtIr4GT8fPXB94fw+N2krH9Y8oL9xCVOoaeF16PwXh+BAN11FVwcPWbOOrKeXPu29x1x+0dbVJHoIsnHZ1uwjk5ntPpZO7cufz5z38mPz+fyNi+9Bl6HSbr+TcQ2NFYTf7BlRzN2YjN5s9DDz3Er3/9aLeOUJ6Tk8O8efOYN28eGRkZWCxWopNGk9RnAiZLWEeb16lw2KvYu+ld6quP0mPEVGIGpJ133cBuRwOZa+ZSW5rDM3/6K08/+T8dbVJ7o4snHZ1uwlk5XmlpKW+++Sb/+c9/yM/PJzw6hV4DJmML7nXevRBOpr62mCMHl1NasAeLxcKds2bx6CMPM2DAgI42rc3xeDxs3ryZpUuX8sUXX7Bjxw4AImJ6E5M0ktDogRhNtg62svNRW5XPvo1v4/E4SZ1wG6GJXbcr+0xobheHvp9H5ZE9zL7vfua8+hIGQ+eePdiK6OJJR6eb0GzHc7lcrFy5kg8++IBPPvkEp9NJZGw/evSdiH9Iynkvmk6mobaEwuy1FOZuRcTD8BGjuP8XP+P6668nPDy8o81rFRwOB1u3biU9PZ3vv/+e9PR0KioqMBgMhEamEBHTn4i4oZitoR1taqel7OhuMrZ/jMkvkL4TZ+Mffv7P3BRNI3fLQkoOrmPyNdNZsvATLJb2WZOvg9HFU3dAKeUBdp+QdJ2I5LSwjFnAchE52oqmtQtKqWRgqYgMPlO6UuoZoE5EnmuFenOAUSJSdq5ltQKndbzKykpWr17NsmXL+OyzzygvL8fiZyMqYQQ9ek/AZNXH/Tgbaykr2E5R3mbqa4sxGIyMGTuOG2+YwWWXXcbgwYMxGjv3tHy3201+fj4HDx5k165dx7d9+/bhcrkACAqJISCkB9EJ/QkITcVk1mfNnQ4RIT9rDTn7vyIgoid9L5mF2T+4o81qN0SEwr0ryd/xFReMHMt3q5cTFBTU0Wa1Nbp46g4opepE5JymeSil1gCPiciW1rHqtHWZRMTdiuUlcx6KpxY+p+OO53A4OHDgAFu3bmXr1q1s2rSJbdu2oWkaZouV8JgBxPcciX9IynkzyLU1ERHqqo5QVXqAsqN7qaspBCAgIJAxY8dy4ehRDBw4kAEDBtCvX792e5E4nU5KSkooKiqiqKiI4uJiioqKyM/P5/Dhwxw+fJicnBzc7v/7yvgHhGELjCEoNJ7QyGSsQYmYO3AZna6GprnJ2vkZxUe2EN5zGCljb8Zg7hYtLz+i9NAmsjfMp0dyb9anrz7fY6bp4qk7cCrxpChXif4AACAASURBVJQaBrwG+AOHgNkiUnmqdOAy4B2gALADDwMPi8j1SqnpwMdACGAA9olIilIqFXgFiAIagHtF5IBSairwe8AClAO3iUixT7TEA8lAmYj89ARbA4FFQBhgBn4vIot84ucrIB0Y77NvuojYlVIjgbm+utOBq1sqns7iHiKAj3zXbwKuAkaKSJlS6g/AbcARoAzYepZ1NPmcTsc999wjhw4dIivrEAUF+RzzQ7PFSmBIAmFRqYTH9MUvIKHDFyftajQ2VFJTkU1DTR4Vpdk01JYgmuf4+YCAQOLj40lMTCA6OpqgoCCCg4MJCgoiMDAQo9GIwWD4wd7lcuFwOH602e12qqurf7BVVVdTU11NbW3tKe3zswZi9Q/HYgsnMDiSgMBIzLYw/PyjMVu69zpz54LLWc/+ze9TXX6Y+CFXkDD0ym7XpX0yVUcPkLX2Xfz9A3nphecZPnwY/v7+BAQE4O/vj7+/P2az+Xx4Trp46g6c1G2XLSIzlFK7gAdF5Ful1LNAsIg8cpr0NfhanpRSJiBTRHoppZ4DLgEeAUzAz0XkVqXUSt9xplJqDPBXEblUKRUGVImIKKXuAQaIyK99omAqMEFE7CfZbwL8RaRGKRUJbAD6AD2BLLytOzuUUp8Ai0Vk3kn38Q+aFk/7gYwTkmOB53zCpqX38CJeQfOsUupaYCleUZQMvAmM8z2jbcDrZ1lHk8/pdPhZg8TqH4E1IAJbQAT+QVH4B8djC4js9EtEdDU0zUNjfTkNtcU0NpTjbKzBYa/G0ViN29mAx+PE42rE43E2u0xlMGIwmDAYzZhMVoxmK0aTFZPJisns2yz+WKxBWCxBmP0CMfsFYfEL0lsP24CGulL2bnwbh72SXmNvJjJlZEeb1GmoLz9Cxuq30FyNaOIBTfvBeaUMGE0WjAYjymBAGQwYDN4fDkoZjx8bDEavyPIJLXVMrxzfHTtQJ5V/7LM66bQ66fzZkzp8tmHtosfbVczoXtwx2EVk2LEPSqkQIFREvvUlvQvMbyr95MJExK2UylJKDQAuBJ4H0gAj8J2vpWi8r8xj2fx8+0Tgv0qpOLytKtknFL24CUGggL8opdIADUgAjkXiyxaRHb7jrUDyKe7jfeDqJp7NoZOezTO+/dncQxpwve8ZfaGUqvSlTwAWHbs3pdSSc6jjdM+pScZc+VRLLtc5BwwGI/5B0fgHRZ/2OhHNK6BEvC2BIohogIAyeMWSwYQ69hLR6RSUF+0jY9vHKKOR/pf/gqDoXh1tUqciICKJQVc/zMFVc7DXlBKbPI7A4Dg0jxOPx4Xm20Q03+ZBNA0R8R770jXRQDTwuoaPk/SK78T/pcoJOzn++cfnz1n3/Ab4+7kW0hJ08XT+8B1eQeICvsHbrWcEHsPbfVd1oig5gZeA50VksVJqIvDMCefqm6jrNrwtOCNFxOUbS3QsKqPjhOs8gA2v2DpX7zjbezhVvU29+Vr7OTXJ2kWPtzSLjo7OCWiaxp/+9CeefvodQmN60jttFga/jh0YrnncOBuqcNZXobmdaJrb2zrpF4DZFoTFP7RDhLdfQBgDrnyQQ9+9R1HOeh54+Ne8+K9/nE8/AtpVOIEunjoFIlKtlKpUSl0sIt8BM4Fvm0r3ZasFThz5uhZ4D3hPREp9431igb2+rqZspdRNIjJfeT1mqIjsxDs2qsBXxp3NNDkEKPEJp0l4u+tOd39VSqlqpdQEEUnHK75ahK+LsKX3sNZX15+UUlfjHaMF3jFXryul/orXB64F5pxlHTo6Ou1MTU0Nd9xxB4sWLSK2z4X0GH09GMztbofb0UBVwT5qSw5TW5pDY03JaVtRjGYrtrB4gqJTCI3vR2Bkz3ZbqNlksdFn0j3kbvqUl1/4J5lZWXy+4GOs1q6/GkFHoIunzsOdwGtKKX/gMHDXGdLf8aXb8Y7d2Yi362yt7/wuvALnmCffBryqlPo93kHeHwM78bagzFdKFeAdu9ScNu8PgCVKqS3ADuBAM/LcBcxVSjUAXzfj+lPR0nv4I/CRUmobXtGZByAim5VSi315c4EtQPVZ1qGjo9OO7N27lxtuuIHMzCxSxt5AROq4H42zaUs0j5vKvF2UHt5MbVEWIhpGi42AmJ6Epg7FEhyOJTAcg9mCMpoQjwt3YwOuukrs5YU0lBVQuHclhXu+wWQNJKLXSKJSR+Mf2vbL6RgMRpLH3IRfYARff7GIocNHs/qbZSQkJLR53ecb+oBxnW6JUipQROp8onQtcJ+IbGtHE3TH09FpASLCnDlzeOSRR8BooU/aHVjDk9utfldjHcUHvqMkawPuxjosQeGEpl5AaK+h+EcntWiih9vRQG3+QSozt1Odtxc0jeD4fsQPuoyg6PYJfFuRt4vD6z7C3z+AJYs+Y+LEiW1eZxuiz7bT0WkPlFIfAgPxjtV6V0T+2s4mdBnHc7vdFBUVUVhYSFFREY2NjcdjE4WEhBAaGkpMTAw9e/bEZNIbs3Van6qqKu677z7mz59PRNIAUsbfijK3T1gHt6OBov3fUnTgOzS3k+CeA4gaeBFBPfq1ysxYl72O8v0bKN29Fre9jsDoFHqMmEpgZI9WsP70NFQVcWjtOzTWVfC3v/+Dx3/9SFcdB6WLJx2dbkKndDxN09izZw+rVq1i27Zt7Nq1m/379+F0nnkav9FoIjEpiREjhnPR+PGMHTuWUaNG4efnd8a8OjpNkZ6ezsyZM8nLO0KPEdcQ1S+tXcJ5iOah+OA6CnZ9jcdpJzTlAmJHTsYW0Tbda5rbSfn+jRRt+wa3vZaIlJEkDbsWi39Im9R3DLfTTva6D6nM38c1U2fw0bx3CA7uchHZdfGko9NN6DSOV1NTw9KlS/n8889ZtWo15eXeAOzWwFCsIbEERSTgHxyFwS8QZQ7AYDIff3l5XA5vrKTGWtz1FTTUlFBTegRHXbm3DJuNiRMnMeO66VxzzTUkJiZ22H3qdC0aGhp48skneeGFFwgIiaT3hNuwhCa1S921JYfJ2fQZ9qpCghL7Ej92Kv6R7TMuyONspHjbN5TsXovBaCJpxDSiUi9s0xYhEY2ju1dSsPtromPiWfz5p4wZM6bN6msDdPGko9NN6FDHs9vtfPbZZ3zyySd8/fXXOBwObIGhBMb0JiKhP9aIZCwBYWcuqAlcjbXUleZSX5JJ+ZG9OOq8IbZGjxnH3XfdyU033XTeLOKr0/qkp6dz1113kZWVRdyACSQNuxaMbb/MisfZSN62xZRmbcQcEEri+OmEpAztkK4sR3UpeWs+oa7wEMFxfek15ib8AtvWZ2pLDnP4+w9x2Wv4w9PP8Icnf9fp14f0oYsnHZ1uQoc43oEDB3jjjTd4+513qKqsxBYUTljSECKTL8AvrGWDXpuLiNBYXUxV/h7Ksrdiry7BaDJx1VXX8NCDv+Tyyy/HYNCjqutAaWkpv/vd73jrrbcIDI0iZdzNWCPaZ2JrTVEWh9d/jLOhiuihlxA7cjJGS8dO4xfRKNu3nqMblqKUInnszUT0GNqmdbodDeRsmk9F7i4GXzCCTz6ax4ABA9q0zlZAF086Ot2EdnM8h8PBwoULef3111mzZg0Go4nwpMHE9b8Ia0Ryuy4HIyI0VBRQmbeNkqwtuB31xCUk8eAvf8Hdd99NdPTpo4DrnJ+43W5ee+01/vCHP1BTW0vcgDTiB09Gmdq+tUlzuziy4wuKD3yHX3AkPSbdQmBcSpvX2xIcNeXkfPM+DSV5RPUdR88R0zGY2i6ulYhQnr2VvK2LELeTJ578PX/4/ROYze0fS6uZ6OJJR6eb0OaOd+jQId544w3mzn2bsrJSbMGRxPYbR1iPkZhsQWcuoI05Fi+n7NBGqouyMBpNXDtlKo88/CATJ07sqrN+dFqAiLBkyRKefPJJ9uzZQ0RiP5IvvB6jf2S71G+vLiZr7XvYq4uIHHQR8WOu7fDWpqbQPG4KN31Jyc412MLi6J02C1tQ2z4nl72WvC0LKc/dSc9evXnzjVe5/PLL27TOs0QXTzo63YQ2cTyXy8WSJUt4/fXXWb58OcpgIDxxMHH9x2OLSu20iw7bq4spO7SR0qzNuJ0N9OiZwkMP3s+sWbOIiIjoaPN02oDVq1fzxBNPsGHDBoLCYkgafi0BcQPbTTSXZ28je+N8DCYzPS/9KcE9On3XFADVefvJXfkBIKRedDuh8f3bvM7KI3s4sm0xjbXlXHHlNbz6youkpqa2eb0tQBdPOjrdhFZ1vOzsbN566y3mzp1LYWEh/kHhRPUeQ0TqaEzWtp3q3JpobhcVeTspy9pATUk2ZrOF62+4gQcf+CXjx4/XW6O6OB6Ph0WLFvHcc8+xfv16AoLDiR8ymZCeIzC00zIlmsdF3pZFlGSuJyC2F8mXz8QSGNoudbcWjppyDi+bS2NlEYnDryVuQNu31GoeF0X713J0zzco0bh95h08+8en6dGj7eNRNQNdPOnodBPO2fGcTieLFy9mzpw5rFixAlCEJQ4gvv94bFF92m3NrLaiobKQisMbKc7ajMfVSO8+/XjowV8yc+ZMQkO71suuu1NZWcm8efN46aWXyMzMJDA0ipj+aYT3Go0ytt84msbacrK+e4+GinyiL5hE/IXXoLrGbLIf4XE5yFv9MVWHdxKePIxeY2/G2A5jxJwN1RTtXUlx5gYMSnHnrLt48onfkpLSoePEdPGko9NNOCvHExG2bdvGhx9+yLx58ygpKSEgOIKIlNFE9b4QYxdqZWouHreDypwdlGZtoLYsD4ufHzNm3MCdd9zO5Zdf3pkHsXZrNE1j7dq1vPnmmyxYsACHw0FIdE8SBl9KQOxAVDvPsKzI2032+o/BoOg58VZCeg1u1/rbAhGhZMcqjm78Elt4PH0uuQvrOYQYaQmO+kqK962iOHMjiMYVV17N/zz+ayZNmtQRLcS6eNLR6Sa0yPEOHDjARx99xEcffURmZiZGo4nQhAHEDxiPNaJ3u7+IOor68nzKD2+kNHs7Hqed4JBQfnLTTdx++21MmDChq8SkOW/xeDykp6fz6aef8tlnn1FQUICf1Z/w5BHE9RuHKSi23W3SNA/527+gaP+3+EclkXzFHfgFn1/j6Kpz95Gzch4Go5k+abMIikput7qdDdWUZa2n+OB6XI119ExO4Z677+L2228nObnd7NDFk45ON+G0jud0OklPT2fp0qUsXbqUzMxMlFKExvUhKmUEwfGDMFj828vWTofmcVN99ADVR3ZSlrfHu+ZYSBjXXH0V06ZN5corr9SDcLYTeXl5fPPNN8e30tJSTGYLIfH9ie41DP/YAe3SnXQMzeOmtuQwNcVZ1BYfpr4iH9HcKGXAZAvEHBCCLTKRoPhUgnsM6LSz61qKvaKIw8vewlVXRfKYm4hKHd2u9WseF+U5O6jI3kx10SEARo4ewy0/uZEpU6bQr1+/tmyR0sWTjk434QeO53Q62bp1K99++y1r164lPT2d2tpajCYTIbF9CE8aRHDCIEzWLrfmVJvjcTuoyt9HXVEG5Uf24XbUowwGBg8ewqWTJpKWlsaECRP0GFKtgN1uZ/v27WzZsoXNmzezYcMGsrKyALAFhBAQk0pM8gVYo/pgNLfvmoaNtWUUZ3xPefZW3I56UAaskbFYwqMx2QJQBhMeRwOu6grsJQVozkaU0URI8iCih04kIKZnu9rbFrgb68le/i51R7OIGXgJPYZN6ZBWaUddBZW52ynL2U5DZSEAST2SmTrlmuP+mJDQqsvd6OLpfEUpJcA8EZnp+2wCCoGNIjLlLMrLAUaJSNlJ6dOAgSLyt3O3un04zb3kALWAx5e0VkQeUkq9AywVkQUtrCcZGC8iHzZxPh54UURubEm5vrwtsmnjxo2yY8cOtm/fzo4dO9i1axd2ux2AoIh4/COTieoxCL/wXu3+EurKiKZRX36EuuIMqosOUVuai+ZxARCfkMiI4cMZPnwYQ4cOZciQISQnJ+sLF5+Ex+OhuLiY3NxcMjIyyMjI4MCBA2RkZHDw4EE8Hq872gLDsIUlEJ7Qj8CYVMyB0R2zjEl9JUd3Laf08BaUUgSlDiKk/3ACk/s12aokotFwNJeajB1U7tuC5rATmNiHxHHTsUXEt/MdtC7i8ZC/7nPK9n5PcEJ/el90OyaLrcPscdRXUnN0P9VH91NVmIXm9i4ynpCYxLixYxk27AKGDh3K0KFD6dGjx9l+h3TxdL6ilKoDMvG+vO1KqauBvwL5rSmeWgvl/QYrEdHaovyT6sqhafF0qvR3ODvxNBF47FTPWyllEhF3yyw/e5t8YhqL1R//sAT8w+MJi+2NX1gPTNbAszVD5yQ0j5v6inzs5bk0VORTW16AvaYEfP/3lFLExMaRmpJC796pJCUlER0dfXyLiooiIiKCoKAg/P39u9QyMh6PB7vdjt1up6GhgYaGBiorK6moqKCiouIHx0VFReTn55OfX0Bh4dHjAgnAYDThHxyJOTCKoPA4gqN7Yg6Ow2zr2MkJonkozkgnf+cyRDTCh44jcvQkzEEtm4npcTZSuXMDpZu+weOwEzn4IuIvvLbL/2gp27eOI+mfYQ2KpO8ls7EGR3W0SWiah4bKo9jLc6krzf7BIuIAVquNHj170js1hZSUFHr16kV8fPxxX4yOjiYiIgKTyXRy0bp4Ol/xiacXgW0iskAp9R6wF7hYRKYopS4E/g3YADtwl4hkKKWMwN+BK/F29cwRkZd8wuJdYCpgBm4SkQNKqVl4BccDvhd6DTAKiAV+c+zlrpR6HPgJ4AcsFJGnfS0zXwGrgXHA50CoiDzqy3MvMEBEfnXSvb0KjPbZvkBEnvalN2VjBPAREAVsAq4CRp6NeFJKjQSeBwKBMmCWiBQqpXoDr/nq8AA3AR8AA4Bsn12VwLWAFQgAZvvKHXya5/6U735swDrgZyIiLRVPfS65SwLCE7AEhOmxi9oZze3CXl2EvboYZ30FjbUVOOrKcdSV47TXHBdWP0ZhsvhhtvhhttgwWfwwGIwYjUYMRhMGg29vNPqOjaiT/6c3428tmoaIhqZ5EE1DEw3xHEvTEM1z/Pj4NZoHj9uF2+XE7XLicTvRPM35LaAwWayYrUGY/UOw+Idg8Q/FEuDdW4Oi8AsM73RhLxpryziUPo/68iME9hpA/KXXYwk9t0Hgbns9Jd8vo2Ln9/iFRtPzstsIiEpqJYs7htqCLLJXvAOa0PviOwiJ69vRJv0Ij6uRhqoi7FWFOGpLT/DHCjyuxlPkUFis/t7Nzx+L1UaPi+81bHz/V+0qZn4k33TalI+Bp5RSS4GhwFzgYt+5A0CaiLiVUpcDfwFuAO4DegHDfedOHAVbJiIjlFL3A48B95yizjhgAtAfWAwsUEpNBvoAF+JV7IuVUmlAHtAPr3C7XykVAOxSSv1GRFzAXcDPTlHHkyJS4RMcK5VSQ0Vk12lsfBpIF5FnlVLX+u6xKVYrpY79DH5XRP517IRSygy8BEwXkVKl1M3An/GKoA+Av4nIQqWUFTAAv+WElief0BwHDPXZn3xCvU0995dF5Flf/veBKcCS09h/SsJ7DGlpFp1WwmAyExCRREDEj1+Momm4nQ24G+twNdbhctThcTTgcTvwuBxobicelwOP23esaThdbsThRMTjFTY+QSOa54dlN3OCpVLKGwleGVDK4B2zogy+dCPKoHyfzSiDHxgVymDEYjBhNVkwGM0YTGbv/sRjkwWjxYbJ4o/Jzx+TxR+j2drlZmqW52wne+N8lMFA0jW3E9x/eKv8ADHZAoi//AaC+w4l/6sPObjwBRIvmkHUoItaweqOISihN/2uf5TDX71Fxqo59Bg1nZi+F3WqH2xGs5WgqOQfzRAUETxOO67GWlyNdT6frMXVWI/bUY/H1YjH1Ui9vRHgn8CvTlF8m6GLp3ZERHb5XtC3Al+edDoEeFcp1QdvS8ex4DWXA68d61ISkYoT8nzm228Frm+i2s99XW/7lFIxvrTJvm2773MgXjGVB+SKyAZfXfVKqVXAFKXUfsAsIrtPUcdPlFL34f0+xQEDgWPi6VQ2ph07FpEvlFKVTdgOMOk0XZP9gMHACt8/AyNQqJQKAhJEZKGvjkagqX8YK056psdo6rlPUkr9BvAHwvG2HrZYPP3pl9dSVlnX0mw6nRS3puHxaLjdGm5NQ9METdPwaIKIIOIVT001aikFCuXdK+/eoBRKKYwGA8oARmXAYFAYjb69wdD+fRUdiObx8NHbL7EpfR6BCb1IunYmxhZ20TWHwB596H3HYxR89RH5332KvaKQpPEzumwwTb/gCPrOeIi8VR+Qt3khyaEa9zzwW0znUXy0f3/47bz2rlMXT+3PYuA5YCJwYjvz/wNWi8gMn8Ba40tXND2t3eHbe2j6b+k44VidsP+riLx+4oW+eutPyv8m8ATelrG3Ty5cKdULb4vSaBGp9HVfnThKsykbW6OJVQF7RWTcSTa1ZErayfd7Ytk/sNHXgvUfvF2JR5RSz/DDe202V4ztdzbZdHS6JfX19dx22218sWgRUSMuJjptWpuKGZMtgB7XzaY4/QvKNq/GUVNGyuS7uuw4KKPFSvLkuyja/BVrVyzCXlvKl0sWERnZPgswtzW3Xj1yW3vX2bXaa88P5gLPnqIFJwQo8B3POiF9OfBz3+w8Tuq2O1u+BmYrpQJ9ZSYopU45j1tENgJJwE/xjlM6mWC8AqTa17J1dTPqXwvc5qv7auBsQ+JmAFFKqXG+ssxKqUEiUgPkK6Wu86X7KaX88c7cC2pm2ad67seEUpnv2bV4Vp6Ojk7LKCkpIS0tjcVLlpB0+Q3ETGqfViBlMBCbNpWEK2+hLj+LrKWv4mps6rdW50cZDMSNuZael97Gls2bGHzBMHbvPlVHgk5z0MVTOyMi+SLywilO/S/wV6XU93i7n47xJt7utF1KqZ14Rcy52rAc+BBYr5TaDSzg9KLiE+B7EflR95qI7MTb/bcXrzD8vhkm/BFIU0ptw9t9mHeaa1crpXb4tvdOqtuJV8D83fdsdgDjfadnAg8ppXbhHdgdi7cr0a2U2qmUevQMNv7ouYtIFTAH2I13MP3mZtyrjo7OWZKfn09aWhq79uwl9fp7Cbmg/ccfhQ2+kB5T78ReVkDm4ldw1te0uw2tSXjfkfSZ9ksqqmsZfeEYFi5c2NEmdUn02XY6Z8Q3wP1fIrKyo205j+j0jiciHD58mIyMDHJycsjNzaW6upq6ujoaGxvx8/PDZrMRFhZGYmIiSUlJDBw4kD59+ujLpOicM4cPH+ayyy7jaFExvW64D3NsxwaxrMvLJO/ztzAHhtF72v1YbM1txO6cOOuqyFn+DvWlR/jDU8/wx6f/0KkGkrcQPVSBTudBKRWKN5TAThG5qaPtOc/odI7n8XjYtGkTy5YtY/369WzevIWqqv9rbDQYTZj8bBjMfiijCc3jRtwu3I4GNLfr+HVWmz+Dhwxh0iVpXHHFFUyYMAGbreOC9Ol0PQ4cOMBll11GeXUNydffizm6c4QMqM8/RM6nb+AXEknvqfdjtgZ0tEnnhOZ2cuTb/1KRuZ2rp83gkw/eIzCwS8aZ08WTjk43oVM4XmNjI19++SXz589n2ddfU1VZiVIGAqLisUUmERKXjCk4ClNgOCb/QO8U+pMQETyN9TjrKmmsKMJZWUhdcR51xbmI5sFi8SNt4kRm3vZTpk2bRmho68+Q0jl/yM7OZsKECVTU1pE04178olp1GY9zpi73ILkL38QvPJbeU36B2a9r/zAQEYq3r6Rw01fExCey6LP5jBkzpqPNaim6eNLR6SZ0mONpmsbq1av54IMPWPDpp9TW1GANCCYwqT8RvQZhiU3F5Hfuiw57XA7qCg9jP5pJ+aFdOGsrMJnMXHr5Fdz/8/u45pprMJ9H06V1zp2CggImTJhAQXEJSTPuwz+uR0ebdEpqs/eTt2gu1sgE+kz5RZedhXcitUezyFv1Ea6Gan73xB949pk/dKXud1086eh0E9rd8SorK3n33Xf5z3/+Q2ZmJmY/GyG9hhDdfxSW6F5tGkVaRGgoyaMmeyflB7fhaqghLCKSu++ezc/uvZfevXu3Wd06XYOSkhJGjhrF0cIiet5wHwGJqR1t0mmpydxN3pJ3COrRj9TJd3fZOFAn4nY0UPDdp1RkbWfI8FF8+t8P6dOnT0eb1Rx08aSj001oN8fbsWMHr7zyCvM++IBGu53guF7EDr0YW9JADCZLe5lxHNE81OTtpzJjE5U5e0GE8RPSePThB5k+fbreGtUNWbZsGTfddBP1DXZ6zLiboOT+HW1Ss6jYtZ6jK+YT1m8UPSfe2pUHXB9HRKjM3Ep++kLQ3Dzx5O/5/RO/xWJp//8VLUAXTzo63YQ2dTyn08mCBQt45ZVXWLduHSazhbA+I4gefBGW8M4zhsRZV0Xlwc2U7d+As7aS8Igofv6z+/j5z39GUlLnGCSs03Zs3bqV3/3ud6xYsQKUgZ7TZxOUOrCjzWoRJeuXU7JuGVHDJ5E4ZmpHm9NquOprOLr+cyqydpCc2pcP3nub8ePHnzljx6CLJx2dbkKbON6RI0d4/fXXmTNnDiUlJfiHRRE9eAJBvUe2yjimtkI0jZoj+6ncv57KnP0og+LKK6/ioQcfYPLkyV1p7IXOGRARvv76a/7xj3+watUqDAYjmmgkTbmDkL4XdLR5LUZEKFz5GRU7vyd+/DRihk7saJNaleqcveSnf4qzroppM27gxX/9k549OzZsxCnQxZOOTjeh1RxP0zS++eYbXn31VRYvXoyIEJo8iNghF+MXl3rKGXKdGUdNBVUZGynZtx63vY6EpB48cP8vmD17NtHRpwyEr9MFqKur47///S///ve/2bNnD7bgMDD6Ya8sIuGqnxI2aFRHm3jWiKZx5Iv3qTm4kx6X/ZSIPl33Xk6Fx9lIyc7VFO9Yg9EADzz4EE/9/knCws52cYhWRxdPEvQ78AAAIABJREFUOjrdhHN2vIqKCt5++21ee+01srKysAYEE9ZvNNGDLsIQ0PXDAWgeNzU5eyjft46agixMJjPX33A9v7z/fi6++OLzYnzJ+Y6IsGXLFubMmcNHH31EXV0dQdGJRF+QRvnhvVQd2kncpTcQMbz9I4e3NprbTe6nr1N/NJuUq+8hJKlrjNtqCc66Soo3L6MsYzNWmz8PPPAAv3n8MaKiojraNF086eh0E87K8TweD6tWreK9995jwYIFNDY2EpqQSvTgCdh6DMJgPD/X+m6sLKYqYyOl+zfidtjp268/D/zyfmbOnKnHjeqE7Nu3j/nz5zN//nz27t2LyeJHWOowYgaPxxiWQP7a+ZQf2EjMxVOIuvDSjja31fA47GT/9xWcVWX0nno/AdGdM9TCuWIvP0rpjpWUZ+7A4ufH7NmzeeThh+jXr8MWPNfFk45ON6HZjici7N27l/fff5958+Zx9OhR/GwBhKQOI2bIBEwhMW1pZ6dCczmpyd5Jyd511Bfn4me1ccsttzDrzjuYMGECJtP5KR47Oy6Xi40bN/L111/z2WefsW/fPpRSBCf0JqLPCIJ7XYCyWBERCtYtonT3WqLGXEHMhOasI961cNXVcPijF9FcDvpOfwhraIe3yrQZjZXFlO5YRXnmNkTzMCHtEh59+CGmTJnS3rPzdPGko9NNOK3jaZrGxo0b+fzzz1m4cCGZmZkYjEZCew4gqv+FWOP7YTB17yn9DaVHvK1RB7aguZ2EhIUx47rruOnGG7nsssvw8+v6gQs7Kx6Ph3379pGens7y5ctZtWoVNTU1KGUgOD6F8D7DCOo5GKMt+Af5jm76iuJtK4gYfjGxk647b7teHRUlHP74JQxmP/pe9xAW/+AzZ+rCuBpqqczYSOnedTjrqggMDuGmG29k5u23kZaW1h4TPnTxpKPTTfiR4+Xl5bFy5UpWrVrFN998Q1FREQajkeDEvoSnDCEweQhGv669llZb4HE5qD1ygLrcvVQc3o3H5cDPamPCxRO4+sorufzyyxkyZAgGQ9caON9Z0DSN3Nxc9uzZw5YtW1i/fj0bN26kpqYGAP+QCAIS+hLRayCW6F4Ym5jVWbR9JYUbvyBs8BjiJ//kvBVOx2goyiPnk/9gCYmk79RfYuziy7g0B9E81BzJoDZ7J+WHdqK5nASFhHLV5MlMmXItV111VVtN+tDFk07HoJQSYJ6IzPR9NgGFwEYRmaKUmgYMFJG/tbEda4DHRGTLKdLjgEagDpgtIhlnWcczQJ2IPHcWeR8B3hCRhrOp+xgNDQ2yfft2Nm/ezJYtW9iwYQOHDh0CwBoYjH9cKpGpQ7HG98VoOf//6bYWmsdNbf5B7EcPUpl3gMbKEgCCQ0IZPXo048eN5cILL2TkyJHExsae9y/wllBdXU12dvbxbf/+/ezZs4c9e/ZQV1cHgFIGAqMSsEb3ICwhFXNEIuagiDM+x9I935GfvpCQ/iNIvOqnKGP3ELK1OQfIXfgmAXG96H3Nz87bMYmnQnM5qc7bR0N+BpW5+3A11AKQ0rsPl1w8gYsuuogxY8bQr1+/1giMq4snnY5BKVUHZALjRcSulLoa+CuQLyJTWrEehfd7pzVxfg1Ni6fHRGSLUuo+YIqITDvpGqOIeJphwzOcvXjKAUaJSFlL856IyWQSj8drqi04DGtkIqFJfQmI640pJFp/qbcSzroq6o9mYS/OpqYoF3tFIfj+5wUFh9C/Xz8GDx5E//79SU5OJjExkaSkJOLi4rr8+CkRwW63U11dTXV1NSUlJRQXF/9oKygo4PDhw1RWVv4gv8U/EGt4HLbwOIKi4rGExmIKjWnxOm7lBzaSt+a/BPceQtKUO86LZUxaQtW+LeR/9SEhqRfQ67KZqG7YAiqiYS87SsPRg9QV5VBbmI27sR4Ak8lMap8+DBs6lEGDBpKSkkLPnj1JTk4mLi6uuV1+unjS6Rh84ulFYJuILFBKvQfsBS72tTzNwisaHlBKvQPUAKOAWOA3IrLAV87jwE8AP2ChiDytlEoGvgJWA+OA64DfAqMBG7BARJ725V/DmcVTf+AzERnos/t54Erg18CFwGxftjdF5N++/E8CdwBHgFJgq4g8d1K5kcAWEUlWShmBv/vKFWAOXgd9DsgAyoDLgbd8z0GAuSLyr+Y874TRV0pwbDLmsHhMAef3eIjOhMflwF5WgLOiEGd1CXXlhTRWluBqqPnBdQaDgYjIKCIjI4iMiCAiIoKwsDDCw8MJDAzEZrNhs9mwWq0/ODaZTBgMBgwGA0qp48cnpnk8nuOb2+3+weeT09xuN42Njcc3u93e5Ofa2lqqqquprqqiurqa2tpa3G73KZ+DUgqLfxAm/yCM1iCsIRH4h0ZiDYlA2UIxBYZh9PM/ZxFfmbWdnG/mEdizLz2m343B3LUF6dlStmUNRd8uJmLIBJLGz+j2P45EBEd1KfbSfNzVxdSXHaW+vBBnbcUPrjOZzMTExhIdHUVMdDRRUVHHt5CQEIKDgwkODmbq1Knt/kC75zdZpyk+Bp5SSi0FhgJzgYubuDYOmAD0BxYDC5RSk4E+eAWMAhYrpdKAPKAfcJeI3A9eMSMiFT6RslIpNVREdjXTzqnAbt9xALBHRJ5SSo0E7gLG+OrfqJT6FjAAtwDD8X7ntwFbz1DHfUAvYLiIuJVS4T57fwVMEpEyX30JIjLYd0/NnjMfM+qq5l6q04oYzX4ExqVAXMoP0t0OO666Spz11bjrqnDWV+Gsr+ZoQwNHKo/i3puFx2HH42hAczs7yHovymjGYDJjMJpQRhMGk9m7N/thtFgxWsIxxicQYbF6P/vZMJr9MFoDMfsHYbIFYbIGtHkLSMXBreSu/hD/xBR6TLur2wongMhRE3HV1VC+dQ1mWxBxI67oaJM6FKUU1tBorKHe8U/H5iNqLifOukrvVluBs7aChvoaskrrOHBkDx57Pe7G+h/54PCfP3/ZtlcfXdme99B9v806P0JEdvlaiW4FvjzD5Z/7ut72KaWOzZWf7Nu2+z4H4hVTeUCuiGw4If9PfN1vJrxCbCBwJvH0gVLKDuQAD/rSPMCnvuMJeFu76gGUUp/hFX8GX3qDL33xGeoBb6vSayLiBhCRilNccxhIUUq9BHwBLG9GuQBYLSacLg/d/Adop8Fo88fP5g9RP173TwDR5PgIfxENcbvRPC40twvx7TW3CxBExNs1KIJwwrGItzTlbYFSBiMohVIGbxR4g/cYZUD5WqlQRgwmEwajGWUyowzGJlstlAJDJ/lClR3YRO6qjwlISqXndXdj6NyLyrYLsZdMwWOvo2jTVxiNRuKGX9bRJnU6jH5+mP1iCYiI/dE5EdB8PWWay4nH1YjH6d3w9mjo4kmnQ1mMt2tqIhBxmuscJxyrE/Z/FZHXT7zQJ8jqT/jcC3gMGC0ilb5uQGszbLvt5O48oPGEcU6ne3M01T/txiuuOMkGdZo83gK9tl+At2vvl3i7K2efLs8x1r3w4Jkv0tHpgrz55pvc9+rHhKX0J3HaLMTYvUNqHEMpAwlX3ox4PBSsX8qsq8byp6ee7Gizzhf+1N4V6uJJ52TmAtUislspNbGFeb8G/p9S6gMRqVNKJQCuU1wXjFdMVftara4G1pyDzcdYC7yjlPobXvEzA5jpOz6WbsLb7XdM4OUAI4FNwI0nlLUc+LlSas2J3XZALRAElPnGSDlF5FOl1CHgnVa4h05FbW0t69evZ/v27ezevZuCggKKiotxuVwYjEYiIyJITEhk4MABjBw5krFjx3aGpRp0OogXX3yRhx9+mLDeg0iYcifSjWaXNQdlMJJ4zU8R0fjz07/HbDHz9G9/09Fm6ZwF+jdb5weISD7wwlnmXa6UGgCs93Ut1AG34+1aO/G6nUqp7XgHpB8Gvj8no/+v3G2+VqxNvqQ3RWQ7gFLqv8AOIBf47oRszwGfKKVmAqtOSH8T6AvsUkq58A4Yfxl4A/hKKVUIPAK8rf5v5d3ftcZ9dDTl5eV89NFHfP7556xduxaXy6t/rSHhGANDMQUEYjDbQPNQeKSErfsOMn/+fEBQSjF0+Ahuun4Gt99+e2dcfV2nDRARnnjiCf72t78R3u8C4q++HbrZrLrmogxGkq65nSOah2d+9z9oHg9/fPK8+NfRrdBn2+nodAydzvHS09N5+eWXWbhwIU6nk4CoOAJTBhLSqz+G8FhMtqYDdHqcDhpLCmgsOERN1l7qi/JQSjFh4iR+9dCDTJs2TQ9SeZ7icrm45557eO+994gafhHRE2d0y+n4LUXzuMn/4n1qMnfzwK8e58Xn/t7tZ+GdA3qoAh2dbkKncDwRYdmyZfzlL38hPT0dv4BAgvuPIGLIWEynGLTZXJzVFVTv3UTFno24aqtJ6pXCs0/9gdtuu601AuLpdBKqq6u55ZZbWLZsGfETribswst1AdACRPNwdPknVO7dzE9n3c37b72h/8g4O3TxpKPTTehwx1u9ejWPP/44W7duxRYaTtToSwkcMAqDufVmRonmoebgLso2r8RecpSYhET++fe/ceutt+oviS7OwYMHmTZtGplZWSRNvomggRd2tEldEhGNom+XUL71W66YMp0lC/6rr8vYcnTxpKPTTegwxzt48CCPP/44ixcvxhYaQcxFV+Hf54LTLh0hIriqK2g4mo2zuhxPYwPKZMEcEIwtNglrTOIZ89ce3kfZ+q9pKM6n78DBvPrSC1x66aVtcYs6bcyyZcu45ZZbcGpCz6mzMMUld7RJXRoRoWzTSorTv6Tf0GGsXfF1W60Bd76iiycdnW5CuzteRUUFzz77LK+88grKZCZ6zOWEXHDRaVuaPE4Hlbs3ULlnE46ywuPpBosfmssFvlV2DH42QvoNI2L4xVgjm+7uE9Go2r+N0u+/wllTycWTLuO1l19k4MCBrXejOm2Gy+Xiqaee4u9//ztBsYn0mD4bAkI62qzzhuqDOyn46kOCw8JZvfxrhg27oKNN6iro4klHp5vQbo7ndDp59dVXeeaPf6S6upqIIWOJGn8VRv/Apo3TNCp2pFOyYQUeez3W+B4EDxmBrWcqftGxKKMREcFTV4P9SA61B3ZTt3834nYT3H8YcWlTMQc1HXBdc7so3/YdZZtWorkc3HHXbP73L3/Wf213YnJycrj11lvZsGEDUcPGE3PJdDDp49daG3vxEfI+n4s4G3np5Zf5+b33dLRJXQFdPOnodBPa3PFEhCVLlvDYY4+RmZlJSK/+JEyajiEs5rT5GsuLKPj6Y+yFefgn9yHy0quxJSWfsT6PvZ6K79dQuXEtymAgJm0q4UPHnXYAsbuhjrINKyjb8T1Wm40nn3ySx371KFZrc2Km6rQHmqYxZ84cfvOb3+BwuUmY/BP8ew/taLPOa1x1NRR89QF1eZlMu+EmPnhnLoGBTf/Y0dHFk45Od6FNHW/r1q089thjrFmzhoCoOOInTseS1OeMM6Gq9m+lYPknGMwWoq+eQdDg4S2ePeWsLKd4ySc0ZGcS1GcIiVfegtHPdto8jvJiStK/oDprDzHxCfz7n89x88036zO3OpiDBw9y33338e233xLaqx+Jk2+GwGYv4ahzDoimUbpxBSXrlxOTkMQnH8wjLa2ppUa7Pbp40tHpJrSJ4x05coQnn3yS999/H2tgMNHjJhM0aAzqDAELRfNQtHYp5Vu/xdYjhfgb78AUFHzWdogIlRvWUrpiCebQCHpedzfW8DN3ydXlHqR47RLsJQVcMGIkr778EuPGjTtrO3TOjqqqKv7yl7/wwgsvoExmYi+ZRuCAUbqY7QDqj2RR8PXHOKsrmHX3vbz4r38SFBTU0WZ1NnTxpKPTTWhVx6uoqOC5557jX//6F26Ph8iRlxB54aVgPnP3l+Z2k/+lN1hf6OgJRF85/Yxiq7k05B7m6CfvgAg9ZtxDQNyZI46LplG1dzPF33+Fu76GaTOu54Xn/0lycnKr2KTTNA6Hgzlz5vDMM89QUVFB+ODRxF08BWx6l1FHorkclHz/FWVbvyMsKorn//G/3DFzph7u4//QxZOOTjehVRyvvLyc559/npdeeom6ujrCBowkPu3aZs+A0lwOche9TX3uQaImTyd83CWtYdYPcFaUkj/vDdy1NSRNvZPglObNrPM4HVRsWUPJ5lUYgDvunMVTv39CF1FtQH19Pa+//jr//Oc/OXr0KCHJ/UiYNA1DeFxHm6ZzAg1Hcyha/TkNRXn0GzSYV196kUmTJnW0WZ0BXTzp6HQTzsnxcnNzeeWVV3j11Vepr68nrP9w4sZPRoU2f7aax9lI7qdv0FCYS+zUmwkZ3nZBDt11teR/OAdnSSFJ02YRnDKo2XldtVWUbVxBxe5NKIQbb76Fp3//pB7eoBXIzMzkjTfe4O2336a8vJzQ5L7EjL0CU3yK3kXXSRHRqD6wnZL0L3HWVDJ81Gieffoprr322u78N9PFk45ON6HFjicirF27lpdeeomFCxcCENpvWItFE3i76nIXzqH+yCHib5hJ0KC2jyfjsTeQP+91HMVHWyygwCuiKrd9S+mOdYjbxbgJF/PoQw8yffp0LJbWi4p+vlNRUcHnn3/Ohx9+yMqVKzEYDIT0GULMhZdiik7qaPN0monmclK5eyPlW9fgrKmkV5++PPrgA9x+++2EhYV1tHntjS6edHS6Cc12vIyMDObNm8e8efPIycnBLyCQ0MFjiBo+4awCFIrm4cjS96jJ3E3s9FsJGTa6xWWcLT8UUHc1uwvvRNwNdVTt3kDFrg04ayoIi4hk5u23cesttzBmzJju/Ov7lIgIhw8fZsWKFSxevJgVK1bgdrvxD48idNBowgePAX99AHJXRTweqjO2U7H9OxqKjmC2WJh+3Qxuu/UWJk+ejL+/f0eb2B50H/GklBJgnojM9H02AYXARhGZopSaBgwUkb+1Un3vAEtFZIFSag3wmIhsaY2y2wql1DPA00AfEcnypT0KPA+Mbm37lVIPAb8AtonIbS3M+wjwhog0tKZNJ5RfJyKnHLWqlJoBfAYMEJEDTVwTCvxURP7j+xwPvCgiN56mzjW03fekScdzuVysW7eOL7/8ki+++IK9e/eiDAZCkvsSPmg01l6Dznr9ORGh4Ov/UrV3E9FXXkfY2LSzvoGzxWNv4Mj7r+EsKaTHdfcQlNzvrMoRTaMu5wA1ezdRdWgf4nETG5/ATTfewJWTJ5OWltYtZyW53W7279/P5s2bWb9+Pd988w05OTkA+IdFEthnKBEDRmCIiDut0NTcblzV5bgaanHX1+Kx1yEeD6J5QASD2Q+DnxWjnw1zUCiWkAiM1tOHpNBpW+zF+dTs20zFvq14Ghuw+Fm5YvIVTJ86lUsuuYQ+fc4crqSL0q3EUx2QCYwXEbtS6mrgr0C+iExpg/reoWuKp+uBT0TkT76074FQ4M42EE8HgKtFJPss8uYAo0SkrAV5TCLibua1pxNPnwBxwEoReeYU541AEt6//+AW2LeGNhZPIkJhYSHbt29n/fr1rFu3jk2bNlFfX4/BaCQoKZWQ1EEE9r0Ag//Zhw44VlfRt4sp3/otEWmTiZx0VavcyNngsddz5N1XcZaX0vP6ewlM6n1u5Tns1B7aS13mTqpzDiJuF0ajiRGjRpE24SJGjRrFqFGjSE1NPW9eHi6Xi+zsbDIyMjh48CAHDx5k7969bN++nYYG728Ys80f/8RUwlIGYE3qjTE44pT3r7mcNBTm0lCQTWNJAY3lxTiryo4vv9NcDFYb1sh4bDGJ2GIS8Y/vhSUkvFXut60REZyVpcfv391Qi+Z0oAwGDBYr5qBQrFFx2GKSMJ0mOn9nQDwe6vMP0ZC9l8qMXbjqqgGIiIrmkrQ0Ro0cwbBhwxg2bBixsbHng090O/H0It5WjgVKqfeAvcDFvpanWXhfxg8opW7C2wLjAapFJM33Qvw7cCXeF9EcEXlJKTUSb8tMIFAGzBKRwqbEk1LqVWA0YAMWiMjTPvtygHeBqYAZuElEDiilAoCXgCGACXhGRBYppazAq8AowA38SkRWn3gfvnKXAs8B3wFv+a4XYK6I/OukZ/QMYMAraEYrpVKAlwH/c7D/GaBORJ7zXbcHmAL8FpgNZABzge+Bf/vKtQN3iUjGqZ473i/uc768ZSIy6USxo5S6EZgiIrN8f4cKYDiwDfgP8AoQBTQA9/rs7AV86HvGy4BHTyWelFKBvnonAYtFpL8vfaLvO1MIDAN2AdN9167w1blURAaf5rt04vdkMvBHwA845HsedUqpvwHTfH/z5SLy2Mk2norZs2fLvn372H/gADXV3n9symAgMDYRv9iehCX3xRSfitGv9SJtl2z8hpL0/8/eecdHVaX//32mJJPeO4TQAoQiINJEQBAFsWFDVIpiA/v+dNUt3y2ua91111VBsCAiiIooKCC9ShUQpIoQWkjvmWTafX5/3AnGGJIAIYXc9+s1r3vn3HvPec6dOXM/85znnLNIn45gxKgG/8F0lxRz/MO3cOXnkXTLgwQktK6TfDW3C3taKo4Thyg8+hP2jBOIR9fofv4BtG3blk4dO9CuXTvatGlDbGwsMTExxMbGEh0d3WAr2rvdbgoKCsjLyyM/P/9X26ysLNLS0jh58iRpaWmcOHGCjIwMNO0XceMTEIRPWBT+sS0JTkjCEhGPOTQCpX47nF1EKMs8SdHhPRQd2U9pxnHQNEBhDY/ENzoW36hYrBFRWIJCsAQFYfYPQJkt+jQWSqE5HWhlZXhK7bgL8nDl5eLMy8Zx6iSOjLTT99waGkFgYnsCE5MJbNWhUXmnRITS9GPk79lK0eF9uIry9ANKYQ4IQPn6giZopXa0sjLvVQpbXEuC23YhrEtvrAHn96fmQlMuCktPHqb0xM8UnTyCsyD39PGg4BDatGlDcnu9PSQlJRETE0N0dPTpV3BwcIP/XtRAvRt35mXQ64dPgP/zCopu6A/tqqZQ/T/gGhE56e1+AXgAaA30EBG3UipcKWVFFzY3ikiWUmo08AK6KDgTfxSRXO8DdIVSqpuI7PIeyxaRnkqpycBTwH3AH4GVInKv15YtSqnlwEMAItJVKdURWKqUSq6m3O5AQrknpEK9KlMIHFdKdUF/+M8F7jkP+6tERB5SSg0HrhSRbKVUMDDQe2+vAv4J3EIV991b/u/Kr62mzuUkA1eJiEcptQJ4SER+Ukr1QRdTQ4D/AlNEZKZS6uFq8roJWCIiB5VSuUqpniKy3XusN9BFRI4opZK8+90BvO/L+U2dKhaglIoE/uS1uUQp9QzwO6XUm8AooKOISDWf4W+Y9ek8fMKj8U3qQnxEDL6RsfjFtsRkvTAP7pydG8hcv4igrj2JHnFTo/ghtAQE0nLsJI7NeJOj86eTdOsk/GPPP2DZZLF6H9btieg/AvF4KMtJpzTjOI7sUxzNy+bg8tU4583zCoZfY7b6YPG1YfW1YbX5YbX5YfHxxWQ2614Ik9m7bz6dJpqGiIZoom9FEE0D777m8eBxu/A4nXhcTtwul3erv/e4XGhuV7X1Mtv8sQaGYAkMxhrekshWXfANi8InNBJrWBQWv4BqrxfRsJ84TMGBnRT+vBd3cT6gsCW0JLzflfgltsavZRJmv9rFyJgsVij3wCQk/rosjwdHVjqlRw9jP/ITBQd2krdrE5hMBCS2J6RdV4LadsEa2DDCQzQP+ft3kL11FY7sUyirD/7JHQhJHootsRXW6ChM1l+v2+ex23Gmn6L058PY9+8lc/0iMr9bQnByN6L7XoMtovpljxoKpRS+4dH4hkcT2rUvcYCnrJSy7DTKMk/izMvi5/wc9i1fjavgC71btnIeZrPeFnxtv7QN777F6oPJbNHbgtl8et9Uvm/S2whK6QpHqV/tK5RX+ij9d6nivtd+Tp9TNZvmvle3N60WNKh4EpFd3ofYGGBRNaduAGZ4u2e+8KZdBUwt7/bxPsC7AF2AZd4bb0b3PFTH7UqpB9DvRRyQgu6loEJZ36N3nwFcDdyglCr3MNiARGAAunDD6zk5ii4SzsRhoI1S6n/AN8DSas79BLgD3TMylF+Lp7O1v7aEAB8qpdqje2PKf0l+c9/PMl+Az7zCKRDoD3xW4WFerh4uRxdrAB+he4aqYgy6hwz0+zQG3aMFsKWWXZA11akv+n3d4LXTB9iILmzLgHeVUt8AX9eiLAA6PPRXFNSLiMnfv51TK74goH0KcTeOqdIT0VBYgoJpOW4Sx2e8Req8qbS5fTL+0S3quBALATEtCIj5db4ejxtXcQHuEj2mx10e2+MoQ3M50JwO3E4HTmcZWokdEQ00jy6UvC+8okn/0fc+ILz7SikwVXhvtmKyWlEWGyZbEGaLFavFgrJYMVmsmCw+mGx+mH39MNv8vdtf3pusPuf0nSnLOkXevm3k79uOqygfZfUhoG0HApOHE9C+E5bAuo8LU2YzttgEbLEJhPW5AtE8lJ08TvH+Hynav5u05Z/D8nn4x7citEN3gpMvwaeahaTrChGh4MBO0jcsxpmXhU9sHFGjbiWwew9MftV7ec3+/vi1aYtfm7aEDxuGMzOTws2b9NeBHwhJ6Un8gOuqXRC7sWDy88fash1Bv+ouFzSPhqukELe9GHdpMW57MR67vtVcDjSXE81ZRpnTib2oGE9ODuJxn46FE82jtxGP9sv7eujd6tqyy627X3vy8wteUAUa2vMEsAC9y2cwEFHVCV6vSB9gJLBTKdUdXYdW/lQUsEdEarWeg7dr6Cn04Os8b5dSxRbk8G49/HKvFHCLiByolNeZftHc6F1v5di8dcpTSl2CLogeBm7nzB6yhcCrwDYRKaygyM/F/irtqYLngVUiMsorcFeXV5XajRSreE7lMkq8WxOQX+4NqiGP36CUikD3UnVR+gAEMyBKqd9XKqcmaqqTApaJyJgqbOiNLmjvAB7x2lMj70+6jZyi2pp37mzHWoJvAAAgAElEQVRZt4a/vz6HwKS2xN02rs5mDq9LrCFhtBg3iRMz3uL4/On894OPadW2fUObdRoRcGseHC4PLo8Hl0fD49HwiIamyW++OCal0HWTwmwyYTGZsJhNWM1mrBYTFpOZC62Z7SXFrFr0NYvmzeXwgX16l3C7jsQOvwFbu06YfOq3a1KZzPi1TMKvZRKRV43EmZVByf7dFO39gbRVX5K26kvad7mEK4dfy4CrriEqJrbObThx9Ahvv/g8xzZ/h198Agk33otvx066V+Qc8ImOJvL6GwgbMoSCNavJX78e+897Gffw44waMxZzI2xrdYnLo1HmcuFwuXG6PTjdettwuT24NQ2PprcTl9uNx6OhiYbH40EEPF4vrd5+vB5b9EEgWrnYEt2Li+ii90w/0BazibWHM3bWV71Pl1vfBVbB++hxTLu9cSq/QSnVVkQ2A5uVUtejB/8uBR5SSq2u0NVyAIhSSvUTkY3ebrxkEdlzhrKD0R+wBUqpGGAEv4iEM/Et8KhS6lFvV00PEdkBrAXuAlZ6u+sSvfYEA5OV/nc/Ab0rqbwryCki85RSPwMzzlSgN6D+GeBgHdifih7jhFKqJ3p3VVWEACe9+xMqpP/mvns9NUVAEHqcGUCGUqoT+j0Y5T1euV6FSqkjSqnbROQzrwDtJiI/oHsb7wBmod/XqrgVmCkiD5YnKKXWoHsBK1NuX1WcqU7lbALeUkq1E5FDSil/oAWQBviLyCKl1Cbg0Bny/w2Xta1j70oVrF+/npeeeQK/2HgS7rgXznGEXn3gExZBi3EPcXzG2zx9/3i+37yJ9u0bj4BqKuzZs4cpU6bw4cyZFBcVERDfkhbX34atQ1fMAY0jyFkppcdURccSPnAYzpxM7Pt2cXzPD0x77UWmvfYil/Xpy513jObWW2+lRYvzaysej4dXX32Vv/zlL2CxEHfzrfj17nPOoqky5oBAwq+9jqA+/cj58gve+9dLbFy1lMXz55OYmFhzBgZ1Qa1/e+uKBvffi8gJEflvDae9qpTa7Q1uXgv8ALwLHAN2KaV+QB+G7kR/oL7sTduJ3i10prJ/AHagB6qXB0nXxPPoXVi7vPY8701/GzArpXajxyVNEBGHN88jwG50D1t5l1ICsFoptRNdOD1XXaEi8kmFWJ7zsX8eEO4tdxK/FWTlvAK8qPTRfRX/Qv3mvnvTpwGLlVKrvO+fRe/GWkn1Xad3ARO9ee1Bj+sCeBx4WCm1FV3IVcUYYH4V9buz8okikoPe7fajUurVSofPVKfya7PQBeQcpdQudDHVEV2Mfe1NWwM8WU0965Xt27czcuRITEEhtLjrAajDwPMLhU9ENC3GPYTd4aD35QM4cuSsB302S5xOJ3PnzmXQoEF06dKFqdOmYWnbkXYPPEnCfU8Q0LNfoxFOVeETEU3ogKto9eD/o/UjzxI7dCS7jx7nySefpGXLlvTt14///Oc/nDhx4qzzPn78OEOHDuW5557Dr1MKiU89g3/ffnUmnCpijYgg5t77iB49hv179pDcuTOzP/uszssxaBwYk2QaGDQMF6zh7du3j4EDB2LXIPHeR5BGPhqoMmXpJzkxcwphoaHs2LL5vD0PFyvHjx9n2rRpTJs+ncyMDGzhkYT3vhy/rpc2+qH0tcGZk0nZ/h/J+3EHZem6E7x3n76MqaVHasmSJYwZM4aSsjKib7oZ3x49622ghCs7m8zZsyg7cZwHHnuMKa+/bizie2FpPlMVGBg0cy5Iwzty5AgDBgwg315K4oRHkJCmuUxD6cljnPhoKlHR0ezYvIm4OGOBWgBN01i+fDlvv/02CxcuRBMhKDmFyD5XYE1q16gGA9Qlzpwsyg7sJm/3L0KqV+/ejBk9mmuuuYaUlJTTwkhEeOWVV3juuefwT2hB3NhxSFj9zzUlbjfZX82ncPMm+g8bxtL58wkIqH5EpME5Y4gnA4NmQp03vBMnTjBo0CDSMrNodc/DEH526901NuzHjnDy43eITWjBzs2biIqKamiTGozc3FxmzJjBlClTOHToEL5BwYT06ENwz76Ym6hAPlecOVmU7d/9K49UWEQkVw0dysArBrB48WIWLVpESI+eRN56W4PG+okIBRvWkbNwAS3atWPjypWGJ/XCYIgnA4NmQp02vNTUVIYMGcLJjAySxk1CxSTUZfYNhj31ECc+nk5CUhI7Nn5HZGRkQ5tUb4gIW7ZsYcqUKcydO5eysjICW7Ulos8AfNp3xmRpDON9GhZXfi6lqYdwHP2ZgkP78RTr41LCrxlB6JChjWI+M4CS/fvI/PgjAkND2bx2LR2Tq5vFxuAcMMSTgUEzoc4a3qFDhxgyZAhZeXkkjn0IFR1fV1k3CkoO7efk3PcJj4ll46qVF/0ovJKSEmbPns2UKVPYsWMHVl8bQd16EnHZAExRdT+E/2LAXVTA8Vnv4MrJJnrMnQR2u6ShTfoNZcePk/7+dKwWK+tWrqBXz54NbdLFhCGeDAyaCXXS8H788Ueuvvpq8opLSBz3ECry4ny42o8dIW3u+1jNJpZ8/Q2DBla1EEHTZu/evUyZMoWZM2dSWFhIYFwLQnv1w79zT32ZEIMqceZmc+KjqbjtJcRNuBe/due3TuKFxJmRwan3pqGcThYvWsTQQYMa2qSLBUM8GRg0E8674a1YsYKbb74Zl8lMy7EPopp4jFNNOHOyODl7Ou7CfF597V88+dijjaZb5lwpLi5m3rx5vP/++6xduxazxUpQyiVE9bkCFdeiydfvQuPISOP4rHcQzUPcvfdjawLzKrnyckmfPg1PcRGLvvmGq4fUal5dg+oxxJOBQTPhvBrehx9+yH333YdfVAwJd96HBJ5pKqyLC7e9mIz5syk+tJ9rR93M3JkfEhjYtIbliwjr1q3jgw8+4LPPPqOkpAT/qBhCevYhqNtlKH9jRFZtKD2eyonZ01E+PsTf9wA+sU3H6+ouLOTUO2/jKSzim0XfcI0hoM4XQzwZGDQTzqnhORwOnnrqKd58801C2nUk7rbxSD0vtdHQiGjkrltB9uolRCe04JOZM7nyysENbVaN/PTTT8yZM4cPP/yQw4cPY7X5Edj5EiJ69sNkeJnOipKfD3By7gdYgoOJu+9BrBH1PxXB+WIIqDrFEE8GBs2Es254R48e5fbbb2fLli1EXX4l4VdeCxf5+lnVYU89RMaCuTjzcrhrwgT+8+qrjW403uHDh/n000/59NNP2bFjBwBBbZMJ79EH3/YpqGYmfOuCor0/kDZvFj4xMcRNfABLcN0vbFxfuAsKODVtCp7CIhYvXsSwK69saJOaKoZ4MjBoJtS64YkI06dP56mnnsLh8RB34xhsyZ0vpG1NBs3pIGfVEnI3r8XPP4A//OE5fvfEE/j7+zeIPSLCjh07+Oabb1iwYAHbtm0DIKhVa4JSuhPYqSsqKLRBbLsYyN++iYyvP8PWqhWxE+7D7O/X0CadN+6CAk69MwVPcRFLlizhKiOI/FwwxJOBQTOhVg3v4MGDTJo0iZUrVxLStgOxN4yGYOPhWxlHZjq5K7+h8MAeAoNDeHjyZB579BHi4y/8tA1ZWVmsXbuWRYsWsXjxYk6dOgVKEdiyFcEp3Qno1A2T8ZmdN7kbVpK1/Gv8kjsSO248Jp/Gu9D12eIuKCDtnbeR4mKWLVvG4AFVrW1uUA2GeDIwaCZU2/AyMzP529/+xjvvvIPZx4foYTfg3723ERdTA/ZjRyjcvIaCfbtRSjHgioGMH3s3w4cPJyHh/CcOdbvdHDx4kO3bt7Nu3TrWrVvHvn37ALD6+ePftgNhHbtgTWqPqREvxtuUEBGyV3xD7oaVBHbrTvQdY1AX4QSh7vx80qa+jVZSwr9ee5V7xo0jOLhprUvZgBjiycCgmVBlw0tNTeWNN95g+vTp2O2lhPXqR9TgaxA/YwTW2eDMzaJk1/fk796OMzcbgKQ2bRnQvx9du3YlJSWFhIQEoqOjCQsLw2w2YzKZ0DSN/Px88vLyyM7O5ujRoxw5coQjR47w448/smvXLsrKygCw+vnh17I1ga3b4ZfYBnNsAsrUfGPQLgSiaWR88zkF2zcR3LcfkTfdjLqIF9h15+dxcspbeErsoHno3LEj/fr1O/1KTk42FhiuGkM8GRg0E043PIfDweLFi/noo4/48ssvQSlCOncnevBwCItoSBubPCKCIyMNR+oh7KmHsJ86gbuw4Kzz8Q0OwRoZgy02nsCERMyRMZgjYy7qB3lDIx43p+bPpmjPTkKvHEr48BHNwvPqysslbcrbaGWl+EbH4crKwF1qByAkNJS+ffqcFlPdunUjJiamWdyXGjDEU2WUUh5gN2AB9gHjRcReB/kWi8hZ+9WVUjOAQUABoAEPi8jG87SlFzBORB47n3yqyb8v8F/A1/uaKyJ/VUoNBpwi8t2FKPdC4v0cvhaRz6tIvx2IEZEib9p/gceAKBHJribPP4jIP2tRdirQq7q8aiIzM1OWLVvG0qVLWbhwIXl5efgGBRN8SS8i+gxCApvuCKLGjqfUjjMnE624GFVmRyuzgwgioBSYfW2Y/PxRNj8kMARraBimBlxctjmiOR2kffYhJYf2E37tdYQNrptRaCKCuFwoi6VRC19Xbo4uoJxOWox9CJPFinbqBCXHj1B8/AiOzHTwPruDgkPolNKJrp07k5KSQqdOnejQoQMtW7bEarU2cE3qDUM8VaaiyFFKfQx8LyL/Po/8zCLiOU/x9LWIfK6Uuhp4TUS6VVXGudpY1yilDgC3i8gPSikz0EFE9iql/goUi8hrDWvh2VODeOoJvCIis5RSJmAnEA50r0E81eo7URfiSSklAD4Bgfi37UBE996YE9ugmvHUAwYGAJ7SEk7Mfpeyk8eIuvlWgvv0Pad8RNMoSz2C/eABHMeP4czIwFNcDJoGgLLZ8ImKwicuHv/2yfgld8Ds13hG77lysjk59W3E5abl+EnYKqxZ6XGUUZZ2HC0nE2dWBvbMUzizMnCXFJ8+x2QyERMXR+uk1rRpnURSUhKJiYnExMQQGxtLTEwMMTEx2Gy2BqhdnWOIp8pUEk8PAd2Ap4H/AV3RPVJ/FZGvlFJJwEdAeYDIIyLyndfD8hfgFPoDNKU8X6VUHDAXCPbmNUlE1lVjzwx+EU82IFdE/L0P1PeBq4E3gVzgb+ienp+Be0SkWCl1GboXKABwAEOBS4GnROQ6pVS4N582gB14QER2VRY6SqkfgeuALOBToAVgBp4XkbmVbM5DF0yZFdKSgE2Ax5vHo8Axb9lR3rR7ROSYt86FQC8gFvh9uWhRSj2N7unxBeaLyF+UUgG1sOl+4AHABzgEjBUR+5nKUrpf+n/AEOAIemN5/wzi6QDQX0SuV0oNAW4DRuAVPEqpu9E9UT7AZmAy8AL692o3sEdE7lJKfQm0BGzAf0VkmreMVK99pTXV80zEDh0pge07Yo6Ob9T/gA0M6hNXYT4nZr2DKy+H6DF3E9i161nn4S4ooOC79RRt24qnqAhMJnwS4rAmxGEODsbk54s4XWgldlzpmTiPn0QrLQWzmYAuXQnp1x9b6zaNoivMmZVF2jtvg0ejxfhJ2KLiqj3fYy/BkZ2BlpeDVpiPIy+HstwcXAW5uAryT3urKhIYFERUdDThYeGEh4USEhJCcHAwISEhp1/+/v7YbLYzvnx9fbFYLJjN5ipfJpOpyrQ6vMf1/mE1mSELSikL+gNwCfBHYKWI3KuUCgW2KKWWA5nAMBEpU0q1B+agP+QAegNdRORIpazvBL4VkRe8XpmzmSDmevSHbTllIjJAKRUJfAFcJSIlSqlngN8ppV5CF2qjRWSrUioY/QFckb8BO0TkJu+DfybQvRobhgNpIjISQClV1TodrwMHlFKr0e/fhyKSqpSayq8F2UJgpoh8qJS6F3gDuMmbRxwwAOgILADKPW/t0e+tAhYopQaii6+abPpCRKZ7j/8DmIgujqosCxgFdEAXzDHAXnShVxU/ATcqpcKAMcAs9O8OSqlOwGjgchFxKaXeBu4SkWeVUo+ISMV7fa+I5Cql/ICtSql5IpJT4Xht7n2VhF5xVW1PNTBoFjizMzk+6x08ZXbi7r3/rBf4dRcVkbf0Wwq3bgYR/LqmENCrO35dOmGynXkyUvF4cKQew759NyWbtlHyw05srVsTPvxa/Fq3Od9qnRc+UVHEPzCJtHfe5sTMqbQcPwnfahb/NvsH4J/YBhJ/a7d4PLiLC3EXF+EpKfJui3EXF5FdUkRGXiFaeiZaWRmaoxRPWRnicl7I6v2WSmLqF3GlfrUp3yk/3P6Pr0Tu/+uT59wTcC40BfHkp5Ta6d1fB7wHfAfcoJR6yptuAxKBNOBNpVR3dI9KcoV8tlQhnAC2Au8rpazAlyKys4pzKvOqUupP6N6ZiRXSy70OfYEUYIP3w/cBNqI//E+JyFYAESkEKqvvAcAt3uMrlVIRNTyUdwOvKaVeRveI/cZrJiJ/93Z5Xo0uFscAg6vIqx9ws3f/I+CVCse+FBEN2KuUivGmXe197fC+D0QXU+tqsgno4hVNod7rvq2hrIHAHG93aJpSamXVt+M0XwB3AH2AByukl3v6tnrvux+66K6Kx5RSo7z7Lb11qyiearz3ZyLY5ovD7aYB/jAZGDQ67CeOcuyjqWBSJDw4Gd8WLWp9rXg85K9dQ96K5YjbRdCAvgQNHYQ1qnZLtiizGVvb1tjatib0xuGUbNxGwZIVpE15i4AePYi87kYsQQ0Xg+gTHU38g5NImzqF4zOn0PaeR7FFncM6fhYL+EZBRFQ1JwkeTdBEf4nmQXOUoblciNvtfbnQvFtxuxGPG3G5ENFAE+9WQ0S8W033eFWVphfJr3ZOb850vJL3TH9/E/Du2d+Uc6cpiKfSSt4AvF04t4jIgUrpfwUygEsAE1BW4XBJVZmLyFqvt2Qk8JFS6lURmVmDTU9X7i6qVIYClonImEr2daPmyRGrepoK4EavUzk2r/0HlVKXAtcCLyqllorI33+TgcjPwBSl1HQgSylVm2FcFW11VGGjAl4UkXd+U4mabZoB3OSNw5rAr8VcVWVVtqcmPgG2o3vZtAoCVXnTnqvuYm9X71VAP2934mq89/y0MbW891Wx5dnJZ1EVA4OLl6+++oo7X3wW34AA4u97EAkLq/W1zox0MufOwXHiBH5dUwgbdR3W2OrEQfWYfHwIGtSfgH69KFy6moKlKyk9sJ+I628i+NJeNWdwgfCJjiH+wYdIe2cKJz6awpYNG+jcqVOD2dMIqVfhBL9+GDclvgUe9YoolFI9vOkh6J4dDRiLHodSLUqpVkCmtwvpPfRgY5RSM5VSvc/Rvk3A5Uqpdt68/JVSycB+IN4b94RSKsjbHVmRtcBd3uODgWyvhyq1gm09gdbe/XjALiKzgNfKz6lUx5HqF/XQHt0rlw8UARX/Un2H7q3Ba8P6Gur5LXCvUqo8Ji1BKRVdG5u85Z7yevzuqqEc0O/LHUopszdOrdrhNyJyDL179+1Kh1YAtyqlor02h3u/AwAurz2gf5fyvMKpI7o38VfUsp4GBgZVICL861//YtSoUZijo0mY/EithZOIULDxO07893VceXlETryb6En3nJdwqojJx4fQ664m/g+/wxoXS9bcOWR8OgfN6aj54guET0wscQ88hMPlolffvmzasqXBbDFoGp6nqnge+A+wyysKUtGDp98G5imlbgNWcQZvUyUGA08rpVxAMTDOm94NPcD8rBGRLK83ZY5Sqryz/U9eT8Vo4H/eOJpSdO9GRf4KfKCU2oUeMD7emz4PGOftwtwKHPSmd0XvRtQAFzCpCpPGAq8rpezoHqy7vCMOF6LHLt2IHjD+GHoX5tN4A8ZrqOdSbwzRRq82KwbuBtrVwqY/owdrH0Xv/qrJLz4fPVh8t7fua2o4n6o8Yt5Rhn8Clip9JJ4LeNhrxzT079R24F7gIe/ncABdEFemNvf+osBut/Pzzz+TkZFBYWEhpaWl+Pr64u/vT3x8PElJSYSGGkuQGNQOl8vFI488wrRp0wjt3oPI20aj1XJYveZ0kvXF5xRv/x5bSkcix43GHHxhZnO3xkYT8+RDFCxaRsHiFTiOHSNm7Hh8Y86h26wO8I2NI37SI6S/O40rBg/m6wULuOYqI36yIWj0o+0aAm8g93sicltD22Jw0dJoG56I8MMPP7Bq1Sq+++47Nm7axMkTJ2q8LjQigt6XXcYVl1/OkCFD6NOnD2Zj6gWDSmRnZ3PHHXewYsUKIq8aRvBVV9d6xKk7P49TH7yPM/0UIdcOI2TE0HobrVq6/yeyP5iNuN3E3D2OgPYd6qXcqnAXFJD+7jRcOTnM/HgWd91+e4PZ0kgwpiowMGgmNKqGJyJs2rSJzz77jHlffMGxo0cB8I2IwCexFQHx8VgjItECAlA2G8pi1YNFnU59xu6CfFzp6RSnpuLMzAAgOCyM66+7jvFjxzJ06FBjWQkDtmzZwq233sqp9Ayib7kVv56X1vpaR1oap96fjuZ0EnXvXfh16XgBLa0ad04umVM+wJWeSeSomwnp06/ebSjHY7eT/sG7lB07xkv//jfPPPFEg9nSCDDEk4FBM6FRNLy8vDw++ugjpk2bxp49ezBZLPi3Tyb0ku5Y2rbDHFLr2RdO47HbKT14AMeB/RTu+RGtrIyouDgm3nMPD0+aRIuzGEllcHEgIkydOpXHH38cn9BQYu8eD3HVz1lUEfvBA6R/9CEmPxvRkyfi06L219Y1WmkZWe/NomzvAUKHDCH8mmsbbE4ozekg8+NZlOzby10TJzJj6lQsF+GiybXAEE8GBs2EBm14x44d45VXXuG9996jrKwM/8RWhPfvjzWlC6Y6nHFYc7mw7/mRku3bKD5wAJPJxA2jbuaPz/yeXr0abvSSQf2Rn5/P5MmTmTNnDiEpnYm+YwyarfYzeRft2E7m3DlY42KInnQvlvCGj60Tj4fcufMpXr+ZoP79iLqh4RYsFk0j55uvKVi3hksHDGD5woXNMf7QEE8GBs2EBml4P/30Ey+99BIzZ85EA4J79iLs8gGYzsILcK64cnMp+m49BZs3oTkc9Ozbl5f+/neuuuqqRjGbs0Hds2LFCiZMmEDaqVNEXj2cwEGDz0pkFG7bStZnc/Ft14boBydg8m88S4mICPlfLqJw2WoCevYg5rYxDbq8UuGWzWR98TnRCS1YunABl1xySYPZ0gAY4snAoJlQrw1vz549/POf/+STTz5BmS2E9OlLyKBBmELq/x+qVlZG0ZbN5K9bg7uggM49evDKP/7BiBEjDBF1kVBSUsKf/vQn/vOf/xAYG0fMmDshLr7mCytQuHkTWV98jq1DO6IenIDJt/EtziwiFH67ivwFi/HrnELsneMwNeBivKWHfyZz9iyktIx//+d1Hp00qbm0KUM8GRg0E+ql4X3//fe88MILzJ8/H4vNRki/ywm+YiCmwAsztPtsELebwm1bKVi1AldeHh26duOVfzzP9ddf31x+8C9KFixYwKOPPsqxY8cIH3AFYSNGwlkKioKN35E9fx62lI5EPzAO5dNwgqQ2FK3ZQO7cL/Hr1JHYuyc0qIByFxeR/clsSg4e5Jobb2T2++8THl672dabMIZ4MjBoJlzQhrdhwwb+8Y9/sGTJEqwBAYRefgWB/S/H5H82SzfWD+J2U7T9e/JXrsCVm0P7zp158W9/Y9SoUcYIvSZEamoqTzzxBF999RWBCS2IuvkWTC0Tzzqf/PXryFnwJX5dU4i6byzK2jQCoIvWbyJ39jz8OnUkbuw9qAYM3BZNI3/1SnKXfktQaCgz3n2Xm0eNqvnCposhngwMmgl13vBEhG+//ZYXX3yRtWvX4hscTMgVgwjs0xdVh0HgFwrxeCjasZ2ClStwZmeR2LYtf//zn7nzzjuxNuA/eYPqycrK4oUXXmDKlCloShEx7BoCLx8A5xD/k79mNTnfLMTvki5ETbyrQQXIudCYBBSAI+0k2Z/NpezkSa69aRTT3vwfCQkJDWrTBcIQTwYGzYQ6a3gej4cvvviCF198kR07duAXHk7IwEH49+qN8ml8cSI1IR4Pxbt3Ubh6JWVpacQkJPCnZ59l4sSJ+PnVfpSWwYUlJyeHN998k3/9618Ul5QQelkfIq6+BjnHRXTzVq4gd8ki/Ht0I/LeOxs0+Pp8aGwCSjwe8letJG/lciwWC8899xzPPv30xdaWDPFkYNBMOO+GV1RUxMyZM3njjTc4ePAgAbFxhA6+Et9ulzT4D3ZdICLY9++jcNUK7KmphISH8+Tjj/PQgw8SExPT0OY1W1JTU3n99dd59913sdvtBHftRvS1I5GIyHPOM3fZUvKWfYt/rx5Ejh/dZIVTOUXrNpI75wv8UjoRd/eERtEeXbk55C36hqJdPxAZF8ff/+//mHjvvfg0wT9YVWCIJwODZsI5N7x9+/bx1ltvMXPmTIqKighslUT44CuxdEppsLlmLiQiQtnhwxSuWUnx/v2YLRZuHDWK3z3+OP379zeCy+sBl8vFokWLeO+991i0aBECBPe8lIjBV0JU9DnnKyLkLV1C3orlBPS5lIixt1803+HGKKAASg8dIu/bRZQePUpkbBz/98c/cM+ECQQ2gkEk54EhngwMmgln1fBycnL49NNPmTVrFt999x1mi5XA7t2JGDAQFX92Q8CbMs7MTEo2byR/6xa0sjLaJCczcfx47rrrLlq1atXQ5l1UaJrGxo0bmTdvHrNnzyYjIwNbaCgBPS8ltP8ACA4+r/xFhNzF35C/ehWB/XsTfuctF41wKue0gGoEo/AqIiKU/nSQguXLsKcewS8wkAnjxvPIw5NJSUlpaPPOBUM8GRg0E2pseGlpaSxatIgFCxawePFi3G43AfEJBPa8lIBLe6ECAurDzkaJ5nBQvGM7Jdu/x556BIBeffty5+23M3LkSJKTkxvYwqZJdpXQ5QUAACAASURBVHY2q1evZtmyZSxYsID09HTMFgv+HTsR0bcvprbt66RLTUTIWbiAgvVrCbyiH+Gjb7rohFM5p2OgOnYgduw9jUZAgf45OI4dpWTTRgp27kA8Hjp26cK4O+9k9OjRtGnTpqFNrC2GeDKoGaWUB9gNWIB9wHgRsSulikXkrH2vSqkngGkiYve+XwTcKSL5dWn3WdiTBHwtIl2qSN8HHAB8gG3ARBFxVZPXX4FiEXmtUvpg4CkRua7uLD8rftPwCgsL2bhxI+vWrWPJkiV8//33ANgiIvDv2o2wSy9DoqONbqpKuHJzsP+wk6Id23GkpwPQsnVrbrruOgYPHszll19uxEhVgdvtZv/+/Xz//fds27aNtWvXsmvXLgAsNhv+HTrqaxy2a1+nozVF08j+aj6FG78jaPAAwm67oVF8p8XlwnHkGK70DNzZuWhlZaAJyuaLJSwUa1wMvq0TMZ1DoHXRhs3kfvw5tg7JxI27t1EJqHI8xcWU7NhO8a4fKD2aCkC7Dh0YOXw4w4YNY+DAgQSd42CAesAQTwY1U1EkKaU+Br4XkX+fh3hKBXqJSHYdm3pO1CCevhaRLkopM7AMeE9EPq4mr79yAcSTUsosIp5zuRYgNzdXdu/eza5du9i9ezdbt25l165daJqGMpnwT2xFYEpn/FNSUFGGYKotrtwcHAcOYN+/j+JDPyEuXVe3TEpiQP/+XNKtG127dqVLly60bNnyor+vIkJubi6pqan89NNPHDx48PR21+7dlJWWAmDx9cU3sRWB7ZPxb9ceFRd3QYK2RdPI+vxTirZtJXjYlYTe1LCzymtOJ6U/7KF48zbKDh4Gt1s/YLFg8rehTArNXoY4vf/PlMInqSUBvboT0KsH5qDa/9wWf7eFnI8/x9a+HXHjJzZKAVWOKy+X0t27KT14gJIjhxGXC2Uy0S45mX59+tD7ssvo1q0bycnJRDeOP3SGeDKomUri6SGgm4hMLk9XSgUCXwFhgBX4k4h8pZQKAD4FWgBm4HkgBngN3ZuTLSJXVhRTSqlxwFPonpJdIjJWKXUb8BfAAxSIyMBK9p2p/CRgMbAe6A+cBG4UkVKl1KXA+4Dde3xEdeLJ+/4lIFdEXqlkcy/gNREZ7BVPbYEEoCXwiohM94qnvwM5QAdgLTBZRDSl1NXA3wBf4GfgHhEp9pbxPnA18CYQDTwEuIG9InLHWXyGpxueNSAQn/g4/Fu3JbBNW4iPr9PFeZsr4nbjOHkC97FjlKYewX7sKO6CgtPH/QICSExMpE1SEklJSbRq1Yro6GgiIyOJiIg4/QoODsZqtTbIA0LTNBwOB2VlZae3paWlFBQUUFBQQH5+/q+2eXl5ZGRkkJaWRtqpU6SfOoXT6fxVnrbwCMwREfjGxRGY2AoVG4c5MvKCd5uJx0Pm3DkU79xByLXDCBk5rMEeup4SO0Wr11O0aj2avRRzZBj+PVOwdWqDT1IC5tCg0/dDRNBKSnEeTcNxIBX79r24jp8Ci4XAvpcSPGww1qjajTQs3riVnFmf6QJq3L2YmsBIN83loiz1CJ5jRyk9dgz78WN4iotPHw8ICqJ9+/Ykt2tHXFwc8fHxp1/h4eGEhoYSEhJCcHAw5gs3itIQTwY1U0EkWYB5wBIRmVIp3V9ECpVSkcAmoD1wMzBcRO735hMiIgWVPU/l79GF1RfA5V5REi4iuUqp3d58TiqlQit371VTfivgkLesnUqpT4EFIjJLKbULeFRE1iilXqUG8aSUsqELscdFZFcN4mkU0BcIAHYAfYBkYAmQAhz17r8DrPbWeYSIlCilngF8ReTv3jLeFpFXvPakAa1FxFHVfaiOiJHXi29cHD6xcZiDgxvDP7dmgcdux5mRjis9HVdWJq68PFx5ebjz89Ds9jNfqBRmX18sPj6YfXww+/hitlpQJjPKpFDKpG9NJpQygdL3EUFEQzTvSwTxeLen07xbjweP243mdOFxOdHcbrRyT0htMJkw+/lhDgzCHByEOSgYa0gIlqBgLKGhmCMjsUZENojHQ9xuMuZ8TMnuXYTeOIKQa4bUuw3gnYh17Ubyv/4WKS3Dr2cKwcP649ux9VmJR+eJDIqWfUfx+u0gQvCVlxMy4qpadekVb9pGzkefYmvXVvdANQEBVRERwZ2fjyszA3dWFs7sLJxZmbjz8vEUFaI5HGe81mKzYfX3x2S1Yrb6YLZaf/Uy+VgxmS16O6rQnpRScLqd6e+V6Zd2tm/hgnr/AW0cYycNzhY/pdRO7/464L1KxxXwT6XUQEBD97rEoMdJvaaUehldhKyroZwhwOflokpEcr3pG4AZXvHzRRXXnal8gCMiUm7790CSUioECBWRNd70j4ARZ7Cprbfu7b227aqhDgBfiUgpUKqUWgX0BvKBLSJyGEApNQcYAJShC6oNXkHjA2yskNfcCvu7gI+VUl8CX9bCjtOEDb4Sk1L1/3epmWMOCMCnTVto0/Z0mqA/EDwOB56SYjwldjR7CZ6SEjx2O+J0IC4XmtOFuJz6vsuFx+UCkdMCCRHE5dbTvKJIKQXKBKYKDwCrFZTS07wPgPKHgMVqRVks3pcVZTHrW+uv35tsNsx+fphsNkw2P0x+NpTVR3+owOltY8BTVsapDz+g9NBPhN1yA8FDr2gQOxzHTpDz0ae4Tp7C1qU9YaNH4JMYd055+bSIIeKeUYSMGkrBvGUUrlhH8ebvCb/jZgJ6dKv22sC+vUApcmbO5dQH00kYPxFzU5qwUiks4eHYwsOhY6fTyQJoImhlZbiLivAUFuIptaOVlaKVlv1qK243Hrcbt9uNuN1ISTHi9uj7bvev25Sm/dLONAH57ft2r/77/kNP/256fd4GQzw1TUpFpHs1x+8CooBLRcTl9ZjYROSgt3vsWuBFpdRSEfl7NfkoqghsFpGHlFJ9gJHATqVUdxHJqal877GKf0s8gN+ZyjkDP4tId6VUHLBaKXWDiCxA7zor/+tYuc+rct5STboClonImDOUX1JhfyQwELgB+LNSqrOI1MpVsOTe8eSXltXmVIMmgiaCIGgiv/5mKVAoXS8pReORNRee7MxMnhg/DseRw8RMuBNb7x71boNoGoXL15C/YAnmkEAiH74L/8s614m31xIaTMTEWwgc2pfcD+aTPf0jSvv0JPy2mzD5n1kQBfa5FGUykf3hJxTP/IAPP/2MiKio87anKSIILo+G0+PG5dFwa7+8NBE8p7dyuo2JiPdPj57HC6tWL6hvuw3xdHESAmR6hcuV6N1lKKXi0WOEZimlioEJ3vOLgCCgcsD4CmC+Uup1Ecmp0G3XVkQ2A5uVUtejxxJVFE9Vln8mRCRfKVWglBogIuvRxVe1iMgppdSzwHPAAiAVuBS9K++WSqffqJR6Eb3bbjDwLHq3XW+lVGv0brvRwDT0Lsa3lFLtROSQUsofaCEiBytmqJQyAS1FZJVSaj1wJxCI7tGqkXYREbU5rdGgaRrp6emcPHmSrKwsNE0DIDIykvj4eOLi4oz15wx+xaFDhxh9260cT0sj/uGJmDu2r3cbPEXFZL//MWUHDuHfqwvhE0ZhDqr7xbF9kxKI/fMkChauomDBKhyHjxL1wDh8Es48B1vAZT0w+fuROW0md95wHVvXrG1KUwM0Ku7p1TOjvss0xNPFycfAQqXUNmAnsN+b3hV4VSmlAS5gkjd9GrBYKXVKRK4sz0RE9iilXgDWeKdH2IEuuF5VSrVH99KsAH6oZfnVcQ/wvlLKDnxby3p+CfxVKXUFeoD3e0qpPwCbK523BfgGSASeF5E0pVQyenfcS+j3ZS0w3xswPgGYo5Ty9V7/J+BgpTzNwCxvl6MCXm+oqR0uBC6Xi/Xr17NkyRI2b97Mtu+/p6RCkGhlrD4+pHTtyoC+fRk+fDhDhgzB37/uH1IGTYM1a9Zwyy23UOJyEf/kQ9Cy/hejdZ48ReaUD9CKigi/52YCB/W6oLGFymImdNRV2Lq0J/vNj0l/9U0i7r6NgF5n9rb5de5IzOMPkPn2B3S77DLWrVxJj0suuWA2GtQdRsC4gUHD0OganoiwceNG3nvvPeZ98QUF+fmYLBZ8Wybgm9QSv/hYVEgIWoCfHseDoJXYkYJCtMxsSlOPU3r0GOJwYvX15erhw5n8wANcffXVWBrJ0hQGF57p06czefJkfKOjiJ50D1pEWL3bYN+1l+wPPsZk8yXq8bH4tm1Zr+V78ovIems2joOphFw7lJCR11Qr3Jxp6WS9+S7K6eSzTz/lxpENNf1ck8UYbWdg0ExoNA3P4XAwc+ZMXn/9dfbt24fF5otf926E9OiKat8Gk8235ky8iMtN2c+Hcf24n8It2/EUlxAeHc0Tjz3Gow8/TGho6AWsiUFD4nK5eOqpp3jjjTcI7ppCxL13ovnW/rtTVxSt3Uju3Pn4tIon6vGxWMJD6t0G0EcY5sz4ipJ12wjo34uIMbdWO3eWOzeP7KkzcJw8xQuvvMJz/+//GaNwa48hngwMmgkN3vAKCwt55513+Pfrr5N+6hT+SYmEDOqP5ZIuZyWYzoS43ZT+uA/7+s2U7D2Ar78f993/AH969lliY2ProAYGjYWjR49yxx13sGnTJsKuGkTQTdfW+3IrIkLht6vIX7AYv0s6EDn5Tky2hp0GQEQo+HIFBV+uwNY5maiJ46ptW1qZg5wZc7Dv2sPt48cxa/q7Rixh7TDEk4FBM6HBGp7T6WTq1Kk8//zzZGdnE9ApmYjhV0G7pAv2T9d5/CTFK9ZStG0nVh8fHn7kEf7yxz8anqiLgK+++op77rmHEoeDyLtvxdq9a73bICLkz/+GwuVr8O97CZH33YayXrAJGc+aotVbyZ0xH982iURPvg+T35knwRVNI3/BEgqXriKl16Us/fIrEhLqP2asiWGIJwODZkK9NzxN05g7dy5//OMfOXLkCAEdk4kcdW29BvO6MrMp/GYpxVt34BcUyDPPPMPTT/7OCC5vghQVFfHMM88wZcoUAlu3Imri3Wjh9S+GRdPInfMFxRs2EzikL+Fjr2+UiwyXbN1N9pRP8ElMIPrhiZj9q1/Yu3jLdnLnzMPPz5/PZs/m2hFnmvrOAEM8GRg0G+q14S1fvpxnnnmG7du349eyBZE3j0Qlt22wmArniTQKF35Lye69hERF8tLz/+C+iRONwPImwvLly7nvvvs4duwYoUMHEnz9cLDW/2cnIuTOmUfx+s0EXzeY0FuvbtRxQvYd+8h682N84mOIfuR+zIHVr43nSs8k591ZOE6l88jvfse//vlPfJrYjOT1hCGeDAyaCfXS8Hbt2sXvf/97vv32W2xREYRfPwJLz66N5p952c9HKPxyMaU/H6FFm9b899XXGDVqVKN+ADZn0tPTee6555gxYwYBcbFEjr0dkup3JFs5IkLep19StOY7gkcOIvS26ke0NRZKdx0g641ZWKIjiHnsQcxBQdWerzmd5H+2gKINm0nqkMy82XPo2bNnPVnbZDDEk4FBM+GCNryTJ0/y5z//mRkzZuATEEDw8CH4XdFXXxqkkSEilO7aQ8FXi3GmZ3JJr17879//5oorGmYZD4Pf4nA4eOONN3j++eexl5YSMnQgQdcOaxBvE3iF07yFFK1cR/DwKwi9Y0STEE7llO45RNbrH2KJjdIFVED1XXigT7+QO/tztBI7v3v6KV7469/wbYDRjI0UQzwZGDQTLkjDKyws5OWXX+b111/H6XYTPPhygq8ZAtUsFdFYEI+Hkk3bKPhmGe78Aq4aMZz/vPoanTt3bmjTmi0ul4sPP/yQF154gdTUVIIv6ULELTegRdb/3E3liAj5Xy6icNlqgq7qR9jd1zcp4VRO6e6DZP5nJj4JccQ8dj8mv5rj/jwldgrmLaRo0zZiExOZ+r//ccP1TbP+dYwhngwMmgl12vDsdjtTp07lpZdeIisri+DePYm4cQRaWNMbzaY5nZSs3kD+tysRh5Mxd93FSy+8QMuWDdM91BwpKSnho48+4uWXXyY1NZXANkmEXT8cU4e2NV98gclf+C0Fi5cTeGUfwsff2KSFg33nPrLe+BifVgnEPHI/JtuZR+FVpHTvAfI/X4AzPZP+Vw5m6n/foGvX+h/l2IgwxJOBQTOhThpeuWh6+eWXyczMJLBTMpGjrkNanNtq8Y0JT3EJJUtXkb96PWaTmYcmT+K5p39PfPyZ1wszOD9+/vln3nrrLd5//30KCgoIaN2K8OuvQXVo1yhESv6iZRR8vZTAgb0Iv2dUo4ndOx/s2/aQ9dZsfNsmEj35fky+tQsIF4+HotUbKFi0DK20jOtGjeLlf/yDlJSUC2xxo8QQTwYGzYTzanhZWVm88847vPnmm2RkZBCU0pHwkVdD64vPO+POyaPom6UUbv4es9nM6DFj+OOzzzbXh0Sdk5WVxWeffcbs2bPZsGEDJrOZwJ7dCBsyEElMaBSiCaDg25Xkf7WYgMt7EHHfrReFcCqnZPMusqd8gq1DW6IeuheTT+1jEz0ldopXrKVg1XrE6eSakSN57qmnGDhwYKP57OoBQzwZGDQTzqnh/fDDD7zxxht8/PHHOBwOAjt3JOLaYdA6sa7ta3S4snMoWbmOwg1bEJeLAVdeyWOTJnHDDTcYgbNngYiwa9culixZwpIlS1i3bh0ejwf/FvH4X9qdgL69IKT6EWD1TeGKNeTN+1qfAPPB2y8q4VRO8Ybt5Ez/HFvnZKLvn4A6y2B8T3EJxSvWUrh+E1qJnfYpnfh/jz3O6NGjm8NktIZ4MjBoJtS64WVkZDBnzhxmzpzJjh07sNh8Ceh9KWFDByJRERfSxkaJp7iEknUbKVq/GXdePsFhYYwbO5Yxo0fTt29fTBfhg/V8KC0tZfv27WzatIlNmzaxfv160tPTAQhIbIFvSgeCeveA2JgGtrRqCldvIO/TL/Hv1YXISXegLOc/c7hoGq7j6ZTtP4zrVDbu7DzE4QSTwhwciCUqHN82LfHt2BpzYP1N4Fq0eiu5H3yBX7dORN03DnUO855pThf2rdspXr0Bx8lTWHx8GHHttdwzbhzXXHPNxTohrSGeDAyaCdU2vEOHDrFw4UK+/vpr1qxZg8fjIaB1KwJ798T3sh6oJjB67kIjmkbZvoOUbvqeop27weMhPCqKW26+meuuvZYrrriCsLCGGxVWn4gI+fn5HD16lP3797N371727dvH3r17OXjwIG63GwBbdCSWVi0J7twJc4e2mEKCG9jy6ilav4nc2fPw65FC1MN3nveSK86TGRSv3UbJdzvQCksAMAX5Y40KxeTng2iCJ78YV2Y+eDxgNuHXuR0BAy7Fv1fnahf2rSuKVmwid+ZX+HVPIWriuHMuU0RwHj2BY9sOCrfuwFNUjNXHh4GDBnHTDTcwbNgwkpOTL5auPUM8GfwWpZQH2A1YgH3AeBGxn2eefwfWisjyMxx/CLCLyMzzLCcJ+FpEupzDtROApSKSdj421BXeuvQXkdl1kN3phici/PTTT6xfv57169ezbt06Dh06BIB/i3hsXVMI6t0TYqLqoNiLE620lNIf9+PctZei3XsR5/9n77zjoyj6P/6eu0vu0gtJICFAACH0Lk1AAUUUFBRBLNh7fez6e/RBUewNsRcEH1ERRYog8IgK0nvvvYT0crlLcm2/vz/ugiEmEEN69g372t3Z2ZnZzc7tZ7/znRknSinad+rEwAED6NatG507d6Zdu3a1polPRLDb7aSnp5Oenk5GRsap7fT0dJKTkzl27BhHjx7lyNGj5Nntp85VBgOWmGgMDaOwxMUR2KIZNInDEFqzmuPOhG3VOjL++z0BnRKJfvBGlH/5x5RyHj1Jzpwl5K3fAUYDQd0TCe7dlsD2zfGL+ruA1JwuHAdPYlu7m9yVO3CnZWOKiSDsikEE9etW6c2G1v+tJOvreQR27UDUbTees2gTj4eCfQdw79hL7raduFLTAAhv0IB+ffsyoH9/unXrRseOHYmJiamIS6hqdPGk83eUUjYRCfZtTwc2iMjbRY4bRcRTbQU8A+conv4AHheR9SUcq/JrVkpd5CvP8HNN67333pPt27ezfft2tm3fji03FwD/kGD8WjQjuG0i5nZtUNU4nk5tRVxuHIeP4jlwiLzd+8k/fBRxOgEwmkw0TWhGy+YtaNG8OQkJCcTFxREZGXlqiYiIwGKxYDabMZvNZ20G9Hg8FBQUkJ+fX+o6Pz+fvLw8cnNz/7ZYrdbT9nOK7DsdjpIzNSj8QkIwRYSjwsMwN4jA3CASU2Q40iASY0z0P/aZqUnY1mwg46sZWNq1JObhm1Dm8g3uqtnzyfphEbbf12IIMBM+rDdhQ3viF372QSkLEY+Gbd1uMmf9ieNAEv7NGxN50wjMLSq3c4Z18Qqypv9MYLeORN16Q4VavVypaTj3HcJ96Aj2fQdxpaWfOhYZFUWnjh1pk5hIQkLCqaVZs2ZER0djrALrWznQxZPO3ykmnu4BOgHfA+OBk0AXoCPwKnARYAY+EJFPfOc8CYwDNOAXEXlaKTUVr6j5QSn1KnAl4MZr6XlcKfU8YBORN5VSXYCPgUDgAHCbiGT5xM0aYCAQDtwuIn8WK3uCL58OPkvSlb50WgI/iciTSikj8AXQA69FZgpwDJgKnADygT54rW5TgCHA+8A9+MSVUioKWC8iCb58RgJGoAPwFuDvuwcO4HIRyVRKtQQ+AKKBPOBOEdntuzdWX3kaAU/67tNqoC1wCJgGLAa+9KVtAEaJyL4y/ElRSolfSDB+sY3wi21IULN4jAlNUTFRddIZtjoRTcOdloHrRBJyIhlHajqO9Ay0zCzcubaznm80mfDz8wMFogmapiGahuZbyovRYsFoMaMsZpTZjDL7g8WM0WLBFGDBaAnAFBKMMTgQQ1AgEhCABAViCA7CEGCps8+JfcMW0qdMx5zYnJhHbsZgKd9cbnkbd5Ix9Sc0q53wy3sROfoiTCHlb+4WEXL/3EbaV4vx5NgJu/Iiwq4cVKlNedaFy8n6dj6B3TsRdcv1lZaXJ9eG80QSnEzFmZRM/vEk3BmZeGz20+IppQgNDycqKoqGMTHEREcTERFBcHAwQUFBBAcHn7ZtNpsx+epPaYvJZEIpdWoxGAyn7Z9tMRgMREVFVbl4qr2fJvUQpZQJuAxY6AvqCXQQkUNKqbuAHBE5XyllBlYopRYDbfAKiV4ikqeUiiyWZiRwFdBGREQpVVK3jK+AB0Vkqa+5bzzwL98xk4j0VEpd7gu/+CyX0QXoilfE7FFKTQZigMaF1imlVLiIZCulHqCI5cnXNl8gIv18+/ecIZ8OvnwswH7gKRHpqpR6B7gJeBf4FLhHRPYppXoBHwKDfOfHAv18928u8APwNEUsT76yTxKR6Uopf7xirUzEv/IchtCQuuJvUKNRBgN+DaPxaxgN3TpT1OagOZx4cnPR7Hl/LXn5iNtdZPGA2w1KnbYog2/bYECZTCg/P99S0rYJg78/ymLGYDGj/P3rrPg5FwotTubzmpVbOInTRdaMX8j9dRXm5rHE/PsGAlqe+9hgSilCB3QiqHtrUj+fT87s3yjYvo+o+2/AFBl2zumXROjQfiBC1ncLSDcYiLppbKUIKGNIMAFtWkOb1gQAhVejFRTgzsz2CqnMLDy5Njy5dk7a7RxPTUY7uB8tvwBxONEcDjiHj4lzodmHb7Q8fO/jB6oyT1081Q4ClFKbfdt/4rXS9AXWisghX/gQoJNS6hrffhjQCq+Y+bLQR0pEMoulbQUKgM+VUvOBn4seVEqFAeEistQXNA2YWSTKLN96A5BQhmtZIiI5vrR3As2AHUALnxiZj9eiUxozypAHwO8ikgvkKqVygHm+8G1471Mw3ns4s4iAKeoMM1tENGCnUqq0bkirgH8rpeKBWWW1OgHExsaS73ZXva1Z53T8zXCWiVl1qobMZSvJ+O8MLG2aE/3wTeUSTu7MHNLe/QrnkSTCr+hD1PUXYzgHX6mSMAZZiH14FEHdW5Py0VySX3if6AdvxHxeswrNp5DQy/ojmkb29wvJUopmt91UIT0Oy4S/GULDIKHka/OIoImGRxM8ouFxufA4nIjDiTgc3o8Pj4Z4PKD51h4P4tF8aw+iaVDYAiZy2rZ3U3weor5jxcJ80bvjbRWpMnTxVDvIF5EuRQN8L/yiNlWF1zq0qFi8oZyhZ5eIuJVSPYHBwFjgAf6yvpSFQqcMD2V7noo6cXjwWq6ylFKdgUuB+4ExwG2lnF/0mt14m8vAa2EqLR+tyL7mK6cByC5+X0s5v0SNIyLfKKXWAMOARUqpO0Tkt1LSO421N99blmg6OvWC9957j4e/+o7QLm2JfOB6pBz+Wo6Dx0h7979oTiexT19PyPmJlVDSvwjt1xFz04YkvfoNya98RtSd1xDUu7Sfk3MjbNiFoBTZM37BEhTKsvm/EBCg97gtwvdVnaFuN647LALuVUr5ASilWiulgvBacW5TSgX6wos32wUDYSKyAG9T3Gm132clylJKFU5xPw5YSgXi81cyiMiPwHNAN9+hXOBMZoHDeL84AK45Q7y/ISJW4JBSarSvDMon4M7EaeVRSrUADorIe3ib9jr9kzLo6NR3RIRXX32Vhx9+mLDzOxL5wA3lEk5567eT8vKnKLOJJi/fUenCqRBz0xiavnYXAa3jSf/4e3J/W1VpeYVdPoDIW65i/R/L6HZhP6xWa6XlpXN2dMtT3eFzvM1mG5XXLJUGjBSRhT6H7/VKKSewAPi/IueFAHOUUha8FpZHSkj7ZuBjnwA7CNxawWVvDHyplCoU88/41lN9+RY6jBfnTeB7pdQ4oEwWn2LcAHyklHoW8AO+A7acIf5WwK2U2uIrmwW4USnlApKBCeUoQ43F7XazadMm1q1bx549e9i3bx+paWlkZGbicjnx8/MnMDCQ+MaNada0Ke3ataN79+507dqV4ODg6i6+Tg3H4/HwGcm3JQAAIABJREFU6KOP8t577xHWtyvht49CytEcZVu2nowps7C0iif2qev+UU+6isAYEkjjZ8dx8u2ZZE6bi2bPI3T4oErxZwwZ2BNDoIXdn8ygQ++ebFj6J9HR+hAm1YHe205Hp3qokRUvJSWFn376iTlz5vDn8uXYbd7eaEaLGb9GUajQIExBgRhMJsTtQStw4MzKwZORjSfX26Jq9DNxfu/ejLh8GFdffTWtW7euzkvSqYHk5+dz4403MmvWLCIuG0DImEvL5UBvXbScrG/mE9i5JbFPjMUYUL6eeRWBuD0kfzCb3GVbCRs5kPCrhlRaXvlb9pD2/nQiG8aw4tffSNTrmD5UgY5OPaHGVLyCggJmzpzJlClTWLZsGZqmYYmLwdy2JcHtzoPmcRgjw876Je3OtuI8nIRn3xHsW/fgOHoSgPZdu3D3rbdx/fXX06BB/ZtORud00tPTGTFiBKtWrSLqhisIvKQko/LZyZ69hJyffiW4dzsaPjwKYwU7hpcH0TRSPpqL9bdNhI8eQtjwgZWWV8G+I6RP+i8mpfh59lwuHlh5edUCdPGko1NPqPaKd+jQIT788EOmfPklmRkZBMTGENi7E4Hnd0TFRZ9zs4M7M4f8tVuxr9iM42gSfmZ/xlx3HU89+hgdO3asoKvQqU1s3LiRq666iqTkk8TcfS1+PdqXK52ceb+T/cNiQi7qQqP7rqySaVPKing0kt//idxlW4m4/jJCLx1QaXm5UjJIf/crXKkZvP/xR9x3+52VllcNRxdPOjr1hGqreHv37uXll1/m66+/RoDA7u2JGNwHldis0sadch49Sd5va7Cu2Ig4XfQa0J+Xxz/PwIED9bGu6glff/01d955J4aQIKIfvBGaNSpXOoUjb4cM6ESjB6+qkeNlicfDyXd+xLZqB5E3X0HIoL6VlpfHnk/G+9PJ33mAcXfdyeeT38ffv/qaL6sJXTzp6NQTqrzi7dixg4kTJzJjxgyUn4mQgb0IG9ofIqpunCOPzY596XpyF6/EnW2lY4/uvDbhRYYOHaqLqDpKfn4+Tz75JO+//z4h7c4j6r7r0co50nfu0nVkTplFUM+2xD0+ukZZnIojbg9Jb8zAvmEvUfddS1DPs3XmPbe8smf8gnXxChK7dmbx7Lk0bdq00vKrgejiSUennlBlFW/z5s289NJL/Pjjj5gCLIQO7kPwpRegQqu2V1JRxOnC9ud6rPOX4c7IJrFzR159fgIjRozQRVQdYtu2bVx//fVs376diKH9CR19KZRzgEf76i2kfzyDwM4tiXv6Ogy1YO4+zeHi+ISvcOw/Qczjt2Bpe16l5mdft43Mz3/EbDYzfdpXXDViRKXmV4PQxZOOTj2h0iveunXrePHFF5k3bx5+gQGEXtKXwCF9MARXn2gqjrjd2JZvInf+UlypGbRs15ZXnn+BUaNGnXVCXp2ai9vtZtKkSfz73//GEGihwZ2jMbZvWe708jbuJO396QQkNiHu3zdiLOd8d9WBJzePY89OwZVhpdEzd+LfrHGl5udKTiPjg29xHD3JNTdezxcffERoaGil5lkD0MWTjk49odIq3ooVK3jppZdYuHAh/sFBhFx6AYGDe2MIqrkjEovHg33VFnJ//gPnyTSaJ7bmpf+M59prr62ps7jrlMKGDRu466672LhxIyHd2xN12yi04PI/e/k79pP69lTMCY2IH38zxkDz2U+qYbjSczj2f58jHo2Gz96DX3Tl9joVl5ucn34lZ8EyIhs15L9fTOHyyy6r1DyrGV086ejUEyq04okIS5YsYeLEifzxxx+Yw0IJGdqPwIE9UQG152Ujmkbemq1Y5/2B80QKTVu24MX/jOf666/HZKr5zTT1mbS0NCZMmMCHH36IOTyUiBuuwNS97Tk1wxbsPUzqG1Pwi40k/vlbMIUGVmCJqxbHsVSOPTsFY0ggDf/vboyhle9r6Nh/lMzPf8B5Mo1Lhg/js/c/oFmzypmDr5rRxZOOTj2hQiqepmnMnz+fiRMnsmbNGgKiIggZ2h/LgO4oc+1p2iiOaBp5G3aQO/d3HEdPEtesKROe+w833XQTfn5+1V08nSLY7XbeffddXnvtNWx2O2GDehF+zaXIOYp2x6ETpLz2GabwYOJfvA2/iNo/an3+7qMcf2Ea/k0aEvPUXRiqoI6Ky4114XJy5v2GEQP/euQR/v3UU4SHh1d63lWILp50dOoJ51TxcnNzmTZtGpMnT2bv3r0ENIwibNiFmPt2gVrgSFtWRNPI37yb3Lm/U3DoOJENY3jo/vu59+57iImJqe7i1WuysrL46KOPmDRpEqmpqYT26ECD0UPRGp17k5TzeDIpL3+KIdBM/Eu34R8VVgElrhnY1u4m6Y3vCOjUiugHb0KV04H+n+LOyMb6/UJyV28hMCSEJ594nEf/9QghIVXX27YS0cWTjk49oVwVb+fOnXz22WdMmTIFq9VK8HnNCBtyAcYe7Wp0t+1zRUQo2LoX+6+rsG/dg9HPj1Gjr+FfDzxI79699R56VUjhM/j5559js9kI6dSGyJGDoWV8haTvSk4n5eVPwQDxL96GOTby7CfVMrIXryf1k3kE9+9G5O3XVOnz6zySRO7sJdg27iQgJJg777iDRx56mISEhCorQyWgiycdnXpCmSteRkYG3377LdOmTWP9+vUYjEaCe3Ykcmh/JCGuMstYI3GdTCNvyRpy/lyHFDhp0qI5d95yK+PGjavtL4AaS0ZGBrNmzWLKlCmsXr3a+wz26kTk8IFI44qbmNadkU3ySx8jLhfxE27F0rTuWhfTZ/xO5vd/EHblRYSPurTK83ccPIZ90Upy125FAYMvHcLdt93O8OHDsVgsVV6ec0QXTzo69YQzVrwjR44wZ84c5syZw7Jly3C73QQ1jyeobzcsvTuiQmu//8e5ouUXkLduO/krN5O36wAAnXt0Z/TIqxgxYgTt27fXLVLlREQ4cOAACxYsYPbs2SxbtgyPx0Ngk1iC+ncnsG8XCKnYIS/cWVZSXv4EzZZH4+dvIaBlbIWmX9MQEVI/nkfOrxuIvPlKQgaVb46/c8WdkY39t7XkLl+PJzuXwJAQRl9zDVePHMmgQYMIDq4VvzW6eNIpH0opD7ANMAG7gJtFJK96S3U6SqmLgMdFZHgJ4XOAQ76gdBG5+BzzugXoISIPlHK8CxAnIgvKkNZDwL3ARuA2YD4QBbwiIjPKWcTTKl5KSgrLli1j6dKlLF26lO3btwMQGB+LuUsbQvt2gcZ19yv8XHGnZZG/Zgt5G3dScOAYALFN4hky+GIuuvBCBgwYQPPmzXUxVQoOh4OdO3eydu3aU89gUlISAIFNYrF0bUtIjw5I00aVcg89VhvJL3+KJyuHxv+5icDEJhWeR01EPB6SXveOQh79wHUE9qi+OR9F0yjYdRDHqi3krtuGVuDA5OdHvwsHMPTiS+jbty89evQgIKBGDnmiiyed8qGUsolIsG97OrBBRN4uctwoIp5KyrtMaZ9FPP0t/BzLdAtnFk9nPF4s7m7gMhE5pJTqDbwmIheeS/nmzp0rmzdvZvPmzWzavJnDh7y60WQxY27VjKCOrbF0bYuKqXv+HpWNO9tKweY9OLftxb77IJrN+w3RICaabl270r1rNzp37kzHjh1p3rw5gYG1t/v7P0FEyMzM5ODBg6eW3bt3s3nzZnbu3Inb7QbAHB6KX2ICIe3Ow9SmBYYKcAA/Ex5bHimvfoY7JYPGz95IYPuESs2vpqE5nBx/fhqOQ8nEPHErlsQW1V0kxO2mYO8R3Nv2Ydu8C2dSKgBGk4n2HTvSo2tX2rdvf2qJi4ur7kFtdfGkUz6Kiad7gE7A98B44CTQBegIvApcBJiBD0TkE594mQBkAInAMuA+EdGUUh8B5wMBwA8iMt6Xx2FgCjAEeB/IBF7wpXsAuFVEbEqpocC7QDpey02LsoonpdR1wP/hrRjzReSps4TfCjzju969gENEHlBKjfbdBw+QA1wM7Pdd0wngFaAtYBORN31pbQeGA0/jtTbtAb4G7gSi8VrJRvn2rwTcwGIRefxsfytf+oJSBMRGY4hvRFCLJpjbNEc1aVRlvW/qA6JpuJJSce89guvAMfKOJOFKSkU8f2n9BjHRtGzRgvNatCQ2Npbo6Giio6OJiYkhOjqasLAwgoODCQoKIjg4uNqGStA0DafTicvloqCggNzcXGw226l14XZubi7p6emkpqaSkpLiXaemkJycjC3Xdlqa/hFhmJo0IqBZYwIS4iC+IYaGDarMQqflFZDy+uc4jyUT98wNBHcp/yjktRlPbh5H/+8LPDk2Gv7f3fjHl2/S5MrCk2vHceAo2oET5O8/jON4Mh6r/dRxP39/YuPiSGjWjIRmzYiPjycqKooGDRqctoSGhhIYGEhAQEBFj9umiyed8lEonpRSJuBHYCHe5rv5QAef1eQuIEZEXlJKmYEVwGigmS9+O+CIb/sTEflBKRUpIplKKSOwBHhIRLb6xNOHIvK6UioKmIXXOmNXSj2FV0S9DuwDBuEVKzOAwDI0280EvgRWA92BLGAx8B6wtpTwNb6lO16B9DuwySeetgFDReSEUipcRLKLW56UUs9TgngSkcO+a+0hIulFhZ5SKhJYBbQRESlMuyx/r0bP3Sv+TRphsNSeASzrCuJ240pKw3UiBU96Fq60TNypmbjTsvBYbYjTdcbzDSYTRosZg78fBqMBZTCijAYMRiMGkxFl9O4rZQDf76uI/G37rzXetaaheTxoLjfi8aC53WjuwrUbtH/wW60UxpBADCHBGEODMIQGYwoNxi86EmN0JMaYCEzRkVUyzlBpaAUOUt/4EsehY8Q+MZaQ8xOrrSw1AVdqFkef+RyMBho9ey+myJo9DpPHasN1IhVXUgqejBzc6dm4M7JxZ2bjybKeet5Lw2AyYTT7exeLGYOfyVuHjEaUwVuflNGAMhq99czoq1sGA0oBSnlFvlIc/WNVlYunujMgjE6AUmqzb/tP4AugL7BWRApFyRCgk1LqGt9+GNAKcPriHQRQSn0L9AN+AMb4RJcJiMUrsLb6zi/09+ntC1/h+2L1xycqgEMiss+X7tfAXaWU/8+iokopNQL4Q0TSfPvTgQF4fYVKCqdY+AygtS98BTBVKfU9XpFXUViBAuBzpdR84Oeynmhp1QwFqKr/YNIx+WFsGoel6ek9FTWfG5rmcKJZ7XhybXisdqTAgVbgRBwOxOFCK3AgDifi9ngtWB4N0TQ8Hg23xwOahng00DRQBt83sfL+L7To+H70KbKvDApMvpeH0QiFQsxkhMIXickERgPKz4TBYkZZzBgs/r61GWXxx2AxYwgKQPmaUWrCc+ax51Ow5yAFuw/hSkrFlZKOJysH8WgYAi1kzviN3GVbsLSMI6B9ApaWcafKX1/wi4kg/rlxHHtuCmlvf0mjp+/GWIPmoSyOITQEv9AQaHu6tVDD9yGQV4Bmz0Oz5aHZ8vHY8pACB+J0oTmdiMOFOF2Iw4nmcOLxeHD76o1oGng8iMsFBYX7f62Lf4gkfPXqo4dvevrtkspZWejiqe6QLyJdigb4fqjtRYOAB0VkUbF4F/H33l+ilGoOPA6cLyJZSqmpQNE+rIVpK+B/InJdsXS7lJBuWSnt1/5Mb4ES8xKRe5RSvYBhwGZfuYrjBor+Wp+1r66IuJVSPYHBwFjgAbxWtrOyccxD2F3OskTV0amVuN1uFv08nx+//Y7f//crHrcbo9mPgKZRWBJjMAY2wWA2oRW4cWXZyD94AtvKHQCYIoIJvqAD4Zeej39cVDVfSdVhTmhE3JNjOfHS17je/5b5i34lLLzuDBD6TxDALRqapuERwSMamoh3wWux1fCKp1ELv/64qsuni6f6xSLgXqXUbyLiUkq1xuvzA9DTJ5aOANcCnwKheAVSjlKqIXAZ8EcJ6a4GPlBKnSci+5VSgUA8sBtorpRqKSIHgOtKOLc01gCTfE2CWb5zJ+NttjtTeAO8FqHRwBYAX/5rgDVKqSuAJkAuUHRo3cN4fZxQSnUDmp+tgEqpYLzNkAuUUqvxNk2WiUhLIJGW+uGorFO/KCgoYMqUKbz55pscOnSIgKgwGl11PpG9WuPfKgaDf+mvHVdOHjnrD5K1ci85v6wl++fVBHVvRYOxg7G0qNtDFxQS2LEFsU+O5eTr3zF82GVs+XMVYWH1U0CVlcM3PV3lPct18VS/+BxIADYqr1kqDRjpO7YKrzN5R7wO4z/5HMY3ATuAg3ibv/6GiKT5fIi+9flSATwrInt9TX7zlVLpwHKgQ1kKKiInlVLP4PVdUsACEZkDcIbw533XcRKvc3qh5/UbSqlWvvhL8Iqqo8DTvqbOV/D6id3k21+H1+H8bIQAc5RSFl/aj5Tl2moTLpeLbdu2sWXLFg4dOsSRI0ew2WwUFBRgMpmIiIggOjqaxMRE2rVrR5cuXepN7zWd0xERZs+ezWOPPcahQ4cIaxNP+/HXEnB+AspYtiY4v7BAogZ3IGpwB1yZNlJ/2UzK7HUcfeJjQvq2I+rmofjVoalaSiO4e2tiHx/DkTdm0G1gPzYvXVlXplGpM+gO4zqVMlSAzlmpsRXv6NGjpwboXLFyJQX5+QAog8IvMgxDoD/4mRC3B81egDvHjri83dyNfia69ujO8EsvY8yYMbRt27Y6L0Wnijhw4AB33303S5YsISShIQl3X4K5c3yF9Npz2wpInrWWlFlrQCkaXDeI8Mt61enpiArJXb2Tk2/NpGWXDmz4bZlugSodvbedTtWji6dqoUZVPLvdzsyZM/nss89YuXIlAAFNGhLYqQUhbZpB8xj8osNLHEZBNA13Wg6Oo6m49hzHtv0g+ftPgAgt2yZy1y23cfvtt9OgQeWOF6RT9Wiaxscff8wTTzyBxwDxN19IxGWdymxp+ic4UrI58sFictYdIKBVHA0fHoV/bN33h8pdtYOT7/xAk9YtWf/Hcn1C7JLRxZOOTj2hRlS81NRUXn/9dT777DOsVisB8TGED+pKQM9ETLHlFzvurFxsq3ZiX74d+56jmMz+jBo9mmcef4LOnTtX4BXoVBepqamMGzeOxYsXE9G9JS3+NQxDVOX2DhMRsv7czeHJCxGPRswdlxNyYZc6P3K8fdM+kl6fQYPYGNb9sVyfw/Hv6OJJR6eeUK0VLz09nTfeeIPJ779PQUEBYRd0oMHQXhgSG1f4i8hxJIXcRevJXroZrcDJwKFDePWFF+nZs2eF5qNTdaxcuZIxY8aQkp5GszsvJuLyTlUqYBxpVg6+Phfb9mOEXtiJmLuvqNYxq6qC/N1HSXp5OgFBQSxbvISu+kdIUXTxpKNTT6iWipeZmclbb73FpPcmYbfnEd6/Ew3GXIQxtvKngfHY88n5ZS1ZP6/Ck5tP74sG8OZLL3PBBRdUet46FYOIMGnSJJ544gksDcM5799X49e8eppjxaOR9N1Kkqb/iSWhIbFPjsWvjk9n5DiczImXvoYCF9Onf82Yq0ZVd5FqCrp40tGpJ1RpxcvOzuadd97h7Xfexmazey1NYy7C1LjqfUa0fAc5i9aRNXcl7hw7fQcO4M2Jr9KnT/XMKq9TNpxOJ3fffTdTp04l6oI2JDwyDBVU/dae7HUHOPjaHDAYiH1sNIEd6/YUL64MK8mvf0f+gSSeef4/THxufJ1vtiwDunjS0aknVEnFs1qtTJo0iTffegtrTg6hfdoTNeYiTE2r3+lUczjJWbSOzNkr8OTYGTB4EK9PfJlevXpVd9F0ipGdnc0111zDkiVLaHLjABpe37dGvbALTmSy74UfKDiRScxtQwm/rHd1F6lS0RwuUj6cQ+7ybVw0bCiz/vsNERER1V2s6kQXTzo69YRKrXg2m43JkyfzxptvkpWZSWjPtkSNHYSpWfWLpuJoBU5yFq4lc84KPNY8Bg25hFdfmsj5559f3UXTAY4cOcKwYcPYvWcPLf81jLDB7aq7SCXisTs4+OY8slfvI/KKXjQYN7RSev3VFESErLkrSZ/+KxHRUcz+/gcG9O9f3cWqLnTxpKNTT6iUime32/nwww95/fXXSU9PJ7RHIjFjB2No3rAysqtQtHwH1oXryJi9HI8tn0svv4yJE16ke/fu1V20esv69esZfsUVZNlySHzuGiyd4qu7SGdEPBrHPv+NlNnrCOnZmoYPj8Zgqf6mxcqkYP8Jkt/+AVdaFg899iivTngJi+Wss0vVNXTxpKNTT6jQipebm8sHH3zAW2+95RVNXVsTc91gDC0bVWQ2VYKW78D6yzoy5nhF1OXDh/PShAl07dq1uotWr5g3bx5jx46FUDOJE67F1KT2NAulzFnP0U9/JaBFI2Kfvh5TRGh1F6lS8eQVkD5lITm/byI2oSlff/ElgwaVaZrNuoIunnR06gkVUvGys7OZPHky77zzDllZWYR1SyR6zEUYWsVVRPLViievANsv60ifsxyPvYBhV17BxAkv6uNEVQHvv/8+Dz/8MMGtYjlv/DUYI2rflDvZq/dx4NU5GMMCiXvmBsxNa7719VzJ23qQ1E/m4UzOZPioq3j3tTdo2bJuO9D70MWTjk494Zwq3p49e3jvvfeYNm0adrudsJ5tiRk9ENWi7r0gPPYCchesIX3uSrS8AoaNuJIXnvuP3pxXCXg8Hp544gneeecdGvRJJOHJ4bWy2Utzecjdcpj033aQ9ecuEDAEmjEGB2CMCMbcPJaAdgkEdW2FwexX3cWtUDSHi6xZf5I5byXKrXHLHbfx0vgXiI2t0xMr6+JJR6ee8I8rnsPhYMGCBXz66acsXLgQo5+J0H4dibqiL6oGOoJXNB57Ptaf15Dx80q0PAftunTiX/c9wNixY/VJUyuAvLw8brzxRn766SfiRvYi7o6Lap3DtTPTRsqc9aQt2IjH5sDgbySkRRQBjUIwWkx4HB4K0mzk7k/DU+DGEOBP6IWdiLiyH34Na0+zZFlwZ+WSPXMZmf9bj9FgYPTYa3m67o7wr4snHZ16QpkqnqZprFmzhq+//prvvvuOzMxMLA3CCL2kB+FDekBY7WtOOVc89nxsS7eR87/1FBxNwRIUyMiRI7n+2rEMGTIEs9lc3UWsdaSkpHDllVeybt06mt4xmJira1dPR0+Bi5PfryT5hzWIR6NR/5bEDW1DdPcmGM2mv8XX3BqZW05wfNFuTi7Zi2hC5LCeRIwehDGobjlbO5MzsS5YS/aSDWgFTrr36c09t93O6NGj69JEw7p40tGpJ5Ra8Ww2G7/++ivz5s1j/vz5pKSkYDT7E9KzDQ0GdcPQvmm9mFH+bIgIBXuPY1+yiZw1O/HY8gkMCeaK4cMZdtnlDB48mLi42u/7VZmcPHmS6dOnM2HCBGz5eTR/fDgNLqyZQxGUhnXrUQ69NQ9nqpW4ixM575aeBDcJL/P5Bek29k1dx7Gft+MXHkT0vSMI7p5YiSWuHjy2fHJ/3UDOb5twnEjHz9+fSy4dwlVXjuCyyy6jcePG1V3Ec6HmiSellAfYBpiAXcDNIpJ3hvh/AI+LyPpzKphS0cDPgD/wkIj86QsfAdwqIiN9+88At4vIeb79K4A7ReTKc8zfJiLB55JGGfLoD3wMuIA+IpJf5Fg88AHQDjDgvRdPiIhTKdUFiBORBb64zwM2EXmzgso1FbgQyPEFTQGigGUi8qtS6jDQQ0TSKyK/f1i2w8AxEelfJGwzYBKRDmc4LwHoKyLflCPPlSLS9yxx/unzIuAVAEePHmX9+vUsX76c5cuXs2nTJjweD35BAQR2OY/wnm3x69YSQ2Dd+iKuSMTlJm/7IfJX7yZn7U48Vu9PVMvEVlwycDA9e/akR48etG3bFpPp75aIuo7H4+HEiRNs27aNzZs3n1r2798PgDHYQqvnryGkfZNqLmnZ8U7PsoKkb1YQGBdGh8cHEdW1/AIge3cKW19bgu1gBg2u7E3kDUNQprr3kSIiOA4kYV+6FevaXbjSvT/zie3bMbD/APr27UufPn1o2bJljRoI9SzUSPF06qWglJoObBCRt88Q/w8qRjyNBS4TkZuLhUcD20WkoW9/LhAPDBWRVKXUK0C2iLx2jvmXSzwp79OmREQrQ9yPgTUi8mUJaawBPhKRL5VSRuBTIFNEnlBK3YJXvDzgi/885yCelFJGEfEU2Z8K/CwiP5QS/zBnEU9KKZOIuMtTnrOU9TCQDVwhIseUUm2Bbzm7eLoI73M5/B/kddp9OUvcf/S83HXXXbJt2za279iBLTcXAKO/HwGtmxDYpgnBnc7DmNi4xv14aw4XnhwbWoET5e+HMTQQYw0TdaJpOI6k4Nx2GPvWA9h3H0XLdwBgtlho3SaRdoltaN26Na1atSIhIYFGjRoRGxtLcHClfi9VOCKC3W4nLS2N1NTU05Zjx45x8OBBDh48yOHDh3G5XKfOC4iNQrP44TicjKVJA1pNGIOlYe1pwvHkOzn42hyy1+yn8aVtaPfwhfhVwFQxHoebXR8u5+jsbYR0TiDmsbEYgwIqoMQ1ExHBeSyVgk0HsG/eT96+46fqSkBQEG3atKFThw60bduWhIQE4uPjadKkCXFxcTXtI6TGi6d7gE7A9xR5ESml3gfWi8jUouJJKWUDPgEGAlnAWBFJK5Z+M7yWjWggDbgViATmAgHACf5uldkLXC4i+5VSG4BZwA4Rma2UWgo8Cxwtnq6IHC0pP194c+AbvBa2hcAjJb0MlVKPArf5dj8XkXd9Vo1fgN+BPsBIETlS5JzBwJu+tNcB9wLjgNfxWndWisgNxeKPF5EBRcJCgUNAc2B7kXvzCtAWaAq08K3fFZH3fOfdCDyE14K3BrhPRDy+v83bwKXAYyKyvEheUykmnoqG+QTMDLx/V4DrfX+LqUAm0BXYCPwXr2UtEDgA3CYiWcWekSi8z06CUqo98KWvrAZglIjsK3b/D+MVkk4ReVMpNQGwA+NEpIPPw0UsAAAgAElEQVTvb/FfIMh3ygMislIptdp3nw4B04D3gFeBiwAz8IGIfOITWeOBk0AXEWlXWAeUUsHAHCAC8AOeFZE5vnL9I/FkCQsRU5NozE1jCEqIw69ZDMaEGJRfjfpBQnO6yNtyANv6PeTvOIwrOfNvDY6m6DACWscTdH5bgrq1qnE+I6JpuE5m4jyQhPtgMnnHU3EkpeNKywbt9IsJCAokpmFDIiMiCA8NIzQ0lNDQUEJCQggJCcHf3x8/P7+/Lf7+/hgMBgp/T0XkjNsejwen04nL5cLlcp3aLinM4XBgt9ux2WzYbDasuVZyc23Y7TbsNjseT8n63hQcgH+jSIwx4VgaNsDSMBJTkyhUfBRZs/4ka84KQru3oOUzIzEF1R4/MWdGLvuen0newVTaPTiAhKs7VXgexxfuYtsbv2GJi6DRMzfW+QmHCxGPhvN4Gs59J3AfTSPvWAqO42m4M62nxTMYDIRHRhARGUmDiEiiGjQgIiKC8PBwAgMDCQgIwGKxEBAQcGqxWCyYTCaMRiNGoxGDwXBqu/hiMBgwGLydFZRSpyxgRddFtzt16lTl4qnMv9RKKRNwGV5hUVaCgI0i8phS6j94X0oPFIvzPvCViExTSt0GvCciI33xT1lXirES6OuzyOwDVgOXKqV+xivu1gEzi6cLjCwpP1/4JLyWnq+UUveXcg+64xV3vfAq3TU+sZYFJOIVYvcVO8cCTAUGi8hepdRXwL0+0dWPki087YENRQNExKqUOgokAKfdG5/lqQ1eMRMC7FFKfQScB1wLXCAiLqXUh8ANwFd4/zbbReQ/JV0r8IZS6lnf9rgSjltFpKdS6ibgXaDQotMauNgn0LYCD4rIUp/IGQ/8q5T8AO4BJonIdKWUP1Ca2eUHvPf0TeAK3zUVljEVuERECpRSrfBapXoAT3O64L8LyBGR85VSZmCFUmqxL42eQAcROVQs3wLgKt/fIgpYrZSaK+VwHGw65fEabRJ3Z+WSvWANOb9uwGPN8/ZK6pJA4KB2+EWHYQzwQ3O4cGbYyD+cSu7Ww+Su2IEy+xF6YWcihvfBvxomHS4JZTDg3zjKW54BnSj0hhGXG1dKFq4MK54sG+7sXNxZNjKzbaTZc5HkdDwHHWj5DrR8J5LvQNxlMkSWD6MBZTKijEaUyQCnto0YLP4YAvwxWPxRDfwxNG6IIaApYRZ/bxf80CCMYUGYwrxrY2hQiV3wtXwHyZN/wrZmF9HDutL0niEYTLWnR50jJZs9T3+DOyeP7i8Pp2GfhErJJ35oWwJiQtjw3AJOPPcFceNvxT+uZjzPlYkyGjA3a4i5mXfIk8L+h568AtzpVtwZObjSc3CnW/FY7aTY8jlpS8Oz+yiarQBPXgHidCHOCm90OCOtf3yh656r/7OpKvMsi3gK8PmUAPwJfAGc0f+jCBpeCwXA13gtRMXpA1zt2/4vXmvM2VjhK4MRWAWsxSsougJ7fC/O0tItLfwCYFSR8JKa/foBP4mIHUApNQvoj9dKdkREVpdwTiJwSET2+vanAffjFRyloSjZobi0cID5IuIAHEqpVKAhMBjoDqzzvagD8IoLAA/w4xnK8EQxy1Px498WWb9TJHymTziFAeEistQXPg2voD0Tq4B/+/y9ZhW3OhUhE8jyNe3uAor64PkB7/v8wjx4xVxJDAE6KaWu8e2HAa0AJ7C2BOEE3vv/slJqAN5nuzHe+5x8luv6G/FBETg8LqrB2nxG3HkFJP34O0mzl6K53IT3PI+Yy7sS0iUBg1/pTYiiCbbdJ0hftIWM3zeR8+sGYob0pOkNQ/GvqaM7m4HgcCh1DEHBI4JHNDQRNNHwiIZ4NDxuD5rbjXg0xO1Gc3lAQJC//qRKndpWGP7aVgplNGIwGTAYjSg/E8powKAMvlO8/wyF20phUAoD3nV5n5n846nsnvgl+SfSaHLXYBqOPL9GC/jiFJzMYs/T36DlOej5zlVEtK3cMc0adIun93tXs+aRnzj5/Je0m3gfAfF1bxy1MmEOhogo7y/k3xA0Ob2ueDxuPC43HocTj9OFx+lCc7pAE0TTfGsBTTu1PnVMfMdECj1DC7PxreWvl+CpOFT5WC1lEU/5ItKlaIBSyo23WaWQstrpy/KFXpY4K4EH8Yqnz0Qk12fhuQivsPon6UoZ4hRypl8aeznOKY0d/CXkvIl4m+2a4G3+Kml0QEeRbQ/ev60CponIMyXELyirP08plHbfSrsPRSn6/Jx6dkTkG6XUGmAYsEgpdYeI/FZKGjPwOtTfUiz8ESAF6OzLo6CU8xVeq9ii0wK9zXalXcMNeJt7u/sseYcp+7N/Gr8Nfag8p1Uqs2bN4v6H7ic5OZmoC9vT5OYLMcWWzQ9GGRQh7eIJaRdP/K0XkfzdKlJ+Xkf20i28OPElHn/4kVNmeJ2qZ+7cuYx78gUwCB1fubHGz1FXnIKkLHY/OR1xuej5zlWEt46uknxDW0bR+92rWfvobPY++zGrl62gQ9tSXSt1qo9FZ49SsZT31+wI0E4pZfZZGAafIf3CL/vrgeUlxFkJjPVt31BKnOLsBOLwWn0KTXWb8Tb7rDxLuqWFrygWXhLLgJFKqUClVBBwFV5r3JnYDSQopc7z7Y8Dlp4hPsASINDXJIavefItYKp4ezrm4m2eOxtLgGuUUjG+dCJ9Pl8VwbVF1quKHxSRHLzWocJecUWv+zB/CcDC5wOlVAvgoM9fay7eJtjS+Amv1bB4pQkDTvoc9sfxV9Nf8Xu2CLhXKeXny7u17296JsKAVJ9wGghU1L2sVlJTUxkzZgyjRo0iL8RAl0m30/zpK8ssnIrjFx5Ek3supsMndxLUIZ6nHn2czn16sG9faYZEncrC7Xbz3HPPMWLECAyxobSffGutE05uax57/zMDcbro9fbIKhNOhYS0aECvd6/C7XFzweABHD1+tErz16mZlEs8icgxvE7jW4Hp/CVgimMH2vucugcBE0qI8xBwq88/ZhzwcBnyF7zOz+kiUtiFZBVeh+lC8VRauqWFPwzcr5Rah/clWVK+G/H62qz15f+5iJyxnVVECvD6Sc1USm3D29zzcRmu7ypgtFJqH7AXrwXl/3xRfscrXjcrpa4tJRlEZCde5/nFvuv9H1BRY/SbfVaih/Fae0riZry+U1uBLvz1938Tr3BZiXcIhEKuBbb7monb4PXNKhERyRWR10TEWezQh8DNPgfx1vxlRdoKuJVSW5RSjwCf4xXhG5VS2/F2bDibJXY60EMptR6vwN59lvg1nqVLl9K5c2dmzf6JZrcOotXbN+LXumIs4JbGkbR84RqaPzqM3Tt30a5jBz78/JMKSVvn7Bw5coSBAwfy0ksv0fDSLrR6/XpU1Nm+D2oWmtPNvhd/xJlqpfvEYYS1qlrhVEhwQiQ9Xr+SvBw75w/sQ3pGlY/SolPDqNRBMv9pDyQdnXpEtY5Oq2kar732Gs8++yyBjRvQ6v+uxpRQeT2KnBm5HHpjHtYtRxh+7dV8+/m0WjcsQG3i+++/56677qLA7STh/ksJHdi2uov0jxERDr4xj8zfd9DpuUuJv7g098WqI2PjcdY9OZeEDi3ZtnwTgYH1b4T/GkrNG6rgnBLXxZOOTmlUm3jKzMzkpptuYv78+URd2J5mDw3FEFj5k7+eGtRw+nIaNW/Kwp/m0rlTnZxnq9rIzMzkkUce4auvviKibVNaPjUC1bB2/gSf+O8ykr5ZQavbe9PqppozXUzysv1sHL+Qnpf0ZdWCZbovX82gboknHR2dUqmWird27VpGjx7NiaQkEu6+hIhhnau8x5V1yxEOvj4XsTt574PJ3Hv7XVWaf11ERJg5cyYPPvgg6ZkZNB7Tl5jr+mCoYYOslpX0/23l0NvzaXxZWzo9NbjG9Qo8/MMWdk5exg0P3sLX73159hN0Kpsqf0B0yayjUw8QESZPnky/fv3IcObS4e2biRzepVpeSqGdm9H+/dsIahvHfXfczahxY8nLK3XGJ52zcOjQIUaOHMm1116LM8KfzpNvp9G4frVWOFm3HOHwe7/QoFs8HR8bWOOEE0CzUZ1oOqIj0ydP5eUP36ju4uhUA7rlSUeneqiyime1WrnjjjuYOXMmDXq3pvljw1HB1T+itHg0kqYvJ+m7FTRLPI9Fs38mMbHuTchaWeTm5vLKK6/w9ttvoylofGN/okZ2Rxlr7zdx/tF0dj32FZYGgfT9YDR+IdX/nJaG5tZY//Q8MjYeZ9aC2YwcckV1F6k+ozfb6ejUE6qk4m3evJnRo0dz8NBBmt58EVGjeqIMNetLPmfDQQ6+MQ+DS+OLzz/nxutKGylEB8DpdDJ16lTGjx9PcnIyDS/uRJNbBqIa1G7nZVe2nV2PTEMcTvp8OIaguBo6uGoRXLkOVt0/E2dWAetXr6WjPgZUdaGLJx2dekKlVjwR4dNPP+Xhhx/GFBZIy6dHYG5bUaNUVDzONCsHX51D7s7j3Hz37Xwy6QPM5pprdagOXC4XU6dOZeLEiRw5coTwdk1JuPti/FrX/lGvNYeL3U99Q/7hVHq9exUR7RpVd5HKTF5SDivu+Z6A4ED2b95NdFT1DKdQz9HFk45OPaHSKl5WVhb33Xcf3333HQ3Ob0XLx4cjoTVrst6S0NweTny5lORZa2jduR2/zJpHixYtqrtY1Y7VauXLL7/k3Xff5fDhw4S3bUL8jQOwdG1SI/2B/imiCQde/omslXvoOuFyYgeUOl9OjSVzaxJrHv2J0MaR/DTlewYOHHj2k3QqEl086ejUEyql4v3yyy/ccccdJKem0OTGAUSP7lXjmunORtbKvRx6+2cMGrz66qv864GH6mV38P379zN58mS+/PJLcnNzCW/flPjr+mHp1rROiKZCjn3xO8k/rKbNvRfQYmy36i5OuTm+cBdbX/mVgNhQenU8n0lvvE2nTmeaJEGnAtHFk45OPaFCK15mZiZPP/00n332GaEJjWjx+HD8Wtbe5gNHmpWjkxaSveEA3fr25LupX9OqVYmzktYprFYrM2fOZNq0afz5558YTSYaXNiWuJE98Tuvyuc+rXRSF2ziyOSFNB3RkfaPXFjrReHuT1dycPoGAuLCyD9pZciwy3jh38/Ru3fv6i5aXUcXTzo69YQKqXiapvHFF1/wzDPPkJWdRexVvYgd1x/lXzu7qRdFREhfvJVjny5BnG7uf+gBXho/gdDQmu9I/E+w2+0sWrSIH374gdmzZ5Ofn09Ik2giB3egwSUdMUbWrilVykrO+gPsHT+TqPOb0uPl4RhMtd+6KJqw8bkFpKw8RMzFHchcuQ+3rYCe/fow/plnGTp0aL20olYBunjS0aknnFPFExEWL17Ms88+y/r164nsmEDCfZdirMQpVqoLZ6aNk9OWkfq/LYRGRvDi889z1x13YbHUfD+u0khOTuaXX35h9uzZLF68mIKCAsyhQYT3TyR2SFdMraJrvRXmTOQdSmXXY/8lKC6U3pNH4RdU+SPcVxXuPCerHvyRvCQrrSeOxb4rieRZa3Cm5xLbNJ4H7r6X22+/nYYNa7+jfw1CF086OvWEclU8TdNYvHgxL774IitXriS4USSNb76QkAsT6/TLFsC+7yTHP/0N6/ajRMQ04JknnuKuO+8iLKzEebxrFFarlaVLl7JkyRJ+/fVXduzYAUBgwwjCep9H9AVt8W8XW6vHaCorzoxcdv5rGgbR6PPRGAJr6fQxZyI/1cbKu2eg/E20eecWjEEWslbsIWPhFnK2HMZoMjLksqHcfMM4hg8fTlBQ3bQuViG6eNLRqSf8o4qXnp7O9OnT+eCDD9i3bx+BMeHEXduX8Es6oPxqfxNdWRERcrceJWXGKrI3HcLfYuaa0aO5+4476devX41oEtE0jd27d7N69WrWrFnDmjVr2LZtG5qmYTT7Edq+CeHdWhDSNQH/5lF1XvQWxZPnYPeT03GcyKTX5FGEt669fnlnI3tXMqsfmkVwq4a0evkGDP4mAPKPZZC5cAtpf+zAlWnD32Lm8mHDGDXyKoYMGUJMTN3zbasC6rd4Ukp5gG2ACTgEjBOR7ApM/7SJipVStwA9ROQBpdQ9QJ6IfFXsnATgZxGpsNHPlFK9gUmA2bfMEJHnlVLPAzYRebNY/AnAMhH5tQLLcBjvtaefQxpdgDgRWeDbf54Syl8TOMO9fR64E0jzBS0UkaeroEhnrXgnTpxg8eLFfP/99/zvf//D4/EQ3q4psSN6ENjnPAz1SDSVhH3fSTIXbiPtj2148pxERDVg5JVXMuzyYfTt25fY2Mod10pESEtLY8eOHWzfvv3Ueuu2beRarQD4BwcQ2DqW0LaNCeuUgH+bRqdeovUNze1h3/MzsW46TPdXhtOwd0J1FwkRIS/JSubm41j3pZF30oozOx9EMPibsEQHExQfTkSHWMI7xP7j5sWk3/ay+YVFRF/cnmaPXnGaUBaPRu6O41j/3EP68l24su0AtO/ckcuHDKV///706tVLF1Nlo96Lp1PiRik1DdgrIhMrI33f/i34xNMZzkmg4sXTHmCMiGxRShmBRBHZWZXio4LE0y0UuX/nWn6llFFEPOUtz1nSfp7SxVO5ynyO5T2t4rlcLnbt2sWmTZtYt24dv/32G7t27QIgKDaS8P5tiL6oPX7No8qZXd3FU+Ake/U+clcfIHPdfjx5DgAaN21Cn569aNOmDYmJibRo0YKYmBiio6MJDQ09o8XH5XKRkZFBenr6/7N33uFRVOsf/5wt6b0nJJAACQmEGghNEaRIBwUUVBAVu3KxYPfKtYKiYkHFwgX8CXJBUJqK0kE6RCC0hCQEkpBCerLZen5/7AYREkwwJBsyn+fZZ2dnzsy8MzvvzHfe855zyM3NJTc3l6ysLFJTU0lLSyM1NZXUtLQLIgnAwd0F53A/nFr44x0ThmNkINpm3o2uq4hrgZSStDnryFt/iNhnbqb5iHYNak9Fbilnfz5GxvrjlKVb38+1rlrcm7nh4uOMUAtMFWbKsssoySpFmiUqrYqAHi0IGRRDYO+IGlexJi3YTdJ/99D8vj4EjutdZRlpkZSfOkfZgdMU7D9FydGzSLMFgNAWzekR3532sbG0bduWmJgYIiMjcXC4fvLE6gBFPF0knh4GOkgpHxVCxANzAGdAB9wrpTwhhFgHPC+lPCSEOAislFK+JoR4HTgtpfyquu3bfk/mz8jTDGwPUSFEHDAfKAe2A0OklLE2oTMT6Is1YjRXSjlPCBEMLAU8sEbNHpFSbrvCcRZgFUw5l8y/2IYHgNtsn8+wCrjlNtGzEBgBaIFxUsrjQoibsEazwPpg7iOlLLmCDWlcIp6EEP7A50Bz26xpUsodVZ1/rJHBZNu8DOBtIMa2bkvb9xwp5Ue2bd8NTAUcgN3Ao1JKsxCiFHgfuAV4Wkq5vRp7RwAv29Y/D9wlpcy2nbPq9vkSMAk4gzWytL8m4qkKUbgGmC2l3HypvcBwYCRgAtZLKZ+p7pxfzOzZs2VaWhqVn+TkZPR660Nf4+SAe2wYXp1b4tE5HG24b5Oq2vknWIxmypPPUXE8i5KjZyk5dQ59diFY/nqf02i1ODk74aB1QOugRaVSYdAb0Osr0FfoMRqNVW5f4+yAU6AXmkAPnIO8cQnxwTnMD3ULH7Tersr/VA0Z324n8/+20WpSN9rc33DN9svOFnLq2/1krD+ONFkI6hxIxMAWNOsajFd41YLaqDOScziP09vPkrI+Dd15Ha7NPIiYEEfokLZ/20pQSknCa7+QtTGJyJdH49U75m/tNFcYKU8+h/7EOUqOZ1CSlIk+pxhsz2shBP5BgTQPCyO8eQvCwsIIDg7G29sbHx+fC99eXl64uLjg7OyMs7MzavV1G61WxJOU0s0mUr4DvpZS/iyE8MBapWYSQgzAKk7GCCGeB0qAb4ANQL6U8hYhxCbgYSnliUu2X1ktWIkPsKoK8XQIeEJKuUUI8S5/iqcHgQAp5RtCCEdgBzAOq8BxklK+abPd5W+Ey7+BJ4HNwM/AQillRaUNQAUwCKsw0gshFvBX8fSelPJjIcSjQBcp5RQhxGpgpk3suAEVUkrTFWxI43LxtBj4VEq5XQjRHPhFShlzhfM/mcsjT4OAfoA7cAIIAloD7wC3SSmNQohPgV1SykVCCAncIaX8X3W22rbtDRRKKaUQYgoQI6V8+gr77AAsALpjFbQHgM9rUG33HBBM9eLpgr1CCB9gJxBts8urptXMQgipcXPCIdAThwBPnJv54NIyEOdWATg182kSicP1hcVgQn+uEH12EeaickyF5RiLdUijCYvJjDRZwGxBOGhQXfTReDij8XRB4+GM2tMFrZcrGk9nRSDVktz1h0j7YC0ht0TT8YUBDXL+TOUGkhftJXVZAiqVoM2o1sTe2RbPUPdabcditnB6yxkSFhwh79h5PFr6EPNEH3y7hF1xPbPexK5/raDkVB5Rb9yBe/sWtT4Gc4WRirPnqUjPQ59RgCG3GH1eMYbcYgy5JVj0VQv+i1Fp1KgdtKgdrR+VSoVQqxAqFSq1CoRApVYhVOKyeVXpk2r/yqoWVFO4yrnVla1mf2d2H633i8reKt+dhRAJQDiwH/jVNt8TWCiEiMQaVdHa5m/DGs1IBdYCA4UQLkD4pcLJhk5K2anyR+XD/+ICQghPwEtKucU26xtgiG16ENBBCDH2Irsigb3AfCGEFvhBSplwpYO0Rce+tW3vTmAC1mgWwETgLDBaSlmdN6ywfe/HKtzAKuTet213hZTy7JVsqIYBQNuLbm4eQgh3qj//VbFWSqkH9EKIHCAQ6A/EAXtt23YGKqNuZuD7GtgWCiy1RfkcsP7nV9rnjVgjkeUAQohVV9j2B1VEnqrjYnuLsQrdr4QQa4E1NTgOADovexKNW+Ntat+YUDlocG7uh3Nzpcqzvsnfdpy0D9fh26057aff3CDCKWdXGoff2YD+fDmRw1vR7dHOuPpf3SDKKrWKiJtbEN6vOWmb0tk1Zx+7n/yBsMFtiH7iJrRuVY/HqHbU0G3mCHY+vpzk/yynzay7cGlVu/H71E5aXFsH4dr68vWklFgqjJhKKzCX6DCVVmAqqcBcWoFFb8RiMGHRm6wvDHqT7bcRaZFgsdi+JdIiMdt+S4vlz2WmKoIs1QReqpxbXZCm6sJVF71CnCf+5xef3TP4rXeqL1H32Jt40kkpO9kEzBrgMeAj4HVgk5TyVlsO0mZb+b1YxU8KVqHlhzWKsP8f2CCoPplXYI1I/XLZAiH6AMOAb4QQ716aeH4pUspTwGdCiC+BXCGEr23REaATVrGQWs3qetu3Gdt/KKWcaXuADwV2CSEGSCmPX8mGKlABPaWUukuO7WOqPv9Xsu1i+wTW6NoLVZSvqGHe0MfA+1LKVUKIvsCMv9knXH1fSias56KSi1XOBXttkbh4rOJwPPA4cHNNdrB3zGws0nKV5jUMUkqKi4vJzs7GZDKhUqnw9fXF19fXLlq5KdgX69auY+w77xIQG0qX14fXewMHk87I8c92kP7jYbxaeTHo3ZsIal83rfuEEETc3IKwXs048PVhDi06wvmEDDq8OAifjs2qXMfBy5n490az6/HlpL26nD2/7yKydVSd2FMfSKz3gMrpi2+vVQkbeW3HPv8LfX/7T703UrI38QSAlLJICDEV+FEI8RnWyEeGbfHki8oZhBBngNuxCix/YLbtc7X7LhRCFAkhbrDl39x10eJfgEeEEBtt1U9RNrv8gAwp5ZdCCFegC7BICLEI+ERKuefifQghhgHrpPVKjMT6wK+s7jmINcdplRDiFillZk3sFkK0klIeBg4LIXoC0cBxIcRxKWV0DQ9/PVYB8K5tm51sUbQqzz/WKtOaxL03YP0vP5BS5tiqu9yllKerOI63gT1SypWXLLrYhntqsM+twAIhxEys1/kIYF4N1gNIAx4VQqiAZkB8VYVs1aMuUsp1QohdWHPAaoRaqFAL+xYc+fn5/Pzzz+zYsYO9e/dyJDERXXn5ZeW0DlpaR0US3zWeG3r3ZujQoYSEhDSAxQr2wsaNG7lj3O14RQYSN3M4wrl+hVPpmQIOvLSW0vQCYu9qS9eHO6N1qnsbNE4a4h/rTIsbQ9n06nZ2P7mSto/0pvnYTlVG2ZwD3en27ih2Tf2eG/rfxKFdBwltFlrndjU19gx+q97fRO1SPAFIKQ8KIf7A+kb/DtZqo6eAjZcU3Qb0l1KWCyG2YY3YVJusXUPuxVoNV45VMFXyFdYqxQPC6hm5wGisVW7ThRBGrDlLk2zlOwBZVWx/IvCBbfsmrMnP5kpns+UcPQOsFUIMrKHN04QQ/bAKsaPAT0IIP66cSHdICFF50f0PaxXoXFvOlwarAHmY6s//JuB5W1Xr29XtRFpbEr4MrLcJEiPWqOJl4gloD1RVxTYDWCaEyAB2ARFXOC6klAeEEEuBBNt+anNN7MAa9TuMNRJ4oJpy7lhFoRPW8/xkLfZhl+h0OpYtW8aCBQvYunUrZrMZB1dHPKL8CRkWjYu/O44+LqAWSIvEVFyBLreU/ORclqxcysIFCwCI7dyBBybfz8SJE/H29m7Yg1KoVzZt2sTIkSNxDfWi6zvDEa71+5jJ2ZlKwuvrUWtVDPl4IKHdr22XFQCBHfy57ZthbJ6xg8RPtlN8Moe2z/RH7Xj5sbuF+9B11kj2PLmSLjd048C2vYSGKgKqsWFXCePXE7Yk66+llOMa0IbhQMvK1meNASHEL1LKWxrajnrArhzvzJkzvP/++yxYsIDCwkI8Qn0I6teawN4tcYvyrVECu5SS0tR8cn9P49yWZApP5qB1dGDMuDG8/PxLtGvXsM3TFa4969atY8yYMTiHeBD/3mjUPlXnAF0LpJSkLN7PiS934hPlw8B3+uIRUr+9l0uL5OD8w+z/IgGfmAC6vD0SBy/nKsvmH85k3/RVeAf4sn/bHsLCrpx0rnBFmnZrO22iXMgAACAASURBVAWFJoRdOF5qaiozZ87kv//9L2ZpIfim1kSM6oh7h4B/nNxbdDKXjLVHOfPzUcwVJm4ZMYQ3X32duLi4OrJewZ5Yvnw5d955J56t/Il7ZwRqz/rrh0iaLSR+uJX0Hw/TclA4fV7uhda54SpWUjels+mVbbgEuhH3zihcgqseQqjgSBZ7n12Fp48X+7ftoUWL2rfCUwAU8aSg0GRoUMc7f/48M2bM4LPPPgOVoPmwdrSa0AWHoLp/UzcU6jj9/SHSVvyBsVTPsNtG8NG7c2jZsmWd70uhYfj000954okn8G0XQtdZI+q1qs6sN5Hwxnqyt56iw6R2xD/exS66kzj3Rw6/PLURlVZN11kj8YisuqfwwmPn2PvMKlzd3dj662bat6uz/pibEop4UlBoIjSI4xmNRj799FNmzJhBUXEx4SPb03piN7R+VVct1Om+ywykfneQ1P8dAJNkysMP8OaMN/D19f37lRXsErPZzPTp0/nggw8I6d2KDi8PQuVSf8LJWKJn/0tryP8jk+5PdaPDhL/vgLI+KUgp5Kepv2EsN9Ht3VF4xlTdPUHRyVz2PbcaYbSw+sfVDOjXv54tbfQo4klBoYlQr44npWTdunU8/fTTnDhxgoBuLWj3WB+cI7zq0wwAKvJKSZ6/h/SfjuLi5sK/X/k3T06dpgw30cgoKSlh4sSJ/Pjjj7Qa25moR3vVa+euhiIde57+kdLU8/SZ0ZvIW67YhqTBKMkqZe3D66ko0tPtnZF4xVbdErU8q5h9z62mPLOIr+Z/xb13T65fQxs3inhSUGgi1JvjJSYm8tRTT7F+/Xo8mvvS7rE+eHVv1uBVGyUp5znx2Q5y9pymWUQYH7/3IaNHj25wuxT+nsOHDzN27FiSkpNpP/UmQm+t36omQ6GO3U//QFl6AQPf7UvzXlX3rWQvlGaXsfaR9ZSf19Ft1ki8O1Rtr6G4ggMvrSP/UAYP/esRPpn9ERqN3TaKtycU8aSg0ES45o6Xl5fHq6++yrx589C6OBA5uTvNRrWt984K/46cXWmc+HQHJafz6dGnF599OJdOnTr9/YoK9Y6Ukv/+9788/vjjqF21dP73YNw7BtarDfpCHXueXEn52UIGzO5H856No0+xstxy1j6ynrKccrq+PRyfzlW3rjMbzByfu43TPxymS+9urPt+NYGB9XuOGyGKeFJQaCJcM8czGAx88sknvPbaa5SUltBiVHsiJ3dH41l/zcZri8Vk5szqRJL+uxtjsZ677rmbd96aRXDwte+jR6FmZGZm8tBDD7FmzRoC41rQ6ZVbUHvX7zWlLyhn95Mr0WUWMfC9foR1bxzCqZLy8zrWPforJZmldJ01Ap9O1ffvlPHLcY68twlXDzcWfb2QUSNG1qOljQ5FPCkoNBHq3PGklPz4449Mnz6d5ORkgnq0pN2jN+LYwqOud3XNMJZUkLJoPykrEnB0cOCFF15k+tPP4Ox87RPaFarGYrGwYMECnn76acp05bR5oCdht8XW++DV+nybcMoqYtD7NxMa3ziFtS5fx5qH11OaVfa3Aqr4VB6H3viV4pQ8xt9zJ/M++gwPj8bjz/WIIp4UFJoIdep427dv5+WXX2bLli14RwQQ89gNeHWz7zyQK1F2tpCT83aStTWZwNBg3p81mwkTJij5UPXMzp07mTp1Kvv27cO/QygdnxuIQ2j9djwJUHG+jN3TVlKRU8Itc26mWVztBtW1N8rP61j7iE1AvTMCn47VCyizwUzygj2cWrIfbz9v5syew8S771Z84a8o4klBoYlQJ463e/du/v3vf7N+/Xpcfd1pfU83gofFoNLY97h5NeX8wbMcn7uDoqQcYuM68PaMNxk2bJjy4LjGHDx4kNdff52VK1fi5u9Jm4d6EtC/NUJV/+e9Iq+U3dNWos8r5ZY5/Qnpcn3k/1wQUOfKrEnk1QwoXEnhsXMcnbOVwuPZdO7ehbkffELPnj3ryVq7RxFPCgpNhKt2PCklv/76K++99x7r16/HxduNiAldCBvVDpXT9dcyR5otnP3lOKcW7qX8XDFR7dow46VXuf3221Gr7Sv5vTEjpWTbtm3Mnj2b1atX4+TuTIuxHYm4vRMqF22D2FSRW8quaSsw5Jcz+MP+BHequqPJxkp5no41j6ynLLuMru+MxKeaVniVSIvk7LqjnPhyJ4ZCHX0G9GXW62/To0ePerLYblHEk4JCE6HWjldSUsLSpUuZM2cOiYmJuPp50GJMB5qPjm2wh1t9YjGZyfztJKmLD1ByOp+gsGAee+gxptx/P0FBjbsapyHJz89n8eLFfP755yQmJuLk4UL4uI6Ej+mIyrXhritdTgm7p63EUFDO4I/6E9zx+hJOlZTnlbPm4fWU5ZbT9Z1R+LT/+yR4U7mB9B8Ok/LdAQxFFXTrFc/TU5/i1ltvbar9pSniSUGhiVAjxzObzWzdupUFCxawfPlyysvL8YkMJOL2zvj1bYnaoelFXqRFkr39FGd+SCR3fzpqjZqhI4Yx+e57GDJkiJJcXgPy8vL48ccfWbZsGRs2bMBkMuEbE0KLUbEE9GuJyqlhxbguu4Td01ZgLNIx+KMBBHXwb1B7rjVXI6DAKqLOrErk9A+HKc8qwifAj8kTJzFh/ATi4uKaUvW2Ip4UFJoI1TpeWVkZv/32G6tWrWLNmjXk5OTg6O5MUN/WtBjSDte2fk3ppnhFStMLyFh9jDO/HMVQpMPJxZnhI4Zz68jR9O/fX+kfx0ZBQQF79uxhw4YNbNiwgYMHDyKlxKOZDwF9WhLavw0ukT4NbSYAunPF7Jq2ElNJBUM+HkBgrF9Dm1QrLGYLQiVq7aPleeWseWg9ZXnldHt3FN7V9EReFdJsIXdvOmd/TCR7dxrSbCEsojm3jbqNWwYNok+fPri6utb2UBoTiniyd4QQLwF3AmbAAjwkpdwthJgGfCGlLK9HWyKBD4AYoBAoBl6VUm4VQkwGukopH68ve64GIcQCYI2UcnkVy54BpgAmrOf7PSnlonq07SvgfSnl0WuweQnWPJOMjAz27dvH9u3b2bZtGwcOHMBkMuHo7ox/9+aE3BiJd88w1I7XXz5TXWExWchPOEvullQytiRhKNIBEB3bloH9+hMfH0/Xrl2JiopCpbo+kumrwmAwkJKSQlJSEseOHWP//v3s27ePlJQUANQaNT6xIfh1CSOwZwTOkd52JcTLs4rYPW0lpjK9VTi1s1/hJKUk/2QBZ3ZmkHfsPPnJhejO6zCUGREqgcZJjXuIG54tPAjqGEhIfDDeLT2veL7LcstZ+/B6yvJ0dHt3ZK0EVCWG4gpytqWQvfkUuQlnsBjMaLQa4rp1pXePXnTt2pWuXbvSqlWr68kXFPFkzwghegLvA32llHohhB/gIKXMFEKkYRUrefVkixNwCHhGSrnKNi/WZsOCxi6ehBAPA7cC46SUxUIIT2C0lHJhDberkVKa6tzgOuLhhx+WR44c4ciRIxQVFQGgdtDgExOEd/sQ/OOa494hAJWm6VXL/VOk2UJRUi6F+zPJ3ZdOfmImZr31UnBxdSGmXVuiI9sQGRlJZGQkzZs3JygoiMDAQNzc3OxKTIC1n6WSkhIKCwspKiqioKCArKysyz4pqSmcTjuNxWK5sK5bsBfukX74xATj1SYA17b+aJztMz+uPLOIXdNWYinXM2TuQAJi7HPA6PLzOo6vOMmJNcmUZpYB4B3mQlAbT9wDnHD21GIxSwxlJgrOlpOTXEJhhvWd2qelB62Ht6bNyEicqum0tiy3nDUP/UL5+YqrFlCVmPUmCg5nWn3hj7MUJ+ViNlh9wdHZiVatWxHTJpo2UW0IDw8nJCSE4OBggoODCQgIaEwNMhTxZM8IIW4D7pVSjrhk/lRgNnACyJNS9hNCTABexPqnrpVSPmcrWwp8CAwHdMAoKWW2EMIf+BxobtvsNCnljivYcj/QR0p5TzXLJ2MTT0KIEcDLgANwHrjLts+bbLaANRLSB3ADlgIegAZ4REq57Qp2PAA8aNt2MjBRSlluE0XFQFcgCHhWSrlcWJ9MHwM3A6m28zO/CvGUDvSTUp6qYp9xWEWsG5AHTJZSZgkhNgO/A72BVcDJao57BhABBANRwFNAD2AIkAGMkFIabdt7Rkq5TwgxGHgLUGP9j/tXdf6klCXVnauLcfR0lm4RPrhF+OIR7ot7pB8eUQFNMofpWmMxWShLL6DoZA7Fx3MoSc+nPKMIXXbJZZWnGkctLr5uOLq74OjiiIOLI1oXRxxcHXFwdkSlUaFSq1GpVQi1CpXGOn1B5EqJlBJpsX2kRFosF6axSMxGM2ajCZPeiMlg/bb+NmE2WOcZKwzoSyrQl+owlOmhmvu0SqvGydcVB18XnAPdcQv1xjXUE+dQL1zDvHDwcLrGZ7duKD1TwJ6nfsBSYWTI3AEERNufcCrNLuPAl3+QtC4Fi9FCy55+tLulGW1uCsTd78o9rRdmlnNyWw5/rD7L2T8K0LpoaDs2ig4TY3Hyuvw/KsspZ83DNgE1exTe7eqmQ1CLyUxpWj5Fx3MoTcun7GwhZWcLKc8sRpotfykrVAJHd2cc3JxwcnPG0c0JR9u3xlGL2kGD2kGDRqv5c9pBg1qrQahU1qpLW/Wldbqqebb5Qlwmf8TlMy75/eeMZY99rogne0YI4QZsB1yA34ClUsottmVp2CJPQogQYBcQBxQA64GPpJQ/CCEkMFJKuVoI8Q5QLKV8QwixGPhUSrldCNEc+EVKGXMFW94HTkspP6xm+WT+FE/eQKGUUgohpgAxUsqnhRCrgZlSyh22Y6sA/gU4SSnfFEKoAZcrCQIhhK+U8rxt+g0gW0r5sU08uQJ3ANHAKilla5sAfQQYDAQCR4EpF4snIYQ7kC6l9K5if1pgC1bRmSuEuAO4RUp5n03sHJVSPmorW91xzwAGAP2AtsBOYIyU8ichxEpgoe2/2gw8A5wGDmAVR6lCCB8pZX5V56+m0a6hW56Q9hbhaGqY9SbKs4qpyC1Ff74MQ4EOfUE5+vxyTGUGzDojpnIDJp3ROq0zIs2Wiz61vHeqBEKA0KhRO6hROWhQOahRaS/57aC2PojcHNC6OaJxdUDj6midts1z9HHB0dcVrbuj3UXKaktxUi57pv+IQDLk4wH4t7GP3KtKjDojB78+zJHvjoFF0mVMc7pPiMC/5dV1Fpp9spitXyWT+EsGju4OdH2kM21GR6K6pMf20uwy1jy8nooCq4DyanvtelS3mMzoz5ejP19Gxfky9Hll6PPLMZZUYCw1YCozYCrTYywzYCo1YDGYsBjNFz619oU6ZuiWJ25e2+ejTfW5TyWJohZIKUttUY8bsT54lwohnpdSLrikaDdgs5QyF0AI8S3WqM4PgAFYYyu3Hxhomx4AtL3oRughhHCvaSTD9tCPBE5KKW+7ZHGozdZgrFGYVNv8HcD7NvtWSCnPCiH2AvNtIuUHKWXC3+w61iaavLBGgn65aNkPUkoLcFQIUZm52wdYIqU0A5lCiI1VHQ7VJ1S3AWKBX23nSg1kXbR8aQ2OG+AnW3TpsG0bP9vmHwbCL9lnD2CrlDIVQEqZb5t/2fmrxubLeDp6Iuf1hTUtrnCtaFP9IglUmA1UmPVUWPQYzEYM0oTRYsIszRjNJkwmEyazCbPRhETa3qpVoBKoVCpUKhVqlRq1SoVKqFALFWqhRiPUaFTWb61Kg4NKi1alxVGlRavSoKr/WogG4fjeI8x88mscXTUM/XggHuH133v5lcjYm8W2N3dSklFKh+HN6PdYND6hLv9om4FRHox7pwt9HmjNurePsH3mbk6uSuKm/9yAV7jXhXJuga4M/3wQax9ez/7pq3nl/2YR2bna9+l/TusrL7YgqTDr0ZkN6M169BYjeosBo8WE3qC3fioM6A0GLBYzJrMJi8Vi9Q+LBWmxYLFILNKCxWzBYptnjdJaLtzwZeXUxU8AedF8rPlmlTirncBai1OvKOKpltge+puBzbYH7z3AgkuKXenOZ5R//vNm/vwPVEBPKWVNL4JErEKk0q5bhRBdsVYfXsrHWBOfVwkh+gIzbOvMFEKsBYYCu4QQA2zJ5n2AYcA3Qoh3/yZJewHWXKQ/bNGuvhct0180ffE5ueJrii3HqUwI0VJKmXLJYgEkSimr61q37KLpKo/7YtuklBYhxMX/iYXL/aJKMVfN+Tt+pWOrpH9gfE2KKShct6xbt46ZE1/GNdCFIZ8MwCnQfgauNunN7PpgL8e+P4l3c1cmz+9FRLe6rUoMjPRg8tc9OfJzJmvfOszKiWvp/kQXYsZFX4gmugW6Muwzq4B6c+LzbPh1Iz27K72KV8Gu+t7hdZNqXx8IIdrYWrhV0glrlQ5ACeBum94N3CSE8LNVfU3AWtV0JdYDF5K7hRCdbN/xQoiqxMtioLcQ4uKhtqt7JfLEmssDVrFXuY9WUsrDUspZwD4gWgjRAsiRUn4JfA10sZVdJISo6onvDmTZIlV3/c0xAmwFxgsh1LaIUL9qyr0NzBVCeNj27yGEeBBrXpm/LXkfIYRWCNGuNsd9FezE+n9G2PbpY/u+7Pz9g300GqSUmM3mhjZDoRGzaNEiRo0ahWe4B8O+GGRXwqnoTDGr7lvHse9P0mNSSx5Z1qfOhVMlQgjaD2nGYyv6Eh7nw45397Ll5S0YdcYLZdyCXBn2+UC0HlpuHngzW7b/3aNEoT5QIk+1ww34WAjhhbX5fDLWZGmAL4CfhBBZtoTxF4BNWKMW66SUP/7NtqdiFQuHsP4vW4GHsSaQXxaNklLqhBDDsVYbzQGysQq4N6rY9gxgmRAiA6tCj7DNnyaE6Ic1AnYU+AkYD0wXQhiBUmCSrWwH/lo9VskrWMXiaaxVXu5VlLmYlViTxQ9jTeiu7k7wGdbzvddmixFrVwUGIcRY4CNbCzwNMAdrJK6mx10rbLlVDwIrhBAqIAdrdWtV5++64fz582zfvp2dO3dy/PhxTiadJDv7HCXFpRiNRjQaDU4uTgQGBdIqoiVtY9oRHx9Pz549CQ8Pb2jzFewQKSWvvvoqr7/+Os3jQ+n/zk1oXO2nkUTqpnS2/GcHajVM+CSe6Jvqp58wd38n7v6sO9vnn2LDR8coSCmi/7v98Aj1AMAtyI1hnw9k3aO/MWDAABZ9s5AJ4+6sF9sUqkZJGLdzhBDvAt9IKQ81oA0ewNdSynENZcN1iN05npSSxMREvv/+e1auXMkff/wBgFqrxjPMA48wN9z83XB0d0TjqMFsMGPSGSnJKaMoo5jCtCJMFdZ8+YjICEaPGM1tt95G7969G31Ss8I/p6Kigvvvv5/FixfTdlQbej7XDZXWPio/pJQkLDjCvk8PEhLrxbjZcfg0+2e5TVdL8u85LJt+AIRg0Hv9COz4p4DTFVTw69ObyD6Sy1vvvsULT7/QIDbaIUprOwWFJoLdOF5xcTH/93//x7x58zh06BBCCII7BdK8VxhBnf3xjvZG4/j30QGLyUL+qQKyD+ZydkcmZ/dnYjFaCIsI5YH7HuTeyfcSGhpaD0ekYG+cO3eOsWPHsmPHDro/1pX298TYjaA2G81sf3sXJ1efov3QZox6rSPaGlzv15L8M2V888huis/puPmNG2nRt8WFZaYKE5te2U7a5nTuf+w+5n34RWPqj+laoYgnBYUmQoM7XkpKCrNmzeLbb7+lrKyMgBh/YkZGEda3Gc5+/7x/IEOZkdNb0klalULG/ixUahWjx4zmxWdfJC4urg6OQKExsG3bNm6//XbyC/Pp++oNtBhgPwJaX2Lg12c3k7XvHH0eiuLmx6LsRtSV5ev59vE9ZCYWcsOz3Yge82dLO4vZwq4P9pG49Dg9+nZnzfK1+PraX99Y9YginhQUmggN5nhJSUm89dZbfPPNN6g0KloPjqDdmGi8Y7z+fuWrpPhsCcdXJHF0xQmMZUbib4hnxoszGDx4sN08rBTqFiklc+bMYfr06Xg182TgO31xb2U/XRHo8nX89MRvFKQUMnJGRzqPCmtoky7DoDOxbPoBTm7JpucTnYid1OEvy4//kMSOd3bjF+THuh/WEdelyb6UKOJJQaGJUO+Od/z4cd58800WL16M2kFN29uiaD+xXZ1EmWqKodTA8R+TSVxyjNLsMtrHtWfmazMZMmSIIqKuI3JycnjggQdYtWoVLfuGc9OrvdG42U/VUum5UtY99htlOWXc8X5Xom4MaGiTqsVstLDixYMc+TmT+Ifa0+H+Tn/xlZzEPDY8t4WKQj1zPpzDow8+2hR9SRFPCgpNhHpzvKNHj/LGG2/w3XffoXHS0G5sNLF3xeDs23BDd5iNZpLWppAw/zAlWaV06Nqema/NUiJR1wGrV69mypQp5BfmE/9oHG0nRCFU9vOfFp4uZt1j6zGWGbjrk3jC4+y/ustilvz47wQSVp0l7t62dH4k7i9+osvXsemV7WTsyWLg8IEs/u9i/Pzsd1Dla4AinhQUmgjX3PEOHz7M66+/zvLly9E6a2k3ziqanLztp08ds9FM0ppTJMw/Qsm5Ujp268is12cxaNAgRUQ1MvLz85k+fTrz588nsE0A/f5zg11V0wGcP5HPT1N/Q0gLd3/eg2ZtPRvapBpjsUjWvHaI/d+n0+nuaLpO7fYXH5EWyeElx9g79wCe3h4s/HoRI4aPuMIWrysU8aSg0ES4Zo6XkJDA66+/zooVK3B0daTd7dHE3hmNo5f9iKZLMRvNnFx9ioT5hynNLqNDXAfe+s9bDB06VBFRdo6UkoULFzJ9+nTyC/LpOLE9XR5oj8rBProhqCTnSC4/Td2Ak6uaifN6EHCVY9M1JFJKfpqZyO7FqXSYEEX8k90v84/zSQVsfmU7+acKGD5mOPM+mkdISEgDWVxvKOJJQaGJUOeOt3PnTt58803Wrl2Lk5sTseOjaTs+GkdPh7re1TWjUkT9seAIJVmlxHZux5sz3mLEiBGKiLJDdu7cyfTp09mxYwfNOgVzw/M98Gj1d/3k1j/nErL5edpGXL213PNVzwbrw6kukFLy8zuJ7Pq/6gWU2WDmj28SSZh/GAcHB177z2tMfXwqDg6N515QSxTxpKDQRKgTx5NSsnnzZt588002bNiAq5cr7SZE03ZcFFp3bV3sokGwmCwkrbNW5xVnlBDTPprX/v06t956q9KnjR1w7NgxXnrpJVauXIm7nxtdH+lMq+HhdpXbVEnm/nP88uRGPAIcueernngFOTe0Sf+YvwqoNsQ/GV/ly0XRmWJ2vruPMzvP0iw8hJlvzOLOCXeiUtlXVLAOUMSTgkIT4R85XkVFBUuWLOHjjz/m4MGDuPu70/6uGNrc2hqNy/Uz6pLFZCH551QS5h+m6EwxIc1DeGrqU0yZMgVPz8aTr3K9sGfPHmbNmsXKlStxdHWkw91tiZ0Qg9rFPgXt2d2ZrH96E97NXLjnqx54+DdcI4m6RkrJL+8eZec3KbQfH0X3py6PQFWWO7szk31zD5J3Mp+odlG8+uKr3H777Wg01829QhFPCgpNhKtyvJSUFL7++mu++OIL8vLy8GvlS7s7Ymg5pDkap+vmRngZFpOF01vPcPS7E2QePIezqzOT7pnEg/c/SOfOnZUqvWtIRUUFK1asYN68eWzduhVnD2fajo2i3fgYHL3ttxoofcdZfnt2M77hbtzzRQ/cfO035+9qkVLyy+yj7FyUQvs7ouj+dNUCCqwJ5ad+SSVh/hEK0goJDgtm+pPTueeee/Dx8alny+scRTwpKDQRaux4BQUFLFu2jEWLFrFjxw6EEIT3aU7H8bH4xfk0OeGQd/w8R787SdL6U1iMFtq0a8OUyVO46667CA4ObmjzrgssFgt79uxhyZIlfPPNNxQUFOAd6kXM2CiiRrdG62rfQj1tSzobnt9KQKQ7k+b1wNWORd4/RUrJ+veO8vvCFGJvj6LHM9ULKLCKqPRtZzn8f8fISjiH1kHDiFEjeWjKQ/Tv37+xVosr4klBoYlwRcdLS0tj9erVrF69ms2bN2M0GvFr6UurIRG0HhyBy3WQt/FP0RfrSfn1NElrUsg+kgNAXHwcY28dy6hRo4iOjm5ywvKfUF5ezvbt21m9ejUrV64kIyMDjYOGiH7NaTs6Bv8uPnaZ03QpKb+lsenlbQS39eLuz7rj4tl4c/9qysURqNhxUfSYfmUBVcn5E/kkrUnl5E/J6Iv0ePl6MXL4SG4dfSsDBw7E1dW1HqyvExTxpKBQU4QQvsAG288gwAzk2n7HSykNNdjGi1LKty76/buUspcQIhxYI6WMrVurL/AXxzt9+jTbtm1j27ZtbN26lePHjwPgG+5D6I0hRA5siVe0pyIGqqEgtZD0jWdJ3ZJO7rE8AIJDg+l3Uz/63tSXPn36EBkZeT0myl41OTk5HDx4kJ07d7Jx40Z27dqF0WhE66QlrGcIrW5uSUjvIBwaUcOD5J9T2PzqDkI7enPX3Hic69B2i1miLzWCEGgcVQ0+ePClWCNQx/h94SnajYuk5/QeNb5fmA1m0ref5czmDFK3pWMoNaDRaujStQv9+/anT58+dO/eHW9v72t8FFeNIp4UFK4GIcQMoFRKObuW65VKKS/r8OVai6eFCxfKQ4cOUfnJybFGTpzcHAno6E9YfChhN4bgHtb4+qJpaEqzyzizLYNz+3PIOJCJLr8CABc3Fzp06EBc5zg6duxIZGQkERERhIaGNtaqir/FYrGQmZlJcnIyycnJnDp1isTERA4cOEBGRgYAQiUIiPYnuGsgYd2a4dvRG61z4xFMlZxYlcTWN3YS3tWPCR93w+kfVC1KKck+WUzSthzO/FHAuRPFlORWYDH9+bx09XHAJ8yFsE4+RMT70bKHHxqHhr2OpJSsf/8Yvy84RduxkfSa3qPW0UKLyULWgWzO7bH6T+6x81hMFgBCQkPo1LETnTp2IiYmhoiICFq2bElQUFBDv9gpggvZowAAIABJREFU4klB4WqoFE/AJuB9wA3IAyYD5cAeYKSU8oQQYgmwEWgFTAcOA4lSyrsqxdTF4kkIoQZmAn0BR2CulHKeECIYWAp4ABrgESnlthraK7VOWnxaeuPd2pOA6AACOvnh2dIdlVqJjtQVUkqKTheTnZBLQVIRuSdyyU8uwFBmvFBGo9UQGhZK87DmBAUG4e/vT0BAAP7+/vj4+ODm5nbZx9nZGa1Wi1arRaPRoFar6/ThYTabMRqNGAwGjEbjhWmDwUBJScmFT3Fx8YXpgoICsrOzOXfuHNnZ2WSdyyInOweD4c8ArFqrxivME+8oL4JiAvBr44NnGw8c3Bp3TtCh/0tk94f7adnLn/EfdMXxKluc6oqN7F9+mgMr0zmfVgZAUIQz4bGu+DZzxN1biwQMOjPnMw1knSon9VApJqPE2UNDu4HBxN/ZksAojzo8utohpeTXD46x479XL6AuxqgzknMol4LjRZxPLiD3ZB6Fp4uQ5j+1g6OTI2HNwwgOCiYwIJCAgAACAgLw8/PDw8PjL77j7u6Om5sbTk5OODg4oNVqL3z/g8iwIp4UFK4Gm3gqA24FRkkpc4UQdwC3SCnvE0IMBF4DPgQmSykH29b7S+SpGvH0IBAgpXxDCOEI7ADGAbcBTlLKN20Cy0VKWVITe29fPlp6hClCqSGQFklJViklZ0soySylJKOU4owSyvJ0VORXUFFYgb74b2t8L0OlUaHWqlGpVag1KrhYTF1yn73stislZpMFs8mMxWRBWmp/XxYqgbO3E86+Tjj7OOPs64yzrxMeIe54hLrhHuqOW6ArKs31c81JKdn36UESFhyh3S0h3PpWZ7RX0bO5rtjItq+S2Ls0DUO5mahuHvQY7kfcQB88/a4chTPoLRzfXcTO1XnsX5+PQWehTR9/bp4aQ1CbhulOQ0rJr3OOs2N+Mm3HRNLr2X8moC7FpDdTkmn1n9KMMuv0uTIqCirQFVSgy69AX6Sv9XaFWqDWqFFpVGi0aoRKhRDWa9tqv7gwLQQIYZ2+bflw5y+6LqyoswOsAfbdZEJBoXY4ArHAr7YogBrIApBS/iqEGAfMBTrWcruDgA5CiLG2355AJLAXmC+E0AI/SCkTarpBvwg/TNKIqP8XpiaPUAk8m3ng2ezy6IC0paKZjWYqCvXoiw2YKkwYy42Yyk0YdUZMOhOmCqvIsZgsWMzywrQ0W7CY5IVqjr/u+Mq/VRqVVYDZvlUaFSrtX6fVWhUaZy0Orlq0rlq0LhocXB3QumjQumj/8oC83q8ti9nCjnd2c2zFSeLGtWDYi+1Ra2pZRWWW7Ft+mk2fHEdXZKT7MD9uuT+EiHY1T5R2cFTRoY83Hfp4U/qSkQ3fZrN+YRaf376VrmPC6PtYTL13kyCEYOC0aAB2zE8CCb2f61lnAkrrqMEnwhufiMtzoCp9yGKyUFGkx6QzYSwzYtQZMZZbfclYbsRssGAxWi74jrnSn4x/fksprS8SkiqmASmxBYAeA96rk4OrIUrkSeG6wBZ5MgNDpZQ9q1iuArYAEbYyh2zzaxJ5+h74Qkr5SxXbDQGGAVOBd6WUi2posuJ4CgpXSUVFBZMmTWLZsmX0fSCavk+0rnW16fn0Mla+dJAzCQW0ifdgwovhhLetm9ZlZUUmfvzkLBu+PYeTu4bhL7en7aBmdbLt2iCl5LcPj7P962Qm3n8nC7745nptNFHvbwrX5VlUaLLoAX8hRE8AIYRWCNHOtuxJ4BgwgT+jRQDGi6ar4xfgkcpyQogoIYSrEKIFkCOl/BL4GuhSx8ejoKBwCbm5ufTv359ly5YxZHp7+k2NrJVwklKyZ2kan43dQl5KCQ+805rnv2lbZ8IJwNVTw50vhfPajx3wb+bA0qcPsOK5fejLTHW2j5oghGDAv6K5cUok33y9mElT7sRiqSIqqlBrlGo7hesJCzAW+EgI4Yn1+p4jhDACU7B2X1AihNgKvAy8CnwBHBJCHJBS3lXNdr8CwoEDwnqXzgVGY00gn27bfikw6ZodmYKCAidOnGDo0KGczTzDhPd7ED3Qv1brG8pNrJpxiMM/ZRB7gxf3vdUSn6BrV6XWLNKFl5fGsvaLTH785AxZx4oY90E3AlrVX0K5EIL+U9uAkHz75VJMFiPffv2/67aFaX2hVNspKDQMiuMpKNSCTZs2MWbMGCxqA3d+FE9Q+9p145F/pozv/rWXnOQSbnuyOcMeDEFVj51+Ht9TxKf/SkKvMzPqPx1pNzi03vYN1ojbxk9OsPWLJPoO7s3qZT/j5nbddIWitLZTUGgi2L3j6XQ6EhMTOXToEKmpqWRmZnLu3Dl0Oh0Go7U1mpenJ97ePgQHBxMVFUVUVBQdO3ZUBu1VqDOklLz//vs899xzBER4cNfc7riH1K4fqrS9eSz51z5UKsnD70XSoY/XNbL2yhRkG5g79STJB0sYNC2KXvdF1Xv/SLuXpPLTzCO0iW3Fxp+3XS9DGiniSUGhiWB3jldeXs7WrVvZsGEDGzduJCEh4UJ+hFAJ3P2ccfNzQONka4oPVJQYqCg2UZJbgclgKysEbdpG0ad3HwYMGMgtt9yCh0fD9Xuj0HgpKSnh/vvvZ9myZcQOCmPUfzrg4Fa7VN0jP2ew4sUE/MMcmfZFNEHNna6RtTXDoLfw9QvJ7F5znvhxoQx+seMFf6ovTmzJZvn0/Xh6e/DbT5vo0KG2DZDtDkU8KSg0EezC8crKyli3bh3Lli1j7dq1lJeXo3FQE9bBm/A4f4KjvfCLcsYrxPmKN3iLWVJ0TkdeailZiSWkH8wn/Y889KUmNFoNvW/syfhxd3L77bdfDyO4K9QDhw4dYvz48Zw4cYKB09rSc3J4raM0vy88xS+zjxIZ584Tn7bBw9s+ek63WCQrPzzD6s8yiL7RlzHvxePgXL8pyJlHC1n8+F4MZWa++uor7p7QqFM2FfGkoNBEaFDHO3DgAHPnzuW7776jvLwcd19nYgYE0e7mZoR0dq+TG7nZZOHsHwUkbcnl2OYs8lJL0TpoGDz0Fu67ZwrDhg1Dq7WPh5mC/WCxWJgzZw4vvPACzh5axszsQovutatmu7iX7bhbfHjo3UgcnOyvcfnm77JZ+GoKLbt6ccfHPXH8B0PKXA3FORUse3o/6Qn5PPTE/Xz83meN1ScV8aSg0ESod8erqKhg2bJlfPrpXHbt2o2Ds5YOw5rRaWhzmnXxQKW+dvcfKSXnjhdzaHUmf6w9Q1m+Hv8gXx5+8BEeevBhmjWr/z5wFOyPM2fOcO+997Jhwwba3RzKyFc74ORTu1ZhFovkp5lH2LMkjX4TApn4akS9JobXll1r8vjy2WRCY9wZ/1kPXDzrt0NNk9HC+veOsvvbVDp3b8/Kpatp0aJFvdpQByjiSUGhiVBvjnf69Gk+//xzvvzqS87nncc/woPu41vSfkQQTnU46nxNMZssJO/IZd/SdJK2n0OoVAwfNZRpjz9F3759G3qAUYUGwGQy8cknn/DKK69gNBsY8lwsnW4LqfW1YDFLVr9+iAPfp3PLfcGMf65Fo7ieDm7IZ+7UkwREuHDXvF64+dV/XtbhdRms+s8hNGoNH334MfdNvr9RnDsbinhSUGgiXFPHs1gs/Prrr8ydO5e1a9cikUT3DaLHhFa06O5lNzfF/DNl7PtfOgdWpqMrMtA6uiXTHn+KSZMm4e7u3tDmKdQDe/fu5aGHHuLgwYNE3xjCsJfa49Gs9gMVm00WfnglgUNrMhj+SDPGTAuzm+u8JiTuKOTDR0/gFejIxK974xHgXO82FJwt54eX/yBtfx6DRw5k/ucLG0trPEU8KSg0Ea6J4xUUFLBgwQI+/fRTkpOTcfd1Jm5MC+LGheER1LCtjK6EscLMkZ8z2fvdaTISC3B1c2bSPfcw9fF/ER0d3dDmKVwDUlNTeemll1iyZAme/m4MfT6WNgP9rkrwmIwWvn/uAEd/zeLWaWGMerR++1CqK07uK+a9KcfwDHBk0vzeuPvXv4CymCU7v0lh48fH0To48NprrzHtiSfRaOy6T21FPCkoNBHqzPGklOzbt4958+axePFidDodLTr70WN8K6IG+KJxaDw9CUspyThcyL7vznDo5zOYjRb63tyHfz3xJMOHD7f3G7hCDcjKymLWrFl8+umnqNTQ4+6W9L6vFY7uV3edmgxm/vf0fk5szuaO51sw5L6QOra4fqkUUJURqIYQUGAd+++ntxJJ2pFNm9jWfDj7EwYNGmSv0TxFPCkoNBH+seOVlpayZMkSPv/8cw4cOICjs5b2Q5vRfUIrAtq41IWNDUrpeT0JK8+yZ2kqRed0hIQF8fgjU5kyZQr+/rUblkOh4Tlx4gSzZ89m0aJFmExGutwazs2PRuMacPWC2Kg3s/TJfSRty+Guf0cw8O6gOrS44bggoIKcmPhVrwYTUFJKjv2WxS+zj1GYWU7PG+N5b9Yceva8bOz1hkYRTwoKTYSrcjyLxcL27dv59ttvWbJkCSUlJYRE+dD19hbEDg2+6rd3e8ZssnBySzZ7v0vn1K4ctA4ahg0fyr333M/gwYNxcKh9foxC/WAymVi3bh1ffvkla9euReOgpvOoMHpPjsQr7J+1KjPqzXz3r70k78hl0mstuXl8YB1ZbR/8RUB93Qt3v4YRUGCN7u1bls7WL5Ioy9fT+6YePP/MSwwdOhSVyi66gFDEk4JCE6HGjiel5PDhwyxevJglS5aQnp6Oo4sDbQcEET+uFcEdXe01lF7n5KaUcGDZWf5YZ+3uwNPbg/F3jOeuO++mV69eymCndoCUkoMHD/K///2PRYsWkZWVhae/K51vC6P7+Ahc/P551auxwsySqXtI2ZXHPa+3pO/t15dwquTE3mLef8A+BBRYB1be+7/T7P6/VIqydUS0bsEjDz7G3Xff3dCJ5Yp4UlBoIlzR8QwGA1u2bGHNmjWsXr2a1NRUVGoVkb0D6TSsOa37+uLg0nSFgtlo4dTOXI6sPcfRjRkYK8x4+XgyYvgIRo+6lYEDByqt9eoRnU7H77//zrp161ixYgVpaWmo1Cra3BhE1zERRPT2Qq2tmwiFQWdiyRN7Sd2Tx+Q3W3HT2IA62a69UimgvIOduPurhhdQYPW/o79lsfvbNM78kY9KJeg/6GYm3TWZIUOG4OvrW98mKeJJwb4RQvgCG2w/gwAzkGv7HS+lNDSIYVUghOgEhEgp19WmnBBiJNBWSjnzGpr3F8czGAzs27ePLVu2sHXrVrZv305paSlaRw0te/gT0zeEqH7+uPo2yt5/ryn6MhPJ23M4uSWPE1sy0RUbUWvUdInrRP9+A+nbty+9evVSxFQdkp+fz4EDB9i1axcbN27k999/R6/Xo3FQ06pnALEDmtH6Jj9c6ng4FEO5iW8f38Ppfee5b2Zrbry1aeS+XRBQQU5M/Lp3g/QDVR25KSUcXpNFwup0is7pUKlUdO8Vz6jho+nTpw9xcXH1UbWuiCeFxoMQYgZQKqWcfdE8jZTS1HBW/WkHcDfQVUr5+N+UnVyTcnXJzp07ZUJCApWfQ4cOUVFRAUBQay+ad/GmzY0hNO/uUe9jXjVmzEYL6QfzSd2ZT+reXM4mFmAxSYQQtIqMoGtcPF06d6Fjx45ERUURFhamVPVdgaKiIk6ePMnJkydJSkri6NGj7N+/n5SUlAtlmsX4EB7vQ+sewTTr7HbNhhjRl5v49tHdpB/MZ8qs1vQe1TSEUyUn9lpzoHwqI1ANlEReHRaLJDOxkOSt5zm+JZOsY0UAODo5ENc1jt49b6B9+/bExsYSExODk1OdCkBFPCk0HirFExAL5AOdgQPAUmAO4AzogHullCdsImUk4AK0AlZKKZ8VQqiBr4GuWCMy86WUHwghNgMJQDzgAdwnpdwjhPAB5gMtgXLgQSnlIZs9IUA4kAfcYLMhA3gbSL3ULtu85EvKOWMTU0KIFrZ9+WONsN0rpUwXQiwAim02BwHPSimX1+LcSQAXTyeC2ngQHO1BeJcAmnV2x9VHSYCuKwzlJs4kFJDxRzFZx/+fvfMOjKJo4/Azd5dcGmmENCCEQOgoVQWkigiKiiCKqKAIqICAvaCin4pKE0WxoAjCJ6IU5bOBUkWqBKQ36RBIIb1de78/7tCAAZKQcCnz4Lq7s7uz79xmbn/3zjszqZzYnUJafM7fxz08PagdE0292PrUrFGTiIiIc5bg4GACAgLw9/cv9yJLRMjNzSUtLY3U1NRz1snJyZw8eZKTJ08SHx/PyZMnOX7iOMlJyX9fr5QiuIYf4Q2qULNJVSIbBxLawAfvgNL/e83NtPLf4Rs5/mcKQybUpU3PkFK/Z1nkrAfKv5qZ+z9tS0B42e1Vm5mUx9GtZzixNZ3DcYnE707DbnMAYDAYqFU7ipjoGKKja1OrVi1q1apFeHg4ISEhfy8+PoUunxZPmvLDeeIpBLhdROxKKX8gW0RsSqmuwKMi0sclnl7GKbLygL04BU4o8JaI3OjKN1BEUl3iab+IDFFKdQCmiUgTpdRUIElEXlVKdQEmi0gzlz23AteLSM75HqVL2JX/vL/3lVL/A+aLyCyl1CDgNhHp5RJPvsDdQANgsYjULexn1/+9ayS8oT8B4d6VJti7rJCVkkfCgQySj2Rz5mgWZ45kknw0i4yEXHLSrRe8zuzjgXcVT7z8zHiaTZg8TXh4GjF5GDF5GjF5mjB5GDB5GFEG5Xyuyik6nAuudCB/mlI4HIKIIA7n8q/9fNvi4Nx9EexWO9Y8O1aLDZvFjjXPds62zWLHkmfDbnVcsHzKoPCraqZKNTNVQr3wC/GiapQvVWv5UTXah6AaPm4ZMyzrTB6zH9nA6f3pDJ1Ql+tuqZzC6Sz74zKYPHg33gEeDPi0LUE1fN1tUqGwWx2cOZZFwv4MEg5kknQog9T4bFJP5JCZnFfgNR5eJnz8zZi9PTD7eLrWHnh6/bM2eRpZNnvzFf8S1e0BmpLiGxGxu7YDgFlKqVicnqT8gQ/LRCQNQCm1C6gF7ARiXKLoB2BpvvPnAojIaqWUv1IqEKfg6uNKX66UqqqUCnCdv1hEciiYi9l1IdoAvV3bs4Hx+Y59KyIOYJdSqkjdfRp0CQfUlf+5pMEvyAu/1l7EtD43XQCbxUZmUh4ZiXlkJuWSm24lN9NGbqaVvEyba7FisziwW63kWfLIznS49v9ZREAcAs7//tkWQQRwrcXhvLMyqL+F1b+3XQLsnO18aQoMJoXJbMTkYcDTz4C3pwmTpxmTpwGT2YDRw4DJbMTLz4SXvwdefh6Y8217B3jgG2x2TQ5ddv4u007lMGvoOtJOZjNyWn2adQpyt0luJ7ZFFZ6Z1YiJg3Yx88HfGTC9LSHRZT+ez+RhJDTGn9AYf7jpn3QBrHk20uJzyE6xkJ1iISvVQk6qhexUCznpVqzZdiw5Nqw5eaSlZ2M9bcOSY3fWO4ud/+y4bdTLTRa/e0XLcyVvpqnQZOXbfg1YISJ3KKWigZX5juX/iWEHTCKSopS6GmeVGg7cBQxynXO+a1Qo2EV79rysAo4Vxq7Ckt+e/GUp0vvm3lqvkmlLKcbtNaVO7cKfKjiwiRW7w4odOw6x4RA7DnHgwIGIHTn7z6maLtrNUrn+f9Ybqc7+UwbXlgGlDBjyrQ3K+PdixLl2QytGiXP4wDGGDniKzPQ87n+pDlUjPEk4mktgqAeeXuW7CfVyqd3Uj2e/aMyEB3cze9B6pn/7HnUbxrjbrMujUOYLNrFideRhEys2hwW72Pg9af6S0jbvfLR40pQGATjjhwAeuNTJSqkQwCIiC5RSfwEz8x2+G1ihlLoeSBORNKXUauBe4DWlVCecTXjpBTR/ZQD5f5JdyK7zz8vPWqAfTq/TvcCaS5WnMNSp0rwkstFoKgxWq5VVq1axbNkyfvr5J7Zv34bD7pSaM17cf865weEe1Ij1oV7rAOpf40+dq/1cXrPKQ1RDX56b04gJD+zmoVtH8vOPv3Ddte3cbZZbuCF8wJ4rfU8tnjSlwXiczWNPAMsLcX514HOl1NmBYJ7PdyxFKbUWV8C4K+0V1/nbcAaMD7xAviuA55RSW3EGgl/IrvPPy89IYIZS6mlcAeOFKI9GoykkO3bs4JNPPuGrr+aSmJiE0aSIbeRJjzurULOOmeAQA96+Buw2ISdbSDhp4/hhC/t35jB/srNHV2A1E61uqsr1vUOJbuLn5hJdOarX9eG5OY2YNGgPnTp3Yt68r7j91j7uNqtSoAPGNWUWV8D4UyLyh7ttKQXKRcVLT09n9+7d7N69m4MHD5KUlERKSgoOhwOj0Yivry/h4eFERkbSuHFjmjZtSlCQjkvRXJq1a9cybtw4fvjhBzzNRtp08aVLT39adzTj41u4ATVTz9jZ/Hs2q37MZP2KLCx5QmxzX264P4LW3UMwmiqHNyo10cKUoXs5uieL96dN4dGhI91t0pVG97bTaM6ixdOVJycnh6VLl7Js2TJWrVrJ9u07OPsdoRT4BXri42/CYASHXcjNspN+xuIKfHYSFV2drl1upGvXbtx0000EBwe7qTSassjBgwd55plnWLBgAYFBZvo8GMDt9/vjH3h577/MdDs/L8hg0axUThyxEhFt5rbHanLtzSGVokkvJ9POByP3sWNNKs+9NJpxr06uTD15tXjSaCoJZabiWSwWFi9ezNdff80PP/xAdnY2Zm8TdZv70bB1MDUb+hIWY6RaDa8Cf8k77EJKgoUT+7I5sTePv/7MZNf6M2Rn2DGZjHS+oQP9+w3gjjvuICAgoAALNJUBq9XK22+/zWuvvYbR6KD/o8Hc+ZA/3j4l+95zOITff83i83eSObjHQs1YL/o+U4urOlZ8EW+zOvh8zEF+/zaRO/rexJyZC4syVlJ5RosnjaaS4PaKt3//fqZPn87MmZ+TmJhEYDUvWnQNovVNocS28sLkWfy5yBx24fCOTDYvTWPDT4kkHc/F28fM3f3u4rHho2nRokUJlkRT1tm+fTsPPPAAcXFxdLklgGEvhhISXrr3dDiE1T9l8umkZI4fstKiSwD9XoghNKrsTG1SGogIP3x8kgXvHKVh09r8uHgFtWrVcrdZpY0WTxpNJcEtFU9EWL58OePHj2fp0qUYjQaa3xBMl37VadDGu1SaN0SEg9syWf11Euv+l4Al10Gzlo15+okXuOuuuzCZdL+VioqI8NFHHzF69Gj8/A2Mfi2MDt2v7Aj6Vouw4PNUZk1NxmaFW4ZG0vORGpf146A8sHVFCh8/uR+zp5mv5y3kxq43Xfqi8osWTxpNJeGKVjy73c6CBQsYP348mzdvJrCaNzfcG0aHO0MJCL1yY+ZkpdtY+20SK748zcmD2dSICuOZp57noYeGVJbmhUpDZmYmQ4cOZe7cuVzXyZ/nJ4UTEOy+903SaRsfjkti2eIMoup58cC4usRcVfYHl7wc4g/mMHX4PuIPZvPE04/x5uuT8PCokJOLa/Gk0VQSrkjFy8nJYebMmUycOJGDBw8SEe3LzYNrcO3tgXiai/bLOyfTxqqvE9i2KpXUhDyqBHnQ4Dp/Ot0dTlBY0bwJDofw54oUfpx+iv1xaQQG+/HYY6MYOWI0ISGVe/qNisDevXu544472Lt3D4OeCKX/o1UwGMpG8PL6FVlMGpNA8mkbPQaFc/vIqAo96GZetp0v3zjCqm9O06xVQxbM+56YmHI+oOa/0eJJo6kklGrFS01NZdq0abz77rskJCRQ5+oAeg6pydU3FG8wwbhfzzDjhb/ITLVRv6GJ6GgjCacdbN1ixdOs6PtkTW4YEFms3j37N6fz4/RTbFmejJePJ4MGPcgzTz1fGeI0KiRr167l1ltvRVQ2L78XQfO2Za9ZNjPdzkdvJfH93HQiY8wMnRhLdJOK7YXa+FMyM188iDgMvPHGG4wc8Xi5n+w6H1o8aTSVhFKpeCdPnmTKlCl89NFHZGRkcFWHqvQcWpPY1l7F7rb83QfHWfTuMRo18WDcWwFcffU/L8OjR2y8MjaDFcvy6HR7EPe/Wb/YY+ucOJDNz5+eZu3i0yCKvnf15vnnXuKqq64qVn6aK893331Hv379CAlXjJ9Zg8gyrn83/57NW0+f5kyijd4ja9BjSI0KPaxB8sk8Zr50iO2/pdC8dWNmfTaXpk2butuskkCLJ42mklCiFW///v1MmDCBWbNmYbNZufbmUG4ZWpMaDS4vvmHxtOMsnHKMXr29efNtf7y8ChiqwCG8/14W70zKpHOvAO5/q+FlNdGcOZXH0s9Ps2JePHnZDm7s3oUXnx9L+/btK9O4NeWOjz/+mGHDhlG/qRfjPo0gKKR8BGRnpNmZNCaBlT9k0rCVLw9NqE9IdbO7zSo1RIR1/0ti7htHyEq3MXjog7z+6ltUq1bN3aZdDlo8aTSVhMuueCLCypUrmTp1Kt9++y0enkba9wnl5odqULXm5bvjN/2czAcj99GrtzcTJ/tjvMQv8vffy2TShEz6jQij+8jLj6nITLWy/MtEfvniJBlnrLS65mrGPP8Kt956a0Vqbij3iAgvv/wyr7/+Otd1rsLY90Px9ikfwuksIsLShRm8+0oiAPe/Ups2t4W62arSJeOMlW/fO8GKeafw8THz/PMvMPKxx/HzK5fT22jxpNFUEopd8TIzM5kzZw7vv/8+O3fuxD/Ii453V+PGAZH4l9Cv/RMHsvnPndtp2MDI3HnBBXqczkdEeObJdOZ/k8OzH9ehYeeSeflYcu38tiCRnz+LJ/F4LtVrhvHwkGEMHjyEiIiIErmHpnhYrVYeeeQRZsyYQfc7A3jqzWqYyvGUKPHHrLzx+Cl2bM6lzS3B3PdqHXz9y17MVkly8kA230w8zpblyQQE+TF61OOMGvl4eZtmSYsnjaaSUKSK53A4+O2335g9ezbffPMN6enpxDQJpOt9EbS62R9Pr5L7pW+zOvjPndvJTMzlfz9WJTKi8F6e3Bz6J9t2AAAgAElEQVShd69kEhIcvPp9M/yCS675w24T4n49w8qvEtm5NgWTycgtt3Zn6OBh3HjjjRW1C3aZJSUlha5duxIXF8e9jwYx+OmqFaJZ1WYTvvwwhZnvJlM1zIPBE2Kp37rij4x/YGsGP358irhlSfj4etH/3v4Me2QEzZs3d7dphUGLJ42mknDJiicixMXFsWjRIubMmcORI0fw9vWkZbcgOverTkwzz1J5WZ2Nc5r2SRA9ehRd/OzebeX2W5LpcJMf908unWDUU4dzWD0vidULT5GZYiMwqAp39unLPffcS8eOHXWzXimRlZXFkiVL+PLLL/n2229xOOw8NrYavQcGutu0EmfXllxef/wU8Uet3PpwBLc9FoXJo3w1RxaHY3uyWDozgQ0/Oge0bd6yKYMeGErv3r2JjIx0t3kXQosnjaaSUGDFS0tLY82aNfzwww8sXryYEydOYDAomrQLpt3t4TTr6oe5FONJTh7I5qXbt9G9u5n3pxX/hfjelEzemZTJ8x/XoX4JNd8VhNXiYMeaVDb9kMrmZYnkZTsICvanW7fu3NzjFrp160Z4eCnPA1KByc3NZePGjSxfvpwVK1awfv16LBYLBoPCaIKX3gunw03lMkamUGRnOpj6n0R++iadOlf5MGRiPcKjvd1t1hUhK83Guu+SWfn1aY7vy0IpxbVtWnFn77vp2rUrTZs2xWAoM2JSiyfN5aGUWgm8KSJL8qWNBuqJyLASukczIFJEfrzEeQ8ArURkRAHHMkWk0N+6SqnDQAbgAE4DA0TkVFHszpfXTOB7EZlfjGtfEJFxxbnveYiIcOjQIeLi4li/fj0rV65ky5YtOBwOvHw8aHJ9AC1vCKVxR1/8g69M3MWkh3ZzaGs6y1ZVJbRa8b03VqvQo1sSVpvi5e9bYPIsfU9QXo6dbatS2bYinW2/JZOWZAWgXoM6tL2uPW3btqVNmzY0bNhQe6bOQ0SIj4/nwIEDbNu2jbi4OOLi4ti5cyc2mw2lFNGN/ImoY2bryjOYjMIb0yNo2rJyCImVP2Yw6YUErFboPyaa9neGVogmysJy4kA2m5eksWlJIsf2ZAEQHBJIl0430L59B1q2bEmzZs3w9fV1l4laPGkuD6XUw8B1IvJgvrT1wNMi8lsJ3eMBLiCKCnteMcVTKxFJUkqNA/xEZGS+4wrn37OjEHnNpPjiqUh2X4jOnTvLli1bSEtLA8DD00jdZv7Uv8afRtcGEd3MXOQRwC+XP1em8M7QPbzwchWGDLn8L8FVK/N44P4UBj8XyvWD6pSAhYXH4RCO7clmx5oM9v+RzoE/08hMsQFgNntSr35dmjZpRqNGjahbty5RUVHUrFmTiIiICiesbDYbqampnDp1ivj4eOLj4//ePnbsGPv37+fAgQNkZ2f/fU1AVS9qNfYhunEV6lwVQN1WZv7amsEHo/YRGGzk7ZmRRNe5snPUuZuEeCvjnjzN1nU5tO4WxMDX6uAXVPni7JLj89i9LoO9GzLZsTaZlNMWAAwGA/Xq16FRo6bUi61HbGwssbGxxMTEEBYWVtpzWGrxpLk8lFJVgT1ADRHJU0pFA6uBWsCNwKuAGfgLeFBEMpVSNwOTgSQgDogRkZ5KKV9gKtAUMAGvAD8BBwBv4ATwJnAImOJKy3Hlu9clnu5w3a828KWIvOqy828RopR6GrjLdd4iERlbQLkO84946g6MBIa57FkBtAF6ASOAHjibxV4XkXkuYTUV6OKyVQEzRGT+efm2AiaKSCellJ/rmlauvF4FWgNPA9uBncBQ4GugBmAEXhOReYV5TvWaV5UaDT2JaRxEzYZeRNbzvOJiKT82q4MXe/6Jl7Kx5JeqeHqWzHfRQw+msGG9hbeXNsMvxH2z2YsIp4/k8teWLE7us3D8QAYnDmSRdCLvnPOMRiPhEaGEhYVRNTiEoKBggoOdi7+/P97e3nh7e+Pl5XXOtoeHBwaD4e9FKfWvfXDOMehwOLDb7ecsF0qz2Wzk5eWRm5t7wfXZ7ezsbNLS0lxLKmnpaaSnpZOVlV3QR4KXj4mgMDOhtTwJj/YlvJYvYbW8CK9rJCjs3Hi63xYm8PmYv6hd38zbMyIJCavYPdAuhMMhzJueymeTkvAPNjH47Vgata148V6FRURIPW3h8M5sju7M4/DOdE4eyibpeC522z/aQilF1ZAgIsIjiIisTlhoGAEBAQQEBODv7//32t/fH7PZfM7i5eV1zr7RaMRkMmE0Gv9eDG6Y+0eLpwqIUuoH4BMR+U4p9RxQFXgbWAj0EJEspdSzOMXKeGA/0EFEDiml5gJVXOJpHLBLROYopQKBjUBzoC/5PEpKKX8gW0RsSqmuwKMi0sclnt4EmgDZwCbgARH546x4Ukp1A+4EHsYpahYD40Vk9XllOsw/Iud9IAv4EDgItBWR9UqpPsAjQHcgxHW/a3EKq0dd6WHALmDwJcTT24BZREa77h8kIinnib4+QHcRGeLaDxCRtMI8o1n725apirfyq9PMfPkgH30WxE3dSq6H3MGDNrp1SaLXfYHcOqZhieVbUuRm2Uk6kceZ+DyS4y2cic/jTLyFjBQr2ek2MlNtZKU5F4fd3daei4fZgMlT4WE24OFa+1Qx4V3FiHcVIz5+zm2fKkZ8/E0EhHgQUM2TgGoeBIR44u13aQ+biPC/D0+wcMoxWrTz4T/TwvHzr1ieueKwb0cur406xfFDVno8FM4do2vh4Vlm4n/cjt0mJJ/M49ThHJJO5JGWaCUt0UKqa51+xkZupo3sDDuXbiu4NDP3tYkcGLs2/vJzKjyV8+dDxWcu0A/4zrUeBFwHNAJ+d/2i9ATWAQ2AgyJyKN+1Q13b3YDblFJPufa9gKgC7hcAzFJKxeL00uT3Zf8iIskASqmFwPXAH/mOd3MtW1z7fkAsTm/Z+axQStmBbcCLQCBwRETWu45fD8wVETtwWim1Cqe3qEO+9JNKqeUF5H0+XXF+dgCISEoB52wHJrqE1vdFaRb1MPhhd+ThBm/zv7BZHXz/8Qmubu5BtxtLtikmJsZE37u9WTA3lc4PWvCPLFvBxT6+EFXPm6h6BR0VBAeCHRHBkuPAmufAkuda5zqw5gnWPAd2qyAiiDi9E+IAEaf4EAeIw6mVDUaFMigMBue2waBQRjC40pQrzXA2zajyCSQDHmaFh6cBo4cqIOZGoTCgMFASf1c2q4NZr+xn1TenuPGOKjz9ZhieZvf/vZYF6jXxYvr3UUx7PYnFn55i99p0hk5sRPW6bov5KVMYTBAeZSY8yr+Ao+KsUzgQEfKyHeRk2snJsJGbZcdqEWwWB1aLYLU4sFkc2P7eFhx2weEQHDZnXXPYBZytDh9eyTJq8VQx+RaYrJRqAXiLSJxSqjpOIXNP/hOVUhcbxEMBfURk73nXXHveea8BK0TkDlcz4cp8x873sJy/r3AGuH98ETvO0llEkvLZEYjTA5U/rwtxIU+PDTj7kzF/u5K6yDXODEX2KaVaAjcDbyqllorIfy52zVn611lamNOuCDNmzCDpxG9MGBdOacTAPjbKj4Xzc1j3aQ5zZv9x6Qs0bicjI4O77rqLVT+fYuDIUB4Y7V+pAqQLg5e3gSfeCOXaTj6Mfy6BV/tsZcKE8QwfNlp/VleeKyqc4J+XhqYCISKZOAXMDJyeJID1QDulVF0ApZSPUqoezvioGJfoAbg7X1ZLgMdcMUP5hVYGkH8K8gCc8U8AD5xnzo1KqWCllDfOXwe/n3d8CTDIFWOEUqq6Uqq4fdtXA3crpYxKqWo4PU4bXen9XOkRQOd81xwGWrq2++RLX4ozfgqXXWeH27UqpTxcaZE4myvnABOBFsW0223YbDbeeON1ml5lpmPn0mlJjIw00v8+H76au4tdu1eVyj00JcfJkyfp0KEDv/yylGfeqs6DjwdoMXAR2t3ox4yfomjaysxjI57ghm7XceTIEXebpSlltHiquMwFrga+AhCRRJzCZq5SahtOMdVARHJwBl7/rJRag3MYgLNxO6/hbILbppTa4doHZ4B2I6XUVqXU3Tjjpt5USv2OM3A6P2uA2cBWYIGInON6EJGlwJfAOqXUdmA+5wqzorAIZ5Pen8By4BnXcAaLcMZ1bcf5CyX/G/xV4F2l1G9A/qiW14EgpdQOpdSf/CO4PsH5efwXZyD9RqXUVmCM65pyxZdffsnBg4cY/liVUn1BDhvhi6en4uWXh5TaPTSXzx9//MG1117Lvv27eOuzWtx8t4+7TSoXVA018fbMCB5/rRrr1/1Bo8b1+OCDd3E4SiCgR1Mm0QHjGpRSfq5edwr4ANgvIu+4264Kjtsrnt1uJzq6Fr5+p/lpaelPrfHmGxl8+kkW23esoFHDTqV6L03RmTNnDkOGDCEoxMjrH0dSp5G7LSqfxB+3Mun5RP5Yk0X7ji2ZOeNrYmIuf6JszUW54q5R7XnSAAxxeU924myCK0z8kaYck5ycTJcuXTh+/ASPDve9Is0yg4f44OEBw4ffxoEDB0r9fprCYbPZePLJJ7n//vtp2MyTj76toYXTZRBRw4MJX0Tw1JuhxMVtoUnTBkye8jZ2exnrrqm5LLTnSaNxD26peCLCV199xciRI0lOTqJurImff6nKlRom5ZWX0/nv7GzCw008OvwFnnnqpdIePE9zEU6cOMG9997LqlWr6D2wKsPGBGOqfOM+lhoJJ61MGpPEhpWZXNWsLtM//i/XXHONu82qiGjPk0ajKR2OHj1Kz5496d+/P2bfDETgsVG+V0w4AQx9xBeloF4DI2Oe/w/NW9UjLi7uit1f8w8//PADzZo1Y+OmtTw/sQYjX9HCqaQJjfTgrRnhjJ0azomTh7nuumsZMvR+UlIKGvlEU57Q4kmjqeDY7Xbee+89GjVqxIqVvzDipXA8zUKduiZuvuXKjvodGWmkT19v1vyWx5iJ1Th54hjXXNOKp54ZQU5OzhW1pbKSnZ3N448/Ts+ePQkKzWP6/2pzU5/KMUedO1BK0blnFb74NYo7BwXz+Yw5xNaLYsbnn+qA8nKMFk8aTQVm165dtG/fnlGjRtGklYmZS6IJjVQc2mdhxEhfjMYr3wX90WG+2G1wdE8Os36N4qY+/kya8AGNmtRm+fLCjF+qKS6rV6/m6quvZsqUKfQeWJX3F4ZTI0aHblwJfKsYGf5iVT5eHEV4lIOHBg2hecuGrFixwt2maYqBFk8aTQXEYrHw+uuv07x5c3bv3cKL79Tkrc+rEVpdmPVeMrVjjNx6m3vmmouqZeK2Xl7M/28WYhOeeTuUyf+tjtWewg033MADg/rpZo0SJi0tjREjRtCxY0dyrfFM+TKGka8EYy65mXg0haRuIzNTv4lkzDthnE48RJcuXbil5w3s3r3b3aZpioAWTxpNBWPTpk20bt2al156ifY3+TJzSS269vJCKcXaX7P4a7eFYSP83OJ1OsvwEX7k5grffe4cML5FWx9m/FyTex4JZs4X86jfIJpvvpmH7tByedjtdj799FPq1avHtGnT6DuoKtN/rE6zNnp+OndiMChu7OXPF79GMfTZEFatXknTpo0ZPOR+PcBmOUH3ttNo3EOJV7ykpCTGjBnD9OnTCQnz4vHXQmnb9Z+56kSEh28/Rk6ajeWrQjCZ3Dtq9IhHU1m1Mo+v1kTjF/BPj7v9O3OZ8FwS+3bkcHPPTrz/3gxq167tRkvLHyLCkiVLeOGFF9iyZQtXtfLnsbGhxDbRI4WXRVKTbcx6L5X/zU0FUQwY2J8Xx/xH/90XHt3bTqPRFA2bzcYHH3xAvXr1+OyzT+k7KJjPl9Q4RzgBbFiZzb7teQx/zNftwglg+EhfMjOF72edOSc9trEX0xZV59EXQlj26yoaNIzl6WdGk56e7iZLyw8iwk8//USbNm3o0aMH8Ql7GDs1ine/1sKpLBNY1cSoV0P4cmUtbr0nkNmz/0tsbF0GPnAPO3fudLd5mgLQnieNxj1cdsVzOBwsWLCAsWPHsnv3blq182fkK+FE1f131iLCsN7HSU+ysmJ1CB4eZeNFOmRQChs3WJj7WzS+/v8e7ykh3spnE1NYsjCNqiFVePXVNxgy+GE8PT0LyK3ykpOTw7x585g6dSpxcXGEV/fhvuFB3NTHGw/PsvGsNYUn8ZSNeZ+ksfjLFCx5QqfObXni8ee4+eabMRp1k2sBXPE/ci2eNBr3UOyK53A4+P777xk7dixbt26ldj0/HnoihHbdTBccKXzDyiyeffAkb7zlT/97y858ZTt3WOnZI5mHHw/gnpEXng96z7Zcpr2ezLZN2URWr8pzz77M4MFD8Pau3F3sd+zYwezZs/nss89ITk4mOtaXOx8MLFA02e1CRpqD9BQ7eXmC0QgeHorgakZ8q+gXclkk9YydH77K4NvZKSSeshFdO4KHBj3KgAEDiYqKcrd5ZQktnjSaSkKRK15WVhazZs3i3XffZd++fdSI9uWBUcF0vtV80eBvEWHYHcdIS7axfGUIZnPZ8kQ8PDiFdesszF19buzT+YgIm1ZnM/v9VLb/kU1oWCDDHh3J4MFDqV69+hW02H2ICPv27WPhwoXMnTuX7du3YzQqru/mT+/7Q7jqOoVSCrtd2L8zj63rcti7PZfDBywcO2jBZi04Xx8/Rc3antRrYqb+VV5c08GH0Eg9YmZZwWYV1izNZNEXGfy5MQuAjp3a8MDAofTq1YvAwEA3W+h2tHjSaCoJhap4IsLvv//O7NmzmTdvHmlpaTS8qgp9HwqiQw9PTIVoflu/IovnBpU9r9NZdu2ycstNyQwe6c99j4dd8nwRYeuGHOZ+mM7G1RkYjQZ63noTAwcMoXv37hXOG5WSksKaNWv4+eef+emnnzh06BAAV7WqQpfb/OnYw5ugEIXVImz+PZvl/8tg7bIsMtOdAzDWjDJSr56JOnVNhEcYCAw04OWtcNghL09ISHBwKt7O/n02du6wkpbm/NOMqe9Buxv9uKmPPzWidTNpWSH+mJVfFmWxZFEaJw5bMJmMtO/Qljt69eW2226jVq1a7jbRHWjxVBFQSr0DHBGRKa79JcAxERns2p8EnBCRyZdxj07AUyLSswRMvmS+SqktwIMislUpZQLSgIdFZI7r+GZgiIgUe64NpdQrQKaITCwgfQiQCJiAF0RkcTHv0Ylifm5KqV7APhHZVZx7n8cFK15ubi6rVq3ixx9/ZPHixRw+fBhvbxPtu/ty+73VaNSCQk/kKyI82usYGWdsLCuDXqezDHskhd9WOWOfqgQWfq67E0csfD83k5/mp5KabMfXz4uet9xCz5696NKlC5GRkaVodcmTlZXFrl27+PPPP1m3bh1r165lz549AHj7mGjR1ofrOvlzTSczYdWd/X2OH7bw7ew0li5MJz3Vgb+/4sabvLi+gyft2npSLbTwTXIiwoH9dlauyGP58jw2rrfgcMDVrby4fWAAHbpXKROdDTTOZ7Vray6/L81jzS9pHP3LAkDtmJp07nQjnTt3pmPHjtSoUeOKTPztZrR4qggopfoCfUXkLqWUAdgEWESkjev4OmC0iGy4jHt04sqKpw+AnSIyTSnVEpgOrBeRYUopX+A4ECIixZ46/BLiKVNEJiqlGgK/AaEi4sh3jklEbMUtXyHtmwl8LyLzi3ptAQg4vwATEhLYtGkT69evZ/369axbt47s7Gy8vE00b+NNl55BtOvmiY9v0b8f1i3P4vmHTjLubX/u6V/2vE5n2bvHSo9uyTw4zJ8BT13a+3Q+NquwdX02q37KY/WSVNLOOP8MY+vVpmOHG2jRogXNmzenadOm+Pr6lrT5RSI9PZ0jR46cs+zZs4edO3dw6NDhv8e2CgjypHELM41b+NKkhTcNmxvwNDsFk4iw+fcc5n+ewoYV2RhNcFN3L3rd4UWHjmY8SyhI/FS8nUULc/h6Xg6HD9mJrGnizocCufmuALy8dWftssSxgxbWr8jhzw25bN2Q+bfnMTQsmObNWtKyZWuaN29O/fr1qVOnDj4+Zff7oBho8VQRUEpFAhtFpIZSqinwFBAB3A1kA6eBUKA9MBGnN2UT8KiI5CmlbrhAendgCpAExAExBYicaGA2cPYNMUJE1rpEwyuua5sAm4H7REQKmW9/4GYRuU8p9RiQBzwgIm2VUp2BF0XkBqXUE8Ag12Wf5vO+XSh9DDAAOIbTs7T5YuLJtX8KuAr4GlgLtAMWA1uL8rkVkO8OoKeIHFZKDXA9NwG2AR8C3+P0uKUBfYBbgEcAG7BLRPpRSB566CHZvXs3e/bsJiUlFQCjUVG3oQ+NW5pp0ymQq65TmL2K/4JyOIRHeh0jK9UZ61RSL9TS4rFhqSxflseXq2oRGFL8eBu7XTi4J48tay3Erc1m55ZsMtL+0fQRkaHUrh1DTO26REVFUbVq1XMWHx8fzGbzOYszX/u/ltzcXLKyssjMzCQzM/Pv7fT0dJKSkkhMTPx7nZiYQEJCAqmpaefY62k2EBllpnY9EzH1fYmp50WtelA9+t8dAESEzWuymfnuGXZsziWkmoH+93rT/14fwsJLL+jb4RB+/SWPjz7MYstmK9XCjAwcFUz3vgHaE1UGsduFg3stbN9oYf9OC/t3ZnFovwW77Z/3fWT1MGJj6xFdK4aIiIhzlmrVqhEQEEBAQABeXl7lwXOlxVNFQSl1GOgA9MD5YKsD63C+eN8EugH7gRtEZJ9S6gucL/aPLpHeBTgAzAN8ChA5PoBDRHKVUrHAXBFp5RJP3wGNgZPA78DTwB+FzDcaWC4iMUqpucCrOAXFbcBIwOzKfyZwnavMG4D7cI4ndrH0a3EKnjjgo0t4nq4FFrk+zxU4RcswpZRXUT+3C4knnMJzIdBORJKUUsEicuZ8z5NS6iRQ2yXQAkUklUISXM1Doup4EFXHk6g6ntRrbKb+VeYS/TW/bHEGr406xYTJAdzZt+zHAf11wMZNXZPo09+PYf+JKLF8RYSEkzYO7Mrjr90WTh6zcuq4lfhjVpJO2bAX21d6cYwmCAgyERhsJCDY4FqbCIv0IKyGibDqRsJreBBU1YjBcOnv/j/WZDNzSjI7NucSEWlk2Ahf+t7lfcWbYtevszD+7Qy2bLZSK8bE4GdDuP5Gv/Lwgq3U5OU5OHrAwrFDVo4fsnHiiIUThy2cPmnjTKIN+wX89iYPha+fB37+Hvj6euBpNuLhacDT87y12YjJpDAYFMqgMCic63OW/GnO8IOC/m7OT/rXKeclfDjhzyv+x1f44AJNUfkdaOtaJuN82bfFKZ7WAvWBQyKyz3X+LGA4TkFQUPpKV/p+AKXUHGBoAff1AN5XSjUD7EC9fMc2ishx1/VbgWggszD5urwxnkqpcKABsBend+daV7mmAtcDi0Qky5XXQpzeNXWBdIMrPduVfrE4pseVUvcBGcDdLo8ZOMUQF/k8C/u55acLMF9EklxlP3OB87YB/1VKfQt8e4k8z2HRpto4P5bSafqw5DmYPiGZBo1M9O7jnjnsikqduibuudeHuf/N5NYBFmrWLRnBpxSEVTcRVt2LdjfmP+LA4XCQlensvp+e4iA9zU5ejmC1CBaLc23Nc/7ANBidi9GgXNsKT7PC28eAl49z7e1rwNtb4e1nwK+KwfViyL8UnUP78vhwXAIbV2UREWnktXH+bhFNZ7mujScLFgXzy5I8JrydwUsPn+LaDj6MGBtOzRgdWF5WMZuNxDb2ILbx+Uec9SA9xU5ygp3kBBtpKXayMx1kZjjIynCQneHczsm2YrVYsFqErGzBkvpPHbFaBJtNEAFxgN0hiAMcDhBxei//2RccDnCU0A+XfsPrDegYve+LksmtcGjxVHqsxSkqmgI7cDZLPQmkAzO48Dfpxb4RC+MmfBxns+DVON/MufmO5eXbtvPP8y+s+3EdcCcQ7xIv63E2mV0DrMcpqgricssE8M75HikXWZdxDxvnqpezKkMV0q5bcHoXbwNeUko1LkzcFUDLyO+w2ktv8ttpU7/i1PGpjP9vWKG8GmWFUY/78u3CHGaNt/D1d1+62xy3knD6DG+9/ilffL6YKlWMjHkpiPsHepaJoH+lFN26e9Glq5k5s7OZPCGTh3ocZvjIPjz53CP4+JQPwa7JRwTQqHCnCoKIBYdYELHiwIKIzblgQ8SBYEdwgDica8R1pUtNIfm+ZOUCa86Z39J53/O+msXIicyPfi1iaS8bLZ5Kj99xiqWDriDqM0qpQJzNZkNwenyilVJ1ReQAcD+wCthzkfTaSqk6IvIXcM8F7hsAHBcRh1JqIHCpQIjC5nu2TI/jbGoDp5iaAJwSkVSl1GpgplLqLZwC5A6X/aoQ6SbgVuDjS9h7sXIU9XM7jLOZDqVUC+DsRFLLgEVKqXdEJPlssx1Or1cV1/kGoKaIrFBKrQH6A35AoZru/DwbFrOYlyYlJYVJb82hQ0df2ndw/4u2KISEOJujxr8Vz4ZVe+jefdClL6pg5ObmMmXKFMaNG0dOThYDHvBj5GhfgoLcbdm/MZkUDzzoyy23ePHmuCzemfgN38z7lfenfsbtt9/hbvM0lYS6IU+cvNL31N0lSo/tQAhOj0z+tDQRSRKRXOBB4Bul1HbAgTPe52LpQ4EfXC/rC029PQ0Y6PIK1eMfz0yBFCFfcIqnGJyiCRGJxynO1rr243AKq40445o+FZEtl0ifhzPQewHOXnTFopif2wIg2NWE+Siwz5XXTuANYJVS6k+cza4AXwFPu4ZtiAXmuO61BadnrNAxT6XJmDFjSEtL5bkXAtxtSrEY9JAvNWoaGTlyJLm5uZe+oIIgIsybN48GDRrw/PPPc20bBz//Gs7YV8umcMpPtVAjk6f4M29+ML4+mfTq1ZvbbuvM0aNH3W2aRlMq6IBxjcY9lErF++OPP7jmmmsY+KAfY191b5f8y2HF8jwGDUxhzIt38/prX7nbnFInLi6OUaNGsWbNGho18ubFsYG0aVPHem4AAA9eSURBVFs+v5utVmHGZ9m8OzkTpUy88sorjB79NB4eesRyTamhe9tpNJWEEq94drudNm3acOTIdn5ZEYS/f/mu2yMeTeWXpXls2bqBRg1bu9ucUuH06dOMGTOGGTNmEFzVk6ee9qPv3aaLTrdTXjh+3M6rL2fy6y85NG5Sm08+nkPbtm3dbZamYnLFK4xuttNoKghTp05l06ZNvPBilXIvnADGvloFsxcMGdwLh8Nx6QvKEXl5eUyYMIHY2FhmzfqcwUOqsHxVVfr196gQwgmgRg0j02cE8PGngaScOUq7du0YMmQAZ85cqPOqRlN+0J4njcY9lGjF27NnD82bN6fd9Samz/CtMGPufP1VNs8+nc5/XhvMSy9Od7c5l42I8P333/PEE09w4MAButzgy5iXA4mJKaXBpsoIWVkO3n0nhxmfZhAYWIVJk95jwICBFebvVON2dLOdRlNJKLGKZ7PZaNeuHfv3/8nPv4QQGlZxXsQiwvBHU/llSR6rVy+hTZtu7jap2Pzxxx88++yzLF++nLp1fXhxrD8dO7nbqivL7t1WXnw+k7jNeXTo0JqPPppFw4al1/NUU2nQzXYajaZovPjii2zcuJH/vOFfoYQTOMcTevOtAELDjPTrdwdJSYnuNqnI7N+/n7vvvpvWrVuz9c/fGftqMD8urVLphBNAw4YefLMwkHFvB/Dnn5u5+uomvPDCU2RnZ7vbNI2mSGjPk0bjHkqk4i1cuJA+ffpwz71VGPdW+e1ddym2xFnod1cKrVtFs3z5Hjw9y/5I1qdOneK1117jk08+wdMTBg/xZfDDPlSpor9zAZKS7Lz5RjYL52cRFRXCK6+8zf33D8Bk0sMPaoqMbrbTaCoJl13xdu3axXXXXUedug6++sYfs7li1+XvFuUwemQa997Xhdlf/Fpm42WOHz/O+PHjmT59OjabhX79fRk5yp9qoRXLK1hSrF+Xx7jXs9i+zUL9+jV57bVJ9OnTB4NBN4xoCo0WTxpNJeGyKt7Ro87eSxZLEov+V5XIyMrxYp4yOYN338ni4Yd78+GH88uUgDpy5AhvvfUWM2bMwOGwcUcfH4YN9ye6dsXqKVgaiAhLfs5j8sQs9u+z0rhJbZ584iX69++P2Wx2t3maso8WTxpNJaHYFS8hIYEOHToQH3+YefNDaNCwcggncL5kx72ewaefZDN48O18+OF8tzbziAhr167lvffeY8GCBRgMQt+7fXh0WAA1alae51JS2O3C4u9y+eTDHPbssRAeHsTw4aMZNGgwkZGR7jZPU3bR4kmjqSQUq+IdPnyYbt26cfz4IWbNqUbraypf/RURJrydyYcfZNG1a0u++eZXAgMDr6gN2dnZzJ8/n/fee4/NmzcTEODJXf28ePAhXyIiKt8zKWlEhN9WW/h0ei6/rcrBYFB069aJBx98hJ49e+Lj4+NuEzVlCy2eNJpKQpErXlxcHD179iQ7+wwzZgXTomXlrrtfzc3mpRfSCQ8PZPbsBXTq1KVU73fWyzRz5ky+/vpr0tPTiY31ZuAgH+7o7YF+n5cOhw7ZWPCNhYXzs4iPt+Pt7UnXrl24/fY76dGjh/ZIaUCLJ42m0lDoiiciTJs2jSeeeIKqIQZmflGVevV1kxDA1i0WHh+ZzuHDNvr378Wbb75LVFRUieVvt9tZu3Yt3377LYsWLeLQoUP4+Jro0cNMn77+XNfGUabirioydruwYb2FX5Y4+OWXTE4cd9aBmJiatG/fmfbtO9C6dWsaNGhQLnpjakoULZ40mkpCoSrevn37eOyxx1i6dCmdu/gx8Z0AgoO1cMpPdraDD97L5tNPM3HYDfTufSuPPDKK9u3bFzkeSkTYu3cvq1evZtWqVSxdupSkpCQ8PQ20befFLbf60eNmha+vFkzuRETYvdvG2jV2Nm208semHM6ccQbmm0xG6tWvw9VXtaB+/QbExMRQu3ZtYmJiCA8P1734KiZaPGk0lYSLVryjR48yceJEPvroI7y8FE8948d9AzwwGPRL+0KcOGFn5oxc5n2VSUa6EBTkR+fOXWnZsjUNGzYkNDSUqlWropTCbreTlpbGqVOniI+PZ/fu3ezYsYPt27eRnOycey001JM2bU106+5Ph46Cn5/+7MsqIsLBg3Z27bCzdy/s2Z3Hnj15nDxhJ/8rzmz2oGbNSKpXjyIysgaRkZFERkZSvXr1v7cjIyPx9vZ2X2E0xUGLJ03FQSn1DnBERKa49pcAx0RksGt/EnBCRCYXMr+VwFMi8kcJ2VcN+B7wBEaKyG8FHD8JjBCRjy+Sz2jgExEpyjDJ/6p4VquVn3/+mdmzZ7No0SLAQe8+Pjz1TIAeI6gIZGc7WLXSwrJf7WzakM3Ro5f+7Hx9jdSr70m9+gZatPCl9bWK6Gh0k1w5Jy9POHHCzrEjdo4dN3DsiJ2T8TZOxVtISHBw+rSdvNx/vwODgvwJjwgjIrw6ERHVCQ8P/9cSERFBcHCw/hspG2jxpKk4KKX6An1F5C6llAHYBFhEpI3r+DpgtIhsKEReRmAZJSue+gE9RGTgBY4PA+4B7CLS6SJ2/QW0EpGkItxeMjIy2LVrFxs2bGDZsmWsWrWKtLQ0gqt60quXmUFD/KleXYumyyU93cGxo3aSk4WUMwaUMmAwgp8fVKvmICREERpm0C/BSoiIkJ4mnDpl5/RpBwmnDSQkuPZPWUlKspKYKCQkFCyyPDxMhIVVIzw8gvDwyHOEVX6hFRISgp+fn24yLD20eNJUHJRSkcBGEamhlGoKPAVEAHcD2cBpIBRoD0wETDgF1qMikqeUOgzMALoB7wOPuPKIAz4HjgFjgc+AVji9OTNE5J3z7KjlyqcakAg8CAQDiwFv4ATQRkRyzrvuN+BJ4Eugo4iccKVnApOBm4AfgBeBvUCSiHQuzGdTu3a0HD585O/9WtFetGlrpOuN/nTo6MDDQ7/INZqygoiQkSEkJjpITHCQlGggMRESE+0kJlpJTHCKrMREB8lJNhwFjIuqlCIgwI+AgAACAwMJDAwmICCQwMBAqlSpgpeXF97e3hdczGYzRqMRk8l0znJ+2tn9s0JNKfX3kn//YscKc25ZwtcNQYhaPGlKFZcA6gD0wPnroDqwDkgD3sQpjPYDN4jIPqXUF0CciExxXTtNRMa78loJPAeMAnaIyBtKqZbAWyJyo+ucQBFJPc+G/wHzRWSWUmoQcJuI9FJKPYDTYzSiALtrAstFJFYpNQ6nMJrsOibA3SLydb4yFsnzdHsvb4mtZ6JefRONGntQo4axsJdqNJoyjN0unEl2/C20EhLspKYKGRkO0tNd67T8+0JWpoPcXMjNFfQruegcOhZeK7pG/NEreU89A6OmtPkdaOtaJuMUT21xiqe1QH3gkIjsc50/CxgOTHHtzzsvv4+Br0XkDdf+QSBGKTUVpxdoaQE2tAF6u7ZnA+MLYXc/4GvX9lc4vVtnY7PswIJC5HFBpk6L5TxHl0ajqQCYTBAa5lwujQMRO+D4e9tiEfJyhdxzFrBaBZsNHA7n2m4Hm02w28DuALtNsNn/WYs4F86uyZeG05smnHvswue6lhL6jEoSlwPoepwtBFcMLZ40pc1anGKpKbADZ1Pbk0A6zqa0S7lbswrIr7NSapKI5IpIilLqapxNaMOBu4BBl8izMN8B9wBhSql7XfuRSqlYEdkP5IrzG6/YREVuu5zLNRqNRvMPV1Q4AejoNU1p8zvQEzgjInYROQME4vQGrQP2ANFKqbqu8+8HVl0kv8+AH4FvlFImpVQIYBCRBcBLQIsCrlmL05MEcC+w5mIGK6XqA74iUl1EokUkGmcTY78LXJIBVLlYnhqNRqOpOGjxpClttgMhwPrz0tJEJElEcnEGcH+jlNqO03/90cUydMUexeFsgqsOrFRKbQVmAs8XcMlI4EGl1Dac4mzUJWy+B1h0XtoCV3pBfAL8pJRacYl8NRqNRlMB0AHjGo170BVPo9FoSoYr3ttOe540Go1Go9FoioAWTxqNRqPRaDRFQIsnjUaj0Wg0miKgxZNGo9FoNBpNEdDiSaNxD6q8L0qph91tgy6TLpe7bdDlKhPluuJo8aTRaIrLUHcbUApUxDKBLld5Q5erjKPFk0aj0Wg0Gk0R0OJJo9FoNBqNpgho8aTRaIrLJ+42oBSoiGUCXa7yhi5XGUePMK7RaDQajUZTBLTnSaPRaDQajaYIaPGk0WiKhFKqu1Jqr1LqgFLqOXfbU1IopQ4rpbYrpbYqpf5wtz3FRSk1QymVoJTakS8tWCn1i1Jqv2sd5E4bi8MFyvWKUuqE65ltVUrd7E4bi4pSqqZSaoVSardSaqdSapQrvVw/r4uUq1w/r/zoZjuNRlNolFJGYB9wI3Ac2ATcIyK73GpYCaCUOgy0EpEkd9tyOSilOgCZwBci0sSVNh44IyJvuQRvkIg86047i8oFyvUKkCkiE91pW3FRSkUAESISp5SqAmwGegEPUI6f10XKdRfl+HnlR3ueNBpNUbgGOCAiB0XEAnwF3O5mmzT5EJHVwJnzkm8HZrm2Z+F8kZUrLlCuco2IxItInGs7A9gNVKecP6+LlKvCoMWTRqMpCtWBY/n2j1NxvhQFWKqU2qyUqjCD+bkIE5F4cL7YgFA321OSjFBKbXM165Wr5q38KKWigebABirQ8zqvXFBBnpcWTxqNpigUNBVCRWn7byciLYAewHBXM5GmbPMhUAdoBsQDk9xrTvFQSvkBC4DRIpLubntKigLKVSGeF2jxpNFoisZxoGa+/RrASTfZUqKIyEnXOgFYhLOJsqJw2hWHcjYeJcHN9pQIInJaROwi4gCmUw6fmVLKA6fA+K+ILHQll/vnVVC5KsLzOosWTxqNpihsAmKVUrWVUp5AP2Cxm226bJRSvq7AVpRSvkA3YMfFrypXLAYGurYHAt+50ZYS46zAcHEH5eyZKaUU8BmwW0Qm5ztUrp/XhcpV3p9XfnRvO41GUyRc3YunAEZghoi84WaTLhulVAxObxOACfiyvJZLKTUX6ASEAKeBscC3wNdAFHAU6Csi5Sr4+gLl6oSzCUiAw8DDZ2OFygNKqeuB34DtgMOV/ALO+KBy+7wuUq57KMfPKz9aPGk0Go1Go9EUAd1sp9FoNBqNRlMEtHjSaDQajUajKQJaPGk0Go1Go9EUAS2eNBqNRqPRaIqAFk8ajUaj0Wg0RUCLJ41Go9FoNJoioMWTRqPRaDSa/7dbxwIAAAAAg/ytx7C/KGKQJwCAIaclW7U8wb5TAAAAAElFTkSuQmCC\n",
"text/plain": [
"
"
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"fig, axes = joypy.joyplot(sector_features_log, colormap=plt.cm.viridis, figsize=(8,8),\n",
" title='Distribution of mis-invoicing across sectors (log transformation)');"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"source": [
"The Yeo-Johnson transformation is similar to a Box-Cox transformation, but allows for zero values. When $x=0$ and the tuning parameter $\\lambda=0$, it will apply the same modified log transformation, $log(x=1)$, as described above."
]
},
{
"cell_type": "code",
"execution_count": 27,
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"outputs": [],
"source": [
"sector_features_yeo = power_transform(sector_features, method='yeo-johnson', standardize=True)"
]
},
{
"cell_type": "code",
"execution_count": 28,
"metadata": {
"slideshow": {
"slide_type": "slide"
},
"tags": [
"hide-input"
]
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAmsAAAI1CAYAAACJyL1jAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4yLjEsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy+j8jraAAAgAElEQVR4nOydeXxVxfmHn/duWchGEpYQICHsi7KDgmwCbli1Ki51X2ht3Vq1LrX9VetarVaxahe11mrRuuMKakVFkEVWQUDZEwIEQsh+1/f3xzmBS8wKSe5NmCef+8m958yZeWfOzJzveWfOHFFVDAaDwWAwGAzRiSPSBhgMBoPBYDAYaseINYPBYDAYDIYoxog1g8FgMBgMhijGiDWDwWAwGAyGKMaINYPBYDAYDIYoxog1g8FgMBgMhijGiDVDm0RE/ioiv2uiuLqLSKmIOO3f80Tk6qaI247vAxG5rKnia0S694rIHhHZ2QRx/UZEnjmM4y4SkblHmn4D0ikVkZx6whxyng2tExEZICJLI21HXYjI8yJyb6TtiFZEZKyIfGe3x7MibU91mqrPFpEbROTBBoU166wZWhsisgXoBASAILAWeAH4u6qGDiOuq1X140YcMw94UVUPR5zcBfRS1Ysbe2xTIiLdgA1AlqrujqQthrbNkbSXw0zvdeBVVX1ZRF4CvKp6Zdj+CcAbwCBVzW/CdC/H6ktOaEDY54FcVf1tU6XflIjIRKxz1jVC6X8CzFbVxyORfjVb7qKZ+mwRiQW+B4bV1w8bz5qhtfIjVU0EsoAHgduAZ5s6ERFxNXWcUUIWsNcItdbF0eb1E4sGX6dEJAOYBLxlb7oBOE1Eptr7Y4F/ADc3pVA7GmnmvjELWHM4B7amPltVK4EPgEsbEth8zKdVfYAtwJRq20YBIay7ZYDngXvt7+nAu0ARUAh8gXWj8m/7mAqgFLgVyAYUuArYBnwets1lxzcPeABYDOwH3gZS7X0Tse6Yf2AvcArgA/x2eivD4rva/u4AfgtsBXZjeQyT7X1Vdlxm27YHuLOOckq2jy+w4/utHf8UO88h247nazh2IpBrl8luIB84CzgNyyNXCPwmLPxdWHfiALHAi8Beu8yXAJ1qsfFyYH7YbwWuAb4D9gFPAgLE2HENCgvbwc5HR/v3DKy71EJgNtClWry97O9xwCN2mewH5tvbajrP9wBfAiXAXCA9LM5L7Tj2Ar+jhnoZFnYasBwoBrYDd1XbfwKwwM7jduDysHr8NPA+UGafu/62bUVYF7QzwuI5DcvTXALkAbfU1QZqsFOAP9vnfD+wioNtKgb4E1bd2wX8FYgLO/ZMYIWdx41Y9f0+LO93JVZd+4sddoxdL/bb/8eExTPPPu5L+/z2wqonm+x8bQYuqqWcLwU+rrZtun1MO6x2+4G9/biwMl8JTAw7pgtWHSrEqlMzGtAvXc6hdbmu8/Q8Vt1+z87TIqBnfe3A3tcL+Mwuuz3AK2HH1VeutdbnsHDtOLR/KLXL4y7gNay2XQxcjdXvLrTzmA/8BfAcST7suhPeL8fUdT5qsWsecK99fkuBd4A04CU7zBIgOyyOx7HaXTHwNTDO3t7sfTZwEfBpvfWrvgDmYz7R9qGWi6LdGH5uf3+eg2LtAawLi9v+jAvrMA6JK6xxvWB3WrVdxPOAQXaY1zkoVCZSi1izv99VFTZsf3jDv9LujHKABKzhmn9Xs+0ftl2DAS/Qv5ZyegFLSCbax24ArqrNzmrHTsQaZv4/u8xmYIm+/9jxDcS6AOdUzxfwM6zOMR5wAsOBpFrSuZwfirV3gRSgu53mKfa+54D7wsJeC3xofz8RqyMchtW5PwF8Xi3eKrH2pF3mmbZ9Y+xjajrPG4E+dnnPAx609w3A6rxPADxYIsZP7WJtInAMVsd+LJbYOcve1x3r4nmhXdZpwJCwerwfGGsfm2jXj9/Y6Z5oH9vXDp/PwQtNe6zhFaijDVSz82Ssi1UKlnDrD2TY+x7DumCm2na8Azxg7xtl2znVtjMT6Fe9ftu/U7Eu3JcALjvf+4C0sPDbsOqYC+umozgsjxnAwFrK+WHgyRq2v2bbvtcu70z7+2m2vVPt3x3s8J8BT2HdeAzBqoeT6+mXLseuy3YZ13WenscSHqPsPL4EvNzAdjALuNO2OxY4oRHlWmN9rqW+Vu/H7sKq42fZacdhte3j7PSygW+BXx5JPmrpl2s9H7XYNc8u/55Y9WctVv83xbb1BeCfYfFfjNXuXMDNwE4gtiX6bKw+q7CuuqWqZhjU0KbYgdVhVceP1cFnqapfVb9Qu5XUwV2qWqaqFbXs/7eqfqOqZVhelfOaaIjqIuBRVd2kqqXAHcAF1Vz7d6tqhaquxPIIDK4eiW3L+cAdqlqiqluwvEmXNMIWP5Y48gMvY3lnHrfjW4PlLTi2luPSsMRRUFW/VtXiRqT7oKoWqeo24FOszhksoXhhWLif2NvAKrfnVHWZqnqxyu14EckOj9geUrsSuFFV82z7FtjH1MQ/VXWDXQ/+G2bLucA7qjpfVX1YorbWOqWq81R1taqGVHUV1oVqQpjtH6vqLLt+7lXVFWGHv62qX6o1H3MI1gXhQVX1qer/sC6GVeXiBwaISJKq7lPVZWHbG9IG/FhCrB+WmPtWVfNFRLAE+69UtVBVS4D7gQvs467CKv+P7Dzmqeq6WopjGvCdqv5bVQOqOgtYB/woLMzzqrpGVQNYNw0hYJCIxKlqvl3/aiIFSxRV51oswfQHu15dDLyvqu/b9n4ELMUaMu2GJcJvU9VK+1w8Q+PaznHUfZ4A3lDVxXYeX+Jg3aqitnbgxxom7GLbN9/e3pByra0+N5SFqvqWXWYVdtv+yk5vC/A3Dtbrw83HITTwfBxiV1heN6rqfqyhxo2q+rFd3q8CQ6sOVtUX7XYXUNVHsG7e+jawTI60zy7BEpR1YsSaoS2RiXW3Wp2Hse585orIJhG5vQFxbW/E/q1Yd9LpDbKybrrY8YXH7cJ6oKKK8Kc3y7EuCtVJx7qjrx5XZiNs2auqQft7VQe4K2x/RS1p/xuYA7wsIjtE5CERcYvIOPvprlIRqWs+Sm35+x8QJyKjRSQLq9N/0953SLnZneZefpjfdKy78411pN8QW7oQVgdUtdxOr0Zsmz8VkQIR2Y81NFRVX7rVY094XesCbNdDH6QJP6/nYHmLtorIZyJyvL29QW3AFhV/wfI+7hKRv4tIEtaQczzwtYgUiUgR8KG9vSF5CKd6Ha+eh0PybN8QnY9VZvki8p6I9Ksl7n1YYrN6vnZheV6r6l0WML0qL3Z+TsAStF2wPB3hom8rkCkiMWF1uOrzeS15rOs8Qf3tuLb9t2J5PReLyBoRqXp4oiHl2pC+oy4O6RdFpI+IvCsiO0WkGEvAV+8HG5uP6tR6Pmqzy6Z6X1Vr3yUiN4vItyKy364LyTXkozaOtM9OxPJK14kRa4Y2gYiMxGq8P7g7sz1BN6tqDtZd5k0iMrlqdy1R1ud56xb2vTvWXeIerHlF8WF2OTl4QWtIvDuwLiThcQc4tKNpCHs4eOcaHldeI+NpNLbn5m5VHYA1xHg6cKntzUmwPwMPI94QljfgQiyv2rthHfgh5SYi7bC8e9Xzuwdr+LZnY9OvRj5w4Ek5EYmz06uN/2ANw3VT1WSsIUmx922vx57wOrMD6FZt0v2B86qqS1T1TKAj1iT7/9rb62oDhyamOlNVh2MNQ/YBfo1VbhVYw48p9idZVasuOnXloXqdr17HD8lDTceo6hxVnYolptZhDSvVxCrb5vrYjuUdTwn7tFPVB237UkUkXPR1B/JU1RtWh6s+42uIv87zdCSo6k5VnaGqXbCmHDwlIr1oWLk2OJkGbn8a63z0VtUkrGFf+cFRNUVUez6qU+v5aIC99SIi47AeUDsPaK+qKVjiqSofzd1n98fyttWJEWuGVo2IJInI6VjDdC+q6uoawpwuIr3soZxirAnPVR6jXVhzDRrLxfZ6TvHAH4DXbC/UBiBWRKaJiBtr4mlM2HG7gOw6nnCbBfxKRHqISALWneortuu+wdi2/Be4T0QSbU/UTViTcJsVEZkkIsfYQrUYSzQG6zmsofwHy8tyEQeHQKu2XyEiQ0QkBqvcFtlDMwewBd9zwKMi0kVEnCJyvH1MY3gN+JGIjBERD3A3dV+kErG8A5UiMgpLbFbxEjBFRM4TEZeIpIlIbcNTi7BuCG61vZUTscTXyyLiEWvdumS1hq6r6np9beAAIjLS9gK67XQqgaBdbv8A/iwiHe2wmSJysn3os1jlP1lEHPa+Ku9X9Tb2PtBHRH5i5/d8rDmA79aUYRHpJCJn2ALcizVXsLb69BEwTKynPuviRazzd7JdB2JFZKKIdFXV7VgT0x+wtx+LNcz7Uj1xhlPreWpEHDUiItNFpOpGYR+WmAjSyHKth11AmojUNzyXiFWfSu3z/fOGJlBHPg6hic5HXSRiiasCwCUi/wckhe1v7j57AtYwbZ0YsWZorbwjIiVYd8h3Ao8CV9QStjfwMVYnvxB4SlXn2fseAH5rD4Xc0oj0/401SXgn1rDaDQD2/IhfYM2pyMPqsHPDjnvV/r9XRJbxQ56z4/4c6wm2SuD6RtgVzvV2+puwPI7/seNvbjpjiZlirAnHn9FEIlFVqy6CXQjr4FT1E6y5g69jeb16cnA+VXVuAVZjPRFWCPyRRvaF9pyp67EuvvlY8052Y4mJmvgF8Ae7zv4ftsfLjmsb1tDlzbY9K6hhHqId1gecAZyK5e16CstrWTU/7BJgiz0kdQ3W3Cyouw2Ek4QlyvZx8EnXP9n7bsMaSv3Kjv9j7Hk9qroYq/39Gcsr8RkHvQ2PA+eKyD4Rmamqe7G8rTfb8d8KnK6qe2opO4cddoddPhOwyrOm8tmFNVx+Zi1xVYXbbof5DdZFejuWB7GqHlyINTl8B9ZQ++/teW31oXb89Z2nI2EksEhESrG8tTeq6ubDKNfaM2HZOQvYZPeNXWoJegvWjUcJVr155UjzUUvYwz0fDWEOVl+yAavOV3LosGqz9dn2TcVpwL/qDav1zrM2GAwGQ13Yd9RFWMNBtV1wDC2AiAzAuviN0ha8wInIDcCJqhp1K+4bohMRuR5rasSt9YY1Ys1gMBgaj4j8CPgEa/jzEWA01lIZplM9yrA9JO9hrZdlXiNlaHLMMKjBYDAcHmdiDcvswBpmvMAItaMPETkGazpEMdaTtAZDk2M8awaDwWAwGAxRjPGsGQwGg8FgMEQxRqwZDAaDwWAwRDGt5u30BkMbw8w/MBgMhqahQQvxtmaMZ81gMBgMBoMhijFizWAwGAwGgyGKMWLNYDAYDAaDIYoxYs1gMBgMBoMhijFizWAwGAwGgyGKMWLNYDAYDAaDIYoxYs1gMBgMBoMhijFizWAwGAwGgyGKMWLNYDAYDAaDIYoxYs1gMBgMBoMhijFizWAwGAwGgyGKMWLNYDAYDAaDIYoxYs1gMBgMBoMhijFizWAwGAwGgyGKMWLNYDAYDAaDIYoxYs1gMBgMBoMhijFizWAwGAwGgyGKMWLNYDAYDAaDIYoxYs1gMBgMBoMhijFizWAwGAwGgyGKMWLNYDAYDAaDIYoxYs1gMBgMBoMhinFF2gCDwWAwNC+qSmlpKWVlZQe2ud1uUlJScDqdEbTMYDA0BCPWDAaDoY0QCARYvnw58+fPZ+3ataxbt47vv9/I3j178Af8PwgvIiQmJNIhvQM9e/ekd+/e9OrVi2OPPZZhw4aRkpISgVwYDIbqiKpG2gaD4WjENDxDk1BUVMTs2bN59dVX+fTTeZSVlQIQ64wjLpRAO0cisa44YiQWB84DNS9EiAA+fOqlMlRBaaCYCsoIcFDUde+axQnjxjL1pKlMnjyZbt26RSKLBkN9SKQNaG6MWDMYIoNpeIbDRlVZsGABM2fO5M0338Tv99POlUiadqKDJ4P4iiRiJO6w4vXjpYQiylwllLCPvYFd+PAClnj78Tlncd5553HcccfhcJhpz4aowIg1g8HQLJiGZ2g0qsrbb7/NPffcw7Jly4hxxZKhWXRxdSfOm4RI01+zVJVS9lPkKGCfo4A9gZ2ECJHePp3pF5zH1VdfxbBhw5o8XYOhERixZjAYmgXT8AyNYu7cudx5550sXbqUJHcKWY6+pHszcErLTj0OqJ8C8tnrymd3II8QIfr26sd1N17LRRddRPv27VvUHoMBI9YMBkMzYRqeoUFs3bqVX/7yl7z11lskepLIkYGkeTNwSOSHIP3qY5dsZ4dsoTi0D4/bw8UXXcJtd9xKnz59Im2e4ejBiDWDwdAsmIZnqJNAIMDDDz/MPffcQ8AXpKdjAF38OVEh0mqiWPexw7mZHcEthAgxecIUfnvXnUyYMKFZhmcNhjDafAUzYs1giAym4RlqZf369VxyySUsWbKEzq5u9HUMwe2PibRZDcKrleTJJnJ1Iz68HNP/WO5/6D6mTZtmRJuhuWjzFcuINYMhMpiGZ/gBoVCIJ598kttuuw0NwADHcFJ9nSNt1mER1CD5bGGrbKBCy+jbsx8PPHw/Z555pnmK1NDUGLFmMBiahTbX8Px+P9u3b6e8vJyUlBQyMjLM6viNoKioiEsvvZR33nmHTq5M+jtG4PK7I23WERPSEPlsZausp1xL6ZXdi/v+eB/nnnuuEW2GpsKINYPB0Cy0iYZXVFTEiy++yGuvvcbCBQvx+X0H9sXGxHL8cWO44qrLOffcc4mLa/y6X0cLq1at4uyzz2bz5i30cw4hw5/d5oYMQxpiF9vZ4lhPWaiY7K7Z3PPAPVxwwQW4XOZlOoYjom01lhowYs1giAytuuGVlZXx4IMPMvPxmRSXFJPsak+adCbJmQJBBwF8lEoxu/15lGspSQlJ3HX33Vx3/bW43a3fW9SUvPjii/x0xk+RgJPBruNp502OtEnNiqqyi1y2OtZREtpP14yu3HXPXVx66aWmbhgOFyPWDAZDs9BqG95HH33EjBkz2Lp1KxnO7uS4BxDnTagxrKqyjwK2OtezN7iL7K45vPXuGwwePLiFrY4+fD4fN910E08++SRpzk4MYhTuUOt4iKApUFUK2MEWxzqKQ/vo3KEzv7vrd1x11VXExBw95WBoEoxYMxgMzUKra3jBYJDf//733HfffSR72jPQOYL4yoZ5gawLcz7rZRl+/Nz9+z9w5//d0eaG+hpKXl4e06dPZ+HChfRw9aNHYEDULsnR3Kgqe9nJVsd69oX2kNY+nTt/+xt+ds3PiI+Pj7R5htZBm+9IjFgzGCJDq2p4ZWVlnHPOOcyZM4durp70Dg7GQePFhU+9rJNl7NY8zjj5TP779itHnRdl3rx5nHfe+RQVFnGMexSp3tb5tGdTY3lhd9te2N0kJyRz7fXXcv0N19O5sykjQ50YsWYwGJqFVtPwioqKmDZtGgsXLmSQeySd/N2PKD5VZTPfsom19M8ZwPwlX5CamtpE1kYvqsojjzzC7bffTjtHIkMcY/D4jOeoJvZpAbnO79kVzMPldDH93PO49fZfM2TIkEibZohOjFgzGAzNQqtoeAUFBUydOpVvVn/DYPcYUn2dmizuXZrLGhbTKS2DJSsXkZmZ2WRxRxslJSVcccUVvP7662S4utMvNAynmicg66NcS8hzbiI3uJkgAUaPOI5bbruZM844A4/HE2nzDNGDEWsGg6FZiPqGl5uby5QpU9j43SaGuseS7Etv8jQKdTcrWUBSuyS++nohffq2vfdJrl27lnPOOYf169fT1zWETH/OUTtX73Dxq498xxa26/dUaDntk9pz5Ywr+dnPfkbv3r0jbZ4h8rT5BmXEmsEQGaK64W3atIkTTzyRHbn5DHeNJ8GX0mxp7ddCVjAfT4yHzxd8xrBhw5otrZZm1qxZzJgxA/XDsY7jSPC2j7RJrZqqhxF2uraxK5CLohw/egzX33gdZ511llnL7+jFiDWDwdAsRG3DW7t2LZMnT2ZfQRHDXeOJ9yU1e5qlWsxy+QJxKnM/nsu4CeOaPc3mxOv1ctNNN/HUU0/RwdOZQTIap8+sIdaUeLWCnc5t5IY2UaFltItrx3nnn8eVV13J2LFjjffy6KLNn2wj1gyGyBCVDW/ZsmWcNPUkKoorGe4cT4yvXYulXaFlLJcv8IuX2e+8wymnndxiaTclW7du5bzzzmPx4sX0cPUnJ9gfOYwnZw0No+op0t2uXPID2wkSIDOjK1fNuJLLLruMnJycSJtoaH6MWDMYDM1C1DW8+fPnM23aNEIVMEzG4/HHtrgNXq1gucynglL+859ZnHfB9Ba34Uh44403mDFjBmUl5Qx0jGzSBzIM9RPQAAWSxy7HdvYEdwIwcvgofnrNDKZPn05yctt+O8RRjBFrBoOhWYiqhjd37lzOOussPMFYhso4XL7IPWnnUy8rZQHFWsjfnv47M665OmK2NJTS0lJuvPFGnnvuOdJiOjJIRuH2trzYbSxeraCYfZRTQjll+PESwE+IEA4cOHERQywxxNGOJBJJIZb4VjHEWKnl7HJuZ0doK2VajMft4fRpP2LGz65mypQp5n2kbYvor5BHiBFrBkNkiJqG98orr3DJJZeQ4EhmiJ6A0x/5i1hA/ayShRTqbv5430Pc+ptfH1Y8lZWVuFyuZr0wf/XVV1x88cVs2rSJHNcAsgN9o3bYM6RB9rKLAvIpooBySg/sc0sMHonD5fDgwEFIQwTx4w2V41fvwXB4aE9H0uhEGp2IleheK05VKWYfu13b2RHYih8f7ZNTufiSi7j8issZOnRoqxCfhjpp8yfQiDWDITJERcN78sknuf7660n3dOKY0PE4As5Im3SAoAb5RhZRoDv4+VW/4C9/fwKHo34RVFZWxmOPPcbz/3ye7zd+j8PhYMjgYdzy65s4//zzGxRHQygpKeHOO+/kL3/5CwmeJAY5RtGuga/faklUlf3sJY/N7CaPIAFceGjv7kx7V2dSXJ1o50rB46jdExhQP6WBQooDe9gfKGCvPw+vlgOQTBqd6EYnuhIj0e1NDGmIPeSz25XH7kAuIULkZPfkyquv4OKLLyYrKyvSJhoODyPWDAZDsxDRhhcKhfjd737H/fffT4anGwOCI5FQ9HmDQhpiPcvJYzPjjpvAu3Nmk5RU+9OpK1eu5Oyzz2bTpk10SOhBertuBDVA/v71lHj3Mmb0eN794C3atz+yJTRmz57NtddeS15eHt2dvempA3GEokfogiV289lCLpsoZT8u3HTy9KCTpwdpnkwccvj2qiqlwX0U+Lax07eRkmAhIKTRmW7kkEbnqPdW+dVHgeSx07GdwuBuAI4bdTxXXn0F55577hHXEUOLEt2VrQkwYs1giAwRa3jFxcVccsklzJ49m27uXvQJHBu1w3ZgCYNcNrKBlXTpmMl7c99l8ODBPwi3YMECTjvtNII+YUjn00lwdD4kju3FK1i3dx6ZnbNYtmoR6emNX+R39erV3HLLLcydO5f2MWkMcIwgrjLxiPLX1AQ0QB4b2coGfHhJdKbRLaY/GbG9cEnzLB9SGtjHDu935Hk34NMKYmlHV3rQhR54JPrf/VqhZRS4cskLWvPbXC43006bxuVXXMapp5561L2/thVixJrBYGgWItLw1q9fz9lnn826devo5xxKhj876j0gVRTqbtbIYgL4ueeee7jtjtsODGl+9913jB49mpDXyYgu03FrzUuOFJRvZvnOt+iWkcO3369s8CKqW7Zs4d577+Wf//wnMc4YsulHhr8HDokekRvQANv5jm18hx8fqa4u5MQNIdXdpcXOcUhD7PZtYVvlWvYF8nHgpAvZdKc38ZLQIjYcCapKCUUUuPPI82+2xG5CEhdceD6XXXYZY8aMaTXt5SijzZ8UI9YMhsjQog1PVfnrX//KzTffDEFhsOP4Vrmavk+9rHMsY3cojwF9BvLcC88ycOBARowYwbYteYzpdjFurVsU7CzdwIpds5k87jQ+/vy9OsOuWbOGBx98kFmzZoEK3R29yJZ+OAORfwijClVlB1vYyBp8VJLu7kZO7BDaezrXf3AzUhrYx5bKVezwfo+idJKuZGkfkqR11LuQhihkNwXuPHb6txEkSGZGVy69/BLOOecchg0bZoRb9NDmT4QRawZDZGixhrdhwwZuuOEG5syZQydPJgMdI3B4W+9q+qrKTrbxvXyDVyvIzspm69atjMn+CYnOjAbFsWHvF2wqWsRjDz3Fjb/++SH7KisreeONN3jmmWf49NNP8bg8ZNKDbEdfnP7oeXl41auXvmM1ZRST4uxIn/jRERdp1akMlbG14htyvd8SUD+p0ols7UuqdIy0aQ0moH4KJJ/dju0UBHcCSqcOnTj7nLM586wzmTRpknmxfGQxYs1gMDQLzd7wCgsLeeihh3j00Udx4KQXA+ncioY96yOgftaxjJ1sp3vSUAZ0mNzgY0Ma4qu8l/AGS9jw/XoSEuOZO3cub7/9Nu+//z7FxcUkepLJ0GwyNRtnMLrEbYkW8R2rKGQ3cY5E+sSPopOnR1Sf20DIx/bKb9lSuRqfVpAiHcjR/rSnQ1TbXR2fetkrO9nr3ElBYAdBgsTHxXPipBM56ZSTOPHEExkwYECrylMboM0XthFrBkNkaLaGl5eXx8yZM3nqqacoLS2lqyuHPs5jcLSxd1MGNchXzEVcbsZ0vRSXs3GejRLfHhZsf4H0xK4UlGwDIM7djrRgR7rG5NCuIiXqLriVWs5G1pDPVtwSQ07cULrHDjiiJztbmqAGyK1cx+aKlXi1nBRJp4f2J5WOUVfe9RHUIPvYzT73bnb7d1BBGQCp7VOZPHkyY8aOYdSoUQwdOtS8ZL55aV0V5zAwYq0BiMiPgTeA/qq6rgHhnwEeVdW1R5huNvCuqg46kngaG6+I/Ap4AOikqvsbEN/7wE9UtegI7ZoI3KKqp9ew/W1gExALvKyqdx9BOqWq9Uxsqvm4IUAXVX3/cNMOo0kb3r59+5gzZw4vvPACc+bMQVXJcGbRyz0QT2XzXyRUlXJK2U8hlZShKG48tCOJFNJxNoOY2Kzr2Mg3jOh8Luntsg8rjvV7P2Nz0RJ6xhxLRzoR702KSsEQUD9bWM82vkNRsmIH0vnN4fwAACAASURBVCN2CB5ndK9rVhdBDZDnXc+mipV4Q2UkSxo52p9UOkXlOWgIFVrGfuceihx72OPfSSUVADgcTvr368/o40YxcOBA+vfvT79+/cjKymqydf+OclpnhWkE0TNLNrq5EJgPXADcVV9gVY3+9+PUzYXAEuDHwPP1BVbV05rbIOALVT1dRNoBK0TkXVX9umqniLhUNdDMNgwBRgBNIdaOiB07drB06VKWLl3KvHnzWLBgAcFgkHbuRHpIfzJd2Xj8cRBsXjsC6ieXTeSxmYqw1fDDceAkXTPoTi+SSWuSC7FXK9jCOjrG9zxsoQbQs/1x5JWsYU9oF9n+3lEnEkIaYgeb2cRafHjp7OlJ77gRxLtqX2uuteAUF91jB9I1pp8t2lawXOeTJGnkaL9WsVZbdeKkHXGhdnQOZYHYr/OSIspd+9m1fg8vrn0JHwffBhETE0tOdg+yc7LJysqie/fudO/enczMTNLT00lPTyctLQ23u215xQ2Nx4i1ehCRBGAsMAmYjS3WbG/PXcAeYBDwNXCxqqqIzMPyEC0VkVLgSWAKsA/4DfAQ0B34parOtj1d/waq1hu4TlUX1GPT20B7wA38VlXftuP5AEtYjgHygDNVtUJEhgPPAeX2/tri7gkkAL+2bX3e3n45cAYQD/QE3lTVW+19W7BETALwoR3/ccBK4J/A3UBH4CJVXSwio4DHgDigArhCVdfXZlM4qlomIl8DPUXkR0AXIBvYIyJ32HnsABTY8W4TkR7Af7Dq+4dheZ1ImCdPRP4CLFXV50VkJPA41jnxAlOBPwBxInICludxpx0GLE/ZeFUtaUg+SkpK8Pl8NX68Xi8lJSUUFhayb98+CgsL2bt3L1u3bmXz5s1s3LiR/fsth6cgJLtSyZZ+dIrNJK4y0brAhRpixeFTtfbZRtYQwE97VwbZnmNJdXch3pmE4MCnlRQH9lDg20a+73t2ay6p0pk+egwJcmQr/W9mHSFC9E2dcETxuBwx9EkdxzcFcyjw7KGjv8MRxddUqCp7yOc7VlNOCe1dnRkaP5oUd+uZlN9QHOKkW+wAMmP6kufdwKaKFazQL23R1p+0Vuxpi5E4OhAH/gyyAMSa81ZOCZXuMioopfD7EnLXL+QT+R++sNd6hZOUmERaahpp6WkkpySTkJBQ4yc+Ph6Px4PH4yEmJubA95p+O51OnE4nDocDh8Nx4HtN26rvF5Eaz0lLbDtaMWKtfs4CPlTVDSJSKCLDVHWZvW8oMBDYAXyJJeqqC6F2wDxVvU1E3gTuxbrwDwD+hSUAdwNTVbVSRHoDs7DET21UAj9W1WIRSQe+EpHZ9r7ewIWqOkNE/gucA7yIJZquV9XPROThOuK+0E7/C6CviHRU1d32viF2nr3AehF5QlW3Vzu+FzAd+CmWd+4nwAlYQu83dnmuwxI2ARGZAtxv21kvIpKGJQTvwSrD4cAJtiB9B3hBVf8lIlcCM+30HgeeVtUXROTaBqThAV4BzlfVJSKShCVy/w8YoarX2eHeAa5V1S9tAV3ZkDwAda7CXxMOnMQSTxzxJJJOJ7JJoj2JpOAM2s04SIsMBpRpCWtYTDH7SHV1oU/8KJLdPxQ5MRJHB083Oni60UdHkVu5jo0Vy1nEx/RgANna97DWKfNqJTvYTJeEAbSLST3i/HRJHMjmoiVs0m/ooBMjfoEo1n18xyr2UUC8I5kh8VPp6MmKuF3NjSXa+pMZ0ydMtM1vE8Oj4XgkBg8xEAhblNnOVpAAlVTgpQI/Pnx48ePFX+KjvMRL8dbtBNhMkMCBT4AAoeZ2oUc5U+Tczh+FXt0ZaTuaEyPW6udCLC8QwMv27yqxtlhVcwFEZAWWh6e6WPNx0JuzGvCqql9EVtvhwfKO/cWeExUE+tRjkwD3i8h4LB9KJtDJ3rdZVVfY378GskUkGUhR1c/s7f8GTq0l7guwhGBIRN7AEl5P2vs+qZrDJiJrgSyguljbrKqr7TBr7GO0Wn6TgX/ZwlTt/NfHOBFZbuf3QVVdIyLTgdmqWmGHOR44OyyPD9nfx3JQDP4b+GM9afUF8lV1CYCqFtv5qR7uS+BREXkJeKOqLjSEgXHD8VcEcdh/csh/wYUbF27ceHDhwSlOHE4HLrf1P1Ls8G9llfcrRJwcGz+JzjE9G3QBdYmb7Lhj6BLTm3VlC9jkW0OhczfDY04gztG4F4Fv9q4l5Fdy2o863GwcgkMc9Eodw8pd77I3YS9dyWySeBtLeaiU9b6V5AW24JFY+seNoWtMPxyO1vPwQFNwiGirXM+mSmt4NMXRgb6eY0h3tr7h0YYTQztqXtC5ClUlFFI0GCIUUkKhEBpSW7wFUUKECB34X/171W9FAT3wR9gvathafdsP7KrZ2sMuCW3csafQgCk7rRkj1urA9uKcCAwSEQWcgIrIrXaQcJ91kJrL068Hn+IIVR1ji6Gq8L8CdgGDAQf1e2guwhrqG24Lvy1YE+9rsikOS9zVW/NF5Fgsz9xHdmfowZrUXyXWGpLf8DChsN+hsPD3AJ+q6o/todt59dmGPWethu1ldRyjtXyvIgCHvGepqgwbVF6q+qCIvAechuXdnNKQB1AAvilf2pBgUcUf//hHbr/9JdLjujA48URcwcY/uOBxxHJs4ol08GaxtuwLFuknzH77bSadOLFBxxcVFdGtWze6xPWjnefIvWpVdG7Xl42er9gYWM1XRXOIiWm5NbP279/PAw88wGOPPUaIEL0ShtEjbjCO0NHdPTvESbe4AWTG9iXPu57NlStZVPk/hg8ZwQMP3c+UKVPasGgzNJLnI21Ac2MeQ6mbc7GG1bJUNVtVuwGbsYb1mpJkLE9OCLgESxTWF363LdQmYXm4asV+SnO/PdcKLLFXExcCd9l5zVbVLkCmiNQZ/2GQjDWfDuDyJox3AZZnEKw8Vnk5v6y2vYqtwAARibG9j1ULda0Dutjz1hCRRFtYlwAHXgQpIj1VdbWq/hFYCvRrwrxEDarKHXfcwe23305mfG+GxZ9yWEItnIyYnoxOOhP1CVOmTObRh//coOOefPJJSktLyUlpGq9aFSJC79SxlFTu5Z47H2nSuGujoqKCRx55hJ49e/LQQw/R0ZnNhLQL6Bkz/KgXauFUzWk7Ifk8BiScwJrV33LSSScxeuRxfPzxx5gVDQxHA0as1c2FwJvVtr2ONQ+rKXkKuExEvsIaAq3LWwTwEjBCRJZiiY+GeHOuAJ4UkYVARS1hLuCH+X2Tg0KnqXgIeEBEvqR+YdoYbgCuEJFVWKL3Rnv7jcC1IrIESygCYM+3+y+wCqtMl9vbfcD5wBMishL4CMvr9imWuFshIucDvxSRb+wwFVgPd7QpgsEgv/jFL3jwwQfJajeQgbHjkSY6ZQmu9oxOOpM0dyY333oTV1xyNcFg7XNvysvLefTRP9MxoScJNcyRO1I6xvciwZ3GU399vE47jhSfz8fTTz9Nr169uOWWW3CVt2N8x+kMiBuPM9B6l+JobhzipFtMf8Yln8+AhBNYvXwNU6dO5bjRx/PJJ58Y0WZo05h11gyGyBD1Dc/v93PZZZcxa9YseiUOJcc9vFmGnUIaYn35IrZVfsPY0eP54KN3SUxM/EG4mTNncuONNzKm+0UkuRv2WqnGkleyhtW7P+BP9z7JzXf+oknjDgaDvPjii9x1111s2bKFDvGZ9EkYRUIwvf6DDT8gpEHy/OvZVLaCylAZx40+nvsfuI9JkyZF2jRDy9Pmx8ONWDMYIkNUN7yKigqmT5/Oe++9R/+k4+nubtJ1mWtke+Vavi1bQFa3Hsz74n9kZR0cfff5fPTokUNlkTAqo6kdvQcJaZDPtz1DckIa+YWbmkScBoNBXn31Ve6++27WrVtHWnxnercbSVKwbTzdGGmCGiDf/x0by5ZTGSpjzPFjue/+e5k4cWKkTTO0HG2+IZlhUIPBcAjFxcWccsopvP/e+xybMqFFhBpAt9gBDEs8hdzcXI4dOJiFCxce2Pfiiy+yY0cevdKOb1YbHOKkR8pIdhVt4V9//+8RxeXz+Xj22Wfp168fF154ITu37GFk+qkMjz2d5FBbfqKxZXGKi66e/pyQch4Dksby9aLlTJo0iXFjx/PZZ5/VH4HB0AownjWDITJEZcMrKCjglFNOYcWKlQxtP5n0up9daRZKg0WsKJ2DV8t5/vnnueDCC+jfrz+7c4s5rsvFzS5ygiE/87b+na6dcti045tGH19RUcEzzzzDww8/zPbt20mN60zPdkNpH8o0Aq0eVJX9gQL2+nMpDu7FGyonqH7cEkOsI4EUdyfS3V2Jd9a+TmFQA+QHNvB96XK8oXJOGDuO++6/l/Hjx7dgTgwtTJtvWEasGQyRIeoaXm5uLlOnTuX77zYyvP1JpGiXiNniC1WysuxjCn35/Piss3nzrTcY0e0s0j29WiT9jfsW8l3hl7z31kecduaUBh2zc+dOnn76aZ5++mkKCgpIj8ukd8IwEs1wZ70EQj5yvevYWrmGypD12rJ4Vwpx7mSc4sYfqqTcX4Q3aO1r7+5CduwgOri711q2QQ2wI7CBjWGi7f4H7mPcuHEtli9Di9HmG5gRawZDZIiqhrd+/XpOPvlkdu7YxYiUU0kIRX7Se0iDrC2fT17lBuLd7RnX7QrkMN54cDj4g5XM2/o3BvYawcoNtb75DYCvv/6axx9/nJdffhm/30+nuGx6JQ41Dw40ANUQud71fFe+BL96aR/blczEQXSM74nHFVctrFIR2E9+yTpyS1ZRESgmxd2ZAfFjSXTVvuZeUAPs8K9nY9lyvKEKxh5/Avfefw8TJkwwIrrt0OZPpBFrBkNkiJqGt2jRIqZNm0ZFqZcRyacSF0yJtEkHKPBuY1npHPqnTyYreWiLpr1uzzy27v+axV8tZ8TowYfsKysr47XXXuMf//gHX375JR53DJmePmQnHIMnUPcK9AaLsmARq0o+pTi4h/axmfRNnUhKXMOe8g1pkNzib/i+cD7+kJee8cPoETu4zteXBTVArm8dm8tX4A1V0LdXP359+y1cdNFFxMaaJVNaOUasGQyGZiEqGt6HH37IOeecg1tjGZ58Km5/41791Nws3v8OFVrK+KwZOKRlX7tUGSjhs63/YPyok5m36H1UlSVLlvDss88ya9YsSkpKSIpNpVvMADLcvXBqQ96aZlBV8rwbWFe2AIfDRf/0E8lI6H9YXi5fsJy1BZ+ws2w9aZ6uHNtuEh5H3cIrqAHyvd+zzbeGEn8hyYkpXPPzn3Hd9dfRtWvXw82WIbIYsWYwGJqFiDY8VWXmzJncfPPNJMekMyzxFJyBlnvFUkPY59/J4uJ36Jc2ieyU4RGxYfXuD8kvXce1P7+WOR9/wIYNG3C7PHTy9CA7YSDxgVQzlNYIQhrk27IF5HrXkRrbjWM6nkqcu/aHBRpKbvFq1hR8TKyzHcMSTiLB1b7eY1SVwkA+ef5vya/YhEMcTJ1yEj+/9hpOO+003G4jvlsRbb4RGrFmMESGiDW8yspKrrnmGv71r3+R0S6HQfETovL1RsuKP6QoWMCErJ/ickRGSJb69jJ/+z9JiemC2+EkM64X6WThFHMhbyy+UCUrSj5mXyCfnJTR9E4d26RzEIsqd7Bs51uohhieeArJroa/5aI8WMwO/3pyKzbgDZXTPjmVK668nCuvupKBAwc2mY2GZsOINYPB0CxEpOGtWbOGiy++mBUrVtAncQTZ7iFR6RkqDuxl4f436NV+LL1Sm3dttfpYvvNt9lZsY0LKBbgkuryPrYWKYClLi9+jIlTKoA4nk5nUPAKozL+PpTtexResYGjiVNLcmY06PqQh9vi3szPwPTsrtqCE6N2zDxdd8hPOP/98+vVrk6//bQtEXyfWxBixZjBEhhZteMFgkJkzZ3LHHXfgxM2gxPG018ZdyFqSlSX/o8C/nQndZ/zgqcCWpqgyn6/yXqJv4hiyPcbL0ljKg8UsKX6PgPoYlvFjUuO6NWt6lYFSlu54lfLAfoYnnUqqq/NhxeMNVbDbv5ld/s3s9e4AoHfPvlzwk/OYNm0aI0aMwOls2XmUhloxYs1gMDQLLdbwPv/8c2644QZWrlxJRnwOgxLH4Yiy+WnhlAX3M7/oVbKTR9AvfUKkzQFgcd4rlPn3MT75vBZ/0KE1UxYsYknx+4QIMjzjXFJiD084NRZvoIzFO16hMlDCiKRTSXF1OqL4KkNlFAS2ssu3mb3efEBJTkrhlFNP4fTTpzF58mQyMprnfbWGBmHEmsFgaBaaveEtWrSI++67j3feeYfEuBT6xo8mVbtF5bBnON+Ufka+dyPju88g1p0QaXMAKCjfzNf5rzMoaRKZ7pZZmLe1UxooZEnx+yAwImM6SbEdWzT9ykApi/NexhcsZ0TSaY2aw1YXvlAlhYE8CkN57KrYii9UCUBWt2wmTZ7I+PHjGT9+PDk5OVHf1toQbb6gW61YE5EfA28A/VV1XQPCPwM8qqprjzDdbOBdVT3iFyaKyPPAQlX9W9i2s4CfquppRxq/HV82MEZV/1NPuInALap6eg37tgAjVHVPA9OcB2QAFfame1X1tVrC/hL4u6qWNyTuI0VE7gJKVfVPNez7KXCT/bMYuElV59v7DtSfxpZHLTRLwysrK+P111/n2Wef5fPPPyfOE0/3mEFkxQxCNPo9QhXBEr4oeoVuSUMY0GFypM05gKqyIPffhDTA2MSzzUW4HooDe1la/D4Oh5MRGdNJjInMAsEVgWIW571MIORndNLptHM27RqCqkpxcA/FuptCfz57vfn4bfGWktye4cOHMXLUSIYOHcqwYcPIycnB4TCv5G4G2nyDjL5HwBrOhcB84ALgrvoCq+rVzW1QfYiIU1WDYZtmAbcDfwvbdoG9vanIBn4C1CnWmoGLVHVpA8L9EngRaBGxVhsicjrwM+AEVd0jIsOAt0RklKrujIb6UxOqyrZt2/joo494//33+eijjygtLSUpNpUByWPIdPfFoa4oWdWtfjZVrACEHikjI23KIYgIOSmjWLn7XXYHc+nkat55V62Z/YEClhZ/gMvhYUSX6SR4an+7QHMT50piRMZ0FuX9h69L5jA66UfEOJpuLUERIdnVgWQ60M09EI1TyoJFFOkuSoN7WfL5Sj7936eECAEQGxtLr569GThoAH379qVv37706dOH7t2706FDB3MTYKiVVulZE5EEYD0wCZitqv3s7ROxhNseYBDwNXCxqqrt7blFVZeKSCnwJDAF2Af8BngI6A78UlVn2x6pfwNVy5Ffp6oLavOsidXKHgJOxbo03quqr9g2/R7IB4ao6oCwY5xALjBMVfNFJB7YBvQA+gCPAgl2fi63w4wEngXKsMTqqao6yI7rQWAiEAM8qap/E5GvgP7AZuBfwJu15Gsi8AdgL9AX+Bz4haqGwj1JInIxcAPgARbZYcIFKOFlHbbtaWAkEAe8pqq/F5EbgD/Z53KPfT6eBUbYZficqv65Wtw/An5rp78XSxTusj1m3YEc+/9jqjrTPuZO4FJgO1AAfF3dsyYiXwC/V9X/hW27B0BVf1et/myxbawA/gt0BZzAPar6Cg2jwQ1PVSkvLyc/P5/NmzezZcsWNm3axIoVK/h66dcU7CkAICEmmVRnJt0T+rXK9b8qgqV8UfQKXZOOYWCHqZE25weENMT8bc/hcng4LuGMVle+LcE+/y6WlXyA2xnHyIzziPdEx9sw9lfuZPGOV4h3JTMyYRruFlwKJqRBSoP7KA0VUi77KfEWUhoooiJYgoZ1Ax6Phy4ZXcjKyqJ7VncyMzNJT08nLS3tkP+pqam0a9eOmJgYUwcP0uYLorV61s4CPlTVDSJSKCLDVHWZvW8oMBDYAXwJjMUSNeG0A+ap6m0i8iZwLzAVGIAlaGYDu4GpqlopIr2xvF0j6rDpbGAIMBhIB5aIyOf2vlHAIFXdHH6AqgZF5A3gPOBx4AzgU6ASeAI4U1ULROR84D7gSuCfWMOkC0TkwbDorgL2q+pIEYkBvhSRuVieuwPDm7YgrC1fo+wy2Ap8aOfpwPCliPQHzgfGqqpfRJ4CLgJeqKE8XhKRqmHQycCdqlpoi8pPRORYVZ0pIjcBk2whOBzIrBLCIlJTTz8fOM4W4FcDtwI32/v6YQn4RGC9LRCPxfJWDsWq78uwRHx1BtawfSlwWQ1hqzgF2KGq02x7k+sIewhDso8nGAoSCgUJqv0/FCSk1v9A0E+lvxyvv5JKfwWhQ/UwgoMEV3uSnGkMSOhDe1dn2jnaW513kFbZdW2pXAlAj+RREbakZhzioGfq8aze/QG7g9vo5MqKtElRRaE/n2XFHxLjSmBEl+nEuxvcHJqd5NjODO18Jl/nv8Hyso8ZkXByiz0o4hAnSa50krCHgu0l+oIaoDxYTHlwP5VajldLqdhZysq8dSyavxRvqAK1PXI1IQgupwe3043b6cHjisHldON0OHE4nDjEgcPhxClORBw4HWH/7Q7iULEnHPwpB8IgHPxu7+GQcJFnycbPIm1Cs9NaxdqFwGP295ft31VibbGq5gKIyAqsYcDqYs2HJUYAVgNeW3ystsOD1aT+IiJDsC5/feqx6QRglu1l2iUin2F5koptmzbXctws4GEssXYBlvDpi+UZ/MhuTE4g3xYviapa9Wbp/wBVc8xOAo4VkXPt38lAbzuv4dSVr8WquglARGbZeQqfazYZGI4lRMHyku2uJV+HDIOKyDX2nDAX1ny2AcCqasdsAnJE5AngPWBuDfF2BV4RkQws71p4ub6nql7AKyK7gU7AOODNqjlxIjK7FntrQqjbA7Ya+JOI/BHL2/pFQyNet32V3R06cOBAxGn/t347xEmMJNFO0nHHxOB2xOCROOKcicQ5EolxxNudsUAbuLuuCJaQW7mezMQBxHui5yJfnS4J/dm0bxHfly+lU0pWne+iPJrY48vl6+I5xLmTGJkxnVh3YqRN+gHp8dkc0/EUVu1+n9UVnzMkYVKTLsrbWBx4SHalk0z1+XyKhpRQSAmqH59W4lcvvlAlfq3EH/ISJEBQ/QQ1QFADBIJ+goEAPgKE1I8SQgkR0hCKhn0Pofa2H6QZ9v3Qb1pzOK2+L3Kckv7TGR/u+fs/Im1Hc9LqxJqIpAEnAoNERLGEjIrIrXYQb1jwIDXn0a8Hx39DVcfYQ35V4X8F7MLylDmwvF11mlbHvrI69n0JZIjIYGAMlmDrDaxR1UNWAxWRut6hIsD1qjqn2jETq4WrK18/bME/TONfqnpHHXb80DCRHsAtwEhV3Wc/WPGDF/jZ+wYDJwPXYnkcr6wW7Amsif6zw4a9q6jt3DekR1mLJUT/F7ZtmL29RmzP7nDgNOABEZmrqn9oQFp8s/xbtqzLw+lw4HA6cLqduFxO3DEuPDFuPLHuo2qI4/bf34LjfaFvxxMibUqdiDjonTqWFbveod8ZHfjFtTMibVLE+d9nH3PDrc+RHJ/G8IxzcRHZdfHqokviALzBMtbv/QwZPYg/P/Jom2tnqhDwBwj4AgQCQQL+IKFAiGAwSCioBIMhSwyq9V9Diqqiak25qOotqy6Rh0yVig5tdigCT9zy0huRNqO5aXViDTgXeEFVf1a1wfZiNXUvnwzk2gLuMixRWBefAz8TkX8BqcB44NdYQ3O1Yg/n/Rdr+PV9e3hyPdBBRI5X1YUi4gb6qOoaESkRkeNU9SssYVfFHODnIvI/20vYB8gDSrCGBRuSr1G2sNqKNdz592rmfgK8LSJ/VtXdIpKK5enbWk/ZJGEJ1v0i0glrXt88e1+VfXtEJB3wqerrIrIReL6GuJLtfEHdQ5RVfA48bw8Zu4AfcegDHVU8BPxRRE5R1b225/FyYHRtEYtIF6BQVV+050Fe3gB7AOh1bHd6Hdu9ocHbNKtWreKtd98gJ3UkbqJjqY666NSuD4meDjz30l958C+/Iza27heHt2VeeeUVrv/1z0mJ68ywzmfjCEXv+n1V9EgZiTdQxgfz3qLXP3KY+fQjkTbJcIRMu3zC3kjb0Ny0Rh/+hViT5MN5HeuJx6bkKeAye4J+H+r2jmHbtApYieWduVVVdzYwrVlYnq6XAVTVhyVK/ygiK4EVWF43sOam/V1EFmJ5uvbb25/B8gItE5FvsASJy7YpICIrReRX9eRrIdZDCt9gDS8eUs72sie/BeaKyCrgI6whzTpR1ZXAcmAN8ByWN7GKvwMfiMinQCYwzx6+fh6oyYN3F/Cq/UBAvUtn2HMZX8Eqw9eBGocqVXW2bdsCEVkH/APr4ZT8OqI/Blhs23sn1txHQyO5/fbbifHEkdO+Vl0cVYgIfVLHUVJZyI3X3B5pcyLGc889x4UXXkhqfFeGdTqnVQi1KvqmTaBLwgCe+Ouj/OH/7o+0OQZDvbTKp0GPZkQkQVVL7e+3AxmqemOEzTI0HtPwgE8++YQpU6YwoNMkuicMj7Q5jWJp/usUVe5g46bv6Z7VNdLmtChPPPEEN9xwA52TezK4wxmtYg2/6oQ0xIpds9ld9j1PPPY01914TaRNMhw+bWssuwZao2ftaGeaiKywvWfjMN4cQyvF5/Nx3XXXkRSfxv+zd95xUlXn/3+fadt777tsY+m9dxQQEDRBFMWaxEKipkhiorHFksTElnzzS6IxxG4kAlIUBQGlSZPOLgtb2N5n2+zUe35/zCwiLLDgzs7sct+v1+7O3HvuOc859z47n3lOSwwY5GlzLpm+EVNwKDZuu/HKGbemKAoPP/wwDzzwAPEh2QyK7JlCDZyzewdHzyXCL5kHfvpj3nnzPU+bpKJyXtTImoqKZ7jiHe+5557jN7/5DWNSFhKq65nj947VbqK4cS8fffgx114/y9PmXBSbzUZxcTGlpaWUl5djNpuxWq34+PgQGhpKVFQUWVlZHS7QajabufPOO3nvvfdICx9GZuiUXjEb1q5Y2VPxAU2WalauXMW1bpZz9wAAIABJREFU8+Z42iSVS6fXR9ZUsaai4hmuaMcrKiqiX79+hBmSGRR5rafNuWzsioWtJcvw9w+grKrQ6yYbtLS08Pnnn7N+/Xp27drFoYOHsFgtF70uKDCYQYMGM236FCZPnkxOTg433XQTX375JTkxU0kOGNarZlFaHW3sLn+fNkcjK1euYs7cazxtksql0XsexvOgijUVFc9wxTqeoihMnz6dHdt2MjHlLnSy67b/8QTtm7zfsuAu3vrgX542B7PZzOrVq1m2bBkbNmzAarWi1/kQ7B9PaGACwYEx6EUAem0gGo0ejdCgKA5sDjMWWzMWu5E2ax31TaU0tlYAEo1rIdXU0KGkh45HI3riQgIXxmJvZU/lB5hsRpZ/sJzrvjff0yapdB5VrKmoqLiFK9bx/vSnP7F06VKGxM8h1i/H0+Z0CQer1lHRcow1H33C7GtneMSGsrIyXnrpJV577TWMRiMBfqHEhPYjOiyLQEMCGs2ljy2zOyw0tBRT1XCMmqZ8bHYTBq0/8UH9SQoaRIDhQks/9jysDhN7KpbTYq3j7bfe4aabF3raJJXOoYo1FRUVt3BFOt7+/fsZNWoUUf59GBgxt9d0pdkcZnaUvYVGBycK84iJie62svPz83n22Wd5++23sdsdxIX3Izl2OEGGpC5doV+RCvVNBZTW7qOmMQ+JJDoggz6howj1je+ycjyNzWFmT+X/aDJX8ac/vsDPl6qT7XsAveMfyQVQxZqKime44hyvtraWkSNHUlvVwLiE29BIH0+b1KU0Wqr4quwd+mcP4evDX6HVuneWZFVVFU8++SSvvvoqQmhJiBhCaswYDFr3b9dlsTVTUrOXkprd2BxthPklkh46lkj/3rFfql2xcqBqNTWmQu754Y/52z9eQaPp+ZMpejGqWFNRUXELV5Tj2Ww2Zs6cyZdfbmV88s34iShPm+QWSpoOcKTmMxbMv5n/rnjLLZFDs9nM888/zx/+8Afa2swkRQ0nPW4SOk33j/2zO6yU1e6jqHonFlsT4X7JZIVPJNT3omtlez2KVDhWu5GSpgNMnjCdFR99QFhY7+r27UWoYk1FRcUtXDGO53A4uOWWW3j//fcZmjCXGN8L7sDW48mt3UxR4x5+9sAveeHlP3Rp3hs2bGDJkiXk5+cTF9Gf7MSruiWSdjEUxU5JzR4KqrZis5uIDsgkK3wCgYYIT5v2nZBSUty4j7y6LURGRLN67UpGj+4ZO21cYahiTUVFxS1cEY7ncDi4++67ef3113vkLgWXg5SSg9XOCQc/e2Apf37pD985wlZdXc3Pf/5z3n77bYIDouiXOptgH+/rcrQ7LBRX7aSoegeKYiMpZCgZYWMxaL13c/fO0GAu52D1GiyOVn7z60d47PFH0ev1njZL5RtUsaaiouIWer3jtbW1cfPNN7Ny5UqyoyaQFjzG0yZ1G4pUOFyznvLmI9x8420se/O1y/5w//jjj7njjjuor6snLW4CyZHj0Gq8e+kMq62VExWbKa3dh17rQ0bYeJKCB/foRXStjjaO1n1GZfNx0tOyePf9txg5cqSnzVJxooo1FRUVt9CrHa+goICFCxeyb98++sdMJzFgiKdN6naklOTVbaGocQ8D+w9l9doVpKR0PhpmNpt5+OGHefnllwkNjGVw+gJ8tOFutLjraTZVkVu6noaWIgJ9IukbPrXHT0Koas3nWO1GzPZWbvj+Qv74p9+TmprqabOudFSxpqKi4hZ6peMpisJrr73GL3/5S6xmGwNjriFcn+ZpszxKefMxjtR+ik6n5Zmnn+H+B3+CwWC44DXHjh3jpptu4uDBg6TGjiY9drrXR9POh5SSamMux8s+o81qJDogg74RU/DXh3ratMvG5rBQ2PgVRcZ9CAG33XY7v/zVQ/Tt27vHY3oxqlhTUVFxC73K8aSUbNy4kUceeYRdu3YRHZTKwNhr0CsBnjbNKzDZGjlWt4Ga1kJiomJ57InfsnjxYoKDg7+VTkrJP//5T37605+BomFQn+sJ9e/jIau7Fodip7hqB4VVW5FSITV0JH1CR6HTXFi4ejNmezOFjV9R0ngIRTqYMmkqP75/CXPmzMHPr2eP0+thqGJNxTMIIa4HPgRypJS5nrbnQgghUoE1UsoB5zn/M+A5IEZK2diNpp0XIcQI4DYp5QNCiCmAVUq53XXuXsAkpXzDjSb0CsczGo0sX76cf/zjH+zZs4cA3xCyIycRZcjqNQvedhVSSuraijlp3E5DWzkGgw/XXnstc+fOYcqUKQQGBnL33XezYsUKIkPSGZAyH4Mu0NNmdzlmaxP5ZRuoaDiMjy6I7PDJxAVm9+jnxWJvpaz1EMXG/VjsLfj6+nHt3GuZe+0cpk6dSlJSkqdN7O303Ienk6hizUsRQvwXiAM2Simf6OC8Vkrp6HbDOqATYm0XYAH+JaVc1n2WdQ4hxBNAi5TyT91YbI90vIaGBg4dOsS2bdvYuHEjX375JVarlRD/KFJDRxDjl42Gntld111IKWm0VFJpOkp5Ux5WhwnAJVYEmQlTSYka16PFS2doaDlFbsknNLdVEuaXSE7ENIJ9um/nB3egSIWGthJqzPmue9sGQEpyKmPGjGbI0CEMHjyYvn37kpiYqM4o7Tp6t7OgijWvRAgRCOQBU4GPpJR9XcenAI8DFcAQYAnwJFDlev8hcAh4EPADrpNSnhRC3OC6zgE0SikndVDeKiAM0AOPSilXuUTYx8BWYBxQBsyXUrYJIYYDrwMm1/lrOhJrQoh0YDVwH/AbKeVM1/E7gOsALTAA+DNgAG7FKexmSynrhRCbga+B4UAUcBvwa2Ag8L6U8tGzxaIQ4iEgUEr5hOv6r1xtGQr8QEr5pastHwJ+Aux0tU0NcD8wHZd4E0IMAf4O+AMngbuklA3ny7eD29kh5eXlUkpJ+w/Ahd67O43VaqW1tZWWlhZaW1tpbW2lqamJyspKysrKKC8vp6CggPLy8tN10Gp0SOkUGT7aQAL04UT4pRAbmIVvL4wIuQOHYudY7UZKmw/h7xPOgJTrCA1M9LRZ3YaUCmW1X5NfsQmbvY2k4EFkho/HoO3+BX67GiklLdZajLZS6ttKMJoqabM3nT6v0WiIiY4lNTWFuPg4wsPDCQsLO/3Xz88PX19ffH19v/Var9ej0WgQQqDRaC74I4TwiOjv7jLj4+N7vVhTvwJ7J9cBn0gpjwsh6oUQw6SU+1znRgEDpJSFLsExGMgB6oEC4DUp5SghxIM4hcdPgceAmVLKMiFER6N6zcD1UsomIUQksFMI8ZHrXCawSEr5I1e07/vAW8C/gfullFuEEM9foC6LgHeBL4FsIUS0lLLadW4AMBTwBU4Av5JSDhVCvIhTlL3kSmeVUk5y1WkVTuFWD5x0pb0YOlebzMYpWq9qPyGlLBJC/J0zImtCiOlnXPvGGfV8ynX9Ty+W78VISEjobFKPohU6fHRB6DW+2BULAg0SBYMugGD/ePwMoQgEFnszTaZKaupOkle3iejALDJCxxDk0zt3KugKTDYjB6rW0GipJCFiCNmJs9Bpe+74rctBCA2JUcOJCevHyYotlNTspqIll4zw8SQHD+nRS30IIQjyiSLIJ4qkwKGAc9/RZmsNJpuRNnsjbS1N5O4v4dDe49gUMzbFjOIdHSY9ilnpD2V9fOL54562w52oYs07WcQ3QuU91/t2sbZLSll4RtrdUsoKACHESeBT1/FDOKM+ANuAZS6x9WEH5QngWSHEJEABEoAY17lCKeV+1+u9QKoQIgQIlVJucR1/E7jmPHW5CacQVIQQHwI3AP/nOrdJStkMNAshGnFG4NptH3RGHh+dcfzIGfUtAJIA43nKbqe9znuB1IukPU0H9fwP8MF3zRdgZOpcTK0W2qP34pwovvjmt+gojTjjlTj99uJpxLeOnn4lNOiEAa1Gj1aj/+a1Vk9p89fk1nyJotiJDR9IUuQwQgKSOvz23Gquo7R2H2V1+6hqOU5a5FAGJ0xHr/XtXMNcIRTXHWRf6ccgNAxK+z6xYf09bZJH0ev86Js0i8TIYeSWrie39nPKWw4xNGkW0UGpnjavC/EjnHO3rFIUid3uQHEoWG0WLLY2FOnAIe0o0o6iOFCkHYe0I1FcEXGJ5JtI+en38ozjHhlt0b1lujoHBgCqWFPpPoQQEcA0YIAQQuLsJpRCiF+6krSedYnljNfKGe8VXPdXSnmvEGI0MAfYL4QYIqWsO+O6W3B2MQ6XUtqEEEU4o11n5+/A2b0q6IRHCiEG4YzMfeb6YDfgjP61i7WL2n5WOqWDa3SAHTjzK/jZyqD9Ggdd+8xfdr67CldfPJGHKSws5MYbb+TIid3EhGXRL2U2ek3wBa8J8I0gO/Fq0mLHU1j1JYVVu2h0lPDuu28xY+aMbrLce2lqamLJkiXsensVESGpDEq7Hr0myNNmeQ2BftEMz1jsXOqj/DO25L/J3Lnz+etfX76kNepUrjg6CkL0KnpujLn3sgB4Q0qZIqVMlVImAYXAhMvNUAiRLqX8Skr5GFCLMxp1JiFAtUuoTQUu+F9RSmkEGoUQ7Tbdcp6ki4AnXPVIlVLGAwlCiK7+r1sFRAshIoQQPsDcS7y+GTjnE9M1c7VBCDHRdehWYMvZ6Xojq1atYujQoRw8eIThWQsZlHrjRYXamRh0/mQnzGRU9p1Y2hRmzprF0od+jaIobrTau9m5cydDhgzh3XffJStpGkP7LFaFWgcIIYgJy2Fczn1kJkxl3bp1ZGZm8cgjj2IymTxtnoqKR1DFmvexCFhx1rH/ATd/hzyfF0IcEkIcBr4ADpx1/m1ghBBiD07h1ZmlQu4E/k8IsQNoO0+amzi3Litcx7sMKaUNeArngP81dM7+M1kNXC+E2H+GMGvndpztdxDnJI6nvqu93oyUkt/97ndcd911aGUQ43LuJiKw72UPGA4NSGRM37uJCx/In/78eyZPupqmpqaLX9iLsNvtPP3000yYMIHa6kbG9vsBqVETevR4rO5Aq9GTFjOR8f2WEBWcxbPPPkNqSjpvvfXWFS36Va5M1NmgKiqewescz2q1cs8997Bs2TISo4aQkzgHIbRdkreUkpKa3eSVfkpiQirbdmy+ItaeKigo4NZbb2X79u0kRA4kJ2k2GuHjabN6JPXNRRwv/5Sm1koy0rN56eU/M3v27F6/xIlKp+j1D4Eq1lRUPINXOZ7RaGTBggVs3LiRrMSppERNcMuHYG3TSQ4WLsffL4DPN3/G8OHDurwMb0BKyRtvvMH999+PzeogJ3k2UUH9PG3WOSiKA5vD5BqgLtBotOi1fl4rgKSUVDYc4WTlJkzmBoYPHclLr7zAhAmXPUpEpXfgnQ9sF6KKNRUVz+A1jldWVsasWbM4diyXgWnziA7ucG3jLqPZVMnXBe+hSCvLly/n2nlz3Fped1NXV8e9997L8uXLiQ7rw4C069Dh2XXnFMWBsbWUxtZSmtuqaGmrxmxrwu4wn5NWCA16nT9+hlAC/aIJ8o0mNDCRIL9YhJd03SqKg7K6rymo/AKLrYVpU6/mD398lhEjRnjaNBXPoIo1FRUVt+AVjnfs2DFmzpxJdVUtQzNuJNg3uVvKNVub+LrgXVraanj5pb9w/wNLuqVcdyKlZPny5dx///3U1taRmTCVpIjRHhM4doeVamMuVcaj1DcX4VCsAPj4hBAYEIufbxh6QwB6fcDpBV0UxY7V1oLV0kKbuY6W1irsdueQVJ3Wl7DAFKJDs4kOyUav8/zel3aHlZLa3RRVbsPmMDNp4lSefuZJJk48e+ipSi9HFWsqKipuweOOt2PHDubOnYvF7GB4xs346rp3AVubw8zBwuXUNRXw4yU/5ZW//BmNxjsiN5dKeXk5S5YsYdWqVYSHJDIgdR6+2kiP2NJkqqC4+iuqjMdQFBs+PiFEhmcTHp5JaGgaen3ndweQUmKxNGI0FtFgLKC+4QQWixEhNIQH9SEhYgjRodloumhs4+Vid1gord1DUfVOrLZWRgwfzdPPPMmMGTO8tktXpUvp9TdZFWsqKp7Bo463Zs0aFi5ciEEXxLCMm9GLzi/L0ZUo0kFuyceU1u5j1oy5rFj1Ab6+PWcBXYfDwauvvsrDDz+MqbWNjPgpJESM6vaZnlJK6ppOUlS9nfrmIrRaH2KiBxIbPZSQ0JQui+5JKWluLqO65hBV1QexWBox6ANJiBhCctQofPSe7e51KDbK6r6mqGo7ZmsTGelZLP3lL1i8eDH+/j1/CyuV86KKNRUVFbfgMcd77bXXuPfeewkNimdo+k1opGe7s6SUFFXvIL9sA/1yBrN5y2dERXn/NlVffPEFDz74IPv37ycqtA8D065FJ0K63Y6GllPkl23E2FqCjyGYpMRxxMeNRKd3732VUqGu/jhlZV9RV38cjdCSEDmU1Jhx+Bm6vx3ORFHsVDQcpqR2F02tlQQGBnP33T/k/vvvJzU11aO2qbgFVaypqKi4hW53PLvdztKlS3nppZeICc9iUOr3Eei724zzUtlwlMPFKwkLCWfNuo8YM2a0p03qkMLCQh5++GH++9//EhQQTlbiVYT7Z3d7d5vJUk9e6WfUNOZhMASRljKNuLjhaDTdvzGNyVRH8anNVFY5d6aLjxhCRtxkj0fapJQYW09RWreHyrpjICQTxk/innt/xPXXX69G23oPqlhTUVFxC93qeEajkZtuuon169fTJ24sfWKne+WirI2tZRwsXI7F3sIfnvsjv1j6M68Zc1RSUsLTTz/N66+/jhAa0mLGkxI1FiG6Vxwpip2iqu0UVG5FCA0pyZNJShyHVuf59dvMZiPFp7ZQXrEbjdCRGjuO1OixaDWe/1JgtjZS3rCfstoDtFmM+PsFcMPCG1i8+BYmT56MXu95G1UuG+/4J+FGVLGmouIZus3xdu/ezaJFiygqKqZ/yhxiQwd3V9GXhdVu4sipj6gxHmfypKt4+51lJCQkeMye/Px8XnzxRf71r3/hcCgkRQ6jT/xEdCKg222pby7m6Kk1mCx1REcNIDN9Nj6+od1ux8UwmWo5WbCemtoj+BiCyU6YQUxojlcIbyklDS3FVDUeorz2CA7FSlBQMPPmzWPBgu8zY8YMNeLW8/D8g+VmVLGmouIZ3O54iqLw/PPP8+ijj+LnE8ygtO8RYIh3d7FdgpSS4uqdnCjfhI+PD88//0fuve8etNrumXUopWTTpk28+OKLrF27Fo1GS0LEYDITJqMV3d+151DsnCj/nOLqnfj6hpGdOY+IiOxut+NSMRoLOX5iDS0tFUSEZNIv8Rr8fLxHXDoUG3VNJ6lryaeyLhebow293sCYMWO55pqZTJ8+neHDh3fbc6dy2ahiTUVFxS241fEOHTrEvffe69rmaAD9UuYipMGdRboFk7meY6VrqWsqJDUlnRdf+hPz5893W4SmoKCAN998kzfeeIOCggL8/YJICB9OctRwtJruj6QBNJnKOVS0ilZzDQnxo0jvMwudrufMmFUUB6VlOygs3IBEkh43iZTosV7XDa9IBw3NxTSYCqkxnqDZVAVAYEAQo8eMZvz4cYwZM4ZRo0YRERHhYWtVzkIVayoqKm7BLY5XW1vLs88+yyuvvIKPwZ+shKuJCurvFd1Pl4uUkmpjLicqPqfVXEdKch9+9vMHuO222wgLC/vOeX/99desXbuWNWvWsGvXLoQQRIWmkxA5mPCAbLQeGLDfblth5VZOVmxBbwggJ/v7RERkecSWrsBsNnI8fzW1dccICohnQPJ8gvy8d9avxdZKQ0sRjW3F1DeW0NJWjXS5bXJSKkOHDWHw4EEMHDiQAQMGkJGRgU7nmWdFRRVrKioq7qFLHa+qqoq//vWvvPTSS7S2mkiKHkZWwnQ0eH7QeVehSIXK+sOU1e2hoaUUrVbL+HETmH/dPEaNGsXgwYMJCgo6//WKQklJCXl5eezdu5cdO3awY8cOamtrEUIQHpxEVEg2cWED0GvPn093YLG1crhoBXXNBURHDSI7cx56Q+8YR1VdfYi8/FU47FbS46eQGj3Ga7axuhB2h4UmUzktlkoaW8tpaq3EZK4/LeAMBgMZGVnk5GSTnZ1NZmbm6Z+oqKge/YWpB9DrG1cVaypuRwjhAA7hdCgH8BMp5XY3lfUE8DiQKaU84Tr2M+AFYKSUcs8Frv0p8E8ppekiZWwGHrpQXp3gOzuezWZj8+bN/Pvf/2b58uXYbDbiIweQlTgVg+a7RZy8nSZTObVNeVQ25NLSVgPgFFzhEcTHxxMREYFOp3Uu3WA0UldXR0VFJRbLN3thBgdGE+QbT0x4OiF+aei13iGG6puLOFj0IXa7mczMucTHjex1H/RWawt5x1dRU3uE4IBEBqTMI9DXMzs+fBccio1Wcy2tlhrarLU0tVbT0lZLm9WIlMrpdIGBQaSnp5OT05c+ffqQmpp6+ic5ORkfn97zpcpD9C4H6QBVrKm4HSFEi5Qy0PV6JvAbKeVkN5X1BPA94L9Syqddx7YBocDtFxFrRcAIKWXtRcrYjAfEmpSSoqIitm7dyoYNG1i9ejUNDQ34GPyJDx9MSuxIDBrvGbzdXZitzTS3VdBmq6HN2kibuQmb3Xw64qHT+GDQ++PnG0SQfyS++nB8dREYdN4hztpp7/Y8UbEZf78I+ve7iaCgnjEh5HKQUlJVfZDj+R+hKDYy4qeREjWqR0TZLoYiHbRZjLRZ67E6GjFZ6mhuraXFXIfZ2vQtIQcQEx1LWp/Ubwm5lJQU4uPjiYuLIzw8vNcJ9i6m1zeO2sGu0t0EAw0AQohAYBUQBuiBR6WUq4QQAcB/gURAC/xOSvm+EGI4zghZIFAL3CGlrOigjJXAfOBpIUQfoBGwtZ8UQswAngR8gJPAncBdQDywSQhRK6WcKoT4f8BIwA9YLqV8/MxChBBa4F/ACJzi63Up5YvfpXHa2tqorKykqqqKyspKSkpKyM3NJTc3l8OHj1Bd7Rz07GPwJzI4k6x+swk0JHfbOlbti4zWNxfRZKrAajchpYKPPpAA30gigvoQFpTSrXtF+hqC8DUEAT13PNeZ3Z4x0YPIzrwOnb7nTCK4HIQQxMYMJiw0jbzjKzle+ilVxmMMSJ5HgG/PHsCvEVoCfCM6rIciFSy2ZtosRmxKMxZ7I6a2Bo4fqeTg13m0WRvPEXN6vYHo6Gji4uJISHAKuOjoaEJDQwkLCzv9t/11cHAwfn5+GAwGVeT1EtTImorbOaMb1BeIA6ZJKfcK52qi/lLKJiFEJLATyMQZGZslpfyR6/oQwARsAeZLKWuEEDcCM6WUd51V1hNACzAOeAynaCvFKcgeAoqAD4FrpJStQohfAT5SyqfOjqwJIcKllPUuUbYReEBKebA9soZToP1eSnm1K32olNLYmTaJj8mQdrsVm82CzeH8a3dYURTHOWl1Wl8CfSPx94kgNDCBkMAkAn2iu/WfsEOxUVq7l+LqXZitRkAQ4B+FwRCEEBos1iZMphqkVDDoA0mKHEFy9Cj02t4tOLqC+uZiDhV9iM3eRmbGHOLjR11xH7BSSiqr9pN/YjWKYicjbhop0b0jynapnCnmrLYWrI4WLDbXj7XZ+dfejM1u5uIBeoFOq0OrNaDT6dFp9ei0BrRaLUJo0Gg0zr9C86333xwTHd8DcfbbCz+v5z7P56Y/95HvvA8cO7Gz1zuMGllT6Q7apJRDAIQQY4E3hBADcHrjs0KISYACJAAxOIXdn4QQfwDWSCm/dKUfAHzmcnwt0FFUrZ33gJuAmcB0nGINYAzQD9jmyscA7DhPHguFEHfj9JM413UHzzhfAPQRQvwFWAt82rnmAEubglbjj68uhACDHm2AHq1Gj1ZrwEcXiEEfiI8+EB99EAZdgOufJngi2l/ZcJTckk+w2JoJDUmjT5+riYzsh+6sFfPtdgsNDScoK9/FyYrNnKrZRUb8FJIiR1xx4qMztHd75pdvws8vnOGDbu/V3Z4XQghBXOxQwsPSnVG2sk+pbjzGgJT5PT7KdqlohRZ/n1D8z7MeXXuARUqJ3WHB5mjD7jBjc5ix251/HQ4LDmlHUWw4FDvKma8VO4rNgUQBKZHYkVIipYJEuqJ68vSxc8q/qECUF3nbmQDRpQWRZg5//Kfr9z750iVd1MNQxZpKtyKl3OGKokUBs11/h0spba7Ilq+U8riry3M28JwQ4lNgBXBESjm2k0WtBp4H9rgid+3HBfCZlHLRhS4WQqThjJ6NlFI2CCGW4YwMnlmXBiHEYJyC8MfAQpzdqRflVNlRzGZrJ6viGerr6/n5Lx7gwN7VhIYkMDjrZgIDUs6bXqfzISqqP1FR/WluLuNkwSccO7UOQ2gNy/79OklJyd1ovXdTV1fHkh/fTf6+z4mLG0x25vVoND1vHbyuxscnmIEDbqWqaj/5J9awM++f/PrhR/nJj3+iLkzrJqQEh0NBcSgoikRRnEJNUSRSkafFlZTOX+2dcd+lV66re/Tuv/Wff+/SDL0QVaypdCtCiL44o2J1QAhQ7RJqU4EUV5p4oF5K+ZYQogW4A/g9ECWEGOsSfHogS0p5pKNypJRtri7O42ed2gn8nxAiQ0p5QgjhDyRKKY8DzUAQzvFwwUAr0CiEiAGuATafVZdIwCql/J8Q4iSwrLPtEBDkS0CQ93YR7t69mwULFlBeXkFW5jXEx41Do+n8h2VQUAKDB91FReVeDh9Zy5hxo3n77bf4/vevd6PVPYPt27dz4403UllZRb+c64mJViOPZyKEIDZ2KGFh6eSf+IjfPf0YK1au4O23lzFo0CBPm6fihazf+6T54ql6NlfegAAVT+AnhNgvhNgPvI9zVqYDeBsYIYTYA9wC5LrSDwR2udI/AjwtpbQCC4A/CCEOAPtxjks7L1LK96SU+846VoNT/L0rhDiIU7z1dZ3+J/CxEGKTlPIA8DVwBHgd2NZBEQnAZpedy4Bfd7aU4CzqAAAgAElEQVRBvJlly5YxYcIE6utbGDniXhITJl6SUGtHCEF83AhGjbgfH0MYCxZ8j5/97FcoyrldK1cCUkpeeOEFJk+eTFOThdEjlxAb0/uW5egqfHyC6d/vFvrlLCQv7zhDhgzl7rvvw2js1LBQFZVehTrBQEXFM3id40kp+d3vfsfjjz9OVGQm/XJuQqv165K8HQ4becdXUln1NZMnX826dSuvqM2yGxoauPPOO1m1ahVxsQPpm/09hFDX1uosNpuJwqINlJZ9RUhIKC+88GfuuON2NBo13qACXAFLd6hiTUXFM3iV49ntdpYsWcKrr75KQvxwMjPmo+nibZaklJSUbuPEyY/JzOzP9u2biIzseQuhXirbtm1j8eLFlJSUkJkxm7jYMWo07TJpai7jxInVGBtPkZnZlxdf/BOzZ89W21Ol1z8AqlhTUfEMXuN4ra2t3Hjjjaxdu5Y+faaRkjTdrR9+1TWHOXrsv0RExLB16yaysjLdVpYnsdlsPPXUUzz77LMEBEQwoP+N+PlembM9uxIpFaqqD1JUtAFTWz3Dho3ixRefZ9KkSZ42TcVzqGJNRUXFLXiF49XW1jJ37lx27dpNv5z5xESP7JZyGxuLOXj4TfR6HZ9++jHjx19w+GGP4/jx4yxevJjdu3eTmDCSzIy5OOfEeBdSSmw2E1ZbC1JxIJEIBHp9AAZDQJdHV7sSRbFTUbmHoqJNWKzNDBkynMcee4T58+er3aNXHqpYU1FRcQsed7zi4mJmzpxJQUEhAwcsIjQku1vLN5lqOXBoGTZrC2+8+QaLFt3YreW7A4fDwd/+9jcefvhhpKIhO/s6wsP6edosABTFQVPTKYyNp2hpKae5pQKzuQHnXJ+O0RsCCQyIIcA/hpCQZMJC0zEYArrR6ovjcFipqNxLSek22trqSU5OY+nSn7N48WJCQ6+87deuUFSxpqKi4hY86niHDx9m1qxZ1NUZGTLoNvz9kzxih9XawsHDb9LUVMpjjz3FE0880mPHHx09epQf/vCH7Nixg+iovuT0/R5abaBHbbLbLdTWHqW65jANxgIcDgsAvv7hBATH4RcQicE3GINPEEKjQwiBlAo2ays2SytmUx2tzZWYmqtQHM4d2wID44iKGkBM1CD8/b1nwVpFcVBTe4TSsq00NpZiMPjw/e8v4L777mHChAk99rlS6RS9/uaqYk1FxTN4zPG2bt3Ktddei90GQwbfhcHg2UH+DoeNY3nLqa4+xA033Mzbby9Dr/e+LsPz0dbWxh//+EeeeeYZdDpfMjPmEBE+0GPiQEpJY2MRZeW7qak9gqLY8PENISymL2FRWYREpqM3XNpMXKk4aDaWYqw5QUN1Lk0NxQAEBSeRGD+GmOiBXtVl2txcRmX1XsrLv8bhsJCYmMLixTdz0003MmjQIFW49T56/Q1VxZqKimfwiOO999573Hnnnfj4hDB40J3otMGeMOMcpFQoKNxA8anNDB06mk8/XeP1M0WllCxfvpylS5dSXFxMfNxQMjPnotV0zXInl4qi2KmqPkRJ6TZaWsrR6XyJTBhMdMJQgiNSu3SfTbOpgdqyA1Se2k1baw16QyAJcaNIShyHXu89S7I4HFaqaw5RU3OIuvoTSKmQlprOLYsXMX/+fIYNG6aOb+sdqGJNRUXFLXSr4ymKwmOPPcYzzzxDZGQ6A/vfjBCeERUXoqJyH7l5KwgJCWPVqg+ZNGmip03qkF27dvHQQw/x5ZdfEhaWSFbGHAIusBWXO3EOtN9LUfFmLJZG/AKjSegzgeiEoWj17l3LTUoFY80Jygu3UV91DK3Oh6SE8SQljkev967ny2ptobbuqEu4FQCSiIgo5s2by7x587jqqqsIDPRst7XKZaOKNRUVFbfQbY7X2NjIHXfcwcqVK0lKGk1Gn7kI4b37LDY3l3Hk6Hu0mRt45JHf8vjjj6LTeUcX2+7du3niiSdYt24dfn5B9Em7muioYV0ateosiuKgqmo/hcWfYzY3EBSWTHLWVYRFZ3ukm6+1qYLivM+oqziMVudLSvIUkhPHeVX3aDtWayv1DccxGvOprsnFbjej0+mZMGEi1147hxkzZtC/f3+1u7Tn0OtvlCrWVFQ8Q7c43o4dO7j55ps5daqE7Kw5xMaM7hEfQHa7mbzjK6mqPkh2dn/ef/9tBg8e7BFbFEVhw4YNvPTSS3z88cf4+QWSmDCBhPgxHtt8vb7hBPn5a2g1VRMYkkBK9gzCYvp6xb1taSyn+Ngn1Ffn4usXTkb6bKIicrzCto5QFAeNjcUYG49TXXOM1tYaACIjo5k1awazZs3iqquuIiYmxsOWqlwA73y4uhBVrKmoeAa3Op7FYuG5557j6aefJiAgnP79et6CrFJKamoOc/zEauz2Nm6//U6ee+7pbvvQbGho4J133uEvf/kLeXl5+PuHkJAwloQ4z4m0trZ6TpxcR03tUXz9wknrP4eIuAFeKYQaqo9TcPgjTC3VhIVnkJ0xD39/7x6HCGA2G2kwnqSx8SQ1tcex2UwA5OT0Z86ca5gxYwYTJkzAz8+7unmvcLzPAboYVaypqHgGtznepk2buO+++8jLyyM+fihZmfPRCM+Ii66gfV/IsvJdGAwG7rtvCQ8+eD+pqaldXpbJZGLNmjW88847rFu3DpvNRnhYMslJ4wkNzfFYl57DYaWoeBOnSrYiNFqSM6eR0GcCGp1331dFcVBRtJPi3PUoip3UlKmkJE30yq7RjpBSobmlgsbGk9TX51PfUISUDgwGH8aNG8/MmVczZcoUhg8f3qNmMPdCVLGmoqLiFrrc8fbu3ctjjz3GunXrCA6OIjtzHkFB6V1djMcwmWopPrWRyqpDAFx11dUsXnwzc+fOJTw8/LLytNvtHDlyhM8//5xPPvmELVu2YLFYCPAPJTJyAAnxw/D1je3KalwydXV55B1fhdliJDpxGKk51+DjF+JRmy4Vq7mJk4c/orb8IP4BMfTNup7QkGRPm3XJOBxWjMZCmpoLqK7Jo7W1GgA/P3/Gjh3HVVdNY/LkyYwYMQKDwbuFdC9DFWsqKipuoUscz+FwsHbtWv72t7+xfv16/PwCSUqcSHzcGDSa3vlN32w2Ulm1h7LyPVgsTWg0Wvr3H8D48WMZMmQIKSkpJCQkEBAQgK+vLwDNzc00NTVRVlZGQUEBJ0+e5MCBA+zbt4+2tjYAQoJjCQ3NIDamH/7+yR6ZNHAmVmsL+SfWUFV9EL/AaDIHfY+QyD4etem7Uld5lJMHV2AxN5GQMIr0tJnodL6eNuuysVpbMDYW0txSTG3tSVpbqwDw9fVj9OgxTJw4nlGjRjFy5EhiYz0r+ns5qljr6QghYoGXgJGABSgCfgrEAw9JKee6ocztUspL3uxQCPEE0CKl/FNX29RBWVO4QP2FEC8DC4AkKaXiOnYHMEJK+ZMzbRVCPAV8IaXc0MmyU4E1UsoBnTl+kbxO29TZa8649jdSymcvcH4dcLOU0nipeXeCy3Y8u93OF198wYoVK/jwww8pLy8nICCM+LhRrkHv7l2uoSNstjaMjUWYTDU4HBY0Gj1+vmGEhqbi4+OeKJCUCs3NZTQYj2M0FtPYVIrdbu7UtQaDPwEB0QQHJRIeloy/fyI+Pt6xNZGUkorKfZw4uQ6Hw0pS1jSS0qeg0fUO8e2wWyg69gnlhdvx8QkmK3M+UZF9PW1Wl2C1ttDYWOQUb3UFtLRU0u7qcXHxjB49mlGjRtK/f3/69etHWloaWq33zszuQfR6sdYzBg5cJsI56nYF8B8p5U2uY0MAt45Qvhyh5k0IZ0jheqAEmARsvlB6KeVj3WCWO/gNcI5Ycz03Qko5u/tN+jYWi4X8/Hzy8vI4cOAA27Zt46uvvqK1tRW9zkB4eCbDh15FUFAmGk33/tOXUqGu7jglZdsxGgtwafpzCAyMIyF+DLExg9Fqu65rSAgNwcFJBAcnkZLstMdiacZsMWKzNSOEA0XaEYBW54tW6NFoA/D1Cfe6NcDaMZlqyT2+EqOxgODwVDIHfQ//4N4VkdHqfEgfOJ+oxKHk71/OocNvEB09iKyMuRgMPXudM4MhkKioAURFDaBPmrPbtLm5HFNbOU1NZaxf/wUrV644I72BzMws+vfvT1paKsnJyaSkpJCcnExSUhIhISFeOXlEpfvp1WINmArYpJR/bz8gpdwPpyNLgUKI5cAAYC+wWEophRDDgReAQKAWuENKWSGE2Ax8DQwHooDbgF8DA4H3pZSPuvJukVIGul7/ErgVUICPpZQPCyF+BNwNGIATwK1SStOZhgshHgDuBezA0Xaxecb5VOBNoH1X5Z9IKbe76vWEy+6z6zULZ5SxFth3kXY7DLwPLOIiYk0IsQxnRGz5BdpuOPA6YAK2Xig/V553APMAfyAdWCGl/KXr3J04270COI4zYvotO1zvW6SUgUKIOFddgnE+8/cBcwA/IcR+4AjwCPAxsAkYC1wnhNiCM2pXK4RYDDyA8559BSxxmfovYATOr8+vSylfvFjdAD744ANMJhOtra2YTKbTr+vq6qiqqqKyspLKykrKy8tRFKW9TQgJSSAifDB9szMJDEjrUvFzKTQ2niIv/yNaWsrx8Q0hMX0yYdHZBITEodP74bBbaWutwVidT3XZ1+QdX0Fh8UbS02YSGzPYLV2MQmjw9Q3B17dnjecC50D8UyVbKSreiNDoyBj0PWJTRnm8K9adBIclM3TyA5Tmb+JU/ufUN+STmT6H2JihvUagaLUGQkNTCQ1NJT7OecxuN9NqqsFirqHNXEt1VSUFBRuwWIwoiuNb1+t0ekJDQ4mMjCQqKpKoqChCQkLw9/fH39+fgICA03/9/PzQ6XTn/Gi12m+9P3PHhjPb2R2vu4sRI0Z0e5ndTW8Xa+1i5XwMBfoD5cA2YLwQ4ivgL8B8KWWNEOJG4BngLtc1VinlJCHEg8AqnMKtHjgphHhRSlnXnrkQ4hrgOmC0lNIkhGgfBf2hlPJVV5qngR+4yjyTh4E0KaVFCNFR/0w1cLWU0iyEyATexSkazlevPcCrwDScAvH9C7TLIld+q4BnhRB6KaXtAunb66vn/G33b+B+KeUWIcTzF8vLxRBXXSxAnhDiLzjF65M4270Rp7j6+iL53Aysl1I+I5yrwfpLKb8UQvxESjnEZXsqkA3cKaVc4jrWXq8c4EZgvJTSJoT4G3ALTpGX0N5te5771CELFy4855hG6NDp/TAYAjHoAzEYokhOysTfP5oA/yj8/SM9Js7aURQ7JwvWU1K6DYNPMFlDFhKVOPScqJ5WZyAwJIHAkAQSMibTWHeSwiPrOJb7AZXV++mX/T23dY/2NJqbyzmW9yEtLeVExA0gY8B8DD1sAsHlotHoSM6+moj4QZzYv5xjucupqj5AduZ1+PmFedo8t6DT+RISnATBSd86LqWC1dqC2dKIxWx0RYhN2Gwm6mpbqawowWbLw+6w4HBYURw2FGn3UC28i2lTnh25cdOvd3vaDnfS28XaxdglpSwFcEVYUgEjTpH3mevDWoszgtPOR66/h4AjUsoK1/UFQBJQd0baq4B/t0fNpJT1ruMDXCItFGcEan0Hth0E3hZCrARWdnBeD/zV1a3rALIuUq8WoFBKme86/hbO6N63EEIYgNnAz6SUzS7xOgNY24ENZ5NNB20nhAgBQqWUW1zp3gSu6UR+G6WUjS67jgIpQCSwWUpZ4zr+/ll174jdwOsuMbmyPbraAcVSyp0dHJ+OUxzudtXLD6dYXg30cYnItcCnnagTADNn/prmRhtanQG9zge93oBWq0Or1aDVatDpNGg03hVdaG2tY9uOf2E0lhKXOo7UfrM6NThcCEFoZAZDJv2EiqKvKDy6hq/2vMKokYtJjB/YDZZ7Jw6HjaPH1pObtwG9wZ9+I24l4gptj4CgGAZNuI+Kop0UHV3Hrj0vM7D/HDIyJ6PpxdHFcwnGOZz6XKQERZE4HAqKorheO7DZrNjtFux2K4ricP5IiZTK6R+kgiIVpHScMVr2m2Gz3x5AKzt8eenpuxXv2OTYjfR2sXYE5yD582E547UDZ3sInCJs7EWuUc66XuHc9hR0/PguA66TUh5wdfdN6SDNHJzjxeYBvxVC9JfyW1+jfgZUAYMBDXDmyOqO6sV5bDmbWUAIcMglTPxxdl12Rqx12HauiNPluPGl1sOOsy3ax50ZAKSUXwghJuFs0zeFEM9LKd/o4PrW8+QrcI57/PU5J4QYDMwEfgws5JsI7AX55JPzzmvwSg4fPsyMGTMwm5sYPO4ugi9jQLgQGuLTxhIalcHxfe+wfftr/PJXv+H3z/2u13R7dZbt27fzgx/8gNzcXOJTR9Gn/1yEtufOiuwKnM/HOMJjcig4vJL9B1fgoIh33n6DAQM6PedI5cpko6cNcDe9/SvL54CPa4wYAEKIkUKIyRe4Jg+IEkKMdaXXCyH6X2b5nwJ3CSH8XXm1d4MG4Yw46XF2p30L1wD/JCnlJuCXfBOBO5MQoMI1U/NWnFGsC5ELpAkh2hfeWnSedIuAH0opU6WUqUAaMKO9Dhehw7ZzzaZsFEJMcKU7p86XwFfAFCFEhKv9bjjjXBHOCBjAfJzRR4QQKUC1q+v5X8AwVxqbK4+LsRFYIISIduUXLoRIEUJEAhop5f+A356Rb69ix44dTJw4CWNTG4MnLrksoXYm/oFRDBx3H1EJg/njH55h5jXzsFgsF7+wF9DS0sKDDz7IhAkTKC2vYejEe0gftOCKF2pn4usfRs7IO8getojc3OMMGTKUX/3q15jNnZvpq6LSG+nVYk061yW5HrhaCHFSCHEE5+D78gtcY8UZjfuDEOIAsB+4rNmdUspPcHab7nF1Rz7kOvVbnKLjM5wi6my0wFtCiEM4x2O92MHyEX8DbhdC7MTZDXi+qFC7LWac3Z5rhRBbgeKz07gE2UzOiKJJKVtxTgi49sK1vWjb3Qn8nxBiB9B2sbwuUEYFznu4A9jAtydKvApMFkLsAkbzTZtMAfYLIb4Gvg+87Dr+T+CgEOLti5R5FHgU+FQIcRDnfYsDEoDNrnu7DOekh17F+vXrmT79KmwOHYPGL8HgF9Ul+Wp1BrKHLSI1ZxafrV/DiFETaWxs7JK8vZXPPvuMgQMH8sorr5CQPp4hE39KYFjvWbS4KxFCEJ04lOFTHyIyYTB//OPvSUlN591336O3LzelotIRvX6dNRUVL8XrHe+///0vixcvxjcgmv6j70LvE+SWcqpK9pK//wMSktL4ascXxMf3rD1ML0ZdXR1Lly7l3//+N8FhsWQNuQG/oKSLX6hymoaafIqOraXFWM7AwcP4x//7K2PHnm+kisoVSK8fR6GKNRUVz+DVjvePf/yD++67j5DINHJG3I7OzeuSNVQf59juNwgKDmXr1s3075fj1vK6A0VR+M9//sPSpUsxGo0kZUwmMXM6wot2lpBSwW5rQyoOpFTQ6nzQ6ny8cskQKRWqSvZSnLseq7mJq66exXPP/u6KWLZB5aKoYk1FRcUteKXjSSl57rnneOSRR4iM60fWsFvQartHXDQbSzn61etoNLBu3RqmTrnQ0FLv5vDhw9x3331s3bqViOh0Modcj9432mP2SCkxNVXSZDxFi7GM1qYKLG1GrJZmOGcxY4HBNwi/wCj8A2MIDk8hJCINHz/v2OHBYbdSXvglpSe+wG5rY/KU6Tz7zFOMG9ej1yJX+W6oYk1FRcUteJ3jKYrC0qVLeeGFF4hNHk76oAXdvitCW2sdR756HWubkWX/+Q+LbznfPBjvpKWlhaeffpo///nP6A1+pPabTUTcUI9EqhwOGw1VudRXHaO+Og+bpRkArd4X/7B4fALDMfiFoPMNdN5njQbFZsVuNWFtNdLWXEObsRLF7pz8ERASR2TcIKLiB+EX2DVjF78LdpuZyuIdlJ74Apu1lQEDh/CLnz/IjTfeiJ+fd+5QoeI2VLGmoqLiFrzK8ex2Oz/60Y9YtmwZSRkTScmZ47GuMJullWO7/0NjfTFPPvUMj/3W++dtOBwO/vOf//Doo49SUVFBfNpo0vrNRqPtXtEgpaSpvoiqkj3Ulh/CYTej1fsREpdFSHw2QdF98AmK6PS9lYoDU0M5TZUnaCg5REutc15SSGQ68WnjiYjJQXSzoD8bh91KVcluKot20tpcRVBQCD/4wV3cfvttDB48+IpbFuYKpdffZFWsqah4Bq9xPJPJxKJFi/joo4/o028m8enTPP4B53DYOP71e9SWH2LxbT/g3//6Ozqddy4L+fnnn/Pzn/+cAwcOEB6VRvrAefgGJnSrDYrDTk3ZfsoKvqS1qQKNzkBY0kAi04YTHJvRZYLK0tpAXeE+qo9vx2oy4uMfTlLWdGITh3lctEkpaawroPrUTqrLDiGlQp/0TO64/VYWLlxIdna2R+1TcSuqWFNRUXELXuF4dXV1XHvttezcuZOswdcTnTzG0yadRkqFwiNrKSv4kkFDRrD+49XExnrPpuZ79uzh8ccfZ926dQQFR5LabzYhUf27Veg6x29to+zkl9isLfiFxBLTdyIRqUPQ6t23dptUHDSUHqXi8AZa60vxDYgkOftqohPcs+/rpWKztlJXcYja8gM01JwEICUljeuvn8+8efOYMGECer33TPRQ+c6oYk1FRcUteNzxiouLmTVrFidOFpAzYhGhUZe79rN7qS7dR/6B/xEYGMSH//uA6dOnedSevXv38uSTT7J69Wp8/QJJTJ9MbOq4bp3l6XDYqCjaQWn+JmzWVkLisonNmUxwXFa3ikUpJcbSI5QdXI+poZyg8BT6DJhHcKj3LE1iaTNSX3WUhupc6qvzkYqDgMAgpk6ZwsyZM5g2bRo5OTkejyarfCd6/c1TxZqKimfwqONt2bKFG264geYWEwNG34lfcLInzbkorU0V5O55C1NLDT/44T28/NKfCQgI6LbyFUVh/fr1vPzyy6xfvx5fv0AS+kwiLnUsQuvTbXZIqVBdso+i3E+wmpsIjs0kYdBMgqLTus2G89lVW7CHkq/XYje3EpMykrSca9Abuu8edQaH3UJDTT5Ndcepq8zDbGoAIDIyiulXTWfG1Vczbdo0UlNTPWuoyqWiijUVFRW34BHHk1Lyyiuv8Itf/ILAkGj6jbgNnW+EJ0y5ZBx2K8XHPqascBvRMQm88vILLFx4g1sjInV1dbz77rv89a9/JS8vD//AUOJSxhGbOhZNN4o0gKb6Yk4eXkWLsZSAiGSShs4hODajW224GHZrG+WHPqMq90u0Bj/SB1xHVPwgr41amVvraaw7QXN9AXVV+c6lTID4hCSmTZ3ClCmTmTx5Munp6V5bBxVAFWsqKipuotsdr7q6mnvuuYeVK1cSkziIrCELQWPobjO+M8bakxQe+YiWxgoGDBzCs888xZw5c9BoumasVFtbG59++ilvvPEGq1evxmazERqRTFLGJIKj+qHRdO9EB6u5iYIja6kp+xq9XzBJQ+cQkTbMK8aGnQ9TQzmFO96ntb6U8Lj+ZAy8Dh/fEE+bdUGklJiaq2iuP0ljfSEN1SexWZ071kVFRTNlyjfiLScnp8ueN5UuQRVrKioqbqHbHE9KyfLly/nxj39MQ4ORtH7XEJMyzqs/7C9G+2r2JXmfYW4zkpCYzI9+eBcLFiygX79+lxQFURSF3NxctmzZwrp169i4cSNtbW34+QcTGT+E+NSR6P2iuz2yIqWk6tQuCo6sRVHsxOVMJq7/NLSG/8/eecdHVaV9/HumZSa99w4JEDokdJCiKEiRooKiImvvbdfVd3dFt+la1ld9dVlX17o2FMGGWEAUkN5DJyGkt0mZZPo97x8zsAHpJDMD3O/nc3Nnzr33nOeezJn7m+c55dxY9F0qbip3Lqd082I0Gh1ZeZeTmD7gnPFQSSmxWqppNhfTVF9EffVeHLYmACIjoxgxYsRh8da7d2+0Wv+Ohr3AOTc+VGeBKtZUVPyDTxreli1buO+++1i6dCmRMWl07T8TvTHWF0X7BEVxU1exjaqSnzHX7AckcfEJDB82jJ49e5CVlUVSUhJGoxG9Xk9zczONjY2Ulpayd+9edu3axdq1a2lq8jyEQ8NjiYjtQkJqD0zhmT6fFPgQrZYa9m7+mMa6/YTFZ5M58EpMEf5bAeFssDXXUrTqA5qr9xMZn0NOr+kYg6P8bdZpI6XE1lqPxVxMk7mI+up92FrqAAgJDWXokKGMGjWSYcOG0bdvX5/2qVRRxZqKikrH0KENb926dTz11FN8/PHHGE2hpHcZS1xKvt/nwupIHLYm6qsKsZgPYK4t8nYeP341G4KCMYXEEhKeTHR8FqawVIKCY/3q+ZGKm9J9P3Bg17dotDrS+k0krvOAc9oLCt6BEbtXcXDj54Agq9t4kjIHnvP3Zbc20GwuxmIupq56L63N1QBoNBpyu3Rl0MABFBQUUFBQQK9evQgK8m0/xwsIVayptD9CCDewtU3SFVLK4tPMYzawREpZ3o6m+QQhRCbwuZSyx8nShRBzAYuU8pl2KLcYyJdS1p5tXu1Auze8xsZGPvzwQ9544w1WrlxJkDGYpMwhpGQPR6O78JbfUdwu7/qXFqR0AQpajQGNLgiDMRydPjigQnLWljp2bXiPZnMJUWk9ySiYgiE4sPt5nS52Sz1FP39IU+UewmOzye19JaaQc2OAy6ngsFtoNpdgs5TTWH+QpvqSw/3eNFotmZlZ9OrZg7y8vMNbp06dCA8P97Pl5zyB05A7CFWs+QEhhEVKGXqWeSwDHpJSrmsfq05Ylk56nnbtlV8m56FYO816OuuG19LSwubNm1m+fDmLFy9mxYoVuFwuwqOSSEjLJz5tgM9HLKqcPof6pu3b9hlCoyVzwDRisvr626wOQ0pJzd7VHNzwGVJxk9ltHMlZ53YfyuMhpcRubcDSWIq9pRJLYyXNjZXYWuqQUjl8XnhEBOywy3gAACAASURBVBnpGXTqlE1mZibp6ekkJiYSHx9PQkIC8fHxxMTEqP3ijs95L9YCc/2WCxAhRB/gH0AwsA+YI6U0HysdGAPkA+8KIazAvcC9UsqpQojJwPtABKABCqWU2UKITsD/AXFAK3CzlHKnEGIi8DvAANQB10opq7wiKRnIBGqBa9rYGgosBKIAPfA7KeVCr9j6CvgJGAKUAZOllFYhRH/gdW/ZP51hHZ3uPcQA73nPX0ObBi2E+D1wLXDQe3/rpZTPtGc9nQ0OhwOz2Xx4q6ur4+DBgxQVFVFcXMz27dvZuXMniuL5wo+MTiOl0wjiU3sRFJzU4R4jKSVulw0pJTq98bx80PoCh93Cns3zqa8sJDyhM9lDZmAIOff6c50OQgjicwYRkdyF4tXz2b9tETXlW8jtcyXBAbBAfHsihMAYHOXto9fzcLridmFtqcVqqcblaMDe2kB5TR37ildht36J2+U4Zl5RUdHExMQQERFBVFQkERERv9hCQ0MxmUwEBwdjMpmOuQUHB2M0GtHpdGi12oDyMKscG9Wz5geOCoMWSSmnCCG2AHdLKX8QQjwBhEsp7ztB+jK8njUhhA7YI6XMEkI8A1wE3IdHjN8mpZwphPjO+3qPEGIg8Fcp5WghRBTQIKWUQoibgG5Syge9ImQiMExKaT3Kfh0QLKVsEkLEAj8DOUAGsBeP92qTEOJDYJGU8p2j7uNpYNxxPGs7gF1tkhOBZ7xC6nTv4QWgVkr5hBDicuBzPCIsE/gXMNhbRxuAeWdYxnHr6UTEJWZJxe3C7d0Utwu34t173x8LodFiCo7GGBJLaGQKYZGphEakYTCGnWrRZ0xrcxXVpRtoqN2HpbEcqRyyURAcnkB4dBbxKb0Jj85Sv/xPgbrKQvZsmo/LZSOtz3gSug2/4ESvlJK6ovUcWPcpistJRtdLSe104dVDW6SUuJytOO0WHHYLLkeL57XDgtPejNNhxeW04XbZjtgr7l8KvFNFaLRohAaNVotGaBEaDRqtzpOm0aLRahEarefXrhAIxOGfvp7X4hfHxOEThHcnPGcL71Xt+B3Rqe8czfKFvz6vxYzqWfMPVilln0NvhBARQKSU8gdv0pvAR8dLPzozKaVLCLFXCNENGAA8B4wAtMCPXk/YEG+ehy47FB9LBT4QQiTh8RoVtcl60XEEiAD+IoQYAShACpDgPVYkpdzkfb0eyDzGfbwNjDtO3ew7qm7mevdncg8jgKneOvpCCGH2pg8DFh66NyHEZ2dRxonq6bgomBB6HYYgz5egRqNFCJ1nr9Gi1QWh05s8myEYnd5EkCkCQ1CYzx9kjXXFHNi5mMa6/QihISQmnYTcIeiDIxAInHYLrfVlVJeup7J4FaaweNJzxhAXIOtEBhpul4P92z+j8sBqTJFJdBl6K8FRyf42yy8IIYjNzic8MZfiNfMpLvyC2oqt5PaeTkh44KwD60uEEOgNIegNIQSHJZz8Ai+K4sbtsuN22VHcThTFieJ24nZ79oc35dDehVQUpFSQ0n34teJ9TZvXh87xdN74ryaSSP7r8JF4IrttNJOU3nfSm6z893174Sn/N8BT7Zdp4KGKtfOHH/EIICfwLfAGHrH2EJ5waENbEdSGF4HnpJSLhBAjgbltjrUcp6xr8Xio+kspnd6+YIcmf7K3Oc8NmPCIu7NtnWd6D8cq93g/6dq7no5LXWXh6V7ic6qqqrjnnnv4ccWHmEIiyCqYRFRGf3TGY3e3dLvsmEu2UrVjGbs2vAfWbbz37pv07Xv+9r86XVavXs2sWbOoKtlHas/RJPa4FI1W/Ro2BIeTc9GN1Bdv5MC6T9m4/Hluvvk2nnryz0RGRvrbPJXA57wWauB5OKn4GSllI2AWQgz3Jl0H/HC8dO/rZqBt7Gs5ntDnKillDRADdAW2SymbgCIhxJUAwkNv73URePqWAdxwiiZHANVeoTYKT/jzRPfXADQKIYZ5k649xXLa5nEm97D8UFlCiHF4+tiBp8/cRCGE0etNu/wsyjgv+fTTT8nLy+PjTxaQ3ncc3Sc+TFyXi44r1AC0uiBis/PJG/8A2UOvYX9RMf3z87n/oYdxudptfMo5icvlYu7cuQwdOpSKajM9L7uL5N6Xq0KtDUIIYrL60XPib4jvPIh/znuF9IwsXnnlH7jdbn+bp6LiV1SxFjjcADzt7dvVB3jiJOlvAP8QQmwSQpiA1XhCkcu9x7cAW+R/fdTXAr8SQmwGtgOTvelz8YT9fsTTQf5UeBfIF0Ks8+a78xSuuRH4PyHEKuC0QoZtON17eBwYIYTYAIwFSgCklGuBRcBm4BNgHdB4hmWcV0gpeeqpp5gyZQpuXRi9Jz5IYveL0ehOfVSpEBpis/rTc+JviM3sx/PP/o1+BUMoLz/nZplpF3bv3s3QoUN5/PHHicnsS974BzDGZPrbrIBFbwwlY8A0uo+/H2GK4Y47bqdb9558+eWXbUJuKioXFuoAA5ULEiFEqJTSIoQIxiNwb5FSbvChCQHX8BwOB7fddhv//ve/icvqR8bAq9Do9Gedb+3+dRSv+RiTKZgvPl/IRSNGtIO1gY+Uknnz5vHggw+ioCFz4DTCU3r526xzCikl9Qc2Ubb5K2zNdfTtX8Bzz/yNkSNH+ts0lcDivB/RpIo1lQsSIcR/gDw8fe3elFL+1ccmBFTDq6urY+q0aSz/4QfS+1xKQvdL2nW0lrWxij0/vI6jpYEXX3qZO267ud3yDkQqKyv51a9+xZdffklMajeyh1yNMHT8iN3zFcXtonbfGsq3fYujtZHBQ0fw5z/OZeTIkerIYxVQxZqKikoHETANb/fu3YwfP56i4gPkDJtJRNqxxlecPU57C/t+fIumyr3cesc9vPzi39Fozr+eGAsWLODmm2+mqamZtP4Tiek0KCBHxUopcbSYsTXVYGuuxWVvQXE7kIqCVm9CF2QiKDQGU0QChpDIgLgHxeWkes9KKrZ/j9NmIa97L/7w+0eZNm0aOp3a/+8CRhVrKioqHUJANLylS5cydeo0rA4XXUbOwRid3qHlKW4XB9YuoGbvz4wYNZYvP/vkvFnwur6+nvvvv5+33nqLyPgMOg+7Bk1wrL/NOgK3w4a5dBsNZTtort6P09p0xHGh1QEC6XYeka4LCiYsoTPhiTlEpfXAYPLv8kiK20nd/nVU7lyOtbGaxKRU7rnnTn41Zw7x8efmgvcqZ4Uq1lRUVDoEvze81157jdtuuw1jWBw5o36FPtg3M+dLKanauZySDZ+RmZ3Lj8u+JTU11SdldwRSSubPn89dd91FbV0dKT3GkJg3xit8/I+UkqbKPVTvWUVDWSHS7UIXHE5oUjahSdkYoxIxRsahM4UhvJ5O6Xbjsrdib6zBVl9BS9UBmsv34rQ0gBCEJ3QmJqs/MZl90GjPvl/jmd+bQkPpdqp3/Uhj5T60Oh2TJl3B3XfdoYZILyzO+3+0KtZUVPyD3xqe2+3mkUce4emnnyY6tRtZQ69Fq/f9Qu8NpYXsW/EOwcEhLPn6SwYNHOhzG86W8vJy7rzzTj799FMi4zPIHnwVurDAmMxVUdz/9T41VKIzhhLZqTdRnfsSkph52mFNKSU2cxXmvRsw792Io6kOnTGUuM6DSMgd4vdF560NldTtX0PV3jW4HVaSU9K44YbruG7WLLp16+ZX21Q6HFWsqaiodAh+aXgWi4VZs2axcOFCkroNJ7XvRITGf4tDtzZUsGfZ67hszbz+739z/azTnoLPLzidTl5++WUee+wxWlqtpPW+jNjcYX6ty0NIqVBXvImyzYuxW+owxSQT13M4UTn9221eNykllrI9VG9dTtOBHQiNhricQSR3H+N30aa4nNSXbMZ8YAPm8t0gJd3yenDj7OuZPn06WVlZfrVPpUNQxZqKikqH4POGV1xczOTJk9m6bRtZA6YQ23mIr004Jk6bhX3L36Cpuoh7H/g1z/7tr2i1/hc9x+Pbb7/l3nvvpbCwkJi0bmQNmIrGFO1vswBoqtzLgXWfYm2owBidRPKA8YRn5HVoONDeWEvVxu+p270GITTE5wwmucfF6E8wgbKvcFibaCjZTF3xRpprDgCQ26UbV06fyhVXXEG/fv3Oy0EuFyCqWFNRUekQfNrwli1bxvTp02lptdN5+CyC43N8WfxJUdwuitfMp3bfWvoVDObzhR+TlJTkb7OOYNu2bfzud79j4cKFhEXFk9Z/EiEJXQOiX5TL3srBDZ9Rs28NhrAYkgeMI7JzH5+O4LQ31VG5fgn1u9ej0RlI7nExiV2HB8wqDbbmOprKtmMu3U5j1T6Qkrj4BCZNmshll17K6NGjiY4ODNGtctr4vxF2MKpYU1HxDz5peIqi8Pzzz/Pwww8THBFPl5E3IgLEC3Q0Ukpq96/lwNoFmEzBvP3Wv5lyxRX+Nos9e/Ywd+5c3nvvPQxBJhLzRhHfdThC47+O9YeQUmIu2ULx2gW47C3E976IpP6XotEb/GaTzVxF2apFNJXswBAaTVrfCUSn9woIUXsIp72FxrIdNJcXUl+2E7fTjhCCnr36MH7cpYwdO5YhQ4YQFHTqK3eo+JXA+XB1EKpYU1HxDx3e8CorK5k9ezZff/01sRm9yB4yA7SB//CxNlSyf8U7tJgruHziFbz26j9ISEjwuR1r1qzhueeeY/78+Wi0OhK6DCOx20g0hmCf23IsHK2NFK/5mIbS7ZhiU0m/6EqC49L8bdZhmg7uomzVImz1FYTGZ5ORP5mQ6MAb9SsVN5a6Elqr92Iu20VzzQGkVDAYgsgvKGD0qJEMHz6cwYMHExamTmwcoKhiTUVFpUPosIYnpeT999/n3nvvpaGhkYyCyURlDQwoz8bJUNwuKguXUrb1G4xGIw8//DAPPfhAh8/JZrPZ+PTTT3nppZdYsWIFQaYQYjsNIClvJBqD//tggWcAQc2enzm48QsUxU1SwaXE97ooIAY3HI1UFOp2rqZizZe4bK3EdR5Iap9xAdGf7Xi4HTaaqvZirSuioWIflvpSkBKNVkvPnr0YNfIiRowYwbBhw4iLi/O3uSoezp0vtzNEFWsqKv6hQxrejh07uOeee/j222+JTMig05CZaEPO3QeKtbGKss1fUl+yjcjoWB64/15uveWWdp341OVysXLlSv7zn//w/vvv09jYSEhELAldhxOTXYAIIG+ktbGaotUfYaneT2hKDunDpxMUGfj/X5fdSuW6r6nZ/hNanYHknmNJ6DIMTQAKzKNxO21Yag5grT9AY+U+mmuKUdwuANLSMxk2dAhDhgxm4MCB9O7dG4PBfyHoCxhVrKmoqHQI7drw9u/fzxNPPMHbb7+N3mAktc94orMHHp7k9FynubqIym3fYC7fhU6nZ9z48Vx91ZWMHz+eqKjTm8xXSsmePXtYtWoVS5Ys4auvvsJsNqPTG4hO70Vi7kCCojIDqu48nsZllG1dgkZvIGXQJKK7DjinvKXg6c9WuuJTmkt3YYyIJ73/ZCKTu/rbrNNCcbtoqTuItf4AlpoDNFYXH14JQm8w0LdvP4YOGcygQYMYNGgQaWlp59z/6RzkvK9gVaypqPiHs254iqKwdOlSXnrpJRYtWuTpV5U7lOQeoxH6wOhX1d5YG6uo2/czNUWbcFqbEEKQk9uFwYMGkZubQ1paGrGxsQQFBaHVamlubqaxsZGqqir27t3Lnj17WL9hA+b6egCMweGEJ3clLqMnxthstHqjn+/wl1hqSyj6+UOsDRVEZvcmdegV6EP8O5fZ2SClpKmkkLIVC7E31RKRkkdG/0kYwwPfQ3gspJQ4WhtoqSvBbi6loaqIlrpSFO+SXbFx8RQU5JPfvz99+vShT58+ZGVlqQKufTnvK1MVaz5CCCGBd6SU13nf64AKYLWUcsIZ5FcM5Espa49KnwTkSSmfPHurfcMJ7qUYaAbc3qTlUsp7hBBvAJ9LKeefZjmZwBAp5X+OczwZeEFKOf108vVee7o2nVHDs1qtrFq1igULFvDxxx9TUVGBMSSc2E4DSMgditbo+zUbFbcTp80CgN4Y5pOpGqRUsNSW0FK9B0vtQZprS3Bam094jcEYgjEsFmNEIlFJ2Zii0tCHxQXEAuXHwu20U7p5MVU7f0QfEk7asKlEZPX0t1nthuJ2UbNlOZUbvkG6XSR0HU5Kj0vQGgJPMJ8uiuLGai7HWn+QlroSmmpKsDZVg/d5GxIaRq9evcjv34+8vDxyc3PJyckhJSVFnfftzFDFmkr7IISwAHvwiAWrEGIc8FegtD3FWnshPD/7hJRS6Yj8jyqrmOOLtWOlv8GZibWRwEPHqm8hhE5K6To9y8/KphM2PCkl9fX17N69m8LCQrZv387q1atZu3YtTqcTnd5AZEo34rL6EJLYzafrM0opsdQeoL54E43lO7FZag8/hEBgikwkPCmXuOwCgqN8N1ea2+XA0dqI296KorhAKmh0QWgNJvRBIeiCzh1vY0P5TopXz8fRYiY2bwjJAy9HG+T7JcF8gbO1ifLVX1C/ay06YxipfccTl50fsCL6TFFcTlobKrA3VWBrqKCp5iCt5nLcLsfhc4KMRjp16kzXLl1IT08jNTWVlJQUUlJSSE1NJT4+nuDgYNUr90vO+wpRxZqP8Iq1F4ANUsr5Qoi3gO3AcCnlBCHEAOB5wARYgRullLuEEFrgKeBSPA/4V6WUL3qFzJvAREAPXCml3CmEmI1H4NzlFRBNQD6QCPzmkJgQQvwauAoIAhZIKR/zep6+ApYCg4FPgUgp5f3ea24GukkpHzjq3l4BCry2z5dSPuZNP56NMcB7QBywBrgM6H8mYk0I0R94DggFaoHZUsoKIURn4B/eMtzAlcC7QDegyGuXGbgcMAIhwBxvvj1OUO9/8N6PCVgJ3CqllKcr1gZfNks6HTacDhtOuw2X047TbsPa0kRLcz2tzQ2HOzEDaLR6gqOSCUvIJjw+m9CETmh1vu/43lS5l9LNi7HUFCG0OsJScgmOTUEfGgmA09KApaqYlor9SMVNWGJn0vpcTmhsus9tPRdx2iyUrF9EXdF6giLjSR9xJaHJnfxtlk9oqS6h9KcFtFYfICQmjYz8KYTGZfjbrA5FSgVnaxO25hrP1lSLrakaW3MtjtZGlDZC7hAajRaDKZQgUwjG4FCCTKHo9UFodXp0egNavQGdznD4vUarRQiNZ9N49hqNBoRAcyhNo/EKwONrnjMRiCe+5gTHTrOoxe88fd6LtcCYWvrC4X3gD0KIz4FewOvAcO+xncAIKaVLCHEx8BdgGnALkAX09R5rO6NprZSynxDiDuAh4KZjlJkEDAO6AouA+UKIsUAOMABPs1gkhBgBlABd8AjFO4QQIcAWIcRvpJRO4Ebg1mOU8T9SynqvwPlOCNFLSrnlBDY+BvwkpXxCCHG59x6Px1IhxKEw6JtSyr8fOiCE0AMvApOllDVCiKuBP+MRXe8CT0opFwghjIAG+C1tPGteYTsY6OW1P7NNucer95eklE94r38bmAB8dgL7j8nPX78LgEZnQKsLQqMzoNEZ0BtDCYrKICy5J/rgcIJCojFFJhIUEu3XDu9tRYQ+JJLUoVOIzs0/rrfHZWuhbudqqjcvo3Dx/xLbqYD0/pPRGc5P79DZIqWkrmgDJesX4nbaSOx3CQl9x/h1cltfExKfTu6UuzHv3kD56s8p/PoFYrL6k9b3cr+vN9pRCKHBEBKJISSS8MQjVxWRUuJ22nC0NuJsbcTR2oDT3oLb0YrLbsXlaMXqsNJsqUZxOVDczsObdLuQivs4pZ5/DBRJl6x++4Fv/G1HR6KKNR8ipdziFQQzgS+POhwBvCmEyMHjyTkU17oY+MehEJ2Usr7NNZ949+uBqccp9lNvKLNQCHFoZtGx3m2j930oHvFWAhyQUv7sLatFCPE9MEEIsQPQSym3HqOMq4QQt+D5PCUBecAhsXYsG0ccei2l/EIIYT6O7QCjThDq7QL0AL7x/oLTAhVCiDAgRUq5wFuGDY77K++bo+r0EMer91FCiN8AwUA0Hu/oaYu1txauYPW2UoKCDBiD9ISY9ISYgggPMWI0BFaz3LF1Ay88+ReaGhtI6j+W+L5j0OhOHHbVGUNI6DOa2LwhVG38lqpNy7DV7eee3/yJHn0KfGT5uUFVRSmvv/RX9m9cTVhiJukXXY0hyveTAAcCQmiI7pJPRHZPqjd+R9WmpTSVbWfy1TcyYdosDIbAmUYlUHC43LRYHVhtDmwOFzaHE4fTjc3mwGqz4nQ4cLrcOF0uXC43ituNS1FQ3J7XbkVBKm6klEjpEYmH+O9r2eZvG04QmJNnOobqNKN9piA9ZhfH+g4/rwisp8KFwSLgGWAkENMm/Y/AUinlFK+gW+ZNFxy/Sdi9ezfH/1/a27wWbfZ/lVLOa3uit9yWo67/F/AoHs/fv4/OXAiRhcdjViClNHvDgW17CB/PxvaIvwtgu5Ry8FE2nU4v+6Pvt23eR9jo9dC9jCc0e1AIMZcj7/WUuW7SEK6bdCZX+g4pJc8++yx/efS3mCLj6Hn1Q2gjTk9EaA1GkgdOICKzJyVL3+Ovv7uTPzz+Rx77n0cu+H43DoeDZ599lieeeAIpNGRddCURXc6f6VbOBq0+iKQB44nuOpDKnz9j/tuv8NN3n/H0U08yc+YMtNrAn59Nxaes97cBHY36reB7XgeeOIaHKgIo876e3SZ9CXCbd/QoR4VBz5SvgTlCiFBvnilCiGPOMiqlXA2kAdfg6Wd2NOF4BE+j13M37hTKXw5c6y17HHB6E2X9l11AnBBisDcvvRCiu5SyCSgVQlzhTQ8SQgTjGVl6quvFHKveDwmzWm/dnfao0XMFt9vN7bffzq9//Wsis3vR+Yp7T1uotSUkIYPcqfcRkdGdx3//P4yfPA2bzdaOFp9brFy5kv79+/Poo48SmtaVvKt/S2S3wapQO4qg8Bgyxs6m04TbaLIrXHfdLDrlduX9999HUTp87JOKSsCgfjP4GCllqZTyf49x6G/AX4UQK/CE8w7xLzzhyS1CiM14RNPZ2rAE+A+wSgixFZjPiUXMh8AKKeUvwpVSys14wqnb8QjRFadgwuPACCHEBjzh2JITnLtUCLHJu711VNkOPILpKW/dbAKGeA9fB9wjhNiCZyBAIp7QrEsIsVkIcf9JbPxFvUspG4BXga14Bl+sPYV7Peew2+3MmDGDefPmkZw/lrTRsxD6sw8/aQ1GMsfeQFLBOBZ/toB+g4ZhNp8oAn7+YTabuf322xk2bBhFpRV0mXAzaWOuhwBefikQCE/NJXf6A2RefD3VDRZmzpxJ5y7d+PDDD1XRpnJBoI4GVTkp3gERf5dSfudvW84jArLhNTc3c8UVV/D999+TMXwK0d2Hn/yiM6B+z3pKlr5PfEoaq3/8gYyM83u0qNvt5rXXXuPRRx+l3mwmodcIkgouA+2FM4CgvZCKQsP+zVStX4LVXEVGdid+98hvue666wgKUvu0XaCc930qVLGmclyEEJF4ptbYLKW80t/2nGcEXMOrqalh3LhxbNy4kewx1xDWqV+Hltdctoeir/+NKTiYZd99S/9+fTu0PH+xcuVK7r77bjZs2EBkWg7pw6aeVUi5I5CKG2dLEw5LAy5rs3dEoRuNTo/WYEQXHI4xMg6NLnDEpVQUzPs2UbtlGS01pUTFxPLgA/dz5x13EBkZ6W/zVHyLKtZUVFQ6hIBqeCUlJVxyySXsLyqm82WzMaX4Zr1Ga105+798Fel2sOCTT7h83GU+KdcXlJeX8/DDD/POO+8QEhlD8qCJhGT09PvACiklNnMllvK9tNaU0lpbht1cdQpTPQgM4dGEJGYTltKZ8PRu6E3+D99KKWku3U3t1h9oLNmJ0RTMDbNnc989d9O167m17qjKGaOKNRUVlQ4hYBpeYWEhY8eOpabeTM7lN2OI9e1EpA6Lmf1f/gtbQzUv/t/L3HnbiabdC3yam5t59tlneeaZZ7DZHST2GUVc39EIP4Y8XXYrTQe203RwJ82le3B5l+bSBodiik/FGJeMISIGfVgkutBwNDo9QqtFcTpR7FaczY3Y66uw1ZTTUroft60FNBrC07oSnVtAZFYPhMb/IzRba8uo2/oDdXs2IhU3g4cN56H772PSpEnodOrkB+cxqlhTUVHpEAKi4a1atYoJEyZgdSrkTLjVb+E5t91K8Tdv0lS6mwd+8wjPPPlnv3ugTheHw8Grr77KE088QXV1NbE5fUkZPAFN8JkOdj47XPZWGou20bB/M82lu5GKG21wKKFpOYRm5BKSnoM+POq061lKBVt1OY07N9KwcwMuSyOG8Gjiel1EbNdBJ52Dzxc4rc2Yd66hpnAljmYzsfEJ3HH7bdxy882kpKT42zyV9ufc+rI4A1SxpqLiH/ze8L744guuvPJKtKZwOk+4BeEnUXEIxe2idPlH1O1ay6RpVzH/vXfQ6/3/4D8ZiqIwf/58Hn30Ufbt20dUei6pgyaii/a9KJBSoblsL3U7fqaxaCtScaMPjyIipzfhub0xJaW165qbUlFo3redmrVLsVYUow+LInnA5UR17hMQa3tKRaGppJD6HatoOLADodEwctQY7rjtFiZOnKgOSDh/UMWaiopKh+DXhvfWW28xZ84cQuNT6TTuJqQhxJ/mHEZKSeX6JVSu+5ruffrzzZefkZTku8XgTwe3280HH3zAn//8ZwoLCwmPTyVl8ASCEnN87hV0WS3U7viZuh0/42iuRxtkIjIvn4hu/TElpvnEHsuB3VT+8Bm2mjKC49NJG3ElwbGB48WyN9bSsGcdtTvX4LA0EB4RyfXXX8fNN91Er169/G2eytmhijUVFZUOwS8NT1EU/vSnP/HYY48RndGVjEtuAD8sCH8y6ves5+APHxEcEsLCTz5m9OhR/jbpME6nk3fffZe//OUv7Nmzh/C4FBL6XewZPODjSW1tDdXUrGHBywAAIABJREFUbFlO3a41SLeLkLQconoOJDynp1/CkVIqNBSup3L5Z7htrST0GU1iv0sCIjR6CKkoNJftpmH3Wur3bUUqLvJ69uL2W25m5syZxMTEnDwTlUBDFWsqKiodgs8bnsViYfbs2Xz88cfEdRtAyvDpCE3gdrq21ldS/M0b2Btruff+B3jyz3/ya9iqpqaGf/7zn7z88suUl5cTnpBGUv5YTKndfB7ys9aVU7HuaxqLtiE0GiLz8onpPxJjbGBMCeKytlC5bBENhWsJioonY8wsQmJT/W3WL3DZWmjYu4G6nWtorS1Dq9Uy5pKxzJl9AxMnTiQ4ONjfJqqcGqpYU1FR6RB82vB27NjB1Vdfzbbt20kfMpmo7sPOiQ78boeNspWfUrdzDenZnfnPW28wdOhQn5UvpWT16tXMmzeP9957D7vdTlRGNxJ7X0RQku/DnbaGairXfY157yY0hiBi+g4nps8wdKGnuoqab2ku3knZ4vdx21pIGjiB+J4jAvZz11pbRtO+jdTuXo+zpRFTcDBTpkxl9g3XM3r0aHU90sAmMD9U7Ygq1lRU/INPGp6Uknnz5vHAAw+AVk/mmGsxJuX4ouh2pbFkB6XLP8JhaeCy8RN4/rln6NKlS4eVV1RUxDvvvMPbb7/Nnj170AcZicrNJ6nXCDRhsR1W7vFwWS1UrF1M7Y6fEVodMf2GE9t/JLrgwOhreCJcrRbKlnxA877thGV0I2PkDPSmwBSX4AmTWir20bRvI3V7N+F22IiOjWPWNTO59tprKSgoCFjBeQFz3v9DVLGmouIfOrzh7dq1i7vuuotvv/2W6Mw8MkbNgCD/T2J6priddmq3LKdy0/coLgeXjL2UXz/4AGPGjEFzln3FFEVh/fr1fPbZZ3z++eds3LgRgMi0XGK75BOS0QON3tget3FaSMVNbeEqKtZ+hdthJ6bPUOIGXowuJHDFzrGQUlK/aQWVPyxCawwm8+IbCEvK8rdZJ0VxOWkqKaRx30bMRduRipv4xCSunD6N6dOmMWzYMHX+tsBAFWsqKiodQoc1vPr6ev72t7/x3HPPodEZSBownsiuAwNiKoX2wGltpm7bT9QUrsJltRAdG8eUyZMZN+4y+vfvT0ZGxgk9H4qiUFpayq5du1i7di0rV65k5cqVmM1mhNAQnpxFREZ3Ijv1QRviv2WLWqoOULL8I2x15YSk55A0agrG2ES/2dMeWKvLOLjoDRzNZlIGTyKux/BzxkvlsrfSdGA7zcXbaTiwA8XtJCIqmilXTGbqlCmMGjWK0NBz98fQOc658SE6C1SxpqLiH9q94ZWXl/Pyyy/zwgsv0NzcTFzXAtKGTAqYaTnaG8XlpKFoKy0l26kvLkRx2gEIDQsnLTWVlJRkQkND0Wq1uFwu6urqqK2to/hAMTar9XA+obHJGOPTiU7LxZicgzbIv/WluBxUrP2a6i3L0IdEkDhyMuG5vc4ZUXMy3DYrpYv/Q/O+7UTm9CV9xFVo9YE3IvlEuJ12mkt2YinZRt3+bShOOzqdjgEDB3H5+HFceuml9OnTR+3n5jvOj8ZxAlSxpgKAEEIC70gpr/O+1wEVwGop5QQhxCQgT0r5ZAfbsQx4SEq57hjpSYANsABzpJS7zrCMuYBFSvnMGVx7H/BPKWXrmZTdhnZpeC0tLSxZsoS3336bRYsW4Xa7icnpS+qAS9GExbdHEecEituFtbYMR305NnMl9uYG7C2N4HaBVECjQRsUjDYoGFN4NCHRiRgi49CGx6MzBo6YtVQWUbL0feyNNUT1HETiiElojb4Pv3Y0UirUrvmeqhVfERSVQNbY2Zgiz83Pq+J20VKxn9aKvTQc2EFrbRkAIaGhDBgwkOHDhjJ48GAGDhxIVJR/J54+j1HFmsqFgRDCAuwBhkgprUKIccBfgVIp5YR2LEfg+dwpxzm+jOOLtYeklOuEELcAE6SUk446RyulPNlq1Gcr1oqBfCll7eleexRn1PBsNhvr169n1apVLFu2jO+++w6bzUZQSBjRuQXEdx+CJjT6LE07NRSXA2tdBfbGGhSnA40hiKDwWIJjUxGqR+G0kIqbirVfU7XxO/RhkaSMvZrQzFx/m9XhWA7s5uAXbyPdLtJHzSQq69yfnNbZ2oylbDe2mhKayvbRWl8B3udsYlIyvXr2pHfvXvTo0YPOnTuTkZFBUlLSWfe7vMBRxZrKhYFXrL0AbJBSzhdCvAVsB4Z7PWuz8YiUu4QQbwBNQD6QCPxGSjnfm8+vgauAIGCBlPIxIUQm8BWwFBgMXAH8FigATMB8KeVj3uuXcXKx1hX4REqZ57X7OeBS4EFgADDHe9m/pJTPe6//H+B64CBQA6yXUj5zVL6xwDopZaYQQgs85c1XAq/i+UJ4BtgF1AIXA69560ECr0sp/36KVS4BXC4XNpsNq9V6eG82m6mpqaG6upqamhrKy8vZvXs3u3fvpri4GEXx6NyQ6HhCU7sS27kX+pgMnwgkKSVNJTuo27mappIdSLfrF+do9AbCM/KI7TaE0ORO5034rqNwWMwUf/sOLZVFRHYfQNKoK9AGnX/etOPhaDJzcNEbWKsOEt9nFMkDxgfEovDthdtho7W6BEd9Gdb6Siw1Zdgaqo9oO3q9gZTUVDIzMkhMTCAuLo7Y2Fji4uKIiYkhLCyMkJCQX2xGoxGdTodOp7vQxd55/yWjDmNRacv7wB+EEJ8DvYDXgeHHOTcJGAZ0BRYB84UQY4EcPIJJAIuEECOAEqALcKOU8g7wiCcpZb1XFH0nhOglpdxyinZOBLZ6X4cA26SUfxBC9AduBAZ6y18thPgB0AAzgL54PvMbgPUnKeMWIAvoK6V0CSGivfY+AIySUtZ6y0uRUvbw3tMp90bXB5lwuxxI5ZgOxiPQ6IMIiogjKDKO+L4XExyXSnBChs+nP7CU76N01UKsNaXogsOI6jmI0LTOBMUmojEE4bbbsNdWYCnZQ+OuTTTs3URIUjYpgyYSkpDRbnZY68qxVBThslnQGUMJTc7GFB2YS1KdjMYDhRz4/j9IxU3quGuJzOvvb5N8jiE8iqwZd1O59FOqNy3FUlVM1pjrMIT6b3BHe6I1GAlLzYXU/3pKpeLG3liLvbkeZ7MZh6WehqZ61u4owrVhKy5bC26H9QS5HgMh0Gi0CI0GodGi8e6FEOD9wSQOaZrD0sabLo6XfkQBtE0MJHWUc9VvjRteud/mbzs6ElWsqRxGSrnF6wWbCXx5ktM/9YYyC4UQh6ZNH+vdNnrfh+IRbyXAASnlz22uv8obztThEX55wMnE2rtCCCtQDNztTXMDH3tfD8PjzWsBEEJ8gkdsarzprd70RScpBzxes39IKV0AUsr6Y5yzH8gWQrwIfAEsOYV8AYjtNgip0aHR6RFaz16j1SG0erRBJnSmUHTGUHSmkMOdrzVC4A8nlctupXTVZ9QWrkIfHkXK2KuJzMv/hSdPHxqBMSaBiC59SBo5GfP2tdSsWsLuBS8Q33sEqQPHo9EZztiOlqoSSlYsoKWy+BfHQpKzSBs8mdB2FIUdieJ2UfbzF1RtXoYxLpm0CdcTFH1u9tlqDzQ6HcmXTCc4NYvyb+az8+NnyRpzDZHpef42rWPQ6NDFJBISc+ToXgkoiifaJd1uXPYWXLYWFKcdxelAcTlwe/eK04F0u5BSQSpukApSObS5kVIBReFwj5OjomjyUE8M2bb0Y7w/Ikn+4liAcCvwv/42oiNRxZrK0SzCE+obCZxokTx7m9eizf6vUsp5bU/0CsCWNu+zgIeAAiml2RtWPZW4z7VHh0cBW5t+aieSMsf7dnHhEXMcZYM4wTWeDD2298YTKr0TT/h3zomuOUTFpqWncprf2bp1K1OnTqVu/34SBowmdtAliFMYuafRG4jpM5TIvP5U//gF1Zt+QGs+wDdffkH37qf3AJZS8tRTT/HoK88TFB5ByuXTMObkoQ2LwNXciGXHVupXfMfOT/6X3/7+D/xl7mMBHXotKipixowZVG1eQ1y/YcQNnxhQa2f6k8hu/TElpFH6+Vvs/fxV7rrvAf7+9FPqXGYqJ+O8Fmrw34eUisohXgeekFJuPemZv+RrYI4QIhRACJEihDiWuyAcj3hr9Hrlxp2xtUeyHLhCCBEshAgBpgA/etOnCCFMQogwPGHUQxQDh2JP09ukLwFu846KRQhxqNd+MxDmTYsFNFLKj4HfA/3a6T4Cgvfee4+BAwdSWl1L7sy7iRs+4ZSEWlu0BiNJY6aROf02amrr6Nu/P+++/8EpXy+l5Pbbb+eRRx4homdf0m9/mND8oegiohAaDfqIKKIGjSDzrkcIz+vDk088zuSZ1x7u1xdofPLJJ/Tt25dNW7bRacqNJIyaqgq1owiKjidr5j1E9xrMS88/R98BgygqKvK3WSoqfkUVaypHIKUslVKe0a8UKeUS4D/AKiHEVmA+XmFz1Hmb8YRKt+MRhyvO3OIj8t0AvAGsAVbjGWCw0Zv+AbAJT8j0xzaXPQPcLoRYCbRdR+hfeMK3W4QQm4FrvOn/BL4SQiwFUoBlQohN3nIfaY/7CASefvpprrnmGgxxKXSedT/6xLMLL4Zm5NJp1v3ooxOYNXMGDz7yP5xscJOUkgceeIB58+YRP+Ji4q+4FnGchdy1QUYSp80ietgYPvvgPabMuv6k+fsSm83G3XffzbRp01BCosi54UFM2T39bVbAotEbSL7kSlLHX8uOwu10zevO/738SkD9T1VUfIk6GlRFxT8EZMNTFIWHH36YZ555huhu/UgaOwPRjiEoxeWkfMkHNOzYwLRrruODt/593IlDn3/+ee6//35iB19E9CWTTim0KaWk5tvPMa9cyoN/eJxnHv9Du9l+puzZs4cZM2awYcMGEgpGEjN0PBqtGtY7VRxNZiqWvE/zgT0MGzWaD955m+TkZH+bpRJYBG6/h3ZCFWsqKv4h4Bqe0+nkpptu4q233iKu33DiL5qM6IDpAKRUqPrxS2rXfs/gUWP47ovPMJlMR5yzfPlyRo8eTWhudxKuvP60lsqSUqH8wzew7NrOfz5ewMwpk9v7Fk6Zd999l9tuuw2nhLTLZmLM7OY3W85lpFQ8a4su/xyj0chTTz7JHbfdqq4QoHIIVaypqKh0CAHV8FpbW7nqqqv44osvSBo2jugBF3d4J/26DT9SsfRTOnfvyc8/fE9MjGc8S11dHT169KBZgZQ59yDOYM4xxWHnwL+eB7uNol07SU707ZqaFouFu+++mzfeeIOI9M6kXT4LgsN9asP5iL2+morv5mMp2Uu3nr146/XXyM/P97dZKv7nvBdrap81FZULnPr6ei655BK+/PJL0i+9ipiBl/hkNGVMv+GkTbyefTsL6da7L/v37wfgzjvvpKa2lpTpN5yRUAPQGIJImjoLZ4uFMVOm+7Sv0+bNm8nPz+fNN98kaehlpE67VRVq7URQdDwZ028ndfy17N1fTMGAAcyafSPl5eX+Nk1FpUPRzp071982qKhciMz1twEAZWVljBkzhs1btpI56XpCu/p2UlZjTCIhqZ2o3LiSf/7rNZAKL77wAgmjxmHsdnYd8HWh4QidgZLl3+I0hTBm2NB2svrYuFyuwwMzLHYn2VN/RWi3/NMK4aqcHCEExrhkonoORLhd/Pz1Z7z44kvUNzQwoCD/FyF1lQuCx/1tQEejhkFVVPyD3xvejh07uPTSS6mqrSNr8hz0Kdl+s8VeV0Xx/Hk4LQ2EpKSTMufudllySEqFg2++gqO6nN07d5GdntYO1v6SnTt3Mnv2bFavXk101z4kXzwdgoI7pCyVI3E01FH789fUb1+PKSSEO++4gwfuv4+kpHNzVQuVM0INg6qoqJx/rFy5kqFDh1Lb2Eznq+/0q1ADCIpJICS9MwhBzGVT221tSCE0JEyYjuJwMPn62e2SZ1scDgd/+9vf6NOnD5u3FZI96QaSxl+nCjUfYoiMIfmya+h8/YMYUzvxzNNPk56ewawbbmDr1jOZLlJFJfBQPWsqKv7Bbw1v4cKFzJgxA31YJBnTboWQCH+ZchhrdRn73nmOyIKhJIyb2u751y5bTN0PS/jHu+9x6zUz2iXP7777jrvuuoudO3cSlduLlIungym0XfI+13A7bLhtnrUsNVod2uAQv4V/7eYaGjYup3brGqTLSY/efbjztluZOXMmERH+/6yrdAjnvWdNFWsqKv7B5w1PSslf/vIXfv/73xOWkknGFTchg/zfv0dKSdEHL2E3V5N15yNog9vfK6W4nBT/4xl0QPWBIkJDQs44r3379vHoo4/y4YcfEhoTT9KoKQRldGk/YwMcxenAUrwTS8lerFUl2OuqUBz2I0/SaNCHRWFKSCU4OZOwrG4+X/vUZW2hacd6zNvWYK0pR28wMHrMxcy46komTpx4ePSxynmBKtZUVFQ6BJ82PIvFwpw5c/joo4+I7VFA4pjpECDLHDXsWE/pl++SMOEqIvsP6rByWov2cPCtV5h0400sfP3V076+rKyMP/7xj7z22msgNMQNHENM/ii4ACa4lVLSUrKH+s0raS7agXQ5EXoDxqRUghKT0YVFog0ORiBQnA5czU046muxVxzE2VAPgCE6nshu/YnqMRB9qO9Gx0opsVWV0rxrA+bdW3A2mdFotRQMGMj4yy5l9OjRDBgwAIPB4DObVNodVaypqKh0CD5reGvXruXaa69l7759pFw0iYi+wwNmoXO3w8ae159EFxFB+k33dnjorPyTd7AUbmH1+vUU9O51StcUFhby97//nbfffhuX2010r8EkDLrkggh5SsVNQ+F6atZ8j8NcjTY4lLDufQjt2pPgjGzEKUxK62w0Y9m5jeYdW7Ae2AcaDeGdexJbMIrgxHQf3MV/kVJiqy6lZd92mop20FpVClISZDQxaPAghgwaRH5+PgUFBaSmpgZMO1E5Kef9P0oVayoq/qHDG57dbuepp57ij3/8I0FhEaSOvwZ9YlZHF3taVC7/jNq1S0mfcy+mtLNbf/RUcFmaKHrpSdK7dWf/hrXHfRjb7XY+//xz/vWvf7F48WJ0egOR3QtIGDQGERLZ4Xb6Gykljbs2Ub1yMQ5zDUGJqUQNGkFY9z5ozmL5MUddDQ3rV9G4cTWKzUpIZhfiB15CSKp/Bri4ba20HNyHvWwfTaX7sdWUIxUFgOiYWPr27UPPHj3o1q0beXl55OXlER0d7RdbVU6IKtZUVFQ6hA5teN988w133XUXu3fvJiavP0kXTwP9mU0w21HY66vZ++bThPXsR9IVM31Wrnn1cqoXf8qz817lgVtuOpxutVr54YcfWLBgAR9++CENDQ2YwiOJ6j2U6F6DwHjm/dzOJWw15ZR/9zGtZUUY4pOIHXkZoV17tKuXSbHbMK9difnnZbhbLIRmdSVx+ASMcf5d81NxObHVlOOsKcNadZCWqnLs9VUoTsfhc2Ji4+jarStdc3PJycmhc+fOh7eQs+gLqXJWqGJNRUWlQ+iQhvfTTz8xd+5cvvvuO0JjE0gePRVDWk5HFHVWSCk58MmrtFYUk3XnI+jCwnxXtuLmwKvPI2ytfPj2WxRu387y5ctZunQpVqsVnSGI8M49iOs1EF1SdoesjxqIuO02qld+Rd3GFWhNJuLGTCC8b0GHhqYVp4OGNSuo++lbFJuNiLz+JAy9DEN44HivpFRwNjVgr6vE3ViLvbaS1roq7OZaXK3NR5wbF59ATm4OXXNz6dy58xFiLjT0/A+b+xFVrHVYwUJI4B0p5XXe9zqgAlgtpZwghJgE5Ekpn2yn8t4APpdSzhdCLAMeklKua4+8OwohxFzgMSBHSrnXm3Y/8BxQ0N72CyHuAW4HNkgprz3Na+8D/imlbG1Pm9rkb5FSHvPbTggxBfgE6Cal3HmccyKBa6SUL3vfJwMvSCmnn6DMZXTc56TdGp7VauWjjz5i3rx5rFy5ElN4JDH5I4noORgRIIMIjqZp7zZKFr5O3NjJRA++yOflWw8WU/L6CxjiEnHUVBIck0BIRi7ROT3QJmSg0V9Ync1bDu6ldPF7OJsaiMwfTOyocWiDfeclcltbqf/pO8yrfwQk0X2GETfwYnSmwPZUue02HA21OBtqUZrN2M3VtNbX4DDX4mxpOuLc2Lh4cnJy6JKbQ05ODp06dSI7O5vs7Gyio6PV/nFnx3lfef4cxtQC9BBCmKSUVuASoOzQQSnlImCRv4wLILYCM4A/ed9PBwo7qKw7gHFSyqIzuPY+4B3glMWaEEInpXSdQVlHMxP4CU89zT1GOVogEs/9vQwgpSzHU5fnJNXV1SxZsoRFixaxePFimpubCY1LJG3MVMJ7DEDoAldsKC4nFcsWYohNIGrAML/YYErLJKLPABq3rCNz5t2EJgdWXz5fobhcVK/4itp1y9BHx5A+525MaZk+t0NrCibukolEDhhG7bKvqVu/HPO21cTmjyKm33C0hsAK4R9CG2TElJCKKSH1F8fcDhuOhjqvkKvHbq5la0kl67ZsxWk5UsiFhoaRmZ1FbufOhwXcoS0jI0MdqariV7EG8BVwOTAfzwP3PWA4gBBiNpAvpbxLCHElHg+TG2iUUo7wPoCfAi7F46V4VUr5ohCiPx7PUyhQC8yWUlYczwAhxCtAAWAC5kspH/OmFwNvAhMBPXCllHKnECIEeBHoiaf+5kopFwohjMArQD7gAh6QUi5tex/efD8HngF+BF7zni+B16WUfz+GiZ8Ck4E/CSGygUbAeRb2zwUsUspnvOdtAyYAvwWygUVCiNeBFcDz3nytwI1Syl3Hqnc8v2qSgaVCiFop5ai2njAhxPT/Z++846Oq0v//PjOTSe+dANKbdBApShEBQaWrlBWwY2F1lXVX3f2tZfl+7bt+dXXXBvayFkCpgvRO6F16CSSkTSZtyr3P74+5YAyBBMkwSbzvV+Y1M+fee85zb+bM/czzPOcc4CYRmWR4OHOBTsAmpdSbwL+ARHxC7x7DzsbAp8Y1nn+B/18E0Avoh0/cP22U98X3mTkJdAS2AU2VUluAH4w2vxeRtuf7LJVrZyC+9eeCgQPG9ShUSj0PDMX3P18oIlPPZ+vFIiIUFRVx+PBh9u3bx759+9ixYwdr1qw5u+h5SFQM4Y3b0qptV6wpjWrFr/PsjUvxOHKo/7vJVRpN6C8Srr8J557tZK2aS/joB2rFtatOSk9ncGzuJ7iyTxLdpSdJA27GEhwcUJuComNJHTaGuB59yP5xHlmr5pGzeQWJ3foT16EnlhrqKa4Iqz2E0KQ0QpPSztmme1y4Hbl48nOQwnzcjhyO5p1m/7JVuGfPRvf+/BvWYrGQkJhEar1UGtavT2pqKvXq1Tv7HB8fT2xsLDExMcTGxhIc4P+hiX8ItFj7HPh/hoBpD7yPIdbK8f+AQSJywghnAdwLNAY6iYhXKRWnlArCJ6SGichppdRtwDTgzgvY8JSI5Bo37MVKqfYiss3Yli0inZVSDwBTgbuBp4AfReROw5b1SqlFwGQAEWmnlGoFLFRKtbhAux2BNBFpC2fDdBVRABxTSrXFJ9q+AO64BPsrREQmK6VuAPqJSLZSKgrobVzb64H/AUZRwXU32n/0zLEXOOcztACuFxFNKbUYmCwiPymlrsbn+boOeA14S0Q+VEo9eIG6hgPzRWSfUipXKdVZRDYZ27oBbUXkkFKqkfG6I4Dx/gznnFPZBpRSCcBfDJuLlFJ/Ah5VSr0BjABaiYhc4H94Dh2HjMbrdqN5zjw8eD1uvG4XriInJU4HrsICNI/nF8cFRUQTmtKQlN43E16/CSEpDWrVQuFuRy6n1y0ionV7wpteqHv4H1t4BIn9byRzzlfk791E7GVexD5QiK6Tnb6UrFXzsISEkTbmbiJatgm0Wb8gOCmVtDF3UnL8CNmL53Jq6Syy05eR1GMgMW26Yqnlc9tZgoIJSUglJOHc9UtFdLxFTp9XzpGD25GDx+ngQL6DvcfT8RYV4C0uPG/d1iA79rBw7KFh2OzBWIPs2ILsWIPsWO0/v7bYbFiUBWUp8yj3/sx2KvghU9mPm3O3qwu+rdIx52HN5xc/b2JtI6CfeBHZZtw0xwJzL7DrKmCGUupLfLlJANcD/z4TRjMEQ1ugLfCD8U+34vOsXIhblVL34rsWqUAbfF4YyrSVDpxZA2cgMFQpdcaDEgI0BK7BJxQxPENH8ImS83EQaKKUeh2YAyy8wL6f4wvxDQL680uxdrH2V5Vo4AOlVHN83qYzP2nPue4XWS/Afw2hFgH0BP5bppOe+VnYC584BPgIn+erIsbi8wCC7zqNBc6ItfVVDOlWdk7d8V3XVYaddmANPiFdCryrlJoDfF+FtgDYOu9rlC0Iiy3IeLadfW8NDcee2pjQ0AhsYREERUYTHJeEPSYRa3AIllrsATq1dBYoRdLAYYE2BYDozt1xbF7HqWWziW7SBlsdX9PT7cjl2LxPKDp+kIhW7Ui+8RZsNTjxPbT+FTSYeD9FB/eRvXguGQu/JGvNQhK69Ca+fY8aGx69JJQVa2QMwZEx0KDpOZtFBE3z4i1y4i0qQCstRistQXOVoJUWo7tKzr53eT2I24NeXIJ4Pehez8/PmgaiI6KDLr7nWjrgsF39NqO2v/yHrwNthz+pCT9PZuMLC/YFKlz/w/D6XI0vZLpFKdURn+Qu/8lSwE4R6VGVho1Q21R8yfp5RoiubO8/s4aKxs/XSgGjRGRvubrOdwf1AmVdHyHGOeUppTrgE2APArdyfg/gd8BLwEYRKTjT1K+0v0J7KuA5YImIjDAE9dIzp0rVkuPL7lO+jSLj2QLkn/F2VVLHOSil4vF54doaA1asgCilHi/XTmVUdk4K+EFEzplfQinVDZ+AHgM8ZNhTKQu27GX9geMEWS3YbVaCbTZC7DbCg+2Eh9ix1cERiBtXreCv+7eT3P9GgmJiA20OAMpiIfnG0Rx595+9p662AAAgAElEQVREHUrnb8/9T6BN8gsiwqLvZvLWm6/i0TXqjxhHWLsutSb0G96kBWGNm1O0fw/5q5dwauls8jf8yE23jmPobeNITE4JtIk1FhFweb2Uur24vF7cXg2314tH0/FqOl5Nw6sLuu57r+kamteLV9PQNB1d0xARBEEE43WZyo3nsl+gUv7rtPzbCkWh/EIrVnXwo91mZfmhrK1V2rkWUxPE2vv48tC2G3lG56CUaioi64B1SqmbgQb4PFGTlVJLy4Su9gKJSqkeIrLGCIu2EJGd52k7Ct8N3aGUSgYG87MoOR8LgClKqSlG6KuTiGwGlgPjgR+N8GdDw54o4AHli1Wl4QvNnQmtuUXka6XUAWDG+RoUkRIj9LavGuw/jC9HDaVUZ3zhv4qI5ucBH5PKlJ9z3Q1PlBOIxJcnCJCplGqN7xqMMLaXP68CpdQhpdQtIvJfQ/C2F5Gt+LypY/ANWjjfyNTRwIcict+ZAqXUMnxezvKcsa8izndOZ1gL/Esp1UxE9iulwoD6QAYQJiJzlVJrgf3nqf8cBnZowcAOgQ0DXk5cLhdTbrmJ8KQUortf/tGfFyKkXgOiO/dg7ZxvCX/qca7tfnWgTapWsrOzue+++/jmm2+IbNSMhiPGQVTtm9hXKUVE89ZENG9NyfEjONYu46sZ7/D1B+8yYNANPDLlIQYOHIg1gHmQJgGjyt+9tZWA/3wXkeMi8lolu72klNpuJMMvB7YC7wJHgW1Kqa34pmVw47uBv2CUbcEXZjtf21uBzcBOfKJxVRVMfg5fSHCbYc9zRvmbgFUptR1fXtkkEXEZdR7CN6rzZX4O0aUBS42E9xnAExdqVEQ+L5OLdSn2fw3EGe3ez7kC8AwvAv+rlFqFz2N1hnOuu1H+NjBPKbXEeP9nfGHBH7lwKHo8cJdR1058eXkADwMPKqU24BOOFTEW+LaC8xtXfkcRycEXxtyhlHqp3ObzndOZY0/jE6yfKaW24RNvrfCJv++NsmXAHy5wnr9pXnjhBfbv30/y4JGoS5gB318k9h+MNTSM2yZOQjdmsK8LzJ07l7Zt2zJr9mxSBw0j9fbJtVKolSe0/hWkjJ5A4ylPktDrOn5csYIhQ4aQ1vAKnn76mbMDcExM6grmpLgmJoHhN9Pxdu7cSadOnYho1Y6kkb8LtDnnxbFlA6dmfcZDT/6F16c9V/kBNRin08ljjz3GO++8Q0RqGvVG/g6VkBxos/yGaF7f+qOb1+I8+BOI0KXb1dxz5x3ceuutxMbWjLC7id+oHfH8S8AUayYmgeE30fE0TaNnz55s272HRg/8CQkJDbRJ50VEyPjifYoO7GXl6jX0vKproE36VaxYsYKJEydy+PBhEq65jtjeg2qkN9NfeBx5FO7YjGPrRlynT2ELCmLQ4MHcfccdDBkyxJyzrG5iijUTExO/8JvoeK+88gpTp06l4S0TCW3TIdDmVIq3yMmRt14iKi6e43t3Expac8VleVwuF3/96195+eWXCYtPJHX4OKxpDQNtVsAQEVynTlC0fRP52zbiLSokMiaG340fzz133UWnTp0CbaJJ9WGKNRMTE79Q5zvetm3b6NatG6FNWpB0y6RaM/KwcN8uTnz2LoNuuY35X34eaHOqxJo1a7jnnnvYuXMn8V17kTDwJggyJ0c9g+gaRQf2UbR9I45d2xBNo1nr1jxw7738bvx4EhMTA22iyaVRO75cLgFTrJmYBIY63fGKi4vp2rUrhzNOcsV9U5HQ2jV/WdaCWeStXca0f7zGk4/8PtDmnBeHw8GTTz7JW2+9RWhsHCk33kJQk3NHGYuu48nPxZ2dhTvnNFphAVqJb34u8I20VDYb1rAIrGHhBEXHYk9Mxp6QVOfWSdVKinDu2IJz6waKTxzFarMx4IYb+P0DDzBo0CAsdXDanN8AplgzMTHxC3W6491zzz289957NJn4ALYrzp3Ys6Yjusbxj9+m5NghFi5azPV9egfapF8gIsyaNYsHH3yQkydPEt+9N/H9bjjrTRMRXJkZFP20m5KjByk5dhjdVfpzBVYr1rBwLKGhvtnpRRCPB62oEHG7f9FWUHwioQ0aEdqgMWGNmmGPS7icp+pXXFknKdy6kfytG/AWFZLaoCGPTHmIu++6i7i4uMorMKkpmGLNxMTEL9TZjvfWW2/xwAMPkNR7ALH9BgfanF+Nt7iQo+++hnK7WL9mDR3atQ20SQDs2rWLRx99lAULFhBRrwGpQ2/Fkuxbf7L01AkKtqVTuHsbnnzfVIFBScmENm5CcP0G2JOSCEpKxBIWft6wtO52483NxZ2ZiTsrE9eJ45QePoReXOyrLyGRiOZtiGhxJaENm/iWI6rliObFuXs7zvTVFB4+QJDdzujbbmPqI4/QuXPnQJtnUjmmWDMxMfELdbLjLVmyhAEDBhDZvLUvT62W38jduac5Nv0Ngu12tm3cQJPG55tD2v/k5uby9NNP8+abb2ILDiG+9wAiuvZCdA3nji3kp6+m9MRRsFoJa9ac8LbtCGt9Jbao880FXXVEBE9WFiU/7aNo9y5KDh4ATcMaGUXklR2JbteF4NT6tSYv8UKUZmbg3LiavK0bEY+b9l268KdHH2X06NHmSNKaS+3/4FWCKdZMTAJDnet427Zto2/fvnhDwkibNAWpIze20lMnOP7Bm4SGh7NqyY+0b9fusrbvdDr5v//7P15++WUcBQXEde1BYr/BaMpC/sbV5K5ZhlbkJCgxiairexDZpSvWcP/mCOouF8V791C4eRNFe3aDphGUkEh0x6uJ7tQNW1jNXW+0qmilJRRsWY9j42pcOaeJiU/gwfsn88D991OvXr1Am2fyS0yxZmJi4hfqVMfbvXs3ffr0oUjTaTjpQSSy9s+SX5bSUyc48ek7WDSN72bNYuD1/f3eptPp5K233uLFF18kJyeHmNbtSOo/BImKJW/NMnLXLkMvKSa0eQti+/UnpGnTgHi2tOJiirZtw7lpI6WHD4HVSmSbDsR07Ulog8a13tsmolN8YC8FG1ZR8NNuLBYLw0aM4LFHHqFnz561/vzqCHX+n2CKNROTwFBnOt6WLVsYPHgwjpJSrpj0EBJTNxOzPfm5nPjkHVw5WTz+5FNMe/pv2Pww2eyhQ4d4/fXXee+99ygoKCC6RRuSrhuMSkqlYGs6p3+cg+YsIKx1G2L7DyCkYc2ZS8196hSOtaspTE9Hd5ViT0ohtntvotp1xVIHJuZ1557Gmb6G3E3r0EtLaN22LVP/8AfGjh1bq+bkq4OYYs3ExMQv1ImOt2DBAkaPHo1uD6bBuHshvm7PV6W7Ssma+zWObek0admK6W//h969L32kaGlpKd999x0fffQRc+bMAaWIbtuJhB59sCSnUXzkIFnzv8V16gTBDRoSf9NQQgOYP1cZuttF4eYtOFavwH3yJNaISGKuuobYrj2xhoUH2rxLRne7KNy+ibz1KynNOklkdAz33nM3Dz34II0aNQq0eb9FTLFmYmLiF2p1x/N6vUybNo1nn32W8JQ06o+/Gz3s0hPZawMiQuHubZxeOBuPI49uPXvy56lTGTx4MCEhIVWuJycnhx9++IF58+Yxc+ZMCgoKCI2JJaJ9F+KuuhYiItFKijj9w/c4Nq/DFhNL3OAbiejYsdaE3kSEkp/2kb98GSX79qKC7ER1vIq47n3qxBQgIkLJkQM4N64mf/c2FNCnXz/uvuMOhg8fTnh47RemtYTa0SEuAVOsmZgEhlrb8bZv387999/PqlWriOvUjcTBI36Ts+XrbheO9LXkrV2Kp8BBaFgY113Xn549utOmTRtSUlKIjIxE13UKCwvJyMjgyJEjbNmyhU2bNrFr1y5EBHt4BGHNWxPfqRvW+o1RFgsignP7JrIWzEIrLSamdx9i+w/EElx7B224Tp7EsXwZzi2bQISodp2Jv+Z67AlJgTatWvA48nBuWkf+1g14HHmEhIYybPhwJt5+O9dddx3Bwb+9PnIZMcWaiYmJX6h1He/YsWM8//zz/Pvf/yYoNIzkwSMIvdJcX1F0jeJD+ynZsx3noZ9w55y+4P4h0TEEpaQRnnYFEc1aYUmu94spTjyOPE7N/oLig/sIbtCQxFG3EFyHRh96HQ7yly2lYN0axOslsm1H4q8dQHBiSqBNqxZEdEqOHqJ4x2bydmxGLy0hNCyMAQMGMmL4MIYMGUJSUt0QqDUIU6wFGqWUBmwHbMBuYKKIFFdDvYUictHjy5VSM4A+gAPQgQdFZM0l2tIVmCAiflnXRinVHXgNCDYeX4jI00qpvoBbRFb7o11/YvwfvheRryoovxVIFhGnUfYa8HsgUUSyL1DnkyLyP1Vo+zDQ9UJ1VYGa3fEMNE1j6dKlzJgxg88//xxd14nt2pPEfoOREDOhuiK00hI8eTnohQUorxdltaCsQRAegTUq+rzTWogIBdvSyZr3DSJC/OAhRPXoWevnqjsf3kInjmXLcKxZhXg8RLRuT3zvAYQk1x1hqns9FB/8idL9u3Hs3YG3wAFA0xYt6d+3D3369OGaa66hQYMGtSa0XUOp8xevNoi1s6JKKfUJkC4ir15CfVYR0S5RrH0vIl8ppQYCL4tI+4ra+LU2VjdKqb3ArSKyVSllBVqKyC6l1NNAoYi8HFgLL55KxFpn4EUR+VgpZQG2AHFAx0rEWpU+E3VZrOm6zqFDh1i9ejVLly5l7ty5nDp1iqCQUKI6dSOhR1+IjD67v4iOaBoWW1DgjK4DeIsKyZzzXwp3byekUWOSbh1LUEJ8oM26LGhFheSvWIFj1QrE5SLiyg4k9huMPb5ueZ9EBNepE5Qe3EfJ0YMUHjl4dgmwqJgYOrRvT+dOnWjXrh1NmzalcePGpKWl+WXEcR3EFGuBppxYmwy0B/4IvA60w+dxe1pEZimlGgEfAWeyOh8SkdWGB+lvwEl8N+w2Z+pVSqUCXwBRRl33i8iKC9gzg5/FWgiQKyJhxg38fWAg8AaQCzyDz5N1ALhDRAqVUlfh83KFAy6gP9AFmCoiNyml4ox6mgDFwL0isq28sFJK7QBuAk4DXwL1ASvwnIh8Uc7mPHwCLatMWSNgLaAZdUwBjhptJxpld4jIUeOcC4CuQArw+BmRpJT6Iz5PVjDwrYj8TSkVXgWb7gHuBezAfuB2ESk+X1vK97PzdeA64BC+zvn+ecTaXqCniNyslLoOuAUYjCGwlFK/w+dpswPrgAeAafg+V9uBnSIyXik1E2gAhACvicjbRhuHDftKKjvPC1BpxxORannouk5JSQlFRUW/eOTl5XHy5Mmzj71797Jr925KjGWF7OERhDRqRnz7LtgaN8cSZEcrKca5aytFP+2iNOM4XqfPU6CCgrAnphDWsAmRbTsRUs/0FFSVwr07OPXdl2ilJcQNGkxM7z511pt2IbTiYhzLl5G/cjni9RLV8SoSeg8kKDo20Kb5BdF1XJkZuE8cxZN1kqKTx3FlnkT3/Lw2q9Vmo169NNLS0khJTiIxMZGEhAQSExOJiYkhPDz87CMsLIzw8HBCQ0Ox2WxYrVZsNts5D6vVitVqrWv9s06dTEXUGsmulLLhu+HOB54CfhSRO5VSMcB6pdQiIAsYICKlSqnmwGf4bqoA3YC2InKoXNXjgAUiMs3wOl3M1N8347u5n6FURK5RSiUA3wDXi0iRUupPwKNKqefxCcPbRGSDUioK3w2/LM8Am0VkuCE0PgQ6XsCGG4AMEbkRQCkVXcE+/wD2KqWW4rt+H4jIYaXUv/mlAPwO+FBEPlBK3Qn8HzDcqCMVuAZoBcwGzngWm+O7tgqYrZTqjU/sVWbTNyLyjrH978Bd+MRYhW0BI4CW+AR6MrALn7CsiJ+AYUqpWGAs8DG+zw5KqdbAbUAvEfEopd4ExovIn5VSD4lI2Wt9p4jkKqVCgQ1Kqa9FJKfM9qpc+wqxBtnx/VASQ7YJZ384XeYfUMoWhC0ikqC4BELadSUqKYWQtIYEJ6Xgc0yC1+ng9KI5ODb58oxscfGENGtKUFw8ymZDKyrClXGC/I2ryFu7jOCUesT3HUREi7Z17aZQbWiuUk7Pn4ljy3rsqfVIvWcywfVSA21WwLCGhRF3w2Ciel1D/o+LcaxdjXNbOjFX9SLumv51YlWEsiiLhZDU+oSk1gcgHp+n2pOfhycvB09+Lp68XPLzc8g5mcWmAwfRiovQiotA1/1k1Ll99ef+W2abOufFz4cGoL83f/KFhD1P/+FSIh01ntog1kKVUluM1yuA94DVwFCl1FSjPARoCGQAbyilOuLzGLUoU8/6CoQawAbgfaVUEDBTRLZUsE95XlJK/QWf9+muMuVnvCrdgTbAKuODbgfW4BMbJ0VkA4CIFADlb2bXAKOM7T8qpeIrEQHbgZeVUi/g8/id4xUUkWeNEPJAfOJ0LNC3grp6ACON1x8BL5bZNlNEdGCXUirZKBtoPDYb7yPwibcVldkEtDVEWoxx3IJK2uoNfGaElzOUUj9WfDnO8g0wBrgauK9M+RlP5gbjuofiE/kV8Xul1AjjdQPj3MqKtUqv/flI6tkHt2Z84SoFKONPGd9/5z6f/ZxU8KzK1VO+PhVkxxJkx2K3+17b7VhCQrFFRGEJDkEpRZDVgkX90qMjuk7O+hWc+uF7dK+HyM5diO7RC3v9iteB1EpKKNyyBcfypWR8Pp3wxs2pP3wMwXF1e/61i6Xw0E8c++YTPI48Yvr1J27AQJQZ7gLAFhlJwrDhRPfuTd7CheStXY5j01oSevYjsdd1WIOrPj1KbSQkMRkSk8uVCroImi5ouo5eWoLuKkV3u9E9LsTtRve40d1uxOsF0RHd9+Dss/Zzmehnqv1FG+XLpIKyn/er4Edl4CJ1w4F3A9X45aA2fDuUlPN2YITERonI3nLlTwOZQAfAApSW2VxUUeUistzwBt0IfKSUeklEPqzEpj+WD7+Va0MBP4jI2HL2tafy8FdFP0sE8OI7pzOEGPbvU0p1AYYA/6uUWigiz55TgcgB4C2l1DvAaaVUVRJiytrqqsBGBfyviPznnJOo3KYZwHAjj24SvxSPFbVV3p7K+BzYhM+LqJcRFsooe+JCBxuh8+uBHkZ4dinGNT9rTBWvfUWcXPbDRZxKYDhx4gRjxoxh+8qVRLZqRfKIUUjshVcnsIaGEt2jB1HdulGwfh258+aw/18v8D/PP88fH3nkN+9lKy0t5S9/+QuvTn+D0MQkGkx5GFW/QaDNqpEExcaRdNsYYvr2JX/hArKWzKdkyzqe/utfefCBB8ypMEzKUqeFGvzy5l+bWABMMUQbSqkz8wdE4/Nc6cDt+PKILohS6gogywjJvYcvOR2l1IdKqW6/0r61QC+lVDOjrjClVAtgD1DPyFtDKRVphHfLshwYb2zvC2QbHrjDZWzrDDQ2XtcDikXkY+DlM/uUO8cb1c93yeb4vI75gBMoO5PpanzeKAwbVlZynguAO5VSZ3IK05RSSVWxyWj3pOHRHF9JO+C7LmOUUlYjz7DfhXYWkaP4wuVvltu0GBitlEoybI4zPgMAHsMe8H2W8gyh1gqft/QXVPE8ayWLFi2iU6dOrEtPJ23seBLvuLtSoVYWZbUS3aMnDR57nJAmTfnTo48ycNhwCgsL/Wh1zWbLli1cddVVvPLKK8T26Enqw4+YQq0K2JNTSLp9ImlTHkZPSOCxRx+lYdOmfPDhh2hajRnHZWLiV2qrWHsOCAK2GYn2zxnlbwITlVJr8YVAK/SmlaMvsEUptRlf+PE1o7w9vgEJF42InAYmAZ8ppbbhE2+tRMSNL1/qdaXUVuAHynlrgKeBrsZxzwMTjfKvgTgjJHw/sM8ob4cvZ28LPnHy9wpMuh1fztoWfOHN8UY48TtghFJqi1LqWnxJ93cYbd8OPFzJeS4EPgXWKKW248sti6yiTX/Fl9z/Az4RWxnf4stF2w68BSyr7AAR+Y/hUSxbtgv4C7DQOM8f8OXIAbyN7zP1Cb7cPpuxz3P4/oflqcp51jpef/11Bg4cSLEtiIZTHiGkU+df7RGzRUeTPOlO4m4YwqLvv6N5u/YcPHiwmi2u2WiaxgsvvEC3bt04cPw4V9x7H7HDR0JQzZngVvd48OTm4M7Kwp2ViVZU+HMOZQ0hpEFDku++j9S776UAxaSJE2nZti1z586tcbaamFQ3NX40aCAwEv/fE5FbAm2LSZ2lxnU8Xdd5/PHHeeWVV4hq147E28aBvfoERfFP+8j65CPsQUEsnDuXa3r2rLa6ayoHDx5k4sSJrFy5kpgOHUkYOQoJvZgxTP7BnZlJ0a6dlB45jOvYMTRnwTn7KJsNe2oqwQ2vIKxFK8KaN68xeXWi6xRu20r+wvm4s7Pp2qMHr7/6Kt27n+MAN/ltUOfzK0yxZmISGGpUxystLWXixIl8+eWXxPW6lpibh/pl+gh3Vian3n8PrdDJ9A8+YMKYMZUfVAsREd5//30eeeQR3LpO4vCRBHcI7JqeWlERBevX4dy0EU9mJgC2pESCGzXAlpSALSYGFWQDAa2wEG9uPu5jx3EfOYa4PVhCQojo3JnoXr2xJ9aMASPi9eJcv47cRQvRCgu54aabePXFF2ndunWgTTO5vJhizcTExC/UmI6Xn5/PsGHDWL58Ock3DSX82t5+FRXeQieZM6ZTeuwof/3733nmiSfq1MCDEydOMHnyZL7//nsim7cg5bax6FFRAbPHk5dH/o+LcW7aiHg8BDdtTFjnDoR1bIsttvLZZsTjpWTPTxRv3ELR5q3g1Qi78kribxiCPblmLBGlu1w4V64gd+mPiMfD+Ntv53+ee44GDcycwN8IdecL5DyYYs3EJDDUiI6XkZHBoEGD2L1nD6ljxhHcvsNlaVf3eMj67BOKdmxn3F138eF//oPVWul4oBqNiPDuu+8ydepUil0u4m8YTHiPXgGb4FYrLCTvx8U41qwCIOLqLkT2vQZ7/V8/l5vmKMC5fA0FS1YiLheR3boRP2gI1oiaMQeaVlhIwdIfyVu1EqvVypSHHuIvTz1FXFzVB8eY1EpMsWZiYuIXAt7x9u7dy6BBgziZlUW9iXdgbdL0srYvuk7OnO9xrFhGr+uvZ8HMmYSHh1d+YA3kwIED3HPPPSxZsoSoFi1JHn0rekxMQGwRXT87bYpeWkp4967EDB6ALaH6VgLQCotwzFuEc9lqLKGhxN88jMhLGIhS3XhycylYtJD89I2ERUTw1BNP8MjDDxMWFvh8QRO/UDM+eH7EFGsmJoEhoB1v/fr1DBkyhCKPl7S77oHUwM2c71i1kuzZM2l65ZWsWrSI5OTyE4LWXFwuF//4xz949tln0ZQi/sabCe16VcBEi+tkBqe//grX0SMEN29K3G0jsNfz3/V0Z5wi5+P/4j58lNDWrUkafRu2yMjKD7xMuE6exLFgHs5dO4lLSmLaM89w1113ERRkrmVbxzDFmomJiV8IWMdbsGABo0aNgrAwUu++96LmT/MXRbt2kvnpx8TExbFy8WLatGkTaJMqZf78+fz+97/np59+Irpde5KGj0QPkFARXSd/2VJyF87HEhpC7MibCb/68ni6RNdxLl1F3sy5WEJDSLptHOEtWvq93Yuh5NBB8ufNofjwYRJTU3nqz3/mnrvvNj1tdQdTrJmYmPiFy97xRIQ33niDP/zhD4Sm1iPlrruR8JqRawRQeuwYmTPew6LrfPbJJ4wcNizQJlXIgQMHeOyxx5g1axbhySkkDhuOtVnzgNnjyc0l64vPKD10kLBO7YkbMxJr5OUPJ7tPnCT7vU/wnMokul8/4gcORtWgPEQRoXjPbgqWLqH40EEiY2N57JFH+P2UKcTG1s3F4n9DmGLNxMTEL1zWjud2u5kyZQpvv/020W3bkThmLGKvecv1eHJzyfpwBqUZJ3jgkT/w2ksvYqshc3udPHmS5557jnfeeQdlsxHbfwCRva6BANrnTN/I6ZnfgFLE3Tr8snnTzofudpP339kUrlpHcJPGpIyfgC0ycCNhz0fJoYM4ly3FuWsnwWFhTJo0iUemTKFVq1aBNs3k12GKNRMTE79w2Tre0aNHGT9+PCtXriSh//VEDRgUsBGKVUH3eMiZPZOCdWtp07kzMz//nObNA+e5On36NP/4xz/45z//icvtJrp7D+KvHxBQr6Tu8ZA961uc69cR3KwJCRPGVOsAgkulaMNmcj7+L5awUJJ/N4HQKxoH2qQKcZ3MwLl8GQVbNiOaRo9rr+Wxhx9m6NChZl5b7cIUayYmJn7hsnS8r7/+mrvvvptil4ukUbdctqk5qgPn5k1kz/wGpWk8/fTT/Gnq1Mt6Az1w4ACvvvoq06dPp7S0lOjOXUgcNDhgozzP4MnJ5tRHH+DOyCDqhv7E3DSwRopv9/EMTr/9Id68fOKHDiW6e68aM1q0PN5CJ0Ub1uNYuwZPXh6xCYlM+N14Jk2cSIcOHWqs3SZnqfP/IFOsmZgEBr92vKysLKZOncpHH31EZKPGJI8dj9TCvByvw0HOzG8o3LmDtEaN+OdLLzFq1Ci/3Ty9Xi/z58/nvffeY/bs2SirlcjOXUjo2w+JT/BLmxdD0c4dZH3xGVgU8RPHEtauZs/UrxUXkzP9M0p27iGiSxcSR96CpQZ7rETXKd69i+L0jTh370I0jaYtW3LXxImMHj06oB5ekwtiijUTExO/4JeO5/F4ePfdd3nqqacocDqJ7Xcd0f36BzSv6lIREYp37yJv3lxcmado3qYNf3r0UcaNG0doaOgl16/rOmvXruXbb7/l008/JSMjg5CoaMK7diWm17VQA6aiEE0jd8E88pcuwd6wPol3344tIfCjeKuC6DqOeYtwzPkBe1oaybdPwB4XeOFbGVpREcXbt1G4eRPFhw4C0LhZM0aPGMHQoUPp0aNHrZ/IuQ5hijUTExO/UK0dz+Px8Nlnn/HMM89w8OBBIpu3IHnkqBrhDaouRNNwblHbwS0AACAASURBVEqnYOVyXCdPEh4ZxdChNzNqxAj69OlDQkLVzlXXdfbv38+KFStYsWIF8+fPJzMzE4vNRniLlsR174G1eYsaM5LR63SS+clHlB48QMQ13YkbPQxlr33iu3j7LrJnfIZSisRbxxLR5spAm1RlPHm5lO7eRfGuXRQd2I9oGuGRkVx77bX079ePPn360KlTpxozGOY3iCnWTGoeSikN2A7YgN3ARBEpVkoVishFZz0rpR4B3haRYuP9XGCciORXp90XYU8j4HsRaVtB+W5gL2AHNgJ3iYjnAnU9DRSKyMvlyvsCU0Xkpuqz/KKolo53+PBhpk+fzttvv82pU6eIaNCQ+BsGY23WvM7m2YgIpQcOULwpnYKdO9BLigFIa9CAjh060KB+fVJTUwkODsZms1FYWEhubi5ZWVns27eP3Xv2UFLsO8YeGUlwk6bEduiItWkzLNXgqatOSo8c5tRHH6CXlBA3bhQRV3cJtEmXhOd0Ntnvfoz72IkaOb1HVdBLSyneuwfPwQMU7v8J9+nTAISGh9OhQweuvuoqOnfuTOfOnWnZsqU5UOHyUDe/7MpgirVaSFlRppT6BEgXkVcvQawdBrqKSHY1m/qrqESsfS8ibZVSVuAH4D0R+eQCdT2NH8SaUsoqItqvOdbgV3U8t9tNeno6ixcv5ttvv2XTpk0opYhs3Ya4ntdgaX55RZqI4MnKpGT/T3iys9GKilBWK7b4BILrpRHavLlfc5RE0yg9chjt+HFKjx2lJCsTvaAAb1HRL/azhYZhCw/DGp9AcFIS4fXSsF7REEt8Yo0UtSJCwdo1ZM+eiS02hsR7J2CvXy/QZlUL4vGQ+9/ZFK5c65veY+zt2KIrX1C+puItKMB16CCeI4cpPnaM0owTiMf3+9FitdKgYUNat2xJy5Ytad68OQ0bNqRevXqkpaWRmJhohlKrh5rXiasZU6zVQsqJtclAexF54Ey5UioCmAXEAkHAX0RkllIqHPgSqA9YgeeAZOBlfN6qbBHpV1a8KaUmAFPxiYttInK7UuoW4G+ABjhEpHc5+87XfiNgHrAS6AmcAIaJSIlSqgvwPlBsbB98IbFmvH8eyBWRF8vZ3BV4WUT6GmKtKZAGNABeFJF3DLH2LJADtASWAw+IiK6UGgg8AwQDB4A7RKTQaON9YCDwBpAETAa8wC4RGVPV/yEXEGu6rpOTk0NmZibHjh1jz5497Nmzh507d5Kenk5paSkAEY2bEH5lW8LbtUdd5sEDuseDc+MGHCuX4zE8CyokGGtEBOL1ouU7fGX2IMLbdyC2dz/sKSmXzT7RNETXQdNQQUG1ynujezxkf/MVzvSNhF7ZivhJY7GG172Z9gvXpZP72dcoezBJY8YS3qJuzHEmuo7n9GncGSeQ7Gxcp7MozcrCk30a3e3+xb5Wq5WEpCSSk5NJjI8nLi6O2NhYYmNjz74ODw8nLCzsgs9BQUE18kfHZaTOn7wp1mohZUSZDfgamC8ib5UrDxORAqVUArAWaA6MBG4QkXuMeqJFxFHes3bmPT4h9w3QyxBBcSKSq5TabtRzQikVUz5ceoH2rwD2G21tUUp9CcwWkY+VUtuAKSKyTCn1EpWINaVUCD7h97CIbKtErI0AugPhwGbgaqAFMB9oAxwxXv8HWGqc82ARKVJK/QkIFpFnjTbeFJEXDXsygMYi4qroOlyIRtdcK5rbhdflRnO58LpceN0uPMXFuAoKfEKjDNbwcIKSkgiu34Cwxk2wX9EoIGswighFO3eQPXsmWn4+9isaENHjKkKvbIU1LubsDUN3uXEdPEzxpm0Urd+EeDxEXHUV8YNvxBYR+IT9moonN4dTH36A+2QG0YOvJ3rI9TVyWo7qwn0yk+x3PsJzKpOonj2JH3IzFrs90Gb5BRFBKyjAW+BAczjQnE40hwNPgfG6pAS9pBi9pAStuBjKfQdUhsVmQ9lsWKw2LDYbVpsVi832i4fVFvTze6sVLAplsaCUQimL77OmFOpsueXsdl+55eeHUVYVKhSS1Xjszm+/qfNizcyGrJ2EKqW2GK9XAO+V266A/1FK9QZ0fF6lZHx5bi8rpV7AJ3pWVNLOdcBXZ0SciOQa5auAGYbY+qaC487XPsAhETljezrQSCkVDcSIyDKj/CNg8Hlsamqce3PDtm2VnAPALBEpAUqUUkuAbkA+sF5EDgIopT4DrgFK8Qm4VcaXhB1YU6auL8q83gZ8opSaCcysgh1nydizGxVkR9mDUEF2LKGhqKgogoKDCYmMxBYZiTUiEmtUFPakJKzhESjAEsBfz1pxEZlffkHRzh0E1UshYeJ9BLdoWuGXqSXYTmjrFoS2bkHMsMEULFxCwY8rKN6xg8QRI4nuVLtzr/xB0d49nPz0YxAhcfIdNX5ajurAnppMyp8fJn/WPAqWrKDkp59IGTOW0IaNAm1a9aMUtpgYgs8zT5/gE3Rnn91un3hze3yvPW7j2ff+F681r8+b7NUQzQuaZrz3omkaXuM9mhdxuXzbNC+IgAgi4hOHIoguZcp10Mu8Nvbz7V+Ro6eCsio6hKrsOKpgv2YvvXrH/j8+Or1qFdROTLFWOykRkY4X2D4eSAS6iIjH8AiFiMg+I9w4BPhfpdRCEXn2AvUoKuh9IjJZKXU1cCOwRSnVUURyKmvf2OYqs58GhJ6vnfNwQEQ6KqVSgaVKqaEiMhtfKPKMCyKk3DHl65YLlCvgBxEZe572yyZD3Qj0BoYCf1VKXSki3qqcRPqOHRzJy8dutRIcZCPUFhRQIVYZ2zel8+QDD1CSmUnCyJsI63dNlUOL1ohwYkfeRESPq8j99CsyP/2E5oUFTHvxZcLCL/8aljUNXdeZ8cYb/Pu9dwitn0bivRMgvvbNifdrsdiDiLtlKGHt25Dz0Zcc/9cbjJg0iYcf/5P5+fADXl1H03W8xkPTdTSRs8+6Luj43usi6CI+jSaCIGUEJcZ73/OZb1MxXpTVVFLFr/dfE+ezoHhx+Yq5v+LQWoUp1uom0UCWIZT64Qs/opSqhy/H62OlVCEwydjfCUQC5QcYLAa+VUr9Q0RyyoRBm4rIOmCdUupmfLlgZcVahe2fDxHJV0o5lFLXiMhKfGLvgojISaXUn4EngNnAYaALvtDoqHK7D1NK/S++MGhf4M/4wqDdlFKN8YVBbwPexhey/ZdSqpmI7FdKhQH1RWRf2QqVUhaggYgsUUqtBMYBEfg8dpXSLiWFdpcxh+tSmD17NvffeiuW6CgaPD4FfmWie1BqMkmPTMYxbxErv/ue23bsYMWChTRr1qyaLa49ZGVlMWHCBBYsWEB0ty7Ejh+F/EZHD4a0bEbqU3/AMXMu37z/PkvmzOHtN97w6yTIJnWDe6++KjPQNvibupsM8dvmE6CrUmojPuGzxyhvB6w3wohPAX83yt8G5hkhwrOIyE5gGrBMKbUVeNXY9JJSartSage+xPytVWz/QtyBTyStAUqqeJ4zgTCl1LX4BgS8ppRagc9jV5b1wBx8Quw5EckwytcAzwM7gEPAtyJyGp+I/czIo1sLVJT5bAU+NvL3NgP/CNRUJ/5kxowZjBw5Emu9FJL/+OuF2hmU1UrMTYNI+v29ZGVm0rZLZxYsXlRN1tYuli1bRseOHVm85EeSx99C9MTbfrNC7QyW0FBix44iZeqDFAdZueWWW+g9YAC7d+8OtGkmJgHFHGBgYhIYanzHe+WVV5g6dSrhbVoSf/ftqJDgaq3fk5VN9r+n4zmdw0v//CePPfRQtdZfU9E0jWnTpvHMM88QmpxE4t2/Q1KTKz/wN4ZoGs6lq3DM+QFxuxk3YQIvTptGvXp1YwoTk2qlzrteTbFmYhIYamzHExGeeOIJXnjhBSK7dCB2whhUkH8yJvTiErLf/4SSXXu586EHeee1/8NSh0c/Hj16lEmTJrFkyRKiu3clbsxIdLt/vWm6y40n4xTuEyfx5uSiFxahl5SeHQloiQjHGh2FLT4Oe/162BLiatQIVK2wCOf8xTiWrSbIZuOhKVN44vHHSUxMDLRpJjUHU6yZmJj4hRrZ8bxeL5MnT+a9994jundPom8d5vcbt2gauf+dReHyNVwzaCDzv/6G8DqWWC4ifPDBBzz88MOUeDzE3zoMe7fO/luQPjePovStlOzYjevA4Z+ngbBYsESEYQkLBdERr4ZeWIy4fp7/S4UEE3xFA0KM0bxBaak1Qrx5snNwfrcA58YtBNnt3HPvvTz5pz+RlpYWaNNMAo8p1kxMTPxCjet4paWljBs3jm+//Zb4GwcSPuT6y5bYLSI4l64i76vZNG7dipU/LKoz4a7MzEzuvfdeZs+eTWTL5iRMuA09tvpn7BcRSnbswblsFaW794EIQQ1SCG3XguBmVxDUIAVbQsw5wktEkBIXnswc3EcycB/JwLXvEJ7jvpxta0wUYV06EN61E/aG9QOe7O85lUXhD0soWLcJq9XK+Ntv58nHH6dly5YBtcskoJhizcTExC/UqI5XUFDA8OHDWbJkCUm3jSC0T8+A2FG8fRfZ739CZFQUSxcspFOnTgGxozrQdZ3p06fz+OOPU1DoJHboEEL79qx2L5VPpO3GMWch7qMnsMZGEXFtV8Kv7UJQUtyvrtebV0Dp9p8oTt9JyfZ9oGnYkhKI6HU1ET2uwhoRWO+nJzuXokVLKVi9HvFq9O7fnz8/9hiDBg2q06F0kwoxxZqJiYlfqDEdLysriyFDhrB5yxaSJ43F3qVDQO1xH8/g9FvToaSUzz/7lFHDRwTUnl/D9u3buf/++1m1ahURLZqSMHY0kpxQ7e14srLJ/fJbSnftw5YYR/TQfoT37ISyVe/yWlphMcUbd1K0ahOufYdRQTbCunYksk8vghvWr9a2Lto2ZyFFK9dSsGw1WoGTBk0a88dH/sCECROIrsVrjppcFKZYMzEx8Qs1ouMdPHiQQYMGcfjYMVLumYC1TYtAmwSA11FA9lvTcR07wRN/+3/8/a//r1Z4S3Jycpg2bRqvv/46trBQYkbciP2qTtXvTdM0HAt+xDH/R5TNSszIAUT2717tIq0i3MdO4fxxLUWrNyOlbkJaNSd60HXnXc3iciFeL8Wbt1O0dBUlh44QFBLM6NG38MB999GrV6+Ah29N/Eqd/+eaYs3EJDAEvOOlp6czZMgQHCUlpDx4JwTYQ1Ie3eUm96MvKNq0jat6X8t3X/6X5OSaOcVFSUkJr732Gs8//zwFTidRvboRN2wIelhotbflOZ1N9ozPcB86Sli39sSOuxFbbFS1t1MZekkpzh/X41ywEs3hxN64IdE3XEdo2zYBF0auI8coXbOBgvWb0EtdXNGsGQ/ddx8TJ040R5HWTUyxZmJi4hcC2vHmzJnDmDFj0ENDSH7obvTE+ECac15EhMKVa8n76jvCIyOY/s67jB45MtBmncXpdPLOO+/wyiuvkJGRQVSHtsSPGIKe5B9BULRhMzmffgUWC/GTRhDevb1f2rkYxO2hcOUmHHOWoWXnEdykITFDBxPSIvArU+guN8WbtlK8egMlBw5hsVrp278/d9x+O8OGDSMyMjLQJppUD6ZYMzEx8QsB6Xi6rjNt2jT+9re/EX5FA5LuvwMtMiIQplwU7oxT5M74DNfxDK4bPJgZ//kPDRo0CJg9GRkZvPnmm/zrX/8iPz+fiFbNib/pBmjS0C/tiaaRP3MuBYuXE9y8EQmTb8OWUPGC4IFCvJpPtM1chJZXQEibFsQMHRzwnLYzuE9mUrouHefGLXhz87CHhHDjTTcyYfzvuOGGGwgJKb+ksEktwhRrJiYmfuGyd7zc3FzuvPNOZs2aRXT3rsSOHYX4abJbfyCahnPxcvLn/IAFuG/yZJ7+618vW1jL6/Uyb9483n33XebMmYOu60R0akf8oP5IA/9NM6IVFZP93seU7vmJyP7diR17EyrI/7lpvxbd7cG5aA0F3y9FLyohrGsHYoffiC2uZixOL7qO69AR3OnbKEjfguYsJDg0lP79+zNi2DBuvPFGUlNTA22mycVhijUTExO/cFk73oIFC7jzzjs5lZlJwqibCenTM+B5Rb8Wb04eznmLKFizAXtwMGPHjeORKVPo2LFjtbdVUlLC4sWL+eabb5g1axa5ubmExEQT2r0LUT2vhoRfPzVGVfCczibrjXfx5uUTd/swIvte5df2qhO9uJSCucspmL8CgKjr+xA18DoswfYAW/YzommU7t2PZ8cenNt24s3NA6Btx44MHjCAPn360KtXL2JiapYX0+QcaueX2UVgijUTk8BwWTpeZmYmTzzxBNOnTye8fj0SJ45F0lIuR9N+x3Mqi6LFyylYvwnxeGjSogW3jRrFkCFD6NKlC6GhF5/cf+rUKbZu3cqaNWtYsmQJa9euxe12ExQeRkjb1sR07YRq1QxlvRyjLk+Q+ca7IDqJD08gpMUVfm/TH3hz8sn7Yh7F67ZhjYkiZtgQwv0wQvZSERE8Gafw7NxD0Y49lB46gmgaSinatGvHtT170rlzZzp16kTbtm3NsGnNwhRrJiYmfsGvHa+wsJA333yTadOmUVRcTHT/3kTeOABstSfsWVW04mJKNmymZMtOin86ALqO1WajVZs2tGrRgsaNGlGvXj3Cw8MJCwtD13WKi4spLi7m9OnTHDt2jGPHjrF7zx5OZ2UBoCwWQhvWx968CVGtW0KzRqjLeO1K9u7n9H9mYAkPJXnqnQTVq/0jGEv3HSbvk+9xHz6BvXED4m4ZTnAj/+T4VQe624P70BG0g0co3ref0iPH0EtdAFhtNpo2b86VrVrRvHlzmjVrRrNmzWjatCn16tXDVgf7WQ3HFGsmJiZ+wS8d7+TJk7zzzju89tpr5ObmEtmuDYm3DkOL92+4rqagFRXjOnAIOXqCkiPHcGfn4M3NQzzeCvdXNiv2mBgssdHYEuMJb1ifoLR6kJrsWz8zABSlbyX7g88ISk4gaeod2OLqzsSuousUrdpM/n8XoDmchPfoSuywIVijav6oTNF1vNm5eI9noGecovR4Bq6sbLzZOYj358+XUor4xETq10+jYf0GpKWlnX2kpqaSkpJCcnIyiYmJWC+Dh/Y3ginWTAKPUkoDtgM2YDcwUUSKL7HOZ4HlIrLoPNsnA8Ui8uElttMI+F5E2v6KYycBC0Uk41JsqC6Mc+kpIp9WQ3XV1vFycnJYsGABn3/+OXPnzkXTNCI7tCV+8PVIQ3ORa9F1pNSF7nYjbjcohbLbsdiDUMHBNSoc51y2itwvZxHc/AoSH56ANSIwgtHf6CUuHLN+pGDhKpTdRsyQAUT26XVZvZfVheg6Wp4Dz+lsyMlDCgrw5Dlw5+XjzXeg5TvQis79urZYLMTGx5OSkkJavXqkJCeTkpJy9pFc5n1sbGytzTG9TNT5i2OKtVqAUqpQRCKM158A6SLyapntVhHRAmbgBbhEsbYUmCoiGyvYdtnPWSnV17Dnpmqo7ld1PE3TOHz4MOnp6WzYsIFVq1axbt06dF0nODaGsKs7E92jG+LHedO8+Q6KN26hdN8B3Bkn0YuKUVYr1thoghtfQWibloS2a3NZ8rrqCiKC4/sFOOYtJrRTaxLuH4slOCjQZvkdz8nT5H7yPaXb92FLSSRu9DBC29S9Bdl1twfN4UArKESchajCIvQCJ15HAe6CAryOAvSCQrwFzl946c4QFBREckrKOYKuvKhLSUkhIqLmT8XjB0yxZhJ4yom1yUB74Evgb8BJoCPQDnge6AsEA/8Skf8YxzwO3A7owDwR+bNSagY+EfWVUup5YCjgxefJmqqUehooFJGXlVIdgX8DYcAB4E4RyTPE1DqgHxAD3CUiK8rZ3shop63hKRtq1NMU+FZEHldKWYH3gK74RMz7wDFgBnACKAF64PMqvg8MBN4AJmOIOaVUArBRRBoZ7QwHrEBb4BXAblwDFzBERP4/e+cdHkW1/vHP2ZKebBoJgUAKvXeQ3hQQBFFQbAh2xXL1iorlWu71Z78WrmJXROyFqtJUkCYivXdCT++7m23v748dMEQCAZLsJsznefbZmTMz57xTzs533/eUHKVUI+AtoA5gBW4Tke3atSnQ7KkLPKxdp9+BFsA+4BNgAfCxlrcBGCUiuypwS9mzZ4+UlJRw/ONwOE4s2+12cnNzycnJITs7m+zsbA4fPsyevXtJ278fp9MJgMFkIqhhIsEtmhLWpiWSmFClXiLH0XTyf1iAdd0mEMFcLw5zwwSMlnBwuXFl5mDftR+xlWCMCCd8QC/C+/XGEFD7Rcf5IG43OV/OoGj5KsL6dCF6/OUXlNAVEWwbtpP72VxcGTkEt2tF1KjhmGP9c6DmqkRE8NhseAqKkMJCDEVW3AWFOAsKKMnLx1NQBIVFuAsKcRQUIh7P3/IICQ0lPj6ehFJiLjIykpCQkBPtNkt/goKCMJvNGI1GTCbTiU/ZdYPBcMK7V9rLV9lp50J0dHStF2s1z+d8AaOUMgGXAvO0pK5AaxHZp5S6HcgXkS5KqUBguVJqAdAcr3DpJiJWpVR0mTyjgSuA5iIiSqlT9VGfBtwrIku08OlTwP3aNpOIdFVKDdXSLz7DabQHOuAVTTuUUv8D4oD6x71vSqlIEclTSt1DKc+aVqHtItJLW7/zNOW01soJAnYDj4hIB6XUa8CNwOvAe8CdIrJLKdUNmAIM0I5PAHpp12828C0wiVKeNc32N0TkM6VUAF5xWCEaN67g6O4mE8bQEIyWCEyx0QT370V4bAwBDesTUK/uSWGjqvq18jic5M+dT8HPv6ECzEQM7UNY786YE/4+Mbm43dg27aJw4QryZv5E4ZIVxFx7JcGtW1aRdTUbj8NJ1sefYduwBcvw/lhGXXLBhbuUUoS0b0FwqyYUzFtG/pxfOfLvV4i4uA+WwQP9aqiPqkYphTEkBGNICNSNA7wv6UCgrL9MPB48xVbc+QW4Cwq9H03IpRcUcjQ7A/e+PbgLCvHY7HAKYVdbSJrycur+uybu9bUdVYku1moGwUqp9dryUrxeqB7AHyKyT0sfBLRVSo3W1i1AE7zi6ePjbdxEJKdM3gWAHfhAKfUDMLf0RqWUBYgUkSVa0ifAN6V2+V77XgMkV+BcfhaRfC3vrUASsAVI1cTPD3g9VuXxVQXKAPhVRAqBQqVUPjBHS9+E9zqF4b2G35R6OQaWOn6miHiArUqp8iakXAk8rpRKBL6vqFcNoOEtN2AVQZmMXsFlMqFOfIwYQkIwhIVgMJsxG42YDAZMBgOqmr39tgOHOPDuxzjSMwnr24XI0YMxRoSWu78yGglp35yQ9s2xb9tDzqdzyJjyMZF9ulN/zJUYAgPLPfZCw11sZf9bH2LbvZeo64cTMaiHr03yKcpswjK8H6E9O5D39TwK5v2CddVaEq4aiaVLhwtOxFaIoGCIObUH0iOCWwSPeHCL4Ha6cDtK8DiciMOBOJzax4GIB9wer6fOo32XWvemHY/ClYrGHY/MnRSgKz/tpEBe5Ub1OgO6WNPxOTYROWnET+2Hq7h0El7v1/wy+w3hNO2jRMSllOoKDASuAe7hL+9SRSjRvt1U7HkqKbXsxuuZy1VKtQMGA3cDVwM3l3N86XN24Q0/gteDVl45nlLrHs1OA5BX9rqWc/wp3xIi8rlSahUwDJivlLpVRH4pJ7+TSPvg04rs5lOmT5/O7S8/giEkiAaP3YGhWfJZHR/UohEJT99N3oxF5P20lPCMbH77aT7JyWeXT23k0KFDXHrppZTsS6Pe3ddh7nLWTTprLaZoC7F3jiFsQDfyps/h4HtTSdiyk/femkK7du18bZ6Of/K1rw2oavynG5TO+TIfuEspZQZQSjVVSoXi9VLdrJQK0dLLhkHDAIuI/Ig3tHmSeNG8YLlKqd5a0lhgCZWI1t7MICLfAf8COmqbCoHT9enfD3TSlkefZr+/ISIFwD6l1FWaDUoTjKfjJHuUUqnAXhGZjDdU6vtZtSsBEWHSpEmMHTsWY3I96j5991kLteOoADNRYy4l7oFxHD5wgBbt27Hw1wrp2VrL1q1b6dGjBzv37qHeQ7foQq0cgpomE//03cSOv4I/N6ynQ8eO3HHXnWRnZ/vaNB2dakcXa7WHD4CtwFql1GbgXbxeq3l4hcSfWih1YpnjwoG5SqmNeEXYA6fIexzwsrZPe+DflWx7fWCxZt9U4FEtfSrwjlJqvVLqVGMYvIJXoK4A/t6A6sxcD9yilNqANxR7+Rn23wi4lFIblFIPAGOAzZrdzfG27avRuFwubrvtNl588UUiB15E9MSbkNOEPStKcLtm1H1qAu6QQAYPGsxHX3xWCdbWPJYvX06vXr3IKi6k3uN3YGie7GuT/BplMBDavyv1XnwQy8DuvPfue6Q0bsSUKVNwu/2yA7yOTpWg9wbV0fENflfx7HY7119/Pd9//z0xIy8mdOSASm8n5C6ykvX6NOy7D/Dsf1/h8Qf+Wan5+zMzZ87k2muvxRhtIW7izXhiInxtUo3DceAo+Z//gHXbHpq2askHb79D7969z3ygTm2n1jdo1MWajo5v8KuKV1hYyMiRI/nll1+Iu2EEwZd0r7KyPCUOst76AtuG7Ux4eCJvvvBSrW48LiK8+OKLPPbYY4Q2akidB8bhqaWD3VYHIoJ19WbyvvwRV3Yel181mjdffY3ExERfm6bjO2rvD4iGLtZ0dHyD31S8rKwshg4dypq1a4i/9SoCepTX56LyEJeb7I9nULxsDaPGjeWrDz+ulVPv2O12br/9dj799FMs3TsQecuVYPa/fl0igqewGE+RFY+9BClxgMHg7Z0cFIAp2oIh2L8mLveUOCj68TfyfliCyWjinnvu4YlHHyU6+sKYWk3nJHSxpqOjUyX4RcU7dOgQgwYNYuee3dS9+wZM7ZtWW9ki4h2i4cff6DNsCAu+m0lgLRra4+jRo4waNYqVK1cSM2oQocP7+YUH0ZWTjyPtSO0yVwAAIABJREFUCI79h3GkHcGVno0rKxdxOE97nAoOxFw3loCURAJTEglq0QhTnahqsrp8nJk5FH67gMJVGwkKDeGf9z/AwxMnYrHUnjlVdc6I7ytWFaOLNR0d3+Dzirdjxw4GDRrE0axMEh4Yh2qa5BM7CuYtJfeLH2nbvRtL5y0gIqLmt+VatGgR119/PbkF+dS5/WrMnXw3KLC7sBj71j3aZzeuDG2oRaUwJ8QQkFgHc1wkpjoWTJYwVFAAhqAAlAgehwuPrQRXdgHOrDwcBzMp2XsEj9U7so05MZ7gDi0I69EBc704n50jgOPQMQpn/kzR6s2ERETwyEMTuf++f9SK50nnjOhiTUdHp0rwacVbvXo1Q4cOpcjloO6DNyMNyxv3t3ooWr6O7A+/JalZU1b9spj4eN/ac6643W6eeeYZnn32WUITE6hzz3V46lb/tEmunHysf27GumYLJTv2gwiG4ECCWyUT3DqFoMb1CUqOxxB89p5M8XhwHM6ieN1uitfsxLY1DTweAhs3JKxfF0Ivao/yYajXkXaEghmLKF63jaCwUO66404m/vOf1KtXz2c26VQ5uljT0dGpEnxW8RYuXMgVV1yBhAUT/9DNePwglAVg27CDzLc+I7pOHVYt/o1GjRr52qSzYvfu3dx0000sW7YMS58uRI0dgQRUn2jx2Eqwrt5E0W9/UrIrDYCABnGEdWtBSMcmBDeuVyVzjrryiyhYvIH8n9fiPJyFMSqCiCG9COvXFUOQ78LaJfsOUzxvKYWrNmI0Ghlz3bU8/sgkWrbUpz6rhehiTUdHp0rwScWbNm0at956K4H144l7cDzuShhDrTIp2X2AjNc+IdBkYs73MxnYv7+vTTojHo+HyZMn89hjj+E2Goi5/rJq6aRxnJJ9hyj8+Xesf2xCShyY68cS0acdYRe1JDDxXIYfPDdEBOuGPeR8vxTblv0YwkKwXD6A8AHdTprDtrpxZuRQvGA5BUtWIw4nXXr24IG77+HKK6+sVW0kL3B0saajo1MlVGvFc7vdTJo0iVdeeYXw1k2Jufs6JMQ/X1TOo5lkvfEpzowcnnvpRR554J9+0TD/VKxevZr77ruP33//nYgOLYm56Qo8lrJTblc+4vFg27CDgnlLKdm+DxUUQHjP1kQM6Ehws0SfXy/bzoNkff4Ltk17McXHEHnVYEI6t/apXe7CYqxL/qRwyR84M3IIj4rk5vE3cevNN9O6tT6LRA3HP38gKhFdrOno+IZqq3hZWVnceOON/PTTT0Rd0oOIa4aCyb+HyfBY7eS89w3F67Yy6IrL+fLDj4mK8o9wLXh7ej722GNMnTqVoCgLUWMuxXxR2yoXI+LxYF21kbxZv+A6mokp1kLksIuIGNgRU6h/Da0hIljX7SZz2gIcBzMIaplK9LiRmOvW8a1dHg/2rXuwLV5N4dot4PbQqHkzxl13Pddccw1NmjTxqX0654Qu1nR0dKqEaql4P//8MzfeeCPpGRnEjh1BUL8u1VFspSAeDwU/LCFvxiIsMTF88ck0Lh0yxKc2HTlyhJdffpl3330Xh8uFZXAvLMP74QkKqNJyRQTb+u3kfbsA56FjBDSMJ/rK3oR3b4nyc+Etbjf5C9eQ9dnPeBxOLMP7YRnWz6edEI7jLijCtnoz1lUbse3YB0DzNq25cvgIhg0bRrdu3Wrl+H+1EF2s6ejoVAlVWvHy8/P517/+xZtvvklI/brUufMapIFvh1Y4V0r2HSbnva9xHMlg0PDLeOeNyaSkpFSrDZs2bWLKlCl8/PHHOF1Ownp0JHrkQCQ2ssrLdhw4Ss6nsynZuR9zQgwxY/oT3rMVylCzpnZ25RaS8fE8ipZvxpwQQ/T4Kwlqnuprs07gys7Dvnoz1rVbse3y9nANj4xk8KBBXDJwIH369KFZs2Y+DzHrnJJaf1N0saaj4xuqpOJ5PB6++OILJk6cSHp6OpaLuxN59RAkwFwVxVUb4nBSMG8Z+XN/xSAw/qabefyRR6pUtOXl5TFr1izef/99li9fjjHATFj3DkSN6F8tIs1dZCX/+4UU/rIKQ1gwsdcNxDKwQ5X06KxOitftJv29ubgycgkf1IPI0YMxBFatZ/JscRfbKNm8C+fm3RRu2I47vxCAyJgY+vTuRd/efejcuTPt27fXx3HzD3SxpqOjUyVUasVzu93MmDGDp59+mi1bthDWqCEx40ZCUkJlFuNzXDn5FM78mYJla1EIQ4YO5dbxNzF06FCCgs6vzZaIsHfvXn755RdmzJjBokWLcDqdhNSLI7RfV0J6doCwkEo6k9NT/McmcqbNwlNkxTKkCzFjBmAKrz3ziXrsDjKnLyT/pz8wxUcTc+tVBDVN9rVZp0REcKVn4dyZhnNnGkXb9+LK9A4srJQiuVEq3Tp3oVOnTrRt25aWLVtSv3593QNXvdT6i62LtVqCUsoNbAJMwDZgnIhYfWvVySil+gETReSyU6TPAvZpSVkicvF5ljUe6Cwi95SzvT1QT0R+rEBe9wF3AWuBm4EfgFjgeRH56hxNrJSKd+DAAaZNm8b777/PgQMHCE2sS+TIizF2alHjwmRngysnH+vClRQsW4O7oIjgsFB69+7Nxf0H0LFjR1q0aEFCQkK5L0ybzcaRI0fYtm0bmzdvZuPGjSxdupRDhw4BEBQXQ1DnVli6tkWSEqrtWroLisiZNhvr6k0ENqpH/F2XE5RSt1rK9gXWTfs4NmUmrsx8Iob0xHLlIAw1wAvszivEkXYYOXAM2/7D2PcdwpWdd2J7SFgYzZo1o23r1rRo0YIWLVrQuHFjkpOTCQmpHsF/gaGLNZ2agVKqSETCtOXPgDUi8mqp7UYRcVdR2RXK+wxi7W/p52nTeE4v1k67vcy+24FLRWSfUuoi4EUR6XueJp5TxbNarfz5558sXryYWbNmsXbtWgDC2jQlckB3DO2bVqtIE48HRHwWmhO3G/vWPTjXbqdo226cRzNPbAsIDMASGUl0dDRmkxmXy4XD4SArK5OC/IKT8gmMjcLcqAHhLZtgbpYEdWOr3TNSvHoTOZ/MxGMrIebqfkSP7FnjQ54VwWMrIXPaAvIX/Ik5IZaYW0cT2Ng3U5+dD+6CIpxHMpCjWbiOZmI7dAznkQxcuSc/azFxdWiUmkrj1EakpKSQkpJCYmIiCQkJJCQkEBMTg6EW/9GqInSxplMzKCPW7gTaAl8DTwFHgfZAG+AFoB8QCLwlIu9qYunfQDbQDPgNmCAiHqXU20AXIBj4VkSe0srYD3wEDALeBHKAZ7R89wA3iUiRUmoI8DqQhdczlVpRsaaUuhZ4DG9F/EFEHjlD+k3Ao9r57gRKROQepdRV2nVwA/nAxcBu7ZwOA88DLYAiEXlFy2szcBkwCa83bQcwHbgNqIPXCzhKWx8BuIAFIjLxTPdK45QVT0TIz88nIyODjIwMDh06xM6dO9m5cyfbtm1j48aNuFwuUIrQJkmEdGxJcOfWqGqahcCdV0jxyvXYtu7Gse8wnsJiAAxhwQQk1SeoRSqhPTpgiqn6Nl2ntC+/EMfhDDiWhScnH1eRDVdRsVdUGhTKaMQcEY45MhxTZDiG+FhUvToYQnw37IXH4SR3+hyKlqz2etPuuYKghjWzM8j5ULxhD+lTZuHKLiBiSC8sV15SI7xsZ8JTbMN5NBNPZi7k5OPIyMaeno07Kwdndh54Tv4pMJnN1ImPo15CAvUT6hEdHU1UVBSRkZFERkaeWLZYLAQHB//tExQURFBQ0IUWhq31J6uLtVrCcbGmlDIB3wHz8IZDfwBaa16h24E4EXlWKRUILAeuApK0/VsCadryuyLyrVIqWkRylFJG4GfgPhHZqIm1KSLyklIqFvger/epWCn1CF7R9hKwCxiAVxx9BYRUIAz6DfAx8DvQCcgFFgCTgT/KSV+lfTrhFWS/Aus0sbYJGCIih5VSkSKSV9azppR6mlOINRHZr51rZxHJKi0slVLRwEqguYjI8bwrcr/qdmwjrpIS3HYHbocDV0kJ7hIHLqsdj8tV9uZiionEFB9DYEoiQY0bYm7cEGN49c0+4EzPIn/mzxT/vhE8HgIaxBHUpD6mGAsocOUUUrL7MCX7j4FShHRsgeWKSwhoUHtDeJWB80gGmW99gfPQMaKu7E3MmP4Y/HwojqrEbbWTOW0BBQvXYE6IJfrmUX7blq0yEJcbV04+7rwC3HmFePIKTyy78gpw5xfhsdrwWG2I3XFWeRvMJpTBgDIaUUbvt8Fo8KYZvGkGo9G73aC8ywYDKIUyKBTK+wdHE33ebaDU8W8F2ked9ptyt5dLOZtUORv2Lfyt1os13w90o1NZBCul1mvLS4EPgR7AHyJyXAQNAtoqpUZr6xagCeDQ9tsLoJT6AugFfAtcrYk8E5CAV9Bt1I4/3l7rIi19uVaxA9BEDLBPRHZp+U4Hbi/H/qWlRZxS6nJgsYhkauufAX3weqROlU6Z9K+Aplr6cmCqUuprvKKysigA7MAHSqkfgLkVPTCvsBAVaEZFhKACLRgCzBgDzAQFBWKMCMUQHoYxIhRjZASm+JgTHgZDNf+BFJeLvDm/kjfnV5TRSOSwblgu7lzuNEbOjFzyF60l76dVWNduI+KS7kSNGuzTOSL9laIV68iaOgMVYKLeE2MJ69DY1yb5HGNIEHXvHEFEj9YcmzKL9Ofe8z5Do4f4XY/RSsFkwhgXA3Exp9wsyAkXvLjceGx2r3grtuGxlSAOJ+J0ad9O77fD5V12usAjiMft/XZ7wOPRvt2IR3C7PV6vs9tzYj9EAAHxIG5tXdC+vcsiHq9RnuP7ereL/H3/Ew6hE9uOl3Fqyt9UzgaB5Gkv3Lf/xkmTT3epazq6WKs92ETkpAkJNeFUXDoJuFdE5pfZrx9/rwmilEoBJgJdRCRXKTUVKB0vOp63AhaKyLVl8m1/inwrSnmq5HRqpbzQ4p1KqW7AMGC9ZldZXEDphiJnjIuJiEsp1RUYCFwD3IPXi3hGDm7cQpGzBJPy37Ypu3bs4O7xN5O3ZSuRfdpR58bBqKjTe/PMcVHEXjeQqOHdyf5qMXnzVmLcvIcPpn5Cl4u6VZPl/o3NauWphyfx5bSvCG2ZTML9ozHEhPvaLL8ipG0qya9NIPuzn8n9aQUB2/bz1jvv0r13L1+bdkHhQfCI9yMiJ9YFTqSdWEY0naYJTG3b8X2AE9LzhH4r9ZN92hfFGSKA1y388oNzOsEahC7WLizmA3cppX4REadSqineNlsAXTVxlgaMAd4DIvAKsnylVDxwKbD4FPn+DryllGosIruVUiFAIrAdSFFKNRKRPcC1pzi2PFYBb2gh1lzt2P/hDYOeLj0Gr8frKmADgFb+KmCVUmo40AAoBEq/IffjbaOGUqojcMYBvJRSYXjDuj8qpX7HG+qtEHWCQ6kT7F+TqJfmu+++Y/z48bhMiuTHxhLQ6ey8PsbwEOJuHUp4z1ak/28mo4cO49kXX+DRBx680NrSnMT27du56qqr2Lx5M3FX9cNyVZ8LohPBuWAIDqTOrUMJ7d6SjCmzGDNsODfedguTX/4vFovF1+bp+BH7b5zkVyMfVAX++7depyr4ANgKrNXaZL3LX4J9Jd7OB5vxth2bISIbgHXAFrydCZafKlMt9Dge+EIptRGveGsuIna8Yc8flFLL8ArBCiEiR/F2FvgVr+haKyKzzpD+tHYei/B2ZjjOy0qpTdo5/6Yd9yvQUim1Xik1Bm87v2gtlHwX3g4KZyIcmKud8xLggYqen78iIjz11FOMHj0a6keT9PKdZy3UShPcIokGL91OaPvGPP7gQwy/9iocjrNre1Nb+Oyzz+jcuTO7Du4n5anxRF7TXxdqFSCkVTIN/3sXUZd1Z9oHH9GwcSoff/LJX+E1HZ0LAL2DgU6VDJ2hc0b8ruK5XC4mTJjA+++/T/TATsTcNrTS5m8Uj4fsb5aQ8/ViWvfoyrIfF1ww3hGr1cp9993Hhx9+SHirFBLuHw3RYb42q0Zi332YrA9+xLrrEO0v6sq09z6gTZs2vjZLx/fUene9LtZ0dLHmG/yq4tntdq699lpmzpzpDc+N6Vcl4cr8X9eT/vYs6qYm8cfPS2jQoEGll+FPnBT2HN0Xy9V9dW/aeSIeDwW/rCNr+iI8VjvjbrmZF/79LPHx8b42Tcd36GJNR0enSvCbipeXl8fll1/O0qVLSbhlGGGXdqnS8oo37OHoy18REhbKbwt/oUO7dlVani8QET755BPuvvtuPAFGEv4xCnPb6p18vrbjLrSS88Wv5C78k8CgQB6cOJFHH3qYsDDda3kBoos1HR2dKsEvKt6RI0cYMmQIW7dto/79ownq3qJayi3Zf4zD//cZqsTJ7JmzGHLxJdVSbnVQWFjIhAkTmD59OpY2jah7/ygk0n87k9R0HIezyP3iF/JXbiEiJoonn/gXd91+hz6t04WFLtZ0dHSqBJ9XvJ07dzJ48GAOZxyjwSPXYWpdvVP8ODPzOPJ/n+E4ms37H33ILWPHVWv5VcH69esZM2YMu3bvJu7qfkRc2Rtl9K9+XG6rnZK9RynZexRHeg6u7AJcuYWIwwVuD8psxBAegskSSkBiHQIS4whulogpOsLXpp8W286D5Ez/meIt+4iIjuKhBx/kvnvuJSLCv+3WqRR0saajo1Ml+LTi/fHHHwwbNowil4MGT4xFpfhmeiN3kY2jL32Jdct+/vXsv3nmsSdq5NAebrebV155hSeffBJjeAj17h+NsaV/tMcTtwf7zoMUr91F8bpdlOw7dmKbMSyIgDoRmKPDMAR6R7z3OF24Cmw4c4pwpOef2DegfiwhHRoT3qsNQY3r++19sm5NI3/GMgrX7iQ4PIwJd93FfXffQ8OGDX1tmk7V4Z8PYyWiizUdHd/gs4o3b948Ro0ahbKEkPivsUi8b+bxPI7H6SJ98gwKV2zmhttvYeqUdzHWoEb4O3fuZPz48axcuZLI7q2Jv/0yJCLY12ZRkpZOwZINFC7diCunEAyKsJaJRLRPJrRpAqFNEjBHnj5U6LY7sKVlUbjpIAXr91O4IQ1xuQlIiMYyuAsRAzpiDPXdvKqnw77nCPkzlpG/aisKxaWXDWXi/f+kX7+q6Tyj41Nq/Q3VxZqOjm/wScWbNm0at9xyC8FJdan3+PWIxT/a9YjHQ9a0BeTOWUmfoYP48evvCQ3173ZeLpeLN998k8ceewyP2UjcLUMJ6tnSp0JA3G6K/thO7pyV2HccBKMBS+dUovu1IrJLKqbzFFauIju5y3eStXADRVsOYQgOwHJxJ6Ku6IXJ4p8N+50ZeRQuXEPuwj9xF1pJbtqYCbfezg033EBCQoKvzdOpHHSxpqOjUyVUa8Vzu908+uijvPzyy0S0bUzCw2OQYP+bazF37koyp86nfuMUfp7zI82aNfO1Sadk2bJl3H333WzcuBFL5+bUvWuETzsReBxO8heuIXfOClyZ+QTERxI3ohMxA1oTcAbv2blSvOsox2asJmfJVgyBZqIu607kiB4YQ/zT0+YpcVK0fDMFC9dg3XkQZTAw4JKLuf3mWxgxYgRBQf5pt06F0MWajo5OlVBtFS8vL4/rr7+eH3/8kdhLuxE9fjCY/DfMWLxhD8de+xaDW/joww+54ZqzmaWsajl48CBPPPEE06ZNIyQumjo3DSGgS1OfedPE6SL/57XkfPcbrpxCwlolEn9FV6IualJtHRtsB7M5PO03cpdtxxQVRuy4wYT3auPXoUbH4SyKl2wkd/E6XNkFhISHMXz4cK69egyDBg0iONj3YWyds8J/H7ZKQhdrOjq+oVoq3ooVK7juuus4ePgQCbcOI/SSTtVR7HnjzMzj2KvfYtt5kMtGX8HUd94nJibGZ/ZkZGTw/PPP8/bbb+PyuIke0ZOoUb0h0OwTe8TjoXDpJrK++BlXZj6hLROpP7YPlvbV26O3NEU7jpD21nysu44R0jqZuNsuIyCxjs/sqQji9mDdvA/biq3k/74Fd5GNoNAQhg0bxrVXj2Hw4MH6uG01A12s6ejoVAlVWvFKSkp44YUX+M9//kNQXBQJ94/G0Lhmtc8Rp4ucGUvJ/vY3wiMtvPrSK9w0bly1dj7Ys2cPb7zxBh999BFWm42o/h2Ivbo/xIZXmw1lse06ROZHP2HfeYiQxnWpP64vlk4pfuHJEreHzJ/Wc+iTJXjsTmLG9CPq8p41YtYGcbmxbtmPfdV28lZuxl1gxRRgpkevnoy8bARDhw6laVPfeVF1Tkutvym6WNPR8Q1VVvEWL17MXXfdxfbt24nq2564W4chIf7XPq2ilOw/RuY7c7DuOkTjVs159fmXGDZsGAZD1YT5nE4nCxYs4P3332f27NkYjEbCe7UhbnRfSIiqkjIrgiu3kKzPFlHw63pMUaEk3tSP2IFtUAb/e08584pJe3M+uct3ENysPvH3XEFAPf/2spVG3G5s2w5Qsm4PBWt2UHIwA4DElCRGDL2MgQMG0LdvX596e3VOwv8qQSWjizUdHd9Q6RVv/fr1PPnkk8yZM4fQhFjibrsMc7vaMcWRiFC0YgvZ0xfhyMilYeNUHvrHA1x99dXExZ3/GHF2u52lS5cye/ZsvvzyS7Kysgi0hBFxSWeiLu0KPuw8IB4P+YvWkPXpQsThIv6KLiSM6YEpNNBnNlUEESFnyVbS3lqAx+Ei9vqBRA69CFVFIrsqcWbkYVu3G+u6XRRu3IOUOAFo3roVgwYMpH///vTu3VsXb75DF2s6OjpVQqVUPI/Hw/z585kyZQpz584lMDyUyOHdsVx2kc/aU3lKnNi2pmHbeRBXVj7i9mAMCyawYRwhHZpgjjn3EeXF5aZw5Vby567EtvswymCgR+9eDBs8hJ49e9KpU6czDvkhIhw7dox169axdu1ali9fzpIlS7DZbBgDzIR1aU5Mvw4Y2yShzKZztrUycBzJIv3t2di2phHeLomke4YQnBjtU5vOFkd2Ifvf+In81XsIaZNM/N1XYK7j27H9zgdxurDvOYJjaxrFm/dTvC0NcXjFW4OUZHp2u4hu3brRtWtXOnTooHdWqB50saaUcgObABOwDRgnItbT7L8YmCgif56XYUrVAeYCAcB9IrJUS78cuElERmrrjwK3iEhjbX04cJuIjDjP8otEpEpbliqlegPvAE6gu4jYSm1LBN4CWgIGvNfiIRFxKKXaA/VE5Edt36eBIhF5pZLsmgr0BY4PX/4REAv8JiKLlFL7gc4iklUZ5Z2lbfuBgyLSu1TaesAkIq1Pc1wy0ENEPj+HMleISI8z7HO2z8s5izW3283KlSv5/vvv+f7770lLSyMo2kLEoE5EDrsIQnzjcXHlFJAzazkFi9fjKbKDQWGOCkWZjLjyrXjs3hdacMskokb2IrRjk3Nu/yMiONLSsf2+jfzft54IUwHExseRkpxMlCWSsLAwTCYTxcXFFBcXc/TYMdLS0rDbtKqmFCGJcQS1TSWyY1MMzRMxBPk+ZCwuN7mzV5D99a+oABMNbxtI7KC2Nba9lIiQtWAjB95dBAZF3C1DCe/TrsaeT2nE6cK++zDOnYex7zpM8a6DOLO8P50Go5HkRqm0b92G1q1b06pVK1q1akWTJk0ICPD9c1aLqPkP0hmoiFg78RJSSn0GrBGRV0+z/2IqR6xdA1wqIuPKpNcBNotIvLY+G0gEhohIhlLqeSBPRF48z/LPSawp76+PEhFPBfZ9B1glIh+fIo9VwNsi8rFSygi8B+SIyENKqfF4xdI92v5Pcx5iTSllFBF3qfWpwFwR+bac/fdzBrGmlDKJiOtc7DmDrfuBPGC4iBxUSrUAvuDMYq0f3ufysrMo66TrcoZ9q0SsuVwu9u/fz/bt29mwYQPLly9nxYoV5OfnYzSbCG3biOh+HTB3aeIzL5C43OTMWErOjGXgdhPZoxmxA9sQ3rYBRk34iEewH8omZ/kOsuZtwJGRT3DzROLuGEFgw/jztsFdUIxtx0HkUDaOYznYM3Jx20qgxIG4BUOQGRVgxmgJJSg+mqD4aMwN4zAkx2EI9q9won3vEdKnzKJk3zEiezSj4YRBBMbUjh6J9qO57HtlLkVbDxHevSVxdwzHGO4fAzNXJq7cQkp2H8a19xj2tHRsB9JxpOeAx1vtlVLEJySQmppKo5QUUlJSSE5Opm7dusTFxREfH09cXJwu6CqOLtbKiLU7gbbA15R68Sml3gT+FJGppcWaUqoIeBfoD+QC14hIZpn8k/B6buoAmcBNQDQwGwgGDvN3r9NOYKiI7FZKrQG+B7aIyEyl1BLgCeBA2XxF5MCpytPSU4DP8XoQ5wEPnOrlq5T6J3CztvqBiLyueW1+An4FugMjRSSt1DEDgVe0vFcDdwFjgZfweq9WiMj1ZfZ/SkT6lEqLAPYBKcDmUtfmeaAF0BBI1b5fF5HJ2nE3APfh9VCuAiaIiFu7N68Cg4EHRWRZqbKmUkaslU7TBNNXeO8rwHXavZgK5AAdgLXAp3g9hyHAHuBmEckt84zE4n12kpVSrYCPNVsNwCgR2VXm+u/HK1wdIvKKUurfQDEwVkRaa/fiU+B4LOweEVmhlPpdu077gE+AycALQD8gEHhLRN7VRN1TwFGgvYi0PF4HlFJhwCwgCjADT4jILM2usxJrc+bMkeLiYqxWK6W/s7OzSU9PJz09nWPpxziQdgCHw3HiuJCGdQlsloilbWNM7VMw+HgAUseRbI6+/i0le44Q1as5iTf1I6je6Rvhe1xushdt4tDHi3EVlxB7TX+iRvaqkW2ZKhNPiZPsrxeTO3s5JksISRMGE93LPwcFPh/E7eHot6s4Mv03jOEhxN99OaEdmvrarCrHU+LEcSQL18FMPOl5ONJzsKXn4MrIw5ldAKd4F0dEWoiJjSXSYiHKEkl4eDgREREnPiEhIQQGBhIQEHDKb7PZjNFoxGAwYDAYUEqdWD7V+vG045+qoCrIuLPJAAAgAElEQVTybdu2ba0XaxX+K66UMgGX4hUyFSUUWCsiDyqlnsT7ErynzD5vAtNE5BOl1M3AZBEZqe1/wntUhhVAD83jtAv4HRislJqLV0yuBr4pmy8w8lTlaelv4PVkTVNK3V3ONeiEV0x2w6vkV2niMBdohlf4TShzTBAwFRgoIjuVUtOAuzSR14tTe7BaAWtKJ4hIgVLqAJAMnHRtNM9ac7ziKRzYoZR6G2gMjAF6iohTKTUFuB6YhvfebBaRJ091rsDLSqkntOWxp9heICJdlVI3Aq8Dxz1WTYGLNUG4EbhXRJZoouop4P5yygO4E3hDRD5TSgUA5fX3/xbvNX0FGK6d03EbM4BLRMSulGqC1+vWGZjEyX8wbgfyRaSLUioQWK6UWqDl0RVoLSL7ypRrB67Q7kUs8LtSaracQ8PPESNOHaU3hAVjsoRijAzDFBdGaKsuRNWvQ0BiLAH1YzGG+k/7l6I/d3D0tW8xmI00evzKCgsLg8lInSHtiezelLS3FpD12c/Yt6URf9+oWullqQjWLftJf3sWzqM5xA5qS+ItAzD7wfyiVYEyGqg3pjuRnVPZ8/JsDj/7GZGDOxN742C/CEFXFYZAM0EpCZDy9yF0xOnCmV2AO78Yd14Rrvxi3PlFuPKKySq0kmErxHM0C/eeEsTmwG0rwWO1g/uMAZwLgqbfPdNhx5VPrvO1HVVJRcRasNYmCGAp8CFw2vY7pfDg9cAATMfrAStLd+BKbflTvN6mM7Fcs8EIrAT+wCtgOgA7tBd1efmWl94TGFUq/VRh1F7ADBEpBlBKfQ/0xusFTBOR309xTDNgn4js1NY/Ae7GK3DKQ3HqMFl56QA/iEgJUKKUygDigYFAJ2C19m8mGK+YAXAD353GhofKeNbKbv+i1PdrpdK/0YSaBYgUkSVa+id4BfTpWAk8rrXX+76sV60UOUCuFirfBpRuQ2kG3tTa9bnxisdTMQhoq5Qara1bgCaAA/jjFEINvNf/OaVUH7zPdn281/nYGc7rb7R//QFylRNDgBlDkBlzUCDGADMmowmTMmAyGDAqA/7o3RcRjs5eypEPZxOSGk+TJ0cRUOfsOw2YLSE0evRyMts24MC7P3PosQ9o+cxtBCfUnCEezhdXsY20j38gfd5KAutG0uy5a4nokOxrs6qFkEbxtJp8E4c+WUL6jD+wb9pHkwevJ7yZ7wb29RmBQNiZOl0IbhHc4sEjgtvjxuN243a6cDtdeBxO77fLjbhciMuNON1ej50I4hFtGe+6iDcse3z5+McjVTeuUFV0aPRmef5dwv2ciog1m4i0L52glHLhDVMdp6KxmIrcqYrsswK4F69Ye19ECjUPVj+8Qu5s8pUK7HOc0705i8/hmPLYwl/C0ZuJNwzaAG848VTD0JeUWnbjvbcK+EREHj3F/vaKtscqh/KuW3nXoTSln58Tz46IfK6UWgUMA+YrpW4VkV/KyeMrvB0wxpdJfwBIB9ppZdjLOV7h9frNPynRGwYt7xyuxxs+76R5KvdT8Wf/JNb9o9xmn36NiDBp0iReen8WsT2bkzTxMgxB597rVClF3GWdCE6JZ/e/v2XbQ2/y05wf6Nerz5kPruHMmjWLCQ9MIOPYMepdeREJY3ud17WsDMQjuIvtiNONMhkwhARiqMKpyQxa54nIbo3Z/98f2Pzwmzw86RH+89QzmM2+vRY6NYr5Z96lZnOujUTSgJZKqUDNgzLwNPkf91xcByw7xT4rgGu05evL2acsW4F6eL1ax12f6/GG0VacId/y0peXST8VvwEjlVIhSqlQ4Aq83sbTsR1IVko11tbHAktOsz/Az0CIFmJEC/f+F5iq9cQtxBvuPBM/A6OVUnFaPtFam73KYEyp75VlN4pIPl7v1/Fem6XPez9/Cc7jzwdKqVRgr9bebjbekHZ5zMDrFS1bSS3AUa2Dx1j+CqWWvWbzgbuUUmat7KbaPT0dFiBDE2r9gQvKBSAiTJw4kZdeeom6wzqR/OjllSYuwlsl0uLVGyHYzMUDL+azb76slHz9kfT0dK6++mpGjhxJcbDQ7vWbqH9b/2oXauL2ULj5IIen/caup79hw7i3+HP4i6y7+nXWX/8/1o15gzWXv8yGcW+x84kvOfL5Mgq3HPJ6aCqZiLZJtJxyM3UGtObF/3uetl06sn379kovR0enpnJO3ce0XnhfAxvxthkrL1ZcDLTSOgHk89cLvjT3AR8ppR7irw4GZypfNA+MRUScWvJK4Hb+Emvl5Vte+j+Az5VS/6Cc8KCIrNUa0f+hJX0gIuu0Ru3l2WpXSt0EfKO1+1uNt9H9mc7vCmCKUupfeEXvj8Bj2i6/ApO08PTzp8lnq9bubIFSyoB3iJC78Yrt8yVQuwcGoLyZtscB7yilQoC9/HWtXwG+VkqNBUp7zsYANyilnHhDi/8ur3ARKUQLVZcJ0U4BvlNKXYX3Oh33km0EXEqpDXjbu72Bt/3fWuXNIBNv28XT8RkwRyn1J94/BxfM20REuP/++5k8eTIJl3el/h0DKr2hcFD9aJq/eiO7n/mWG665jsPHjvLwvQ9Uahm+RESYOnUqDz74IAVFhSSN60ed0V1RVei5OpUNRVsOkbVgA7krduIuLkEZFKENo4hpU5fghKYEWIIxBBjxON04C+zYjhZQsDuLw9OXwqdLCYgNJ7p/K+KHdzqn8Hd5mEKDSPrnMMK7NWb35J9o074tjz7+OI899AhBQb7tSKOj42uqdFDcs+0hp6NzAVFjRqP2eDzce++9TJkyhXpXdKPebf2rdHwst93B3udmkrd6D/+YNJHXnnupxo/HtXnzZu69914WL15MVJtkUu8biiHRUm3le1xucn7dwtFvfsd+MBtjsJm6fRpRp0cKdTo3wBx25uFLnIV2Mn5P48jPO8lclYZSipj+Lak3tg+BcZV7Ls6cIg68vZCcZdtJSErknclvMXz48Br/HOhUGbX+wdDFmo6Ob6gRYs3j8TBhwgTeffdd6o/uTsLNfavlhelxuUmbPI+shRu5atx1fP7BJ5hMvp1N4FzIz8/nmWeeYfLkyZhDg0gc15fIIW2rbT5PcXvIWriRI18sx5FRQHijWJJGt6de/8aYgs897Go9WsD+7zZwYNYmEKh7ZRfqXtPzxLh6lUX+un0cemcR1gNZ9Lq4H/97+TXat29/5gN1LjR0saajo1Ml+H3F83g83HHHHXzwwQckjulJ3XG9q9WzISIcnvYbR79cQd8hF/Pjd7MICakZQ3t4PB6mT5/Oww8/TEZGBvGXdqDBuH4QUX0D8BZsTOPAu4uw7c3A0rIujcZ2Jr57cqXeQ1tGITveW8mRhTsIqhdJ8gPDCG/dsNLyB69wz5i9hiNfLMddZOfSyy/jxf88R5s2bSq1HJ0ajS7WdHR0qgS/rnhut5tbb72VqVOn0uC63sTf0NNnIaiMuWtIm7KA1p3as3jeIr+eLFtEmDdvHpMmTWLjxo1ENm9A8oRBmJtU38gCzjwrB95eQM5v2wiKD6fZnT2p179xld6/7PWH2fjiImxHC0gY3Y364/qhjJU7yLGryE7GzD85NuMP3NYSLhk2hEcemMiAAZXfflKnxlHrHwBdrOno+Aa/rXhut5vx48czffp0Go7tS/x1FR1WserIWbadvS/Npl5SA5YvWkxSkv91xP3999+ZNGkSS5YsIbxeLPVv7ENY76bVFvIEyFm6jbQ35+O2ltDohs6kXtsJU1D1hI9dVgfbpizn4JzNRLRNJHXSlZijztTB+hzKKbSRMeNPMn5cizPfSkqzxtx7xwSuueYaEhL+PuCszgWBLtZ0dHSqBL+seC6Xi7Fjx/Lll1+SNL4/cWMu8rVJJyjcdIBdz3xLWGgYv85fSIf2HXxtEiLCkiVLeO6551i4cCHB0REkXNOD6CFtUebq6+XpKrSxf/I8cpdtJ6JZHG0euRhLI994IA/P386m//6KKSyQRv8aRViz+lVSjsfhImfJVjLnrqNo5xGUwUCvvr259qoxDB48mNTU1CopV8cv0cWajo5OleB3Fc9ms3Hdddcxc+ZMkm8ZSJ3RXX1t0t+w7stg15Nf4yks4dXXX+WeOyb4JATmdruZO3cuL774IitXriQ4OoL4K7oQM7Q9hpDqnTKpcOsh9r4wC2duEU1u6kbqNR0xmHw7z2rBnizWPP4DJTlWGj0ygsjuVTvHqe1gNvlLtpH56xbsR3IASGqUwqWXDKZ79+507dqVpk2bYrjA55+txehiTUdHp0rwq4qXnZ3NiBEjWLlyJSl3DSZmuO+9VuXhzCli33/nkr92H4MuH8qn731MXFz1tAlLT0/nww8/5N133+XAgQOEJkRTd1Q3oi5ujQqs3t6q4hGOffs7hz5ZQnDdcNo/OYSoFvHVasPpKMmx8uejc8jfkUHSXRcTN7xLlZcpIpQczqFwbRoFa/aSvykNt80BQGh4GC1atqB1i1a0aNGCZs2akZqaSlJSEhERlTdenI5P0MWajo5OleA3FW/Pnj1cdtll7N67hyYPjySsZ+MzH+RjjguVw5/+RlBICC+98CJ33nZ7lQzvYbfb+eGHH/j888+ZM2cOTqeT6A6pJAzvTHDXlEpvSF8RXMV29r44m/zVe6jbrzGtJw4gILz6eppWFJfNyfr/zCdj+T7qj7mIhHH9qrdHsduD/VAO1p1HKdmVTtGBTGwHs3DkFJ20X1hEOA0aNiA1OYWkhkk0bNiQpKQkUlNTadSoEdHR0XonBv+m1t8cXazp6PgGv6h4P/zwAzfccAN2j5OmT40msGU9X5t0VtgOZHHwrQXkb0yjXnIDnn3yGa699trzHvG+oKCARYsWMXv2bGbMmEFBQQHB0RFE9m1OwtBOGBPPNOl21WE/ksuup7+h5EguLe7tTdLINn4tJMTtYfNrizk4Zwt1L+9I4u2DqrXTxalwFduxH8rBmZ6PJ6uYkox8bOl52DPycGQW4iq0nbR/uCWC5NQUmjduSpMmTWjVqhXt2rWjWbNmNXL8v1qI/1aASkIXazo6vsGnFc/hcPDMM8/w3HPPEdmkPo2fuAIVV5HpZv0PESHv910c/Ww5xXuOEWoJ54brrufy4SPo06cPoaFn7pGYlZXF6tWr+eOPP/jll19YsWIFLpeLgNBgIns0JX5AWwLb1POJF600BRvT2P3s9xgUdHjmUmI7JvrUnooiImyfsox9X68nbnBrGt47zOfX8nS4rSWUZBRQciwP99F8HEfzsB7NwXYkh5L0fMTtAcAcGECT5s3o3L4j3bp2pXv37rRp00YXcNWPLtZ0dHSqBJ9VvPXr1zNu3Dg2btxI/OD2NLzrEqjm9lZVgYhQuD6NnIWbyF6+HY/DhdFkJKVRI1q3bEmd2DpYLBaUUlitVnJzc9m/fz979+3l2NFj3kyUIrxRXSI6pRDTpQnmZvEYqnHuztOROW89aW/OJ6S+hU7PXUZYA995984FEWHX1D/YPfUPYvs2I+nByzFUY4/ZysLjcmM/mI1tXyaO/VkU702naM8xnHneaYiDQoLp2LkzfXv2okePHnTv3t2vxwasJehiTUdHp0qo9oqXmZnJM888wzvvvENgZBjJ9w0htGvtHN7AU+KkcMshbJsPYU3LwnooC3eRHVeRHaUUxiAzxpBAAuIsBMRHEN4wjtCm9TA3isUY4l9tv8Tt4eAHv5A+czWxXRrS/qkhftk+raLs/XIt299eTlS3VFIfG4UhoHb8UXBk5FO87TC27Ucp2HqI4j3piMfrgUtt2pi+PXvTq1cvevbsSdOmTf06dF0DqfUXUxdrOjq+odoqXnp6Om+99RZvvPEGRcVFxA/tSP2xvVHh59euS6fqcRXb2fvCLPL/3EvSqHa0mNDL58NyVAZpszax5bXFWNo1pNGTV2EMrt7hTqoDt91B8c5j2LcfoXDrIQq2HMRVZAcgMjqKnj160ruX1/vWuXNngoODfWxxjUYXa9WJUsoNbAJMwD5grIjkVWL+J00sr5QaD3QWkXuUUncCVhGZVuaYZGCuiLSuRDsuAt4AArXPVyLytFLqaaBIRF4ps/+/gd9EZFEl2rAf77lnnUce7YF6IvKjtv40p7DfHzjNtX0auA3I1JLmicikajCpSiue2+1m8eLFTJ8+nS+++AKHw0FMj2Ykje+PoZIbx7uK7LitJV5vVViwzxuP1xZKdyRoeX9fkkZU2k+QX3B4/nY2vLCI8OZ1afzMNZjCavefB/EI9kPZ2LYdoXjbYfI2H8B+2DsmnMlson3HDvTp2ZvOnTvTpk0bmjVrhtls9rHVNYZa/6Pjb/5nm4i0B1BKfQLcDfxfdRQsIu9URzkanwBXi8gGpZQROO2IkSLyZPWYdda0BzoDP1ZGZkopo4i4KyOvs+S1cxGYPrT3b4gIBw8eZMmSJSxatIgFCxZw7NgxAkKDiL64NfWv7IahnqVSyvI43eT9sZuc37ZRtOkAztziE9uMIQGEtaxPVO+WRPdq5nchxZpCwcYD7Pm/70E8dH7lcurUkI4EZ0P9wc0xBptY98x8dk6aTpNnr8McGeJrs6oMZVAEN4wluGEs0YPb0gBw5luxbjuMbdtRdmw5wNr/TcbjdAFeAdekWTM6tGtHi+YtSE1NJTU1lZSUFOLi4vQw6gWGv3nWTni+NE9XWxGZoJTqCrwOBAM24CYR2aGU+hGYJCIblVLrgBki8m+l1H+ANBH5oLz8tfXx/OVZexrN86KU6gR8BFiBZcClItJaE1YvAP3wesTeEpF3lVIJwFdABF4BfJeILD3NeeYCzUQko0x6aRtuA67UPm/j9e59q3nEPgGGA2bgKhHZrpTqi9dbB16vTR8RKTyNDfsp41lTStUB3gEaakn3i8jyU11/vJ7P3VraYeB5oIV2bKr2/bqITNbyvgG4DwgAVgETRMStlCoCXgUGAw+KyLJy7B0OPKEdnw1cLyLp2jUrr8zHgRuBg3g9Z2vK8ayd5HEr/Vxo63OBV0RkcVl7gcuAEYALWCAiE8u75mWocMUTEaxWKwUFBRQUFJCRkcHBgwc5ePAgBw4cYMuWLWzYuJG83FwAgiLDCG3XkPjerQjunIQhsHL+nYvbQ9aCjRz5cjmOjAICooKp0zWJsJQYTGGBuG1Oig/kkr32INbD+RhDA0kY3Y24kV0wBtW+MFdVkTl/A2n/m0dIPQudnq95HQnOlsxV/8/eecdXUaV/+Dn33vRKKgQISWgJgRB6FVARBASxIKKCLqsu9t7QVda199X1Z8HuqsuKCiKgIL0X6SAJJCEBElJIT25ufX9/3AsETCAotxDn+XwmM3fmzDnvzJ1z55v3nPOeXH55Yj7+LcPo+Ox1+Eadn6OSzwV2i426Q0cxHSjBlFtCdU4hNTlFmIsrT0rnHxhA6zataRXbipaxscQ6l5iYGEJDQwkNDSUkJOSkdUBAAL6+vvj4+DRHodfsLuhUvM2zBjg8FsDFwIfOXXtxiA+rUmo48BxwFbASuMApPKzAIGf6wcB/Gsg6QCm1rd7nCOD7BtJ9DNwlIiuUUi/X2/9XoEJE+iil/IA1SqlFOATVTyLyrNP2M/17+DqQoZRaDvwIfCoidfWu/05gBDBeREwNVKwSEemplLodeBC42bm+wymugoG6U09qAv/C4WVarZSKB37CIcB+c/9F5Cql1JOcLGpmAMnAhUCI8xrfAToAE4FBImJRSv0fcD3wGRAE7GqC93A10F9ERCl1M/AwDrFEI2WmAdcCPXA851uAXxrJ+z6nmAR45Ax2HLdXKRWB4xlNdtrV5LdqXM/OiM2G3WbHbrMhNrtj2+rYd+yYtc6MpbbueKiAU9EH+RHQJpKA/u1ISOpLUEprAhJjznlTpDG3hJw35lOzN5+wlFi63juEmH7tGuw/JSKU7Sog+6stHPp0JSU/bafdvaMJ7Z5wTm1qbojNzsEPl1L43SYi+8TT48lL8Q1t/p7J6H7t6PPy5Wx+dB4ZD39Op+cn4RfbwtNmeQSdj57AxBgCE0+ekcNusmAqrMB0pBxzQTmmgnLKSqsoKjvA5pzdWMprsVU3/Sdf52NAZ9Cj99Gj8zGg9zGg8zGgdDrHb4dSKKVQOufauc3xfTqUAnQ653HgTALwDMfP+It1mvMPbdxzprPPe7xNrB0TUwk4XqyLnfvDgE+VUh1xeCSOuQpW4fDW5ADzgUuUUoFAgohkNJD/8WZWOOFBqZ9AKRUGhIvICueuz4FRzu0RQJpS6up6dnUENgEfKaV8gDkiUl8Q/gan9+8LZ37XAZNweOsAJgOHcAg1SyNZfOtc/4JDKAKsAV5z5vutiBw6nQ2NMBzoUk8chiqlQmj8/jfEfBExASalVBEQi0N49wI2OfMOAI55FW3AN02wrQ0wy+nF9MXxnZ+uzAtweFprAZRSDYnyY5zUDOp8Lhqjvr2VOETxB0qp+cAPTbgOAKqtdY44Uz4KpfdB6XUonQ693rE4Pit0fo5Ri/ogP/SBvugD/TCEBuAbHYpvVIhbmhmLf9xG7tuLMAT6kPb4CFpfcvqRbEopIrrFEdEtjtLth9nx0lIyHv2KVlf2ofXUi7w6vpansNWYyHpxLhWbsmh3ZRopd1zQLAYSNJXI9Nb0e308mx76nowH/0PH5yYR0DbK02Z5DTo/n+NNqI1ht9iwVtZiqzVjqzVhrzVjMzq2bUYzdpMVsdoQqw27xbEWi2OxW22IxYoIYBcQQZwLdudacOy3C4jNuQZszuOn44zHz3QHGk8gAn1/nP7wxkufe+lMuZzPeJtYM4pIulMw/YCjz9qbwD+BZSJyhbPD/3Jn+k04xFY2DmEXhaOzeGMelKagaPzJUDg8bj/95oBSQ4AxwOdKqZdPHahwKiKSBbyjlJoJFCuljgXi2YWjL1gbThYk9TE51zac36GIvOAUDKOB9Uqp4SKy93Q2NIAOGCAiJ4XvVkq9RcP3/3S21bdP4fAePtZA+rom9vt6C3hNRL5XSg0DZpyhTPj9nfitOO7FMer3fD5ur9PT2BeHGL0WuBO4qCkFlG7Lxo54te/eZDJx3z338sHMhcT2TaD74yMwhJ+dOIzo3poLPryWve+uJffbTcQU2Vn4zQ9ERWkv4mNkZWVx5fgrqMrIofsDF9N6XBdPm+QRwlNa0u9fV7LpgblkPfQl3377LRcPa1J10vAQDv0mx7c5dauBX2BxwdiqYT//w+sGtZ1rvE2sASAiFUqpu4G5ziatMBz9ogBuqpfOrJQ6CFyDQ9BFA684l99bdrlSqkIpNdjZf+r6eod/Am5TSi11Nud1ctoVBRwWkZlKqSCgJ/CZUuoz4N8isrF+GUqpMcACcTzlHXEIjGOjXrfi6KP2vVJqpIjkN8VupVR7EdkJ7FRKDcDRNLhXKbVXRJKbePmLcAiOl515pju9hA3ef6AKR9PjmViC47t8XUSKnM2HISKS28B1PA9sFJHvTjlU34Ybm1DmSuATpdQLOJ7zscB7TTgP4ABwu1JKB7QG+jaUyNncHCgiC5RS63H04WsSBp13BwOtqqri8ssvZ9myZXS6vg/t/9r3d3vE9P4+pN47lLDkGHa+uoxuvdJYuXgFXZJTzrHV5x9LlixhwoQJ1NnNDHz1KkJ7tPS0SR4ltH0UA/7vajY/+gNjRo7m/957h79NvcXTZml4ORsvfa7hfiLNCK/1s4vIVmA7Do/FS8DzSqk1wKlvuVVAobO5axUOj1SjnfubyF+At5VS63B0qD/GB8AeYItSaheOl78BRxPmNucgh6s40dE/DShoIP/JOPpWbcPRzHp9fe+SUyQ+CMxXSjXVBXGvUmqXUmq70+aFznNP57zZoZQ65Fxew9Gk3FsptUMptQeY5kzX2P1fhqPZdJtSamJjhYjIHhyDAxYppXbg8IK2aiR5N+BIA/tnAF8rpVYBZww3IiJbcAz62Iaj2fJsnok1OLyaO3EI/y2NpAsBfnBe0wrgvrMow2spLS3lkksuYcXKFfR6/FI63Nr/nDRdtrk0hf5vXkl1TQ29B/Zl9fq158Da8xMR4d///jcjR46EFj4Mfm/in16oHSMwLowBb19FRFoc0/56K3c/ch92e7N/F2tonBavGg3anFBKhQIfisgED9pwGZB0bHTk+YBS6icRGelpO9yAV1a8wsJCRowYwe5f99B7xmgiB7c752XUHCpn04PfYy438vXsrxk/etw5L8ObMZvN3HXXXbz//vvEDepA2uPD0QW5N56WqayWsp35lO4ooCavDGNhFdYaE2ITDAE++EUFEdgmnBZdWhKR3pogD0xcb7fa2P3acg7O30O/YQP4ftYcYmJiznyixp8Rb+5Rck7QxJqGhmfwuoqXl5fH8OHDOXAol77PjiWsV5zLyqo7WsPmh+dRlXOUmZ9+wF+v/4vLyvIm8vPzmThxIqtXr6bT5L60n9rXbUGETeVGCpZkUrBsH2U7HQ5/vZ+e8IQwglsF4xfii9IrLLUWaotqKcsux1RpBiC0QyRxwzvT9rJUfNw484WIcHDebva8tZLQFmF8O+sbLhw6zG3la5w3aGJNQ0PDJXhVxcvMzGT48OEUlZfQ78XLCU6NdnmZlmoTv0yfT+mOw7z4xss8fHdTQ9Sdn/z8889cd911VNRU0v2h4URf5J55WSuzSjgwezv5P2dgN9to0T6cxOEJtO7TiuguEegbmUxdRKjIqyJv9SGyfz5A8a4S9P4G2o5Oof3kvvhFuC+AbeX+YrY+9RO1+eVMu+t2XnnuJQIDm28AXY2zRhNrGhoaLsFrKt6OHTu45JJLqLbU0veV8QR2cF+MK5vJyrYZP1K4NoeHnnyUF2c81+wCdtrtdp555hlmzJhBi8RoevxjFH7xoS4vtzKrhMwP11O0Jge9v4GOo5NIubozUR1/3/d7dF8ZO7/aw/4F2eh99SRO7EHSpF7o/d3ThGupMZPxzhry5u0iLrENn838hIsvvtgtZWt4Pc3rR6MBNLGmoT4b0DkAACAASURBVOEZvKLirV+/nlGjRmH1g36vjsevrfujx9utNna+uJTDi/Yy9Y6bmfnme+h0Xjv26azIz8/npptuYvHixcSP7ELq/cNQ/q4dCVxzqJzMD9dTsGwfPkG+dLu+C12u7kzAWYZdaYyKvEo2vbOVnJ9zCYoLIfWBi4jqHX/mE88RR7ccYtcry6g5XM7wMSP496tv0rnzaWfs02j+aGJNQ0PDJXi84i1evJjx48fjExFA31cvx6dlkMdsEbvw6/+t5sDX27h80pV8/el/z/tJrGfNmsVtt91GtbGG1LuG0GpMsku9htZaM/s/20TO19vQGXR0vTaFtBu64B/mmsDJBb8cYeWz66g8WEXbUckk3zUUnyD3TCtmM1k58PU2sr74BbvJyrU3XMcTj0wnJUULB/MnRRNrGhoaLsGjFW/27Nlcd911hCZE0vulcegjPD+tkYiQ9flmMj9czwWXDuOnbxcQEBDgabPOmpKSEu666y7++9//Ep3amu7TR+DbJvjMJ/5ORIT8nzPZ++4aTCU1dLysPX1u70lQtOvvndVkY8sHO9jx2S4CWwaT9sRIWqQ2FpXn3GMqqyX781/I+2EXNpOVS0aP5N477mbEiBEYDF4ZRlTDNWhiTUNDwyV4rOK999573H777UR1bU2v58eggr3Lg5U7Zye731hOap80lny/iNjYWE+b1CTsdjsfffQRjzzyCBWVFXS6qR/tJvVw6bRRlVkl7H5jBWU78olKiWTAg31pmeb6wSGncmR7Ecv+voqaolo6T+1L4qTebp1WzFRu5OB3Oznw3Q7MFUYiY6K4cfIUrplwDX369Gk2zeoajaKJNQ0NDZfg9opns9l48MEHeeONN2g1oD3pM0a6vP/U76Vg6T52vPAzIeGhLJg7nwH9+nvapNOydetW7rjjDtatW0dMelu63XchfglhLivPZrKy/7NNZH+1Bd8QX/rc3oPkyzu4LQxIQ5iqzKx+fj3Ziw8Q07ctaU+MxDfMvZ5Ru8VG0foDFPyUyZG12YjNTkR0JJeNHsOoS0dxwQUX0Lp1a7fapOEWNLGmoaHhEtxa8SoqKpg0aRILFy6k/YSedJw2wOsnCq/ILGbr3xdgOlrDS6+9wn133ON1I0WzsrJ48skn+fLLLwlsEUzybYOIHdHRpXYe3XaYnS8vofZQBR3HtKffPb0IaOG+2GenQ0TY+90+1r6ykYCoQNKfHk1YJ894Rs2VdZRsyOPo+jyOrM/GUu2YQrhNQluGDh7KoIED6dGjB2lpaVoYkPMf7/phcAGaWNPQ8Axuq3jr169n0qRJHDx0kG73XUjcZedPJ2xzuZHtzy6meGMugy4ewqxPv/QKz0hmZiavvvoqH330EcqgI/HqdBIn9UAf7LoO9paqOva+s4aD8/cQ0jqEQY/2o21/1wUu/iMU7S7h54eXYyw30e2+obQenepRe+xWO1VZJVTsOELZrnxKdhzGVFoLgE6no0PnDvTu2ZuePXoeF3BRUU2d6U/DC9DEmoaGhktwecUzm8289NJLzJgxg6CYUNKfvJTgLuffC0jsQt7cnex9dw0+Bh+e/PuT3H/Pffj5uXdQhIiwcuVK3njjDebOnYveoKftmFQ6TumLIdJ1ni0R4ciKLHb/awWWCiNdJ3Wh163d8Qnw7g70xrI6lk5fSf7mI7Qb14Xku4ah9/WOZncRoa6omsp9xdTuL6Uss5DyzCLqiquPp4lpFUtatzR6dE8nLS2NtLQ0kpOT8fV1z4hXjbNCE2saGhouwaUVb9WqVUybNo09e/bQ9uJkUu8bhi7EuwYSnC01h8rZ+9ZqCtfnEJfQhqf/PoMbrr/B5aLtwIED/Oc//+GTTz4hKyuLgLAg2o7vSsIVaRhc3PxoLKpm9xvLKVqTQ0TnCC54fAAxKZEuLfNcYrfa2fzOVrZ/tpsWKdGk/2MMAbHuj+XXVEzlRir3FWPMLqMq+yhlWUVUHyjFbrEBoDcY6Ni5Iz27O7xv3bp1Iy0tjdatW3tdE/2fjGZ/8zWxpqHhGVxS8Xbs2MGTTz7J3LlzCWnZgq73DqXFgLauKMpjFG/MJfO9dVTsLyYiJpLbbp3GdZOuo0uXLuckf7PZzC+//MKCBQuYN28e27dvByCmZzzxo1KJuKAdhgDXCl8RIX9RBrvfXIFYbPT6WzrdJqV4fT/DxshZmsuKp9eiM+hIe2IE0X0TPG1Sk7FbbdQcLKc6u5TanDLK9xdRmV2CsbDqeJqwFuF0T0sjrVvacS9camoqwcGuC9micRKaWNPQ0HAJ56zi2Ww2Fi1axDvvvMO8efPwCw4g8Zp0Eq5JR+flTWW/FxGhZPNB8v63ncJNB0CgY0onRlx0CRdccAHp6ekkJiaescmqqqqKjIwM9uzZw+7du1m/fj0bN26krq4OpVNEdWtN7KAkYoe0x6+Ve168prJadr26jMJV2cR0j2HokwMJd8P0VK6mPLeSnx9ZTll2OZ1u6kP7Kf08Onr1j2KpMlGVXUJdTgUV2SWU7y+iOucollrz8TRJ7ZPontb9JC9cUlISer13NAc3I87fB6mJaGLtLFFKPQ5cB9gAO/A3EdmglLoXeF9Eat1oS0fgdSAFKAcqgadEZKVS6iagt4jc6S57fg9KqU+AH0RkdgPHHgRuBqw47verIvKZG237AHhNRPa4IPs/VPEsFgurV69mzpw5fPfddxw8eJDAiBDaju1CwoR09CF/nn41dUdrKFqeReGaHEp352OrswKg1+uJaRlDixYRtAgPx8fgg9VqxWw2U1RcRGFhEcbaE9VVZ9AR3jGW8K4tiUlrS0j3GHzcHHriyMosdr26DGuNiV7T0km7vgs6N8YrczUWo4XVz29g/8JsR3iPx0fiG37+BT5uDLELxiOVGHPKHc2o+wupzi6l+lAZYndU+YDAALqmdj2pH1y7du2Ij48/L4NAewmaWNM4gVJqAPAaMExETEqpKMBXRPKVUgdwiKMSN9niD+wAHhSR7537ujpt+OR8F2tKqWnAFcAEEalUSoUB40Xk0ybmaxAR6zk3+NzR5IpXVVVFZmYmmZmZ7Ny5k3Xr1rFx40Zqa2sx+PkQ1Tue+BEpRAyKR+fj+v/Y7RYbZbsKKP+1kNqCSux1FgxBfgQnRNCia0tC2kd5rP+O3Wqjcn8JxtxyjIerMBZXYq4yYaoygghKr0MZdPiFBhAQGUxARBBBbVrg1zaEgNah6Aye8XhYqkzseWslh3/aS2TnCIbMGERUh9834bq3Uz+8h39EAOn/GE14SktPm+VSbHUWqg+UHvfCOUTcUUzlxpPSRUZH0a5dOxLbJdCmTRtiYmKIjo4+aYmKiiIkJOS8n47tHKOJNY0TKKWuBP4iImNP2X838AqQAZSIyIVKqUnAdBwP0XwRecSZthr4F3AZYAQuF5FCpVQ08C5wbEbke0VkzWls+SswRERubOT4TTjFmlJqLPAE4AscBa53ljnUaQs4xMMQIBiYBYQCBuA2EVl1GjtuAW515r0fmCwitU4RVgn0BloCD4vIbOV4i78FXATkOO/PRw2ItTzgQhHJaqDMXjhEczBQAtwkIgVKqeXAWmAQ8D2Q2ch1zwASgVZAJ+B+oD8wCjgMjBURizO/B0Vks1LqUuA5QI/jO764ofsnIic6spyGMU9fL1aTBYvJgrXOgtVswWqyYDGaMZbVUFtWTW1pFTVlVdSVn/D+KL0itGMMLVJbEpnehsg+bV3ef+oYdcXVZM/aSv6ivZgr6gDwb+GPwV+PqdKMpcYCQEi7FrS5LJX4cV3R+2svlDNRvCmPnS8uwVRaQ/ebutHzr93Qu0F0e5riPSX8/OgKaouNdL6lPwnX9Dyvm0XPFhHBVFpL7aFyjEeqqCuqxnikktrCKoyFldQV12AzWho9X+ejxzfQD99AP3yOrf190fvo0Rn09dYGdAYdeh8DeoMenUGHUjqUTjkWpcC51ul1x/c51jrHsfr76qVF1T928rkoheN/Nsd3evz/t+P7T+w8OZ3zoDp527FSJ2SZOpH+f7e/0+wfHE2snQVKqWBgNRAI/AzMEpEVzmMHcHrWlFJxwHqgF1AGLALeFJE5SikBxonIPKXUS0CliDyjlPoS+D8RWa2Uigd+EpFGA2IppV4DckXkX40cv4kTYq0FUC4iopS6GUgRkQeUUvOAF0RkjfPa6oB7AH8ReVYppQcCTydAlFKRInLUuf0MUCgibznFWhAwEUgGvheRDk7BextwKRAL7AFuri/WlFIhQJ6I/Ma1oJTyAVbgELnFSqmJwEgRmeoUV3tE5HZn2sauewYwHLgQ6AKsA64SkYVKqe+AT53f1XLgQSAX2IJDjOUopSJEpLSh+9dUb57zOTiBTqH3M6D31eMTFoBfiwB8wwPwDQ/EPyaY4Phwgtq0ILB1GHo/9/ZDs9VZ2PfpRg7M3o7Y7CQMjSfp0kTiesTgH+4YDSkiVOVXc3hDAZk/ZFG0sxj/yEA63TqA1iNTtJFyDWA1Wtj77hry5uwkLCGMoTMGEZt6/oVW+SPUVZhY+cw6cpfnEdUzjm6PjSAgxntHi7obm8mKucKIubzeUlmHzWjBWmt2ri1YjRZstWZsJit2qx2x2rFbbc61HbHasFvt2C12xGYHEUezrAhiB7HbPTxb8R9j9Iq7Lpo/5M1lnrbDlTTP3scuQkSqnV6dC3C86GcppR4VkU9OSdoHWC4ixQBKqS9weK3mAGbgB2e6X4BLnNvDgS71XmqhSqmQpnpqnCKjI5ApIleecriN09ZWOLxMOc79a4DXnPZ9KyKHlFKbgI+comiOiGw7Q9FdnSItHIen66d6x+aIiB3Yo5Q6FsZ8CPCViNiAfKXU0oYuh8Z/OjoDXYHFznulBwrqHZ/VhOsGWOj0nu105vGjc/9OIOGUMvsDK0UkB0BESp37f3P/GrH5N7y9+nPWVu7EL8CfgAB/Anz98Tf4EaD3I1DvT7AhkGBDIDoPi5y9m3bxzoOvcuRAPp3GtKfnLemEtA76TTqlFKGtQwi9MoSUKztRsKWQTf/ewo7nl2BbU8QdLz1CZCv3z1nprWRs3s3bD7xCUW4B3a5Lpfdt3TH4//l+jv3D/LjkpaFkfL+fda9uYt3U/3Lr8/cyaOyFnjbtvMSOYLFbsditWMWKxW7DJjasYsNmt2FHsIkNuwg2sSMIdufaZrdjt9uw2+3ObbvjHOf2scVma2Cf3Q52caS32RERxzGxA45/5gSnKAQEQURAwC5O0ei8BsHxGXu9z848jiU67mQSCND7gaOVqlnz5/t1+IM4RcZyYLnzRX8j8MkpyU73hrXICXemjRPfgQ4YICJNfeh24xA+x+y6QinVG0dz7Km8haOj/PdKqWHADOc5Lyil5gOjgfVKqeHOwQlDgDHA50qpl8/Qqf8THH3Jtju9ecPqHTPV265/T077P5yzj1qNUipJRLJPOayA3SIyoJHTa+ptN3jd9W0TEbtSqv53Yue39aJB8djI/dt7ums7xu2DbuD2piT0ECLCq6++yj8eeYSwuFAuf2c0Mb2b7vVp1TOWsR9cyu6v97Lp31t5ePQ0Zs+azcjhI11otfdjMpl46qmnePnllwlpGcy490YT0+P8iZvmCpRSJF/ekVY9Yln+5BrevPMFclf+ysx/zyQ6WhP4Gk1ivacNcDXNZ5iRG1BKdXaOwDxGOo4mMoAq4Jj/fgMwVCkV5WxKnISj6e50LAKODwZQSqU7132VUg2JpS+BQUqpcfX2NTbBXRiOvljgEJfHymgvIjtF5EVgM5CslGoHFInITOBDoKcz7WdKqb4N5B0CFDg9cdef4RoBVgLXKqX0To9XY/9CPw+8rZQKdZYfqpS6FUe/wGjnYA+UUj5Kqcbmsmnwun8H63B8n4nOMiOc69/cvz9QhtdQW1vLtddey0MPPUTihe0Y/58xZyXUjqF0iq4TU7ji8zH4hBsYNXIUM16YceK/4j8Z27Zto3fv3rz44ot0HteB8V+O+dMLtfqExYcy9oOR9Ly1O/O+nUdSpyQ+/PjDP+3zoqFRH02snR3BwKdKqT1KqR04+jvNcB57H1iolFomIgXAY8AyYDuwRUTmniHvu4HeSqkdSqk9wDTn/ngacPE6PXCXAdOUUtlKqXU4OtM/00DeM4CvlVKrcHTIP8a9SqldSqntzjIW4vCMbVNKbQWu4kQH+jRObm48xt9xiNPFQFO8St8B+3A0N75D4yL2HRz3b5NSapczXa2ImIGrgReddm8DBjaSxwwavu6zwtmcfSvwrbPMY02tDd2/85rS0lKGDx/O7NmzGXBXHy58fjCGoD/W2T08IYxxH40i4cJ4/vHYP7julknYbLZzZLH3Y7VaeeaZZ+jTpw8HjuQw5o0RDH68P75B2uCLU9EZdPS6pTtXfnEZwe0CuXnqzQy+eDCZmZmeNk1Dw6NoAwy8HKXUy8DnIrLDgzaEAh+KyARP2dAM8bqKd/DgQUaOHMm+rH0Mf3YobYed2wnTRYRNb29l+6e7GDLqAhbO/pHAwMacwc2DjIwMpkyZwsaNG+k4MokBD/bBL9y9c5o2hs1sw1RlxlxtAREM/np8g33xdeFk9GeD2IVfv81k07+3YDXZuHXaLTwz41kiIzVvpMZvaPYjmDSxpqHhGbyq4u3Zs4eRI0dSUl7Cpa9eRHRP141K3P2/vax9ZSMpPZNZ9dPqZvnytdvtvPXWWzz66KPo/HUMfqQ/7Ya38Zg9FqOFwh3FFPxSSMmvRyk/UEH1kZoG0/oG+xDaOpiIzhHEdo2mZc+WhLfz3AwKxlIjW97bwa9zMgkKDeKpvz/Jnbffhb+/a+dl1Tiv0MSahoaGS/Cairdu3TrGjBmDVW9h1JvDCevo+hdzztJclv19NbFtY1nz8xoSEhJcXqa7OHDgAFOnTmXZsmUkDI7ngscH4B/lfm+atc5K3prDZC/KIW/NYWwmG0qviO0YSnRSMBHtgghs4Yt/sA9KgaXOhrHSQkWBkdK8GvL3lGMsd8T5Cm8XQvwFbWk/MpGoZM+I69L9ZWz81xYOrj9MZGwkjz3yGLf97bZm753VaBKaWNPQ0HAJXlHx5s+fz4QJEwiI9mfUm8MJbO2+6W4Kthay+IFlBAQGsHzRCrqndXdb2a5ARHjvvfd46KGHsIiFgff3pf3YBLfHmKsurGHP1xnsnZOJqcJMUKQfqSNa0XFILO16ROAX1LQgACJCaV4N+9eWkLH8CDkbS7BbhejkFnQa15EOo5Lc3mQqIhT8Usi2D3dyeHMBLaJacM/d9zDt1mnExsaeOQON5oom1jQ0NFyCxyvexx9/zC233EJ05yhGvnERvi3c3+G9dH8ZP96zBLvRzg/fz+eiYRe53YZzQW5uLjfffDM///wz8X3bMPTvA/Fv6d5muqqCarZ8sIN987NAhOQLW9J7YgJJfaPQ6f/4u8xYYWbHgsP88k0ehRmV+AX7kHJ1Z1KvTSEw0v1zWh7ZVsj2j3eTt/YQBh8DV1x1BXffcTeDBg3SgjD/+Wj2X7gm1jQ0PIPHKp6I8MILLzB9+nTa9W/LRS8M+cMjPv8I1UeqWXjXEqrza/jsi8+YdPUkj9lytogIM2fO5MEHH8RsM9Pv7t50ujLJrWLBWGpky4c72PvtPpQOel3djgGTk4ho45rmQRHh8K5y1nycxZ6fC9D76Og8rgM9/ppGYJT7myTLcyvJ+GYfe7/PxFxjoXV8a26YdAPXXXcd3bp104Tbn4Nm/yVrYk1DwzN4pOLZ7Xbuu+8+3nzzTTqP6sDgv/dH5+P5CD515XUsemA5hTuLeOVfr/DAXQ942qQz8uuvv3L77bezfPly4vu2YcgTAwlo5T5vmt1qZ883Gfzy7jYsRis9rmjL0Fs7Ed7KfV6ukgPVrP4oi+3zDqIz6Oh6bTJpU7rhF+L+EaWWWgsHlueRsyiPvPWHEJvQul1rxo4ay+jRo7nooosICvrt7BsazQJNrGloaLgEt1e8qqoqJk+ezNy5c+l+fVf63N3DqybOttZZWTp9FbmrDjLtvmm89dJbGAzeN8lKbW0tzzzzDK+88go+AQb63NGTjuOT3Hovj2wvYs2LGyjdV0ZS/yhGPdaVmCTPzalZerCGpf/OYOeCw/iH+pB2YzdSJ6Zg8POMx9ZYVkfusoMcWpvPwY2HsRqt6A16uvdI44KBQxg8eDADBgwgLi5O87w1D5r9l6iJNQ0Nz+DWipeVlcXll1/Or3t/ZeB9fUmZ2MmdxTcZu9XOulc3sWd2Bn2H9OGH2fO9ZsohEWHOnDncf//9HDhwgOTLOtHv7l5u7etnMVrY9PZWdv9vL6GxAYx8sAupI1p5jeAo2FvBz//ay/7VRYS1CaLP3b1JGBbvUftsZhtHthVxZFMRR3YUUri7GJvJEZQ5MjqS9O7p9OzRk/T0dNLT0+nUqZNX/pOgcVq8owK4EE2saWh4BrdVvDlz5jB16lRMdhPDXxhKbG/vED+nI3Pefla/sIEWUeH874uvuXCYZyf2XrNmDQ8//DBr164lun0Ugx/tT1R6hFttKNhayMqn11J5qIo+kxIYfk8K/k0c2elustYVs/DF3RRnVdGmTyz97u9LRIcWnjYLAJvFxtHMMkp2HaVsXzlFGSWUZZVhszhmDvfz96NL1xR69+hDjx496NGjB926ddOaUL0bTaxpaGi4BJdXvNraWh544AHeffddWqbEcvHzQ9wamuOPUrL3KEseW0XV4UpuvfNvvPbCa26PqbVx40aeeeYZ5s2bR2h0CL3+1p2kMQnoDO7r52cz29j49hZ2ffUr4XGBXP50d5L6ui5o8bnCZrWz+etclr2dQV2VhZQrO9Lrbz3wD/e+YLZ2q53yAxWUZpZTlllBcWYJJRklmCrNAOh0OhI7JNCzRy969+xNeno6ffr0oUUL7xCgGppY09DQcA0urXgLFizgzjvvJCcnhx5TutFzWnevGEhwtliMFja9tZXdX+8ltm0sr7/0OtdOvNalzWp2u53Fixfz4osvsmzZMgLDAul6XQqpkzpjCHCvJ6viYCVLp6+kZG8pvScmcMl93utNa4zaCjPL/i+TTbMO4BtooOct3ekyIdmtgvf3ICLUFNZQklFKeWYlJRmlFGcWU11wYuaHDp07cMGgCxg0cBADBw6kc+fO6HTefV3NFE2saWhouASXVLw9e/bw+OOPM2fOHKISIxn8aH+ie57/0znl/3KE9a9t5mhmKd17p/HU9BmMGzcOvf7cdWDPz8/nk08+4YMPPiAnJ4fQmBC6XpdCp/Ed8PGAQMpalMOq59aj18P4f6aTclFLt9twLinaX8XCl3aRva6EFgmh9LuvN20Hem4Krt9LXYWJoxmllOwqpWhnMQU7CzFVmAAICQuhX/9+DBk0hAEDBtC3b19CQz03VdefCE2saWhouIRzWvG2bNnCa6+9xpdffolfkB/dp6TS9YaU89Kb1hh2m51987PY9tEuKg9X0TaxLX+98a9cc801pKSknH1+dju//vorCxcuZM6cOaxduxYRoW2f1qSM70ybYa3Q+7p/NKO1zsq6Vzexd84+2qS34OoXe9IirnlMqSQiZK4o5MeX91CaV0P8oDj63duH8IQwT5v2uxERKnIrKdpRTMmuUvK3H6EspxwElFJ07tKZwQMGM3DgQAYMGECnTp0079u5RxNrGhreilIqElji/NgSsAHFzs99RcTchDymi8hz9T6vFZGBSqkE4AcR6XpurT7OH654BQUFzJ07l08++YQNGzbgG+BL6oTOpE3uim+4+2cjcBd2q50DKw7y6/8yyd9aAAJtE9syZNAQ+vXtR1JSEu3atSMsLAxfX1/sdjsVFRWUlJSQlZXFvn372L59O2vXrqW0tBSA2OQY4oe0ocOliQS39VxH8rLscpZMX0lZVjmD/9qBi+7ojL4ZCe5jWC121v8nh5XvZ2Kps9H1mmTSb+7ukfhsrsBUZaZ4dwlHd5VyZEcRR3YWYa52/ByFhYfSr18/Bg4YRFpaGmlpaSQmJmoC7o+hiTUNjfMBpdQMoFpEXjnL86pFJLiB/Ql4mVgrLy9n/fr1rFmzhqVLl7Ju3TpEhKikSJKv7EiH0Yn4hDRfkdYQNcW15C49SMEvhRzZUUjtUeMZz9HpdYTHhxHTLYrWPeKI6RVNcCvPeq5EhH0/ZLHmpQ34Bui54rkedBoc41Gb3EF1iYklb+1ly3d5BIT50eu2dDpf3hGdvnkJF7EL5bkVlOw8SvHOo+TvOOF9AwgICqBLly6kp6XTuXNnkpKSSExMJCkpifDwcM8af36giTUNjfOBY2INWAa8BgQDJcBNQC2wERgnIhlKqa+ApUB74CFgJ7BbRK4/Jt7qizWllB54ARgG+AFvi8h7SqlWwCwgFDAAt4nIqiaaLCKC2Wymtrb2+FJRUUFhYeHx5eDBg2RkZLB3717y8/Md16pTxCRH025IWxKHxROSFOy2OFbmGgvVBdWYKkwYAgwExQR6ZIqhhhARjEeNVBXUUHvEiN1ow25x/L75hvjgE+JLYFwAoa2Dvapzu6XWwuoXN7B/QTYJfSK58oWehMV434hJV1LwawULXthF3pZSojqF0+/+vsT1Or/76J0JS62FsuxyyrMqKd9fQfG+Ekr3l1Hn7P92jLAWYcTFxdGqZStiY2KJiYkhNjaWqKgoQkNDCQkJITg4mJCQkOPbfn5++Pr64uPjg4+Pj9fE4XMhzf8CNbGm0RxwirUa4ArgchEpVkpNBEaKyFSl1CXA08C/gJtE5FLneSd51hoRa7cCMSLyjFLKD1gDTACuBPxF5FmnoAsUkaqm2OsX5CeWOgtiP3398w3xJTwhlLD4MMITQonuEk1M10h8At3nQasurCHzhywOLMujdF/Zb2wOjg2kTf84Oo3tQExa9J/hxXDOOJpZypLHVlJ5qJKh0zoz9NaO52TS9fMREWHPogJ+enUPFQVGki5qS5+7exPa2nMzM3gCoX85ggAAIABJREFUU5WZqvwqqg5XH19qjtZiPFpHXVkdxlIjllrrWeWpM+jQ++jRO9dKp0MpQKkTa075rBx97pRS4Nw+vvYyxs8a7fd+70/P2O3lfOb8GgOuoXF6/ICuwGLnD4oeKAAQkcVKqQnA20D3s8x3BJCmlLra+TkM6AhsAj5SSvkAc0RkW1MzTB7fEb2/DoO/wbnoMfgb8An0ISDSn4CIAAIi/DH4O6qo8sA/jjVFNfwyczsZ8/YjNiG+RwSpt3QkpmMIgaE+WOpslB2uJW9LKfsW5bB37n5iu0bS+/aetO4T53Z7zydEhF+/yWDd65sICPNlyswB50XsNFeilCJ1ZBydhsay5tMsVn+wn9xVc+l6TTLd/5KGf5ifp010C/4hfvh39iO682+fB3G2m1rrrNSV12GusWKptWCttWCuPbFts9ix2+zYLXbs1hNrm3MtNuGYo0bE+Uec24hzn2O/1D8m4plJjU+Hw6A7cbSoNFs0z5pGs8DpWbMBo0VkQAPHdcAKINGZZodzf1M8a98A74vITw3kGweMAe4GXhaRz5postdWPLvdzltvvcVjjz2GxWqmz4QE+t/QnvC2jb8sTTVWtv9wiNUz91NRaGTc1aOZ+fbHxMQ0/35XZ0tFRQU333wzs2fPptPgVlz5bDoBEdr/zadSccTI8rcz2To3j6DQIB6f/jj33n0f/v5/riZijSbhfe6+c4wm1jSaBU6xVgvcCkwWkXVOj1cnEdmtlHoA6Ax8DrwODBARi1KqDEcTp8WZT2PNoKOBCc5zOgGHgSjgsIhYlVL3Agkicm8TTfbKipeXl8eNN97I8uXLSR4ax+jHuhHWuukj9CwmG2s+zmLl+/sIDArg008+44rLr3ShxecX69evZ9KkSeQdzOOSe7rQ/8YEdG6cAP58pDCzkiVvZJCx6ggtW0fz3DMvMmXylHMaY0/jvKfZVyJNrGk0C+oNMPgZeBNHU6UBeAOHR20ujnAeVUqp14AqEXlKKfUiMA7YcpoBBjrgGWAsjh+FYmC8c3kIsDjLniIiOU002esq3oYNGxg3bhxVtRWMergraeN//wThRVlVfDd9G/l7yrnzgdt4/YU3/9STY9vtdl5++WWeeOIJwmIDmfBiL1p1/80gZI3TkLOphJ9f28uhXWV0Tu3A6y+/yaWXXuqVfag03E6zfwg0saah4Rm8quJ988033HDDDQRF+zD57f60SPzjTU0Wk40fX9zN5q9z6Te0Jwu/+/lPOZfikSNHmDJlCosXL6bbiLaMfaobfqHu9wqJCBVHjBRmVlFZaKTmqBmb1Y7SKQLCfAiL9Se8dSAxHUMxeGlsNxFh908FLHlzL6UHaxg0tD9vvPIWvXv39rRpGp5FE2saGhouwSsqnojw8ssv88gjj9AuPZJr/9WHwIhzO9J063d5zHt6B3EJLVn240rat+9wTvP3ZhYtWsTkyZMpryxj1CNd6XFVa7d6giwmGxnLCslcWcj+NUXUlJ48YE7pQOwnn6P3UbRKDiWxfzSdh7akdbdwr2uqtVrsbP5fLivey6S2zMzocSN54ZmX6datm6dN0/AM3vWAugBNrGloeAaPVzyLxcIdd9zBzJkz6XZpGy5/Jg0fP9d4fHI2lTDr3s34+Pgwb858hgwe5pJyvAWj0cj06dN54403aNUxggkv9SKyg/s6xpcerGH9FznsmHcIY6WF4BYGug4Kp0PPEOKTA4lu609ICwMGX51jwvJyK6VHzBzJqSN7ZzVZ26rI2laF3QYhUb6kjW1DzyvaEZXoXU23ddUWNvznAGs+3Y+5xsYVEy7nuadfoHPnzp42TcO9aGJNQ0PDJXi04lVUVDBhwgQWL17MsFuTGXpHB5d7T0oOVPPlHRupOFLHzI/e56brp7q0PE+xceNGpkyZQkZGBv2ubc8l9yfjE+CeZsWyQ7WseC+T7fMOodNBzxERXHB1DKn9w846flt1uYWdq8rZuKCU7ctLsdsgoWcL+k9pT+cLW3qVt622wsy6T7NZ/59srCY7114/kX/OeJakpCRPm6bhHrznYXQRmljT0PAMHqt4ubm5jBkzhr0ZvzL+qZ6kjW/ltrJry838957N5G45ymNPPcSzT73YbDqIm81mnn76aZ5//nnCY4MZ/3R32vV3z1RBljobqz7cz5qP9qMUDLs2ltE3x9Ei9tzMtVlebGbNd8Us+28hJYdMRCcEMuCmDnQf2waDBya7b4zqoybWfpTNhlnZiA2m3DSZGX9/mvj4eE+bpuFamsePyGnQxJqGhmfwSMXbuHHj8RGfk97oS3zfMLfbYDXb+P6pHWz/4RBXThrHlx//Dz+/8zvg6Zo1a5g2bRq7du2i1/gELn04Fd8Q93jTstYVM+8fOyg7XEv/y6K45uF2RLR0zYToNquw+aejzJ+ZT96eGsJb+TP0tk50H9sWvRdN4VVZVMfqmVlsnp0DKCZdfy1PPPak1jzafNHEmoaGhktwe8X75ptvmDx5MoGRPtzwdj8ikjwXXFREWPHePpa9nUHvgd358fslREZGesye30tpaSmPPPIIH3zwARGtQhjzeDc6DHXPdVhMNpb8ay/rPs8mNjGAKTMSSR3gHvEtIuxeU8E3r+eRs7OG6MRALrwjmZRL4ryqebS8oJZ1n+Sw+ZsD2MzCuCsu48nHZ9CzZ09Pm6ZxbvGeh85FaGJNQ8MzuK3iiQj//Oc/eeqpp0hIj+baN/oQEOkdTVc7Fxzmuye20bJNNIvnLyMlJcXTJjUJm83Gxx9/zPTp0zlaepSBk9sz9LZO+Aa6x7tUnF3F1w/+QuG+Ki6+oSUTHozHP9Az4UC2/FzGt2/kcXifkdZdQhnxYCoJfbxr6qzqoyY2fHGADV9lY6q2cuElQ5n+8BNcfPHFzaYZ/k9Os/8SNbGmoeEZ3FLxamtrmTp1KrNmzaLnuATGPJmKwc97mqsA8raW8tU9m7CbYeb7M7nhuimeNqlRRISFCxfy8MMPs3v3bhJ6RDP28e5EdQ5wmw1Za4uZ9cBmfP0Uf32+PenDPB+7zm4T1s0r4ZvX8ygtMJM6PJbh96cS0TbI06adRF2VhU2zcln3eTY1pSY6dE7i3rvu58YbbyQ42LtGumqcFZpY09DQcAkur3i//vorEydOZNeuXYy4L5UBNyV4rReh4oiR2Q9tIW9bKTfdegNvv/4egYGBnjbrJFavXs1TTz3F0qVLiWkXzvB7k+l0cZRb7+nmr3OZ/+xO4joEcO97yUTFeVdfP3OdjYUfFrBg5mFsFmHADYkMvrUT/sHnNnbfH8VisrH7p3w2fpnL4d1lBIUE8pe//IW/3TKNrl27eto8jbPHO3/YziGaWNPQ8Awuq3giwscff8xdd92FIUBx5XM9SBzoee/LmbBZ7Cx5ay9rPs6ibWIrPv/4K4YOHepRm0SERYsW8eyzz7Jq1SpCIgMZemtHekxoi8HHfe8Hu01Y/Poe1n6aTdrQcKa91onAEO9oym6IskIz37yex+pviwmO8OGiO5PpcWW7sw4f4mpEhEPby9j4VR67Fh3CbhXSenTllql/Y9KkSedlP8o/Kd71YLkATaxpaHgGl1S83Nxcbr/9dhYsWECH/i256vkeBEadX3NyZm8o4fsZOyg7VMP1N17LS8+9SlxcnFttqKys5IsvvuDdd99lx44dtGgZzMAbk+hxVRt8Atwrksy1Vr55bAt7lxZy8Q0tuW56AnrD+fFuOrCrmi+fO0Dm5ipadQpm5CNdSewb7WmzGqSm1MTOBflsm3uIgr3lGHwMjBg5nAlXTWTs2LGacPNuzo8K8QfQxJqGhmc4pxXPaDTy5ptv8s9//hObWLjormT6TIr3Ok9GUzHXWln2diYbvszG4OPDPffcw/33PkBsbKzLyrRaraxYsYL//ve/fPXVV9TU1NCmSyR9r00kdUyMR+KJVRbV8dVdGynYW8Gk6QmMmOK+mHjnChFh04+lzHopl6OHTV7bn60+BXsr2PF9PrsXH6biiBG9XsegIYO4avzVXHLJJSQnJ3ttl4I/Kc3+y9DEmoaGZzgnFa+uro7PPvuMp59+msOHD5MyNI4xj6cR0sq7+gj9XkoP1rD0X5ns/OkQPr4GJl47kZun3sLgwYPR6/+4eKqoqGDFihUsWLCAb7/9luLiYvwCfUkd0Yp+E9sTmxrosZfykYwKvrhjI6YqC9Ne70iPC72/Kft0mOts/PhRAfPfd/Znm5LEBbd0wi/Iez2/IkL+ngoylhSxZ0k+xdlVAMS2imH4RcMZPvwSBg0aRIcOHTTx5lma/c3XxJrGWaGUigSWOD+2BGxAsfNzXxExN3iiB1BKpQNxIrLgbNIppcYBXUTkBRea94cqXnZ2Np988gnvvvsuxcXFxKdFMfK+rrTpHXKu7PMqSg5Us/GLXLbMzcVitBEdG8mY0WMZOmQo/fv3p3379vj4nF6g1tTUsG/fPrZt28bWrVtZv349mzdvxm634xfgQ6ehsaSNjCdhUBi+AZ4VEJkrC/n6oV8ICtVz73vJtEvxXi/U2VJ2xMT/Xs1j3dwSQqJ8ufieFLqPa+tV8dkao/RgDTkbjnJgYylZG4qoKTUBEBoeQu9evenfbwA9e/akS5cudOjQ4YzPpMY5w/sfnj+IJtY0fjdKqRlAtYi8Um+fQUSsnrPqhB3ADUBvEbnzDGlvakq6c8xZVTybzcb27dtZsmQJX3/9NZs2bUIpRfLQVgya3JE2fULc/p+9iFB91ISpyopPgJ7gSD/0Pq4NC2KqtbJvZRG/Li4ka30hxkoLAHq9ntZt44iJiiEsLJzAwEDMZjNGo5Hy8jLyDh6kvKz8eD6+AT60Sg4jqV8U7fu1pFVaoNdMm7T+ixx+fGkX8SlB3PNOsstmI/A0Wdur+OKZA2Rvr6ZNaigjH+1GfHqEp81qMna7ULy/isM7KyjYXUnezqMU7avEbnNUbYNBT2L7RLqmdqNjh47Ex8fTrl274+uwMPfPHtKM0cSahkZjHBNrQFegFOgBbAFmAW8AAYAR+IuIZDhF0TggEGgPfCciDyul9MCHQG8cIuYjEXldKbUc2Ab0BUKBqSKyUSkVAXwEJAG1wK0issNpTxyQAJQAg502HAaeB3JOtcu5b/8p6QJwijelVDtnWdE4PIh/EZE8pdQnQKXT5pbAwyIy+yxuX4MVz263U1RUxMGDB8nIyGDHjh3s3LmT9evXU17uEBttUiPpOjKO1JFxhMa590VuNlrZu/QIu37M5+C2UmrLLcePGfx0tE4No9OwlqSPbUtwlGvDStjtQklONfm7Kqg4aOLowWpqKuow1Viw1tkx+OrR+yr8gg2EtwyiRctgWrQJJLpTIC3iA72uP5/dJvz40m42fJlDj4tbMO3Vjvh5INCtO7HbhfXzSvjfy7mUF1lIG9WK4fenEtbSfXHrziWWOhtFWVUcza7haI6RoqwKirIrKTtci81iPyltcEgQ0dHRxMbGEhMdS0xMDDExMURHRxMZGUlYWBihoaEnLWFhYef91GwuwrsqswvQxJrG7+YUsRYFXC4iNqVUKFArIlal1HDgNhG5yinWnsQh6kxABg5BFQO8ICKXOPMNF5Fyp1jbJyK3KKWGAP8nIl2VUm8BJSLyD6XURcBrIpLutGcsMFhEjKd6zM5gV/10xz8rpeYBs0XkU6XUVGCciIx3irUgYCKQDHwvIh2aeu8untxLjNUm6qrNGKtMGKtNVJUZqSiqxmY98aOu99ERnRRCXGoYiX2iaNc7wiMvMqvZxqZZuaz6YB81pWYi4vxIHRBK25RggsL0mIx2juQYydxUyYFdNegMit5XtWXI3zoTEu25aa3OF0w1VmY//AuZK4sY8ZdWXPuw94W5cCWmWhvz3z/Mwg/zQSkGT+3AwJvae7w5+lxhtws1pSYq8o1UFBgpL6ij8oiRmlKTYykzU1NqorbMfNwz1xgGHx1+wb74+fvg42fAx9+Ar5/BsX3q4qtH76NDp9Oh0yt0ep1zcWzr9afs1ymUszn6JEe9OnnfcS9+vTSKU85TDX/+Td7ngA8fmd/sK0vzqAka3sDXImJzbocBnyqlOuLwINXvuLFERCoAlFJ7gHbAbiDJKcLmA4vqpf8KQERWKqVClVLhOATeVc79S5VSkUqpY20K34uIsREbT2dXYwwArnRufw68VO/YHBGxA3uUUmc1THHdvF34BxvwCzbgF2TAL9JAeFIoqbExhMYGEBrrT0R8EJHxQeh9dMd/CD3Bwe2lzHlyG8XZ1aQMCOOyv3UgpX9oo32M8rOMLP6sgJVfH2T7vMOMfKALvSZ4b0BeT1NxxMgXd26gaH8Vk2ckcvF1LT1tktvxC9Rz5b3xDJkQy6yXcln2f5ls/TaP4fd1oduo1uf9s6PXKUKjAgiNCqBt2m+PH5NndruduioLxnIzphqrY6m2Yqq2UFdd/7MVq8mG1WTHYrJhNVkxmc3UVDj2WU02rGY7ljobYhfsthOL2AS7XRD7b+04X2k3Ztz4J7t+P8fTdrgSTaxpnCtq6m3/E1gmIlcopRKA5fWOmept2wCDiJQppboDI4E7gGuAqc40p/6bKTTs8j6WrqaBY02xq6nUt6f+tZzV22Rz7lLyjfvx1fnhpwvETx+IwrumgbLb7f/f3n3HN1W9Dxz/nO69aEtpQYbsIRtkCyqiIkOUIQjIVpYI/FgqAoKgCKgIqF9EFAUExC8gWwFlKrIKyB6yWwrdbebz+yMBK19GgaZJy3m/XmmSO859btKTPDnn3HuZNelrZn+4nNCCPrzxRUUeaXTnAxiiH/aly5gSNOtWiLlvn2LZuFgu/GZm0ufvEhYekguR5x0H9xxhQKdRpKdn8MYXFahYP38eIJJd4THe9P2oNIc7JfPd+NMsHraLw4uTGT7xDSpULePs8FyaYMVsNWIWE2YxYRETFjFjETNWsWAVMxax2B5jwWq1YLFYMJnMWKwWLGYzFosFqwhWsYKIrVR775uI2D78RODaY0AQ+7LX77jeY3fj8yzL5BQPN0+ucvRQzpbqenSypjlCMLbxXwBd77SwUiocMIrIEqXUceCrLLPbARuUUvWBJBFJUkr9CnQEximlHsPWJZp8k1/fKUDWb79bxXXjclltBdpja1XrCGy+0/5kR/ngepQPrpcTRTlEYmIiHTt3ZOXKldRvHUWnt4riE3B3yWTBor4M/aosG+ZfYv57h+nQuBv/Xbqa2jUfdVDUecuSJUvo0XkwAWFuvLmgMtGl9JGD15SpGcToJRX57Yd4lkw5TcfHX6NT53a8P3EqhQrlvXPNaQ6X75M11/opr+UX7wPvKaW2ANkZIR0DbFRK7cGWqI3IMu+qUmorMAvobp/2DlBDKbUPmAh0uUW5G4DySqk9Sql2t4nrxuWyGgC8Yt/Wy8DAbOxPnnb69Glq167N2nVr6PJOKbpPLHbXido1SimavBTFqAUVsJBJgwb1mDvvixyOOG8REcaNG8cLL7xATBlv3vq+ok7UbsLNXdHoxUgmravCMz0KM3/+95QsVZxx498hLe12Deialv/oAww0l2U/wGCIiOx0diwO4JIV78CBAzRt2pTktARen1mekjVy7uCAlCsmPh1wlEO/JzH2vRG8OWx8nh+LdLcyMjLo1q0bCxYsoH6rKLqMK46nPrgvWy6dzmDhpDPsWp9AeMEQxox+l549eulzmWmgjwbVNOfRyVru2rZtG88++yzKM5MhX1YgunTOfwmajFa+GHqM31cl0LPvS8z6+Bvc3B6MBv7z58/TqlUrdu7cSdvBxWnWM/KBS1ZzwpGdySz+8CxH/kyiaPFo3hs/mXbt2j0w/0faTeX7iqSTNU1zDpeqeGvWrOH5558nKMKNIbPLEf6Q44azWq3CgomnWfvVBZ5t/RiLv1uFj0/+Pr3Hzz//zEsvvURKWiJ9PixD5SYBDt9maqKJiyczuRpnJDPNgljBx9+dwDAPoor5EhLpmWeTRRFh78ZElkw5w5nDaVSsXIbJkz6iadOmeXaftPuS7990naxpmnO4TMVbsGABnTt3JrqkL2/8pxzBEbnTQrFq9nkWTjpNrXoVWbPiN0JC8t+RolarlfHjxzN69GhiHg6i38eliSrpmETYZLSyb+NV9m5M5OC2RC6fu/2V33wD3ChVNZCyjwZTqWEIhUs77zqo98pqEbavuMzSj84SfzaTug1qMH7sBzRq1CjP7Yt2X/L9m62TNU1zDpeoeDNmzKBfv36UrRnKgJml8Q3M3c+8bcvj+c/w45QoFcOGtduJiYnJ1e070qVLl+jcuTNr166lXosoOo8pjrcDLvF55aKB1V9eYMuP8aQlmgkIcqPqo76Ur+7LQyU8KRjtiX+gGyjISLNyJd7C38eNnDxsZN/ODE4ftSV1hUv6UPOZcOq3iaRAobw1kM5stLJhwSVWfHaepHgjtetWY9w7E3niiSd00vZgyPdvsk7WNM05nFrxRIQxY8YwZswYqjWJoM+0Enj5OGfMz4EtiXzS7wghoUH8vOY3ypev4JQ4ctKSJUvo06cPySmJdHyzBA3bhuV40pAYZ2Tpx2fYvDQeRGjYLICn2gRRo74fHh7Z31ZCvJnfVqfyy4pUYv/IQLlB9SdCeaJzNKVr5P41Z++HMdPCr4viWfnFea5cNFC95iOMfec9nn766Ty1H9pdy/dvrk7WNM05nFbxLBYL/fv3Z+bMmTR8vhBd3i2K+118uTvC6YNpTOlxCKvZjZ9WrKFBvYb3VZ6IsHbtWubOncv+/bF4e3tQv34j+vXrz8MPP5xDUf+vxMRE+vfvz7x58yhRMZSe75ekUA53e5qNVtZ9c5H/Tj+D2Sg82y6I9r1DKVT4/g8IuXDWxI/fJLFyYRIpSVZKVfGnRf8iVKwfkqeSHZPRyuYf4vnps/NcPpdJhUdK83+DR9G+fXu8vHL3erparsg7/5z3SCdrmuYcTql4BoOBl19+mUWLFvFsz4d4YUi0y3wJx5/J5MPuh7hywcjcr+fQvu3L91ROQkICXbt2ZcWKFYSHe1G5ihvp6fDnzkysVjfefnsoo0ZNyNGjB0WE7777jsGDB3P5cjwtXivCs30K4eGZs6/t2SPpfDbkKGcOpfNoE3/6vhlOkeI5n3xkZlhZsySZb2deJe68mZKV/Wk1sAgV64fm+LYcyWyysvW/l1k9+wLnj6cTGRXGwP5v0KfPq4SFhTk7PC3nuMaHmAPpZE3TnCPXK96lS5d4/vnn2bp1K+2HlaBZ97u6nGmuSL5i4uNXj3BsdzKvD3mVyRM/wd09O+dVtjl37hxNmzbl+PHDDB0ezMudPfHysn2Ox12yMG5MKiuWZ9C5czPmzPkpRxK2gwcP0rdvXzZu3EjJR0LpMuZhilTI2dOeWK3CurkXWPzh3/gHujF4QiQNmjr+iFKTUVi9OJlvPr1C3Hkzj9QP4sX/K0aRsg4YfOdAIkLsb4ms+yqO2M1X8PH1omOnl3i1dz+qV6/u7PC0+6eTNU3THCJXK97u3btp2bIlcZcv0uO9UtR8JvjOKzmJyWjlu/Gn2DD/EvUb12DRd8uJirrzxc2Tk5OpW7cup04d4T9zCvBonf9dRkSY+mEqn3yURq/ezfls1vJ7jvPs2bOMGzeO2bNn4xfoyQuDH6LBi2G3vMD9vcpINfP50GPs/vkqdZ/wZ8iESMIicvdKgSaj8OM3iXz9yRVSk600bBNOq4FFCS2Y97oUzxxOY93cOLYtj8NksFKpSjn69OxHx44dCQ523Xqh3ZZO1jRNc4hcqXgiwuzZsxkwYAD+Ie4MnFE2x1t9HOXXxXF8884J/AL8+Hzmf2jbtv0tl7VarbRq1YqVK3/im+8iqVP31uWKCOPHpTD7i3Q+/3w0PXu+c1dxnT9/nilTpjB9+nQsVjON20fRom9hAsNy/gCN88cz+Pi1Q8T9nclroyJo0zXYqd3WyYkWvpl+haVfJ+LuoXiuTwxPdY/B0yvvnZA2LdnM9mUJbPo+jr8PpeLj60XLVi15qX0nnnrqKby989YRsQ84naxpmuYQDq94V69epXfv3ixatIgKdQrQe3IpgiLy1mfa+WPpfDHsBCdjU2je8kk+nvoZxYsX/5/lZsyYQd++fXlnbBhdXrlza4/ZLHTueJVdu0zs+nMr5cvf+eLysbGxTJkyhW+//RaLxUy9lgVpPaAoYTGOSVR2/3KFzwYfxdtb8c6nUVR91M8h27kX504bmTnhMpvXphFV1IsOo4pT+bG8OQZMRDi1P43fFiWwY3UcaYlmAoP9ad2qNe3adqBx48b4+vo6O0zt9vLWB9s90MmapjmHwyqeiPDtt98yePBgEq5c5oVBxXiqe2SOd8/lFrPJyqr/nGf5rHNgdWPAgH4MHTKCyMhIAE6cOEGlSpWoXhPmfpP9U03EXbLw5OOXKV8unC1bLt50/FpycjILFy5kzpw5bNu2DR9fTxq8EMlTXWMIL5L9sXR365f5F/lmzElKVfBh7MwoomJcszX0j1/T+HhMPGdOmKjWJJj2I0sQ+VDevRqF2WTl4NYk/liZxM51cWSkWvDx9eaxxxrS/NmWPP3005QoUcLZYWr/K29+uN0FnaxpmnM4pOJt3bqVkSNHsmnTJkpVCaXrmIeJKeeaX/R368pFA4s/PMu2ZXF4eXvycudO9OnVl+HDh7NjxyZWr48gOtp6V2UuWpjO/w1JZuq0V3l94AwA4uLiWLFiBcuWLWPt2rVkZGRQuGQQ9Z8Pp8ELEfiHOK7LT0T44aMzLJ9xjkcb+/P2J1H4+bt2F6PJKCyZk8jcTxIwm+CZntE80ysGb1/HJbO5wWS08tf2JPb/msreTZe5dDoTgMIPFaJhg8do2KARDRo0oGzZsvq6pM6nkzVN0xwixyqe1Wrl559/ZsqUKaxevZqQcF9a9S9Mw7YFcHPP/c8wESEp3kTSZRNu7hAW5Y1/cM4NiL9wIoM1cy6x+YeLmE22l/HN0cF073FcPKWEAAAgAElEQVT3XVUiwssvXWV/rJn27TuxbdseYmNjEREiYvyp3CSY+i0LUbSS46+jaTZZmTv6BL8tjueZtkG8MT7yrk5u62zxF83Meu8yPy9LITzak/YjilO9ac6fDNhZLp7KYP+vyRzZmcrhnVdJumwCICg4gMqVK1O9Wk2qVKlC1apVKVeuHJ6e+eNHUh6RP/7JbkMna/mMUmoj8J6IrMky7XWgtIi8lkPbqAJEi8jKOyzXFaghIv1uMi9VRLJ97gGl1CkgBbACl4DOInLxbuLOUtZXwAoRWXwP644UkQn3st0b3FfFExEOHjzI0qVLmTt3LseOHSM4zIdm3aN5vGMkXn65+9klIhzZmcLGhZc4sCWR5ATzv+ZHFvaicpMwHmtfkJiSOTP2KjHOwFst9lEgWFj7czie93hOs0N/mXi2WQI1anqR7hFA2ZrBVGkcRkzZ3LvQuSHdwqcDj7BvUyKd+4fxyqC8m+Ts3ZHBR6PjOHHYSKV6QbQfVTzH3nNXISLE/Z3JkZ2pnIrN4NSBZM4cTsOYaWvZ9fBwp1jxhyhduhxlSpehdOnSlC5dmuLFixMTE6NPzJvz8mZluQs6WctnlFK9gUdF5JUs07YDQ0XktxzaRldukYRld7l7TNZqiMhlpdQEIEBEBmSZr7D9P9+xH+w+k7W7ivs27qrimc1mTpw4wfbt29m6dSu//PILR48eBaBMjVCatI+mWrMApxyVd2RnMvPfO8XJ2DQCgtyo08SfslV8CC/ogdUiXDhjYt8fmfy5OR2TUaj+eAgvDitGVLH7G7S9/psLzBt3itlfh9Kk8f0duTdsaBJLl2Tw/qpKhD7k+POXZZV8xcS0Xn9xan8aA8dG0rJj3j99hNksLJuXxOwpCWSkW3m8QyQt+z9EQGj+bW2yWoSLJzM4/VcGF44auXgqjQsn07h0OvN6EndNZMFwihQpQpHCRSlSpAiFCxcmIiKCiIgIwsPDr98HBQXl2aQ9l+X7F0kna/mMUqoAcAgoLCIGpVQx4FegKPAkMAbwBo4Dr4hIqlLqGWAKcBnYBZQQkeZKKX/gE6AS4AG8A6wCjgG+wDngPeAkMM0+LcNe7mF7stbavr3iwHciMsYe5/WkRyk1FGhrX26piIy+yX6d4p9krRkwAHjNHs8GoA7QCugHPI0tGXpXRBbaE7lPgCb2WBXwpYgsvqHcGsBkEXlMKRVgX6eGvawxQE1gKBALHAB6Ad8DhQF3YJyILMzO+5SSkiLp6elkvWVkZJCUlMSlS5e4dOkScXFxnDlzhsOHD3Ps2DGMRtsFt/0CvShZLYBqjSOo8ngQIQVz95xb1xjSLcx/7xQbF8YRHuVB5wFhNG0ViI/vzRPGxCsWls5NZNGXiRiNQqu+MTzTq/A9ddWaTVaGPbmbYjGw+If7Pwox7pKFRvXjafx0AO0mVbrv8rK93b8z+bDHX1y9YOCtj6Ny5US3uSnxioU5UxNY/l0SvgHutOpfmMYvReHh+eCM8bJahauXjFw6mUnCeTNXL5q5cjGThAsZXLlo4MoFIxmp5puu6+npQYHwMEJCQwkKDCI4KITAwEACAwMJCgq6fu/n54ePjw/e3t54e3tff3zjNC8vL9zd3XF3d8fNze3645vdrs3PI+PxdLKm5T1KqZ+Az0Xkv0qp4UABYBLwA/C0iKQppYZhS47eB44CDUXkpFJqPhBoT9YmAAdFZJ5SKgT4HagKvEiWFjOlVBCQLiJmpdQTwKsi0saerL0HVATSgT+AriKy81qyppRqCrwA9MZW4ZYB74vIrzfs0yn+SaqmA2nATOAEUFdEtiul2gB9gGZAuH17tbElcq/apxcEDgI97pCsTQK8ReR1+/ZDReTqDUlmG6CZiPS0Pw8WkaRsvkd3rHi+ge6ERHgRVdyHQiV8iSruS/FK/sSU9HPKWLSszh5JZ3r/w1w6lUnbnqF0HRiGr1/2PtQT4sx8MjaejT+lUrFOAD0+KENI5N11C235MZ4v/u8Yn88J5ckncuZ8WO+OTWbO7HSmrK1IyEOBOVLm7Zzan8qUnocQi5XxXxTikRr59/QQJw4b+PTdy/y5OZ3oEt60HVaMyo+F6lYju8w0CylXTKRcNdvusz6+aiI92UJmmu2Wkfrvx3fuS7h/bu6KrG/V9fct67Qb52WZeNN1szM/m2b8WSOsS6mtV+96xTzEOT/JNUebD7QH/mu/7wY8CpQHttgrgxewDSgLnBCRk1nW7WV/3BRooZQaYn/uAzx0k+0FA3OVUqWwtUJl7etYJyIJAEqpH4D6wM4s85vab7vtzwOAUthaA2+0QSllAfYBbwIhwGkR2W6fXx+YLyIW4JJSahO21rCGWaafV0r9cpOyb/QEttcOABG52QdBLDDZntituJtu5g7DSuLhY8HL1w1vHze8fN3x8nHDx9+d4HBPAgt44uVtS37c8ABc59ft3k0JfPr6X/j5Kz74JoYa9e5uPFKBSA9GfxJF7UbJTHs7nrFt9jLos0coWj57CZLVKqz64jyly3jwxOM5N/andx9/5n2dzvpZp2k7oVqOlXsz+367wvQBBwkOcWPSV4UpVjJ/j2EqUcabyV9Hs31DOjPGxzOt92HK1w6izaASlKqW97t975efP/j5+1KwyJ2WFAQrgtX2WARjphVDhhWz0YrZKJiMVkyG/31sNloxGQWrVRCrrdvWahWsFhCr2J/bposV+7x/lskSgu0uS0PPzdp85CbLZR38cX3yTWbfQyNSW+Czu10pL9HJWv70IzBFKVUN8BWRXUqpGGyJU4esCyqlqt6mHAW0EZHDN6xT+4blxgEbRKS1vdt1Y5Z5N9a6G58rbAdEZKeiNRaRy1niCMHWwpa1rFu5Ve03808mlPUEUeo269gKFDmilKoOPAO8p5RaKyJjb7fONd9NPJqdxVzOzJkzmdqvHyXL+zHhi2jCo+6tZV4pxdMvBlOmkg/Du19gwkt7WbBgPi2ee/GO6y5fvpyzR1sw7eOIHG2ZiYh0p2MnP+Z+lcLk8WMpU7phjpWd1VdffcXUXj0oUcaPiV8WokDBB6N3QylFnSb+1Gzgx7Lvkpg3/Srj2u+h6VMNeW/CVKpVc2yCrOVr+TpRA1f6ua7lGBFJxZYwfYmtpQxgO1BPKVUSQCnlp5QqjW18Wwl7kgXQLktRa4D+9jFfWRO7FCBrM0gwtvFrAF1vCOdJpVSYUsoX25iyLTfMXwN0s48RQykVo5SKvJv9zeJXoJ1Syl0pFYGtRe13+/T29umFgMZZ1jkFXLuSc5ss09diG/+GPa5Q+0OTUsrTPi0aW/fvPGAykK+/bT788ENee+01Hm0cyLQFhe45UcuqRFlvZvxQmCIlPGndqi3/+XLaHdeZOHEChYt48uxzOf/x1auPP+4eMG5snxwvW0QYN24cr7zyCtXqBvDRggcnUcvKw1PxfJcQvt1UlF7Dwtm2fQvVq1enZaun2L59+50L0LQHkE7W8q/5QGVgAYCIxGNLpOYrpfZhS97KikgGtoH6q5VSm7GdFuPauKtx2Lo09yml9tufg21Af3ml1B6lVDts497eU0ptwTbQPqvNwDfAHmCJiGTtAkVE1gLfAduUUrHAYv6dCN6Npdi6SPcCvwD/Zz+9x1Js4/JisY1z25RlnTHAR0qp34Csjf3vAqFKqf1Kqb38k+B9ju31+BbbgRe/K6X2AKPs6+RLEydOZMiQITR+NoSxMyPw88+5ssMLejBtQQxV6/jRs/sgPpo+7pbLbt68ma1bt9OzV5BDzkFWMMqddu39+P77v/j7zO47r5BNZrOZ3r178/bbb9Ps+TAm/CcSv8AHL1HLytfPjZf6hDL/16J0GViAXzasp06dOtStV51ly5ZhtebCYCxNyyP0AQYaSqkA+1GhCvgUOCoiU50dVz6XZyre2LFjGT16NE+0DGH45HCHnajVYLDyzmsX2fZLGuMnDmXksPf/Z5nmzZ9l27Y1bN4ejq+vY+L4+7SZxg0v069/HT6atvW+y0tMTKRDhw6sXr2al/tG0G2wcy/G7qrSU6389H0yi79M5NI5Ew+XKsKrvQfSpUsXwsPDnR2e5tryfYXSyZqGUmoQ0AXbQQe7gZ4iku7cqPI9l694IsLbb7/Nu+++S7M2oQydVAB3Bx+FajYJ4wddZMNPqYx481XGj/30emKzb98+KleuzOChYfQb4NgB+X1fTeS3X438/fdpQoIL33M5hw8fpkWLFpw4cYxB4wrxbPv8dXJYRzCbhI0rU/jx6xT270rHy8uDlq2eo1fP12jcuDHu7nn7MlaaQ+hkTdM0h3DpiicijBgxgkmTJtG8fRhvjA/LtQvBWyzC5BFxrFqUzGv9OzL9o29QStGpUyd+/HEBW7YXINiB1+cE2LvHRKvnEhg/oRUjRyy9pzJWrVpFhw4dcPMwMHZmDJVq6lEnd+vEYQM/LUhj7dJEUpIsRESE0KZNW9q2bU/Dhg114qZdo5M1TdMcwmUrnogwePBgpk6dSqtOBRgwJjTXErVrrFbh03GXWfJVIh1fbs47b0+lbNmyvNI9gFFv5c75yNq9kMDZM8LJk4l4eWV/kJ7FYmHChAm88847lCjjz4QvChEZ47Jvd55gMFjZtj6NTasy2fZLEpkZQnh4CM2aPcPTTz/Lk08+SUREhLPD1JxHJ2uapjmES1Y8EWHgwIF88skntOlagH5vO+/EpSLCVx9dYe5HVyhWPJpzZy+waUsEhQrlTgvVz+sz6fFKIl/M7kePbp9ka50LFy7QqVMnfvnlF55sGcqg8RH4+bvkW51nZaRb2bExjc1rDPzxWzJJVy0opaharSKPN2lGgwYNqFu3LgUKFHB2qFru0cmapmkO4XIVz2q10rdvX2bNmkW7nuH0GRHiEgPhv56ewJwpV3j+BV8mT8m9E6harcJTT1zGy9OL2NjUO152Z9WqVXTp0oXUtEQGvhPJUy/4usTrl5cYMq0c3J3Jkf0G4i6YSU224OWtCAnzoEQZLypU8yEy+p9zblsswtH9Bv74zcjvm1L4a28GZpOtapUp+zAN6jemXr161KxZk7Jly+pu0/wr31c0naxpmnO4VMUzmUz07NmTuXPn0vHVCHoMdZ0jFmd/mMC8T6+wcm0BypbN3QuBL1yQzvChySxf8T7Nnx1602WuXLnCoEGD+PrrrylZNoC3pxfioYdzNcw8TUTYtTWDnxYmse2XNDLSbFXDP0ARFKQwGCAp0YrFfmKdMhW9eKpNEM1eCMYv4N8JtCHTyqG9Bg78aWbfzjT270wjNcV2ChA/Px+qVHmEmjXrUL16dWrUqEHp0qV1Apc/uMaHlQPpZE3TnMNlKl5qaiovvvgiq1evptugSF7uH+QyiVp6qpW29U5Sr54nsz4PvfMKOcxgEBrUjadcuTA2bYz/1zwRYdGiRQwYMICEhHheerUAnfoG4+XtGq9dXrDtlzTmTEvgSKyBkFA3mjXz5omm3lSu4kl4+D9JlMEgHD1iZvNvBlb+lEnsPjMBgYqOr4Xx/CsheHvfvNXTahX+Pm7kSKyRI7EWDsWmcvSAAUOmLYHz9/ehatUq1KxZhxo1alCjRg1KliyZVy5erv0j31c6naxpmnO4RMW7ePEizz33HLt2/cng8dEud2qJhV9cZeaEy/ywLIyqVZ1z/cyZn6by/sRUtm9fRO3aLwDwxx9/8MYbb7B582bKVApg2KRClCjnlPDypLOnjEwfG8/2Dek8VNSd3q/606aNL94+2fvO3b3LyCcfpbHhFwPRhd0ZNL4gNRtm7yAQs9mWwB2ONXJ0v5lD+9I4djATo8FWJYOC/alWrQo1a9SlZs2a1KxZk6JFi7rMDxjtpvL9m6OTNU1zDqdXvG3bttGmTRsSky4z+pMYHm2Su12Md2I0WHmp0SlKPuzO/IVhTosjOclKvUfjefyJ4ox/dxnjx49n/vz5hIX70H1wAZq96Ovw88/lFyLC8vnJzHg3Hnd3GDgogC5d/fDyurfXb8tmA6PfSub4MQutOgbSZ1QkPr533ypmNgmnjho5HGuwtcDtS+P4oczr49/CCgRRvXp1atWsS40aNahZsyYxMTH3FLPmEPm+AupkTdOcw2kVz2q18umnnzJ48GAKRnsxblYhipd1vc+6ld8n8f6wOL6aF0qjRt5OjeW98Sn85/M0QsMU6eketOkaTMdXQ/ENcGpYeUpyooUJgy+y/Zd06jXwYtLkYGKi73+8WGaG8OHkFGZ/kU6psp68Myua6IfuvxXWaLBy4rCtBe5IrJlDe1M5ddRwfexc4SJR1Ktbn7p1bUefVq5cGU9P1/rB8wBxvQ+wHKaTNU1zDqdUvDNnztCtWzfWr19P3SbBjJwSRUCw612D0WIRujY9TaCfsGJlAad3QV26aKFB3Xgee9yXfhMKE5z7w+fytBOHDLzZ+zxxF8yMGBVI11f8cvzcfRs3GHi9fyIi8NbHUdRslPOZdGaGleN/Gfhrj4mDuwzE7kol/oIZAF9fL2rUrEa9uo9Rr1496tSpo08fknt0sqZpmkPkasUzGAx89NFHvPvuu1gsmbz2ZiTPtnfdU0tsWpXC6Ncu8tH0YFq0zJ2T4N7JsCFJ/PfHDBZuLkZIuG5Bya6NP6UwceglAgMVMz4LoUYNx409/Pu0mT69Ejly2MzQCRE0axvisG1dE3fexIFdmRzcZSZ2VxpHD2RgseVvlCpdjHp1G1GvXn3q1KlDuXLl9MELjuGaH2Q5SCdrmuYcuVLxjEYj8+fPZ+zYsZw4cYK6jwczYHRBooq4br0XEXo9dwZTupn1G8JdZjzY8WNmnmxyme79guj0RkFnh+PyRIT5n13l80kJVK3uycxZIRSMcvxpMlJTrbzW23Zt1+6vh9JpQO62zGZmWDm8z8CBXSYO7Mpg/59pJF219Z0GBPpRs0Z1ateuR61atahVq5Ye+5YzXONDwoF0suYASqmpwGkRmWZ/vgY4IyI97M8/BM6JyJT72MZjwBARaZ4DId+xXKXUbuAVEdmjlPIAkoDeIjLPPv9PbBeA33Uf234HSBWRyTeZ3hOIBzyAkSKy7B638Rj3+LoppVoBR0Tk4L1s+wYOrXhnz55l3rx5TJ8+nXPnzlGqfAB9RkRSvb7rn1Nq+4Y0hnc7z6TJQbRt51pHp/bucZUd243M31IcP3/Xfy2dxWIRpo+NZ+nXSTRv4cMHHwbjk80jPXOCySQMH5rED0syadUhkP7jCjot6RcRzp40cWC3gcN7zRzcm8rxvwzXD14oFB1BrZp1qF37UapUqUKlSpWIiYlx2VZvF5XvXywPZweQT20FXgSmKaXcgHAgKMv8usDrzgjsPmzFFvceoDJw2P58nlLKHygB7HXg9qeKyGSlVDngN6VUpIhcH2yllPIQEbMDtw/QClgB5ESylqNEhH379rFu3TpWrlzJxo0bERGq1Qnk9fHFqdHQPU98+IsI30y/QqEYd1q1do3uz6x6v+rP2jUG1i24Ssvu4c4OxyUZDFYmDLrEplWpdO/px8g3A3P92rKenorJU4MpGOXOzE9TyMywMuSDQnh45H4dUEpRpIQXRUp40awNQCgGg5XjB40c2mvm0L5M/ty9mv/+95/fn0HBAVSsUIFHHqlKhQoVKFWqFCVKlKBo0aJ4eTnnFDaac+lkzTG2AFPtjysA+4FCSqlQIB0oB+xWSj0OTMb2PvwBvCoihttMbwZMAy4DN23BUkoVA74Brp10qJ+IbLW3KL1jX7ci8CfQSUQkO+Xa9+kZYAa2JG0W0NU+rxawS0QsSqk3gG726f/J0rp4q+mjgM7AGWwtZ3/eYvsAiMhfSikzEK6U+h5bElkPWKaU2nM3r9uNLXlKqf1AcxE5pZTqDAzB1gK2D5gJtAAaKaXeBNoAzwJ9ADNwUETa3y72nJCZmcnZs2c5c+YMp0+fZv/+/ezZs4fdu3dx5cpVAIqX9uOV1yN4omUw0UUdHVHO2rM9gwO7MhnzbtA9n87BkapV96L2o57M+yyJp14KxcdXt65llZJk4c1eF9j7ewYj3wqkZ6/snfvMEZRS/N/wQPz9FZPfT8VoOM+IadF4usD/lbe3G+Wr+lC+KkAAEE5KkoWTh42cPGzh5BETxw/tY963O0lNsVxfz83NjZjCUZQo8TAPFSlGVFQUUVFRFCxY8Pp9WFgYQUFB+Pv754kfaFr26GTNAUTkvFLKrJR6CFtisw2IAepg6z7cB7gBXwGPi8gRpdTXwKtKqVm3mf4F0AQ4Biy8xebjgCdFJFMpVQqYD9Swz6uKLXk8jy35qqeU2pnNcrcC79of1wXGAB2UUoH251uUUtWBV4Da2JqldyilNtn39VbT29vj8sCWSN02WVNK1Qas2BI7gBARaaSU8gGO3sfrlnUbFYBRQD0RuayUChORK0qpZcAKEVlsX244UNyeEN7VSObuAypiNlmxWASzyYrZYsVsEiwW6/XphkwLqSkmUpKNpCYbbY+TTP8qx8tLUbysN48+4UWlmlHUqO9LRFTerdbffHqF8Ag32rZ1vVa1a15/I5AOba+w+rurtNKta9fFXTDxf13Pc+6UkWnTg2npIgeG9O0fgK+vYtyYFAyZ53h7RjTePq43yD8w2J1HavnySK1rU0IRES5fsnDhbxMXzpg5f8bEhb9TOf/3Hxz6ZRtX4y0YjTcfUeHmBn4BHvgHeBIQ6Imvvyeenm54ebnj6WW79/B0w8vbDU9P2025KdzcFEqBst+7qRueX5uv/ln2vt1nITM/cGSnjmvIu5/qrm8LtiSmLjAFW7JWF1uythUoA5wUkSP25ecCfYENt5i+0T79KIBSah7Q6ybb9QSmK6WqABagdJZ5v4vIWfv6e4BiQGp2yrW3NnkppaKAsti6Qf/AloDVBT4B6gNLRSTNXtYPQANsCdrNprvZp6fbp99uHNogpVQnIAVoZ28RhH+Sr1u9ntl93bJqAiwWkcv2fb9yi+X2Ad8qpX4EfrxDmf8yd+YBPDwUHp4Kd3dw91C4eyg8PLDfKzw8ISDInchoN4qXccc/0JOQAu5ERntSMNqDyEIeRBXxxMPDDdtLnLd/Re/elsauLRmMeDMQH1/X3ZdH63hRr74XX89Momn7cD12DTh11MDQLmfJSLUw5+tQ6tVz7nnxbtSthz8+voo3RyTzZvdzjPn8Ifz8XS9hu5FSEBHlQUSUd5Yk7hpBxEJaipUr8RauxJu5ctlCarKV9BQraalW0lOtpKVaSE+1kJFmxmQSUtMEU6JgMgpmo2A0CmaTYDIJCFitIGK7Wa03ThPbfZZlXEH7vqVfblTsyDfOjsORdLLmONfGeFXC1g16BhgMJANfcutv1tt9S2WnagwCLmEbV+YGZGaZZ8jy2MI/7392q9w24AXggj1Z2o6tC7IWsB1bEncz97tPYB+zdpPpafexDTO21+ganyxlZSeuZ4GG2LpH31JKVcjuuLn45G0kGf5A4Qa4oZQ7CneU8sQNT9yUF27KGzc3H9yULyqPJ2J3IiK8MaUXhaK96dzZeV1n2fXGkADatLrClu+LMHj4OGeH41Q7tsfyeruheHm6s3BxBOXLu8g3+A1e6uiHr69iyKAk3u6WyqIfvyQ4JNDZYd2/KKBUdhcWrGLEKkZETLZ7TFjFjGABsSBYEKyIWABBsALXMjOxfzDa/14fNvy/77lk86P9vg9yFHfOpc76+f4KcX06WXOcLdiSsxNi+6+/Yu8qq4DtyMZUoJhSqqSIHANeBjYBh24zvbhS6mEROQ50uMV2g4GzImJVSnUB7vSzP7vlXtunQdi6acGWvH0AXBSRRKXUr8BXSqmJ2BKe1vb4VTamewDPAZ/dId7b7cfdvm6ngOYASqlqQHH79J+BpUqpqSKScK0bFFurXqB9eTegiIhsUEptBl7CNvgkMTvBhvo+Sqjvo/e4q/nPDz/8wK6dB5n0QTg+rtF7dlvVqnvxWGMvPv14I28MLEZYWLSzQ3KK5cuX067dIKIKKb6eF07hIpY7r+RErZ/3xddXMaDveVo81Y3163cTGRnp7LC0+1Qy/I3zzo7B0Vy/HTjvisV2FOj2G6YlichlEcnENo5rkVIqFts4rFl3mN4L+MmeHJy+xXZnAF3srV6l+afl6abuolywJWslsCVpiMgFbMngVvvzXdgSud+BHdgOJNh9h+kLsR1hugT47XaxZmM/7vZ1WwKE2buEXwWO2Ms6AIwHNiml9mLrxgZYAAy1n8akFLYjYWOB3dha/rKVqGn/ZjabGTVqFCVL+fH8C3mnS3HosECSkqyMHt3R2aE4xZw5c2jdujWlSrux6IdQl0/Urmn2tA9ffBnK0aMXqFe/AmfOnHF2SJp2R/o8a5rmHLri2X322Wf06dOHWV8U5Klmeau7d9jQJJYuyWDfvu2ULVvb2eHkChFh4sSJjBw5koaNApjxWRD+/q53ybI7+X2HkR6vXCUkJJCff/6DUqVK33klzVXlrQ+Oe6CTNU1zDl3xgMuXL1OmTBlKlzHw3cKAPHeqgfg4C40bXqZBw+KsWnnc2eE4nNFopE+fPsyZM4dWrQOYNDmAvHzar/2xJrp0uoqHhzfr1m3hkUeqOjsk7d7krQ+Oe6C7QTVNc5qRI0eSlJTI2HEheS5RA4iIdOe1fv6sXnWCH3+c7uxwHCohIYGmTZsyZ84cBrwewofT/PN0ogZQsZInCxeHoZSRhg1rs379SmeHpGk3pVvWNM05HviKt2PHDurUqUP3noGMesu1Lit1N4xGocUzCSSnuPHXwYsEB4c6O6Qcd+jQIZo3b87Zs6d5f3IoLVrlnbGF2XH2jJluXZM4ecLMrFnT6N59gLND0u5O3vuld5d0y5qmabkuPT2dLl26EFXImwGvu/6pOm7Hy0vx3gdBXLxgZPDgVs4OJ8ctWrSIWrVqkZh0lu8WRuS7RA2gcBEPFv8QSu06XvToMZDhw1/Fas174/C0/Esna5qm5brhw4dz+HVgxO4AAA26SURBVPBhJk8JJTAw7zcyVq3qxSvd/Jg9+1dWrJjj7HByhNFo5PXXX6dt27aUKm1l2U/hVKue99+rWwkKdmPO3BDav+TLpEmzaP5cPa5everssDQN0N2gmuYsD2zFW7t2LU899RRduwUxekze7f68UWaG0KpFAvFxir17j1C4cDFnh3TPjh07RqdOndixYwfdegQxbIRfnh+fll0iwtdz0xk/NoXo6DCWLFlD9eo17ryi5kz5vhtUJ2ua5hwPZMU7efIkNWrUICIykx+XBePjm79ehuPHzLR4NoHKVQqzaeNxPD09nR3SXbFarcyYMYNhw4bh6WnmvUkhPP3sg9kBs3u3kX59kkhIEMaPH8OgQSNxc3swX4s8IN8na/o/T9O0XJGamkrr1q2xWNKY9XlovkvUAB4u6cH4iUFs23qGHj2fvv9L6eSiI0eO8OSTT9K/f39q1nZj9bqIBzZRA1vX9vJVBWjQ0IshQ96iYcMqHD+e/0/PormmB7cmapqWawwGA61bt2b//limfRJCseJ542z396JVa1/6D/Tn67k/89ZbvZwdzh2lpqYyYsQIKlasyB9/bGbCxALMmetPVKH8+x5lV1iYG5/PDmby1GD2xR7gkUfKMnHSWAwGw51X1rQcpLtBNc05HpiKZzAY6NChA0uXLmXy1HDavJD/L0ksIvzf4GQWL8pg1JuvMm7spy53HjmTycRXX33FmDFjOHfuHG1eDGTY8CAiInWSdjMXL1h4a1Qq69dl8PDDUUyZ8hnPPfecy72vD6h8/yboljVN0xwmJSWF5s2bs3TpUt4ZG/ZAJGoASikmfhDEi219Gf/uTPr27YDJZHJ2WIAtSZs7dy5ly5alV69eREReZfHSaCZP8deJ2m1EFXLniy+D+eqbUJRbAi1btqR+/aqsXbs2T3V3a3mTblnTNOfI9xXv0KFDtGnThsOHD/H+h2E83+bBSNSyslqF98an8J/P02nQsBLzv1tFTEyMU2KJj4/n888/Z8aMGZw/f56KFf0YNCSIxk1Etw7dJZNJWPBdBjM/TePCBQs1a1Vk6JC3adWqVZ47qCSfyPf/wDpZ0zTnyLcVz2KxMGPGDEaMGIG3j5mPp4dSr76zo3KupT9kMHJYMl5eXnwweQrdu/XG3d3xJ5c1GAysXLmSb7/9luXLl2M0GmnYyJ+u3QJ5rLFO0u6XwSAsWZzJrBlpnPnbTMGCoXTv3ptXXulOyZIlnR3egyTf/yPrZE3TnCPfVTwRYf369YwcOZKdO3fSsJE/Ez8IoZAeqA7AyZNmhg9N4fcdBsqUKcLbb0/khRdewCuHT2B28eJF1qxZw+rVq1m9ejWJiYmEh3vTvIUXHTsFUrKUPjN/TrNYhE0bDXw3z8gvP6cjAlWqlOPFFzvRqlUrypUrpxNjx8r3L65O1jSHUUpNBU6LyDT78zXAGRHpYX/+IXBORKZks7yNwBAR2ZlD8UUAKwAvYICI/HaT+eeBfiLy2W3KeR34XETS72Lz+abiJScns2TJEmbNmsXvv/9OoUI+jHwrkGebu+kvqBuICKtXGZgyOY1jR00UCA+ifbuOPPNMcxo2bEhAQMBdlZeWlsbhw4fZuXMnv//+Ozt27GD//v0ARER40egxT55rGUTdelY8PPR7kRvOn7ewcoWRlT9lsnuX7ajRqKgCPPlkMxo3fpxatWpRtmzZXGlZfYDk+39unaxpDqOUehF4UUTaKqXcgD8Ao4jUsc/fBrwuIjuyUZY78DM5m6y1B54WkS63mP8a0AGwiMhjt4nrOFBDRC7fxebzbMVLT0/nwIEDbN68mXXr1rFx40YyMjIoXsKXnr38eP4FT7y9nR2la7NYhM2/Gvl+oZH169MxGgQ3N0XxEg9RsUJloqNjKFCgAMHBwSilsFqtZGRkkJCQwOXLlzl37hxHjx7h/PkL18sMDfOkcmUPatbypdFj3pQrb8XNLd9/h7m08+ct/PariS2bzWzdnE5Cgq1V08/PhypVHqFy5eqUKlXq+q1YsWJ468pzL/L9P7pO1jSHUUpFA7+LSGGlVCVgCFAIaAekA5eASKABMBnwwJbQvSoiBqXUKeBLoCkwHehjL2MXMAc4A4wGZgM1sCVAX4rI1BviKGovJwKIB14BwoBlgC9wDqgjIhk3rPcbMBj4DmgkIufs01OBKcBTwE/Am8Bh4LKINM7Oa5OWliYiwrUbQNbnN5uWU8vcaj2TyURqaiqpqamkpaWRmppKcnIyFy5c4Ny5c5w7d46TJ09w9Oix6+s8/LAv9Rq407J1IFWrWnVL2j3IzBB27jSy8w/h6BETR48auBwvJCVZuPFa4kFBHoSEuhERoShWzJ3iJXwoXsKLChUsPFRUt2S6MqtVOH7MQmyshf2xQuy+DI4cMZGc9O83OSwsmEKFooiKiqFQoWjCwsIICgoiKCiIwMDA6/c+Pj54eXnh5eWFp6fn9cfXniulUErh5uZ2/XHW262mX7vlJf7+/nkr4HugkzXNoewJV0PgaWy/fmKAbUAS8B62ROwo8LiIHFFKfQ3sEpFp9nVniMj79rI2AsOBgcB+ERmvlKoOTBSRJ+3LhIhI4g0xLAcWi8hcpVQ3oIWItFJKdcXWItbvJnEXAX4RkVJKqQnYErEp9nkCtBOR77Ps4121rNnLyBOUgogIN6Ki3IiOcadMWQ/KlvPkkcqeREfrrhxHsVqF9HTbv4mbG3h6Kjw98/130gNFRLh6VTh10szJExbOnbMQH2chPt5KXJyVuDgLyclCaoqgv6pv7eSZqKLFCl/429lxONKDdyy9ltu2AHXttynYkrW62JK1rUAZ4KSIHLEvPxfoC0yzP194Q3mfAd+LyHj78xNACaXUJ9haudbeJIY6wPP2x98A72cj7vbA9/bHC7C13l0bW2cBlmSjjFsaMSoSIQOFLRm69kP22mOluN6wf30a156rfy+Hbdn/Ked/ylbXl7uxXKXA3UPh76/w87Pd+/op/P0UBcLd8PBwBzxRyuOfwDSHcneHwEBnR6E5klJQoIDtdtNrxYsZwYKImYwMC6kpQmqaLXkzGgWTSTCZ+OfeKBjtz0WwJXgCViv254LA9XlizfL42i2XX4P7ZW9wqo+tByTf0sma5mhbsSVnlYD92LouBwPJ2Lom7/TNn3aT8horpT4UkUwRuaqUqoytS7Iv0Bbodocys/N51AEoqJTqaH8erZQqJSJHgUwRua9DHCe8e+l+Vtc0TdP+ka8TNdBXMNAcbwvQHLgiIhYRuQKEYGvt2gYcAooppa6dlOhlYNNtypsNrAQWKaU8lFLhgJuILAHeAqrdZJ2t2FrKADoCm28XsFKqDOAvIjEiUkxEimHrsm1/i1VSAN0GommapjmETtY0R4sFwoHtN0xLEpHLIpKJbcD/IqVULGAFZt2uQPvYsV3YujRjgI1KqT3AV8CIm6wyAHhFKbUPWzI48A4xdwCW3jBtiX36zXwOrFJKbbhDuZqmaZp21/QBBprmHLriaZqm5Yx8P5BWt6xpmqZpmqa5MJ2saZqmaZqmuTCdrGmapmmaprkwnaxpmqZpmqa5MJ2saZpzKGfdlFK9nbl9vX96//T+OT+OfLZ/+Z5O1jTtwdPL2QE4mN6/vE3vX96W3/fPKXSypmmapmma5sJ0sqZpmqZpmubCdLKmaQ+ez50dgIPp/cvb9P7lbfl9/5xCX8FA0zRN0zTNhemWNU3TNE3TNBemkzVNewAppT5QSh1SSu1TSi1VSoU4O6acpJR6USl1QCllVUrVcHY8OUEp1UwpdVgpdUwpNdzZ8eQ0pdSXSqk4pdR+Z8fiCEqpIkqpDUqpv+z/mwOdHVNOUkr5KKV+V0rtte/fGGfHlJ/oZE3THkzrgIoi8ghwBBjh5Hhy2n7geeBXZweSE5RS7sCnwNNAeaCDUqq8c6PKcV8BzZwdhAOZgcEiUg54FOibz95DA9BERCoDVYBmSqlHnRxTvqGTNU17AInIWhEx259uBwo7M56cJiJ/ichhZ8eRg2oBx0TkhIgYgQVASyfHlKNE5FfgirPjcBQRuSAiu+yPU4C/gBjnRpVzxCbV/tTTftOD4nOITtY0TesGrHJ2ENptxQBnsjw/Sz76on/QKKWKAVWBHc6NJGcppdyVUnuAOGCdiOSr/XMmD2cHoGmaYyil1gNRN5k1SkT+a19mFLbumW9zM7ackJ39y0dudkkd3WqRBymlAoAlwOsikuzseHKSiFiAKvYxsEuVUhVFJF+OQcxtOlnTtHxKRJ643XylVBegOfC45MFz+Nxp//KZs0CRLM8LA+edFIt2j5RSntgStW9F5Adnx+MoIpKolNqIbQyiTtZygO4G1bQHkFKqGTAMaCEi6c6OR7ujP4BSSqniSikvoD2wzMkxaXdBKaWA2cBfIjLF2fHkNKVUxLWjypVSvsATwCHnRpV/6GRN0x5M04FAYJ1Sao9SapazA8pJSqnWSqmzQB3gJ6XUGmfHdD/sB4P0A9ZgG5j+vYgccG5UOUspNR/YBpRRSp1VSnV3dkw5rB7wMtDEXuf2KKWecXZQOagQsEEptQ/bj4t1IrLCyTHlG/oKBpqmaZqmaS5Mt6xpmqZpmqa5MJ2saZqmaZqmuTCdrGmapmmaprkwnaxpmqZpmqa5MJ2saZqmaZqmuTCdrGmapmmaprkwnaxpmqZpmqa5MJ2saZqmaZqmubD/B6qFCuPtHtBlAAAAAElFTkSuQmCC\n",
"text/plain": [
"
"
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"sector_features_yeo = pd.DataFrame(sector_features_yeo,\n",
" index=sector_features.index,\n",
" columns=sector_features.columns)\n",
"fig, axes = joypy.joyplot(sector_features_yeo, colormap=plt.cm.viridis, figsize=(8,8),\n",
" title='Distribution of mis-invoicing across sectors (Yeo–Johnson transformation)');"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"source": [
"The two figures below display the results of running the PCA analysis on transformations of the data using a modified log and a Yeo-Johnson transformation, respectively.\n",
"\n",
"The top loadings on the second principal component are the same and refer to Works of Art, Pearls, Precious Stones and Metals, and Arms and Ammunitions. These sectors refer to extremely high value-added sectors where the traded commodity is a finished product.\n",
"\n",
"By contrast, the loadings on the first principal component (in either transformation) refer to heavy industries, where the commodity is an intermediate product (as opposed to a finished product). Even after applying normalizing transformations, the first principal component recovers sectors which were responsible for a large amount of the dollar value of mis-invoicing in the continent during 2000-2016. "
]
},
{
"cell_type": "code",
"execution_count": 29,
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"outputs": [
{
"data": {
"text/html": [
"\n",
"\n",
""
],
"text/plain": [
"alt.LayerChart(...)"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"biplot_PCA(sector_features_log, 10, 1, 2, obs='reporter.ISO')"
]
},
{
"cell_type": "code",
"execution_count": 30,
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"outputs": [
{
"data": {
"text/html": [
"\n",
"\n",
""
],
"text/plain": [
"alt.LayerChart(...)"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"biplot_PCA(sector_features_yeo, 10, 1, 2, obs='reporter.ISO')"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"source": [
"Finally, transforming the data improves the performance of the PCA analysis, in the sense that the first two principal components now explain 90% of the variance in the data."
]
},
{
"cell_type": "code",
"execution_count": 31,
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"outputs": [
{
"data": {
"text/html": [
"\n",
"\n",
""
],
"text/plain": [
"alt.LayerChart(...)"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"scree_plot(sector_features_yeo)"
]
},
{
"cell_type": "markdown",
"metadata": {
"hideCode": false,
"hidePrompt": false,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"### Country features"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"source": [
"The second view of `IFF_Sector` is to consider the reporter countries as the feature space. Below, I use the function `create_features()` and specify `reporter.ISO` as the features in order to generate the data-set for PCA. In this case, we have $p=46$.\n",
"\n",
"The interpretation in this application is to understand the variation in where the illicit outflows originate. This is because the values have been aggregated using the GER strategy which captures outflows only."
]
},
{
"cell_type": "code",
"execution_count": 32,
"metadata": {
"slideshow": {
"slide_type": "-"
}
},
"outputs": [
{
"data": {
"text/html": [
"
"
],
"text/plain": [
" PC1 PC2 PC3 PC4 PC5 PC6 PC7 \\\n",
"AGO 0.064538 -0.127775 -0.044675 -0.081190 0.015199 -0.030508 -0.020684 \n",
"ALB 0.044858 0.100240 -0.085332 0.010378 0.222166 -0.056160 0.016405 \n",
"AND 0.002434 0.006593 -0.006567 0.005445 -0.015707 0.021064 -0.006253 \n",
"ARE 0.091433 -0.038099 0.067933 -0.046062 0.123878 -0.061712 -0.030800 \n",
"ARG 0.129513 0.139207 -0.082968 0.019367 -0.043149 0.085106 -0.014389 \n",
".. ... ... ... ... ... ... ... \n",
"VUT 0.000000 0.000000 0.000000 0.000000 -0.000000 0.000000 0.000000 \n",
"YEM 0.040005 -0.060918 0.007451 0.143530 0.037673 0.037506 0.085598 \n",
"ZAF 0.008847 0.007834 0.091261 -0.022447 0.026785 0.001632 -0.043753 \n",
"ZMB 0.040152 0.020620 -0.037492 0.009481 0.093282 -0.176393 -0.033166 \n",
"ZWE 0.058102 -0.112442 0.020694 0.215291 0.042842 0.010566 0.044425 \n",
"\n",
" PC8 PC9 PC10 \n",
"AGO -0.075254 0.026087 0.018444 \n",
"ALB -0.068677 0.098802 -0.006931 \n",
"AND -0.004508 0.001468 -0.016877 \n",
"ARE 0.190913 -0.147428 0.060691 \n",
"ARG 0.038525 0.024086 0.000942 \n",
".. ... ... ... \n",
"VUT 0.000000 0.000000 0.000000 \n",
"YEM 0.261330 0.309931 -0.017295 \n",
"ZAF 0.104236 -0.037778 0.124183 \n",
"ZMB 0.069316 -0.109787 0.018559 \n",
"ZWE 0.149634 0.182897 0.017658 \n",
"\n",
"[167 rows x 10 columns]"
]
},
"execution_count": 47,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"biplot_PCA(partner_features, 10, 1, 2, show_loadings=True)"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"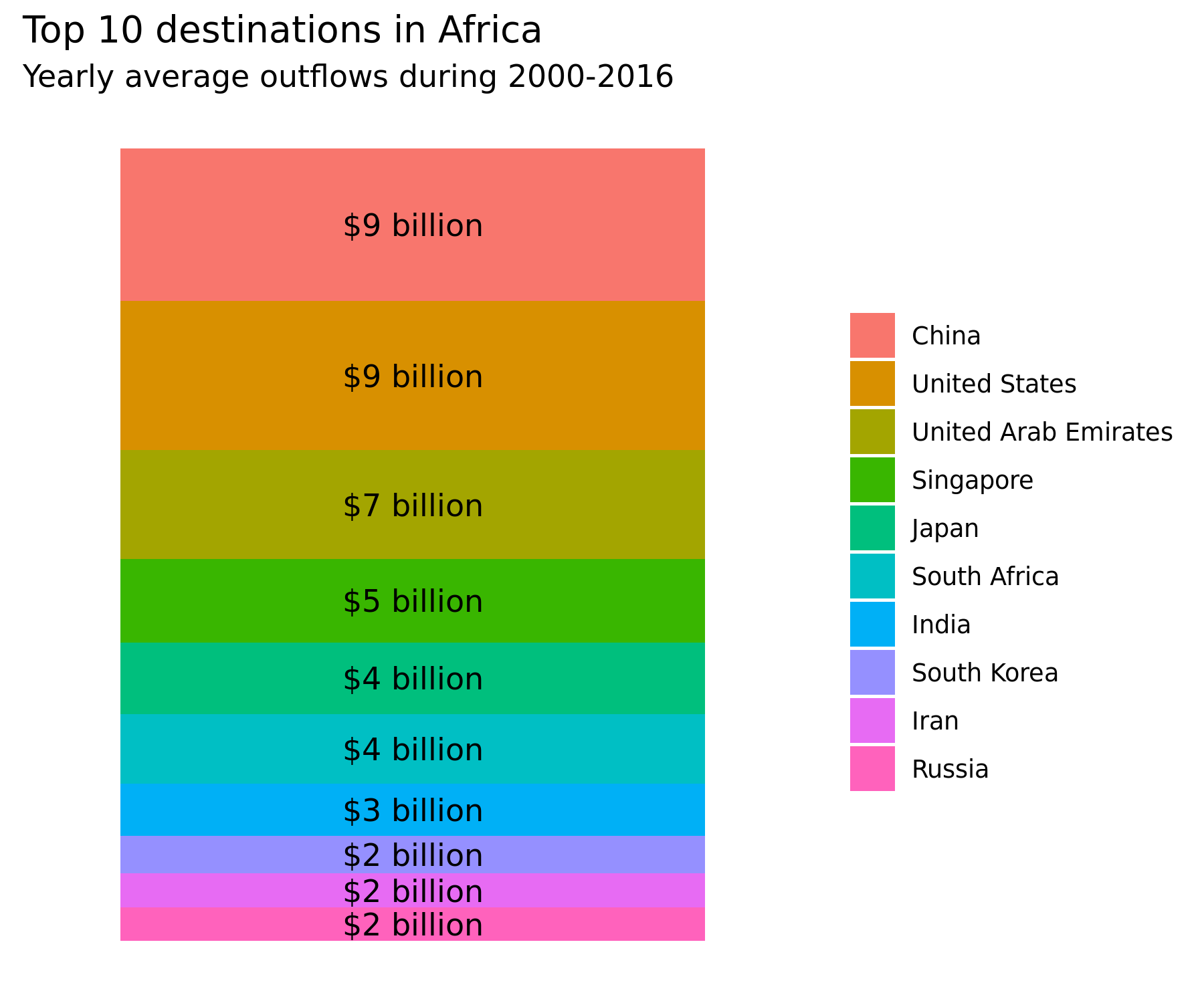\n",
"*Source*: generated by `Data Visualization.R` in "
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"source": [
"The top loadings on the other principal components reveal some unexpected sources of variation for destination countries.\n",
"\n",
"The top loadings are:\n",
"- Second principal component:\n",
" - Top loading 1: El Salvador\n",
" - Top loading 2: Dominican Republic\n",
" - Top loading 3: Nepal\n",
"- Third principal component:\n",
" - Top loading 1: Belgium\n",
" - Top loading 2: Norway\n",
" - Top loading 3: Panama\n",
"- Fourth principal component:\n",
" - Top loading 1: Iran\n",
" - Top loading 2: Suriname\n",
" - Top loading 3: Papua New Guinea\n",
"- Fifth principal component:\n",
" - Top loading 1: Central African Republic\n",
" - Top loading 2: Kuwait\n",
" - Top loading 3: Albania\n",
"- Sixth principal component:\n",
" - Top loading 1: Ecuador\n",
" - Top loading 2: Slovenia\n",
" - Top loading 3: Algeria"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"source": [
"These dimensions of variation are much harder to interpret. Nevertheless, a few points stand out.\n",
"\n",
"First, apart from the first principal component, the loadings do not appear to be driven by the magnitude of the illicit outflows. Second, the loadings recovered are surprising. One \"usual suspect\" which appears is Panama (on the third principal component) which is one of the oldest and best-known tax haven in the Americas. Third, this suggests that the analysis of the destinations of illicit outflows from Africa merits much deeper analysis to \"follow the money\" (which is outside the scope of this project)."
]
},
{
"cell_type": "code",
"execution_count": 48,
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"outputs": [
{
"data": {
"text/html": [
"\n",
"\n",
""
],
"text/plain": [
"alt.LayerChart(...)"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"biplot_PCA(partner_features, 10, 3, 4)"
]
},
{
"cell_type": "code",
"execution_count": 49,
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"outputs": [
{
"data": {
"text/html": [
"\n",
"\n",
""
],
"text/plain": [
"alt.LayerChart(...)"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"biplot_PCA(partner_features, 10, 5, 6)"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"source": [
"#### Explained variance"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"source": [
"With a feature space of $p=167$, 12 principal components are required to explain at least 50% of the variance in the data."
]
},
{
"cell_type": "code",
"execution_count": 50,
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"outputs": [
{
"data": {
"text/html": [
"\n",
"\n",
""
],
"text/plain": [
"alt.LayerChart(...)"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"scree_plot(partner_features)"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"source": [
"#### Variance-stabilizing and normalizing transformations"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"source": [
"The sections below explore the effect of variance-stabilizing transformations on the `partner_features` data-set.\n",
"\n",
"Korea and Nicaragua appear as top loadings on the first and second principal components, respectively.\n",
"\n",
"When running PCA on the transformed data, the projection of the principal component scores on the first two principal components takes on a half-moon shape.\n",
"\n",
"Expand the code chunks to see the details."
]
},
{
"cell_type": "code",
"execution_count": 51,
"metadata": {
"slideshow": {
"slide_type": "skip"
},
"tags": [
"hide-cell"
]
},
"outputs": [
{
"data": {
"text/plain": [
"['ATG',\n",
" 'BLZ',\n",
" 'BMU',\n",
" 'DMA',\n",
" 'GNB',\n",
" 'GRD',\n",
" 'KGZ',\n",
" 'KNA',\n",
" 'LCA',\n",
" 'SLB',\n",
" 'TON',\n",
" 'VCT',\n",
" 'VUT']"
]
},
"execution_count": 51,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# Figure out which columns are composed of all 0s\n",
"partner_features.apply(lambda x: (x == 0).all(), axis=0)\n",
"noIFFpartner = partner_features.loc[:,partner_features.apply(lambda x: (x == 0).all(), axis=0)].columns.tolist()\n",
"noIFFpartner"
]
},
{
"cell_type": "code",
"execution_count": 52,
"metadata": {
"slideshow": {
"slide_type": "skip"
},
"tags": [
"hide-cell"
]
},
"outputs": [],
"source": [
"# Drop the corresponding features\n",
"partner_features = partner_features.drop(columns=noIFFpartner)"
]
},
{
"cell_type": "code",
"execution_count": 53,
"metadata": {
"slideshow": {
"slide_type": "skip"
},
"tags": [
"hide-cell"
]
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAjIAAAI4CAYAAABwVwM/AAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4yLjEsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy+j8jraAAAgAElEQVR4nO3deZhkVX3/8ffHGRCQAURUBBVkUSOIIyqu6LhEjcEYlxiXKBhXEpcY+UUjanBf4haj4i6oAVziSlxQcATcFQcBN0BQEBABgRkWgeH7++Pehpq2a7qqu2c53e/X89TTVffce865dZf61F2qU1VIkiS16CYbugOSJEkzZZCRJEnNMshIkqRmGWQkSVKzDDKSJKlZBhlJktQsg8x6lOR9SV45R3XdPsmqJIv618uTPGsu6u7r+0qS/eeqvjHafV2Si5JcMAd1vTzJh2Yw3VOTHDPb9kdoZ1WSXaYZZ43lrHUjyWFJXreh+7E+JNk5SSVZvA7qPjDJ7/t19hZzXb+Gm8vPl9bE35GZG0nOBm4NXAesBn4GfAz4QFVdP4O6nlVV3xhjmuXAJ6pqJh/chwC7VdU/jDvtXEpyO+BXwE5VdeGG7IsWliSHAedW1Ss2dF/WtSQ7A2cBm1TVdXNY7ybA5cB9qurkuap3mjYL2L2qzlgf7W0ISQ6g+zx4wIbuy8bKIzJz69FVtQTYCXgT8FLgw3PdyLr4JrWR2Am42BDTlvV9tGger/+tuzWwGXDaum5ofawDLa1nC/6IbVX5mIMHcDbwsEnD9gGuB/bsXx8GvK5/vh1wNHApcAlwAl2w/Hg/zVXAKuDfgJ2BAp4J/BY4fmDY4r6+5cAbgR8AlwFfALbty5bRfdv8s/4CjwSuAa7t2zt5oL5n9c9vArwC+A1wId2Rpq37sol+7N/37SLg4LW8T1v30/+hr+8Vff0P6+f5+r4fh00x7TLg3P49uRA4H/hb4FF0R3IuAV4+MP4hdEepoNvBfgK4uH/PfwjcekgfDwBOHHhdwPOA04E/Au8BAty0r2vPgXFv2c/HrfrXzwbO6Pv2RWCHSfXu1j/fHHhb/55cBpzYD5tqOb8W+DawEjgG2G6gzqf3dVwMvJIp1suBcf8a+Andt+hzgEMmlT8A+E4/j+cABwysx4cCXwau6JfdX/R9u5Tug+xvBup5FN0RypXA74CD1rYNDOlrAf/cL4Oz+mH/1ffrcuDHwL6Tlv2n6Na1lX2f7jlQfnfgpL7sk8BR9NvmiMvtn/q+rOyXx67Ad/u+fArYdMh87AZ8q1/GFwGfHCibbn4+TbcOrwROAe4I/DvdtnAO8PCB8ZczfH+wM2uuU1vTfeE6v18+rwMWDen/TYF3Auf1j3f2w+7YrwtFt/0eN8W0E+0+p5/2fOAlk/aX3+3Xh/OBdw++j5PXAbr9YPXtrgL+nhv3ES/hxn3EMyb1/610+6rfA+8DNp+0f3kpcAHw8SHvwbOBn/fL4WfA3v3wtW0Dy+n3p2PuY/4CuJruKP8q4NK1bIOHseY6vB+wou/Pd4C9Bspe2i/rlcAvgYfO5HNvY3ls8A7MlwdDPjD6DebA/vkNKxrdTuZ9wCb9Y19uPNW3Rl0DO4CPATdj+Afc74A9+3H+lxs/xJcxJMj0zw+ZGHeg/IYND/hHup36LsCWwGcnNvKBfnyw79fdgD8BfzHkffoY3U51ST/tr4BnDuvnpGmX0Z26e1X/nj2bLhAd0de3R7/R7zJ5voDnAl8CtgAWAfcAthrSzgH8+U7maGAb4PZ9m4/syz4CvH5g3H8Gvto/fwjdh9XedDvQ/waOn1TvRJB5T/+e79j37379NFMt5zPpPjg271+/qS+7C93O7gHApnQ77GsZHmSWAXelC5J70e3Y/7Yvuz3dTu7J/Xt9C2DpwHp8GXD/ftol/frx8r7dh/TT3qkf/3z6D2Xg5ty44x+6DUzR1wK+DmzLjR88/9D3azHdB9cFwGYDy/5quhC1qG/re33ZpnRh78V9u0/o36fXjbHcvghsRbfO/Qk4lm772Jruw23/IfNxJHBw/75tBjxgoGyU+XlEX/4xug/zg7lxWzhr0vY7bH+wM2uuU58H3t+Pdyu68PPcIf1/DfC9frxb0n1AvnaqeqeYdqL8yL6tu9JtSxP7oXsA9+nnb2e6sPAv06wDN2xDk/YRr+nfl0cBVwI378vf2S+7benW2y8Bb5w07Zv75b75FPPwd/37ei+6oLEb3ZHkTVj7NrCc6YPMsH3MGuMO2QY3Y83Pl73pgty96db//en2+TcF7kQXfHcYWC67jvI5t7E+NngH5suD4UHme/RHKCataK+h+0Dfbbq6BnYAu0wxbPAD7k0D5XehO9KyiNkHmWOBfxoouxPdjn9ih1PAbQfKfwA8aYr5WkS307/LwLDnAsv753/Wz0nTL6M72rGof72kb/veA+P8mBs/jG+YL7owtsa3krW0s8aOo29j8APnU8DL+ucPA349UPZt4On98w8Dbxko27J/33YeqHc3uh3RVcDdpujLVMv5FQPl/8SNwelVwJEDZVv068CUQWaKtt4JvKN//u/A54aMdxjwsYHX+9J96N5kYNiR9Ed46ML8c5kUHFnLNjBFmwU8ZJpx/jjxHvbL/huTtoer+ucPpDsikIHy73DjtjnKcrv/pHXupQOv3wa8c0gfPwZ8gIHtZYz5+fpA2aPpQuvkbWGbgfVk2P7ghnWK7nTQnxj40KYLr98c0qczgUcNvH4EcPZU6+pa1uU7Dwx7C/DhIeP/y+A6ONU6wNRB5qrBPtB9oN+HLnhcwcCHNnBfbjzCt6x/jzZbyzL5GvCiKYZPtw0sZ/ogM2wfs8a4U22DA8Mm1uFD6QPmQPkvgQfR7XMupNt3bTLdetjCw2tk1r0d6Q5PT/afdAn+mCS/TvKyEeo6Z4zy39B9S9hupF6u3Q59fYN1T+wEJwzeZXQl3c5/su248dvwYF07jtGXi6tqdf/8qv7v7wfKrxrS9sfpdkJHJTkvyVuSbJJk3/4Oi1VJ1nZuf9j8HQdsnuTeSXYClgKf68vWeN+qahXdKZ/J87sd3TeqM9fS/ih92YGBdaCqruzbm1Lf528m+UOSy+gObU+sL7ebpj+D69oOwDm15kXtg8v18XTfjH+T5FtJ7tsPH3cbWGP9T/KSJD9PclmSS+mOhgyu75Pfp8366x52AH5X/d59oL+D8zPdcpu8zo2yDkJ3WjTAD5KcluQfx5ifyW1cNMW2MNjuKPuDiaMJ5ye5tG/3/XRHXKYy1b5ghyHjDjO5XzsAJLljkqOTXJDkcuANU/R3un0gdPuIwYuYJ7aRW9KF+x8PzOtX++ET/lBVV6+l7mHbxXTbwChG2YcOWtt7sRPwkon57Of1dnRHYc6gC4mHABcmOSrJuMtwo2KQWYeS3ItuRT5xcllVrayql1TVLnTfrv41yUMniodUOWz4hNsNPL893bfIi+i+hWwx0K9FrLnxTlfveXQbxmDd17HmjnUUF/V9mlzX78asZ2xVdW1Vvbqq7kJ32mY/uiMnJ1TVlv1jjxnUez3dt6cnA08Bjq6qlX3xGu9bkpvRnTqYPL8X0Z022HXc9ic5H7jtQHub9+0NcwTdYfbbVdXWdKd50pedM01/BteZ84DbJRncn9ywXKvqh1X1GLoPx8/TvV/TbQNrbTPJvnTn+Z9Id9pgG7pD7Rky7aDzgR2TDI57+0nzM8pyG1tVXVBVz66qHeiOUr03yW6znJ9hhu0PBp1Dd0Rmu6rapn9stZZtYap9wXmz7NfE9IcCv6C7C2krutM0k+d/un3V2lxEF/j2GJjXratqMDBMV/+w7WKt2wCT9sHA9mP0eyafB+fQnfLeZuCxRVUdCVBVR1R3F9ROfT1vHqM/Gx2DzDqQZKsk+9FdQPiJqjplinH263dgobu4b3X/gC4grPX3RYb4hyR3SbIF3WH7z/Tf2H5F9230r/tbJF9Bd650wu+BnSdthIOOBF6c5A5JtqT7pvTJGvPWzb4vnwJen2RJfwTjX+kuYFynkjw4yV37EHc53U599TSTjeoIugsNn9o/Hxz+jCRLk9yU7n37flWdPThxH4Y+Arw9yQ5JFiW5bz/NOD4DPDrJ/ZJsCryatX8QLgEuqaqrk+xDF8Qm/A/wsCRPTLI4yS2SLB1Sz/fpdtT/1h/lWkYXTI5Ksmm63+XZuqqu5cZ1fbptYDpL6ML0H4DFSV5Fd83KKL7bT/vCft4eR3eh6YSRlttMJPm7JBNh8490HyKrZzk/wwzbH9ygqs6nu2D8bf1+6yZJdk3yoCF1Hgm8Isktk2xHdzpz3O33lUm2SLIH8Ay6i62hew8uB1YluTNw4Ah1jbyv7LezDwLvSHIrgCQ7JnnEGH3/EHBQknuks1u/Hxu6DfTTrQAe18/3bnQ3bozq98Bt+216VB8EntcfdU2Sm/X7/yVJ7pTkIf26fTVduJurfeEGYZCZW19KspIuDR8MvJ1uQ53K7sA36M5zfxd4b1Ut78veSLezuDTJQWO0/3G686QX0J2qeCFAVV1Gdy3Fh+i+IVxBd3X+hE/3fy9OctIU9X6kr/t4ugsMrwZeMEa/Br2gb//XdEeqjujrX9e2p/ugv5zuIsJvMUcBqqomdmI7AF8ZGH4s3Z1D/0t3FGBX4ElDqjmI7k6UH9KdinwzY26fVXUa3ft7VN/eSrpz4X8aMsk/Aa/p19lX0R8p6ev6Ld3poJf0/VlBdyH3VO1eA/wN8Fd033rfS3e06xf9KE8Dzu5PFzyP7qJWWPs2MJ2v0b3Xv6I7hH81o512mOjv4+iuPfgjXQj97ED5OMttXPcCvp9kFd3RsBdV1VnMYn7WYsr9wRSeTnfK92d078dngNsMGfd1wI+An9Ktryf1w8bxLbpTiscCb62qiR+fPIguTK+k+yD+5NSTr+EQ4PB+X/nEEcZ/ad/29/r18Rt01/yNpKo+Dbyebr+1ku4I47YjbAPvoLv+5vfA4XRfFEZ1HN1dUBckmXxEbVg/f0R3Afi76ZbpGXTrO3RfYt/U9/MCuiOlLx+jPxsdfxBPmqf6o2eX0h2qP2tD90frT2bxA5nrStbRD/FJHpGR5pEkj+4PX9+M7vbrU+juUJOkeckgI80vj+HGHyvbne42eA+7Spq3PLUkSZKa5REZSZLUrFb+KZaHjSRJWriG/pSER2QkSVKzDDKSJKlZBhlJktQsg4wkSWqWQUaSJDXLICNJkpplkJEkSc0yyEiSpGYZZCRJUrMMMpIkqVkGGUmS1CyDjCRJapZBRpIkNcsgI0mSmmWQkSRJzTLISJKkZhlkJElSswwykiSpWQYZSZLULIOMJElqlkFGkiQ1yyAjSZKaZZCRJEnNMshIkqRmGWQkSVKzDDKSJKlZBhlJktQsg4wkSWqWQUaSJDXLICNJkpplkJEkSc0yyEiSpGYZZCRJUrPGCjJJdk5y6qRhhyQ5KMlhSZ7QD9s2yU+SPKOf5qokK5L8LMnHkmwylzMhSZIWpjk/IpNka+BrwAeq6qP94DOrailwV+C2wBPnul1JkrTwLJ7j+rYEvgIcUVWHTi6sqtVJfgDsOE6ld95m2dz0TpIkNecXly4fWjbXQebtwIeq6h1TFSbZDLg38KJxKr36sjnomSRJatKrQ/1HkanKxg0yNc3w44DHJHlrVV04UL5rkhXA7sBnquqn4zR65jXLuf7aMXsqSZLmhTfcjJsOKxs3yFwM3HzSsG2Bs/rnRwEnAl9O8uCqWtkPP7Oqlia5DbA8yd9U1RdHbXTRJt1DkiQtPP9RXDOsbKyLfatqFXB+kodCd3cS8Ei68DIxzjuBY4HPJdl00vTnAy8D/n2cdiVJkqYyk7uWng68oj9VdBzw6qo6c3CEqnopcA7w8Sna+DywRZJ9Z9C2JEnSDVI17LKXjUoTnZQkSevElBf6gr/sK0mSGmaQkSRJzTLISJKkZhlkJElSswwykiSpWQYZSZLULIOMJElqlkFGkiQ1yyAjSZKaZZCRJEnNMshIkqRmGWQkSVKzDDKSJKlZBhlJktQsg4wkSWqWQUaSJDXLICNJkpplkJEkSc0yyEiSpGYZZCRJUrMMMpIkqVmzDjJJVidZMfDYOcmyJEf35QckuT7JXgPTnJpk59m2LUmSFrbFc1DHVVW1dHDAFCHlXOBg4O/noD1JkiRg/Z1aOhrYI8md1lN7kiRpAZiLIzKbJ1nRPz+rqh47xTjXA28BXg7sP24Dt912GatXz6KHkiSpWQ+/0zc/c/gP8oSpytbJqaUhjgAOTnKHcRtYvRqqxu+YJEmaFx41rGAugsxIquq6JG8DXjrutOdftnzuOyRJklqxxbCC9X379WHAw4Bbrud2JUnSPLReg0xVXQO8C7jV+mxXkiTNT6k2Lj5popOSJGmdyLACf9lXkiQ1yyAjSZKaZZCRJEnNMshIkqRmGWQkSVKzDDKSJKlZBhlJktQsg4wkSWqWQUaSJDXLICNJkpplkJEkSc0yyEiSpGYZZCRJUrMMMpIkqVkGGUmS1CyDjCRJapZBRpIkNcsgI0mSmmWQkSRJzTLISJKkZhlkJElSswwykiSpWYtnMlGS7YF3AvcC/gScDXwNeMakuvcA7gLcGvgCcNZA+UFV9Y2ZtC9JkgQzCDJJAnwOOLyqntQPWwosqar/GhjvDcCKqvp5klsDJ1TVfnPUb0mSpBkdkXkwcG1VvW9iQFWtGBwhyQOBJwJ7z657nR13e9BcVCNJkhr0uzO+NbRsJkFmT+DHwwqTbAN8FHh6VV0+ULRvksHA8/iqOnOUBlddOYNeSpKkeWHfA6+pEw7dNFOVzegamWkcCnyiqr49afiMTy2dctJyLrikZt8zSZLUnJf893V7DiubSZA5DXjCVAVJ9gd2Bp42g3qHuv324fbbTxnEJEnSPHfCoZueNqxsJrdfHwfcNMmzJwYkuVeSBwGvB55aVdfNoF5JkqSxpGr8UzZJdqC7/foewNV0t19vRndx728mjf4CYBF/fvv166rqMyM26XklSZIWrqGnZWYUZDaAJjopSZLWiaFBxl/2lSRJzTLISJKkZhlkJElSswwykiSpWQYZSZLULIOMJElqlkFGkiQ1yyAjSZKaZZCRJEnNMshIkqRmGWQkSVKzDDKSJKlZBhlJktQsg4wkSWqWQUaSJDXLICNJkpplkJEkSc0yyEiSpGYZZCRJUrMMMpIkqVkGGUmS1Kw5CTJJVvV/b5LkXUlOTXJKkh8muUNfdnaS7eaiPUmSJIDFc1zf3wM7AHtV1fVJbgtcMcdtSJIkAXMfZG4DnF9V1wNU1blzUenKlSvnohpJktSgJUuWDC2b6yDzKeDEJPsCxwKfqKqfzLbSrbbaatYdkyRJbbrNe1e+5LwDt3zbVGVzGmSq6twkdwIe0j+OTfJ3VXXsbOpd8rjXz0n/JElSk94KTBlkUlWzrj3JqqracorhBwE7VdULkpwN3LOqLppBE7PvpCRJalWGFczp7ddJ9k6yQ//8JsBewG/msg1JkqQJc/07MrcCvpTkVOCnwHXAuwfKf5rk3P7x9jluW5IkLTBzcmppPWiik5IkaZ1YP6eWJEmS1ieDjCRJapZBRpIkNcsgI0mSmmWQkSRJzTLISJKkZhlkJElSswwykiSpWQYZSZLULIOMJElqlkFGkiQ1yyAjSZKaZZCRJEnNMshIkqRmGWQkSVKzDDKSJKlZBhlJktQsg4wkSWqWQUaSJDXLICNJkpplkJEkSc0yyEiSpGZNG2SSVJKPD7xenOQPSY7uXx+Q5Pokew2Mc2qSnfvnWyY5NMmZSX6S5MdJnj33syJJkhaaUY7IXAHsmWTz/vVfAr+bNM65wMFDpv8Q8Edg96q6O/BIYNsZ9FWSJGkNi0cc7yvAXwOfAZ4MHAnsO1B+NPDAJHeqql9ODEyyK7AP8JSquh6gqv4AvHmcTm57zweMM7okSZpHLvnRiUPLRg0yRwGv6k8n7QV8hDWDzPXAW4CXA/sPDN8DOHkixMzUpdfVbCaXJEkN2/ybF9ZVD75VpiobKchU1U/7a16eDHx5yGhHAAcnucOwepIcDPwdcKuq2mGUtgE+dcyxnLrqulFHlyRJ88ibf3Pl/sPKUrX2ox1JVlXVlkleBbwIWAbcAjioqvZLcgBwz6p6fpLnAHsDDwD2owtKxwC7DR6VmahzjHnwkIwkSQvXlEdjYLzbrz8CvKaqTlnLOIcBDwNuCVBVZwA/Al6XZBFAks3W1iFJkqRRjRxkqurcqvqvaca5BngXcKuBwc+iO4JzRpIfA98AXjqDvkqSJK1h2lNLG4kmOilJktaJOTm1JEmStFExyEiSpGYZZCRJUrMMMpIkqVkGGUmS1CyDjCRJapZBRpIkNcsgI0mSmmWQkSRJzTLISJKkZhlkJElSswwykiSpWQYZSZLULIOMJElqlkFGkiQ1yyAjSZKaZZCRJEnNMshIkqRmGWQkSVKzDDKSJKlZBhlJktQsg4wkSWrWyEEmyS2SrOgfFyT5Xf/80iQ/mzTuIUkO6p8f1o970/71dknOntO5kCRJC9LIQaaqLq6qpVW1FHgf8I7++VLg+mkmXw3848y7KUmS9OcWr6d23gm8OMkHZzLxLe9732mTkiRJmp+2/5//2fe0XXY5Yaqy9RVkfgucCDwN+NK4E19ZNecdkiRJzTgeyFQFcxFkhqWMycPfAHwR+L9xG7jie98bdxJJkjR/TBliYG7uWroYuPmkYdsCFw0OqKozgBXAE+egTUmSpNkHmapaBZyf5KEASbYFHkl3Kmmy1wMHzbZNSZIkmLvfkXk68IokK4DjgFdX1ZmTR6qq04CT5qhNSZK0wKXauJC2iU5KkqR1Yp1eIyNJkrRBGGQkSVKzDDKSJKlZBhlJktQsg4wkSWqWQUaSJDXLICNJkpplkJEkSc0yyEiSpGYZZCRJUrMMMpIkqVkGGUmS1CyDjCRJapZBRpIkNcsgI0mSmmWQkSRJzTLISJKkZhlkJElSswwykiSpWQYZSZLULIOMJElq1khBJsn2SY5KcmaSnyX5cpI7JtkjyXFJfpXk9CSvTJJ+mgOSVJKHDtTz2H7YE9bVDEmSpIVj2iDTB5PPAcuratequgvwcuDWwBeBN1XVHYG7AfcD/mlg8lOAJw+8fhJw8hz1XZIkLXCLRxjnwcC1VfW+iQFVtSLJM4FvV9Ux/bArkzwfWA68px/1BGDfJJsANwV2A1aM28mdHnjvcSeRJEnzxG+O//7QslGCzJ7Aj6cYvsfk4VV1ZpItk2w1MQj4BvAIYGu6Izh3GKHNNVxRq8edRJIkzRN/s+on9cUt756pykYJMsOELqhMZXD4UcAL6YLMS+hOS43lP7/xBX65+oqxOyhJktr3s+uveP+wslGCzGnAVBfnngY8cHBAkl2AVVW1sr/ml6r6QZI9gauq6lcTw8fxjJvuOPY0kiRp3njesIJR7lo6DrhpkmdPDEhyL+B04AFJHtYP2xx4F/CWKer4d2ZwJEaSJGltpg0yVVXAY4G/7G+/Pg04BDgPeAzwiiS/pLtD6YfAu6eo4ytV9c257LgkSVK6nLLRa6KTkiRpnRh6XYq/7CtJkpplkJEkSc0yyEiSpGYZZCRJUrMMMpIkqVkGGUmS1CyDjCRJapZBRpIkNcsgI0mSmmWQkSRJzTLISJKkZhlkJElSswwykiSpWQYZSZLULIOMJElqlkFGkiQ1yyAjSZKaZZCRJEnNMshIkqRmGWQkSVKzDDKSJKlZBhlJktSsGQWZJAcnOS3JT5OsSHLvJIuTvCHJ6f2wFUkOHphmdT/s1CSfTrLF3M2GJElaiMYOMknuC+wH7F1VewEPA84BXgfsANy1qpYC+wKbDEx6VVUtrao9gWuA582285IkaWFbPINpbgNcVFV/Aqiqi/qjK88Gdq6qq/vhK4FDhtRxArDXqA3utuweM+imJEmaD/b75lu3fWcefMlUZTMJMscAr0ryK+AbwCeBPwK/7cPLWiVZDPwV8NVRG7ya1TPopiRJmicuBjJVQapq7NqSLKI7dfRg4LnAG4BnVNXd+/JnAC8CbgHcr6rOSbIaOKWv4gTgJVV1zYhNjt9JSZI0X0wZYmCGQWaNCpIn0IWZvelOLa0cKDsV2K+qzk6yqqq2nGEzBhlJkhauoUFmJhf73inJ7gODlgK/BD4MvDvJZv14i4BNx61fkiRpVDO5RmZL4L+TbANcB5wBPAe4DHgtcGqSlcBVwOHAeXPUV0mSpDXM+tTSetJEJyVJ0joxd6eWJEmSNhYGGUmS1CyDjCRJapZBRpIkNcsgI0mSmmWQkSRJzTLISJKkZhlkJElSswwykiSpWQYZSZLULIOMJElqlkFGkiQ1yyAjSZKaZZCRJEnNMshIkqRmGWQkSVKzDDKSJKlZBhlJktQsg4wkSWqWQUaSJDXLICNJkpo1dpBJsjrJiiSnJvlSkm364cuSHD1p3MOSPKF/vl+SnyQ5OcnPkjx3bmZBkiQtVDM5InNVVS2tqj2BS4B/nm6CJJsAHwAeXVV3A+4OLJ9B25IkSTdYPMvpvwvsNcJ4S/q2Lgaoqj8Bvxy1kT2WLZ1R5yRJUvtOW75iaNmMg0ySRcBDgQ9PN25VXZLki8BvkhwLHA0cWVXXj9LWtVxHUTPtqiRJati76jMnvzBPuNtUZTMJMpsnWQHsDPwY+Ho/fFjSKICqelaSuwIPAw4C/hI4YJQG3/DNd3MeF82gq5IkaT5L1XhHOpKsqqotk2xNd2Tl01X1riR7Au+vqvsPjPtF4G1V9a1JdWwHnFVVS0Zs1sMxkiQtXBlWMOPbr6vqMuCFwEH9xbynAzsk+QuAJDsBdwNWJNkyybKByZcCv5lp25IkSTDLi32r6idJTgaeVFUfT/IPwEeTbAZcCzyrqi5LsgT4tyTvB64CrmDE00qSJEnDjH1qaQNpopOSJGmdmPtTS5IkSRuaQUaSJDXLICNJkpplkJEkSc0yyEiSpGYZZCRJUrMMMpIkqVkGGUmS1CyDjCRJapZBRpIkNcsgI0mSmmWQkSRJzTLISJKkZhlkJElSswwykiSpWQYZSZLULIOMJElqlkFGkiQ1yyAjSZKaZZCRJEnNMshIkqRmGWQkSVKzxg4ySW6d5H4VKeUAABJUSURBVIgkv07y4yTfTfLYJMuSXJbkJ0l+keStA9NsmeT9Sc5MclqS45Pce25nRZIkLTRjBZkkAT4PHF9Vu1TVPYAnAbftRzmhqu4O3B3YL8n9++EfAi4Bdq+qPYADgO3moP+SJGkBWzzm+A8Brqmq900MqKrfAP+dZNnAsKuSrAB2TLIrcG/gqVV1fV/+a+DXoza69wP3HLObkiRpvjjp+FOHlo0bZPYATppupCQ3B3YHjgf2AVZU1eox27rBtXXNTCeVJEmNO3rVobXflgdmqrJxg8wakrwHeABwDfD/gH2T/BS4E/CmqrqgOxs1OycdfwrXGWYkSVqQjr3yE9sOK0tVjVxRkocCr6qqBw0M2w74Ed11LwdV1X5J7gicCDwcWAl8Hdht4tTSDIzeSUmSNN8MPSoy7l1LxwGbJTlwYNgWk0eqql8BbwReWlVn0gWdV/cXC5Nk9ySPGbNtSZKkNYwVZKo7fPO3wIOSnJXkB8DhwEunGP19wAOT3AF4FrA9cEaSU4APAufNqueSJGnBG+vU0gbURCclSdI6MWenliRJkjYaBhlJktQsg4wkSWqWQUaSJDXLICNJkpplkJEkSc0yyEiSpGYZZCRJUrMMMpIkqVkGGUmS1CyDjCRJapZBRpIkNcsgI0mSmmWQkSRJzTLISJKkZhlkJElSswwykiSpWQYZSZLULIOMJElqlkFGkiQ1yyAjSZKaNVaQSbI6yYokJyc5Kcn9Bsr2SbI8yel92f8luWtfdkiS3/XT/izJk+d6RiRJ0sKTqhp95GRVVW3ZP38E8PKqelCSWwPfB55SVd/pyx8AbFdVn09yCLCqqt6aZHfgx8AtquraEZsevZOSJGm+ybCCxbOodCvgj/3z5wOHT4QYgKo6caqJqur0JFcCNwcunEX7kiRpgRs3yGyeZAWwGXAb4CH98D2Aw0epIMnewOlVNXKI2ec+uwHXj9lVSZI0H3z0iP3fv8cu//HcqcrGDTJXVdVSgCT3BT6WZM/JIyX5Pt0Rm2Oq6kX94BcneTawC/DIcRotVuPZJUmSFqznAHMSZG5QVd9Nsh1wS+A0YG/gC33ZvZM8AdhvYJJ39NfIPI4uAO1aVVeP0tYPv3fWTLspSZLaN/QamRnffp3kzsAi4GLgPcABg3cxAVtMNV1VfRb4EbD/TNuWJEmCmV8jA1062r+qVgMXJPl74M1JdqS7iPci4DVD6nkNcESSD1aVF79IkqQZGev26w2oiU5KkqR1Yu5PLUmSJG1oBhlJktQsg4wkSWqWQUaSJDXLICNJkpplkJEkSc0yyEiSpGYZZCRJUrMMMpIkqVkGGUmS1CyDjCRJapZBRpIkNcsgI0mSmmWQkSRJzTLISJKkZhlkJElSswwykiSpWQYZSZLULIOMJElqlkFGkiQ1yyAjSZKaZZCRJEnNmlWQSVJJ3jbw+qAkh/TPD0ly0KSyXyQ5NcnJSZ4+m7YlSZJme0TmT8Djkmy3tpGSPA/4S2CfqtoTeCCQWbYtSZIWuMWznP464APAi4GD1zLey4EHV9XlAFV1GXD4qI088J67zaaPkiSpYcf/6IyhZbMNMgDvAX6a5C1TFSZZAiypqjNn3MJ1V854UkmS1Larvnlgbf7gQ6c8kzPrIFNVlyf5GPBC4KopRglQs2lj+fHf4forfz+bKiRJUqOu/flh+w4rm4sjMgDvBE4CPjq5oA86VyTZpap+PZPKb7LVztxkq51n2UVJktSixdvf+8RhZXNy+3VVXQJ8CnjmkFHeCLwnyVYASbZK8py5aFuSJC1cc/k7Mm8Dht29dCjwTeCHSU4FvgV44YskSZqVVM3q8pX1pYlOSpKkdWLoT7b4y76SJKlZBhlJktQsg4wkSWqWQUaSJDXLICNJkpplkJEkSc0yyEiSpGYZZCRJUrMMMpIkqVkGGUmS1CyDjCRJapZBRpIkNcsgI0mSmmWQkSRJzTLISJKkZhlkJElSswwykiSpWQYZSZLULIOMJElqlkFGkiQ1yyAjSZKaZZCRJEnNGjnIJFmdZEWSk5OclOR+A2X7JFme5PS+7P+S3LUvOyTJ7/ppT0/y2SR3WRczI0mSFpbFY4x7VVUtBUjyCOCNwIOS3Br4FPCUqvpOX/4AYFfglH7ad1TVW/uyvweOS3LXqvrDKA2vXr16jG5KkqT5ZNGiRUPLxgkyg7YC/tg/fz5w+ESIAaiqE4dNWFWfTPLXwFOA/xqlscWLZ9pNSZLUunrvYw7gwM8fNlXZOAlh8yQrgM2A2wAP6YfvARw+Zp9OAu486siv2W/kUSVJ0vzzUeCwqQpmemrpvsDHkuw5eaQk36c7YnNMVb1oSF0Zo11e+aWfjzO6JEmaX4bmhhndtVRV3wW2A24JnAbsPVB2b+CVwNZrqeLugOlEkiTNyoyCTJI7A4uAi4H3AAcM3sUEbLGWaR8PPBw4ciZtS5IkTZjJNTLQHeLZv6pWAxf0dyK9OcmOwIXARcBrBqZ9cZJ/AG4GnAo8ZNQ7liRJkoZJVW3oPoyiiU5KkqR1Ym6vkZEkSdoYGGQkSVKzDDKSJKlZBhlJktQsg4wkSWqWQUaSJDXLICNJkpplkJEkSc0yyEiSpGYZZCRJUrMMMpIkqVkGGUmS1CyDjCRJapZBRpIkNcsgI0mSmmWQkSRJzTLISJKkZhlkJElSswwykiSpWQYZSZLULIOMJElq1oyCTJLVSVYMPF7WD1+c5A1JTh8oOzjJw5N8N0n68Rb1Zfeby5mRJEkLy+IZTndVVS2dYvjrgO2Bu1bV1UmWAC+pqmOS/CPwTOBDwAuAH1bVd2bYviRJEqmq8SdKVlXVlpOGbQGcA+xcVSunmOY2wInA3wBfAPapqktGaW/ZbjuM30lJkjQvLD/jvAwrm+kRmc2TrBh4/Ubg58BvpwoxAFV1fpJ3At8FXjhqiAHgylUz7KYkSWregfsUh/5gyjAzl0dk9gIOr6q796+fAbwIuAVwv6o6J8lNgJVVdbOxGjzhs8U5vxy7n5IkaR444XP/yqE/eMdURev81FKSU4H9qursYdOOwFNLkiQtXENPLc3Z7ddVdSXwYeDdSTaD7u4kYNO5akOSJGnQXF0j89WqehlwMPBa4NQkK4GrgMOB82bXTUmSpD83o1NLG0ATnZQkSevEuj+1JEmStL4ZZCRJUrMMMpIkqVkGGUmS1CyDjCRJapZBRpIkNcsgI0mSmmWQkSRJzTLISJKkZhlkJElSswwykiSpWQYZSZLULIOMJElqlkFGkiQ1yyAjSZKaZZCRJEnNMshIkqRmGWQkSVKzDDKSJKlZBhlJktQsg4wkSWqWQUaSJDVr5CCTZOckp04adkiSg/rn/5rkF0lOSXJykrcn2WRg3LsnqSSPmLvuS5KkhWxOjsgkeR7wcOA+VXVX4F7AhcDmA6M9GTix/ytJkjRri+eonoOBB1bVpQBVdQ3wponCJAGeAPwlcEKSzarq6lErX7b9LaCun6OuSpKklizf6WZ78oNzT52qbC6CzObAllV11lrGuT9wVlWdmWQ58CjgsyO3cOWqWXVQkiS17GanAJmqZJwgU0OG32SwrL8G5s3ANsBTquo7dKeTjupHOQp4GmMEmeWX/2mMbkqSpHlmyhAD410jczFw80nDtgXOBq5IcgeAqvpaVS0FTgU2TbIIeDzwqiRnA/8N/FWSJWO0LUmS9GdGDjJVtQo4P8lDAZJsCzyS7gLeNwKHJtmmLwuwWT/pw4CTq+p2VbVzVe0E/C/wt3M3G5IkaSEa9xqZpwPvSfK2/vWr++teDgW2AL6f5E/AKuDbwE+A/wI+N6me/wUOBD4+455LkqQFL1XDLn3ZqDTRSUmStE7MyTUykiRJGxWDjCRJapZBRpIkNcsgI0mSmmWQkSRJzTLISJKkZhlkJElSswwykiSpWQYZSZLULIOMJElqlkFGkiQ1yyAjSZKaZZCRJEnNMshIkqRmGWQkSVKzDDKSJKlZBhlJktQsg4wkSWqWQUaSJDXLICNJkpplkJEkSc0yyEiSpGYZZCRJUrMMMpIkqVkGGUmS1CyDjCRJapZBRpIkNcsgI0mSmmWQkSRJzTLISJKkZhlkJElSswwykiSpWQYZSZLULIOMJElqlkFGkiQ1yyAjSZKaZZCRJEnNMshIkqRmtRJkMsojyXNHHXe+PRbyvC/0+XfeN3w/nH/n3Xlf54+hWgkyo3rOhu7ABrSQ5x0W9vw77wvXQp5/513A/AsykiRpATHISJKkZs23IPOBDd2BDWghzzss7Pl33heuhTz/zrsASFVt6D5IkiTNyHw7IiNJkhYQg4wkSWpWc0EmybZJvp7k9P7vzacY53ZJvpnk50lOS/KigbJDkvwuyYr+8aj1OwfjS/LIJL9MckaSl01RniTv6st/mmTvUafd2I0w70/t5/mnSb6T5G4DZWcnOaVfzj9avz2fGyPM/7Iklw2sz68addqN3Qjz/v8G5vvUJKuTbNuXNb3sk3wkyYVJTh1SPp+3+enmfd5u8yPM+7zd3melqpp6AG8BXtY/fxnw5inGuQ2wd/98CfAr4C7960OAgzb0fIwxv4uAM4FdgE2BkyfmZWCcRwFfofvRoPsA3x912o35MeK83w+4ef/8rybmvX99NrDdhp6PdTz/y4CjZzLtxvwYt//Ao4Hj5tGyfyCwN3DqkPJ5uc2POO/zeZufbt7n5fY+20dzR2SAxwCH988PB/528ghVdX5VndQ/Xwn8HNhxvfVwbu0DnFFVv66qa4Cj6N6DQY8BPlad7wHbJLnNiNNuzKbtf1V9p6r+2L/8HnDb9dzHdWk2y2/eL/tJngwcuV56th5U1fHAJWsZZb5u89PO+3ze5kdY7sM0v9xno8Ugc+uqOh+6wALcam0jJ9kZuDvw/YHBz+8PS35kqlNTG5kdgXMGXp/Ln4eyYeOMMu3GbNz+P5PuW+qEAo5J8uMkLf4S5qjzf98kJyf5SpI9xpx2YzVy/5NsATwS+N+Bwa0v++nM121+XPNtmx/FfNzeZ2Xxhu7AVJJ8A9h+iqKDx6xnS7qd279U1eX94EOB19Kt8K8F3gb848x7u85N9T8mJt8zP2ycUabdmI3c/yQPptupPWBg8P2r6rwktwK+nuQX/TeeVowy/ycBO1XVqv56r88Du4847cZsnP4/Gvh2VQ1+k2192U9nvm7zI5un2/x05uv2Pisb5RGZqnpYVe05xeMLwO/7Q6j0fy+cqo4km9CFmP+pqs8O1P37qlpdVdcDH6Q7JLcxOxe43cDr2wLnjTjOKNNuzEbqf5K9gA8Bj6mqiyeGV9V5/d8Lgc+x8S/ryaad/6q6vKpW9c+/DGySZLtRpt3IjdP/JzHptNI8WPbTma/b/Ejm8Ta/VvN4e5+VjTLITOOLwP798/2BL0weIUmADwM/r6q3Tyq7zcDLxwJTXh2+EfkhsHuSOyTZlG6n/cVJ43wReHp/J8N9gMv6026jTLsxm7b/SW4PfBZ4WlX9amD4zZIsmXgOPJyNf1lPNsr8b9+v7yTZh26bvniUaTdyI/U/ydbAgxjYD8yTZT+d+brNT2ueb/NrNY+391nZKE8tTeNNwKeSPBP4LfB3AEl2AD5UVY8C7g88DTglyYp+upf3CfYtSZbSHXY7G3jueu7/WKrquiTPB75Gd2X6R6rqtCTP68vfB3yZ7i6GM4ArgWesbdoNMBszMuK8vwq4BfDefvu+rqruCdwa+Fw/bDFwRFV9dQPMxoyNOP9PAA5Mch1wFfCkqipgISx76L6MHFNVVwxM3vyyT3Ik3R0q2yU5F/gPYBOY39s8jDTv83abH2He5+X2Plv+iwJJktSsFk8tSZIkAQYZSZLUMIOMJElqlkFGkiQ1yyAjSZLWiUzzjzAnjbtTkmP7X95fnmSkfz9hkJEkSevKYXT/QmQUb6X7H2J7Aa8B3jjKRAYZSZK0Tkz1jzCT7Jrkq/3/xDohyZ37orsAx/bPv8mI//jSICNJktanDwAvqKp7AAcB7+2Hnww8vn/+WGBJkltMV1mLv+wrSZIa1P8z5/sBn+5/hRngpv3fg4B3JzkAOB74HXDddHUaZCRJ0vpyE+DSqlo6uaD/p5+PgxsCz+Or6rJRKpQkSVrnqupy4KwkE/8nMUnu1j/fLslELvl34COj1GmQkSRJ60T/jzC/C9wpybn9P3x+KvDMJCcDp3HjRb3LgF8m+RXdPwF9/Uht+E8jJUlSqzwiI0mSmmWQkSRJzTLISJKkZhlkJElSswwykiSpWQYZSZLULIOMJElq1v8HlIhHTDdmCf8AAAAASUVORK5CYII=\n",
"text/plain": [
"
"
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"# Plot the distribution of illicit flows for a random sample of partner countries\n",
"fig, axes = joypy.joyplot(partner_features.sample(n=15, axis=1, random_state=234), \n",
" colormap=plt.cm.rainbow, figsize=(8,8),\n",
" title='Distribution of mis-invoicing across random sample of partner countries');"
]
},
{
"cell_type": "code",
"execution_count": 54,
"metadata": {
"slideshow": {
"slide_type": "skip"
},
"tags": [
"hide-cell"
]
},
"outputs": [],
"source": [
"# Apply a modified log transformation\n",
"partner_features_log = partner_features.apply(lambda x: np.log(x+1) if np.issubdtype(x.dtype, np.number) else x, axis=1)"
]
},
{
"cell_type": "code",
"execution_count": 55,
"metadata": {
"slideshow": {
"slide_type": "skip"
},
"tags": [
"hide-cell"
]
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAj0AAAI2CAYAAAC7VjnCAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4yLjEsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy+j8jraAAAgAElEQVR4nOzdebwkVX3//9enqrvvOjPsq8CwCAiyiBJXDG7RKImJazRR1MREY77ZMDERY0yCJvHngknUxGiCOy6JRomoUcQlcRcEBhRBQJaBWRhm7n67qz6/P87pvtV9u+/tO3Pv3Jlb7yePok6dc+rU6epaPrX0HXN3RERERNa6ZLU7ICIiIrI3KOgRERGRUlDQIyIiIqWgoEdERERKQUGPiIiIlIKCHhERESmFZQl6zOyfzewvlqmtY81s3MzSOH21mf3WcrQd27vSzC5crvaWsNxLzGybmd27DG291szeuxvz/bqZfXFPl9/HcsbN7IRF6rR9z7IyzOwyM7tktfuxN5jZRjNzM6usQNuvNLP74jZ78HK3L70t5/mlo91fMLNPF6bdzE5a7uWsJjMbMrPPmtlOM/vEaven03Kdk8zscDO7ycwGFq272N/pMbPbgcOBBpABNwIfAN7j7vkSO3Y78Fvu/qUlzHM18CF3352T/BuAk9z9N5Y673Iys2OAm4Hj3H3LavZFysXMLgPucvfXrXZfVpqZbQRuA6ru3ljGdqvALuBR7v7D5Wp3kWU68GB3v2VvLG81mNlLCOeDx63S8r8H/J67fytOr8g6353z3jIu+0XA/wMes5z7xG72ZSMrsH8W2n8XcJO7/+NC9fq90/NL7r4OOA74O+A1wPv2rIvzrcQV2j7iOGC7Ap79y96+C7WGt//93eHAILBppRe0N7aB/Wk7W6l90MzOBTY0A57VtMLfx3HAzbsTZOxP20n0YeB3Fq3l7gsOwO3Akzvyfg7IgYfG6cuAS2L6EOAK4AHgfuDrhODqg3GeKWAc+FNgI+DAbwI/A75WyKvE9q4G/hb4DrAT+C/goFh2PuEqdl5/gacBs0A9Lu+HhfZ+K6YT4HXAHcAWwh2sDbGs2Y8LY9+2ARcvsJ42xPm3xvZeF9t/cvzMeezHZV3mPR+4K66TLcBm4FeApxPuEN0PvLZQ/w2Eu18QDsYfArbHdf5d4PAefXwJ8I3CtAOvAH4C7ADeCRgwENt6aKHuofFzHBanXw7cEvv2GeCojnZPiukh4K1xnewEvhHzun3PfwP8LzAGfBE4pNDmi2Mb24G/oMt2Waj7DOAawtX5ncAbOsofB/xf/Ix3Ai8pbMfvBj4HTMTv7iGxbw8QTnq/XGjn6YQ7n2PA3cCrF9oHevTVgVfF7+C2mPeO2K9dwPeB8zq++48TtrWx2KdHFMofBvwgln0MuJy4b/b5vf1u7MtY/D5OBL4Z+/JxoNbjc5wEfDV+x9uAjxXKFvs8nyBsw2PA9cDJwJ8T9oU7gV8o1L+a3seDjbRvUxsIF2eb4/dzCZD26P8AcClwTxwujXknx23BCfvvVV3mbS73t+O8m4GLOo6X34zbw2bgn4rrsXMbIBwHPS53HHg+c8eIi5g7Rry0o/9vIRyr7gP+GRjqOL68BrgX+GCPdfBy4Kb4PdwInBPzF9oHriYeT5d4jHkIME14ejAOPLDAPngZ7dvwBcC1sT//B5xZKHtN/K7HgB8DT+rxWV8PvLfLvtg8bnU9nseylHBM2xa/r9+jsN11tNnXeS/W/UT8fnbGbeD0QjuXxXX33/GzfRs4MZYZ8Pa4XewErgMeCvwV7efA36S/c17xfPwSwjH57XF9/xR4TMy/M7ZxYT/H3thmcz8aBx7N/O3lMYRz2M44fkzHtrbQOaICTBKeqPSOaRYqjA3dTpeTS/wAryx8Ic2g528JO1w1Ducx9xitra3CSv4AMELvk+Hd8UscAf6DuRP++fQIegoH1A91lF/NXNDzMsIJ4ARgFPhP4gGh0I9/jf06C5gBHtJjPX2AcABeF+e9GfjNXv3smPd8wuPD18d19nLCzvaR2N7phAPECZ2fixDZfhYYJuyMDwfW91jOS5h/QLoCOAA4Ni7zabHs34A3Fuq+Cvh8TD+RsMOfQzjY/iNxx+1y8HhnXOdHx/49Js7T7Xu+lXCSGYrTfxfLTiPsJI8DaoSDe53eQc/5wBmEHfxMwkngV2LZsYQd5gVxXR8MnF3YjncCj43zrovbx2vjcp8Y5z0l1t9MPIEDBzJ3kui5D3TpqwP/AxzE3EnqN2K/KoST3L3AYOG7nyYEXGlc1rdiWY1wMPujuNznxPV0yRK+t88A6wnb3AzwZcL+sYFwIrywx+f4KHBxXG+DwOMKZf18nqfG8g8QTiQXM7cv3Nax//Y6HmykfZv6NPAvsd5hhEDpd3r0/6+Bb8V6hxJOpn/Trd0u8zbLPxqXdQZhX2oehx4OPCp+vo2EwOIPF9kGWvtQxzHir+N6eTrhAH9gLL80fncHEbbbzwJ/2zHv38fvfajLZ3huXK/nEk6iJxHuElRZeB+4msWDnl7HmLa6PfbBQdrPL+cQTrSPJGz/FxKO+QPAKYQT7VGF7+XEHt/ZJ4A/6bIvNo9bCx3PX0HYFx5E2O+/xMLbx+0sct4rnI/WMReAX9uxXu4nBNAVwl2Ny2PZUwkXEwcwF1Ae2e0cSH/nvOL5+CWEbeelcX1fQjj3vzP28xcI28NoH8feZvuVQn9a2wBh290BvCh+xhfE6YMXO0cU2ruOQlDe9ftYqLDbF1bI/xbxzgftG+Vfx43lpMXaKqyEE7rkFU+Gf1coP40QvabsedDzZeB3C2WnEE4SzYOTAw8qlH8H+LUunyslnCBOK+T9DnB1YUNYLOiZIl6FEjZ8Bx5ZqPP9wsbT+lyEjbjtameB5bQ2sMJOXjw5fRz4s5h+MvDTQtn/Ai+O6fcBby6Ujcb1trF48CBs+FPAWV360u17fl2h/HeZC7JeD3y0UDYct4GuQU+XZV0KvD2m/xz4VI96lwEfKEyfRzhBJ4W8jxKvXgg7/+/QEWSywD7QZZkOPHGROjua6zB+91/q2B+mYvrxhDsNVij/P+b2zX6+t8d2bHOvKUy/Fbi0Rx8/ALyHwv6yhM/zP4WyXyIEuJ37wgGF7aTX8aC1TREeSc1QOMETDqJf6dGnW4GnF6afCtzebVtdYFs+tZD3ZuB9Per/YXEb7LYN0D3omaL9hLGFEEwZ4a7IiYWyRzN35/D8uI4GF/hOvgD8QZf8xfaBq1k86Ol1jGmr220fLOQ1t+F3E4PRQvmPgZ8nHHO2EI5d1UW2wf8BXtFtnbP48fwqCsFzXN7uBD0nLNC/A2Kd5l2YyyjcmSIEvT+K6ScSgrJH0XFHmflBTz/nvOL5+CXATwrTZ8Q6hxfythMvHLt8juKxt9l+r6DnRcB3Oub/JnN34q+mxzmikNc6T/Ua9uTXW0cTIs9O/x8hkvyimf3UzP6sj7buXEL5HYSrj0P66uXCjortFdtuHjCbir+2miScKDodwtxVdrGto5fQl+3unsX0VBzfVyif6rHsDxIOWJeb2T1m9mYzq5rZefGXJuNmttC7CL0+31XAkJk90syOA84GPhXL2tabu48TNvzOz3sI4Urt1gWW309fjqKwDbj7ZFxeV7HPXzGzrWa2k3Bl1txejlmkP8Vt7SjgTm9/Yb/4vT6bcPC5w8y+amaPjvlL3Qfatn8zuyj+EmGnmT1AuMtS3N4719NgfP5+FHC3x72/0N/i51nse+vc5vrZBiHctjfgO2a2ycxetoTP07mMbV32heJy+zkeHBfzN5vZA3G5/0K4k9NNt2PBUT3q9tLZr6MAzOxkM7vCzO41s13Am7r0d7FjIIRjRPHdjOY+cijhQuD7hc/6+ZjftNXdpxdou9d+sdg+0I9+jqFFC62L44CLmp8zftZjCHd3biEElG8AtpjZ5WbW6zvcQQiou1nseN52PFqkvwtpzWdmqZn9nZndGreR2wt9aeq6Ht39KsIj03cC95nZe8xsfY9l9nPO6/w8nfsn7t71uLDIsXcxnX1r9q+4rS22La0jPIbrabeCnvgS2NGE9zPauPuYu1/k7icQrtr+2Mye1Czu0WSv/KZjCuljCZHpNsLVzXChXyntO/pi7d5D2ImKbTdo/5L7sS32qbOtu5fYzpK5e93d/8rdTyM8OrqAEOl+3d1H43D6brSbE67KXgC8ELjC3cdicdt6M7MRwuOLzs+7jfDo4sSlLr/DZsKt5ObyhuLyevkI4Vb/Me6+gfCoyWLZnYv0p7jN3AMcY2bF/aT1vbr7d939mYQT6acJ62uxfWDBZZrZeYT3Ep5HeHRxAOF2v/WYt2gzcLSZFese2/F5+vnelszd73X3l7v7UYSr4neZ2Ul7+Hl66XU8KLqTcLV+iLsfEIf1C+wL3Y4F9+xhv5rzvxv4EeGXQesJj4o6P/9ix6qFbCOceE4vfNYN7l48ISzWfq/9YsF9gI5jMHDEEvq9O+eDOwmP3Q8oDMPu/lEAd/+Ih1+DHRfb+fse7VxHeEzSzWLH87bjEe3fezf9fM4XAs8k3DXaQLgrAn3uJ+7+D+7+cMJj6ZOBP+lRtZ9z3p5siwsde5d6Pm72r6/jU7zwOwlY8BeWSwp6zGy9mV1AeDnyQ+5+fZc6F8SDnRFeZsriAGHFLvj3W3r4DTM7zcyGCY8OPhmvBG8mXOU+I/6s9HWE54xN9wEbO3bYoo8Cf2Rmx5vZKOEK7GO+xDfdY18+DrzRzNbFOyN/THg5c0WZ2RPM7IwY8O0i7KzZIrP16yOElyh/PaaL+S81s7Pj30V4E/Btd7+9OHMMnP4NeJuZHRWvZh7dz99S6PBJ4JfM7DFmViO8oLfQwWAdcL+7T5vZzxEOKE0fBp5sZs8zs4qZHWxmZ/do59uEg/qfxrtn5xOCmMvNrGbhb0xscPc6c9v6YvvAYtYRDkJbgYqZvZ7wjk0/vhnn/f342Z5FeAegqa/vbXeY2XPNrHki2EE4wGV7+Hl66XU8aHH3zYQXHd8aj1uJmZ1oZj/fo82PAq8zs0PN7BDCI9Wl7r9/YWbDZnY64R2Ij8X8dYTtYNzMTgVe2UdbfR8r4372r8DbzewwADM72syeuoS+vxd4tZk93IKT4nGs5z4Q57sWeFb83CcRXoLt133Ag+I+3a9/BV4R7yiYmY3E4/86MzvFzJ4Yt+1pQiDYa7/7HOGR2Dx9HM8/DvxBXMcHEIL6xT7nYt/lOkKQvp0QRL5pkfotZnZuXB9VwnfVfEG8m2U55y1goWPvVsJL3b3WxeeAk83shfH49XzC4+sr+lz2zxEeSXfeLWrTb9DzWTMbI0TZFwNvI+zU3TyY8GLXOOEg/C53vzqW/S3hwPKAmb26z2VDeIRzGfEFSOD3Adx9J+G53nsJ0eAE4VcKTc0/xrTdzH7Qpd1/i21/jfDy5DThbxrsjv8Xl/9Twh2wj8T2V9oRhKBgF+EFya+yTMGWuzcPeEcBVxbyv0z4BdV/EK56TgR+rUczryb8Iue7hMehf88Sg21330RYv5fH5Y0Rnt3P9Jjld4G/jtvs64l3YGJbPyM8kroo9udawkvq3ZY7C/wy8IuEq793Ee6i/ShWeRFwu4Xb0a8gvLALC+8Di/kCYV3fTLi1O02ft89jf59FeE6+gxCw/mehfCnf21KdC3zbzMYJV3p/4O63sQefZwFdjwddvJjwmOJGwvr4JHBkj7qXAN8j3AG4nvALuKX+UcevEh5rfhl4i7s3/+jaqwkH/zHCSftj3Wdv8wbg/fFY+bw+6r8mLvtbcXv8EuF9jb64+yeANxKOW2OEO5cH9bEPvJ3wvtB9wPsJFxX9uorwa7B7zazzTl2vfn6P8HL7PxG+01sI2zuEC96/i/28l3AH9rU92vkBsNPMHtljUQsdz/+VEFBfR/il0ueY+zt23fRz3vsAYf+4m7C9LuWn9Otjn3Yw9wvXt/Sou5znvG4WOvZOErax/43r4lHFGd19O+FJxUXxM/wpcIG797VtEC7O/3mxSov+cUKRfU28QnmA8LjgttXuj+w9tgd/rHSl2Ar/0TVZGWb2C4SXen9lD9v5ReCf3b3z0YzsJfEO51eBhy3y7pr+7S3ZP5jZL8Vb6COEq5jrmXvZT0RkSdz9i7sT8Fj4px2eHh/BHA38JXM/8pBV4O5b3P0hiwU8oKBH9h/PZO4Pxz2Y8KcDdJtSRPY2I7xXuIPweOsmwqMc2Q/o8ZaIiIiUgu70iIiISCko6BEREZFS2N/+FdV9nZ4ViojIStiTP+gpke70iIiISCko6BEREZFSUNAjIiIipaCgR0REREpBQY+IiIiUgoIeERERKQUFPSIiIlIKCnpERESkFBT0iIiISCko6BEREZFSUNAjIiIipaCgR0REREpBQY+IiIiUgoIeERERKQUFPSIiIlIKCnpERESkFBT0iIiISCko6BEREZFSUNAjIiIipaCgR0REREpBQY+IiIiUgoIeERERKQUFPSIiIlIKCnpERESkFBT0iIiISCko6BEREZFSUNAjIiIipaCgR0REREpBQY+IiIiUgoIeERERKQUFPSIiIlIKCnpERESkFBT0iIiISCko6BEREZFSUNAjIiIipaCgR0REREpBQY+IiIiUgoIeERERKQUFPSIiIlIKCnpERESkFBT0iIiISCko6BEREZFSUNAjIiIipaCgR0REREpBQY+IiIiUgoIeERERKQUFPSIiIlIKCnpERESkFBT0iIiISCko6BEREZFSUNAjIiIipaCgR0REREpBQY+IiIiUgoIeERERKQUFPSIiIlIKCnpERESkFBT0iIiISCko6BEREZFSUNAjIiIipaCgR0REREpBQY+IiIiUgoIeERERKQUFPSIiIlIKazLoMbONZnZDR94bzOzVZnaZmT0n5h1kZteY2UvjPFNmdq2Z3WhmHzCz6up8AhEREVluldXuwGoxsw3AF4D3uPu/m9lG4FZ3P9vMUuB/gOcBH169Xi6duzMzM8Pk5CQTExOLDpOTk0xNTTE7O0u9Xl9wcHeSJMHMuo6TJKFSqTAwMMDg4OCC45GREUZHR1vj4jAyMkKtVlvtVSkiImtMWYOeUeBK4CPu/u7OQnfPzOw7wNEr1YFGo8H09DRTU1NMTEwwPj7eGjeHzumueWMTjI+F/InJCaamJ8mybEl9qdgAKVUSq4YxVRKvzKUJ+bgBHv/LYzrHzYEcJyenQYMZMmZoME3DZ2gws+T1U61UGR4aZXQkBkKjI6xbP8q69SEoag7Dw8NLnq7VapjZkvska4e7k+c5WZaRZVlbunO6mS6OO4du+f3mLVbX3QEwsz0e0jSlUqm0xp3p3S1LkjX50EDWoLIGPW8D3uvub+9WaGaDwCOBP1hKo4849NnU8+nuQzZN3eemQ9DQvwqD1Bilxgg1RqkyGqcPYZgRDmCEmo1QLY4ZoeqFdJdxlWESjwcsX1KX5iwyn+NkzNJoBkJMU2eSOhPMMj432PhcXjbO7Hgc7p1gjHG2M84s9zBLqFdnklkmyJhdUncTUmrJMJVkgIrVwjipUbEaaVKjGvPTmFdNBlrpxCoklpCQYpaQWIrRYxzrFdN7I9hyD2FpK0D1vDWdewxWY15neWc+MZQNZTHIxcG753ddVrHdbnnk5J7hnpOTzUvnnrXqdC3rZz5imWc4WeyjLBfDMFJSq5BYGvYT4tjCPpBaJdRJupe15iuOO9vsUmad8xf2OcNavWtON9Nz+YYR6xbSYV81EpKYH8us2WYS5431Cm0W10zbeirs/73qFfOL9d+56bnL8E3JWg16eh3RmvlXAc80s7e4+5ZC+Ylmdi3wYOCT7n7dUhZ65/abqfggFQapMMwABzFCmE4ZiPmdw0AMXkZjMDJaGEZa+Wnxq1rKeXMfuKFhGBUGqDAArN+dBrqL32ZGoy0ICoHTxIJ59XySRj5DxmxhmJueYpaMXfGu1Vx5TvOkmcd03nU6J2P3o8i9pXCw75E2CieHRdMLt7VQu0Y4ibWnU4xaOImRUiEp5M+l58/X2cbyzNdtujgkXfPn53Wv17tu2AHaA9ndHTe3zZxGTDfiUEzvflnuDdy7LaM4Pb/MyWi06s3gTLaVzW9j8bJ9f/9bmsPMn/2Xzn+sdj/2d2s16NkOHNiRdxBwW0xfDnwD+JyZPcHdx2J+852eI4GrzeyX3f0z/S70qsuvZ9uPIK1BOgDJWl27+5wKsCEOy8Ahq0M2C3k9pFvjRvvgWRjyOPY8pnPIs3A3I8tysjw8Kmk7DocbJq10WxcK011vDllHWcdFo5mRWLy6jY82mu9fhbTFenQfx5t/Fi5yiRex7eXWXt4rry2/OBhYWhh3lhfnl7XN4z6Vte9bzeniPtbKyzv2v7yQl8/tg3nueO4xnZPnHoccb5bl8c6kO7k7eRYeKzaH3GNdL9619Nbjx9bdT89bnyfUmft8zZ3cY1lnfkgV5inkJzWHm7ln5b6A8liTp2V3HzezzWb2JHf/spkdBDwNeAfwhFjn0hjcfMrMnt4x/2Yz+zPgz4G+g57Tn7d8n0HWAgPSOOiHgCJ7X4zS14ZvrnYH1oK1fA31YuB18XHVVcBfufutxQru/hrgTuCDzF8XnwaGzey8vdFZERERWVnmvraee64yrUwREVkJa+aW1Wpay3d6RERERFoU9IiIiEgpKOgRERGRUlDQIyIiIqWgoEdERERKQUGPiIiIlIKCHhERESkFBT0iIiJSCgp6REREpBQU9IiIiEgpKOgRERGRUlDQIyIiIqWgoEdERERKQUGPiIiIlIKCHhERESkFBT0iIiJSCgp6REREpBQU9IiIiEgpKOgRERGRUlDQIyIiIqWgoEdERERKQUGPiIiIlIKCHhERESmF0gQ9ZpaZ2bWFYaOZnW9mV8Tyl5hZbmZnFua5wcw2rlafRUREZPlUVrsDe9GUu59dzOgS0NwFXAw8fy/1adm5O41Gg6mpKaanp5menmZqaorZ2dl5Q71eX3S62Wax/W7pJEmoVqtUq1UqlUor3WsYGBigVqstOk6S0sTlsgLcnSzLaDQaraFzulfectcFMDOSJMHM5g3d8jvz0jSlUqm0Dc19brG8bvnd9tlKpYKZrfI3J7IyyhT09OMK4PFmdoq7/3ipM997772tYKEZQCwlPTMz0wpSigFLr/TU5DSThbzp6SlmZqbJ83wFVs3qqFQq1GpzgdBArcbAYGG6z+Cp37r91GkGYsWTUXF6KWXu3jbkeb7geDnqFE/GWZatSHqhvH4DhkYjo15v0Kg3qDfCOMtiXtu8cf6sQdZohHHWIM8ysjxbha12/xeCoirVSpVKxwVLrVqlWqtSqy18YbOUi6DdHRZqO03TRYNKBXflU6agZ8jMro3p29z9V7vUyYE3A68FLlzqAo488sg96F67xGqkyRBpMkhqg1SSIZJCOk0OJbVB0mSIkWSA9dUh0tpgqN+cr5m2AVIbJElqJFYjsWpo32rz8pKYl1oNswpG86BQPDhYIRXSTkbu9Tg08Fa6fWjmZ/ksuc+Q+yxZPkPuM2Qe8/Jm3ixZc9pnyPMZ8sk69YkZZnyWB2Kd3GfI8l1z7TXreqGdfAZHJ8C9yUgwS+N2lJJYBbNKGBPHsbw9L+SHvBpmw626Cc3yClWrULM0tJ1WsEqFZLBz/kKbnX2wSmyvWx8W61dHHh3txuXN5c3dsXR3nBxwcMfxkMZxz9uncSjkuWdxX2vg3ijsb422PKfRlh/2vZhHcd7ivtktrzA90yCfqjPjdaa77t/TXfd79zo5DfK8vc2wDvYFFo5jZnGbtfY8S+JxzubKLGmr063FXsual9M18Jqf9+wz7jnw/d+xHUv4YNJFmYKeeY+3evgIcLGZHb/UBTz2pHeRN6qFACKmk0K6UGZWjcFFyE+TgVaQUjxINsX9Deu+n62yKjC415bmPjfgi1YHIPcsBEl5R2Dk8wOkuWAqjmPwlftMPBEVT1bQOkE1O1ecLtTzLmVGPIC2DqRJ6wDczG8ddLuUtecbEOp3ljXTxZP6XCCQFk7Sc+lmftc6lmKtoCEtBBDNen1spBYP78XxPrdtLzcD0tXuxPLwuHXHTdz73BcB3POFg6zF8ptBFO3Bmrfys9a+Gva5EGi274N5a7qZ557THnQWgtS2+Zt5nZ+r10rolt9l/t71fhd448JrVRZTpqCnL+7eMLO3Aq9Z6rzf+MkrV6BHsnwqcRhe7Y6ICGkc9t7F0n5OAc8y0Fui3V0GPBk4dJX7ISIiIstEQU8X7j4L/ANw2Gr3RURERJaH9X7+KLtBK1NERFbCmn/bbW/QnR4REREpBQU9IiIiUgoKekRERKQUFPSIiIhIKSjoERERkVJQ0CMiIiKloKBHRERESkFBj4iIiJSCgh4REREpBQU9IiIiUgoKekRERKQUFPSIiIhIKSjoERERkVJQ0CMiIiKloKBHRERESkFBj4iIiJSCgh4REREpBQU9IiIiUgoKekRERKQUFPSIiIhIKSjoERERkVJQ0CMiIiKlUFntDqwkMzsCuBQ4F5gBbge+ALy0UK0CnA6cBhwO/BdwW6H81e7+pb3RXxEREVk5azboMTMDPgW8391/LeadDaxz93cU6r0JuNbdbzKzw4Gvu/sFq9LpvcTdmZmZYXJyksnJSaamplrjmZkZsiyj0WiQZdm84f777+fKK6/kWc96FsPDw6Rp2jZUKpVWemBggMHBQYaGhhgaGmpLp2m62qtBRERKZs0GPcATgLq7/3Mzw92vLVYws8cDzwPO2ct9m8fdqdfr84KQfsa98iYmp5iYmGRyslk2yfT0FDPTU7j7HvX3s3fuIP/B13Z7/rRSYXBgiMGhIQYHBhkaHmJ4eJiR4SFGRoYZGgrT3cYLlXUb12o1QgwsTe5Onuc0Gg0ajQb1er2V7hx6lRXzm4HySg/N5dTrDerFsnooy93xziEP49wdOsoAnC7zxDIzI0mSMFiCmWFJQtrMS5K5Omn7dKtOmpA089KkdWFQqVR6DouV70mdYl6vdD/1kkRvR8j+Zy0HPQ8Fvt+r0MwOAP4deLG77yoUnWdmxeDo2e5+az8LPOWcF5Bls+RZvTU0p9vHDfLGLFleJ2/MkmezNEhOnJwAACAASURBVOqTuOe79UGTyjBpZYikMkxSGSJJm+lB0sqBJNVh0nVDDB04xGhliKQ6TJIOk1YGsea8aZjX0hpmKWYVSNKYTsFSLEnZdMUzmJ3czOCpT+CUky7F8wZ4hucZ7nGIeXk2Q57N4I0p8myKPJsmb8RxM92Yot6YZiab4v4Hpsi2TZE3xskbW8kbk7HeJFljirwxuVvrBzMq1WEq1SHSyhBppUaSpCRplSSpkCQVLK200nPTc3UsqWBYq70wKgZSHWU9psMJNgfP8TzHPY/rLaZbeR7qFIc8a5/ubCPPyPNG2PbyDM8aYTpv4HEcysL0arOkgllct4U0VsGSdC7P0h51algyPNeGJYCBWVjfZnPTxXSxjOJ3OZffquNORk4W1zee43jr+yOL+cx9X61x8bsmD1U8A5/C80ZrX3FvtI/zDFp5HXXy+up8Wd2YYZbO7TPxO2um5/KT1j6UxHxLKySWtvY7s5Qk7nPNem3fZww4saT13VgznXTJa9W3VjutNiDkFdulsI10+Zzzsvqt1/Via/fqffNzf9GljizVWg56FvNu4EPu/r8d+bv9eOvOn34XkipJUsOSajwoV0nSESw5AKvUqCTVEFgkVZKkGuqlNdLKcAxWmkMzkJmbTtKhQl4zwBmc25Hj/1q7ygrc3HALV8CNbbez7qTTl38BAF4YeWsyXIFnM+TZFFl9MgRSMXDKGpOtdJ51TDfz6iHP83rrJJJ7gyxv4FkDb4QTjueTbXXcG3hWb+8cc3fK5u6aeUdRe767tx1sIYnTSQwsi9Od5cV6KUYhP2mmwwkkbQUH1XAimhdYVDumi3WqPYORedMxME6SagxCOtrq1YZV5k5KUa9ttusmvL/ftOtyk3VelvcuC8Hu3LZJMzBqC46a6awjcKrPBVVt8+U92ssK+0EGedY1v1mfVn77cslDfp43yDwE5O4NfCYDn+7obzMobwaNPpcOkWOcDoFmZ1kIMAt5rYDUoVlGx7yxzX3Zea98zSu//u7au1e7H/u7tRz0bAKe063AzC4ENgIvWs4FfucHN3PHvU6aQiWBNLGQTiGNFy37s0a9znnvvi9MTG3lza9ajc2nCoyuSMt5DlkGWR7TuZN7Mx2Oi3k8NubNYy9hPBeYtbfZPK9b57QVBkLcApCEi1QSCwOE7cjCBW3IT9bG9iR7orbaHdgzcR9q27eK+1yc9uLYC+OcVj2IdYj7YnFgLp4Jd1kLF1OFa5TiPjzv2oWOfb3LqwGtR6XdZirIu0a8vdsrrrD//BpfnD+zLJXt6bsd+6r4IvO3gPe6+7/GvHOBYeDDwOPd/acd85xP+LXW7r7IvDZXZnTXXXdxzDHHAJCc+Sga1/6f3pUREdk7dLBdBmv2To+7u5n9KnCpmf0ZME34yfogMAL8Z8cJ+//Fcec7PZe4+yf3Qpf3effff//cxM4dTOYwoh9hiYjIfmLNBj0A7n4P4ddZS7FhJfqyFuzYsQMAO/p4fNd2ttVzRvTTcxER2U/oN4fStwceeABoBj072D6brXKPRERE+qegR/rWutNzxLGQZdzzwPgq90hERKR/Cnqkb62g57CjALhv587V7I6IiMiSKOiRvrUebx0Sgp7tO8dWszsiIiJLoqBH+rZr1y6S4REYWQfAtgd2LTKHiIjIvkNBj/RtfHwcGxqF4fDHAe8fU9AjIiL7DwU90rexsTEYGsFi0LPtAT3eEhGR/YeCHunb+Ph4uMszpDs9IiKy/1HQI30bHx/HB+fu9OzcpTs9IiKy/1DQI33bOTaGFV5knhhX0CMiIvsPBT3St7GxcZKhERgcBjOmxhT0iIjI/kNBj/RtfHycZHgk/MvqQyNMT+gvMouIyP5DQY/0bXx8jGQ4PNpiaJRZBT0iIrIfUdAjfXF3Jsfj4y3Ahkep650eERHZjyjokb5MTk7i7hCDHoZHySZ1p0dERPYfCnqkL+PjIcCx5p2eoRHyyfEQCImIiOwHFPRIX5pBT/FOD5PjTOar1ycREZGlUNAjfRmLP0/P4x8mZHgUpsYZayjqERGR/YOCHulL805PPtB8vDWKT04wmevxloiI7B8U9Ehf5u70xMdbI+vwqXHGMwU9IiKyf6isdgdk35LnOXfccQd333039957b2u45pprQoXCi8zMzvCmt76d02yaI444ojUcf/zxHHLIIeGPGIqIiOwjFPSU2JYtW7j++uu5/vrrueGGG/jhddezadMmpiYn2upZkkKlFtJDhXd6gE989vPk3//KvLZH1x/AiSc9mNNPPZmHPORUzjzzTM4++2yOOeYYBUMiIrIqFPSUwPj4OJs2beKGG27g+uuv57rrr+e6629g+9YtrTrp6MFUjjqdoUe/mHVHPQQOPJZ89HCSDYeTjBzM5Ff/hV2f+NP2X28B6194KYMXPoh8bCvZrvvId24m2X47jW23cvO9t3DD579G9pEPt5azbsOBnHHmWTziYWfysIc9jLPOOouHPOQhDA4O7tV1IiIi5VOqoMfMxt191MwS4FLgiYAD08Dz3P02M7sdeIS7b1vFru6WyclJfvzjH3PjjTdy0003ccMNN3Dd9ddz209/2qqTDAxTOeIhDJz8VA55wmn4EaeTHnU66frD5rWXFtI+0/6T9eYdn3x2DBuqkR54NOmBR7fq14DhmM6nx2jcvYn87hvI77mO7915Pd/89nvx2cnQpzRl4wkP5pyzzuDMM8/gjDPCcPzxx5Mkeu1MRESWR6mCnoLnA0cBZ7p7bmYPAiYWmWfVuTvbt2/njjvu4Pbbb+eOO+7gjjvu4NZbb+XGm27i9ttua/2xQEtSaoefSHLkWRz8zBdSOeo08sNPIz3keGw3Aol8ZgIqVaw2EDLinR6fWfyfokgG11E78VFw4qPCrIDnGdnWW2ncdQN27ybuvWsTn776e3zyk59ozTc4PMKDTz6Fk086gRNPOIET4rBx40aOPPJIRkdHl/w5RESkvMoa9BwJbHb3HMDd71qORrdt20aj0SDLsr7G9XqdiYkJJiYmGB8fb0uPjY2xdevW1rBl6za2bdtKfXa2bZnp0DoqBx9LcvjDOPChL2DgyFPIDzsVO/RELL6H07Qn90x8ehwGR1rT1gp6du+forAkpXL4yVQOPxl4FjGUIp8ep7H5JnzzJvLNN3LLvbdw09evJfv0Z/BG+2cfHBrmsMOP4Kgjj+DIIw7ngAMOYP369axfv55169a10oODgwwMDFCr1ajVam3pWq2GmZEkCWbWGjqnO/PcvTXked423U/Z7syzu/V2d+jVPtB1vFDZ3q7TzWJ/PXxPywGSJGkNzW1mJaZ3Z97mAMzbtvvJ25vz7Sv2pb7oIm95lDXo+TjwDTM7D/gy8CF3v2ZPGz300EP3uGMAWIINriMZPTgOR5Ecdya10w9maMMRpAcdS3pwGGzogHk75ko8EPKZ8VagA7Tu9OS7GfT0kgyOUjv+XDj+XACGmsvPM/IHNtPYdjvZ/XeQ79pCPraFLbu2cO/995Hf/iPy6TF8egyf3gX65zFEZA058l1jD77nlaM/We1+7O9KGfS4+11mdgrhnZ4nAl82s+e6+5f3pN0jf/0tTGSV8PgorYClWByTVsKvoJIUkphOq1htGBsYwWrDJAPD2MAoVAZIEyM1SA0qCaz29cbY7PjcS8zQCnqS2THWVfdGD1I4/EFh4HHzSnOHhkPm0Gjk5LOT+PQY+dROaMzi2Sw0ZvBGPaZn8TiAhyDJ80J6btqdGETFPHcwAwwsAbMwiRXy58qK+dYtv5C2HvmdeV3baRvT3tYCbXav19l2bK+ZFzLi2i9Md8srTFu3+bvO06tOc7KPdrpZ9Mp9kfKF5i9uI3lOvJEMeR63m7DtuLdPN9Ne3O76qZ8Xt8m5Mo/L79qXtn564eLA2/Np3tlauE77tBey5qYXW57Py9tH7Et9CevyiYCCnj1UyqAHwN1ngCuBK83sPuBXCHd9dts9H7poObq2T3raJ6f50uRwa7r5IvOpIxN897f2xduu64EjVrsTIiLL5V9WuwNrQSl/GmNm55jZUTGdAGcCd6xur/ZtY2NjeJfHW2Pjy/t4S0REZKWUMugBDgM+a2Y3ANcBDeCfCuXXmdldcXjbqvRwH7Nj505sZH1r2qo1qNaYHNu1ir0SERHpX6keb7n7aBx/Hvh8jzob92af9hcPPLCT9Nh17ZlDo0xP6E6PiIjsH8p6p0eWaNeunSSjG9rybGSUGT3eEhGR/YSCHllUlmVMjI2RjMy/01OfWPyPE4qIiOwLFPTIosbGQmCTDHcEPcOj1Cd1p0dERPYPCnpkUbt2hZeVbXR9W74Nj5JPjPf1l2pFRERWm4IeWdTOnTsB8M47PUOj+OQ403mXmURERPYxCnpkUa2gZ96dnhGYGmdXpjs9IiKy71PQI4tqBj2Noc53etbB5Di7GrrVIyIi+z4FPbKo1p2ekfY7PQyP4lMTPFBX0CMiIvs+BT2yqGbQYx0/WbehUXDnvgf0s3UREdn3KeiRRTWDHjr/Ts+GAwG4c+u2vdwjERGRpVPQI4vatWsXllZgYKgt3w44BIC77r1vNbolIiKyJAp6ZFE7duwgWbcBM2vLtwMOBmDz1q2r0S0REZElUdAji9q6dSu24eD5BTHvni0KekREZN+noEcWtXXrVrxL0NN8vHXffVv2dpdERESWTEGPLOq+rVthw0HzC4ZGoDbIjm260yMiIvs+BT2yqK1bt1I5oMudHjM44GB2btevt0REZN+noEcWVK/X2bF9O+mBh3Qttw0HM7Vdd3pERGTfp6BHFnTPPffg7qSHHd213A48hPoD2/UvrYuIyD5PQY8s6K677gIgO/So7hUOPBS/fwvb6wp6RERk36agRxZ05513AtA4pHvQkxxxLL5tMz/ZObE3uyUiIrJkCnpkQTfffDOYYUce27XcjtoI7nz7x7fu3Y6JiIgskYIeWdCmTZuoHnkcNjjctdwedDwA3990497sloiIyJKtmaDHzNzMPliYrpjZVjO7Ik6/xMxyMzuzUOcGM9sY06Nm9m4zu9XMrjGz75vZy/f259jX/OCaa8g3ntKz3E44DdIK3/7O9/Zir0RERJZuzQQ9wATwUDNr/quYTwHu7qhzF3Bxj/nfC+wAHuzuDwOeBnT5i3zlcdddd3HLT37C4NmP7lnHBoawkx7KHd/5un7BJSIi+7S1FPQAXAk8I6ZfAHy0o/wK4HQza7t1YWYnAj8HvM7dcwB33+ruf7/C/d2nvec97wmJR/3CgvXSx/0iszd8j09959q90CsREZHdU1ntDiyzy4HXx0daZwL/BpxXKM+BNwOvBS4s5J8O/LAZ8Oyuo3/5ha102z2P4h2QXmnouFPSvZ4vMD895u85z7z555KNiTHu/+7XSH/+l8kedCILSS94MY1P/AvPefL5HHLu46mMjELHv8je1D2XnvVFRATu/q8Pr3YX1oQ1FfS4+3XxHZ0XAJ/rUe0jwMVmdnyvdszsYuC5wGHu3uMP1Mx3z7e/RttpvXAibzunt090LnzxdI9l9D9P+yxd50mrpM9/FZUX/fHitwM3HMTA2z9F/UNvZ9ttN+FTk93r9Xz8pcdiIiILGfrKls1TTzjsyNXux/5uTQU90WeAtwDnA/P+wSh3b5jZW4HXFLJvBM4ys8Tdc3d/I/BGMxtfyoJvvf12bp/ao5tF+wQDqgkcVkuo9nsH5lGPhRc8lvHMub+ekymOWREGpAbVxBhIYMAMM6jnzlQexg1f+TAyMagY1MwYSo2KQeYwnTszsQ/5XuiHSFk844cPPHS1+7AWrMWg59+Ane5+vZmd36POZcCfAusA3P0WM/secImZ/YW7Z2Y2yAJPY7o5YajCCUOL1xMREVmKqScctn21+7AWrLUXmXH3u9z9HYvUmQX+ATiskP1bhDtDt5jZ94Ev0X43SERERPZjpp8ZLyutTBERWQn6tccyWHN3ekRERES6UdAjIiIipaCgR0REREpBQY+IiIiUgoIeERERKQUFPSIiIlIKCnpERESkFBT0iIiISCko6BEREZFSUNAjIiIipaCgR0REREpBQY+IiIiUgoIeERERKQUFPSIiIlIKCnpERESkFBT0iIiISCko6BEREZFSUNAjIiIipaCgR0REREpBQY+IiIiUgoIeERERKQUFPSIiIlIKCnpERESkFCqr3YHlZmYHA1+Ok0cAGbAV2Ajc4+6nFeq+ARh397eY2WXAU4AT3H3GzA4BvufuG/de71eeuzM7O8vExATj4+PzxpOTkzQajdaQZdm8NECapl2HSqVCmqYMDg4yPDzM0NBQayhODw8PMzAwgJmt8hoREZGyWHNBj7tvB86GeUHNRuCKRWbPgJcB717BLvYlyzImJibahsnJyVa6W8DSOR6bmGDX2FiYnphgcmKCqfFxsixb7Y8HgJkxODzM8MgIIyMjDA8Ps25khNE4vdgwPDy8YHmlsuY27zUpz/O2QHs5h2LQvrvzA63g3MzmpRcqS5KESqWybEO1WqVarS4p3bwQEZE1GPTsoUuBPzKzf92dmd/1rncxMzPD7OxsX+OZmRmmp6cZj0FJK7iZmGB2ZmZJy04GBkiGhkiGh7HhYWxoiHR4mPTAA0kf9CDSoSFGRkZYF/MtDgwNwcgINjREMjKCDQ5i1SqWppCmWBxIU6xSgSQ+Ec1zPMsgy/A8bx83GvjsLPnUFD49TT49jU1Pw/Q0zMzg09P41BT59DT51BTZ5CTjU1PsnJzkrqkp8l278Pvuwycn8akpsqkp8qkp8np9SeukVqu1AqrRRYKkWq225BNQkiSLnvT6Tbs7eZ6T53nX9J6WN4ded++WI11vNKgX8uvdgoguY3df0ve6EqxSCdt6YUyaYsncGwDuDs2+FtMLlLX2ieZ+sUoXHGZGpRgIFdK1mK7tRjC11CAsTdPWftPPeCl1i+PivtW5Hnqtn309/5xzzulaV5ZGQU+7nwHfAF4EfHapM7/qVa9qz0jTEEDUam3jZGBgbrpWIxkdxQ47rBW0rGsGL3GcFMbWnB4ZaRtbCe5qeL0egp/JydbYO6bzqal5eRNTU4wV62ze3F5nagpvNGCJQdWaEE/yrQA3BrbWkU+lgsV8ugTCVq1ig4PzytoCiHjSS5ttd5Z31O1ap9ivzr72qttPG3vpMau7t4IgYhDkjUa4iGgGRcX8ZrDUTNfrc9NxXBw68xaano3DeK86s7P41FSYrtfn+lRIe70+18eYT3wELsvrtFtvfdymE074xmr3Y3+39s+Uc3pdTnbmvwn4DPDfS13A4777XR6oVEhqNZJqlaRSwaBtSMzCOA4Wp6UPaQqDg3Dggbs1uwO5exh3TDeHPM/J48E7bzTI40E8z7K2tDca4Sq+29X9AncEetZJkrm7CkkCZmE65rXSZq0yM5ur26xfKGuWF6fb7mg086G1Dc5LN+9KdSvrKJc+7eMXKE7YPov7RXGgo4yOdF4I4PJ6nbwZxNXreLz7SBx7nof54r7U2qfi4HneKsO9NW/X6Wbbnftc64P1OAX0yO95B3KpdyaX2k7vvh+ytAVLN/v23re8tgOdZ8uDgNuKGe5+i5ldCzxvqQv4+iMesfu9ExER6e3Tq92BtaA0P1l393Fgs5k9CcDMDgKeRnic1emNwKv3YvdERERkhZUm6IleDLwu3sm5Cvgrd7+1s5K7bwJ+sLc7JyIiIivH9oVfTqwhWpkiIrIS9OrcMijbnR4REREpKQU9IiIiUgoKekRERKQUFPSIiIhIKSjoERERkVJQ0CMiIiKloKBHRERESkFBj4iIiJSCgh4REREpBQU9IiIiUgoKeqQvu3bt4h3veAdPetKTOPPss3jO857LlVdeif4ZExER2V/o395aXmtyZX7pS1/iwgsv5J577uHAM06hdvTh7Lz2Rqbv3cbPPfHn+a8PX84RRxyx2t0UEVnL9G9vLQMFPctrza3M973vffz2b/826x+8kYe98/WMPvJMAPJ6nZ+9/9Pc+Nq3M3rgAXzzK1/lISefvMq9FRFZsxT0LAMFPctrTa3MD3zgA1x44YUc+ZTHcs4H30wyMjSvzs7rfsy3fvmV1Ko1vnX1Vzn9lFNXoaciImuegp5loKBnea2ZlXnVVVfx1Kc+lYMfew7n/uc/YrVqz7q7bryFbz3jdxgaHeGmb3+fIw47bC/2VESkFBT0LAMFPctrTazMTZs28djHPhY76lAe88X3kR6wbtF5dnzvBv7vF1/OsWedzqarvs7w8PBe6KmISGko6FkG+vWWtNm8eTNPf/rTaQzWeOQn39FXwANw4CMeysPeewm3f+canvLiF5Dn+Qr3VEREZGkU9EjL+Pg4F1xwAfdu38ajPvkOasceuaT5j3rmkzjtb/6A//uPz/CSP/nDFeqliIjI7qmsdgdk3zA7O8tznvMcrr32Wh79sUsZPnv3Xkg+4fdfxOSdm/ng2/6RE445jjf84UXL3FMREZHdo6BHyPOcl73sZXzhC1/gnH96PQc97XG73ZaZ8dC/fzXTd2/hr/74Tzju6Afx0uc+fxl7KyIisnv0eKvkGo0GL3vZy/jwhz/M6X/5exx94a/scZuWppzzb2/kwHPP4Ld+/Te47GMfXYaeioiI7BkFPSW2c+dOnv3sZ/P+97+f0y5+Bcdf9NJlazsdGuSR//mPHPDwh/KyF/4Gb3rH2/RPVoiIyKpaU0GPmR1hZpeb2a1mdqOZfc7MTjaz083sKjO72cx+YmZ/YWYW53mJmbmZPanQzq/GvOes3qdZWd/61rd4+MMfzhX//d+c/dY/48Q/+23iKlk21Q3reOSn38nhT30cF//hRTzj+c9hy5Yty7oMERGRfq2ZoCcGMZ8Crnb3E939NOC1wOHAZ4C/c/eTgbOAxwC/W5j9euAFhelfA364Vzq+l11zzTW88IUv5NGPfjRbpid4/OfeyzG//bwVW15lZIhHXP42Tv3L3+Pzn/oMG09+MH91ySVs3bp1xZYpIiLSzZr544Rm9kTgDe7++I783wR+3t1fXMg7kRAcHWNmLwHOBc4DHg4MAF8lBEJXuPsnl9CNfWZlujvj4+PcfffdbNq0ie9+97t8/vOf54c//CHVoUFO/L3f4IQ/upB03che69PYj2/jR699O/d+8RtUajUef/75/OJTnsJZZ53FqaeeymGHHcbAwMBe64+IyH5Ef5xwGayloOf3gePd/Y868t8G3OHu7+jI3wEcBzwLeAQwC1wFbABOAo5niUHPgx59TlidcZ26eyuNe9t0t3reVpe5NN3bKNYrttGYnGbq/gfI6/W5z1upcNCjzuLIX3oCR7/gAmoHru/3Yy27sR/9lJ+9/9Pc94VvMPGT29vKautHGdiwnrRWDUO1SlKtYEn7Tcmuj+I68no9rWvb5IvfQWdhZ1lb3gJtLNJu8btt5dGt3kJ5HdP99mNe5zt0rrTC9Lx1vtD6nlfWe7q17eZh+/U8x/NmXj6vDGKdJXyMZqaZYZa00iQxL4l5i01bghmtacxIEot1k9Z4mZ8Uy2JKsMLP+eJ708+MPkx/9XUPleEn60bvOzDF/MuB3ycEPRcRHo0tyexgFY8HwtY+GKdD0kJ3jLlpM+LLRa0TQcinfT5rzRSSbdNWWBakg4PUDtpA9aANDBx+MOtOPYHRU46nMjz/HwxdDetOPYHT//aPOf1v/5iZrfczduMtjN/6M2a3PcDsth3Ud47jjQb5bJ18tk5Wr3cNRormZXU7I7q3rbemtu9qXlmrcK4d6yyj7XvszJv7fmgr69bGon3rNq/N79vin6HLSWL+SiwU+cJ1uwSBfc0bv5NWEJEUgpK2YIK2QKS5X3ULfnteyDUDpUIwRe5tQVe4cOgoa86X53F6Lh938tyBQt18bVxI7jfWyIV7HyaBwdXuxP5uLQU9m4BuLx5vAjofeZ0AjLv7WPOg6e7fMbOHAlPufvPuvNS75SvfXvI8pTcKHP+kRauJiJScAp5lsGZeZCY8mhows5c3M8zsXOAnwOPM7Mkxbwj4B+DNXdr4c3bjDo+IiIjs+9ZM0OPhnvavAk+JP1nfBLwBuAd4JvA6M/sx4QXl7wL/1KWNK939K3uv1yIiIrK3rJkXmfcRWpkiIrIS1v7b2nvBmrnTIyIiIrIQBT0iIiJSCgp6REREpBQU9IiIiEgpKOgRERGRUlDQIyIiIqWgoEdERERKQUGPiIiIlIKCHhERESkFBT0iIiJSCgp6REREpBQU9IiIiEgpKOgRERGRUlDQIyIiIqWgoEdERERKQUGPiIiIlIKCHhERESkFBT0iIiJSCgp6REREpBQU9IiIiEgpKOgRERGRUlDQIyIiIqWwpoMeM7vYzDaZ2XVmdq2ZPdLMKmb2JjP7Scy71swuLsyTxbwbzOwTZja8mp9BRERElkdltTuwUszs0cAFwDnuPmNmhwA14BLgCOAMd582s3XARYVZp9z97NjGh4FXAG/bu71fPe5Oo9FgenqamZkZZmZmmJ6ext0xMwDMbN7QzE+ShFqt1jakabqaH0lERARYw0EPcCSwzd1nANx9W7xr83Jgo7tPx/wx4A092vg6cOZe6Ct5nrcCjOK4W95CZZ150zMzTM9MMzU93RoX683OzDAzPcPszAyzM7PMxABnOSVJQrVWo1qtUq1V5wVFAwMDDA0OMTgwwMDAAIODgwysYLpWq7UCNdn/uDtZltFoNGg0GtTr9Va6ON3veHfm6Xc825qepdHIyPMMj5+h+Hk6073KAdI0bQ2VVrpCpVLpyOs+VCqVPRqq1eqKzZumqfZNWVFrOej5IvB6M7sZ+BLwMWAH8LMY6CzIzCrALwKf73eBP/fiC8hm6zRm6jRm6zRmZuP0LI3ZRiEd6mStOg3yLNvNj9kurVVJB+IwWCMdqFKJ41beaI3K4AaqA4cyOFAlHahRKdRvm2ewRjpQo3kc8nDEDgdid/Bmfpj23MnrBEpDZAAAIABJREFU4bNmsw3y2WK6MG5k5LN16jN1pmbqbJ+eJpsZIxufJZuuk83Mks3UaUyHcTPNMgVklfiZK4MDVAeqYXpwIOQN1KgO1mKdGpVmulalOjhAWq1giWFJEsZWSCdJGMza67TymUsnhYN720mOHvk9ToRLnBd38tzxPI9DezrPskKek8+rN1e/1Y7Pby/PHY9tNdvIGxlZvUHeyEK60egynZE3CnmxPGvM5a8GSxOSSkpSrXSM03n5VklJqylWSUlqFZLhlKRSwdLaXHvFk3sh3Up2K3fHs5w8y/Esx7MGeTYb0rNh/XqWddTJ8SxrTYc6eWv9ehznjYy83ljBNdifJI3rs5KSNsfVCkml0pY3fzrkFafTSoWkWshLm/Ur85bRtf00vAHS+q7M2r6f9vzmHW9a35eZdaRppbvNi3Uua27ey1745yuyvstmzQY97j5uZg8HzgOeQAh63lSsY2YvBf4AOBh4jLvfCQyZ2bWxyteB9/W7zB9//fukA1WSZuBRq4Tx8DC1ZroWhqRWpTJQJalVWoFKUqvMCzYqgyEoWSiIqQzUQlmtgiVr9zUtdw8nv5k62fRs18Aoa6VnaRSCp2Z+o1ud2fl1pqenyHbt6rqsvJ7FAG/uBI8Txvu5tiAtnUszL4CbG9MjvzVOQ5CHMRcYVFKSwQpJZYhKc7o6d7KyeMKy4gktzmtd6heDja4BSY9gxeIJtTjuFsQkzc9QAs3gdF5QVAhO5wKlfH7g1CWQWrROr+l6R17We55GI8Mbs+STxeXmCy5nXwv4FnLACx71vEvtCR9f7X7s79Zs0APg7hlwNXC1mV0P/A5wrJmtc/cxd/934N/N7Aag+eJJ652epbr6pz/kLsZIMVKSOA7pBN2y3WMGVOMwurxNO06DnAyPQ0jnhaE47VBI///t3Xu8JHdd5//Xp6q6+1znkkwymZlwvy93FgMiYkDuGxGBSIR1YV0RfSCysAiIumQB8bLwe+hPI95Qwz6W27qALOvv54WNoBKBABGCgCGBkMxkMpPJZM69L/X97B9V3V19O3POzDnTZ7reT6h8v/Wtb1V9u7qr693VfZLCvDshZF9jpHkQCiEl7dz9CPmdlkCahvxTYHYXxqxz42yduwDWfSVlHykBiLofFLufLLGe/mZRp08cR1gUE0VGHMVYFBGZZet0ttqtR4WW9rzl88V6d5kR9dSz+W69dz3ZQSKyXz9WT9fx3PENnIdhSHu2Xnf9bjud87ZYpiG7o9hqtmg1m9kdTM/PcXeCh+wcdQier9Xp027PP/y4530G68WvMbvN3XY8dG/UuhO5UYfvbt8RLg/b6t9v7BRm9jAguPvN+fw7gT3ACrAfeHX+Q+YY+DrwbHf/jpktufuZXlIn82CKiMi46dPBFpjkOz1zwG+b2R6gBXwL+CngFPAO4CYzWwRWgWuBI+MaqIiIiGy/ib3TMyY6mCIish10p2cLlOOXeSIiIlJ6Cj0iIiJSCgo9IiIiUgoKPSIiIlIKCj0iIiJSCgo9IiIiUgoKPSIiIlIKCj0iIiJSCgo9IiIiUgoKPSIiIlIKCj0iIiJSCgo9IiIiUgoKPSIiIlIKCj0iIiJSCgo9IiIiUgoKPSIiIlIKCj0iIiJSCgo9IiIiUgoKPSIiIlIKCj0iIiJSCgo9IiIiUgoKPSIiIlIKCj0iIiJSChMbeswsNbMbzewmM/tfZrYnb7/czD7Z1/dPzewlef0KM/uymf2Tmf2zmb16HOMXERGRrZWMewDbaNXdHwdgZtcCrwF+Zb0VzKwC/AFwmbvfYWY14P7bPdCz4e7U63Xq9Tpra2vr1s9keaPRwN179mlmI+tJklCpVKhWq1QqldPWq9UqtVptYBrWPqwtiiY2t0sJuTtpmhJC6EzF+Y3WzQwzI4qis57iONZ5JhNjkkNP0fXAYzbQb57smJwAcPc68M0N7+T662k0Gp2wcLqyv604dYJIfY21tTXW+kJJfW2NRj3bxlaIk5ikVsmmqbysJSTVBIsiIAs+xfxTDEMGhOCEVkpopqTNlFajRdpsEYr1NGzJeNuSJNlwQDrbgNXfVq1WiaKoc4E528ndxz6FEAbK7Zi2c9vrbX8joaE4n4aUNE1JB/qlPeu0hqzvA+v4kHbHC312qvYHmqRSIUniQj3pfNBp19vzlbxerVSH9hu2Tn89juOBcljb6crN9i2Gxv76sLb16sUPhjJ+Ex96zCwGfhB43+n6uvs9ZvYJ4DYz+xTwSeCD7r6hd6OnPOUpmxpbXM1CRVKrdOt54KjkZTyTULmgSrU2z0ztgm4wKfTphpRCWy0hmapmZU97ZWAfSS0hiuNNjf1MhRDyUNSi1WjRqrdIGy1a9WY+ZfVuW2FZ3n9033afrG213mSxvkirfg+tpXa/we2mjWwssrNZFGGRYVF+Ucnr2ZTP25C2vD8GURwRxVF3WRwRFfpmy7L5Tr3S7ldcJ8GiKkln/azdosJ81L9Ovp98u1H/Ov3r9+2z87jXXd86d2VCCODgIeDBOwHLg+dTtx5GtHsIpK2Ap9kHmdBKSVuB0GxlZSslbWXtodXts9JKCa1GNt9ICSvrrN8srN+3bFJ0XpdmYNlzh9lAe9a3u06x4Vfv+ZOLfs5ecnwc458kkxx6ps3sRrKvp74I/HXe7iP6O4C7/6SZPRp4JvBG4FnAKzeyw9f8xS9jtagbYmpJXlZ6w00tIa4kIz8B5C99JvHzQRTFUIuhVt22feT3pEY+0UPXcR8SnnoDVn84Sxut7oXFHdyzO2GdOyfden+fYf3bb3xmdN8QC3WMnj7D+rf7DOu/0T5RX2AYHTYG6xtZF7MN9+20b8OnZVu3JtvBC7XTnZ/uWegKaSC02mXaW45Y5mk7rAXSfL63z4jt5e0952p+jhfPdQ/ePc9D4RwPoXNOh3afYW0928j3QeFOunvnGBQO3KuAd23Zk1FS1v97jUlhZkvuPmdmu8nu2PwPd/9/zexRwO+7+/cV+n4CeI+7f7pvG/uAb7v7/AZ3O5kHU0RExk2ZfAtM/K/T3P0U8HPAG/MfKt8MHDSzRwCY2f2AxwI3mtmcmV1eWP1xwG3neMgiIiKyDSb5660Od/+ymf0TcJW7/zcz+7fAn5jZFNAEftLdT5nZPPAmM/t9YBVYZoNfbYmIiMjONrFfb42JDqaIiGwHfb21BSb+6y0RERERUOgRERGRklDoERERkVJQ6BEREZFSUOgRERGRUlDoERERkVJQ6BEREZFSUOgRERGRUlDoERERkVJQ6BEREZFSUOgRERGRUlDoERERkVJQ6BEREZFSUOgRERGRUlDoERERkVJQ6BEREZFSUOgRERGRUlDoERERkVJQ6BEREZFSUOgRERGRUlDoERERkVJQ6BEREZFSmNjQY2b7zewDZnarmX3RzK43sx8xs8vN7JSZfdnMvmFm7y6sM2dmv29mt5jZ18zsM2b2pHE+DhEREdkaybgHsB3MzICPA9e6+8vytvsBLwBOAn/n7leY2TTwZTP7mLv/A/BHwLeBh7h7MLMHAo8Yz6PYes1mk5WVFVZXV1lZWemZ2m3NZpM0TWm1WqRp2lNvl+5OHMdDpyiKiOOYJEmYmppienr6tGWSTOTLUEREdphJvdo8A2i4+++1G9z9NuC3zezyQtuqmd0IHDKzBwFPAl7u7iFffitw63YPNk3TgRByJlM7uCyvLLOyslxoW2V1ZZVWq7XdD+WMJEnC9PQU0zMzzMxMMz09w+zMDNPTM8zMZNP09PSG66OWT01NEUUTe3PzrLk7IQRarVZP0C1O/W2b7TMqUJ9NfeN9W4QQCO6dx+uFem+bn2Z5sW4AmBlRFI2cisvjKCKK4pHL+6ckSUiShEql0qkPmz+btmF9NrIsSRKdV3LemNTQ80jgS6frZGZ7gYcAnwEuA2509/RMd/oDL3gyzUaLZqNFq9mi2WjSyuebzVZfvUmz0SJtpqRp2PS+osiozdaoTVWozVapTVepzeTl3iq7D9S4eGa+t71dTidD26vTFeIkJo4jojgiSqK8bkRx3KljRkhDNgXv1gvzaTOl2WjRWG3SqDezcq04tbr11Qb1tSb1lQaNtQb1lSb11TXuXV3grhNN6rc3aOTL2/1ajTMLcNWpClMzNWpTVapTVeIkuzMVJ4UpjnrLJCbK60kSYVGEdS50hY1b9+LX19TT1ml0JwTH8wuxh/z4hW7dQxZEesusPqy9u43uslYrzZ6TVkraysoQ2vPdtjN5HW63OMlfi3HUrUfRYPuwtjgiiix//oyoGmGRYWbd58O6z43lE2Y9z1u23NoL8zbaHTrru2fPV3bcm3hwUndanTbPnvPU8Wb3+fLg+fPvnW2Ewjrtc6v7XAVCK6XVNx+Cn7PnpV/7OGdT+/zJ5pPKkHMrn5IkJq7E+d3hwrpJ3HmuIsvec6L2c9duj/rbI8zolJFF6/QtvA5s+GPqOWc31L657YxaYVT3P3z7B4YvkE2Z1NDTw8yuAZ4KNICfB77fzL4CPAz4NXc/OvKFuQm3f/swcTWiUklIqjHV+YSZSpWkmlCpJtnJX4lJqnFnPqkmJNWE2nRlMJx0yspAe1KJh5xMZ/8YdqbBN/M0DVlYWs3DUqFeX2vkASqfX23QWG1SX+1tb9RbWQBIvXNB6Vxc0gaNRiBdCaRpSmhfXPILEIB7cYQ+MNT+uwQ967hjkXU+4Wf1Yhn1trXfqKOo25Zky5M47ukTRe03e4jaITYPsO0A0L44RUPa4rjQnkSdYNjTpydgdC9WUWz5xS7bZzGAFLfRLfuCSWE8Z3b3YJLOgc2FmCzIdkNQ2soDb6s3MPWG3e58q5mdC+110/a50Cz0TfPzJF+vu/3CPtLC/pvt86p/f92y0WoS6oX9tbIPTZ0Q6d27ap3g2FPSM9/uWwyh7tnx6e/bcxIXj/yIQ++jFpwDP/ym73/NFXM/c83YBjAhJjX0fA14cXvG3V9jZvuAG/Km9m96Hgr8vZl9LF/nsWYWtb/e2qwv3fhFVnyRiAgjIiJist6Ed5jZ7dqw4wS887+QvYHm/6NTMlAWtzGc9dXa/+wts1qhzQzra7P83oR171GInFfa51lWC3S+Vuw71wbOPaenDSgsp6+Nvnr7w0i3PjiuUefvYPt6MWhUSDqT9tv8q3+xzq5kg2ycyXW75D9k/kfgT939vXnbfcm+xnol8EZ3vyJvfz1wmbv/mJl9BPgm8J/d3c3sIcC/cvc/3+CuJ+9giojITqBPNltgIn995lmSeyHwA2b2bTP7PHAt8OYh3X8PeJqZPQD4SeAS4Ftm9lXgD4Ej52jYIiIiso0m8k7PGOlgiojIdtCdni0wkXd6RERERPop9IiIiEgpKPSIiIhIKSj0iIiISCko9IiIiEgpKPSIiIhIKSj0iIiISCko9IiIiEgpKPSIiIhIKSj0iIiISCko9IiIiEgpKPSIiIhIKSj0iIiISCko9IiIiEgpKPSIiIhIKSj0iIiISCko9IiIiEgpKPSIiIhIKSj0iIiISCko9IiIiEgpKPSIiIhIKSj0iIiISCko9IiIiEgpJOMewHYwsxT4KmBACvysu382X3YZ8BvAIWARuBN4i7t/1cyuBl4FHAeqwDvc/YPn/hFsr3q9zuLi4mmnpaUlms0mIQTcnRBCT93dqVQqVKvVzlScr9VqzM3NMT8/z9zc3NCpVqthZuM+JCIiUgLm7uMew5YzsyV3n8vrzwHe6u4/YGb7gc8BLyuEoKcC+9z943noWXL3d5vZQ4AvAhe6e3ODu96Wg9loNFheXt5QUClOCwunWFxc6ASYxaUllhaXaDZbG9pvpZpQqcSYQWRGFBnkZRRlQaXVCjSbKc1mi2Yj3fRjS5KE+fk55ubn2DU/z65du5mf38WuXbuYn58fKIe1tcvp6WkFqAnRDtZpmg5MrVZraHtx2ozNvGbiOCaKIqIo6tTXaxu1TK9TOQN60WyBibzT02cXcDKv/yxwbTvwALj73w9byd1vNrMVYC9wbCM7+tSnPkW9XqfRaPSUw9oajQZra2ssLy+ztLTUVy4W5ldoNjeWuZIkYna2xsxsjZnZCrOzNWZnaxy8tMbs3EXMzl7KzGyN2dkqs7NVZmYTZudqzMxW875VZueycmamSqW6uZeHu5Om7RCU0qi3WFlpsrLSYGW5zspyI5tfbrGy2mB1ucnycj2bluosLa2xtHSMo8fu4JZvN1heqrO83GBpcY2NhPM4jpmfnysEoV09YWl6epparda5C9Uuh7VVKpWBi1X/NKzdzHD3LZmAkRf+nTVlIaSVpqStFmlISVuDy9M0fywhaw+d5cXHmNVDCJt67Z2PeoPQ4OsqjrN6cYrimCROOv2yKRno1+kfDW7jTPpsdb+z3VYU9f4yoxgiR9XPdNlW9ztTu3fvPuttyOSGnmkzuxGYAg4Az8jbHwlcu5ENmNkTgJvdfUOBB+CZz3zmhvrFsVGpxFRrCdPTVWZmq0xPV5iZrTIzX2Xf/iozsxczPX0oX1ZlZqZSCCw1ZueqA/PVajLWT5BmRpLEJEnM9PTWbdfdWV1t5iGoztJiFqCWlrqBKQtHffNLxzh67Ha+dWud5aUGjUaLRiO7I9U4g7tSkyKOjSiOiKMRZWz5xaZQxhFRZPnFua+MjTiKiBKjUs3nO8tjoigZ3r9Y5stPO44oIklGbKOwrQ1/Jt7Evdns7lPflAZCuz31rJ6GwX4h9PYprpv29cmnNA2E1ElDb9num6YtQmiQptm20uA0WoHQyNctbqdQhjRk64R2Waz37bPvscj43HTL1Q975APf9s1xj+N8N6mhZ9XdHwdgZt8LvN/MHtXfycw+R3Yn6K/c/XV58+vN7FXAA4Hnbman137wp0kqTar510LVapx9RVTN6u32OI7I3pWzyci+NurUpZfB3OwUc7Pzm17VccDBPZ/LS3darZRmo5XdlWrkd6caLRqNlFYzJQTvudD1XPTyi5e35wt1s/yTXV4aednfbvkzPqw9L8FGh5QR4eR0/ToHtXiAC3Urttmo5f3tsnN4nuW8p607O2L50HqhtRDW0v4y7Ya23kAVekJZu/T+MLZuuBvcTs+dX+8dY7c+/KgMW8aI9frvMI9aNngjer1lZ+xpgELPWZr43/Tk83cBjwZeCwR3f1th2UuAK9z9lX2/6XkR8NvAg9x9bYO7nryDKSIiO4E+ZWyBif+TdTN7OBADJ4BrgFea2VMKXWaGrefuHwVuAF6x7YMUERGRbTepX2+1f9MDWTp+hbunwFEzeynw62Z2iOwHyncDbx+xnbcDHzCzP3T3yf9lpYiIyASbyK+3xkgHU0REtoO+3toCE//1loiIiAgo9IiIiEhJKPSIiIhIKSj0iIiISCko9IiIiEgpKPSIiIhIKSj0iIiISCko9IiIiEgpKPSIiIhIKSj0iIiISCko9IiIiEgpKPSIiIhIKUzqf2VdtkGz2eTWW29lcXGRAwcOcPDgQcz038ATEZHzg+70yGl99rOf5Ud/9EfZu3cvD3/4w/me7/keLr30Uu5/30O8+U0/z5EjR8Y9RBERkdMydx/3GCbJRB3MI0eO8IY3vIEPf/jD7N01zYsvfxBPftRB5qdj7ji+zN984Xb+8nPfYapW5W3/+Zd4/X96M5VKZdzDFhGZRLqtvgUUerbWxBzMz3zmM1x55ZUsnDrJG1/2BP7jlY9iZmow0Nxy+BRvfu/1/MVnv8OTn/hoPvLR/8197nOfMYxYRGSiKfRsAYWerXXeH0x355prruH1r389Dzy4iw+943k8/D7zp13vf/yfb/Ga93yaWq3GBz74YZ793Oefg9GKiJSGQs8W0G96pGNtbY2f+Imf4LWvfS3Pvuw+fPp3XrihwANw5TMezD/83ou5ZG+N5/2bK/ivv/p2FKhFRGQn0Z2erXXeHszbb7+dF73oRdxwww289RWX8dYffzxRtPkPFsurTV79G3/LRz99C1e95Id437UfYmZmZhtGLCJSKrrTswUUerbWeXkwr7vuOq666ipWlxf4o1/4QX7oKWf3mxx35z0fvJG3ve9zPOaRD+Xj/+svuf/97781gxURKSeFni2gr7dKLITAO9/5Tp75zGeydybwmd998VkHHgAz440vezwffdfzue07t/HExz+GT/3NX2/BiEVERM6cQk9J3XzzzTzrWc/il3/5l7nyGQ/h7373R3jYBn+/s1HPedJ9+czv/ggX76nwnOc+l7f8/OtZXV3d0n2IiIhsVClCj5m5mb2nMP9GM7s6r19tZm/sW/YNM7vJzP7JzP7dGIa8be69917e9ra38ehHP5obPn8917zxGfzxL1zO3FS8Lft78KV7+NvfeSEvf/ZD+fV3/yaP+VcP5SMf+TAhhG3Zn4iIyCilCD1AHXiRme1br5OZ/TTwLOAyd38U8DQm5HvUm266iTe96U3c73734+1vfztXPOW+fPnaq/j3z3/otv+nJOZnqvzez1/OX7z7h0h8mZe+9Coe88iHcc0113DixIlt3beIiEhbKX7IbGZLwK8Ac+7+i/mdnTl3vzq/47Pk7u82s+8CT3f3W85wVzviYJ48eZKbb76Zf/mXf+H666/nuuuu4+tf/zpxHPGCpz6QN//49/CYB+4ey9jSNPDRT9/Kuz94I1+95W4qlYTvfdJlPP0Hn8XjH/94HvGIR/CABzxA/2ZnEZFeE/EBfNzKFHoOAl8BHgu8ir7QA/w+8F1333um+3n5FU909+yvlxynXafTlpfeLYG8b2/78P7eSVXF9mYrcGpxlZOLK5xaXGVppdEZ09x0hSc/6hKe96T78eKnP4iL906f6cPbUu7OV245wUc+9S2u+9Id/NO37qb4UtwzP8WFe2a5YPcstWpCrZpQTWKqlYRKEnXvThXeBtptxRtXhvUs6x9Dp17Iq/2nRM854sPb+8+inmWj1unfT88YTr/+utseNf51x9PXb8Q2Tjee4E4ITgihUM/PibwePHTaQ/7aLvbt1Nuv+zC4HLLn1Sx7njt1y551yxb0tEfW369Qt9Hbi/qXj1q3MCaG7a+z7VHrZW1D1zvNPjGIIusZu0yO//7JG/SMboHS/FfW3X3BzN4P/Bww7Ne0xlneqfmHL96MmRfemAbfCLvz9LwxGe036CFvikPWp7CNShLxgP01HvegXeyZq3LgwlkedOluHnxoNw+97x6SOGKnfUgwMx774It47IMvAmBhuc43vnuSb952ku/etcQ9C2vcfe8aJxfXaLTWWFpIabQCjWZKs5X9HmjYRX7YxbkYLq3vOPQEpCEBqjPP8GUbX+f062fr9CS24euv+xhGjK13N9v6GOLISMyI4kJYiIzIIiIzosiI2hdo69a7y4woyvZe7Ftc3t7n0A8IxXpn2eAHjsEPFvR8WOnfVuhfn8HtMLAsXy+0t7H+Porj7QRFJ/vgtKH1nBB6A7RMhtXrfubY9NPfe/G4x3G+K03oyf0m8CXgT/oX5KFo2cwe6O63nsnGv/2d2wird5/tGEfI008WifLEE4NFEFUgitlpwWYzLsqn7x+61CE0IaTgKXgAD903du/8Q4CB14ENzgyNNgO3Bop302xIX+sro/x1ufNC9oa5A6GvJHvN4YXbXJ0kQue1V1g2EMcHXp56vcrmNL78noeOewyToFShx93vMbOPAP8B+OMhXX4VuMbMXpqHoF3AVe7+BxvZvtX2ENf2bOGIRUREYPrp77133GOYBGX5662i9wCj/orrvcB1wBfM7Cbg08DKuRqYiIiIbJ9S/JD5HNLBFBGR7XCefme8s5TxTo+IiIiUkEKPiIiIlIJCj4iIiJSCQo+IiIiUgkKPiIiIlIJCj4iIiJSCQo+IiIiUgkKPiIiIlIJCj4iIiJSCQo+IiIiUgkKPiIiIlIJCj4iIiJSCQo+IiIiUgkKPiIiIlIJCj4iIiJSCQo+IiIiUgkKPiIiIlIJCj4iIiJSCQo+IiIiUgkKPiIiIlIJCj4iIiJRCMu4ByM7UaDQ4efIkS0tLNJtNGo1Gp0zTlCRJqFarPdP8/Dx79uwhjuNxD19ERGSAQk+JLC4ucvjwYY4cOcKRI0c69cOHD3P06FFO3nOCkydPcu+pU6yurp3xfnbNz7Fn9y727t3LBRfu45IDBzlw4AAHDw6W8/PzW/gIRURERjN3H/cYtpSZpcBXAQNS4Gfd/bP5ssuA3wAOAYvAncBb3P2rZnY18CrgODCbb+OX3P2fN7H7sRzMZrPJ0aNHOXz48MB05MgRjhy+g8OHj7C0vDyw7q7pKof2THFgV40LZqvsmamxZ7bKnukqe2YqzFVjaolRiYxqDJXIiCNoBafRcpoBGsGpt5yFtRYnV5rcu9rg5HI2nVha4+hCnTsX1lhtpAP7n5ud4eCBSzh06X05eOgQhw4d4uDBgz3lgQMHqFar5+JQiojsVDbuAUyCSQw9S+4+l9efA7zV3X/AzPYDnwNeVghBTwX2ufvH89Cz5O7vzpe9FPgt4NHufnyDu9+yg7m2tsbx48e5++67ufvuuwfq7Ts0h++4g7uOHaP/eawmMQf3THNod42Du6c4dMEsB/fMZPPzCQd3T3Fw9xRzU+fmZp97FoqO3LvGnQtrHDlV586lbP7wyRWO3LvM4XvrHDm1SqMVBta/aN+FWRA6dGlPINq3bx8XXHBBdlcpL2dmZjDT+4OITBS9qW2BSQ89VwIvd/cXmtk7gODubxux3tUUQk/e9n7gi+7+WxvZ95/92Z95o9GgONXrdYa1LS8vs7i42JmWlpZYXFhgcXGBxaUl1tbqIx4fXDiXBZZDu2sc2juThZm9WaA5NJ9waM8U++aq5+WF3905sdzg8L1ZMDq80OTIQp3DJ5c5cnKFw/eucfjUGscWRn/9Vq1WuGDPHvbs2cPc/Dwzs7PMzMwyMzPD7GxWtqdqtUqlUiFJknXLKMp+829mneParvfPj6q7+8AUQjijtrM+Ah5OAAASoklEQVRZr93Wrp+L+YG2NMW9XQ+EkObL027/0Dc/sI923Qvrt+dHjckJ3jffXk7fvJPVPXSew8giosiIoqgwtdt7J7P+foUpjoiiuDMfx0lWJnkZx8Rx3Kn3l1u5bLv3UzwXRpn05VvhiU984vn3hr4DTeJveqbN7EZgCjgAPCNvfyRw7Sa39SXg4RvtfOWVV667PImMahJRjSNmazHztYS5WsL8VML9phLm9yXMXzrPXG0vF8xU2DdX5aK5Gvvmqp36npkKcTS5r30zY99cjX1zNR576eh+zTRw56k1Tiw3OLnS5J7lJidX8npenlxZZnltgZWFlBONFrc3UlYaKcuNlJVGi+VGyoRl/i1jBpEZkZFf7EfNW0/fjcxHkWG063mfYfORddaL6S4bOoaIDYwpyueTwvL29grzERi96wIEz0J5cAju+UQepPra8kDlpARPO/P9/dJmoR6yehqcZnDqfW3tPmm+rXTIesV+nTZ3QqBnPb3uzz/+uz/8NH7m458Z9zjOd5MYelbd/XEAZva9wPvN7FH9nczsc8Au4K/c/XUjtrWpdPGVd72YWv3eLNgkcT616wlRHGXvrhhYlE/F+iYfaYlVgPvugvtupLMDHsA9L0PW6E6atmi1As000EpTmqnnZaCVOs28rXO3pL1JB6d78XDofMWYLWv383xZ/lST3/mBzsU/a+9eqLv98otv1F2ezRfW69yBsL7t5+tZVGiPiON2wIi6AaNzsW8HiPw12tb5FGt983mbFZZ15k/XX0byzj/ophMfXh+5fNQ2stLz4JWm2Z2vTkhKQx6aCm0hC2rF0DQsXHVCWV9bOE3COl0AO10+O923Fadff3u3v4X2nLtdTa5JDD0d7n69me0DLgK+BjwB+PN82ZPM7CXAFets4vHADRvd36N/4c/OYrQyDnE+1cY9EJFzyOi+9uW88YlxD2ASTPS/nNDMHk52Xp8ArgFeaWZPKXSZWWfdFwPPBj64rYMUERGRc2IS7/S0f9MD2QeaV7h7ChzN/yLr183sEHAMuBt4e2Hd15vZvyX7k/WbgGds4i+3REREZAebuL/eGjMdTBER2Q76NdwWmOivt0RERETaFHpERESkFBR6REREpBQUekRERKQUFHpERESkFBR6REREpBQUekRERKQUFHpERESkFBR6REREpBQUekRERKQUFHpERESkFBR6REREpBQUekRERKQUFHpERESkFBR6REREpBQUekRERKQUFHpERESkFBR6REREpBQUekRERKQUFHpERESkFBR6REREpBQUekRERKQUJjr0mFlqZjcWprfk7YmZvcvMbi4s+0Uze7aZXW9mlveL82VPGe8jERERkbOVjHsA22zV3R83pP2dwCXAo919zczmgf/k7n9lZj8B/Afgj4DXAl9w98+euyFvvxAC9Xqder1Oo9EYqK/X1mq1iKJoQ1OlUqFarVKr1TrlqHq1WiWKJjqDy3nC3Qkh0Gq1eqZmsznQNmo6k74hBKIowswGzqWNtLXPt0qlMlBfb1mxHsfxuA+/yLYydx/3GLaNmS25+1xf2wxwO3B/d18css4B4O+BFwB/Dlzm7vdsZH/u7mma0mw2aTQaZ1RuJIAMLF9bo762SqNep762lpXtfs0G9XqDeqNBo9mk3mySpuHsD+42SJKYqVqNWh6EpqamsnA0NcXU1DS1fL7TPqJ+uuWj6nEcd6Yoigbm8xuA5y1371zQ2+VG62madi7S7fqwttMtP5O2TYWIZjPr22zSarXLVl4v9EtbtFrZudpq7ytNabVSWmk67qdqbKIoolqpUK1W8rLaCUbVao1qrUa1ltd7lg2f1lt+Nsva52T7PJ2E83MDJv4BnguTfqdn2sxuLMz/KvB14LvDAg+Au99pZr8JXA/83EYDD0AcR2xXhowNanFENTZqUbu0bltsVKOI+Thvi4xaJaI2ZVT3JNTiStZWXD6wfjbf3tZAW2wkZjgQHIJ7VpKXhbbUnVZw6sGpp4FGWqxDPQTqqdPI2+ppviw4a61APQ2spUvUmwvU15y1vM+pNHBX3rfe6evUQ2CtFUi3McObQWxGHFleRkSFtshs5BvvsNZR79E24r3N28c5eP4cOMEd9249eHFZftciX36+iQ2SyLLJsrJSqCcR3brl84XlUz198yk2kkp7HUii6uB2+7fVN1+JBvfVs16hbf3xFseRvX7cnQDd55TueTVw3hXaUneaIZsaaaEewpB2Cu0M7dcITiMNNEKgka7SCCs0605jxfM2Zy04C+2+IWTbzc/hRmc7Wd9zwQwiy45jbEaUz7fPzU571F6e9Wmfx8Xz13q229vWPm+L57qdpm/WZuT/P6P1//H594957+fLm8i3yKSHnoGvt8zsMX3z/x54HXAh8BR3vx24Bvg1d//Tzezsl/71ISoG1fzNrhrnZXs+iqjExfliv4hKJ5R0Q0c7oMSRQv5GpHmIWkt7y3raDU6j2lPPpvZFJPVsewNtxX6h2xZGvLcPax51h3XU5cHJfoCXvTGvUzeIyN7Mradueb9N1PP1zehc0OP8Yt0JJPlFJTHrCSmxdS/ww9ehZ93i8jjfVgk+uZeC5+fNqEDUHNLW7Rf6lmdtoXDOBbLzMAuI3XOzp08+hmI5bDlkHy66Y2+39ZWFE7XdP2vzgb692/G++WF9Cn173xDeBbx5A4dc1qGvt7rtNwFXuPt3Rq27AZN7MEVEZJz0KWALlO6Xo+6+ArwP+B0zm4Lsr7SA6lgHJiIiIttq0r/e6v9Nz//v7m8BfhF4B3CTmS0Cq8C1wJExjFFERETOgYn+emsMdDBFRGQ76OutLVC6r7dERESknBR6REREpBQUekRERKQUFHpERESkFBR6REREpBQUekRERKQUFHpERESkFBR6REREpBQUekRERKQUFHpERESkFBR6REREpBQUekRERKQUFHpERESkFBR6REREpBQUekRERKQUFHpERESkFBR6REREpBQUekRERKQUFHpERESkFBR6REREpBQUekRERKQUknEPQHaeNE05ceIE99xzD/V6nUajQaPRoNls0mg0CCFQqVRIkqRT1mo15ufn2bVrF7t27aJarY77YYiIiPSYuNBjZvcHPunujyq0XQ0sufu7zewNwE8BTSAAnwLe7O7NvO/jgS8Bz3X3vzy3o98+zWaT48ePc9ddd3WmY8eOZfWjR7nr8OGsPH6c4ydPEkI4q/1N1arsmptj7549XLx/P/sPHuLiiy9m//79PeUll1zCgQMHmJmZ2aJHKiIiMtzEhZ71mNlPA88Gnuzu95pZFXgDME0WggB+DPj7vNzRoader/eGl/7pziPcdeRO7jp2jBOnTg3dxlRk7E8i9lcT7ldLuKyasP8+e9lfibkwNqZwqjhVD1TNqBqYQcuzqelOC6gTsehwKsBCcBZSZ6GVcuLUMY4dP8xNX/oCd7UCJ1vDw9T87CyX7L+YSw4e4sDBg1xyySU904EDB7jkkku46KKLiON4G4+qiIhMKnP3cY9hS613pwd4HfA0d//2iHUNuAV4FvB3wAPdfW0Tuz+jg5mmKUtLSywsLLCwsMDi4iL33nsvx48fHz4dO8bx48c4tbA4dHtzccT+SpSFmVqV/bUkm4/IpkrE/krM/krEXGRkD/vcaATneCtwrJlytBm4yyOOps7RRsrRepOj9SZ3tgJHm4GFVjqwfhRFXHThhVkwyoNQe9q/fz979uxh165d7N69u1POzc0RRfr5moic187dG/UEK9OdnmlgblTgyX0f8G13v8XM/hZ4PvDRje7gl57wCNbSlHoaqKcp9RDyej6fBuohsNZKWWq2WGg0WWy2WBpycS9KDC6qxFyUROyLI/51JeKi6Zj9u3Z3w02SBZ2Lk4iZeOde4KuRcagac6h6+rs1K2ngrlbgaDPlaNPzMJRytLHC0du+ydFv/TNfa2ZtzXXipgHzlYTd1YTpOGYqiZmKY6bzciqJsvY4phZHJJERm5FEEbFZ7xQZSV6226JteCtyzxJ0cO+UwcHpK0e1F5ezmX79+/SBcXRKh4B3xlrcl3ceQ289FPr29Okbk4/oF4au11vv9hk+js7yYfspPLaBPkP30f8Yu4+jX2RgGEZ2tzTCMMten1mbEeXl0D55e1Qoo7xPp2599aHLuvPd7WT7HujLqG32tQ/sp7fNNrTOxra13ti28lTcqq1t1WfKl3/q81uzoZKbxNAz6vIXFZeZ2XOAXwf2AC9z98+SfaX1obzLh4AfZxOh59du/AY1M2oGtciyepTPd+rGrggeFEXsmo3ZFVeYj41dsbErjrplZJ2gszvO78Z0zp5yBP6ZJOIBCTxgalSP7CrjHjiZOnc1U06lzqk05JOzkJenWoGF4KyGwFpIWWs5a2vOyeCsBWfNycrgtNxJgdTpqZ/dr5y2V/vCGeUXyKgzb915G9Hes551+m10W1ZYp3sBL9TpXvT6l0ejlg/ZRnv/I/vYkG309cm2YaOX9weRM+jTv7wdpjohkUKoLSzrBKaeefrm26Gzuyzk2+2U/W3e7ldc1tdG9nX1afut1zaw/97t+zrrTtb3Ddvj5Zdd+lI+f8eHxz2O890khp4TwN6+tguALwLLZvYAd/92/iPlvzSzTwJVM4uBFwMvMLNfJHu/utDM5t19+PdIfVr/38fgs9dBkkClCpVKPtWgWoXaVDYlk3jYx8fInuALNrtimkK9Ds0GNNag2YRGA1rNfGplfdIWhIC3WoS0RasVSNMWaQikIcVDKCQiz97doVuOHLj1lu0wm18toyjKLqJRnF2soyhrMyPKv5aMogiL4vyKa9D+Gi+K8raoUC/06bRTqI9oM8sTUNS7/rB2rLCN/IEUl3XGsdknS7ZMcAhpNqUBPGSvdffs9d5eFrzz2u9MHrrLQtq7LKR5sgmFsr0sj3Dtts5yAMfTNLtTGEIWiEIgeMg3HTp3HYOHbNchZKGpsCx17z3nNvvTjUL/rfrVx1aFOa9U4LZv3LpFmyu1iftND4CZ3UD2F1mfMrMLgH8Engc8B3gBcFX+Q2YD/hp4J1AD3uDuzyls51rgb9z9v21w15N3MEVEZCfQR4UtMKm3HP4dcI2ZvSef/y/573TeC8wAnzOzOtmPm/8B+DLwW8DH+rbzP4GfATYaekRERGSHmsg7PWOkgykiIttBd3q2wM79Mx8RERGRLaTQIyIiIqWg0CMiIiKloNAjIiIipaDQIyIiIqWg0CMiIiKloNCztQb+zfSTOJnZq8c9hp026ZjomOiY6Jhs8zGRLaDQI2fip8Y9gB1Ix2SQjskgHZNBOiaDdEy2iUKPiIiIlIJCj4iIiJSCQo+ciT8Y9wB2IB2TQTomg3RMBumYDNIx2Sb6b2+JiIhIKehOj4iIiJSCQo9sipk918y+aWbfMrO3jHs8O4GZfcfMvmpmN5rZDeMezziY2R+b2TEzu6nQdoGZ/bWZ3ZyXe8c5xnNtxDG52swO56+VG83s+eMc47lmZvcxs+vM7Otm9jUze13eXtrXyjrHpNSvle2ir7dkw8wsBv4FeBZwB/AF4Mfc/Z/HOrAxM7PvAE9097vHPZZxMbOnAUvA+939UXnbbwD3uPuv5QF5r7u/eZzjPJdGHJOrgSV3f/c4xzYuZnYAOODuXzKzeeCLwAuBV1LS18o6x+RHKfFrZbvoTo9sxmXAt9z9VndvAB8CfnjMY5IdwN0/A9zT1/zDwLV5/VqyN/LSGHFMSs3d73T3L+X1ReDrwCFK/FpZ55jINlDokc04BNxemL8DnZwADvyVmX3RzPQvFeva7+53QvbGDlw85vHsFD9rZl/Jv/4qzdc4/czs/sDjgc+h1wowcExAr5Utp9AjmzHsX4Wu70fh+9z9CcDzgNfkX2uIDPNe4EHA44A7gfeMdzjjYWZzwP8E/qO7L4x7PDvBkGOi18o2UOiRzbgDuE9h/lLgyJjGsmO4+5G8PAZ8jOxrQIG78t8rtH+3cGzM4xk7d7/L3VN3D8AfUsLXiplVyC7u/93dP5o3l/q1MuyY6LWyPRR6ZDO+ADzEzB5gZlXgKuATYx7TWJnZbP7jQ8xsFng2cNP6a5XGJ4BX5PVXAH8+xrHsCO0Le+5HKNlrxcwMeB/wdXf/fwqLSvtaGXVMyv5a2S766y3ZlPzPJn8TiIE/dvdfGfOQxsrMHkh2dwcgAT5QxmNiZh8ELgf2AXcBbwM+DnwEuC/wXeBKdy/ND3tHHJPLyb6ucOA7wKvbv2UpAzN7KvB3wFeBkDe/lew3LKV8raxzTH6MEr9WtotCj4iIiJSCvt4SERGRUlDoERERkVJQ6BEREZFSUOgRERGRUlDoERERkVJQ6BEREZFSUOgRERGRUlDoERERkVL4vxe+PTQG6friAAAAAElFTkSuQmCC\n",
"text/plain": [
"
"
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"# Plot the distribution of illicit flows for the transformed data\n",
"fig, axes = joypy.joyplot(partner_features_log.sample(n=15, axis=1, random_state=234), \n",
" colormap=plt.cm.rainbow, figsize=(8,8),\n",
" title='Distribution of mis-invoicing across random sample of partner countries (log transformation)');"
]
},
{
"cell_type": "code",
"execution_count": 56,
"metadata": {
"slideshow": {
"slide_type": "skip"
},
"tags": [
"hide-cell"
]
},
"outputs": [
{
"data": {
"text/html": [
"\n",
"\n",
""
],
"text/plain": [
"alt.LayerChart(...)"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"# Biplot for the first 2 principal components for the transformed data (modified log)\n",
"biplot_PCA(partner_features_log, 10, 1, 2)"
]
},
{
"cell_type": "code",
"execution_count": 57,
"metadata": {
"slideshow": {
"slide_type": "skip"
},
"tags": [
"hide-cell"
]
},
"outputs": [],
"source": [
"# Apply a modified Yeo-Johnson transformation\n",
"partner_features_yeo = power_transform(partner_features, method='yeo-johnson', standardize=True)"
]
},
{
"cell_type": "code",
"execution_count": 58,
"metadata": {
"slideshow": {
"slide_type": "skip"
},
"tags": [
"hide-cell"
]
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAnQAAAI2CAYAAADZ+RWoAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4yLjEsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy+j8jraAAAgAElEQVR4nOzdeXxU1f3/8ddnJisJARIIYZMdBERR3HdcuiiutbZa12/br9W2LtW2tmpLW+1iv1brT61Va627rYrWXQFZFEFZZUeQQIAECHvCkmTm/P64NzBJZiaTjZDM+/l45JGZe88953Nnzr3zmXOXMeccIiIiItJ2BVo7ABERERFpGiV0IiIiIm2cEjoRERGRNk4JnYiIiEgbp4ROREREpI1TQiciIiLSxjVLQmdmj5rZXc1U1yFmVmZmQf/5ZDP7XnPU7df3jpld3Vz1NaDdu82s1MxKmqGuX5rZE41Y7jtm9n5T20+gnTIzG1BPmRrvs7QMM3vKzO5u7TgOBDPrZ2bOzFJaoO7rzWyD32fzmrt+ia05P19q1fsVM3utuettLmY2zsyebe04DlZmNtTM5prZTjO7sbXjqa25+q2ZnW9mLyZUtr770JlZIdAdqAJCwGLgaeAx51y4gYEVAt9zzk1owDKTgWedc41JYMYBg5xzVzR02eZkZn2A5UBf59zG1oxFkouZPQWsdc7d2dqxtDQz6wesAlKdc1XNWG8qsAM43jk3v7nqradNBwx2zq04EO21BjO7Bu/z4ORWan8W8CNgJjAFmOCc+23E/KuBXwEjnXO7mqnN0/E+z3onUHYcB8HnVywttb01oP1/ADucc7cc6LajxHINLdiXzWwhcLlz7vN45RIdoTvPOdcR6Av8Efg58I+mhVhXS3yzPkj0BTYrmWtbDvToYTvu/21ddyADWNTSDR2IPtCW+llLbYNmdgzQyTk3w3mjGt8FfmJmI/z53YD/w/uQbpZkLhm1cF/rSyO3yba0DfheAP633lLOubh/QCFwVq1pxwJh4DD/+VPA3f7jrsCbwDZgCzANL3F8xl9mN1AG/AzoB1RvTGuAqRHTUvz6JgN/AD4FtgOvA7n+vNPxRh/qxAt8DagAKv325kfU9z3/cQC4E1gNbMQbeezkz6uO42o/tlLgjjivUyd/+U1+fXf69Z/lr3PYj+OpKMueDqz1X5ONQDFwIXAO3sjeFuCXEeXH4X3LA++D5llgs/+afwZ0jxHjNcBHEc8d8APgC2Ar8DBgQLpf12ERZbv565HvP/8+sMKP7b9Az1r1DvIfZwL3+a/JduAjf1q09/l3wMfATuB9oGtEnVf5dWwG7iJKv4woey4wF29UpQgYV2v+ycB0fx2LgGsi+vHfgLeBcv+9G+bHtg1v53F+RD3n4I1Y7wTWAbfF2wZixOqAH/rvwSp/2l/9uHYAs4FTar33/8brazv9mI6OmH8kMMef9xLwIv62meD7doMfy07//RgIfOLH8m8gLcZ6DMIb5diOt628FDGvvvX5D14f3gksAIYAv8DbFoqAr0SUn0zs/UE/avapTnhfPIv99+duIBgj/nTgAWC9//eAP22I3xcc3vY7Kcqy1e3+r79sMXBrrf3lJ35/KAYeinwda/cBvP2g89stA77F/n3ErezfR1xbK/7/w9tXbQAeBTJr7V9+DpQAz8R4Db4PLPHfh8XAUf70eNvAZPz9aQP3McOAPXhHfcqAbXG2waeo2YfHAvP8eKYDh0fM+7n/Xu8ElgFnxljXXwFP1Jr2U2AG3n77BeDRBNqL+drEaPd0Ij6zgJ542+EWvO3y+w3Y1guB24DP8baFl4CM+vZB9byfT/nv0Vt+mzOBgTHWZQ37t4sy4AT//f8YuN9v9268fcgkvH13KfAc0Lkp6+HXF8LrQ2V422nUz+CIflk7rqeAR4B3/Do+Bgrwtv2twFLgyIg4bwdWsn/7uCji9YzVlxuy762znUTMPwn/8yFu/6q3QIwPTv/NvL524Hg720eBVP/vFPYf2q1RF/t3hE8DWcT+oF8HHOaXeYX9yczpxEjoIjaIZ2vNn8z+hO5//Bd4AJANvIq/s4uI43E/riOAvcCwGK/T03gfLh39ZZcD340VZ5SNvApvJ5Pqv/GbgOf9+kb4HWZA7fUCrgPeADoAQWA0kBOjnWuou7N9E+gMHOK3+TV/3pPAPRFlfwi86z8+A2/DPArvg+T/AVNr1Vud0D3sv+a9/PhO9JeJ9j6vxNswM/3nf/TnDcfbUE4G0vA+uCqJndCdDozE2/APx/uAu9CfdwjeBnmZ/1rnAaMi+vF2vI0n4L/2K4Bf+u2e4S871C9fjJ+cAF3Y/wEYcxuIEqsDPgBy2f8BfIUfVwreB3gJ+3dw4/y+cI7/ev4BmOHPS8Pbkd3it3uJ/zrd3YD37b9ADl6f2wtMxNs+OuHtxK6OsR4vAHf4r1sGcHLEvETW56v+/Kfxkpo72L8trIqoazKx9wf9qNmnXgP+7pfLx0sCr4sR/2/xPszz8b68TAd+F63eKMtWz3/Bb2sk3rZUvR8aDRzvr18/vKTp5nr6wL5tqNY+4rf+63IOsAvo4s9/wH/vcvH67RvAH2ot+yf/fc+Msg7f9F/XY/ASrkF4IyCpxN8GJlN/QhdrH1OjbIxtMIOany9H4SW0x+H1/6vx9vnpwFC8LwA9I96XWMnIf4Cf1poWxEtgXsX7fOtYT3txX5s4+6bIhG4KXlKRAYzyX58z69vWIz7rPsVLCnPx+tUP4u2DEng/n8JLOI7F66/PAS/W0+9TIqZdg9fXfuwvn4nXl872X7NueF9YHmjKesToe/E+g6PF9RTe/nC0//pPwtv3XOW/3ncDH9baRnri9ctv4X3h6FFPX27IvjfqduLPz/XLRP1s31cu3syIFztaQjcDf8SqVuC/9V/UQfXVFdEhBsTqJER8sPvPh+ONvAVpekI3EbghYt5QvA/A6h2vA3pHzP8U+HaU9QriffgNj5h2HTA52kYcYyPfjT96gNchHXBcRJnZ7E9K9q0XXlJa41tjnHZqdDq/jcgP3n8Dt/uPzwK+jJj3MXCV//gfwL0R87L9161fRL2D8Dr+buCI+nYG/vtyZ8T8G9ifQP4KeCFiXge/D0RN6KK09QBwv//4F8D4GOWeAp6OeH4KXvIRiJj2Av6IH95O/zpqbWTE2QaitOmAM+ops7X6NfTf+wm1tofd/uNT8UaIIr/ZTWf/tpnI+3ZSrT7384jn9xGxI64V49PAY0RsLw1Ynw8i5p2Hl7zX3hY6R/STWPuDfX0K7zDpXiKSF7wk/sMYMa0Ezol4/lWgMFpfjdOXD42Ydi/wjxjlb47sg9H6ANETut3U/PDciJcoGt6Hy8CIeSewf8T3dP81yojznrwH3BRlen3bwGTqT+hi7WNqlI22DUZMq+7Df8NPtCPmLwNOw9vnbMTbd6XW0wc/wE8aak0f4cd8QQLtxX1tYrR7Ov5nAdAHb1SnY8T8P+AfxSHOtu4/LwSuqNXnqkcVo+6DEng/nyJi5BIvmVxaT7+vndCtqee1vxCY25T1qN33qP8zuE5c/ro+HvH8x8CSiOcj8UfbYqzHvIh+cg3xE7pE9r1RtxP/eapf5pB4r21TrnLthZfJ1/ZnvG8A75vZl2Z2ewJ1FTVg/mq8leuaUJTx9fTri6y7+sOgWuRVqbvw3ojaurJ/dCSyrl4NiGWzcy7kP97t/98QMX93jLafwdsZv2hm683sXjNLNbNT/Cvyysws3nkGsdZvEpBpZseZWV+8b4/j/Xk1XjfnXBnecHrt9e2K981nZZz2E4mlJxF9wHnntGyOVYkf84dmtsnMtuMNZVf3lz71xBPZ13oCRa7mxT+R7+s38HZ4q81sipmd4E9v6DZQo/+b2a1mtsTMtpvZNrzRscj+Xvt1yvDPCekJrHP+HiAi3sj1qe99q93nEumD4J0uYMCnZrbIzP6nAetTu43SKNtCZLuJ7A/6+tOLzWyb3+7f8Ubgoom2L+gZo2wstePqCWBmQ8zsTTMrMbMdwO+jxFvfPhC8fUTkyefV20g3vC85syPW9V1/erVNzrk9ceqOtV3Utw0kIpF9aKR4r0Vf4Nbq9fTXtQ/eqNwKvGR5HLDRzF40s1jv4Va8Lws1OOeq95XV/2O2Rz2vjb8dVO+DT4kSQ09gi3NuZ7TlfbG29Vjzq1/bWPugRN7Phr5ftdXen+X778U6v/8/S93+39D1qC2Rz+Bo/Srh/Z2ZXWVm8yL6wWFR1iOWRPa98V736r66LV4jjUro/BNKe+GdD1WDc26nc+5W59wAvG/bPzGzM6tnx6gy1vRqfSIeH4KX2ZbifSvtEBFXkJo7sfrqXY+3wUbWXUXNNzURpX5Mteta18B6Gsw5V+mc+41zbjje4cyxeCNp05xz2f7fiEbUG8b7lnAZcDnwZsSOp8brZmZZeIfUaq9vKd4hg4ENbb+WYmDfVWFmlum3F8vzeIef+jjnOuEN2Zs/r6ieeCL7zHqgj5lFbif73lfn3GfOuQvwkoTX8F6v+raBuG36O/6fA5fiHU7rjHcIymIsG6kY6GVmkWUPqbU+ibxvDeacK3HOfd851xPvm/EjZjaoiesTS6z9QaQivG/sXZ1znf2/nDjbQrR9wfomxlW9/N/wzscZ7JzLwTvcVXv969tXxVOK9+EzImJdOznnIj8Q6qs/1nYRdxug1j4Y7xykRDXm86AI71SQzhF/HZxzLwA455533pWGff16/hSjns/xTu+oT7z26ts/jIjYB0+LUvd6INfMOkZbvini7IPqez8b1EyC0//gTzvc7/9XkOD234B9aSKfwY3exvxBjcfxrorO8/djC9m/Hg3KNRqx7x2Gd8RgR7xCDUrozCzHzMbinWj9rHNuQZQyY/0dueGdBB3y/8BLlOLenyyGK8xsuJl1wBuCfdn/Br8c7xvLuf6tBe7EOz5dbQPQr1bnjfQCcIuZ9TezbLxvzi+5Bl6C7cfyb+AeM+vov/k/wfsm0qLMbIyZjfST2R14nTpUz2KJeh7vXIHv+I8jp19rZqPMLB3vdZvpnCuMXNhPCp8E/mJmPc0saGYn+Ms0xMvAeWZ2opmlAb8h/g6hI9433z1mdixeQlrtOeAsM7vUzFLMLM/MRsWoZybeB9bP/FHP0/F2Ki+aWZp59/Xr5JyrZH9fr28bqE9HvC8Vm4AUM/sV3jltifjEX/ZGf90uxjsXplpC71tjmNk3zaw66d6Kt4MLNXF9Yom1P9jHOVeMd2HNff5+K2BmA83stBh1vgDcaWbdzKwr3mH+hm6/d5lZB/OulLwW7+Ru8F6DHUCZmR0KXJ9AXQnvK/3t7HHgfjPLBzCzXmb21QbE/gRwm5mNNs8gfz8Wcxvwl5sHXOyv9yC8C9wStQHo7W/TiXoc+IF5o/BmZln+/r+jefclO8Pv23vwktxY293beIdNG90e9b82cTnnivBOifiDmWWY2eF4r99ziSwfT5x9UJNirmUT3sV+9fXTjvgXC5hZL7yLTxKS6L70AHwGZ+Ht0zb5cV2LN0JXrb6+3NR972l4F2/ElWhC94aZ7cT7tnIH8Be8HVY0g4EJeG/gJ8AjzrnJ/rw/4O00t5nZbQm2Dd5hxafwT6YGbgRwzm3HO9fqCbxMtxzvaq5q//H/bzazOVHqfdKveyreyZB78I6jN8aP/fa/xBu5fN6vv6UV4CU8O/BOJp1CM3Vi51z1xt+TiM7knJuId6XpK3ijQgOBb8eo5ja8Kxc/wztE/yca+EXCPwzyY7ydTjHeSbwb8UZgorkB+K3fZ3+FP3Lm17UG7zDprX488/AueInWbgVwPvB1vG+Aj+CNfi71i1wJFJp3GOEHeN88If42UJ/38F7r5XhD9HtI7HBcdbwX453PsRUvGX81Yn5D3reGOgaYaWZleKOjNznnVtGE9Ykj6v4giqvwDsMsxns9XgZ6xCh7NzALb+RmAd6Vwg29IfMUvMNDE4H/c85V38T7NrwvFTvxEoSXoi9ewzjgX/6+8tIEyv/cb3uG3x8n4J0TnBDn3H+Ae/D2WzvxRpxzE9gG7sc7P28D8C8aloxMwju0WWJmtUdYY8U5C+9CmYfw3tMVeP0dvC/zf/TjLMEbOf9ljHrmANvN7LjGtpfAaxOz2ojHl+Gdi7Ye75SWXzvnPqhn+URE3Qc1IeY6/FNf7gE+9vvp8TGK/gbvYoDteFfPvhqjXMLrEaNsi30GO+cW451D/AleXx+Jd155tbh9uRn2vZfhnTISV703FhY52PijqdvwDmGtau145MCxJtxovKVYK99gVRrHzL6Cd1HchQewzfOB3zrnYh0VEKnBzM4DrnTO1fvFTr/lKm2CmZ3nH9bJwrttyQK8q6NERBrMOff+AU7mUvAupJp1oNqUts8590YiyRwooZO24wL23/R1MN7tYzS8LCIHPTPrhHeKxyF4hyBFmp0OuYqIiIi0cRqhExEREWnjlNCJiIiItHEp9RcRAZp241MREWmaptyMW5KARuhERERE2jgldCIiIiJtnBI6ERERkTZOCZ2IiIhIG6eETkRERKSNU0InIiIi0sYpoRMRERFp45TQiYiIiLRxSuhERERE2jgldCIiIiJtnBI6ERERkTZOCZ2IiIhIG6eETkRERKSNU0InIiIi0sYpoRMRERFp45TQiYiIiLRxSuhERERE2jgldCIiIiJtnBI6ERERkTZOCZ2IiIhIG6eETkRERKSNU0InIiIi0sYpoRMRERFp45TQiYiIiLRxSuhERERE2jgldCIiIiJtnBI6ERERkTZOCZ2IiIhIG6eETpLaM888w/nnn8/ChYtaOxQREZFGM+dca8cgbUO76yhFRUUMHDiQyspK+ueMZsXWzwgErLXDEhGJRjsniUsjdJK0XnrpJSorKzkx8BNW7ZjNB08vbO2QREREGkUJnSStl19+mV7B0RwXvgWAFx5+t5UjEhERaRwldJKUysvLmTVrFoMDX6cTvcnnMKZ//l5rhyUiItIoSugkKX322WeEQiEOCZwAQF9OY3XFTLavDbdyZCIiIg2nhE6S0owZMwAo2HscAD05mgrK+Gj88tYMS0REpFGU0ElSmjt3Lrkp/elAHgA9GQ3ARx/Mbs2wREREGkUJnSSlBZ8vID80ct/zrgwjhQzmzJ7bilGJiIg0jhI6STp79+5l+RfLKUjdn9AFSaErw1i9cXErRiYiItI4Sugk6SxbtoxQKER3O6zG9G4MZ0PVYvZsa6XAREREGkkJnSSdBQsWAJC3d2SN6d0YzjZWUzirrDXCEhERaTQldJJ0Fi5cSNBSyWNIjendGA7Apx8uaY2wREREGk0JnSSdRYsW0TUwhCCpNaZXJ3TzZug8OhERaVuU0EnSWbxoMd3CI+pM78IAgqSxZIkSOhERaVuU0ElS2b17N6sKV9E9dXideUFSyGMohaWLWiEyERGRxlNCJ0ll+fLlhMNhugWGRZ3fjeGUVC6iorz523bO8fHHHzNt2jScc83fgIiIJC0ldJJUFi/2Dqfm7q07QgfVV7oWUjSv+TO6u+66i5NPPplTTz2Vn3x/XLPXLyIiyUsJnSSVxYsXE7AguW5w1Pn5eOfWfTqpea90nTp1Kvfccw9HpVzD4VzJA//4Le//+7NmbUNERJKXEjpJKkuWLCEvOJAU0qPO7+YndHNnNu95dHfeeSedU3vy9apHOJeHyaIbP71+XLO2ISIiyUsJnSSVxYsX0zUU/XArQC6DCJLGooXNl9DNnTuXadOmcZL9jFQySacjo7mOBVveZf6ktc3WjoiIJC8ldJI0Kioq+OKLL8hPiZ3QVV/puqqk+RK6J598ktRAOodVXLVv2iiuwRHmL3c83WztiIhI8lJCJ0ljxYoVVFVV0T0Y/QrXavmMoHjvIqr2Nr3NPXv28Nyzz3EoF5NJl33TcxlIX07lnU+fJlSlK15FRKRplNBJ0qi+wrVLRewROvDOo9vGalbPafpvur722mts3baVo1P/p868w/g2m8LLmPDMwia3IyIiyU0JnSSN+fPnE7AgXcP1j9ABzPig6b8Y8eSTT5Kb2pc+e8+oM28YF2ME+OfD/25yOyIiktyU0EnSmD17Nt2Dw0klM265fEYC8Nm0z5vUXlFRERMmTOCI8NUEomxq2XSnH6czcd6/CYd12FVERBpPCZ0kBeccs2fNpnvoqHrLdmEAGXRmzvym3Sfu2WefxTnHqMBVMcuM4FJKQ8uZ8uqCJrUlIiLJTQmdJIXi4mI2btpIn/TR9ZYNEKAnx7Bi86c09he6nHM89dRT9E89hU6VA2OWqz7s+uSDOuwqIiKNp4ROksLs2bMBKAjXP0IH0Itj2BBeQPHSXY1qb+bMmSxfvpwjA9fELZdFN/oxhvdm/Fu/7yoiIo2mhE6SwsyZM70LIiqOSKh8L44lTIhJ/5nXqPYef/xx0oKZDNl7Sb1lR3Apmyq/YPoHTTtnT0REkpcSOkkKU6ZMoVdwNOlkJ1S+F8cCMOntjxvc1saNG3nuuecYxdVkkFNv+WFcRIAgj/9Zh11FRKRxlNBJu7d7924+/fRT+rrTEl6mIz3oxnCmz5/Q4PYefvhh9u7dywkpNydU3jvsegZvT9VhVxERaRwldNLuTZo0iYqKCgalntmg5QbyFVbumcqmVbsTXmbDhg385S9/YUTKN+iyd2jCy43gUjZVrGDKfxt3iFdERJKbEjpp98aPH09mSg6994xp0HKDOZcq9vDPe99KeJlf/vKX7N61h7ODf2hQW4dyIQGCPPr7lxq0nIiICCihk3Zu165dvPrqqwwOjyWFtAYt258xZFPACy89k1D5V199lSeffJITA7fSee/gBrWVRVeGcB6vf/ooG9dvbdCyIiIiSujaGDPrZ2YLa00bZ2a3mdlTZnaJPy3XzOaa2bX+MrvNbJ6ZLTazp80stXXW4MB67rnn2Lp1K8emX9fgZQMEGcW1zN/6BjMnLI1bdurUqVxxxRX0ST+a06p+26hYT2cce9jOrVfc26jlRUQkeSmha4fMrBPwHvCYc+6f/uSVzrlRwEigN3Bpa8V3oOzcuZNx48bRJ+0Yeu0+pVF1HM/NpJDJdVfdSDgcrjO/srKSv/zlL5x99tl0CvflcvdWg0cCqxVwBIdzJc9/+Gfee21ao+oQEZHkpISu/ckG3gGed879rfZM51wI+BTodaADO5B27tzJpZdeSklxCecEHsSwRtWTTT5f4T7mF3/Auad9m/nz51NSUsJHH33EuHHjGDx4MLfeeisD3Ve4NvwRmRX5TYr7HB6iM/25+JLzefP1d5pUl4iIJI+U1g5Amt1fgCecc/dHm2lmGcBxwE0NqfSHI14GvFtqVN9aw+H2T6sxr+a0yOXqTMNF3KojSr2ubl37HkfMq54WCldQvHspsze9SnnVVsba3+mx5/iGrGodR3Mde9nO+x/dxbuj/rNvumH0tzP5jj3MoMpzGp00Rsoghyv5gOdDYznvwnPo2+FoDs09jdz0PnRI6UTAUghYkKClYPo+JpI0Hlr0jdYOQQ5ypvtetS1m1hd4yzl3WMS0ccBOvMOp2f7/U5xzG/35/YAlwDJgMPCyc+7qBrbbZjpKBp3pxxhO4mf0saYlc5F2uHUUMoW9bCeH3vTiOLLJpxnyuDoq3W5m8zgLeYFi5hCiovkbEZE2Yxzu4V87ftTaccjBSyN0bc9moEutabnAKv/xi8BHwNtmNsY5t9OfvtI5N8rMegCTzex859x/E2103OGfs2ebRYxCef/NokzDaj1uXHmzGHVEKW9mBFOMtA4BuvXoQsEoI7tHomuXqF7A5c1daQyZnMeN4G6kdJlj9aLNbCvdScXeEFVVVYRdlW5CLJJM1qDfBpS4NELXBpnZLODnzrmJZpYLzAC+DtwFvOmce9nM/gSMBs4BevrTD/OXvwj4mXPuhAY0q44iItJ6WuBYgLQnOgmnbboKuNPM5gGTgN8451ZGFnDO/RwoAp6h7vv8GtDBzBp36aeIiIgcVDRCJ4lSRxERaT0aoZO4NEInIiIi0sYpoZOkMWvWLB577DHKy8tbOxQREZFmpUOukqg23VFmzZrFiSeeSGVlJcePHssns95o7ZBERBpCh1wlLo3QSVIYN24cacHOjOhxKzNmv8kzT0xu7ZBERESajUboJFFttqOsWLGCwYMHc9Qh4zi02095ZX5fBh9yBgtWvtTaoYmIJEojdBKXbiws7d4rr7wCwIC8a0gJZNK3yyUsLXyadavL6NU3u1nb2r17N2+//TZr165l5MiRjBkzZt8NkkVERFqKDrlKuzd+/Hjyc46mQ8ohAPTLvZSq8C6eeOj9Zm1n+vTpDB06lEsuuYSbb76ZM888k0MHH8nnn+sG7yIi0rKU0Em7tnXrVj777DN6dT5n37Ru2SeSEsjm7bc+aLZ2PvzwQ8466yx2bk3ja4e9y6WjNnBS/39RVLSBo486njf/O6HZ2hIREalNCZ20a1OnTiUcDtMz58x904KBNApyxrBk1QdUVjT91MBVq1ZxySWX0CG1P1879GPyM79CRmo3Bna9krHD55CdPpCLLj6fqZM/a3JbIiIi0Sihk3Zt4sSJpAYz6Zx+XI3pPXLOYueelXz49pdNqt85x7XXXsvu8hBnDHqNNMuvMT8ztYCzhkwgPdiN8869mHVrS5rUnoiISDRK6KRdmzRpEvkdTyEYSKsxvWfO2QC88lLTDoX+85//ZMqUKYzucy+ZwUFRy2Sm5nP6oPGU7ynl62f+D7qyXEREmpsSOmm3NmzYwKJFi+jV5Yw683IyhpKZ2pNpH09qdP0bN27ktltvo6DTKfTv/N24ZfOyjuSo3n9kwfJ3uOdXTzW6TRERkWiU0Em7NWmSl6wVdKyb0JkZPXLO5MviSewuDzWq/ltuuYWdO8s5sf+jmNW/KR2a/yPys0/h7j/+hLVrNjWqTRERkWiU0Em7NXHiRDLSOpOTdmTU+T1yzmBvVSlvvbqgwXW/++67PP/884zseTvZqcMSWsYswPH9/kZF1U6uvfzXDW5TREQkFiV00m5NnDiR7tljCFgw6vwC/8rX115u2Hl05eXlXH/99eRmD2V4/i8atGznzOEMyf8BEz/+O5MnNDyRFBERiUYJnbRLX09eXloAACAASURBVH75JYWFhfTOrXu4tVpWWm9yMoYwfWbDzqP79a9/TWFhIScO+DvBQHqDYzui1zhSg5247ru3NXhZERGRaJTQSbs0ceJEAPKzz4xbrqDjGRRtmsrmjXsTqnfWrFncf//9HNrjf8lNP7VRsWWk5HF4z7tYvuZ9nnrsvUbVISIiEkkJnbRLH3zwAdmZPclOGRq3XO/O51AVLuepv0+st87Kykq+973vkZXRnaN6/alJ8Q3Nv4Hs9AHcfvvPqKqqalJdIiIiSuik3dmzZw/vvPMOvXLOxczilu2RczapwRz+/dLL9dZ75513Mn/+fI7v9wgp1qlJMQYDaRzV+/ds2Po5fxj3dJPqEhERUUIn7c77779PWVkZA/IvrrdsMJBOn87nM3/Z65TtrIhb57333suhPf6XHlkXNEucfbt8k65Zx3HvfXdRVlbeLHWKiEhyUkIn7c4rr7xCZnpnctPGJFS+X+632Fu1hQf+MD7q/JUrV/Kd73yHbp0O4+je9zdbnGbG6D73UrZnPbdc33z1iohI8jH9DJEkqE10lG3bttGzZ0/6dLyc4/s+ntAyYRfi9QWHkp2Vy9pNMwgE9n/P2bRpEyeddBLrijZz7ojpZAaGNHvMH35xMcU73mfOnHmMPGJws9cvIu1C/PNHJOlphE7alccee4zdu3czvNcNCS8TsCAje95B8ZbPGPfLx/ZNX7lyJaeeeiqFq4o4Y8jrLZLMARzb90EClsaFY6/WBRIiItIoGqFrB8wsBETepfZCoB9wm3NurJldAzwJjHLOfe4vsxAY65wrTLCZg76jlJaWMmTIELLtWMYMfKdByzoXZsLyr7Fh52R+cN2PyMwK8uijjxKuSuXMoa+Tm35KC0Xt+XLz83z05RV884IbeGn8Q/VezCEiSUc7BYkrpbUDkGax2zk3KnKCmfWrVWYtcAfwrQMU0wG1d+9errjiCnbuKGfMEX9u8PJmAU4b9DIzV1/HI4/+FTOjX95FHNfvftKsdwtEXNOAvMvZsmsu/3n9PoKXVvHUsw+Snt7wmxaLiEhyUkKXPN4ETjWzoc65Za0dTHNwzrFx40Y++ugj/vSnP/HZZ59x8qDHyA4e1qj60oI5nDLgBU7o+w/MAgQDGc0ccXyje/8JI8iLL9/L5Knvc+tPf8gZZ5zBkCFDyMrK0qidiIjEpEOu7UCtQ66rnHMXmdnp1DzkejTwKXCmc+7qhh5y7ZjZwzn/qKvXZ/zHONjXhxzVZXARj3G4FigTqUNaL47pcz99cy9JZHUOauu3T2DeursoLZ+5b1rAUkhNycYsgGGYBQDzkzzDdDRGpF27eOS6gn99ahtaOw45eGmErn2oc8g1hueBO8ysf0Mb6NFxLDUTB6P6lI7qpKJ6emSZ/aNKEeUjHmMx6sTAopSvVWd6MJcuHY4gv+PJpKSk0B4GsfrknUWfvLPYXl7I5vJZ7Ny7korQdipDO/ES2erENuwnu/pSJpIEZgF9WjsIOXgpoUsizrkqM7sP+HlDl12+MbFbgEhz6u//iYgomZP4dNuS5PMUcBbQrZXjEBERkWaihC7JOOcqgAeB/NaOpTXMmTOH3/3ud6xdu7a1QxEREWk2uihCEtXmO0pJSQmDBw+mrKyMgt4jWPPlPFJTddaBiLQJ7eAMYWlJGqGTpHHvvfeya9du+h//G0rWLuLXf/p3a4ckIiLSLDRCJ4lq0x2lqqqKgoICgl3GMPjMZ5j9wgg65fWj5MuJrR2aiEgiNEIncWmETpLC1KlT2bx5Mz2GfhOzAF0HfoONhVP4fOnmOmV37drFnDlz0JcdERFpK5TQSVJ49913Caak0aHgKwDk9Tsf50I89q+6v/n67W9/m9GjR/Ozex440GGKiIg0ihI6SQpTp04lu9vRBFM7AJDd7SiCaTlM+nBqjXIrV67kjTfeAOCvf/0rFVXhAx6riIhIQymhk3avvLyc2bNn06XXyfumWSCFnIITWb1sCpVV+w+tTp48GYDsM39IZelqXv6k4T97u2bNGt566y3mz5+vw7YiInJAKKGTdm/GjBlUVVXRqcdJNaZ36nkqu7YtZ9qs4n3Tpk+fTkp2LhnHXgbAa5M+TbidsrIyrrzySvr27cvYsWMZNWoUIw4/lkWLFjXPioiIiMSghE7avWnTpmEWILPrCTWmd+pxKgCvvj5537SPp08npf8xpPQcDqmZfPrZZwm1sWPHDsaMGcNzzz9P39E/ZdRFkxl06kOsWLmaUUcdy9vvfNhs6yMiIlKbEjpp96ZNm0bHboeTkt6pxvTsbkcSSMli6tSPANi7dy9fLF9Oh0OOwIKppPYeyYblc+s9bBoOh7n88suZM2cuh5/zH/occzfZ3U+gYPj3OfKSz0jL6ssFF5zH9BnzWmwdRUQkuSmhk3atoqKC6Z98QqceJ9eZZ4EUcrofx6rlH+GcY+XKlYTDYVILhgCQ0uNQKkq+oHR3/ITuX//6F2+99RaDTv4zHXuPrTEvLasHh419h0BaJ75+7jfYVLql+VZORETEp4RO2rU5c+awZ/ducnvVTegAcnqeQlnpQhYu28qyZd4FEKGugwFIyR9IeOcm5q/ZFrP+7du38/Of307nHsfTbdgNUcukZfXg0LOfZ+e2Ir52wXVNXCMREZG6lNBJuzZ1qndbkvSuJ0adn1NwEuB4+Y1p+xK6YP4gAFL8/9M/Xx6z/t/+9reUlm5i0Cn3Yxb7Ru45BSdwyNG/Ys70l/nzgy82ZlVERERiUkIn7dq0adPomDuYtA7do87v2P1YLJDKhInTWL58OamdCwhk5gD7E7v5i6MndEuXLuXBBx+kx7Brycg9qt5Yeo/6CdndjubO23/E6qKSRq6RiIhIXUropN0Kh8N8/PHHZHWPfrgVIJiSSXa30SxZ8DFr1qwhkHvIvnkpXfsDsPyLFXWWc85x0003EUjJovcxv0koHgukMGTME1Tu3cl5l9yge9SJiEizUUIn7daiRYvYunUrXfucFLdcpx4ns61kFiu+LCSY22ffdEvLJJCTz8b1RXWWeeONN3j//ffpd8ydpGXmJxxTh9xhHHLMr1jw6XgeeOTfia+MiIhIHEropN2aNm0aAJnd4id0OT1OwoWrWFtURHpe7xrzgl36sHNjzYRuz5493HLLLXTMO5Suh17f4Lh6H3EL2d1G84uf/Zjiko0NXl5ERKQ2JXTSbn344Yd0yOlFWnb/uOVyCk4EjFBVBSl5fWrMC+b2pnJLETsr9h8evf/++/nyyy8ZdMp9BIKpDY7LAikMHvM4FXu2cdG3b2rw8iIiIrUpoZN2qaKigvfee49Ovb8a9+pTgJT0zmTlHeE96VR7hK43oS1rWbsjBEBRURH33HMP+QPPJ6vgrEbHl5U7gj6jf8nMKS/y+FOvNboeERERUEIn7dS0adPYuXMn3Qeek1D5rLyRALjOtUfo+uAqdrGkqBSAm266iYrKMANPurfJMfYe9VOy8g7nph9fz6bSzU2uT0REkpcSOmmX3njjDYIp6WTmn5FQ+fRsb2QumFtzhC7QxXu+4Is1vP7664wfP55Djr6TYIf4h3ETEQimMnjM4+zZVcqF39KhVxERaTwldNLuVFZW8uKLL5J7yFcIpmYltEyoqhxLy8Q6dKkxvfqq1/mLl/Dd736Xzt2PoGDEjc0Wa3bXUfQ+8namT3qOu//0WLPVKyIiyUUJnbQ7//3vf9mwYQO9RlyT8DJ7y4oIdulT53y76oRu6sczKCvfy7CvPIcF05ozXA4Z/Us69z6TX9/xYz6cMrNZ6xYRkeSghK4NMrMCM3vRzFaa2WIze9vMbjKzeRF/C83MmdkwMzvdzLbXmt/4M/oPYuFwmHvuuYeOuQPI6vG1hJfbW1ZEMOKmwtUC2V0hNYNdO7cz5Ix/EMwa3JzhAmCBIEPPeoa0Dj0459yxzJ4zv9nbEBGR9k0JXRtj3hDSeGCyc26gc2448EtgjnNuVPUf8F/gOefcEn/RaZHznXMTWmkVWtTDDz/M3LlzOWT0nVggJeHlvBG63nWmmxnBLr0Jl29jy7qZlG9Z1Jzh7pOakceIsW/jSOfkU87gjTffaZF2RESkfVJC1/aMASqdc49WT3DOzXPOTat+bmanApcCN7RCfK0iFArx2GOPccstt9BtwNfpPODyhJcNV+2hctcGgl36RJ0fzO1D5erZrJv/Fz7/+DLCLtxcYdeQ2WkQh53/PsHMHpx/3jlcfMkVzJ07Vz8RJiIi9Up8CEMOFocBs2PNNLPOwD+Bq5xzOyJmnWJm8yKef8M5tzLRRk8453eAl1h4CUbEYz/hcOx/DC4iEYnxuHY91SXqTN9f3kU+9pfZXbaRktUzKdtWROfeYxh4+jP13nsu0t7ytQBRR+gAAp17EV4+FYDQumWUBpaQ70YkXH9DZHYaxOEXfUzRrLt5/fW/Mf6V5+jQsSe5PYaT0+UQUtOzSUnNJJiSHrGO+9c12jQa8FqIyMHpk7fubO0Q5CCnhK79+RvwrHPu41rTpznnxja20hnv/KoRS1lEMmG1kg3/sRkW8Xh/IlKrfJRlzS/v3Rj4KHofcy95Ay4kGGzYwHNFuffTXoG86CN0gawuEA6RcsF3qXr9H2ze8REFnVomoQMIpGUy4MR76H3kTyhd9Qbb101m29Yv2LB2IeHKckJV5dBCo4QicnA65fqfTZn2t7TTWjsOOXgpoWt7FgGXRJthZlcD/YArm7vRJ14vZ0d5xAhQrUSsenpDRsaaKmCQmgLZmUZBHmRlNq7tN8evY8F/IZgXfYSOUKXX3unnwXvPYxWLuPeHB2LT6Q58D/geoRCUbndsL4Pde8JUVoUJhSBMxOFYF2W0Ex2uFWkPxk/l9taOQQ5uSujanknA783s+865xwHM7BigA3APcKpzrqq5G/3u+R2au8qDxnsvrwUzgp16Rp3vdu/wktYhh2OHDGHbl0s4dpgd0OS1pmArtSsireUnl/FJa8cgBzcldG2Mc86Z2UXAA2Z2O7AHKAQygCzg1VqJxo/9/7XPobvbOffyAQj5oLdmzRpSO3XHUtOjzg/v3AT5vbHMLKzfUEKzp1Ba6eiWpnPTRETk4KCErg1yzq3Hu4q1ITq1RCztwerVqwl0jnG4FQjt3IT1HgBAoN9Qqt7/N7OLS/la3/wDFaKIiEhcum2JJL3CwtUE8ureVLhaaMsaLL8XAFbglZv9xaoDEpuIiEgilNBJUguHw6xes5r0rtETuvDuHbjyLVi+N4Jn3b3/C78sPFAhioiI1EsJnSS1kpISKisqSOvaN+r80ObVAAR6evOrE7plq1YfmABFREQSoIROklphYSEAgdzo96CrTuisl3cOHV26QVoGxWvXHIjwREREEqKETpLa6tVewhbqHGOEblsxANbdP4fODMvvxfZ1RQcmQBERkQQooZOkVt8IXXh7MQSC0LnrvmnWvRd7S9YS1m+siojIQUIJnSS1wsJCUjvmEUjPijo/tL0YcvOxYMTNfPMKcFs2UlqphE5ERA4OSugkqRUWFhLMi364FSC8vQTL615jmuXm47ZsZP2eZv9BDhERkUZRQidJbcXKlVhu7IQutL0YyyuoMc3yukNlBctKSls6PBERkYQooZOktXfvXgpXrSKz55CYZWImdMCytetbND4REZFEKaGTpLVixQrC4TBpBdETOle5F1e2JcohV+/5KiV0IiJykFBCJ0lr6dKl3oNug6POD+0o8R7UGqHDT/C+XFfcUqGJiIg0iBI6SVrLli0DwMVI6MLV96Crfcg1Nx+A9SVK6ERE5OCghE6S1tKlS0nP7UUgIzvq/NB2b4TOutU65JqZBR2y2VpS0uIxioiIJEIJnSStZcuWYfnRR+fAv6kw1DmHDrzz6Mo3KaETEZGDgxI6SUpVVVUsWLiQtJ7DY5YJbS+BYArk5NadmdeditINuBb+tYhJkyZx5JFH0qffAO574MEWb09ERNomJXSSlJYuXcruXbvo0P+omGXCO0qwLvlYoO5mYrn5sGUDW6paLsH66KOP+PrXv87SkjJK03pw2y03cdOv/9xi7YmISNulhE6S0qxZswBwvY+MWSa8YyPk5UedZ3ndCW/ZwMaKcIvEV1ZWxuWXX04wtw+5t02i803vkHHkhfy/39/BBzPmtUibIiLSdimhk6Q0Y8YMUjrkYN0GxSwTivKzX9Ustzvs3sWqzdtbJL7f//73FBUV0eXqR3EdumCBAJ0ue4BAhy5ceuV3qarSz46JiMh+SugkKU2YMIG0QSdFPZxaLeQfco2mJX8tYuXKldx3331kH38Zru/x+6YHsvPIueSPbFsxh1vvfazZ2xURkbZLCZ0kncLCQlauXEnW8DExy7hQJW5nKeRGH6GrPhT7ZQskdDfffDMumEbOhb+pMy/j6G+SNvgUHv79nRRv2NTsbYuISNukhE6SziuvvAJAcNhZMcuEd3rJksVI6KqnF65b16yxvf7667z55pt0POd2XE6Puu2akfOt+wjt3sk3r7+9WdsWEZG2SwmdJBXnHE8//TQdBhyNxfiFCIi4qXBut6jzrav36xFF65vv1yJ27NjBjTfeSFaf4aSffkPMcqk9h5F1xg18PP5J3v5werO1LyIibZcSunbCzMr8/wEze9DMFprZAjP7zMz6+/MKzaxr60baut566y0+//xzsk66Om65cHVC1zXGIdesHEjLoGRd8xxyDYfDXHPNNaxdt47Olz8IwdS45bPPuZ1g55586ztXUVpa2iwxiIhI26WErv35FtATONw5NxK4CNjWuiEdHDZu3MiPfvQjMgsGEjz2O3HLhndsAKL/SgR4hz4tL5/StaubfMXprl27uOqqqxg/fjydL76HcN/j6l0mkNGRzt/9F+Wb1nLEyV9h7dq1TYpBRETatpTWDkCaXQ+g2DkXBnDONcsnfVlZ2b5fKWhr/7ds2cL06dO57777KN6wifzb3sXVMwIW8hM6ukQ/5ApAXgHh7VsYdcLp3PGTHzJy5Ejy8vJITU0lJSWFQCBAKBSq81dVVUVFRQWrVq3i008/5YknnvBuUXLhr0mLc6i1trSBx9P5+89S/M//YcCQYXzvu9fy9a+cTf/+/enSpQupqamkpaURDAYxs4TrPdAO5thEDhZZWVmtHYIc5Ew/JdQ+mFmZcy7bzHoDH+GNyk0EnnXOzfXLFAJHO+cafIzOzNp8R0ntdzQ5l/4faf1G11t2+ws3s2v+eDJeWxKzTMW47+EKl2JluwhvafzFEWmDTiL7vDtJH3xyo5av2riSnW/ezZ55/4WqikbHISIHrx6P7Dxt/fXZU1s7Djl4aYSunXHOrTWzocAZ/t9EM/umc25iU+rteNHvAIPq0ZR9oyrmP635vPb8WMvFer5/0Kbp9QXSs0jpOYKUbgPITjMSGQ/asbPE+3mvOCwvn/DsKRzy4GrKln9OaNMqwru2QbgKF6oEF8YCQbAgBLw/CwQgkAKBFFLy+hDsPoT0nG5kpJBQXFH1GkiX6/7Jnl1llK9dTGhzEW7PdlyoCldVAeFQY2s+ANr89wSRA+VXQOxL8yXpKaFrh5xze4F3gHfMbANwId5oXaPtePXO5gitzTj+iVJmxbogwmd5BVC+g2fOMU75n1OBUw9McDFlAwWtHIOItBAlcxKXLopoZ8zsKDPr6T8OAIcDq1s3qrZnXXFxzHvQVau+YGLxmua9F52IiEhDKaFrf/KBN8xsIfA5UAU8FDH/czNb6//9pVUiPMg559hQUkJqXvxDrtW/IrGimW5dIiIi0lg65NpOOOey/f/vAu/GKNPvQMbUVm3ZsoXKigrS87oT74Yk1feo+7JICZ2IiLQujdCJ1LJ+vZegxboHXbV9P/+1XgmdiIi0LiV0IrUUFRUBUNmtV/yCOV0gNY2Nxc33818iIiKNoYROpJbVq71rSFx+77jlvF+L6M62Yl0UISIirUsJnUgta9aswVJSoZ770AFYQR92FxcdgKhERERiU0InUsuaNWtIye/p3QS4Pt37EN6wlu1V4ZYPTEREJAYldCK1rFmzBlff+XM+694HV1rMqh17WjgqERGR2JTQidSyes0ayE80oesNzjF3le7dLCIirUcJnUiEqqoq1q9bR2pB/AsiqllBHwA+X7mqJcMSERGJSwmdSITi4mJCoRApDRmhA5Z9qRE6ERFpPUroRCIUFhYC4BJN6Lr1hECAFas0QiciIq1HCZ1IhOXLlwNQ0WtAQuUtNQ3yCthYpBE6ERFpPUroRCIsX74cS03DuvdJeJlAr/6UrV6Jc64FIxMREYlNCZ1IhOXLl5PSqz8WDCa8jPUdQmj1F5TsDbVgZCIiIrEpoROJsGz5csK9EzvcWs36DILyHcxYpZ8AExGR1qGETsS3d+9evli+nLS+gxq0nPUdDMBHCxa3RFgiIiL1UkIn4lu0aBFVVVWkDBrZoOUC/Q4FYMa8z1siLBERkXopoRPxzZ07F4DKAYc1aDnL6w553Vk6d3ZLhCUiIlIvJXQivrlz5xLIzML16t/gZQNDR7Ft8TxCutJVRERagRI6Ed/UqVMJDjsKCzR8swgMHUW4aAUz1m1ugchERETiU0InAmzatIkFCxaQctTJjVo+MOokcI5/vf1+M0cmIiJSPyV0IsCECRMACB55UqOWt2FHQVZH3nn33eYMS0REJCFK6ESAF154gbT8HlQOHd2o5S0llcAxY1g36W227drTzNGJiIjEp4SuDTAzZ2bPRDxPMbNNZvam//waMwub2eERZRaaWT//cbaZ/c3MVprZXDObbWbfP9DrcbBas2YN77zzDoy5qFHnz1ULfv1y3PbN/Orpl5oxOhERkfopoWsbyoHDzCzTf342UPtnCdYCd8RY/glgKzDYOXck8DUgtyUCbSuqqqpYvnw54XCYX/ziFzgLkH7x95pUZ2D0aVjfIfz97nGUl5c3T6AiIiIJUELXdrwDnOs/vgx4odb8N4ERZjY0cqKZDQSOBe50zoUBnHObnHN/auF4D1rOOcaOHcvQoUM5/PTTef7550m9/MdUduvVpHotECDlx/dQsX41x5x7IcXFxc0UsYiISHwprR2AJOxF4Ff+YdbDgSeBUyLmh4F7gV8CV0dMHwHMr07mGqvX+ZcDsO8ua5H3W6t+HDHN7Xtct5yrZ9nqZeotVz0pShtRY/H/V2wtZcfC2aTk57Poo49Iv/hK3BW3YtTlqioJvfwYgcOPIzD86CglagoedSrulj+z5MFf0LNPH7IGDqdDj94E0tIJpKZBMBi1nYNZzDvrxbvnXqx5cZZxce/h14z1NSbu2K9CM7cTuykXJ4Zmfb0bG3eM+OK+r80Yg8NB2BEOVeGqqnChKu9xKIRZgEBKChYIYMEULBj0/gcCWEoKBIL+tCAWCO4vYwZ2cGyx615/rrVDkIOcEro2wjn3uX9O3GXA2zGKPQ/cYWYx74xrZncA3wTynXM9E21//cypUJ2K+Du4Gvu5fU+s7jSLMq1R5WrPa0B9EbG7kiIsK4u+zz3HyrPPJr1Hd6qCQaKpfPMZqh77LYGsDmS+ugiX2iFquUhpY68kcOTJhN59kd1fLGBX0WqoqoTKClwoVO/yrcNBvFQzxoda3M+6mDMb3k7cefGDaN124s1qTAyNee0O1OtTb1sNXKYx7QSCEEzBgmmQ1gGCQW9aOOz9haogHMJVhmDvbv/5/umE/L9wyNtWm/Y9uFllfrixePeY/B6tHYccvJTQtS3/Bf4POB3Iqz3TOVdlZvcBP4+YvBg4wswCzrmwc+4e4B4zK2tIw7O+WMX2qrb9KwgGhMMhLhjYg7SvfpX0AQPIHD2aqinvsuDeP3jfxmu5bNy7zATC5bv4wbZp/PC8yxNsLQ++4Y3o7Qo5tleFqfQGEOKNs4hIAgwvpwsAQYNUM9ICkBHw/luMRDXkHHvCsDfsqHDe85C/XcLBvW2eO39bw36TUJKOErq25Ulgu3NugZmdHqPMU8DPgI4AzrkVZjYLuNvM7nLOhcwsg7hf9esanZPa+KgPIkuWLKF8x3byTzgBgKyTTqL0oYfYvHMzx3TvXqNsKBRiwexZ9LvmYta88CYfT5/C/116ZWuELSJJbveYfP0MjcSliyLaEOfcWufcX+spUwE8CORHTP4e3ojeCjObDUyg5ihe0pg1axYANmIEAFnHHQfhMC9Onlyn7KJFi9hVXk73k0fTcfhAChcuPpChioiIJEwJXRvgnMuOMm2yc26s//gp59yPIuY96Jwz51yh/3yHc+4651x/59xo59zJzrmHDtgKHERmz55NIDOT9IEDAcgcNQqCQT785JM6ZauTv6zRI+h46AC2LVnJDld1QOMVERFJhBI6SSqfzZ5NxrBh3pVtQCAjg/TBg1k1b16dsl988QWB1FQ69O9F9tAB7Fm/kYVbSg50yCIiIvVSQidJIxQKMWfOHDqOHFljeuZhh1G2YAGlVTVH31asWEFW355YMEjHQwcAMHPxggMWr4iISKKU0EnSWLZsGXt27SL9sJoXi2UcdhhVW7YweeXKGtO/WLGCzAG9AcgadAgAC1csb3C7RUVFzJ07t577rImIiDSeEjpJGtXnxKVESegAJn766b5pzjlWrFhBzgAvkcvsUwDAl6tXN6jNv/71r/Tr14+jjjqK484+mz179jQ6fhERkViU0EnSqH1BRLWMYcMgGGTm7Nn7ppWWllJeVkZ2P+/nwFI6ZJLWtQslq4sSbu+9997j5ptvJufMM+l+2218NnEi5914Y/OsjIiISATdh06SxqzZs8kYPhyr9asQgYwM0gcNYvXnn++btnbtWgAyeu+/N13mIT3YWrQuobaqqqq46aabyBo4kB4PPIBlZFC5cSMT/vEPJtxwA2eNGtUMayQiIuLRCJ0khVAoxNy5c8mudUFEtYzhw9mxcCHlYe+nftavXw9ASo9u+8p06NOD8jXF7HH1/3zXP//5T5YtW0bBz36GZWQAJf/2DQAAIABJREFU0PXGG7H0dG66996mro6IiEgNSugkKSxdupTdu3aRFSuhGzGCqk2bmO6fI1ed0KVHJHSZfXqwe20Jm8IVcdtyzvHAAw+QPXIkaWeeuW96SpcudL74Ypa88goL1iU20iciIpIIJXSSFGb758cF/F+IqK36wogJ/oUT6/yEK6Og674ymb27E9q9hy+3bIzb1pQpU1i8eDFdr7yyzu/D5l59Na6igrv+8Y/GrYiIiEgUSugkKcyaNYtghw6kDRgQdX7GsGEAzPATv/Xr15PRLZdA6v7fsE33k7sV69bGbeuRRx4hrXNnMs49t8689IEDyTjiCD546SXCuo2JiIg0EyV0khRmz55NZpQLIqoFs7NJ69+fZfPnA94IXXrP/BplMgq8w69frot9pev69esZP348nb/5TQL+uXO1db7gAnYtXsyLEVfVioiINIUSOmn3qqqqmDtvHpm17j9XW8bw4WxZsIAq51i7fn2Nw62w//BrYcn6mHU8/vjjhEIhulx2WcwyOeeeC8EgDz79dAPWQkREJDYldNLuLVmyhN27dtX5ya/aMkaMoHLdOmaXlLB+/XqyetQcoUv3R+jWr4ue0FVWVvLYY4/R8dRTCfbtG7OdlK5dyT7lFOa8/DJ7QvVfMSsiIlIfJXTS7s2YMQOAwBFHxC1XfWHEm9OnU7pxI5m1DrmmZGWSkpNNacmGqMu//vrrrF+/nu5XXFFvTJ0uuIDK4mIeef/9RFZBREQkLiV00u598sknpOfmktqvX9xyGcOHAzBp2jTveUG3umUKurK9OHpC99BDD9GhTx9STjut3pg6nn02gawsHn/mmXrLioiI1EcJnbR7n3zyCemjRtW5hUhtKV26kNqnD0v8Eb20nnUTuvSCrpSXbCJU6wrVhQsXMmXKFDpffnnMCy8iBTIz6fjVr/L/2bvv+Kqr+4/jr3Nv9iBkQBYjJIyw91JwoCh1odaKe/Nz1lUXdRTbOutsHYiKSisOHK0DARfIDHtvEiJ7hDASyLzn90eGSci4WWTc9/NRzL1nfq5NzIfz/Z7z3fT11xzIzKzGpxERETmREjpp1g4ePMiGDRsI7tvXrfaBQ4ZwePVqALyjy1mhi25F1p79HLF5pcpff/11nL6+hFx2mduxhVx8Ma6MDJ6bOtXtPiIiIuVRQifN2ty5cwEI6N/frfYBQ4bgOnYMAL8ymyIA/CIjyN5zgIMlnhaxe/du3n//fUIuuggTFuZ2bIFDhuAVFcWHuuwqIiK1pIROmrWZM2fiFRCAs08ft9oHDhkCgPH2wic85IR63+hW5Gdl82v6geKyf/zjH+Tk5hJ1++3Vis04nbS85BJ2z5rFvE2bqtVXRESkJCV00mxZa5k+fToBgwfj8PV1q493VBSOoCB8W4djHCf+eBQfLryr4NFgu3fvZsKECbQcPRoqOaqkIqFXXw3G8Mirr1a7r4iISBEldNJsLV++nK1btxI2cmS1+jlDQvArZ0ME/Ha4cMqugsd/PfDAA+Tk5xN11101itE7OpoW557L/MmT+XX//hqNISIiooROmq0PP/wQh7c3fueeW72ODlPu/XPw2+HCv+7exbRp05gyZQqtbr21RqtzRSLuugvXsWPc9OSTNR5DREQ8mxI6aZaOHDnCO++8Q4tzzsHRsmW1+uYfOoRv6/By64of/5WayrXXXktw166E3nZbrWL169KFlpdeyk8TJ/LzkiW1GktERDyTEromxBgTboxZUfhnjzFmZ+HrQ8aYdWXajjfGPFD4+v3Ctr6F7yOMMdsa4COcNE899RRHjhwhauzYavVzZWbiOpqBX0z5K3ReQQF4BQeybfMWMl0u2v7rXxg/v1rH2/qRR3CGhXHJFVewb9++Wo8nIiKeRQldE2KtTbPW9rHW9gEmAC8Xvu4DuKrong/cVN8xNgZTp07lhRdeIPzyy3FU8fzWsnILkym/NlEVtvGNakXO4aPET54MHTrUKtYiXqGhxL7yCkd27KDXaaexcuXKOhlXREQ8g1dDByAnzSvAfcaYt2vSedmyZdjCpyNYa0u9dresPvu4XC5SU1OZPn0633zzDSH9+hH52GPV/px5ewse6+VXzqHCRfyiIsg5eAjTvVu1x69M4KBBtHv3XXbecw99+/XjtLPP5twzziA+Pp7w8HACAgJwOBw4HA6MMcVfq3oChog0fX3dPBxdPJcSOs/xKzAXuBb4urqd+7t5MG9D82rVioi77ybittvAzaNKSipK6PwrS+hiW3NwwQocBly2wmY1Ejh0KPEzZnBw0iQWTJvG7Jkz63YCEWmSum3deufa+PjXGzoOabyU0DUPFaUVZcufBr4Cvq3uBG0nTABjCv5A6ddFSq4WldeuRHtTWX2JslKrT5X0McbgFRlJYGQkwU4njhquWmUVHh3iX8E9dAV1kWTt2keE02JtPfwIRUQQ/dBD2Ice4kh6Ohl79pB76BA2KwusxbpcYG3BH1dVV9pFpJno2NABSOOmhK55SANCy5SFASklC6y1W4wxK4DLqzvBr7feWvPompD7jh/n9cKNDxXxi2mFzc3jMSecFVvz40rcUovjUESkWbmvoQOQxk2bIpoBa20GsNsYcxaAMSYMGEXBJdayngIeOInhNSk7d+7Ev4Iz6Ir4xUQCsHlH6skISUREpEpK6JqP64DHClfgfgKetNZuLdvIWrsWWHayg2sqdu3ahW8l988B+McWJHTJ27efjJBERESqpEuuTZS1dnyZ9+uAMytoe0OZ95fWW2BN3I6dO/EdUvnuVb/YghW8bTuU0ImISOOgFTqRQtZadu/aRWBU5ZdcfVuFYby82Lljx0mKTEREpHJK6EQKHTx4kJycHAKquORqHA78oiPYv2vPSYpMRESkckroRArt3LkToMLHfpXkFxPJ4Z276zskERERtyihEym0o/ASqld0RJVt/WNbk7lzL7lW58CJiEjDU0InUiglpeDYPr/2MVW29Ss8XPiAK6e+wxIREamSEjqRQikpKXj5+eIbWfUKnV9sa/KPZ5F8cO9JiExERKRySuhECqWkpBDYLsath90XnUW3dltKFS1FRETqnxI6kUIpKSn4xVV9uRUgIC4WgPVbt9RnSCIiIm5RQidSKDklhcD2sW61DUxoB8CGLZvrMyQRERG3KKETAdLT0zl86BDBbiZ03i2C8GkVxq9bTni6moiIyEmnhE6E33a4Bsa1cbtPYHxb9m/ZVk8RiYiIuE8JnQiQnJwMgHdctNt9AhPacTT5V7J1Fp2IiDQwJXQiwLp16zDGENCpvdt9Aju2JWv3frYcPViPkYmIiFRNCZ0IBQldUPtYvAL83e4TVLgxYtGm9fUVloiIiFuU0IkAa9euJTAxvlp9grp0AGDRmpX1EZKIiIjblNCJx8vNzWXjxo2EdE2oVr+gznE4fH1Yvnx5PUUmIiLiHiV04vFWrlxJbm4uYX0Sq9XP4e1Nix6dSF25pp4iExERcY8SOvF4CxcuBCBwYI9q923RqwtpK9dzKD+nrsMSERFxmxI68XgLFy4kMKoVfm2iqt03bGgfcg8d5dvlSfUQmYiIiHuU0IlHc7lc/Pjjj7Q8pS/GmGr3jzhtIABf/fxDXYcmIiLiNiV04tGWLVvGnj17iB11Wo36+8dGEtgpjrnTZtZxZCIiIu5TQice7ZNPPsHhdBI6cmiNx4i5dCS7flnEqp3b6i4wERGRalBC10QYY6KMMR8bY7YaY9YZY6YZYzobY7obY34yxmwyxmw2xjxuCq8dGmNuMMZYY8xZJca5pLDssob7NI1DZmYm7777LjEXjcAnIrTG47QZcx64XPzl9VfrMLrGLysriy1btrBjxw6stQ0djoiIR1NC1wQUJmhfArOstQnW2m7An4FI4CvgWWttZ6A3cApwR4nuq4ErS7y/AtBJuMDjjz9Oeno6ne+6tlbjBHVqT/TFZ/PNvyayevPGOoquccrIyODTTz9lzJgxhEdE0KlTJ9q2bUtoqwiuvfEGpk+fTl5eXkOHKSLicYz+Zt34GWNGAOOttaeVKb8ZON1ae12JsgQKEr+2xpgbgIHAcKA/4AvMpiDJ+8Za+1k1wmg23ygHDhzgxRdf5NlnnyX+5j/Q/ZVxtR7zWOou5gy/mqCQFvznzYmcM3IkTqezDqJtWLm5uaSkpDBr1iy+++47pk+fTlZWFn6twoi5cAThg3uTe+wY6QtXsmv6L+QeziC0VQRXXT6GSy65hL59+xIWFtbQH0OkOaj+ri3xKEromgBjzN1AB2vtfWXKXwJSrbWvlilPB9oDlwIDgBzgJyAE6Ah0oJoJXZuh/SxA8bdL4YtS3z9Fryupc6e/LTNOuf0or02ZsnL652YeI2P3PgDaXTuanq/+GYe3dwWfunrSl6xhyTUPkrVzL05fH1q0i8HLzw8vP18czrpdDLe24B/W2oI3JV4X17lcJ5Zhy+lXfntXXh6Ze/ZjXS6gYANI5AVnEHPx2YQN7YMpk7DmZ+ew//v57Pz0O/Z89wuurGwAfEKC8Q8PxSfAH+N04nA6ir9Sg53FIp6o38x3nF8F9XU1dBzSeHk1dABSK4aKV85Kln8M3E1BQvcnCi7XVku2n/dvv3wLvxb/Li75S7m4rriydLQl64zBlNPflGpDqbqy/cvOf0JMpeoMDh9votvF0LJPIlHnnV7ZR6620AE9GLHyf+z9dhaHlq7l+I495GflkJuVXSq5rDVrCz6XMQUfr/i1AUzB/4zBOBwFX01BWXGb8vo6HKXbYDBOB9GxkQS0jyF0UC+COsdVerSL09eHqAvOIOqCM8g9kkH64tUcWbWRrF37yEk7RN6xLMjPx+VyYfPzsfn63SRSDccAv4YOQhovJXRNw1qgvE0Ma4Gyl2HjgQxr7dGiX77W2kXGmB7AcWvtppqct7b/5+ZxcO7+/fvp168fm595i2dee4lH7ryv6k7VEQRcNxiuq7Jl8xYEjB4Ooxs6EJFmQ8mcVEqbIpqGnwBfY8zYogJjzEBgMzDMGHN2YZk/8E/g+XLGGEcNVuaam1dffZWdO3cS3q094//8OAczjzR0SCIiIrWmhK4JsAU3h10CjCw8tmQtMB7YRcEayGPGmI0UbHZYDLxWzhjfWWt/PnlRNz55eXm8/fbbxF8wlDNeu4fsI5m89N8PGjosERGRWtOmCHFXk/9GmTdvHsOGDWP0p0/S/tJTeS/+KmL7dGH9/35p6NBERKqiHURSKa3QiceYPn06DqeT6LP7YhwO2p87iORZy0jPPdbQoYmIiNSKEjrxGD/++CPRgxLxbRkEQNuz+pFzJJP/La6fK9GzZs3ijjvu4L333sPl0o5OERGpP0roxCPk5OSwbNkyood2Ly5rc0ZvAL6fN6vO55s6dSpnnnkmE956i5tuuolr7761zucQEREpooROPMLKlSvJzs4mZnC34rKA1qG0iItixaKldTrXgQMHuOWWW2hzSg/uOPw1fe75PVNef4fJ0z6v03lERESKKKETj7Bo0SIAwgd3KVUeNbgr2xetI8vW3fNH//73v5ORkcHZbz+AV6A/w577P1p2asODDz5IXn5+nc0jIiJSRAmdeISkpCSCosIJbtu6VHnkoESO/rqXpXu21Mk8aWlpTJgwgW7XjyKkazsAnD7eDH78WvatS2Hi9E/rZB4REZGSlNCJR1iYlETk4MQTHl0VNagrAD8umlsn80yZMoXs7Gz63n1pqfJOY84kKDaCl156qU7mERERKUkJnTR76enpbN60idhB3U6oa92vEw4vJ/OTFtZ6Hmst7777LlH9uxDWO75UndPbi563j2brT0uYt2VVrecSEREpSQmdNHtF98+1HpR4Qp2Xvy8RveLZuGhFredZtmwZK1eupOeNvyu3vut154AxvPTBhFrPJSIiUpISOmn2kpKSMMYQMbBzufWRg7qya/EGDudn1WqeSZMm4e3nS8JVI8qtD27TinYj+/PD5C/Iya+7TRgiIiJK6KTZS0pKIqJbHL4tAsutjxrclZwjmczesKzGcxw/fpwPP/yQjr8fXnxwcXm63TCKI7/u5YNZ/6vxXCIiImUpoZNmzVrLwoULiRxy4v1zRaKHFGyM+GnhnBrP8+WXX3L48GF63nhepe0SRp+KT0ggb78/qcZziYiIlKWETpq1zZs3c/DgQdoM6V5hm5ad2uDbMohFSUk1nufdd98ltEMMUWf0qrSdl78vXa4YwfLPf2TXoQM1nk9ERKQkJXTSrC1cWLB7tfWQEzdEFDEOB1GDu7IlaRXW2mrPkZyczE8//US3G0ZhHFX/SHW7cRR5x7N5+ZN3qz2XiIhIeZTQSbO2cOFC/FoE0bLwkN+KRA7qyoE1KaRk7K/2HBMnTsThdNLtplFutY8cmEh49zg+ef8/1Z5LRESkPEropFlbuHAhkYO6VLlyFnNKd6zLxdfzf6zW+NnZ2UyaNImEC4cSEBvhVh9jDN1uGMX2hWuYvXZJteYTEREpjxI6abbS0tJYuXIlsadWfl8bQMywHjh9vJn+/cxqzfHll1+yf/9+ev/fRdXq1+Was3F4OXnxvTer1U9ERKQ8Suik2frhhx9wuVzEnTugyrbegf5En9KdZT/Mdfs+OmstL7zwAmEJbYg5p1+1YguMDKPDRafw/XufkZ5xpFp9RUREylJCJ83WjBkzCAhtQXgFBwqX1fbs/uxbuYU1e1PcHn/p0qUMfORKtzZDlNXv/j+QdfAIf530arX7ioiIlKSETpoll8vF9OnTaXN2PxxOp1t94n43CID3vvq0yrb5+fmMGzeO0HZRdLr27BrFGHNKD6JP7cF7L71Bdk5OjcYQEREBJXTSTP3yyy/s3r2bzqOHud2nVZ+OhHZpy38/mlpl2wkTJrBixQqGPX8rTh/vGsc58JGrOJy6h7+8/VKNxxAREVFCJ83S+++/j29QAO0uPsXtPsYYEq89h5RZy/h59aIK261evZoHH3yQDmcPoMMfTqtVnHHnDabNmX345xPPsHv/3lqNJSIinksJXRNkjHnUGLPWGLPKGLPCGDPYGONljHnaGLO5sGyFMebREn3yC8vWGGOmGmMCGvIz1Kft27czZcoUul53Dt4BftXq2/PWC/AK8OORvz1Rbv22bdu48MIL8W4RwLmTx2GMqVWsxhhOf/WP5GQc56Ibr8DlctVqPBER8UxK6JoYY8xQ4AKgn7W2F3A2sB34OxAD9LTW9gGGAyWvBR631vax1vYAcoDbTm7kJ4e1lvvvvx9rYOCDY6rd3z88hAEPX8miqTN45f23So377bffMmTIEA4cSWf0N0/jGxVaJzFH9OjA8BduY8m3s7j+nttq9LQKERHxbF4NHYBUWzRwwFqbDWCtPVC42jYWiLPWZhWWHwXGVzDGHKDqw9mamPz8fB577DE+++wzhj81loD2kTUaZ8DDV7Bj9gruu/E2Znz5NR1i27FgwQJWrFhB624d+MMnzxLSvX2dxt7rzos5nLKH/7z8Nr9uTeGdV9+gU6dOdTqHiIg0X0arAU2LMSYImAsEAD8AnwDpwAfW2r6V9Muw1gYZY7yAz4Hp1lq3T7W94aNnLYXfK9ba31aRSr2m3HJrLRQXWyhVXvS6dN/y6iuc32VJS9nJuu/mkZaykx63nM+ICffV6CiRInnHs1n09/+wYcoP5B45Rli39nS56iy63fQ7vHx9ajxuZay1rHr9v8x9eCJ5WTm06Z9Ih0E9adkmEv+WwTh9vHB6e+H09qaWV3rrVqMKRqR5em/Mw/pBk0opoWuCjDFOCi6pngncCjwN3FiU0BljbgTuAcKBU6y1240x+cDqwiHmAH+y1rp9VoYxplF/o/gEBxA5uCu97xhN/OhTq7y3LSv9KL4tg2p9D1x9yNx7kLXvTCN15mIOrEom53BmQ4ckIg3sHtdPE14xZ97e0HFI46WErokzxlxGQVLXj4JLrkdL1K0BLrDWbitaoavpPI+u+9weN/m/JUDG/LYwY0xxuTGmeMXGGEq8dqe8aGzKzFN6TlOi3IHByzgJb9GSaBNIGP5VfpaJjz7Hv5/5F8P/MIqnPn67USZ1ABZLOlnszDzIwaOHOJ6TQ25uLnklzqxr6J9e/fdD5OSw3SJvecWc+W5DxyGNlxK6JsYY0wVwWWs3F77/O9ASOAZEArdaa7MKV/HWA+fURUJHw+cOdSIlJYWEhARCYkI5tPMgH3w7hevOu7KhwxIRqUrj/JunNBra5dr0BAEfGGPWGWNWAd0o2PzwKLAbWGOMWU7BZdUPgF0NFWhjNHHiRIwx3D37bwRGBPPG+xMaOiQREZFa0wqduKtZfKMkJibiaO/PbdMf5bM/vsuCd35kZ9puWgeGN3RoIiKV0QqdVEordOIxtm3bxsaNG+k+qh8A3c/vR152Lv+d+00DRyYiIlI7SujEY/zwww8AdDqnJwDxw7vi9HYy/ccZDRmWiIhIrSmhE4+RlJREYGgwkV1jAfAN9KPdoI6smLNUuzVFRKRJU0InHmPRokW0G5RQ6piS9oM6sX15Cvtz0hswMhERkdpRQiceITMzkzVr1hA3sPTjtOIGdyIvO5dfVs+vl3nXrl3LqFGj6N6zB2++NUErgSIiUi+U0IlHWLp0KS6Xi3aDSid07QZ1BOCXpDl1PufWrVsZPnw4C5YlcdQ3iztuu53nJ7xU5/OIiIgooROPsGjRIgDaDoovVR7WvhVBrUNYtmhpnc6Xl5fHNddcQ47N5f4FT3F/0tMkntubx//0Z7buSKnTuURERJTQiUdYtGgREXGRBLcOKVVujKH9oI5sWbSBfOuqs/kmTZrEwoULufz1sYTGt8bhcHD5G2Ox+S7u/dsDdTaPiIgIKKETD7Fo0SLaDkoot679oE7s3bCT5EO/1slcmZmZjB8/noRTu9L7iqHF5eEdIhlwzWnM+Pc3bE/TAzxERKTuKKGTZm/v3r2kpqYSP7BzufXtBxfcR/fz4l/qZL5XX32V3bt3c9Ez15TaUQtw+j3nkXs8h2ffeaFO5hIREQEldOIBkpKSACpZoeuIMYZ5SfNqPVdaWhrPPfccvS4aSNywExPImJ7t6Xh6N6a+/RF5+fm1nk9ERASU0IkHSEpKwunlJLZ/h3Lr/UMCaZ0Yw4qk5bWe66mnniIjI4MLn7qqwjZDbzmb/Vv3MHX2l7WeT0REBJTQiQdYuHAhsb3i8AnwrbBN3ODObF24gWxXbo3nSUlJ4bXXXmPIDWfSunubCtv1unQQ/i0DmfDuxBrPJSIiUpISOmnW8vPzWbx4cfF9chWJG9KJzLSjLE6u+Srdo48+isPLwXlPjqm0nY+/LwOuHs78z2exO21vjecTEREpooROmrX169dz9OhREoYkVtqu/eCCA4d/XjirRvPMnj2bjz76iDPvu5Dg2NAq2w+95SzysnP553/eqNF8IiIiJSmhk2Zt4cKFALQZXP6GiCJR3dviG+zPnDlzqz3H8ePHGTt2LJHx0Zw1brRbfWJ7x9FuYAIfvjNZjwMTEZFaU0InzdrcuXMJCgsmolNUpe2cXk46ndmd5T8swlXNBOvhhx9m8+bNjJl4Gz6Bfm73G3rzWWxfs41Zi+rmuBQREfFcSuik2bLW8v3339Pp7J4nnAdXnsSRvTmQvJekLe4/BmzKlCn861//YsS9F5Iwolu14ut3xan4BPjyyjv/qlY/ERGRspTQSbO1Zs0adu3aRY9z+rrVvss5vQH4Yub/3Gr/888/c9NNN9FpeHcueK7iY0oq4tcigL6Xn8KMj7/lyNGj1e4vIiJSRAmdNFszZ84EoOM5Pd1q36pjFBEdo5j25TdVtk1KSuKiiy6iVccobv7iAZzeXjWKcegtZ5GdkcXrn+gIExERqTkldNJsffnll7TpGUfLNuFutTfGMOCq4az/aSVrt2+ssN20adM466yzCIxswe0zH8c/PKjGMcYN7Uxk11jemfi2NkeIiEiNKaGTZik5OZl58+bR/8ph1eo36PrTwRj+9srTJ9RZa5kwYULBylyXaO7+5a8ERYfUKk5jDKfffT7Jizfy/v/+U6uxRETEcymhk2bptddew+F00v/q6iV04R0iGXDNcL5442OWr11ZXJ6ens4VV1zB7bffTtdz+nDnz3+pdTJXZMjNI4hMjGXcg4+QkZFRJ2OKiIhnUULXxBhj8o0xK4wxa4wxXxtjWhaWn2GM+aZM2/eNMZcVvr7AGLPcGLPSGLPOGHNrQ8R/Mmzfvp233nqLAVcNI6Ste5dbS7rwmavxDfZj5LkjeeWVV3jooYdISEjg888/Z/TT13DzVw/iE+z+8SRVcXo5uey1m9m3dTdX//EGXXoVEZFqU0LX9By31vax1vYADgJ3VtXBGOMNTAQutNb2BvoCs+o1ygaSnZ3NddddhwsX542v/BFcFQmJDuWOmY/jHeLHfffdx0svv0SbYR15aMnzjHhkNA6ns46jhs4jejLyz5fy1fufc/Mf/4+cnJw6n0NERJqvmm3Nk8ZiAdDLjXbBFPx/nQZgrc0GKr7rvxGz1havYJV8feDAAebNm8czzzzD0qVLuX7yPYR2aFXjeWJ7x/HI6hc5vPMgfiEB+AX710n8lTnvr2PIOZbNey+/wy8/zeKe2+/mtNNOIz4+nqCgILfO0hMREc+khK6JMsY4gbOAd6tqa609aIz5Ckg1xvwIfAN8ZK11uTtfSOuWWMtvlwNLJVZF/yhKsiinjYXirrZEe/fGdFfLNuHcOPVP9Pn9ELf7VMQY4/YO2bpgjOGSF6+n0xnd+eaxj7j77ruL65xeTrz9fXE4DBhT/NU4jBI9EQ/wtz1vR99tLtvd0HFI46WErunxN8asAOKApcD3heUVZT0WwFp7izGmJ3A28AAwErjB3Ul7XjqoIIEwhuL8wZRIJgwlXpffxpiifxS2LW5uSpRXPU7J8qK+fi38ienVnvhhiXh7Ne1v614XDqTnBQPYu3kX25cmc3jnQTIPZpAduj+3AAAgAElEQVR7PKcg6XUVJL7WZbEut3NyEWnaFgLtGzoIabyMbsBuWowxGdbaIGNMCAUrbVOttf80xvQA3rLWnlqi7VfAi9ba2WXGiABSrLXB1Zi62XyjzJs3j+PHj3P22Wc3dCgiIu7SUrxUSpsimihr7WHgbuCBwk0Pm4EYY0xXAGNMe6A3sMIYE2SMOaNE9z5A6kkOuVH49ttvGTZsGCNHjuRfb7/S0OGIiIjUCa3QNTFFK3Ql3n8NfGqt/bcx5lTgRcAPyAX+bK393hgTDHwCJADHgUzgHmvtkmpM3Sy+UQYMGMCeQzvwDfIhM/0YqVt24uvt29BhiYhURSt0UikldOKuJv+Nsnr1anr16sWtz19BWEwwz1zzNu//9y2uH/1/DR2aiEhVlNBJpXTJVTzG119/DcDwy/oycFQP/AJ9+e83XzZwVCIiIrXXtLcDilTDvHnzaJcYQ0irgr0gfc5MZN70JPJcuXg5vBs4OhERkZrTCp14BJfLxYIF8+k6OL64rO9ZXdm/I50VWxY1YGQiIiK1p4ROPMKGDRtITz9E1yEdi8u6DilI7n6c+31F3URERJoEJXTiEebPnw9A4uDfzuVs1zWGgBZ+zJ8/r6HCEhERqRO6h048wrx58wgJDyKmY+viMqfTQeKgeFYuWIfLunCYuvv7zeHDh/nyyy/ZvXs3ffr04dxzz8Xh0N+fRESkfiihE48wb/48EgfHn/Dc08TB8Xz09LdsP5hM+/COFfSunq+//ppbbrmFffv2FZf1GdCLLz79Lx06dKiTOURERErSkoE0e/v372fzps10H9LphLqug+Ox1jJ74U91Mtdnn33GJZdcQkiMPy/++Aif7n6J+yZez6ZNmxh0ygC2pabUyTwiIiIlKaGTZm/BggUAdB4cd0Jd5/7tMcYwd/6cWs+zatUqrrvuOhIHxfP3affSeVA7/IP8GHHlYJ6b+SeOHTvGyAtGcPz48VrPJSIiUpISOmn25s2bh5e3F536tTuhLqCFP+27x7AsaUWt5sjNzeWqq64isKU/j/xnLAHBpR8nFtc9lgcn3cSWNdu474m7ajWXiIhIWUropNmbP38+Hfu0w8ev/MODEwd1YP3iLWTnZ9V4jjfeeIO1a9dy+0tX0LJ1ULltBpzbg5HXncLbL7/PinVLazyXiIhIWUropFnLzs5m8eLFdBuSUGGbxEHxHDuSxaLVc2s0x969e3niiSfof3Z3Bp7fvdK2148fjV+gD3c/dGeN5hIRESmPEjpp1pYtW0Z2djZdB1e8gzVxUMHO09nzf67RHOPGjePY8WOMfe4PJ+yiLSukVTCX3XcOc75N4tuf/1ej+URERMpSQifNWtGBwl2GnHj/XJGYjq0JDgtk4cKF1R5/4cKFvPfee4y+cwSxnVtX3QG46M4RhEWH8Ojjf8ZaW+05RUREylJCJ83a7NmziU2IJDQypMI2xhgSB3VgVdK6aiVYLpeLP/7xj4RHhXL5Q6Pc7ufr78PlD45i5bx1fDH9U7f7iYiIVEQJnTRb+fn5/PLLL/QYfuL5c2UlDopn+6Y9pO7f4vb4kyZNYsmSJdz090sJCParVmznXHcKrduF8fjjj2uVTkREak0JnTRby5cv5/Dhw/Q5LbHKtt1PLbjH7tsfv3Jr7LS0NMaNG0f3oZ0Yfnm/asfm7evNmId+x/qlm/n0f1Oq3V9ERKQkJXTSbP30U8HTH7oNr/qRXomDOhAUGsC0b791a+yHH36Y9PR0bn/pyio3QlRkxFVDiE5oxeNPPI7L5arRGCIiIqCETpqx6dOn0z4xlrCoFlW2dXo56T+yO/NmLCE3P7fStnPmzOHdd9/l4rvOon2PqBrH5+Xt5Kpx57N5dQofTv2gxuOIiIgooZNmKS0tjV9++YUhF/Zyu8+Ac3tw+MBRvptT8XEiGRkZ3HLLLUS2jeDKcefVOs7hlw2gXWI0T/zlCfLz82s9noiIeCYldNIsffbZZ+Tn53PKRe7f3zb4vJ74B/nyzqSJ5dZba7nzzjvZsmUL90+8Ht9An1rH6XQ6uOrR89m2cQdv/2dCrccTERHPpIROmh1rLW+99RbxPdrSoXdMhe12bNrLd+/+wvGMgkd++Qf5cdofBjJj6ixSdpy42/WFF15g8uTJXPHweXQbVvGTJ6pr6EV9iO/Vhr+O/ytHjx6ts3FFRMRzKKFrYowxkcaYKcaYZGPMUmPMAmPMJcaYM4wxh40xy40xG4wxL5ToE2SMecsYs9UYs9YY84sxZnBDfo76NH36dJYvX855Y0+rcMNC5uHjjBv1Em/c+zFv3Pp+cfll95+DK9/FHfffVnyciLWWZ599loceeojTfj+QMY+4f+acOxwOB7c8dxl7Uvdz413X6BgTERGpNiV0TYgpyE7+C/xirY231vYHrgDaFDaZY63tC/QFLjDGnFpY/g5wEOhkre0O3ABEnNTgT5KMjAzuvfdeouNaM+KainPWOZ8v5dD+owwa2oFZX63iYPI+AKLiIrhy3PlMn/ojl115CRMnTuT0009n3LhxnHH5YO596xocjrr/sek5rDNjHv4dn0/+ij+Nu0dJnYiIVIsSuqZlBJBjrS2+2cpam2qt/VfJRtba48AKINYYkwAMBh6z1roK65Otte6dz9GE7Nq1iwsvvJDNmzdz9+vX4O3jVWHb2VMX0yEhgif+dj4Ay/+3rLjusj+dw5iHf8dXX37LrbfeytpNq7nr1Wu4/53r8Pb1rrf4rxx3HufecCovP/cvzr1gJGvWrKm3uUREpHmp+DeeNEbdgWVVNTLGhAKdgF+AQcAKa22ttlCOfeIqiheNSlyKLPG21CXKghcnllU8xon17owPkJOdw69bdrFq/nocTsN9E6+jx2kVnz137GgW6+Zv4ebbhhHXIYKETq1YMGMNZ91XcCnV4XBwzWMX8vt7R3L4QAat2obhdNb/330cDgd3/vMq2nWNZvKTX9GzZ09iOkTSsWccEVFh+Pr74uXtxMvbC4fTQQ2Pv2sQNT2rT0QKTHzyw4YOQRo5JXRNmDHmdWAYkAM8CAw3xqwCugDPWmv31NUv0nf+9pG7MRV+LS4o/lIcS5k2v5WXHaNEu0r6eHk5iYyL4OK7RnDujcOIjm/122Dl2LRkGy6Xpf+g9gAMHtKBLz9fDtm54PvbzlX/IH/WzN3Ck5e+zm3P/4HeZ3d3699BbRhjuOiOszhjzCBmT13Mqtmb2Lb5V5bPWUN2Vg75ufnk5+kQYhFPc9GDw+ZeEHT7sIaOQxovJXRNy1rg90VvrLV3GmMigCWFRXOstRcYYzoDc40xXxb26W2McRRdcq2JDZmLyCWnnGSr4VZeDGBw4DRe+Bg//E0wlSVyRWYt2ojDYejTp+DWw9792jDl34vwWhdI/6HnFrez1nL/Yy+yY/NePnnwU/5v3RJO2rJYLIy890q4F/LJJcuVSS7ZuGw+LptPfhN6soTuBxSpvVS7+v6GjkEaNyV0TctPwNPGmNuttW8WlgWUbWSt3WSMeQZ42Fp7pTFmCfCkMeYJa601xnQCullrKz5Bt4wuAQPr5AM0BuuWbqRj50iCgv0A6N23LQDLFy5n1PCbi9tt27aNzRu3EBfdgtVb9nFs06+0735quWOKiNSnngxb1NAxSOOmTRFNiC1Y6rgYON0Yk2KMWQR8ADxcTvMJwGnGmA7ALUAUsMUYsxp4G9h1ksJudFasWE5i198e2RXbpiUhLf1ZuWJlqXZLlhQsfN43pg8AC3+ZdvKCFBERqQat0DUx1trdFBxVUp5ZJdodB2JL1I2tx7CajH379rF79x4Su/72BAljDJ27RLJhfSrW2uLLyIsXL8bby8kfRiRw76u/sGbVUsY0VOAiIiKV0AqdeJSVKwtW4bp0jSxV3jkxkk0b95KVk1ZctmzZMnokhNMyyJeE2BDWrE8+qbGKiIi4SwmdeJQVK1YA0KVrq1LlnRMjOX4sh42blhaXbd68ic5tQgDoFhfGuuT92PyckxesiIiIm5TQiUdZsWIFUdEtaRlaei9J58SCFbsVy5MAyMnJYfv2HXSIDQOgS/uWbN11mNyjHnvroYiINGJK6MSjrF69ms6JrU8o79ipFcbAylUFK3ipqam4XC7iY1sA0D4ymPx8y47kdSc1XhEREXcooROPkZOTw/r16+ncJeqEOn9/H9rHhbN27RYAtm7dCkB8VBAA7aOCAUjZsv4kRSsiIuI+JXTiMTZu3EheXh5dEqPLre+cGMmGdTtxufJITi7YABEXXTqh25a8sdrzrlu3jhEjRhAbG80999xFdnZ2DT+BiIhI+ZTQicdYtWoVAB07h5db37lLJDu2p5OWvo3t27fj7eUkKqzgXru2rQsTum2p1ZozNTWV4cOHs2rVErp0a8k///k611x7sZ6eICIidUoJnXiM1atX4+3tJC6+goQuMRJrLcuXz2fHjh1ERwTicBScSefr4yQ6PIDU7Xvcns/lcnH99deTk3Ocf396M/966wruuvdMPps6nSkfv1Unn0lERASU0IkHWbVqFfEJrfH2dpZbX3Q23YqVS9i5cycx4aV3wsa2CmLXvnS35/viiy+YPXs2Dz06inZxLQG45fZhdOrSmscee4K8vNwafhIREZHSlNCJx1i9ejWdytnhWiQmtiVBQb6sWrWaHdu3E9sqqFR9dHgAuw9kunUWnbWWp59+mvYdIhj9+57F5V5eTm7/4+lsS97Pf6a8WvMPIyIiUoISOvEI6enp7Nixgy5dyt8QAYWPAEuMZN3aZHbu2klMq+BS9TERgexOy8RmH6pyvhkzZrB8+XJuuXU4TmfpH7OzzulKh/hwXn75Nd1LJyIidUIJnXiE1atXA9ApMbLSdp0TI9m4YQ/Hjh0ntkxCFx0RSPrRbI4d2l3lfE899RTRMS25YHT3E+qcTgeXXzWQVStSWbRkZjU+hYiISPmU0IlHKHqGa6cKdrgW6ZIYybHMgkuqMRGl76GLLrynbteOyp/pOmfOHObOncuNY4fh7eNVbpuLLumFj4+TNye87Fb8IiIilVFCJx5h8eLFtGrVgtaRwZW269L1t0OHY8L9StVFhwcCsGv7tkrHePrppwkLD+KSP/SqsE1IywBGjurGl5/NJiPD/Y0WIiIi5VFCJx4hKSmJnr1jMMZU2i6xaxROZ0Gb2FZlVugiqk7oli1bxvTp07nuxlPw9/epdK7fj+nHkSNZ/PvDf7rxCURERCqmhE6avYMHD7Jp0yZ69WlXZVsfXy9aFR4iHBUWWKqu+JLrzh0V9n/mmWcIbhHAmGv6VTnXwMFxtI8L4913J1fZVkREpDJK6KTZW7RoEQC9+rZ1q32LEH9Cg33x9Sl9Xl1osC++3k527dlXbr+1a9fy+eefc+U1AwkO9iu3TUnGGC67oj9LFyezbMVst2ITEREpjxI6afYWLFiAw2Ho3qPiM+hK8vFxElXmUGEoSMCiIwLYvS+t3H5//etfCQjw5bqbhrgd2+hL++Dl7eSNN19yu4+IiEhZSuik2fv+++/p0astgUG+brXPzc0/4VDhItHhgezef+SE8+PWrFnD1KlTufr6wbQM9Xc7trDwQM4+J5GpH88kM/OI2/1ERERKUkInzdqhQ4dISkrilOHxbvdJTztGVFj5SVnR0yLIzyous9Zy3333ERzsX63VuSKXXzWAI0eymPjOc9XuKyIiAkropJn7+uuvcblcDD+9s1vt8/NdpKVl0DrsxEuuULhCl3YMm3O4uOyzzz7jhx9+4K77R1Rrda7IwMFx9OgVw8svvUVurp7vKiIi1aeETpq1KVOm0KZtOL36VPzIr5LSD2aSn2+JqeiSa0QAR4/lcOTALgD27t3L3XffTbfubRhzVdU7W8tjjGHs7cPZ/msab054ukZjiIiIZ1NCJ83Wpk2bmDFjBueP7lnl+XNF9u09ClDhPXQxhWfR7dyeTFZWFldccQWHDqfz1D8uOeGZrdUxYmQi/Qe24y9/eZ79B/bWeBwREfFMSuiaEGNMvjFmhTFmpTFmmTHmlBJ1g4wxs4wxmwvrvjXG9CysG2+M2VnYd50x5sqG+xQnz/jx4/Hx9ebKawe53WffvoKELqbCe+gKErptWzdy6aWXMmvWLJ586kI6dan8kWJVMcbw6JPnk5GRzZgxF5CXl1er8URExLMooWtajltr+1hrewPjgGcAjDGRwKfAn621nay1/QrrEkr0fdla2wcYDbxljPE+ybGfVO+//z4fffQRN409lYiI8u+HK8+BfRnAb4lbWUXln3/+KTNnzmT806M5f3SP2gcMdO4SyWPjz+Pnn5Zw6e/P4+jRo3UyroiINH/lPzlcmoIWQNFDQO8CPrDWzi+qtNbOLa+TtXazMeYYEAqUf0JuOQ4dOlR8VEdNvtamr7tj5OTksHnzZqZOncqUKVMYempH/u+OU939iMBvK3SRFa3QFSaHNj+PSR/eSP+Bbao1flUuu6I/mZnZvPjs98THt+Omm8YybNhw4uLiCA4OJiAgAC+v0j+2JS8nl7207O6lZhFp3EJCQho6BGnklNA1Lf7GmBWAHxANjCgs7w584M4Axph+wGZrrdvJHEBoaGh1mjeowCAfbhx7CnfeeybePtX7Ft+/9yitQv3x9nKWWx8c4ENwgDc+/l51nswVuf7mU+jbvx1v/nMWL730Is8//496mUdEmo41W8ef1T3+Lz82dBzSeCmha1qOF142xRgzFJhsjDnhep8xJomCFbyZ1tp7CovvM8aMBeKBUdWd+KFHz6VgsccUzlE8V6XvKfHeVNCXqsaixPtK2jochjZtQ+nUpTUBAYGYGtxRsH9fZoWXW4vERASyd38mDuPeQcU10advAm+9l8DRIxls2bKH3bsOc/x4LseP5eBy/XaocenzjUsfdlzm7GMRadoeAJTQSYWU0DVR1toFxpgIoBWwFugH/K+wbrAx5jLgghJdXrbWvmCMuZSCRDDBWpt1wsAVeO7v0+sw+sbr6OHPiA4/Vmmb6PBA9hzIpGuHR05KTIN6n5RpRKRx+11DByCNmzZFNFHGmETACaQBrwM3lNz1CpS7E8Ba+wWwBLi+3oNsgnbt2klUePlHlhSJiQhk14EMbJ7b+bCIiEi90gpd01J0Dx0UXHy83lqbD+wxxowBnjPGxFKw2eEA8NcKxvkrMMUY87a11lXvUTcR+fn57N27j+iI9pW2iw4PYE/aMfKzDuIVFHOSohMREamYEromxFpb/p36BXULgdMrqBtf5v1SoEudBtcM7Nu3D5fLRXRE1ffQ5ea52L8rhejOSuhERKTh6ZKrSKFduwoe5xUdXvm5dUUJ385fk+s9JhEREXcooRMptGPHDgCiw3wqbVeU8O3asa2+QxIREXGLEjqRQtu2bQOgfVRwpe2Kn+f6a0p9hyQiIuIWJXQihVJTUwnw8ya8hV+l7SLDAnA4DNu37zhJkYmIiFROCZ1IodTUVNpFtajycVk+3k5iIgJJ3bHnJEUmIiJSOSV0IoVSU1Np27ryHa5F4qKC2bYzrZ4jEhERcY8SOpFCqanbaBdZ+f1zReKig9m2+7AOFxYRkUZBCZ0IkJmZyYEDabSLCnGrffuoFuxOyyTr8K56jkxERKRqSuhEKLjcCgWJmjviooOxFrZtWVOfYYmIiLhFCZ0IvyV0j745h8Xr9lbZvn3hpdmUzevrNS4RERF3KKETARYsWADAzgOZPPbPOVW2j4suWMlL3rKxXuMSERFxhxI6EeDHH38E4Mah7Zi7+QDpBzIqbR8dHoCPt4PkZD3+S0REGp4SOhFg06ZNxIUHcMOQtlgLCxb/Wml7p9NB57YtWb9l+0mKUEREpGJK6MTjuVwu0g8e5PRO4QyKC8XXy8Gclbur7Ne1fRjrU/Zj83NPQpQiIiIVU0InHm/Dhg3ku1z0a9sSP28nfduGsHJbepX9EuNCSd1zlIwDeqariIg0LCV04vFmzpwJQJfIgqdE9IhpwZpdRyAvv9J+XduHArBm+bz6DVBERKQKSujE482fPx+Azq2DAOgeHcyBjBwO7D1aab++nSMAWJKkhE5ERBqWEjrxeGvXrsXbaWgb6g9Aj5iCM+bWbTlQab92kcG0DvUnadHSeo9RRESkMkroxKNZa0lJSSEuPAAvZ8GPQ9eogoRuUxX30RljGNg1ksWrt2FdlV+eFRERqU9K6MSjbdmyhbycLBIiAovLolv44evlIHVP5ZdcAU7tGcWm7YfYvnFxfYYpIiJSKSV04tGmT5+Oy0LH1r8ldA6HIT4igOQq7qEDOHdwOwC++fLDeotRRESkKkroxKNNnjyZfJelY6vAUuXxEYEkH8gEl620f2L7UDpEt+Dz/06rzzBFREQqpYSuiTPGWGPMiyXeP2CMGV/4erwx5oEydRuMMWuMMSuNMdc1QMiNxqpVq1iyZAlAqUuuRe+37j8GOXmVjmGM4brfdeGnxcmsWz633mJtCPn5+Xz33Xc8+eSTPProo/z73/8mLS2tocMSEZFyeDV0AFJr2cClxphnrLUVbss0xtwGjAQGWWuPGGNCgItPVpCNjcvl4oEHHiDAz4djWTl0al12hS6AjOw80tIyCY9tWelYN5zXlRemLOfB++7im5+XY4ypz9DrXVpaGpMmTeLNN98gJWUbxhgcDsjPt/j6eHPN1VfywEPjSExMbOhQRUSkkFbomr48YCJwXxXt/gzcYa09AmCtPWyt/aC+g2uM0tPTue222/j+++8Z1jsah4G4sIBSbeILV+y27ThU5XiRYQE8ceNAps1eyR23XM2RI0fqJe76lJGRwbRp07j66qtp06YNDz30ELEtcpj8xCjSvruZQ9PHMufNS7nm3M58+OGHdO3alZFnnc7HH3/MgQOVH+8iIiL1Tyt0zcPrwCpjzPPlVRpjgoFga+3Wmk5w1fkDgIJjPgAsv91bVlhUXFfY4IQySzll5bUrKis1hy1VV2UZ5bfbfzCDdcl7yM7J44Er+/LrvqO0DfXH19tZ6vMmtCpI8FJ2HKb/YKp012W92HXgGK9O+oj3/vMp3TtGExXeAh9vJ97eTrycpccv9e+qzGct+5nKa08V9eXd+Ve2TVZ2HgePHGP/wQySd6RhrSU02Jdrz0lg7EXd6REfXqp9/y6t6d+lNY/fMIBJ36zjna+XcuWVVwLQJjKEtlGhtAjyw9/XG19fLwwVr1RWtorZxBc4RerFh98saegQpJEzJ/yikCbFGJNhrQ0yxvwVyAWOA0HW2vGF99JlULCCt81aG1bTeTrEtLBFv6BL/sItel3yF7ShnLJK25X6PCeWFbUsb16qmKNM19BgX7p3COeKkZ3o3TGC0+/4ghbWxQ/3nFrq8x7LySPw3m958tLuPHjXabhryYa9TP1pC+u3HWRv+nHy8lzk5rvIy3edkOCUTVxOfF+mPVXUV9G/7Bje3g7Cgv0Ia+FL17gwBiS25oy+sfj6OMuZ7UR5+fks27SfWct2snn7IbbvyyDjeC5Z2Xlk5VR8Ll9l/8kpm9iKSIF1H1693//MN1s3dBzSeGmFrvl4BVgGvFe2ovCeuUxjTLy1Nrkmg2/dtB6bd7y2MTYcYzDGCU4/cPoUFyfv/Zjf9ww/oXmAjxfRIb6k7M/Bd+jf3Z7m1KFw6o2Fb/KzIT+78NDhxpSomBL/PrzB6Ys7CVxZvsDwYTD8pqISC/m54Cr8zNbSuD63SNOVs/zFzg0dgzRuSuiaCWvtQWPMp8DNwKRymjwDvG6MGVOY4LUArrDWTnRnfEdQbB1G2zgcOnSItPRDdIqMK7c+ISKQrbvTcfjVeGFTRKRO+J/5ZtU39IpH06aI5uVFIKKCujeBn4HFxpg1wGzg2MkKrDHaurXglsKEML9y64vPosvOOJlhiYiIVJtW6Jo4a21Qidd7gYAS78eXeG2B5wv/CAWP/QLoGOFfbn1Cq0AmJ23n+N5U/Nt1P5mhiYiIVItW6MRjFSV08REB5dYnFJanrFtx0mISERGpCSV04rG2bt1KdMsAAn3LX6hOKHwc2NaN605mWCIiItWmhE481pYtW+hYweoc/PY4sK2b1p+skERERGpECZ14rC2bN9OxdVCF9RFBPgT7ebE1JfUkRiUiIlJ9SujEI2VmZrJ7zx4SWreosI0xpuDokp17T2JkIiIi1aeETjxScnLB+cpF98lVJKFVAFv3HAZXxU8+EBERaWhK6MQjbdy4EYDO4b6VtkuICCQl7Rj5R/afjLBERERqRAmdeKTihK51VSt0geTmu9ixQUeXiIhI46WETjzSpk2biA0LJMiv8rO1i3a6Jq9fdTLCEhERqREldOKRNm7cSJcqVuegxFl0G9bUWyxffPEFw4cP56EH/kReXl69zSMiIs2XHv0lHsday8aNG7iyV3iVbduG+uPj5WDzpk31EsuMGTO47LLLiA31Z+7cuRzbncxrH35ZL3OJiEjzpRU68Tj79+/n0KHDdI4OqbKt02FIjAxiTfKOOo8jJyeH2267jW6xLdn4xAjuPiOeNz76L0t/nlbnc4mISPOmhE48TtGGiC6VHCpcUq/YFqzafhDysus0jsmTJ7Nt2zZeuLQHAT5O/nZhIi38vPnHXx6q03lERKT5U0InHmfVqoINDj2j/N1q3zOmBTvSj5OeUnfPdLXW8vrrr9OzTSjndgkFoIW/N2NPbc9n89bx6+rFdTaXiIg0f0roxOOsWLGCsCA/Ylv6udW+V2zB0yRWJ82usxiSkpJYsWIFd5wejzGmuPyPZ3TAWsuE55+os7lERKT5U0InHmflypX0adOiVCJVmaKEbtWSpDqL4c033yTI34er+0eWKm8XFsD5PaKY9NUscrOO1dl8IiLSvCmhE4+Sk5PD6tWr6dO2pdt9okP8CA/0Yfmq1XUSQ1paGp988gnXDmpDsJ/3CfW3DmvP3iNZfPXuy3Uyn4iINH9K6MSjLFu2jKysLE5JaOV2H2MMQzuEMm/dr3XyTO5GzHYAABnZSURBVNdJkyaRnZ3N7ad3LLd+VPdI2ob689bb79Z6LhER8QxK6MSjzJ07F4BhccHV6jesYzgb9x5l/6ZltZo/Pz+fN998k9O6RFa4KcPpMNxyanu+X5lC8prazSciIp5BCZ14lJ9//plOUSFEtvCtVr/hCQWHEM/65rNazT9jxgxSUlK48/T4StvdfEo7HAbefuHJWs0nIiKeQQmdeIyMjAx+/PFHzu/u/uXWIoPiWhIW6M1X33xb4/mttTzzzDPEhgVxSc+IStvGtvTngp5RTPpyJjlZx2s8p4iIeAYldOIxpk2bRnZ2Nhf3aVvtvl5OBxf0iOKbxZvIOpJeo/lnzJjB3LlzeXRUZ7ydVf/o3TY8jn1Hsvj3S+NrNJ+IiHgOJXTiMd58803aRQRzapx7T4go69rBbTh0LJdP33iu2n0zMjL44x//SHxkCDcPaeNWn1HdWjM4LpTH//EamUePVHtOERHxHEromhBjTL4xZoUxZqUxZpkx5pQSdYOMMbOMMZsL6741xvQsrBtvjNlZ2HezMeYLY0y3hvskJ9+sWbOYNWsWd54Wh5cbq2PlOatLK7pFB/P0P98iOyvL7X75+fmMHTuWrVu38t61/fDxcu/8O2MML/2+B7sPHeOuay7BWlujuEVEpPlTQte0HLfW9rHW9gbGAc8AGGMigU+BP1trO1lr+xXWJZTo+3Jh307AJ8BPxpjq30zWBO3YsYMbb7yRDq1DuOv09jUexxjDi5d2Z+PuQ9x9/WXk51d9hMmOHTu45JJL+Pjjj3n64h6cFt+iWnOekhDGE+d14f2vfuKBO24mLy+vpuGLiEgzZvS3/qbDGJNhrQ0qfP0H4Gpr7cXGmL8BLmvtXyroNx7IsNa+UKJsMrDUWvuqO3MvXrzYFn2vWGsp+bq8sqrqT0afzMxMli5dyvvvv09u1jF+um84A9sEuvNxKzXuv+t4duZm+nTrzJhrb6Rjx474+/vjcDg4cuQI6enppKamsnjxYmbNmoWX0/D8JT24u4bJpMtluXvqal6fnUJ82xguu+JqevXuTVhYGMHBwRhjMMbgcDiKXxf9EZHmYcCAAfqBlkopoWtCjDH5wGrAD4gGRlhrlxpjvgA+sNb+r4J+/9/evcdHWd15HP/8MpOZzORGwiVI5JYgCAJett5b6mUFtVhdsdvaWquttmVVtGxt1e5a2lWrVkCp1K0urXbr2pZ6KQh9VQQEFZSiyEWBYMJNDFdJIIRcJnP2j5mQACFMQsgwM9/36zVmcp7nOec3j8/oL+c85zwTODyhuwsY5JwbG2PbCXmh+LxpjBrcg19eO4RBBW1be+5InHM8v+QTfvn6x6zY0vK9bekeY2ivHP55UHfGjuhH/27HnkjOXLGVx17/mMXrP6O+ISH/dYhIO7lfX30XY1+J6Q9wSU3eeAcgbbLfOXcGgJmdD/zezIYeupOZvQvkAK855+48Ql1t+mtv5thzsUjd0TaaKjhQFi1v2t60b9P2pn0P7NfS8c2ObX58Y3tHOr552z6vcUpBLumBLPAe/oit9jLghku6csPFp1NRWcnG7buprW8g7BzZfi95QR/dcjLxZWSA19f0AY7RVefnc9V5Q6ipqWZD+WdUVNewtyaEc+CAsHOR986hdE8k6cQ2m0pSlhK6BOWcW2xm3YDuwIfAWcBfo9vONbPrgNGtVHEmsDTW9kb/+p1jiDZ5dYm+OlMGcGontykicXd3vAOQE5smRSQoMzsV8AC7gKnATc1nvQLBVo4dA4wEXjiuQYqIiEinUA9dYgmY2QfR9wZ8yznXAGw1s68Cj5hZIbAd2An8vNmxPzCzG4BMYBWR++92dGLsIiIicpxoUoTESheKiEj8aJartEpDrpISnHOMHz+ezMwgP7v3R/EOR0REpEOph05ildAXyuuvv85ll11Gvxw/G/bU8s7Mv3Du6DHxDktEJFbqoZNWqYdOUsLDDz9MYU6ApdcOIdfnYeJ/HN9eul27djFr1ixWr159XNsREREBJXSSAsrLy5k3bx63ntqdrhlebh7UjVdWrqdyw7rj0t6f/vQn+vfvz+jRoxkyZAi33XRDTI8JExERaS8ldJL0Xn75ZZxzfKU4D4DrivKoDztmP/14h7c1c+ZMrr/+eobneJh7zWncOayAXz/3PPfd8s0Ob0tERKSREjpJeq+99hr9uwQZkusD4PyeWfQIeHl19uwObWfjxo3ceOONnFmQw2tXFHNJzyCPX9iH7w3pzqPPvsA7s1/u0PZEREQaKaGTpNbQ0MCCN97g4pOyDpSlmXFJYQ7z1m3B7a/qsLbGjRtH/f59TL9sAEFv01frsfN7c1Iwnbu+/13CGnoVEZHjQAmdJLXly5dTUVnJxX3yDyq/pFcOW6vrWTvnlYPK16xZQ11dXZvbmT17NjNmzOCnnzuZosyDv1ZZ6R4eOudk3t28kxlPPtL2DyEiInIUSugkqc2fPx+Ai7v7Dyq/pDAbgHmvvHig7Omnn2bw4MGMPPss2rKcT01NDePGjePUrlncOSS/xX1uGNiV/tl+Hv7lRFw43NaPISIi0ioldJLU3njjDU7JC1KY5TuovCjHT58sH/MWLwEiCw8/8kik92zBig9Z8vv/ibmNiRMnUlpaypQv9MPnafkr5U0z7j6jJ+9u+YyFf3i6nZ9GRESkZUroJGmFQiEWLlzAxb2yD9tm0fvo3tiwnXBVJWVlZZSVlfFA/24AzPntMzG1sWnTJh588EHGDOjGZT0Dre5706Bu9Ah4efQXD7X9w4iIiLRCCZ0krWXLlrFnz97D7p9rdElhNrtqQiyf9RfefPNNAK7O8jAs4GXhqo9iamP8+PHQEGLShX2Pum/Am8Ztp/Vg9prNrHlzbuwfRERE5CiU0EnSmjs3kjRd3D2jxe2XFuZE9pv5Mm+//TZ5Pi9D/B5GZPtZVFFNw6ebW61/zpw5vPjii/zkrF70CcT2VRp7Wg/8HuPxCfe24ZOIiIi0TgmdJK158+YxtHs2BUFvi9t7ZfoYnJfB3HeW8tFHH3F6hpc0M84KprMv7Fg/f84R666rq+OOO+5gQNdsfji8e8wxdQ+kc+PAbjy34D12bt7Q1o8kIiLSIiV0kpRqa2t56623uKTZ+nMtubQwh4Ubd1C6di3FgcjEidMC6QB8uOitIx43efJk1q5dyxMX9sGf1rZnZt81rICahjD/ff/dbTpORETkSJTQSVJavHgx+/fv59K+XVvd79LCHKpDYbbt2kVxMLK0yeBApEfvo2XLWjxm7dq1TJgwgWuKu3Flr2CbYxuSH+CK3rk8+ecZ1FTva/PxIiIih1JCJ0lp3rx5pJnxxW7pre53Ua9sPNEOtmJvZO25HE8avX0ePtz8yWH7NzQ0cPPNNxP0GE+N6Nfu+MafXsC26jpeePRn7a5DRESkkRI6SUqzZs3i3J455Ppbvn+uURe/l+H5kV62ovSmodNBGV7WVeyBQxYBnjRpEosXL+ZXn+9DT3/bhlqbu7Qwh+FdA0x66mktNCwiIsdMCZ0knbKyMt5//33GFLc+3NrolC6RodbiZslfkd/D+toQ7Nh6oGzRokXcd999XDugO9f3O3xtu7YwM/59eE9Wba/kpSl6HJiIiBwbJXSSdKZPnw7AmP65Me2f6fXQxWPkeZu+Dv39XnbUh9m75kMAtm7dynXXXUe/3CDTLuqHWft75xp945SuDM0P8OOfP0hdbe0x1yciIqlLCZ0kFeccf/jDHzi7Zy79Mlsfbm20ZV8dAw4Zmi3yewBY/8H7VFRUcOWVV1KxaycvjRpAl9iqPSpPmvHY+b0p3b2Px3/4bx1TqYiIpCQldJJU5s+fz6pVq/j+0IKYjymtrKEo49CELjrT9b1/MHLkSFatXMFLlw9kWI6nQ+Md1TuXa/p14T+f+h0r313UoXWLiEjqUEKXgMyswcw+aPa6J1ruNbOHzGxds20/MbORZrbYouOEZuaJbrsgvp+kY4XDYe6991565QT5eoz3uIXCjo1VdQw4QkK3YM5rfLjiA168fBCXt2OJklj85ov9yPN5ufpLV7D100+PSxsiIpLclNAlpv3OuTOavR6Olj8A9AKGOefOAL4ApDvnXgM2At+J7ncH8A/nXFJ1CT344IMsWbKEX5x7Mhne2C7tTVW1hBwU+w/uecvzGDkeY3+ogXfGDOOqkzOPR8gA9Aik89fLB7CtsooR/3Q6qz+K7TmyIiIijZTQJQkzCwK3Anc452oAnHN7nXMTorv8ALjXzE4Dbgd+HJdAO5hzjpKSEsaOHcv999/PN07twTeLcmI+vrQyMhmhyHdwD52ZUeT3sjMU7vBh1pacW5DF3780kIrKSs44fThjb/k2CxcupLq6+ri3LSIiia+Dbu+WThYwsw+a/f4LYDWwyTm3t6UDnHPlZvY4sBgY55z7rC0Nnte3AOciC++6pjoPen/wtpbK3EHbI9tc0/7N3h/1OOdwOHbuq2VvbT1pBj8YXsCj5/Vu0wzUsr2RhO7QHjqITIxYvT8UWYsu7fj/7fP5k7JZ8ZXT+I8lW3j22Wf572m/w4CuQT95QT+BdA9pZgdeZkaagXHsM25F5MS2+Mq+Hp5a0hDvOOTEpYQuMe2PDqkeYGbDD/n9ZuBOoCtwgXNuMzAVeNg592xbG8wN12DNkgeL/iNS1thm9GfjPs23tbBP9I6+ZvtYi3U0Ht9SHV16BRncJcCX+3Xh5CxfWz8WpZW1+A0KfYcndP19XmZX1OBqQliw7XW3R89gOv9zUT8mXdCbuVv2sHJXNeXV9eyubaCmIYzDEXaOsCPyCrujVyoiyaAKCMQ7CDlxKaFLHh8DfcwsOzrU+jvgd2a2CvAAOOfCZtauDODvmys7MNQTR+mYMfQvmUlaC716RRkeahyUX3sfva7+106NKwf4l+hLRAQlc3IUuocuSTjnqoFpwJNmlgGR2axA53QtJajSdesOekJEc40zXdevXNGZIYmIiLSZErrEFDhk2ZLGWa4/AcqBVWa2DHgTeA7QWhgtcM5RWlpKcaa/xe2NiwuXrdasUxERObFpyDUBOedanHbpnKsH7om+jnRs1vGKK9Hs2LGDqupqinu1fEr6+rwYUFZa2rmBiYiItJF66CRllUYTtSJvy7NE/WnGyT4PZVu3dmZYIiIibaaETlJWWVkZAMXeI88TKfJ7KNvd4kowIiIiJwwldJKySktLMaD/ESZFQGRiROn+Oqje13mBiYiItJESOklZpaWlFGb4yEg78sK8RX4P5fUNVJeVdGJkIiIibaOETlJWaWkpxb7WvwKNS5dsWPZeZ4QkIiLSLkroJGV9vG4dxRmtT/RuTOjKVizvjJBERETaRQmdpKTKykq2bd/OwKzWF18v1lp0IiKSAJTQSUpat24dAAMDrffQdfOmkZVmlG3Y0AlRiYiItI8SOklJJSWRSQ4Dj/JoWzOLLF2yfWdnhCUiItIuSugkJZWUlGBAsf/oX4Eiv5fSqv0Qqj/+gYmIiLSDEjpJSSUlJfQN+ltdsqTRwAwvH9eEqN9QdtzimTZtGoMGDmTM6NFUVFQct3ZERCQ5KaGTlFRSUsLAoyxZ0mhoIJ0651i3aOFxiWX69OnccsstBMs3M3P2LK495yyca30oWEREpDkldJJywuEwa9esYVDAF9P+w4KRiROr3lnc4bFUVVUxbtw4zs4N8u6gfKb27cL8det5/v77OrwtERFJXkroJOWsX7+eqn37GJ7d+pIljU7NSMcDrFq2rMNj+c1vfsPWrVt5ol8evjTjO92CnB5I56HHHydcr3v2REQkNkroJOUsXx5ZJPh0/9HvnwPISDNOyfCyauPGDo0jFArxq19NYURukPOjnYVpZvzopCxWV9Xw6iP/1aHtiYhI8lJCJyln+fLlpJkx1BdbQgcwNOBl5e69UF/XYXHMmDGDjRs3cWdh7kHl/5ofoI/PwxNTp3ZYWyIiktyU0EnKWbp0Kadm+gnEMMO10ZlBHx/XhPjsvSUdFscTTzxB36Cfq4MHx+E147Yemczb+hmr/jazw9oTEZHkpYROUko4HGbRore5INj6EyIOdUFWZEx08YyXOySOZcuWsXDhQm4vyMJjhyeW3+keJMOMJyf8Z4e0JyIiyU0JnaSU1atXU1FRyYV5WW067pzMyMSIt+fP7ZA4Jk+eTGa6l1vyM1rc3tXr4YauAX6/dAW7yz/tkDZFRCR5KaGTlDJ3biQhG5ER+3ArQNCTxtmZ6bz+UQkc4xpx5eXl/PGPf+Tb3YJ0aeUbeEdBFvvDjmn33n1M7YmISPJTQicpZcaMGQzODlAU46LCzY3uEuAfe/ZTvmTRMcUwefJkQqEQ407KbXW/4cF0vpjtY+r0F2kIhY6pTRERSW5K6CRlbN++nQULFnB1jr9dx3+5S2R49C9TJrU7hk2bNjFlyhS+2T2LAZ7wUfe/o0cWG6pr+fMDP213myIikvyU0CUQM+tnZqsOKZtgZj+Mvh9vZmvMbKWZLTezSWaW3mzfM83Mmdmozo79RPDMM88QCoW4qUfb7p9rNCyYzueC6Tw1YzYufPRk7FDOOW677TasoYEH+uTFdMw1eRmcGUznR48+RlVlZZvbFBGR1KCELkmY2feBkcB5zrlhwNnAdqD54xCuB96K/kwpO3bsYOLEiYzKz2SQt/33wN1ZEFn0939/2vZHcz3wwAO8+uqrPNqnC72tIaZjPGY82SeXT/bX8d0rRuoZryIi0iIldMnjJ8BY51wFgHOuzjn3sHNuD4CZGXAdcBMw0sxanl6ZhCorK/nqV7/K3spKJvXrekx1fb1rgPMzfdz+8C95a+7rMR2zbds2br31Vu6//36+0SOH2/Nje4Zsowuy/TxUmMMLi5dw01VfYs+ePe0JXUREkljbFuOSE1UAyHLOrW9lnwuB9c65UjN7A7gSeCnWBp6/9JwDkzsdjsZ+ooPKDrxvuayxd6lpewtljgO1t1jmDq7/sLJm9TU4x9qKKmZtKmd3bR3P9c9niCe2nrEjSTNj+oB8vrhmB1/458sYUZDPmd3zyfOnk2aGA/bVh9gXClFRW8/ayire37kbA+7umcUvTs7CWlh37mjuOSmLOuf42ay/8XLXfEb1LmBofi55fh9Z6V7SDAzDDBprP/R3EUlcX5/bcYuaS3IyDeEkDjPrC8xyzg1tVjaBSP5yp3MuP1o2CngE6AJ83Tm3yMymAh84554xsy8D33TOfaUNbSfkhdLDm8YXsn38uGc2Z2f76aj0Zk9DA1O27uWl3TWsqwlRFW46PX6DLE8a2WlGcYaX8zJ93NgtwMCA75jbf6+qlie3V7Fgby3ra48tORWRxOHOLpzGkk9uiXcccuJSQpdAzCwLWOucK2xWNgV4D3gAGNG8l87MXgUeA94EtgD1QAORrKIrcJJzbm8sbZfccJWzqj1NvT/RHiGg5bJooR203Zr1HrVWdqR6rNn2VuoxA48H8/sJdC/ABgyG/GMbaj2ihjBsXo/buY1wXS0AHp8ffH4IZkK3AsjN6/husup91Jd8xJ5Pt7B37x5cKIRrCB/Wa6lvt0hyGPhp6bdY8snv4x2HnLiU0CUYM1sK/Ng5N9fM8oF3gCuAUcCXga855yqi98zNIZLo+YHxzrlRzep5DnjdOfe/MTatC0VEJH5094S0SvfQJZ4bgalmNjH6+8+i98U9BQSBd82sFqgC3gaWAU8Ahz6E9EVgLBBrQiciIiInKPXQSax0oYiIxI966KRVWrZEREREJMEpoRMRERFJcEroRERERBKcEjoRERGRBKeETkRERCTBKaETERERSXBK6CRWphdmZt+LdwwnykvnQudC56JTz4VIq5TQibTNd+MdwAlE56KJzkUTnYsmOhfSaZTQiYiIiCQ4JXQiIiIiCU4JnUjbPB3vAE4gOhdNdC6a6Fw00bmQTqNnuYqIiIgkOPXQiYiIiCQ4JXQiMTKzy81srZl9bGb3xDueeDKzDWa20sw+MLOl8Y6nM5nZb81su5mtalaWb2ZzzGxd9GdePGPsLEc4FxPMbEv02vjAzK6MZ4ydwcx6m9l8M1ttZh+a2Z3R8pS8LiQ+lNCJxMDMPMBU4ApgCHC9mQ2Jb1Rxd7Fz7gzn3OfiHUgnexa4/JCye4C5zrlTgLnR31PBsxx+LgAmR6+NM5xzszs5pngIAf/unBsMnAfcFv3vQ6peFxIHSuhEYnMO8LFzrsw5Vwf8Ebg6zjFJHDjnFgKfHVJ8NfBc9P1zwDWdGlScHOFcpBznXLlz7v3o+73AaqCQFL0uJD6U0InEphDY3Oz3T6JlqcoBr5nZe2amxVOhwDlXDpH/uQM94hxPvN1uZiuiQ7IpNcxoZv2AM4F30XUhnUgJnUhsWnr0TipPEb/QOXcWkSHo28xsRLwDkhPGU0AxcAZQDkyMbzidx8yygBeBu5xze+Idj6QWJXQisfkE6N3s95OBT+MUS9w55z6N/twOvExkSDqVbTOzkwCiP7fHOZ64cc5tc841OOfCwDOkyLVhZulEkrnnnXMvRYt1XUinUUInEpt/AKeYWX8z8wFfA2bEOaa4MLNMM8tufA+MBFa1flTSmwF8K/r+W8Bf4xhLXDUmMFH/QgpcG2ZmwDRgtXNuUrNNui6k02hhYZEYRZdfeBzwAL91zj0Y55DiwsyKiPTKAXiB/0ulc2FmLwAXAd2AbcBPgVeAPwN9gE3AV5xzST9Z4Ajn4iIiw60O2AB8r/E+smRlZp8H3gRWAuFo8X1E7qNLuetC4kMJnYiIiEiC05CriIiISIJTQiciIiKS4JTQiYiIiCQ4JXQiIiIiCU4JnYiIiEiCU0InIiIikuCU0ImIiIgkOCV0IiIiIgnu/wF9Ug8knYPz6QAAAABJRU5ErkJggg==\n",
"text/plain": [
"
"
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"# Plot the distribution of illicit flows for the transformed data\n",
"partner_features_yeo = pd.DataFrame(partner_features_yeo,\n",
" index=partner_features.index,\n",
" columns=partner_features.columns)\n",
"random.seed(234)\n",
"fig, axes = joypy.joyplot(partner_features_yeo.sample(n=15, axis=1, random_state=234), \n",
" colormap=plt.cm.rainbow, figsize=(8,8),\n",
" title='Distribution of mis-invoicing across random sample of partner countries (Yeo-Johnson transformation)');"
]
},
{
"cell_type": "code",
"execution_count": 59,
"metadata": {
"slideshow": {
"slide_type": "skip"
},
"tags": [
"hide-cell"
]
},
"outputs": [
{
"data": {
"text/html": [
"\n",
"\n",
""
],
"text/plain": [
"alt.LayerChart(...)"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"# Biplot for the first 2 principal components for the transformed data (Yeo-Johnson)\n",
"biplot_PCA(partner_features_yeo, 10, 1, 2)"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"## Intra-African illicit financial flows"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"source": [
"The analysis will now be restricted to intra-African illicit financial flows, that is, illicit capital that originates from African countries and which flows to African countries too."
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"source": [
"### Data wrangling"
]
},
{
"cell_type": "code",
"execution_count": 60,
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"outputs": [],
"source": [
"# Import bilateral trade mis-invoicing data\n",
"IFF_Dest = pd.read_csv('Data/GER_Orig_Dest_Year_Africa.csv')\n",
"\n",
"# Restrict to destinations in Africa only\n",
"IFF_Dest_AFR = IFF_Dest[IFF_Dest['pRegion'] == 'Africa']\n",
"IFF_Dest_AFR = IFF_Dest_AFR.fillna(0).drop(columns=['reporter', 'rIncome', 'rDev', \n",
" 'partner', 'pRegion', 'pIncome', 'pDev',\n",
" 'Imp_IFF_lo', 'Exp_IFF_lo']) \\\n",
" .set_index(['reporter.ISO', 'year'])\n",
"\n",
"# Extract trade mis-invoicing in imports and exports, respectively\n",
"IFF_Dest_Imp_AFR = IFF_Dest_AFR[['partner.ISO', 'Imp_IFF_hi']]\n",
"IFF_Dest_Exp_AFR = IFF_Dest_AFR[['partner.ISO', 'Exp_IFF_hi']]"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"source": [
"Let's create the feature space from the African partner countries which are the destinations of illicit ouflows originating from the countries listed in `reporter.ISO`."
]
},
{
"cell_type": "code",
"execution_count": 61,
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"outputs": [
{
"data": {
"text/html": [
"
\n",
"\n",
"
\n",
" \n",
"
\n",
"
\n",
"
partner.ISO
\n",
"
AGO
\n",
"
BDI
\n",
"
BEN
\n",
"
BFA
\n",
"
BWA
\n",
"
CAF
\n",
"
CIV
\n",
"
CMR
\n",
"
COG
\n",
"
COM
\n",
"
...
\n",
"
STP
\n",
"
SWZ
\n",
"
SYC
\n",
"
TGO
\n",
"
TUN
\n",
"
TZA
\n",
"
UGA
\n",
"
ZAF
\n",
"
ZMB
\n",
"
ZWE
\n",
"
\n",
"
\n",
"
reporter.ISO
\n",
"
year
\n",
"
\n",
"
\n",
"
\n",
"
\n",
"
\n",
"
\n",
"
\n",
"
\n",
"
\n",
"
\n",
"
\n",
"
\n",
"
\n",
"
\n",
"
\n",
"
\n",
"
\n",
"
\n",
"
\n",
"
\n",
"
\n",
"
\n",
" \n",
" \n",
"
\n",
"
AGO
\n",
"
2009
\n",
"
0.0
\n",
"
0.0
\n",
"
0.0
\n",
"
0.0
\n",
"
0.000000e+00
\n",
"
0.0
\n",
"
7.356525e+05
\n",
"
0.000000
\n",
"
0.000000e+00
\n",
"
0.0
\n",
"
...
\n",
"
0.000000
\n",
"
0.0
\n",
"
0.0
\n",
"
0.000000
\n",
"
1.628157e+06
\n",
"
0.000000e+00
\n",
"
0.0
\n",
"
1.016827e+09
\n",
"
1.060946e+05
\n",
"
309894.487818
\n",
"
\n",
"
\n",
"
2010
\n",
"
0.0
\n",
"
0.0
\n",
"
0.0
\n",
"
0.0
\n",
"
2.025235e+05
\n",
"
0.0
\n",
"
5.577699e+07
\n",
"
53088.378146
\n",
"
1.402793e+08
\n",
"
0.0
\n",
"
...
\n",
"
0.000000
\n",
"
0.0
\n",
"
0.0
\n",
"
252999.300576
\n",
"
1.137066e+08
\n",
"
5.529461e+03
\n",
"
0.0
\n",
"
3.315930e+08
\n",
"
2.665205e+04
\n",
"
420951.156359
\n",
"
\n",
"
\n",
"
2011
\n",
"
0.0
\n",
"
0.0
\n",
"
0.0
\n",
"
0.0
\n",
"
5.501246e+03
\n",
"
0.0
\n",
"
6.262938e+06
\n",
"
257786.746458
\n",
"
3.466061e+07
\n",
"
0.0
\n",
"
...
\n",
"
0.000000
\n",
"
0.0
\n",
"
0.0
\n",
"
0.000000
\n",
"
4.623718e+07
\n",
"
1.745372e+06
\n",
"
0.0
\n",
"
3.281534e+08
\n",
"
4.525653e+05
\n",
"
0.000000
\n",
"
\n",
"
\n",
"
2012
\n",
"
0.0
\n",
"
0.0
\n",
"
0.0
\n",
"
0.0
\n",
"
0.000000e+00
\n",
"
0.0
\n",
"
1.425377e+07
\n",
"
222663.224270
\n",
"
2.587614e+07
\n",
"
0.0
\n",
"
...
\n",
"
8435.069683
\n",
"
0.0
\n",
"
0.0
\n",
"
0.000000
\n",
"
1.262796e+07
\n",
"
1.253616e+05
\n",
"
0.0
\n",
"
7.944924e+08
\n",
"
1.180964e+03
\n",
"
0.000000
\n",
"
\n",
"
\n",
"
2013
\n",
"
0.0
\n",
"
0.0
\n",
"
0.0
\n",
"
0.0
\n",
"
2.945193e+05
\n",
"
0.0
\n",
"
2.125395e+06
\n",
"
0.000000
\n",
"
4.357466e+06
\n",
"
0.0
\n",
"
...
\n",
"
957.605075
\n",
"
0.0
\n",
"
0.0
\n",
"
0.000000
\n",
"
4.438123e+06
\n",
"
1.035603e+05
\n",
"
0.0
\n",
"
4.272753e+08
\n",
"
2.855892e+05
\n",
"
0.000000
\n",
"
\n",
"
\n",
"
...
\n",
"
...
\n",
"
...
\n",
"
...
\n",
"
...
\n",
"
...
\n",
"
...
\n",
"
...
\n",
"
...
\n",
"
...
\n",
"
...
\n",
"
...
\n",
"
...
\n",
"
...
\n",
"
...
\n",
"
...
\n",
"
...
\n",
"
...
\n",
"
...
\n",
"
...
\n",
"
...
\n",
"
...
\n",
"
...
\n",
"
\n",
"
\n",
"
ZWE
\n",
"
2011
\n",
"
0.0
\n",
"
0.0
\n",
"
0.0
\n",
"
0.0
\n",
"
8.741233e+07
\n",
"
0.0
\n",
"
0.000000e+00
\n",
"
0.000000
\n",
"
0.000000e+00
\n",
"
0.0
\n",
"
...
\n",
"
0.000000
\n",
"
0.0
\n",
"
0.0
\n",
"
0.000000
\n",
"
0.000000e+00
\n",
"
1.295280e+06
\n",
"
0.0
\n",
"
3.088036e+09
\n",
"
5.016118e+07
\n",
"
0.000000
\n",
"
\n",
"
\n",
"
2012
\n",
"
0.0
\n",
"
0.0
\n",
"
0.0
\n",
"
0.0
\n",
"
3.187848e+07
\n",
"
0.0
\n",
"
0.000000e+00
\n",
"
0.000000
\n",
"
0.000000e+00
\n",
"
0.0
\n",
"
...
\n",
"
0.000000
\n",
"
0.0
\n",
"
0.0
\n",
"
0.000000
\n",
"
0.000000e+00
\n",
"
2.729399e+06
\n",
"
0.0
\n",
"
1.242790e+09
\n",
"
1.704507e+08
\n",
"
0.000000
\n",
"
\n",
"
\n",
"
2013
\n",
"
0.0
\n",
"
0.0
\n",
"
0.0
\n",
"
0.0
\n",
"
0.000000e+00
\n",
"
0.0
\n",
"
0.000000e+00
\n",
"
0.000000
\n",
"
0.000000e+00
\n",
"
0.0
\n",
"
...
\n",
"
0.000000
\n",
"
0.0
\n",
"
0.0
\n",
"
0.000000
\n",
"
0.000000e+00
\n",
"
0.000000e+00
\n",
"
0.0
\n",
"
0.000000e+00
\n",
"
0.000000e+00
\n",
"
0.000000
\n",
"
\n",
"
\n",
"
2014
\n",
"
0.0
\n",
"
0.0
\n",
"
0.0
\n",
"
0.0
\n",
"
0.000000e+00
\n",
"
0.0
\n",
"
0.000000e+00
\n",
"
0.000000
\n",
"
0.000000e+00
\n",
"
0.0
\n",
"
...
\n",
"
0.000000
\n",
"
0.0
\n",
"
0.0
\n",
"
0.000000
\n",
"
0.000000e+00
\n",
"
0.000000e+00
\n",
"
0.0
\n",
"
0.000000e+00
\n",
"
0.000000e+00
\n",
"
0.000000
\n",
"
\n",
"
\n",
"
2015
\n",
"
0.0
\n",
"
0.0
\n",
"
0.0
\n",
"
0.0
\n",
"
8.142369e+06
\n",
"
0.0
\n",
"
0.000000e+00
\n",
"
0.000000
\n",
"
0.000000e+00
\n",
"
0.0
\n",
"
...
\n",
"
0.000000
\n",
"
0.0
\n",
"
0.0
\n",
"
0.000000
\n",
"
0.000000e+00
\n",
"
8.238550e+06
\n",
"
0.0
\n",
"
6.474374e+08
\n",
"
0.000000e+00
\n",
"
0.000000
\n",
"
\n",
" \n",
"
\n",
"
604 rows × 46 columns
\n",
"
"
],
"text/plain": [
"partner.ISO AGO BDI BEN BFA BWA CAF CIV \\\n",
"reporter.ISO year \n",
"AGO 2009 0.0 0.0 0.0 0.0 0.000000e+00 0.0 7.356525e+05 \n",
" 2010 0.0 0.0 0.0 0.0 2.025235e+05 0.0 5.577699e+07 \n",
" 2011 0.0 0.0 0.0 0.0 5.501246e+03 0.0 6.262938e+06 \n",
" 2012 0.0 0.0 0.0 0.0 0.000000e+00 0.0 1.425377e+07 \n",
" 2013 0.0 0.0 0.0 0.0 2.945193e+05 0.0 2.125395e+06 \n",
"... ... ... ... ... ... ... ... \n",
"ZWE 2011 0.0 0.0 0.0 0.0 8.741233e+07 0.0 0.000000e+00 \n",
" 2012 0.0 0.0 0.0 0.0 3.187848e+07 0.0 0.000000e+00 \n",
" 2013 0.0 0.0 0.0 0.0 0.000000e+00 0.0 0.000000e+00 \n",
" 2014 0.0 0.0 0.0 0.0 0.000000e+00 0.0 0.000000e+00 \n",
" 2015 0.0 0.0 0.0 0.0 8.142369e+06 0.0 0.000000e+00 \n",
"\n",
"partner.ISO CMR COG COM ... STP SWZ \\\n",
"reporter.ISO year ... \n",
"AGO 2009 0.000000 0.000000e+00 0.0 ... 0.000000 0.0 \n",
" 2010 53088.378146 1.402793e+08 0.0 ... 0.000000 0.0 \n",
" 2011 257786.746458 3.466061e+07 0.0 ... 0.000000 0.0 \n",
" 2012 222663.224270 2.587614e+07 0.0 ... 8435.069683 0.0 \n",
" 2013 0.000000 4.357466e+06 0.0 ... 957.605075 0.0 \n",
"... ... ... ... ... ... ... \n",
"ZWE 2011 0.000000 0.000000e+00 0.0 ... 0.000000 0.0 \n",
" 2012 0.000000 0.000000e+00 0.0 ... 0.000000 0.0 \n",
" 2013 0.000000 0.000000e+00 0.0 ... 0.000000 0.0 \n",
" 2014 0.000000 0.000000e+00 0.0 ... 0.000000 0.0 \n",
" 2015 0.000000 0.000000e+00 0.0 ... 0.000000 0.0 \n",
"\n",
"partner.ISO SYC TGO TUN TZA UGA \\\n",
"reporter.ISO year \n",
"AGO 2009 0.0 0.000000 1.628157e+06 0.000000e+00 0.0 \n",
" 2010 0.0 252999.300576 1.137066e+08 5.529461e+03 0.0 \n",
" 2011 0.0 0.000000 4.623718e+07 1.745372e+06 0.0 \n",
" 2012 0.0 0.000000 1.262796e+07 1.253616e+05 0.0 \n",
" 2013 0.0 0.000000 4.438123e+06 1.035603e+05 0.0 \n",
"... ... ... ... ... ... \n",
"ZWE 2011 0.0 0.000000 0.000000e+00 1.295280e+06 0.0 \n",
" 2012 0.0 0.000000 0.000000e+00 2.729399e+06 0.0 \n",
" 2013 0.0 0.000000 0.000000e+00 0.000000e+00 0.0 \n",
" 2014 0.0 0.000000 0.000000e+00 0.000000e+00 0.0 \n",
" 2015 0.0 0.000000 0.000000e+00 8.238550e+06 0.0 \n",
"\n",
"partner.ISO ZAF ZMB ZWE \n",
"reporter.ISO year \n",
"AGO 2009 1.016827e+09 1.060946e+05 309894.487818 \n",
" 2010 3.315930e+08 2.665205e+04 420951.156359 \n",
" 2011 3.281534e+08 4.525653e+05 0.000000 \n",
" 2012 7.944924e+08 1.180964e+03 0.000000 \n",
" 2013 4.272753e+08 2.855892e+05 0.000000 \n",
"... ... ... ... \n",
"ZWE 2011 3.088036e+09 5.016118e+07 0.000000 \n",
" 2012 1.242790e+09 1.704507e+08 0.000000 \n",
" 2013 0.000000e+00 0.000000e+00 0.000000 \n",
" 2014 0.000000e+00 0.000000e+00 0.000000 \n",
" 2015 6.474374e+08 0.000000e+00 0.000000 \n",
"\n",
"[604 rows x 46 columns]"
]
},
"execution_count": 61,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"partner_features_AFR = create_features(IFF_Dest_Imp_AFR, 'Imp_IFF_hi', \n",
" features='partner.ISO', obs='reporter.ISO')\n",
"partner_features_AFR"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"source": [
"There are strong regional dynamics in international trade, so it is useful to extract information on which regions the countries belong to. The `crosswalk` data-set includes information on the geographical groupings of each country. The codes are taken from the UN Statistics Division M49 standard ()."
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"source": [
"The `UN_Intermediate_Region` code is nested within the `UN_Sub-region` code. In the M49 standard grouping for Africa, there are two sub-regions: Northern Africa and Sub-Saharan Africa. The latter contains further geographical groupings: Eastern Africa, Middle Africa, Southern Africa, Western Africa. Therefore, we need to reconcile both so that the regional labels include Northern Africa and the 4 groupings within Sub-Saharan Africa. The code below achieves this, and this is automatized by the `region_labels()` function further down."
]
},
{
"cell_type": "code",
"execution_count": 62,
"metadata": {
"slideshow": {
"slide_type": "skip"
},
"tags": [
"hide-cell"
]
},
"outputs": [
{
"data": {
"text/plain": [
"['DZA', 'EGY', 'LBY', 'MAR', 'SDN', 'TUN']"
]
},
"execution_count": 62,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# Merge in UN Intermediate Region groups\n",
"partner_features_AFR = pd.merge(left=partner_features_AFR.reset_index(), \n",
" right=crosswalk[['ISO3166.3', 'UN_Intermediate_Region']].drop_duplicates('ISO3166.3'), \n",
" how='left', \n",
" left_on='reporter.ISO', right_on='ISO3166.3')\n",
"\n",
"# Which African countries do not have a UN Intermediate region?\n",
"noregion_mask = partner_features_AFR['UN_Intermediate_Region'].isnull()\n",
"countries_noregion = partner_features_AFR[noregion_mask]['reporter.ISO'].unique().tolist()\n",
"countries_noregion"
]
},
{
"cell_type": "code",
"execution_count": 63,
"metadata": {
"slideshow": {
"slide_type": "skip"
},
"tags": [
"hide-cell"
]
},
"outputs": [
{
"data": {
"text/plain": [
"array(['Northern Africa'], dtype=object)"
]
},
"execution_count": 63,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# Which UN Sub-region do those countries belong to?\n",
"crosswalk[crosswalk['ISO3166.3'].isin(countries_noregion)]['UN_Sub-region'].unique()"
]
},
{
"cell_type": "code",
"execution_count": 64,
"metadata": {
"slideshow": {
"slide_type": "skip"
},
"tags": [
"hide-cell"
]
},
"outputs": [],
"source": [
"# Assign Northern Africa as a group for those countries\n",
"partner_features_AFR.loc[partner_features_AFR['reporter.ISO'].isin(countries_noregion), 'UN_Intermediate_Region'] = 'Northern Africa'\n",
"partner_features_AFR = partner_features_AFR.set_index(['reporter.ISO', 'year']).drop(columns=['ISO3166.3', 'UN_Intermediate_Region'])"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"source": [
"The figure below displays the biplot for the first two principal components estimated using the intra-African bilateral matrix of illicit flows."
]
},
{
"cell_type": "code",
"execution_count": 65,
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"outputs": [
{
"data": {
"text/html": [
"\n",
"\n",
""
],
"text/plain": [
"alt.LayerChart(...)"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"biplot_PCA(partner_features_AFR, partner_features_AFR.shape[1], 1, 2)"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"source": [
"The countries with the top 3 loadings on the first principal component are Mozambique (MOZ), Madagascar (MDG) and Comoros (COM). Madagascar and the Comoros are islands in the [Mozambique channel](https://goo.gl/maps/wY7AajqRV9AoD3cz5), where two well-known conduits of illicit financial flows are located: the Seychelles and Mauritius."
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"source": [
"The second principal component seems to capture Northern Africa, with Algeria and Tunisia scoring the second and third largest loading, respectively."
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"### Removing outliers"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"source": [
"There are vibrant debates in the field on estimating trade mis-invoicing based on mismatches in official trade data, much of which is outside the scope of this project. However, suffice to say that there are some outliers that might have large values of mis-invoicing due to benign reasons. For example, South Africa does not report gold exports to UN Comtrade (the underlying source of official trade statistis), and so any discrepancies found by looking at its mirrored trade statistics would result in spurious mis-invoicing estimates. "
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"source": [
"I remove outliers based on extreme values on the first two principal components. This effectively removes most of the observations for South Africa. Further work is needed, though, to remove outliers based on domain knowledge, especially if using this data to do a deep dive on certain dimensions (rather than looking at aggregate patterns, as is the case here)."
]
},
{
"cell_type": "code",
"execution_count": 66,
"metadata": {
"slideshow": {
"slide_type": "skip"
},
"tags": [
"hide-output"
]
},
"outputs": [
{
"data": {
"text/plain": [
"MultiIndex([('AGO', 2010),\n",
" ('CIV', 2013),\n",
" ('EGY', 2012),\n",
" ('GHA', 2002),\n",
" ('MAR', 2005),\n",
" ('MAR', 2006),\n",
" ('MAR', 2007),\n",
" ('MAR', 2008),\n",
" ('MAR', 2009),\n",
" ('MAR', 2010),\n",
" ('MAR', 2011),\n",
" ('MAR', 2012),\n",
" ('NGA', 2011),\n",
" ('ZAF', 2005),\n",
" ('ZAF', 2006),\n",
" ('ZAF', 2008),\n",
" ('ZAF', 2010),\n",
" ('ZAF', 2011),\n",
" ('ZAF', 2012),\n",
" ('ZAF', 2013),\n",
" ('ZAF', 2014),\n",
" ('ZAF', 2015),\n",
" ('ZAF', 2016)],\n",
" names=['reporter.ISO', 'year'])"
]
},
"execution_count": 66,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"features_data_std = StandardScaler().fit_transform(partner_features_AFR)\n",
"pca = PCA(n_components=partner_features_AFR.shape[1])\n",
"princ_comp = pca.fit_transform(features_data_std)\n",
"outlying = (princ_comp[:,0] > 6) | (princ_comp[:,1] > 4)\n",
"partner_features_AFR[outlying].index"
]
},
{
"cell_type": "code",
"execution_count": 67,
"metadata": {
"slideshow": {
"slide_type": "-"
}
},
"outputs": [],
"source": [
"partner_features_AFR_noout = partner_features_AFR[~outlying]"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"source": [
"The figure below displays the projection of the data without outliers on the first 2 principal components. Some interesting regional patterns appear.\n",
"\n",
"Top loadings on the first principal component seem to capture a western African hub, with Cote d'Ivoire and Togo scoring highly. By contrast, the second principal component seems to recover a southern African hub, with top loadings going to South Africa, Malawi, and Botswana."
]
},
{
"cell_type": "code",
"execution_count": 68,
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"outputs": [
{
"data": {
"text/html": [
"\n",
"\n",
""
],
"text/plain": [
"alt.LayerChart(...)"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"biplot_PCA(partner_features_AFR_noout, 46, 1, 2)"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"source": [
"In order to discern better any groupings, the next section will color the observations according to an aggregate class label."
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"### Coloring by class label"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"source": [
"The function `region_labels()` extracts the regional labels from the `crosswalk` and further divides the \"Sub-Saharan Africa\" group into its 4 corresponding subgroups, as discussed above."
]
},
{
"cell_type": "code",
"execution_count": 69,
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"outputs": [],
"source": [
"def region_labels(features_data):\n",
" \"\"\"\n",
" Return regional labels for countries in the data\n",
" \n",
" features_data: as Pandas dataframe, data-set of features\n",
" \"\"\"\n",
" # Extract observation labels from features data\n",
" obs_labels = pd.DataFrame(features_data.reset_index().set_index('reporter.ISO').index)\n",
"\n",
" # Merge with UN intermediate regions from crosswalk\n",
" obs_labels = pd.merge(left=obs_labels,\n",
" right=crosswalk[['ISO3166.3', 'UN_Intermediate_Region']].drop_duplicates('ISO3166.3'), \n",
" how='left', \n",
" left_on='reporter.ISO', right_on='ISO3166.3') \\\n",
" .drop(columns='ISO3166.3')\n",
"\n",
" # Create a mask for the Northern African regions and replace the missing intermediate region\n",
" noregion_mask = obs_labels['UN_Intermediate_Region'].isnull()\n",
" countries_noregion = obs_labels[noregion_mask]['reporter.ISO'].unique().tolist()\n",
" obs_labels.loc[obs_labels['reporter.ISO'].isin(countries_noregion), 'UN_Intermediate_Region'] = 'Northern Africa'\n",
"\n",
" return obs_labels"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"source": [
"The function `biplot_PCA_classes()` projects the data in the two principal components chosen by the user, and further colors the observations either according to their UN regional grouping (by specifying `classes='UN_Intermediate_Region'`) or according to their World Bank income group classification (by specifying `classes='Income group (World Bank)'`)."
]
},
{
"cell_type": "code",
"execution_count": 70,
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"outputs": [],
"source": [
"def biplot_PCA_classes(features_data, nPC=2, firstPC=1, secondPC=2, classes='UN_Intermediate_Region'):\n",
" \"\"\"\n",
" Projects the data in the 2-dimensional space spanned by 2 principal components\n",
" chosen by the user, along with a bi-plot of the top 3 loadings per PC, and colors\n",
" by class label.\n",
"\n",
" Args:\n",
" features_data: data-set of features\n",
" nPC: number of principal components\n",
" firstPC: integer denoting first principal component to plot in bi-plot\n",
" secondPC: integer denoting second principal component to plot in bi-plot\n",
" classes: {'UN_Intermediate_Region', 'Income group (World Bank)'}, as string, class label\n",
" by which to color observations\n",
" Returns:\n",
" plot (interactive)\n",
" pca_loadings (if show_loadings=True)\n",
" \"\"\"\n",
" \n",
" # Unit of observation is the reporting country\n",
" obs='reporter.ISO'\n",
" \n",
" # Run PCA (standardize beforehand)\n",
" features_data_std = StandardScaler().fit_transform(features_data)\n",
"# features_data_std = power_transform(features_data, method='yeo-johnson', standardize=True)\n",
" pca = PCA(n_components=nPC, random_state=234)\n",
" princ_comp = pca.fit_transform(features_data_std)\n",
"\n",
" # Loadings\n",
" cols = ['PC' + str(c+1) for c in np.arange(nPC)]\n",
" pca_loadings = pd.DataFrame(pca.components_.T, \n",
" columns=cols,\n",
" index=list(features_data.columns))\n",
" \n",
" # Scores\n",
" pca_scores = pd.DataFrame(princ_comp, \n",
" columns=cols)\n",
" pca_scores[obs] = features_data.reset_index()[obs].values.tolist()\n",
" pca_scores['year'] = features_data.reset_index()['year'].values.tolist()\n",
" \n",
" score_PC1 = princ_comp[:,firstPC-1]\n",
" score_PC2 = princ_comp[:,secondPC-1]\n",
" \n",
" # Plot data\n",
" plot_data = pd.merge(pca_scores, obs_info, on=[obs, 'year'])\n",
" tooltip_obs = ['reporter', 'year', 'Income group (World Bank)', 'Country status (UN)']\n",
" \n",
" obs_labels = region_labels(features_data)\n",
" plot_data = pd.merge(left=plot_data, right=obs_labels.drop_duplicates('reporter.ISO'), on='reporter.ISO')\n",
" \n",
" if classes == 'UN_Intermediate_Region':\n",
" color_scheme = 'paired'\n",
" else:\n",
" color_scheme = 'dark2'\n",
"\n",
" # Return chosen PCs to plot\n",
" PC1 = 'PC'+str(firstPC)\n",
" PC2 = 'PC'+str(secondPC)\n",
" \n",
" # Top loadings (in absolute value)\n",
" # TO DO: use dict to iterate over\n",
" toploadings_PC1 = pca_loadings.apply(lambda x: abs(x)).sort_values(by=PC1).tail(3)[[PC1, PC2]]\n",
" toploadings_PC2 = pca_loadings.apply(lambda x: abs(x)).sort_values(by=PC2).tail(3)[[PC1, PC2]]\n",
"\n",
" originsPC1 = pd.DataFrame({'index':toploadings_PC1.index.tolist(), \n",
" PC1: np.zeros(3), \n",
" PC2: np.zeros(3)})\n",
" originsPC2 = pd.DataFrame({'index':toploadings_PC2.index.tolist(), \n",
" PC1: np.zeros(3), \n",
" PC2: np.zeros(3)})\n",
" \n",
" toploadings_PC1 = pd.concat([toploadings_PC1.reset_index(), originsPC1], axis=0)\n",
" toploadings_PC2 = pd.concat([toploadings_PC2.reset_index(), originsPC2], axis=0)\n",
"\n",
" toploadings_PC1[PC1] = toploadings_PC1[PC1]*max(score_PC1)*1.5\n",
" toploadings_PC1[PC2] = toploadings_PC1[PC2]*max(score_PC2)*1.5\n",
" toploadings_PC2[PC1] = toploadings_PC2[PC1]*max(score_PC1)*1.5\n",
" toploadings_PC2[PC2] = toploadings_PC2[PC2]*max(score_PC2)*1.5\n",
" \n",
" # Project top 3 loadings over the space spanned by 2 principal components\n",
" lines = alt.Chart().mark_line().encode()\n",
" for color, i, dataset in zip(['#440154FF', '#21908CFF'], [0,1], [toploadings_PC1, toploadings_PC2]):\n",
" lines[i] = alt.Chart(dataset).mark_line(color=color).encode(\n",
" x= PC1 +':Q',\n",
" y= PC2 +':Q',\n",
" detail='index'\n",
" ).properties(\n",
" width=400,\n",
" height=400\n",
" )\n",
" \n",
" # Add labels to the loadings\n",
" text=alt.Chart().mark_text().encode()\n",
" for color, i, dataset in zip(['#440154FF', '#21908CFF'], [0, 1], [toploadings_PC1[0:3], toploadings_PC2[0:3]]):\n",
" text[i] = alt.Chart(dataset).mark_text(\n",
" align='left',\n",
" baseline='bottom',\n",
" color=color\n",
" ).encode(\n",
" x= PC1 +':Q',\n",
" y= PC2 +':Q',\n",
" text='index'\n",
" )\n",
" \n",
" # Scatter plot colored by observation class label\n",
" points = alt.Chart(plot_data).mark_circle(size=60).encode(\n",
" x=alt.X(PC1, axis=alt.Axis(title='Principal Component ' + str(firstPC))),\n",
" y=alt.X(PC2, axis=alt.Axis(title='Principal Component ' + str(secondPC))),\n",
" color=alt.Color(classes, scale=alt.Scale(scheme=color_scheme),\n",
" legend=alt.Legend(orient='right')),\n",
" tooltip=tooltip_obs\n",
" ).interactive()\n",
" \n",
" chart = (points + lines[0] + lines[1] + text[0] + text[1]) \n",
" chart.display()"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"source": [
"The following graphs suggest that the first two components of PCA seem to partition the feature space remarkably well according to regional groupings, and to a lesser extent according to income grouping. It should be noted that there is less variation in the income groupings in Africa as a whole, with few countries belong to the high income group.\n",
"\n",
"The biplot which uses African partner countries as the feature space (after removing outliers) and which colors by regional grouping is the most striking (scroll down below to see it). Recall that the loadings refer to the *partner* countries (i.e. the destinations of the illicit outflows) which have the heaviest loadings on the first/second principal components, while the observations are colored according to the *reporter* country (i.e. the origin of the illicit flow). This biplot suggests that the partner features which have the highest weight on the first principal components correspond to a western African hub (Cote d'Ivoire and Togo), and that those observations with the highest principal component scores in that rotated space correspond to western African reporting countries.\n",
"\n",
"Similarly, the largest weights on the second principal component refer to a southern African partner hub (South Africa, Malawi, and Botswana), while the observations with the highest scores correspond to northern and southern African countries.\n",
"\n",
"Therefore, it appears that there are strong sub-regional dynamics in intra-African illicit financial flows. The policy implication of this finding is that existing sub-regional policy initiatives could be leveraged to combat illicit financial flows within the continent. For example, the Economic Community of West African States (ECOWAS) could anchor policy efforts in western Africa while the East African Community (EAC) could attend to the east."
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"source": [
"**For sector features**"
]
},
{
"cell_type": "code",
"execution_count": 71,
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"outputs": [
{
"data": {
"text/html": [
"\n",
"\n",
""
],
"text/plain": [
"alt.LayerChart(...)"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"biplot_PCA_classes(sector_features, 21, 1, 2, classes='UN_Intermediate_Region')"
]
},
{
"cell_type": "code",
"execution_count": 72,
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"outputs": [
{
"data": {
"text/html": [
"\n",
"\n",
""
],
"text/plain": [
"alt.LayerChart(...)"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"biplot_PCA_classes(sector_features, 21, 1, 2, classes='Income group (World Bank)')"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"source": [
"**For partner features**"
]
},
{
"cell_type": "code",
"execution_count": 73,
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"outputs": [
{
"data": {
"text/html": [
"\n",
"\n",
""
],
"text/plain": [
"alt.LayerChart(...)"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"biplot_PCA_classes(partner_features, 46, 1, 2)"
]
},
{
"cell_type": "code",
"execution_count": 74,
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"outputs": [
{
"data": {
"text/html": [
"\n",
"\n",
""
],
"text/plain": [
"alt.LayerChart(...)"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"biplot_PCA_classes(partner_features, 46, 1, 2, classes='Income group (World Bank)')"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"source": [
"**For partner features, restricted to African partners**"
]
},
{
"cell_type": "code",
"execution_count": 75,
"metadata": {
"slideshow": {
"slide_type": "skip"
},
"tags": [
"hide-cell"
]
},
"outputs": [
{
"data": {
"text/html": [
"\n",
"\n",
""
],
"text/plain": [
"alt.LayerChart(...)"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"biplot_PCA_classes(partner_features_AFR, 46, 1, 2)"
]
},
{
"cell_type": "code",
"execution_count": 76,
"metadata": {
"slideshow": {
"slide_type": "skip"
},
"tags": [
"hide-cell"
]
},
"outputs": [
{
"data": {
"text/html": [
"\n",
"\n",
""
],
"text/plain": [
"alt.LayerChart(...)"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"biplot_PCA_classes(partner_features_AFR, 46, 1, 2, classes='Income group (World Bank)')"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"source": [
"**For partner features, restricted to African partners, without outliers**"
]
},
{
"cell_type": "code",
"execution_count": 77,
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"outputs": [
{
"data": {
"text/html": [
"\n",
"\n",
""
],
"text/plain": [
"alt.LayerChart(...)"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"biplot_PCA_classes(partner_features_AFR_noout, 46, 1, 2)"
]
},
{
"cell_type": "code",
"execution_count": 78,
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"outputs": [
{
"data": {
"text/html": [
"\n",
"\n",
""
],
"text/plain": [
"alt.LayerChart(...)"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"biplot_PCA_classes(partner_features_AFR_noout, 46, 1, 2, classes='Income group (World Bank)')"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"## Clustering"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"### Agglomerative clustering"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"source": [
"This section investigates clustering techniques to see if they recover some of the groupings observed above."
]
},
{
"cell_type": "code",
"execution_count": 79,
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"outputs": [],
"source": [
"# Run PCA on first 2 principal components on intra-African partners, without outliers\n",
"features_data_std = StandardScaler().fit_transform(partner_features_AFR_noout)\n",
"pca = PCA(n_components=10)\n",
"princ_comp = pca.fit_transform(features_data_std)\n",
"X = princ_comp[:,[0,1]]"
]
},
{
"cell_type": "code",
"execution_count": 80,
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAlIAAAF1CAYAAAAjngRgAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4yLjEsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy+j8jraAAAgAElEQVR4nOzdd5xU1fnH8c8zZRu99440QYqIgl1ULNi7xh5rjNEYa0w0MWo0iT+7iTERY7AXsECsqKAUAUWkIyC9s8C2qef3xwy4y85SZmdntnzfrxcvdu/cOfeZu3d3njnn3OeYcw4RERER2XeeTAcgIiIiUlMpkRIRERFJkhIpERERkSQpkRIRERFJkhIpERERkSQpkRIRERFJkhIpkV2Y2WVmNinTcSTDzC4ysw/TeLzOZubMzJeuY+4mlr+b2e8yHccOZtbRzArMzJvpWCor/jPuXsFjn5nZz+Nf7/X1V5N/z0RKUyIlNVr8j/gWM8vOdCzpliiJcc6Nds4dn8m4klH6zThZzrlrnXP3pSqmynLOLXfO1XfORVLZrpkNNbNtpRM0M/tnBdv+nspj70lNvf5EKkOJlNRYZtYZOBxwwKkZDaYK1IaejHSpY+dqOuAFBpXadjiwepdtRwBf7EvD1aFnUaSmUSIlNdklwBRgFHBp6QfMrJmZvRv/lP61mf2p9DCCmR1vZgvMbKuZPW1mn1fUI2Jmw+JtbI3/P6zUY5/F2/4qPozzbvzYo0sdu3Op/XuZ2Udmtjl+/HNLPTbKzJ4xs3FmVggcbWYnm9k38bZWmNm9pULb8SaZHz/20NLDJfGhrr/u8lrGmtmv41+3NbM3zWyDmS01sxsrOtFmlmtmfzOzH+PnYZKZ5SbYb5mZHVvq+3vN7L/xr3PM7L9mtsnM8uPnppWZ3U8sEXgy/jqeTPJcjTKzP8UfP8rMVprZLWa23szWmNnlpZ6/2+tjl9d0lJmtrOh1mtkQM5seb2udmT0S316mxzB+rdxnZl+a2XYz+9DMmpdq85L4+d1kZr/b9Vzu4JwLEbvuj4g/ryWQBby6y7YewBfx+CbHz/kaM3vSzLJKHdeZ2S/MbBGwKL7t1vi+q83sikTnpYJzVWa4Lt72tWa2yGI9x0+ZmVXw3L/Er6tGe7jud3uuzMxjZneY2Q/xx18zs6Z7+xpE9pUSKanJLgFGx/+NMLNWpR57CigEWhNLsnYmWvE3rzeAO4FmwAJgGAnE/wC/Dzwe3/cR4H0za1Zqt/OBi4F2QDdgMvA80BSYB9wTb6se8BHwEtASuAB42sz2L9XWhcD9QANgUvw1XAI0Bk4GrjOz0+P7HhH/v3F8CGnyLuG/BJy3443LzJoAxwOvmJkHeBeYFY97OHCTmY1IdB6AvwIHxs9TU+A2IFrBvhW5FGgEdCB2Lq8Fip1zvwUmAjfEX8cNSZ6rXbWOH68dcCXwVPwcwG6ujyQ8BjzmnGtI7Of/2m72vRC4nNhrygJ+A2BmfYCngYuANqXirsgX/PTzP4LY65+0y7alzrmVQAS4GWgODCX2s75+l/ZOBw4G+pjZCfG4jgP2A8olc/toJHAQ0B84FyhzjcUTn38CBwDHO+e2spvrfi/O1Y3x13Mk0BbYQuznLVIllEhJjWRmhwGdgNecczOAH4i9Se0Y5jkLuMc5V+Scmwu8UOrpJwFznHNvOefCxJKktRUc6mRgkXPuRedc2Dn3MjAfOKXUPs87536IvwGMB35wzn0cb/t1YGB8v5HAMufc8/G2ZgJvAmeXamusc+5L51zUOVfinPvMOTc7/v13wMvE3iD2xkRiw56Hx78/G5jsnFtN7I2thXPuj865oHNuCfBPYklhGfGk6wrgV865Vc65iHPuK+dcYC/j2CFELIHqHm9jhnNuWwX77vO5quB4f3TOhZxz44ACoOdeXB/7KgR0N7PmzrkC59yU3ez7vHNuoXOumFjCNSC+/WzgXefcJOdcEPg9sZ9dRT4HDosnyYcT+1lPBg4pte1zgPh5nhI/j8uAf1D+GnrQObc5Hte58Ti/d84VAvfu7YmowJ+dc/nOueXAhFKvGcBP7JpuCpzinCuKx7y7635P5+oa4LfOuZXxa/Re4GzTsKVUESVSUlNdCnzonNsY//4lfupVaAH4gBWl9i/9ddvS37vYyt1lhm522ffHXbb9SNlPwOtKfV2c4Pv68a87AQfHh1jyzSyf2Kfq1hXEiZkdbGYTLDb8tpVYL05z9kL8db1CrDcHYonm6FKxtN0llruAVuVbojmQQyxZrYwXgQ+I9YitNrOHzcxfwb77fK4S2BRPZncoIvaz2NP1sa+uJDaMNj8+TDhyN/uWTth3xAPlr8kiYNNu2pkSf25fYr1PE51zBfE2dmz7AsDMepjZe2a21sy2AQ9Q/hqq8PeD8tf/vqroNQN0B04D/hBPiojHvLvrfk/nqhPwdqnrZh6xXrlE17ZIpSmRkhrHYnNzzgWOjL85rCU2dNHfzPoDG4Aw0L7U0zqU+npN6cfin+BL71vaamJ/mEvrCKxKIvQVwOfOucal/tV3zl1Xap9deyFeAt4BOjjnGgF/B6yCfRN5mdin8U7Ehm7eLBXL0l1iaeCcOylBGxuBEmLDVntSCOSV+n5n4hPvGfqDc64PsSHCkcSGbxK9lmTO1d7a0/WxqzKvKd6j1WJnEM4tcs5dQGy47iHgjfjQ5L7Y9ZrMJdZ7l1C8B+5rYuewjXNufvyhifFtB/DTHLpniPWi7hcffryLn66hnU3uEkvp89FxH1/LvphHbKhzvJn1LLV9d9f9ns7VCuDEXa6dHOdcMr+zInukREpqotOJfcLsQ2yYYADQm9ibyCUudrv5W8C9ZpZnZr346Q0bYnOe+pnZ6fHu/l9QtqejtHFADzO70Mx8ZnZe/LjvJRH3e/G2LjYzf/zfQWbWezfPaQBsds6VmNkQ4sOXcRuIzVPqWtGTnXPfxPd7DvjAOZcff2gasM3MbrfYRHKvmfU1s4MStBEF/g08YrEJ6l6LTWxPVHLiW+D8+GsbTKmhODM72sz6xRORbcSGxHaUBli3y+tI5lztlb24Pna1EMiJT4D2A3cDO1+7mf3MzFrEz9OO87uvJQ/eAE6x2I0NWcAfKJ/s7OoL4Cbgq1LbJsW3rXXO7ehBbEDsfBfEX+t17N5rwGVm1sfM8ojP8asq8eHyu4CPzWxHsr67635P5+rvwP3xDw+YWQszO60qX4PUbUqkpCa6lNgcjuXOubU7/gFPAhfFk6MbiE1CXUtsSOllIAAQHw48B3iY2JBAH2K3lJeb8+Oc20TsE/4t8X1vA0aWGlLca8657cQme59PrKdrLbEejN3VwLoe+KOZbSc2F2TnROb4kMb9wJfxYYxDKmjjZWIThl8q9dwIsXleA4ClxHqdniN2zhL5DTCbWC/I5njcif5+/I5Yz9UWYm9wL5V6rDWxN8FtxHoiPgf+G3/sMWI9Z1vM7PEkz9W+qPD62FV87tv1xM7PKmI9VKWHgk8A5phZQfx1nF/BnK0KOefmAL8kNhS7BtgOrK8oprjPifWClZ5oPym+rXTZg98QS0S2E5sH9+oeYhkPPAp8CiyO/1+lnHMvAH8EPrXYXa67u+73dK4eI9ab9WH8+VOI9caKVAmLTaMQqd3M7CGgtXOu3N1Z8cnUK4GLnHMT0h6cZNzuro9MMLP6xHq39nPOLc10PNWZzpVkmnqkpFayWA2iAyxmCLEJwW+XenyEmTWOD0/tmDOyu7utpBbZ0/WRoZhOiQ811iNWbmI2sCyTMVVXOldSnSiRktqqAbF5MIXEhgX+Bowt9fhQYnehbSQ2xHV6/NZvqRv2dH1kwmnEhjFXE6vfdL7TkEFFdK6k2tDQnoiIiEiS1CMlIiIikiQlUiIiIiJJykjJ/ObNm7vOnTtn4tAiIiIi+2TGjBkbnXMtEj2WkUSqc+fOTJ8+PROHFhEREdknZlbhUkka2hMRERFJkhIpERERkSQpkRIRERFJkhIpERERkSQpkRIRERFJkhIpERERkSQpkRIRERFJkhIpERERkSQpkSrFOUcoEsl0GCIiIlJDZKSyeXXjnGP07Fk8OvUrthQX06JePW4dehhn9emb6dBERESkGlMiBYyePYsHJ31OcTgMwPrCQn7/2Sf4vV5O7dk7w9GJiIhIdaWhPeCxqZN3JlE7FIfDPDLlywxFJCIiIjVBnU+kwtEom4uLEj62Zvv2NEcjIiIiNUmdT6R8Hg+t6tVP+FjHRo3THI2IiIjUJHU+kQK49dDDyfGVnS6W4/Nxx6FHZCgiERERqQk02Rw4o1cf/B4Pj0z5klXbttGpcWNuH3YEw7t2y3RoIiIiUo0pkYob2aMXI3v0ynQYIiIiUoNoaE9EREQkSUqkRERERJKkREpEREQkSXudSJnZv81svZl9X2pbUzP7yMwWxf9vUjVhioiIiFQ/+9IjNQo4YZdtdwCfOOf2Az6Jfy8iIiJSJ+x1IuWc+wLYvMvm04AX4l+/AJyeorhEREREqr3KzpFq5ZxbAxD/v2XlQxIRERGpGdI22dzMrjaz6WY2fcOGDek6rIiIiEiVqWwitc7M2gDE/19f0Y7OuWedc4Odc4NbtGhRycOKiIiIZF5lE6l3gEvjX18KjK1keyIiIiI1xr6UP3gZmAz0NLOVZnYl8GfgODNbBBwX/15ERESkTtjrtfaccxdU8NDwFMUiIiIiUqOosrmIiIhIkpRIiYiIiCRJiZSIiIhIkpRIiYiIiCRJiZSIiIhIkpRIiYiIiCRJiZSIiIhIkpRIiYiIiCRJiZSIiIhIkpRIiYiIiCRJiZSIiIhIkpRIiYiIiCRJiZSIiIhIkpRIiYiIiCRJiZSIiIhIkpRIiYiIiCRJiZSIiIhIkpRIiYiIiCRJiZSIiIhIkpRIiYiIiCRJiZSIiIhIkpRIiYiIiCRJiZSIiIhIkpRIiYiIiCRJiZSIiIhIkpRIiYiIiCRJiZSIiIhIkpRIiYiIiCRJiZSIiIhIkpRIiYiIiCTJl+kAaqJFmzYxeva3rCko4MhOnTmjVx9y/f5MhyUiIiJppkRqH334wyJu+mAcoUiEiHNMWr6Mf387gzHn/Yz6WVmZDi9jlm/N53+LFxFxUY7v2p1uTZtlOiQREZEqp0RqH4QiEW77+ANKwuGd24rDYVZt28YL387kF0MOyWB0mfPirG94YNLnRJ3DAU9Mm8K1Bw7hxoOHZjo0ERGRKqU5UvtgwaaNRKKu3PZAJML7ixdmIKLMW7N9Ow9M+pxAJEIoGiUcjVISDvP3GdNYuGljpsMTERGpUuqR2gf1srKIuGjCxxrU0WG9j5YsxrBy20ORCOMXL6RHs+YZiEpEapOPJs7jH6Mnsm7jNlo0bcDVFx7GCUftn+mwRIAU9UiZ2c1mNsfMvjezl80sJxXtVjddGjehU6PGeKxs4pDn83Np/4EZiiqzzIwEeVTssYoeEBHZSx9Pmsefn/6AtRu24Rys37Sdvzz7EeMnzMl0aCJAChIpM2sH3AgMds71BbzA+ZVtt7r65ymn065BQ+r5/dTzZ5Ht9XJ+336c2L1HpkPLiOO6dsO58sOdfq+3zp4TEUmdf4yeRCAYLrMtEAjz7MsTMxSRSFmpGtrzAblmFgLygNUparfaad+wERMuvZLpq1exsaiIga3b0KZBg0yHlTGt6zfg90cewx8//xQA52K9VDcOGcp+zXTnnohUzrqN2xJu37CpAOdcrFdcJIMqnUg551aZ2V+B5UAx8KFz7sNd9zOzq4GrATp27FjZw2aUx4wh7dpnOoxq44K+B3BEp858+MNiItEox3btRufGTTIdlojUAq1bNGT1uq3ltrdoVl9JlFQLqRjaawKcBnQB2gL1zOxnu+7nnHvWOTfYOTe4RYsWlT2sVDPtGjTk8gGD+PmgwUqiRCRlrrnocLKzy37mz8n2cc2Fh2coIpGyUjHZ/FhgqXNug3MuBLwFDEtBuyIiUscNP7QXd14/gjYtG2IGrZo35DfXHK+79qTaSMUcqeXAIWaWR2xobzgwPQXtioiIcOxhvTn2sN6ZDkMkoUr3SDnnpgJvADOB2fE2n61suyIiIiLVXUru2nPO3QPck4q2RERERGoKLREjIiIikiQlUiIiIiJJUiIlIiIikiQlUiIiIiJJUiIlIiIikiQlUiIiIiJJUiIlIiIikiQlUiIiIiJJSklBThERkb2xOb+QT79aQGFRkCEDOtG7e5tMhyRSKUqkREQkLSbPXMLdf3kHgFA4wotvTeHIQ3pw9y9PxMwyHJ1IcjS0JyIiVS4QDHPP394jEAwTCIaJRh0lgTBfTF3El9N/yHR4IklTIiUiIlXu2zkrSNTpVFwSYvxnc9IfkEiKKJESEZEqt7uhOw3qSU2mREpERKpc/z7tcQm252T7OeGovmmPRyRVlEiJiEiVy87ycd8tp5Cd7SM7y4fXa+Rk+zhmWA8OHdw10+GJJE137YmISFocPLALb/796lLlDzrTs2urTIclUilKpEREJG0aN8zjzBMGZjoMkZTR0J6IiIhIkpRIiYiIiCRJiZSIiIhIkpRIiYiIiCRJiZSIiIhIkpRIiYiIiCRJiZSIiIhIkpRIiYiIiCRJiZSIiIhIkpRIiYiIiCRJiZSIiIhIkpRIiYiIiCRJiZSIiIhIkpRIiYiIiCRJiZSIiIhIkpRIiYiIiCRJiZSIiIhIklKSSJlZYzN7w8zmm9k8MxuainZFREREqjNfitp5DPifc+5sM8sC8lLUroiIiEi1VelEyswaAkcAlwE454JAsLLtioiIiFR3qRja6wpsAJ43s2/M7Dkzq7frTmZ2tZlNN7PpGzZsSMFhRURERDIrFYmUDxgEPOOcGwgUAnfsupNz7lnn3GDn3OAWLVqk4LAiIiIimZWKOVIrgZXOuanx798gQSIlki5TV67goS+/YNHmTbSp34Cbhx7Kid17ZDosERGphSqdSDnn1prZCjPr6ZxbAAwH5lY+NJF9N23VSi5/5y1KwmEAFm/ZzG8+HE9BIMA5+/fLcHQiIlLbpKqO1C+B0Wb2HTAAeCBF7Yrsk4e+/GJnErVDcTjMw19NJOpchqISEZHaKiXlD5xz3wKDU9GWSGUs3LQx4fZtgQAFwSANs7PTHJGIiNRmqmwutUrbBg0Tbs/2+ajn96c5GhERqe2USEmtcvMhh5LrK9vRmuvzcfWgwXg9utxFRCS19M4itcoJ3ffj3iOPoVluLj6Ph/r+LK4dPITrDzok06GJiEgtlKolYkSqjXP278fZffpSEAyS5/erJ0pERKqMEimplcyMBppYLiIiVUwf1UVERESSpERKREREJEka2pOMcc6xYNNGwtEovZu30FwmERGpcZRISUbM27Ceq98by5aSYoxYnacnThjJ0A4dMx2aiIjIXlMXgKRdSTjEhW+9xqrt2ygKhSgMhdhcXMzP3x3DhsLCTIcnIiKy15RISdp9vOQHwtFoue1RF+Xt+VrvWkREag4lUnVYMBKhKBRK+3E3FRclTKQCkQjrCwvSHo+IiEiyNEeqDtpaUsJvP/2Ij5YsJuocPZs358HhI+jXslVajj+kbXvMrNz2PL9fc6SkRlmyfCM//LiB9m0a06tb64TXtYjUbkqk6hjnHJeOeYN5GzcQivcKzd2wgQvffJWPLr6c1vUbVHkMvVu05Liu3fl4yWKKw2EAcnw++rRoyVGdulT58UUqKxgKc+dDY/l2zgq8Xg/RqKNLh2Y88vuzaVAvJ9PhiUgaaWivjpm9fh2LNm/emUTtEIpEeWn2rLTF8X8jTuK+o4/lwDZt6d+qNXccegQvnn62SiBIjfDvV7/imzkrCATDFBUHKQmEWLRsPX979uNMhyYiaaYeqTpm+dZ8vAmGH4LRCIs2b05bHB4zzuy9P2f23j9txxRJlXc/nk0wGC6zLRyO8tmUhYQjUXxefSAQqSv0217H9G7egrArP9E7x+tjQOs2GYhIpOYJhsIJt0ejjkik/O+XiNReSqTqmG5NmzGsQ0dyfD91Rhrg8Rh9mrfAOZe54GqxwmCQt+fN5d/fzGDuhvWZDkcq6eABXfAk6Nnt2bUV2Vnq6BepS/QbXwc9fdKpPPX1FEbPnsWW4mI8ZoQiEa59/x0GtWnDc6ecQbZPl0aqzFq7hovHvEHUOUKRCF6Ph+O7dueRESclfDOW6u+GS4/k27krKC4JEQiGyfJ78fu83Hbd8ZkOTUTSzDLRAzF48GA3ffr0tB9Xyjrj1dHMXr+OaKlrIMfn45dDDuG6wQdnMLLaI+ocQ//1DzYUla3Ynuvz8+Dw4zi1Z+8MRSaVta2ghPc+mc3chavp0rE5px8/gGZN6mU6LBGpAmY2wzk3ONFj6naoozYWFTFv44YySRRASTjMq3NmK5FKkdnr11EUCpbbXhwO8eqc2UqkarCG9XO48LSDMh2GiGSYEqk6KhKNUtGgUqKq45KcaDQKFZzpunyeN20p5F+vfslX038gNzeLs04cyJknDMTj0VCniNQsSqTqqFb169O+YSN+2FK25EGW18upPXplKKqarygUYsz8uXy9ehVdGjfhrN774/d6YJeVeHJ9fs6qo6UftheWcMWt/yF/W3HsDrcthfz9v1+wcMl67rrhhEyHJyKyT3TXXh326IiTqJ+VtfMOvjy/n06NGmtYL0mbi4sY8d9R3D/xc8YumMfT06cyYvQobjp4GLk+H9leLxA7z4Pbtq2zNbTe/Xg2BYWBMmUCSgJhPp40j7Xrt2YwMhGRfVfreqQ2FRUxdsE8Vm/fxpB27TmmSzd8qpad0P4tW/HFZT9nzPx5rNy2lUFt2nJc1+7442/4sm8enfIV6woLdg7ZBSMRgpEI//nuGz677Oe8s2A+m4qKGNahI8M6dKyzd+zN/H45gWD5Okx+n5cFS9fTumWjDERV9zjnmL1gNfMXr6VV8wYMO7Abfr9+90X2Va1KpGauWc2lY94gHHUEImFemTObbk2a8spZ55Hr92c6vGqpcU4ulw0YlOkwaoUPfliccN7Tym3bALhy4IHpDqla6ti2KdNn/Uh4l8KVkaijVfOqX+tRYgVFb7nvTeYvXks4GsXv85Kb7efp+y+gXevGmQ6vVtteWMIzL37BJ5PmE3WOI4bsxw2XHUWTRnmZDk2SVGu6apxz3Dj+PQpDIQKR2KfdolCIhZs28fy3MzMcndQFORXU3nLO7RzWEzjrxIH4fGX/9Pi8Hjq0bULPrq0yFFXd8vLYr5m7aA3FgRChUISi4iBbthXxh0ffz3RotVo06vjF3a8wfsIcCouDFJeE+PjL+Vx9x38rrJYv1V+tSaSW5m9hS0lxue2BSJgx8+dmICKpay7se0C5ZMprxuC27WiYnZOhqKqfdq0b8/CdZ9K6RUOy/D78Pg+D+nXkkd+djdXR4c50e++T78sNr0ajjkVL17Nla1GGoqr9ps1axpr1WwmFIzu3RSJR8rcV88XUxRmMTCqj1gzt+T1eKiot6lNvgKTBFQMPZObaNUxcvgyPGQa0rFef/xtxUqZDq3YG9evI689cxcbNBeTk+GlQT4lmOkUqKL1hFkuopGos+XEDoVCk3PbikhCLl63n2MN0x3RNVGsSqQ6NGtGuQUOWbNlcJqHK9fk4f/9+GYtL6g6/18s/Rp7Ggk0bmb1uLe0bNmJIu/Z1dlL5npgZLZppTlQmHHdYL157f2a5N/V2rRurOnsV6tC2KVlZPsLFZYv05ub46dSuaYaiksqqNUN7AM+cfCpNcnOp588i2+sl1+fj0A6duLBf/0yHJnVIz2bNObtPXw5p30FJlFRLl5x1CB3aNCE3J3YTTna2j3p52fz+ppMzHFntNvTArjRqkIO3VOFZj8fIzfFz9LCeGYxMKqPWrbUXCIf5ZOkS1hcWcGDbdvRrqcmrIlKec46xH87iP29NZXN+IV07NueGS49iUN+OmQ4tLcLhCBO/XsychWto06Ihxx3Rh4b1NcRa1TZtKeThv3/IlJlLcMCB/Tpy27XH00ZlP6q13a21V+sSKdm9SDTKK99/x+jvvyMQDnNKj15cNWgw9bKyMh2aSFq9+NZUXnhjCiWBn8rOZ2f5eOzec+nbs20GI5O6IBKJ4ojdsSrV3+4SKf0E65hfffA+D0z6nPkbN7A0fwv/mDGNs15/mWCk/ARIkdoqFIrw4ltTyyRRAIFgmGdfmpihqKQu8Xo9SqJqiZT9FM3Ma2bfmNl7qWpTUmvBpo18unQJxeGfbnsORCKs3LaV/y1emMHI6q5INMqmoiJCSmTTasu2ojJL1JS2dPmmNEcjIjVZKu/a+xUwD2iYwjYlhb5Zs5pEU5+LQiEmr1zBqT17pz2muuyV77/j4a8mUhQK4TMPl/YfyK+HHopXSxpVucYNcyusWdW+bZM0RyMiNVlK/mKbWXvgZOC5VLQnVaNlvfp4rPyPPMvrpV0D5b/pNH7xQu77YgL5JSUEIxGKwiFGzZrJ/035KtOh1QlZfh/njhxETnbZpaOys3z8/PxDMxSViNREqfro+yhwG5C4rxwws6vNbLqZTd+wYUOKDiv74ohOnamf5S93S77PPJzTp2+GoqqbHpv6VZkhVoDicJhRs2ZqmC9Nfn7+YVxy1sHUr5eNAW1aNuLem0/mwH514649EUmNSg/tmdlIYL1zboaZHVXRfs65Z4FnIXbXXmWPK/vO5/Hwylnnc/24d1iyZTMeMxrl5PDoiJNpVb9+psOrU9Zs355weygSpTAUpLE3N80R1T0ej3HJWYdw8ZkHE4lE8fm0AoKI7LtUzJE6FDjVzE4CcoCGZvZf59zPUtC2pFinxo15/8JLWLV9G4FwmC6Nm2h9swzo1bwFX69eVW57g+wsrcuXZmamJEpEklbpoT3n3J3OufbOuc7A+cCnSqKqv3YNGtK1SVMlURly+6FHlFvgOMfn4/Zhh6sauohIDaLbg0QyYFCbtow+4xwObteehtnZ9G7egkdHnMQ5WhdSRKRGUWVzEal2AoEQYz6cxUeT5pOT7eOMEQM4ZlhP9aDuJecccxetZcvWIvbv0ZomjbQQsUhl7K6yeSrrSImIVFooFOH6u19h2cpNBIKxOxvnL17HN9+v4DfXHJfh6Kq/tRu2cfMfXmfjlgI8ZoTCEThguIIAACAASURBVM47ZTBXX3iYElGRKqChPRGpVj6fuojlqzfvTKIASgIhxk34nlVr8zMYWc1wx5/fZtW6fIpLQhQWBwmGIrz+/kwmTluc6dBEaiUlUiJSrUz9ZinFJaFy271eD7PmrsxARDXHyjVbWLF6C9Fo2SkbJYEQr4+bmaGoRGo3De3VEPklJTwxbTLLt+ZzVKcunN2nL9k+/fik9mnWtD4+n4dwuGx9XzOjSaO8DEVVMxQUBfBWsBDu9oKSNEcjUjfonbiaWVdQwJcrfiTPn8VRnTuT4/Pz8Q+Lueb9sez4jPnJ0iX8dfKXfHTx5TTP0xuL1C6nDO/H6+/PKJNImcWWbzmof6cMRlb9devYIuE8qCy/lyMP7pGBiERqPw3tVSNPfT2Fo154jt9/9gm3fvQ/Dn7u70xduYLrx7/LrvdWbg2UcNtH/8tInCJVqV3rxtx3yyk0qJ9DXm4WOdl+2rZqzBN/PE+FM/fA7/dy27XHkZ3lw+OJJVTZWT5aNmvAOScPynB0IrWTyh9UEzPXrObit18vt/5ajtdHSSSc8Dk+j4eFN9ycjvBE0i4cjrBo2Xqys3x06dBcd5ztg0XL1vPWuG9Yv2k7hwzqysnH9CUvNyvTYYnUWCp/UAO8Nmc2JeHyCZMr1xclUjf4fF56d2+T6TBqpP06t+T260dkOgyROkFDe9VEUSiUMGXyYFT0OfyQ9u2rMiQRERHZAyVS1cTRnbsm3F4cCXPNoIPKJVN5fj+PjRhZ9YGJiIhIhTS0V01sC5TgMSO6y5y1LK+XQzp0ZHjXbjw2dTIbigoZ3qUrNw4ZSpbKH0gG/DBrGT/OWUGHXu3Yb1DiDwBVqag4yFP/+ZyPJs4jEoky7MCu/OqKY2jetH7aYxER0TtxNbEkf0u5JArAgGX5W7ik/0D+c8bZ6Q9MJK6kKMDdpzzI/KmL8XgNF3V069+ZB8b/lrwGuWmJwTnHjfe8yg8/biQUjgCxSujfzV/FK09eSW5O7Z1QvXTFRuYsWEPTJnkMGdAFXwX1okQkvZRIVRP9WrYiz++nKFS2orPX46FX8xYZikrkJ/+6czTzJi8kWKrq+MIZP/DMzaO45bnr0hLDrLkr+XHV5p1JFEA06igqCvLJpAWMPLZfWuJIp0gkyp+eGMcXUxdjBh6Ph9wcP0/ddz7t2zTJdHgidZ4+0lQTI3v0pFF2Dt5St3hneb3s17QZB7Vtl8HIJB2i0SjrV2ykcFtRpkOp0IejPiuTRAGEAmE+GT2RdJVRWbJiY7nlTwCKAyHmL1mblhjS7f1PZzNx2mICwTAlgTBFxUE25xdy18NjMx2aiKAeqWojx+dnzHkX8eCkz/loyQ/4PB5O79Wb3wzduxXbI9Eob8ybw2tzZhN1jrN678+5+/cjy6sChtXdxLem8vj1/6R4ezHRaJRhpx7ELf+6jtz66Rku21vBQPn17wBCgRDhcBi/31/lMXRo03RnocnScrL9dO3YvMqPnwljP/yOkkDZ0ijOwaq1+axel0/bVo0zFJmIgBKpaqVFvXo8MuKkfX6ec45fjHuXicuX7SzouXDTRv63eBH/OeNsPCpkWG3Nm7qIhy55nEBRcOe2r96ZTskFj/Knd+/MYGTlDRzej6/Hf1Nuu3mMsU/8j7N/fUqVx3Bgv460at6QlWu2EI7ElpAxM7KzfIw4ok+VHz8TAsHEBXk9ZhU+JiLpo6G9WuC7dWuZuPzHMlXRi8Nhvl23hi9X/JjByGqfQHGAlQtXU7S9OCXtvfrwGILFwTLbQoEQ33wymw0rN6XkGKly1UM/S7jdRR1jnhyflhg8HuOpP53P4Qd3x+f14PEYg/p24Nk/X0S9vOy0xJBuxx3Wiyx/+Z7lvLwsOrVrloGIRKQ09UjVAtNWryQcjZTbXhQKMW3VSg7v2Dn9QdUyzjleuv9NXnloDGZGJBxhxBXH8ItHL8dbifXfVi9eS6LpRb5sPxtXbaZF++rzRtmsTRO8fi+RUPlrrXh7SdriaNQgl/tuOZVo1OGcw7sPd69t3FzAxi0FdGzbtMYsmXLOyAP59KsFrF6/leKSEH6/F6/Hwz2/OjnhMKeIpJcSqVqgWW4efq+XUDRaZnuO10fzvLwMRVW7jP/XJ7z85zEEigI7t304agK59bK56qGLk273gCP7sGL+KsK7JCfhYJiOvavXTQYNmtandeeWrFq0psx2j9fD4BMGpD2eWBKxd4lEUXGQex55lxmzl+P3eQlHolx2zlAuPvPgqg0yBfJys3ju4YuZMGUhM2cvp1XzBpw8vB8tmzXIdGgigob2apyCYJDX537P019PZfrqVTjnGNFtP7xW/kfp8Rin9OiVgShrn5cffLtMEgUQKAryztMfEImU76HZW+feeho59XLK9Czk1Mvm3FtPpV7D6pUEmxm3PHcdOXnZeONDTVk5fuo3qcfl953P6h/Wkr9ha4ajTOz+J8YzY/ZygqEIhcVBAsEwL7wxhQmTF2Q6tL3i93s5/vDe3HH9CC4/d5iSKJFqRD1SNch369Zy8duvE3GOQDhMts/HkHbteXbk6fz3zHO49r2xbA3Ehljq+bN48qSRNM2tXm/GNVX+hm0Jt4cCIYLFwaTvsGvZoTlPT3+IUfe8yrefzKZRy4ac+5vTGH7R4ZUJt8r0O7w3/5j1V8Y8MZ7l81fR55D9CJSEuHbgbwgFI7holL6H9ea3L99Eo+YNMx0uANsKSvhq5hJCu/T6lQRCjH57GkcP7ZmhyESkNlAiVUM457j+/XfYHvxpYnJRKMTUlSt4dc5sLurXn0mXX8X8TRtxztGreQvdrZdC+w3swuyJ88ptb9K6ccK6RvuiTddW3PnijZVqI53admvN9Y9ezpLvfuSWo++hYEthmcdnfzGXu056gKem/TlDEZa1vaAEr8dDiPI9h5vzq2/dLhGpGTS0V0Ms2ryJ/ED5Cb3F4TCvz5kNxIZeejdvQZ8WLZVEpdg1f72E7LzssjW9DLas28rZLa/k96c/xLbN2zMXYJpFo1HuOun+ckkUQDgUYfnclSydXT3uGG3VomHCu948HmPwAR0r3f6GTdv5etaPrF6XX+m2RKTmUSJVQ+yuzyM9NaXrtp4HdeexL//EsNMG07R149icJgeRUIRwMMzX//uW3570QKbDTJu5kxfutgSE1+9h46rNaYyoYj6vh5uuPIbsbF+ZbfVys7j83GFJtxuORLnv8XGc94vnuPuvY/nZTaO47YG3CFRQuFREaiclUjXEfk2b0TC7fJ2cXJ+Ps3vvn7Y4XHQrrngsrngMLrolbcetDrr178y9b93GEWcPxTxlf3XCwTBLv1/Bku+qRy9MVSspDOy24n6wJEz3gV3SGNHuHX9EHx65+2yGHtiVLh2acerxBzDqkUtp07JR0m3+960pfDZ5YWwCe1GQYDDM9O9+5PFRn6Uu8Gpke2EJ/3lzCtfe+RK//ctYZs1dmemQRKqFOj9HyjnH+sJCcv3+hIlKdeEx4+mTTuXit18n6hwl4TC5fj8DW7fh/L4HpCWGaPH7sPVOfsq/I7iG9+HJOz0tx68uVixcTSRcfr6N1+dh7bL1dD2gUwaiSq/9h/UgEo4mfMyX5eOUa4+jSTVbuqR/n/b079M+Ze29Of7bcpXFg6EI4yd8zy1XHVurajxtLyzh8lv+w+b8QoLxSftTv1nKDZcexekj0l/6QqQ6qdOJ1FcrlnP7xx+wsaiQqHMc1rETfzv+RBrnVK81znYY0LoNky6/mvcXLWBDUSFD2rbnkPYd9motvspykfWw9Q6gbAkAtv0Olz0E87at8hiqiwOO6M3sL+aWW8A3HAzTfUDnzASVZrn1c/nlU1fyxPXPEQqGiEYcGGTnZnPD41cw4vKjMx1ilSvapSL9DqFwlEgkisdTe9a5fOP9b8okUQAlgTBPvvA5Jxy1PznZVb/Ookh1VWcTqSVbNnPVu2+XWVZl0vIfuWzsW4w576IMRrZ7jXJyuLBf/4SPOeeYuXY1y/Lz6dWsOfu3bJW6A5d8UMEDDkrGQ70rU3esFHKh+bii5yG8HLIOxupdgnmaVqrNkdccz9uPjSMcihCNr/eWnZfFkecOo2XHFqkIu0YYcenR9BjUlff/+TFbN2xj2GlDOPysg/H568aflf592vP1rGXlKtN37dgcf4LJ7TXZl9MXl0midvB6jEVL19OvV/UqHiuSTnXjL14Co76dSXCXQoqhaJRFmzYyb8N6erdomaHIkpNfUszP3n6DZfmxeUvOOQa2bstzp55Oji8VnxaDQKKhnAi4xJ/MM80FPsNtuZGdsYdm44pehuZjMW/rpNtt2KwBT894mFG/e4Vp42eS1yCX0244kdNuOCFlsdcUXfp14obHq2cSXdVuvPxorrljNIFQmHA4itdj+P0+br3muLTHsnV7Me9/MpulKzbRq1srTjhq/5SuPdikUeJ6dOFIlEYNqmcPvki61NlEall+PpEEi5x5PR5Wb99e4xKpuz/9mEWbNpZZJmbGmlX835SvuPOwIyt/gOyjYPujCR7wxx6rZpyL4rbeDZQuGREEF8EVPIE1ur9S7bdo34xbn/9FpdqQmq1z+2b859HLeO29GcxdtIZunVpw3sjBdGjbJK1xLFu5iWvveolQKEIgGGbC5AW88OYUnnv44pRVQD935GC+mbOCksBPPfher4dO7ZrSsV3lenhFaro6m0gd3K49X69eRSCyy2TRSIQ+NSyJCkejfLRkcbm19gKRCG/M/T4liZT5uuHqXQ6Fo4j18DggB/LOx/y9K91+ykXXQjRRNfIIBD5PezhSO7Vq3pBfXpbZ+WAPPfMBhUWBnUOMJYEwwVCEJ0d9xh9vOSUlxziofyeuuuAwnn1pEj6fh0gkSvs2TXjozjNS0n6ytheWMOq1yXz61QL8fi+nDO/H+aceVOuGVqV6q7OJ1EUH9GfUrG+IlEQIx/8C5fp8nNqjN20a1Kx1rCLRaMLeNYglU6niafBrXPZwXPG7QBTLPQXLGpiy9lPK6pN4KBLwJH/Lu5S17scNvP3EOJZ8u4yeQ7pz2g0n0ryteijSJRSKMGfhmnLztKJRx+QZS1J6rPNOGczI4f1YuHQ9jRrk0rVj85S2v6+CoTBX3z6atRu2EYrfRTvqjSl8O28Vf7v7rIzGJnVLnU2kGufk8t4FF/N/U75kwrKl1M/K4rIBg7iogonc1Vm2z8cBrVoza+2aMsU5PWYc1Tm1tXwsqz+WVf3PkXka4rIPhcAkoPTddbmQd3mmwqpVFs1cwi1H3UMoECYcCvP9l/N595kPeXzyA3TMwOTj/G1FTJr2A+FIhKEHdqVVNVnrryqZx/CYEU1QltdXBb0y9fKyGbh/h5S3m4wJXy1k45aCnUkUQCAYZtbcFcz/YS29uiU/D1JkX9TZRAqgVf36/PnYEZkOIyUeHH48577+CsFImEAkQq7PR54/i7tSMT+qhrJGD+O2XAuhOWB+cAHIOxfLrZufVrdvKWDNknW07tKShk0r3+v62HXPUlzw0xy0UCBMOBjmmZtH8eD431a6/X3x6VcLuP+J8ZgZzjkef34CV194GOefelDKjrFm/VaefWkiX8/6kfp52Zwz8kDOGDEgo/WifF4Phw/pzsSvFxMuVdcry+/lpKPTV6g3E76bv4rikvJV5J2D+YuVSEn6VDqRMrMOwH+A1sTGUp51zj1W2XZl3/Rs1pxPL7mC1+bOZsHGjQxo3YYze+9frYuMVjXzNMKavYwLL4HIGvD1wrzN0nZ85xxzJy9kynszyK2fzdEXHEabLiksSbGXIpEIT934bz54fgK+LB/hYJjjLjmSXz75c7y+5HotIuEIC6eXHzpyDmZ9NqeyIe+TrduLuf+J8eWKY/7z5S85eGAXunSo/BDU5vxCrrz1RQoKA0SdI39bMc+8+DlLV2zkN1en/y690m695jiWr97C6nX5OOcAo2e3Vlx1wWEZjauqtWvViOwsX7mfu9fjqRO9kVJ9pKJHKgzc4pybaWYNgBlm9pFzbm4K2s6IcDTKFz8uY+W2rfRt2YqBrdukpehlZTXLy+O6wQdnOoxqx3xdwdc1rcd0zvHwZU8y6a2plBQF8Pm8jL7/LX79z2sZfuHhaY3l5Qfe4sMXPiNYEtpZRPTj/35B45aNuOyP5+9VGz/MWsarD49l5YJV9BnWk3NuORV/tq9cUVKA3PrpTd4nTluc8PczFI7w8cR5XJWC8/36+zMoLgkRLTUZqSQQZtyn33P5OcNo1qRepY+RrIYNchn1t0v4bt4qVqzZQrdOzendvU3G4kmXE4/uy6g3ppTZ5vEYDepnM6SOFMaV6qHSiZRzbg2wJv71djObB7QDamQitWb7ds5542W2lgQIRyN4zUO/Vq0ZddqZZPtq10ho7NNrFDPd4ZJq0z/4NpZEFcYqwYdDEQhFeOSqv3PIyYOo1yh9b7xvPz6OQFHZWl+BoiBjnhy/V4nU9A9nce+ZDxMsCeGijqWzl/Pxi18w9LTBTB47vUwylZWbxclprqMUjkQpN9ua2PUdTLCUTzJmzVtVZi7ODn6/jyXLN2Q0kQIws5QvgVPdNWmUx+N/OJf7HhvHmvVbcQ56dW/FPTeNxOvVMrKSPim92sysMzAQmJrgsavNbLqZTd+wYUMqD5tSv/5wHOsKCigMBQlEIhSFQ3y7dg1PTy/3kmos5wJEt/4Rt64/bl0fohvPwAVnJdivBBfZFE+4ZF9MeOXLnUlUaV6flxkffVfh87ZvKWDiW1OZOm4mwUD53p5kFOQXJdxetLV4jz9b5xyPXfssgaIgLhrbNxyKULStmEBhkAOO7ENWbhb1GuWSlePn4JMGcvHvz0lJ3Hvr0AO7lukp2iE7y8fRQ3um5Bgd2zbFm2AuVDgcoVULDSNlSq9urRn9+BW8/szVjHnuWp65/0Ja6+chaZayLhYzqw+8CdzknCtXwMc59yzwLMDgwYOr5TvztkCAmWtWlyslEIiEeX3u99x8yKEZiix1nHO4jWdBZOFPG8NzcFsugWbvYL5OOFeM23ovlLwfe9zTBBr+Acs5JnGb0fxYzSZvu33q3XIuCK4YrGGNGDrdF16/F7PyHSUGFc5LGvfcxzx147/xZcV+Lc2MP717B30Pq1ydrv0GdWHB1z+U2961f6c9nvftWwrYuHpzue3OOb6fNJ+3N49i5cLVrFq0ho592mdkDliLZg249mdH8I/REwmHI0SdIyvLxynHHkCf/VIzxHXeKQfy8aR5REoVpPT7vPTp0YaOKveQcZnuEZS6LSWJlJn5iSVRo51zb6WizUyIugrqDhGbN7U7zjkmr1zBuwvn4zHjjF59GNy2+q0/5bb9qWwStfOBIK7w31ijP+Dyb40XrYwPB0XX4fJvgmb/xfwH/PSU6Hbc1tsgMBHwguXgGv4BT+7ul0pxLhiLo/htIAqe5tDwXiyn9ix0e9zFRzLh5S8JFJXtlYpGoxx4fPnyEcvmrODpXz1fZh4TwG9HPshra/5Jdm7y846uf+wKbjv2j4RKgkSjDvMYWTlZ3PD4FXt8bk69nAqTrQZNY29e7Xu0pX2PzC5afe7IAxkyoDMfTZxHOBzlyEP2S1kSBdClQ3MevP0MHnrmAzblF4JzHHpQN+68vnbc9SsiyUvFXXsG/AuY55x7pPIhZU7jnFy6N23GvI1lhx79Hg8n7bf7IYK7J3zMmPnzKA6HMGDM/Llc0n8gtx96RBVGvG+cK4HiVyt4NALh+bjI+ngSteuwVABX8A+syVM/tZf/Swh+zc46Ta4Ytt6G87bZba0pt/UOKPn4p2NE1+DyfwVNX9yrGlUutAC3/SEIzQRrDPWuwPJ+hln1mRdxwBF9OO2GExjz+DgAPF4PzsHvX7+FnARroH0wagKhXe4+AsA5po37hsPPOiTpWPoc0oMnpz7ISw+8xQ/fLqXrAZ248K4z6dKv0x6fm5Xt56jzh/H5q1+VSfCy87I569epqZqdKp3bN6vSO9UO6t+J15+5ivxtReRk+8nNyaqyY4lIzZGKHqlDgYuB2Wb2bXzbXc65cSloO+3+dvyJnPfGq4SiEUrCYfL8flrk1ePmg4dV+Jzv1q1lzPy5FIdjb4QOKA6HeWHWN5zTpy9dm1STrv/IWnY7Lc7fL1YmYEfNpTIcBKfhit+HnOMgsh6CMyhb7BIggCt8Dst6IuEhXHQzlHzIzt6uMs/7O5b1zG5fggv/iNt8Hrj4vB9XBNv/housxBretdvnpttVf/4ZJ145nK/Hf0Nu/RwOPWMIDZrUT7hv4dYiopHyvZ7OuTK1mpLVef8O3DX6V0k998anrqJgcyEzPpqFP9tPKBDi5KuGc+p1yfXGhENhpo37hk2rN9N7aA+6D4gVjd2+pYAvx3xNsDjIQScOyMgw4Z6YGU3SeKOAiFR/qbhrbxKxqR+1Qq/mLfj8sisZM38ey/K3MKB1W07svt9u79j7ZOkPBMLlexOiUceEZUurTyLlaQkJKiDHeLF6l4M1BFfBJGe3Fbf1t1D4DDS4EywrccIVWVlxDJE18eftmkg5CC/b40twhf9IcMxiKHoZV/8XWDVb/qX9fm1ovxdDTIeePiQ2QX2XpCkSjjLouAMqeFZ65ORl88ext7N+xUbWL99Ix17taJjkYrirFq/h10f8nuLCEiLhCGbGgcf3Z8RlR/PABY9iHiMadfzjNy9w3u2nc8k956b41YiIpFbtup8/RRrn5HLZgEF7vX+e34/X4yG6yzwqj8fIrUYlE8yTh8u7EIpeBkq/YRs0/DPmjc3pii1O/AJQnKCVIgj/CIEvEyRDAH7IqriWlbNG4BL1sHggay8ShuAsIMEt7eaPJWI1YPmaRA46YQADju7Lt5/OpqQwgJmRlZvFBXeeUW3WrmvZoTkt48UtA8UBJr01jbVL19N9YGcGnzAAr3fPNxr88Zy/sWXd1jJ3C07/4FumjfuG8C5Dm6/9ZSxDThxIryH7pfaFiIikUPV5l6/BRu7Xi0enTCbRIrkndK9ebwLW4DacpwEUPg9uO3i7YA3vxrJ/Klpo9W/GeTtAwTMQTdS7FICS/4GnGURXl24drB5WL/Ek5mjxeNj6a8onQgaWi9W7bs8vwNcNIosp17PmQuCt2sn94VCYSDhSqYnfFfF4PPzh7Vv5auzXfP7aZHLqZXHCFcPZf1hqbt9f/O1SZn8xj8YtGzH01MEJ52ntrTVL1nHjsN8SKApQUhjAn+3DAdFIlKatm3Dx78/mhCuOKTdJff2KjaxcsLpcyYVgcQhLUFogWBLioxc/VyIlItWaEqkUaNewIQ8OP447P/kInyc2Byniojw24mSa5uZlOLqyzLxY/Rug/g04F0lYrsDMsLxzcNmH4zYcR/mJ50B0E7Gi9qV5oMHtmLdl+d0j22HrTSQcWvQdgDV6APN13nP89a/FBT6jbI9aDuQMx7xVsxp9QX4hj133LJPenkY0EqVr/07c8s/r6D4wtQtCezweDjvjYA47I3XV6aPRKA9e9BiT351ONBLF5/fx+C+8/OXje5KO/+FLn2Trxm0760qVnoS+YcVGnvrV8xQXlnDmjSeXeV44GE6YMAEJLwsXdURCqSmoKSJSVarPbU413Om9+jDlymt4YPhxPHTs8Uz7+XUc1617psParT3VfDJv6/jSKrteJtnEJovvOpcqEi9pkEDxKCqcn2V5mD/W6+CiBbjAl7jQdwmLRZq/D9bkGfB2BLyxWHLPxBo9tNvXkiznHHeM+BOT3p5GOBgmGomyeOZSfn3UPQnrK+2rH+etZOKbU1g2Z0UKoi3vk/9OZMp7MwgUBQkFwhQXlFCwpZB7zng4qUKrRduLmTdt0c4kKpFAUYAX732dSKRsEtSmaysatyg/h82f7cPjLZ9g5dTL5shzK77JQ0SkOlCPVAo1ysnhlB699vl5zjkWbd5EOBqlZ7PmeD3VJ7+1xk/gNl8QuzvOhQEDf38Ifw+usPwTohVUrQ/vbgL6sthTC0fD9ofAfOysL9XkX5iv7G36ln0o1uJjXLQQLBuzqruMF81cwo9zV5SbvxMOhnnv7x/u9Vp1uwoUB/jDWX/lu8/n4vV7iYQjdO7bka79OrJ5bT4HnTCA4y87mtx6OZWK//1/fpSwwvq2zdtZOns5XQ/YcwmEZASKgxRsKaRRqcVjzYy7XvoVd4z4E5FwhGBJiNz6ObTp2oqTrz6Wf9z6IpFwhEg4Qk5uNkedO4wBR/etkvhERFJFiVSGLdi0kWveG8OGwkI8ZuT4fDx6wskc2iH2BrctUML01atpkJ3FgW3a4UlzBXDzdYQWn0HgC4iuA/8A8HXHrU9U18gP2Ucmbij7CCipoLcqup5oYHIsiaLkp46ryArc5suhxScJi0Kap+pvQ1+9eC2eBIltKBBi2ffJ9yL9+7cvM+uzObFhsfic/gXTFrNg2mIAvp0wh7ceG8fTX/+5UuvyVTQ0ZmZE9nEduuXzV/HMTc8TDe++OC3EepnqNy4fd5+hPXlh0RN8+J/PWPfjRvof0YdDzxiCz+/jwOP78+nLkygpKGHYaUPoM7RHrat4LyK1jxKpDAqEw1z45qtsKflpvk9hKMTV747l00uuYNzihTz85Rf4vV6cczTMzuaF08+me9NmaY3TzA85w8tscw1+C9v+wE9zlfzgaYjVuypxGzknxApxJppvZTlQ8ESCxxxEV+OK38HyTqvkq0hOlwM6JUw4snKz6H1I8pOg//fvT8vMLdpVoCjAxpWbePPR9ytVAuDYi49g6ffLyy1anJWTRdf+e98btXH1Zm4cehdF24oSrQ9cRnZeNufffnqFS+E0adWY8249vdz2dt3bcPHv0rtOn4hIZVWfMaQ6aMKypQQTFGGMuCiPT5vMX7+aSCASoSAYpDAUYk1BAae+/CIrt21jaf4WXv3+Oz78YVHCGlZVzZN3Ftb0X5B9DPh6Q73LsGbvYd4WCfc380L28ISPAeAKSDyHoE5Y5QAAIABJREFUKgrb7saFl/y0q4viovm4iupdpVCn3u0ZcExfsnJ/qmLt8Ri59bI58ee7eT17ECzec+zBkhATXp6U9DEATrrqWHoO7k5u/dgQYVaOn5x62dz9ys17Va5gh7FPjidYEiyXRHl9XkZeezytOsd+7g2b1eey+87j/DvOqFTcIiI1hXqkMmhjUSGRBGv4BSMRpqxcTkmCBKkkEuHY//wbM/CY4TEPfq+H0WeeS+/miZOYqmJZB2FZB+39/nnn4IITYkvJlOYikHM6FDxK2bvxdgjhCp7BGv+FaNE7UPBniG4FfLi8C7EGt1TpPKl73vwNo+97g/f/+QmBogAHnTiQqx++mIZNkytKCdD/qD7M/Hj2Hid8r/txI9FoNOHw4t7wZ/n5y6f3MP2DWcz8ZDbN2jTm8LOH0qh5fZbPX4U/27dXFcQXfP0DoUD56zE7L5uDTxrEr56+ikg4Uq4XauXC1Sz9fgXtureusvlYIiKZpEQqg4a0a5+wJnye30+e///bu+/wqKr0gePfc6elN0LvvaN0ERClKBaaioi9NwR1VQTRxbp2/a2ydlRW7J21I4hYQZDepHdIQiB1+j2/PyYEhrmTDqG8n+fJQ+aWc89cbjJvTnmPM2oOcp95SFeTH66b8Rm/XH390T2mxHkqxAwF9xeEZv3ZAQOSn0TF9EO734XgFosTTfD9ivbOhdz7OBBs+aHwHTTBEpeH0cFMdOFb4J0P9gao+GtRjrIPYnY4HVz18Giuenh0mc8pzZjnr2Fcr0n4PL4Su/iUgqU/razUoGvDMOhxdmdadG7CM9e9xOsT3sEMmihDYXfYqd+yDpM/vqvEhYebndSYZXNXEfCHB1NBf4D6LesAhAVRfp+fhy96loXfL8HutBMMmLTs0pRHv7qXuMTYCr8XIYQ42kjXXjVqVSOds5q3JNbuKN4WY7fTqkY6ozt0wlGOVogcr4cVmRmHo5pVRimFkfwwqsa7qIRxoZakmjMxYgejVCykvU0opYEFMwudcy+RLVYeKHw/tCCzBR3chc46L5SpPbAEPN+g91yC6Z5ZlW+t3Bq2rs8bq/6PURNG0PO8rtSPsoyMzW5jz469lb5eMBjk9j73s+C7xcVr+mlT4/f62bxiG3eePjkiSDrYiLHn4HCF/93ljHHQoW9bGraOTIQ6/eGP+WvmUnweP4W5bryFXtb8uY4Xxk6t9HsRQoijiQRS1eyZM8/m4TMG0KVuPTrUqs3dp/bhvfMv4oK27WmQVPZ14wyl8AaP/FipilCODqiEW8A1EJ33BObunpiZg8DzI7jOjH6iWUKgaO4L5aAyw3M76fwXQOdyYJFkE/BA7iS0Ln322eGUWjuFK/45kkdmTGDU+GHExEdmGw8GgpUa1L7fgu+WsC8zBzMY2c6ptcZd4OXPbxdbnBlSu3FNnpnzIK17tAgtXxPjYNCVp/PAp3dbHv/Vqz/gdYcPcPd7A/z0wa8R+aWEEOJYJl171cxQivPbtuf8tu0j9n01+nIGvP0Gu/Lzo3bzFZeDolOtOlVSJ23mhLrYbPVRxuFZ500HM9B7RhQNMjchuDeU/sBWgSSmyobeNxH880Nl2xqGEnQqO7hnYLk2n96Hdn+FihtSqfdRVfpf0ocPn/qC3Zuz8HtDXX2uOBenX9SLes1L/3/1+/yYQTPq8jU71+8m4IsewJjBINk7S275atmlGVP+eIxgIIhhM0rsRvZa5K6CUDqGYMAs10B3IYQ4mkmL1FEsxuHgq0uu4NyWrXEYBoZSdKlTj/Y1axHnCHUHOgyDGLudZ846G0clP5y0NjFzH0Zn9EFnX4nOOA0zZ+JhmR2nC6cVDTo/uFXIDcFlJZxlAM5DtsWGvvzzCGVa90NwAzr7cvSei7FMt7Bf/nMVyu59OLhiXUyZ9xgX3TWEBq3q0aJzU259/hr+8XrJ6w/mZOXy4AVPMzTxcoYmXcG4XvdaZklvdlJjbI4Sng8N7cq4rp/Nbit1LF7ngR0tl4Np0aUpTpfD4gwhhDg2qer4IOnWrZtesGDBEb/usSxomgS1xmmzETBNZm1cz9zNm0iPi2Nkuw7l6gaMxsx/BfJfpDhDJAAxEHcZRtL4Spcfdq09F4E/eleStSRIew3ynwX/CjBqQ8w5UDg1lHm93OyoWr+jjMrfu+qgteaGk+5k25odBIoSbyoFcUlxTFv7QlhWca01406dxNpFGwhatEyl1knhwx2vWV5n7V8b+OCpL9i2Zgcd+rThoruGUqtRyTNEd27YzZgeE/AWevF5/DicduwuO8/8+CAtuzSrxLsWQogjTym1UGvdzXKfBFJiPzOjV9FixIdQcahai6p0RqCZc0/R7L2yjlNyomq8HzHbTrtnoHP/WcFAyomqvRClrLvDjnaLf1zOxLMfjVi+xma3ceVDoxh9SC4nd76bRy9+jnlfL4ooyxnr5Nk5D9K6e3jX6vxvFvHQyKfxuf1orbE5bMTEuZgy/3EaRBkgv9++zBy+fPl7Vs9fR9OOjRh6y2BqNjiyyWSFEKIqlBRISdeeOMDMtd6u3ViOM6oEFXcNkd10RekQIo+G1OmWKQu0mV/hIIqYs454EGVqE2/QWyVdip89/1VEEAWhAeqf/N+X7Ny4O2x7bEIsdaONt9Ka1UXL0xzYpPm/m17BW+grrm/QH6Qwz83Uie+UWr+Umslcdv9IHvnfRK7916USRAkhjksSSIkDHB2tt9taVHnCS+VojUp9EYx6hAIqJ7gGgbOP1dFQGNntpANbIO/xKFcwsEzShSt0LXsrSLinotUvt4AZ4L0tH3DjwjHctPBW7l46kaX7ShoPVrJgMMjCmdHPz8nI5dp2t3NTl7vZvfnAQtK1m9QMy9K+n91hjwh0crJy2ZeRE3GsNjVL5qyocN2FEOJ4IoGUKKaSJoGK5cBjYQCxqOTJ5S5La432/YkueAPt+Q6tfRHHKFcfVM0fUTV/QtWaj5H6b7A4Dkzw/oQOhnc7avdHQLSUDyYRS87YuhYFbkBwE2QNxCx4s5zvrGKmbZrO7N1z8Jk+TEwyvZm8sO5F1udvKP1kC+48D35fyZMA/N4AG5du5q7+D2AWZdAfdHk/7IdkH1eGIiYhhh7ndA7bvn9ZGStJNSqe1V0IIY4nEkiJYsrREVXjE4gZArbm4DorNC7J2aNc5WjtQWdfgt57PTrvGXTOBHTmGaEWpEOvqRTKVgNlxIU2mLuilGpHe2ehvT8fSL4Z2Ez0QMpCcAmYWwBfUdoFD+T9H9r7czneXfkVBAr4bc/v+A4JEn2mjxk7vgx7vSJnJatz1xDU1l2pnkIv374xm/GDHsIMlD6+zDQ1OZm5LP9lNQDJ6Uk8OWsy9VvWwRnjwOFy0LJLU/7v54exO8JbHV2xLvpddCrOmPBZdjFxLi688+hIGyGEENVN8kiJMMreApXyVKXK0PmvgX85xakHtB+0G51zF6rGh9bn+NdCYDnYmhQtE3NokFAIeY+hUYCJThgP3p/KWTOroMuNLngD5epbzrLKLtu3F7uyE9CR19/p3gnA/D0LeH3jGxjKQGuNw3BwR6txNE84MMMtd08et/aYQPbufXgLrVruolCwd9e+4petuzXnzdXPk7ltD3aHjbQ6qVFPHffi9eTvK+SvmUuwOx0EfH6G3HIm514/sOzXF0KI45gEUqLStH8FeOeCig+lI3B/QmT+JhP8izHzX0fFX41Soe4lrf3ofWPB+xsoA4oHYSsiuuZ0wYHv8x6i7DP+SmFmVU05RXymn0V7F7HXv48W8c2oH1sf02KwvkLRJL4JGZ5MXt3wOv6D8nV5TA9PrXmW5zs/i9MIjWl6+6GPyNyebTnAvCRBf2R2dKUUtRqml3pubHwMD39xD5nb9pC5NYuGbeqTmJpQrusLIcTxTAIpUWFaa3Tu/UXZw/2AHfKeBhV9bA35z6MDq1Apz4TKKHg9FEThOShusoEq+pDX2Vi3JFXV8i5OcJ1eRWXBDvdOHl31OAHTT0AHsCk7LRNbMLDWAH7ImI3PPNCS5DQcDKs/hJ+zfsG0WK5Ga83ifUvokdYdgJ8/nVfuIMrusHH2tQNKzftUmpoNasisOyGEsCBjpETF+X4G9/8ILSQcJNQK5SkafxQt55QHPN+jAxtDLws/IHIh4iDoveDoQMUCJhvRZ+0dzAlGCir+6gpcw9qUdS+RH8jHY3oJ6CBe08vfeWtJsicxquFIajhr4DSctE1swz1t7qa2qxb5gQKCFi1WJiYFgQOpHSqSEfyOV29izPPXVOo9CSGEiE5apESFaffnhGdB3y9IRLfcwZQN7VsUGg8VdQkXDb6fiB5IOQgFSlZjhYKE0hwEiJ7/SkHsSFTiOJQRfYxQeezx7iHDE7mwss/08fOeX/hXx4cZWLs/+3z7eGPjNB5Z+RgA9WLr4VTOiMHoWmvaJbUtfn3uDQP57wMf4vOUbcmermedxJlXnl7iMQW5hfzvxe/45fP5JNVIZMS4c+h+1snh9ff4+H3GAvbs2EubU1rStmfLKk3OKoQQxzIJpETFWXRHFe0o5TwP5E5A504GWz0gh4juO6MRmJuil+HqBySD95MoB5Swxh4AtlBrVBUFURBqQVIWQ7uA4ll4QR3k4ZWPke3LxiwKEre7t2MoIyyYMrbZSJ5Tk4/Vl/Qa2p3O/TswfNw5vP/45xGBlFIHDS0rYtgM/vHKjSXW153vZkz3CWRuzSouc9nclVx09zAK89zMnDYHn8cf6k5UCjMYxO500LFPGx7+34SIWX5CCHEikt+EouLsTUuPVyztD8C8ENzG/nxVodYtJyg7KvVJdN5z4PudiFYpRxdUygvgX4L2fkVk12DptA6wMW8pcfYd1IutV5E3ESHdmU6SPZksX+Tg9TquUEbxJfuWkR/ILw6iADQau7LTM60He/172f1FNiseWMfOQC5LA6v59o3ZdB10EnHJsRTkRmZxDwuiFLQ/tQ33/PfWUsdFff36LLK27QkLzDwFXt5+8CPsTjt+b2TLVzDgZclPK/j8hW+48B+SAkEIIWSMlKg4e3MqH4v7AQ3x10DMeRB/Iyr9e5SjEyrpYVCpQFGOKRUHRl1UygsoZUMHs4vOLz+vNvg4cx/3L3uQ/23/qpLvoah6SlHbVcty3/LcFczN/IUthVvCBpwX18f0kmCP56baN7DywQ34PQGCgVArlqfAy29f/MkPb89FmyW39sXEuTj3+oHUbVobgIKcAl6fOJ3Lmt3C1W1u46NnZhDwh1r//vhyIV53ZF201pZB1H5+b4BvXp9VYj2EEOJEIS1SosKU61Q0NiJn1ZU0fsmKH+ztMBJvCy/f3gBqzgLP1+jAOrA3g5jBKCOp6Ih8KrIGoNdULPekssqbDAT4ePunxNliGVCnf7nLOlhBoIA1+X9b7gvoAO9ufg+f6Q9rjdrPZbhoFN+IRbOXY3fY8B0y9ExrXWqPKYSCrr9mLWXQFf3wef2MO3USOzfsxu8N/R9Nm/wBS+eu5OEvJpBWJxWlVIXW/bNqGTuStq7ZztyP/0BrTd/ze9K4XcNqrY8Q4sQlgZSoMGWkoRPvgbwnCQVNZqjVyHFKqLXK/UlR+oKyCG8B0dqLLvwUvN+CVhDcDuY0yH0Q03UGKvkR8JS/VSSgYWZeAz7NaczBs/qmb3mPBvENaJ3Yqtxl7pcXyMembJaJNwHcZvQuyAR7PN1Su7DQubTC14dQq9gfXy5k8ognad2tORlbs4qDKABvoY9Fs5azbvFGRow7m18/nxeW3DM0hrz04Krdqa0B2LNzLx89M4Olc1ZQt1ltRt41lDY9WpZ4bmV9+PQMpk3+gKA/NKnh/cc+Y/TEEVx634WH9bpVZeeG3fzy2XyUgt4jehS3Hgohjk2qKlahL69u3brpBQsWHPHrisND+1ej3Z+FEmbaGkPBi4AGXdZWCxsq7T2UMzRbTGsfes8oCGzAelagAqMhONqD95ty1dVrGjywqzO7AnER+wwMBtc5k5ENL8BQ5e/1DpgBbl10O+6gVZ1L1q9mX65pehU+j4+Rda6jMLf8ZRxMKYVhUwQtlpFxxTq56dmrOO/GQXzzxixevO1NDJtBMGBSp0lNvG4fmdv2FAUq1oaPPZvW3Zvzn9vexFPgIeALopTCGePgnrfH0ff8npWqfzQ71u/i+o7/iBhw74x18tLCJ2nUpv5huW5V+fi5L3lz0ruYZihHvzIU1z5+KeePO7e6qyaEKIFSaqHWupvVPmmREpWmHG1QjomhNfYyTg3PQF6mApLB0fHAa/f/IBgtiALQoTXzjFM5MEi9dD5T8bc3yTKIgtCsu5m7fyDOFsuQ+ucVby8MFPL+1g/5Y898TG1yUkonLm08mjRn+Iw/u2FnVMORTN/8btRWqWhW5YbWwnPGOHnws/H8c9gToTqZmmAgGBrXZPU3jwKHw04gEAwbP6W1JhjQlgniTa3ZtXE37nw3Z18zgP6j+7D2r40kpsbTuF1D9mbk8Ox1L/HHVwujdifOePE7lFLF47j2X9Pr9vH8La/Re3h3DKPqh2D+9sWflq1lQX+QXz+bT6OJI6r8mlVl+7qdvDnpvYggcOqEd+g1pJu0TAlxjJLB5qLqeH8px8EOIA5UPCr1xeIlYwC0dyboMgRHnp8gdjgQEypPxRL62yA8x5HW4DMNfimozZSsdiUW6dcBPtsxozjTuNaax1c/xa9Zv+M1vfi1n7/2LuLBFY/gDUZOWTyjVj9ua3krdVzl+1BMsB9YdqVDvzY8tf5+Rvz3LLp+1IYz5nWj2+0dLc9zxTp5ceET0fM6WQRCfq+fGS99x6h6N7Bo9jJcsS469G5D43YNKcgt5KOnZ7B+8SZi4lxRyzWDZlgQdTB3voeMLVW77M5+hs2wrJNSoX1Hs18/m48ZjLxnWmt+/Wx+NdRICFEVpEVKVB3tpUwjohPuCY3FUakQcybKOGTtNqMGoRi/lKzmeifYW6FqfAS+X0AlQMxZoJLRZibgYqN7D0+segKv9lN6pvOQoA7yW9Yf9Kl5Kqvz1rDbszushcnExB10My97PqfVjFzsuENyewBs2Cwzlh/KZbgYXOdMILR48ZubpuEzfQTqFV3TC86LndTvnErmzfn4CvwYhsLhcjDkprPYtTETw2ZgBiPvV2xiDKm1U8jYmkVg/1gpDe680HitycOf5MNdrxMT52L7up2MO3USedn5pc4OLIkZDJKQEl/h80vSZ0QPpk58J2K7YTPoe8Hh6U6sKlFHUegS9gkhjnpV8iecUmqwUmqNUmqdUmpCVZQpjkGuXqBLSkdgA1tHjIRrUfHXouLOjwyiABV3MeAs2zXzHkH7VxaVNwplpBSND6qFYUtmXf56vDpAWYOo/b7YMQOAbe7txck0D+Y1vWwq2GJ57orclezz55QaRLkMF3ZlZ1DtAfRI686Wwq28tnEqhcHCiK5Bn/bhbG1j6PSB9B7RgzY9WxI0Tb56bSb3D33ccg0+V5yLC/8xhLfWPM/pF52KMqxachQLvlvMotnLuL7jP8jNyosMohTYnWX7m8vhstN9cOfDFkjValSTm//vapwxjrCv6564jHrN6xyWa5YmGAjy1w9L+fnTeeRk5UY9rveIHpatZspQ9Dm/x+GsohDiMKp0i5QK9cn8BxgEbAP+VErN0FqvrGzZ4tgSmsU3EfKeoHgWHxCK123g7FG8WHHJBaVAzCDwfAvKVdTNFy0oCULuPZiez1HJT6Fs4XmcPMHyJ+sEyPBmss+3j7oxdbApG/5DAhuX4aJhbPjA5kxvFtm+bFblrrbMFXUwp3JwTt3BnFGzH8nOZAB+2D2bgBl9bJVX+3C3LWDEuHOYdO5jBLyBA61MFnqc3ZlL77sApRQ2m2HZyqTReAt9TBn3RtjsvoPZ7AYX3TWUxXNWsPqPvzEPKscoCs5iE2Pxe/20792G8dNuLfG9V9Z5Nwyi5zld+PWz+Wit6T28e6UXZa6o9Us2MeGsh4vHPfm9Aa5+5GJG3jk04tgGLety5UMXM+2fH4S6+JTCMBTX/OsSGR8lxDGsKrr2egDrtNYbAJRS7wPDAAmkTkBG/KVoZze0+5PQoHPXQLA1QdmSUUZaqeeb+S9A/quEWpDsRTP/ytCa5JuPzr4M0r9FHTTjblvh9gq/lw+2fsTVTa4kyZGM37unuIVJoXAaTk5JD3UluYNupqx9iTV5f2MohbeUIArAp/18s/M7fsv6g/vbTSTRkRi2bIwVhSLeHsfnL3yDt7DklPLKUPQ4uzM2W2js2WkjT+Wnj37HUxB+XsAfJCEljn0ZOVHLcsa4aH5yEwZf059xve7FU+jFU+DF4bSTXDOJZ+Y8SPaufaTXT6NOE+uEpFWtZoMaDB979hG5VjTBYJCJgx9hX0Z4K9S0yR/Qrldr2heliDjYRXcNpffw7vzyaSj9QZ/ze1ZbS5oQompURSBVH9h60OttQMRgBaXUDcANAI0aNaqCy4qjlXK0RjnuLfd52rcE8l+jYuvOBMHMBN98cJ0ChBJkZvoyK1BWyO975vFn9kIURevoFQV07ZPaclXTK4i1xQIwdcNbrM5bE+qOK8dYF4/pweP1MHbRHdSPrYfTcGJgRA2mHIaDM2qdzn8y3iq1bG1qajZKL37dffDJ9Dy3C/O++gtPgRfDZmB32ul/SR8eGvlMiakOYuNd9BraDYfTwdNzHuT2Pvdh8wUwgyZ5e/N58qopPPH9/bhiXWV/88eB5T+vxmMR0Prcfr585XvLQAqgfou6jBo/7HBXTwhxhFRFIGXVXBDxcaK1fhV4FUJ5pKrguuI4oLWG4HrQQXThZ5Q9G7pVYSZe/xZ+ys7j613fkOPPxajEMECNxn/QmC+HcjCg1hmMbjyqeJs76GbRvsWlpjsoaeC5RrPNHb3lzIYNQxlc2OB8WiQ0p/fwHqxduMFyeZeDNWp7oOtRKcWk9+7grx+W8stn84lLiKH3+T0ZP+DBiOn4B6vdpCZP/TAZh9MBwL9vfo3CXHfxwPZgoY+1Czfw7qOfcvUjo0usz/GmMM9tOYNQa03+vnKmABFCHLOqIpDaBhy8PkMDYEcVlCuOc9q/Er13TFH2cwXapNSZeiUoNA0eWj+fDO8+dFEsX5ZZc2Xl135mZ85hZMMLsBuhHx1P0FOcKqEkDWLrs9W9rcSuu0PVcKbRN70PjeIa0jqpVXGKhHNvGMiMl79n57pdUc9VKpRBu2b9GgdtU3QddBJdB50EwM+f/IFhtw40laE47cJe3PvubcX5oApyClj1x98RswN9Hj/fT5tzwgVSHfu2tRzkHxPv4rQLe1VDjYQQ1aEqZu39CbRUSjVVSjmBi4EZVVCuOI5psxCdfQWY20ODyXUhULGB4QA7/Sn8a3cXdnv3FgdRh4Opg3iCHna6d7HDvQOlo3fF7ec0nAys05+TUjqVq4XMHfQwosEwuqZ1CcszFZsQS68hXUs8V2sYP/AhpoydGvWY/JwCAlG69Pqc35P73r8jLKmmaUafp5+9ax+Pjn6ODUs3l1iv40lCSjw3Pn0Frjhn8YzImHgXzU9uyumjTq3m2gkhjpRKt0hprQNKqVuB7wAb8IbWekWlayaOb96ZRC52DKFHyCjaZyPUQhUtUFGgUtnkS+bxXY3wlqFlqLIMDCYuuw+P6UWhcBgO7MpGwCJFgkJhV3Z6pvWgT3pv2iS2YWPBJnL9uWVqmSppxuH8r/4q9fygP8h3b/1I/0v60K5X+Hid2e/9zAtjpuL3RnbrxcS7GHbL4IjtiakJNO3YmHWLNkTEU2bQZM4Hv/HTR78zesIIrnxo1GHJbH60GXrLYFr3aMlXr84kb08efS84hdNG9sLukBR9QpwoquSnXWv9NfB1VZQlThBmFmirMT5BiBkCRnooU7mKgfxnsUx/YNRA1fyVd1c9jlevq/IqKlRE65ZP+/EFDgQfXjP6wPhYWywPtL+PWFsc/147hWU5yy1zUkUTY4uJui8pPQn+3llqGd5CHz999HtYILUvM4dnrnvZMohyuBycc/1AOvWzzgA/ftqt3HHa/QS8AcuB1trUvPfYZ+zeksWE/44ttX5VYdemDD5/4Ws2Lt9K254tGTZmMKm1U47ItQFad2tO627Nj9j1hBBHl+P/T0ZxdHJ0I7RMzCFUHCp2KEbSeIzEsaj4y8FIjTwOBcnPoZRiY8GmMl2yvAPP4+1xnJTcsXi2Xnm5g4XEGrHcs/ReFu9bUq4gCiDJnhT22m/62efLwdQmF95xHrYo45sOpgyF3W4L2/b7jAXF+Z/CjlWKgZf15eZnr4q6NEyT9g2ZvuE/3PD0FZYJPiE02Prnj39n47Kq6eZbPX8tEwY/wqj6N3BX/wdY9vOqsH3Xd7qTL6Z8y18zl/LhUzO4pt3tbF9XepAphBBVQQIpUT0cncC1f9Hh/WLA3gGcB8aXKBWDqvEpOPsSelwV2JpB2qcYrlCWjTjbwWVEV56B3gD5gQJ6pvXAaZQxy/oh7MrBP1c8RGGwsELnZ/lC69UFdZC3N73DzQvHcteSexj71+0E+ngZeddQy4DoYA6Xnf6Xhi9jo01tPdRJQWJaZKb5Q8UnxzPkpjNJTk+MeozWsHTuqqj7y2rp3JXc1f8BFn6/hOyde1kyZwUTBz/CvK9DXZvP3fgKnnxP8Vgvv9dPQU4hr979dqWvLYQQZSGBlKgWSilUyguQeC/YO4K9PSTehUp7IyyhJoCy1cFIm4qqvQpVezVGzW8xnO2L959ZZ1CFg53SfLvre3QFxl45lIMWCS3IC+RV+Np27Pyc+Su3L7qTHzJm49d+/NpPfrCAd7e+T+e72/HR7qnc98Ed3PXmGM6+bgA2uy20bEqsE2eMg8vuv5DmJzUJK7fneV3RZuR7csY4OG1k2QdJjxh3LnaHzXKf3WkjpWaS5b7yePkf0/AWhncBe90+XrrjLbxuL5uWb404R5uav2Ytq/S1hRCiLJSuhtUyu3XrphcsWHDErytcalK3AAAgAElEQVSOT6Y2mb75XeZm/kJA+6t8zl6McuHRpScJ3Z/vycSkbkxd0p1pLM5ZWuI5TsNJwAygUOVO1dA4rhEPdZgcti0nK5dfP/8Tv9dPz3O7RM00PuOl73jlzmkEgyba1DicdoaOGcwNT15e5usHg0Geve5lvp82J2JfYmo87217pdJJOs92XWw5s1Ap+LLgHYanXmm5tE1q7WQ+3Pl6pa59osjdk4fX7SO9flrULl0hTnRKqYVa625W+2RqiTjmGcrgiiaXcX6D4UxZ+zKr8irfpXSwsgRREMpZtX8c1Db3Nra5t0U9VqFoFNeQDG8mDpudggp0/+3xZUdsS05P4pzrBpR67tCbz6LroE789OFvBHwBTh3egxYnNy3X9W02G3e/OYZeQ7rx9LUvEgyYoDRJaYk89MU9VZLpPLlWMnu2R77PuOQ4HC4H/Ub15qcPfgsbOO+KdTLklrMqfe3jXdaObB679N+s/P1vDENRo14q46eNpUPvNtVdNSGOKRJIieNGgj2BfjX7VHkgdThoNJsLt1SqjCZxjcNe7/FmM3P3D2wu3ELjuEb0r3U6mwu3sNOzi3ox9Tg5pRO7vRm8vekd/s5fi9Nw0u+yvoxucD4Ow2LgfwkK89x8PuUbfv74d+KS4rjjlRup07QWdqedZp0aV1nLxugJw3n9nnfCZgi64lyMvHMoSinGvnAtmVuzWD1vLXaHHb/XzylDujF6wogquT7A3wvX8+6jn7BpxVZadG7KpZMuoGnHxqWfeBQzTZO7+z/AjvW7ixOs7tyQwcTBjzJ15XPUapheSglCiP2ka08cV7TW3PLXuAoP8D5W2JSNf7abRJP40Af61sJtPLLyMQLaT0AHsSkbpjZxKDt+HcCpHChl4DN9YYPuHcpBh+R23N5qHFneLOZkzGWPbw/tk9vTI607TosAy+v2cku3e9i1MaN4eZmYeBfn3jiIKyZfhCvWic1uPXaqvLTWTH/kYz588oui1zDs1sFc+69LwvJUbV61jR3rdtGkQ0PqNq0NwIalm3npH2+x8re/SUiJY8Rt5zDyrqHFCzmXxeIfl3PfkMfwuX1oHZoF6Yxx8tSsybTt2bJMZZimSfaufSSkxBMTd3SsR7h07kruO+8x3PnhucocTjsX3T2Uqx4+sbLUC1Ea6doTJwylFMPqD+G9LR9Ud1UOq3gjHpfhwm/6cRgO/rtpOh7zwIfi/i5GX9FagV7ts1xQ2a/9LM9ZyS+ZvzJt83SCOtQ9uXDvIr7a8Q3/bH9v8eLM+/3w9lwytmSFrdHnKfDyybNf8vnzX+NwOjj3pkFc99illU5MqZTi8vtHMuruYezZuZe0OimWXYaN2zagcdsGxa93rN/F7X3uKw4Usnf5mP7wx+zelMltL91Q5uu/MHZq2GB3bWq8hV5euuNNJn9yNzmZuTRoVRdnjPVkh9nv/cyLt78VqofW9L+kL2OnXBv1+CMlY0uW5Xa/L8D2EpYeEkJEkkBKHHNMbbLDvQOn4aJWTM2I/Q7lwI6dgEXm9ER7AvmBgsO6jMyRkBvMZcKySdiUjZOSO7E2v+IJSe3KzvQt7+EzDwQMXtNLpjeT73bOZHiDoWHHz/92EZ4C63FjwYBJMODly5e/x1vgLVfQUhJnjLO4paksPnjyC3yeQ2b7Ffr4ftocrnxoFCk1k0stIxgIsnWV9Ti31fPWcXmzMTicdrTWXPfEZQy9OXxc1uIfl/Ps9S+HBWKz3/sZv9fPhLfHlfm9HA6tuzcnGIgcxB8T76JTv/YWZwghopH0B+KYsixnOeMW/YOHVv6LScvvZ9Kyyez2ZIQd0y6preUYHQODFEcKaU6rBJ9HB4XCwCDWiClTItCgDrJ435JKXdOv/QTMyKDTr/3My54fsb1mgxoYtpJ/dewPWgpyI7tY3flufnz/V759YzaZ2/aUWM7mlVv5fMo3zHrnZ9z57lLeyQFr/lwXGvx+CIfLwbYyZIQHMGwGsQnWOcq01vi9fgrz3LjzPbx699ss+D78/+GdRz+JSN3gc/uZ+/Ef5O3NL+M7OTwatq5Pr6HdccUdaBmzO+0kpycx8PLTqrFmQhx7JJASx4xMbxbPr/0PeYE8vKYXn+lnu3s7j616EvOgXE91Y+twWs2+uIzwLiATk63ubWT79h7pqpdJTWc6nZI7clOz6/HrQJlbzUzM4nX9ysuu7DRPaBZ1v1V+riE3nYnDVfq1bA4b2TvD7/XiH5czqt4NPHfjK/zntje4stVY3nn0k4hztdY8d9MrjOk+gdfGv82/b36VixvcyMo//i7Du4KmHRtZJiv1efzUbVa2li2lFMPGDg4LNqLxFnr58Kkvwrbt2phheazdGXlfqsPE6eO4+pHRNGhVl/QGaZx34yD+8+fjxMZHX5pICBFJAilxzJiTMTdimRWNxh10szL3wEw9rTVdUzvTKqElNZ3p2LBFnHM0yvRlsSbvb17bOJWAtlrQOTqNpl5M3XIvZ9M2sTW3txxLnZg6oMG7JEDhlz58K4I4lIMBtftHnNO4XUPu+e844lPiiEuMjb5UjKmp1ejA7C+v28s/hz+JO9+DO8+Np8CL3+Pnvcc+iwiQfv18PrPf+Rmv24fP48ed76Ew180/hz1BMFh6vq1R44fjOGQckjPWyanDulGjbtlbJK98YBSDLu+HM8ZBXFIsDpcdu9N6sHpWUeua1prv3vqRvGzrVietKXMwdzjZ7DYuuP083lz9PO9teYUx/76G5PTKJ1EV4kQjgZQ4ZmT79liuV6fR7PPnhL7Xmtc3vhFaJDh3OZm+rHInuqxOHtODv5xBFITuweVNLsVQ5fuRXpu/ngnLJjEiZRjZV7nJvr2QnGc87BlTQMGYIN1iu1ie1/f8nny8eypPzppMq67WC/Z26tc+bGD4wplLscqK4HP7+P6tOWHbvn1jtuU4LJ/Hz6o/1pb6vpq0b8i/vr6Xxu0boAyFK9bJOdf2Z/y08i2kbLPbuO2lG/hgx2s8N/dh3t38EnZn5ExGm8NGl0GdAHjzvveYMnYqBTmR3ZqueBeX3X9htQ82F0JUHRlsLqqcN+hlRe4qTB2kfXK7iFlfFdU+uT0L9y7Ca4Z/wJrapGVC6MN8Td7f/Jm9AK/psyriuJbiSMGubOVaHNljevCaXl5ZNJXARo0+6LblLCvg1bun06Z7C/buzqFj3za0792mePyZ3WGnYet6rF+yybLsrWu2h732e/yWMwe11njd4f+nVtnKIZTRPHhIpvNta3fy/uOfsXreWhq2qc/oiSNo1bU5nU5rx+vLnsPn9WN32MLSJZRXQko8CSnxAFz/+KW8On463qLcVjaHjbikWC6+Zzj5+wr45Lkvw2Y07pdUI4GxU67j9FG9K1wPIcTRRwIpUaWW5SznhbUvFncxmZhc0+RKeqWfUumye6Z15+ud35DhycRfNK3fZTjpkdaD2jGhrpKFe/86IYOo1gmtSHOmYlN2oHzvX6PxpBVixgfDTvV7/Xz1ykxmTZ+Lz+PHGeOgY9+2PPTFPdgddjyFXmb+9yfLdfsA3HnhOYo6D+xIwB8ZIMXEuzj9ovA1/gZefhorf19j2SrVtler4u83LtvMbb3vw+v2YQZNtqzazp/fLOKBz8bT7cyTAHC6ypdstDRDbxlM3eZ1+PCpL8jank2XgZ0YPWE46fVrsPL3NdiddstAqmaDdAmihDgOSSAlqkxBoJAX1r4Y0WI0deNbtEhsQU1XxbMle4IebMrG/e3u5ftdPzAvez4uw8WAWmdwanqv4uPyA0dmNlRNRzpn1xvMmrw1zM9eUOq4K4dyFAd/ZaFQOA0HQW2WabzUZY1HYzfsjGo4kncOSWWwn4GBUsq6xUoDUfJU7g9mPAVels5dxTdTZ9P+1NbcdcZk/L6A5ew4w2bQ45zOYduS0hK55d9X8+LtbxH0h86LiXfRfXBnup8dfmz/0X348b1fWPbzajwFHhwuO4ZhcO87t4UFRq+Onx6WVDLUuuXj+VteY9raFw7b2nHdzzqZ7medHLE9vUENAr7I/y+lFPVa1jksdRFCVC8JpESVWbj3L8vtGpPfs/5gaP3zylXeytxVvLnxv2R4Q7OfDAy6pJ7MNU2vYlj9IZbnFATKltG8c/LJLM1ZVur4qTquOlzSaBTPrv138bbXur1cnPF7QO0zGOHexcfbPmVl7ircQXdYUOVUTnqn9+Kqpldw9+KJZPisZ3I5lAONJqADOJSDGJuLia3HM2nFZMvjD2bDVhw4nV7rNNKcqczY8RVbC7fgNX04DScaTYPY+rRIaM7sjDkRwZltrwMzq/RB+N5CL2/c+y6eAo/lYsJAaGB2YixXPXRxxL5zrx9Eh95tmPn2XArz3PQe1p0uAztFBDw2u41HvpzIolnL+PO7JSSnJzLwstOo2aBG2HErfl1tWYeMLVkU5rmJT4or9T1VpVoN0zm5fwcWzVoetv6fM9bBqLuHHdG6CCGODAmkRJXxBr1haQj2C+ggnqDH4ozo1uat49k1/w5rxTExWbh3EVnePTzQ/n7L1oayzMiLt8UzrtUYNJo1uWvZVLiJWFssszN+JMOTgdf04TKcOA0X/2g9jtoxtZnWY2rU8urG1mFsy1sAWLJvKW9vfpc93j04DAf9a53OyIYXAHBBw+FM3fBmcbZxCLU8tYhvzpiWNzE74ye2u7fRPL45/Wr1ZUvh1jLdqyDBsAHqnVI60imlIwDZvr1sLdxKmjONhnENimc4Znmz8JhenIYTm7JxesEZTOX9Ml0vf19B1H2xCTFcNH4YQ28+i6QaiZbHNG7XkOseu7TU6xiGQddBJ9F10ElRj0mqkRixzAmAzW7giq2eAd33vX8Hz17/Mr9+/idKQWJqAuNevJ7W3VtUS32EEIeXBFKiynRM6cAHWz+K2O4yXJycGv3D0Mqn2z+37ArTaHZ6drKpYDNNE5pE7O+e1o01eWuijpNqldCC21uOK57d1i65De2SQ6vd96vZlxU5K9lUuJl0Zw06p3bGE3TjM/2Wa85ZOSmlEyeldMIb9BYvBPzNzu/4dvf3FAYKSbQnEvTn4jScmASpHVObW1veQoozmQsaDA8rK2iG1swrS9deiwTrmXNpztSwBKSxtlge6jCZRXsXszZ/PbVc6ZxS4xRefnlamd5faeo0rcVl911YJWWVxYV3DuH1Ce8UD/yGUJqDs64+o9LL01RUbEIsk967A3e+m4KcQtLqplZqoLsQ4ugmgZSoMnViajOo9gB+yJhd3NXkMlx0Se1My4Ty/TW+3b2jhL2KDG+GZSB1ao1TmJPxE9vc2/GaXhQKh+Hg/PrDGVR7AHYj+iNvKIOOKR3omNKBXzJ/5c4l4/EGQx/Q/WqexuhGF5V4/sFcttC0/7c3vcvcrJ+L78de/16chpNRjUbSLL4pjeIaRh3H0yqxZSjgK6WRzWW4ioO2srApG93SutItreuBbTYbSoVyHB3K4bIT8AUpbYFzV6yTQVf0K3M9qsKwMYPJ2JLJF1O+xe604/cG6D28Bzc9c+URrYeV2ITYqJnRhRDHDwmkRJUa1WgknVI68mvWbwR0gF41TqFTcsdyD/qtF1OHnKLcUIcytUnDuIbFr/2mn/nZf7IsZwVpzlSubXo1mwo3s2DvQhLtCZxR83TLoCuaJfuWMm3z9LAB23Mzf0ZjckWTy8pcTkGggJ8y50a0rAXMAGvz1nFGrZKDDpfNxfVNr+XVDa8T1EFMLJY8UQ7Orju4zHWKZuBlfflh+tywlh0Ije257rHLyNubz/uPfx427udgSiladGnKsDGVr0t5KKW44ckruOTeC9i+bhe1GqWTWqv0dfSqyq5NGbw6/m0Wfr+EmHgX5954JpdMHFGlrWGmaRIMBHFY5K8SQlQ/CaRElWub1IY2ia1Zm7+OPb5sMrwZxekJyur8BiN4cvUzEUGIgUGH5PbUi60LhMZlPbzyX2R4M/GaXmzYmLl7Fre2uJnbWt5aofp/vn1GxKw3n/YxN/MXRjUcWdzaVJrdngzshh1/MPw9mJhsKthUpjJ61OhG04Qm/Jb1O/mBfHZ7M1i+bwVOw0FAB+lbszfD6pVvEL+VDn3aMvzWwXz2wjdo08Rms6G1ZtL7d9BrSDcACnIK+ezfX1m2WtkdNu5+c0y1JZpMSImndTfr7s3DJXdPHmN6TCA/Ox/T1BTmuvnwic/ZtGwz//zorkqX7/P4ePXut/nmjdn4vX6atG/IuP9cR4c+baug9kKIqiKBlMDUJn/nraUwWEirhJYkOBIqVd4+3z4eW/0Ue317UYSm23dP68r1za4tc+btVoktua3lrfx38zvFs/ZijBjOqjOIoQcFDjN3z2KXZ3dxwBUkSNAM8uqG13m+83PYVJQ5/SXI8lkvpKuUIj+QX+ZAKt2VTsCMbMFRKOrH1S9zfWq60sNmKeYH8sny7qGmK514e3yZyynNdY9fxuBr+jPvq7+IiXfR5/yeYUuGXPf4pXz35o+WGbttDptlGoSq4nV7mfXOL/z57SJqNkjjvJvOolGbst/Dw+HLV2fiyfdgmgciS6/bx7yvF7F93U7qt6hbqfIfv+IF5n21EJ879AxtXLaFCYMf5T9/Pk7jtg0qVbYQoupIIHWC2+7ewVOrn8Ed9KCAgA4wov5wzq13doXLfHH9K2R4MsK6ohbs/YvmGc0YWHtAmcvpmNKBp1IeQ2sdtWtwXvZ8y0HpATPAtsJtNI5vXO76N4tvwuJ9SyO225WNZEfZu42SHIn0rNGD+XsW4DsoZbjDcDCk3rnlrtd+CfYEEuyVC3ajadCqHg1a1bPc53A6uGj8MN55+OOIhJMJqfE0bG19XmUV5rkZe8pEMrZk4SnwYrMbfP36LCZOv43ew3sclmuWxcrf1lgm3rQ7bGxYuqVSgVTW9j3M+3JhRPl+r5+PnvqCu94YU+GyhRBVS6aSnMBMbfL0mmfZ69+Hx/TgLlrn7fMdM1idu6ZCZeb681ifvyFiPI/P9PHD7h8rVGZJ46tchnXrkInGGWVfaS5ocD4u45AFbw0nFzQ4v8yDzfe7usmV9K99Oi7DFWqJiq3Hna1up9FBY7yOJeffdi6N2zUgNiEGCOWMiol3Mend2w9b8svPp3zDrk2ZxYlBgwETb6GPp6990TJT+pHSuF1DywWMzaBJveaVW5R4x/rdOCwysptBk43Ly5YWQwhxZEiL1AlsQ/4GCgPuiO0+08esjB9pk9S63GX6TV/x8jCHOjTjeVUYUOsMthRuDStboUh31qBOOcdl7dcoriGT2k7k422fsqFgI6mOVIbVP4/uad3KXZbdsDO60SgubngRQR0sdyB2tImJc/HCH4/x2xd/suSnFdRsmM6ZV/QjtXbKYbvm3I9+x+eOTGdhBkw2LN0cddHkw23YmLP430vfEfAdSEzqcNpp1qkxzU9qUqmyG7auZ9naZbPbaNND8lEJcTQ5tn+ri0pxBz1RWxEKAtGTLpYkzZlGkiORPb7ssO12ZaNbapcKlVmSU2r0ZE3e3/yS9RuGMlAoYm0x3NZqbKVaSBrHN+LO1rdXWT2VUtjV8fHjZrPb6HvBKfS9oPLrJ5ZFXKJ1CoFgMBh135FQq1FNnpo1mWdveJnNK7aiDIPeI3pw+8s3VLrs1NopDLysL7Pf+wVv4YEg0hnr4MI7rbP6CyGqx/Hxm11USIvE5gTMyK4Rp+GsUOsLFE1Hb3Ydz/79fwR0kKAO4jScJNoTwwaJVxWlFFc1vYJz6p7N2vy1JDmSaJ/UrsyD2q3scO9k0d5FKGXQPa1bpdYIFJU37NazWfvXhrAFjJWhqNO0dtTxXEdK6+4teGXR07jz3did9ipNUXDbyzdQp2ktPnvhGwpz3LTv3Zqbn72Suk0r120ohKhaqrQke4dDt27d9IIFC474dUWk2RlzeG/LB/hNPxqNy3BSN6Yuk9pNLHM2byuZ3ix+zJjDbk8G7ZLa0Dv9VGJsMVVY88Pj8+0z+HLH15jaRCmFQjG60SgG1D6juqt2wtJa8/I/3uJ/L8/E4bSj0SSlJfLUrMnUbSZBhRDi8FNKLdRaW7YwSCAl2JC/kR8z5pAbyKNbahdOqdGzXJmyjxdbC7fx0MpH8B2SssChHDx50mNhS62IIy9jaxarfv+blNrJdOzbVpZdEUIcMSUFUtK1J2iW0JRmCU2ruxrV7s/sBQTMoOW+RXsXMaB2/yNcI3GwWg3TqdVQulmFEEcX+ZNOiCLRZhuGth+eqf1CCCGObRJICVGke1pXy0zoGk2X1JOroUZCCCGOdhJICVGkQVwDhtU/D4dyYFM27MqOQzm4tPFoUmV8lBBCCAuVGiOllHoKGAL4gPXA1VrrfVVRMSGqw5B659E9rTt/7V2EoQy6p3alhqtGdVdLCCHEUaqyLVIzgQ5a607A38DEyldJiOpVJ6Y259QdzOA6Z0oQJYQQokSVCqS01t9rrfdndPwDkCXJhRBCCHHCqMoxUtcA31RheUIIIYQQR7VSx0gppX4A6ljsmqS1/qLomElAAHinhHJuAG4AaNSoUYUqK4QQQghxNCk1kNJaDyxpv1LqSuA8YIAuIU261vpV4FUIZTYvZz2FEEIIIY46lZ21Nxi4B+intS6smioJIYQQQhwbKjtGagqQCMxUSi1WSr1cBXUSQgghhDgmVKpFSmvdoqoqIoQQQghxrJHM5kIIIYQQFSSBlBBCCCFEBUkgJYQQQghRQRJICSGEEEJUkARSQgghhBAVJIGUEEIIIUQFSSAlhBBCCFFBEkgJIYQQQlSQBFJCCCGEEBUkgZQQQgghRAVJICWEEEIIUUESSAkhhBBCVJAEUkIIIYQQFSSBlBBCCCFEBUkgJYQQQghRQRJICSGEEEJUkARSQgghhBAVZK/uCgghhBBClEfAH+D3GQtYt2gjdZvVpt9FvYhNiK2WukggJYQQQohjRv6+AsadOomsbXtw53uIiXfx2oTp/PvXR2nQsu4Rr4907QkhhBDimPHm/e+za8Nu3PkeADwFXvL25PPU1VOqpT4SSAkhhBDimPHTB7/h9wXCtmmtWfPnegrz3Ee8PhJICSGEEOKYoQwVfV/0XYeNBFJCCCGEOGYMuKwvDpcjbJthM+jQu021DDiXQEoIIYQQx4wrH7iIJh0aEpsQg81uIzYxhtTayYx/a0y11Edm7QkhhBDimBGbEMuUeY+xaNYy1i/eRJ2mteg1tBsOp6P0kw8DCaSEEEIIcUwxDIOug06i66CTqrsq0rUnhBBCCFFREkgJIYQQQlSQBFJCCCGEEBUkgZQQQgghRAVJICWEEEIIUUESSAkhhBBCVJAEUkIIIYQQFSSBlBBCCCFEBUkgJYQQQghRQRJICSGEEEJUkNJaH/mLKpUJbD7iFw5JB7Kq6drHIrlf5Sf3rPzknpWf3LPykftVfnLPDmista5ptaNaAqnqpJRaoLXuVt31OFbI/So/uWflJ/es/OSelY/cr/KTe1Y20rUnhBBCCFFBEkgJIYQQQlTQiRhIvVrdFTjGyP0qP7ln5Sf3rPzknpWP3K/yk3tWBifcGCkhhBBCiKpyIrZICSGEEEJUieM6kFJKPaCU2q6UWlz0dU6U4wYrpdYopdYppSYc6XoeTZRSTymlViulliqlPlNKpUQ5bpNSalnRfV1wpOt5NCjtuVEhzxftX6qU6lId9TxaKKUaKqV+VEqtUkqtUErdZnHM6UqpnIN+Zv9ZHXU9WpT2cybPWDilVOuDnp3FSqlcpdTthxxzwj9jSqk3lFIZSqnlB21LU0rNVEqtLfo3Ncq58nl5KK31cfsFPADcVcoxNmA90AxwAkuAdtVd92q8Z2cC9qLvnwCeiHLcJiC9uutbjfep1OcGOAf4BlDAKcC86q53Nd+zukCXou8Tgb8t7tnpwJfVXdej5au0nzN5xkq8dzZgF6H8PwdvP+GfMeA0oAuw/KBtTwITir6fYPW7Xz4vrb+O6xapMuoBrNNab9Ba+4D3gWHVXKdqo7X+XmsdKHr5B9CgOutzFCvLczMM+K8O+QNIUUrVPdIVPVporXdqrf8q+j4PWAXUr95aHfPkGYtuALBea11dyZ+PWlrruUD2IZuHAdOKvp8GDLc4VT4vLZwIgdStRU3eb0RpqqwPbD3o9Tbkl/t+1xD6a9eKBr5XSi1USt1wBOt0tCjLcyPPVhRKqSZAZ2Cexe5eSqklSqlvlFLtj2jFjj6l/ZzJMxbdxcB7UfbJMxapttZ6J4T+6AFqWRwjz5sFe3VXoLKUUj8AdSx2TQJeAh4m9MvoYeAZQsFBWBEW5x7XUxlLumda6y+KjpkEBIB3ohTTW2u9QylVC5iplFpd9FfOiaIsz80J92yVhVIqAfgEuF1rnXvI7r8IdcXkF41p/BxoeaTreBQp7edMnjELSiknMBSYaLFbnrGKk+fNwjEfSGmtB5blOKXUa8CXFru2AQ0Pet0A2FEFVTtqlXbPlFJXAucBA3RRx7hFGTuK/s1QSn1GqMn3RAqkyvLcnHDPVmmUUg5CQdQ7WutPD91/cGCltf5aKfWiUipda31CrvdVhp8zecasnQ38pbXefegOecai2q2Uqqu13lnUPZxhcYw8bxaO6669Q8YKjACWWxz2J9BSKdW06K+Yi4EZR6J+RyOl1GDgHmCo1rowyjHxSqnE/d8TGqBudW+PZ2V5bmYAVxTNrDoFyNnfdH4iUkopYCqwSmv9bJRj6hQdh1KqB6HfUXuOXC2PHmX8OZNnzNpoonTryTMW1QzgyqLvrwS+sDhGPi8tHPMtUqV4Uil1MqGmx03AjQBKqXrA61rrc7TWAaXUrcB3hGYkvKG1XlFdFT4KTAFchLoRAP7QWt908D0DagOfFe23A+9qrb+trgpXh2jPjVLqpqL9LwNfE5pVtQ4oBK6urvoeJXoDlwPLlFKLi7bdCzSC4nt2IXCzUioAuIGLo7WKngAsf87kGSuZUioOGETR7/uibQffsxcQgwIAAAB3SURBVBP+GVNKvUdo9mK6UmobMBl4HPhQKXUtsAUYWXSsfF6WQjKbCyGEEEJU0HHdtSeEEEIIcThJICWEEEIIUUESSAkhhBBCVJAEUkIIIYQQFSSBlBBCCCFEBUkgJYQQQghRQRJICSGEEEJUkARSQgghhBAV9P8N4IpiNxtfdAAAAABJRU5ErkJggg==\n",
"text/plain": [
"
"
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"# Perform agglomerative clustering\n",
"from sklearn.cluster import AgglomerativeClustering\n",
"clustering = AgglomerativeClustering(n_clusters=5, linkage='ward').fit(X)\n",
"plt.scatter(X[:, 0], X[:, 1], c=clustering.labels_);\n",
"plt.title('Agglomerative clustering using Ward linkage');"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"source": [
"Agglomerative clustering with Ward linkage results in better identified clusters on the first two principal components (compared to single, complete, or average linkage; code omitted)."
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"source": [
"However, the groupings do not correspond to the ground truth labels of either region or income grouping. Let's briefly investigate the observation labels in each cluster to see if discernable patterns appear. The labels in the first cluster are given by:"
]
},
{
"cell_type": "code",
"execution_count": 81,
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"outputs": [
{
"data": {
"text/plain": [
"MultiIndex([('AGO', 2013),\n",
" ('AGO', 2014),\n",
" ('BEN', 2008),\n",
" ('BEN', 2010),\n",
" ('BEN', 2011),\n",
" ('BEN', 2012),\n",
" ('BEN', 2013),\n",
" ('BEN', 2014),\n",
" ('BFA', 2004),\n",
" ('BFA', 2005),\n",
" ('BFA', 2010),\n",
" ('BFA', 2011),\n",
" ('BFA', 2012),\n",
" ('BFA', 2013),\n",
" ('BFA', 2014),\n",
" ('CIV', 2001),\n",
" ('CIV', 2003),\n",
" ('CIV', 2005),\n",
" ('CIV', 2006),\n",
" ('CIV', 2007),\n",
" ('CMR', 2001),\n",
" ('CMR', 2002),\n",
" ('CMR', 2010),\n",
" ('CMR', 2011),\n",
" ('COG', 2011),\n",
" ('COG', 2013),\n",
" ('DZA', 2002),\n",
" ('DZA', 2003),\n",
" ('DZA', 2005),\n",
" ('DZA', 2006),\n",
" ('DZA', 2007),\n",
" ('DZA', 2008),\n",
" ('DZA', 2009),\n",
" ('EGY', 2002),\n",
" ('EGY', 2005),\n",
" ('EGY', 2009),\n",
" ('EGY', 2010),\n",
" ('EGY', 2013),\n",
" ('EGY', 2014),\n",
" ('EGY', 2016),\n",
" ('ETH', 2015),\n",
" ('GAB', 2005),\n",
" ('GHA', 2000),\n",
" ('GHA', 2001),\n",
" ('GHA', 2003),\n",
" ('GHA', 2007),\n",
" ('GHA', 2008),\n",
" ('GHA', 2009),\n",
" ('GHA', 2016),\n",
" ('GIN', 2004),\n",
" ('GIN', 2005),\n",
" ('MAR', 2000),\n",
" ('MAR', 2001),\n",
" ('MAR', 2002),\n",
" ('MAR', 2003),\n",
" ('MAR', 2014),\n",
" ('MLI', 2007),\n",
" ('MLI', 2008),\n",
" ('MLI', 2010),\n",
" ('MLI', 2011),\n",
" ('MLI', 2012),\n",
" ('MLI', 2016),\n",
" ('NER', 2004),\n",
" ('NER', 2005),\n",
" ('NGA', 2001),\n",
" ('NGA', 2002),\n",
" ('NGA', 2003),\n",
" ('NGA', 2006),\n",
" ('NGA', 2008),\n",
" ('NGA', 2010),\n",
" ('NGA', 2013),\n",
" ('SDN', 2006),\n",
" ('SDN', 2012),\n",
" ('SEN', 2005),\n",
" ('SEN', 2006),\n",
" ('SEN', 2007),\n",
" ('SEN', 2008),\n",
" ('SEN', 2009),\n",
" ('SEN', 2010),\n",
" ('SEN', 2011),\n",
" ('SEN', 2012),\n",
" ('SEN', 2013),\n",
" ('TUN', 2002),\n",
" ('TUN', 2003),\n",
" ('TUN', 2005),\n",
" ('TUN', 2006),\n",
" ('TUN', 2008),\n",
" ('TUN', 2009),\n",
" ('TUN', 2010),\n",
" ('TUN', 2011),\n",
" ('TUN', 2012),\n",
" ('TUN', 2015)],\n",
" names=['reporter.ISO', 'year'])"
]
},
"execution_count": 81,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# Show labels in first cluster\n",
"partner_features_AFR_noout.index[np.where(clustering.labels_ == 0)[0]]"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"source": [
"Let's extract the unique country labels per cluster."
]
},
{
"cell_type": "code",
"execution_count": 82,
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"outputs": [
{
"data": {
"text/plain": [
"{'AGO',\n",
" 'BEN',\n",
" 'BFA',\n",
" 'CIV',\n",
" 'CMR',\n",
" 'COG',\n",
" 'DZA',\n",
" 'EGY',\n",
" 'ETH',\n",
" 'GAB',\n",
" 'GHA',\n",
" 'GIN',\n",
" 'MAR',\n",
" 'MLI',\n",
" 'NER',\n",
" 'NGA',\n",
" 'SDN',\n",
" 'SEN',\n",
" 'TUN'}"
]
},
"execution_count": 82,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# Countries in first cluster\n",
"cluster_labels = partner_features_AFR_noout.index[np.where(clustering.labels_ == 0)[0]].to_list()\n",
"country_labels = [i[0] for i in cluster_labels]\n",
"set(country_labels)"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"source": [
"No immediately discernable pattern appears in the first cluster. This is the case for the remaining clusters too (code hidden)."
]
},
{
"cell_type": "code",
"execution_count": 83,
"metadata": {
"slideshow": {
"slide_type": "skip"
},
"tags": [
"hide-cell"
]
},
"outputs": [
{
"data": {
"text/plain": [
"{'AGO', 'CIV', 'CMR', 'DZA', 'EGY', 'ETH', 'GHA', 'NGA'}"
]
},
"execution_count": 83,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# Countries in second cluster\n",
"cluster_labels = partner_features_AFR_noout.index[np.where(clustering.labels_ == 1)[0]].to_list()\n",
"country_labels = [i[0] for i in cluster_labels]\n",
"set(country_labels)"
]
},
{
"cell_type": "code",
"execution_count": 84,
"metadata": {
"slideshow": {
"slide_type": "skip"
},
"tags": [
"hide-cell"
]
},
"outputs": [
{
"data": {
"text/plain": [
"{'AGO',\n",
" 'BDI',\n",
" 'EGY',\n",
" 'MWI',\n",
" 'NGA',\n",
" 'RWA',\n",
" 'SDN',\n",
" 'TZA',\n",
" 'UGA',\n",
" 'ZAF',\n",
" 'ZMB',\n",
" 'ZWE'}"
]
},
"execution_count": 84,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# Countries in third cluster\n",
"cluster_labels = partner_features_AFR_noout.index[np.where(clustering.labels_ == 2)[0]].to_list()\n",
"country_labels = [i[0] for i in cluster_labels]\n",
"set(country_labels)"
]
},
{
"cell_type": "code",
"execution_count": 85,
"metadata": {
"slideshow": {
"slide_type": "skip"
},
"tags": [
"hide-cell"
]
},
"outputs": [
{
"data": {
"text/plain": [
"{'BDI',\n",
" 'BEN',\n",
" 'BFA',\n",
" 'BWA',\n",
" 'CAF',\n",
" 'CIV',\n",
" 'CMR',\n",
" 'COG',\n",
" 'COM',\n",
" 'CPV',\n",
" 'DZA',\n",
" 'EGY',\n",
" 'ETH',\n",
" 'GAB',\n",
" 'GHA',\n",
" 'GIN',\n",
" 'GMB',\n",
" 'GNB',\n",
" 'KEN',\n",
" 'LBY',\n",
" 'LSO',\n",
" 'MAR',\n",
" 'MDG',\n",
" 'MLI',\n",
" 'MOZ',\n",
" 'MRT',\n",
" 'MUS',\n",
" 'MWI',\n",
" 'NAM',\n",
" 'NER',\n",
" 'NGA',\n",
" 'RWA',\n",
" 'SDN',\n",
" 'SEN',\n",
" 'SLE',\n",
" 'STP',\n",
" 'SWZ',\n",
" 'SYC',\n",
" 'TGO',\n",
" 'TUN',\n",
" 'TZA',\n",
" 'UGA',\n",
" 'ZAF',\n",
" 'ZMB',\n",
" 'ZWE'}"
]
},
"execution_count": 85,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# Countries in fourth cluster\n",
"cluster_labels = partner_features_AFR_noout.index[np.where(clustering.labels_ == 3)[0]].to_list()\n",
"country_labels = [i[0] for i in cluster_labels]\n",
"set(country_labels)"
]
},
{
"cell_type": "code",
"execution_count": 86,
"metadata": {
"slideshow": {
"slide_type": "skip"
},
"tags": [
"hide-cell"
]
},
"outputs": [
{
"data": {
"text/plain": [
"{'BDI',\n",
" 'BWA',\n",
" 'KEN',\n",
" 'MDG',\n",
" 'MOZ',\n",
" 'MWI',\n",
" 'NAM',\n",
" 'RWA',\n",
" 'TZA',\n",
" 'UGA',\n",
" 'ZAF',\n",
" 'ZMB',\n",
" 'ZWE'}"
]
},
"execution_count": 86,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# Countries in fifth cluster\n",
"cluster_labels = partner_features_AFR_noout.index[np.where(clustering.labels_ == 4)[0]].to_list()\n",
"country_labels = [i[0] for i in cluster_labels]\n",
"set(country_labels)"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"### Hierarchical clustering and corresponding heatmap"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"source": [
"Rather than specifying *ex ante* the number of clusters, I now perform hierarchical clustering, restricting myself to illicit trade in 2016. I have explored various transformations, scalings, and types of linkages. I find that a (modified) log transformation on standardized data (with mean 0 and unit variance) with Ward linkage (which minimizes the sum of squared differences within all clusters) performs rather well."
]
},
{
"cell_type": "code",
"execution_count": 87,
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"outputs": [],
"source": [
"# Create data for African bilateral trade matrix in 2016\n",
"data = partner_features_AFR_noout.reset_index() \\\n",
" .query('year == \"2016\"').drop(columns='year').set_index('reporter.ISO')\n",
"\n",
"# Select the columns which have at least 1 non-zero row \n",
"data = data.loc[:,(data != 0).any(axis=0)]\n",
"\n",
"# Log the data\n",
"data = data.apply(lambda x: np.log10(x+1) if np.issubdtype(x.dtype, np.number) else x, axis=0)\n",
"\n",
"# Scale the data\n",
"scaler = StandardScaler()\n",
"# scaler = MinMaxScaler()\n",
"data_scaled = scaler.fit_transform(data)\n",
"data_scaled = pd.DataFrame(data_scaled, index=data.index, columns=data.columns)\n",
"\n",
"# Extract region labels for the observations\n",
"obs_labels = region_labels(data).set_index('reporter.ISO')\n",
"\n",
"# Extract unique regions\n",
"color_labels = obs_labels['UN_Intermediate_Region'].unique()\n",
"color_labels = np.sort(color_labels)\n",
"\n",
"# List of RGB triplets for the region labels\n",
"rgb_values = sns.color_palette('Paired', 5)\n",
"\n",
"# Map region labels to RGB triplet\n",
"color_map = dict(zip(color_labels, rgb_values))\n",
"region_color = pd.DataFrame(obs_labels)['UN_Intermediate_Region'].map(color_map)"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"source": [
"The reporting countries are plotted in the rows of the heatmap below, while the partner countries (restricted to non-outlying African countries) are displayed in the columns. Dendograms for each dimension are displayed. In addition, the first column colors the observations according to their ground truth regional label.\n",
"\n",
"On the origins dimension (i.e. reporters), the two highest-level clusters correspond broadly to western African (in pink) countries on the one hand, and eastern (in light blue) and middle African (in dark blue) countries on the other."
]
},
{
"cell_type": "code",
"execution_count": 88,
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAsgAAALTCAYAAAALuvQuAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4yLjEsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy+j8jraAAAgAElEQVR4nOzdeZhcZZn38e9NABsIyr6DUWBQQGQpZUR5ARUFRRQZheACbsF9RnHJDDOm1ZkBFRwZwKVRDKBssigiCLgERFksMMKwI4tsgqAICWkg4X7/qNNyaHqp6vSpqq58P9fVF33Oec65797Cr59+6pzITCRJkiQ1LNfpBiRJkqRuYkCWJEmSSgzIkiRJUokBWZIkSSoxIEuSJEklBmRJkiSpxIAs9YiIuC4idu2CPg6KiEvHOH5+RBxYZY0xzpsbEf+5NLUnQ0RsEhELImJaB3sY8+vQLZ+rkUREf0R8b5Rju0bE3aXtpn8uIuKOiHjtJLUpaQozIEtTwEj/4x4eEjNzq8yc1/bmWpSZe2bmCZ3uY6KGB7CJyMw/Zub0zFwyWX1NoIe/fx0m+gvHkIi4ICI+U9reMCJylH3rLV3nrZkqPxeSuosBWVrGRcTyEzinYzOfU91EPt9TwCXALqXt/wfcOMK+WzLzT61cuEc/X5K6nAFZ6hHlWeaIWC4iZkfEHyLioYg4PSLWKI7NKGby3hcRfwR+Uez/QUT8KSL+FhGXRMRWpWvPjYhvRMR5EbEQ2C0iNo6IsyLiz0WNY4b1c0RE/DUibo+IPUv750XE+0vbH4iIGyLi0Yi4PiK2L/YP9T+0f58WPheviojfRMTDEXFXRBw0wphnzZoWn5fNivffUNR9NCLuiYhPRcQqwPnABsUSiQURsUGrn+/SvuVLn5MvRsSvi3oXRsRapb7eHRF3Ftf+j9GWAkTEC4qPebli+9sR8UDp+Pci4l/KX4eIeDHwTeAVxcfzcOmSq0fET4qeroiITUf5lF8CvHKoLrAz8DWgNmzfJUXto4qvyyMRcVVE7FzqsT8izih6fQQ4qPi4Li76uAhYiyYN+7noL742JxbXui4iaqOc96Lie3f/Ynusn481I+LHxcfz24j4z/L3VnGtiyLiLxFxU0S8vdn+JXWGAVnqTR8H3kJjBm8D4K/AscPG7AK8GHh9sX0+sDmwDnA18P1h4w8A/gtYFbgMOBe4E5gBbAicWhq7I3ATjSDzZeA7ERHDm4yItwH9wLuB5wJ7Aw8Vh/9AI1Q9D/g88L2IWH+8DzwiNik+lqOBtYFtgfnjnTeC7wAHZ+aqwNbALzJzIbAncG+xRGJ6Zt7LxD7fwx0AvIfG539F4FPFx7Ml8HXgHcD6ND4fG450gcy8HXgE2K7YtTOwoAjB0JjFvXjYOTcAHwQuKz6e1UqHZ9L43K8O3Erj6z+SK4HnAC8t1bmoOKe875Li/d/S+LqsAZwM/CAi+krXezNwBrAaje/Dk4GraHw/fRFYmjXse9P4Xl0NOAc4ZviA4pe0C4GPZebQ9/VYPx/HAguB9YreDixdaxUan4uTi3NnAl8vB2xJ3ceALE0dPyxmBx8uZvm+PsbYg4FDM/PuzHycRgj9p3jmn6v7M3NhZi4CyMzjM/PR0viXRsTzSuN/lJm/zsyngG1oBMFPF9cYzMzybOydmXlcscb2BBrBbt0R+nw/8OXM/G023JqZdxb9/CAz783MpzLzNOAW4OVNfJ7eAfwsM0/JzCcz86HMnEhAfhLYMiKem5l/zcyrxxjb8ud7BN/NzJuL46fTCJAA/wT8ODMvzcwngM8BOUYvFwO7xNNrfc8otl9A45eQ349x7nBnZeaVmbmYRiDcdqRBxcd8BfD/ipnz1TLzNuBXpX1bFr2Rmd8rvi6LM/NIGuF6i9IlL8vMHxbfa2sDLwP+IzMfz8xLgB+38DEMd2lmnld8b57E0wF+yM40gvOBmXlu6WMc8ecjGsuN9gXmZOZjmXk9je/5IXsBd2Tmd4uP92rgTBpfV0ldyoAsTR1vyczVht6AD48x9vnA2aUwfQOwhGeG1LuG3omIaRFxeLFE4BHgjuLQWiONBzamEYIXj1L/7+tMM/Ox4t3pI4zbmMZM8bMUywrmlz6GrWnuT+ujXrNF+wJvAO4s/rz/ijHGtvT5HkV5be5jPP352qB8bvH5fIjRXQzsytMztvNozF7vAvyqCJ3NGq2nkVxS1NwZGPpl6dLSvruGfvmJiEOisazmb8Xn63mM/r22AfDXYvZ+yJ0tfAzDDf+Y+ob9IvNB4DeZ+cuhHeP8fKwNLD+s5/L7zwd2HPbL7TtozDZL6lIGZKk33QXsWQ7UmdmXmfeUxpRnIQ+g8Wft19IIKzOK/THK+LuATWLpX0B1F/Csda0R8XzgOOCjwJrFLwT/N6yflq45goXAyqWazwgsxaz2m2n8WfyHNGZ1YeTZ21Y/3624D9io1OdKwJpjjL+YRiDdtXj/UuCVNALyxaOcM9Heyi4p6v4/GjPHAL8uav99eUWx3vizwNuB1Yuv7d8Y/XvtPhproVcp7dtkEvodzQdpfG//T2nfWD8ffwYWU/oa0fglbchdwMXDvjemZ+aHqvoAJC09A7LUm74J/FcRNImItSPizWOMXxV4nMbM5MrAf49z/StpBJfDI2KViOiLiFdOoM9vA5+KiB2iYbOi51VohKQ/F/2/h8YMcjO+D7w2It4eEcsXL6AaaWnA74GtImLbYv1r/9CBiFgxIt4REc/LzCdprOsduiXb/cCaw5aftPr5bsUZwJsiYqeIWJHGmuBRf1HIzFuARcA7gUsy85Gi530ZPSDfD2xUXH+ifkNjXe87KQJyZv6VxtfwnTy9/nhVGoHyz8DyEfE5Gks/Rvt47gTqwOeLr8urgDctRZ/jeRTYg8bSkMNLPY/481Es1TgL6I+IlSPiRTTW1A85F/iHiHhXRKxQvL2stC5cUhcyIEu96Sga6ygvjIhHgctpvHBuNCfS+LP1PcD1xfhRFaHgTcBmwB+Bu4H9Wm0yM39A44VfJ9MIJj8E1ijWcR5J48WA9wMvoTEb2cw1/0hjacQhwF9ovEBv+DpTMvNm4AvAz2isbx5+H+B3AXcUf1L/II2QR2beCJwC3Fb8yXwDWv98Ny0zrwM+RuOFZffR+Dw9QCOwjeZi4KHiczG0HcDvRhn/C+A64E8R8eAE+3yMxgvpnkNjtn/Ir2jMwg8F5AtovODtZhrfc4OMv/zkABqfz78Ac2h8v1YmMx8Gdgf2jIgvMv7Px0dpzCz/ica65lMovj6Z+SjwOmB/4N5izJdofJ4kdanInIy/rEmS2iEipgMPA5sXd61Ql4mILwHrZeZSPTFSUuc4gyxJXS4i3lT8+X4V4AjgWp5+oZg6rLjP8TbFMqGXA+8Dzu50X5ImzoAsSd3vzTT+PH8vjXvx7p/++a+brEpjHfJCGi/mPBL4UUc7krRUXGIhSZIklbR0i6aI6Ko0nZnN3PJJkiRJalqrAbmqPipR3LrpEhqvFl4eOCMz53S2K0mSJHWzlgLycstNq6qPqjwOvDozF0TECsClEXF+Zo55CyuparVabTbQ1+k+pGXUYL1eP3z8YZKWVS3OIE+t1/QVL2JZUGyuULx11TIRLbP66vV6f6ebkJZFtVqtv9M9SOpuvT6DTERMo3Hz+s2AYzPzig63JEmSpC7WYkDurhnkiJgFzCrtGsjMgfKY4olf20bEasDZEbF1Zpaf8iRJkiT93ZQOyEUYHhh3YGPswxExD9iDZz4GVZIkSfq7FtcgT60lFhGxNvBkEY5XAl4LfKnDbUmSJKmLTekZ5CasD5xQrENeDjg9M8/tcE+SJEnqYj39Ir3MvAbYrtN9SJIkaero9RlkSZIkqSU9vQZZkiRJapUzyJIkSVKJAVmSJEkq6ekX6UmSJEmtanENsjPIkiRJ6m3OIEuSJEklrkGWJEmSSpxBliRJkkpcgyxJkiSVuMRCkiRJKnGJhSRJklTiDLIkSZJU0uIa5Kk1gxwRGwMnAusBTwEDmXlUZ7uSJElSN+v1GeTFwCGZeXVErApcFREXZeb1nW5MkiRJ3amn1yBn5n3AfcX7j0bEDcCGgAFZkiRJI5rSM8gRMQuYVdo1kJkDo4ydAWwHXFF9Z5IkSZqqpvQa5CIMjxiIyyJiOnAm8C+Z+UjljUmSJGnKmtIzyM2IiBVohOPvZ+ZZne5HkrpFrVabDfR1uo8OmFGr1fo73USbDdbr9cM73YQ0VfR0QI6IAL4D3JCZX+10P5LUZfrq9Xp/p5tQ9ZbBXwikpdLTL9IDXgm8C7g2IuYX+/4tM8/rYE+SJEnqYi2uQZ5aM8iZeSkQne5DkiRJU0evzyBLkiRJLenpNciSJElSq5xBliRJkkp6eg2yJEmS1CqXWEiSJEklLrGQJEmSSpxBliRJkkpaXIPsDLIkadnTA4/lnuqP1/ZR2WorZ5AlSRqfj+XuoCke7jUFtTiD7EPpNHV0+YxPN8/mOFMjSVqm+SI99TJnfCagi4O7pEnQ5ZMHo+nmSYWxOOEwRXkfZEmSli1OHrTJFA31whlkSZIk6Rl6+kV6EXE8sBfwQGZu3el+JEmS1P16fQZ5LnAMcGKH+5AkSW3QZWusu2XttGuhW9TTa5Az85KImNHpPiRJUtu4xnqYLgnpU0prM8jTuisgR8QsYFZp10BmDnSqH0mSJE19U3oNchGGDcSSJEmaNFM6IEuSJEmTrbU1yNN8kp4kSZJ6W0/PIEfEKcCuwFoRcTcwJzO/09muJEmS1M2m9Iv0xpOZMzvdgyRJkqaWnp5BliRJklrV2hrk5VyDLEmSpN7W00ssJEmSpFa5xEKSJEkqcQZZkiRJKmlxBtk1yJIkdYtarTYb6GvxtBm1Wq2/hfGD9Xr98BZrSFNaiy/ScwZZkqQu0lev1/urLNBimJZ6gkssJKkLTXBmsFWtziROhLOPkqYcX6QnSd2p8pnBdnD2UdJU1NoSi2muQZbarU0ziWXtmFUczllGSWrSBP6/MJF/15fpf5edQZa6X1fOJE5ycH/RJIbyZfofdWkqmuR/Tybzl/xu/ffEtecVMyBLmqhuDe79ne6hlzlzpYr474m6ii/SkyS1wpkrST2vxdu8Ta01yBGxB3AUMA34dmY6IyFJkqQx9ewMckRMA44FdgfuBn4bEedk5vWd7UySJEndrJfXIL8cuDUzbwOIiFOBNwMGZEmSJI1qSgfkiJgFzCrtGsjMgeL9DYG7SsfuBnZsV2+SJEmamqb0fZCLMDwwyuGRms0K25EkTRHejUPSWKb0DPI47gY2Lm1vBNzboV4kSd3Fu3Esg/zFSM3q2RfpAb8FNo+IFwD3APsDB3S2JUnLogk+BKHV/zH7P2VpfP5ipKb07AxyZi6OiI8CF9C4zdvxmXldh9uStGzyf8qSNIW0OIPcXWuQx5OZ5wHndboPSZIkTR0tPihk6swgS5IkSRPRs0ssJEmSpIno5RfpSZIkSS1rcQZ5aq1BlrqRtxmSJKm7tfigEGeQ1Rk9dpss72ggSVIXcw2ypgpD5TKox34xkiRNEa3NIIdLLCS1lb8YSZLarqfvgyxJkiS1yvsgS5IkSSWuQZYkSZJKvA+yJEmSVOJ9kCVJkqQS74MsSZIklSyza5Aj4m1AP/Bi4OWZWe9sR5IkSeoGy2xABv4PeCvwrU43IkmSpO6xzN4HOTNvAB9+IkmSpGea0vdBjohZwKzSroHMHOhUP5IkSZr6pvRt3oowPGogjoifAeuNcOjQzPxRZY1JkiRpyurpNciZ+dpO9yBJkqSpxfsgS5IkSSXL7H2QI2If4GhgbeAnETE/M1/f4bYkSZLUYT29xGIsmXk2cHan+5AkSVJ3aSkgT+uhgCxJkiSNpMWA7BpkSZIk9bbWAnI4gyxJkqTetsyuQZYkSZJG4hpkSZIkqcQ1yJIkSVKJa5AlSZKkEtcgS5IkSSWuQZYkSZJKXIMsSZIklbgGWZIkSSpxDbIkSZJUEpnZ9OD67bc3P7gNai94gWs+2uTHd3xlUr/2N//qhZN5uY659KxfVV4j2vCXm+VXaOl35Qm5+aarKq/x4q1fXnmNe/74h8pr7HXQvpXXmP/L31deA+CV+7yy8hqDCwcrr7HCc1aovMbggkWV11iy5KnKa7z05VtWXuOEw06uvAbAZttvWnmN6auvWnmNtTZcq/IaH3jD7j2VyZbZNcgR8RXgTcATwB+A92Tmw53tSpIkSZ3W0tTUtFiuq96W0kXA1pm5DXAz8K9Le0FJkiRNfcvsGuTMvLC0eTnwT53qRZIkSd1jSt8HOSJmAbNKuwYyc2ACl3ovcNrkdCVJkqSpbEqvQS7C8KiBOCJ+Bqw3wqFDM/NHxZhDgcXA9ytpUpIkSVNKa0sspth9kDPztWMdj4gDgb2A12Qrt/OQJElSz5rSSyyWRkTsAXwW2CUzH+t0P5IkSeoOy2xABo4BngNcFBEAl2fmBzvbkiRJUm+JiDWBnxeb6wFLgD8DM4B7M3PL0th+YEFmHhERc4HdgRdm5uMRsRZQz8wZVfc8pdcgL43M3KzTPUiSJPW6zHwI2BaeFYBnAOeOc/oSGjdT+EaFLT5LT69BliRJ0pT2NeATEXFcO4suy0ssJEmS1N3+CFwKvAv4cbuKthSQi7W6Wgq1Wm020NfpPlo154z9Ot2CJEnqUhN8NsVodxAbvv+/gXOAn0ywvZY5g9x+ffV6vb/TTbTqx3d8ZU6ne5AkSd1pvGdTjOIhYPVh+9YAbh927VsjYj7w9ol32JrWArIzyJIkSZoEmbkgIu6LiNdk5s8jYg1gD+CoEYb/F84gS5IkaRnwbuDYiDiy2P58Zv5h+KDMvC4irga2b0dTrd3FwoAsSZKkCcrM/mHb1wO7jTL2oGHbb62ssWGcQZYkSZJKXIMsSZIklTiDLEmSJJW0eh9kp5AlSZLU05wSliRJkkpamkHWsmvPi543qde7eco9S3BkTz75ROU17rrrxsprbLDBppXXWGedTSqvcetN8yuv8a5Pf6jyGoMLFlVeY9vdXsoqq02vvI66yyZbVv9zeNJXTq28xnPXem7lNQAeuvcvldeYvvqqlddQ65xBlqRlkOFYkkZnQJYkSZJKDMiSJElSiQFZkiRJKjEgS5IkSSUGZEmSJKnE27wVarXabKAdNx+b0YYakiRJmiAD8tP66vV6f9VFarVa5TUkSZI0cS6xkCRJUqUiIiPipNL28hHx54g4t9g+KCKOGeG8OyJirXb2CgZkSZIkVW8hsHVErFRs7w7c08F+xmRAliRJUjucD7yxeH8mcEoHexmTa5C7XBtfPDimyw+e1ekWJElSl4qIWUA5LAxk5sCwYacCnyuWVWwDHA/s3KYWW2JA7n5tefHgeBYfNzCn0z1IkqTuVITh4YF4+JhrImIGjdnj89rQ1oQZkCVJktQu5wBHALsCa3a2ldEZkCVJktQuxwN/y8xrI2LXTjczGl+kJ0mSpLbIzLsz86hRDh8UEXeX3jZqa3MlziBLkiSpUpk5fYR984B5xftzgbkjnDqjuq5G5wyyJEmSVGJAliRJkkoMyJIkSVKJAVmSJEkqMSBLkiRJJd7FQloKK6ywYuU1XrzVyyqv8cCf7q68Rl/fKpXXGBxcWHkNLZu+95VvVl7jnz50YOU1fvrtn1ZeY8mTSyqv8dgjj1VeA2CFvhXaUqdq18z7ffVF3rB79TXayIDcfoO1Wq2/hfEzKupDkiRJIzAgt1m9Xj+8lfEthmlJkiQtJdcgS5IkSSUGZEmSJKnEgCxJkiSVGJAlSZKkEgOyJEmSVGJAliRJkkoMyJIkSapURGREHFna/lRE9Je23xkR10TEdRHx+4j4dkSsVjq+dkQ8GREHt6NfA7IkSZKq9jjw1ohYa/iBiNgD+ASwZ2ZuBWwP/AZYtzTsbcDlwMw29GpAliRJUuUWAwM0gvBwhwKfysx7ADJzSWYen5k3lcbMBA4BNoqIDatu1ifpdb9WH01dicsPntXpFiRJUpeKiFlAOSwMZObAsGHHAtdExJeH7d8KuHqMa28MrJeZV0bE6cB+wFcnoe1RGZC7XKuPpq7K4uMG5nS6B0mS1J2KMDw8EA8f80hEnAh8HFg00piIeAlwErAq8G+ZeRqwP3B6MeRU4DtUHJBdYiFJkqR2+RrwPmCV0r7raKw7JjOvzcxtgfOBlYrjM4GDIuIO4BzgpRGxeZVNGpAlSZLUFpn5Fxqzwe8r7T4MOCIiNirtWwkgIrYAVsnMDTNzRmbOKMbvX2WfBmRJkiS105HA3+9mkZnnAf8LnB8R10fEb4AlwAU0Zo/PHnb+mVR8NwvXIEuSJKlSmTm99P79wMrDjp8AnDDCqf0jXOsaYMtJbvEZnEGWJEmSSiY0g1yr1WYDfZPcS6fN6HQDkiRJ6ryJLrHoq9fr/ZPZSKd1w72GJUmS1HkusZAkSZJKDMiSJElSiXexUEcc87nPV3r95ZZrz+9+a65Z+ePgWXPNDSqv8c5/fd/4g5bS2f97ZuU1MrPyGucMVP9xvO6AN1Re4yffPqfyGgDLLTet8hq77feaymtssGGlzyQA4OIzf1l5jXU2Wr/yGstNq/7f36eWPFV5DYC+lXvj5VZ33nhHp1uYcpxBliRJkkoMyJIkSVKJAVmSJEkqMSBLkiRJJQZkSZIkqcSALEmSJJUYkCVJkqQSA7IkSZIqFxHrRsTJEXFbRFwVEZdFxD4RsWtEnDts7NyI+KfS9toR8WREHNyOXg3IkiRJqlREBPBD4JLMfGFm7gDsD2zU5CXeBlwOzKyoxWcwIEuSJKlqrwaeyMxvDu3IzDsz8+gmz58JHAJsFBGVP8bWgCxJkqSqbQVcPcbxnSNi/tAbsPfQgYjYGFgvM68ETgf2q7ZVWL7qAr2oVqvNBnrjAe1NuvzgWZ1uQZIkdamImAWUw8JAZg6MMf5Y4FXAE8CngV9l5l6l43NLw/enEYwBTgW+A3x1cjofmQF5Yvrq9Xp/p5top8XHDczpdA+SJKk7FWF41EAMXAfsWxr/kYhYC6g3cfmZwLoR8Y5ie4OI2Dwzb5lww+NwiYUkSZKq9gugLyI+VNq38ngnRcQWwCqZuWFmzsjMGcBhNGaVK2NAliRJUqUyM4G3ALtExO0RcSVwAvDZcU6dCZw9bN+ZVHw3C5dYSJIkqXKZeR+jz/zOGzb2oOLdM0a4zjXAlpPZ23DOIEuSJEklBmRJkiSpxIAsSZIklRiQJUmSpBIDsiRJklRiQJYkSZJKvM2bmnL+7n+b1Ot9tK/aB/Od8fUTK73+kE23eEnlNRYtWFR5jXOO/VHlNVZba43Ka7z/gE9WXuOsb5xSeY12eOP7925LnXO+dWZb6lTt1Qe8pvIag234Wa9fcFXlNQYXPVZ5jU9+6SOV1wA49/Sft6VO1dbZaL1OtzDlOIMsSZIklRiQJUmSpBIDsiRJklRiQJYkSZJKDMiSJElSiQFZkiRJKjEgS5IkSSUGZEmSJFUqIpZExPzS2+xi//IR8d8RcUvp2KER8bqIuCwiohg3rTi2Uzv69UEhTxus1Wr9TY6dUWEfkiRJvWZRZm47wv7/BNYDXpKZgxGxKnBIZl4YEe8F3gd8G/gY8NvM/E07mjUgF+r1+uHNjm0hSEuSJGkEEbEy8AFgRmYOAmTmo0B/MeQTwKURcRnwUeDl7erNgDyJarXabKCv031UYc4Z+3W6BUmS1KUiYhYwq7RrIDMHStsrRcT80vZhwA3AH4tQ/CyZeV9EfA24DPh4Zv5lsvsejQF5cvXV6/X+TjdRhR/f8ZU5ne5BkiR1pyIMD4wx5FlLLCJim2Hb7wH+GVgT2Ckz7wKOBQ7PzLmT2/HYfJGeJEmSOuFWYJNi3TGZ+d0iRP8NmFbsewrIdjdmQJYkSVLbZeZjwHeAYyKiDxp3qwBW7GhjuMRCkiRJ1Ru+BvmnmTkbOBT4IvB/EfEosAg4Abi3Az3+nQFZkiRJlcrMaaPsfxKYXbyNdu70qvoajUssJEmSpBIDsiRJklRiQJYkSZJKDMiSJElSiQFZkiRJKvEuFmrKnhc9b1Kv95Ev/vukXm+4jTd+UaXXH/Lwg9U/9fLNH96n8hrnfuucymv86e67Kq9x5tdvrLzG2z72rsprDC5YVHmNdtn74H0rrzG4cLDyGr1ihees0IYqK1de4fivnFJ5DYC1N167LXWqtuNeO3a6hSnHGWRJkiSpxIAsSZIklRiQJUmSpBIDsiRJklRiQJYkSZJKvIvFxAzWarX+EfbPaHMfkiRJmmQG5Amo1+uHj7R/lNAsSZKkKcQlFpIkSVKJAVmSJEmVi4hDI+K6iLgmIuZHxI4RMS8ibiq250fEGcXY/oh4LCLWKZ2/oF29usRCkiRJlYqIVwB7Adtn5uMRsRawYnH4HZlZH+G0B4FDgM+2qc2/cwZZkiRJVVsfeDAzHwfIzAcz895xzjke2C8i1qi8u2GcQe6wWq02G+jrdB/jufzgWZ1uQZIkdamImAWUw8JAZg6Uti8EPhcRNwM/A07LzIuLY9+PiEXF+xdl5qeL9xfQCMn/DMyprvtnMyB3Xl+9Xu/vdBPjWXzcQFu/MSVJ0tRRhOGBMY4viIgdgJ2B3YDTImJ2cXi0JRYA/wvMj4gjJ7XhcRiQJUmSVLnMXALMA+ZFxLXAgU2c83BEnAx8uOL2nsGALEmSpEpFxBbAU5l5S7FrW+BOYOsmTv8q8FvamFt9kZ4kSZKqNh04ISKuj4hrgC2B/uLY90u3efvZ8BMz80HgbOA57WrWGWRJkiRVKjOvAnYa4dCuo4zvH7b9SeCTk97YKJxBliRJkkoMyJIkSVKJAVmSJEkqMSBLkiRJJQZkSZIkqcS7WEyuwVqt1t/iOTMq6KPrbbLJlpVe//7776j0+kP6+latvMZFJ1xUeY2FCx+pvMZbP7Jf5TWeGHy88hpqze9/Ob/yGlu8/EWV1+gVbzj4DZXXuPTMSyuvseTJxZXXAFj5uSu3pY66jwF5EtXr9cNbPWcCgVqSJEkVcomFJEmSVGJAliRJkkoMyJIkSVKJAVmSJEkqMSBLkiRJJQZkSZIkqcSALEmSpMpExJoRMb94+1NE3FPaXjciTo6I2yLiqoi4LCL2KZ37qnbdKY0AACAASURBVIi4MiJuLN5mtaNn74MsSZKkymTmQ8C2ABHRDyzIzCMiIoDfACdk5gHF8ecDexfvrwecDLwlM6+OiLWACyLinsz8SZU9O4MsSZKkTng18ERmfnNoR2bemZlHF5sfAeZm5tXFsQeBzwCzq27MgCxJkqRO2Aq4epzjVw3bVy/2V8olFp03OBUeN335wW1Z8iNJkqagYm1wOSwMZOZAi9c4FngVjVnllwEB5AhDR9o3qQzIHVav1w/vdA/NWHzcwJxO9yBJkrpTEYZbCsTAdcC+pWt8pFhnXC8drwHnlM7ZAbh+KVptikssJEmS1Am/APoi4kOlfSuX3j8WOCgihl7gtybwJeDLVTfmDLIkSZLaLjMzIt4C/E9EfAb4M7AQ+Gxx/L6IeCdwXESsSmPJxdcy88dV92ZAliRJUltkZv+w7fuA/ccYfwnwsorbehaXWEiSJEklBmRJkiSpxIAsSZIklRiQJUmSpBIDsiRJklRiQJYkSZJKvM2bmrLZbRtO6vU+dvABk3q9TllltVUqrzFt2rTqa6xQfY3BBYOV11D3eelu21ZeY3Ch31vd5E0H7lF5jZVXXLHyGgAPPPJI5TX+cM1tlddQ65xBliRJkkoMyJIkSVKJAVmSJEkqMSBLkiRJJQZkSZIkqcSALEmSJJUYkCVJkqQS74MsSZKkykXEocABwBLgKeCvwOrAdGBt4PZi6IeB/wbWBwaBBcB7M/OmdvVqQJYkSVKlIuIVwF7A9pn5eESsBayYmfdGxK7ApzJzr9J4gHdkZj0iZgFfAfZuV78usZAkSVLV1gcezMzHATLzwcy8t8lzLwE2q6yzERiQJUmSVLULgY0j4uaI+HpE7NLCuW8Crq2orxG5xGIZUavVZgN9E77A7p+fvGYkSVJPKZZBzCrtGsjMgaGNzFwQETsAOwO7AadFxOzMnDvGZb8fEYuAO4CPTX7XozMgLzv66vV6/0RPnvGvP5kzib1IkqQeUoThgXHGLAHmAfMi4lrgQGDuGKe8IzPrk9VjK1xiIUmSpEpFxBYRsXlp17bAnZ3qZzzOIEuSJKlq04GjI2I1YDFwK89cktFVDMiSJEmqVGZeBew0yrF5NJZelPftWnlTY3CJhSRJklRiQJYkSZJKDMiSJElSiQFZkiRJKjEgS5IkSSXexUKSlkELH17AKqtN73QbUld7+447Vl7jsGtuq7yGWucMsiQtgwzHkjQ6A7IkSZJUYkCWJEmSSgzIkiRJUokBWZIkSSoxIEuSJEklXX+bt1qtNhvo63QfPWBGpxuQJEmaCro+IAN99Xq9v9NNTHW1Wq2/0z1IkiRNBS6xkCRJUuUiYr2IODUi/hAR10fEeRHxDxGREfHF0ri1IuLJiDim2O6PiHsiYn5x3syqezUgS5IkqVIREcDZwLzM3DQztwT+DVgXuA3YqzT8bcB1wy7xP5m5LfBm4FsRsUKV/RqQJUmSVLXdgCcz85tDOzJzPnAXsAi4ISJqxaH9gNNHukhm3gI8BqxeZbMGZEmSJC2ViJgVEfXS26xhQ7YGrhrjEqcC+0fERsAS4N5R6mwP3JKZD0xK46OYCi/SkyRJUhfLzAFgYCku8VPgi8D9wGkjHP9ERHwAeCGwx1LUaYozyJIkSaradcAOox3MzCdozDAfApw5wpD/ycwtaCy/ODEiKr0FsAFZkiRJVfsF8JxiFhiAiHgZ8PzSmCOBz2bmQ6NdJDPPAurAgVU1CgZkSZIkVSwzE9gH2L24zdt1QD+ltcaZeV1mntDE5b4AfDIiKsuxrkGWJElS5TLzXuDtIxzaeoSxc4G5xfv9w45dBWwx6Q2WOIMsSZIklTiDLEmSpJ5TvJBvMyCBP2TmYLPnOoMsSZKknhERy0fEl4G7gROA7wF3RcSXm30CnwFZkiRJveQrwBrACzJzh8zcDtgUWA04opkLGJAlSZLUS/YCPpCZjw7tyMxHgA8Bb2jmAq5BVlNufeE9k3q9o1hzUq8nSZJUyOK2csN3LomIZ+0fiQF52TFYq9X6J3ry5QcPf6S6JElSV7o+It6dmSeWd0bEO4Ebm7mAAXkZUa/XD1+a8xcfNzBnsnqRJEmq0EeAsyLivTQeX53Ay4CVaDysZFwGZEmSJPWMzLwH2DEiXg1sBQRwfmb+vNlrGJAlSZLUMyJiZeDJzPwF8IuI2AJ4Q0Q8NzPPbuYa3sVCkiRJveSnwAyAiNgMuAx4IfDRiDismQsYkCVJktRLVs/MW4r3DwROycyPAXvSuAXcuAzIkiRJ6iXlW7m9GrgIIDOfAJ5q5gKuQZYkSVIvuSYijgDuATYDLgSIiNWavYAzyJIkSapURGREnFTaXj4i/hwR5xbbBxXb8yPixoj4RES8vtieHxELIuKm4v0TR68EwAeAB2msQ35dZj5W7N+SJh817QyyJEmSqrYQ2DoiVsrMRcDuNGZ4y07LzI9GxJrATcB2mbktQETMAz6VmfXxChXXf9bzHzLzN8BvmmnWgCxJkqR2OB94I3AGMBM4Bdh5+KDMfCgibgXWB+5qtUhEXMsz1yEPv/42413DgCxJkqSlEhGzgFmlXQOZOTBs2KnA54plFdsAxzNCQI6ITYA+4JoJttPUnSrGYkCWJEnSUinC8PBAPHzMNRExg8bs8XkjDNkvInYDtgA+kJmDE+zlzomcV+aL9CRJktQu59B4odwpIxw7LTO3ojGrfGRErDfZxSNizBA/xIAsSZKkdjke+EJmXjvagMy8DDgJ+OeJFomIaRHxiREOfauZ8w3IkiRJaovMvDszj2pi6JeA90TEqhOsswR48wj7r2rmfNcgS5IkqVKZOX2EffOAecX7c4G5pWP3AuuVtnedQNlfR8QxwGk0bjM3dK2rxzvRgCxJkqRetFPx3y+U9iWNx0+PyYAsSZKknpOZu030XNcgS5IkqedExLoR8Z2IOL/Y3jIi3tfMuQZkSZIk9aK5wAXABsX2zcC/NHOiAVmSJEm9aK3MPB14CiAzFwNLmjnRNchqyvm7/21yL/irNSf3eh3y85N+XnmNiKi8xh7v36PyGr1i7uFHV17jgQf+WHmNzTbbvvIaAJlPVV5j7/e/vfIaat7Rs4+pvMaKK/ZVXgPgJzu8qPIaa6y/RuU1lmELI2JNGi/MIyL+EWgq0BiQJUmS1Is+SePJfZtGxK+BtYG3NXOiAVmSJEm96DpgF2ALIICbaHJ5sWuQJUmS1Isuy8zFmXldZv5fZj4JXNbMic4gS5IkqWdExHrAhsBKEbEdjdljgOcCKzdzDQOyJEmSesnrgYOAjYAjeTogPwL8WzMXMCBLkiSpZ2TmCRFxEjAzM78/kWu4BlmSJEk9JRv3mDx4ouc7gyxJkqRKRcQS4FpgBWAxcALwtcx8KiL+C3hjafjKwKbA8zJzQXH+j4B1MvMVLZS9KCI+BZwGLBzamZl/Ge9EA7IkSZKqtigztwWIiHWAk4HnAXMy81Dg0KGBEfF94PRSOF4N2B5YEBEvyMzbm6z53uK/HyntS+CF451oQJYkSVLbZOYDETEL+G1E9GdmDh2LiHcCmwEHlk7ZF/gxcD+wP3BYk3VeMNEeXYMsSZKktsrM22jk0HWG9kXEDOBw4B2Zubg0fCZwSvE2s9kaEbFCRHw8Is4o3j4aESs0c+5EZ5AHa7Va/wTPbdWMNtWpTK1Wmw2058HxFZlzxn6dbkGSJHWpYkZ4VmnXQGYOjHda6fxpwPeA/8jMW0v716Uxo3xpZmZELI6IrTPz/5po6xs01jx/vdh+V7Hv/eOdOKGAXK/XD5/IeRPRxiBepb56vd7f6SaWxo/v+MqcTvcgSZK6UxGGxwvEfxcRLwSWAA8Uu/4duC8zvzts6H7A6sDtEQGNh33sX4wfz8sy86Wl7V9ExO+b6c8lFpIkSWqbiFgb+CZwTDEr/I80Huwxa4ThM4E9MnNGZs4AdqARkJuxJCI2LdUdCuXj8kV6kiRJqtpKETGfp2/zdhLw1eLY52nc2u2XxSzxkH2BTYDLh3Zk5u0R8UhE7JiZV4xT89PFNW+jsZzj+cB7mmnWgCxJkqRKZea0MY69foxTNxxh/PZN1vx5RGwObEEjIN+YmY83c64BWZIkST0nIvqADwOvonH/419FxDczc3C8cw3IkiRJ6kUnAo8CRxfbM2ks7XjbeCcakCVJktSLthh2F4tfehcLSZIkLct+V9whA4CI2BH4dTMnOoMsSZKkXrQj8O6I+GOxvQlwQ0RcC2RmbjPaiQZkSZIk9aI9JnpiTwTkKfAo5xmdbmBpLfhr048+b8r5Jxw6qdcbbs8D9670+kNe867XVF5j2rRR74yjDlh55edWXuP++++ovMa66z6/8hoAm2yyVeU1Tjry6+MPWkrrrfeCymu8+u27V17jnKPPqbzGpltvUXmNwYXj3oRgUjzy0COV11hj/TUqr7Gsysw7I+JVwOaZ+d2IWAtYNTNvH+/cngjIdPmjnHvkcdmSJElTRkTMAWo07oP8XWBF4HvAK8c71xfpSZIkqRftA+wNLATIzHuBVZs50YAsSZKkXvREZiaNh4QQEas0e6IBWZIkST0lIgI4NyK+BawWER8AfgYc18z5vbIGWZIkSQIa93CLiLcAnwUeobEO+XOZeVEz5xuQJUmS1IsuAx7OzE+3eqIBWZIkSb1oN+DgiLiT4oV6AGM9IGSIAVmSJEmViogEvpeZ7yq2lwfuA67IzL0ioh9YkJlHlM65A6hl5oMRcShwALAEeAo4ODOvGKfsnhPt14AsSZKkqi0Eto6IlTJzEbA7cE8zJ0bEK4C9gO0z8/HigR8rjndeZt450Wa9i4UkSZLa4XzgjcX7M4FTmjxvfeDBzHwcIDMfLO5pXBlnkNtjcKo/Te+Q437Y6RYkSVKXiohZwKzSroHMHBg27FTgcxFxLrANcDywcxOXv7A472Yat2o7LTMvnoS2R2VAboN6vX54p3tYWqf87u45ne5BkiR1pyIMDw/Ew8dcExEzaMwenzf88Oin5YKI2IFGmN4NOC0iZmfm3KVqegwGZEmSJLXLOcARwK7AmqX9D9FYSlG2KvAwQGYuAeYB8yLiWuBAYG5VTboGWZIkSe1yPPCFzLx22P5LgL0jYlWAiHgr8PvMXBIRW0TE5qWx2wITfgFeM5xBliRJUltk5t3AUSPsvyYijgEuLW4J9wDw/uLwdODoiFgNWAzcyjPXO086A7IkSZIqlZnTR9g3j8ayiaHtbwHfGmHcVcBOFbb3LC6xkCRJkkoMyJIkSVKJAVmSJEkqMSBLkiRJJQZkSZIkqcS7WKgj9jxw7063oJKffvunldf4618eqLzGG9/75sprvP3jB1ZeY+8Fb6+8xhnfPLHyGgAPPHBH5TUGBxdWXmPhwr9VXqMd9v5Y9f/2XvmTKyuv8fiixyuvAdC3XF/lNb78mX+pvMZOO+1TeY0PvGH3ymu0kzPIkiRJUokBWZIkSSoxIEuSJEklBmRJkiSpxIAsSZIklRiQJUmSpBIDsiRJklRiQJYkSZJKfFCIJEmSKhMRawI/LzbXA5YAfwYCWAF4ojR8G+CNmXl+ce4ngMOAdTOzbU/sMSBLkiSpMpn5ELAtQET0Awsy84jh4yJiFvAO4ILS7pnAb4F9gLlV9zrEJRaSJEnqqIj4B+BzwLsy86li36bAdODfaQTltnEGGajVarOB6h+4PoUdctwPO92CJEnqUsXs76zSroHMHGjy3BWAk4FPZeYfS4dmAqcAvwK2iIh1MvOByep5LAbkhr56vd7f6Sa62Sm/u3tOp3uQJEndqQjDTQXiEXwRuC4zTx22f39gn8x8KiLOAt4GHLsUbTbNgCxJkqSOiIhdgX2B7Yft3wbYHLgoIgBWBG6jTQHZNciSJElqu4hYHfgu8O7MfHTY4ZlAf2bOKN42ADaMiOe3ozdnkCVJktQJHwTWAb5RzBIPOYzG8oo9h40/u9j/paobMyBLkiSpLTKzv/T+YTTC8EhOG+HcT1bU1rNMhYA8WKvV+scZM6MNfUiSJGkZ0PUBuV6vHz7emCYCtCRJktQUX6QnSZIklRiQJUmSpBIDsiRJklTS9WuQJVVvj/fvUXmNwQWDldd4YvDxymv8+qxfV17jkb/9pfIaB87+cOU12uWCuedXXuO173xd5TUGFyyqvMZFJ1xUeY1p06ZVXuN9nzmg8hoAZ373J5XX+MyXv1Z5jXPnnl55jV7jDLIkSZJUYkCWJEmSSgzIkiRJUokBWZIkSSoxIEuSJEklBmRJkiSpxIAsSZIklRiQJUmSVKmIyIg4qbS9fET8OSLOLbYPKrZ/FxG3RMQFEbHTsGt8MiJujIhrI+L3EfHViFihin4NyJIkSaraQmDriFip2N4duGfYmNMyc7vM3Bw4HDgrIl4MEBEfBF4H/GNmvgR4GfAAsBIVMCBLkiSpHc4H3li8PxM4ZbSBmflLYACYVew6FPhQZj5cHH8iMw/PzEeqaNSALEmSpHY4Fdg/IvqAbYArxhl/NfCiiFgVmJ6Zt1fd4JDl21VIz1Sr1WYDfZ3uo1mHHPfDTrcgSZK6VETM4unZXoCBzBwoj8nMayJiBo3Z4/OauWzpv1mq9XrgS8BqwAGZ+ZuJdz4yA3Ln9NXr9f5ON9GsU35395xO9yBJkrpTEYYHxh0I5wBHALsCa44zdjvghsx8JCIWRsQLMvP2zLwAuKB4gd+KS9P3aFxiIUmSpHY5HvhCZl471qCI2IXGjPRxxa7DgG9ExGrF8aDCv8Q7gyxJkqS2yMy7gaNGObxfRLwKWBm4Hdg3M28ojn2j2H9FRDwOLAB+Dfyuij4NyJIkSapUZk4fYd88YF7x/lxg7hjnJ42lGUdU0d9wLrGQJEmSSgzIkiRJUokBWZIkSSoxIEuSJEklBmRJkiSpxIAsSZIklXibtwo0+RjpGW1oRWrKjVfcWHmNGVvNqLxGO7zyra+svMbggkWV17joxAsrrwGw+7tfV3mNXd62W+U1esXuB+5eeY0Lj7+g8hqnfOPsymsArNhXyUPa2m7atBU63cKUY0CuxriPka7VamMelyRJUme4xEKSJEkqMSBLkiRJJQZkSZIkqcSALEmSJJUYkCVJkqQSA7IkSZJUYkCWJElS5SLi0Ii4LiKuiYj5EXF+RHypdPz5EXFbRKwWES+PiEsi4qaIuDEivh0RK7erV++DLEmSpEpFxCuAvYDtM/PxiFgLeA7w84iYm5k3AEcB/1Hs/wGwf2ZeFhEB7AusCjzWjn6dQZYkSVLV1gcezMzHATLzwcy8B/gk8PWI2BNYNTO/D3wEOCEzLyvGZmaekZn3t6tZA7IkSZKqdiGwcUTcHBFfj4hdADLzPOAvwInAh4uxWwNXdabNBpdYdM7gVHrc9CHH/bDTLUiSpC4VEbOAWaVdA5k5MLSRmQsiYgdgZ2A34LSImJ2Zc4FjgZUy86Z29jyWXgnISxs2Z0xSH02r1+uHt7vm0jjld3fP6XQPkiSpOxVheGCcMUuAecC8iLgWOBCYCzxVvA25DtgB+FEVvTajJwLy0obNqTSTK0mSNNVExBbAU5l5S7FrW+DOUYYfA1wZET/JzCuK898J/Cwz/1R9tz0SkCVJktTVpgNHR8RqwGLgVp65JOPvMvP+iNgfOCIi1qExu3wJcFa7mjUgS5IkqVKZeRWw0yjH5tFYelHedxmN9cod4V0sJEmSpBIDsiRJklRiQJYkSZJKDMiSJElSiQFZkiRJKvEuFlKXu+QHl1ReY7cDdqu8xuCCwcprqHk77b0Tq6w2vfI63/3voyuvMfOfP1B5jV5x4he+U3mNl7xiu8prLGrTvyfTV1+1LXWq9uLtqv+a9BoD8jhqtdpsoK/F02ZU0IokTZp2hGNJmqoMyOPrq9fr/a2c4JP5JEmSpi7XIEuSJEklBmRJkiSpxIAsSZIklRiQJUmSpBIDsiRJklRiQJYkSZJKDMiSJEmqVEQsiYj5EfH7iLg6InYq9s+IiEUR8buIuCEiroyIA0vnHRQRx7S7X++DLEmSpKotysxtASLi9cBhwC7FsT9k5nbFsRcCZ0XEcpn53c606gyyJEmS2uu5wF9HOpCZtwGfBD7e1o6GcQa5zSb46OqOO+S4H3a6BUmS1KUiYhYwq7RrIDMHStsrRcR8GhlofeDVY1zuauBFk99l8wzI7dfyo6u7wSm/u/v/t3fn4ZJV5b3Hvz+mgAwqokZBaSUqGmRsckEJjqgkcQQVjGO84BRHjAMmgpeoqKBRgka8V0WjoF5n71VxQkVxaEYZzFUBFTVhcAQBBd77x96H3hSnD92nVlX1ab6f5zlP1967znrXOaer6t1rr/Xuw2bdB0mStHbqk+HjFnjKcIrFnsD7kuywiuemdf/WlFMsJEmSNDVVdSqwFXD7VTxlF+D86fXopkyQJUmSNDVJtgfWBy6f59gy4CjgmOn26sacYiFJkqRJm5uDDN0UiqdV1XVJALZLcgbd/OTfAcfMsoIFmCBLkiRpwqpq/VXsvwjYZIHvey/w3ol0agFOsZAkSZIGTJAlSZKkARNkSZIkacAEWZIkSRowQZYkSZIGrGIhreWqauIxvvLBr0w8xp6P2nPiMbT2ecahz594jKuvvHriMdYV11577cRjXH/95N+zfnPZbyYeA+Ca318z8RhHHvrsicd45COfN/EY6xoT5Mm4evny5Yev4tiyKfZDkiRJa8gEeQJWrFhx5KqOLZA4S5IkaS3gHGRJkiRpwARZkiRJGjBBliRJkgZMkCVJkqQBE2RJkiRpwARZkiRJGjBBliRJ0kQlWZbknJF9hyd5af/4JUm+n+R7Sc5K8uYkGw6eu0uSSvLwafTXBFmSJEkzk+TZwMOAParqvsDuwCXAJoOnHQic0v87cd4oRJIkSbP0KmDvqvo1QFX9AbjhpmtJAuwP7AN8PcnGVTXRe8ybIE/fQrehXmsd8q5PzLoLkiRpLZXkYODgwa7jquq41fjWTYDNqurCBZ5zf+DCqvpRkpOBvwI+tujOrgYT5Clb6DbUa7MTzrj4sFn3QZIkrZ36ZHihhLhWsX+94bF+jvEbgNsAT6qqb9JNqzixf8qJwFOYcILsHGRJkiRN2uXAbUf2bQlcBFyZ5G4AVfX5qtoZOAfYKMn6wH7Aq5NcBBwD7Jtk80l21hHkzkLTHpZNsR+SJEnrnKq6Iskvkjykqr6UZEvgEcBbgdcD70hyQFX9up9zvHH/rQ8FzqqqG6pXJDkeeAzw/kn11wSZhac9LMX5wpIkSWuhpwLHJjm6335NP6/4HcCtgG8nuQa4AvgGcAZdAv3xkXY+CjwHE2RJkiQtZVV1HvCgefYXcFT/Nerp8zz/U8CnWvdvyDnIkiRJ0oAJsiRJkjRggixJkiQNmCBLkiRJAybIkiRJ0oBVLLRajj5736btHbje4U3bW5c94AkPmHiM8791/sRjSJNy9MtfPvEY22x9z4nH2P85T5t4jHvtvMPEYzx0v8m/Z5393em8Z51/6nkTj/G64z448Rhbbb3VxGOsaxxBliRJkgZMkCVJkqQBE2RJkiRpwARZkiRJGjBBliRJkgZMkCVJkqQBE2RJkiRpwARZkiRJE5XkuiRnJjkryelJ7pfkNkkuT5L+OXsmqSTb9Nu3TvLLJOv12y9OcnWSW0+6vybIkiRJmrSrqmrnqtoJeCXw+qr6NfCfwL3759wPOKP/F2AP4NtVdX2/fSDwXeCxk+6sCbIkSZKmaQvgV/3jb7AyIb4f8JaR7W8CJNkO2Az4R7pEeaJMkCVJkjRpm/RTLL4P/E/giH7/N1mZEN8d+AiwvN++H10CDV1SfALwdeBeSe4wyc5uMMnGb2mWL1/+CmDjWfdjIp4/6w5IkqS1VZKDgYMHu46rquMG21dV1c79c/cE3pdkB7oE+BVJ7gZcVFVXp7MZsBvwnf77DwAeW1XXJ/kY8Hjg2En9PCbIbW28YsWKw2fdiUlYfvx9D5t1HyRJ0tqpT4aPu9knds89NclWwO2r6gdJbgs8Eji1f8ppwDOAC6vqiiQ7AvcAvtCv59sIuIAJJshOsZAkSdLUJNkeWB+4vN91KvBCVibIpwIvop9/TDe94vCqWtZ/3RnYOsm2k+qjCbIkSZImbW4O8pnAh4CnVdV1/bFvAHcBVvTbp9LNR55LkA8APj7S3sf7/RPhFAtJkiRNVFWtv8CxNwFvGmxfBGSwfbd5vucljbt4I44gS5IkSQMmyJIkSdKACbIkSZI0YIIsSZIkDZggS5IkSQMmyJIkSdKAZd60Wg7Z8bNN2/v5Od9u2p7Gs8Nf7jDxGFdfcfXEY2j1nfKxU6YSZ6/H7TXxGIe84Q0Tj/HZ4z818RhvedWhE4/xgAftP/EYp51y1sRjXP7zX048BgDJzT9nCfjk20dLCLd30F/tM/EY0+QIsiRJkjRggixJkiQNmCBLkiRJAybIkiRJ0oAJsiRJkjRgFYubd/Xy5csPX83nLptgPyRJkjQFJsg3Y8WKFUeu7nPXIJGWJEnSWsopFpIkSZqoJJXk/YPtDZJcmuQzg32PSXJ2ku8n+V6Sx/T7109y5sjXZUk+NKn+OoIsSZKkSbsS2CHJJlV1FbAP8LO5g0l2Ao4C9qmqC5PcDfhCkguq6mxg58Fz7wR8BzhiUp11BFmSJEnT8Fngr/vHBwInDI69FHhdVV0I0P/7euAfhg0kCXA88KaqOmdSHXUEeS22fPnyVwAbz7ofAIe86xOz7oIkSVpLJTkYOHiw67iqOm7kaScCr+6nVewIvBv4y/7Yn9ONIA+tAJ43su/FwLXAMS36vSomyGu3jVesWHH4rDsBcMIZFx826z5IkqS1U58MjybEo885O8kyutHj/ztyOEAttK+fhvEiYPeqGn1uU06xkCRJ0rR8im6k+ISR/ecCy0f27QqcB5BkE+ADwHOr6r8m3UlHkCVJkjQt7wZ+U1XfS/LAwf6jgI8k+XJVXdSPNB8K7D848+AJlAAAH1xJREFU/tWq+gxTYIIsSZKkqaiqi4G3zrP/zCQvBz6dZEPgj8DL+v13Bp4LfD/JmYNvO7eq/nYS/TRBliRJ0kRV1Wbz7DsZOHmw/THgY/M87+d085GnxjnIkiRJ0oAJsiRJkjRggixJkiQNmCBLkiRJAybIkiRJ0oBVLLRajj5736btHbje4U3bk7Rm9nrcXrPuwpLyqIP3m3iMrz/lIxOPsemtb1JIoLnd9tpp4jHOOf0/Jh4D4LKfXTaVOJP26Oc+dtZdWHJMkNu6evny5Yc3bG9Zw7YkSZK0GkyQG1qxYsWRLdtrnGxLkiRpNTgHWZIkSRowQZYkSZIGTJAlSZKkARNkSZIkacAEWZIkSRowQZYkSZIGTJAlSZI0UUkqydGD7ZcmOXzkOWclOWFk33uT/D7J5oN9b+3b22pS/TVBliRJ0qRdAzxuVUltknvT5aV7J9l05PAPgUf3z1sPeBDwswn21QRZkiRJE3ctcBzw4lUcfxLwfuAk4FEjx04Antg/fiDwjb69ifFOemu31reuXrznz7oDkiRpbZXkYODgwa7jquq4kacdC5yd5I3zNPFEYB/gXsDf0yXFc34APDrJbYEDgX8H9m3V9/mYIK/FWt+6ehzLj7/vYbPugyRJWjv1yfBoQjz6nN8meR/wAuCquf1JdgcuraofJ7kYeHeS21bVrwbf/jHgAOC/Ac9q/gOMcIqFJEmSpuVfgGcCw3nGBwLbJ7kI+BGwBbDfyPedCBwBfKGqrp90J02QJUmSNBVV9Uvgw3RJ8tyiu8cDO1bVsqpaRrcg78CR7/sJ8Crg7dPopwmyJEmSpuloYK6axd7Az6pqWJXia8B9ktxp+E1V9c6q+tE0OugcZEmSJE1UVW02ePxfwK0Gh/cYee51wFxy/PRVtLesbQ9vzBFkSZIkacAEWZIkSRowQZYkSZIGTJAlSZKkARNkSZIkaaiq/PKr2Rdw8FJqd9ox1qWfxRi3vBjr0s9ijFtejHXpZ1lXYqzNX44gq7WDb/4pa1W7044xrTjGMMZSjmMMYyzlOMZYB5ggS5IkSQMmyJIkSdKACbJaO26JtTvtGNOKYwxjLOU4xjDGUo5jjHVA+onYkiRJknAEWZIkSboRE2RJkiRpwARZkiRJGjBBliRJq5TkLkn+Ydb9kKbJBFljS/InSZ6U5NAkr577GqO9LRf6atn3kbjbJfnHJOc0bPO9rdpam0zid3Uz8XZv1M6+Sb6W5LIklyb5apK/atH2SJz1k2w12N4oycFJzm/U/sZJbj/P/jsk2bhFjL699ZNsNtjeI8ne/dfmreLME3fTJE9O8n8atXdCknuv4tj7G8WYyftWH7t5AptkqyTPSfI14GTgjo3avTDJBYOv4faPWsQYxNqjZXvrsiS7J/nTwfZTk3wyydsm/f93bbXBrDugdcIngd8ApwHXNGjvNKCAzHOsgLs3iAFAkjsBTwSeBOwIvB44sFX7fZsTk+R3dL8TWPn7KrrX9kZV1ew1PoXf1Wi8+wAH9DF+Aywfs72DgGcBLwNW9LuXA0cm2aaqmpQ0SnIA8E7gyiQ/AA4H3g98F/jbFjGAtwGfAz42sn8fYC/gOY3ivAG4BHhjv30CcA6wMXA68PJGcUiyEfBXdP+/HgF8FPi3Rs0/FLhfkjdW1bEjx/68UYzLgIuBa/vt4ftX0/ct6BJY4PF0r4+tgY83aHNz4LF0f4N79m3evaq2GbftgdHX8XrAE4CXAmc0jAPwjiTfAV5eVb9u3DZJTqqqh/WPX1lVr28do2/7GFa+z99EVb2gQZh30r1OSLI3cCTwfGBnunJv+zeIsaRY5k1jS3JOVe0wpVhbV9XPGrRzEN0HyzbAh/uvT1bV3cZteyTO9/s48yX7VNXpjeNtDjyXLhH8eFUd0qDNqfyu+ljb9rEOpEs0tgWWV9VFDdo+D9irqn45sv92wClVNe8I4yLinAM8pqp+mGRX4FTggKoaO4EZxDivqu6zimPnVlWTpC/JGcDuVXXt3HZV7ZIkwNeraq8GMfah+3s/HPgK8CHgmKpaNm7bgxhnAPsCxwN/BJ5eVZf1x06vql0bxHgr8EDgG3QnEqdU4w/YVSSwT2yVwCa5CvgO8I/0/U9yQVU1Te77WOsBTwH+ATgTeF1VnTeBGC+ge088oqqaXC0YtH9GVe3SP27y/2gVcZ620PGqOr5BjLOqaqf+8bHApVV1eL99ZlXtPG6MpcYRZLXwzST3rarvTSHWqcBdG7RzbN/Wk6pqBUCSSZwtbg0czapHwx/cIkiS2wAvAp4KfJAuqbm8RdtM6XeV5JvArYETgf2r6gdJLmyRHM+FGE2OAarq8i7fa+YPVfXDvu3T+5+hWXLcW6jDLafOrTeXHPdeDtAnTput4nvW1OeBr9OdvFwINySbLVVV/Sfw8CQvAVYkeU5VfZaFf5drEuCF/YnDA+kSv2OSnAS8Y+7nauASbprAPrZR2wCH0l21eQfwwSQfatg2AEk2BP4OeDFwCvDoqmo6tWJOVV0P/Ev/dzg1ydtZeXWyqmqLcUOM28fVCtIgAV4N6yfZoH+9PwQ4eHDsFpkr3iJ/aDW3F/D0JBfSTbGYe/OZxPSCVpnMnekuT745yR3pRkU3bNT20A+rqkkSPJ/+MushdFMf3g3sUlW/aRxmWr+rS+lGqe8I3B74AW0/gH6bZKeqOmu4M8lOwO8axrlDn4TN2Wy4XVVvbhDjkiR/UVXfGe5MN1f70gbtz9koyeZV9TuAqjqpj3NrumkWLexGl5R9MckFdCdI6zdq+yaq6s1JvgT8e7r55xs1bLuAr/Qj1gcAR9D9P35XoxATTWCr6i3AW5LcnW5U/xPAnZO8nO6K1P9rEOZCuqtD/wL8BNipfw3O9WF02tBYkjwTeAXwKuDYxqP6d0/yKbrPpbnHN6iqR7UK1I8ivxC4V7/rfOBtVfW+RiFOAL6a5DLgKrqTVpL8Gd0Ut1scp1hobP1l8Zuoqh9PINZPqqrFCPKwzW1YOdf1VnQfBIc2avuGS3DzHNu0qq4cs/0r6RKi9zBPktcoGRvGm9jvqm//1sB+fft/BtwGePhoIrjItvcCPkD3u5qb57478DTgyVV1yrgx+jiHLXS8ql7TIMZf0J2ovJfuZ4FubudT6aZzfHvcGH2cl9DNS3x2Vf2k37ctXYL2pao6ukWcQbz70/3t96O77P7xFnPD53sdplvMeDTdzzZ2Qp5kU+DRdCert6ebH/6hqvrpuG3PE2sugT0AuAdwGO0S2NFY9+1jPbGqtmvQ3ntZ9YlvVdXfjRtjEOubwEXAS/orCE0lecBCx6vqq43iPJVuxP0ldHP/A+wKvAl4a6skuV/UeCfgpLnPpiT3BDZrPR1wKTBBVhP9CMBf9ptfHx2lW8O2VrUgIcDTGlwWWyj2PYEDWyQxfXsPA86le9M5u6r+kOQOdNMhnl5Vdx6z/cNZePFGk59jFbGb/q7maf8OdMnGgcBdquouDdr8U7r5iH9O9//pXLpRpeYfnpOUZAu6EdznAXPz/88F/rWqLmkc69l0I5eb9ruuAI6sqne0jDMScz26xPzAqnpGi/b6y+3zHbtTVf2iQYwr6UaLTwB+yMjrsvXI6CBuswQ2ycOr6vOrOPaEqvrwOO1PW5J9quoLg+2tWXl14ucj04daxr0L3Ynqmxq1962+vYtG9i8DTqyqsat15KaVKgr4det59EuJCbLGluSFwEGsXFH/WOC4qjpmke1NY0HCFsAdq+oH/fbjgU36w5+vqv8aN0bf7ovoLu39EPgT4K3Am4H3AW9s8cE8aUket9DxVh/8SW5VVb9fxbG7V9UFLeJMWpK3LXS8Gqw4T1cO61VVdeK4ba1BzM3oPjNaTkchyfrAJlV1Rb+9ByunPZzRKl6SHegqmNyH7sP/POCoVmsnpjEymuRy4FvAN+kWA35nVa+ZRbZ/HfA1uisqPxs51mox40tGdhVdBZBTGs7Vnov1SmDDqvof/fZPgF/T/f86vhpWncg8VUWq6qWN2l5oUe4qj61hjAu5aUWkzYCzgP/ecC3IkmGCrLElORvYc3BJZlPg1AnNQW4iyXHAN6vqvf32D4HP0iXJ11bVsxvFuaFyQpK70iXKe1fVtxq1/+GqekL/+A1V9fLBsRtKEI0Z4z2DzUcCnx5sN7skmuSPwOuA14yO9rX4cE7yaGCb6st8Jfk23aVw6MpAfWSc9gdx/kBXCu3DwM8ZmTff6ARvW7o5nJsBz6l+UeAkJLkX3YKd7ftd59OdADe5nJ/kKOCSqnpjv30hK0vJnVZVr2gQ49HAUXSlCVfQ/U12A14JvLSqPjlujJuJf8cWJ939if0ewP36r92AC+gT5nFHePu5028HXk03LeEjw2Ormi62hjHmm4K0JV0Vk8NbnvQlOR34y8Fn01wVlvWBr9aYVVgy4aoigzinVdVua3qsUezHAQdX1SMmFWNtZYKssSX5Hl3VhKv77Y2B71bVfRfZ3qcWOt5i4UP/QbDr3OWj3LhczynjvnEO4twosUvjknhZoMxQqw+0VcVrLcl/0NUK3o6uYsaFg2Njx03yDbrLlD/tt8+kW629KfCeqnrIOO0P4tyObiTpiXSLkT4EfLSqftWi/ZFYj6ArXfZd4IaTihavkb79PemuDB3HyrmPu9BdMXpcixO9TKeU3Fl01RIuGtm/jK5k4U7zfNu4Mefm0z8JuHdVbT2BGJsCz6CbsnW3cedSz72H9NOnPkB3ovK8qvp9qxHkBWJvCXyxZYx53hOfPhgUGTuxzJTK4iX5Pd3gyk0O0dWp3nSeYy3jT/Rvv7ayioVaeA/w7SRzpaweA/yvMdrbE/gp3Vy+b0OzyhVDG4zMrXrK4PFtGsbZZuSS+x2G2w0uty90hjuJs99JnlFfWVVPTvJk4GtJXlUrF5+0iLtR3XjB1CnVlcK7vE80mujb/Dfg3/o5jwcC5yZ5eTWsw9qP7L6MbrX5sQwS5IZeTTcP+OTBvk8k+TLdwrB9G8SYRim5Dee7RFxVF6UrO9ZEkk2AR9ElxbsCm9O9H36tUft3ZuXo8dzdJU+jS9BObREDoKr+X39y9M/AGekWiU1Uf5Wt9Xv9Zkk2rKo/9jHeC5DkT4AWa1kmXhav16RG+2L0r8Fb5F2XTZA1turKJp1MV+4twDOqapw7Iv0p3R3BDqT7oPk/wAlVde64fR24PsmfVr84q6rOgRsWcbRMNEZv/3ravM9avFsl2YXuDWyTdDemgO7vsMmqv23tVVX/nuQU4P3pynA9q1HTtx2J8/eDzZvctnlc/d/iQLr/y5+l4d8+yZF0idgh1dXynZTtRpJjoFud309TamEapeT+mOSu1VfimNNPVWmyUCvJB4C9gZOAfwW+TFfm8eQW7fcuphvJfwvwiqr6Q8O2YVDyrj9peUWSz9ENVjR/jQwleTDQ+irL/wbemeTv5+Zq9yfD/9ofG0tNpyzevBWh+jnPl48M9CzaPHPDoXvPfBTd7+sWxwRZi5Zki6r6bX9p7KL+a+7YljXPTRlWR1VdR3cb3c/1Z/oHAicn+R+1yIV/83gT8Okkh7Dy9qa70s1TbLLyGKZS4P0XrLwRyX/S9X9Ok8oMST7NyhHcYa3PuXrXrWp93jB61I/sPQD4J7q/T4tk/9tJDqqqG9WkTfIsusukTSR5DfA3dHN1TwReWe1Xy98XeGhV/byP+VS6y/k/ppvHuajX3jwWWiA3VonCgXcBH0oyXym5VvWDD6Ors/w6blzi7xW0u132DnQJ3vnA96vqurS/oc796a6wPRZ4SZKL6EaOTwVWVNU1Y7Z/k/+nVXVykt1odKKa7k6To4MQW9LN1289Uv1PwGuBnySZSzLvSneF85/GbTx91Y/qFhC/FnhtVlYV+SzddLGxpVu4eiTwS7ra2u8HtgLWS/LUqvpcgzCbj2wX3WfIk2s6NwFb6zgHWYuW5DNV9Te58epXWJk4LXoeVp8Y/zXdG80y4FPAu6vBbaYHMR5Bd4ls7ra859CVr2o2Ijfp+dTp6uH+tPpqGOkqgOxHd7LSJFHK/LU+b1jtXO1qff5zVf3jPPv3oPtZxlokkq5s3CfobmYzV9NzN7rqIo9psYiqj3M93cKpq/pdo+W+xl682i8+emh/WXpvukT8+cDOdPNd9x83Rh/nkr7tmxwCnlBVd2wU51l01V42pft9XUnjUnLpSlEewo1L/B1VY5SknCfG9nRXvZ5Id9e77YH71oTKCPZzqB9JdwOJbapqrBH3acw1TfIruv+nc4puJLTVCdd8MTehq6sO3aj+VQs9fw3aXajqR7P1GklW0H1W3ZpuPcC+VfWt/v/bCZNaF3JLZ4KstU6S4+lGYz5LV+PxnBl3adGSXMoC86nHTS6nkSjlptUfvkN3ubVoWP1hJObtAaqq2V3hBguQHkJX6gvg3Kr6cqsYfZx70N0NcPQGEdvS1V4du+JEkjOrauf+8bHApVV1+OixBnGmUXJx7tLu3LSg9ehO8L5ejct+TVOS5XTJ8v7AxVV1v0btbs/Kecj3p7sMfipdFYujFvre1Wj7YroylPOqBjcemuaCryQvq5XVUR5fN67K8boa8yZHWbjqR7Ofc+T1fn5V3XtwrFV1kYkvjl9qnGKhsQ3mvQ79BvjxIi8tP4VuBOmewAsG6zbmRqbHXlyR5NULHK6qOmLcGL1Jz6defzBK/ES68lsfBT6arkpDCy+jW4gyZyO6u7ZtSrdAs1mCnO7GJ39P97deL8m1wDHV1zEdt3mAqvoS8KUG7a3KW4BDR+cN9kn/W+hG/Ma1QZIN+tfXQ+jKsN1wrEH7wFSmCMFNL+1CN7J/aJImZb9m8eFfVSuAFf00rr1btJnuNsC/oCvr9nW6UfaWJf7WpysdOImF0XNGb8V+Iy2S8IEDgDf2j1/Jjd+r5q4gjqOq6l1Jvgp8oF8z8bx+vnPL3+FwSsro6HerUc5pLI5fUkyQ1cLb6ebvnk33orovXXHx2/XzCk9ak8aqahorZue7nLcp8EzgdnTzvMY2hfnU608hUZpK9YckL6YbEdt9buSwX/zyjiQv7hfEjOP2U/pgXlZVZ8/T/or+kngLJwBf7ROmq+iSJZL8Gd3JaRPTSCxrFXdi7Nc2fJH5p3isqYl/+N/MSTdAi6lI21XVjf6+jRdr/aLRyehCppGEz8kqHs+3vWg1f9WPlpfnd0ryW/qrLP1j+u1WC1mnsTh+STFBVgsXAc+ceyEluQ9d9YYj6GqorlGCPA1VdfTc43TF3l9IV0/0RLpFb83MM5/6bay86+C4ppEoTav6w1OBfarqskGsC9KVfTuJbvR1HNP6YF7oA6tJZZGqem2SL9HdwvykQXK0Ht0Um1ZmNqpUbct+TePD/+ZOulsknvdO8nq6xYCTWKw1jb/vNJLwObWKx/NtL8ZwYfHEqn7UmPWtVzPGNBbHLykmyGph++EHTVWdl2SXPrmZZb8W1I9QvQT4W7qbLexajW/mMDKf+jWt51NPKVGaSvUHulq1l43urKpL06ZW7bQ+mL+7it/XM2lY6q3muUlHNSorNTCzUaU0LPs1jQ//KZ10/ysrF2t9mZHFWnQ/4zia3CznZkzzQ2HSI683ufpRjat+TNOEB3OWHBfpaWzpiqP/kpWXQp9IN6rxFLrL8buv6ntnJcmbgMfRrQg+tqqumFCc61k5sjRfpY8WxeonaorVH1a5qKXFgpeWq8pvJs4d6W45+wdWJsTL6eZuP3ZSFQ0mbZBYvglollimuxPn6AfRDWW/qur7jeJMozLO6En3W1uedE9jsdakZYwSoJqcdWlxfCsmyBpbX0Lnuay8UcgpdPOSrwZuNankcxx94noNXd3PJZm4Tls/ojdXEm8S1R+uY/7L1AE2rqqxRpGn/cGc5EF0Hzgwgd/XtEw6sUxX83ioedmvaXz4T+Oke3iiOHrSOM3qEFr3rAuDOa2ZIKuJPkm+a1X9x6z7IqmNdWVUaRof/tM46R6cRM6VxPv9IMbYJ5GSVjJB1tiSPIrusutGVXW3JDvTXYK9xdVNlNYljipJuqVykZ5aOAz4C+BkgKo6s2E5K0kzMqWSi5K01vHNTy1cO1qbU5IkaalyBFktnJPkSXQ3rbgH8AK6Oz1JkiQtOY4gq4Xn01U3uIauFudv6GqASpIkLTku0lNzfdH6Q6rqoFn3RZIkaU05gqxFS7JjkpOSnJPkiCR3TPJR4IvAebPunyRJ0mKYIGsc7wI+COwHXEZ3l7ULgD+rqrfMsmOSJEmL5RQLLdrwtqf99k+BZVV13Qy7JUmSNBarWGgcGyfZhe6mAQBXADsmCUBVnT6znkmSJC2SI8hatCRfWeBwVdWDp9YZSZKkRkyQNXFJ9qmqL8y6H5IkSavDBFkTl+T0qtp11v2QJElaHVax0DTk5p8iSZK0djBB1jR4mUKSJC0ZJsiSJEnSgAmypuGiWXdAkiRpdblIT2NLcivgEOCuVXVQknsA96qqz8y4a5IkSWvMEWS18B7gGmDPfvti4J9n1x1JkqTFM0FWC9tV1RuBPwJU1VVYuUKSJC1RJshq4Q9JNqGvVpFkO7oRZUmSpCVng1l3QOuEw4HPAXdJ8gHg/sAzZtojSZKkRXKRnppIcjtgD7qpFd+qqstm3CVJkqRFMUHW2JJ8qaoecnP7JEmSlgKnWGjRkmwM3ArYKsltWbkwbwvgzjPrmCRJ0hhMkDWOZwEvokuGT2Nlgvxb4NhZdUqSJGkcTrHQ2JI8v6qOmXU/JEmSWjBBVhNJdgDuA2w8t6+q3je7HkmSJC2OCbLGluQw4IF0CfL/BfYFTqmq/WfZL0mSpMXwRiFqYX/gIcB/VtUzgJ2AP5ltlyRJkhbHBFktXFVV1wPXJtkCuAS4+4z7JEmStChWsVALK5LcBngXXTWLK4DvzLZLkiRJi+McZDWVZBmwRVWdPeOuSJIkLYoJshYtyfZV9f0ku853vKpOn3afJEmSxmWCrEVL8q6qOijJV+Y5XFX14Kl3SpIkaUwmyJIkSdKAi/S0aEket9DxqvrYtPoiSZLUigmyxvHI/t87APcDvtxvPwg4GTBBliRJS44JshatvykIST4D3KeqftFv3wk4dpZ9kyRJWixvFKIWls0lx73/Au45q85IkiSNwxFktXByks8DJwAFHADMV9lCkiRprWcVCzWR5LHA3v3m16rq47PsjyRJ0mKZIKuJJNsC96iqLya5FbB+Vf1u1v2SJElaU85B1tiSHAT8b+Cd/a6tgU/MrkeSJEmLZ4KsFp4H3B/4LUBV/YCu9JskSdKSY4KsFq6pqj/MbSTZgG6xniRJ0pJjgqwWvprkUGCTJPsAHwE+PeM+SZIkLYqL9DS2JOsBzwQeBgT4PPA/y/9ckiRpCTJBliRJkgacYqGxJfmbJGck+WWS3yb5XZLfzrpfkiRJi+EIssaW5IfA44DvOa1CkiQtdY4gq4WfAueYHEuSpHWBI8gaW5LdgSOArwLXzO2vqjfPrFOSJEmLtMGsO6B1wmuBK4CNgY1m3BdJkqSxmCCrhS2r6mGz7oQkSVILzkFWC19MYoIsSZLWCc5B1tiS/A7YlG7+8R/pbhZSVbXFTDsmSZK0CCbIGkt/F709q+obs+6LJElSC06x0Fiq6nrgqFn3Q5IkqRUTZLVwUpL9kmTWHZEkSRqXUyw0tsEc5OuAq3AOsiRJWsJMkCVJkqQBp1hobOk8Ock/9dt3SfIXs+6XJEnSYjiCrLEleQdwPfDgqrp3ktsCJ1XV7jPumiRJ0hrzTnpq4b9V1a5JzgCoql8l8ZbTkiRpSXKKhVr4Y5L1gQJIcnu6EWVJkqQlxwRZLbwN+DhwhySvBU4BXj/bLkmSJC2Oc5DVRJLtgYfQlXj7UlWdP+MuSZIkLYoJssaW5P1V9ZSb2ydJkrQUOMVCLfz5cKOfj7zbjPoiSZI0FhNkLVqSV/Z30dsxyW+T/K7fvgT45Iy7J0mStChOsdDYkry+ql45635IkiS1YIKsJpJsDWzLoLZ2VX1tdj2SJElaHG8UorElORI4ADgPuK7fXYAJsiRJWnIcQdbYkvwHsGNVXTPrvkiSJI3LRXpq4QJgw1l3QpIkqQWnWKiF3wNnJvkScMMoclW9YHZdkiRJWhwTZLXwqf5LkiRpyXMOsiRJkjTgCLIWLcn36KpVzKuqdpxidyRJkppwBFmLlmTbhY5X1Y+n1RdJkqRWTJA1cUlOrao9Z90PSZKk1WGZN03DxrPugCRJ0uoyQdY0eJlCkiQtGSbIkiRJ0oAJsqYhs+6AJEnS6jJB1jQ8ZdYdkCRJWl1WsdCiJbmQG88vzmC7qmq76fdKkiRpPN4oRONYPrK9HvAE4KXAGdPvjiRJ0vhMkLVoVXU5QJL16KZR/ANwJvDXVXXeLPsmSZK0WCbIWrQkGwJ/B7wYOAV4dFX9aLa9kiRJGo9zkLVoSS4GrgX+BfjJ6PGq+tjUOyVJkjQmE2QtWpL39A9HF+pBt0jv76bcJUmSpLE5xULjOIcuOb4hKQYuBU6pqgtn1itJkqQxWAdZ49gM2Lz/d+7xcuCzSQ6YZcckSZIWyykWai7JlsAXq2rXWfdFkiRpTTmCrOaq6pd4e2lJkrREmSCruSQPBn41635IkiQthov0tGhJvseNK1gAbAn8HHjq9HskSZI0Pucga9GSbDuyq4DLq+rKWfRHkiSpBRNkSZIkacA5yJIkSdKACbIkSZI0YIIsSZIkDZggS5IkSQMmyJIkSdLA/wfnlDOQq3/prwAAAABJRU5ErkJggg==\n",
"text/plain": [
"
"
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"# Plot heatmap and corresponding dendograms\n",
"g = sns.clustermap(data_scaled,\n",
" method='ward',\n",
" cmap='bone_r',\n",
" row_colors=region_color,\n",
" );\n",
"g.fig.suptitle('Hierarchical clustering with Ward linkage', y=1);"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"## Network analysis"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"source": [
"The matrix of bilateral mis-invoiced imports between African reporter countries and partner countries can be conceptualized as a *weighted directed graph*. Recall that the data-set `IFF_Dest` contains the mis-invoiced imports and exports for a reporter-partner-year tuple. The underlying data has been aggregated across commodity sectors using the Gross Excluding Reversals (GER) method, which ignores all inflows of capital (i.e. negative values), and simply sums up the positive outflows across trading partners."
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"source": [
"The table below shows the `IFF_Dest` data-set that we are working with:"
]
},
{
"cell_type": "code",
"execution_count": 89,
"metadata": {
"slideshow": {
"slide_type": "skip"
},
"tags": [
"remove-input"
]
},
"outputs": [
{
"data": {
"text/html": [
"
\n",
"\n",
"
\n",
" \n",
"
\n",
"
\n",
"
reporter
\n",
"
reporter.ISO
\n",
"
rIncome
\n",
"
rDev
\n",
"
year
\n",
"
partner
\n",
"
partner.ISO
\n",
"
pRegion
\n",
"
pIncome
\n",
"
pDev
\n",
"
Imp_IFF_lo
\n",
"
Imp_IFF_hi
\n",
"
Exp_IFF_lo
\n",
"
Exp_IFF_hi
\n",
"
\n",
" \n",
" \n",
"
\n",
"
0
\n",
"
Algeria
\n",
"
DZA
\n",
"
UMC
\n",
"
Developing
\n",
"
2001
\n",
"
Andorra
\n",
"
AND
\n",
"
Europe
\n",
"
HIC
\n",
"
Developed
\n",
"
7.925637e+03
\n",
"
1.609561e+04
\n",
"
NaN
\n",
"
NaN
\n",
"
\n",
"
\n",
"
1
\n",
"
Algeria
\n",
"
DZA
\n",
"
UMC
\n",
"
Developing
\n",
"
2001
\n",
"
Argentina
\n",
"
ARG
\n",
"
Americas
\n",
"
HIC
\n",
"
Developing
\n",
"
1.914238e+07
\n",
"
4.717459e+07
\n",
"
NaN
\n",
"
NaN
\n",
"
\n",
"
\n",
"
2
\n",
"
Algeria
\n",
"
DZA
\n",
"
UMC
\n",
"
Developing
\n",
"
2001
\n",
"
Australia
\n",
"
AUS
\n",
"
Oceania
\n",
"
HIC
\n",
"
Developed
\n",
"
1.589172e+06
\n",
"
2.027641e+07
\n",
"
NaN
\n",
"
1412.374399
\n",
"
\n",
"
\n",
"
3
\n",
"
Algeria
\n",
"
DZA
\n",
"
UMC
\n",
"
Developing
\n",
"
2001
\n",
"
Austria
\n",
"
AUT
\n",
"
Europe
\n",
"
HIC
\n",
"
Developed
\n",
"
1.511117e+07
\n",
"
7.641706e+07
\n",
"
NaN
\n",
"
NaN
\n",
"
\n",
"
\n",
"
4
\n",
"
Algeria
\n",
"
DZA
\n",
"
UMC
\n",
"
Developing
\n",
"
2001
\n",
"
Belgium
\n",
"
BEL
\n",
"
Europe
\n",
"
HIC
\n",
"
Developed
\n",
"
9.357981e+06
\n",
"
2.285729e+07
\n",
"
NaN
\n",
"
NaN
\n",
"
\n",
" \n",
"
\n",
"
"
],
"text/plain": [
" reporter reporter.ISO rIncome rDev year partner partner.ISO \\\n",
"0 Algeria DZA UMC Developing 2001 Andorra AND \n",
"1 Algeria DZA UMC Developing 2001 Argentina ARG \n",
"2 Algeria DZA UMC Developing 2001 Australia AUS \n",
"3 Algeria DZA UMC Developing 2001 Austria AUT \n",
"4 Algeria DZA UMC Developing 2001 Belgium BEL \n",
"\n",
" pRegion pIncome pDev Imp_IFF_lo Imp_IFF_hi Exp_IFF_lo \\\n",
"0 Europe HIC Developed 7.925637e+03 1.609561e+04 NaN \n",
"1 Americas HIC Developing 1.914238e+07 4.717459e+07 NaN \n",
"2 Oceania HIC Developed 1.589172e+06 2.027641e+07 NaN \n",
"3 Europe HIC Developed 1.511117e+07 7.641706e+07 NaN \n",
"4 Europe HIC Developed 9.357981e+06 2.285729e+07 NaN \n",
"\n",
" Exp_IFF_hi \n",
"0 NaN \n",
"1 NaN \n",
"2 1412.374399 \n",
"3 NaN \n",
"4 NaN "
]
},
"execution_count": 89,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"IFF_Dest.head()"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"source": [
"Thus, the values in the import column of `IFF_Dest` correspond to import over-invoicing which result in an illicit outflow from reporter $i$ to partner $j$. Therefore, we can consider each entry in `IFF_Dest` to represent an edge going out from the reporter into the partner country."
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"source": [
"### Data wrangling"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"source": [
"Let's download some indicators from the World Bank that we can use as node attributes."
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "skip"
},
"tags": [
"hide-cell"
]
},
"source": [
"The covariates `control-corruption` and `rule-of-law` refer to the percentile rank that each country achieves on these governance dimensions. The control of corruption measure captures perceptions of the extent to which public power is exercised for private gain, including both petty and grand forms of corruption, as well as \"capture\" of the state by elites and private interests. The rule of law variable captures perceptions of the extent to which agents have confidence in and abide by the rules of society, and in particular the quality of contract enforcement, property rights, the police, and the courts, as well as the likelihood of crime and violence. The underlying source for these data is the World Bank's [Worldwide Governance Indicators (WGI) database](https://info.worldbank.org/governance/wgi/).\n",
"\n",
"*Nota bene*: these will be used in further work and are not exploited in this project."
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"source": [
"The variable `gdp-pc` measures each country's GDP per capita in current US $ and is sourced from the World Bank's [World Development Indicators (WDI) database](http://datatopics.worldbank.org/world-development-indicators/)."
]
},
{
"cell_type": "code",
"execution_count": 90,
"metadata": {
"slideshow": {
"slide_type": "skip"
},
"tags": [
"hide-input"
]
},
"outputs": [
{
"data": {
"text/html": [
"
\n",
"\n",
"
\n",
" \n",
"
\n",
"
\n",
"
country
\n",
"
control-corruption
\n",
"
rule-of-law
\n",
"
gdp-pc
\n",
"
\n",
"
\n",
"
ISO3166.3
\n",
"
\n",
"
\n",
"
\n",
"
\n",
"
\n",
" \n",
" \n",
"
\n",
"
AFG
\n",
"
Afghanistan
\n",
"
3.365385
\n",
"
5.769231
\n",
"
547.228110
\n",
"
\n",
"
\n",
"
ALB
\n",
"
Albania
\n",
"
40.865380
\n",
"
41.826920
\n",
"
4124.055726
\n",
"
\n",
"
\n",
"
DZA
\n",
"
Algeria
\n",
"
27.884610
\n",
"
18.750000
\n",
"
3946.443977
\n",
"
\n",
"
\n",
"
ASM
\n",
"
American Samoa
\n",
"
87.500000
\n",
"
87.980770
\n",
"
11696.955562
\n",
"
\n",
"
\n",
"
AND
\n",
"
Andorra
\n",
"
87.500000
\n",
"
90.865390
\n",
"
37474.665406
\n",
"
\n",
"
\n",
"
...
\n",
"
...
\n",
"
...
\n",
"
...
\n",
"
...
\n",
"
\n",
"
\n",
"
VIR
\n",
"
Virgin Islands (U.S.)
\n",
"
72.115390
\n",
"
73.076920
\n",
"
35931.541252
\n",
"
\n",
"
\n",
"
PSE
\n",
"
West Bank and Gaza
\n",
"
51.923080
\n",
"
40.865380
\n",
"
3074.291152
\n",
"
\n",
"
\n",
"
YEM
\n",
"
Yemen, Rep.
\n",
"
1.442308
\n",
"
3.365385
\n",
"
1033.733043
\n",
"
\n",
"
\n",
"
ZMB
\n",
"
Zambia
\n",
"
41.346150
\n",
"
43.269230
\n",
"
1280.578898
\n",
"
\n",
"
\n",
"
ZWE
\n",
"
Zimbabwe
\n",
"
9.615385
\n",
"
8.173077
\n",
"
1464.583529
\n",
"
\n",
" \n",
"
\n",
"
223 rows × 4 columns
\n",
"
"
],
"text/plain": [
" country control-corruption rule-of-law \\\n",
"ISO3166.3 \n",
"AFG Afghanistan 3.365385 5.769231 \n",
"ALB Albania 40.865380 41.826920 \n",
"DZA Algeria 27.884610 18.750000 \n",
"ASM American Samoa 87.500000 87.980770 \n",
"AND Andorra 87.500000 90.865390 \n",
"... ... ... ... \n",
"VIR Virgin Islands (U.S.) 72.115390 73.076920 \n",
"PSE West Bank and Gaza 51.923080 40.865380 \n",
"YEM Yemen, Rep. 1.442308 3.365385 \n",
"ZMB Zambia 41.346150 43.269230 \n",
"ZWE Zimbabwe 9.615385 8.173077 \n",
"\n",
" gdp-pc \n",
"ISO3166.3 \n",
"AFG 547.228110 \n",
"ALB 4124.055726 \n",
"DZA 3946.443977 \n",
"ASM 11696.955562 \n",
"AND 37474.665406 \n",
"... ... \n",
"VIR 35931.541252 \n",
"PSE 3074.291152 \n",
"YEM 1033.733043 \n",
"ZMB 1280.578898 \n",
"ZWE 1464.583529 \n",
"\n",
"[223 rows x 4 columns]"
]
},
"execution_count": 90,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# Specify indicators of interest to import from World Bank\n",
"indicators = {'CC.PER.RNK': 'control-corruption', \n",
" 'RL.PER.RNK': 'rule-of-law',\n",
" 'NY.GDP.PCAP.CD': 'gdp-pc'}\n",
"\n",
"# Import covariates\n",
"covariates = wb.get_dataframe(indicators, \n",
" data_date=(datetime.datetime(2016, 1, 1)))\n",
"\n",
"# Merge in ISO codes from the crosswalk\n",
"covariates = pd.merge(left=covariates.reset_index().rename(columns={'index': 'country'}), \n",
" right=crosswalk[['country', 'ISO3166.3']], \n",
" how='left', on='country').rename(columns={'date': 'year'})\n",
"covariates = covariates.dropna(subset=['ISO3166.3']).set_index('ISO3166.3')\n",
"covariates"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"source": [
"Now, let's create an auxiliary function that transforms `IFF_Dest` into an appropriate format for network analysis, and applies some thresholding.\n",
"\n",
"The function `create_graph_data()` accomplishes the following:\n",
"- Extract data from a specific year, in order to perform network analysis at a specific snapshot in time.\n",
"- Ignore illicit flows that are less than a certain value specifid by `flow_threshold`. The default is to ignore flows that are less than $10,000. This is necessary because the mis-invoicing estimation procedure, by construction, will locate IFF as discrepancies between a country's reported imports and the mirror exports declared by its partner country (after adjustment). But any discrepancy, no matter how small, would result in the creation of an edge between a given dyad. If no thresholding on the value of the mis-invoiced flow were applied, then the directed graph would simply recover the topology of international trade networks.\n",
"- Further restrict the graph, if `threshold` is `True`, to reporting countries which are considered \"conduits\" because they have the highest value of IFF in relation to either their GDP or total trade value."
]
},
{
"cell_type": "code",
"execution_count": 91,
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"outputs": [],
"source": [
"def create_graph_data(year='2016', threshold=True, threshold_var='GDP', flow_threshold=10000):\n",
" \"\"\"\n",
" Returns data-set to be used to generate a directed graph.\n",
" \n",
" year: as string, specify which year to use for the network analysis (between 2000-2016)\n",
" threshold: as boolean, indicate whether to restrict reporting countries to conduits\n",
" threshold_var: as string, indicate which variable to use when determining which \n",
" reporting countries are conduits ('GDP' or 'trade')\n",
" flow_threshold: as numeric, specify the cut-off under which to ignore the dollar values\n",
" of mis-invoiced imports\n",
" \"\"\"\n",
" flow_data = IFF_Dest.reset_index().query('year == @year')\n",
" flow_data = flow_data.loc[flow_data['Imp_IFF_hi'].notnull(), :]\n",
" flow_data = flow_data.query('Imp_IFF_hi >= @flow_threshold')\n",
" \n",
" if threshold:\n",
" conduits = 'conduits_' + threshold_var\n",
" flow_data = flow_data[flow_data['reporter.ISO'].isin(eval(conduits).index)]\n",
" return flow_data"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"### Thresholding"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"source": [
"The figure below displays the distribution of over-invoiced imports by African countries in 2016, as a proportion of their GDP and of their total trade value, respectively. The distribution of outflows relative to trade value has a higher variance than that of outflows relative to GDP, with some countries' experiencing up to 30% of mis-invoicing in their total trade with the rest of the world."
]
},
{
"cell_type": "code",
"execution_count": 92,
"metadata": {
"slideshow": {
"slide_type": "slide"
},
"tags": [
"hide-input"
]
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAlkAAAGDCAYAAAAYtQWTAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4yLjEsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy+j8jraAAAgAElEQVR4nOzdeXycZbn/8c+Vyb6nTbol3VvovtMFCmUtBZGigmxKQQVcOHqOokflHEXE4++g5xxxRVwQZJFFBKqsIlCgC7SlLdC96Zau2dNmz8z9+2OmNYSkmTQzeSaZ7/v1yqvJPNs1SZp8c9/X3I855xARERGRyErwugARERGRvkghS0RERCQKFLJEREREokAhS0RERCQKFLJEREREokAhS0RERCQKFLJEepiZ3WNm/xmhcw0zs6Nm5gt9/KqZfS4S5w6d7zkzWxKp83XhuneaWZmZHeyh611rZi9G6dxpZrbUzKrN7PGeun7b7w0R6XkKWSIRZGa7zKzezI6YWZWZLTezz5vZ8f9rzrnPO+e+H+a5zj/RPs65Pc65TOecPwK1325mD7Y5/0XOufu7e+4u1jEU+BowwTk3qJ3tZ5tZSauPXzWzhlCgOPY2L7TNmVltq8er2rumc+4h59zCbtZ9feh6n2yz6XJgINDfOXdFtK7fzjlP+nvDzOaa2UtmVmFmpWb2uJkNbrXdzOy/zaw89HaXmVmr7d83s3fNrMXMbm/n/AVm9nDo/0ilmT100k9UJIYpZIlE3kedc1nAcOD/Af8O/C7SFzGzxEifM0YMB8qdc4e7cMwtoUBx7G1Fq21TWz2eG+FaW1sCVIT+bW04sNU519LeQTH6dcwD7gVGEKz/CHBfq+03AZcBU4EpwCXAza22bwe+Afytg/M/CRwMnXsA8OPIlS4SOxSyRKLEOVftnHsGuBJYYmaTAMzsD2Z2Z+j9fDP7a+gv+goze93MEszsj8AwYGloBOYbZjYiNFLyWTPbA/yj1WOtf1GPNrO3QtNTT5tZv9C1PjACFHpsl5mdb2aLgG8DV4autz60/fj0Y6iu/zCz3WZ22MweMLOc0LZjdSwxsz2hqb7bOvrcmFlO6PjS0Pn+I3T+84GXgCGhOv4QgS9Fp0KjUG+0+tiFRiC3hUZaftF6pKad44cDCwiGjwvNbGDo8e8B3+Gfn9fPhq71ppn9n5lVALe3c/2JrUaSDpnZt0OPzzazFaHvlwNm9nMzS+6gpg98b4S+lt8PXfuImb1oZvntHeuce84597hzrsY5Vwf8HDij1S5LgP9xzpU45/YB/wNc3+r4+51zzxEMZ23rWggMBb4e+j/S7Jx7p6PPrUhvppAlEmXOubeAEuDMdjZ/LbStgOCU0reDh7hPA3sIjoplOufuanXMAmA8cGEHl7wO+AwwBGgBfhpGjc8D/wU8Grre1HZ2uz70dg4wCsgk+Mu3tfnAqcB5wHfMbHwHl/wZkBM6z4JQzTc45/4OXATsD9VxfWe1R9ElwGkER2s+ScefbwjWv9o592dgE3AtgHPuu3zw83psRHMOUExwFOcHrU9kZlnA34HnCX4NxwAvhzb7gX8D8oF5BD/PX+zCc7oGuCF03WTg1jCPOwt4v9XHE4H1rT5eH3osHHOBLcD9oanGt81sQZjHivQqClkiPWM/0K+dx5uBwcDw0F/0r7vObyh6u3Ou1jlX38H2Pzrn3nPO1QL/CXzSItP8fC3wv865YufcUeBbwFVtRtG+55yrd86tJ/iL90NhLVTLlcC3nHNHnHO7CI6EfLobtf00NLpTZWZr22xb22pbp4Gzlf/nnKtyzu0BXgGmnWDf64CHQ+8/zIenDNva75z7mXOupZ2v4yXAQefc/zjnGkKfo1UAzrk1zrmVoeN2Ab8mGFLDdZ9zbmvomo918pwAMLMpBEfjvt7q4UygutXH1UDmiUb7WikCFhL8nA4i+LV/uqNRNZHeTCFLpGcUEuzXaetHBPtXXjSzYjP7Zhjn2tuF7buBJIIjH901JHS+1udOJDgCd0zrVwPWEfxl3FY+wVGUtucq7EZtX3bO5YbeZrTZNqPVti934ZzhPBfM7AxgJPCn0EMPA5PN7EQB5kRfw6HAjg6udUpoevmgmdUQHCXrytc2rOfU6npjgOeArzjnXm+16SiQ3erjbOBoGH8gANQDu5xzvwv9YfEngp+PMzo5TqTXUcgSiTIzO41ggHij7bbQKMXXnHOjgI8CXzWz845t7uCUnf0iG9rq/WEER8vKgFogvVVdPoLTlOGedz/BRuXW524BDnVyXFtloZranmtfF88TK5YABqyz4JITq0KPX3eCY070ud4LjO5g26+AzcBY51w2wenlcEaPuizUZ/Z34PvOuT+22fw+HxylnMoHpxNPZAOdf6+J9AkKWSJRYmbZZnYJwRGOB51z77azzyVmNiY0zVJDsOfm2EvuDxHsWeqqT5nZBDNLB+4Angi9jH8rkGpmHzGzJOA/gJRWxx0CRlir5SbaeAT4NzMbaWaZ/LPXqN1XzXUkVMtjwA/MLCv0y/yrwIMnPjL2mFkqwX6tmwhOvR17+xfgWju5Vw7+FRhkZv9qZimhz9Gc0LYsgt8nR81sHPCFbj+JdphZIfAP4BfOuXva2eUBgn8QFJrZEIK9hX9odXxS6HOTACSaWWqrKeu/AHmhF0n4zOxygn+EvBmN5yLiJYUskchbamZHCI5I3Ab8L8Fm4/aMJThacBRYAfzSOfdqaNsPgf8I9RKF26AM8EeCv/AOAqnAlyH4akeCTdK/JThqVEuw6f6YYwtllrfT1wTw+9C5lwE7gQaCYeJk/Evo+sUER/geDp2/t7mM4PTXA865g8feCC7Z4QMWdfWEzrkjwAUERzYPAtsIvtgAgo3q1xB81d5vgEe7/Qza9zmCAf+71mr9sVbbfw0sBd4F3iO4VMOvW23/DcHPy9UE/w/UE+q5c85VAJeGnks18E1gsXOuLErPRcQzFt4UuoiIiIh0hUayRERERKJAIUtEREQkChSyRERERKJAIUtEREQkChSyRERERKIgFu/+Tn5+vhsxYoTXZYiIiIh0as2aNWXOuYK2j8dkyBoxYgSrV6/2ugwRERGRTpnZ7vYe13ShiIiISBQoZImIiIhEgUKWiIiISBTEZE+WiIiI9Izm5mZKSkpoaGjwupSYl5qaSlFREUlJSWHtr5AlIiISx0pKSsjKymLEiBGYmdflxCznHOXl5ZSUlDBy5MiwjtF0oYiISBxraGigf//+ClidMDP69+/fpRE/hSwREZE4p4AVnq5+nhSyRERExDOlpaXMnz+fSZMm8dRTTx1/fPHixezfv7/D4x588EGmTJnCxIkTmTp1Kp/73OeoqqoC4Oyzz+bUU09lypQpjBs3jltuueX4NgCfz8e0adOYNGkSV1xxBXV1dVF5burJEhERkeMeXrUnoue7Zs6wE25/5JFHWLJkCVdddRWLFi3isssuY+nSpcyYMYMhQ4a0e8zzzz/P//3f//Hcc89RWFiI3+/n/vvv59ChQ+Tm5gLw0EMPMWvWLJqamvjWt77F4sWLee211wBIS0tj3bp1AFx77bXcc889fPWrX43gsw5SyBIRERHPJCUlUV9fT2NjIwkJCbS0tPCTn/yEpUuXdnjMD37wA3784x9TWFgIBEemPvOZz7S7b3JyMnfddRdjxoxh/fr1TJ069QPbzzzzTDZs2BC5J9RKWNOFZrbIzLaY2XYz+2Y728eZ2QozazSzW7tyrIiIiMSva665hhdeeIFFixZx++2388tf/pLrrruO9PT0Do95//33mTFjRtjX8Pl8TJ06lc2bN3/g8ZaWFp577jkmT5580vWfSKchy8x8wC+Ai4AJwNVmNqHNbhXAl4Efn8SxIiIiEqdycnL429/+xurVq5kxYwZ//etf+cQnPsGNN97I5ZdfzooVK054/Lvvvsu0adMYPXo0jz76aIf7OeeOv19fX8+0adOYNWsWw4YN47Of/WzEnk9r4UwXzga2O+eKAczsT8BiYOOxHZxzh4HDZvaRrh4rIiIiAnDHHXdw22238cgjjzBz5kyuueYaFi9ezCuvvPKB/SZOnMjatWs555xzmDx5MuvWreOWW26hvr6+3fP6/X7effddxo8fD3ywJyuawglZhcDeVh+XAHPCPH93jhXpUyLdTBoJnTWkioj0lG3btrF//34WLFjAunXrSEtLw8zaXZfqW9/6FrfeeitPP/00RUVFAB0GrObmZm677TaGDh3KlClTovoc2gonZLW3KIRr57FuHWtmNwE3AQwbph/8IiIi8eS2227jBz/4AQBXX301l112GXfffTd33HHHh/a9+OKLKS0t5aKLLsLv95Obm8ukSZO48MILj+9z7bXXkpKSQmNjI+effz5PP/10jz2XY8IJWSXA0FYfFwEdL1xxksc65+4F7gWYNWtWuCFOREREIsirEe7HHnvs+PsDBgxg+fLlJ9x/yZIlLFmypN1tr7766gmPPXr0aJfrOxnhvLrwbWCsmY00s2TgKuCZMM/fnWNFREREeq1OR7Kccy1mdgvwAuADfu+ce9/MPh/afo+ZDQJWA9lAwMz+FZjgnKtp79hoPRkRERGRWBHWYqTOuWeBZ9s8dk+r9w8SnAoM61gRERGRvk73LhQRERGJAoUsERERkShQyBIRERGJAoUsERER8UxpaSnz589n0qRJPPXUU8cfX7x4Mfv3t79i1FNPPcXGjd2/ecyIESMoKyvr9nk6Elbju4iIiMSJ1fdF9nyzbjjh5kceeYQlS5Zw1VVXsWjRIi677DKWLl3KjBkzGDJkSLvHPPXUU1xyySVMmPDh2yG3tLSQmBgb8UYjWSIiIuKZpKQk6uvraWxsJCEhgZaWFn7yk5/w9a9/vd39ly9fzjPPPMPXv/51pk2bxo4dOzj77LP59re/zYIFC7j77rtZunQpc+bMYfr06Zx//vkcOnQIgPLychYuXMj06dO5+eabP3DT6AcffJDZs2czbdo0br75Zvx+f7efm0KWiIiIeOaaa67hhRdeYNGiRdx+++388pe/5LrrriM9Pb3d/U8//XQuvfRSfvSjH7Fu3TpGjx4NQFVVFa+99hpf+9rXmD9/PitXruSdd97hqquu4q677gLge9/7HvPnz+edd97h0ksvZc+e4D1lN23axKOPPsqbb77JunXr8Pl8PPTQQ91+brExniYiIiJxKScnh7/97W8AVFZW8t///d88+eST3HjjjVRWVvK1r32NefPmdXqeK6+88vj7JSUlXHnllRw4cICmpiZGjhwJwLJly3jyyScB+MhHPkJeXh4AL7/8MmvWrOG0004DgjebHjBgQLefm0KWiIiIxIQ77riD2267jUceeYSZM2dyzTXXsHjxYl555ZVOj83IyDj+/r/8y7/w1a9+lUsvvZRXX32V22+//fg2M/vQsc45lixZwg9/+MOIPI9jNF0oIiIintu2bRv79+9nwYIF1NXVkZCQgJnR0NDwoX2zsrI4cuRIh+eqrq6msLAQgPvvv//442edddbxacDnnnuOyspKAM477zyeeOIJDh8+DEBFRQW7d+/u9nNSyBIRERHP3Xbbbdx5550AXH311fzhD39g7ty53HrrrR/a96qrruJHP/oR06dPZ8eOHR/afvvtt3PFFVdw5plnkp+ff/zx7373uyxbtowZM2bw4osvMmzYMAAmTJjAnXfeycKFC5kyZQoXXHABBw4c6PZzstad9bFi1qxZbvXq1V6XIRJRD6/a43UJH3LNnGFelyAiHtu0aRPjx4/3uoxeo73Pl5mtcc7NaruvRrJEREREokAhS0RERCQKFLJEREREokAhS0REJM7FYn92LOrq50khS0REJI6lpqZSXl6uoNUJ5xzl5eWkpqaGfYwWIxUREYljRUVFlJSUUFpa6nUpMS81NZWioqKw91fIEhERiWNJSUnHbzsjkaXpQhEREZEoUMgSERERiQKFLBEREZEoUMgSERERiQKFLBEREZEoUMgSERERiQKFLBEREZEoUMgSERERiQKFLBEREZEoUMgSERERiQKFLBEREZEoUMgSERERiQKFLBEREZEoUMgSERERiQKFLBEREZEoUMgSERERiQKFLBEREZEoUMgSERERiQKFLBEREZEoUMgSERERiQKFLBEREZEoUMgSERERiQKFLBEREZEoUMgSERERiQKFLBEREZEoUMgSERERiQKFLBEREZEoUMgSERERiQKFLBEREZEoUMgSERERiQKFLBEREZEoUMgSERERiQKFLBEREZEoUMgSERERiYKwQpaZLTKzLWa23cy+2c52M7OfhrZvMLMZrbb9m5m9b2bvmdkjZpYayScgIiIiEos6DVlm5gN+AVwETACuNrMJbXa7CBgbersJ+FXo2ELgy8As59wkwAdcFbHqRURERGJUOCNZs4Htzrli51wT8CdgcZt9FgMPuKCVQK6ZDQ5tSwTSzCwRSAf2R6h2ERERkZiVGMY+hcDeVh+XAHPC2KfQObfazH4M7AHqgRedcy92o16RTj28ao/XJYiIiIQ1kmXtPObC2cfM8giOco0EhgAZZvapdi9idpOZrTaz1aWlpWGUJSIiIhK7wglZJcDQVh8X8eEpv472OR/Y6Zwrdc41A08Cp7d3Eefcvc65Wc65WQUFBeHWLxJ3Glv8NLUECLi2f+uIiEgsCWe68G1grJmNBPYRbFy/ps0+zwC3mNmfCE4lVjvnDpjZHmCumaUTnC48D1gdsepF4kBdUwvr91ax7fBR9lfVU9PQcnxbfmYK4wZlMXFINsP7Z3hYpYiItNVpyHLOtZjZLcALBF8d+Hvn3Ptm9vnQ9nuAZ4GLge1AHXBDaNsqM3sCWAu0AO8A90bjiYj0NeVHG3l582He21dNS8CRn5nMqIJMBmalgBnN/gB7K+pYUVzOG9vLmFSYw0cmDyYnLcnr0kVEhPBGsnDOPUswSLV+7J5W7zvgSx0c+13gu92oUSSu1Df5+fvmQ6wqLicxIYFZI/oxa3geQ3LT2t2/scXPm9vLeXXLYbYePMLlM4uYVJjTw1WLiEhbYYUsEekZO0qP8sSaEmrqmzltRD/OGz+ArNQTj0ylJPo4d9wApg3N5bHVe/nT23u4PDCUaUNze6hqERFpj0KWSAwIOMeL7x9k2bYy8jNT+MLZoynKS+/SOfplJHPDGSN4YMVuHl+9l0DAMWN4XpQqFhGRzihkiXisodnPo2/vZcuhI8we0Y+LJw8mOfHkbiuakuhjybwR/HHlLv6ybh+DclI7nGYUEZHo0g2iRTxUXd/MvcuK2Xb4CIunDeGy6YUnHbCOSU5M4KrThpGR7OORt/bQ2OKPULUiItIVClkiHqmqa+I3rxdTUdfEktNHMGdk/4idOyMlkU/OGkpFbRNL1+tOViIiXlDIEvFAZShg1Ta28JkzRjJ2QFbErzGqIJOzTx3A2j1VbDt0JOLnFxGRE1PIEulhtY0t/P6NndQ3+/ns/JEM69e1BveuOOfUAvplJPPcewe1QryISA9TyBLpQU0tAR5YsYvq+maWzBvR5VcQdlWiL4GFEwZysKaBd/ZURvVaIiLyQQpZIj0k4ByPvr2Hksp6rjxtaI/dBmdyYQ5D89J4aeMhmloCPXJNERFRyBLpMS9vOsymg0f4yJTBTBzScyuymxkXTRpMTUMLK4rLe+y6IiLxTiFLpAdsPlDDK1sOM2NYHvNGRe5VhOEakZ/BmAGZrNhRRktAo1kiIj1BIUskysqPNvLYmr0MyU1l8bQhmJkndZwxOp+ahhbe21ftyfVFROKNQpZIFPkDjsdW7wXgmtnDSfJ5919u7MBM8jNTeHN7OU6vNBQRiTqFLJEoenXLYfZW1nPZtEL6ZSR7WkuCGaeP7s++qnr2VNR5WouISDxQyBKJkr0Vdbyy5TDThuYypSjX63IAmDEsj7QkH29sL/O6FBGRPk8hSyQKWvwBHl9TQlZqEh+dMsTrco5LTkxg1vA8Nh2o4Whji9fliIj0aQpZIlHw6tZSyo428rHphaQl+7wu5wOmD88j4GBDSZXXpYiI9GkKWSIRdrimgde2ljK1KIdTBkb+noTdNSg7lcE5qazbq5AlIhJNClkiERRwjqfW7SPZl8BHYmiasK3pQ3MpqaxnR+lRr0sREemzFLJEImj93ip2ldexaNIgMlMSvS6nQ1OG5mLAX9bu87oUEZE+SyFLJEKaWgK88P5BivLSmDk8z+tyTig7NYkxAzJ5at0+AgGtmSUiEg0KWSIR8trWUmoaWvjI5MEkeLSqe1dMC00ZrtlT6XUpIiJ9kkKWSARU1jXx+rZSphTlMLx/htflhGXC4GySfQk8/95Br0sREemTFLJEIuCljYcwg0UTB3ldSthSknzMG92flzYe0m12RESiQCFLpJsOVNezfm8Vp4/OJzfd21vndNUFEwayp6KOrYf0KkMRkUhTyBLpppc2HiIlKYGzxhZ4XUqXXTBhIAAvbdSUoYhIpClkiXTD7vJaNh88wlljC2JuZfdwDMxOZWpRDi9tPOR1KSIifU7sLuQjEuOcc7y48RCZKYmcPjrf63JO2sKJg/jRC1s4VNPAwOzUni9g9X09d61ZN/TctUQk7mkkS+Qk7SyrZWdZLWefWkByYu/9r/TPKUONZomIRFLv/c0g4rF/bD5MVmoip43o53Up3TJ2QCbD+6fz8iaFLBGRSFLIEjkJu8pqKS6r5ayxBST5evd/IzNjwSkFrCyuoLHF73U5IiJ9Ru/+7SDikVe2HCYjpfePYh0zf0w+9c1+1u6u8roUEZE+QyFLpIv2VtSx7fBRzhyT36t7sVqbN7o/vgTjje2lXpciItJn9I3fECI9aNm2UlKTEpgzsm+MYgFkpSYxfWgur28r87oUEZE+QyFLpAvKjjaycX8Nc0f2JyWp962LdSJnji3g3X3VVNY2eV2KiEifoJAl0gVvbCvDl2DMG93f61Iibv7YfJyDN3doNEtEJBIUskTCdKShmbV7Kpk+LJes1CSvy4m4qUU5ZKUm8oamDEVEIkIhSyRMK4vL8Qcc88f0vnsUhiPRl8Dpo/vz+rYynHNelyMi0uspZImEodkfYNXOCsYNyqIgK8XrcqJm/tgC9lXVs7u8zutSRER6PYUskTCs31tFXZOf08f03nsUhmNu6BWTb+2s8LgSEZHeTyFLpBPOOZbvKGdQdiqj8jO8LieqxgzIpF9GMqsUskREuk0hS6QTxWW1HKxp4PTR/TEzr8uJKjNj9oh+rNpZ7nUpIiK9nkKWSCeW7ygnPdnH1KG5XpfSI2aP7EdJZT37quq9LkVEpFdTyBI5gcraJjYfqGH2iH69/kbQ4Zoz6lhflkazRES6Iz5+a4icpLd2BXuTZvehW+h0ZtygbLJSE9X8LiLSTQpZIh1o8QdYvauCcYOzyU1P9rqcHuNLONaXpZAlItIdClkiHXh/fw21Tf7jyxrEk9kj+1FcWsvhIw1elyIi0mspZIl0YOXOcvplJDN6QKbXpfS4OaOC92bUlKGIyMlTyBJpx8HqBnaX1zFnZD8S+viyDe2ZOCSbtCQfq3dVel2KiEivpZAl0o63d1WQmGDMHJbndSmeSPIlMHVoDmv3KGSJiJwshSyRNpr9AdbtrWLCkGzSUxK9LsczM4blsXF/DfVNfq9LERHplRSyRNrYdKCG+mY/M4fH5yjWMTOH59EScGwoqfK6FBGRXkkhS6SNNbsryU1LYnRB/DW8tzY9NFW6do9ClojIyQgrZJnZIjPbYmbbzeyb7Ww3M/tpaPsGM5vRaluumT1hZpvNbJOZzYvkExCJpKq6JrYfPsr0YXlx2fDeWr+MZEblZ7Bmt/qyRERORqchy8x8wC+Ai4AJwNVmNqHNbhcBY0NvNwG/arXtbuB559w4YCqwKQJ1i0TFO3urcBD3U4XHzBiex9o9lTjnvC5FRKTXCWckazaw3TlX7JxrAv4ELG6zz2LgARe0Esg1s8Fmlg2cBfwOwDnX5JzT3IPEpIBzrNldyaj8DPplxM8K7ycyY1geFbVN7C6v87oUEZFeJ5yXThUCe1t9XALMCWOfQqAFKAXuM7OpwBrgK8652pOuWCRKdpXXUlHbxHnjBnhdSo95eNWeE24/WBNc8f3nr2xnxgmWs7hmzrCI1iUi0heEM5LVXmNK27mDjvZJBGYAv3LOTQdqgQ/1dAGY2U1mttrMVpeWloZRlkhkrdlVSUpiAhOH5HhdSswYkJVCSmICeyo0kiUi0lXhhKwSYGirj4uA/WHuUwKUOOdWhR5/gmDo+hDn3L3OuVnOuVkFBQXh1C4SMQ3Nft7bX82UolySE/Wi22MSzBjWL509mi4UEemycH6bvA2MNbORZpYMXAU802afZ4DrQq8ynAtUO+cOOOcOAnvN7NTQfucBGyNVvEikvLuvmma/Y5Ya3j+kKC+dQzUNNLUEvC5FRKRX6bQnyznXYma3AC8APuD3zrn3zezzoe33AM8CFwPbgTrghlan+BfgoVBAK26zTSQmrNldSUFWCkV5aV6XEnOK8tJwwP6qekbkZ3hdjohIrxHWPUOcc88SDFKtH7un1fsO+FIHx64DZnWjRpGoOnykgT0VdVw0aRAW52tjtedY8CxRyBIR6RI1n0jcW7+3GgOmDs31upSYlJWaRE5aEiWV6ssSEekKhSyJa84F7803qiCD7NQkr8uJWYW5aeyrrPe6DBGRXkUhS+Lavqp6ymubmFKkUawTKcpLo7y2ifomv9eliIj0GgpZEtc2lFTjM2OS1sY6oaK8dABKqjRlKCISLoUsiVuB0FTh2IGZpCX7vC4nphXmBpvfNWUoIhI+hSyJW7vL66hpaGGqpgo7lZbsIz8zmb0KWSIiYVPIkri1vqSKJJ8xfnC216X0CkV56ezTKwxFRMKmkCVxyR9wvLevmvGDs3UbnTAV5qZR09BCTX2z16WIiPQKYS1GKtKbjN7zeKf7vFOdQV3TUBamvM/oPas63b8jO4ZdcdLH9jbHFyWtrGdCWi9d7mL1fT1znVm6sYWIaCRL4tSbFdlk+PxMy671upReY3BOGgmmVxiKiIRLIUviTlPAWF2VyezcIyQlOK/L6TWSExMYmJ2qVxiKiIRJIUvizof7ghAAACAASURBVDvVmdQHfJzer8brUnqdorw0SirrCd6uVERETkQhS+LOmxVZ5CS2MClL015dVZSbTn2zn4raJq9LERGJeQpZElfq/Qmsrc5kbt4REszranqfwlbN7yIicmIKWRJX3qnOoNklMC9PU4UnY2B2KokJRonWyxIR6ZRClsSVt6qCU4WnZmok5mT4EowhuWmUVOnzJyLSGYUsiRtNAWNtdSan5WqqsDsK89LYX1WPP6DmdxGRE1HIkrixoSaDxkACs/OOeF1Kr1aUm0az31F6pNHrUkREYppClsSNVZVZZPj8TNSrCrulKC8dQH1ZIiKdUMiSuNDiYE11JjNzjpKoqcJu6Z+ZTGpSgvqyREQ6oZAlceH9I+nU+n3M0VRhtyVYsPldK7+LiJyYQpbEhdVVWaQkBJiiexVGRGFuGgdrGmgJBLwuRUQkZilkSZ/nHKytzmRyVi3JuldhRBTmpuEPOA7XqPldRKQjClnS5+2pT6GsKYkZuUe9LqXPKMwNrvyuKUMRkY4pZEmft7Y6E4AZOQpZkdIvI9j8vk/N7yIiHVLIkj5vbXUGo9LryUvye11Kn2HHmt8VskREOqSQJX1adbOPbbVpGsWKgiI1v4uInJBClvRp62oycBgz1Y8VcUNCze+H1PwuItIuhSzp09ZUZZKX1MzINAWBSDvW/L5fze8iIu1SyJI+qyUA62symJFTi2mV94g71vyuld9FRNqnkCV91saj6TQEfMxUP1ZUmBmFuWnsV8gSEWmXQpb0WWurM0myAJO0ynvUFOamcbC6gcYWvXJTRKQthSzpk5wL9mNNzq4jRau8R01hXjp+59h6UKOFIiJtKWRJn7SvIZnDTclauiHKjjW/v7uv2uNKRERij0KW9ElrtMp7j8hLTyItyaeQJSLSDoUs6ZPWVmcyIq2B/sktXpfSpx1rfn93X5XXpYiIxByFLOlzjrQksOWoVnnvKUNy09hy8Iia30VE2lDIkj7n3dAq79MVsnpEYV4azX41v4uItKWQJX3OhpoMMnx+xmQ0eF1KXDjW/L5BU4YiIh+gkCV9inOODTUZTMqqJUGrvPeIvPQkctKSeE/N7yIiH6CQJX3KjtJaypuTmKIFSHuMmTG5MEevMBQRaSPR6wJEIun1baUATMmu87iS+DK5KIffvl5MY4uflERf9C4U8ENdGbQ0gr8Z/E3Bx1IyIDUXUrIhIYrXFxHpAoUs6VNe31bGoJQmBqQ0e11KXJlcmEOz37Hl4BGmFOVG7sS1pXBoI9SUQM1+OHowGKo6ZJCaA3kjIH8s9B8LGQXoDuEi4gWFLOkzmloCrCwuZ36Opgp72uTCHCC48nu3Q1bNfjiwHg5ugCMHgo+lZEP2EMg/FbIHQVIG+JKCb+aDpqNQXw0NlVBXDuU74MC64LGpuVA4E4bNg4z87tUmItIFClnSZ6zdU0ldk1/9WB4oyksjNz2Jd0uqYc5JnMAF4NB7UPwqVBQDBv1GwYTLYNBkSO/fxfM5qC2D8q1weCMUvwI7XoaCU2HY6cFzmlpSRSS6FLKkz3h9Wym+BGNilvqxetpJN7+3NMKu16H4tWCvVVpeMFgVzoSUrO4UBJkFwbfhZ0B9FexdCXtWwpr7IGswjPsoDBivqUQRiRqFLOkz3thWxvShuaT7Al6XEpcmFQab3xua/aQmddJ87hxsegZe+g5U7oLc4TDukuAIUzQa19Ny4ZRFMOYCOLgeNj8Lb98b7Nka/1HIHRb5a4pI3FPIkj6hsraJDfuq+dfzToFKr6uJT1NaNb9PHXqCvqySNfDibbBnBQyYALNvDo4o9YQEHwyZAYOmwO7lsO0FeON/Yfj8YNhKTOmZOkQkLqgpQfqEN3eU4RyceYoam70yqVXze7uaauHZb8Bvz4Xy7fDRu+Hm13suYLWWkAgjz4Jz/hNGLoDdb8KyH4X6wUREIkMjWdInvL61jKzURKYU5rDG62Li1LHm93ZXft/5OjxzS3BqcPbNcN5/dq/nKlKSUmHix4IjW+sfhuU/g1EL4NRLwKcfjyLSPfopIr2ec443tpdxxuh8En0anPXKseb3DSWtQlZTXbDv6u3fQN5IuP5ZGHGGd0V2pP9oOOsbsOnp0Cscd8LMG4K9XCIiJ0m/kaTXKy6rZV9VvaYKY8Dkwhy2HjpCQ7MfSrfAb88LBqw5X4AvLI/NgHVMYgpM/mQwXB05EOzVqtjpdVUi0otpJEt6vde3Bm+lc9bYAo8r6TtG73m8awf4+gEwuSGFlkAOhx/9CsN2Pgq+5OD0YMGpsOHRKFQaBYOnQsYAWP07WPFzmPQJGH6611WJSC8U1kiWmS0ysy1mtt3MvtnOdjOzn4a2bzCzGW22+8zsHTP7a6QKFznmje1lDO+fztB+6V6XEvcmZ9dyV+KvGbb9j5AzFM76ujeN7d2VPRjmfzV4a553H4ONTweXnRAR6YJOQ5aZ+YBfABcBE4CrzWxCm90uAsaG3m4CftVm+1eATd2uVqSNZn+AFTvKmT9GU4Weq6+icP3dfDLxNV7OuATmfjF4H8HeKjkdZt8EI84Mrhi//uFO7psoIvJB4YxkzQa2O+eKnXNNwJ+AxW32WQw84IJWArlmNhjAzIqAjwC/jWDdIkBwuYDaJj9nKGR5q6IY3vgfrPYw/5v+ZX7cckV0FhXtaZYAEz8eXMi05G1Y83vwN3ldlYj0EuGErEJgb6uPS0KPhbvPT4BvAFqGWyJuZXE5AHNG9vO4kvhVUPkOrPgF+FLgjH8jMGAyW2sSqW/xurIIMQuGrEmXw6GNsOoeaK73uioR6QXCCVnt3dirbXNCu/uY2SXAYedcp0sXmdlNZrbazFaXlpaGUZYIrNhRzqkDs+ifqZW6e5xzDD30d0btXwr5Y4I9TFmDmNqvGb8z3q9K8rrCyBoxH2ZcB5W7Q0GrweuKRCTGhROySoChrT4uAvaHuc8ZwKVmtovgNOO5ZvZgexdxzt3rnJvlnJtVUKBXiUnnmv0BVu+qZO4ojWL1NAv4Gb3vKYaULedQ3kw47aZgDxMwNS84hLW+sg++eHnIdJixBKr3wlu/Dt7gWkSkA+GErLeBsWY20sySgauAZ9rs8wxwXehVhnOBaufcAefct5xzRc65EaHj/uGc+1Qkn4DErw0l1dQ3+5k7qr/XpcQVn7+BU/c8TH71u+wdcA67Bl/8gf6rAWkBBqf5WV/Rx0ayjhk8BaZfB1W74a17FbREpEOd/qnpnGsxs1uAFwAf8Hvn3Ptm9vnQ9nuAZ4GLge1AHXBD9EoWCTrej6WQ1WOSmms4dfcjpDWWsqNwMWW5U9vdb2q/ZtZX9MGRrGOGTAPnh3cehLd/C7NvDK4JJiLSSlg/BZ1zzxIMUq0fu6fV+w74UifneBV4tcsVinRgZXE54wZl0S9Dv9x6QlrDYU7d8zCJ/ga2Dr+a6szRHe47Na+F5/elUtVk5Cb30fWlCmcG185a9xCsfSC4UnxfeEWliESMbqsjvVJTy7F+LI1i9YSs2l1M2PkHzAXYOOL6EwYsCI5kAX13yvCYolnBJR4OvQfvPq4FS0XkAxSypFd6d1+V+rF6SL/q9xm3+yGaEzN5f+RnqEsb1Okxk/JaMFzfnjI8ZuSZMOYC2LsStj7ndTUiEkPi4Ceg9EUrdmh9rJ4wqGwlww+9SE36ULYOvQp/YlpYx2UnOUZl+dlQ2cdHso459WJorIFtL0JKNsxSW6qIaCRLeqmVxRWMG5RFnvqxosM5hh14geGHXqQiezybh3867IB1zNR+zayrSIyPGTQzmPxJGDgR3vszbP6b1xWJSAxQyJJep6klwOrdFZoqjJIEfyNjSv7M4IpVHOw3m21Fn8AldH3Qe1peC2WNPvbVxcmPmQRfcA2t3KHw58/BgfVeVyQiHouTn37Sl6wvqaKhOcC80QpZkZbUXM05b99M/5qN7B54AbsHXRi8f99JONb8vq6vN7+35kuGWZ+DtH7w8FVQc8DrikTEQwpZ0uus3FGOmfqxIi29/gALV1xHftUGthV9nIP584LTYCdpfG4LKQmOd+IpZAGkZsM1jwZ7tB65CprqvK5IRDyikCW9zsqd5YwblE1uuvqxIiW3ZgsLV1xLWmMpr5z2aypyJnX7nMkJMDmvmXfK4yxkAQyaBJ/4XXDK8C83QSDgdUUi4gGFLOlVGlv8rNldyTz1Y0XMwLIVXLByCc4SeGnu/Rzuf1rEzj2jfzPvVSXS6I/YKXuPUxfBhT+ATUvh1R96XY2IeEAhS3qV9XuraWgO6KbQETKq5C+cvfqLHE0fwotzH6Q6a2xEzz+9XwtNAWNjVZyuFjP3izDtU7DsrmDYEpG4opAlvcrK4mA/1mz1Y3WPCzB1y93Mffc7HO53Gn+fcz/1YSwy2lUz+geb3+OuL+sYM/jI/wRvwfOXz8PhzV5XJCI9SCFLepWVxeWMVz9Wt/j8DcxfdysTi3/LtqFX8OqsX9CclBWVaw1MCzAkzc/aeOzLOiYpFa58EJLS4U9XQ32V1xWJSA9RyJJe43g/lpZuOGmpjWWct+ozDD34d9aOu5W3J/4nLiG6AWh6/+b4Hck6JnsIXPlHqNoLf/4sBOKxSU0k/ihkSa+xbk8VjS0BLUJ6knKObGPhimvJPbqd12f8H5tHLunWEg3hmt6vmX11Pg7Xx/mPm2Fz4eK7YPvf4bX/9roaEekBcf5TT3qTlcUVwX6sEerH6qrBpW+ycMWnSQg089Kc+ygZeF6PXXt6qC9rbTzcLLozsz4D066F10JhS0T6NIUs6TVWFJcxcUg2OelxPvXURWN2P8qCNV/iaHoRL8x7mMqciT16/Um5LSQnuPhcL6s9F/8YBkyAP98I1SVeVyMiUaSQJb1CQ7OftXuqmDtSU4XhSvA3cdp732P2xjs5kD+fl+Y+EJVXEHYmxRdclHS1QlZQcjp88gHwN8PjN0BLk9cViUiUKGRJr7BubxVN6scKW3r9Qc5fdT1j9z7B+6M+x7KZd9OSmO5ZPbP6N7OhIokG9XsH5Y+BxT+Dkrfg79/1uhoRiRKFLOkVVhaXk2BwmtbH6tSA8rdYtPxKco4Ws2z6T1h/6ldw5vO0ptPym2l2xvp4f5VhaxM/BnM+Dyt/CRuf9roaEYkChSzpFVbsKGfikBxy0vRLuiPm/Ezafg/nvnUjjUk5vHD6w5QM6rkG9xOZGWp+X12mr98HXPB9KJwFT30Jynd4XY2IRJhClsS8hmY/7+yt0q10TiCt4TDnvHUTU7b9gj2DL+SFeQ9TkznK67KOy0txnJLdwtvqy/qgxGS44g/gS4THroPmeq8rEpEIUsiSmPfOHvVjncjg0je46M0ryK/awMpJd7B86n/TkpTpdVkfMiu/mTXlSfid15XEmNyh8PHfwqH34dlbva5GRCJIIUti3gr1Y7UrsaWOWe/fyTmrv0B9Sn+eP+NRiod+rEcWGD0Zp/Vv4khzAluqtV7Wh4w9H866Fd55MPgmIn2CftpJzFtZXM6kwhyyUzXVdExBxVrmvvsfZNaVsHnEp1l/ypfx+1K9LuuEZuX/sy9rQm6Lx9XEoLO/BXtXwd++BkOmw8CeXc9MRCJPI1kS0xqa/azbU6WpwhBfSx3TN/+Y81ddj7kAf5/ze9aO/0bMByyAovQAg9P86svqSIIPPvE7SM2Bx6+HxqNeVyQi3aSQJTFt7e5KmvwBNb0DQw4v4yNvfIzxO+9n+9DLeXb+k5T2m+V1WWEzC45mvV2WhFNfVvsyB8Anfgvl29WfJdIHKGRJTDu+PlYc368wreEQ89d+lbPXfAl/QiovzbmPtyd9x9PFRU/W7PxmDtb72F3r7bpdMW3kWbDg32H9I7DuYa+rEZFuUE+WxLSVxRVMLswhKw77sRL8jYzb9Ucm7vgN5vysO+XLbB55PYGE3vu5mFcQvIXMisNJjMjU8u8dOuvrsOuNUH/WDBgwzuuKROQkaCRLYlZ9k591e+OwH8s5hh14nktev5RpW+/mUP/ZPDv/STaOvrFXByyA0Vl+ClL9rChN9rqU2JbgC04bJqUH+7Oa6ryuSEROgkKWxKy1e0L9WKPjJ2QNKH+bC1Z+mvnrvk5zYhYvz/4ty2b+jKMZw7wuLSLMYF5BMytK1ZfVqaxB8PF7oXQzPP/vXlcjIidB04USs1YWl+NLMGYNz/O6lKjrX7meqdt+xqDyVdSlDGDlpO+xs2ix5/ccjIbTBzTxzN5UdhzxMSZbU4YnNOY8OPOr8Pr/wIizYMoVXlckIl2gkCUx69j6WH25Hyu/ch0Td9xLYenrNCT3Y824r7N92Cd7xZIMJ2teQXC9rBWlyYzJ1m1kOnX2t2H3cvjrvwbXz8of43VFIhImTRdKTPpnP1YffFWhcwwufZPzVt3AwpWfJr9qA+tO+TLPLHiOLSOv69MBC2BYhp8haX5WHO674TmifInB9bN8ycH+rOYGrysSkTBpJEti0prdlTT7HfNivOl99J7Hw97XAs30r36fQRVvkdFwkKbELHYPXMjhvBkEfMkM3/+3Ex6/Y1jfmCoyg7kDmnj1QAoBBwmxeReg7ll9X+TPOekT8PZv4MGPw+RW3wuzboj8tUQkIhSyJCYd78fqA+tjpTRVMqBiNQVV60jy11OXUkDxkI9SljMZlxCf/wXnFTTz5O40ttb4GJejvqywDJwIo86B4leg/5jg1KGIxLT4/AkvMW9FcTmTC3PITOml36LOkVO7g4Hlb5N7dBtgVGaP42C/0ziSPjxmb+LcU04fEFwv641DyYzLUV9W2MZdAhXFsOFRyBkKGfleVyQiJ6CeLIk5dU0trN9bxbxeuHSDz9/AoPKVTNn+C8btfpjM+v3szz+Tdad8hW1Dr+BIxoi4D1gAhekBxmS18NohrZfVJQk+mHFd8Hto7f3g1422RWJZLx0mkL5sze5KWgKuVy1CmtZwiIEVq8mv2oDPNXMkrYjthQuoyB4ft1OCnTlrYBMPFafR4IfUvrdSRfSk94epV8Pq38OmZ2DOjV5XJCId0E9/iTm9ZX0sc37yajYzsOJtsuv2ELBEynImcajfadSlDfa6vJi3YFATv9+ezsrSZM4e1OR1Ob3LoCnBexzuXAab/grjL/G6IhFph0KWxJwVO8qZUpRDRoz2YyU1H2FA5VoGVK4hueUoDUm57Bl4PqW503rlTZu9MqegiZQEx7KDClknZdylULETnv4iDJoMecO9rkhE2ojN32ISt442trChpJqbzhrldSkfkl5/gEHlq+hf8x4JLkBV5mh29ruEqswxYGpv7KpUXzBoqS/rJPkSYcYSWP5TeOIzcMNzkKjPpUgsUciSmPLWznJaAo4zxsTIq6ZcgLwj2xhUvpLsut34E5I4nDeLg/1OozGl9/SMxaoFg5r4/vosSmoTKMoIeF1O75ORD5f+NLhI6T/ugIV3el2RiLSikCUx5c3t5aQkJjDT436sBH8TBVXrGFTxFqlNFTQmZbN74PmU5s3o8yuy96QFA5v4PrDsUDLXjNJK5idl4sdg5+uw/Gcw4kw45UKvKxKREIUsiSlvbi9j1og8UpO8eblZYstRBpevZEDFWhIDDRxNK2Rb0SeoyB6vKcEoGJ3lpzDdz2sHFbK65cL/gr1vwV9uhs+/CTmFXlckIihkSQwpPdLI5oNH+MaiU3v82knNRxhcvpwBFWtIcH4qssdxsP9cjqYP7fFa4okZnDOokSd3p2oph+5ISoUr/gD3Lgj2Z13/t2DPloh4Sn+aS8xYvqMMgDNG91w/VmJLLcMPPM+0bT9lUPlbVORMZMOYL7J96BUKWD3kgiFN1PkTWH5YTdvdkj8GLvkJ7F0JL9/udTUigkayJIYs315Odmoikwpzon6tBH8jg8tXMrh8BQmBZkpzp7K/YD6Nyb3/Xom9zdyCJjITA7y4P4VzB2sph26ZckUwZC3/GRTODPZriYhnFLIkJjjneGN7GfNG98eXEMXbzrgAAyrXUHR4GUn+Wsqzx1My4BwaUmLk1YxxKMUHZw9q4u/7kwnMgGh++ePChT+EA+vhqS9BwXgYMM7rikTilqYLJSbsqahjX1V9VJduyKrdxeQd9zLywHPUp/TnvZGfYfvQKxSwYsAFQxopa/TxToX+7uu2xGS44n5ITodHPwUNNV5XJBK3FLIkJry5vRwgKiErubmaMXufYMKuB/AFGtk69Ao2jVhCbXpRxK8lJ+fsQU0kmuPFfSlel9I35BTC5fdBRXFwRXjnvK5IJC4pZElMeHN7GYOyUxmVnxG5k7oAA8tXMWX7L8k7spWSgrPYMOaLVGaPD76sTWJGTrJjbkEzLx1QyIqYkWfCBd+DTUvhzbu9rkYkLmlsXjwXCDiW7yjj3HEDsQiFn7SGw4zcv5Ss+n1UZY5m1+CLaUyO7RtOx7uFQxr5zrosttX4GJvt97qcvmHeLVCyGl7+HgyZBqPO9roikbiikSzx3KaDNVTWNXPGmAjcpsbfTOHh15hUfC+pTRVsL7yMLcOuUcDqBRYVNZKAY+leragfMWaw+OfQf2xw/azqEq8rEokrYYUsM1tkZlvMbLuZfbOd7WZmPw1t32BmM0KPDzWzV8xsk5m9b2ZfifQTkN7vze2h9bG6249Vth1+t5Ci0teoyJ7AhjFfpDx3iqYGe4kBqQHmFjSzdG+KWogiKSULrnwQWprgseugpdHrikTiRqchy8x8wC+Ai4AJwNVmNqHNbhcBY0NvNwG/Cj3eAnzNOTcemAt8qZ1jJc69ub2cMQMyGZh9kiMYzsHq38Ovz4SKYrYVXc6Ooo/TkhjB/i7pEZcOa2Dn0UTeq1InQ0QVnAKX/RL2rYHn/t3rakTiRjgjWbOB7c65YudcE/AnYHGbfRYDD7iglUCumQ12zh1wzq0FcM4dATYBuqmWHNfUEuCtnRWcMfokpwrrKuCRq+Gv/wZD58AXV1CRoxzfWy0qbCTJHEv3qgE+4iZcCmd8BdbcB6vv87oakbgQTsgqBPa2+riEDwelTvcxsxHAdGBVV4uUvuudPZXUN/tPbqpw71twz5mw4+XgAoyfehKyh0S+SOkxucmOswY1sXRvKgFNGUbeud+BMefDs7fCrje8rkakzwtnTL69hpa2P/5OuI+ZZQJ/Bv7VOdfuynhmdhPBqUaGDRsWRlnSF7y5o5wEgzmjujCS5Rys+Dn8/XbILoTPvghDpketRulZ41PKebl+CH98r55xmfXdOteckbF3m6RVOysidq4uPz9fIlz+e/jt+fDop+HGf0C/kRGrR0Q+KJyRrBKg9Z1yi4D94e5jZkkEA9ZDzrknO7qIc+5e59ws59ysgoKCcGqXPuD1baVMKcolJy0pvAMaquFP18KL/wGnLIKblylg9TGn5R4h2QIsK8/2upS+KTUHrv4TuEBwql0rwotETTgh621grJmNNLNk4CrgmTb7PANcF3qV4Vyg2jl3wIKLHv0O2OSc+9+IVi69XmVtE+v2VrHglDBDddk2+M15sPX54PTglQ9CWm50i5Qel+pzzM07wvKKbBr8emVoVPQfDZ98AMq2wp8/BwGtSyYSDZ2GLOdcC3AL8ALBxvXHnHPvm9nnzezzod2eBYqB7cBvgC+GHj8D+DRwrpmtC71dHOknIb3Tsm2lOAdnnxpGyNryPPzmXKivhCXPwLwvammGPuzc/CrqAz5WVWV5XUrfNWoBXHwXbHsBXrjN62pE+qSwXiftnHuWYJBq/dg9rd53wJfaOe4N2u/XEuHVLaXkpScxpegEo1HOwbIfwys/gMFT4MqHIHdox/tLnzAus57BKY38oyyXBf01nRU1p30OynfAyl9C3nCY+wWvKxLpU7Tiu3giEHAs21rKWacU4EvoIIc3N8CTN8Erd8LkK+AzLyhgxQkzOCe/ms1H09nfkOx1OX3bwjth3CXw/LeC9zkUkYhRyBJPvLuvmvLaJs45dUD7O9SWwQOXwruPwbn/CR+/F5LSerZI8dSC/tUk4PhHWY7XpfRtCT74+G+gcGawP6tktdcVifQZClniiVe3lGIGZ7XX9H54c7D/6sB6uOIPcNat6r+KQ7lJfmbmHuW18hyaAvr6R1VyevAVh1mD4OErg1OIItJtClniiVe3HmZKUS79MtpMBe1eDr9bCM31cP2zMPFj3hQoMWFhQSU1LYksr9ByDlGXWQDX/hlw8MfLoKbtSj0i0lUKWdLjKkJLN5zddhRr01/hgcsgcwDc+DIUzfSmQIkZk7PqGJrawLOH83TT6J6QPwaufSJ4u6o/fjz4r4icNIUs6XH/2HwY5+C88a36sdbcD499GgZNDjW4a9V/Cc4SXzywkt31qWw8mu51OfGhcAZc/QhU7ICHPwlNtV5XJNJrKWRJj3tp40EGZacyuTDnn0s0LP0yjD43uAZWxkneLFr6pPn9ashKbOHZQ3lelxI/Rp4Fl98H+9bAo5+ClkavKxLplRSypEc1NPtZtrWM8ycMwJyD5/4d/vF9mHJlsPE2OcPrEiXGJCc4LsivYk11Jgcbwrz9knTf+Evg0p/Bjn/A49dDS5PXFYn0OgpZ0qOW7yijvtnPwlP7wZOfg7d+DfNugcvuAZ9+gUr7Fg6oJNEcTx/SKGePmv4puPjHsOVZeOIG8Dd7XZFIr6KQJT3qpY2HGJDSzPy3vgDv/RkuuAMu/AEk6FtROpaX5Ofc/GpeK8uhtDGsG1VIpMy+ES66Czb/FZ74jIKWSBfoN5v0mEDAsXrjNh5P/S8Sdr0Bi38J/7+9+46PqkobOP57Msmk904okd6kSBWUVUARLKALll0V+7qru7rvqu+uumt51y3quu7aXbsrNkRFLChYEFA60kGkSICQEAIJ6ZOc949zI0NMhcxMyvP9fO5n7tw2556ZZJ4599znjL4p0MVSrcTktDxEDO9ma2uW3434hR2UfeNsmHUtVHoCXSKlWgX9Saj8ZuPGtTxVfjsZIQfh4hnQ66xAF0m1IoluD6cnHeLTQCmUHAAAIABJREFU/XFMSc8jya1f9H518q/AVMLHd9r+WVOfg5CwQJdKqRZNW7KUf2Svo/M755MghZRePEsDLHVMpqTlAWhrVqCM+jVMfAA2v2/TO5QdDnSJlGrRNMhSvrdjEeb5iZR4DPenP0xUj9GBLpFqpZLcHsYmHWR+bhx79E7DwBhxnb1RZcdCmxm+JD/QJVKqxdLLhcq3NtrOsmVRHZly6CZuHnpyoEvUanX7/s1AF6FFmJq+ny/zYpixO4Vbuu0OdHECb/nz/nutoVfax0GXQGi0vePwhXNslviY9OZ9rUCcl1LNTFuylO94ZXF/ouvj5LqSmdA3LdClUq1cXEglk9MOsOxgNJsOhwe6OO1Xn3PgZ29A/g54Zhxkrwt0iZRqcTTIUs3vqCzu4zCXv8vMjcWc2iOZ2Ai9xKOO39mpB0gIqeDlXSlU6ZiGgdPtdLjyQ/s3/9xZsHVeoEukVIuiQZZqXlVVNbK4v8qqfRXsPljC2Sc28+UE1W6FBhkuzshla3E4X+TFBro47Vv6ALhmHsRnwisX+vcyn1ItnAZZqvl4ymvN4j7nm724XUGc0S810CVUbcipCQX0jirmlaxkCjyuQBenfYvNgKs+tOOPzrkZ3r9Fh+FRCg2yVHMpK4QZ036Uxb2yyvD+2j2M6ZlMTJheKlTNJ0jg6s7ZFFe6mJGVHOjiqNBoO/7oqF/Dsv/Ai+dAwd5Al0qpgNIgSx2/ov3w4rmw/UuY8sRRWdwXbt3PvoIyfnpSRgALqNqqzuHlnJ16gM/y4thQqJ3gA84VDGf+GaY+bzvCP/0T2Lk40KVSKmA0yFLH58A2ePZMyNkEl7wKg3521OqZK7KIiwhhbJ+UABVQtXU/Td9PsrucJ3emU1opgS6OAuh/AVw7H9xR9gfYggehqjLQpVLK7zTIUscuazk8c4ZNRjh9NvSccNTqQyUVzF2fzeSBHQgN1j4zyjfCXIZfZe4lpyyEV3ZrMN9ipPSB6z6DPufZG2FePA8OZQW6VEr5lQZZ6thsnGOTEIZG2zuLOg3/0SZz1uyh3FPF1CGdAlBA1Z70jS5hUko+H+fGs6YgItDFUdXCYu0Yh1OegL2r4YlRsG5WoEullN9okKWabslT8PqlkNoPrv4EErvVutnMFVn0So2mf0aMnwuo2qOLM3LpEFbG4zvSKajQltMWQ8R2I7j+S0jsYbPEv3E5FO4LdMmU8jkNslTjVVXB3Dvgw9ug99kw/T2Iqv2urq05haz6/iDThnZERPvJKN9zBxluOmEPhz0uHtuRrklKW5qErnDVRzD2j7D5I3hsGKx82SYyVaqN0iBLNU5FCbw5Hb56FIb/Ai58Cdx1X5Z56auduF1BTBmsdxUq/8mMKGN6pxxWF0Qxe19CoIujanKFwJhb4JeLILU/zL7RdozP2RTokinlExpkqYYV5cFLk2HjbDjzPpj4dwiq+3JMYWkFb63I4pyB6SRFhfqxoErB+KSDnBxfwOu7k1mco7nZWqSkHjB9DpzzMGSvsX21PrgVig8EumRKNSsNslT9cjfDs+Nhz2qY9gKMutH2sajHzBVZFJVXcsWoTL8UUSlvInBdl2w6hJXzq69j2XlY+2e1SEFBMPRK+PUqGHIFLHsG/j3Y9vnUbPGqjdAgS9Vty8fwzHgoLbApGvqd3+AuVVWGl77ayeDOcQzoGOeHQir1YxGuKm7tbtMFXLM4lsIK7RfYYkUmwjkPwfWLoMMg2+fzkSHw/deaW0u1ehpkqR8zBhY+DDMutIO+Xvc5dB7ZqF0XfJvL9v1F2oqlAi4ttILHRx5iW6GLG76OoaIq0CVS9UrtC5e9A5e+BZFJsOY1+PyvkLVMgy3VammQpY5WXgSzroN5d0G/KXDVXIhrfJ6rZxduJzk6lIn9031YSKUaZ1RKBX85qZAF+0K5bXmM3nHY0olA9/Fw7acw7BoIdsPqV+CzP8O2L8BTFugSKtUkwYEugGpB9m+FNy6DnI0w9k449ZYG+195W/l9Pl9+u5/bJ/XGHazxu2oZLjqhlNzSIB5cH0VSaBW3DzjclI91i5Ff4SKrJJS88hAKPC5cYthcGU56RCXdoyvpFFlJm/mzE7F3H6b0hX0bYNunsOFt+PYj6DLaTuHxgS6lUg3SIEtZG96Fd26wt1hfNgu6jW3yIR6Z/y3xESH8fEQXHxRQqWN3Q+9ickuD+M+3EYS6DL/rV9TiAy2PgbUFkSzJj2ZDYQT7yt0/3shrlJqo4CpOTS1nbHo5Z2WUER3SBprtJAjS+tspfwds+wy2zrdTSl/oMsoO3yNtJbpUbY0GWe2dpwzm3QNfPwYZQ+0dhE24PFhtbdYhPtucy60TehEZqh8r1bKIwF2DDlNeJTy6KRKgxQZauWXBzM2N5/O8WAo9wUS4KukXXcyZKflkRpSRFFJBbEglBujfMZ6sIhdbC4NZmRfCp3vdfLg7jLtXV3F+51Ku6F5C95g20p8pPhOGXGnTPOz62naMX/Yf26KVMRQ6DoWo1ECXUqmj6Ldhe5a7Bd662uapGX6dzYEVXMuv5Ub496ffEhsewuUnayuWapmCBO47qRCARzdFUlIp3DHgMEEtJNDaU+rmzT1JfJ0fDcCwuELGJBYwMKaIkKDaW6WSwwzJYR4GJ3qYllmKMbDqQDCvbAvnjR3hzNgWzpQupdzcp4jOUW2k539EAvSaBD0mwL518P1XsHUebP0E4jrbgCttAITr3c0q8DTIao+MgZUvwoe/h5BwuPhV6D3pmA+3YucBPtmwj9+O70l0mCZ/VC1XdaAV6jI8+20EOaVBPDi0gNAAptLKKw9m5t4kPt8fS0iQ4ezUA5yVkk+S29PkY4nASYkeTkos5PYBh3lyUyQvfRfOe9+HcW3PYm7sU0REW/mvH+SC9IF2Kj0Eu1fC7mWwfpad4rpA2ol20hYuFSBt5c9NNdbhHJjzW9g0B7qeBlOehJhjvxOwqspwz3sbSI0J5ZpTT2i2YirlK0ECdw08TFp4FX9bG8W+kiAeG3mI5DD/9mEq9ATxTnYic3PiqUKYkJLP+Wl5xIY0z+W9xFDDHQMPc03PYv6+LpLHN0fy7q4w/jy4kNPT21iyz7BY6Ha6nQqzIXutbaHfNMdOUam2dSvtRIjt1KQbepQ6HhpktRfGwNo3baK/8mI44//g5Btt1uXjMGvVbtZkHeKhCwdqXyzVaojA9b2KSQ+v5H9XxHDOvAQeH3mIIUlNbz1qqtJK4f2cBN7LTqC0KogxiQVMTd9PSmiFT14vNbyKh4YVcnFmKXeuiubKRXFcckIJdw48TGRwG+gcX1N0mp16nAEl+ZC9zgZc3823lxTDYiG5NyT1gqSeEBoV6BKrNky/FduDgr229WrLh9BxGEx+DJJ7HfdhD5d5uP+jTQzsFMeUQToQtGp9Jncuo2fMAa7/KpaLvojnht7F3NCnCLcPblYrq4RXt4fzz3UJHPIEMyyukIs65NIp3D+tSsOTK5g97gD/XB/J01siWJTj5h/DChiW5JvgrkUIj4cTTrVTeRHkrIfs9Tbo2rXEbhPb0d652O106DQSQsICWmTVtmiQ1ZZVemDp0zZrcmUFTPgLjLi+3sGdm+LBuZvJKSzjycuGENRSeg8r1UR94iqZPS6fu1dH86+NkczdE8qfBxcytJmCj7JKmLUzjMc2RZJV7KJvVBG3ZGTRM6q0WY7fFGEu+MOAIsall/O75TFc+Hkc1/Us5n/6FQW0X5pfuCOh43A7mSo4uAv2b7bjs371KCx6GILDocvJkHmKzcXVYTAE6yD36thpkNVW7VgEH9wCORtsBuWJ90Nit2Y7/OKt+3lh8Q6mn9yFkzprUkDVusW6Df8cXsDZHUu5Y2U0Uz+PZ1x6Gf/Tr4h+ccd2CTG3VJi5I5znt4aTU+piQLzNPu8uzg54l6DhyRV8OP4A962J4qktkSzY5+ZfwwvoGdtG0j00RIIgvoudepwJJ06DnYvgu09tZvn599rtgsNs63+X0TYnV8dh4I4IbNlVq6JBVluTvwPm/x+smwmxneHiGfZ252b8r15QWsGtM9dwQlIkv5/Yp9mOq1Sgje9QzqiUPJ7fGsGTmyM4e14CgxMquPiEEk5PLyclrP40CPtLhQX7Qpm72838vaF4jDAquZyHhhUwOqUCEViy3U8n04CoEMNfhxQyPr2M21bEcO78BG4fcJjLu5UEPAj0u9Ao6DnBTgBFeTY1xM5Fdlpwv239CgqxrVuZTtb5TiMgLCawZVctmgZZbcXhXFjwACx/DoKCYcxtcMpvm/1XlzGGu99dz95DJcz85SjC3W39GoNqbyKCbYb4n3ctYeaOMF7bHs7/rrBfpF2jPfSL85AWVkVCaBXlVVDsEXYWudhSEMz2QhcGITmskqt7FDMts7TFJwMd16GcjxLyuG15DHetjuazbDf3Dy1sMKBs0yIToc85dgKbIuL7JU7QtRgWPwIL/+lkpD/R9uXqNNwGXceQzFm1XRpktXbFB2DJk/DVY1BRAiddBj/5/XGlZajPswu3M2vVbm4a10MvE6o2Lc5tuKZnCVf3KGHdwWAW57hZkhvCmgPBfFzioqzKNve4gwwZEZX0jPFwfudSTk8rp2+cp8UkOW2M5DDDc6MP8fJ34dy3JoqzPk7g/qEFjO/QxlI9HKuwWOh5pp3AdqLPWmYDrp2LYdXLsPQpuy4m40jA1Wm4TR3h0vyB7ZUGWa1VwV7bWXP581BRBH0nw9g/QlIPn73kZ5tz+MsHG5nQL5WbxvnudZRqSUTgxHgPJ8Z7+IVzU64xUFoJbhe4WlEwVR8RuLx7CSenlHPT0hiuWRzHz7qWcOeAwraTwLS5uCNtnsGup9nnlR6bfX7XEmdaCuvftuuCwyFjiA24Oo+0/boiEgJTbuV3+qfT2uxdY+8YXPM6VFXCiVPtZcEU3/aNWpt1iN/MWEXvtBj+edEgvZtQtWsiEN5G/3v2iKnk7dPz+cf6SJ7eEskX2W7uHVTIOG3VqpsrGDoMstOIX9hlh3YfCbh2LYHF/4aFD9l1ST29WrtGQGKP485ZqFqmNvpvoo3xlMGGd2HZM/aPNTgcBl8Ko34DCb7Psr7q+3wuf24pMeEhPDN9KBFu/dgo1ZaFuuD2AUWc0aGc21dGc/XiOCZmlHJXj1LSYjWPVKPEZkDsBdD/Avu8vBj2rLKDW+9aCpveh1X/tetCY2yAljHETh1OgpgOmpm+DdBvy5bKGMhaDmteg3WzoOQAJHS1ua4G/cwm2fODr7flcc2Ly0mIdPPqdSPpEBful9dVSgXesKQK3h9/gP9sieDfGyL58qEv+N2ZPblsZBeCXdry0iTuCHtXYuZo+9wYyNtqfzjvXgm7V8DiR6HKyc8WleYEXYOdwGuw3/7vq+ajQVZLYgzs/cb+wlk3Ew5ss3laek2CwT+HrmP91qRsjOG5RTv46wcb6ZwYwYxrRuovWKXaIXeQvdvynI5l/HFbb+55bwMvf7WTWyf04qz+aYi2thwbEduHNqmHvTIBUFFq+3btXuFMK2Hz+0f2Sexug63qcRjTBtg7IVWLpUFWoJUX2Xwsmz+CzR9CQZa9LbjLaDj1d9DnPL/nYcktLOOu2ev4YG02E/ql8sC0gcSE6d0xSrVnXaIqefHKYczbmMP9H23il6+spG96DL86vRsT+6fj0n6axy8kDDoOtVO1koP2MuPuFfZxxyI7Dm216A5OwOVMqf1tN5JmGtlDHR8NsvytvBj2roYdC2Hb5/bafFWF7WfVbSyc/gfoeRZEJvm9aJ7KKl5d+j33z91MaUUlv5/Ym1+M6aq/VJVSAIgIZ/RNZWzvFGatzOKJL77jxhmr6JK4mUtHdGHqkI7ER7oDXcy2JTzOjqvY7fQjy4ryYN9ayK6e1sHWeWCcnGyuUNvqldzLDoad3NM+JnSDYH1//EmDLF/ylEHuJti33jb7Zi2zTcFVHkAgfQCM/CV0/Ql0HhWw4RpKyit5c8Uunl6wjaz8Ek7pnsQ9k/vRLVlHp1dK/ZgrSJg2tBMXnNSRueuzeX7Rdu77YCMPfLyZcb1TOHdgB8b2TiEsRFtTfCIy8egUEmAvNeZust8xuZth/xbYs9JJJWHsNuKyrVzxJziPmXY+PtNOOmRQs2tUkCUiZwH/AlzAM8aYv9VYL876SUAxcIUxZmVj9m31jIGSfNt/Ku8725ExbyvkbLQf8upfFu5oyDgJRt9s86R0Gh7QXCnF5R6WbDvAe2v28PH6fRwu83BS5zjuOrcf4/ukaOuVUqpBriBh0onpTDoxnU3ZBby2dBdz1uzhw3XZhAYHMbJrIj/pmcywzAT6pEdrZ3lfCgk7kkbCW3kx5H0LuVtsELZ/ix1+bdcSKCs4etuoVIjrYu9srJ6i04+e1wGzm6TBIEtEXMBjwBlAFrBMRGYbYzZ4bTYR6OFMI4AngBGN3LdlqiiBov1QvN82zRblOvPOVLgHDmXZqaL4yH4SBHGdbdNs77MhtZ+9Tp7QNWDXyI0xrN51kC37CtmUXciarEN8s+sgnipDdFgwk05MY+qQTgzLjNfgSil1THqnxXD3ef248+w+LNl+gHkb9/HF5lzunWP/3Ue4XfRJj6FXWjTdk6NIiw0jNSaMtNgwUqJDCaknAPNUQbDGZ8fGHQHpA+3krbqBIH87HNhuA6/87ZC/07aGffuJTXRdU3iC7c4SkXhk+uF5km08CI22aSlCo22fYndUu+0j1piWrOHAVmPMNgAReQ2YDHgHSpOBl4wxBvhaROJEJB3IbMS+/vfF/bblqfyw7XheXgRlh49+7impfd+gEPuBik63gVT3M+xYVXFd7DXw+MwWd81bRLj2peXsP1xOeIiL3unRXDumKyO7JjKyawKhwe3zw6+Uan7BriBGd09idPckOBd2Hyxhxc58Vu7MZ8PeAt5fs5dDJRVH7SMCESEuXEFCiCsIV5Dg8iRSWikUeYSu0ZV8dMaBAJ1RGyViA6KIBJsioiZjbEtXwR47Fe51HrOhOM9OB7bZfsXFeUeu2tTFHe0EX1H2rvmQcDsFh9tWuB8ew2xjRZDLjsMrLjtf/fjDfPCRwM0Y+/pVlfbRVDnzVfZYY25p/vprpMYEWRnALq/nWdjWqoa2yWjkvv63Y6GN3N2RR6aIJPsYGgUhEbazYWSyXR6ZbAOryCQbnbfC1p4nLx1CcnQoneIjNFu7UspvMuLCyYgL57yBHQDbsp5fXEH2oVL2FZSSXVDK3kOlFJd58FQZPFVVVFYZPDlbCHMZooINHSLa8WDVgSJix2wMi214RBFjoPSgHUu3+IANzsoKoKwQSp1H72UVpbYho7zYBmgVpeAptVeQPGVHB0xVnuM7j+CwFh9k1faNbBq5TWP2tQcQuQ64znl6WEQ2N6JsbUESsD/QhWhjtE59Q+vVN1pRvV4VsFe+vOm7NKFeA3derVAr+rwCFMAf/dKw0KW2hY0JsrKATl7POwJ7GrmNuxH7AmCMeRp4uhHlaVNEZLkxZmjDW6rG0jr1Da1X39B69Q2tV9/Qem2axnQlXAb0EJETRMQNXAzMrrHNbOBysUYCh4wxexu5r1JKKaVUm9NgS5YxxiMiNwJzsWkYnjPGrBeR6531TwIfYNM3bMWmcLiyvn19ciZKKaWUUi1Io/JkGWM+wAZS3sue9Jo3wA2N3Vcdpd1dIvUDrVPf0Hr1Da1X39B69Q2t1yYQGx8ppZRSSqnmpOndlFJKKaV8QIOsABCRaSKyXkSqRGRojXV/EJGtIrJZRCYEqoytlYic5dTdVhH5faDL01qJyHMikiMi67yWJYjIJyLyrfMYH8gytjYi0klEPhORjc7f/03Ocq3X4yAiYSKyVES+cer1Hme51mszEBGXiKwSkTnOc63XJtAgKzDWARcAC7wXikhf7B2Y/YCzgMedoYlUI3gN4zQR6Atc4tSparoXsJ9Bb78H5htjegDzneeq8TzA74wxfYCRwA3O51Pr9fiUAWONMQOBQcBZzl3uWq/N4yZgo9dzrdcm0CArAIwxG40xtSVbnQy8ZowpM8Zsx96tOdy/pWvVfhgCyhhTDlQP46SayBizAKg5jslk4EVn/kVgil8L1coZY/YaY1Y684XYL64MtF6Pi7EOO09DnMmg9XrcRKQjcDbwjNdirdcm0CCrZalreCLVOFp/vpXq5L/DeUwJcHlaLRHJBAYDS9B6PW7OJa3VQA7wiTFG67V5PAzcBniPa6T12gSNSuGgmk5E5gFptay6wxjzbl271bJMb/9sPK0/1eKJSBTwFnCzMaZAWuFYqC2NMaYSGCQiccDbItI/0GVq7UTkHCDHGLNCRE4LdHlaKw2yfMQYM/4YdmvMEEaqblp/vrVPRNKNMXtFJB3baqCaQERCsAHWK8aYWc5irddmYow5KCKfY/sTar0en9HAeSIyCQgDYkTkv2i9NoleLmxZZgMXi0ioiJwA9ACWBrhMrYkO4+Rbs4Hpzvx0oK4WWVULsU1WzwIbjTEPea3Sej0OIpLstGAhIuHAeGATWq/HxRjzB2NMR2NMJvZ/6afGmEvRem0STUYaACJyPvAIkAwcBFYbYyY46+7ADgnvwV5O+DBgBW2FnF9dD3NkGKf7AlykVklEXgVOA5KAfcBdwDvAG0Bn4HtgmjGmZud4VQcROQX4EljLkT4ut2P7ZWm9HiMRGYDtgO3CNhy8YYy5V0QS0XptFs7lwluMMedovTaNBllKKaWUUj6glwuVUkoppXxAgyyllFJKKR/QIEsppZRSygc0yFJKKaWU8gENspRSSimlfECDLKX8QESMiLzs9TxYRHK9RrY/T0QaPdCqiNwrIseS8La+Y14vIpc3w3HuFpFbalk+pTkG7BaRHSKS1ITtTxWR9SKy2smjdKyvO9h5Hyd4LQsVkXnOsS+qZZ9mf5/8SUROE5FR9axv0udWqfZGM74r5R9FQH8RCTfGlABnALurVxpjZtOExKnGmD81dwGNMU829zFrmALMATbUXCEiwcYYj49e9+fAg8aY5xuzsYi4nGFaaroEWOg8znWWDQZCjDGD6jhOs79PfnYacBhYXHOF85416XOrVHujLVlK+c+H2BHtwX5Rv1q9QkSuEJFHnflpIrJORL4RkQW1HUhEXhCRqc78DhG5R0RWishaEektIkHO8jivfbaKSKqIdBGR+SKyxnns7Kz/oQVKRLo7LTTfOMft5iy/VUSWOfve43XsO0RkszNmZ69ayjsKOA94wGn16SYin4vIX0TkC+AmETlXRJaIyCrntVOdfRNF5GNn+VN4jVEpIpeKyFLnmE+JiKvG614DXAj8SUReEesBp37XVrc+OS02n4nIDGyy0JrlF2AqcAVwpoiEiUgK8F/smHnV57RDRP4kIguBaTXep2Eistip06UiEi0imSLypVPHK6tbjZzyfC4iM0VkU3XZaynXj96nBs5xjte+j4rIFfV8hjKB64HfOud3qnM+D4nIZ8Dfa3xuk0XkLefzsUxERjvLf+Lsv9p5D6NrnodSbZYxRieddPLxhG0NGADMxI4DthrbSjDHWX8F8KgzvxbIcObj6jjeC8BUZ34H8Gtn/lfAM878v4ArnfkRwDxn/j1gujN/FfCOM383Nqsz2Czk5zvzYUAEcCbwNDbICcK2So0BhjhljgBigK3Vx6mrzM7zz4HHvZ7HcyRB8jXAP5z5fwN/cubPxg76nQT0cc4lxFn3OHB5A3X1U+ATbHbwVGzG6nTnvSgCTqijvk8B5jvzM4ALnPkf3kOv9+K2mq8NuIFtwDBneQz2SkIEEOYs6wEs9zruIez4m0HAV8AptZSrtvepvnP0LuujwBUNfIZ++Ex4nc8cwFXL53ZGdRmx2cA3en3eRjvzUUBwoP8eddLJX5NeLlTKT4wxa5zWgUuAD+rZdBHwgoi8AcyqZztv1dutAC5w5l8H/gQ8jx177HVn+cle27wM3O99IKelIcMY87ZT7lJn+ZnYQGuVs2kUNjCIBt42xhQ72zXl8tHrXvMdgdfFDjrrBrY7y8dUl9cY876I5DvLx2EDvGVOI084DQ9WewrwqrGXA/c5rWjDgAJgqTFmex37XQK85sy/BlxG3e/N67Us6wXsNcYsc86jAEBEIoFHRWQQUAn09NpnqTEmy9luNZCJvVyJs6yu96m+c6xPbZ+h2rxpar+cOh7o69XgFuOUcRHwkIi8AsyqPiel2gMNspTyr9nAg9hWhcTaNjDGXC8iI7CtNqudL+AHsf1/9hhjJtWyW5nzWMmRv+uvgO4ikoztD/XnOspUc2ytH12W8lr+V2PMU0ctFLm5lmM0VpHX/CPAQ8aY2WLHSru7njJWl+dFY8wfmvB6dZ1bzbIc2cFegvwpcJ7YsUUFSKznsldtxxFqP4ffYseGHIhtsSr1WlfmNe/9vnofs9Yi17Hcw9FdRMJqrK/tM1SbWuvJOfbJxvY59PY3EXkfmAR8LSLjjTGb6jm+Um2G9slSyr+eA+41xvyo3081EelmjFlibKfp/UAnY8yVxphBdQRYtTLGGOBt4CHspZs8Z9VibMsW2E7hC2vsVwBkicgUpzyhIhKB7ex9lYhEOcsznH5JC4DzRSTcCTzOraNIhdhWr7rEcuRmgOleyxc45UREJmIvKwLMB6Y6ZUBEEkSkSz3Hrz7WRSLicoLPMcDSBvYZD3xjjOlkjMk0xnQB3sIGro21CeggIsOcskaLSDD2nPcaY6qwrWOueo5xlHrep7rOcSe2pSlURGKxLYENaeg98/YxcGP1E+fHQfXnea0x5u/AcqB3I4+nVKunQZZSfmSMyTLG/KuBzR5wOh+vw35hfnMcL/k6cClHX8L6DXCliKzBfrHfVMt+lwG/cbZZDKQZYz7G9rv5SkTWYvuXRRtjVjrHX40NPr6soyyvAbc6nZ+71bL+buBNEfkSG1xWuwcYIyIrsZcrvwcwxmwA7gQ+dsr5CbbvUX3eBtZg6/RTbP+p7AYqKepEAAAAtUlEQVT2ucTZz9tbwM8a2O8Hxphy4CLgERH5xilrGLYf2XQR+Rp7qbCuVqK6/Oh9oo5zNMbsAt5w1r3Ckcu+9XkPG0CvFpFTG9j2N8BQsTdFbMB2mge42emE/w1Qgr0BRKl2obqTqVJKKaWUakbakqWUUkop5QMaZCmllFJK+YAGWUoppZRSPqBBllJKKaWUD2iQpZRSSinlAxpkKaWUUkr5gAZZSimllFI+oEGWUkoppZQP/D8MUccAK+5u2gAAAABJRU5ErkJggg==\n",
"text/plain": [
"
"
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"# Import data on mis-invoiced trade aggregated by destination and sector for each African country\n",
"IFF_Year = pd.read_csv('Data/GER_Orig_Year_Africa.csv')\n",
"\n",
"# Restrict data to 2016 as an illustrative example\n",
"IFF_Year = IFF_Year.query('year == \"2016\"')\n",
"\n",
"# Plot distribution of proportional mis-invoiced imports for each African country\n",
"sns.distplot(IFF_Year['Tot_IFF_hi_GDP'].apply(lambda x: x*100), \n",
" kde=True, label='% GDP', bins=10);\n",
"sns.distplot(IFF_Year['Tot_IFF_hi_trade'].apply(lambda x: x*100),\n",
" kde=True, label='% trade', bins=10);\n",
"plt.legend()\n",
"plt.title('Distribution of IFF in Africa in 2016')\n",
"plt.xlabel('Mis-invoiced trade for African countries');"
]
},
{
"cell_type": "code",
"execution_count": 93,
"metadata": {
"slideshow": {
"slide_type": "subslide"
},
"tags": [
"remove-input"
]
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Mean outflow as proportion of GDP: 0.06371070220761896 \n",
"Mean outflow as proportion of trade 0.006736362224603777\n"
]
}
],
"source": [
"print('Mean outflow as proportion of GDP:',IFF_Year['Tot_IFF_hi_GDP'].mean(),\n",
" '\\nMean outflow as proportion of trade', IFF_Year['Tot_IFF_hi_trade'].var())"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"source": [
"Those countries that experience disproportionately high outflows can be considered as \"conduits\" on which we can perform the network analysis.\n",
"\n",
"We can use the figure above to inform our choice of thresholds for the proportion of IFF relative to GDP and trade, respectively, above which countries are considered conduits. Those thresholds are assigned to the variables `thresh_GDP` and `thresh_trade`, respectively."
]
},
{
"cell_type": "code",
"execution_count": 94,
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"outputs": [],
"source": [
"thresh_GDP = 0.1\n",
"thresh_trade = 0.17\n",
"conduits_GDP = IFF_Year.query('Tot_IFF_hi_GDP >= @thresh_GDP').set_index('reporter.ISO')\n",
"conduits_trade = IFF_Year.query('Tot_IFF_hi_trade >= @thresh_trade').set_index('reporter.ISO')"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"source": [
"The conduit countries respective to GDP are the Seychelles, where illicit outflows represented 22% of GDP in 2016, followed by Mozambique, Mali, and Tunisia."
]
},
{
"cell_type": "code",
"execution_count": 95,
"metadata": {
"slideshow": {
"slide_type": "subslide"
},
"tags": [
"remove-input"
]
},
"outputs": [
{
"data": {
"text/html": [
"
\n",
"\n",
"
\n",
" \n",
"
\n",
"
\n",
"
reporter
\n",
"
year
\n",
"
Tot_IFF_hi_GDP
\n",
"
GDP
\n",
"
\n",
"
\n",
"
reporter.ISO
\n",
"
\n",
"
\n",
"
\n",
"
\n",
"
\n",
" \n",
" \n",
"
\n",
"
MLI
\n",
"
Mali
\n",
"
2016
\n",
"
0.102023
\n",
"
1.401079e+10
\n",
"
\n",
"
\n",
"
MOZ
\n",
"
Mozambique
\n",
"
2016
\n",
"
0.141781
\n",
"
1.098136e+10
\n",
"
\n",
"
\n",
"
SYC
\n",
"
Seychelles
\n",
"
2016
\n",
"
0.216881
\n",
"
1.427525e+09
\n",
"
\n",
"
\n",
"
TUN
\n",
"
Tunisia
\n",
"
2016
\n",
"
0.100490
\n",
"
4.180838e+10
\n",
"
\n",
" \n",
"
\n",
"
"
],
"text/plain": [
" reporter year Tot_IFF_hi_GDP GDP\n",
"reporter.ISO \n",
"MLI Mali 2016 0.102023 1.401079e+10\n",
"MOZ Mozambique 2016 0.141781 1.098136e+10\n",
"SYC Seychelles 2016 0.216881 1.427525e+09\n",
"TUN Tunisia 2016 0.100490 4.180838e+10"
]
},
"execution_count": 95,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"conduits_GDP[['reporter', 'year', 'Tot_IFF_hi_GDP', 'GDP']]"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"source": [
"The countries which experienced the highest level of mis-invoicing relative to their trading activity in 2016 were Burundi, where up to 31% of trade was illicit, followed by Uganda and Mali. \n",
"Mali and Mozambique are conduit countries both when considering outflows relative to GDP and relative to trade openness."
]
},
{
"cell_type": "code",
"execution_count": 96,
"metadata": {
"slideshow": {
"slide_type": "subslide"
},
"tags": [
"remove-input"
]
},
"outputs": [
{
"data": {
"text/html": [
"
\n",
"\n",
"
\n",
" \n",
"
\n",
"
\n",
"
reporter
\n",
"
year
\n",
"
Tot_IFF_hi_trade
\n",
"
Total_value
\n",
"
\n",
"
\n",
"
reporter.ISO
\n",
"
\n",
"
\n",
"
\n",
"
\n",
"
\n",
" \n",
" \n",
"
\n",
"
DZA
\n",
"
Algeria
\n",
"
2016
\n",
"
0.175611
\n",
"
77082785056
\n",
"
\n",
"
\n",
"
BDI
\n",
"
Burundi
\n",
"
2016
\n",
"
0.312707
\n",
"
754378325
\n",
"
\n",
"
\n",
"
MLI
\n",
"
Mali
\n",
"
2016
\n",
"
0.210566
\n",
"
6788467564
\n",
"
\n",
"
\n",
"
MOZ
\n",
"
Mozambique
\n",
"
2016
\n",
"
0.180047
\n",
"
8647421818
\n",
"
\n",
"
\n",
"
NGA
\n",
"
Nigeria
\n",
"
2016
\n",
"
0.179441
\n",
"
68077346474
\n",
"
\n",
"
\n",
"
STP
\n",
"
São Tomé and Príncipe
\n",
"
2016
\n",
"
0.204593
\n",
"
149825956
\n",
"
\n",
"
\n",
"
UGA
\n",
"
Uganda
\n",
"
2016
\n",
"
0.233074
\n",
"
7802352503
\n",
"
\n",
" \n",
"
\n",
"
"
],
"text/plain": [
" reporter year Tot_IFF_hi_trade Total_value\n",
"reporter.ISO \n",
"DZA Algeria 2016 0.175611 77082785056\n",
"BDI Burundi 2016 0.312707 754378325\n",
"MLI Mali 2016 0.210566 6788467564\n",
"MOZ Mozambique 2016 0.180047 8647421818\n",
"NGA Nigeria 2016 0.179441 68077346474\n",
"STP São Tomé and Príncipe 2016 0.204593 149825956\n",
"UGA Uganda 2016 0.233074 7802352503"
]
},
"execution_count": 96,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"conduits_trade[['reporter', 'year', 'Tot_IFF_hi_trade', 'Total_value']]"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"source": [
"Finally, in addition to restricting our graph to certain conduit countries where the capital flows out of, we should also threshold on the partner countries to which the mis-invoiced capital flows in to. The figure below illustrates the distribution of illicit *inflows* as a proportion of their GDP for each partner country included in our bilateral flow data. That is, the weight on the edge from reporter $i$ to partner $j$ is relative to each partner $j$'s GDP in the chosen year. The magnitudes are smaller than the previous figure which considers the distribution of illicit *outflows* for each reporter $i$ aggregated over all partners $j$."
]
},
{
"cell_type": "code",
"execution_count": 97,
"metadata": {
"slideshow": {
"slide_type": "slide"
},
"tags": [
"hide-input"
]
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAlwAAAGDCAYAAAD+nM7XAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4yLjEsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy+j8jraAAAgAElEQVR4nO3debhdZX33//eHhEkBmQJCmBVQQEWhir864KOtQ7VgqxWqgkOL9tFaq+1TrbailacOVZ9a6wCVggMoKgjiBOKAA4IBGQJCZQgQghBAmYRAku/vj3Uf2DnsMyTnrCQnvl/Xta+zzr2me+211t6ffa977Z2qQpIkSf1Zb01XQJIkaV1n4JIkSeqZgUuSJKlnBi5JkqSeGbgkSZJ6ZuCSJEnqmYFLvUnyyST/NE3L2inJXUlmtf+/n+QvpmPZbXnfTHL4dC1vJdb73iS3JPnValrfy5OcsTrWpZXTju/d1vZlrglJXpfk/40zfkGS5/Sw3uOSvHd1r3esOiR5fJKf9Lk+9cfApVXSXmjuSXJnkt8k+UmS1yd54JiqqtdX1b9MclnjvmhV1XVVtUlVLZuGuh+Z5HOjlv/8qjp+qsteyXrsCLwV2KuqHjlk/IFJFg78//0k97Y30ZHHU9u4SnL3QPlvhq2zqj5fVX/Y1zatjCSvSvKjNV2Pvk32w0E7vq+eznWv6jKT7JHk1CSLk9yW5NtJ9hw1zd8m+VWS25Mcm2TDgXFvTDIvyZIkxw1Z/sOSfLx92Lg9ydnj1GUD4J3AB1d2O9Y1VXUx8JskL1rTddHKM3BpKl5UVZsCOwPvA/4B+PR0ryTJ7Ole5lpiZ+DWqrp5JeZ5Y3sTHXmcMzDuCQPlm09zXafV6tinI62ha7u19PjeHDgN2BPYFjgPOHVkZJLnAm8Dng3sAuwGvHtg/kXAe4Fjx1j+0cCWwGPb378dpy4HAZdX1Q2rsB3ros8Dr1vTldDKM3Bpyqrq9qo6DXgZcHiSfeAhTeFbJzm9tYbdluSHSdZL8llgJ+BrrWXm/yTZpbXYvDbJdcB3B8oG35weleS89gn51CRbtnWt0DLUyhYkeU6S5wH/CLysre+iNv6BVohWr3cmuTbJzUk+k+QRbdxIPQ5Pcl37hP6OsZ6bJI9o8y9uy3tnW/5zgDOB7Vs9jpuGXTGh0a1KbVten+SXSX6d5D+TZIx5j0zy5SRfbC2bFyR5wsD4tyW5qo27LMmLR633x0k+kuQ24IvAJ4GnDrbItWPmP5N8vS3n3CSPGljOY5Kc2Y6hK5L82cC445J8Isk3ktwNPGvINmyZ5L+TLGrb+9WBcX+Z5Mq27NOSbN/KH3LsjTpeXpXkR0n+rS3zmiTPb+OOAp4OfKxt58cGnvc3JPkl8MuBske34Q3b8q5LclO6y/Mbt3FDz6Ux9tngMsd9bgdV1XlV9emquq2q7gc+AuyZZKs2yeHAp6vq0qr6NfAvwKsG5j+5qr4K3DqkTnsCfwwcUVWLq2pZVZ0/rB7N84EfjFrGK9v5dOvg+ZfkkUl+O1BPkuzXzr/1kzwqyXfbfLck+XySzQemfWI7ru9M8kVgo3HqNXq71hs4B25NclIefE36VpI3jpr+oiR/0obHPK6H+D7w7Ay0KGpmMHBp2lTVecBCujeY0d7axs2h+8T8j90s9UrgOrrWsk2q6gMD8zyT7hPwc8dY5WHAa4DtgaXARydRx28B/xf4YlvfE4ZM9qr2eBbdJ/dNgI+NmuZpdJ/+nw38c5LHjrHK/wAe0ZbzzFbnV1fVd+jeSBa1erxqorr36IXA7wFPAP6MsZ9v6FobvkTXKnEC8NUk67dxV9Ht+0fQtXZ8Lsl2A/M+Bbga2AZ4BfB64JwhLXKHtvm3AK4EjgJI8nC6kHpCW8ahwMeT7D0w75+36TcFhl2u/CzwMGDvtoyPtGX/L+Bf2/ZvB1wLfGGc52G0pwBXAFsDHwA+nSRV9Q7ghzzYMjn4pntwm2+vIct7P7AHsC/waGAu8M9t3NBzaZL1HPrcTsIzgF9V1UiA2hu4aGD8RcC2g0FnHE+he37f3ULPJUn+dJzpH0f33AKQZC/gE8Ar6c79rYAdAKrqV3SBZDCwvAL4QguOodvP29O9tuwIHNmWuwHwVbpjZEu643y8eo32Jrp9+sy2/F8D/9nGnUD33A9uw87A1yd5XD+gtfTdT/f6oxnEwKXptojuxWq0++neyHauqvur6oc18Q95HllVd1fVPWOM/2xVza+qu4F/Av4s03MZ6eXAh6vq6qq6C3g7cEhWbF17d1XdU1UX0b3ZPCS4tbq8DHh7Vd1ZVQuAD9G9Uayqj7aWjd8kuWDUuAsGxk0YPge8r6p+U1XXAd+je5Mfy/lV9eX25vVhuhaAAwCq6ktVtaiqllfVF+labp48MO+iqvqPqlo6zj4FOLm1sCylu3wyUp8XAguq6r/bMi4AvgK8ZGDeU6vqx60O9w4utIW/5wOvr6pft+NwpOXk5cCxVXVBVS2h2+dPTbLLOPUcdG1VHdP6GB5Pd6xvO8E8/9pakFZ4LpIE+Evgb9v4O+k+JBzSJlmVc2nEWM/tmJLsQBcc3jJQvAlw+8D/I8ObTqIOOwD7tHm2B94IHD/Oh5bNgTsH/n8JcHpVnd321T8BywfGH08XskbOwUPpQhRVdWVVnVlVS6pqMd0x/Mw23wHA+sD/a8/rl4GfTWJ7RrwOeEdVLWz1OhJ4SXvdOAXYN8nObdqX0+2LJUzuuB7tzva8aAYxcGm6zQVuG1L+QbpP1GckuTrJ2yaxrOtXYvy1dC+WW0+qluPbvi1vcNmzWfENdPCuwt/SvQGNtjWwwZBlzZ1C3d5UVZu3x5NGjXvSwLg3rcQyJ7MtIx54zqtqOV1Ly8ilt8OSXDgS+ujeVLceNu8q1mdn4CkDofI3dG9cgzccjLeOHYHb2iWw0VbY5y1o38rk99UDda6q37bB8Z5HGLuuc+ha4c4f2M5vtXJYtXPpIfVk4n1NkjnAGcDHq+rEgVF3AZsN/D8yPBiMxnIPXWh8b1Xd10Lv94Cxbub4NSsGue1Z8Ti8mxUvXZ4K7JXu7sw/AG5vre8k2SbJF5LckOQO4HM8eIxuD9wwKrw+cEyku5N55KaUlw+p587AKQP77BfAMmDbFpq/zoOh+RC6wDsy30TH9WibAkNvjNHay8ClaZPk9+jeoB5yKae18Ly1qnYDXgS8JcmzR0aPsciJPrXvODC8E92L+C3A3XRvWCP1msWDb1aTWe4iuhfBwWUvBW6aYL7Rbml1Gr2smdz594HnvPUb2gFY1D65H0PXWrFVu0Q4n+4SzojRz/tkW2VGXA/8YCBUbt4u0/3VJJd5PbDlYJ+dASvs83aZZyu6fXV3K37YwPTjvRmOtrLH9y10oWTvge18RFVtAhOeS9MmyRZ0Yeu0qhp96fFSVmzVfQJw08Alx/FcvJJVuZju8uqIG1nxOHwY3b4CoLVsnkQXWl5Ja91q/pXueX98VW1G1xI2cozeCMxtLYwjdhpY7vPrwZtSPs9DXQ88f9TxuVE92Nn/RODQdHcWb0wXMkfmm+i4fkC6voUbMHCZVTODgUtTlmSzJC+k6/Pyuaq6ZMg0L0zy6PZidgfdJ7+Rr3i4ia6P08p6RZK92gvue4Avt0s6/wNslOSPWv+idwKDHUxvAnbJGB2N6V4Y/zbJrkk24cE+X0tXpnKtLicBRyXZtIWSt9B9qp6p9kvyJ+0yyZuBJcBPgYfTvZEtBkjyaroWrvHcBOzQ+s5MxunAHuk6TK/fHr83zqWoFVTVjcA36frHbNHmf0YbfQLw6iT7ts7I/xc4t6oWtEtPN9Adb7OSvAYY2tl8nO2c9PHdWg6PAT6SZBuAJHPT3Rk40bk0LZJsBnwb+HFVDWtB+wzw2nb+bUF3jh03MP/sJBsBs4BZSTYauCR/Nl2/zbe36X4fOLCtb5hv8OBlP4AvAy9M8rR27LyHh76XfYauH+Yfs+L5tild69xvkswF/n5g3Dl0H6ze1Or1J6x4SXwin6Q713eGrnUwyUGjtmPnVt8vtv0MK39cHwh8t12O1Axi4NJUfC3JnXSf0N5B1x/i1WNMuzvwHboXu3PoLlF8v437V+CdrTn971Zi/Z+le5H/FV1fojdBd9ck8L+B/+LBForBuxa/1P7eOqQfFHS3sn+W7o3hGuBe4K9Xol6D/rqt/2q6lr8TGPtW+ZngVLp+ab+maz34k9bf5TK6/mnn0AWMxwE/nmBZ36VrKflVklsmWnG7LPOHdJdjFtHt9/ezYpieyCvpWh0vB26mC41U1Vl0fYG+QtfS8SgevPwDXZ+qv6e7dLU3sDJfPvnvdH15fr0Sfev+ge6y4U/bpa/v8GAn6fHOpenyYrobKV6dFb/3bSd44OaTD9C10lzbHu8amP+ddK10b6NrRbqnldH6/x0EvICuH9cxwGFVdfkYdfka8JjWskNVXQq8ge5cupHuWFzhruSq+jFdv64Lqus7OeLdwJPaer8OnDwwz33An9AFtV/THecnM3n/TvdVGme018Wf0t0gMLL8JW15z2l1Hylf2eP65XThTjNMJt/XUtLvsiRHAo+uqles6brod0uSI+i+IPjNKzHPd4ETquq/+qvZ6pXkccDRVfXUNV0Xrby18Qv3JEl6QFUdvTLTt/6kT6JrSVtntO4ahq0ZykuKkqR1RpLj6S65vrldrpPWCl5SlCRJ6pktXJIkST0zcEmSJPVsre80v/XWW9cuu+yypqshSZI0ofPPP/+WqpozunytD1y77LIL8+bNW9PVkCRJmlCSa4eVe0lRkiSpZwYuSZKknhm4JEmSembgkiRJ6pmBS5IkqWcGLkmSpJ4ZuCRJknpm4JIkSeqZgUuSJKlnBi5JkqSeGbgkSZJ6NmHgSrJjku8l+UWSS5P8TSvfMsmZSX7Z/m4xMM/bk1yZ5Iokzx0o3y/JJW3cR5Okn82SJElae0ymhWsp8NaqeixwAPCGJHsBbwPOqqrdgbPa/7RxhwB7A88DPp5kVlvWJ4AjgN3b43nTuC2SJElrpdkTTVBVNwI3tuE7k/wCmAscBBzYJjse+D7wD638C1W1BLgmyZXAk5MsADarqnMAknwGOBj45jRuzyo74dzrJjXdnz9lp55rIkmS1jUr1YcryS7AE4FzgW1bGBsJZdu0yeYC1w/MtrCVzW3Do8slSZLWaZMOXEk2Ab4CvLmq7hhv0iFlNU75sHUdkWReknmLFy+ebBUlSZLWSpMKXEnWpwtbn6+qk1vxTUm2a+O3A25u5QuBHQdm3wFY1Mp3GFL+EFV1dFXtX1X7z5kzZ7LbIkmStFaazF2KAT4N/KKqPjww6jTg8DZ8OHDqQPkhSTZMsitd5/jz2mXHO5Mc0JZ52MA8kiRJ66wJO80Dvw+8ErgkyYWt7B+B9wEnJXktcB3wUoCqujTJScBldHc4vqGqlrX5/go4DtiYrrP8WtFhXpIkqU+TuUvxRwzvfwXw7DHmOQo4akj5PGCflamgJEnSTOc3zUuSJPXMwCVJktQzA5ckSVLPDFySJEk9M3BJkiT1zMAlSZLUMwOXJElSzwxckiRJPTNwSZIk9czAJUmS1DMDlyRJUs8MXJIkST0zcEmSJPXMwCVJktQzA5ckSVLPDFySJEk9M3BJkiT1zMAlSZLUMwOXJElSzwxckiRJPTNwSZIk9czAJUmS1DMDlyRJUs8MXJIkST0zcEmSJPXMwCVJktQzA5ckSVLPDFySJEk9M3BJkiT1zMAlSZLUswkDV5Jjk9ycZP5A2ReTXNgeC5Jc2Mp3SXLPwLhPDsyzX5JLklyZ5KNJ0s8mSZIkrV1mT2Ka44CPAZ8ZKaiql40MJ/kQcPvA9FdV1b5DlvMJ4Ajgp8A3gOcB31z5KkuSJM0sE7ZwVdXZwG3DxrVWqj8DThxvGUm2AzarqnOqqujC28ErX11JkqSZZ6p9uJ4O3FRVvxwo2zXJz5P8IMnTW9lcYOHANAtb2VBJjkgyL8m8xYsXT7GKkiRJa9ZUA9ehrNi6dSOwU1U9EXgLcEKSzYBh/bVqrIVW1dFVtX9V7T9nzpwpVlGSJGnNmkwfrqGSzAb+BNhvpKyqlgBL2vD5Sa4C9qBr0dphYPYdgEWrum5JkqSZZCotXM8BLq+qBy4VJpmTZFYb3g3YHbi6qm4E7kxyQOv3dRhw6hTWLUmSNGNM5mshTgTOAfZMsjDJa9uoQ3hoZ/lnABcnuQj4MvD6qhrpcP9XwH8BVwJX4R2KkiTpd8SElxSr6tAxyl81pOwrwFfGmH4esM9K1k+SJGnG85vmJUmSembgkiRJ6pmBS5IkqWcGLkmSpJ4ZuCRJknpm4JIkSeqZgUuSJKlnBi5JkqSeGbgkSZJ6ZuCSJEnqmYFLkiSpZwYuSZKknhm4JEmSembgkiRJ6pmBS5IkqWcGLkmSpJ4ZuCRJknpm4JIkSeqZgUuSJKlnBi5JkqSeGbgkSZJ6ZuCSJEnqmYFLkiSpZwYuSZKknhm4JEmSembgkiRJ6pmBS5IkqWcGLkmSpJ4ZuCRJknpm4JIkSerZhIErybFJbk4yf6DsyCQ3JLmwPV4wMO7tSa5MckWS5w6U75fkkjbuo0ky/ZsjSZK09plMC9dxwPOGlH+kqvZtj28AJNkLOATYu83z8SSz2vSfAI4Adm+PYcuUJEla50wYuKrqbOC2SS7vIOALVbWkqq4BrgSenGQ7YLOqOqeqCvgMcPCqVlqSJGkmmUofrjcmubhdctyilc0Frh+YZmErm9uGR5cPleSIJPOSzFu8ePEUqihJkrTmrWrg+gTwKGBf4EbgQ618WL+sGqd8qKo6uqr2r6r958yZs4pVlCRJWjusUuCqqpuqallVLQeOAZ7cRi0EdhyYdAdgUSvfYUi5JEnSOm+VAlfrkzXixcDIHYynAYck2TDJrnSd48+rqhuBO5Mc0O5OPAw4dQr1liRJmjFmTzRBkhOBA4GtkywE3gUcmGRfusuCC4DXAVTVpUlOAi4DlgJvqKplbVF/RXfH48bAN9tDkiRpnTdh4KqqQ4cUf3qc6Y8CjhpSPg/YZ6VqJ0mStA7wm+YlSZJ6ZuCSJEnqmYFLkiSpZwYuSZKknhm4JEmSembgkiRJ6pmBS5IkqWcGLkmSpJ4ZuCRJknpm4JIkSeqZgUuSJKlnBi5JkqSeGbgkSZJ6ZuCSJEnqmYFLkiSpZwYuSZKknhm4JEmSembgkiRJ6pmBS5IkqWcGLkmSpJ4ZuCRJknpm4JIkSeqZgUuSJKlnBi5JkqSeGbgkSZJ6ZuCSJEnqmYFLkiSpZwYuSZKknhm4JEmSejZh4EpybJKbk8wfKPtgksuTXJzklCSbt/JdktyT5ML2+OTAPPsluSTJlUk+miT9bJIkSdLaZTItXMcBzxtVdiawT1U9Hvgf4O0D466qqn3b4/UD5Z8AjgB2b4/Ry5QkSVonTRi4qups4LZRZWdU1dL270+BHcZbRpLtgM2q6pyqKuAzwMGrVmVJkqSZZTr6cL0G+ObA/7sm+XmSHyR5eiubCywcmGZhK5MkSVrnzZ7KzEneASwFPt+KbgR2qqpbk+wHfDXJ3sCw/lo1znKPoLv8yE477TSVKkqSJK1xq9zCleRw4IXAy9tlQqpqSVXd2obPB64C9qBr0Rq87LgDsGisZVfV0VW1f1XtP2fOnFWtoiRJ0lphlQJXkucB/wD8cVX9dqB8TpJZbXg3us7xV1fVjcCdSQ5odyceBpw65dpLkiTNABNeUkxyInAgsHWShcC76O5K3BA4s327w0/bHYnPAN6TZCmwDHh9VY10uP8rujseN6br8zXY70uSJGmdNWHgqqpDhxR/eoxpvwJ8ZYxx84B9Vqp2kiRJ6wC/aV6SJKlnBi5JkqSeGbgkSZJ6ZuCSJEnqmYFLkiSpZwYuSZKknhm4JEmSembgkiRJ6pmBS5IkqWcGLkmSpJ4ZuCRJknpm4JIkSeqZgUuSJKlnBi5JkqSeGbgkSZJ6ZuCSJEnqmYFLkiSpZwYuSZKknhm4JEmSembgkiRJ6pmBS5IkqWcGLkmSpJ4ZuCRJknpm4JIkSeqZgUuSJKlnBi5JkqSeGbgkSZJ6ZuCSJEnqmYFLkiSpZwYuSZKknk0YuJIcm+TmJPMHyrZMcmaSX7a/WwyMe3uSK5NckeS5A+X7Jbmkjftokkz/5kiSJK19JtPCdRzwvFFlbwPOqqrdgbPa/yTZCzgE2LvN8/Eks9o8nwCOAHZvj9HLlCRJWidNGLiq6mzgtlHFBwHHt+HjgYMHyr9QVUuq6hrgSuDJSbYDNquqc6qqgM8MzCNJkrROW9U+XNtW1Y0A7e82rXwucP3AdAtb2dw2PLp8qCRHJJmXZN7ixYtXsYqSJElrh+nuND+sX1aNUz5UVR1dVftX1f5z5syZtspJkiStCasauG5qlwlpf29u5QuBHQem2wFY1Mp3GFIuSZK0zlvVwHUacHgbPhw4daD8kCQbJtmVrnP8ee2y451JDmh3Jx42MI8kSdI6bfZEEyQ5ETgQ2DrJQuBdwPuAk5K8FrgOeClAVV2a5CTgMmAp8IaqWtYW9Vd0dzxuDHyzPSRJktZ5Ewauqjp0jFHPHmP6o4CjhpTPA/ZZqdpJkiStA/ymeUmSpJ4ZuCRJknpm4JIkSeqZgUuSJKlnBi5JkqSeGbgkSZJ6ZuCSJEnqmYFLkiSpZwYuSZKknhm4JEmSembgkiRJ6pmBS5IkqWcGLkmSpJ4ZuCRJknpm4JIkSeqZgUuSJKlnBi5JkqSeGbgkSZJ6ZuCSJEnqmYFLkiSpZwYuSZKknhm4JEmSembgkiRJ6pmBS5IkqWcGLkmSpJ4ZuCRJknpm4JIkSeqZgUuSJKlnBi5JkqSerXLgSrJnkgsHHnckeXOSI5PcMFD+goF53p7kyiRXJHnu9GyCJEnS2m32qs5YVVcA+wIkmQXcAJwCvBr4SFX92+D0SfYCDgH2BrYHvpNkj6patqp1kCRJmgmm65Lis4GrquracaY5CPhCVS2pqmuAK4EnT9P6JUmS1lrTFbgOAU4c+P+NSS5OcmySLVrZXOD6gWkWtjJJkqR12pQDV5INgD8GvtSKPgE8iu5y443Ah0YmHTJ7jbHMI5LMSzJv8eLFU62iJEnSGjUdLVzPBy6oqpsAquqmqlpWVcuBY3jwsuFCYMeB+XYAFg1bYFUdXVX7V9X+c+bMmYYqSpIkrTnTEbgOZeByYpLtBsa9GJjfhk8DDkmyYZJdgd2B86Zh/ZIkSWu1Vb5LESDJw4A/AF43UPyBJPvSXS5cMDKuqi5NchJwGbAUeIN3KEqSpN8FUwpcVfVbYKtRZa8cZ/qjgKOmsk5JkqSZxm+alyRJ6pmBS5IkqWcGLkmSpJ4ZuCRJknpm4JIkSeqZgUuSJKlnBi5JkqSeGbgkSZJ6ZuCSJEnqmYFLkiSpZwYuSZKknhm4JEmSembgkiRJ6pmBS5IkqWcGLkmSpJ4ZuCRJknpm4JIkSeqZgUuSJKlnBi5JkqSeGbgkSZJ6ZuCSJEnqmYFLkiSpZwYuSZKknhm4JEmSembgkiRJ6pmBS5IkqWcGLkmSpJ4ZuCRJknpm4JIkSeqZgUuSJKlnUwpcSRYkuSTJhUnmtbItk5yZ5Jft7xYD0789yZVJrkjy3KlWXpIkaSaYjhauZ1XVvlW1f/v/bcBZVbU7cFb7nyR7AYcAewPPAz6eZNY0rF+SJGmt1sclxYOA49vw8cDBA+VfqKolVXUNcCXw5B7WL0mStFaZauAq4Iwk5yc5opVtW1U3ArS/27TyucD1A/MubGWSJEnrtNlTnP/3q2pRkm2AM5NcPs60GVJWQyfswtsRADvttNMUqyhJkrRmTamFq6oWtb83A6fQXSK8Kcl2AO3vzW3yhcCOA7PvACwaY7lHV9X+VbX/nDlzplJFSZKkNW6VA1eShyfZdGQY+ENgPnAacHib7HDg1DZ8GnBIkg2T7ArsDpy3quuXJEmaKaZySXFb4JQkI8s5oaq+leRnwElJXgtcB7wUoKouTXIScBmwFHhDVS2bUu0lSZJmgFUOXFV1NfCEIeW3As8eY56jgKNWdZ2SJEkzkd80L0mS1DMDlyRJUs8MXJIkST0zcEmSJPXMwCVJktQzA5ckSVLPDFySJEk9M3BJkiT1zMAlSZLUMwOXJElSzwxckiRJPTNwSZIk9czAJUmS1DMDlyRJUs8MXJIkST0zcEmSJPXMwCVJktQzA5ckSVLPDFySJEk9M3BJkiT1zMAlSZLUMwOXJElSzwxckiRJPTNwSZIk9czAJUmS1DMDlyRJUs8MXJIkST0zcEmSJPXMwCVJktQzA5ckSVLPVjlwJdkxyfeS/CLJpUn+ppUfmeSGJBe2xwsG5nl7kiuTXJHkudOxAZIkSWu72VOYdynw1qq6IMmmwPlJzmzjPlJV/zY4cZK9gEOAvYHtge8k2aOqlk2hDpIkSWu9VW7hqqobq+qCNnwn8Atg7jizHAR8oaqWVNU1wJXAk1d1/ZIkSTPFtPThSrIL8ETg3Fb0xiQXJzk2yRatbC5w/cBsCxkjoCU5Ism8JPMWL148HVWUJElaY6YcuJJsAnwFeHNV3QF8AngUsC9wI/ChkUmHzF7DlllVR1fV/lW1/5w5c6ZaRUmSpDVqSoEryfp0YevzVXUyQFXdVFXLqmo5cAwPXjZcCOw4MPsOwKKprF+SJGkmmMpdigE+Dfyiqj48UL7dwGQvBua34dOAQ5JsmGRXYHfgvFVdvyRJ0kwxlbsUfx94JXBJkgtb2T8ChybZl+5y4QLgdQBVdWmSk4DL6O5wfIN3KEqSpN8Fqxy4qupHDO+X9Y1x5jkKOGpV1ylJkjQT+U3zkiRJPTNwSZIk9czAJUmS1DMDlyRJUs8MXJIkST0zcEmSJPXMwCVJktQzA5ckSVLPDFySJEk9M3BJkiT1zMAlSZLUMwOXJElSzwxckiRJPTNwSZIk9czAJUmS1DMDlyRJUs8MXJIkST0zcEmSJPXMwCVJktQzA5ckSVLPDFySJEk9M3BN0Qe+dTn/cvpla7oakiRpLWbgmoIzLv0VH//+VRz742u47tbfrpZ1fueym/ju5TetlnVJkqTpYeBaRbfdfR//eMolPHqbTZiV8Llzr+19nb+++1rnd9MAABL2SURBVD7e/MULectJF3Hv/ct6X58kSZoeBq5V9E9fnc/t99zPx/78iTx3n0fyxZ9dzz339RuCjvnh1dy1ZCm/+e39nHbRol7XJUmSpo+BaxV87aJFfP2SG3nzc/bgMY/cjMMO2Jnb77mfr/UYgm69awnH/WQBL3rC9uyx7SYc/5MFVFVv65MkSdPHwLWSbr7jXv7p1Pnsu+PmvO4ZuwHw5F23ZM9tN+X4c1YMQVXFe0+/jHd/7dIph6Ojz76ae+9fxt88e3cOe+ouXLroDi647jdTWqYkSVo9DFwr4d77l/HST53DXfcu5Vl7bsNJ8xZywrnXceJ51/OY7Tbl0kV38P5vXs4J514HwAe+fQX/9aNr+O8fLxh6CbCqeNep83n7yZewfPnYgWzxnUs4/pwFHLTvXB69zSa8+Ilz2XTD2XzmnAX9bKgkSeuQW+9awqd+cNUavTI0e42teYa58977Oe4nC7jpjnv5s/13ZM6mG64wft8dN+db83/FOVffyk5bPZzjf7KAT3z/Kg598k5c/qs7+OdTL+Wpu23FNptt9MA8n/jBVRx/TtfZfptNN+Rv/2CPoev+5A+u4r6ly9l164c/EOYet8MjOP2iG9lru83YdKP1H5j2z5+y03RvuiRJM9Zv71vKa46fx+U33sFz9tqWR83ZZI3UY7W3cCV5XpIrklyZ5G2re/2r4ta7lvCps6/mlruWcNhTd+HxO2z+kGk2nD2L/Xbegvk33MFPr76VI792KX+w17a89+B9+LeXPoF771/G20++5IF0/b3Lb+aD376CFz5+O/70STvw72f9km/N/9VDlnvTHffyuZ9ey747bsHWmzwY8g7YbSuWVfGzBbf1t+GSJM1gS5ct540n/JxLFv6G/zj0iWssbMFqDlxJZgH/CTwf2As4NMleq7MOK2N5FVctvotPnX0199y3jL942m7sse2mY05/wK5dCDrtokU8aact+I9Dn8is9cKj5mzC3z93T866/Ga+fP5Crl58F2/6ws95zCM34wMveTxHvXgfnrDj5rz1pAv5n5vufGB51956N/948iUsXV78r8dss8K6tt5kQ/bYdhPOu+Y2lo1zOVKSpN9FVcU7TpnPdy+/mX85eB/+cO9HrtH6rO5Lik8GrqyqqwGSfAE4CFjjX9VeVSwvWLp8OYt+cy/zb7idSxfdzh33LuURG6/PXzxt1xUuBw6z9aYbsvf2m3HLXUt4/t6P5OQLbnhg3Ebrz2KXrR7GO786n003ms2y5cULH7cdX/1517freXs/ko/ffBeHHP1TXvT47fnZgtv4xY13sF7Csx+7DVs+fIOHrO+A3bbiM+dcy7nX3Mp2j9iYe+9fxpfmXc/6s9Zju0dsxPabb8y2m23E+rPCfcuWc/eSZdy9ZCkAm2w4m4dvOJsNZj+YuZcvL+5bthyADWatx3rrZcrPqyRJq6qqe19asnQ5S5cVG8xej41mr8fsWetRVRz/k2v57X1Lufu+Zdy3dDkbbzCLh7XH969YzHcvv5ln7bkNYc2/n63uwDUXuH7g/4XAU1ZzHVbw1yf+nDMu/RX3LV3OYDvR7PXCHttuyj5zN+Oxj9yMDdefNanlHfJ7O5HAellx566X8KdP2oH/+O6V3Hb3fbzm93dli4EQ9YiN1+flT9mJY350Dcefs4CHbTCLZ+45hwN224rNBvpoDdpj203Z8uEbcPrFN45ZnwRmJSwdoxVs/VlhvTZ+dEvZrPXC+rPCrKz5A3VdYVukJE3O8iqWLF3OsH7us9cL660X7lu6fNxl7LfzFjznsduMO83qktXZYz/JS4HnVtVftP9fCTy5qv561HRHAEe0f/cErlgN1dsauGU1rEdT576aGdxPM4f7auZwX639dq6qOaMLV3cL10Jgx4H/dwAe8n0JVXU0cPTqqhRAknlVtf/qXKdWjftqZnA/zRzuq5nDfTVzre67FH8G7J5k1yQbAIcAp63mOkiSJK1Wq7WFq6qWJnkj8G1gFnBsVV26OusgSZK0uq32Lz6tqm8A31jd652E1XoJU1PivpoZ3E8zh/tq5nBfzVCrtdO8JEnS7yJ/S1GSJKln62Tgmujng9L5aBt/cZInTTRvki2TnJnkl+3vFqtre9ZlPe2rI5PckOTC9njB6tqeddUU99OxSW5OMn/UPJ5TPehpX3lO9WBV91WSHZN8L8kvklya5G8G5vG8WltV1Tr1oOuMfxWwG7ABcBGw16hpXgB8EwhwAHDuRPMCHwDe1obfBrx/TW/rTH/0uK+OBP5uTW/fuvKYyn5q454BPAmYP2oez6mZs688p9aifQVsBzypDW8K/I/vVWv/Y11s4Xrg54Oq6j5g5OeDBh0EfKY6PwU2T7LdBPMeBBzfho8HDu57Q34H9LWvNL2msp+oqrOBYb+y7jk1/fraV5p+q7yvqurGqroAoKruBH5B90suI/N4Xq2F1sXANezng+ZOcprx5t22qm4EaH/Xjt8KmNn62lcAb2xN8MfapD5lU9lP4/Gcmn597SvwnJpu07KvkuwCPBE4txV5Xq2l1sXANeyH/0bfijnWNJOZV9Onr331CeBRwL7AjcCHVrWCAqa2n7R69bWvPKem35T3VZJNgK8Ab66qO6axburBuhi4JvPzQWNNM968N400u7e/N09jnX9X9bKvquqmqlpWVcuBY+ia7rXqprKfxuM5Nf162VeeU72Y0r5Ksj5d2Pp8VZ08MI3n1VpqXQxck/n5oNOAw9odIAcAt7em1/HmPQ04vA0fDpza94b8DuhlX4282DQvBuajqZjKfhqP59T062VfeU71YpX3VZIAnwZ+UVUfHjKP59XaaE332u/jQXdnx//Q3QHyjlb2euD1bTjAf7bxlwD7jzdvK98KOAv4Zfu75ZreznXh0dO++myb9mK6F5/t1vR2zvTHFPfTiXSXoe6n+8T+2lbuOTVz9pXn1Fq0r4Cn0V1avBi4sD1e0MZ5Xq2lD79pXpIkqWfr4iVFSZKktYqBS5IkqWcGLkmSpJ4ZuCRJknpm4JIkSeqZgUtrvSSV5LMD/89OsjjJ6e3/P07ytpVY3nuSPGea6/j6JIdNw3KOTPJ3Q8oPTrLXNCx/QZKtp7qcmSDJm5M8bOD/byTZvMf1zUlybpKfJ3n6qHGzk/zfJL9McmF7vGNg/LJWdmmSi5K8Jcl6bdyBSW5vy/1FkncNWff2Sb7c17YNk2TfJC9YneucTu15/f/GGb9SryvSRGav6QpIk3A3sE+SjavqHuAPgBtGRlbVaTz0CwPHVFX/PN0VrKpPTvcyRzkYOB24bPSIJLOramnP65927csbU923l0/3smcBbwY+B/wWoKr6DgfPBi6vqsOHjHsv8EjgcVV1b5JNgbcOjL+nqvYFSLINcALwCGAkXP2wql6Y5OHAhUlOr6rzR2auqkXAS6Z/k4ZLMpvuZ372B74xTcucVVXLpmNZk3QgcBfwkyF1mb2yryvSRGzh0kzxTeCP2vChdF/QCECSVyX5WBt+aZL5rZXg7GELSnJckpe04QVJ3p3kgiSXJHlMkvVa+eYD81yZZNskOyc5K92P+J6VZKc2/oGWqSSPTvKdVocLkjyqlf99kp+1ed89sOx3JLkiyXeAPYfU9/8D/hj4YGsFeVSS77cWkx8Af5PkRQOtK99Jsm2bd6skZ7TyTzHw22xJXpHkvLbMT7WQMnrd/9zqPD/J0S0kkeRNSS5r2/KFIfO9KsmpSb7Vtu1drXyX1krzceACYMckH2zLvyTJy9p0ByY5O8kpbT2fHGjxObRNOz/J+wfWeVe61stzgXcA2wPfS/K9gX29dRt+S5t/fpI3j6rbMelams5IsvGQbXvIMZBkX+ADwAva87nxwPQPA/4S+Ouquhegqu6sqiNHL7uNuxk4gu7HojNq3N3A+XS/azhYp12SzB947k9uz/0vk3xg2Hra8/H+dgycl+TRrXysY+nIdgycAXwGeA/wsra9L2vjj23H5tVJ3jSwrqHH2qh99tRR9XvIeZTOWMfL6QPzfizJqwa2891Z8Rzfhe4LRv+21enp6V4XPtyOl/dnxdeVOUm+0s6FnyX5/Vb+zDzYYvnzdEFaGm5Nf/OqDx8TPeg+hT4e+DKwEd23Kh8InN7Gvwr4WBu+BJjbhjcfY3nHAS9pwwvo3ggB/jfwX23434FXt+GnAN9pw18DDm/DrwG+2oaPBP6uDZ8LvLgNbwQ8DPhD4Gi6wLMeXWvVM4D9Wp0fBmwGXDmynLHq3P7/PvDxgf+3gAe+yPgvgA+14Y8C/9yG/4ju26m3Bh7btmX9Nu7jwGFD1rvlwPBngRe14UXAhmM9z22f3Ej3rdcb0/0UzP7ALsBy4IA23Z8CZwKzgG2B64Dt2v69F9itjTuTrgVn+zbNHLoW+u8CB7dlFfBnA3VYAGw9+v+B5/zhwCbApcATW92WAvu26U8CXjFk28Y6Bl5FOw5HTf944OcTHeNDyn7dnpMDefBY36ptx96jpt0FmD9Qj6vpWsg2Aq4Fdhyy/AU8+O3mhw2sY6xj6Ui6sLfxsO1t438CbNie51uB9RnnWBu9z0bVb9h5NN7xcvrAvB8DXjXBOX4kA+ca3Tl2OjBryOvKCcDT2vBOdD+pM3Is/H4b3gSY3cdroI9142ELl2aEqrqY7k3lUMa/hPFj4Lgkf0n3ojwZIz/8en5bB8AXgZe14UPa/9B9Cj+hDX+W7ic2HtA+4c6tqlNave+tqt/SBa4/BH5O17LzGGB34OnAKVX126q6g5W7hPHFgeEdgG8nuQT4e2DvVv4MustqVNXX6d7Eobv8tR/wsyQXtv93G7KOZ7XWjkuA/zWw3IuBzyd5BV1IGebMqrq1usvAJ/Pgc3VtVf20DT8NOLG6H0a+CfgB8Htt3HlVdXV1l5lObNP+HvD9qlpc3WXUz7dtBFhG92O+E3ka3XN+d1Xd1eo20ufqmqq6sA0PHg+Dxj0GJpLk1a1F5PokO4436cDw05P8HDgDeF9VXTrBas6qqtura1G7DNh5jOlOHPg70sI01rEEcFrbn2P5elUtqapb6H40eVvGP9aG7rNxzqPxjpfxDDvHh/lSDb+s+RzgY63+pwGbtTr+GPhwa83bvGbgpX2tPgYuzSSnAf/GwOXE0arq9cA7gR3p+rpsleS/2xvcWEFtSfu7jAf7NZ4DPDrJHLr+UycPm5HuE/qgDJ2qK//Xqtq3PR5dVZ8eYxmTdffA8H/QfRp/HPA6uhaBseo4Up/jB+qzZ426xJVkI7rWiJe05R4zsNw/ovuNt/2A89P16Rlt9HpH/h+s91jP11jzjzf9vWO8WY423jKWDAwPHg/jmWj/XQnsNHK5qar+u7r+WrczxoeCJLu19d/cin5YVU+sqv1qcv0FJ7sdNWR4vGNpcN9Ndr3jHWtj7bPxzqNhlrLi+9lGo8YPO8eHGWv71gOeOrANc6u7LPw+ulbAjYGfJnnMOMvW7zgDl2aSY4H3VNUlY02Q5FFVdW51HeNvobuU8ur2IjnpTtNVVcApwIfpLh/c2kb9hK7FC+DlwI9GzXcHsDDJwa0+G7Y+PN8GXpNkk1Y+N13n6LOBFyfZuL0hv2iMKt0JjNc/5BE8eCPBYKfts1s9SfJ8ustF0P2o7UtaHUiyZZLRrSAjb1q3tHqP9Htbj+55/R7wf4DN6S6njPYHbbkb04XWHw+Z5my6fkCzWrh9BnBeG/fkJLu29b2M7rk+F3hmkq1bP6BD6Vo5hhnrOTsbODjJw9J1Qn8x8MMxljHMuMfAaK1l5tN0LSQbwQOd+jcYNn17Hj5JF3r6/rHblw38PacNj3UsjTbRMTliMsfaCsY5j8Y6Xq4F9mrTPYKuFW0ik60/dC2Lbxz5J12fvZHXm0uq6v3APLqWa2ko71LUjFFVC+n6Vo3ng0l2p/skfBZw0RRW+UXgZ3R9OUa8CTg2yd8Di4FXD5nvlcCnkrwHuB94aVWdkeSxwDnp+kHfRdc/6IIkX6Trl3YtY7/xfwE4pl26GHY32pHAl5LcAPwU2LWVvxs4MckFdMHkOoCquizJO4EzWqC5H3hDqwNtmt8kOYauv9OC9lxA1yrzufbGFuAjVfWbIXX6Ed0lt0cDJ1TVvNZZedApdJeyLqJrYfk/VfWr1lJwDvA+4HF0b7SnVNXyJG8HvtfW/Y2qOnWM5+xo4JtJbqyqZw1s1wVJjuPBYPdfVfXzIXUby2SOgdHeAfwLMD/JncA9wPF0feEANm6Xq9ana635LF3Y79uG6Tqsr0cXXmHsY2m07wFva/X+17FWMJljbQwPOY8Y43gBSHIS3aXuX9Jdup/I14AvJzkI+OsJpn0T8J9JLqZ73zybrtP9m5M8i67l7DK6m3ukodL/ByhJv2vaHWL7V9UbJ5p2jPkPpOvQ/MLprJcelGQB3T66ZU3XRfpd4CVFSZKkntnCJUmS1DNbuCRJknpm4JIkSeqZgUuSJKlnBi5JkqSeGbgkSZJ6ZuCSJEnq2f8Pyy+X0rwfWBUAAAAASUVORK5CYII=\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"# Import data where value of illicit flow is standardized for partners\n",
"IFF_std = pd.read_csv('Data/GER_Orig_Dest_Year_std.csv')\n",
"IFF_std = IFF_std.query('year == \"2016\"')\n",
"\n",
"# Merge in with flow data\n",
"flow_data = pd.merge(left=create_graph_data('2016', threshold_var='GDP'),\n",
" right=IFF_std[['reporter.ISO', 'partner.ISO', 'pImp_IFF_hi_GDP']],\n",
" on=['reporter.ISO', 'partner.ISO'])\n",
"\n",
"# Plot distribution of IFF in partner countries\n",
"sns.distplot(flow_data['pImp_IFF_hi_GDP'], kde=True);\n",
"plt.title('Distribution of IFF in partner countries in 2016 (dyad-level)')\n",
"plt.xlabel('Mis-invoiced trade as proportion of GDP in partner countries');"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"source": [
"The distribution of outflows is heavily right-skewed, where the yearly outflow in 2016 from a single country to their partner resulted in an inflow to said partner which sometimes represented up to 2% of their GDP."
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"source": [
"The helper function `threshold_partner_IFF()` thus helps us further threshold our bilateral flow data from the partner country perspective. By default, it restricts those bilateral flows to transactions where the inflow to the partner represented at least 0.01% of their GDP."
]
},
{
"cell_type": "code",
"execution_count": 98,
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"outputs": [],
"source": [
"def threshold_partner_IFF(flow_data, year='2016', partner_threshold=0.0001):\n",
" \"\"\"\n",
" Filters bilateral flow data-set to minimum level of illicit flow relative to partner GDP.\n",
" \n",
" flow_data: as Pandas dataframe, name of data-set which contains bilateral flow data\n",
" (in wide format)\n",
" year: as string, specify which year to use for the network analysis (between 2000-2016)\n",
" partner_threshold: as numeric, specify the cut-off for the minimum proportion of partner\n",
" GDP that a bilateral flow must represent in order to be included\n",
" \"\"\" \n",
" IFF_std = pd.read_csv('Data/GER_Orig_Dest_Year_std.csv')\n",
" IFF_std = IFF_std.query('year == @year')\n",
" flow_data = pd.merge(left=flow_data,\n",
" right=IFF_std[['reporter.ISO', 'partner.ISO', 'pImp_IFF_hi_GDP']],\n",
" on=['reporter.ISO', 'partner.ISO'])\n",
" flow_data = flow_data.query('pImp_IFF_hi_GDP >= @partner_threshold')\n",
" return flow_data"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"source": [
"Let's now create the directed graph data for countries which are conduits for illicit outflows relative to GDP and relative to trade value, respectively, and further restrict the data to edges where the mis-invoiced trade represents at least 0.01% of partner GDP."
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"### Directed graph for GDP"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"source": [
"Let's create a directed graph for the flow data restricted to the top origins of illicit outflows relative to GDP, and applying the standard thresholding described above."
]
},
{
"cell_type": "code",
"execution_count": 99,
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"outputs": [],
"source": [
"# Graph data for conduits relative to GDP\n",
"flow_data_GDP = create_graph_data('2016', threshold_var='GDP')\n",
"flow_data_GDP = threshold_partner_IFF(flow_data_GDP)"
]
},
{
"cell_type": "code",
"execution_count": 100,
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"outputs": [],
"source": [
"# Create directed graph\n",
"graph = nx.from_pandas_edgelist(flow_data_GDP,\n",
" 'reporter.ISO',\n",
" 'partner.ISO', \n",
" 'Imp_IFF_hi',\n",
" create_using = nx.DiGraph())"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"source": [
"This graph contains 33 vertices (or nodes) and 36 edges."
]
},
{
"cell_type": "code",
"execution_count": 101,
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"outputs": [
{
"data": {
"text/plain": [
"(33, 36)"
]
},
"execution_count": 101,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# Check the number of nodes and edges in the graph\n",
"len(graph.nodes()), len(graph.edges())"
]
},
{
"cell_type": "code",
"execution_count": 102,
"metadata": {
"slideshow": {
"slide_type": "skip"
},
"tags": [
"hide-cell"
]
},
"outputs": [
{
"data": {
"text/plain": [
"[('MLI', 'GHA', {'Imp_IFF_hi': 8081515.07373014}),\n",
" ('MLI', 'SEN', {'Imp_IFF_hi': 449650318.36780304}),\n",
" ('MLI', 'ZAF', {'Imp_IFF_hi': 66862258.2240592}),\n",
" ('MLI', 'TGO', {'Imp_IFF_hi': 9367585.98900624}),\n",
" ('MLI', 'MRT', {'Imp_IFF_hi': 1267279.60791437}),\n",
" ('MOZ', 'NAM', {'Imp_IFF_hi': 1165110.23690534}),\n",
" ('MOZ', 'NLD', {'Imp_IFF_hi': 128444043.062896}),\n",
" ('MOZ', 'PRT', {'Imp_IFF_hi': 121508025.10009299}),\n",
" ('MOZ', 'SGP', {'Imp_IFF_hi': 466068356.77873796}),\n",
" ('MOZ', 'ZAF', {'Imp_IFF_hi': 246975704.837192})]"
]
},
"execution_count": 102,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# Print some of the edges in the network\n",
"list(graph.edges(data=True))[0:10]"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"source": [
"In a directed graph, the degree of a node is the sum of its indegree (the number of edges going in to the node) and its outdegree (the number of edges going out of the node). In this case, the GDP conduit countries of Mali, Mozambique, Seychelles, and Tunisia will have a degree of a least 1 (corresponding to the outdegree of at least one edge going out)."
]
},
{
"cell_type": "code",
"execution_count": 103,
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"outputs": [
{
"data": {
"text/plain": [
"DiDegreeView({'MLI': 5, 'GHA': 1, 'SEN': 1, 'ZAF': 3, 'TGO': 1, 'MOZ': 7, 'NAM': 1, 'NLD': 2, 'PRT': 2, 'SGP': 2, 'SYC': 3, 'MUS': 2, 'TUN': 21, 'DZA': 1, 'AZE': 1, 'BEL': 1, 'BGR': 1, 'HRV': 1, 'DNK': 1, 'EGY': 1, 'FRA': 1, 'HUN': 1, 'ITA': 1, 'JOR': 1, 'MYS': 1, 'MRT': 2, 'PRY': 1, 'RUS': 1, 'SVK': 1, 'SVN': 1, 'TUR': 1, 'UKR': 1, 'FIN': 1})"
]
},
"execution_count": 103,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# Get the degree of the nodes\n",
"graph.degree"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"source": [
"The function below achieves the following:\n",
"- color the country nodes according to their GDP per capita;\n",
"- color the edges according to the size of the *logged* illicit flow;\n",
"- size the nodes proportionately to their degree (for use in the map case);\n",
"- only label nodes with an outdegree of at least 1, that is, only the origin conduit countries selected by the thresholding above will have labels (for use in the map case)."
]
},
{
"cell_type": "code",
"execution_count": 104,
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"outputs": [],
"source": [
"def set_graph_attributes(graph):\n",
" \"\"\"\n",
" Sets node attributes and create auxiliary variables to be used in graph visualization.\n",
" \n",
" Returns:\n",
" col: list of values to color nodes according to (node GDP per capita)\n",
" edge_col: array of values to color edges according to (logged flow between nodes)\n",
" sizes: list of values to size nodes (proportional to degree)\n",
" labels: dict of node labels (where a node is labelled if outdegree is at least 1)\n",
" \"\"\"\n",
" # Create dictionary of GDP per capita for each country\n",
" GDP_attr = covariates.loc[:, ['gdp-pc']]\n",
" GDP_attr = GDP_attr.to_dict('index')\n",
" # Set GDP per capita as a node attribute\n",
" nx.set_node_attributes(graph, GDP_attr)\n",
"\n",
" # Create list of colors for nodes in the graph\n",
" col = [nx.get_node_attributes(graph, 'gdp-pc')[n] for n in graph.nodes]\n",
"\n",
" # Create list of colors for edges in the graph\n",
" edge_col = [nx.get_edge_attributes(graph, 'Imp_IFF_hi')[e] for e in graph.edges]\n",
" edge_col = np.log(edge_col)\n",
"\n",
" # Extract outdegree (the number of edges coming out of nodes) and degree\n",
" outdeg = graph.out_degree\n",
" deg = graph.degree\n",
" # Size of nodes will be proportional to their degree\n",
" sizes = [10 * deg[c] for c in graph.nodes]\n",
" # Label the countries if their outdegree is at least 1, i.e. if they are the reporting African countries\n",
" labels = {c: c if outdeg[c] >= 1 else ''\n",
" for c in graph.nodes}\n",
" return col, edge_col, outdeg, deg, sizes, labels"
]
},
{
"cell_type": "code",
"execution_count": 105,
"metadata": {
"slideshow": {
"slide_type": "-"
}
},
"outputs": [],
"source": [
"# Generate graph attributes and auxiliary variables\n",
"col, edge_col, outdeg, deg, sizes, labels = set_graph_attributes(graph)"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"source": [
"We can now draw the network of illicit flows from the top 4 origins of illicit outflows with respect to GDP."
]
},
{
"cell_type": "code",
"execution_count": 106,
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAigAAAHRCAYAAABAeELJAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4yLjEsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy+j8jraAAAgAElEQVR4nOzdd3hUVfrA8e+5U5JJ75AAITQhoYUiAoqiKGJZO8WC4K66rmXtZSvuqqvormVXf1t1BRvY1oqiolIEVEqQLiWhhvTeptzz++MOJCEBEpg7jfN5nnkgM/fOfUfDzDvvOec9QkqJoiiKoihKMNECHYCiKIqiKMrhVIKiKIqiKErQUQmKoiiKoihBRyUoiqIoiqIEHZWgKIqiKIoSdFSCoiiKoihK0FEJiqIoiqIoRyWE2CiEGO/Pa6oERVEURTlpCSGmCSG+FULUCSGKvX+/VQghvI+/LIRwCiFqvLcNQojHhRDxLZ5jphDCI4SoFUJUCyHyhBAXB+5V+Z6UcqCU8msAIcTDQohXzb6mSlAURVGUk5IQ4l7gOeApoCvQBbgFOB2wtzj0SSllLJAK3ACMBr4RQkS3OGaFlDIGSABeBN4UQiSZHL/VzOcPNJWgKIqiKCcdbwXkj8CtUsq3pZQ10rBWSnmtlLLp8HOklI1Syu+BS4BkjGTl8GN04CXAAfRu57ozhRDfCCH+JoSoEkJsEUJMaBmXEOJFIUShEGKfEOJRIYTlsHOfEUKUAw+38/wWIcSvhRA7vBWf1UKIHt7HnhNC7PFWeVYLIca1OO9hIcTbQoj53vPWCCGGtni8QAhxrhBiEvBrYKq3YrTO+/gNQojN3nN3CiF+3rH/E0emEhRFURTlZDQGiADe7+yJUsoa4HNg3OGPeasaNwK1wLYjPMVpwE4gBZgFvNui2jIHcAN9gWHARO/zHX5uGvBYO899D3A1cCEQB/wUqPc+9j2QCyQBrwNvCSEiW5x7KfBWi8ffE0LYDnvtnwJ/AuZLKWOklAeTmGLgYu81bwCeEUIMP8Lr7xCVoCiKoignoxSgVErpPniHEGK5EKJSCNEghDjzGOfvx/ggP2i0EKISOICRIFwupaw6wrnFwLNSSpeUcj6wFbhICNEFuAC4S0pZJ6UsBp4BprW8rpTyb1JKt5SyoZ3nvhH4rZRyq7citE5KWQYgpXxVSlnmPfcvGAla/xbnrvZWk1zA00AkxnDWMUkpP5ZS7vBeczHwGe0kcJ0R1uNXiqIoinIEZUCKEMJ6MEmRUo4FEELs5dhf4LsB5S1+XimlPKOD194nW+/UuwvIAHoCNqDQO0cXbxx7Whzb8u/t6QHsaO8B75ybG73XkhjVjpT2nltKqXv/O2Qc68V4n/sCjGrQKd6Yo4D1HTn3SFQFRVEURTkZrQCaMIY1OkUIEQOcCyw9zmt3Ey0yECAToyKzxxtTipQywXuLk1IObHFsy8SmPXuAPu3EPA54EJgCJEopE4AqoGUcPVocrwHdvXEdrlUMQogI4B3gz0AX73MvOOy5O00lKIqiKMpJR0pZCfwB+D8hxFVCiBghhCaEyAWi2ztHCBEhhBgBvAdUAP89zsunAb8UQtiEEJOBbGCBlLIQY2jkL0KIOG88fYQQZ3Xiuf8DPCKE6CcMQ4QQyUAsxtyWEsAqhPg9RgWlpRFCiCu882juwkiWVrZzjSIgy5vEgLHiKcL73G5vNWViJ2Jul0pQFEVRlJOSlPJJjEmlD2DMCykC/olRaVje4tAHhBA1GEM6c4HVwFgpZd1xXvpboB9QijHR9aqD80SA6zE+8DdhJEFvA+mdeO6ngTcxEp1qjCXPDmAh8AnwI8aQUiNth4veB6Z6rzsduMI7H+Vwb3n/LBNCrPFOGv6l97oVwDXAB52IuV2i9TCYoiiKoihmEULMBG7sxHwVvxBCPAz0lVJeF+hYDlIVFEVRFEVRgo5KUBRFURRFCTpqiEdRFEVRlKCjKiiKoiiKogQdlaAoiqIoihJ0jtpJNiUlRWZlZfkpFEVRFEUJvNWrV5dKKVP9db1JYpIspdSnz7ma1QullJN8+qR+dtQEJSsri1WrVvkrFkVRFEUJOCHELn9er5RSVuHbz1qBSDn2UcFN7cWjKIqiKIEmfLxgJQzWv6g5KIqiKIqiBB1VQVEURVGUQFMVlDZUBUVRFEVRlKCjKiiKoiiKEmi+rqCEAZWgKIqiKEpASZWgtEMN8SiKoiiKEnRUBUVRFEVRAkmgKijtUBUURVEURVGCjqqgKIqiKEqgqQpKGypBURRFUZRAUwlKG2qIR1EURVGUoKMqKIqiKIoSaKqC0oaqoCiKoiiKEnRUBUVRFEVRAko1amuPSlAURVEUJZBUH5R2qSEeRVEURVGCjqqgKIqiKEqgqQpKG6qCoiiKoihK0FEVFEVRFEUJNFVBaUNVUBRFURRFCTqqgqIoiqIogaYqKG2oBEVRFEVRAkr1QWmPGuJRFEVRFCXoqAqKoiiKogSSatTWLlVBURRFURQl6KgKihL6pBuqvwHnbtAbQIuCiJ4QOxaEJdDRKb4mG4AyoAmIA5JBqO9aSohTFZQ2VIKihC5XCZS+BWXzQHpAdwJuEFYQNhB2SL0Gkq4CW1Kgo1VOhJQgl4PnGdAXAjaMArALiAPLnWCZCSIlgEEqyglQCUob6muHEpqqv4Etl0DJy+CpBr0O48NKgnSBXg+eSih6Ebb8BGq/D3DAynHTN4NzILguAf1jjP/P9UAtRhWlBDyPgbMvuO4xklVFUUKeSlCU0FO9BAruMYZzpPPox8omI3nZeQfUrPRPfIrv6N+BaxyQD9QBR/qW2QA0gv4yuC43klRFCRneZca+vIUBlaAooaUxH3Y9aCQenSEboeBuaNpnTlyK78kd4LoIo1LS0TfcepDLwP1zEwNTFMUf1BwUJSSUlZUxYcIEcB3gQFEZFg1SE60U7HeSkWZj07sDDh378N8PEBOlcd+MNGb+bjeLV9cRH6MhETz9h98zYdqLAXwlSkcUFBRw8UXD2LDGfei+hx9xExMDGzZKLr5Q46orLJSXSyZc4OKXt1o4+yyN7Fwn/U9x4nTOYeTIIl586T1sNlsAX4midFCYVD18SVVQlJCQnJxM3uql5L3Rk1uuSubu61LJe7M/efP7owlx1HOfujudvDf78+z9Gdzy4OvG0JAS3GQxxpCOfsRDqqok5//Exc0/s3DDDGO1Vp/egrzv7KxfbWfv3tW8+eab/olXUU7EwT4oaoinFZWgKKGj/CM4RjJyNGOGRLGv2AmVC30YlGIKz7yjPlxbCxdc6uKaqRq/uLntUnKLRTJqZAX79m4zK0JFUUymEhQldNSvA73xuE//9JsaLhsfB/UbfRhUmJJN0LgW6r+C+sXQ9IN/V8foCzjavJN7HnRzxliNu3/Z/ih1Y6Pk2+8kkybGmRSgoviYqqC0oeagKKHDXdXmriMVVFref/8zhTzwbCHF5W5WvtIX3BUmBRgG3Huhei7UvI637ux9QDf6ysTNhNirwZJqahiC6vbv94ZzzniN9z/Uue8uSVpa8//sHTsluaOcbNsuuepyO0OGxJoap6Io5lEVFCV0WKLa3JWcYKGi2t3qvvJqDykJzbn3U3ens/3DATx6W1dm/G6P0WlWaU3qUP4I7DsXql8GWQeyFmSN91YHegVU/h/sGQdV/zI1nORkjYrK1t8CyysgJdlIRqZN1vjFzRoXXuaipqb5uINzULZvtLPyOzcffJhnapyK4jOqgtKGSlCU0GHP5PCiX0yUhfRUG4u+rQGgvMrNp99Uc8aw6FbHaZrgzmtT0HVYuLz9b+cnLalDyR1Q84Z3+fbReog0GbfKZ6H8MdNCiolNIr2rYNGXxiTZ8nLJp5/pnDG2+S3rrjusTDhb4/IpLpzO1m/I6emCJx6N5vEnvjAtRkXxHdUHpT0qQVFCR/Jl7e6tM/eRTB79dxG5U7Zyzk07mPXzrvTpEdHmOCEEv705gyf/udof0YaOiqeg4SvvHjcdJBug5jWoftWcmLTJzH0xmkefcJM7ysk5k1zM+o2FPn1aj+nNfsxKj+6C6T91ox+24OeySwT1DTaWLl1qToyKophKSHnkTGvkyJFy1apVfgxHUY5h2/VQ/8Pxnx9zGvT5p+/i6QyPDnVO0CVE28EW2I0MLRYLgwfnIJu2YbFInv9DEmNHRALwXV4TDzxRzr4iD7HRGulpFp54IJHBA+w8/GwF/55XS2qShtOl8bs//Iurr7net8HJQnBmA8c7KVoD7UqwveLLqJSThBBitZRypL+uN9I2VK5K8e3qQnEg3a+vwQxqkqwSWrrcCAUPGJ1hO0tEQtrPfB/T0UgJG4vgo82woQgs3omnbg90T4BLsmFUj4AkKw6Hg7yvb4Gq51n4dQW/erKCxfPTKSrxMOX2Yl5/LvVQwrLs+0Z27HYxeIAdgLt/Gsd9N8ezrcDKiEtu4arJV/u2IZpIB+1s0D+l411kW4oEy12+i0dRFL9TCcrJRK8C5+eglxp7lWjxYBsN1lMCHVnHxZ0JSZdA+QedS1JEJKRMg9hR5sV2uK0l8LdvoN4Fjd6JvHqLD9s9lfDi9/DS9zB9OIzv47/YDqp+CWQj1bU6ifHGiO/zc6uZcWXMoeQE4IxTI9s9vV+Wm6hIDxUVFaSlpfk2NuufwbkMqOnkiQ7QLgVthG/jURSzHGzUprSiEpSTgWs91P8dmj4GLIAT41upzfjT2h+i7oCISSBCoC14t4dAuqFiQceSFBEJyVdC+p3mx3bQqr3w/HJwHqN3yMHE5eXVUFwHU4aYH5tXQ0MDuZM20tjkobDEw5evdQVg4zYXM66I6dBzrNnQRL+eGmmpib4PUPQB24fgupijbxTYUhSIsWA1d5WRoijmUwlKOJMS6h6B+pcwkpLDPyy9H47udVB9J1gyIfEd0JL9HGgnCQ26/w5iRsCBf4C7FPQmWrdF14y+HfZ06PoLSJjov/h+LO1YctKS0wMLtkBiJJznn4qWwxFB3id9QNayYk0j199byoaFGW2OO+2y/VTXSiaOi+S5WcbvxjMvVfPveTXs3OPm0zndQa8Giwm/N9posC0B11VAEVBP+4mKA9BBm2FUXtqZTK0oQU1VUNpQCUq4khJq7oPGdzG2oj+WOvBsh/KJkPQFaCZ8I/YlISDxIki4EOo3QOlr0LgT9Hqjz0nkKSz9RxcGXDeF1IQu/otLSiwDujA4vsehu94bdw8FdSVcuvQv9I5Oo8Hj5OJuw/nzsGsPHVPSWE3GvNt4fusN/HzMCxBj91/MwJjhkZSWeygp0xnYz8aajU1cOtHoF/Ptexm8vaCOj76sP3T8wTko735ax/X3FLLjUg+R0Ud69hOk5YB9I+Vr3yGu7ytYI77EqP4JjCQ7Diy/BMtMEOY2kFMU06gEpQ21zDhcNbwEje9gfOPsKBfoRVA5zUhwQoEQED0Yej4B/d+E7I+MP3s+yvK/FDH39H9QWeDHzrHbynBYbORd8PihW1aM8aE5LnUAay94nLWTHuejfWv4pmTrodPe2vMto1P68kb+cliy00/BCpBOALbscOLRITlR47brY3n57VqWr24ePqtvaP/34YpJ0YwcHMGcV94xNdLCRTtZeOoPrJv1c7AXg/0HsH0L9u1g3wXW+1VyoihhRiUo4Ui6scTeSO45+xh0ZhmTb6yivt74gLGkF5N7TjmDzizjJ9dVUlml8+vHannwkVrvyS525W+id+/uVFZWBu41nKCm6kaklDirm5hz2v9RsbPcPxf+ePMxD3FY7eQm9mRfQ3Pi9Mau5fxl2LXsrStj3/xvWk+mNUlDQyO5FxWSe+E+pt5ewpw/p2CxCLqmWpn/fCq/erKCvuP3MvbKQt7+pI7br29vXxvB7x84n6efeRb98EYkPrLnf5tYcslrIEGzaSAcILqD1tdISoR6G1NCnWrU1h41xBOOnJ/hiBTkfZkEwLW/qOIfcxu455aoVvfPuKOaF15q4Hf3RDPs3HJmTo0k+xQrd/62hEd+NZKEhIRAvooTUplfgS3KjrOmifrSOl4e9QI3rvslsd3izb1w3n4aPE5yP/kVAL1iUvnfuHtaHVLhrGVbzQHOTB0AwJ66Mg40VDIquS9TMk9j/ubF3FM4GbqZu9Gdx+OBuo+g9CGjlX0Lo4dFsnh+ervnPXxXi+E/EcmIcb9h61ZzVszsfCWPVbd8gO6dTFy7Q+2jpCi+IoQowFgm5wHcUsqRQogkYD6QBRQAU6SUbf7hCSFmAL/1/violHKO9/5ewDwgCVgDTJdSOoUQAngOuBCjtD9TSrnmaPGprx7hqO6FVj+OG21ne37bCZtjRtrYd0DH4RA8/YcYbn2whk8WNVFTq3PtZbtBL/FXxD5XlV+Bp8mNsGoIi0aX3HR0j8nfKtw6uHUcFvuh4Z2WycnSki0MWfAgXf93Kxd3G05Xh5EAztu9nCmZowGYljnWGOapbTI31oOiJp7YhFJLGkQM9108hyn6fAeyRTWpriB0q3qKclSBq6CcLaXMbdHU7SFgkZSyH7DI+3PrUI0kZhZwGjAKmCWEOPjNZTbwjPf8CuBg86kLgH7e283A348VmEpQwpG7eZjB7ZZ8sqiJwdmtP4Q8HsmipU4uOd+YjHnhuREkJWpcf0c1/zc7FkQEuLcSquyxdjJG92DkHWPokpvONV/cSHymyRWhY8zbGZc6gB8unM36C2bz921fkFdRAMAbu1bwcv4Ssj74JZcs/TPrygvYlr/D3FgPEnZI/auxFLvT5zog9XmOuKW0D4yZeyWjX76CyPQYonrE42l0H/skRQk1B/ugBMcQz6XAHO/f5wCXtXPM+cDnUspyb3Xlc2CSt0pyDvB2O+dfCsyVhpVAghCi/TKtlxriCUsNNDRKcs8x5l2MO83Gz65xGI947y/Y42HEECvnndW8WuS2Gxw0NEr697UCEmTobqqXNaEvWRP64nF5eL77E1Tml5PQK8nci9osoB075z8lLp1f5VzC7E0f8vDgK6lzN7Hvsuaq16zN7zLviw/53aTRZkbbzHEWJD8OZb/qePM7EQVp/4SIQebGBuz/+EdyHhjHKb8crRIURfEtCXwmhJDAP6WU/wK6SCkLAaSUhUKI9jowdgP2tPh5r/e+ZKBSSuk+7P6jnVN4pOBUBSUs2Q7NNcn7Mom/PR6L3W58yz14/67VyThd8MJLzUuQNQ20Vl+GHf4N2wQWm4X+Vwxk8/z1/rngwI51U72l77ksKdnCnza+z+XdW2+XcWWf0byx4H9mRHdkMZdB2n/BmmUkH+2+NViMSos9B7q+BY4zTA/LVdPEvg+30vOaIQghsDpCoJGgohwP31dQUoQQq1rcbm7nqqdLKYdjDL/cJoQ4s6PRtnOfPMr9RzvniFQFJRxpKRjJ6ZHFx2n89bEYLp1RxS9mOrDZDvvdkR6wHLX6FjJypg3h87s+ZsxDZ5l/sZ9kU/vjK80dYr3Gd8lhfJecQz87rPZWVZNDbBaGTD6fTZffa3akbTlGQ7cvwZkHVf+GhiXeHY6FkbRET4K4n4G9v99C2vP2RtLOyiIy1awmK4oStkqPtVmglHK/989iIcT/MOaTFAkh0r3Vk3SguJ1T9wLjW/zcHfgaKMUYurF6qyjdgf0tzulx2Dn7OQpVQQlHjpkdOmzYYBtDc6zMe6+dsr4lHSz++yAyU49xWdSX1FG6ub1/Zz6W0wWiTuBbvpRwTl/fxdNZQkDEMHTxGK7vnkF23wo9t0HPHyDlSb8mJwD5c/PodX2uX6+pKAHh5zkoQohoIUTswb8DE4ENwAfADO9hM4D3vcd0E0Is8t6/EJgohEj0To6dCCyUUkrgK+Cqw8/3Pu/1wjAaqDo4lHQkKkEJR45rqc3v3u5Dtfmtm1l9+GoC0ycbQznjT7fz0WsJQLSxN4+Jkx/9SWga2VMGs2neD364mICbTgP7cayMibDApTkQfxwTVn1Iuj14lueBriOLKwL2e1BbUEHlhmIyLgqhzSwV5bgEpA9KF2CZEGId8B3wsZTyU+AJ4DwhxDbgPO/PAOl490eRUpYDjwDfe29/9N4H8CBwjxBiO8aclBe99y8AdgLbgX8Dtx4rQDXEE460ZIi4AJoWYOzB00lCg8hLfR5WIOVMG8KH17/FuIcnIMz+wB2aDjNHGBsAdnQ/nggLjO0JV5g/6fRYPGs3Q5MLAL1gP1pGYDq0Fryyjp5TBmGJUG9TiuJrUsqdwNB27i8DJrRzymjghRbHvQS8dITnbbNtvLe6cltnYlQVlHAV+xRo6XQ+B3VA/FzvRMnwkX5qd3SXh6K8o1YUfWd8H/jl6eCwQeRR/h9EWIzVP5cOhBtHBbxq5SksQebvP7RkWu4vQZrUIfZopJTkv5JHrxlqeEc5SQTPMuN2SSmfl1J+4PMnPgr11SRcaXGQ+AFUXgaefXSskuKA+H+DfazZ0fmdEILsqUPYPO8Hug5ru2OvKYZ3g39eDt/thQ83wb5qsGrGXHaPhGg7XDQAzupt/D0YuNwQGw013s6yHg+yvBqR4t+uwqXLd6NZNZJO7Xbsg0OZdIL7I3AtBFkKWEDLANtksIwNeMKqKIGkEpRwZukKiZ9D3ZPQ+Jpx32EtzSHC+MM2hup55+FcV03Cbyuxdg/dNvdHknP1UN76yVzGPz4R0YF+JT5h9Q7djO0JVY1Q08S27wt46/nF/Orz2/0XRwdZMtOxZKbj+vQbLMMGgNWCSDC35X578ucYk2NNH44LFL0UnM+D80VAB2qbH/MIcL0JIgnsd4J9htFQTwlfBxu1Ka0E17uj4ntaLMQ+AimbIGY22EaDpTdoPcA6CKJ+DskrIXE+RA7BvauC0l+8S+UTX+Ipqgl09D6VOqgL9hg7+1buOfbBZoiPhO7xvPvmapZ9uZWlb68NTBzHIHUJtfWI5Hi05ASExb9vE+4GF3ve2UTWdW2Gx8OD50eoGw3OF4BqWiUngNEaog7kHmj6HdRNAqla/CsnH5WgnCxEJDgmQ+L7kLwCUlZB0iKI+Q1YjCEP+8CuxuoTt07j0nxKfvomrh9Ddz+ewx0c5vHLap4j8Lg9fL9gIwB/vel1qkoP/3AKAvUNEGFHWANTYN33/haSRmYQ1d3kjR0DQS+AunO9wzkdGXZtAH091F3k7UmjhK0gn4MSCCpBUQ6xZia2Kqk7LsrGanZ7eD/LmTaELW9vQPf4f+InQN6irUjvBFRng4u/3vRaQOI4GllTh4gNXGO0/FfCtPeJlFB3OcbmsZ35AHGCvh0a7jn2oUroUglKGypBUQ6xpMUgPToi2oZIdGDP6YKwncBOt0EoqV8Ksd3i2P31zoBcf+GLy3E2uhGaQFgE3364gYqi4NrzSFYHLkFpKKyhdMUeul+WHZDrm8litZJ7+gZyz6gm94xannja2LHa7Zb8+g+N9BtWS+4Zxu2xp5r4bJGbMefWeRPaRjxN75CbO5jly5cH9oUoip+oSbLKIUITxN8/Hvvgruhl9VT89lNs/VOxpvt/kqSZcrzDPFkT/N+xddJNp3PqhQP55J/LmDDjNM6bOQZ7ZJDtL1NTB/ExAbl0wWvr6H5ZNtZgWdXkQw6HIG9Z2+X7v32kiQPFkvUroomMFNTUSP7yfBMTJ1h56VUnL851ceMMO3/7ZwOnDo9h7NjwW2WnhE/Vw5dUBUVpxXFmbyyJUdj6phA9dShVs79CugMzHGKWAVMGs/V/G/E4/b8z7vDzsjlv5hj6DM/E49KDLznh4BCP/xMUKSX5c/PoHY69T/QSoG3Tvvp6yb/nuPjbk5FERhrDq7Gxgod/ZXQTfubxSB5/uomNmz08/686Zs8q9WfUihJQKkFRjijq0kGI2AhqX10d6FB8Kj4zgZTsNPI/3x6wGNIyEynZXX7sAwNAVtch4vzfqK9ibSHuWiep43r6/dqmk7tpaODQEE7uGbXMf8fF9p06md0FsbHtL6dO76px160RjDmvjt/eH0FSYumhJnpKmFFzUNpQCYpyREITxN97Fg1fbKNp3VE3nQw5OdOGsGl+4FbzpGYmUby7ImDXPxLpdIHbAw7/7weUPyePXtNzg643jE/IWu8QT8yh29Qr21bP/vuqk9wzaumRU8OevUbl8rabbHg8MPNaO0bDjHY291RC28E+KCpBaSUM3wkUX7IkOIi/+0yq/rwYvSp83hgHXDWI7R9uwVV/HHsV+UBqZiIlwZig1NRBTJTfG6R5nG52zVtPVjiu3gEQ7Q+Z9e2tsXuvpKbG+EC54To7ectiiI8TeLwjQpomWjSUlUBgN5NUFH9RCYpyTBEjuhN5Vm+qnl1yaIlsqIvuEkv6qd3ZsWBrQK6flpkUnEM8NfWIOP+v4Cn8dDtx/ZOJ7RNey9oPEVm0t7Q4Kkrws+k2br+/kcZG43GPR+I8Ut4sMlT7+3ClKihtqARF6ZDYGSPxlNXT8PHmQIfiMzlTAzfMk5QRT1VpHa4ATNQ9mkAtMc6fm0fW9DCtngBoyTQ0iFZzUB6aZVQkH/t9BOldBING1zLsjFrGTapnxtU2MtIPT0SiwH67/2NXlABRy4yVDhE2CwkPnk3ZPR9iG9gVWxg0cDvlioEsuvdjmqobiYjzb9ncYtFISo+jbF8lXXul+PXaRyNr6tB6dPHrNZvK6ilatJPTXrzMr9f1N0/TUqifDLTeD8tmEzzxh0ie+MORfwdr98cBOtivNjdIJXDCpOrhS6qConSYtVs8cTeOMpYeNwXXN//j4Uh00OOsXvz4fmCqQsE4DyUQXWR3zVtP+gX9sMeH+dwKy1hjD6zj+l7oANvVIMJvE08FDvVBUUM8ragERemUyHP7Ye2VRPW/vw10KD6RM3UImwM0zJOWmURxEM1DObhJILH+XWKcPzdMW9sfTgiI+h+IeDr31hsB2kCIfNKsyBQlKKkERekUIQRxt5+Oc/VeGr8pCHQ4J6zfJdnsXVZAfVm9368ddBWUAGwSWLW5hIa91XQ9r4/frhlInrpkSl99Ekk6HVuNEwWW0RD9AYjw666rtKAqKG2oBEXpNC3aTvwDZ1P9/DI8JXXHPiGI2WMi6HV+P358d6Pfr50aZCt5AjFBNn9uHj2vHYJmCe+3IufeKooe/Zod5/yX8n8V4278AiJ+DRg8QkwAACAASURBVCINOHwJsgY4QMuByGe9VZfAbd6oKIGiJskqx8WenUbUpYOofOorkh6/EBHCHzA504ay+vkV5N50ql+vm5aZyMr3A9cs7nCyps6vS4x1j07Bq+sY/8l0v10zEA78fhE1C7cjPTp4JJbESGxpGcCdYL8DPF+C6wuQJYAVtAywXQ6WIYEOXfGXg43alFZC91NFCbjoyUMQQlD35rpAh3JC+lxwCkVr91Nb6N9dhYOtgkJ1HfixglL05U4iu0STMMi/q4b8LXKw9/V5jA8gx6ndmh8UGljPBccTEPUiRP0TImep5ERRUAmKcrxKCxCr55Nw9nZse17H89ELsPNb8ITe6h5rpI2+l2Sz+a0Nfr1uWmYixbvKg6b5nb8rKMbk2GF+u16gxF3cH2uXaKyZFcRPWUbS9QuAx4B/ALsDHJ0SNNQclDbUEI/ScboOO1fA+o+htgw8LjQkEWlAaSly+XrEijnQfzwMPB8c8YGOuMNypg7hm0e/4tRf+m8r+6g4BxarhdqKemKTAj/HwJ9LjF3Vjez/6EeGP32BX64XKFJ6qHh9NhnPvY295xakSyLsB5P4SOBuYCxwPzAR9Z3xJBYmSYUvqX8NSse4m+CLp2HlXKgqBI+Tw1t3C3cTuBpg0+fw3m+hfE9gYj0OWef2pXxbKZUF/l1Vk5qZGBRLjZs3CYzwy/V2v72JtPFZRKYGPjEzTz2uvWeQeO1jRPRah9Ca0CKcCKEDOlCPsfHfl8BVwMVAQwDjVZTgohIU5dh0N3z+NBT9CO4ObK6nu6GpFj75k5HMhACLzcKAKwb5vSeKMQ8l8EuNZY0x/8RfmwTmz10b5r1PmvBUjcGathotsiObbNYBXwMTgMBsYKkEkmrU1h6VoPiLlFC9Fgrnw56XYP/rUPoFeEJgh+DVb0NpAXhcnTvP1QQLnwLdY0pYvpY9zf9N29IyE4Njomx1HcJPDdpq8yuo3lRCxkWn+OV6geCpug4RsQUtojP/ZhqAPODnJkWlKKFFzUExm7sOShYYCYm7GqTbuGEBzQ7okHoRpE8BR49AR9vGY4/8gdf/+RwWAZqA9IQocnsk8fjkEYeOydtdxtX/WMLmP11O1n1vMSIrhXduPxuQvL1sAx+9eRkvv/1h4F5EB/UYl0VdUS1lW4pJHpDml2umZiZRHBQVFP/tYlzwSh6ZUwZhsYfX209ZWRkTJkxAepwUlWzGYoHUVOOxhQvh7rth5UpITAS7HR54AC6/3Hh82TK45x6orm4A5nDPPTncfPP9AXstSgCESdXDl8LrHSLY1O+EjbeD3mjcWnEbQyEARe9DyUeQdRd0udTvYR7JihUr+OjdN1nzyJVECDelNY1s3FfJDS8ta5WgzPs2n2tG9z7086qCUjbuq2Bgt0Sj6lJREojwO02zaAyYPJhN89czbtYEv1wzNTORnXl7/XKto5E1tWg9upp/HSnJf2UdY1+fbPq1/C05OZm136+m+tOpPP39VmLjdO67zyiejh0LM2bA668bx+7aBR98YPz9wAG45hp47z0YPhxKS+2cf/4zdOuWw0UXXRS4F6T4j+qD0i41xGOW+p2w/mZwV7WTnBzODXoTFDwH++f7JbyOKCwsJMXqJEIYiVRKbCRnDehKgsPOtzuak443vy9g2qheh36+b9Ig/vTR+uYnctZBTbHf4j4ROVcPZdO8dX5b+hssQzyyut4vK3hKv9mNZreQNDLD9Gv5m5SSose/InbCQoSmH7r/yy+NiskttzQf27Mn3HGH8fcXXoCZM43kBCAlpYknn6zliSee8F/wihKEVIJiBk+dt3LSwOErXY5Kb4Q9/4DK700LrTMmTpzInuIKTnnoXW6du4LFWw4AcPXo3sz7Lh+AlTuKSY6OoF/XuEPnTTk1izW7ythe5G18JjSoDo0EJWNUdzxNHorX+WdybzAM8UhdQl29X5q05c8xNgb012Rcf6p8Yz2uPTsQjta9gDZubE4+2rNxI4wY0fq+kSOb2LjRv315lABTk2TbUAmKD8XEePfUKP4U9EZe/riI2/+yE4CZj27n7S/LWh8/wdgRuKCwETF2BX97q9CopOz+B7fffjsvv/yyP8NvIyYmhtUP/4R/zRxDamwkU//+NS8v28a0Ub14+/sCdF0y79t8rm4xvANg0QT3TxrE4x8frKJIcIXAZGCMzRBzpg5h0zz/TJZNzoinqrgGtyuAE4kPbRJoMfUy7gYXe97dRNZ1Q029TiDUrdxD+X/X0PXRkQhx9JHz226DoUPhVO/OClIaGx23ZmvnPkU5uagExdekhP2vdWBYp7W0RBvPvVmI06VDw05jQm0QsNgiGD8gnT9cPoznrxvNO6t20SM5mqyUGBZvPcA7q3Yx5dSsNudNH9uHJVsPsLu8zmj5YHf4PfbjdXA1jz+GeSxWC4ld4yjbV2n6tY5EVvung+ze9zaTdGoGUd3ijn1wCHHuquTAb74gffZEbF3SMH7hmw0cCGvWNP/8wguwaBGUlDQ/vmpV6+dcvdpFTk74rnJS2qEqKG2oBMXXan4w5p10UmqClQkj45mzoMSYPFu/3YTgOmfr1q1sq27+FcnbXU7PZKNKdPXo3tz9xnf0SYuleztdUG1WjbvPH8izn20CqeMqt/kt7hOVNqQr1igb+1b6p9FcWs+kgDZr81cH2YJXwq+1vaemiX13LSD5ttOIGp4BpAKtq2HnnAONjfD3vzffV1/f/PfbboOXX4a8POPnsjJ48EEXDzzwoNnhK0FD9UFpj0pQfKihoYHcMZeSO/1bcmes4/f/6dwH3EPTu/GXN/bj8bjBGfiJk7W1tcz4z1JyfvMeQ373Ppv2V/LwZUZzrckjs9i4v5Jpp/U64vk/G9cPt64jrVFUPpuH3tDJPioBcnCYZ/M8/2yCmJqZGNBmbdIPmwTW76+mdOVeul82wNTr+JP06BQ+9DnRo3uQcEWO995IoPVKPCGMFTqLF0OvXjBqlLGiZ/Zs4/H0dHj1VbjpJhgwwFjx89OfjuQnP7nCr69HUYKNWmbsQw6Hg7yFs2DPfwDJyx8Xs2pLLWCsIjvc4WPMvTIiGZUTw+uflYLU2znDv0aMGMHy71bDvF8are5bSI2LxPWfGW3OKfhz8/LRCJuF/c/PgDNuouqdWmr+voL4e840PW5fyJ46hNfO/g8Tnr4IzWJuHh/wXY1r6hCZ5i4x3vXaD/S4PAdrlN3U6/hT6bMrwKOTeu/phz1yLw8//DFGd1hDejrMm3fk5zrzTPj+0Nz4KIyNBJWTSphUPXxJVVB8TXOAaDvZMDneSkVN8+z+8moXKfFthz1+fX13Zr+6D12aO2Gxw6x2GHAOWI7ng0WAzQE9hhL7izE4NxXR8PUOn4dohuT+qcSkx7JnSb7p10rLTAzoSh6zh3iklMbOxTPCp7V91QdbqF1cQPrsiQjr4W+jo4Asju/t1QL0A46y7EdRThIqQfG1iDQQbT/Mxw+PZ/6iMmMSLPDyxyWcPbztZMEBWQ5yekXx0dIDpofaYcOvhNTeYOnkPBJbBEx6ADQLmsNGwkNnU/OPFbgP1JgTp4/lTBvCpjfMX80TyAqKPzYJrFhTiLveReoZmaZdw58a8gopfXYF3Z67EEt85BGO+gDo7GRg4T3n/ROKTwlBBxu1qTkoragExdcSTqe93icXn57IuKGxjLjhB3JnrOOb9TXMvrVnu0/xmxt6s7eo1uRAO0GzwLl3Q3o2WDvwQaZZkREx6CNvhbjmoQNb3xSipwyl6smvkJ7AD2EdS/aUwWz930Y8TvexDz4BgZyDcrB6YmZfkvw5a+k1fShCC/23G9eBGvY/8Bld/3gO9l6JRzmyN7AESKZjI+lW77FLgfbfFxTlZKPmoPhQba03qUi7GIr+x8yL0ph5UfOeLrN+1oNZP2u7305WeiQbXmsufw8dkIbucRsNzoKF1Q4T7oT872D9Aqgu8m4e2CIZs0aCpsGACcjowXi+3Y7nxyosI7MRXZMQQhB12SCa1uyj9rU1xF4/MmAvpyPieyaS1D+F/C920PfC/qZdJy0zieJd5Ugp/d/AzOQJsh6nm13z1jNx5c2mXcNf9AYX++/+hMTrhhB9xrGTCM/edDzfPI9tymcIMQ/j+2DdYUdFYyxLvhp4FEj3ddhKqAiTqocvqQTFDOmTofgD76aAnaRFQsY1wZWcHCQ06D3auJXvhh0rob7cSFQi4yBjIGTmgmZFOF3w7XaoqMHz1WqIjsQyehBalyTi7z2Tstvfw56bQcSQ4G55njPV6IliZoISHe9AaIK6qgZiEvyzo/BBssbcHiiFn2wjLjuVmN5Jpl3DH6SUHJj1JRF9k0mcfvS5NLKmAfeXPyC37wcZAbwIPAu8ArwBHGzYmAxcC1wHxJoXvBIaVILShkpQzBDZHXrdC/l/MTrDdpSwo9tzqJgFEad/h31IBtZTUtFizJsfcNySMo3bEQi7DSLt0Og05jhU1yOLK6BLEpbEKOLvHkfVnxeT8vzlaHFHGscPvAGTB7N01he4GlzYHOb1ckn1VlH8nqBU16FlmvetPX9uHr2O8YEeCsr/tQr3gVq6//vSo1a53Ku2oS/bDB6PUVyMjvQeHwfc5r0pitIRQfg1PUykXQyZt4HWweRCi4S4oTDgCfTyJhreXU/VE4som/46ZTfNR69zmhuvCURyfPMPfbthGdzn0I8RI3sQOa4XVc8u9dvGfMcjpmssXUd0Y8eCraZeJy1A81DMrKA0ldVT9GU+PSYPNOX5/aXmix1UvbeZjKcvQIs41nc6AchDI58i3r8JpxKqVKO29qgExUzpV8GAP0PMQO/Knnbe3LQosCVDj5sg+2k0RwxR14wAqwaNbkBi6Z6AiAqdTqwHiW4pxtDOhJGwpxi9pHU799gZp+IprqXh480BirBjsr3DPGZKzUz0ezdZqetQ2wAx5nyI7npjPRkX9sN+xJUuwa9paynFf1pCxtMXYE059n8n68i+iFO6gc0CQiCSYvwQpaKEJzXEY7b4ETD439CwGwrfgtoNxm7HWgREpEPXKyH+1FZzThwXDKB+3lpw6yDBmpkAugRLaO0epvXvida/p1HiHjMIz5K1iIvGIiKNqpKwW0h46BzK7v0Q26Cu2LKCc55C/ysG8uV9C2iqaSIi1pzhNmOpsZ8rKHUN4IgwbZPA/LlrGfLIBFOe2x/c5fXsu/sT0h4aR2R2aofO0feVIXcVY/3peegbdiG6Hm2lj6K0ECZVD19SFRR/cWRC73thyH9h2Jsw9BUY8CQknNZmQqwWZccxaQBEWEiYfTHuH0upfuxz9NpOzGcJAkKIQ+P1Wo8uaL274Vmyzvjm7mXtHk/sz0ZRNfsrZJO5y3mPlyMpiu7jstj2/ibTrmEM8fi5glJTh4g1p3pStamYhv01dDm3z7EPDkLS5aHwvoXEXXQKsRP7dvAcN+5PV2OdMBQt1oF1zAAsvbqYHKkSFlQflHapBCVIRV83gsTnLsfWP434Ry7A0jWOyns/wB3AjqMnShvaDwToedta3e84rx/WzERq/vNtgCI7tpxpQ9lk4jBPamaS37vJyup60zrI5s/JI+vaoaZvE2AGKSVFf1qCJTGS5F+M6vB5nmWb0NIS0E7pZmJ0inLyCL13j5OEiLBizTAmmQqrRszNY4iakkvlrxfQtLwgsMEdJ6EJLONy0fML0Xc3d8oVQhB3x+k0fb+HxhW7AhjhkfW7JJu9SwtoKK8/9sHHITVAFRRMmCCre3QKXltHr+tDc/VO5Rs/0LixmK6PnIvQOjasqu8tRd+yF8uEoSZHp4QtVUFpQyUoISRyQj/iZ02k9sWV1L26KiS6sR5ORNqxnJWLZ+VGYxddLy0mgvgHz6b6b8vwlB7ezCrwImIj6DWxH1vf3WjK8ydnJFBZVIPb5THl+dtl0h48RYt24kiPJX5g2rEPDjJ1K3ZT/t+1dHv2ArQOTkw3hnbWYD03FxEVhC0BFCVEqQQlxNj6pZL4l0txbSwKyXkpAFpKApbcU3B/vQbpap53Ys/uQtRPcqh66uugTL7MXM1jtVlI6BJL2f7KYx/sI7LanCXG+XPzQrJ64txVyYHfLiJ99kRsGR3fR8ezdBNaeiJav+BuOqgEOVVBaSP8ExQpwbUS6mdB7c+NW/0s474g7r9xNFqCI+TnpYh+3REpCXhWbGjVByV6ylCklNS9Zf4mfZ3V58L+HFi9j1qTNjv050oe6XQZzcQiffuN31XdyP6Pf6Tn1YN9+rxm89Q0se+uBaTcdhpRwzueaOh7StG37sNyzhATo1PCn+qD0p7wTVBkIzS+BFXDoWYyNL4AzreNW+MLxn1Vw41jZGOgo+20UJ+XIoTAMioHWV2HvqV53omwaCTcfzb172/Aubk4gBG2ZXPY6PuTbLa8td6U5/fnSh5Zbc4mgbvf2kiXs3sRkWJe+3xfkx6dwoc+J3pMD+KvyOn4eU437oVrsJ43FGHibtCKcrIKzwRFL4XqiVD/e9B3A/W03mFYGvfpu41jqica54SgUJ6XIqwWrOOHoa/fgV7U/MFsSY0m7o4zqHryq6DroJs9dYhpq3nSevpxJY9JE2RDcXin9NkV4NFJvef0Tp3nWboRLSMJra8a2lF8QFVQ2gi/BEWvhurzwfMj0NCBExqMY6vPB1ltdnSmCOV5KSImCsvpQ/AsyUPWN1eyIsdmYR/RnernvwmqVvi9zu1D+dZSqnb5PpEwhnj8VEExYYJs7c5yqreUkn5hP58+r5mqPthC7eIC0mdPRFg7/nao7y5B37Yfy9lqaEdRzBJ+CUrtjaAXAq5OnOQyzqm50ayoTBfK81K0bqlo/TONJKVFE7e4m07DnV9O4xfbjnK2f1nsVvpfMZDN830/zJPqx/14zJggm//KOnpOHYTFHhoNqhvyCil9dgXdnrsQSyfa8TcP7eQiHHYTIwww6Qb9fXDfDe5rwf1TcD8MMri3pghJqlFbu8ImQRFCcO/dN4J7GdDEn59v4OHZrXtWDD2ziqtvqm1138zbaonqXk5NTaNxriefO++8EyEEpaWhNewTyvNStMF9wGZFX928KZ+IsBpLj//zHe69VQGMrrWcaeYM86T5sVmbrysoUkoKXskjK0SGd1yFNey/fyFd/3gO9l6da0fvWbIBrVsyWh/zdoEOKFkKnkfA3Q08N4B8AeRbIF8F+SS4R4N7DOjvhOxCAyU0hE2CEhERwbv/e5vSsvbbpW/e6kHXYclyF3V1rf9R9e1l4f1PnICOXv8vvvrqK7p1C91ukK3npaxG6sH/JiKEwHLGUPQ9Rej5+w/db+uVROz04VQ++RXSnz1CjqLHmb2oLayhbGuJT5/XX83apK4b+/D4cJPAkmW70CKtJI0I/vkYeoOL/Xd/QuL0XKLP6Nm5c3eXoG8vDN9VO3IjuIeC/hRQAdQedoAbaAC5Gjw3gmcqyNAZUg5qqoLSRtgkKFarlZunwzN/b38J6OvvNDF9ip2JZ9v44NPWEy+vvsLO/PecgIuvF73I6WPHYLWGRpn6SJrnpRyg+tHPQmJeioiwYR0/HM93m5CVzf8fHRdlY0mJpmbOqgBG10yzaGRPHuTznijR8Q6khLqqjsydOgF1DRDp200C8+cYk2N9vSrI16SUHJj1JRGnJJM4vXNdX6XTZTRkmzgMERmGQztyG7jPAkqBjqxsrAO5EDxXggyOLw8hTSUobYRNggKS237m4LW3nVRVt13JMv89J1Mvt3P1lRG88W7rBKVfHwslpToVlTpvvFvHtKmT/BW0qVrNS7kvNOaliKQ4LCOzcX+91ujVgVFdib9zHI2Ld9K0em+AIzRkTxvKpnk/+HQCrxCCtMxEik2uovh6eMdd72Tv/zaTdV3wt3kv/9cq3AdqSfvNWZ1OpjyLN6JlpqD17mpSdAEk3eCeCNTQesXjsTSAXAb6oyYFppzMwihBgbg4G9dPtfPXf7WuFny/xk1qskbPHhYmnGllzTo3FZWtk5grLrYz710n3652Me6Mgf4M21SH5qVMzqXyNwtoWlEQ6JCOSevTDS09Gc836w8lAFp8JPH3nUXV00vwVJpcYeiAbqN74G5wUfzDgWMf3An+mChr9EDx3fDO3ve2kDSqG1Gd6L4aCDVf7KDqvc1kPH0BWkTnKqT6rmL0nQewjA+tBnQdIYRg+vRzgSpA4nZLUjNcXHyZMVz+8lyd1AwXuSNdDBjk4pnnPCz8TCd3pHFfTGIV/bP/SG7uUK6//vqAvpbQpRq1tSesEhTwcNctkbz4ahN1LebHvvFuE1u2ecjKraTPiCqqayTvfNi6ijLtCju/e7yB88bb0SzB/UZ7PCIn9CP+9xOp/XdozEvRRmZDQxP6xp2H7osYmoHjvH5U/WVxwOMXQhit7+f5dpjHH0uNjU0CY3z2fPmvBH/vk8atpRQ/tpiMpy/AmtK55Ew2uXAvXBu2QzvR0dFs2LCKhgZjWPXzLyTdDptKNHWyRt4qG98stvLYEzo52YK8VTbyVtkYOULw2txo8tY8xNy5cwPwCpRwFUYJigAESYkaUy6z8+KrRhVF1yVvve/ihyXxFOQlUJCXwPuvxvLGO60TlMzuFh77jYNbfxoDIjkA8ZsvlOalCIuG5axc9M270AubV1PFXDcCWdNE/fvmbNrXGQdX8/hymCctM5HiXSZPlPVhBaV+fzXl3+2j+2XZPnk+M7jL69l/9yek/epMIrNTO32+Z/EGtJ6paL26mBBdMJBccL6LjxcYv8dvzNe5emr7Hw3JyYK+fQSFBw7/na8Hz9MmxxnmVAWljTBKUAD7VMDKvbdGUlpuDOEsWe6mW7qgW0bzSz1zrJVNP3ooPNB6mOfnM2Po0/9aEB3bxTQUaYmhMy9FRDuwjBuKZ9kPyDpjWEdYNeIfOoe6+Xm4tgd2GXja0HQsERb2f7vHZ8+Z6oelxrKmHuGjCkrBq+vofnk2Vkdw/pvRnR723/spcRf3J3Zi386fX1CEnl8UlkM7zXSmTXEw702dxkbJD+slp41qf37O7t2SxkbJkMHtPb6znfuUDlF9UNoVNglKbW0tOH4OWOmSplG/N4mHH4xi/Bk2Vn4W3+pYi0VQuCmR9K4aL78Qw1WXHCzbWsFxCwAFBQWkpKT490X4SfO8lKFGv5QVBYEO6Yi0rslo2Vl4Fq9FeoyVAtauscTeMobK2V+hN3amIZ9vCSHI8U6W9RWzlxrLJqd3k8ATH6qQUhqt7WcE5/COlJLiPy3GmuQg+ZZTO3/+waGd84chIoIzAfMNyZAhFgp2wRvzJRdOavuxMP8tnYFDXfTu7+bOOyxERraXoITenmZKcAubBAUAyylgHQ4cz5uJDawjwBI6bbpPVOSEU4x+KUE+L0Ub2AuiItG/b+5g6RjfB9uANGr+sSKAkUHO1MFseWs9uo/2QEozeUdjo3rim00Cy1fvR290k9rJXiL+UvnGDzRuKqHrI+citM6/Xs/X69F6dUHLCtehnYOM4fFLLhbc96Cn3eGdqZM1Nq6zsfQrC/c+4OFAmyEegI5341XaoSoobYRXggIQMwdEKtCZWfpW45yYl00KKniFwrwUIQSWsYPRD5Sjb29eZhz3izE41x+gYUngSsvJA9KI7hLDnqUFvnm+bglUHKjG4zapr0R1HfhoiXH+nDyypgdn75O6Fbsp/+9auj17AVpU57+w6PlF6LtKsJw1yITogo0GuPjpTI3f/0ZjcLvDN4YxozWmX6vx3N/aS8gzTYtQOTmFX4KiJUH8QtAy6VhGH4kUPdAjPzTOPQmFwrwUYbdhHT8Mz+otyDKj7b0WZSfhoXOo+b/luIvab9DnD9lTh7DpjXU+eS6rzUJ8Wixl+81p7e+rHigep5vd89cH5eod565KDvx2EemzJ2I7jqXPstGJ+7OTYWjnIAH0p3t3wZ13HLt534P3afx3rk5NTctv6Q6w3G1ahCcFVUFpI/wSFAAtA+K/BMcDIFKA9iYExhiPOR5AynegFPTiIqTT2c6x4S8U5qWIhFgspw3EvXitMZcCsPVLIfqqIVQ9+RXSR8MsnZU9dQhb392Ix0et+NNMnIcia3yzSWDhgm3E5aQS08l9bMzmqWli350LSLntNKKGH1/bfc/X69F6d0Xrmebj6IKQlNTW1IC4l5bvk+PP0vjoPaMKPfN6jeefa05cMjIEB/bYiI01Ki1ff2Fl5AgriMl+DT28qD4o7QnPBAVAxILjTkjYDDEvgv0asJ1r3OzXGPclbAbHnYhob2fIpgZkcSF6cSHSdXImKsE+L0XLSkfL7GKs7PEu7426YjAi0kbta2sDElNCViJJp6RQ8MV2nzyfmSt5jCZtJ56g5M/No9f04KqeSLdO4UOfET22B/FX5BzXc+g7D6DvLsVyVvg0a2zD5YTGWuPWVIdsqkO6zkMShVFN6awoED8H4fB1pMpJLnwTlIOEBvZzIeZvEDvfuMX8zbhPeF++vcWKBimhqemkraTA4fNSPg+6eSna8P7gdqP/YCQEQhPE33sWDZ9uwbm+MCAxZU/13Q7HZnWTPbRJ4An2QGkqraPoq3wyJwfXh3jpcyvAI0m95/TjOl82OnF/nod10nCEPXyHdqSmte7dIyWyvBbpfAfobPIaCWIYWB7xZYgnpwBVUIQQFiHEWiHER96fk4QQnwshtnn/bLdMKoSY4T1mmxBiRov7ewkhvvXeP18IYffeL4QQfxVCbBdC/CCEGH6s2MI/QekAIQS03BwwPhEt2nedNkNR87yUWCrv/zCo5qUITcNy5jD0bXvQ9xYDYEmKIv7uM6l86mv0Gv8vd8yePIjtH2zG1XDiy55NG+KpawBHBMJyYpsE7npjPRkXnYItLnhWbVR9sIXaxQWkz56IsB7f25rnq/VofbqiZXa+mVvIkBIhde9fpZGo1DcAAhE1CqxfAAlAR5ahR4E4AywfE869o04CdwKbW/z8ELBIStkPWOT9uRUhRBIwfEWXdQAAIABJREFUCzgNGAXMapHIzAae8Z5fAfzMe/8FQD/v7Wbg78cKTCUoB0VEgs0GSalQU4V0B66/RrA4NC/lqiHGPj4rCwId0iHCEYHlzGF4lq9H1hj7GkSc2oPI03tR9exSn3Z37YiY9Di6DM9g5ydbT/i5zBrikdW+mX+SPze4Wts35BVS+uwKuj13IZb440ua9B2F6HtLsZwZxqt2PG5wNoDuad58WNeRdXWI5FTji5oYDta1IG7BmJNy+Bc1DYgC+oHlObB8CMJ3+zqdtALUqE0I0R24CPhPi7svBeZ4/z4HuKydU88HPpdSlkspK4DPgUnCWNJ3DvB2O+dfCsyVhpVAghAi/WjxqQTFSyQmI7pkoEVHI+LikaUlRklcMeal/H4itf9aSd1rwTMvRUtLRBvcB/fXa5DeZbmxN5yK50AtDZ9s8Xs8OVOH+mSYJ62nOfvx+GIFT9XGYhoO1NJlQm8fRXViXIU17L9/IV3/eA7245ywe2ho5/zhCHvnNhEMCbpuJCbuJqTFhl5XD5XlSJcHWVkF9ghEZIvETnQD65/But9IQsQ1ICaC+ImRuFi+ANtG0GaAOLFqnBJwzwIPAC0/7LpIKQuB/2fvvcPjKq/17fvd05vaqMuWe5NtuYONDcYGO5gQwDTb1JQvIQUOECAJJ+Xkl8KhhAAJpBCSQ++JgYQOpmOKbblXbLmp9xmNpmhmv98fe9SsNhqNiu19X5cuy6O93/2ONGXNWs96FtF/u1KL5wHtLbSPRm9zA/VSyvAxt/d0TrfoAUoUIUSbn4MzCUwmZF3toH8SH6606lK2Dy9dijJ5FCLZSeSzHUgpEWYDKbctwfvoRpoPDW5ZauJFUyl+Yx9Bb/9+NxkDZNYmE+CBcuDRIkZfUYhiGPqXDtXfTOlNr5F61Uwc/TCLi6zbijIh98Qr7UgJzUEINYFiQAojsqoCmpsROSNQklLAmYRwd+OYLaygXAXGR8D4HzD+E4z3gTJ3UO/GSUPiMyjpQogN7b6+0+FyQpwHVEopN8az2y5ukz3c3tM53TL0rzLDECEEItWtPbl9Q+evMdwYjroUIQSGBdOQNQ2o+7Tg3DgiBdc359FwxzpkKNzLConD7rYzYtFovvz3rt4P7gFnig01ouJr8CdoZ1H62WKsRlQOPbl1WJR3pCop/8U6LJPSSb1qRtzrqF+WoZbWYjh9eAl++4WUEG6GYBMgkWYb0h9AVpQhnEmIjKxWHZKSnIIwnXgTmo9LEh+gVEsp57b7euiYKy4EzhdCHASeAZYKIZ4AKlpKL9F/K7vY7VFgZLv/jwBKgWq00o3xmNt7Oqdb9AClG4SiINyZyIZ6ZFCfMdHCcNSlCJMR45mzUTfvQ62qB8C2fCLG/BS8D38+qHuZsqqw37N5hBBaJ8+RxAaA/S3xVLy9H1uei+SCofcHqf3bBsKVjWT+dHHcTrbSHyL89glW2mnRmUSawWxFKiatXO31ILJzEa6kYen8qzP4SClvk1KOkFKOBlYD66SUVwIvAy1dOdcALwEIIfKEEO9Eb38DWC6ESI2KY5cDb0it5PAucMmx50fXvTrazTMfaGgpJXWHHqD0gDCZEGnpyJqq1kF1OhrDTZcikhwY5k/ThgoGggghSLp+EYHPDhP49NCg7WPiBVM48kEx/tqmfq2jlXkSp0ORwRCosl9DAjVx7KyE7SlevG/vp+HFXeTeswLFHL8GIrJuK8rEPJSRJ8BQ0HY6E4xmMNuQoRCy7CgYTYicPD1TMqwZVkZtdwDLhBD7gGXR/wPkAGEAKWUt8Gvgi+jXr6K3AfwY+KEQ4ks0Tcrfo7e/ijby+kvgb8D3e9uIHqD0grDZweFE1lTqepRjGG66FCU/C2VsLpEPtiBVieK0kPKjM/H84SMi1b5B2YMlycroZePZu3Znv9bJzE+l8lACAxSvD+Gyx/3pOdQQoPTVfYxaMz1he4qHwJ5qKn/7Prm/X4ExPf7uEXVfKWpZLYbT4zN0GzYcozPBbEcqBtT6OmR1JcKdgZLm1rMmOj0ipXxPSnle9PsaKeVZUsoJ0X9bXojmAw+2O+cfUsrx0a//a3f7ASnlKdHbL5VSBqO3SynlD6SU46SU06WUG3rblx6gxIBISgGhIOuHXnMx3GjRpShZrmExx0eZOREEqJv3AmCemo39vAIafvf+oFnhFyTAtC0jPy2xJR5PE7ji9/Y58vwOspaOweIeupbScG0TpTe9RuZtZ2CdEr+gVTYFCb+9RTNkMx2npZ32OhMpwWIHoxkZDiPLS6E5hMgZoX3A0jk+GD4ZlC6RUj4gpXw54Qv3gB6gxIAQApGWDv4mZFPjUG9n2CGMCq5r283xGUJdilAEhtNnoBaXoh6uAMCxagYyouL757ZB2cO4r06m7IujNJbHL7DOSHgGpRGRFP+bVfFjRUMqjlVDEUpvfp2k8ybhWj6+X2tF1m1FmZyHMuI4Le2okQ46E8xWJALZ6EWWlyAczg5CWJ3jgCHyQRnu6AFKjAiDAZGeobUen8Q2+D3ROsdniHUpwmrBsHgWkU+3a+ZkBoWUH51J09pthHZ3JUhPLCabifFfm8zuF7bHvUZmgluNpbcpboGsd38tnj015KyYkLD99AUpJZW3v48xzYb7u/P6tZa6twS1og7DouOwtCNVCAW0L6MJzDatfViNIKsrkZ56RFYuIilZL+nonBDoAUofEGYLIiVN06Ooumi2K1p1KdvKhlSXoqSnYJg5QTNxaw5jyHCSdN1CGu58F9U38AFmwapCdvWjzJORn0plIkWy/RgSePDxzYxaPR3DEHW61D+1lcDOKrJ/fTZCif+NVzYFCb+zBeM5c46v0k6LziTYBIqilXMMJhACGQggS0vAYEBk5yHMuhD2uEXPoHRCD1D6iHA4wWpD1lTrotluUFJtJP/m3DZdypH6IdmHmDAS4U4msn47UkqsC8dgnp2H54GPB/xvN2bZeKp3VdJwOL777s5Loa7MQyTc/0C4P0MCpapS/PiWISvv+D45TO0jReTddy6KvX/zXiLvbEGZMhIlz52g3Q0wUmplnGN0JgiBlBK1vhZZVYFIc6OkpSMU/eVc58RCf0THgUhJ09r6PA1DvZVhS0ddyitDoksRQmA4dSrS40PdrbUaJ317PuEDNQTe+XJAr20wG5m0cmrcWRST2UhyhpPaMk//N9MY/5DAqo8OY7SbSJ3d48iMASF0qJ7yn71Dzp3LMeW6+rWWuqcEtaoBw8LjpLTTojMJt+lMWqavy+ZmZEUpBINa+7C9//OVdIYBegalE3qAEgdCCE2P4vMi/f3zuzjRGWq/FGE0YFw8C3XbftSKWoTVSPJPluD522eESwc2wCxYM6OfZZ60hJR5ZD8cZIsf1QYDDramIeINUnLDq6Rfdyr22bn9Wkv62pd2hrlwtBudSeuPfY2aENbuQGRmI4zHUalKpweGlQ/KsEEPUOJEGIwIdwaytlqffNwLHXQpv31rUDQg7REuO4aFhUQ+3IxsCmAa48Z5xSzq73gX2TxwWqL8xWPwlnqp2Vsd1/kZ+akJEcrGqz8JN4U4snYno6+M30o+HmRYpewnb+I4bSTJF/Uv4yGlJPz2ZpSp+Si5aQna4QAgJYRDWjlHiA46E9BKbWp1JbK+DpGVg0hK0YWwOic8eoDSD4TFikhK0Scfx0CrLiVzaHQpSl4GyoSRRD7YjFRV7F8rwJBmp/GxXr2C4r+mQWHyJdPizqJk5qcmxE023gzK0bW7SJ8/AltO/8orfaXqvvWgSjJ+uLDfa6l7SpA1HgwLpyRgZwNAe52JqmqBicnSGpgAyGBAc4QVQivpmC1DuGGdAUFvM+4SPUDpL05XdPJxjS6a7YVWXcolhUOiS1EKx4PJiLpxD0IIkm86A/+7+wluOjpg1yxYXcjOZ7bE9djQSjwJaDWOc4rxUFjbN7y4C9+HB8m5cznC2L+XJ+kLEFm3FeOKOQjjMCzt9KAzAS37I+vrkJUViFQ3ijtDF8LqnFToj/Z+0jb5OASN+uTjWBgqXYoQAsOiGahHKlCLy1CSrSTfciYNv/8AtT7Bk4Oj5C3IJ9zUTNW28j6fmzkqMfN44smgNJV4qN1QSt4Fk/t9/Vjxby6j+g+fknffuRiSrP1aq7W0M20USs4wK+2015kYOutMAM0RtqIMGfDrQtiTBT2D0gk9QEkArZOPPfrk41gZKl2KsJgwnjmbyOc7kPVeLDNzsZ01gYbffzAgGTAhBFMui2/CcSI0KDIYirao9s0f4+ATWxh5UQFGW/9ae2OlucxL6a1vkP2rpZjHpPZ7PXX3UahtxHDa4AVYvdKVzsTYpjNpPczXiCw7irDZNb3JQAphpYSID0IVEG4Aqfs76Qwf9AAlQXScfBwe6u0cFwyVLkWkJWGYO4Xwe0XIUDPOq+agegI0vbRjQK43ZbVm2tbXACgzARONWwSyfRFUSim18s41g+N9ovqbKb3pNVKvmolj0ah+ryd9ASLvbsNwzjAp7UgJkbA20E+NgLmzzgTaC2FrtQ6d5AEUwjbXQsn/QdE5sGk5bL0Uir4KG5ZA8f+Cv3hgrqvTPXoGpRN6gJJA2iYfV+l6lBgZKl2KMi4PJdtN5JNtYBAk/3gJvmc207y/JuHXypqZg2IyUPZF37QuzlQ74eYITZ5+lJ+8Puhjead2QylqKEL6wvz4rxsjUpWU/2IdlknppF7V/24hKSXhtzajTB+FktP/TEy/adWZhMBoiZZzOr/symAQWVYCCG3In6V/Ja7u99MMB34Lmy+A0v+DcD3IMKhBkM0gg1D1b9h+Dez4/yAUXweaThzoAUon9AAlweiTj+NjKHQpyrzJ0BRA3VGMMScJ13fmU3/nOtRAYtvGhRCaWPbpvpV5hBD9nmosvX1vMS5+tIgxV80YlDbW2r9tIFzZSOZPFyfkeuquo1Dvw7BgiEs7UoXmY3Qmhs6lGiklsqEeWVmGSElFSR9AIawagN3fg9o3QIa0YKRLItrPmnbC9ishMHAich2dntADlAQjhEC40yHQhPTpk4/7wmDrUoTBgGHxLNRdB1HLarAtHY9pYgbev36a8GtNWVXIrue3oUb61o6emZ/ar04e6embQDYSDHP4ue2MHgRre+/b+2l4cRe596xAMfe/FCMbA0Te3YrhnNlDV9pprzOhe50JRIWwlWVIf5OWNXE4B3BfKuy7DXx7tWxJTOdEtAzLru9Cs+6aPbDoRm1doQcoA4BQDJpotl6ffNxXBluXIhw2DItmEPloC9LnJ+n7pxHaWkbgw8TW4NOnZGLPcHD0o4N9Oi8jP43KQ/HrUPqaQSl9ZS/JUzNxjh7Y8khgTzWVv32f3HtXYEzv+4ygY9FKO0UoM8agZA9BaSdGnUnr4U0+ZFkJwmIbcCGs0+mEhk/AWwQyyCP/qeK6uw8C8Mu/HSXvvCJmXrmdglVbefoNrcQ55sLN7DnkBySE66D0YW688UbuuuuuAdunjs6x6AHKACHMZn3ycZwMti5FyXGjTBlN5P0ihMVAyo+W4HnwYyIViW0bL1jV926ejH6YtWlDAgPgjD0AKH5884APBgzXNFF646tk/vcZWCdnJGRNdecR8DQNTWlHjWjlnF50JhAVwtZUIetqEJlZiJTUwXGELXsc1K61TDetzmbzE9N46e6JXHtHMc1hldXL3DzzVvRxJ8OoFS/zwgvPs2rVqoHf68mIbtTWJXqAMoDok4/7RwddylObBlSXokwdA3Yr6he7MU3KwH7xdOrveg/Zx5JMT0xZNZ3d/9xOpA/2+lonT5wlnsYmsFsQhtie5oEqH5XvHWTkxQM3UE8NRSi9+XWSvjYZ17LxCVlTNvqJvBft2onxvibmwrJNZ6IYu9WZtB4eigphpRxYIWznK0Pjzl6PmpBvxW41UOeJsGa5m2feahOMf1DUwOi8FEaN6n+XlU436AFKJ/QAZYDRJx/3j1ZdytZSPLe/PWC6FCEEhtOmo5bXoO4/iuPiQoTFQOPTRQm7RsqYNFLHuzn4zv6Yz8nIT417YKD0NiFcsesaDj29jdzzJmLqp0lat/uRksrb38fotuH+7ryErRl+swhl5liUrJSErBnDRaM6Ex+96Uxa9ig99ciKMkRyCkp65qA6wvr9fmZeoZVxZl65nV88VNLlcZt2+5gw0kJmmonCCXYUIdiyVxuG+swbpaxZnj5oe9bRAT1AGXD0ycf9R0m1kfzrFSjpDk2XcnRgdCnCbMJ45iwiG3ZDvZfkW87E/+puQtv77gLbHQWrCvs0myejHxkU6WlEuPpQ3nmsaEDLO/VPbSWws4rsX5+NUBJT1lB3HAZvAMP8SQlZr0f6qDOBFiFsObLJh8jOQzgHd64RgM1qZvMTU9n8xDQ2PzGNX30nr8PP732mnEmXbuXUb+7kl99u+9ma5Wk881YN4bDkpQ/qufSsxJTjdLpBz6B04vgJUKSE5s+g8Q7w/hC8t4DvHggPjLlWItEnH/cfYTLg+u5p2C8upP62Vwh+emhgrpPiwnDKVMLvbUJxmEi68XTq734P1Rtj50MvTL50Ovte2kk4xlbm9LxkaksbiMRRapLeppg7eOq3VxCo8JG1dGyfrxMLvk8OU/tIEXn3nYtiT4w7rfT6iby/HcOKQSjtqNG24XCwV51J6/6afMjyErBYEFm5CNPguPL2lZtWZ7Pn+UKe/e04rv5/BwgEtcfamuVunnunlre/aKBwvI1Mtz6kUGdwGf4BivRD06NQOw/qV4H/Xgg8AYHHoOl3ULcCapdA4F+a4dAwpW3ycaU++bgfWM+eSPLPl9P40PoB06UoY3JQRmYR+WgLlnkjsS4YRcP9HyZER+TKTSJzZg77X9sb0/Emi4mkdCd1ZXGUCPswJLD40c2MvnIGygC80YcO1lH+83fIvesrmHITk0GQUhJ+owjDrHEomckJWbObC0FzUDNbUwxa1qQHnQlEhbC11cjaGkR6FkpK2uAIYXtC9D7q4KIlacyd7ODRVzRztnEjrLiTjfzkwaOsWe4G4wD+nnX0DEoXDO8ARa2EumXg+wWoh4EmoP0vPgIEILJDy6o0XAJyGHuPOF1gMuuTj/uJaeLA61KUOZOgOYy69Utc3zyFSJkH/+t7ErJ2weoZfSzz9N0LRUqJ9DbGlEFRwxEOPbWVsQNgbR/xBCi58TXSrzsV26ychK2rbj8ETQGUUycmbM0OdPAzIaozMfdYzgGQoZCWNYlEELl5COtgCWE11Mpawuu3Edm+H7W4FLWyFoQBrU2kd37xrTx+/3Q5ajTwX7Pcze5DflYuzYW0ZQO485Md3QelK4ZvgKLWQd1XIHIAiMXquwmaN0L9yh4cEocWffJx4hhoXYpQFAxnzETdewRZVUvKj5fgfWQD4UP9dwiedNFUDry+l1BjbI/TuKYaB5u1WD6GIYHlbx/APjKJpAS1/LYgwyplt72FY2E+ySsT1xkkPU1EPtgxcKWdDjoTa686E2gRwjYgK0oRSSmI9EyEMgRmccFm5P4S1M17iXyyjcgbn1H30Fqwj2s95OvnZfDAraMB+OW3R3DLlW2B45wpDvY8X4gS1QjdtCabwIfzSHYaIP0rg3pXdHSGb4DScI2WQaEvZZsghPdo+pRhilAURLo++TgRDLQuRditGM6YSeTjrRhSLbi+MZf6O99FhvpXSrSnO8hbOIp9/94d0/HxuMlKr+YgG0tpofixzYy5elaf1o+FqvvWgyrJuOm0hK3Z0rVjmD0OJSPBJQdVjc7NiepMTFatrNPbniIRZFU50tfYKoQdipKObA5r06uRWnCqqmA0YDh3AeRcBYotzpUN4D4HDP031NPpBt0HpUuGZYCy9oX7mXn668xcUsHMJbXMXFKLklXFa+9onzjv/UsT1pFVNHjatBzvfRwieVw1M5eUMvO0v3L22YuHavu9Ioz65ONEMpC6FCUrDWX6OMLvF2E9azyGvGS8//ii3+tqpm1bYjo2I56pxjHqT0INAcpe20f+qml9W78XGl7che/Dg+TcuRxhTNzLjLrtEPhDKKcksLTTqjNp6qgziSHIkP4mZNlRMFkQ2YMvhJWqRC2rJvzxVsL/ehd5qAIyok66RgPGr8xHSXFB6hlgnxCTFqUTRifk/X+J3biOTgwMywBl5fJ9bH7XzeZ309j8bhrf/4aN0+eb+MoS7cn19Nog82YaWftqR+3B6fNN0XOyefullUOx9ZgRNjvC4UJW65OPE8FA6lKUyaMQSQ7Uz3eSdP1CAusPEfjscL/WnHhhAUfeL8Zf13v5UnOTjSODEkOAcvi57WSdNRaLO3Gfjv2by6j+w6fk3XcuhgR6qkhPE5EPdyTOkE1KCDdHdSYyZp2JdqpEra1B1lQh0jNRUgdXCCvrvEQ27Sa89l0im/Yg0lwYzz8D41lzMcyZDAYFw9nzEGlJ2gnCCJPuBevIPgQpChicMPlPYNZbjAccPYPSieEXoEgfBF9GE8DC3v1hfnVPE48/6EJRBPuLIzT6JL+5zcHT/+quRBIA/0ODtuW4SUoGRUHWxz9rRaeNgdKlCCEwLJiGrGlAlFeScuuZeO7/kEht/L42liQro88ez961vbfJZ8aRQWkp8fSGVt5JnDi2ucxL6a1vkP3rszCPSdxMHK1rZxOGueNRMpL6v2AkrJVz1HBUZ2IFEdvLoWwOaY6wkWbNEdYab+mkb0h/kMjOYpr/8xHhdRsAgfGseZi+uhDDlDEIm9YGrKSnYFx1NkrGMb9/gxMK/gHJC6JBSnfdSEIrB1lHwtTHwJ4Yx1+dXtADlE4MvwAlUqJF+0Bzs+Ty73r53S8d5I/QasFPrw2wZqWF0+eb2LM/QmVVW5nnw0+bW0tCv/394WErlm2hbfKxX598nCAGSpciTEaMZ84msnkfxmwr9q9OoeHu9/pVTpqyqpCdMXTzxNXF4+k9g+L9sgbvvhpyV0zo09rdofqbKb3xVdKunoljYX5C1mxde+tBCIZR5vVzrx10JuaYdSbQ0hnlQZaXIlxJiPQshGFghbAyHEEtLiX8zheEX/4AWefFMGcyxpVnYpg9CZHSddt2t/syWGHiXTD9Gci6BBQ7KFZQHFpQIkyQuhgm/RGmPwvWvK7X0dEZBAZuhGa8yEZaWuJ+foePqZMMrF7ZliZ+5sUgax9JQlEEF51r4fmXg/zgW9onmNPnm/jPky3COQtIL4g2cyG1OYJiGqIx7N0gFAO4M5FV5WAyI8xx1Ih1OmE9eyKG/FQ8d7xD+EAN9tWz+u1eKpIcGOZPJfJ+EfYLFxAsKsH3wlacl82Ia73xX53Ea99Zi6/CiyOre38QV5qD5mCYJm8Au6v3komMqNDU+5DAg49vYdTq6Ql5TkhVUv7zd7BMziDlyvh+H92u3eAj8tFOTKtOj98ivqVtONKsBSYGa0ylnNbTIxFkTRVEwlGtycA9T6UqkRU1qAdKkUcrEOkpKGPzEGfMQpgS9JJtzYNRN8HI66C5GiKNWqBicuti2CHhxMl6JJLhF6AIOyB57+MQ//xPiE3vtM3X2LojzL4DEZZdqplWhUIwdpTSGqB0JIwaseHdcJSad4upfmUvjbuqmLV2DamLRg3OfYkRYTZDdPIxWTlD0554AtKiS2m4UwtSXDctRnH0741Fyc9GVjegfryV5FvPpPbGlzDPyME8KbPv+7ObGX/eZHa/sJ05P1jQ7XFCCDKjU41HTc3tfWFfE9itPeo0pKpS/PhmFv1zTZ/33RW1f9tAuMrHiNuXJVSL0WrINncCIj2O0k6LPX04BAaDpjOJsZTTuoTfrz03HU5ERtaAaU1kvRf1QClqcQlYzChj8zDMmoiwD6CXimICS+L8aXR0EsnwK/EoudTVBfnGDV4ee8CFy9m2xafXBvjlrQ4ObnRzcKOb0m1uSspVDh3pYjqscPDBqD+xccXjHLz7Ixq3VyIUgXX0IA0U6yP65OOBQUm1kZJgXYoyUysziJJSkn6wkIY734tblBt7mSct5jKP9PSuP6n68BBGl4XUmdkxrdkT3rf30/DiLnLvWYFiTmxwrW4phlAYZV4cOgg1opVzIs191plAVAhbV4OsqUS4M1BS3QkPTlp1Ja98TPidLwCJcek8TOctwlAwZmCDE53hha5B6cQwDFCS+MsT2VRWq3zvR95WTcnMJbU882KQled2/AS8coWFZ9YeqzUxg/Uapj95MQaHudV8VoZVvlj6f2xZ/RzFd35IzVv7CdUMnwF+IiUNpIr0DMwwvJOVFl2K7aJC6n/Sf12KZuI2A7W4FHO+HfOMHDx/+iSutcYuH0/1zko8R3r+m2dEMyixEEsHz4FHNzPmqhn9fsMN7Kmm8rfvk3vvCozpiS0NyHofkY93YVwxu2+lnRadSSigTRk222LWmbReuznqCNscFcLaEnff2nQlGwi/FNWVzJ6EceUSDLMnI1IHf6Cgjs5wZPiVeIDbfvYnbrtuFZq1fc/8/tdt4+TPXNgSvAiwfRP3kjwWbPguW1Y9S+OOKpLm5TH1ofPxbCrDW1TG4T99jreoDGOqjaRZOSTNzsE1OwdXYTZG5+BrQYQQ4M5AVpQhzZaEvijqgG3ZRIyjEqNLEVYLhsWziKzbiOvyudT89C386/ZhW9o3EafBbGTShVPZ9dw2Tr359G6P68tUY+nxoaR330ET9oU4+uIuZvz27D7ttdM6NU2U3vgqmf99BtZEu9C2dO3Mm4Bwx1jaOVZnYuqbzqTluvi8yLpaREoqOJMSkjWRUiIralEPlCCPVCDcKShjcxFnzEycrkTn+KXFqE2nA8PzmWE8BQwjILKflnbj2DETCs+ndq+RzEkq5kwHc968hi9//g7OwmyseUlY85LI/Jo2nl2qkqb9tXg2leItKqPypd007qrCNipFC1rm5OCalYOzIDPh6euuEAajFqRUR/UoxuE5AfV4RdOlnE/Dnev6rUtR0lOQMycQWb+VlFvPoPZnb2KanIUxt28G75jaAAAgAElEQVRaiYI1hbz7kzd6DFAy81Mpejs251m8Phg7otsfH1m7i/QFI7HlxP9JXQ1FKL35dZLOn4xrWeLbUNXNxRCOoMyNIeBrrzNR4tOZQFQIW1utZU2ychMiWG/TlZSCxaTpSmYOsK5E5/hED1A6MTwDFCEg+RmoWwqygY4DAnvCCEo2j3/vDLa9/DsUo0LaqFSyp2Yz58pZTLyksPOlFIFjghvHBDc5q6YD2ouvb1cVnk2leDaVcfThTfgP1eOcktGaZUmalYt9fFq/O0O6QlisEJ18TGZO/J0LOl2ipNpJ+fUKGv/+GfW3vEzST8/GOCI+bZIyYSSyqh7KSnGumUHDne+S9rvzEH3ojMk/cyzeow3U7qsmbUJ6l8fEmkHRWmF7LvEUP1bEuG/NiXl/XV2j8vb3MabbcV87L+51ul2/vpHIJ7swrTmj9+eXGtFcYEHTmcQpMJcBP7K6Cux2RHoGIo4Ap3UtfxD1YBnyQAnSH0QZk4tx6RxEagL8W3R0TiKGZ4ACWgYl5TWovwBkPdCbCNEKhpGQ8i8u+bONna/fTiQUoXp/DbWH6sicmM6sS2Jrf1TMBlwzsnHNyCbvG9pt4cYQ3q3leDeVUfPmforv+IhwnR/XzGySZufimpVD0qwcLHkJmsPhdEEoiKyrgbT0oR/XfoLRokvxv7WX+ttewXXdIiyn9r27SwiB4dSphF9bj3ViHqEiK42Pb8T1zVNiXkMxKEy+ZBq7nt3Kwp8t7fKYzFjdZIPR54ml68xb09EG6jaVMeLlyTHv71jqn9pKcFcVIx+5KOEBupSS8OubMJwyEZHWQ4ZHqtrQTTUCJjMosVnTd3U9WV8HPi/CnRF3WVWGI8gjFajFpcjKOsTITJRZkxDZ7gH5EHNcIlUIfwDh97U5a8IMIhfMF4BhgKZSH0/oGZRODN8ABcA4DtLeh6YHIfAooGpOs+0RTsBCqPIyGv41j/Rb3STnGFn0vQV8/Jf1hIMRjBYjp1+/qH9bcZpJPS2f1NPaDKhCNU14N5XhKSqj7Mkt7LnldYQiSJqVg2t2bquuxZTad6dJIQSkupGV5drkY5f+6Wsg6KBL2R+fLkUYDRjPnE34tfUkXV1Izf+8i3lWHpZZsZtcFayewWvfXdttgJI+IoWa0gYiERVDT+3D3iaEy9ltQHvwiS2MvHgqBmt8pUPfJ4epfaSI/EcvRrElvvyoFh0AVaLM6aZs1F5nYjBFyznxBQCyuVnLUioKIidPK6/25fxWXUkp8kg5wp2s+ZWcrutKOiA9EHwcgg9q3lS0N6U0QvD3YCgAyw1gOi+u8pzOicnwfxYpbnD+Ahw/geArEPwPyBpAASULLBeBeSnBD3bjf/0jSj57CvcvlrL8Z2ez/m+fYbIrzLt6DvfO/yNr/n4pU86J/5PjsZjddtzLxuFepo0yl1ISLPHg2agFLYfuX493cznmDLuWYZmdq5WICrMx2Ht/cReKAumaaBazWSv96CScROhShMuOYWEhkfXbSP6v02i4533SH1iJkhJbcJq3YCQhT5DKbeVkTu/c+muymEhyO6gr95Ce10M5ytMIrq6zAFJKih/bzCkPXxjTno4ldLCO8p+/Q+7vzsGUm/hOE1nXSGT97q5LO1JqtvTN/dOZaEtJ8DUi62oQyang6psQVjY0oh4o0XQlJhPK2FwMM0/XdSVdETkMjV+NvmZ3NXcqrH1FNkHT98H4DDj+AeJk+12eOK3BiWT4BygtCDNYV2pfXWAalwZmA2qdn+qfvIFlTi4X3/FVLNkuZl5SyKzLZvDE1c8w4+LpfO1/z8VoSfxdF0JgHZGMdUQymRdogZCMqDTtq8VTpOlZKv61E9/uauxjUqNaFi3L4piS0aWjpzCaIDr5mKycPn/K04mNROhSlLwM5ISRiLJybEvH0XDvB6T8cnlMb35CUZiyqpBdz2ztMkCBtlbjngIU6W3q1gOl9osS1LBK+oKRsd2hdkQ8AUpufI30607FNivxxl6tpZ35kzqXdhKkMwHNoE7WVEFzCJGVgzBbej+JdrqS4lJkU0DTlZw5p20Yn05n1FJoXAqyDlB7PRx8EH4XGleB85+tI09OGvQApRMnzCPAkGZHGAQSkM1hAhtKmHnNbCxTswAYv3gctxbdxLPfeZ57F/yRq5+6gqzJfXf/7CvCoOCYnI5jcjo5azSRrhoM07ijEk9RGQ1flHD0rxsIHG3AUZBJ0mwtYEmalYNtrCbCFTY7hEKaiC8zW9ejDBCJ0KUoheOJVDdgm2qnYUs5TS/vxHHB1JjOLVhdyNrLnuaM33Ttxtoyk2dK96azWovx2K5LS8WPbmbMVTP7/PiRYZWyn7yFY2E+ySsL+nRurKib9gOgzB7X7sKJ0Zm0LhcIaCUdmx2Rnder+FyGI8ijlVprcGUdYkQmyswJUV2JXoboESmhcWW0ySGW4KSFAES+gMAvwfabAdqczvHCiROguG3IYATMBpCSnL9fjOmYaaqONDvfeP5qPn34c/5wxp847/YVzP/WKYP+hq9YjNFyTy58S7st7Ani3VqOZ1MZVa/s48BvPiDsCWoi3DmaniV1hgOlvhaR6h7U/Z5s9EeXIoTAsKiQ8CufkHTNNGrvXI95ejamsb3/zbJm5SIMgrINJeTO69wmHMtU4+6mGEeCYQ49t52vfHFtTPejPVX3fQJSknHTaX0+NxZkrZfIp3swXb5Yey5KqWlMwqF+60wgWtJpqEd6PQh3OsLefYeTlBJZGdWVHK5ApCXpupJ4CH8IagnOEdU0Hk1hx64I1//Yz9FSFSnh6tVmfnaLBSEEjzwV5NZfBMjLEQSCcO3XA9z0/X+A9TYQvU/kPiHQfVC65IR5xgmbCdtp+Ti+NoXAp4fxPr+NtB+d0fk4IVjw7VMZs2g0j13+JLvf3Muqv16MPXVoTdGMSRZSF43qMCcoVOXDU1SGZ2MppY8WsW9PNTP+upiaj7egCqsmxp2VjSlGnYNO7PRHlyIsZoyLZxF++wuSvjmT+jvWkf6HlQhrz083IQQFqwrZ+fSWLgOUjPxUSvdVdXt+65BAR+fHcul/9pAyPRPn6O4N3Lqi4cVd+D46TP5jFyGMic8aSDVa2lkwGZHi0AKTFp2J2Q79zFTIcFQIK6JCWGPXfwNNVxL1KzEZNL+S8xYiHPpzKy6CfwS0hga/X3L+5T7+fI+N5UtNNDVJLr7ax58eFvzg21qJbdVKEw/cbaemVmXSPC+XnK8y0vYCWK4ZwjuhM9ScMHlKIQQZd5yDfeEoUq49Bf8nhwhuK+/2+OwpWdy0/npS8pK5e9a97P/wwCDuNjbMGQ7Sl49n7G1nMOO5VSzY/H0MOTnkrhyDUCIcvOdjPin8E+vn/YUd177Mkb98QcNnR4n4m4d66ycELbqUeOb4CHcyhrmTMfprMU1Mx/PQpzGdV7C6kF3PbUOqndPiGflpVB7qIYPS2P2QwOLHtzDm6lkx7x/Av7mM6j98St59KzAkDYxoUd30JSgCZcYozZ4+HJ2bY7b2PzjxNSLLShA2ByIzu1NwIgNBIrsPEn71E8JvfQ6RCMYzZ2M8bxGGqWP14CRe1EotgxLlqRdCLDzVwPKlWmOA3S544G4bd9wX6HSqO01h/FiFsgofBB8YtC0PC/RZPJ04YTIo7VGcFlKuP43auz8k+x8XIYxdi+pMVhMr7z2fScsm8OjqJ5n/rVP4yi/OxtDN8UONEALrKDeyycrIy0zkX38aIPDtqWl1wi1/bju+PdXYx7tbtSxJc3KxT0pHGYBPwCc6rbqUN/f0WZeijBuBrKrH4QxQ/9QBAh8VY100psdz0guysKfbOfLRIfLP6HhsZi/zeLor7wSqfFR+cJAFj18c074Bmsu8lN76Btm/OQtzH7MusSJrvUS2HsR02QJEc1Czpzf0T2cCUSFsbTUEg4jMHISlTQgrI1Fdyf6oriQvA2XGBESOritJGOp+wAJowuYdu1XmzOz4VjNujIFGH3g8Hd9IDx9RCQQkhVMNoB4epA0PE06QoCKRnJABCoB96Vh8r+3B8/RWkq/q+ZNjwblTuGXjDTz59Wf54+I/c9UTl+MekzZIO+07wu5ABoPI2mpEeibOggycBRlwpWZEFwmEadxegWdTGfXrj3D4wc8IlnpxTstqc8KdnYttdIouuI0R2/JJmi7lznV90qUo86Yg3/iM5KsmU//Ax5gmZmDIdPZ4zpRVhex8ZmunAKW3icbS07WD7KGntpL3tUmYXLF1rKj+ZkpvfJW0q2fiaOf7k0hkREU9UILpslMRFpMWnCRi5k0wKoS12rSSjqJEdSV1mti1VVeSq+tKEoB6tBxZXoUYkY3IcGvZO9nY4Rgpu//Tttz+7Npm3v3Iw559Kn+734bVKoAQyAiI4fmBUWfgOWGfnUII0n64iPJvr8WxdBzGvJ7bAZOyk7j21W/x/n0fcu/8P7DyvguYs6ZvKfHBRKSkIqvKkZ56zcuhHQarkeS5eSTPbevmCHsCeIrK8RSVUfXSHvb/z7tE/M1ahqXFWG52Dpasnt88T2ZMkzI1XcodsetShMGAYfEs5KvrcVwwkfq73yPtjnO7LMO0MGVVIY8t+DPL7j8PQ7vW8yS3g+ZAM03eAHZX55KL9PpQMjpnO4of28zMO5fHdB+lKin/+TtYJmeQcmVszst9QkqtK8fXiEhzgt3Rr7bhtmUleOqRHg8izY1wOJEeH5EDJagHSsFo0PxKdF1JQpH+APJIGbKsUpsineRCGe9HadcpPnWywgefhNGyKhoHDkZwOsDl0iKUFg3K+s/DfHWVjxVnm8jOspxEwcmJU5ZJJCd0TtOYm0TSmhnU3vOh9gLWC4qisOSHi/nu69/mjV+9xZPfeIaAt3OddDgghEC4MzXDKX/vU5+NSVbSFo9m9I0LmP7YRSzcfh2nfvxt8qIzWUoe3shnC/7Gx9MeYNvV/+Lgfeup/eAgYc/wvP9DhZJqJ+U3K1Dc9ph1KcJhw7CoELOhEcWq4Htmc4/Hp45NI2VsGofW7e+4jhBk5KdRfaSbLIrHB8dkUOq3VRCs8pG5pOfSUgs1D31BuLqJzJ8uTnx2TY1AyI8M+Am/vQORlopIRHASDmsTwP1+SMtAPVqj6Ure+BSaIxjPnIXxa4swTBunByf9REYiyAYv6tEyIru+1AITgHAEVAn1HtQaBy3lHYArLjXz0acR3n5P08b5/ZL/+rGfH93QOchecIqRq1aZuP8vQRBZg3GXdIYxJ2wGpQXX6un43txH07r9OM6KberqiFl53LzhRtbe8BK/m3M/Vz95Ofnz+m5uNdAIg6Ft8nFmDsLUN+txS7aTjBUTyFihTYyVUuI/WK/pWTaVUfy/H9K4vQJLbpJWGoqayjmnZWHopSPlREaYDLi+t7BPuhQlJx1ZMAqntYy6Z3dhnpGLeVrXhmwQLfM8u5WxX+k4o0TzQqklv6CjWVrrkMBjNCjFjxYx+soZKD1kbFrwvvUlnpd2k//EJYmd3C3VqD19BGkwEl77Ocq0fK1rp79L+xpRq6rAH0GWNyArdui6kgQgQ83g9SG9jUivT/u+0Qf+IDhsWinR5UDkZiHrPIAEownD/BkIdyp4ZxIOforFLLDZBC896eD6Hzfxg1v9RCJw1Soz13276+zjj2+wMvvMRv77v79O4v2KhzF6BqUTJ/y7jDAaSPvR6VT/9C1sp4xEibEOb3GYWf3wpWx+fgsPnfd3lty8mCW3LEYZZi94wmKF5BRkTf8nHwshsI9JxT4mleyLNXMxNazi213VbubQVpq+rMExKT3a5qzpWRyT3D2WLU5E+qpLUaaORVY3kLxqHPV3v6dZ4XfzeJxy6TQ+/vU6wsFwB9fjbqcaB0MgBMLS9qKvhiMcfGorZ737zV7vS2B3FZW3f0Den7+G0Z2glvsu/EzUz/eB2YgyI7aMTneokQjywCHk4UpktReRGvUrWViIMCd+RtCJiJQSAsFoANIuEPH6IBLRAhCnQwtGRo9AcTm04KTda4yUksjOfYiMdJQ509p+99Yb2LG5iHFjtGOnTzXw3n+6Dje+frmFr1/e9v/cHIXyPRmQ9K0Bu+86xwcnfIACYJmWjW3RKOr/+jlpt5zep3NnXjqDUafm8/iVT7Pnrb1c8ehqknOTB2inceJwQTA0IJOPFaOCa1oWrmlZ5F49E4BIUzON2yrwFJVR98FBDt2/nlCFD1dhVoeZQ9b85BNehNtJl/LDxSj2rj8ZCiEwnDZd06Msysbzx49Ivm1pl78jV14ymYXZHHhtLxMvbHNvzYy6yR5LVwLZ8rf24xiVQtKk9B7vQ7imidKbXiPzvxdjnZwRy93umRadSTiozcuJ+pnIag+RDfswXXlm3I8L6fER2XcYeaBE05WMH6l9atdLN90iVRV8/nYBSKOWDfH6wGDQApHoF7lZWiBitcQ2okEIDF85XZsV1u74vzxczB/ur+e+2+P5u1jBdDEofRs1cVyjG7V1yUkRoACkXHsqZVc9R/CcCVh6SK13RWp+Kj9Ydy1v3b6O3825j1UPXcq0rw2M5Xc8aJOP06KTjz3gGtgAymA3kXzqCJJPbTMTa673442KcCv+uYN9P30b2Rxpy7JE3XDNGSeeM2SLLqXx4U+pv7nnOT7CbMJ45ix44zOCe7z439iDvZsBlgWrC9n57JYOAUpGfipb1u3tfLDXB8eWdx7bzJhoUNkdaihC6c2vk3TBZFzLxvV4bEyoES1jIiUYLVrbMNqbZPi1jRgWFSCS+/YYkMEQ6sEy1AMl4GlCZDgxLJiKyNPHPrRHhiPQqGVAOmRFfH4t4Ggpy6SnoowZqX2fgGxT+zbuFr77ve/z3e+cDd6z6Di9uDfMoIwD+9393tdxhx6gdOKkCVCUJAsp1y/QvFH+3r03SncYjAbO+cUyJp41nsevfJrdb+zh/LvPwzwAI+fjocPkY5MFYR3caaCmFBtpS8aQ1k6MGSz1ak64m0o58ucv8BaVYUy2tmpZkmbn4JqRjTHGsttwpi+6FJHiwnBKAS6xm7rHN2Kemo1xZOeAZtLF03j3x68T8oUwR7uFMke5uyzxHJtBCdX7KXv9S+Y+eF63e5ZSUnn7+xjT7bi/M6+vd/nYxbSMSSQCRpNW0mkXPKhf7AOrCaVwdGzLRSLIo1Vaa3BFLSLHjTLSDWn5KJlZ2hDNkxQZDLWWYqTXB43RQCQQAqe9LRDJy0JxRr83DEE3jGEiOF8F3wXR1uPeDCRtYJgCjn+B0DNiOidRgAJgP2scvlf34H1uG0mX9/zJsjvGLhzDrUU38fz3/sm9p/6Bq5+6gpw+ZmQGCmE0aaLZlsnH3dh6DxaWXBcZuS4yvqoJPaUq8R+ojdr3l7H/lb007qjENjI56s2itTw7p2aiDMC06cGggy7lQA32VV3rUpQxuZoe5TyF+jvW4b73fIS54322pzvIO20UX/57FwWrtZbf7szapNeHktnm3XP4uR1knz0WS1r3epL6J7cS3FXFyEcuinnWUOcL9z43R63yENnwJaYrl/SY8ZBSIqvqkQdKUA+VI1JdKGNzYfZ48NQjXEmQfHJ490gpwR/ooAtpyYqgyo5lmYyRWlnGbht+omDjdHB9DIH7IfRE9EZfuwMEYAeRDJbrwPJNEMf/B5a40DMonTg+3wXiRAhB6s2LqPjOi9iXjMOYE59G3J5i4+qnruDzRzfwwNK/sOKXy1n4vQXD4oVTWG3gcmlByjCbfCwUgX28G/t4N9mXTgNAbY7g21WFZ1MZnk1llD6ymaYDtTimZGgeLbNzSJqVi31C2nEjwu2gS9nfvS5FmTMJpaYB6yQH3n98QdJ3O48pbunmaQlQ0kekUF3SQCSiYmj3+5DejhmU4seKKPhx93or3yeHqX20iPxHL0aJJwvYjc6k02ERlcjrGzGcXoBI7jpYkh4fanGpVsJRFJSxeRjPWwg2i6ar8jYgMrIGPSs4GEhVhcamaCakfVbEB0YjwmkHlxOR5ETkZWl/4xj1IcMGJQfsd4DtfyC0FsJvgqwBjCBywbwKjKcnxKhP58TipApQAEx5ybhWF1L7+4/IuOucuJ/oQghO/fo8xpw2mseveIrdb+5h9cOX4UwfBhoLVzKEgsjjYPKxYjLgKszGVZhN3tc1Y7yIL4R3WwWejWXUvHOA4rs/prm6SZvsHBXhumbnYB2RNGxfqGPRpQhFwXjGTPB8jPfTEoKfH8FySsd29okXFvD2Df8mUO/HmmLDZDHhSrNTX+HBnautpw0JDIJTS4t799Xg/bKWnHMmdLm30ME6yn/+Drn3nIMpN44gXVW1wESqHXQmXR76+V6wmVGmj+5we4uuRBaXIr1NKKNzMJwxC5Gm/U1lKIgsL9HKlbkjhl9moI/IcBi8TR3bdr0+aPKDrUUf4kRkpKGMHQnOxOhDhhXCBpbLtS+dY9CN2rripAtQAJJWF1L+xj787xVjXzK2X2tlTszgho9/wKs/e527Z93LFY+uZuLS2PxWBgohBKRlICtKkb5GhOP4coc1OMykzB9Jyvy2N+vm2ibNCXdTKeXPbmPvj99EStkasGhuuDmYE9UimwBi0aUIuxXD4lk4wxvx/PUjjOMvwNCuLGNNtjLqrHHsXbuTwm9opnoZ+alUHa5rDVBobAKHtfVNvPjxzYxeU4hi6qw7iHgClNz4GunXz8c2M6fTz3tEyqifSXN0bo61x0+9alUDkU37MV2llXZkJIIsqUI9UIosr0HkZqBMG4fITW/du5QS6WlANtQhUt0I5/HlhKHpQxrblWSi/4ZC4LAjXE4tGBmRrZVlnPah0YfoDD/0AKUTJ2WAIkwGUm89nZr/eRvrvDwUZ/9qnkazkfPvOo9Jyyby5NVPM/fKOZz76690sCkfbDTRbKbW2WMyIczHd13XlGbHfdZY3GdpAaWUkmCJF8+mUjxFZRx+8DM8ReWY0mytpSHX7BxchdkYnT3b0Q80tuWTMOan4rmra12KkpWGYdYEXGFouOc9Un+9osPPC1YVsuUfG1sDlMz8NCoP1zJ5viZIbl/ekarKwce3cPraNZ32IcMqZT95C8eifJIvnBL7HWjVmTRr2RKLo9d0vIyoRF7biHJ6ATIQRN11QNOVpLhQxuQiTpveKUMgI2FkdRWoKiI7r8/Gg4OFlBKaAkhvY5s+pKVtV7boQ6KBSIa7zT9kmGb7dHSGKydlgAJgnZGDdUE+9Q99QdoPFyVkzUnLJnJr0U089c3nuH/Rg1z15OVkjO/Zg2IgESYzpLq1F/2snBPqk5oQAuuIJKwjksg8X2vTlaqk6cva1snOlS/uonF3NbZRKW1dQ7NycBZkJtYpNQZMk3vWpSiTR2GorMNSW0rTP7fiuLRtDs64r07mtWtfxFfZiCPTqbnJHmoTykpPm4Ns5QeHMCVbSO0iO1J13ycAZNx4Wuwbj4Tb6UysMc/NiXy0A0wg9x8mUnwEZWwuxnNP0zQVXSD9TZpuyulCJKcOizfzNn1IY8fyTKNPC/pbumVSXIiROdr/LeZhsXed4wzdB6VLTtoABSDle6dSdtXzOM6ZiKUgMyFrOjOcfPvlb/DhAx9z32kPcMHvzmPeVXOG7EVL2B1aPb+2CtKzTugXT6EIHBPdOCa6yVk9HdB8Php3VLZ2Dh3920b8hxtwTskgaU6bE659XFr8nSwx0pMupcXEzVztwffpXpoLczFN0kzTzA4z486dyO4XtjPn+/PJyE+j7Muq1nXbDwnszvuk4cVd+D46TP5jFyGMMeg5jtWZKIbesybBEOqhctQ9h5G1HpTxI1Am5SPc3Rv2Saki62qhqQmRnqmJvAcZ2Rzu2j+kKQA2a1sgkulGGTdK+16fgqyjM+Cc1M8yQ5KV1B/Mp/auD8h+OMYX7hgQQnDG9YsYv3gsj13+FHve3MslD67Eljw0vf0iORVZVdHl5OMTHcVsaJ3YTNTxPewN4t1agXdTGTWvf0nx/35IuD6giXBn57b6tFhyXQkP6HrSpQiTEePZc7D7P8H7p/dJ+d/zW7MsBatn8NnvPmTO9+eTmZ/K1nV72hb1+GDsCMK+EEdf3MWM28/ucE1/URnVf/iUkf+4EENSL50wfdSZyIiq6UqKS5BlNYgcN9T6UWYXYDxGGNvp3FBImyNlMiFy8gY0wyel1NyW2+tCWgKR5mZNlNrStjsyB8Xl1DQjx0nnmM4JgJ5B6cRJHaAA2JeN17xRnt9G0prEjpfPLczlh5//Fy/e/G9+N/s+rnryckbP73mo3EAghND8USpKkWYLwjZ8hKRDgdFlIXVhPqkL81tvC1U34SnShiSWPbGFPTe/jjCItoAlGrSYUhMTZHanSxHJToxnFOJo3oznz5+QcvOZAIxZPoH/fOMFPEcbyMhPa7W7bz8k8MhzO8k4bSS27DZhaXOpl9IfvUH2b87CPLqH4FTKaDknpNmfW+xaWafLQyWyuh55oBT1UBki2anNwVkwncgXX4LLgWFa949zKSU0epD1mhAWhzNhgaCmD/Ef4x+iaUVAdPQPyXK3+YecwJlFneMEPUDpxEkfoAghSL3ldCqufRH7krEYsxPbNWC2m7nszxez9cXtPHzhI5xx3ULOvm1pTNNlE4k2+TgTWV0R1+TjEx1zup30ZeNJX6Z1YEkpCRxpaB2SeOi+9Xi3lGPOsLfLsuTiKszCYI/vd9mdLkXJz8YwNR/zp/vxv7MP21kTMFqMTLyggN3PbWPSVTPa3GQDbUMCix/bzPhvz21dX/U3U3rTq6RdMwvHafnd7IK2wESIHnUm0tuEWlyCeqAUhEAZ01FXolbUo24+gOnqrucLQdQhtqYKIpF+CWFlRNXKMo3HGJk1+rS5MC1lmdQklPwccDk6zYvR0dEZ3pw8AcpRYANQD1iAHGARYATTiGRcl07XvFHujN8bpScKL5xG/twRPHH1M+x5ex9XPr6G1C7szQcSYbFAcqqWVs/q3+TjEw1kx+sAACAASURBVB0hBLb8FGz5KWRGO15kRMW3twZv1L6/4p878O2uxj42TXPCjc4cckxO77LFtyu606UY5k7GVFaH//2tmAqyMOYkUbC6kPd++ibzblpIsCmEvzGApakJkeTAd6SBuqIy8s6fpO1VlZT//B0sUzJIuaKw64vHoDORwWbkoTLU4lJkg0/zK1k0o5OupKVrx3DmdISr6yxTqxDW4dSM12J4nsnm5mOcVKP/+gNgtyJcTi0QyUpHGR/Vhwyxg7KOTt/RfVC64sR+JqvAOuAu4AO0wCQCtLwvm4D/Aq6FpMtnUPbNF/B/UIx9cf+8UbojZUQK33/rO7xz13vcM+9+Lv3TRcy4aPqAXKtbHE7NxK22GtwZ+ifKPiAMCs4pGTinZJBzufamrwbDNG7XRLgNnx/lyF++IHDUg2taZruZQ7nYxnbfmdKdLsW4fC5Wz/v4/vIeST8/j1FLxuIrq8Z39P+44cGNqI3XgDAjRmdQ8vJ88i+ZisGqZSRqHvqCcHUTI25f1vm6vehMZERFlkbn4JTVIHLSUQrGIPIyug1qI+t3Q5IdpWBkp59JKaNC2EaEOxNhs3X6uaYPaWynD4n+2xwGVzv/kPzcNv8QPcDW0TmhEVJ2H7XNnTtXbtiwYRC3k0DqgK8Au+h5mKYVrcXrTxCYWUrN/1tHzhOXoTgG1jvj4GeHefyKJ5m4dAIX3ns+lgG+XnukqiIryxEOB2KAJx+fjIQ9QbxbNFM5T7REFPGGcM3SRLgtM4csXYxaaN5dieeudViXTcS+ahayup7wK5/SbA/juOBTwp6HQQGjOdB6jpRG1BCo4RmY0m/D+94Yqn7/CflPXIKxvXHdsToTo7lVZ6LpShqQxSWoB9vpSkZl9+poqpbXEf7nJ5iuWYpwHhN8NIeQVZVgNEJaOiIQ6iBQbS3LCNHRP6RFJ2Kz6kG0zqAjhNgopZzb+5GJYW72CLnhmv9K6Jrirh8P6n0YCE7MAKUOmAOUAKEYz7EDt0NN03sIm4m0GxcO2PZaCHgCvHDdWg5vOMrVT13OiJl5A37NFmQ4jKwoRbgzhqS182QjVOnDU1SKZ2NZ64Rng9XUVhqKerSYkq2odU003LEOJcmC66bFqIf+gyHj+2AMI5SeJ8JK1YbnzZlYCh/BOrndEEs1As1B7XuTpVVnoulKSlGLS0FKlLF5mpGaq31gsx/YC3gBJzAeRHQAZDhC+In3UE6ZgKFA07nISEQLPqqqkTW1CBWkPwS+Js0nxOWIds20C0YsQ2ump6PTHj1AGR6ceAGKCiwANhN7cNKCDSKPhih7/Bky7jwHy5TEeKP0xoYnNrL2h/9m2X+fxeIbFg3aJ0YZ8CNrqhHDYPLxyYaUksCh+tYhiZ6iMhq3lmPJcWmloZlZ2CsaMBi3kHz9PQjhj33tiBVhWQm2P0fLOUFNb2Iyg2JENoeRh8q1Ek5DI8roHMSYPER6O12JDAMvo9VHtwFmtCeXgvbEmowM30Lko7HI+iDK+KxWLxH8QbCYwGpGuFMRKcnRoMSuP850jgsGPUDJGSE3XHN9QtcUd/6kx/sghLDSJn4wAi9IKf9HCJEGPAuMBg4Cl0kp67o4/xrgZ9H//kZK+Wj09jHAM0AasAm4SkoZEtqLy/3AuUAT8HUp5aYe78OJFqD89hu/5anHnsKgGlBQ+Ct/ZQ5z+AW/4Hmex4HmuHkpl/JTfgqAAQPTmU6YMFOcU3jwsZ8R+feXZD+0MmHeKL1Rvb+ax654CofbweX/uAxX1uDMIJGeeqTfjxhmk49PRtSwStPe6tYsi293MTMe+iXGpEDvJ3fCDsZfgbIGjGakMCBLq7U5OGXViBy3VsLJzejs9SH3AmcDDWhZk66RzTYIW1H3PYSwzgKXE0wGpN+LcLoQqWn6Y0rnuGRIApSvX5fQNcUdt/UWoAjAIaVsFEKYgI+AG4D/n72zDI/i7MLwPWtxdw8WggdNcHeKu5UCFaS0RdpS/ypUoKXQQgs1pAVK0eJQvDjFoZBgceJua+/3Y0PCkgQSCCHQvbn2Cjs7885sdjPzzHnPOU9/IFkI8ZkkSW8CDkKIN+7a1hFD2UkTQAD/AI2FECmSJK0G1gkhVkmS9D1wVgjxnSRJPYCXMQiUYGCeECL4Xu/hqcoyO3LkCJvXb+aU/hTnOMdf/IUPPrzDO8QQw3nOc4YzHOQgGgpD5RZYcIYzXOACqhwVy/f/hcxaRcbaCxV27M7VnHnl4CS8gzyZ3ehr/t1x5f4blQc2diCXG5IYTTxWZAoZ1rVdMevhzdA9bzIuehbejRPxCswgqFUm9r7p1G5mnFD1wae5zJlvmLoZMyEHr8AM8vIEkE1C3Of4B9RGd+oq2rX70F+6gczDCUW/dijaNkLm41YgToRej8jMQp9wAKFrghDR3EucAEjKHDBPRV7/OaSAFLCQQ14mMhdXZI5OJnFiwkQlRhi4fUJR5j8E0AdYmr98KdC3mM27AruEEMn50ZVdQLd80dMBWFPM9n2AZfn7PQrYS5J0T8fSpyreGnshFucMZ8wwGOM540w22fzAD9zkJuYYumjaYMMHfFDsGK31rTm3+RyOe8YRN2Ejlu2qonCrGDdguVJOz0+6E9CpBr89u4qgQQ3oNas7CrNH9zEZnI+d852PM5Csniz32KcRJycnzpw+DZn1+GBWPNZWEtOnmHEzXE+vIdn33FYuh5+Xa5gwXgXaNFDrwVyJontzJBtLhE4HGVno4xMLq2UyswyOyDY5yFuNAVkWUilLHg3rZYK+E+j2InnUe6o8n0yYqDAeQ5mxJElyDNGP6sACIcQxSZLchBCxAEKIWEmSist18AIi73gelb/MCUgVQmjvWn6vbWJLOr6nKoLSxaoLkUQSQAATmch+9nOVq/jiiw33v/Bq0bJNbKNeYj2UvvbYDKhDyteHKuDIjanRvjozTr9G0o0kvm7xLXFX4h/p/iSZDMnZFZGaglDnPdJ9mSgluuMgyh7VenWCirkL1Wi1AmS5CFkW6aejyN1/Gu22A+g270V38jwixvCdkjxdkTeui7xnexTt/0FmlszoZ/UF42m1AhdXQa9nDCfPJUsEkycXPZFWqZZKklhsEicmTFQenCVJOnnH44W7VxBC6IQQQYA30EySpLqlHLu48Ki4x/J7bVMiT5VAsc6z5h/zf1jMYlxwYQhD2Mc+o3V+4ReCCMIHHyLzxVwOOQQRRBOa4Isv4/TjALAd2RDNzRSyD9yo6LeClZMVY9c+S/Png5nfagFHfjzGvfKFHhZJqULKdz4WOt0j24+JUqIPe6DNfL1ltGouZ/kqDZIMJLkOTZqWqE1R/PP2GU5+ep3QdcnEntOQmW2BcHFBsrdFkgvgG6ys4MIFyMkxfNd27QKvUhaXSSwD8SD5MiZM/NfJb9RWng9IFEI0ueOxuMS9C5EK7AO6AXG3p17yfxZ3hxwF3Nn0yBuIARIxTN0o7lp+r21K5Kma4sEM5HI57fL/1aMei1hEBBFkkIENNjyX/68uddFhuBDfzkEpIL/iUVLJcZzRhqSP92LexKvAuK2ikCSJli81p1qbqiwd9iuXd4YyZNEALB0ejZdOgfNxUgKUstOniUeEyAS0RotK+jjuXv7WVDN6D8umZ1cFyMB1SmdcAb1GR9blRNJPxZJxOpaY5WfJvpaMVU1nPEffwGO4IXrWvRts2QIDB8LKVTBsKBz8u7QH/gcwqgxv1IQJE0CFT/FIkuQCaIQQqZIkWWDIjP8cQ/nes8Bn+T835q/vhSGHpCOwA5glSdJtg68uwEwhhJAkaS8wEEMlT8H2+eNOliRpFYYk2bTbU0kl8VRFUK5orhB2x53nGc5Qk5qMYxyTmUwuhrs7HTrU96pBdin8r3kjT8wbe5L24+OrZnKv7cbUY1Ow87BldsO5XDt4/ZHt67bbsUhLfWT7MHF/hGSJ0BtPlzg5SqSkGp/EklPA2clYoVSvJiOonozV67XcGVWVKeXY1HPD69kgAr/uTrMD42gd9io1ZnXGttFlZEpDfsvQobDqd8jNFZw7B8H3zLO/kyzgrzK+UxMmTDwmPIC9kiSdA05gSHrdjEGYdJYkKQzonP/89vpaACFEMvBR/nYngA/zlwG8AUyVJOkqhpyUn/KXbwWuA1eBH4CJ9zvApyqCkhmYyct5L5NKKgoUVKc6i1mMHXa8y7vUpS422GCBBc/yLJ54Fh3EEpgAmjwNmSnZZCRnk9nEDet5x7HqWgNVTZei21QASnMl/ef1oWaXAJYO+ZXmzwfT5d1OyBXlO+dv5HxsZnI+rih0uVrSz8SSeiyK1KNR6NWnaPCtcQTF2lrCw01i9z4tHdspSE4WbP9LyysvFf2M3p5uRs/B2ZCfGF4Scksl9iHeIAqFTP36EjdvClauhB7dy/pOEsq6gQkTJiQqPIIihDgHNCxmeRLQsZhNQoAFd6z3M/BzMdtfB5oVs1wAk8pyjE+VQGkc3JjDbx82BKnumgr/LP9fcWTe2QtfDzN/mcv5V66iUMlRminQ5GkZ1rkubb84gNvifkX7RlQgdXrWYto/r7JizCq+bfcdI38djpO/Y7nuw+R8/OjJi8sk5WiUQZAciyLjfBxWAU7YB3vj1q8WDiGdkFtvB9KNtlu2yIJJ03OZ9o7hC/7+m2ZUq1r0+1inlpxG9c04dd62lEdkZvSs9zMwfQbs2wtJSWV5Z2b3X8WECRNPHEKIbyt6n0+VQAHgJQzNLx8EFTAIJr09jFcafUZetgatWodCJcfr2SZI+6PIXHcRm0EVbPB3F3Yetry4bTz7vjrA3OD59J/fl0ZDgsp1Hybn4/JD6PRkXIwn9WgUKfmCRJuWi30zb+yDvanxXjvsGnuisL4rxylvCh/M/AhD00UDtQPl7N1sVex+lnxnbFnw20Jn1NK5Uh6lH4bTgaE/0NixYGcH9epJ7NtXujs7gQzjHDgTJkyUGpObcRGePoHijiEINZk7z+v3R45hhm0eeDu48+m+15jZbi552RrkCjnzn/+NDl3q0P2HRMzb+KOsoE6vJSGTyegwvR012ldn2fDfuLzjCgPm98XMuvzuYCVrG0PSrMn5uExoUnNJPRFN6tFIQ4TknxjMPWywD/HGqY0f1Wa0wirACUl279+nUA5DZH6M7AECWHq9BeEn+vPHC9/QfFJz2rzeFtU9DSmHAV9xW6B4e0u88krxay5ZChs2Fp5Mjx7J/49WhfZCa2ReGcgcTf10TNyBEHAtGxLVht48NgqoZgm2puhsASaBUoSnrtV9AXOBt4HSWJioQLjrEX/pkNUo/IM5suEsn/RbzPi5A+j0bAh/LTlK5tJTuJuboR3XiHbDm2Bu9fhD2nmZeaydspEbh24w6rfh+DYpv7tYIfSIuFtIllZItibn47sRQpB9NdkQGcmfssmJTMOuoQf2wd7Yh3hj39QLlVPZcnn02Rqi3vkLG4fj2E/8FklZemMpndaMc7t8sPFdg7OXA9tnbiP84E06f9yFoJENkZUUDRNNMFhnPBhCWwPdyfXow6KRzFXIanghq+FVxOHYxH+IbC1sT4AV0ZCqAfkdolyjh1ZOMMwTalUuQVvhre49vcTJ518s1zGlD983mQVWarYCr2FwNc7B4HV2J5b5ywZDnPUucs7ewHZkA+yG1EfuYDipXjh4lRpNfDGzMNx96nLUhA9ZxQFNNjuOX6f9qGb0nNgarwC3CntbJXHq9zOsm7KBDtPb0W5am5IvRGXE5HxciC5bQ9qpGFKPRRWIErmVEvtgbxyCfbAP8camrisy5YMnL+fdTCV8ymZcalhg6W6B6iUV6EYhdDnIlPe+y9LlqtAktSU0/H1+GL2asT8NoeEzdYk4GsGW1zah1wl6ftUL/1b+RTcWfwBjMVTjlBUr4BuQxiD0AhGbhD40Gv2NWCQnW2QB3siqeiCZme6Y/zMcTob38i07cu8++eYjA1QyqG0Nn9UCy8oR1K94geIpTr5QzgLlfx+YBMoTwQlgDgYrpEwMjgMuwAQMVdp2kPXXVRLe2w0yCUkuw7JjNRwmNkPhXHS+P/dkFEmf7kcxqxPblx5l109H8K/vRc9JbWjWq265V9aUhaSbyfw6cgVKSxUjlg7FzqO0SZL35r/qfJwbnW6UzJr5bwLWtV3yBYkhh8Tcq3x+xwDpe68T9e5ufDu7o3QyRzW+HZgpODXqS/yH7cch+CgylZI7RYReKyHJzNBEuyJsX+dK/yxqrBhEbGoW83r/SP+PetB2fAhCCM6uPMuOmdvwCfal2+fdcaxyR4K1EBjaF2yndKHH25gDbYHNIBl/94VWh4iIRxcahYhORPJyRh7gjeTnauo6+zSzMx4+vwZ5JQiTu1FJ4GEOi+uD1eM/v5gESuXgvyFQSoE2MYuo/isMYUcACVy+6IpVcXeaQOJHe5DbW+DwcnM0eRr+XnOaLQsOkBSVSrcXW9FlfAsc3MrvwlUWdFodOz/ezZHFRxmyeCB1etUul3FFehoiJwvJ1eOpzEfRa3RknI8zEiT6XK1hqib/YdfIA7lF+UcBhE5P/ILjpGy4iF8Xd+SuNihHt0RSyIn67RzX5x3B0UxG1e87Yll9P+gOgUgCyZKwX5Jw7fQOWR/G4PBaC7KupxK/9AyB64aSEJnCnK6LaDm6CX3e64okSaiz1fz91UEOzztEk3FNafdWe8xt88uRRR4GT6+/KV0SlyUGQ9OtIN17GkvkqdFfi0UfFo1ISkdW1cMwBeRpMhZ8qjibDlMvll6c3EYlQaANLKhbclfCCuKxCJQXi3SifyikD/5nEihPExHdlqJPM5RvOkxvid2Akm0JdCk5xI5ajetXPVEFOBcsv3Y6ki0LD3BozWmadK9Dj4mtqd2y2mM5AV87eJ1fR62kbu869P6iJ0rzh7uwCiEMXWZlMmSOzvffoJKjTsom9Xg0qcciSTkaRfqZW1j42RsiIyEGQWJZ1eGRf3ba1FwiX9+BlKvGvY4lcn8nFIOaIclkqFNy2B/0HQFTgtGcjaX6soFFtj8wYjWenarj5mxJzv4buMzuxo1XtqJ0ssTn/fakxWXwVY/F+Df2ZvTCgQURvvSYdHa+s4Ow7aF0/KATTcY1RSaXgdAB/wPmYbDKyCyyT7htoDkB+ASkst31iswc9GHRBrGSqzbkqwR4I3N6PKLeRDky7gzynxtTz6pqwaINgZ9yMy+WOdGr2Fz7C5bEbWXs1U85E/QL9a2qA1D39Cg2N5yD/7wO0Nj+cR09YBIolQVT7egdmDdwR+5ujeOrLUj/9Sy65JLD3HIHC+xfCiZ59gGErvBOoVpDH6b8MIKfbnxIQDM/5o39jZeDPmXbooPkZFasT0m11lWZcfo1MuIy+Cp4PrEXbz3UeJIkITk6Q14eIjOjnI6yYhB6Qea/CUQuOc35CZs42PA7DtRbQPh3x5GUcqrNaEm7K1NodewF6szvgdfw+lhVc3zk4iTn3wSuDlqFhZ8NHjXNkNfxQjE4uKCs+8q7e3B7pia5B27iOrZxsWO4BPuQeCwK6y7VybuSgDY8Fd+PO5K29wapf13Dzs2GN/dNIik8hW8HLCEv25Bwa+tpy8CfBzF68xjOrDjDt43mc3X3VcM0jfQhBguO78hODyQ3yxzD3KgtUA/4BogD6fMyixMAydoCecPqKAe3RdEzGCQJ7dbjaH7fh+5UGCKjLCV4JioNN7LhZg4WMjPOBC0pePibexRZ1VvlwieRy4wX5uoNCbX/NW43aitfL54nnsc/2VeJcH63HSjkyMwV6FJziH97J+7zeyGVkPBo1aMmWduukLnhEjZ3RVus7S3p82oHnpnSjrO7r7Bl4UGWvbWJdiOa0GNiG3wC3SvgHYGlgyXPrhrJsZ9P8G277+j+YVdavtT8gS+8kkwGzi6I+FugUiGpHn8VU3FoM9WknYwuSGZNOxGN0sGiYKrGf1IzrGu5PNameykb/yX284N4vdIMs39vIG9bE0X7wum4lBPR3PrzMo1/6E38vCPYtPEvdhznYG+uLjmFZKbApl9t0lefx+n1Nvh/1Y3rEzdjWdcNC3drXt00np/H/87sTt/x6qbxWDsZ8qu8Gnnx/N4XuLj+IhteXIdrHTd6zO6Bc4ALMII9y7yIuhzHSwuGPJLfg8zJFpmTLSI4EBGbjD4sCs0fB5AcbQqTa80r1gfLxAOyOhq0pZva6eXYggPpZ7mSHUFNS9/CF06lQUIeuFTOc8sj4ykRFeWJKYJyBzJrM2TmBs1m/3xTZNZmJM89XOL6kkzCcXob0n7+B21C8ZUPMpmMhp1r8c76F5h3+k0sbMyZ2fZr3uo4j8PrzqDTPnrnYEmSCBnXjCl/T+Loj8f5qf9SMhMfpFIjf7wC5+P4SuF8LIQgOzyVmNUXuDR1O4db/sjeanMJ+2Q/2gw1Ps81otXJl2hzbhL1f+iD7/jG2NR1e2ziRK/WEfPxPuIXHqfq5x0xO38VZY8GRuJE6PRceHkrtWZ1ImX1BVzGNi6xb4pjkAcZoUlostTY9KtD9p5r6FJysG7kicvoIG5O247Q6VGoFDy/dDgBbaryccv5JNxMLhhDkiTq9q/Lqxen4t/Kn+9bfseW1zaRk5JNTGg8XgGuj/z3IkkSMk8nFG0boHy2M/IG1RBRCWh+241m23H012IQFfD3YuIhOJEGOsjR5xF0ZgxBZ8bQ79+Zxa4qQ8brXsOZFXVXFEUpgwtPVoTWxKPBJFBKQJJJuHzQgdzTMaSvu1TiesoqDlj3qUXKvJKFzG1cfR0Z/Ulvfon4iC7jWrDhq92M9X+PlR9tI+VWWnkefrG41XTl1cOTcanmxOyGcwndc/WBx5IsrcDSCpGUwL3ymB4F+jwtqcejuPHNUU6PWMO+GvM41mEJcRsvY1HFntpzu9ExYhohu8ZQ8+OOuD1TEzM36/sPXAFo4jO5MWYd6uh0qn7WHrafQjk0BHmzqkbr3Vx0Erm1EsemnuRcTsChd80Sx5SbKbCv60byPzHIHSywbFeVjPWG76z7i4Yp6LhFhlwySZIY/NkzdJzUklmt5hN+xjicrjBT0GZGW169OBVNrpavan1FxF/Xca9asTlHklyOrIo7ii5NUI7shKyKO7qL4WiW7UK79wz6qASE3nTH+bjIuZXBCruP2DdgJdE7wtDfFo7Z+Q7xd0zxrK/1aYnjDHfpzNGMi9zIjSlcqBeQoS1xm6cW0xRPEUxTPPdAZqXC9YtuxL64EVUVe8wbFmMuCNg+24hbo/8g53A4Fi387juu0kxJu+FNaTe8KdfPRLL1u4O8VOsjGnWtTc9JbajT6tEl1SrMFPSZ8wwBnQP4ddRKmo5uTI8PuyJ/gL4dkp0DIiEOkZaKZO9w/w0ekLy4zPxk1ihSjkWScS4Oq+r5vjV9Aqk5qxMWvnaVvhIk62Q0EdO24zikHk4hbmjXHEM1ti2yasbRidzYDMI+OUDzXaNJ/OU0LiODkKnu/afq3MybhGNRuLXxx2ZwPeJe2YzdiAZIZgr853Tlct+VWId4Y93I8B3u/HIb7NxtmdPleyasGk3tDjWMxrN2tabvd/0ImdScOc3mse+1bdjIlNTsUbPCf8+SmRJ5oC/yQF9Dcu3VGHRHLiFy1MiqeyKr4Y3kbFvpP/+nCYWVCm2Whoj1l4jeHgZC4BziQxfLupTlU1BICqZ5DeXzqN8KF0qAwvRZmjAJlPui9LHD5f32JLy7G48f+qLwKNrxUGamwGF6a5I/349HQ09kZShDrRrkw+RFwxnzeV92Lz3GN+N/Q2mmoMfENrQf2RQL63u70T4otbrWZMbp11g59nfmtVrA6BXDca5WtrtkI+djlcoQVXlIhE5P5r8JRqW+6uQc7Jt54RDsTY2322LXxKuob00lRghB0q9nSVh0Au9ZnbGQq9FuOIlqQkdk3kWNHi+9sQufMUGYO1mStvsatXY9d999OAd7E7HBEDVRVXVEFeBM1q6rWPcKROVhg+/HHbk5dTuBfw5HkV9S3GxQEDYu1iwcvJQR8/sRMrRRkXEdqjlyU5fD2K9GsnX6Fo58c4juc3riXrdicqjuRrK2QB5UDXlQNURKBrrQaLQ7ToBCjryGl0Gs2JocuB8WIQR5SdlkRaSRFZ5KZniq4f8RqQXLyI9g6XI0SDIJTXoeeCoMHWPLwBjXHnwRvYIMXX5itEwChyfn77t8eHqiHuWJSaCUAotgH2xHNCD+jR24L+pTrACxaOqNWT130n75B4eJIWXeh7W9JX1eaU/vKe04u+cKWxYcYNlbf9JuRFN6TmyDT63yvyDYuFrz/KaxHPjmEHObf0vfL5+h6ajiK0VKwsj5WKlEUpbtxKJJyyXtZHSBIEk7GYOZmzX2Id44tPSl6tQWWNV0vq9vTWVFn6Mh6r095F1NouqKQcgvR6E7ehXVlC7InIuK3cQ910k5Ekn97yYQv/A4Dr1robC/v0h1Dvbm1MydBc9th9QnZf5hrHoaIh72nauRcSiCyHf34P9194JoQ6121Xl99wTm9viB1Jh0uk1tZzTurWuJuFV1onbvOtTsHsix74/yU8cfqNO/Lp0+7Iy1y+ObOpMcbFAEByKa1UTcSjEk1649iGRvhayGN7JqHkgW/7FEy1Ki1+jIjk4nKyItX3ykkhWeRlZkKln5YkRmpsDK1w4rP3usfOyw9rPHJcTb8NzXnm0tF5MTnYHSzoyWSwfg3T0Afo+GHyLKdCwqmZIpHgN55ca8/IMT0Og/aKthEihFMPVBKSVCCBI/2ofI0+Lycadiw8m65GxiR/+B69xeqGo4PfQ+EyJT2L74b3b+eBifWu70nNSG4N71UTxEG/WSiD4bw7Lhv+HdyItBC/oXNu4qJSIzA5GRbug0W0KLfSEE2ddTDJGRfGffnPBUbIPccQjxxj7Yx+Bb4/x03AHnRaQSMWUr5gFOeL7fHv3Oc+iv3EI1oQOSXdH3qMvTcqDxImrN6oRLhypc6vAzAWuGYeZ7Q//XYgAAIABJREFU/5O1EILVrp/xzNlJWHraIoQgdvQaHCaHYBFs8GbS52q5PGAVrmMa4jyojtH2SREpfNltEfW612LI7GcKbBKOrDvDnqXHeHtjYZfL7ORs9n60m9O/naHNjDa0mNIShVnluNcROj0iMgF9WBT6iHgkDydDjxV/NyRl5TjGikCTkUdWRCqZ4flRj/BUMu+IfuTGZWHuZpUvNuyw9jWIDis/e6z97LD0sUN1n3PAoXHrETo9zeb3LFw3Qwt9joP6AS+2Cgn6u8OUqvdf9xFS4X1QvDzEyUljy3VM6e1ZT3wfFJNAKQP6PC23Jm7CsrUf9mOKhsMBMjdeInPLFdy+71tud/0atZbD686wZcEB4m4k0e2FlnR9viWOHuV7l6HOVrNh6iau/BXKqF+H4x9y/3yaO9EnJ4Jeb/DskSR0ORrST8caPGvyRYnMXFFQ6usQ4o1NPbeH8q2prKTvv0nUW7twndgMxyF10a46ikjMRPVCOyTL4u/qwz47SOrxaJquG0r8klNkn47Ff17PUu9zd6/l1BjXGN9+hmqgzC2Xydp9DbevCsfICUsibPgaAlYNwrya8fRSZnIW83r/hJOvA+OXDEOhUrDms51kJGXx3Ox+RfaXcCWBba9vJf5iHN2+6EGdfnUqVR6IUGvR38jvXBuXgszfHVmAF5KXc4ki+klA6PXkxGUVCI+CKEhkWsFzfZ72juiHPVZ+dlj52mOdL0gsvWwf3d/dh1dgdyI8SMGVSgbLG4LXo5naLi0VLlC8PcTJSfefyi0L0lufmgTKfw1tQhax49bjNKMVlq39i7wu9IK4SRux6lIDm351ig7wkNw4F82WhQc4+Ps/NOpSy5BU27p6uV4Yzq47zx8T19Hm5VZ0erO9obtoKciJSSdl53nSzqWQejqBzIvxBb419s28sQ/2wsL76Q7dCr0g/rvjJP9xAd+vumNZ1xXNkoMgBMrn2iCVkOyadT2Fv1v+SOsjz2PhbculTr/gP68HVg2KNrgqibMf7kWbpabx510Nx6LWET1wBa5f90RVtVCMJKw8R+KK89RcMwTZXZEPdY6a74f/Sm5GLi+vG8sPr64hsHkVujzfssT9Xv0rjK3TtmDhaEGPL3vh1cir1MdcUYjsXPRhMejDohBZuciqeSIL8EZyqXzJ1bpcDVlR6SXmfmRFpaOyNSuIflj55kdBbj/3s8fMyfLxva8UDTx3BpLUhkbEpcVcBs/5wAjvR3ZopcUkUCoHJoHyAOReiCN+xnbcF/ZGVaVo9Yr6ejLxUzbhsWQg8mLMBsuDrLQc9iw7xpaFB5Ar5PSc2Jp2I5thaVM+dx6pUaksH7USSZIYuWwo9t7Graf1Wj0ZF+JIzc8dSTkWhS5Lg30zT+xr2+LQrgZ2wf7ILf877rW6tFwi39iJLlON71fdUVgrUf+wF8nRGuXw5iX2XRFCcKLvShxb+lL99VakbL5C4opz1FgxqEz7j94RxoXPDtB177iCZam//IPuViZOM9sa7e/G5C2oPGzwfqdtkXH0Oj2/vryOq0dukqMUPDu7L3Xb1iiy3t3bnPzpBLs/+IuAbgF0/qQrtuVkVFneiJRMdGHR6MOiQJKQB3gbPIHsHs3fqtG+hUCdknNH7ke+6IjMzwGJSCUvOQdLL9si+R93ChLFI/CDKleic2HiOUjTQGkqhs1kMNADXvJ77D488JgEyuQx5TqmNPMzk0D5r5K55QqpS07h8VN/5LZFQ/ap3x9DG5uB8/86PdLjEEJwbm8oWxYc4NzeUNoOb0LPiW3wrV36O++S0Ov07P58L/vn/83A2b3wdLEtqKxJOxWLha9dwVSNfbAPltUMvjX/RefjnCuJREzZgk1bfzxmtIIcNervdiOr7oaiX5N7TvfFbrzMlXf30Obki0hKGaH9V+I+ORi7jtXKdAx5KTms9ZvD0JS3C6JeupQcYoatwnPFEOSOhXkv2tRcLvf+DZ//dcCufZUiYwkh2DTrL9a+t5WZ+yYT2Lp0x5Kbnsu+WXs5+dMJWrzSktbT2qCspBdTIQQiLtWQr3I1BsnW0tC5tppnidNw90Ov1ZETm3lH4mlh8ultQSLJpLtyP+wKEk+t/ewxd7cuddSyUpOihs+uwolUQAJ1MR1mLeUGcTLBD3q4VfghlsRjESgvP1uuY0pvfm4SKP9lkr8+jPpmCm5zuiMpjE8o+lwNsaP+wHFqKyya+5YwQvmSGJXC9sWH2PHDIbwD3eg5sQ0hfRuUOalW6AVZoUkGE71jUSTsu0FOZDrCzYrqIxrg1NoP+yZeKO9RXVLofOyOJD0FJ9t7kLr5CjGz9uPxZhscegeiT8xAs3A38uBqyLvUvWeoXZupZl/QQoJ+7INzuypkHIsk6r09BG4b/UA5TBsCv6bt6qE41C+s+kr64gByJ0vsxxmfqzJPRHN9yhZqbRyB0rVo9CAzJZsXPd/Byc6aKRvGUj3Ev9THkXw9ie1vbifqeCRdP+1G/aENKt1Uyp0InR4RlWAwMAyPQ3J3NCTXVnE3Sq7VZKkLK15uC5DIwmhITkwGZi6W+WLDLj//w3gKRmVv8Rjf6WMgSQ0bbsGmOENERSfAXA41rQzTOc3sDaXFlQiTQKkcmATKQyC0euKmbkVV3QnHKc2LvJ5zNILkL//GY/kgZA/pJFwWNGotR9afZevCA8RcTShIqnXyLN4hVJulJu1kTEF0JPV4FAp7c4Orb7AP9iHeKLysWTtlI1Gnoxm9YgReDYpvWnebp835uDiERkfs7ENk7LuO7/yeWAS6oI9OQb1oD4ou9VC0CrjvGJdm7iLvViYNfzEkoV5/YSO2HariPLTeAx3T38+uwbWVPwHPF56XNOEp3Jq0Ca+1w4vknMTOP0rmyWiqL+lfRBCFHr/J9xN/Z/T/evHTmJWM+2UYQb3Klld14+ANtk7djEwpp+dXvfANqRix/iAIIchNyCLzWhKZJ8LJPB9N1s0UsnMgK01L9q0stFlqLG9PufjY5Ve9FEZBLL1skVeSiiYTD07FCxR3cXJKOQuUN74wCZT/Orq0XGLHrcd+bGOsexS9ICW+/xcKDxvsXwp+DEcHN89Hs/W7g+xfeZKgToH0mNiaGlXdCsXIsSiyQpOwqe9mmK7Jr7ApqTX8ieX/sGHaJrq804k2L7e8512x0OsRcbFINrZI1kV7fjzJaBKyiHhtG3IrFT5fdEFuZ47+Wjzqnw+gHNgUecP7V0ClX4znaJdltD31EmZu1uReTeLqqLXU3ju2wBOqrFxeeIzkU7G0+LGv0fL4GduwaO2PTe9aRsuFVk/YqLXYtvPH/cWmRq/t+/U4/2y9yLQVz3H9eDjz+vxE/4960HZ82fr86PV6ziw/zc53dlClbVW6zuqGvW/xYvlRolNryc5PPjXKAYlILUhCVVipjHI/rDytsVTqsNBkY2kusGjohzzAB8nNvlJHhEw8HCaBUjkwSf2HRG5njusXXbk1aRNKP3vM6hi3LXd4uTmxY9Zg2bk6qmoP3xulrPjWdGf4c63pVNWbq2svcL3vam4IUNV2pnr/utT6sht2Qe5F7qxLoumoxlRp4ceyESu4svMKw34ego1r8WLGyPlYqUIyezqaZmWdjiXita04DqyD68RgJJmE7mIUmhVHUI5qhTzw/vk/QgguvLyFgHfbFojB+J9P4Tyi/gOLEwCXYG9CvzteZLnN0PqkfPU31s8EGl1YJYUM/y+7crnfKmxCfLBqUDg1FB0aj2e+SWDVZn7M3D+ZL7svJjUmjd7vdin1BVomk9Ho2cbUHViPA1/s59vG8wl+KYQ2b7TFzLr8vhPqtFxj8ZGffHq7F0heQjYWHtZG+R/OTb3wG1gnP/nUDuU9jkekZaEPi0a75zQIgayGF/Ia3kgOlcPnycQTjqlRWxFMAqUcUFV1xHlmW+Lf2onHT/1Q3FG5I3e2wm58U5JnH8RtYZ9H3hE1Lz6L1OOFfUfSz93CspojDsHeBL3aErtm3ly9Gc/WhQdZ9tmftLnZmB5WbfCve+8pmztxrubMKwcnsfW9HcxuOJfhvwwmsEvxZnaSUgUOToikeHDzNHSefUIRQpC84hxxC4/j/XEnbPOTS3UnrqPZeArV8+2R+ZduOitq+Vl0uTr8njd07tUkZJG28yq1do55qGN0qO9O5o0U1Om5Ro22zBt5gkJO7rFILO6aZlF52uLzv/bceHUbtf4cjtzGcJGOCY2nWe/CqSb3AFfePjSFuT0WkxKdxqgFA5ArSv95qqxUdPpfZ5qMb8rOt3cwN/BLOn/UhYbPNipoDFcSep2e3Ft3JZ9GpBk1HxM6Udjvw9fQ+8OhQWCBILH0tEFWhuO9G8nOCnmTAGSNayAS0tCHRqHZeBjJ2tzQubaGJ5Ll4+3fYcLE04RpiqccSf3lFNmHwnFf8IxRRELoBXETNmDdoybWfWqX2/4MvjWJpByLLPStScrBvqlXwXSNXRNPFDbF3xUmRqey44dD7Fh8CM8aLvSc1Ibm/YLKlFQbuucqK8asouHgBvSc1R1FCX0+9KkpoM5DcnF7IkPj+lwt0R/sIfffBHzn98TMzzBFod13Ge3eS6gmdEDmXrppC3VSNvsbfkfT9cOwb2wQhrFzD6NLy8X7gw4PfazbWv1A0Icd8ehg3I0zc1soWTvCcPu6+OZvEe/uRpelxv/LbkiSxKsNP2PSD8Oo0cR4uionI5dvB/yCykLFSytHYWb5YL4pkccj2TJ1M9pcLd0+7YaLr31h2e1t8ZH//+zodFQOFoX5HkbVL4acEJWDRYV/t4Rej4hORB8ajf7mLSQ3h/zkWo8Se96YqPxU+BSPj7s4+cqoch1TmjHniZ/iMQmUckQIQcLbfyGzVOD0djujk6X6ahLxr27GY+kg5E4P1spdm55H6snogjbxaSejUblaFeSN2Af7YB1Ydt8arUbH0Q1n2bzgADGh8XR9vgVdX2iFs1fpLriZiVmsGr+a1Kg0Rv02HLearkXWEUIgEuJApUJmX9QgrzKjjkojfMoWzKo64v1hR2SWSoQQaLeeRX8mHNWEjkiOpQ/zn5u4GUkpp9687gDosjVcav8zAauHFAifh+HE1G2Yu1hSb6ZxjxOh0RE9YAWuc3sUO92oz9Fwud9K3F5sgmPfWgy1mcbP0Z9gZVe06kSr1vLT2FUkXE/i1U3jsXYquYdIgfFcMbkfmeGpRIcmEJORjbWVGQH1PHAOdC1IQC3ofupji7wCE80fBKHRor8ZZ+hcG5uEzNfVYF7o41JiDxwTlZPHIlBeHVmuY0rTv3ziBYpJ4pcjkiTh/G47Yl/YQMbqC9gOKQyPq6o7YdWjJinfHMH5g473HUsIQc6NFEOb+PxmaNk3UrAN8sA+xBu/F5tg/2MfVC4P31xKoZTTalAjWg1qRPjFGLYuPMjkep9Qv0MAvSa1pV67Gve8M7V2tmLc+jEc+v4I81sv5JnPehD8XFPjXAcj52OzcnE+rggyDt4kauYuXF5oitMoQ6ms0OvR/nECfWQSqle6IpXBcTrlWBRxW0Npd2ZiwbLktRexbupVLuIEDMaBN1edK7JcUsqxGVCH9N/P4/xWuyKvyyyUVJnXg7CRa9F4WGFubVasOAFQqBQ8v2w4f7y5mU9azmfCj0Mx00slG8+p5He1Xs83nsv3f1HYqjg8/zB/f3WQxi19aTy1JeZ2T9Z0iaRUIK/hhbyGFyInD/21WHSnwxB7zyCr5mEQK+4OT2QE0YSJx4EpgvII0MRmEDt+PS7vd8CiWWHbZn2OhtjRf+A4ozUWzXyMttHlakk/HWvoypovSCSlDIcQH2PfGlXF5HBkZ+Syd/lxtizYjxDQY2JrOo4OxtL23j0cYi/cYtnw33Cr7cbg7wdgeVfPB6HOQyTEGfqjlNH5uCIRekHCohMkrTyP75fdsGpqaN8utDo0yw9Blhrl+LZIZbir12v1/N3iR6q+1hzvYQbxKnR6/u28BL8vu2HVsPR5QPci82YK21osZmD060Uuhrq0XGKGrMTztyElRvISfj1L5M//sEaTxqyDrxkbz+ULkDtzP0JjkolATZt6/njXdsPKx7j01sr3/sZzt8m4lcGud3ZwectlOr7fiSbjm5Ypz6UyItKz0YdFoQuLBq0OWQ1v5AFeSA5PV2Xb08RjiaC8NqJcx5SmffXER1BMAuURkXMqhoR3/sJjcR+Ud/jP5ByJIGXuIRxmdyfttiA5FkXmhXisAp0Lp2tCvCuFb40QggsHrrJlwX5O77pMm6GN6TmxDf71SvZbUedo2PT6Fi5svsSo5cOo2sq4U2lpnI8fJ7qMPEPL+pQcfOf1QJlfpSTyNGh+3A/mSpSjWyGVsQHe9W+OEbf5CiHbRxUIh9TtYSQsOUWNVUPK7fiFEPzh+QU9jr2IdTHlvElzDiK3M8f++abFG8/dTCFv1zWys9Sk5mjR5WpLbLtund/74+T6cyyfvI6Jv4+mVvt7t8UvDTFnYtg6bTOZ8Vn0/LInNbrcv6dMZUcIgUhMN3SuDYtGsjTLT671QrJ6sqJFTzsmgVI5MAmUR0j62otkrLuI28LeZN9MzY+MRJK0/Sp6rR6Htv4Fyay2jTxQWFXeiAJAUkwqO388zLZFf+NRzZkeE9vQon8QyhKSAS9susTvL/xBixeb0+WdjkZ3wnc7H1cWckOTCJ+yBeuWvni80bogYiUyc1Ev2ovMywHF4GZlFla5MRnsb/I9Lfc8h3WgodJHCEHYoFW4vtAU+y7Vy/V97On7G1WH18enTy0jl9vM8FTyribhfCOZ8/HZZN42nruz94efPSd3XiIwIoeqn3bGqVfNUn1G/+4NY+GQZYz8pj/BQxo+9HsQQvDvn5fYNmMrzjVd6D67B66BRfObnkSEXiBiEg2da6/fQnKxQxaQn1xrVrlzbf4LVLxAcRMnp5azQJk61yRQHhsiAzTbQdwCoQbJDhRNQd7gcR8ZmpQcUk9Ek3I0koTVF8iKzsCimmO+Z403NgFOpH+4G7dvehu5zD4paDU6jv15ji0LDhD57y26jG9B9xdb4exd1DgxLSaN38b8jiZHw6hfh+PoZ1hHCIGIj0WysEKyLSlSJICKEy+pW0OJ+XgfHq+3xqFvYUMzkZJl8NWp54OiV9ADCapTI9diWdWBwA8Lq3QyT0YTMXMXtbaPfqAkSiEE6tRcY9fb/N4fCUciUSfnoNfosfSyMTKas/azx+xQOOYhPjiOCkJRTBXOx898T+e2gViuCyPwz+EoS2l6GXkuhq96LKbb9PZ0fbWoEeGDoFVrOfrtEfZ9to8GQxvQ8f2OWN4jKfdJQ2h1iPA4dKFRiJgkJG8X5AHeSL6upuTax8RjESjThpfrmNJrX5sESoWj+xfyFoBmLSAH1IAOUAIykPmA2aug7AfSow+bCiHICksm9Xap79EocqLTsWvkWVDmm/fHBaxb+ODwfGGnzoy1F8jefQ3Xb3s/8t4oj5KIS7Fs/e4g+347Qb12Neg5qQ0NOhjfcev1evZ9eYA9c/Yx4Jt+NBxsEJFCqzV0mnVyRjK3AFKBJcB8IAbDZ2sGVAdeBwYB5f+ZCo2O2C8Pkb77On7zemBRu/AuXR+Xhvq7PSja1ETR4cFKxBP+usa5iVtod2aCkbvz9Ql/YtvaD+fhxYvqYo3nCjqfGqIhkiQZen/kJ59a5/cByU3I4vqvZ+l+5IVijedyT8WQNOcgnr8OLvb7N6Hmh7y14QXk26+TfS6Oaj/1LfX3NDE8mS+7LaJBrzoM/rzXfXuclJasxCz+en8XF9acp93M9gRPDCmxrP1JReSq0V+PRR8ahUjJQFY1P7nWw7FSRRqfdkwCpXLw5AgUISBvLuTNplCUlIQVSM5gvQVk3vdYr+zosjWk/RNjqK7JfyhsVAVlvg4h3ljXcUV2h3mgLjmbmHHrcZzSHKv2ht4UQqcn7qWNWPcOxPqZWiXt7okhOyOXfb+dYMuCA+g0OkNS7bMhRlUgEScjWTZ8BdVaV6H/vD6YWZsZnI+TI5HcP0WSrQJkQHYxe7hdxvsa8EH+eg+PJjGbyKnbkMzk+MzuhuIOA0R9eCLqH/eh6NUQRXDZnIVvo8vVsr/R99SZ3QW3noV5FLnXkwkb9gdei54x5IDcVXpbYDznbGnsfFtK4zl1ei5rvGYzNPktZMXkygghuDV2HfbPN8WihXHjNq1Gx1CbaaxMm41CLid02B/Yd62O2/jGpX7fmUlZfN37R1yqODHu56HlKiTiLsWxbfoWkq8n0312DwJ71XoqL94iI9swBRQWjVBrDf1Vanghc7J93If21FPhAsXXTZycNqxcx5RenWcSKBVGzgegXkzxF6/ikINkD9YHQFZyQud9dxuVVlDmm3IsiqzLidjUc8O+mVe+KPHG3OP+2fh5VxKIe3Ur7t/0QlXd0INCHZZI/Gtb8Fg+GLnD0+FwKoTg4t/X2LLgAKd2XKL14Eb0nNSWKvUNn0FeZh5rp2zkxuGbjF4xHJ9GVghdK5CuI8lyS7EHS6ADsA5D1OzByT4TS8Rr27DvWwu3ycFG4XTdlVg0y/5GOTQEeT2fe4xSPLeN5658sJf0M7dwHljbqPOpdUIW6jwtWXbmRsZzheLDHkvvhzOe21h3Pq2WDcSpUfHVQZk7QsnaGorbvF5Gy2PC4vlft4UsuvYBAHlRaVzpv4pqP/XFqp5bqfevzlHz3bDlqLPUTF77HBalrOQpLaHbr7Bl2hZsPW3p8WVPPOrf32LgSUWflI4+ND+51lxVIFYk66fjvFHZMAmUysGTIVDUf0DOFCCnjBvKQeYH1sdBKjzRR/16lvQzt6g9p6vR2nq1jvRztwqmalKORSE0ekPuSH7+iG2QB/IH9ErJ3HmV1O+P4/FzP+T5d74p3x5Bl5KD87sP30G0spEcm8aOHw+zfdHfuPk70nNSW1oMMCTVnlp1ho0z1jDtxB/YuN1EktRlGNkC6AOs4EFyVIQQJP9+gbhvjuL9UUds7+q4qjsTjuaP46iea4OsevEX5ALjuYg7Sm/v6v2hMFdglavHoo0PNjVd8vM/7DC3Nyfu9Z0E7nwWVSlzOx6EQ2PX49zUi5oTmhX7utDoiB64Atc5PVDVKGzcdnLLBbZ8e4D3txX2aknZGkrMl4cJ3DgcuXXpk7n1Oj3LJ6/l2tFwpm57AXv38r3712l1HF90nD0f7aZ2n9p0+rAzNm5Pb/muEAIRk5SfXBuL5GRrECvVPE3JteXIYxEo04eW65jSK/NNAuWRIwTrV/jRf2Qk/x63JjBAzoIf8vhhaeEFTauDi//quXTMmrh4QZ8RWVTxvX03LGfO7Pfo1O0d9Fo9l1/fQdTyswC0vTCZtJP50zVHI0k/ewvLqo4FfUfsg72x8C9f19KUhcfIuxiP27weSAo5+mwNsaNW4/RmW8yblu90VGVBp9Vx7M/zbF6wn4iLsfwW9zkD+w1myY+1UVl+gqTQ4OEBwcGwebNhmw0b4L33QK0GpRI++gj69gWdDho3BsMUjz9gQ1RUFB07duT333+/77Hoc7XEfLiX7PNx+M3viVkV48Re7eEwtNvOIY1oQbZGIiv8zpbrd1TCFGM8Z3XHFIyljy2nh63FqZ0/1ae3NNpH7PwjaBOy8PmoU3n8ekskdPEJ4g9H0GrJgBLXSVt+Gk14Ks7vtC9YtnHuHuJvJvP8vIFG64bP3IXQ6fH/ouvdw9wTIQSbPtnFwZ+PMW37i7gHlH8lTk5KNns/3sOpZadoPb0NLV5pibKSd559WIRWh4iINyTXRicieTkXJtc+4b1jHjePRaDMKL9WAwDSlG9MAuWRoz3E4EGdiI3T0LGNgg9mFg0Tv/VhLhFRen5dbMm+g1rmfJvH5t/vuDOVN0Wdt5GTvVeQcSkeodGDBHIrZUEjNPsQb+wbe6GwfbSOu0KnJ/71HSg8bHCa3gqAnEPhpHxzGI+lg5AeIqT/JBD57y1qNPDHQm9LaEQuLp4ZbNsGM2eCt7dBoJw9CwMGwK5dUKUK3LgBnTvDunVQv/6do7UjNnYFzZo1Y9u2bdStW/ee+1ZHpxM+ZQsqXzucJgWTk5B1R/VLCvbp6bhY6Ph7+y0yU9TGxnO3y3BLaTwXs+4SoR/up83xF4ya6+lzDG3tq68YhPkjruBKPhvLgaGr6fvvKyWuo0vPJWbwKjx+HVRgcrnwpZX41fOk5yTjKhxdtobLfVfgMSkYxz6BZT6e/T8dZe3bW3ll4ziqBfvdf4MHIDEske1vbCX27C26fd6dugPqPpX5KXcj8jSFybVJ6ciqeCAL8ELydPpPvP/yxiRQKgeV/mqYmfQVh47lsXeTFb2HZRcRKAcOaVm9XsOp/ffwQtGd5/wL80g/q4P8SgSZUk7NTzrhO670iX/lgSSX4fK/DsSM20DGxn+x6VMLi5Z+ZG67Qtry09iPb3r/QZ5gfGq5G9qkT2jLngN/MmQorFwJw4bBwYOGdebMgbfeMogTMPycORNmz4blywvHEuIIzz47mBkzZhiJE22OhuzINKPS29zzcZiHJpGs0RKz5QqqVecLu5362OHvJGFlZ466Z2O6fub2UMZz2ow8Ls3YScMl/Yp0/k1efwnLhh6PXJwA2NdxJTs6nbyUHMxKyHGS25pj1bk6Gesu4vCCYSooJjSBFgOCiq5rqaTK1925+ux6rILcy9yav+24EOzcbfi61w+M+2UYQb3qlP1N3QfnGs6MXDeaa3uvsXXqZg7PP0Svub3wavx0RidvI5kpkdfyRV7LF5GZgz4sGt2hi4hcdWG+ipOtSaxUWgRIJQcL/qtUeoGy4c/DdOuoIKC6HEcHiVNndDQKMpz0U1MFz03KYdn3FtjaFv7hHTyiJahVRsHztcstaLQikPRLISQfDCdhWxipJ6PJCkuq8PcDILM2w212V2Jf2ojS3x7zBh44vNKSW2PWYNWpOkr/ov1EnjZGjsrkww/V9OkL587B2LGFAuXiRZg+3Xj/ZznpAAAgAElEQVT9Jk1gwQLjZV99qUGXHknIjersG7TS4P8SkYo6LQ8rb9v8vh92WGdpsIpMw3ZyMFU7VTMynhM6PZqVRxGJGahe6IK15cNH0EI/2o9zO3+cWhtHCYROT/wvp/Gd1fmh91EaZAo5To08SToRjec9GsHZDK7HrZc2YDeqITILJTGh8XgGFJ97Y1nbFffJzbjx2jYCVg0us/VCUM86vLr5eeb1+YkBn/Sg7biQMm1fWqq1r8akky9zask/LOu9lOqda9Dlk67YeT3+7syPGsnaAnnD6sgbVkefnIE+NArtthNISoWhGVwNLySbBzMsNWGiIqn0AmXlmlRenWC4mAztr2TlWjWNggx3gxOm5TBysJKWIcZvo3VzhfEUDxJIGdg19MCuoQdVpoQg9I9XrSp97XF+t72hHf6P/VC4WWP3XGOS5xzE9Ztnnvo7nfr1s7h50xA96dHD+DUh4O63f/eys2dh3nw9m74KRH7DFtfmPgU5IBZuVkgyGbrMPKLe3IUmW4vf5pEo3Y2TJ4Vai2bJQdALgyNxOUyvpZ+PI2rFOdqemlDktbTd11HYmWHVpHw8d0qDczNvEo9F3lOgKH3sMKvnTtb2UBSdq5ORlIWzT8nREZfRQaT/HUHs10fwer1VmY+pWrAfbx2YzJfdFpEak07vdzo/ku+7TC6jybim1Btcn32f7mV+g3m0mNKC1tPboCqmOd3TiMzRBllILURwICI2GX1YNJo1B5AcbAqTa83/G7+LSo8pglKESt2mMCkpiT0H8hj/cg7+9dKZ/U0ev6/XIIRg6Qo1NyP0vPt6ae54ZRjKUwuRZNJjb5Bm2dwX2yH1iH9jB/pcDdb9aiNytWRtvfJYj6ti0NC7tyFSMuyu6ro6deDu1KdTp6B2fp+0nBwYMQIWLoQGA6tRd0Yr/AfXwyXEB0sPGySZjNyrSVwbvBqFsyVVlw8oKk6y1ai/32Pw1Xm+XbmIE6EXnH95CzXfb4+Za9HqnISf/8F1XOMKFZ/Owd4kHI+673q2Q+uR/vt5YkPj8ajufM/mapIk4fdZZ5I3Xib9UMQDHZd7gCtvH36FU+vPsXTCH+h1+gcapzSY2ZjRdVY3Jp+cTPy/8cyt9SWnfz2NXv/o9lnZkCQJmacTirb1UY7ugrxBNUR0IprfdqPZdhz9tRiE9l69pUyYqHgqtUBZs2YNo4e5EX7BlpvnbYm8aEsVXxkHDul4++NcfvvBEoWilCd7WcXdtZYF2xENUPrbkzTrAMgkHGe0JvX74+hSylpS/aThxNixhkqdevWMX5k+HT79FG7eNDy/eRNmzYJp0wpfb9sWevWSgKIVIWk7wrg+ei3O4xvj9UEHZHc1CRPpOai/3YXM0wHlyJbl1k48cukZhFaP77hGRV7LOhWDJj4Lu87l67lzP5yDvUk8FsW9kuEBzBp4ILNUkrwzDM9SVNkonSzxm92F8Nd3oEkqbW8iY+zdbXlz32QSriXxzYBfUOeUpdS87Dj4OzJs5XCGrhzOkW8P832L7wg/HP5I91kZkeQyZFXcUXRpgnJUJ2RVPNBdCkezdBfaPWfQRyU82gizEAZ7EhOFSBgiKOX5eAqo1AJl5cqV9Os3Eii8Gx3QW8mSFWqysgT9R2YR1Cqj4HHwsBYozEG5/VizUQfyRzPX/bBIkoTTm23RRKaS/utZVDVdsOpSndSFRx/3oT1ieuDtbcUrxRSYBAXB55/DM89AYKDh5xdfGJbHxBgiJ3v2QFCQRFDQcoKCghgxYgRCqyd29t/EfvE3VX7oi2P/oq3p9YkZqOftQF7fB8WAJuUWRVMnZnP5vT3U+6ZnsWPG/3wKlzGNkBQV+ydn5W2H3ExB5vWUe64nSRK2Q+tjdiiiVAIFwLaFL459axH+xs77CqCSsLA157Utz2NmpeKLTt+RmZz1QOOUBb8Wfrx0eALNJ7dg1dAVrBy2gpTwe/9+nlYklRJ5oA/KZ5qjHNoOyckG3ZF/0fz6F9rDF9EnpD7wZ2uEiAbt+6D2Ao0FaOxAbQXqIND9CqI0TRqfckwCpQiVv8xYZEN6dUrfQfZuLMDsTTAvudSyMqCNzyR23HqcZrbFPMiD2JGrcXqnHeaNHrwLbuUmA3Cj7M337sQPuAFIaJOziZi6HUkm4fNlNxTFVK3oo1NQL9qLonMdFK1rPsR+i3L2pU3ILZTUndutyGt54amEDlpF7b1jkT8Gx+p9A1fi2782VUvw/LmN0Oq43OEnknpXp9X00jUOFBodV4auxvGZQFzHPLiDsV6vZ/Ubmzm7+SLTtr+Is1/FmGiqs9UcnHOAw/MP0+yF/7N31vFN3esff59Ym7pTKtACxd3drcjYhk4YOsbGkMm9zO52tzv5zRmMGT7DGWz4cJfh3pZSqHupR8/vjxQoNG2TNklbyPv16gt6zvd8z5M2TZ488nk60vvNPji4WldqoCYgZuagi4xHHxEPUgnShoGGmUBuZhbXiumgnQri7qIDKiOLijowJa+C9K2SBWhVgM3bjOv6if+8Mar8hWYgvPR9jW8zrtYRFAAEJ1A8S8WHxAmgGG9Ji6yCzM8F348GkPbhXrQpuXi+0o2Mzw8iqrRVbZqVcAWepuJ12k7AvwCB/PNJRI1ahVMrf0IWjTDunFxPQf3dLuSPt7W4c5JxNJaUHVE0+m9vo+dTl53GZ1yLKnFO4E6hbPl1KIJMyhlNIbVv5pq8tyCXEvr1EJIWniD/UkqFbZRIJIz7/DF6v9CVj7svIPZ8QoX3MgeFk4J+7/Zn1rnZZCdk81XjL/hnyUmr1sTUBARPV2QdGyN/pi+yPq0Q81Ro1h9E88chdBdjEAvuORq6yzfR7j1XMtIixoKmI4i7MDgmxpwTgFzDl/4L0D4N4iNaC2OPoJSg+jsoAI7vg6QBYO4LvBKcloLENp/GKotjS388p3ciZe4OHFrXRh7iye1fz1a1WVbkP+h1FZklIsVQezKBjDUXiZn+J7Xf7IX/K12N1pPoLsWhXrIf+bPdkLYNqaTN96PX6rkwcytNPx2A3L2kE63NKCBz8zV8ni2pK2IrfDoFkWZCoawoiuyKiEcekY421fRUi0Mdd4Le7cWNOdvQ5VWutmDQnF6M/eIxPuv/PVf2RVVqL3NwD3Rn9PIxjN80gVMrTrGwwwKu771us/tXVwRBQOLvhaxnC+TPDUDaNgwxMQPN73vQbD2BLjIe3alI9BGx6PYVc1LELND0AxIxDHc1hXwQt4PuZSs9Gjs1jZrhoAhKcP4LJI0xPZKiBOUCkJcMuVdnXB9rjLJTMGnv7sZjVhdyN1xCcyurqs2yCqknpewc/ix6jTlOigzwQq/aRdw7x0j7+Qz1fh2F+wDj04Z1J6PR/H4MxbTeSJtYvlA65tvjOPg4ETDauOhY2srzuA9sgNxIV4+t8G4XQNaFZHTlRONy0vNQiSLOg8PIWXfRrHt4DW+Mc9vaxP1vf2VMBaDT2Da8tPo5vhuzghNrzlR6P3MIah/EtP0v0PutvmyYso5fnviZtMg0m9pQXRGkEiR1ayEb0Bb5+AFI6tdGd+EG5BaAXkQfGY/24AWSkpJ4+unO1GsURbvOhXTpqeGPTXr27dcz7HHNfXtOnKpl3YZ70arU1Dzkyh/48fu5tn54VYyFoyf2CIqNkXiCy05wmAm4czdveR8KwAGk3Q0OjcKyOT1b4TWrM6JGR86Gy7hNaGNI9ViiUK0akbA3mh1Df6bJCzORyI9hiIiUN+TNBQhDnXSI6GdPostVU3/12FJVWbX7rqLZfBbFy/2RhPha+BFAQVw2kZ8dovn8IUZbh/UqLWm/ncN3UsmuHlsid3HAtYEXmeeSylwXH5FCQEM/3Ea3IPevq+jzNWWuf5Dgd3uT+088GVsq3ybfpE8Y//p7Oitf3cTObyrv9JiDIAi0GNWCOZdfpU7nOvzQ9Tu2vraZgqyHvbPOdASFDGmjYCT+nvfmder06C/G8Hi/AfTsFkv0NTmnjslZ9YuMuDjTXr/WrtfTuZPAylXLrGd8dcXuoJSg5jgoAIIjOL4NblHgtBCkvUHSEIS6IGkBimngegJcNoOs5tYGCTIpvh/2J39PNIKrA/o8NXnbI6raLItx888r7Bm7ir6rx1F3RBOgJRAHLEWd3QJdoRyDE+qOqHdDFB2AQcBGco9u5/roA7gPDqPO1+FG6zpEUUSz5Sy6Q9dQzBqIpLZ5kuymcvlfOwiZ1h6Xht5Gz2duvIJTMz+UYcbP2xKfjsGkHostc038tWQCGvohD3LHsXVt8raZ52hInRWEzgsn7v19qGJvV8ZcAOq0CuTtw7PY8/0RVv/7T5vrlsgd5fSa25vZF19Blavmq8Zfcuy7o+jseiH3KFCDuzNCsC+SFqHsFzNwcC9k+rR7ke66dQVmzjBNcXjlGj1ffiolLi6N+Ljz1rLaTg2hZjkodxDkIB8BLhsNDonbOXA9CMoPQWKdIWS2RuqhxO/TQWTOP4brmBZkfX8c3UPwCS7ylzMcemETg7Y8R0CfesXOyIFRnPv8Ky5+uxjYAPwCmjWIMX8jittIXexB7L93Evz5IHxLETwT9Xq0a06gv5yAYvYgJN5lzGiqBCk7orh9OpEGc40rqYp60dBabONZT6Xh07n8OpSEiBQCi1qMXce1JHvNBUQzi0Wdmtei1gsdiHllG6Km8m/kPnW9eOfwLCIP3WDRc7+jVdu+aNy1litP/Pgkk3dO4dIfl1jQ+hsitj8KYorlI+vXBsVTfZEP64yse3Ou6rJp20GFofC1JAcPi7TuoLn79efme8+v2FiRpCSRjh0kjBnlwOpVn9joUVQD7DooRqmZDsojgqKBN95ze5D5w0mU3eqS9d1xw4n8BIj8Hk7PgRPPw6lZcOULyImsWoPL4dKCo/zz9t8M2T0Z3w7Gh7fF743Gu003oC8wHOQD0GU4c2v2Vm7vjKL+6rG4dA42eq2o1aFZcQgxJRvFzP4IrhXt/CobXYGGi3O20WxeOFKl3Oia7H03kDjJcelUPYbU+XYqv5MnoSjFA+DQohYSN0cKjpivFOs3qQ1SNwcSFxyvkK0P4uLtzL92vUhhjoqvhy2iIKdqNDNqt6zN5J1TGPTJYDbP+YvlQ5aSfDm5Smyp1oj3JCFmzNLSqr2GDl0N6cIe3QTOnpTf/Xps2L23oFVr9IwZZfh+3BhYufqQbe22U+2wOyjVHOfe9XAZ1ghVRDr6xBPo978IJ6ZA3EbIugC50XD7EiTugFOz4fhkSN5rUGusJoiiyOkP9nBpwTGGHXgez6bGhcDUOSoyzifh37XO3WOqmCyi3ziD1FlKvV9GoggwXqciqjRoftoHOhH59L5WnS8S9flh3FrWolZ4WKlrUpacwm9K22ozU8mtsS+FqXkUppXenVPcQREEAbexLcheZX6YXZAI1P1sIOnrLpFztOy0kqk4OCl4ef1EfEO9+b/eC8lKyrbIvuYiCAJNhjdl1vk5hA1syOI+P/Hny5vIK+Pn+ijRrFkzTp+9F+ldOF/G7u0yUtPKfz1auUbP8l/0hDRU89jIQs6dSyQysnp/6LIo9ghKCewOSg3AY3I7XNtfwmf4biS6CNCrQXww1K0HvQrybhqiKde+rhZ6AqJez/FXtxGz4TLDDkzFtYxJzUkHY/DtEIisKCpxe2cU0c+uw2dMQwJfb4eklHk5Ym4h6oW7EDyckE/qgSA3b8KuOeRGphPzw0mafTGo1DV555JQx2fjMah0B8bWSKQSvNsHknYi3uh5vV5PYlQatRvcKyZ26l0PbWIOqiupZt9P7uNM3U8HEvOvHWgzLJOalMqkTPhhNG1HNOejbvNJijTfLkshU8joNqc7r1x+FUEi8HXTrzj01cEqSUFVJ/r27UthoYTvf7z32pNvgsbmtWsieXki8TcUxEQoiIlw4825g1m1apUVra1m2B2UEtgdlBqAELcBlyZHEWQmvvjpCyFpF1ybX6WRFL1Wx4Gpf5ByMo6he6fg5F92l078nmgC+9RD1OlJ+uowif93kJAfHsNrVFPEAuNvcmJmHur5O5E0qIXsqc4Wm6tj9F6iyMXZ22jwejeUwe6lrktdegrfCW2s6ihVhDuTjY2RFpuFq7czSpd7KqqCTILb6OZkr65YsaJbj7p4Dm/EzTf+tlgXmiAIjHh3EMPe7M8nPRcQfaJqZ+k4eTszfP5jTDvwAtf3Xueb5l9zeeOlh67rzlQEQWDj+pnsPygQ2lBNx24aJkzV8ulHZf8trFyj44kR9//tjhw1lZUrV1rTXDvVnMqPcLVjXXKiIHoJgr40FcZS0KsMTopXO/DraR3bykBbqGHv02vQFWgJ3zERuQkqqgl7o+ny8UBint+EKIo0WDcWmZcTYmEBpJf8tKxPvo36+z3IejZC1rfk3B1Lk7j+MqqkXEJndip1jSr2NjlHYwn+aIDV7TEXn05BXPv+hNFzCRHJRmfwuAxvzO0VK9Em5yKrZX7BccArXYkYu4a0X8/jO75sqX1z6DW1M261XPh66CKmrniaVkOs//svC7/Gfkz4ayKROyPY8toWjiw4zJAvhxHQunoOKbUmtYPmsOrXbzGmHNu71/1OyPLFhregUU8+8MFCaE7LVo9z+fLj1jKzmvHwRD0siT2CUt25tZqPfomg2eTjtJx6nNbTThD+xlnm/nRPZfNmcgH1nj1CVq6GE1ez6TnnFI0mHKPxc/uY+vw08k2JsVoQdY6KncN/QSKXMmDTMyY5J4Xp+Whu3ib7s0M4NvUjdNHjyLyK5n44OIJag6i7FzbW30pH/e3fyAa3tIlzoslWcfnfO2mxYAiSMiIjqSvO4D26GVKXqpG1LwvfTkGkn4hDNNKua9BAKakVI3FxwDm8ITnrzRNuu3u9QkrI14NJnH+M/KuWTcm0Gd6c2X9NZcnkVRxcZpmC3MoSNrAhM8/MosXoliwPX8qGqevIScqparNsi+AHwiDuCaSYizNIX7ekRXZqKHYHpTqjyeHovr/YfDSV0z904PziTuz6vDWLX2vCpiNpXLlpKMyb/W0k/5tYD5VaZPT7F/j0+QZcW9GZK8s6Mbitkpykir25VITC9Hy2DViGa4gnfX4fg1RhWpDu5peHaVzLldr/7k7t17vdN/VXEARwdIRCQ5pHF5GE+oc9yEd3QtbZuIKspYl4fx++/evj1a1OqWu0WYVkbryCz/iKD82zJkp/V+TujmRHppc4lxCRSmCjWkavcx3dnNzN18wWbruDY4gngW/1JGb2NvQFFdujNBp0DuHN/S+z6YOd/PlhxacqWxKpTEqn6Z155cprKD2d+KbF1+z7eC8aCz/2ao3sQ4pPoTcdBdAIhOEWNqgGYK9BKYHdQanOpOwjMV2Nj7scB4XhV+XjriDQ14GvXmzAS99cY9vxdHIKdDzT35+Fm+KYMLA2XZoZ6iMEQWBUDx9qaY7axNy8hGy29F6Mf88Quv/0OBIT6kH0ai3x7+2hYEcUwhONcS+tsFSphIICdGdvoVlxEPmkHkhbGm83tjS3zyURv/oCTT7uX+a69FXncetbD4W/dbRXLIFPKe3GxTVQHkQe4IZj2wByK6EQ6/1EE5ya+xH3keVVYWs38uOdI7M4ue4cv8xYX20G/Sk9lIR/PoQXj80g/nQcXzf9kvOrjQzVexgRGoHsDwxDPU3FAQgC+RYQ7NUHduwOSvWmIIGB7VyJTVXR8LmjvPTNNfafywRgSCcfvNzkPPfpZb6b3RCAizF5tGv4YCGqHvLLHxRXWbKvp7O55yIaPNOKTp8NNqm9Vp2YQ/T49WgzCojMVxM40vg8GwDB0Qnt8eto1p9AMb0v0jB/S5pfKqJe5MLMLTR6vy8Kn9JfbPVqLam/nsNvctXK2peHbymTjYu3GBvDbVwLciog3Fac4P/2IedILJnbLN866lHbnbcOzCQpIoWFo5ejLqjc0EJL4l3fm2fWjWfU8jEc+Gw/P/b4gdgTlmm/rtZIeoJsF+BD2WMspIATCB1AfgyEmjHc1aLYhdqMYndQqjPaPFyUMk5934GfXm2Mr7ucsf+7xPLtiQDMGBFIh0ZuNAouJ5Sqs64CbcaFJDb3WkzL13vQ6o1eJl2TezyW62NW49a/Pt5vdCcvNRfvVsadDlEU0R67he7oLRQzByIJtp10/K1lhmF1dSaVnbbJ/OsaykY+KBtbfuaPJTE22Vij0pAen4VfSOk/V4fm/kg8HSk4VPGuGamrAyHzwol9bw/qBMvrmCjdHHl16zTkjnI+H/ADuRnVS5ukXq96vHTiZTpM6cBvT/7CmvGryIp9OAeB3kXSDuQxIFsEQnsMw17di77cDN8LY0C2B+S7QSi9O+6hx+6glMDuoFRn5G4ASKUCvVt78v7Eenw7syHrD6YAIBEEJMUCFc1CnDkVYaQgT2a9lEPKsVi2DlhGpy/CaTK9Y7nrRVEkddlpYl/fQdD/DcTv+fYk7rtBQO9QBEnJp6OoF9FuPI3+bCzyEQ0QvG03FViVmse19/bQYsFQBEnpESFRFEldcgq/ydVD1r4svNoGkHU5FW2xeoik6HR863ohK6ct2m1cywoJtxXHuaU/flPbcePV7Yhay6diZAoZ0359hvqd6/Jx9wWk38q0+D0qg0Qqod2k9rxy9TU86nqyoM18dr33N+q86hPxsTiCHCRPgPwwyC+A7E+QrQLZdpDfAvlykFTPui07VYvdQanOuNTjWryOyLh7XThnr+dQt5ZxCfeXRwSxYmcix6/cG9T26+5UklTWSYfE74pi54hf6bX0SeqPa1nuel2emthXt3N7SwT1V43BtajgNH5P9ANzeQyIOj2alUfRx6SimDUQwcf1bqGsLbjy1i4Cx7XAvZTIzh1y9seATIJLV9vUxFQGmVKOexNfMk4n3D0Wfy251PqT4jj1DEWbkovqckqlbKg11SC6l7jQOp03EomEcV+MoOfUznzUbT6xFxLKv8jGOLg4MPDDQcw8PYu0qDS+avwFp1ecsvlARJsj1AFJZ5D0NURXHuWIyYPYIyglsDso1Rnf7uQW6Jjw6WWaTjpGy6nHuXwzn/9OCDW6vJaXglXvNOf1H6JoNOEYTSYd4+D5TNwaPmFx025suMTeZ9bSf91TBA9pVO561Y1Mro9dg8RJTr3fRqEIdLt7LmFvNIF973dQRLUWzdL9kFOI4qX+CM4O4OgEBbZpmU4/dJO03dE0fLd3uWtTlp7Cr5ThhdURnwfqUMqrP7mDQbitRYWF2+7uIxEI+XwQaasukFPOAMPKMPjV3oz5bDif9fueq/ujyr+gCvCo48G4357i6bXPcvyHY3zf+TtiDsVUtVl27FQL7KXS1RmJgnZ9nuVI2AYj0vbQu7UnvVvfLx3fpZk7B78plmrw6gCedS1qVsSyU/zzzi4Gb5+AT5vyhaiyd18n7t091JrVGa8xze97I8++kYFOpcOjWO2GWKBGvWgfgrsS+TNdEWSG1IOgdELMuV1hdQVT0Wt0XJy1jaafDUTu5lDm2vyLyahisvAc0tDKVlkO385BxG2NuPt9fEQKYR1Me44YhNtOo03KQVaOMnBZyP2cqfvJAGJe20GTv55B5mGdwY6dn2qLm58LC0evYPzCkXQc3doq96ksdTrXYfqRlzi38hyrn1lJcKc6DP40HK/QR7Bg9JHk4Yl6WBJ7BKW6E/wESIxPzC0XiQOEPmdRcy58fZjTH+xl6N4p5Tonok5P0ryjJHy0n5DvhuM9tkWJKEP87mgC+ta7e1zMLkC94G8kAR7Ix3e/65wAd1uNrc2NBcdxrO1C7ZHlC8ClLD1dLWXty+LBVmNTIygAEmcFzkMakbOu8to67r1D8RzcgJtvWU4K3xhN+zXk9Z3TWfnKRv5ecMBq96ksgiDQ+unWvHLlNfxb+rOww7dsn7uNwuyqmd5sx4bYu3iMYndQqjuOftDifwZnwxwkDtBwBrhbRmVVFEX++c8urv50kmEHpuLe0KfM9drMAmKm/0n+6QTqrxmHUyl1HAl7DfN3APTpuai/2YG0RTCykR1KFqYqHECnRdRabyBbQextor44TLN54eWmbNTx2eQcjMF7THOr2WMN3MK80dwupCA5FyhbA8Xo9aObk7vlGnoLFHYGvN4NdVw2aSsvVHqvsqjbOpC3Ds1i98LDrHnjr2qtRaJwUtD3nX7MPj+H3NRcvm78JSd+Ol5t9F3s2LEVdgelJuDVBlp9BFKloSK+DESkiFoZ+rovQ8BQi9xe1Os5OnMzsVuvMWz/VFyCPcpcX3AphajRq3Fs4E3o0ieQl6IfIoqiYUBg33roEzJRf7MTae8myMJbGnUODIqySqsWyl56bQchL3bAJaz8VubUFWfwGtkMqauZzmMVI0gkeBcNDsy7XUBhrgqvANOLFWX+rji2DyR389VK2yJxkBE6L5zEr49SEFFS4daS+IZ48fahmVzbf51FE35Hq6n6ad9l4Rbgxqilo3lu80TO/n6Wb9vOJ2p39aylsWMB7BGUEtgdlJqCZxvovBzqjAGZs8FZKV6NIVWCxAEhYAj5iTPI22iOgmPp6DU69k1YT8bFZIbumYLSr+yW5cyNV7jx/Eb8X+1K7bk97pOsf5CsK6nInOQ46zWoF+5GPqINsh7lFNwqrVcom7w1guwLyTT4V/dy12qzC8n44zK+E2pme6RvxyBSj8WREJlC7TA/swt83ca1JHvtRYu0CjvW8yJwbnduzNmKvtB60TEAVx8X/r37JfKzCpg3bBEFOdU/fRLYNpDn906j73v92fjCBn4esYK0CMvONbLz6CEIQrAgCHsFQbgiCMIlQRBmFx33EgThb0EQIov+9Szl+glFayIFQZhQ7HioIAjHi46vFgRBUXRcEARhviAIUYIgnBcEoVxVS7uDUpNw8IH6k6H7BmgyF0InQtBICHkOGs6CHuuh8RycxoajiUxFdSymUrfTFmj4e+TvqLMKGbxtAgr30gsZ9Wod8e/vJeWHk8YAh24AACAASURBVNRbMRIPE4pG4/dE07R/HdSL9yN/tivSdsa7k4ojKJWIVqhD0eVruPTKdpp/E47Usfza8fTVF3HrFYqidsULRauSO4JtCREpBDYyPb1zB4dmtZD5OJF/MMYi9niNbIqyoTdxn1i/RsTBScHMDZPwruvJp30Wcju5+g/zEwSB5k82Z86lVwnpHsIP3b5n85y/yM+w7SBQO1bE9hEULfCaKIpNgM7ADEEQmgJvALtFUQwDdhd9f7+pguAFvAd0AjoC7xVzZD4Fvi66PhOYUnQ8HAgr+poGfF+egXYHpSYikYFfDwh9Fhq+BPUmQO2BRVEVEBzluM7sSe5PR9DfrtibuTq7kO1DVqBwc2DAhqeRKUtPLWmSc7kxYT2alFwarB2LownpEQDNseuEuehQPN8baRMTx9I7OkGh5V+Uoz47hHu7APwGNih3rV6tI23FGXyruax9Wfh0DCL9n3jiryabXCD7IK5jW5K98pxF7BEEgTr/60f2gRiy/rZ+GkMqkzLxxzG0Ht6Mj7rNJzmqZkQkZA4yev6rF3MuvYpWpeXrJl9yZMFhdNU8XWXHBGzsoIiimCiK4umi/+cAV4BAYASwomjZCuBxI5cPAv4WRTFDFMVM4G9gsGAIxfYF1hm5fgTws2jgGOAhCELtsmy0OygPKfImtXDsWZ/cn8wfFFiQmsfWfkvxbOJH759HISmjQyXvZDxRo1fj2iuUuguGmVyPodl7hbqOGpjQA0moGfLwCgXodBYtlM29lkbMT//Q9POBJq3P2nINh/peODWt2Bt7dcDR1xlHX2dSTsWbVSBbHKeeIegzC1BdTLKITVJXB0K/CufWO3tQJ1g/qiEIAo+/N5ghc/vySc9viT55y+r3tBQufi48/v0TTNn9PFc3X2V+q3lc3XK1Whf/2qm+CIIQArQBjgO1RFFMBIMTAxh7gQgEig+Uiis65g1kieJdXYw7x8u6plTsDspDjNNT7dDdzEB1ONrka3Jjs9jcazFBg8LounC4Ufl5MBS4pq04w61XthL0cX/8phvpuinlOs3Wc2h2X+bw2VycW5b5/CyBIAgWrUMRRZGLs7cRNrcHymLicWWtT1l6utoPBTQFn05B5F5KrXAERZBKcB3dguzVluvAcW5TG7+JrYl5bXulBhOaQ+/nuzDhx9F8PXQR57ddsck9LYV/c38mbZ9M+OdD2fr6FpYNXkqShRxGO7bEwtETQwTFRxCEf4p9TTN2Z0EQXID1wBxRFE0dkmXsxV4s43hZ15SK3UF5iBEcZLjM6knuoqPos8pP9dyOTGNzz8U0mtKO9h8OKLVwUp+vIfb1HWRuumKQrO9umsiXqNejXXsS/aU4rrt449klxJyHcw8LdvIkrLmEKi2fkBnlzxECyDl8C0QR154hFrl/VeLdMQgS8ggIq3gkyGVoIwr/iUebaLmIR61p7UEqkPT9SYvtWR5thjdn9qYpLJ60koPLT9jsvpZAEAQaD23M7PNzaDysMUv6LWLji3+Qm5pb1abZqVrSRFFsX+zrpwcXCIIgx+Cc/CaK4oaiw8l3Ui9F/xqbbREHFJ/tEQQkAGkYUjeyB46XdU2p2B2Uhxx5Qz8c+zUk9/tDZYZ/088msqX3Etq805uWr5XexaKKySJq3BoEuYT6v49BEWRae6qo1aH5+TD65CwULw8g9sDNEvL2piIonRAtEEHR3C7k8tydtFgwBEkZ3UbFSV1yCt/JbWuMrH1ZONT3xFOU4uJZ8Y4vibMCl6GNyF5ruSiKIJUQ8sVgUn89R+4p283RadAlhDf2zWDT+zv48yPrisdZA6lcSteZ3XjlymvIHGTMa/Y1Bz7fj1Z1Lx0qiqJpeiq3cyExBRKSITMbatjPosZRBUJtRfUiS4Aroih+VezUn8CdrpwJwKai9YGCIOwuOr4DGCgIgmdRcexAYIdo+KPZC4x68PqifZ8r6ubpDNy+k0oqDbuD8gjgNK4tusRsVPuvGz2fdCiGbYOX0+WboTSa0r7UfbL33uD6M2vxHteCoE8GIDGh2wVAVGnQLNoHWh2K6f3QSyUkHb5F7V4hFXg0WExR9tp/9+EXHoZXF9OG/BVcSaUgMh3PYeXPHqoJ5CnAWRTQ5KoqtY/rqObkbY1AX8l9iqPwd6HOR/2JeXUbWhsqqQY0rsXbh2dxcu1Zfnl5fY0UR3PycmLYvOG8cHA6MYdimNfsKy6uv4Aoivw1cxOL+/5k3PnSaOCfi/D5Evj0J/huJXy/Cr5YAh//CAdPQYHlfsd2qpxuwHigryAIZ4u+hgD/BwwQBCESGFD0PUBtDJ0/iKKYAfwPOFn09UHRMYC5wKuCIERhqElZUnR8KxANRAGLgJfKM9A+i+cRQJBLcZ3di9sf7EDesjZSL+e752K3R7B/wnp6/zqaoAHGO1hEnZ6UhSfI2HCJut8Ow7lNmYXX91+bp0L9414k/u7IxnZCkEpIPXwT9zBvHL0q+MldrgBRj6jRIMgrNgbg9plEEtZdovfZF02+JmXpaXzHt0aieDj+bJJi0tF7OZJ+KgH/XuW3eJeGzN8Vx05B5G6+hpsJU61NxaNfPXIO3+LW27sJnT/EZlErzwB33tz/MgueXMbCMSt44ddnUCgVNrm3JfFt5MtzmyYQtSuSra9tYf+n+0i6kIREKuH4j8foPL3LvcVnr8C6HYb/qzWGf7XFOoNu58D2g7DtAAzqDr062O6BPCrYWFxNFMVDGK8LAehn5FhnYGGx65cCS43sG42h9fjB4yIwwxwb7RGURwRZfR8cBzch97t7qZ7rqy+wf+J6Bmx8plTnRJtVSMyLf5F7Io4Ga8eZ55xk5aH+ZieS+n7InuqMIDU83eJ3XyegT8XSO0ClFWVFnZ7zL2+h8f/6ovA2zUlSJ+WQvS8a73EtKnTP6kh8RAqOYV73zeWpKG7jWpG95oJFhNuKEzi3O6obmaSvuWTRfcvDyV3Jq1unIVNI+WLgD+Rl1ly9kQb9w3j59CxU2Sp0Kh2afA1bX9tKZkzRB96D/8Da7QbH5I5zYgyNBrRa2HkINu2xjfGPEtVcSVYUxW9FUfzT4huXgd1BeYRwGtUKfUY+qj2RXP3pJMdf20r4zknU6lLH6PqCK6lcH7MKh1BP6i17Armvs9F1xtAn30b1zU6kneohH3F/zUb83ugK15/cpRJ1KLeWnEYilxD8nOmTbdN+Povn402QlSFWV9NIiEjBu2MgaScq76A4NPFF5u9C/v4bFrDsHhIHGSHzhpDwxWEKojLKv8CCyB1kvPDbs4R2rMtH3eeTHptp0/tbkthjt0iLSEOQGv4OtQUafur1I1y4ZoiMaMxo29do4cQ52G+7ImY7jyYPR6zajkkIcimuM3uS/u+/uHohg6H7puLewLioWuafV0n8vwMEvN0Lj6Hm1VzoY9NR/7QX2ZDWyLrcH5nR5KtJ/SeB2j1M6/wpDUGpRMw0/w1LlZLHtQ/20XnbeJPaogF0uSrS112i4YanzL5fdSYhIoW603tycdpmi+znNq4lt385i1Ox6dSWQNnAi4DXuxEzZyuN1o9D4mC7ly2JRMJTX47AI8CNj7rN59Wt0whqbnoUsbrgHebDYwsfR52joiCrgMyYTDKvpyGu34mg0eIy7x2OPjOD8VtWAXArJwt3B0fcFY74KJ3ZNXYaZ5LjafvzN2wfNYVBoY1gxyHo2AKUD4/TXqU8JPNzLIndQXmEEEWR0z/+g5BUQM8nGuJW36vEGr1aR9JnB8k5eJN6y5/EsZypxQ+ii0xCs/wg8jGdkLYqGZlJPnILn9b+yF0qOWDP0QkK4xFF0aw3wytv/k3Q0y1xa1HL5GvS11zCtWsdHEzsWKoJ6LQ6km+kE9KrHudUWvLibuNcycen7FaXzG+PobqYjGML49OrK4r3mGZkH7xJ/GeHCP5Pb4vubQrhr/XBo7Ybn/b9jhlrJ9C4V/mKw9UJFz8XOr/Y+f6DlyJh1da737bwrc3Zia8AMHHraobVb8KoRvdqilZeOUv3wBBWXjlrcFAE4J9L0KOdLR6CnUcQe4rnEUGv03N4+iYS90bTfP14JFodhTuv3bdGk5LLjYkbUMdl02DtOPOdk3O30Cw7iHxiD6POCRjm71Sm/uQucrlB4kdbRs78AdIPxJC2L4aG/+ll8jWiRkfqijP4TXm4XoRTbmbgWdsdRycHfDoGWaQORZBKcB3TgpxV5y1g4QN7CwJ1PurH7V3XydptuvCgJenydDteXDmehaNXcHLd2SqxwaLsOwEqtUlLRVFkXcQFloePZWdMBIVajSHVs/+EvQXZIlhFqK3GY3dQHgF0ai17n1lD9vUMwndNRunngsusnuT/9g+6okFpeacSiBq9Gpdudaj73XCkbuZFOLRHo9CsO4Hixb5Iw0r/9JxgifoT7ijKmt5urFfruDBrG82+GITMRDl+gKztkSiC3XAyI+JSE0iISCGgoWHEgKUcFACXIY0oPJOIJt5UQUrTkbk7EvJVOLfe3oU6uWpEyJr2a8jrO6fz2+yN7Pr2YJXYYBH0erhVpgTFfRyOjyHU3Yv6nt70rlOfrdFXDScKCg06KXYqRxXooNQE7A7KQ442X83fj/+GXq1j4ObxKIrenGXBniifaEnOggOk/XKWm7O2EPhBP2rN6GRybQYYPllpd11Cu/MCipkDkQSXPihQdbuQzEsp+HU2TXekXMwolI2efwxlsBv+jzc2eXtRFElZcuqhi56AwUG5M4PnzmRjSyBxkuMyvDE5FhRuK45LuwB8n21lUyn8B6nbOpC3D81k14KDrH1zc40TdAMMeialjLEwxsorZxnXuBUA4xq3YuWVogiSVAL5ttOpsfNoYXdQHmJUWQVsG7QcpZ8z/daMQ+Z4v2aIw4BGpB9LIn3ZaeqvHI2bmcJpoiii3XQa3cloHGYPROJX9iybxAMx+HUKKmFHRRFMbDXOv5nF9a+O0HxeuFn1KrnH4tAXanGrhEZIdSU+IuXuDB6fjkGkn05Ar7XMRFzXkc3I2x6JPsc6ol7+L3YAnUjyT/9YZX9T8A315u3Ds7iyN4rFE39HW9OmCZvxd6DT61kfcYEPju4i5MdPmLl7E9tuXCNHXWhIs9rfRSyDPYJSAvtT6yElPzmXLX2W4NM2kJ5Ln0Qiu38isepWFtHPrkfW2A+v2nJkcvOeCqJOj/b3o+hvpKKYNRDBo/wW5IQ90QT2rW/WfcqkaGhgeZ9gL722g9CXO+FspCi4LFKWnMJvcjuzIko1hYRiDoqDpxKnQDeyLhkbuWE+Mj8XlF2CyfnrqkX2exBBKiHkq8GkLD9L3hnT0xSWxtXHhbm7XyQ3I595wxdTaEElXavj6GBI85jArpuRtPILIHb628S88CY3X3iLkQ1bsDHyEuh04KS0srF2HlXsDspDSM7NTDb3XETIE03pPG9IiYnE2ftjuP7UWjxHNaPOgmG4jGtDzvwDJofMRbUWzdIDiNkFKF7qj+BsWk1H/N5oAixQf3IHQS43fBLUlF4om7z5GrlXUqn/Wlez9i6ISKPgSgqeI0xPCdUkiqd4oCjNY6E6FADXsS3JWXcR0UJRmQdR1Halzod9ufHqNnRWitSYgoOzA7P+mIxXkDv/1/tbbidbbmiiVZEI0MB4IfuDrLxylifCmt13bGTD5vx+5Sx4uIG7qzUsfPSwR1BKYHdQHjKyrqayuedims7oTNt3+96X0hD1IskLjxP/7m7qzh+Kz7OtEAQBx6HNQAKFm8tX6xQL1Kh/3ANyKfLneyOYqElRkJpH7s0sfNsFVPixGUXpBIXG61B0+Rouvrqd5t+EIzVTOyN12Wl8nm1tU80NW6HKV3M7JRefOvciSpYslAVwaOyLLMCV/H2WFW4rjseABrj1COHWf3ZXaR2IVCZl0qKxtBralI+6zSc5KrXKbDGL3h1BYUi35s758L5Ty4eMvdtivHzIWKa37nLf+ccaNGPb09MNezwEgzOrHnsXjzHsDspDRNqpeLb0XUL7//Wn+az7X1B02SpuzviL3CO3DJL1xRwFQSLg+nJP8tefQxuXVer+YnYB6gV/I/H3QP5cN4QH0kZlkbDvBv496pZINVUWwVGJWEonT+QnB/DsGIRvf/PSSpqUPG7vuo7PQyRrX5zEqFRq1fNGKr335+/bKYjU47EWvY/b2JZkrzxvVech6K2eFFxLJ2PDZavdwxQEQeCJ98MJ/1cfPun5LTf+uVWl9phE/bqGVE9FEUVo3cRy9tix8wB2B+UhIXH/DbYP+Znu348g7Lk2950ruJZG1OhVKILcCV32JHK/kvUi0tpuOI1rS24pqR59eq5hrk7zIGSjOpRIG5VH/O7rBFpC/+RBiupQHiTnSio3l5ym6WcDzd4y9ZezeA5vjMzz4cytFy+QvYNnS3/yYrJQW3BysLJbXfS5KlTnkyy254NIHGWEfhNO/P8dojDatlL4xujzQlee+34UX4X/xPntV6ranLKRCPDUUJBXIEool8HIQXcjMHYsgD2CUgK7g/IQcGvzVXaPWUXfVWOpO+L+TzRZm69xY9IG/GZ0IuDtXkgUpUcwHAc3QXCUUbDx/hZRfUIW6m92Iu3VCPmQVhWSMbeU/kkJHA1aKMU/pYuiyMXZW2n4Vk8cA8zLj+vy1KSvvoDvxDblL66hPFh/AiCRS/FsU5v0k/EWu48gEQxRFCsItxVH2dCH2q904cacbehVZsyUsRJtR7Rg1qYpLJ64kkMrTlS1OWVTvw6MHmyekyKXwcBu0Lap9eyyYwe7g1LjifrtLAef38jAv8bfp9AqanQkfHyA5PlHCV36BJ6PlV/sKUgEXF7uQcGfF9HeNHwa1d9IRb1wF/LH2iDrWbGC0dzYLFSZBXhZQexMkMsNeg6ae4qY8SsvoMlSUXe6+SPhM9ZfwqVzMA51PCxpZrUiwUgEBcDXwnUoAM7hDVGdT0ITd9ui+z6Iz1MtUAS5kfDFYavex1TCuobyxr4Z/PHedjZ/sqt6a6W0bgKTRoKbS9kREQeFYe7O6MHQq6Pt7HsUsAu1GcXuoNRgLi88xsk3dzJk92T8OgbdPa5JzSN60h+oYjKpv2Ycysa+Ju8p9XPF+Zl25Mw/gPZCHOpF+5A/0wVp+4prgSTsvUFAn3pmp4VMRqm8m+bRZBVy5c1dtPh2CBKZma3TWj2py8/gN6WtNaysNhhL8YChkyfVQoJtd5Aoi4Tb1lhHuO0OgiBQ9+MBZG6P4raFJypXlIDGtXjnyGyOrzrDrzM3oK8iYTmTaFAH3poOzz0OYXUNha9SKcikhv8H+8OYcHh3hr3uxFrYHZQSPHwtCo8Aoihy9qN9RK44w7D9U3ENvdeNkXcmkVuvbMVrZDP8zFSFvYPDgEZo9l9Ds+IgDjP6Iwk13cExRvzeaOvUnxQhKJ0QCwoQ3D25+u4eag1tiGcxh81UsnZEIq/lgnOrmjet1hyMpXgAfDoFc2L2VrMHMJaH68jmJI5fg/vUDmaPUDAHmYcjIV8O4sbsrTT58xnkvuVr81gbzwB33jzwMgueWMp3Y1cw7ddnUVhIqNDiSARoGGL40uuhUGUohHV0NCjG2rFjY+zPuhqGKIocf3070WsvMuzA83edE1EUSf/9PDdf3kzge32oNbNzhQXGdAcjkAsaCtJ16Cv5FBFFkYQ9ltU/KYHSoCibdSqBpI1XaPxhP7O3eJhl7YuTnZ6LXqvH3a9kbY5zHcM047xblk3HyHydUXarS+6f1i8ade0YhM/YFsS8vgNRXz0+RTq5K3l12wtIZFK+HPQjeZmmjWeoUiQSgwCbs5PdObEV9ghKCezPvBqEXqvj4JQ/SDl2i2H7puJU2/Amoy/UEvfm36SvukD930fjVsFohSiKaLaeQ7f/KopXBuM0vqNBwK0SMt7ZUemIehH3sNJn9FQaRyfE3DwuvLyFxh/1R+FlfvdN3sl49Llq3KzpSFUDEiNTCWjoZzRCIgiCIc1zzLLtxmBoOc5Zd7FSzyVTqf1yJ/SFWlKWnLL6vUxF7iBj+u/PEtIuiI97LCCjjHZ+O3bsGLA7KDUEnUrLnnGryUvIJnznJByKWmDVcbe5/vQaRI2eBqvG4FC3YsWdol5Eu+4k+otxKGYPROLtgkOfMCQ+zuSvrfho+fii6IklUwYPIshk3NpwE6mjlKBnW1Zoj5Qlp/Cd3PahlLUvTmn1J3ewRqEsgKKhD7Jgd/L2RFt87wcRZAYp/OTFp8mzYouzuUgkEp766nG6T+rIh12/If5S1cn026lu2IXajGF3UGoAmlwVO4b/giARGLjpWeTOCgByDt3k+rg1eI5oQvAXg5A4VSy3LWp1aH45hD4xC8XMAQhuBudHEARcX+xO4c6raCqojmnt+hOAwqRcIr+7TPOPe1bIESqMyiD/fDJejz/8bZOldfDcwadzsMUmGz+I27iW5Ky2rnDbHRwC3Qj+bx9i5lStFL4xwl/rw6hPhvFp3++4dvB6VZtjx061xe6gVHMKM/LZOmAZLnU86LNyLFIHGaJeJOX7E8S9tYvgr8LxmdCmwhEKUaVFs2gfqHUopvdFUCruOy/xcsJ5cmeDgJvaPI0JUa83dPBYOW1y5Y2/CRrbGJfQigmrpSw7jc/TLZE4Pvw14wYHpfSiZ+/2AWSeTURvhVSMsksd9PkaVGdtEznwDA/DtWswsf/da5P7mUPXZ9rxwm/P8u3I5fyzwbo6MXZqCPYISgnsDko1Jj8xhy29l+DfPYQeix5HIpWgy1Fxc+ZmsvfH0GDtWFwq0K1yBzFPhfq7XeCmRD65J4LC+Bu0Q496SAM9yF91xqz9My6loHB3xNWKmiJp+26QcfgWYW92h1Ik78tCk5rH7R2R+DxTsdRQTSP+WgqBDUvXo1G4OeIS6kmmFVIjthJuK07Q273Iv5hC+h/VT9W1Wf9GvL7jBX6duYFdCw9VtTl2qhK7DopR7A5KNSU7OoPNPRdRf1wLOn42CEEQKIxIJ2r0auS1XKj380jktVwqvL+YlY96/k4kob7In+qCUEalviAIuLzQlcK9kWiupZh8j4Q90QT2qbh+Snno1TouztpGsy8GIfN1h8ICs9MHab+dw2NoQ2ReTlaysvqg1+tJiEyhdljZbeM+HYNItUIdCoBzeBiqi8lobtmmSFSilBMyL5z4jw9QGFP9ClPrtgni7UMz2TX/AOve3lK9Bd3s2LExdgelGpJxMZnNvRbT/NVutH6rN4IgkLU1guiJ6/Gb3oHAd/uUKVlfHvqUbNTf7EDaoR6yEaYVhko8lLhM7WJI9ZgoJx6/J/o+dVtLEz3vKE71PKn1WCMEqQxkMlCZXm+gy9eQtvICvhMfbmG2O6TH38bZQ4mTq2OZ63w6BVmtDkXiKMd1RFOy11pXuK04Tk188Z/ZiZhXtqFXW7+LyFx8Q715+/AsLu+OZMnkVWht0Olkpxpij6CUwO6gVDNSjseytf9SOn02iKYvdkLU6kn89CBJXx0hdPHjeD5eORVHfWw66gU7kQ5sjqx/M7NqVxy6hSKt50Xeb/+Ufx+tjsQDMVZzUPJvZHJ93lGafz343mNwdIJC0zUmMjZcxqVdAI6hnlaxsbpRmkDbg/h0CiLNCq3Gd3Ad2Yz8v6PQWXAwYXn4jm+F3NeZhK+P2Oye5uDq48Lc3S+Sk5rL/BFLKMytXoW9duxUBXYHpRoRv/s6Ox/7lZ5LnqT+U63QpudzY8ofFEam02DtWJRNy39zKQtdZBLqH/YgH9URWZewCu3h8nxX1IduoLlcdo1C2ulEXILdcapEGqosLr22g3qzOuNUzLkQlEpEE+tQRJ2e1GWn8X3IhdmKU14Hzx08mvmRn5CDKtP8mh5TkHo7oewRQu5G29WFCIJA3f8bQOZf18g+eNNm9zUHB2cHZm2cjHttNz7ts5DslJyqNsmOLbFHUEpgd1CqCTF/XGbv02vot3YcdYY2Iv9sIlGjVuHUJoCQHx9D5lmxDpU76M7Holl2EPmEHkhb1anwPhI3R5xf6GoQcCvUlLoufs91q0VPkv68Rm5kOvVe6XL/CaXT3Zk85XF713Vk3kqc2z7csvbFKU8D5Q4SmRTvdgFWS/NAkXDbetsIt91B5qUk5PNB3Jy7E01ans3uaw5SmZTJi8fSIrwJH3WbT8r1tKo2yY5NsOugGMPuoFQDIpaf5vCMPxm8bQL+PUJIX32BmJf+IuCdXvjPKbuA1RS0x6LQrD2OYnpfpA39K22vQ6e6yJvUIu/nk6WuSdgbTWA/yzso2jw1l17bTov5Q5A6PNB15KgEVWG5hYaiKJKy2CBrb00BueqGqREUMBTKWkOw7Q6KBt7IQzzJ221bHRDXLsF4jWzKzX/vrDZS+A8iCAJPfhDO4Nf78HGPBcScsl66zY6d6ozdQaliLs47wun/7mbonil4NfUj/p3dpP9yjvq/jcatX/1K76/dfQntjgsoXh6ApI7l5Oadp3RGfeIm6vMJJc7pVFqSj8ZSu2eIxe53h8iPD+DZNRgfI91BglQKMjmoyq5tyDudiDazAPf+lf/51iQSIlIIbFR6i3FxrFkoewe3cYaWY1t3rgTM6owuW0XKcvPa5m1Nnxe6Mv67UXwZ/hMXdlytanPsWBt7BKUEdgelihBFkVPv7ebKDycYduB5nFwduP7MWvT5auqvHoNDJQs3RVFEs+k0uuPROMweiKSWu4UsNyBxccDlxe7kfnsQfb76vnPJx2LxaOKLg0fl0lIPknM5hdjlZ2n66cDSFymV5eqhpC45hd+ktpWOTNUkNGotabGZ1Ao1zUn17RRM2vE4qzoPjp2CQaNDdbqkk2tNBLmUkK/DSf7hJPkXTW+brwraPd6CWX9MYtGE3zn8S+kRSzt2HkYenVfoaoSo13N09hZu/XWVYQemIsZmc33cGjyGNSL4q3CkzoryNylrf50e7cpj6K+noJg9EMHDOmPnFe2CkbcMIH/FifuOx++xvLy9KIpcAPzUQgAAIABJREFUmLWVsLd74uhfeuGtoHRCLKMOpfBGJnmnE/B68uGXtS9O8o10fII9kZcixvcgToFuSB1l5FzPsJpNgkTAdWxLslfbXknVIdidoPd6c2POVnR56vIvqELCutXjjb0z2PCfbWz5dPddpzE3vXrW0dipAHahNqPYHRQbo9fo2D9xPelnExmyZzI5m64S98ZOgr8YhO+ktpWuiRA1OjTLDiJm5aOY0Q/B2cFClhvHeVIn1GfiUJ+5lw5I2BttcXn7+N/Oo8vTEPJC+7IXOiqhsPQISury03g/1RKJsmJzi2oq5tSf3MGns3XrUACcB4WhupyK5qbtRdS8hjbCpX0gsR/ss/m9zSWgSS3eOTyLo7+d4rfZf3B++xVm+b9L1NGYqjbNjqWwOyglsDsoNkRbqGHX6JUUphcwcN1TJP1nD9m7rhsk6zsFV3p/sUCN+ofdIJMgn9YbwcH6b8ISZwUuL/Ugd+Eh9HkqNHlq0s4k4t+trsXuoc4o4Mpbu2ixYEj5aZkiB0XU60uc0mbkk7Ul4pGRtS9OhRyUjsFWd1AkDjJcH29C9hrbCbcVJ+jd3uSdSSTjz+pf4+EZ6MGbB2YSdeQG84YtRq/Ts3PefuOLRTVoEkEVBZoE0Nt1VezUPOwOio1QZxeyY8jPyJzk9PxiMDcn/oHMW0m9X0Yi93et0J6iVof2cASiXo+YU4j627+R1HJH/lw3BFnFlWbNRdE6EEX7YPKWHifp0E182wXcnbhsCa69uwf/EU3waB9Y7lpBKgWFwmihbNpv5/EYHIbcxzopr+pM/LVkk0TaiuNrg0JZANcnm5G/OwpdlnV0V8pC6iQn9Otw4j7cj+rWbZvf31zyM/NJuZ6OXqcHEc78eZH828V+buobkPxfuN4Bbg6C2NFwMxyi20PSG6C6VmW22ykHewSlBHYHxQYUpuWxtf8y3Bv50mZ8G2KmbMRnSlsC/9sXiYk1AcbQX4hDu+YEmuUHUc3bjqRZELLRHREktv+1Ok3ogOZSEpl/XrKo/knmyXiS/rpGow/6mH6Ro1OJQll9oZa038/jO+nRkLV/kIpEULzaBZB1MRmdiaMNKorUywllr1ByN1XNQD+nZn74v9iBG69ss6kuS0W4fvwmWpUWR1cHEEBTqGX3wkOgy4a4SXDrMcheA2IBiIUg5hX9XwU5mwwOS+wY0Nr1VexUf+wOipXJi7vN5l6LCexbj/r1vEj+/DAhP43Aa2Sz0i/KjYXEAxC7HRL2QuYlEI2kLPYbwtL6c7EIXi7Ih7SqMl0PiVKBy8s98I5NI7BL5dNVYCj2vfDyFpp83B+FGUJ1glKJ+EAdSsbGyzi18sexvpdFbKtpmCrSVhy5swLXMG8yziZayap7GITbLiFW0awc34ltkHk6kvDNsSq5v6l0HteW77M/4bXtLzD87QG41XLl/F+H4NbjUHDS4IhQmkOpMzgthRcNjozGtt1TdsrCLtRmjIp/fLdjlMKMfPLisvFu6c/tyDS2DVpO04ltcbmRRWFKPg3WjzOuCqvXQvIRuLEWcm+BIAX03PUhZU4Q8iQEDQS5C2JWHuKt9LuXi5FJaI9HIevUwCaP0xhioAfxCXk0vhAHAysmpV+cmB/+Qe7uQODTLcy7UOkEWZn37NKLpC49TfBH/SttU00kP6eQvKwCvAPNbzW/I9jma4EaqbJQ1PNCXt+LvF1RuAxpZNV7GUMQBOp+OpCrj/2Ga9dg3LpWXG3Z2khlUsK6hhLWNZSR7/eD2FGgTgZKV3a+Hy3oMiDuGajzJ0grlmK2Y8fa2CMoFub0f/ewp8cirry3my19ltByUjsU+27i1KIWIYtGGHdO8pPgwBS4OA+yo0CvBl0B6FRF/xaAKh0if4Z94yHtFJot50CnB5kEnBRI2tdDEmQ5IbaKkLD/Buk+bmivp6E6FlOpvQoTc4j8+ADNvxliflTojqJsUaFs9p5opK4OOJtQw/IwkhiZSkCYH5IKpP58OgWRetw2SqZu4wwtx7YWbruD3NuJup8N4ua/dqJJN33oZFUhlUpp3aoRzQf8zfAXbpKVbYg+7Tuez7Bp8fetnTg3iXXbDbN9Nu/Npc2IGFoNOUbTpg358ccfbW67HSPYIyglsEdQTEWrgsIs0BaC3AkcPUB6f5eMXqsj8uczNPN1Qb3qIs17hsK2SGr/ty/uA0uJbOQnwJHZoM3HEDEpgzuV+Kc/QHAZiaRbI2Q9GiH4u1cLyfaEPdHU7lMf18cakf35buRNaiFxr5hY2+W5fxM8qQ2uTXzNvlaQSBAVDoZCWaUTKUtO4fuIydoXJz4i2ez0zh18Owdz4eNSOkUsjGPHIJgvUngqHmX7IJvc80HcutXBa0Rjbr7xN/V/eqxaP2eUSiVn/6wHWgUT/p3Ewt9u8/aLZacwNRqRaf9J4cS6YIL85ag0bsRIetjIYjulckcHxc592CMo5ZF+HQ5/Axueh+1zYdf7sPVfhu9PLYOce/n5uB1RuMkkyCQCggCcTqTW/8pwTrQFcPzfoM2jXOekOHo1cuUGFIN9kNT2qDYvovF7ownsVx95k1o49qxP7k9HK7RP6u5oMo/F0vCtnhU3pmhwYN7ZRDTJuXiU9jt4BEiISCWgofmOHoB7Yx9UafkUplpfFEwQBFzHtSR7pe2F24oT8EoXtBn5pP58tkrtKB896Axp3i5tHIlPLr+YOSdPj1YL3h6GLj8HhY5GQdavMbJjpyLYHZTSyEs3OCR7/gexx0GvMURRtHdSLyqI2g3b5sL+T0FTwD/v7CTQXYlUKjE4DYJAxtLS53189OY0mk38k5YvHqT1jMOE/+cf3lx2fxvg2evZNJl2EICQCftIu21QvTx1LZXQJu05c6Z6zBPJT84lLz4b7zaG6cBOT7VDdzMD1aFos/bRqbRcnL2NZl8ORupUcR0XQalELCggZelpfCe2QZA9uk/1hIgUs1uM7yBIJHh3CLRJuzGAy8AGqCPSUN/ILH+xlRDkUkK/Cifp2xPkX0mtMjvKRTQUvep0IruPFvBY3/Lb5708pDzW15m6vWN46pVEftuUiD57mw2MtVMu9hRPCR7dV+2yyE6EHW/A7TiDI0Ipv2xRZ3Bcki/Bzrdx1RagVMhAKiA4SFE288Otu3HBsqNHjrB563ZOL+jC+e+7s+vjDrwxuh6rDyTdt27V/kSe7l37vmPnb+Qw6qMzrJ7bnDZNLSeIVhkS9lwnoFcokiIhNcFBhsusXuQuPoo+0/R8fvRXR3Bp5I3/8EoWSjo6oYpOJfdYbNkdU48A5gwJNIavlScbF0dwkOH6RFNy1lRtFMWhrgdB7/QySOHnm1p8alsKCjW0fiwG747RZGTpGNDNCYDSAqp3ji/+uBa7VwTSsaUjXyzJYvLsTTay2I4d87A7KA9SmA173gd1ntHWXqPoNZCXSr8P06k1uwMNN4+n2emXCFs3jlovdjR6SWLkCXxcpTgoDL8CH3cFvVp64eEs5/jVe7Lfaw4mMa7XPQflSuz/t3ff4VFV6QPHv2fu1PQyCQQCoSPV0C2o4IIUe0dX1LX3LuuWnx3XtuoqulbWuuIqq7JWsIE1ihoBKQIhaAgkIYT0ZMq9vz9uSCFtEmYm7f08zzzJ3LnlJJnMvHPOe95Txkl3/sBLN41l8kHx8Nt77f9Zg2jHJ1mN6p/YhiXhnDGcsie/DCjxsTyriKzHMhj10OwDb5DTye6lWSSeMfqA1zbqygzDaFcNlPrcU1IpCFMPCkD0yaOo+DQLf1H4C7fVl3DiQUSO7U3O3eHJwWkrl9NK5rI0tn82AI/X4PFXzEJziXEaRSUNX7v2FOu44+uKN44Z7uD6P8Sz4l99Wfp+djibLZojPSiNSICyHy0yjvTr/sPom9/j9Ee+pKKmSJV29muk3/IBo29+n+MfWMXecg9T/rqc9Fs+oP9Vy0i66HXGX/sMxzx6LjvZi7K0nBdyzIREfiuoZNhFq7hi0c+sXGMuynbWtBSWrDTHhL/ZsJfEaBtD+9Z13Z54x48sunwkU0fHm4FRYecYJ8/9NIu+Tay/E3HmOPy7SqleubXF4w3D4Ofr32fw9YcSkRZ3wO3xF1ezd1Ue7tPDP2W1MykuKMNitRCd0P7que4p/Sj8NqfJ5QNCQYt3ETFtEKVvrg/L9VrS77bplGXkUPTuLx3dlCYoQBEbrfHo/yXx4HNFeL0GQwfYyM33sWGLORy8fYeXnzZWkz7CQVm5zmcZdT2amRuqSUs98P83caCkDkpTJECpz+/BZdPIvHcW6x6Yg91q4cmPtgDgsmtk3jubdQ/MISHSzuPLN5Nx9zFk3jubO08fzZmH9ifz3llk/v0kBgwY0Oqlomw+vn/0UJ6+ZhRJsXbOvDeT51fkMO+o3rzxRR66brBk5U7O2m94Z8a4RJ79MAe/v+YJ6C0L9m+hzUqzi/CWeYgf1fhTurJpRF9zJOX/ysDfwuqru97eSEX2XgZde2hQ2rR7yVpijuiDLapzJBB3lAPtPQFw9YrCHuek5JfC1ncOkugzxlD65s8YIa5i2xotys7Af8zhtzs+pTqnk5XCVxooJwDjRjo5+CAHS94txWG38PIDvfnDn/JIP2E7p129k2cXJhMbrWEYcP8zRQyflU36Cdu57bG9PP/M3R37cwjRDAlQ6vsto8HdI4YnsWVX4wDg0KFuduxppvu5LB+KtrV+Lc2OplmYNjaRO+YPZdHlI1n6RR79klwM6OVi5do9LP0yjzOOaBigLLpiBABXPP6zucHS8cMXO2pWL25uNpF1sBvn7BGU/fOLJod6fGUefr7pQ0Y/OheL/cDXENKrfex+OZPk+WMxqjp/PYtQas8aPE1xTwlfHgqYhdvsw9yUr9gStms2J2J0L3pdMpHs6z/A8IWnFykQZaXlYK372/7vqT7MPykGgMMnuPjm9X5kLkvju//2Z+bhZg9adJSF957ty6YPB5C5LI0vXx/DxKkXdUj7xX6kB6URCVDq+7UuQPH5dd7/aSdj+jesvunXdT7+OY8TJjRT9Ev3Qe5PrV5qU04lm3fVJd9lZpWQ1susGXLWtBSuf3ojg1NcpCY5GxxnUYpX/3gwm3LKufXFzeB0B/rThUzup1n0bWX9nYjTDkbfU0H1x5sbPfbL3StJPHIA7qMGBKU9Rcs24hqRjHNUSqM1eXqaYPSggLmycUEYAxQwy9+XLOm4wm31JV8wHkukjZ2PdaJS+EpB/CWg2ldrCBwQd15N1WohOh8JUOqrLqHS4yf9lg+Y+Jfl9E+M4MKaN9592xMvfpM9ZdXMHNvMrAhDNwu6taLMOZTz7v+ekZd8ztjLv2D9r+Xc/nuzVsfpU3vz8/ayBsmx9TnsFt6+bTzLMnbz+PKOHeIxDIMdH5s9KC0xh3qOovyl7/AX1LW55Od8cl76iZF/C04ZekM3yF/8A8kXTgCHEzzVGHrnXgAulNqzBk9T3GFa2bg+56S+YFFUhfm6TVEWxYAHZlH4+s+UfhOeyroBiT4R7IOBtk7J18CWAnHnhKJVoq32FWqTHpQGpJLsfvblmjS3vbjCw3H3r+Lx5Vu4Zvawpk8SQOG0CYccxVf/vhl2fc7+05iT4ux435nV6JjsF6bVfh8baSPzmTkw/d5WrxVKezftxmKzEDOo9UX4rAMScB03irLHPyfmttlgwLqr32XYrdNw9IoKSntKVmZjcWhEHZKKUgrD6YSqKohof5JoV3YgNVDqSxiXQvGGAnyVXqyu9tenaQullNmL8toaXCFeCygQtqRI+v9tJtk3fciI//2+6WUrws1ih76L4bczwZdbs1hga2xgTYTUl8ASnP87EQTdJKgIJulBqc/Z+mJqsRF2Hj1vAg++sxFvU+PRSjPL4Adi4CntzyGxOMzFA1XH/glzP2k5/2R/rlPGYpR7qFq+iZyXf8Jf7SftovFBa0/B4u9Jrl/W3mlWlO2J/H6dvKxCUoa0r4psfVaXjbiRSez5Ibwr4EbOHIJ3yx48WXvCet3mxB41gPhjh7H9Tys6xdATAFoc9P8vRBwBygE095piMx93TTAXCbS2vzaOEOEgAUp9aYcFtNu4gfEcnBbHkq+3N37QokHfAN9wY4fDgJNBc7ShkYCyQcxg89gOtiOA/JP6lGYh6pojKf7Xt2z480eMeWwuSgvO07BibR7VvxUTN7tuJeV9FWV7ot2/7iEmKQpHRHASqd1T+oU1URZA2TWiThlF6Wtrw3rdlvS58XC8u8rY/coavPnl5D70FYa/g5NnLZHQ5wlI+wDizgUVCdjN/BRV8zX2TOj/P0h90QxqROciQzyNyBBPfX0nUfbKueBt/Im77PnTGtz/381168Scf9Qgzj+q5k5MH4htQ3f00HPN1Yp/+6BuMcCWWOwQPQgm3gmWjv3zGbrOzs+2cfgjx7bpOGu/eHKLDRL7RRGb3nSeTXvkL/6epPPGoWz1kv5cEbC7E5crD6Fg5Z/s456SSs47G4N2vkBFnzSC3HlLiLt0ElpCRNivvz+LXWPAI3PYeOK/2XH/F+jVPhJOGYlzQCd407f1haQF4L4R9BLQy8zgxRIrybCiy5EelPo0KwyZ2f43fqsDRpzQtmOUghGXwcgrweEGrZlxbc1l3tJOhCn3g7XjcyoK1+ThdEcQ2TemTccVZeRQuL6QtEN6U/V+cIpxVecUU/rlrySePrrhAw4neL0Y/p6XKBus/JN9ksI81XgfLc5FxNGDO0XhNgDDr5O/+AcMjx+9wovFaaNqc/hqxAREaaDFg60faAkSnHR6UqitKRKg7G/E8WYOSVtzOyw2iB8MqU2Xtm9V6kyY9iKMvxXcE8GRANYIsMdBzFAYdRUcvQSGX2BeqxPY8fHWRuXtW6P7dNZe9S4j75tJ/E3TqXjtR/w7Sw64LQUv/Eji6aPQohoOZyilwOmEqp43zGOuwRO8ACV6aCLeUg+Vu0qDds5AxZw5htI316N3cOE2AH+ph+KPsqBmaFKv8FD5y+4ObpUQ3Y8EKPuzR8LvbgVHTOCfOjQ7xPaFI282c1DaSylITIeJd8H0V2DGUjj6VTjsUehztHmdTqS58vYtyf7nd9gSXPQ5czRa31giTk+n9NFVBzSG7yuuouitDbjnj2t6B5erR9ZDCfYQj1IK9+S+Ya+HAmBLi8cxIonyDxvX0Qk3a5yT0SsvIPVPR6DFOMCA4o9rVu2u3gq5t8GmqbBhnHnbNBVy/w+qOr7onOjEpAelEQlQmhKZBLPvA/dQ0GzNByoWm3lLnQQz7gCbs+n9uiG/18+uL7aTMm1gwMdU5Zay5d7PGfOPubWzbJzHjgILVL7zc7vbUrhkLTHTB2Hv3fSUSeWK6JEVZXN/KQhqgALgDuPKxvuLnjeW0tc6R+E2ZdNI+v3BjPnqYpLOS8c1qBCyzoCs02Hvm+AvAsNj3vxFsPdt2FbzeGXnGKoSnYjUQWmSBCjNccbA726DWffB4KPNmTYWa91Xe5SZb3L8o3DoVZ2udyPUClbvIHpgPC534Lkw6xcsp/9F44k6qK76rbIooq86ksqlP+HLab3A3f50j4+ClzJJvqCFmVM9cKqxp8pL0c5iktNar0/TFu4p/cJesG0f5/g+YNWoyug8hdIsTiv9rreRduG/oOrnmjokTeU7+c3HqtZD9nwo+zzcTRWiy5FZPK2JSYGJF8D4883ZPb5qsLnMW4C1P7qj3E+y6Hv04ID3L/hoK3u/28HBzzROItZSYog4azxlj64i9m/HtWnacdE7m3ANS8R1UAu1PhwO8Pkw/H6U1jOSBXduKaDXwEQ0a3B/XveUVApX70D361iCND08UEopYuaNpWTJWlyH9A/rtZtVuRZ+uwaMqsCPMargt+sgbTFEHBy6tomupZv0egST9KAEymIBRxREJoI9okcHJ1C3QGAg/FU+1l7zPqMeno3WTBVS56wRKJeNyrcCr3dhGAYFz9WUtW+BmSjr6lG9KMFag2d/zsQInMmRFG/omKnbkTMG483ag2drx8+aUUoxf97M2uDE5zNImrqJ4674lZ+3VDFs7hYqq+pyq469/FeWvFdM3m4fx13+CwePP5yRI0cyd+7cjvoRhOjUJEARbear9JKfkUPKEWkB7b/1718SMzqZXnObWRoAc6gn6sqpVC5bh297YFVDSz/fDhZF1GEBfJp2unrUTJ5gJ8jWF+6VjetTNo3oU0dR0gkKt0VGuli3uaQ2CFnxdRl9k81O6VFDnJwyI5qFT5mze976uASvz2De3FhuXZTPzEMj+emtEaz/9hnuvbdjl6sQnYTkoDQiAYpos7yvfyVhTC/sMa0nBZdv2cO2x79l1ION1xban5YcTeQ5E81ZPQEsa5//3H5l7VugXBEYPawHJZg1UOpzTw5/Rdn6ok4aSeWqbfgLO/jvaXiZMzWCd1eai1+++l4JZ82tWy7j1suTeH15CZkbqrjl4Xwe/2tvAHYW+EjtZQO9AnYvZuzYsR3SfNGZSB2UpkiAItpsxyeBlbc3DIN1173PkBsPx9W/9XWOABwzhmGJdVG59KcW96tYn091VhFxLfTKNNDDphqHaogHagq2fdtxiaparJOIGUMoeWMdZSs2U7JkTfgboVeCoTNvTixL3i+mqlpnzaYqpoytK7QY4bLw4E29OPK8bObNiWFomrmkxZVnJXDhrblMPz+bhQ+/S26OTD8WoikSoIg2yw0w/2Tnmxuo2lHCwGumBHxupRRRV0yl8r31+LY1n2dQsPgHks5Lx2IPMAnU7gC/D8PX8YW+wiGUAUr8wb0p3bIHb1kgK+cGn15WjXJYKXnpRwoXfkbp2xvC3wi/OeNs7HAn2bleXn2vhLlHNp7mfvz0aOKiLVwxr2421aypUWR9MJSLT4tn4zYv4yYcSkFBz1yOQdQjPSiNSIAi2sRTWk3hmjx6t5L34SutZv3Nyxn92FwstrbNJNHckUSeN9kc6vHWTdmsWJ/P5rP+w+7/rKV45TYSzxwT8DlrE2V7QB5KWVEF1ZVe4nu3bQmCQGkOK3Fje1P4fXhXNt6n4K8rKP3PWjAAr47F1QGTEY26QPeEadHc9EBeg+Gd+iwWhWW/V9qEOI2zj4vlpfsHMWnCWFatWhXK1grRJUmAItpk1+fZJE/ui7WZ2Tj7/HLXStxHDyRxamCJtPtzTB+ClhRFxeuZtdt8eyqpWJtHzu2fgkdnz7KNDQKYVrl6Rj2U3M1m/kkguTntldSBBdsS/zIdW/84sJkvX6qV52JIaNG1315wShy3Xu5mzLDACjV+8k05FZVmjlVpWRVbt/1G//6dZNq06BhSqK1JEqCINtnxcev5JyVr88j59xpG3DOj3ddRShF12eFULd+Id7PZ/W1xWlF2DXw6eqWXHXd9RtXWwGb8ACiXC6MH5KGEcnhnH3MmT8fkoViTIum9+BRch5pv6kZHrM9jia0tNZDa28a18xMDPvT79ZVMPCOLsSdv5dCzs7jowkuYNGlSqFoqugoJUBqRAEW0iVn/pPkCbYZusPbqdxl++3QcSQe24rIlIYKoCw+h7LFVGB4fFqcVw+MHBZZoO0NeOq3lAm37c0ZADyh5vyPIiwQ2xT0ltUPW5NnH4rCSdM8xRM4dhi0uEe7xwpgqSK2EPpVwUBVc74Et7V/jqUVKUfbrC6Aarj4+bXIk7zzRsDcke8VQ3PF1w1A3X+Bm/f+GsOatUaz7+kluvOmm0LRRiC5OAhQRsKrCCkq27iFpUt9m9/nthUwMv0H/lkrPB8KnQ1E19iEpaMlxVLz6PcpqwfD4saVEc9D/ziGqhXY0yW4Hv47h8x5Y2zq5cPSgRA2MR/f4Kc8pDul1WqJyDNyZh+F+bjI86IOtBuwB9gK/GrDYD5OrYXoV/BCCQCXuROBAzmvUnEMIwt6DopRarJTKV0qtq7ctQSm1Qim1ueZrfDPHnlezz2al1Hn1tg9USmXUbH9NKWWv2a6UUo8qpbYopdYopQJ6g5AARQQs97Nt9J6ahtZM0qtndwUbb/2EMY/NRVnamf+wuRT+9jMc/xn8/ivUxRlEf6FwvVKM9Z0dxB4xkBHvn4u9T9sTQJVSPWK6cTgCFKVUhxZsY40Oh1TD+zpUA01VmvfWbM8w4JhqeK8N+UqB0KLAfVGjXpSAKBck/gG00CQyCxGA54HZ+227BfjYMIyhwMc19xtQSiUAtwFTgMnAbfUCmfuAh2uOLwIurNk+Bxhac7sE+GcgDZQARQRsxydZ9G1hevGGv35M3zNGE5ue0vaT76qESzPgutXw6S7wGuDRoUpH+Qwsuob1w90MyI3B8tRW8Lfzk6uzewcohmGYAcrQ0AYoAElTOqhgW7YOs6rNl79AnwYVwHwPfBnkIMV9OcTMaFuQolwQPR2SrgpuW0QXFv5CbYZhrMLsc6zvROCFmu9fAE5q4tBZwArDMPYYhlEErABmKzMr/2jgjSaOPxF40TB9A8QppVp9o5AARQQs99PmA5Q9X/1K/odbGHbbtLafeFsZXPat+bVab/ZNRxkK5dVhxU5Y8KMZwLSRckVgdOM8lD25xTijHETGtuNTfRu5p6R2zMrG53qgtB3HVQJneMzgN1iUgj5/g4SzQDmAlmYU2cx9Es6EvvfR09fzEp1SL8MwdgLUfG3qk05foH6GfE7NtkRgr2HUzsHft72lY1okAYoISPmOEirzy0g8uHejx3Sfztqr32PU/cdgi3G07cS7q+HGH6DMF/in4WodNpTAPevAaOObjat7LxoYyjV49uee1JfCH3LRfUHulWiGpmmkH5TOqK/Gc3DFFB7yPopumE+az/yrUJUR/M//bu3+x1Wfwmd+s77ItOpZrNa/By9kP5fF0KFD+fDDD4PTMKWg140weBkknA2WCLBEgiWq5hZpbkuYB4Pfhl43g5KXXrGf4PeguJVSq+vdLglWS5vYZrSwvaVjWtQBFY5EV7Tj0yz6TBuI2r/iFJC9KANHryhSThvZ5vNqyRGMiRps7MKDAAAXJUlEQVSIYRhoysKiYVdzWNwosit3MeKbCxge0a923xv6n8q5Kccw4Mvfs3rSE7hXK/hpL6Q3mcfVNJsdDAPD60XZOqB+RoiFI/9kH3uci8jUGPauyyehPcN6beRyucj83beQ6yffm8/Znj9Q7CvmDtv/AZCq+rLQez/Ha8c2e46c0hxmXX8sf3/t78ya1fr6UG1iT4XeCyD5OqhcA/6aBGItFlxjwNLG4F30HPvqoATXbsMwJrbxmDylVIphGDtrhmDym9gnB5hW734q8BmwG3PoxlrTi5IK5NY7pt9+x7Ra6VHCeBGQ3E+y6NNE/ZPKnBI23/8Fox+Z0/bCYGU+XBY7mZOf4qcpT/O3wRfyp63P1T482NWHzClP1d7OTTmm4fHVfvjP9jZdsrtXlA3lIoFNcYc7D+U1P/ggWSXztG0Ri3xPYdT0oh2sxhCrYlnh/7jJQ3cZeRxTfQJ3a7dxwoTjQ9dGix0iJ0LM78xb5EQJTkRXsQzYNyvnPOBtAKVUX6XUvn+sD4FjlFLxNcmxxwAfGuY/4qfAafsfX3Pec2tm8xwCFO8bSmqJBCiiVYZhsOOTrU3mn6y/+UMGXDaJqGGBF6qqtbxhAF3iqyDe2ng9k+YbBvxYZA4TtUU3Xtk4nD0oAO7JYa6HUm+2ziDLQHR08ut9yPur9Y/c7buvyUPP9VzMVdZLOT3qFMjrHoWsRDcS/mnGrwJfA8OVUjlKqQuBe4GZSqnNwMya+wApgA/AMIw9wF3AdzW3O2u2AfwRuEEptQUzJ2XfJ873gCxgC/AMcEUgvxIZ4hGtKt1WhO7ViduvKFr+h1so/nEX6YubSvQOwCd5VPo9pGdcSpXuYWd1IZ+Mf7D24a2VuaRnXFp7/7FhV3FEfMP1dwwLqNWFMLtPwJdVrgiMouYXIuzKwpmDAmai7MbHvwnb9dBokKtk7DeMfYR2OPjgc/+XjQ6doU3nJd+rnG/MJ8JjD3FDhejcDMM4q5mHftfEtkOAx+sduxhY3MQ5szCnHu+/3QCubGsbJUARrdrxibl6cf0hHH+ll3XXvc/of8xBa+9aKMVeXJqdzClPAfB18XrOXX8f66Y8C9QN8bTIo0NxGwuvuVywsxLDMEK6Xk24+bx+CrbvIWWwO2zXjB/Ti/LtxXhKqrDHBLYWzQGpV9U+S9+GhkYyyWxgU+32v1gXsNB3H9b9Xt4WWK/nZd8STt/7e96OXIaVti1iKURIdeLy9IZhLOqI68oQj2jWvtkZOz7Z2mj9nS0PfElsem+SZw05gCs0/Ic8NHYkuz3FFHj3tuEUBr7cNlYztdrMS3ezirL52YUk9InF5ghf8q/FppEwLoXC73aE54IHmQFlgVHAZd5ruMp6aaMg8xhtBkXGXn4y1jY6/GHb/cSoGC687+La3BUhOl7466B0BRKgiGb9e/BDvJhyL9lvbcBX4aGyoByAss2FZD/5HSMfOMBZENEN30g3lv+KH51EWxuqa9otVH2ThV4eeB5Kd60om/tLPn2H9wr7dd2TUyn4JvQLB1ZWVpK+ewqjPBOYUX0cx1h+x23WvzS5719sC8gxGgdNyqF44crF7MzfyYIFC0LdZCHEAZAhHtGsyD7R5NckQH594wdkLfiIQVdMonRtPkMXTMWVeoBluqf1ovKfnto8EwODF0YuQFNm1/v+OSgX9JnNNf1OBmBsxiVYaj45n3zI0dyzOIHoq48M/No1ibIqJvbAfoZOJNz5J/u4p6SS9XJmyK/j9/uhyoD+VVDW8LFp2pFM0+r+/idox2G46hKhP3PU1DyxgP2qCJYPXB7y9grRJt2k1yOYJEARzep79CDyv80BAzSrBYsB259ajeE3SLu0rdPrmzC7D/45HzVZEXaAqzeV099r8rDsw1+puzM+HuOOMRRd/yae737FPql/k8fsTzld3S5RNveXfPqPDn09kv25p6Ty7dXvoOs6vlIP9tgQ5qI4FfzZCnf7zPL1beECjtdgoHQcC9EVyH+qaFavw9JQFoXFrnHYQ3PQnFYMjw5+gx/OeoO8dza1fpKWxNjgMHf7n4VODc5MQ7lsRF91BGVPfoleGuBQjysCKiu6VR5CuGugAOz9OY+slzPxFFXyWvxClsQvxFPS1Mp9QXStFU7XIKINxziBsQqe7n7F+UQ3sK9Qm+SgNCABimhW8pRUDL/BuL8cRfLYFHSPHxRoETZGPngMyXOGHvhFLh4CEe3oyLNbYEwcjE8AwDY6BfthAyl/9uuADlc2m1mi3Nt9EmV3bMqnz7Dw5qCse/ALfrrtE3SvjrfUg7NXVOhn8ygFT9jgCs0MPFqKOSyYgcwMC3zgAHv3mbUluhkJUBqRAEWYCr3wzE44ZT38bi0cvQbXhdmcdc08Jl40lZLMXRhencRpA5m27koGXX0ISgvC06eXCx4YBxFa06s1NMVhgUFRcPuYBguuRZ4zEe/mAqq/zg7sPK4I6CYLB1aWVVNaWI67X1xYrzv5H8fi6lOXi5QyY3B4LqwU3GmHDAf8oaY3JRqIrLnFYAYvJ1ngfQe8ZgeHBCdCdCWSg9LT5XrggRz4usQMEKrrRd57/cTsUnDyelKHRWK/61j6LJgQ/DYMjYEnJsNfMqHQY5awb+oDgE0BCqYmwY0jzV6UepTDSvQ1R1Jy/8fYRvbC0sqKvsrpwqisRMWE9009FHZuKSBliBtLE2slhZI9xsnM5efxzrgn8Ff7SD12WFivz1ALPGKHewxYqUOhAX4gXsHhFkiUoER0Ed2k1yOYJEDpyTZWwKVboNzf/ErCNUvTW9dV02erFaaVwuTo4LclNQKePxTWFZvr63xXCFaL2cfnN8zvT+wLx6dCUvNDCLaDeuE8cghlT31F9M1Ht1yIzRUBhQXB/1k6QLhL3NcXOzyJw54/hc/n/YdeRw3okDYQoWCOFF4TojuRAKWn+rUaLtkMZc1FJk2o1OG6LHh2KIxsS4ZigJQy80rGxEGlD4q84PFDpBUS7BDgkFLE2ePZe8NbeL7chmNq4/WDatXUQukOFWU7MkDBMBh4yh5Sd63B5jwESioAJ1gGgONysM4FJcmpQjSv++SNBJPkoPRUC7ZBRRuCk32qdLhuK+gh/mdyWaGPCwZEmT0mbch3UXYrUdccRdmzX6MXNZ9joqw2sFjA6wlGiztUh9RAMQyofhFKR0L52dgcK8HIBWMvGLvA/w1UXAklQ6DqPjD84W2fEKJLkwClB1JKceOqhbXDOg/mvcjtO58E4PadT/Jg3ouNjtF+nEj6xnmM2nAaB395Gg9dew+63o4AJ0xsw5JwzhhO2ZNftjyV2OWCbrCycdinGBs6VF0PVbeAsRMob2bHMqAYqh+B8lPA6F7Ve4UIGpnF04gEKD2QQ7Pz38JP2O0rCvgYl8VB5kFL+HnEG6wY9ATv/fdd7rjjjhC28sBFnDkOf14p1Su3NLuPckVgdPGS94ZhsGNTXnh7UKr+Cp7/EHi1tErwZ0DFfOlJEWJ/UgelSRKg9DS6gdXQuCTxFB7Of6X1/ZuQbEvgafefWfTYok5d6EzZNKKvOZLyf32Lv7CZT/jdoAeltLAcpRQx7qjwXND3JXiep+2lXKvA9xV4XgpBo4QQ3Y0EKD1Nufnp9cqkM3il6H2K/aXtOs2g6H7ofp38/Pxgti7orIPcuOaOoOyJL5oOppwRUFXZqQOt1uzLPwlHoq+maaSPP5ZRh+Rx8OGlPLSoGr0mH+kvd1WRPrW09jZsQilaQjFlZXW/2xPPKuDQI64081eEEHWkB6URCVB6Go/5xI3Rojg34TgeLVjSvvMousybuuvUdPS9lVR/vLnRY8pqBc2KUVGBUVaK4e86ww9523bz0eKvWf3OOtz94sPy93C5nGR+7uDnb6JZ8VYk763wcse95vICC//PSeYX0bW3SeM1/nSDg6goM3Dau9fghzV+9hZ72LblrZC3VQjRtUmA0tNE1dWKuC7pbJ4rfItyve05GFkVOWiaRnJyB01tbQNltZhDPS99h7+gbhlcvawUPXurWe4+ewvG9iyoDvE6MkG0KSObxy99lbce+phv3vyJMyJvIGPZmhBf1c++kr/JSRae/kcEi57xNAqOXn7Nw5YsndtvcdRuW7rMy/Gzbcw7xcqSf98X4nYK0cVID0ojEqD0NA5LbUn5BGssZ8TN5LnCt9t0igJvEZdl3c1VV17ZZeqHWNMScB0/itJFq6hcsZE9lyzBKK+G8jJqy9YqBc6Wq892JhPmjMJiUfiq/eh+HZvdykGHDgzxVXWgLogbNMCCrhvkF9S9IGZv17nljipeecaF1Vr3/Hh1qYezTrVx1mlWXn19fYjbKURXEuTgpJsEKFKorSeyKnBZoFLnxuT5LCr4T4OH7857lkcK/l17P2f0B1Tq1aRvnIfX8GG1aMyfOY8b7rw9zA0/MI5pQ6hYugbf+jywKIwKhUpwQ1GhmRPhikCFuVT8gYiMdTHskAGsX7UVm9PK9S+fS2xSCKr8tqJ+54nfb3DOpRXc9WcnQwbV9dbl5etsydKZeqiGUgqr1c+6desYPXp02NsrhOgaJEDpgcoKS2DGWgB62RKpSP+q9rHbUy7j9pTLGh3jH7e67o5dwVMjzSJnXYR/dxlFVy81K9PqBjit+PNK0aakYVSUQ1UlRMe0fqJO5ujzprB+1VYOO20ck44bE4YrNuwxy8rW0TRFcpK5/e4HqknppfjDOfYG+732Xy9FxQYDx5pJ2SVlVpYsWcLdd98dhjYL0QV0k16PYOo67zAieCI1ODcZnO0YnnEqmBUPveyt79uJWOIjcJ04Bmya+ayv8uHbVYJSCpU20BzecVnBVwh6ReeeZWIYYOSDsZHJJ9gZNMHJFU/OC9PFLZjLBUPBbp3Lrq/kqovtKKX45jsfz//bw9P/aLwMwqtLvXzwRiTZa2PIXtuL77/6M0uWtDNBWwjRI0gPSk91WQpsq4YviqEqwDdjhzLX4Plr/9C2LQSUZiFy3nhcsw6ibHEGni+y8H77KxzXH7X3DZT1Rfh1j7lmjOEDixPiToX4c8Ce2tHNNxkVYCwB437gN8BObLzBwxkeYDnoN4M6HVTziykeqMpKD+lH7Mbr9WHVYP48OzdcaQart/2tmopKmH5cWYNjlr4Uwa85OodM2jfkYzBw2LXExCwjIyODKVOmhKy9QnQJ+wq1iQZUS1MTJ06caKxevbrZx0UXpxtwfw68XQg+w5yg0RQLYLfA4dGwcID5fRdXnZmNpj+CNWIl5pzppmbv2EBZIGI89Pk7WOPC3cw6+mIwrsd8JStrZqeaQm3qSbCEsEel6u9Q/QD1k2UDZwHrSRC5ONitEiJolFLfG4YxMVzXm3iw3Vj9flJQz6n65ob1ZwiFrv9OI9rPouCWfvDCcJibYPaQRFrMYRxnzfd2BUfHwlND4P6B3SI4Qa/EEfdnrBGrwKhuJjgB8JqPl6+GbSeDd1dYm1lLvxOM6zDXu2kuOKHmsTIwLgb9odC1x/4HUJHsn48SGCc4/xjsFgkhuiEZ4hEwzAV3pMHNqfBdKez1mbNJ46wwPgriu9HTxNAh51qo2mAGHwHxgm83bD8PBi4FLUwl5aGm5+RB2lZWvhKM20BPBcsZwW+TJQEil0HZLMygKdCuaRdEvADa8OC3SYiuToZ4GukGH4dF0ERpMD0OTnbDqW74XVy3CU6UUsyfPx/KPoGKH/B5q0g6/BeOu/w3AG5fVMCDiwsbHDNgxhZ2F/kAWPhkHqNmr2TsmGGkp6eTkZER+kYbFSxceAWjxpYydpyf9Al+MjIMph3tZ/hI8376BD+nnWGOzd1+h05EtJ/8fAMzSLmcqKgQBVPaKIj6GFQS+5Jmm+cCoiDyNbDNDE17hBDdTvd49xGiFZGRkaxbt47KnKdwUcGKr8rpmxzY0//rzAreWVnGD0sH4HDGsTvhTTze0H/a+fqrhbzzro8fvrPgcCh27zbweMzHXnnRwsSJjYdY3G74+0MG992rMJOKfKFroDYcon8C71tQ/Qjov2F+5vEDNQmxKhrsV4PjbFAdmMMjRKfWfYqrBZP0oIgeY87Mw3h3uZn0/ep7JZx1bGB1T3YW+HDHazjsFjD8uB1r6NOnTyibCobBzp0v4Hb7cTjMQMTtVvTp03LexwXnK1573WDPHgMzJ8Ub2nYqF9jPgugMiPoAXA+DcyG4HoTI1yF6PTivkOBECNFmEqCIHmPeccksea+IqmqdNZuqmDI2sLL2xxwWxW87vQybs5Ur7tjCyg+fCnFLAXZzzMxCfsuBYSP8XHGVzsqVdZ+wfn+uXjvEc/MCvXZ7VJQZpPzj0X376ub05HDQxoL9dHBcAPZ5YD3UrC8jhGidlLpvRIZ4RI8xdngE2TuqefXdEuYe2TA3o7n3UaUgKtLC928M5PPvK/g0o4Izr3ife8uf5/zzzw9ha/cQFeXg+289fP45fPqZwZln69x7j9nQ5oZ4AK65WpE+QefGG4zac0Hj4mlCiE5C6qA0SQIU0XMYfk6YHsVND+Tz2Qv9KdxbV/glMU5jZ0HDfI3Scp24aDOXQtMU0yZHMm1yJGNGDeWFpUtDHKBQd91pMG2aYswYgxde1Fs9Ji5OcfY8xRP/3PeCJ70YQoiuR4Z4RM9hTeSCUxK59Qo3Y4Y1rLZ65MQIln1aRmm5GbT8d0UJBx/kQNMUm7ZVsznbU7tv5sYq0tLSQtzYRDZtqmLz5rpPVZmZBmlpgQUbN1yveOoZA58PICE0TRRCBI8M8TQiPSii54g8nNSUf3Lt/MZx+djhTq46O56p52xHAcmJVp69MwWAsgqdqxfmsbfEj9WqMWTYWJ7+1+2hbatyU1bWj6uv3cLeYrBaYchgePpJC6edYfD7c3VcNSk07kT4aLnW4HC3W3HyiYqH/2GYiaxCCNHFSKl70bNsPR48W9t/vHLBsC/AEoY3ff0VMK6k5eqxLYkGywugTghmq4To9sJe6j7dZqz+KLgz3VTSbil1L0SXknjRAfQoWCHu5PAEJwDqVA4sf8QGzA1SY4QQoRPk4Z1uMsQjAYroWWLmgD0N8827LRRo0eC+NBStauaSTnPhP9oTELnAshiUjOIKIbomCVBEz2KxQ//FYOtN4EGKBSxR0P95sAZ3xdHWL30mqLtoW5DiAvUQqONC1SohRLBJD0ojEqCInscaBwPfgIgJZi8FWjM7KlARYO9n7u8cGs5W1rFcB2oxEAdEt7BjNJAIllfBcnF42iaEECEi/b+iZ9KiIW0xVG+GPS9B8TugNMycDwMML0QeBokXgGtCx1dEtZwOxknAMtDvBzIBe82DHmASWBYAc2VYR4iuRgq1NUleyUTP5hgKKXdCrz+BdxfoZWYSrDUZtMDW6gkbZQNOBe1UMCqBopoH4mUqsRBdnQQojUiAIgSYQYljYEe3InDKRfuSZ4UQomuQAEUIIYToaNKD0ogkyQohhBCi05EeFCGEEKJDdZ+pwcEkPShCCCGE6HSkB0UIIYToSDLNuEkSoAghhBAdTQKURmSIRwghhBCdjvSgCCGEEB1NelAakR4UIYQQQnQ60oMihBBCdDTpQWlEAhQhhBCiQ0kdlKbIEI8QQgghOh3pQRFCCCE6ktRBaZL0oAghhBCi05EeFCGEEKKjSQ9KIxKgCCGEEB1NApRGZIhHCCGEEJ2O9KAIIYQQHU16UBqRHhQhhBBCdDrSgyKEEEJ0KCnU1hTpQRFCCCFEpyM9KEIIIURHkkJtTZIARQghhOhoEqA0IkM8QgghhOh0pAdFCCGE6GjSg9KI9KAIIYQQotORHhQhhBCio0kPSiPKMJr/pSilCoDt4WuOEEII0eHSDMNICtfFlFIfAO4gn3a3YRizg3zOsGoxQBFCCCGE6AiSgyKEEEKITkcCFCGEEEJ0OhKgCCGEEKLTkQBFCCGEEJ2OBChCCCGE6HT+H1TmUltmSX1KAAAAAElFTkSuQmCC\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"# Draw directed graph and color nodes by GDP per capita\n",
"plt.figure(figsize = (10,8))\n",
"\n",
"pos = nx.spring_layout(graph)\n",
"nodes = nx.draw_networkx_nodes(graph, pos,\n",
" node_color=col, cmap=plt.cm.spring_r)\n",
"edges = nx.draw_networkx_edges(graph, pos,\n",
" edge_color=edge_col, \n",
" edge_cmap=plt.cm.get_cmap('RdPu'))\n",
"thous_fmt = FuncFormatter(lambda x, p: format(int(x), ','))\n",
"nx.draw_networkx_labels(graph, pos, font_size=10)\n",
"clb = plt.colorbar(nodes, format=thous_fmt)\n",
"clb.ax.set_title('GDP per capita');"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"source": [
"While the network visualization above is informative, the position of the nodes is generated using a force-directed algorithm. However, the nodes have an intuitive positioning in cartographical coordinates. Therefore, I exploit this implicit positioning and project the nodes above in a space spanned by longitude and latitude."
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"source": [
"Thus, let us extract the longitude and latitude of the countries in order to position the nodes on the map."
]
},
{
"cell_type": "code",
"execution_count": 107,
"metadata": {
"slideshow": {
"slide_type": "slide"
},
"tags": [
"hide-output"
]
},
"outputs": [
{
"data": {
"text/plain": [
"[('ABW', (-69.98267711, 12.52088038)),\n",
" ('AFG', (66.00473366, 33.83523073)),\n",
" ('AGO', (17.53736768, -12.29336054)),\n",
" ('AIA', (-63.06498927, 18.2239595)),\n",
" ('ALA', (19.95328768, 60.21488688)),\n",
" ('ALB', (20.04983396, 41.14244989)),\n",
" ('AND', (1.56054378, 42.54229102)),\n",
" ('ANT', (nan, nan)),\n",
" ('ARE', (54.300167099999996, 23.90528188)),\n",
" ('ARG', (-65.17980692, -35.3813488))]"
]
},
"execution_count": 107,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# Create dictionary of longitude and latitude for countries\n",
"geo_pos = {country: (v['Longitude'], v['Latitude'])\n",
" for country, v in\n",
" crosswalk.drop_duplicates('ISO3166.3').set_index('ISO3166.3').to_dict('index').items()\n",
"}\n",
"list(geo_pos.items())[0:10]"
]
},
{
"cell_type": "code",
"execution_count": 108,
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAxwAAAHBCAYAAADjOL3QAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4yLjEsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy+j8jraAAAgAElEQVR4nOy9WYwse37n9Y09conc96zKzNrO0uf2vdd2u8cej7EtPOMetQwjDYM1shjDWPMA0vAAQuIBgYRkrJF4mQeQQMgSL0DLPCAYaeQRGCGDNcx0o3tvd597TtWpLatyr1wi19iDh7oRt+rUlmtlZtX/I6XOqcol/lWVGfH//pbvj7JtGwQCgUAgEAgEAoGwCOhlL4BAIBAIBAKBQCA8XYjgIBAIBAKBQCAQCAuDCA4CgUAgEAgEAoGwMIjgIBAIBAKBQCAQCAuDCA4CgUAgEAgEAoGwMIjgIBAIBAKBQCAQCAuDve/OH/zgB/bFxcVjrWUtMQwDuq4vexmENYGiqBv/Z1kWDMMsa0kEAuEZYBgGDMPALFb4NE2D4zjQNIlVrjJkX/L4UBTl3miaBsMw1673DqZpgqbpW+97CvzkJz/5M9u2f3DbffcKjouLC/z4xz9ezKqeELIs4+zsbNnLIKwJ6XQa0Wh02csgEAhPHNM0cXBwAMMwZnodmqaRz+fh8/nmtDICAFiWBV3XMRqNoCgKNE2DpmkwDAOmabqP+zhQ5XxNURRs24ZlWbBteyYxSVgMjvi4KvYpisLLly/Bst9uwS3Lgqqq7k3TNFAUBYZhwDCMG5hkWRYsyy5E+FuWhXq9DoZhwPM8BEEAz/MTHYeiqNhd990rOAjjEQwGwXEcjo6Olr0UwhrA8/yyl0AgEJ4BlmVd27hOQzAYRDabJVmNBXB+fo5ut/vg44iQWF8sy4JlWde+Z9s2Dg8PEYvFUKvVbtw/LX6/H4VCYernd7td3FfV5GRv7sLr9d77+uQMMie8Xi9evHhBTsqEO6FpGhsbG5AkadlLIRAIz4DRaASO46Z6LsMw2N7exubmJrmuLYinWlZDeBhd11GpVOYmNgCg3+9jOBxO/XxN0+6937ZtmKZ5563X6937fJLhmCM8z+PVq1c4ODgg9ZPPEJZlEQqF3PpMQRAgiiLJaBAIhEfDsiw0Gg00m82pNzORSASpVGothYZlWeh2u+h0OlAUxS1D4XnevYmiuBK9KNOKQQLhLm6rtLlagvfxjaZp96aq6kLXRgTHnKFpGnt7ezg9PcVgMFj2cgiPiGEYuLi4QCwWQyKRWPrFjEAgPC+63S6KxeLUzxcEAfl8fm2DJIPBAMfHx9e+ZxgGVFW983pMURRYlsXOzs61mvqr/PznP3fLmjY3NxEMBuey3nX9PRPWC+e9u+zSPLIjWgA0TWNrawv5fH7ZSyEsgYuLC3Q6nWUvg0AgPDOmDXJRFIWNjQ3s7e2t7SbYsiycnJxM/DzbtqHrOhqNxp2PuVr6dHZ29mDpyLh4PJ65vA6BsA7cm+EYjUZ4+/YtvF4vEonEgw0hhG8xDAOlUmnZyyAsCJZlrzmEfFy6QErqCATCY2GaJrrdLvr9/sTP9fl8yOfza5+RPTk5mSmC2263kU6nb71PkiTIsux+XSwW8ebNG/drp4xLlmWMRiPXNQq4ParMMAwkSUIsFkMoFCIBKsKz4MGSKsuy0O/30e/3QVEUJElCMpmEIAiPsb61ZDgc4vj4eOnpK8Li+NhmUhRFhMNhqKqK4XAIv9+/pJURCITngqqq+PDhw0zXGkEQ1l5s1Gq1mZplgduzDaPRCLVa7YaQYxgGFxcX6Ha7UBRl4l4Z0zTR6XTQ6XTcOvp5Ng8TCKvIRD0ctm2j2+2i2+3C4/FgZ2dnUetaW8hMjueJoiioVCrgOA6ZTIb41RMIhIXDMMzMga1psiKrgGVZaDabqNfrM/8OQqEQNjY2AFwGkxqNBtrt9p0iIBgMolqtznRMBzI/g/BcmLppfDQaodVqXRtS4lhjAZclJ/l8/tnVKI5Go2UvgbBEdF3H6ekpWJYlNskEAmGhsCw7c3Rc0zScnJwgnU6vReWCZVm4uLhAo9GYy0Y9lUohFrucVXZ4eDjWNTyZTGIwGEBRlJmPTyA8F2ZyqSqXy3feZxgGDg8PIUnSs/LxTqVSSKVS6PV6aDab0HXdtUf1eDwYDAZot9szD2MirDaGYaBeryOVSi17KQTCwrk6MdkJQGmaBp7nEQwG4ff7n8014LHJ5XJoNptQVRWGYUwlPvr9Pg4ODsBxHFKp1NxcmOaJY/d7cXEx14xAp9OB3++HKIpjz8V4+/YteT8TCBNC3ffBffPmjf2jH/1o9oN80/vh8Xjg9/ufRM3opCiKAk3T3PSpruvo9Xoz150SHgeKosDz/EQ+1RRF4fXr18/uvU54OjQajXtLVhzjhHFgGAYejweBQACBQOBOC1LC7BiGgcFggGazOdU1hqZphMNhJJPJlTl/HR0dLex6SdM0vvOd7wC4LIs+Pz8nZU4EwhR897vf/Ylt29+77b5HOeNf7f2o1WoAvvW+FgQBXq8XPp8PHo9nZU5u86TT6eD8/HzZyyDMgG3byOVyAIBSqTTWhc+2bbTbbUSj0UUvj0CYK51OB+Vy+cFo+SSbMtM0XQOScrkMiqIgiiIkSUIoFFpbO9ZVhGVZBINBSJKEd+/eTZz1cPojms0mdnd3IYrigla6GliWhU6ng1Ao5P7ezs/P0e12l700AuHJsLQQkxPl13X9WtOaJEnIZrNPJvplGAYRG2sOwzBIJBJuffP29jY0TcP5+fmtwoOmaTAMA47jnvyFmvC0GAwGOD8/fxRbZ9u2MRqNMBqNUK/XQVEUcrkcJEla+LGfCzRN49WrV265lWmasCzL7be0bdv93tWbbdsQBAEej2dlhGA8Hsfp6enCXr9arSIUCgG4/L3lcrmxezoIBMLDrNyuvtfr4d27d/B6vSgUCmuf8ZiXkwVheZimiWq16v4tr9b50jQN27bBMAwYhnEzd7lcbu3fu4T1x7IsDAYDt3xT07Q7o92TlEfdBk3T8Hq9bqa62+2OtVmjKMrNdD83k5HHgKbpJ/F7lSQJgUBgYVmHj/sq6/U6ERsEwhxZOcHhMBwOcXBwgL29vbXeuDEMs+wlEObA1Y3YbZsywzDc2Rzr4PRCeJpomoaLi4sHxcVtTCo2aJpGMBh0hQLHcVAUxc36ZbNZMAyDXq+HXq+Hfr9/6zHi8TgSiYT7da/XcxuDE4kEmWmzJiiKgouLC3Ac5xql8Dw/1+v3xsYGvv7664X0V3Ac5/5/MBigXq/P/RgEwnNmZQUHcGkxur+/v9b2otNuPmeNNhIeF0EQEI1GEQqF1va9SlhfRqMRSqXSo9p0ZjIZsCwLWZbRbDZvHLtWq4HnebdMttFooNls3nider2OXq8HmqYxHA6vnfdOTk5AURQCgQCSyeTKlPcQvsWyLJTL5XunZTvD7ZxSU0eUBAKBia6RiqIs7Lp4dR0nJycLOQaB8JxZacEBXEaO11l0BAIB17LwIRiGgd/vRzweB8uyePfu3SOskDAtoigiGo0iGAyu5XuTsP7IsoxqtTp2z4UkSeB5/t6hZuMQCATg8XgenHKtaRoGgwFisZi7IXWaxX0+H7xeL7xeL0zTxNHR0a2vZds2ZFmGLMtuM7QgCO7tqfT7rSuapt0rNgC4vSKmaULTNPf7jokMx3Hwer0IBAKQJOnO82mpVJrfwj/C6/UCgNvDQiAQ5stanKkNw0CxWEShUFj2UiaGZVns7e0BuCwTa7Va6Pf7sCwLPM9DFEV4vd4bkfH7ZpwQlofH40EsFrv3okggLBLHQajRaDwoGiRJcjfloVAIuq5DVVXE43G0221cXFxMPBNIFEWk02kUi8WxNmaZTAa6riOVSrnnPEeIOG5YTjniQxiGcWuWBPg2ik7TNFiWBcdx8Pl8CIfD5LO6QERRxM7ODs7Ozq6JiUnQdd0VlQDA8zxCoRCi0ei1suStrS23XNAxnZlXT4dTukfTNCRJQq/Xm8vrEgiESx5lDscsCIIASZIQi8WeTSSr2WyiUqksexkEXF58/H4/otEofD7fspdDeMZYloVqtYp2uz3WRt8JdrRaLdi2DZ/PB1EU0e120e/34fV6EQwG0ev1YFkWaJp2N+0A3H6M0WgE0zTh8/kQj8chCAJqtdqDUW3gcuNYKBTQbrfdDeJoNJopuzINTmYkGo0+m7IswzDQ6XTQ6/VgGIZrbJFMJqdyz+v3+2i1WhiNRohEIojH4zce02q15h4sc/52sVjsWp+FQ7VaxcXFxczHoWkamUwGoVAIhmHg+Pj4moMXgUB4mKXP4ZgUmqaRSqUQiUSWvZRHYTQauReGaSNEhPkhCAKCwSAikcizEbmE1UXXdZTL5VsjrpIkgeM41/LUMS8wTRNerxfD4dAtWwEuyzZDoZAbwOl0OtcsUq9urpxsnsfjca1ULy4uIMvy2CUnzhoajcZ8fhlT4mRGms0maJqGz+dDJBKZmwVvuVyGaZpus7TTMP2Y6LqOdruNXq93b69DOBy+Jjicv7dTSuS8D5z5WbIs37gu1Wo1NBoN9zptWRYqlQra7fbcf66rfzuGYdwApPMzpFIpJBKJB/tIHsKyLJyfn6NWqyGXy7mVCaZp4t27d6TMikCYkXt3UyzLIp1Og6Zp1y99kU1bDk4TWrlcBs/zCAQCiEQiTy4ydXp6StK2K8DVDYjP5yPlF4SV4KFGcJZlkc1mIcsyfD4fWJYFy7JuJNu27RtOO6Zpups3QRAQiUQQi8VcZ6irx7p6buJ5fqpgiCiKbrPwpKVbi8KyLNc5C7hcYzgcnqn0ajAY3Nmnd7XEi+d5+P1+BIPBqdfvoCgKOp0O+v0+VFV98LosiiJyuZz7tyyVShgMBlMf37lO12q1R+t7ME0TnU4HnU4HFEXB7/cjFovB5/Pdmv2YBl3XcXh4iJ2dHXg8HpyenhKxQSDMgbFLqrxeL3K5HFiWxWAwwMXFxZ02h4vCaTZ0BhJ5vV4IgrCWG8RSqbSQaBDhJhRFgWEYsCzr1pCv2lArAsHhrkZwp7HWIRAIQNf1O2f9sCw7Vm8ETdOIRCKIRCLQdR3NZnNudfE8zyMejyMQCLhuVuMYaCyLaUuvLMtCsVi8NsT2PqLRKNLp9Nivb9v2DYExDRRFgaIoUiL0AM7ARJqmUS6X0Wq1lr0kAmEtuK+kaqIejlgshlQqde0xiqKgWq2OfaJdFDzPI5/Pr8UMBNKjMT+c5kJn6J6DIyjWUYwSnie9Xg9nZ2e3bgY5jsP29vY121jbtlGtVueaOQgEAkgkEuh0OnOpi3dgGMYVNaqqotlsrnx21+fzIZ/PT3QOOTg4GFsMRCIRZDKZW++zLAv9fh+yLGM4HD7K5HfCt+Tz+WvldkR0EAjjMbcejtvEiSiKKBQKqFQqd7qHPAaapuHg4ACRSASpVGplN5qDwYCIjRmhKArhcBiJRIL0WBCeBPc1vrIsi0KhgEajsfBNT7fbBc/zcx9YapomGo0GLi4ukE6nkcvlsL+/v9Ib6cFggLdv3yKTyYzVT9hqtSbKPLTb7RuC4+zsDP1+f2XKz54jwWDwmtgYDocrL44JhHVg7N0aRVGIRqN33p9Op9Htdpd+AWm1Wuh0Osjn8yvnKqRpGo6Pj5e9jLVGFEVsb2+vrKAkECbBsiycnJy407k/hqZp5PN5dDqdR4uw2rZ9LVs4T5xG7ePj46VfK8alXC6PJTgecmdyNrJ3TeDu9XquLSxhOaTT6Wv7nJOTk6VXbxAIT4UHBQdFUYjFYojH4/du8kql0spcQCzLwvHxMSRJQiQScZsoGYZxfdqXAbmYzEY8HkcymVz2MgiEuaBpGg4PD++MZlMUhXw+vxSXp3kLDoqikMlkIIoijo6OVuZaMS6ObfB9xOPxe/9OgiAgFArdef/HDf6Ex4NhGOzs7Fzr25FlmYgNAmGO3Cs4PB4P3rx5c+8LGIaBo6OjlbRzvepE8jEf12g+BvF4HF6vF+fn52t3wV0mFEWhUCisXMaKQJiWXq+H09PTex+zsbEBwzAevQRzEUYgHMchGAyiWCyu5blP1/UH+wOTySQCgQCOj49v7cOp1+toNBqIRCKgKAqKokDTNBiGQZq4l0gwGEQ2mwVN07Asyx1IOS/jBAKBcMlMBfC9Xm/sabOrxlW3l8fE5/MhEAgstd9lnRBFEVtbW3OvKV8UlmVBURSYpjl3QauqKhqNBgaDwbWpylenK69y/xLhEmeGwX2k02kwDPOgKFkEiyip0jQNp6en2NzcxNnZ2Ux2rBzHgaZp6Lr+KBt1Z1o7cHnNa7fb7ueNYRgEg0E3Mu7xeCBJ0p3ZbNu2ybl/RaAoCpubmwgEAhiNRjg5OSG9MwTCAplacLTbbZRKpXmu5dHw+XxL28BalkXcLh6AZdlrw8lWFcMwcHJyAk3Tbt34OM3t94kARVFQq9WgKApEUUQwGEQgELg27bnRaLjToB8iGAySTNCKYlkWTk9PH9xsO5nQ4+PjpQRzdF1HLBZzI77zYjAY4OzsbGbR4WQbnD49RVHQ6/UwHA6hqip0XZ/L7y0YDLpzqKrVKlqt1q2/j1qtBpZl3T4PUjq7HrAs67qlEYt6AmHxTLWbMwxj4WKD53lEIhEIggBBEMDzPBqNxrWpudNylxXhYzAYDNYyI7RoOI5DOBxGNBpdi2yGYRjY39+/d0Nm2zZarRZarRa8Xq9bw24YBmq1GmRZvvZ8XdfdEkBHcEy64SNiYzUxDAMfPnx4cC7GQ2U5j0G/30ev10Mikbhzxse0DAYDFItF5HI5nJ+fT10jr6oqjo+P3axePB6/dr+Taez3+64QMQzj3nMvwzDgeR4+nw+JRAK6ro+9RsMwSA/GmqHrOnRdnynbRiAQxmcqwXF+fj7vddzAiXBfJR6PIxKJ4PT09E5Xl/vgeR6FQmGpw94kSUIymZyLcFpHKIpySxFomoYkSYhGo2tVBqTrOg4ODibaEA6HQ3z48GHsqPE0m02apqFpGhlmuGJ0u10Ui8UHH5fNZiEIAo6OjpZa2sEwDGRZdmfbzDtAMhwOcXZ2hnw+j/fv38/0sxqGgfPz8xvN2DRNw+v13iidtSwLo9EIvV4Ptm3D5/PdyHh3Oh0cHBysZa8JgUAgrCr3Cg7btjEajaDrOgzDcG+PEaGv1+sYDofY2Ni4VlbDMAy2t7fdSNm4F6tkMnkjCrYs4vE4gsGgW47zVHEme3u9XkiS9GQG8bXb7amjz4uMWluWhf39fYRCIWQymSfxu153SqXSg+UaTi05RVGPXkZFURQikQi8Xi98Pt+tJYyOS1a/35/b2sLhMLrd7tyElWmaY2VGaZp2RcbHGIaB9+/fkww0gUAgLICJJo0vi7uG+VmWhXq9jmazeedFQhAEFAoFcBz3GEudmHmViS0bx4XGuZg/h82upmlQFAWqqkJVVWia5orzZW9aKIrCxsYGgsHgUtfxXBnXvY9hGOTzeaiq+ug9cR6PB1tbWwubpH0XzsTxw8PDuX1OdnZ24PF4br3PNE20Wi0EAoF7naYsy5o540IgEAjPmblNGl8WTh08z/Nunb/jzJNKpZBKpTAYDFwHH+ci9vEQn1XEyXbs7+8veylTE4vFkEqllr2MR6fVarkZQNM0YVnW0oWGg+OGQwTH49Pv93F6evrge4HjOOTzefR6vUcPOkxybjQMA9VqFd1u91qGjmtZECom1CQDPTaeaBFFEclkcq5iA7gU/x8LDtu2UavV3AnutVoNFEVBEAQEAgGEQqFr5Yc0TWNvb+/B3iwCgUAgTM5aCA4HTdNQq9VQq9UgCAJSqZRrPXo1TT4YDCAIwko7HF3FmTq7jhe57e3tpVkMLxPLsiDL8srWeadSqRs9UITFU61W3Q3uQ2SzWdel7LEZR2xomoZSqXRrUy1fN5H970egTBs2TaH8+x6o2YdLmkzThGEYiEQic21Iv60Z//z8/IZjlG3bUBQFiqKgXq+DoiiIoohAIIBwOOxeO0aj0dzWRiAQCIQ1ExxXUVUVp6en8Pv9KBQK1+5bR6cenuehKMqylzERDMM8S7EBXEZDX7586TahyrKMwWAATdOWmuUIBALY2Nh4FiVtq8RgMJh4oGelUkGhUIAkSXcOKF0UqqreWV6kKApKpdK9m27voQFas6GHaLCyBf/XxliCQ9d1HB4eYnNzE4VCAcVicS6Blna77TpMOe/9VCqF4XB479/E6VMcjUZPorSVQCAQVpUHBQdFUe6QMYqikEql4PF40Gg0bth6LoN+v49qtbr2JT2iKK6d4Jj3cLB15OMmVFVVcX5+/ugRUkEQkMvlHpyGTJgviqLg/Px8rM8uTdPgOM4VpBzHgaKoR8+ScRx3a4P1YDBAuVweq0dDizIABTBDG7ABNTH+ucCZR5JOp7Gzs4ODg4OJ1n8biqK4QxKdQEgkEsHLly9xfHxMrE8JBAJhydwrODweD968eXPrfdlsFtlsFpqmoV6v36jvfUwuLi4QiUTW2g40k8ks9Xc4Dc81u3EX9Xr90bz4BUGA3+9HKBS6s1mWsDg0TcPZ2dnYwpKiKGxvb7si3fl3XLEyD1iWRTabdctQHXq9Hsrl8kTCZ7jHoP4DAd6faRjtceh/d3JTDsMwFuLSZ5omer3ejZk2BAKBQFgeM5dU8TyPjY0NAHDrYvv9/qNvnI+Pj/Hy5ctHPeY8oWka29vb+PDhw7KXMhYsy7p/d8IlziwAx7HKMAy3mXwWnDpzSZJuNLoSHhfDMKaakp1IJKCqKs7Ozha0srthWRaZTAaBQODa9y3LQrFYnG74HkWh94s8fvyP/wK+ehQbv/r5RE/neR7RaBSHh4eTH3tC1imIQyAQCE+VufZwiKKIXC43lvf8vNF1HRcXF2vdKCuKIjY2Nh5lsOKs7OzskMjhR/A8j0Qicet9lmW5NrqKokDTtGui5GrfB8uyrsAIBoNrY37wVLEsC61WC+12eypLWK/Xi1Ao9OjBBJZlkU6nb3UqGwwGOD09nWkzrl+MoFWH0C9GiP2dHYh56eEnfYMoiqAoCtFoFM1mc2XNFwgEAoEwHxayk/H5fHMb6jTJpNunsAEOhULwer04Ojq61Xll2fh8PmSz2ZWda7Kq0DQNURQhiuKdj7Es60m8h58ChmGg2Wyi0+nMtBl25qGUy+VHm+8giiLS6fSd5hmtVgvlcnnm43T/eQ0US8E2gcp//TMU/uivgGLHe/92u10Mh0NEo1Hs7Oyg3++j0WjMPOODQCAQCKvJQgRHKBRCKBTCcDhEtVrFcDic6fXi8TgURcFgMLgzIkfTNCKRyEzHWRV4nseLFy9QLpfR6XSWvRwAgN/vvzH1nTBfiNhYLpqmodlsQpbluYl9Z17QY7hQSZKEdDp9b8ndaDSai9iwbRudf3YGWmRhDnQMv26j9WdFRH9YGPs1DMNArVZDo9FAJBJBoVCAoig4OzsjZVAEAoHwxFjo7tHr9WJ7exuWZbkX8kkbJG3bRqPRAM/zbtNlp9NBv9+HqqruhSkejy/iR1gaNE27k6KLxeLSrFYlSUI2myVCg/Bk6XQ6KJfLC9nkLjprRVEUIpEIksnkWMc5Ojqay3HNjgazp4P2sLA1E8HfzIILTeeQZlkWLi4uYJomotHoygzPJBAIBML8uHcXqaoqKpUKBEFwbxRFuaUGmqaBYRiEQiHE4/E7N6U0TSMej7uiQFEUtFot9Hq9scsVNE3Dhw8fIEkSNjc3kUwmAVxerBRFebKOSZIk4dWrVzg+Pl6KbS4RG4SnimVZODk5mTkDex+2bS/UPjqXy91wnXoM2LCAvT/5LZg9HWd/9BNs/AefzfR6Pp8PyWQSx8fHRHAQCE8YGkNEmH8KFjI61m9BsbeWvSTCI3HvTtLJTNyHaZpoNptoNpvgeR6ZTAZ+v//e54iiiEwm4x6j1+uh0+lAURQYhnHvBafX66HZbLrihabpJys2HBiGwe7uLorFIrrd7qMe++zsDFtb5IRAeFr0+32cnp4+yubWyXLMO4PCcdzEYiOZTM5twjdFUWAkDpZmwtJM0PzDg/8+hmEYpFIp+Hw+nJ+fkx4OAuEJcVvAJc78Kfz0V7BsDh72A4r6fwwTgTtegfCUmGvoWtM0nJyc3OuO8jE0TSMYDN54rKZpGA6H7hRYTdNcN59Op/PkSqjGYWNjA+/evXvU+mYyMIvwFHnMMkXLssAwzNw/t9PYUsdiMdTr9bmthaIosEEBRlsFn5ws8BMOh5FMJtHpdPDhwwfSt0EgPCHaxS7+7D/7C4gBAaGchNBmAKzAIPe3z2HYftgQwEIGS3Vg2kRwPAcWUivjeNWXSiVks9mxhMfH8DwPnufd2QYOz/miRNM0CoXC3Oqwx4HMfCA8RRaRcbiLdruNQqGAYrE4twi+IAh3ulA9hCM65gUbFmB0xhccVzPcJycnSykVJRAIi0VKemEoBjqyitrbBhRZQyDjx6/+8PuIe/4ZgBE0OwHNTi17qYRHYqHF+ZZl4ezsDIIg3GsHOgnP3cnH6/UiEomg1Wo9yvE2Nzcf5TgEwmPC8/yj2U7X63Woqoqtra2phgbehrNhn4Z5b/DZsACj/fDEcIZhkEwmIUkSarXayjjwEQiE+TGSVVS+rKP8ZR1qX4c+MsB5OeRexfA7//mvo8cK0I1tMBhgZO/BBglqPhcepRv46sAriqLcmj7HyvauYWmE28lkMuB5HrVabaFlIR6PBx6PZ2GvTyAsC0EQFtos/jGyLMPn88Hj8cxFcJyenuLFixdTGTrM++dmQzyM9v2ZG6d8SpZlHBwcPOtMNYHw1BhcDFH+RmR0K32kPolj69c3kP3FBP7Pf/T/IrYXxl//T/8aPMFLJzvF3lnyignL4NHth2zbdjfJlmWh3+8TwTEFsVgMkUhkobM6SHaD8FTxeDxot9uPeky/34/T09O5vJZlWdjf359KdMw7s8OGBajnt4soj8eDTCbjOoKR8ikCYf2xbRvdSh+VL+sofVGHIqvIfJbAy9/ZRuJlBPQ3A0C1oY7v/O4uPv+91xAD09lmE54OS/c7fe4lUrPgzOpIpVIYjUbu969mPWzbhmmaqNVqE0069hSw0/MAACAASURBVPv9pH+D8GR5bGc7nudBUdRcXZgsy8K7d++QTCYnMtFgGGauU8/5rA9G52ZJVTweRyQSIeVTBMITwLZttE9klL9qoPxFDZZhIfN5Ep/9nVeIbodA0Tftv3kvh1/5B58vYbWEVWTpgmMeHvWWZeH8/ByDwQB7e3vPbm4Ey7IP2mNGIhFcXFyMXYY1jQMOgbAuPLaY9vv96Pf7C3ntWq2Gi4sL5HK5sRrJX79+DVVVUa/X0ev1Zi5vEjcl0BQNhmHcklmapjEcDtFsNkn5FIGwplimheaHjlsuxXoYZD5L4Jf/nU8R2pQWOmOI8PRY+s583MF/d6EoCo6OjtyL2sHBAV6+fEkyJ7fglGFVq9V7m85DodCzE22E58Vjnh94nkc0Gp3b/IvbME0Tx8fH2NraGkt0CILglkxOMt+HZVmIoghJkhAIBMBxHPSeir/8R/8Lful/+tUbj1cUBaVS6VoGlkAgrC6mbqL+voXKl3VUvmrAGxGR/iyBX/uHv4hA6v4ZawTCfSx9VzlLicFoNMLh4eG175mmiaOjI+zu7s66tCcJTdPIZDJIJBJotVqXw7sYBgzDgGVZMAwzN0cxAmGVmXdp0W34fD5sbm6iVquh1+st9FgMw0xl8pDL5VAqldyeFuecwHEceJ53BcbV88LVrAXr52GbFoyhBtbLX3tMt9slfRsEwoqjKwZqby9Q/qKO2tcXCGaky56MH2zDFyXGMYT5sHTBYds2VFWFIEzWUKTr+p3zKBRFwenpKfL5/DyW+CRhWZY06xOeNYt2qopEIojH4ygWi4/iiLWzszN15iabzSKdTl97vmVZGAwGkGUZsizDMAx3+OpVGIaB528kcXJwDDYowLIst3dM0x62yyUQCI+PNtBQ+ekFyl/U0DhoI7oTQuazBD79N16SBm/CQli64ACAVquFdDo99uMty8LBwcG9vQi9Xg/FYhG5XG4eSyQQCE+MaDS6MCEgSRJisRiOjo5mLhsdh3w+P3NfCk3T0DQN5+fnUBRl7N4L0zRh0jZ6nR445vJn9Xg82N3dxfv37xeeRSIQCOMx6igof1VH+Ys6OsUuEq+iyP5SCr/09z4B7+WWvTzCE2clBIeTyvf7/fD5fPdG6SzLwocPH8a6GHa7XZLpIBAIt/KQ0cK4sCyLXC4Hnuexv78PhmGQzWZxenr6KGIjkUjM7WcZDodTiTDlQAYMC9yvpd0ysmq1SsQGgbBk+o1vZmR8UUO/PkTqTQw7v5FD4nUULM8se3mEZ8RKCA7LstBsNtFsNgFcCo9cLncjve88ZhIf+V6vh5OTExQKhXkvm0Ag3INpmmi32+A4Dh6PByzLwjAMaJoGXdeh6zpCodDS7JdpmobH45m6oZmiKKRSKUSjUfd7r169wuHhIcrl8sIbpVmWRSgUmmtp5DgN57euJczD6KiQJAmZTGZuE9UJBMJk2LaNbrmP8hffTPvuqUh/msDrH+4gvvftjAwC4bFZCcHxMf1+HwcHB9jZ2YGqqqjVajOVPvT7fdfBhUAgLB5nMN1DEW6KoiaaITFvEonEVMP4AoEANjY2bmRjaZrG5uYmPnz4MK8lXoNlWeTz+amaw8eB4zjQND2xlS0bFqEcymBZFsPhkIgNAuERcWZklL6oo/JlHZZlI/t5Ap/93itEt26fkUEgPDYrKTiAy6bwd+/eze31BoMBjo6OsL29PbfXJBAINxlXbAQCgaWKDeCyrOrVq1eo1+vodDoPbrR5nkc+n7/X5EIURXi93oX0h0iStDCx4fDq1SuUy+WJhvWxIR5GR0O320UqlQJFUWPN+yEQCNNhGRYuDtuXmYyv6uA8LLKfJfH9P/wUwQ0yI4Oweqys4FgEw+GQ9HQQCAvEMXR4qOwxEAisjKEDy7LIZDLIZDIYjUao1WoYDAagaRo8z8Pr9cLn88Hv94/tArW5uYn379/Pfa2BQGDur/kxNE1jY2MDqVQK1WoViqLA4/HA4/GAYRgMBgN0u91rf2M2IsLoqDBNE4qiwO/3L9wGmEB4bpi6ifq7Fspf1FD5aQO+mAeZz5L49X/4PUip6cohCYTH4lkJDuCyp6NUKiGbzS57KQTCk6Nerz/YKE3TNAzDwLt372Db9rVIXDwev9YT8dh4PJ6J+72c/rJWqwWO47C9vQ2O4xAIBMYeqDcu0/ZY3Iau66jX65BlGTRNY3d399rAT5ZloSgKstksFEXBaDSCaZrw+/1IJBLo9/toNpsYjUaXGY6WCoZhXKFGIBBmRx8ZqP68gfKXddTfNRHMSsh+nsTrH+7AGyEzMgjrw7MTHMClKxbLskgmk8teCoHwpBinDMeyrDvLjdZpboNlWSiVSpBl2f3e1TKijY0NvH37dm7Hczbzs2IYBg4PD68JQ8uy8P79e+zt7V0TC6qq3hiu6giUcDjsTiu3bRvbf1KAmPJhMByi1WrNvE4C4bmi9jVUvroUGRcfLmdkZD9P4PN/8zUEiYh5wnryLAUHADQaDXAch0gksuylEAhPAl3XJ3KQu41l93Tch2EYKJfL0HUdpmnCMIwbPR8M863NJE3TSCaTqNVqczn+PHo3LMu6ITYcbNvGwcEBCoUCWJaFpml39mFcdQ10BEr1v/05Ur/3CpnXm8jlclM14xMIz5VhW0Hlq0tnKWdGxuYvp/C9PyAzMghPg2crOACgXC4jFArNJWpIIDx3Go3GTM9nGOZaSc8qYZom9vf3H2wq39jYuPZ1PB5Ht9udi0VuKBSa+TVKpdK9JW+2beP4+Hii13SyUspQRftDHYbPxsuXL2daJ4HwHOjXByh9Y187aAyR+iSO3d+8nJHBcGRGBuFpsZpX90dCFEUiNgiEOTFrOdQqlzienp4+KDYoisJwOIQgCNfOK1tbW/j6669ncm3iOG4uguNq+de84SICjI4Ky7JgGMbCnLoIhHXFtm3IpT7KX9RQ/rIObaAj81kCb353F7HdMJmRQXjSPGvBsSouOQTCUyCXy+Hg4GCq6drpdHqlyxvv2jjTXRrh/80PSqUh/7CHil1BpVLBJ5988u1jaBqFQmHizMFVFuGsx3Gc67xl2zYsy4JlWe7/gcvGcZZlwXEcBoPBvc5TTEiA0VIBXGa7ksnkTD8zgfAUsG0brWP5ctr3lzXABjKfJ/ELf/c7iGwFiX0t4dnwrAXH/v4+/H4/0un0vb76BALhYWiaxt7e3sTR/HQ6vVRnqllI/eMoxH0eoADflx4U/8sKvKFvnaR0XUen00G/34coilAUZeJjBAIBiKI481oty4LX60UwGITf7wfDMOj3+zAMAxRFgaZp0DTt/p+iKLcvxzRNZLNZjEYjaJqGTqdzo0yMDQkYvW+7z/V6vdja2kK328VwOFz45HUCYVWwDAsXH9qXIuOrOngvh8xnCfyVP/yMzMggPFueteAAvp1qznEc0un0o/jcEwhPFZqmwXHcROVVlcplVoCiKGxtbcHr9S5whfNFPORhREyABsSegIAVAM0z2N/fn6rEbGtrC4ZhQNM06LoO27aRTqfntl6nGbxYLEJV1Yme2+l0IIoiBEFALpfDaDRCvV6HoiigaRqxN2lIn+4i8XIDg8EA5+fnAACv14twOAyO41Aul6EoCgRBwGg0miobRiCsIqZuov51E6Uv6qj+rAFf3IvMZwn8+r//PUhJMiODQHj2gsNB13UUi0V4PB7k8/mVbV4lEFadafuinIbl169fr1xv1V2Ts3u/OoT0f3vBcRy47/LIfprF2/dfT3WMzc3Nuc7Z+BiaptHv9x/sRbkLXdeh6zp6vR6azSbC4TDy+TwMwwDP8xjIA5z+6U/RkYbXpsw7fSMej8cVVKqqIp1Ow7ZtDL+x0SX9HoR1w52R8cXljIxQLoDMpwl853d34Q3PnpUkEJ4SZFf9EaPRCO/evUMymUQ0Gl25jQ+BsOo41rChUAij0WiiSLojOnZ2dha1vKm4K2vT+MM27E8NRJkg8Hs+0BwFlmXvtAfmOO7WqL4kSQgGg3Nf98d4PB4MBoOZX8e2bbRaLbTbbbx+/Rrv37+Hrmg4/tOfYvuv/tqtJSOj0ehGuR3P8wgGg0in0zfmfRAIkyAIAmKxGHieh67rbpbQud1n8zwJak9D5af1b2ZkdBDbDSPzWQKf/x6ZkUEg3AcRHHdQq9Vc/3yWZSEIAkRRhN/vh8/nI0KE8CyxLAuVSgWWZV1zPOJ5Hvl8HoIgIJFIQFVVGIYx1iDAjxmNRqjVaivlWlUoFLC/vw+GYa5F7ykWkD/pwP4fvkT67/9r7mNPT09vCAuGYbCzswNZlt0+CccKeB4zNm7Dsix0u13IsozRaATDMJDL5dx+ElVVMRqN0Ov1Jt6M8TyPcDgM4PIcaXImaJGB2dPBBm7feH18DE3T0Gw2kUgk7swiEQh3QdM0PB4PotEoPB4PWq0WOp3OZcaR4+DxeBAMBt2vK5UK2u32xMcZthVUvqyj9EUN8nkPiddRbP5yGr/8b38KzkO2UQTCOJBPyhgYhgHDMDAYDNBsNkFRFOLxOGKxGBEehGdDr9fD2dkZLMvC9vY2TNNEv98HcLlxPDg4gCRJbmnQNGLDodFouOJ+FeB5HslkEizLIhgMQlVV2LYNkRfQqTXRtT5AO2qB345AFEW8fPkSsiyjXC67AmV7exssy87UIK9pGlqtFnq9HnRdB8dxEEURPp8PgUDgWilosVhEt9u98RrFYhE8z7tBlHA4jGw2i1KpdOvjbyOXy8Hr9aLT6eDDhw9u9ocNCTDa6p2C4zbi8Tj6/T4RG4RboSgKgiC471me593/UxQFVVXRbrdxdnZ273vI7/cjHo+PLTh6tcFl0/cXNQwuRkh/N469f7WAxKsImZFBIEwBERxTYNs26vU6Op0OXrx4sezlEAgLxWkyvuqwJMsygsGgKzgcer0e3r59i52dHYRCIZimiVarBV3XJ+4dOD4+Bsdx8Pl8SKVSS++r8vv9ODw8RLlchiAIYGga1n/zFdRfT4L6jSTO//k7xGKfuFazwWAQwWAQrVYLNE1jOByCoih3Mvc4OJmkdruN0Wh0Y0OlqipUVYUsy6jVashms6AoCpZl3Vs6pWkaNE1zbW53dnauZW7uw+fzged5vH///sZ62Mil4EBeGvtnVBQFoVAIPM/PPMuF8DTgeR7xeNx1U3Per6qqYjgcot1uQ9O0O0sXb2MwGGBzc/NGltLBtm3I5z2Uv6ij9GUN+shA5tME3vzre4jt3D8jw+v1umYPBALhdojgmAFN09Dv9+H3+5e9FAJh7liWhXK5fGum4iGLV6ePIxqNXovoW5aFer2Oi4uLsdbg2MoOh8Oli3tHKNi2DUVRwBzIEA5k8NUhzBdBqFsSisenAENhb28PgiC4gqDVarmbc4ZhEAqFEI/HbxVRThZDluWJXJxM00SxWHS/3t3dhSAIbobWNE1X9Dk9Fs6/LMsiFotBEATIsnyn+BBFEYlE4trPcxUnwzEJsixfm1VCnKueNjRNu/Ndrt44jrv2/2aziaOjo7m9H2zbxmAwQCgUgq7r8Hq9l454FoXy+wre/vkBzn5eQmQnhF/6/TcIF+6fkcEwDILBIDKZDACgXC6j1WrNZa0EwlOECI4ZKZfLS98IEQjzptlsolqt3lmi4MyGCAQCUFUV/X7fdUDa2Ni4M4pP0zRSqRR4nke5XB57PU40XpLGj5zPG4Zhrgkt28dC/800mH0ZdFMFxdKwMl7YMRGHh4d3ZnRM00Sz2USz2YQoiigUCqBpGrVaDe12e2oXqY/58OEDAFzb1DkbqKt/V+f/PM/D7/cjGAyiVCq59zEMA0mSEAqFQFEUOp3OnWUpbOhy2viktNttUBSFnZ0dtNtt1Ot1UmK15kQiEQiCcE1IOALbme9y9TYcDt3/q6o6t8/BVWRZRjqdRrveQfHHZXz95/sAReHN33iBv/YH30cwGoCmaajX63cOuXQ+C36/3y1tdMQMgUC4GyI4ZkTTNBweHsLr9bp11ATCOjMcDlGpVO59zOnpqbt5dfoAnPKhUCj04DEikQi63e6Nkqz7OD8/x+vXr8d+/Cz0ej30ej03M+AIq6tZHSvjg5XxARQFKy7C/CT87X1jbpYURcH79+9B0/TYJU2T4mziHmIwGKDdbmNnZwdbW1uwLMtt5O71ejg/P39weB8bEaCej/83vYrTm/Ly5UvQNI12uz3VoETCcmFZFhsbG6AoCrIsYzAYXBMWixASD2FolzMyfvzFT1H9+QX8CS8ynyex8zdz8Mcv5/6U6yVUGmWk02l4PJ5rgkMQBPcc5wy+LJVK7s8SiUSwtbWFTqeDer2+lJ+RQFh1iOCYA6PRCKPRyI1Ybm9vk2Zywtri9XpB0/S9F82rMxMcMwUAt5YXNhoNdLtdsCx7rZxi0rkLTj9IJBKZ6Hn3YVmWG7E3TdOdkq1p2jUBcG/00rQBZvrJwdFodOKMzyIZDoduGdikTFNSdRVd13FycuKaD5imidPT04WJMcL8cbKfBwcHS/27aUMd1Z9foPLllRkZn1/2ZHhCt8/IsG0bNE3D6/Uim82CYRg3Q9Nut3F8fHxrn4ZTAplKpbC3t4dKpTK2AQOBsAycfkKe50FR1LUbcBkMUxRlrplmIjjmjKIoKzlHgECYhGQy+WCW4zZui4DPszymUqkgFArNJOgNw3DtM2/bPAiCgJ2dHRwcHIy3bssGZogvtNttvHz5ErVabSU21v1+H+l0Gp1OZ+JILRuerqTKwePxwLZtdDoddDod5HI5JBKJqd6LhOXQarXAcRy2trZwcnIyUWP3rKg9DeWvLmdkNA87iO+Fkfk8iV/4u6/B+8Yza2i32xBFEaZpwjRNGIbxYGYPuAyIlEolV6w4fSgEwirAMAxisRg8Hg94ngfLsu6sGsuy3Gud869TEqlpmhtUHw6HM2WdieBYAKQMgLDuRKNR1Gq1mUsD5jVsy8G2bRweHiIej8Pn84HjuInXs7+/f+9jnPpxURTH2mhQlg0w0yuORCKB0Wi0MmUYvV4PgUAA0WgUjUZjoueyQR5mT4dtWqAm/J3E43FEo1Goqupmmlqt1tgGA4TVoV6vQxAEbG1t3dvPNA8GzREqX9ZR/qoOudRD8nUM+V/J4Pt//1Nw4uRbnMFgMFM/xnA4xMnJCba3t6HrOsl0EJZOOBxGMpmELMu4uLiAqqpjmTE4ltQejweiKCIWi7k9iLIsT3xtJ4JjAZBmR8JTQBCEsTbcV9na2rr29aRlU+OgqirOz8/dr2maRiKRQCwWe/C5p6enAACma0Ms2rA5YLRDwWa/LYmiaRocx40fODBt2NNXVMEwDDAMA4ZhHjUafBdO38Y0WSSKpcH4OJhdHWxYmOi5siwjGo2iVCoRe9E1RRRFJJNJeL1e1655EdfDXnWA0hc1VL6sY9hSkP40jr3fLiDxcjVmZOi6jtPTUxQKBei6PvF5lECYF4VCAYIg4OTkZOJguOPI6DyvUqnA7/cjGo0ilUrh+PgYqjp+RpsIDgKBcINmsznxRXJzcxOieL02OhQKodVqLUR4OFiWNdaJVJZlqKoKvmIj+ycmKN0GbEDdoFD+AwY2f6ka/H4/hsPh+Bsla7YejkajAZqmkU6ncXZ2NvXrzINYLIZ4PA5FUaYuY2LDPPS2OrHgcOyAI5EIqtXqrY+5zWWLsDowDAOfz4eDg4O52hvbto3OWQ/lL2sof1mHMTKR+SyBT/7WC0R3Q6BnyDAuCkVRcH5+jlwud2fvB4GwaFqtFmKxGDY2NnB4eDjzudNxpIxEIshkMjg+Ph77uURwEAiEa4xGo4k3m/F4HMFg8Mb3e73eoxgoPDQLx7Is1+o1/k9MwLRhBCjAvsx0+H9qo/dLl5tZSZImcs+67OGYIcWByxKUly9fLn34nRPRmuQi8jFsSIA5ReM4RVHo9/vI5XJoNpuuK5CTAWJZ1s0CFYtFEjVeISiKQiQSQSwWQ6/Xm0svkm3ZaB513GnfNEMj83lirBkZq0K/30etVkOhUMDh4eFK9GgRnhfdbhfdbhcvX76caxbdcaQMhUK3zuq6DSI4FsCyJyITCNNiWRaOjo7GfrxT1/mxFa6iKO4ciMfgIcFRrVbdOnJWBiwn+E5RsCkbwpCB6fWA4zj4/f47I+y3MmOGA4BrPev3+5c6PKzZbCIYDCIQCLi15079ruNgYtu2axfsTFe+GjWbtHE8EokgmUyCoii3UXd7exuapuHs7My9SDrHlCQJ+XwepVLpzlkJhMfD4/Egl8tB0zScnJxMVGLxMZZhof6+hco3jd9iUED28wR+9d/9BQTS/rUQGR/T6XTA8zzy+TyOj49Jdm4MRFFELpfDaDRCp9Mhn/MZ4TjumgPVvCiXy8jn82MHGcjOeI44dnrOtN7bIr4EwirT6/UevCCKoohIJHKvW5RjtbfoiyvLstjd3b1X5H9s8TrcoxD4sQ09ZIP6JtgT+6sb0NO8mwmZJBJJmbNnOIDL39kqNJiORqPLCcy4FAM8z2MwGLhOJjRNX8s48DwPVVUxHA4xGo1gvk5CbysQBMF1QGFZFpZl3Wge9vl8iMViODw8HDuz0+v1UC6XkcvlsL+//+wmk7Msi2g06g5y/HgjMRqN0O12Z9r4T4IzlDMYDCIej09cjmmoBmpfN1H+so7qzxqQUn5kP0/gN/7D77szMtader0OjuOwubmJYrG47OWsNM4w1EqlApqmEY/Hkc1m0el0MBgMoOs6NE1bGZONVccx42g2m3M/VyqKAlmWkclkxioHJoJjDlAU5UbhnPq2ZrMJSZLIPA7CWhEMBt0yltFoBEVRoOs6dF13J+yO856maRr5fB6np6cLFR1OhP02wTEcDtFqtTAajVzXI6/XC/rviaD5IYR/0YNBmaj/DhDfZVGvVqdzp7Fs2HMQHJ1OB/F4fOnRPE3TEI/HwfM8ZFlGp9O5929IURQ8Hg88Hg8kSULwt17DVizwcY/bfO/YjF5cXLjnS+Ay8tbv9ycuIwsEAgu5gK4yjq1lOBx2N1+2bd+ws/T5fMjn87BtG91uF71eb6E9VKZpolwuo1qtIhwOY2NjA5Zl3etkow11VH/WQPnLOhrvWwjng25Phic4We/PulAqlZDP55HJZNyZO07PyziBnueAIzauZi/b7TZ4nkcoFEI4HAbP8+A4DrZtu0EO518iQq6TSCTg9/txeHi4sHOlUzKYTCZRq9XufSx135v8zZs39o9+9KN5r+9J4NiFURR1azQnHo8jmUwuYWUEwmphGMZUDhnj4mywBoMBZFnGaDRyo7upVAqSJH17gZL7GF30oYkWErEEav9kH3/5n/wZfut//7dgsOZU5UzC/3gE7a9nYMduHyY2DpIkYTgcolAooNvtTmxHO08oisKLFy9wdnY21UZVOe7i4n8+xMZ/9Avuhqrf78Pv98Pv98OyLDeD5PV60W63J87shMNhpFIpt8yq3++jXq9PvNZ1gKZpRKNRRKNRdLtd1Ov1seqwRVFEIBBAIBAAwzDo9XrodruuULnveAzDXMucOP+qqjrWxtjv9yOZTLplcQCgyCoqP22g9EUNrWMZ8RdhZD5LIv3d2NgzMtYdmqaxtbXlCvmtrS2Ypgme59Fut9Fqte7cGDrnsFVwslsEt4mN+2BZFl6vFx6PB16vF6Io4vz8fOkBm1UhFAohkUg8Su8QwzDY2dnB+fk5dnZ2fmLb9vduexzJcIwJx3Hwer2QJAmBQADApcXmbRFRn89HxAaBgMvyl2KxuLDoXTgchqqqePv2LYBvS6yOjo5gmiaq1arbj8E1TWT+tAv/wIKSZbH/23VICo2/9Zf/HoYXfRiY8qQ8ZdM4z/Pw+XwIhUJuaZKmaQiFQuB5HrVabSmbC9u2Ua1WkU6ncXh4OPHzr04bN03TFRNO8+I8cESKYyeczWbdgY5PhauN2IPBAEdHRxNlghw7y3q9Dp7nIUkS4vE4Njc30e12IcvyNXMEn8+HcDgMSZJgmuaNzAlw+fmSZRmtVssV9TzPQxRF2Lbtlt05G5zaWR0f/vwUpS9q6Fb6SH4nhq1f28Cv/IPPwArPb/thWRZOT0+xvb2NaDSKVquFRqMBnucRiUSws7OD0WiEdrsNlmUhiiJEUYQgCDBNEzRNQ9M0XFxcLK380skWz3sTu7GxgUajMbZgMAzj2jklEokgEAgQwYHLQE4qlXKvg4vGNE3UajWk0+l7H/f8PvET4kxM5fnrEZiTk5NbxQbHccjn84+1PAJhJXF6IWRZXsjrO02FNE3j3bt37vcNw4Asy8jn82BZFvV63Z32G/oXQzADC4ZEQTw3wP2ljJ/9V/8S+3/8F3j9x78NW+JR//EJEj8sTLaYCZvGRVFENpsFy7Lo9/totVrXfk80TSOZTGJ3dxc0TUPXdVQqlcmcs2ZElmXEYjH4/f6Jj8sEeZhDA7ZugeIWV1LqNJgDQLFYxO7uLmRZfhJOQJIkIZ1OQ1EUnJ6ezpwd1DQNzWYTzWYTLMsiGAwikUhgY2MD/X7fnfDearVQLpfvLE1hWRaRSMSdLyHLMuLxOAaDwbemAoYNQzVx8pNz/K9//GdIfxrHy9/ZQvxFFMwC3w/rgpPx9Xq9rruPpmmoVquo1WoIBoMIh8PQdR2KoqDT6UBRFFiWBYqi4PP5kM1mYVnWo50TOI5zg60ejwfAZcmqLMvodrtzKWVqNBqIx+NotVpTBaj6/f5Ys5ieOjzPY3NzE2dnZ4/qeOjMUboPIjjuIZFIIJFI3Ph+r9e79YNOURR2dnZI3wbhWaOq6liRFYqi4Pf73YiUM3BPFEV4vV74fL4bcz0+xqmFvopj6euIf57nUa1WL4f72bi8AdDOegBNYXjSQf/rC5gchc7/U0H8d3Kg2PE/w5RpAw/oDY7jEAgEIEkSRFFEtVq900rQsixUKhVUKhVQFIVCoeAaUKTTaRiGAVVV0Ww2F9IY7PP54Pf73WbwSaFo2cnsIgAAIABJREFUCozEwZBVcDHP3Nd3G5qmod/v48WLF1BVFf1+H71eD6qqQhRFd5PkiM9VwuPxIJlMotFouEGsZDKJSqWykGitYRiu+HA2kuM2ehuGgXq9jnq97vZ0nZ+f4+znpW/sa+swtMsZGZnPEvib/8W/spIzMpaNpmm3bgZt20an07nz3GDbNvr9Ps7OzpDL5VAsFhfWn8NxHEKhEAKBADiOQ6/XQ7PZdPc+zt8/k8mApmm3n8g0TVQqlYkzMM6GNRaLTVVSqmkaTNPE7u4uer3enb1LTg8Iy7LuvyzLuv2AmqaNPYl7FXEcBqfqR5yRh86vay04rtaYfqyIZynh4HkehULhRlYDuNwM3OUyQdM0zs7OEIvFIEnS1McnENYVTdNwcHBw4/ssy14r0/B4PNja2ppanFuWhXa7jXa7fedjdF3H0dERMpkMdnd3UTZOIdQaEGoGem8ENP6vy5Nj/DcKSP/t76D4f+xj749+ZXLrQNuG/UCGI5fLwTRNNJtN1/FpvJe2UalUEIlEsLm5iXq9DkVREAgEkE6n3bIrwzDmUrYWj8fdpuSTk5OpL7psWITRfjzBAVxmORxjAL/fj0wmA0EQoCgKRqMReJ5HIBDA2dnZytTB0zSNzc1NyLKMbDZ7rQTqMaLXuq5PVYZmWzaO/r9TlL/4lyh/WQfD0ch8nsT3/uAThHKBtbSvXSeGwyHK5TKy2SwYhnHnfcxjk+zxeBCNRuH3+9HpdFCpVG7duN9WIklRFERRxMbGBiRJQqPRcEvtnHK723DKIimKmikrfnh46JpXpNNp15TCMAzX3ts0TdcIxbkpigKWZSEIAiRJgsfjwXA4dM+3iyQQCCAej0MQBGiahtFohHq9PtXfkqZpiKK4tPPbQyJzrZrGKYrC1taWa9n4Me/fv3f/SE79o9frBc9f2l1qmua+wUzTBMuy4HnevQmCAJ7n790EFYvFsZQ7z/N48eLFdD8ogbCmONF5x9nI4/Fgc3Pzmni3LOvWz5gTYbrr8+2IjKv14+PibNAtywJHM9CqfZSOS2gWG3jzW7+A0WgEj9+Lw8oxaI6Z6LXF/+49lN/fATx3x2+CwSAikchMA/WuQtM0stmsG6EDgKOjo5kuNOl0Gl6vF6enpzNfsKp/8jV8n0QgfX+1etkci0hd10FRFHRdx3A4XJrLzebmJgzDcLNZkUgEiUQCuq4/6hybcTB1C439Fspf1FD5aQOekHCZyfg8CSnlIyJjSXAch3A4jFAohOPjY5imeS2C77hnPoQkSYjFYuA4Ds1mE+12e+rPg1MW6vf73Z4PmqZhWRYURYGqqm6PkSM2ZFlGrVaba78fy7KQJAkMw7iui+OUXFIUhXA4jHg8DkVRUKvV5i48QqEQ4vE4TNNEo9FAv993BY9jY2tZltun5gRPer3ejewFx3GIRqMIhUJzFZ/T8N3vfnf9m8YZhsHu7i44jrvzMTzPu7/kqxa1wOUbKBgMIp1OTz2YbzAYjJ0mvDoIzXmDRKPRe9f//7P33sGRJfh93+eFfv0659zIwGDipgt7Qcc7kndHHo/UiTySok2yKAZTsilLskpZLsmmq2zTViItFVVm2VUsskSfaDOJ5JEixaS72wu8vc07M0iD1EDnnF/wHz3vDTAIA8wAM9jZ/lShdhbo8NDofu8Xv98xY97pWIGwNWN8WGJxVEJfKpUolUpIkkQikSAcDmMYBrVa7ZHHh6wWsyzLdH9tGc/agNQ//ibS751FcSjc/Ldf45mf+CYa/6FI8IPJ0z34CXY4Go0G6XQaSZLOZMfAMIx9uuexWIyZmRk2NjZwuVy2Xv1R7PVIEQTBTl7W1tbOJOgemf89Ocf0oygWi9Trdfs9qCgKLpeLeDyOqqoMh0Pa7bY9lneehEIhnE4nW1tbwKibVS6XqdVqF+Y6ofU18m+V2X4lT/6tEv6Ul/SzcRa/bRbPY+xejTma4XBIoVBA13UuXbqEYRhomsZwOETTNNxuN/l8/tDOgSAIBINBotEohmFQKpXOZO/OKjzdj1UIdjqduN1uwuEwoiiyvb19Lh09TdOO7YIfhbXPVK1WCYVCti/Io7w2VoHb6iANBgNyudy+5MFKwqzxMmtEbTgcEggE6PV6JJNJe8St1Wrh9/vxeDxUq9Vzlb89C94RHQ5VVZmdnT0QqFgfKtM07aqopmlsbW0d++Z1Op32bPdJMQyDmzdvnupivNefw0IURXw+H4lE4lTPP2bM08797uTnZRyo/8JNzC8XwOMg+GPPEPv0VdwBL8P+kOXfeB3jxul8ANSff5vef7UID9j7iMfjhMNharUahULhzKrp1viAKIrIskyj0bCDDKvQYlX4RFHE5Rr5Y7TbbarVKqZpkkqluH379pm93rU/2WaY7xL7y/Mnur0klYmFfhFZqlKuf5Zu77kzOY7ToqoqMzMz3L59+1yXz2VZZmFhgbW1tXMf2Tgtg86Q3bvytcXbVcLTAdLPxUk9E39qPTKeFg47ZzqdTmZmZsjlcvbIjTXRYY0cWaOeYw7HihkbjYb9ebWUuiwjwr3nC5fLhdfrtSdsHA6HfVvLiPY05pjZbBZN0+4pLt7dvfJ6vfZ5/KJ4kLwjOxySJNlKGjAyFznuRZVlmWw2i9frZXp6Gk3TKJVKtFqtA9rh/X6ffD7PxMTEiY7FMAzu3Llz6j/oYZrZhmFQr9cRBIFsNnuqxxsz5mlGVdV9F8zzktI1tzvgdYBmUPs/X6FWqFL5oxzpn/kgwbkoySsTaLpmj2BaS4RHdTeFE8riFgoFKpUK8Xicubk5Njc3DwSboijidrsRBIFWq/XA1yAYDNqGS7VaDUyDQOcb6Eae8MSH6HuuUywW7RlmwzDsdrvP5yMcDqOqqj16cFZSm3LISffm4Yuvh5GI/FtU500MQyUV/VnWc/8S3Qg++I5njNXlOG+lK13X6XQ6JBIJ1tfXz/W5TkK33mfntdHSd+VOnfhimMzzCd7zw9dR3Bej2zLmwRx2vrBEFJLJpO2BY3WMH5cb/Tudfr/PysqKPSZmvc6iKNoJhTWiaS2gWwqE1gL6w17PfD4fbrd7326ktXv1TpMBv3AJh9frJZVK4XQ6aTabJzYMs6TmLPMYWZZJJu+NRgwGA2q1GoPBAFEUCYfDJzqebrd7ZmMGe4nH40eOnIwZ8zRhGIatGGKZ8um6bncArTazy+Wy51TPC7OrQXs4UpUyQfjeGcTnIshvVOgsVSjubvHar3yV2f/6WRwOh+1fEIlEaLVaB88Dxt2LyAl9ODRNI5fLEQgEmJ2dpVarUSwW7QQgnU7T7/ftMadqtUqn00GWZTvxsVrt1mu2t6Mb6L5KtPVnGIID89YSpdBn6Smjwsb9r6tVrZudnaXRaJxpkC0HnWi1kwczDjmPrnsxTSeiXEGS6o894XA6nSSTyTPbszkOQRBQFOWJmhW2S52RstSrBRo7LZLXYsx8JMsHfvLd6ZHxNGKdRxRFYWVlBVmWbXPRMadD1/VDVREtrOTDEvE4CyRJIp1Os7m5+VQ40V+os4q10GdV6x7mBe71erTbbVtG0kJRlEMlbo+jWCw+0Kr9Ybl9+zYAly9ffuidkjFj3gmsrq4emkRYHUBN085N2vEAqoT0o5cwM27MX1xGfDaMEHbimPUzXG0S+FiKwm/fobVdR4m56PV6xGIxtre3Dy86GCbmQ5j+ybJsa+vPzc3R7/dxOBz73L0VRSEUChEOh9E0jUgkgqIoNBoN+v0+9Xqdra2tfYmCc1jAQEIX3ch6A0WvYiizxONxFEWh0+nQarVst+lEImHvzpwFsiwjiiJa6J753/1otT7DnQ7DUo/BdovWF3dx/P2/wMQHfxvMNr3eIoNh5kyO5zRYMsCPo+qbyWRotVrn5lNzGKZp0txtk3slT+7VAt1an9Qzo32M2KXw2CPjKcEambSkuDVNY21tbd8+QDQaPbPP/JgR1kL8WZLNZu2i09PAhYl0E4kEjUbjofSXLQRBYHJy8swkaR+HtFitVhub1Yx5qpGk06k+nSeCIMDVEAJgzPkwVxoIERXHrI/uS3k8n8wS+mCSyp9uk/zeeZLJJI1G42g/hFOa/llVdFVVWV1dtRc+LYO9vUnNYDDYV/AQBIGrV68ea8zWVBfx9m7hpIPpcONKPksqOWOrzrjdbtttut/v43Q60TQNh8Nx6mVDS4JWFEUikYg9sgUwyAzQPlQ+1Pxv+3/6OoONJqYOWrGLoIi0zE+xtfsBRLFNvz/Pk7g0NZtN0um07fh+Xrjdbnw+36Hy0WeNaZpU1xt3PTLy6EODzHNxbnx2kehcCOEhkuUxFxev10s2m6XT6TAcDqnVageWpre2tshkMvh8PnK53His6oISDoeRJOmJdkHPmguRcCQSCQqFwiO1jB5V1/9+HtcCzjjhGPO043Q6L+RCorAQwPhaEd4fR5nx0/iVFUzDJPRNaVb/l68T+/Q0Pp/veHlS/WT7GxZOpxNJkvYtaBuGcaIRB9M06fV6ZLNZdnZ2DiQIqUCEgCOLMHuNYWsL3T2JYHr2dU3a7TbFYtHeFen3+4TDYebm5myXY0uX3vJN0XV9n9qfNWoWjUaRJAnDMHC5XNTrdba3t4GRDPHMZ64TvppA03Wq1aqtyR/+y3Ns/5OvYQx1pJBC9Acv4ZzwMRg+ee8iS1L0PBOOTqdDsVhkdnaWjY2NUy2PngRDNyiv1OxxKVmRSD8f530/+gzBCd9YvvYpRhRF2u32PgW7+xkMBqytrREKhZiZmbFN8trt9rnvLo05OfF4/IH7XX6/H6/XS71ev5DX2Pt54gmHNUL1qJxlsgHYTqznjSWD9iBH5TFj3qkEg8GLudw27YXfXMfs6Yg+x8gdO9fBkfXguRyi/WoFnr/X6XS5XMRiMdrtti1GcZIOhxWg67puj06dtrji840CRVmW6XQ6zM3N2fswTsmBKshIgkD/F/8zueejdEMhqDeBwzszhmHQarXs847lAVEsFpEkCVVV7c6U0+kkkUjQ7/ftEY3BYGAnL9b9JycnyWazbG1t0Wg0ePtnXyP87ZMEbsRJJBLMzs7y9hdeo/nHORwpN3qljxxVCX3X9Klei7PC6vY4HA5b677b7T6WC3exWKTb7TI1NUW5XGY4HCKKou2Yflr0oUHhVpmdVwvsvFbEFVZJPxvnw3/9BfxJ7zn8BmMuIlYB4CRUq1WazSaBQIBgMEgmk7Hff9bY5ZgnR61WI5FIMBwObcNCa+TTNE0ikYi9H5lMJpEk6bHFrQ/LE0s4BEHA6/VSLpdRVfWRZ9/K5TKxWOyMjm6kkX5e+xv3s729zdzc3GN5rjFjHjdut5vr16/T6/Xsi9x5VpBPiqBIMOGBtSZcCeKY8zNcazL5vnn8P+GF4ijRuHr1qp0gFAoFnE4nkUgEgF6rg+O/maDsHHUErIuAddG3Ro76/b4tWytJkm2CdaLjFASmpqbQdZ1Go8HOzg75fB6v14trAOI3cvRKDdiuYXo6BBxfJNjTqDg+Rl9KH/m4Ho+HiYkJKpUKq6urx45W+P1+HA7HkeNcpmmysbHB7Ows4XCYSqWCHHIyrPYYDAYUC0UmkhlKv3AL37ekiP/UNbb+wVcIfc8MovvxX4YymQwej4dCoUC320XXdbuj87hotVqsrq4Si8Vsc9pYLHZPcewBaH2N3TdL5F4tkH+rRCDtG3lkfPssnsjYI+PdiCiKp+pSaJq2L0i15FwzmcyFD16fdvL5PPF4nMFgQLlctp3QrWLQzs6OnRQWi0XbT8jv97O5ufnE3MaP44kkHFZFqdlskslk7Aqorut4vV4EQWBnZ+dUizL1ev1MEw5Zlrl8+bJ9ETYMA9M07S/DMOyKo+XqaRiGLVW296IsCALT09NsbGwcejK4KCZPY8acJ6qqkkqlSKVSwKi7t7Gx8USTD2E+gLlcR7gSxDHrx9zq2slE9c4u3/jNr+C+HLTlevcGpG63m5mZGXZ++yuEv/cZXC4XuVwOTdNsd91isbgvkHe73TidzlONbJqmSavVolar2YGoNYbV6muEK1W863V0p4hr8c+QhS6mLpEy/h3rrr+BKRz0+7EMGh/kWWRx0pGvzc1NZmdnRxfJoIJWHTAsdin9+k08Pyjzzb/8X7CyuoKmaUz+7x9EUJ/Mfk8gEDi1r9J5MBgM7DE0GBXOZmZmjhyzG7QH7LxeIvfqyCMjMhsk/WycZz67iOofe2Q8raiqSiaTsSvcllP33nOn2+0mGo0+kmllt9ul2+1Sq9Xsz/GR+2tjzhXTNA8UvY87V3e7XdbX14nFYrbs+kVbNn/sCYdV2RsOh7a77a1bt+xkIZ/PI0kSExMT5HK5E7/ZLcWXdrtNPp+3pXFPys7ODh6PB7/fb39PluVTPYb1/HsvYpaRlGUScxjp9NFVyDFjnlZUVeXSpUsUCoUnthgnzPsx/vPuaHfjhTQTn5lgd3d35LhbKFD74g5Ti88eWvlWVRVd05F9LnZ3d5EkyfbO8Pv9uFwugsGgvZi9urpKp9M59UXAMo86rOptOGXaUwHk5gCpryN4GmiEABHZbCCZHbRDEo50Om071Z4lg8GA9fV1pqamaN0osfnLb9D6kxzBb5+g5G6itlsEAgHK5TKi68lN9JbL5SeebBzGYDDgzp07zM7O0u12GQ6HI4+Mu0vf1Y0G8csRJl9M874ffQZZuTiCDGPOj0gkQrvdptfr4XQ67fOKtW80GAxwu90nLiA8iOFwyMbGBlNTUye2JhhzMbDGNScnJ9nY2LhQScdjP+NbJ3kr2VhfX8c0zQNZuXWRPQ3W7DCMpDgvXbp0ovvt7OxQLpfp9Xr7Eo7TomnavmpmNBq1vUCOSpy8Xu9YFnfMuxqrDXzscvY5IQQV8MqEJS/xS1ne/J//CL4pjBxz4X8uSuE3VulttVCzB+fgK5UKg2KLyGwETyKE2+3GNE17fKparVIqlej3+6RSKSYnJ2m1Wvbe1lEFCMuIz+qSJBIJRFFEkqQD9xF7Gv6lKqUPZTFlkWj7fXh4BYCuNIsmBA48viWRe15+E91ul7U3l7n0sets/MuXSf6j51CSbmAU6E9PT9v/fpwEg0F0Xafb7T62cdmHod/vgwm3/tMaG1/L0cq3SV6LMvfRCeLXYkh3He0VRbHVzS7CiOKY80EURfx+P7dv3z7w+RcEAafTidPpPFRI4lHodruUy2Uikci+LtyYJ4+qqvZ1Yu+XJEm2Wa01lXOReCKRrtvtxu12s7y8fKYvyN6gfjAY8NZbb6Eoiu1gbP0B/H4/weDIVGrvnOKjzrwpisLVq1cP/ZnH4yGZTFKr1exqgTXWMGbMux1VVZmfn38ySce8n2A4xO7uLo6Mh85qEznmQpBFQh9JU/mTbdI/tHjgeBVFob9dJ/8Ht3H8yA2y2Sy3bt3C5XLR7/f3nU+2trYIBAKoqorf70dVVQzDsKuTw0EfZeNreLoFSF2lF76GCfaYps/nY2Ji1H2xq42mSfCNIu1JP4Yp4P5P2wyXM+T+xnUENLriFNynSBQKhQgEAqyurp7Lxcg0TdpfLbDx62skfj5O4INplKSbSCSCw+GgUqmQz+fJZDLUarV9AZQgCKeeQT8MQRDsx7KCNcto9ebNm4/6K54LpmnSyLXIvVqgudnmyr+4wtyNaVJXY6hhxZavFUWRUChELBbbV6gyDINOp2ObacqyzK1bty5cwDHm9ASDQVqt1qGfC0u57rw6EC6Xa2wSeEEQBIFgMGjL5bbbbTRNG3VBu100TUPXdRRFQVEU6vX6mSvgPSpPJOEIhUJUKpUzPxmapmnbysM9I5b7P4yyLBMMBqnX6/s6K/1+n0aj8UhdjqMQRZFoNDqWwB0z5ghUVWVubo6VlZXH+rzCQgBhYJDOpon/5Rg7X1jGGkoIfjjFyk9/Da01wB8P0ul0EEWR6elpOp0OajSO48VrdHs92xzwMHUXwzAO6OFb45a1Wg1P8S28m19GE2SM3SWKE3X06BzZbBav12s7gU9NTdHpdEbJ0UoZsT3EqGkEP7+FVOkzmPTSl6fxeDwE7nZELL8Mq2u8trZ2LvKXenNA+VeWGZZ6JP/6deSQE7M7ep54PE6/38fn89nqVw6HA13XkSSJxcVFe9z2rbfeOvI5rN+j2WweWHJXFIVUKnWkD5MoiszOztomaE8a0zSp3qnf9cgoYBgm6WfjzH58gtW1VWKLYRqNUdXS5/MRDAaP7IaLoojXu78Lp6rqhQs4xpyecDj8SHsZD4soing8Hra2th77c4/ZjyiKTE1N2Xsdx43NXeTxtyeyw+H3+9nd3T2Xx7eSDUsi9/453VAohM/nO9JFfGNjA0VRmJ+fP1OZ3TFjxjwYl8vF7Owsq6urj+9J027Wfu7PML9nCnS49KHL1ActCoUCstfB5HdfZn5uATXkshfCm80m29vbiNtt5D8vMfjM1KmfVpIkBoMB1WoVqbiBouloDhWH2cMxbOELjhKcvcFGoVAgGo0yNzfHoOOgs2vgfnMbs68jP5/B/d1XSc2PJGyHwyGSJOF2u+l0OhQKBTqdzrkE2+1XSlT+/QreFxPEfvQyoiLhdKnUbhdZCL9Ir9fjzp07hz73XklzURS5evUq7XabdrttS//quo4oikxMTNBsNpmaGr3e3W6XarWKYRjMzs4+8Dif9PiqoRuUl2tsvzpy+3a4ZNLPxnn/jz9DIHvPI6M/6FMoFLh06dKpR4vHPD24XC4EQXgiErU+n49Op3Mhd53eTciyzPT0NK1W69zi5sfFYz/7HtZKP4pHcSg+6kNSrVYPVBrvR9M0DMMYJxxjxjwB3G73vk7leSOIAnrEAct1hBcidPMt3EkXly9fRhAEBrMDXvnZL+D5VAK3z42u6/dm5vWHD9673S6yLONyuWgFZgg01pC1DoakEF58P2o4fGDPwjRNioUC/NFNlPfO4vqeZ3D9ly/CQMfoaxiqxPLy8r7XzuFwMDExQSgUOvPARe8MqfzqKv07TWI/cQV19l532DRNou/LEolGWFo5fHw2k8kc8CASRRGfz2d3Kiy/j1arxdLSkn1udzqduFwustksd+7ceeA5ezAYsLS09Ni7G/pQp3CrQu6VPDuvFfFEXaSfTfCR//a9+JKeI++XzWYfKdk4Dwfpw/aIxpwf4XD4gfHKeeHz+cYKVU8IQRBwuVx4PB57IqhUKj3pw3pkHlvCYWnXOxyOE7XoarUaU1NTaJr22EzDrAXN8djTmDFPlsddVRMWAhivlhHfE6Vyc4dYaJql3JLtzVBeL6C9LCC8P3HfgZ7OaRzuBcqNRoNutzuSCY7GcM5fwWyX6ChB3NE0N2/exDQM/PrX8eqv0xMnqcgfxXOnhdHts92rIX19B8+f5hCmgkhfzxP6X7+TcDi8T/VrOByytrbG4uKivWR8FnTfqlD6d8u4n42Q/gfPIzrvFYhM06TZbPKBf/rtlDcKeDwevF4vnU6Her2OaZpMTEwQCBxcarcwDIPl5eV9C9F73xeWPGi73WY4HPL222/jcrnQdd32QkkkEng8Hur1uu10/jgY9jTyb5bYfiVP4WaZQGbkkXH5U3NHemSoqmoHGacRE7HMv1qtFoZh2Pd/1M+QKIq4XC57jM3tHi3+t9ttSqXShVK/edpwOp2Ew2F8Pt8Tq2o3m03i8Tj1en2cZD4GVFXF6/Xi8Xhwu922uer29vZTY8J47glHIBAgnU6j6zr1ep2NjY0TnfR7vR5ra2tMTU0hiuK5Z3fRaJR4PD7uaowZcwF47G38GR/89gbmQKfT7eEOeZBqkt0pCH8sQ/F31gm8L26PvQCjDscJEw5ZlpmdnbWr1uvr6+TzedShgSyIVMt12nE/qmlS3tzENE1S/gr+6n9EFxUC4i6R4ARc/RANp4mv28Vxs0j/22bRE260eS+N7Q3m5ucZDof7KqOmaZLL5UgmkwiCwO7u7kNXL42eRvU31ui+VSX6w5dwLQYPvV0ul6P65zsk3zuJIrtotVr4/X50XbeDqeOwFuofhKXMY5rmgSA4l8ud8Ld6dPqtAbuvF9l+pUBpuUpkLkjmuTjPff8VnL7jOxWpVMr2fzkNy8vLB2a26/X6qR8HRp2wvcmF0+mk2+3S6XSoVCpsbW1hGIbtSq1pGqVSaVwFf0SsLufeL9M0qVarLC8vP7Fgv16v29Llg8GAfr9/T+RiOGQ4HNrTIGOOZq9AyFE/TyaTKIpCo9GwP2tPY5J3ooRDFEWCwSChUGhf1UUQHnyhFUWR9fX1h8rQBoMBq6urtuqGz+ezVacso73d3d2HWoyzFikDgQDBYHCcaIwZ8y5GUCVIu+FOi0t/6f28/fNfxPzmsP1z77Uw+f9vhe5qA/fcvaq8YALSyRIOURT3jch4PB5a9QbGQMPb6GPK4r4g2+FwEHQPoSYgqSGGnTz67Vdphq8hZkLEND/yD76Icdc8T5qass+Fh50TG40GjUaDYDBIJBJ5qECxt1Sn9Mu3URcCpP/BC8e6hJumydbLa2y9skb4U6Odi3K5bDunPwhVVbl69SqNRoNarUa73T5xh0IQBDweDx6P51wlcDvVHjuvFci9WqB21yNj4r1J3vsj11HcJzN0jcfjD5VswNmNTc3PzyPLMp1Oh3a7baspHvZ6W2PJlvpXMpmkVCpRq9UuxDL+OwGPx0MkErF3NCzDvUqlYisOXQTy+TylUslWPnI6nXi9Xtvs2OFwYJomw+GQZrNJqVR6KgPlh8Xv95NOpzEMA1mWbRGjbrfLYDAgHA7jdrspFApPbHTucfLAhMPj8ZDJZOh2u+zu7u47wZ3k5GK5cj8suq7bDuSWhGy/32dra+vUiYbT6SQQCBAKhcbu3mPGXFCe1AVLWPBjLjfo9XuYbQ2jq9nmdIIgEP5YhsqfbO9LONANzFN0OPYS6hkY+SZdl4NYrYegOOgkFTvhUBQFw3ONgeZAGO4gdg1axVmK8QHOP3gZwDFvAAAgAElEQVSb9m6b1icm7A6L0+m05VIdDseRaiXNZpNUKkU8HqdarRKJRNB1nVKpdOQ53Rjq1H5rnfbLRSI/MI/7xskCZDmkordHHQhL9eY0RqdWsSsYDB5azbdQFIVQKITH40FV1X0FpEAgwNra2pl5FLQK7ZGy1KsFWoUOyesx5j46SfxK5NRGfLFYjHg8fuLbW6NTVgB4VgG+oii8/fbbp3o8K4H1eDz2hEC5XKZSqYyr3g9AlmVUVWV1dfVMvTPOA8u75qh4yyqkhEIhFhYW7H2Dd/t7wOl0kk6nbeNEURTtcVq3200oFKLRaLC1tfWuSdSPTTgcDgfZbJbt7e0zd6Q9KQ6Hg2Qyac/6NhoNNjY2TnRfQRDw+/1Eo1FcrsPnZseMGXOxeFKyfsJ8AOPLy9QbdZKfWGB99Q7OKyH754EXE1Rf2kVrDZG9dwsWBqfe4bAQE2Eiw2mMl2+BLIFpMpHJsHpXzandaNJra7gv/Qz5W1/A+VaP0nuuIe92cd6u0fz01L7ntmS9XS7Xsd0LXddZXl4mFouxsLBgX+zq9fqhbf/+epPSL91GSbtJ/8MXkLwnL9bIQQVEwfZZeRQOS0S9Xi/pdPrY5WpFUVhcXLQNXk+LaZrUt1v20ne/NSD1TIyr3zlPdD6EKD98d9zaizgp9xf9LgKWopiqqkSjUS5dukS5XKZYLD7pQ7uw1Ot1YrEYqqpe+ITjQVj2Azs7O5RKJeLxuP0esNzR343JRzabpVAo2NczwzCOTdzeDRybcAiCsE8V5HGiqirpdPrACfkkJ1tFUYjH47a535gxY945PKmASgg7QRFpLOVJvHidxYyfrjSwR3IkVWbmbz2HVu3D3aDb8DoQlJMFnNYsfDg8GtUSHDJi0IeZjiLMpCFfQXW5cDqd9Ho9MqslHJ0BLWGe2MwnWK+9jWmC+ws7dD6cxDxknKnb7WIYBplMhlwud2TlbDgcksvl2NnZwefzkc1mD6gCmppB7fc3aX1hh/D3zuF5T+zga3bX6djlctmdBctdHUAOq4hO+YBHxMOwuLhoj2243W5isdipRmFTqRSpVIp+v8/Ozs6xRTTTNKms3fXIeDWPaTDax/iBK4SnA7YR36Oyvr7OzMwMHs/RalV78Xg85/L5ME0TQRAeqdLa6/XY2tqyVdEcDsdj3aF5p5HP54nH40/VDsxwOGR7extFUYhEIiSTSZxOJ7u7u++KkaG91Go1wuEwtVrtXZlwHYZw3Anm2rVr5uc+97nHdjDWmzQUCh15IalUKkeexCxzlJOevMeMGXM6LCO589x5WlpaemJJh/GH2+CU0OIqrpLAwo+/aLtTq6pK0hPnK3/n9/jIL3yGSqNK5c4uhksE6eSvh9U59ng86K8tI0QCiJlRMG/qBv2vvsmWOEAwTOIbVTp9E99HnsGMeSn90lcY+iR6zx2tpCcIAvPz8w8Mqi2mp6cZDoe43W4ajQaSJNHarZP7lbfotXsEPzuNHHDuu4/H4yEWi9lqKt1ul16vhyAIRKNR2u02lUqFTr2FruksXFu8kF3mQqFgK3oZmkFppUrulQK51wooLgfp5+Kkn43v88g4D+bm5k78+jSbTXK53JlWxq9cucKtW7fOLDASRZHJyUk0TRsbxx3D7OwspVLpqXbzVlWVqakpbt++/a4ZHbLIZrP0+/13Vbfvxo0bXzdN872H/eyJuiBZWsPWjO5JgpijpAJDoRCpVGq8/D1mzDlgBQ57A1hrdldRlEODMUVRbIm/k34u19fXn+jIiDDvx/jjHeT3RtGMLuW76nihUMjeIQtdi7P7J3eY/I5F/Le7DPMd8lccJ1JUgnsytS6HwmStg3xt5t4PRQGHz83kao2dkJOdmQihr+1wp5on2eqT+cEPsV3J0zsmkXC5XPYC8Eno9/sYhkG5XEYSJZpvFHFoEjf+1jfhCnnsyvfefTzDMCgUCqyvrx8IIqwuTjweR52c5M5rK8jaxTwvh4Nhaqstqp0y7piKPtDJXE1x7Tsu4fA9vA/UaVldXeXatWsnuq3P52NhYeFYR/bTYnU4zgrDMFhfX2diYoLJyUmKxSKKouBwOFAUBVkeOaiLonjgq9vtksvlLrRj8llRKBRIJpNPdcJhLUlbfhLvFqzzsKIo76qE4zieWMJxmorOXrxeL36/n8FgYFdbJycnD5hHjRkz5tHRNI3t7e1D2/7W7O5xgcHeE+1JRjbC4fAjj3Y8EhMeiDoRnRJDXUcq6ly/cX3fTab/4hXe+NdfZuJTlzB1E0mWiUQi+xzBT8Kg06UYVEjvGWUSBAHxygxmuU6y1aec75D/yCTC0KDy9RUaikZyKoOv0znQ6XU6nbZZ3GEKQ4qiHJoUlUolpqenqe1WeO2n/xBBFIj+0CXqO+uws+e4RNH+73HJlWEYlEolW8q8+bl14j8ZxeFzHnmfx0m/M+DOn2+y/NId1l/eIj4XZe6DUwSng0jPSkxPT9sBca/Xs13bLRlQ699nOSZx2ve7KIpEIpGH2kl5XJimycbGBul0mlQqxXA4ZDAY0Ov1GA6H+/xSrC/TNAkEAqP3Y61GoVB4ouMoHo8HTdPOrQjSarXQdZ1gMEitVjuX57gIFItFJicnqVarT32XQ5Ik29C0VCq960bJjuOJJBxTU1MP3V63WrVjxow5XzY3Nx9a0/8wTnKhcblc+P1+dnZ2zvwib/kMWPKEVtFib0AjSCLSR1MEazJ6281gqQ43MvseJ3QtjuSU2frqGmHdAFkgFAodmnB4twrE3ljFlER2X1ikFxmJXwiGQajQpJQOEO719hVMzPUdhHAASdSI9huEkxOUPv86rWfj9IZdVlZWmJmZIZlMks/nMU0TSZKYmZkhn89Tr9fJZDIsLCxQr9cplUqk02m8Xi/NZpPd3d19spuDwYCbv/kyz3z2RdLftYgx5zxY7TYHhMX/F7d0i5b+DGU+AxzfARAEgcXFRd5QC/RLHXyz4WNvf5506l1Wv7rB8pfW2H5zl8y1JPMfmuGb/9qHcAfuXYs0TWNlZYXhcIgkSaiqalfmPR4PDofDlgTtdrvUajUajcaZmOydlkQiQaVSObMA7rxGxk67x1Gr1Wg2myQSCRYWFtjd3T3T89BJiEajRCIRNE2zd5uazSbNZtOWZ5ZlGVEU7dff6gLu/XoQLpcLwzDsWf+nlW63S7PZZGpq6tCu6NOCx+Mhm81SrVbZvOulNOYejz3hSKVSDzR8GjNmzJPFMIzHfpEH2N7eJpFI2IaflgJOu922ExCHw4GqqrRarQee0OPxOIFAAKfz+Oq6pmn2HoLSaNN9s4D7uRSlP1o9cNtOp4P3+1LUPR2cVfDIqj1etrfyLw414q8tozskBMMg+fIt7nz8fSAIeBp9dFkEQWB9fZ2FhYVR8NLuYmwXEbIpzNdWkL/7vXR+9VWisxmyz8/S6/VYX1+3x1UuXbpEpVJhOBzS6XTsatrm5iZOp5NoNMqVK1fQNI2lpSWi0Sizs7Ps7u7SaDTQKj0av73Ji//w28itbmHOqxwWdvrlL+CXX0Iz/QTlP6VvTNLSDx3TtclkMiP5z5iHXunxu1I3Sy2WX7rDykvrFFZKTL2Q5co3L/Cpv/stON2Hq1rJsszCwoJtaGf5UtyPIAj4fD6CwSCpVIpWq2UHytbPTxNsWN3C03TqRVFkenqafD5Pt9t9pODmpPe1gu/zlq7WdZ1cLofL5WJmZsbuBJwFiqLgdrtthSjrc28ljaIoEovFWF1dtc85TqcTn89HLBZjYmLCTkSsKQsrWbP+LYoihmHYsv7WV7lctkcdM5kMbrebarX6VCcbFrlcjmw2y9TUFDs7O/teN9M00TTtwviPnAZBEOzJG6/Xy9bW1lPjDH7WPPaE42ENjsaMGfP4sAQY1tfXz+05pLaG/1YdUxaoXw5i3lV7yufz5PN5uyNhmWRJkkS328XlctHv98lkMtRqNSqVyoERH4fDgWEYJ/Y4sIxFfT4fustP9XNvEvrsNe78m6/um28vl8vs7Owg+hw03yjjUt14AiMlvdnZWZaWlu4FRoYJpokpiCAaiNrd75smnnqXSmJUeBkOh9y+fZuZmRnkWxsI6TjGl1aQPnqZwZfXEWQR518Y7Xmoqsri4iLlcpnNzU3ku+NcsVhs3/ia1+tlenqaVqtFu90ml8uhaZrtMD4zM0NxaYev/W+/wzP/9Fto6R2q/SPmyE0TmTomIiYKI6/D45fRJUmyVQKdUTf94uO5AFe3ayy/dIflL92hvttk5v2TPP+Z60w9n0FWTna5E0WReDxOPB7HMAxyudyBgNA0TduHQhRFAoGAbeAnSRJOp9OWwex0OjSbzQfuJKysrLCwsHCsxO/9eDweZmdngdGsfLlcfugRjgd1OEKhEIlEAkEQaDabVKvVcw+sut0ugiCc2ViVtVvUbrfpdrsoikIgEEBVVVv8wPq77e2w9vt9+v0+pVIJSZKO9bmxEEURSZLsL0VRmJiYoFqt2gaYxWLxXZFsWGxtbZFOp5mYmNjXGRIEAYfDgSiK9tji3vFF0zT3dRcdDgeCINju5/1+f19R6ixxOp1IkmQnSNaXLI/U9zweD71ej0ajwe7u7tj48Bie6NL4mDFjLi4+nw9VVW3TIp/PR7PZPJuLv26S+d0tHI2R0o5rp8vOt+0fXRoOh9TrdbvTIssybrfbVuixzKZmZ2f3uXNLkoSmaSf267kfyetEyfjRi21kv5Pueh33dBDDMOyxKUESEESBVqeLEBLs41tcXGR1dXVUMXU6qM5PEFreBAQKz86BIKC2+hiSyFC952ehaRrLt26TGZp4NgyEqSh6V2fw+g7en/jAgWAwEokQiUTo9Xp2EmEFf6qqks1mabfb6Lp+YKm/V+0wjA8YFru8519/mthkYl/QEy42cXX6CIaJaJjIQ51W9BpG9mvIQgPdDNLSnzv2NbRm8kVRRI26qbyy+1B/iwdhmibFtTLLL62z/KU1+q0+cx+Y5sM/8j4y15JI8qMtfouiSDabRRTFIxdeDcOgWq1Sr9cJBoP2kqwoirjdbtxuN9PT07YB2HG/y/LyMpcuXTpSHOU4VFUlk8nQbDbtSrE1FqaqKrIsU6/XDz2G4zocsiyTTqdxOBy2gWIwGCSZTCJJEtVqlUqlci6BltUpOIvRFEVRiMVirK+vH/BC2Cvv7Ha7j92NsboVD8L6DFhqYu12m2azSTKZ5NKlSwiCcGKhiaeJ40bsrEDeSi6sL0EQ0DSNVqtlJyOmadru56qqEovFGAwGVCoVGo3GQ71nrGuM9T5QVdXuvNw/LmdNAWxvb4+TjBPy2BOOQqFApVJBEAR7jGDMmDEXE13X7cqtpmm4XC52dx89eJS7GnJLY+hzgGHi2nmwGZKmafvUXAaDkUdGoVDA7XbbF3cr2HI4Tm5Qdz/uZ5J0XtvFdzVG862CnXDsxTXtw9hsow3uXWxEUWR+fp7t7W2q1SrLmpvtN2Se++9ewFBGx+Otd2kF9++wibpBoNxiO+LFX23gnZ1k8HtvIX/bLLiOPk2rqsr09DSGYbC7u0ulUiEej9vnWRglJ3Nzc9RqNdyKC7On06m0kOe86IZOrVbD7/fT6/VG41myhH+gg2kiGga6LFEKzkLvH+EQSwyNOAb3jt/lctndIbhXDd7d3SWdTqPGPPRLj1YJ1zSNWq1Gp9PBMAxaxTbVrTq1nSaCKBBM+fjATzzP3DPTB/xEzoJ4PP5AhR3DMPbdRtd1e+6/1+sxOTlJoVA4dufDMAyWlpZYXFx8qGujlWzE43FbXt4SdtB13Zaq3d3dPaBidn9Sq6oqoVCIQCBApVLZN5NeqVSoVCqoqko8HieRSJyL54YkSZimab8/TxugC8JovyocDtuPlU6nWVlZ2Xc70zTt1+k8l3w1TaNYLDIYDIhEIuPRm/swTdPuapyEwWCwTznR7/cTDodJJpN29/tBjyWKIuFwmHA4jCiKdDodut0uxWLRPt+MORueSMKx99/JZPJxH8KYMWNOiFX1W1paArDdogVBIBAIIEmSXfk/zWiA5pYZBhwo1QGYUIo6+N1/9WVm3pPCF3bjCat4Qy4c6oNPUaZpHnrhfpSqqPtGgt1/8xW83zpH/Rs7JL7jkq1cZFWzJLcDIdejtLaD/xP7XbQzmQzd9S6YAplPz9nJhqOvIQ91up79YzOBchvTgPBXc1Tek6K5tYP5QgBTq1O41XpgACqKIul0GkEQaDQa+wKzcrlMKpVC1R187b//PK5vSeCc8e+7f6lUYn5+nlqpjGAaiIaBIYroskQ+FcSQJcBD37jncWQZBlqJ4M7ODoZh4HQ6cTqdNBoN0uk0zqibXvH0OxxW5dyar9d6OvXtJo2dFpIs4om5ST0XxekbdXAGdHn77bfx+XykUqlTjSY9CFmWH0k9rV6v2yN+2WyWbrdLpVI5NLhVFIW1tTVmZmZOnXR0u10mJiaQJIm1tTV0Xcfj8diJeqFQwO/3Mzk5ua/jsvf3EgSB6elpHA7HKGleXj5ytt4a44rFDppCngW6rtNqtexgcHX14E7VUQSDQeLxuG30GAqFUFWVzc3NcznW47BGtwKBAKIoUq/X9+2IjDkbrDFHRVEIh8PMz88f+AxZyov9fp9IJEIwGKTZbLKxsfGukGI+D1RVxe/3P1D+94mOVI2Xx8eMudgMBoN9exybm5v2YqsVsLhcLqampk6n1iMKbH8qi2+lgSkL3HELfP1n/5Sv/trbBBNeBFHA5VP4sZ//NLLj9BVrS7XpYXGkR+cmNexi++2iPWdsVXstorKHjS/cYVrTEfeM7+TfzPMHf+c/Ul2vcuXHrhC+FkEQBDy1Lq2AC/ZUk53dAc7OgH51yCDswvlaGak+oP0toxEzXdfRNO1EAXQqlaLdbrO2tmZ/z9jo0s92efUXv4j/h2cRlYOv56DfxxgMSVW7tIFCIkC01kWfyxBLx2i32wckLf1+P8Ph0B43siqJey/at27dIhwI0a90Tuz10Gw22draGo1QFDrsvFZk5c82cAWcpJ8dGfF540ebu1pdBYfDQSwWO7HH01FYniPhcNh2U7fUiUql0gP9TqxEpdlsIssyqVSKYrFIIpFAURTbyV4QBOLxOMFgkM3NTZaWlk49BRAOh1ldXbUr6KlUChj9Hay/jzVuMjU1xerq6oEKsGmaOJ1O+3EexGAwONPkbi+GYbC1tYUgCFy+fNkesToOn89HIpFA13W2trbo9/vMzMzQ6/VYWVl5rMpBe13XG40G29vbB8a5xpw9g8GA3d3dQ7vxHo+HTCZjjwNaqnRjHg6ry97tdu2C5FE8loTDmsuzpOS8Xi/BYHDsnTFmzAUnFArZARFgK0Ydht/vP1WXw3BJ1K+HAAgD3/43X+SPfuHrtCpdZEXivX9p8aGSjWAwSDqdfqQgUxAE3DcSaLtNTBMGhTbOhJdkMomu69TrdRRFwRt04wy7yb+0Seoj0wA0dhr8xl/7NYadAaIksPMHOd73A++nJTRoht3o0p6g2zAJFlt0TBFne0gz7MH9RpHmd07tS0pu376Nx+MZdSoecN60quZGT6Py62vIbeBjN/DetyMDIIkiznafqDIakXK//waKYYBp4lJVmq0WrVYLv99PLBajWq3aC54ej4dSqUQsFjsyCBwOh+RLBYJ/6xKby+s4vM59M9qKotgGcN1ul/W1dfr9Advf2OWNX7+NL+Ul/Wycj/7t9+MOne56MRwOyeVy5HI5VFUlEAgQCoVOvB+haRq5XM7uDvh8vn3eEZZjvDXaZy0475099/l8+P1+e8m6Wq2iqirhcJi1tTUmJyfJZrNUKhUikVFSury8bHfRrJ2OkyLLMrIsMxgM9knPT01N7Qu2m80mhUKB6elp2u02siyTyWT2BeNer/dERm3WUu/ExAStVstOyKwdhbNYirZGnvx+vy1La83R7z3mRCKBz+cjn8/bimGWb4zH4yEUCtHv9wkEAvj9fnsR/DCfoUfBWizPZrPUajXbk2bMk6fdbrO0tHSmYgTvVpxOJ1NTU/Z50uv1Hnv7c0044vE44XD4oRbgxowZ8+SJxWIUCoUjq4JWd2N3d/eRA4vnv2OB1//jCpVcE1M3KKxWKW82iEz4H3hfq6iRyWQeeNI7Ke4bCWq/exvf1RjFN7ZRhBAOh8MegxgOhwx1ncRfmOLOb920Ew6Hy8G177nON375GwiiSL/ep5vrcmkuQHXYpOKS7MVTwTAYiCKulTrVyxHc/3mX9scymM6DiVa73WZ5eRlZlolGo/aYyf30+32G5R75n3sd9VIA/w/OYoqj83GxWEQURZxOJ/FwBPfd10rXdbZ3d9A0zQ4W984vW4FyMBi0jdCq1SrBYJBqtfrApUnJLVPvNRH6B9WtTNPEGBqYhsmdl7aprNVJXInwrf/4Qzi9Z1M5t+bz8/m8vcwtSRL9fh9N09B13X6PWwHz/WNEhwWltVqNYDBojzEJgrDPJFBVVYrFIsPhkGg0akuqWonW2toaiUSCZDJpu3Pv/awNBgO2t7dtl/uTkM1mWVpawuO51wWy1M32jkdZfzfLld76vvX8p6nELy8vEw6H7V0q6ysYDBKJRA7sTDwMtVqNWCxGPB7fJz+bz+cpl8s4nU5CodB+pThG54ZyuYzD4cDv9xMKhajX66ysrOByuYjFYqRSKUqlErVa7aGCUI/HQzKZtBM+qytp+eCMuVic1CdlzOFYey/RaJSdnR27KLN3n+YwhONe9GvXrpmf+9znHvqgEonEuc12jhkz5vHw1ltvHXkR9vv9BAKBM5uLXv16jt/5Zy/xvf/jx2iVu/z5b95k8cOTPPvtc0j3dTui0Sg+nw+Xy3Uu4hPGQGfj7/4eykemKQlNxMWDiYxU7DMVTvLVn/sKz/29jxBcvHe++71/+HmmPjyFPjRI30jg38khvXAJwTOqPOvNDjuvv03DKSE3Bkhv19AjKoNrJzPIEwSBiYkJ/P57CZk+0Hj9j1+m/qUdXFdCuK+PHsvhcNgeSIZuoHe7DLcL7DZqdF2Ofd2U457v/pGqeDxu7wpYiKKIx+OxZUFFUWT7T5eRpzxI3tEuS6fSJfdqgdyrBZr5NqkbMZJXo8QWIziOWZK/qMiyzPz8/IFg1+FwkMlkcDqd9h6U1e23xjgc0jYOqUxvOI9hug99/Onp6VMl0ktLS/T7fWRZxuPx4PP5qFQqDxz/Og9mZmaoVCrn4uujKAqzs7Nsbm4Sj8ep1Wq02217/E1VVXuMr1Kp7OvW7sXn89kdmtOq21kCOPl8nna7/Y70khgz5iSIomgrJLZaLYrF4oE9pBs3bnzdNM1DTZrO7MxuVc28Xq+taz1mzJh3Nlal8nEx80KKH/rnnyR0d4ciczXKS//Pm/zWz3yRD//gDeIzoxEsWZbPXXBCVCTUxSiiKGB8uXJowmEIJrlhjanvusyd37rJc393lHAM2gMqKxU+/j98AtkpY+RKmD63nWyYpglLmyR1F2quSdXvoPf+OOYJluQtTNNkY2PDnqHtrNa49S++hPTpGKG/OIXolPfd1tQN+rUG7a+8StPnouVT4QgDPItAIEA0Gt03njMYDNA0jdXV1X2qYTC6DoRCIbuCaFV65Vkv5Zd2qQ6H5F7N0y51ST0TY+Hj08QXwweSyXcalmymKIr7Eo7hcEi73UZxOGj++xXkOR+Oy0HEu0mVx/kyicDPj26rR9iu/JNDk447d+6MdoA8HiYnJx+YYFtBgFVlfxImnhbFYpFkMnkuxzAYDOx9GKvrZu1rlEolW51rcXHx0PEwQRCIRCJEo1Eqlco+UZv78Xg8tu+CYRgMBgN7f6Xb7T7R13jMmJNg7SEmk0lKpdKpum+BQIBUKkWz2Tzxftf9PFLC4XA4WFxcfJSHGDNmzAWmXC4j6n2c/RKmINFT4yDcC3Y8Hs+ZapALgmAnGwDugMq3/OQL3Hl5hy/88ut88qfeRyDmO9Vc+6PgeTZJ+40CRq4LBnBfnCetNhk+62TqE4us/PvX6ZU7qBE3O6/kiF+NIztH1Wxzs4A4f28sxtwtY7b7GGsN/ItZnF/ZRP3R93Jr/fSjJ71Olze/9CrtX1hj4a++j3bW3N/aNkzS/hDObp/SnS3qqSCGdLKOUL1ex+Px7Es4FEVBURQSicS+hWcYJah7PQz6rQHtYoetL26z8vt3mPmuWa5/5hKR+SDiCY/hnYAkSciyjNPptJMPi0qlgtOhcOPHPsJrf+d3qP3cG8jTPpQrQVI/+fsYpgPD9OKQSqjKbTr9wz1OTHP0d71z545t9ncYF01qtdVqYZqm7eNz1pTLZfs95/F4kGXZ9suxsBTC9prFWY7i3W73yADKktWNRqO2zHE+n0cQBBRFsT0izkIqfMyY8yQWi5FIJOz/t3bwTkIymcTv9z/QS+hBPFLCMVaZGjPm6aZdWGdi49eRjB5g0lVT7KY+iSmOKtLhcJibN2+e6zEIgsDMe9JMPpukuFLjK790G9ff9DN9PX2uzwvgupag/Ktv4lkIM2xr4Nt/yjRVEUkQcHgU0h+dYeN3b3Hph59n68+3yLznboJRa4JpQng0+mQOhujLW1AYIMwm6H7hDu4feB7Z5yKbzbK9vX3kfPHMzAwej8c2uCrmi7S+msfzXJQX/tWnUCMe/P0+q6ur6LqOszMg0tXwXAqysb5B2+888ncNBAKHVmmLxSLh8MExr1gsZgeT3W53lFgZJuW1GrlXRuNSoiiQfi5OKODiAx+bIfX9V0760r+j0HWdnZ0dYrGYvSi8u5FDy3foFbpsi1UWvut5jPoQbaeDttFCW2kw+JEULuU2IAACmn74OJ0gCKiqisPhIBAIHHss93edLgKFQoFUKoWu6+c21iWKIslk0n6uUCi0z4Xa5/PR6XQQBAGfz4coimxtbR15POFw2E5INjc3x+pSY96RWB3wvbvU5XL5QFJ+FNPT05imycrKyiMXFx8p4brVBpwAACAASURBVIhGo4/05GPGjLm4aJqGb/tPkIwemuwG08Td3cbbXKIfe8ZW7XlcLquSLPKxz3yIbHaTX/tnf8il90/z8b/yAdQHjAU9CnJQxRH3gEeh1xwi3Zdw4JSQxdH3pr7rMl/++7/P7PdfJ/fyNje+/xkAjM0CwkT8XhdgeQuha2IKIv23Sjg/MoucGQWRwWCQYDBIPp8/oGluLTMDyJLM4Atlmn+8jPevzBCIh1AjoyVhp9PJ5WSG/PIaTbcT77PXyJfLtIfHa/63Wi3m5+fZ3d21x4PC4fCxhaVIJMLG+gatUoelP7zDzmsFnD4n6efifPCvPoc/7UUQBLrLdcq31458nHcyRkdDz3fJfaXAZr6D2IO5z77A/MQsjWGJjT9/C8+H4mCC70acbrmF+9uyeL93lkqvjyALKPIW9c7HGWiThz6HtSx9EmKxGIqi0Gq1zqWj8DA0m01756jVarG7u3sm5429e0WWv0m9XiccDrOxsWGblbrdbnZ2dk489iRJEslkko2NjQcuwo4ZcxERBIFsNnugQFGpVE6cbAiCQKFQOLMiwUMnHKqqnpv29pgxY54smqZx+/ZtssMGunjXsVsQMBGQ+00C7hAuj4fc77yO+YcrIIsIP36+Y05utxtZlrn84gzT19P8/v/1JX7+r3+O7/ypj7LwnsMDtTN53mcStJYqGPU+Unq/Q7jpknHcrRx50n6CCxFu/sprOFwK/pQfs9PDrLcQr408QcxqAyNXwcx10P1+xJAD5X0TB54zkUhQqVT2BWWGYbCysoJDl2j/0jqSU+aFf/oJlOi9mX+z3cVY28bs9ohMZqlVCuzm8yeqeuu6Ti6XY3p6+oE7AsO+xu2vLjN093jzN5eobjbJPBfnm/72+/HGDu4gyCEnWu18TM6c5iY+8xsMiVIXXgTh7PdBTNPEbA3R8120Qhc930Xf7aIXu5g9HSnuQkq4cC+Emfr4VbyJIJquEX9xmuDz6ZHR33KBqR97D4s//a0UKkVqtRqm6aLW/XGSySQTCS+mabK2tnZgvCcYDJ74WGVZJhKJXLidgkajQavVIhaLsbCwQKFQOJHs7lHMzc2hqqotj9vr9Wy3c0VRmJiYsH07DMOwBS7a7TatVsvecxFF0Tb1tFSmFEVB1/WHmlMfM+YiMD8/j9N5sKN92PcsFEXB7Xbj8/nsLqDlhdNqtR55n/OhEg6Hw3HsDOmYMWPe2RSLRQzDoKsm8TWX0AQZGFUS+ysyzX/+eeZ/+fvo/cYybNbhrp/GebJ3rEf1OPnM3/hmVl7Z5D/8H3/K9I00n/zxD+H2nb1YhftGksZLmxh+GUMzEOV7wbgRVVEc9wovU3/xCv/p732eme+7DoC5VUBMxxAkCVM30N9exyz2MeNBtNUa3p/4wJFmeNPT0/vkRE3TpP31Iu7rYWIfnSL7nZft+5r9Afr6DmaljjiRRLw6iyCKJJ0SW1tbJ/5dO53OkTsC/Xaf1a9usPLldTZe2SZ5NcbUJ5Nc/+5LD1z6lgMKenOIqRsID7m7sf35O/QrPcLPxvAtBJGcErJZIW383wjoCOhItKgIn3yox4e7Er31wSiZuJtYaLsd9GIPTBMp7kJOupESLpQrIaSECzGo2H8Hn8+HGvVy6/YtFEVhZmbGllpNvDDJWy+/gb88IBQKUavVCIfDxONxKpUKy8vLhEIhJiYm9v3drX2B03IRR4AMwyCfz1Or1Uin0/j9ftvk8TSEw2EMw+DNN99EEAQkSdr3GMvLywD7EnZJkuzFb0uu3wqoLGlk67+qqlIul8cJx5h3JEclG/8/e28eJVl6lnf+vrvGjRv7mpF7ZmVWVVdvanWpW2q1FiQQWuEIYzZhA5KxAIFhzLGNB2bOGM9wxjBgQIMxy8zxBhiBQLQEksBoHVpC6pZ6rTX3PSNj39d754+oiKqsyj0jq6qr7++cOF1dFXHjRmTkje/53vd9HmDHz7SiKIyPj+9o9iRJEqOjnQ29TCbTE/VH4cCCo/uLqSjKodNPHRwcXll0d//SkcdR2mWMyjoIWCtOsakP4Xt3i9THXyL2g4+w/HN/Dckq9hfXYcoHg+4DJUofltXVVXw+37Zrz6nXjPATv/W9/I///FV++yc/xrs+/CTnnujvZog26oemhbzeoPuqum5MlRfn8b15rHff8MMDFLZKeP0u7GYLayOD/Ng5AOzFdexUFRSF+oUU5gceRbjUXZ/XMAx8Ph+FQoFWukbur5dxTfqQZJmR93VmIex2G3tlE2ttCykeQTp/DnFDr24gEKBQKByqr//GL51yrsrsVxeY/coCaxc3GXlokKk3jPP2n3wSw+vqVV1utka8GaFIyKZKu9BECe6+w7YXlfUKSx+fYeWTC1jNNq6owcMf1hAPWbTwI1HFsOcOdCzbsrEy9Y6g2Kx0KhabHZEhdLlXsZCH3GivCaMMGAiPuu/nulwuo6qdn2m9Xmd5eZmRkRE2NzfJ5/OMTI+RSqWQZZnJycleRaNer/ccZG4e5DyqtfypU6dYX1+/64bIofPezM/PE41GmZqaOlS7E3SEoaZpTE1Nkc/nb2k/3Kldq91ub/td6KbF7zQvFQgEnBlVh1cEpmnicrmQZRlZlvF6vbtuUCSTyW1ObIqiEAwGtw2T78VeLm4H4cCCw7IsNE3j1KlTjthwcLjH6e4WWrLOeuKdSFYDW8gs/dbLbPz3LxP61mGGf+khSp+dgagL3j8Om1X4qxWotrCnfDDtg3EvQu3P9cK2bTY3N0kkEtv+XnOpvPvDb+L+J0/x1G9+gZe/PMO7PvwknsDOmQaHRQiB+4E49QtbqJfaSG/w99o10ktXUG+4uNeLdSS/TunlJPbr44iQD+HSsMtV2ldWsVNVGjUJ/a1TyIm9Aw0ty6JQKFBfKpL77DLRHzqD5taJRCLYlo29mcJa2kD4PciPnEW4dl7Ij46OMjs7e+Ad70KmyPrXXmT2qwukFrKMPzrM/d92hvf83NvRjO1fZDfOleyHEtRoZusHFhy2bdPMN6islCgvFynO5GgWG7QqTUBgNS0a1hgWOgoZQFASD2w/Rsuina7dUrGwUjWEV+1ULOIG6qQP1+vjnYqF++ijjd3WHtM0KZVKlMtlFhYWiMfjGIaBoii43W5s2yaZTPZS4aGT7K2q6raZgUQiQTgcPtK5uFwuJiYmsCyLCxcuHPk1nSRbW1uUSiUSiQSxWKwXvrdfKFs3td0wOkYL5XL50H3me7WHlEolBgYGcLlcPQtcB4e7jXA4fMv34V503eKCwSAej+dQa/lWq3XsjJlDXVm7fY4ODg73NtFo9HqYnxBYcmeRGHjzEFufWqS5VMEd9/PMX18icsqPel8A7gvAWxPY2TrMFODrKfjkMvaI2REfp3wI7+47+vvR7U3fjbH7B/mxj34PX/jDr/PbP/kx3vGhJ3jordN9qba4H46Tf26d+oUsZ7/vkd7f220bcUOL1eqzq4y/7RSFq1kaV1bQHzvbyaO4uIi9UaWt6EhxN9qjw/s+Z3JxnVa6RvqPZ0j8Tw8THYgRj8exMwWsb1wETUE+N4nwmvsea2JigitXruz6hVHYKLH2XJLUTJb7v2MaxSPz0HeeYerRSRRt96+JQqFwYCGjBHTa2Z0rIbZtU0/VKC8XqSyXOiJjpdQxKhjxYg57iL0xQeFKFkmW8J8Lcd9PvwYtoLNi/xju1iXqWYP88hDt5NL1ikWmjhzUOxWLAQP1vgDGWxLIMQOxQ5p7PyiVSng8np5wqNVqLC4uAvSCEG+2zoXOYPXW1hanTp1ieXmZWq12ZLFxI3f7YrlrS+t2u3vD8d2gwP3OvTsk3nWg2o1u8GXX3W2/47ZaLZrNZm9jodlskkql7koHMIdXL8Vi8VCC46CVjJ3oBpceh0MJjsMMrjk4OLxy8fv9vfaDGxdGrlEvSkDHtmzatRaxd56lfd/2XW8R1OF1UXhdFLvagvkiXC3AF9axA3pHfEz7IOo6sBgwTZOxsbF9d2RUTeHbfvgNnHvjKf7iNz7Py1+e4T0/8Wb8kYOnNO+EcTaKVGtSWilun+NoWyBffw2rz6ww8tgI+riXwlKR2LeaWOsp7LkUBbdCGQvlfJByKoWqqsiy3MsFaDQaNJvNzmKnWKeVqdEqNEn87GtQVIW4x4f14gw0moiJQUTIf+D3T5IkpqamehbGtm2TWy6y9vwma88ladXaDL4mxpl3TOAf8iDJEi0a5Aq5Pd0IV1dXD/wedgfH7bZFdaNyrXJRorLaERiyoeAe9nTExZsHcQ970AJ67zW2G22W/nSW2GMxBl8To/nlDWrJKq2NKnZRRopIyLEcStxAf00EOebqCAvl9lbku85IO7Gfq1sqlaJerzMyMkIymaRare56rINymJ1/wzBwuVw0m83eZ/J2UalUWFxcxOVyEQwGmZiY2NYGtZv/f7FYZHBwcNcUcZfLxdjYGJlMpvd7MDc3t2+ewI1zNN1wQEdwONxNNBoNlpaWGBwc3GZ72282Nzf3dZUbGhraVyPseYY3fpn5fL4dvdgdHBzuTUZGOu5JL730Uu/vlICGbCo0sjW++vOf4cmPfgdX5nbf+RCGAueCcC6I3bZgpQJX8/DxBbDBnvZ15j5GzT2HiQ8iNm5kaDrGh3/9u/nSx77B7/z0n/D2f/w4r33HfUeudki6gnE2ivz3q1RmM3jOdBbhdtvunbdlWaw9t8ajP3Ie5XKT5/9gmeB3VeC5Oax0na37/VgeFbuYh+LO/epWvU3x7zYwH4mgxtxowxLYNmOWSvulWaSxAUQ8gpAO/zokScIqQ3olzbP/7WUkRWLwNXEe/UcPEBzz7fje7Fe9iMfjew4RWs02ldUylZUSqZfSVFZK8JfzaEG9Iy5GvAQeCGOOeFDM69Uv65ojVO1i/lorVGfOYiriQasL2vMl5LiB/ngMM2YghV0Iuf9zQ0chEokcKwiuWCxy+fJloFMdOXXq1LHOZ7efoRCCwcFBDMPAsqxee1x3DqXbB55Kpchms/u2OfWLWq3G+vo66+vrGIaB3+9ndHSUWq3G0tLSLffv5tLsRigUIp1Ok0qlkCSJSCRCOBw+lFhuNBq3zf7bweEwdAV511xienp6x/t1jWCi0WjfxiK62UCmaaLr+r6tm3sKjp7nu6IwPLx/C4CDg8O9h6IovVYcIQTBNw1ijvl57Q8/yUu///dIj5oo/v378oUswZgHxjzYbx+E1LXWqy9vQrqGPeHtiI9T3o5QuYau60e6QMqKzLf8wOs498Qkf/Ebn+elL83wvp96C6GBvYPTdsN8aAD1mxsUL271BMeNFY7U5RRm2MStQxsLbSJG7jPP48+XqTYF7aAOewieyksZ0n90Fd+3DqMEdIYTCdrJDGaujDboRpyZQCiHawNqNdusvLDGzFcWmP3qIuHTfsa/dZAnfuK1eAfMfQXYfovMUCiEaZqdUKhmm+J8nspyZ+aislKitlXDiBu4hz24RzwYLoXRn3kYWZc7jlCFJu3NCs1nU9S6MxabVbDsztD2tRkL7WwAOWYgBbUTMSToJ7lcjnA43JcMjGq1SiaTwe/3H7mdeacBUlVVe4v4lZWV3nt6szgxDGNbm1M2m6XZbB7pPA5LN+QwlUqRz+d3bB2RZZlIJMLc3HazAI/H05u/8Pl8zM93MmAsy2J+fp7x8fFDCY5+VJocHE4S27ap1+u0Wq1t1Y5arcbCwkLvO3xrawuv18vg4GDP4GI/4vE4fr+fxcVFms0mQggURem5vtm2zeLi4r7fF2KvO9x///32H//xHzM9Pb2nd6+Dg8O9y4ULF24ZsJycnKRYLHLxPz9D5UqOkZ988FitK3a5CTPFjgAZdMP5CKJu4TJdDE/vbNd3GNpti6984nn+7uPP8Zbve5TH3vvAoUVMM13hykc+hfrQAFM/9yTJZJLyJy/he999eAN+Lv7JBWzb5uHzIYRpUMzUaXziGcyQn/ZojLVz+o6LNavaIvNnc9Su5Il8YBrX6QBeZIZKTUTIjzSWQOgHt0Vt1JosfmOFmacXmH9mmfBogKk3jHPqDeP4Yp4DDRCfO3eObDbbc0C5mVquSnY2Q24uQ242Q3Yujf9bI9TTNSprZdwjHswRD8aAiVAEVqZO5Zsp8p9axP/6OO1kjfZmFaEI5AH3dVeouIESMxC+/R2h7iSqqhIIBHp2rM1ms9eG1Gq1mJycJJfLHStn4maEEBiGwejo6KHaJ1qtFpcuXUKW5V4IXjAYJJVKkU6nD3QMTdOIRCJ4vV5kWabRaFAul9nc3Dy2N/9OyLJMIpFA0zQ0TaNareJyucjlcrTbbcrlMtVqlUQigW3bbGxs9LLBms0mY2Nj5HI5hBCUy+VtrVCapjE2NnZLT7osywwNDeH1ensDsje+Nl3XWV5evitdvxwcumiaRjQaxe/3s7a2Ri6X2/cxsVjsQMGijUaDarXay+jYKaD2wQcffNa27fM7PX5fwfGFL3zhyLZ8Dg4Or2x2c7iZmJhgc3OTcrnM2n+6hBrQib2/f3a0Q00/1oUMlRc3kVwKxoNx3A8NoE8Gj5zjAJBazfEXv/F5AL7zn72VyHAnP6RYLJJMJrEsa9suTSQS6bWSWpbFzL/7WwoBgetNAwDIL2dp3985xtLHl3jtdz6AXErhum8c4+uz5D49S9vvJ/YL34bQOpWira0tstkslmXRLjTIf24VoQr8bxvGbbfR6k2qHoPTp08jzIPtqtZKdea/vsTVpxdYfn6VgTMxpp+YYPLxUTyh7UPlS0tLu/aiezweTNPsXfNt26ayVb5BXKTJzmVo11sEJ8METoUIngoRmAyBR2JxeZHG5RztlXLPFaq9VUO4FURAo/BskviP3d+rXkjm0U0EThJZlvH5fMhypxIjy3Jv8dvdfMvlcjQaDVRV7d00TSOdTiPLMqFQiJmZmb7PQQghGB0dPZRt6+zsLOPj41SrVSqVCsVi8cg5HZIkoaoqkUgEwzBYWlrqy2sUQjAwMIBpmqiqSqVSYWVlBUmS8Hq9KIrS+1l4PB4URUEIwebmJj6fD13vCHrDMFheXt71M26aJrFYrFf1kCQJj8dDIpEgl8uRTCaRZRlV7YheSZIwTROv14tt2ywtLd22Ko+Dw+1AlmXuu+++Iz12bm5u25zYkQXHAw88YL/wwguODa6Dw6uUarW6bXiySzedt9lsdoKzsnVqyyW8D+8+YHxQJicncbs7lra2bdNYzFN5cYPqi5u0MlWMB2K4HxrAOBdDcm3f6e1aWNZqNer1em9I17Ksbf9NLxV47q9meOAtk4SnPXuWgoUQ2LZNIBCgmM5T+Owi+vkoSsSF8dsXqX7kHFbbIvNihuhDIWwhMFo2Q19YpbRWZ9HSePRX373tmO16i5n/+izZbA7PmwbAlFCbbcxijaLXhXC7OHv27J7vUzlbYfari1x9ep6Ny8lORsYTE0y8bgRjjwDE7o73LdgQ1IO01+sdgTGbITufQdZkgpMdURE4FcY/4kdqtqmvFqmtFqguF6itFGhsluBtURjQaVzI9qoWSsxAuGRsy2bun/8dk7/yRN+skvfD7Xb3qg/d4DfTNFEUhUKhQLFYxLbtXnic1+vF5/NhGAalUolGo4EQove5EkIQj8d72Rk303VDulG4HqZ15zBomoaqqui6jq7rGIaBpmmUy+VeBeCkZw+6Hv5ra2vHHqh2u90MDg6ysrKy70A3XK8yGYZBPp/v5Xjour5nLkw3uDiTyWAYBqZpUq1WewP7qqqiKAqqqmIYBl6vl2q1SrVaRZIk/H4/W1tbB64OOTi8EnjggQf2v9NNlEolcrnctirKXoJjz7qsbdtkMpk9XUocHBzuXXRdJxqN4vF40HW9Zyk5ODjY24iwLIsL33iZ/HoSfaCCFj96/sXY2FhPbEBnsa+PB9DHAwTfd5ZWpkLlxSSlv1ti8+Mv0HzIT3vYwPYq2IdYw/oSBk/+8P0UkhWefeoS448kCA3vnIth2zaSJJFIJChe2aT56WWEX0MJ6djXhrfr2TqyW8bM1ygFDMIX07RLFt7vf5TC//01CnMZfJOdSknhcorL//5pPFMhXvtDb0BOp7AKZVIBk/Q1C9qBXa65+c0iM19ZYObpedJLOSbOj/DQO8/yvp//NrQ9QgRvRFEUouEoyc1NmqUmqa9vknshje9sgNxQGnkFApNBpt5zBpemQLFBdbUjKnJfXWMrXUGLezBGfLiGfQRfP4xr2Idr0Icl2Vy6dAl14tbddyEJFJ9GK19HjdyefviBgYHezreqqtsW44FAgKGhod59LcuiVCqRTqcplUq3iFCPx8PQ0BCrq6u7LmibzWZvsFmSJKanp3G5XAdaQB+WrovUnWzxyWazVKtVRkdHcbvdlEqlXnL3YasepmlSLBYP/F41m81b2jmAfUMom80mc3NzTExMIISgWCyi6zqjo6O99rjufyuVCuvr69tEWzqdZnBwENM0dxxid3B4JSBJEpqmYZomPt/emVA70Z0NOQz7NoIWi0VHcDg4vEqRJGmbd/dOfZ6SJDF2ZhxLslj93ZcZ+tH7kW7KOAiHw/h8vl6yr2VZCCG23W50xtkN26uSGrGohD1gm5BvYs/lOvMfAIMGTPpgwNh3BkCSJfwDJp6wm8989GucfdMoD3/7KWT11uFcj8dDpVKhFdFQDYXGy1ncr4vCNcEx9+ezTD0epez3M7xZQ7tagAfH0V87wti78yw8dYkHPvI4i//9RTb+ZpZTH3qEyLCKNTuPGIqjnB4nIUvELYtcLtezF7Rtm8xyjqtPzzP7lQVK6QqTj4/y+Pc+wvBDgyg7nOvNtGpNcvPZbW1RxdUCZsKD7/EQ8TcNMvCmwU6rmm3jms9S+9wCyWID16C3IyaG/YTfOo4x4keLe67bAt/8ngKnT5+mVqv12lGgk1BbLpcJf9ckrUJjm+AIBoP4fL5eVSCfzx944HpwcJBQKNQbri6Xy9sWuqqqsri42Avku5GD9DZDp91gYmIC27ZZX18/8LlZlsXW1hbxeLyXw3EvUqvVmJ2dJR6PEw6HkSQJwzAOFTYohMDr9R47yfigBAKBntioVquk02lqtdqBnLgajQaLi4ucOXMGTdPu+pwTB4cbGRkZ6c1gHAeXy9Wr/h+UfQWH88vk4OCwH16vF384gP0j95H/6gaBNw/2hlzHx8f7Ehi6tbW13WtfCAhoiEci2A+HYbUCM3n45DI02p208ykfjHl2beERQnD6iRGG74/y9B+9xFP/7u944wceJDYR3Ha/bkuOkATqwyGaF+ZwKaCPLNIWGrmZFNF3D1Np27i+ukbT58Xzvk6Jevjbp/n8D3yM6sUtzGEfj/yr16EUcth2APnRcwjtemVCkiSCwSCbMylmnp5n5isLtOptpt4wxlt+9A0Mnovv+UVRL9bJzabJzWV6bVGVdBnfSABvwovbozP+YALl7ADNzSLVz6ex/nYLddyHa8CDMeDF8+7TuIZ9aLH9Xax2ojvrcCMTExPUajVevlJAG/Vsu28ikdj2mgKBAOVyuScUdkIIwfj4OKbZmU8xDIOhoSHS6TTr6+tAJ6W73W4fOoH6ZrqzAjMzM4d+bDabJRwObwsCvBdpt9vb7JHPnDmDqqr7zjpomobH4yEajfaqTydN12J7dnb2yMnJtm2Ty+U6v6u75H84ONxtDA8P4/cfzaVxJ4LB4KGMMfYVHI73tIODw0EYGxujWW8iv6WzgBZCMDExcaSdlFqtRi6X6/Wh75TMfCNCEjBidm7fAnbmmuXu32/BU0vYYyZM+WHKi9hhUNntd/H2Dz/K/LPrfO53v8GpxwZ55D2nUbSOUKrX6+iahqFdIP79n0SrPosS9iK/p0HDq/D+XxSopKiKt5ENGcT+4WMIVcZqW2x8+irtzRLuh8KceUcEiSbSw6cR7utzFlbbYvXCBrNfWWDmK4sousz0ExO882e/hfhU5JaFv23bVDPV6+JiJk1uLkujVMc74MX0u3BpCsNDfqSgm8ZaCZFvog370Id8uMb8uN44gmvIhxq6tRrUaDR6sw39wuVy4c+7EFdtxt5/dk+nJdM0OXv2LNlsdlv1S1XVbZ+nbn5El3A4TKFQwOfzoarqLXapR6HbjnUUulWR4eFhisVib07gXqfZbPZmvG5GkiRGR0cxDKMnCBcXF0+k7WwnZFkmnU4fWWx0yWazTE5O9gbcy+Xyq+Jn6/DKQ5IkBgcH+x7eHY/H+ys4TsLyzsHB4d6jXq9Ta9Swam1KFzN47gtx8eLFQznqtFotlpaWjr0rLUI6PBaFx66lnc9dSzv/3Bp2WIfpjvggcj3tXAjB5PlBEmfC/P2fXuATv/RlnvzAgwxMh7GtOjT+dwZDn8ZqS9SeN7E9bqjqVJoCj6eJ7noKs/Jplt72r7CDLiqrBS7/+6eRhMUTv/Ao2Zc3EKdGkSOdHaZWs83y86vMPL3A3NeW8ERMpt4wzvt/8Z2EhgO987Jtm9J6gexst2qRJjeboV1rYQYNDLeKLkkMujTsuo1StzFUFdeQD9eIv9cWpfoPZi3cbDa5cuUKkiT1yu/dvnxZlo9VrdIjbiorhQPZukqSRDgcvuXvK5VKzyENdh52TCaTfdss67Z6ybJ8pGOWSiWuXLlCKBRicnKSmZmZe97lyLZtBgcHSafT5PP5bZsFwWCQdrvN5cuX78j6YmNjg6Ghod6Q+VGp1+vMzMz0jAgikUgvOLE7THu7whIdHHaia3JxUmMRXfe+g3ZC7XvV36+n2sHBwQFgeXkZAMklI2SJ+f/jGcZ//lEWFxdv6fXs7lq73e6e5WUulyObzfb9vIShwP1BuP9a2vlSuVP9+JMFEJ2085/8w38LhrxtR79aqPOHP17E8Gl89/e5+NEfbvEjP7bAL/2b+xh3Cax8E1uXaZeb/JvfXmU8pPDBD8ZIBH6Vf/y+/8ji82n+zYd+ire891HkiSGuPpPnqV/5Pb52Y23EfgAAIABJREFU9Xk+8IYfYeHZFSJjQaaeGOfx73sEX8yL1WpTWCmw+LlZcnNZMldTZC4mkWwwPDqGKqO2beJ1G/eAD2PYf23GwodryI9ryItiHu+a3W1Jsixrz9kDn89Hu91mfHz8wJUQV9Qk8831Q59POp3eFkDZZWJi4pb797stx+Vy0Wq1jiVgLMsilUr1EnnvZcEhSRIul4v19XX8fj+JRKKXhKzrOpqmMT8/f8c2MyuVCrIs7/h5OizNZnObS4+qqsTjceLxOD6fj6WlJUd0ONwRdF3n1KlTJ+4ye5hr2Z6CQwjB1NTUsU/IwcHh3qZcLm9rifA+FKY2X2Dt9y8w/BMPdqaJb8C27Z7LTi6X67lAnYTguBEhSzDhhQkv9rcOwlYNZgr80us/DNk6jHl5yVrhD7/8FL/20f+LRrVF8qVP8NibPottTwALneMENNobVdqKQFcFUtvGFhINlw+pXkJWnycyfh+f2foaT5z9Hq4+s8LMVp4v/fnXqQyXGf6nCZ78x6+jmauRm8tw+Q9fIPXiBvnZDKoi4dIVNFug2TA9HsRzKoxryHtdYAx6kfSDh78dBp/PR71e71ke70bXBvUwrVd6xE09dbDqVTdwcnBwkLNnzyJJUicXpFJha2uLycn+5b7shc/n60tquCRJvYXuvYzX66VSqfQW4oqi9EwBDjOcfVJ0c1T6IThuJhKJ4HK5mJ2dJZFIMDQ0xMrKSl+fw8FhP4QQTE5OnrjY2K/V+Wb2vPLpuu5kcDg4OOzJbjvhkfeOsfxbL5H6ywWi77t1J/rmY6iqSigU6ms6814IISBmQMzA/0Qcu9SE2SLG5xZgsYTvL1Mw7eWR98+huWKsrtRo1FpYbQsp4IalMs1aG09QwW5ZNBSBVWoi6W4Uj8356Sn+8q+e53/9rl/iTW96kolHRxj+opf5SoH5//gML65+Dk2V0WUJXZIJTQaZfs99mONBXNcsZ/UB766OUCdFIBDY1uvbaDS4evVqzx646z4lSRKBQOBQ3xGuqEktfbAKhKqq1Ot1Njc3SSaT2LZNKBSi0Wjs2dbVFSb9WtR6vd5e1eeouFwuRkdHKZVKx27ludvx+XzbXmOr1bptv9P74Xa7GR0dZWNj40AzI6Zpomka9Xq9l+uzE92UckmSmJubw7IslpeXGR8fJ5FIHPvz4+BwGIQQlEqlvg6I78Rhw0P3rXA4ODg47MX6+vqOO+FClhj84bMs/PI3MCZ8eB64tR//5uNMTEyQy+XuSLuF8KjwcAhhDcJVDzwWRd+6gF5fQg9MorTTSDZsLeQYjqkoqkDCQjQsGm0boUoIt0IhWaNWahKQvsEj2iM89/KXeGA9RE1VIVen1Swz+T1DhH/wtbjHAx1hEfN0Bt/vQjRN4/777+/LsVSfjlVr0a63kPep0IyNjTEzM9Nb5AkhaLVaJBKJXasElmUhyzLT09O0Wi3m5+eP1b7UTRA/7kxRNBolnU7f82FxQgg8Hs82x6q7CZ/PRyaTOZAlcigUIhqNUiqVCAaD6LqObds98dHNMdA0DSEE+Xye9fX1ntC1bZvFxUUmJiaIRqM7ZoY4OJwEXcG7vr7O0NDQgWcoD0vXJfCg3Nu1XQcHhxOlVqvt2Qal+DSGPngfq793gdGffQ3aHoFv3TYeTdNum2PNbghJIKZ8+M5L6H4f9XIdq95CQRCRVZpLJVptC4+QyK5WEB6NRq1N9vkUwgYaMv5olu9983v41a/9Lp5/FOc7vu/91D/lZ+GX/oBTP/4Y7rhn3/O41xBCoIdN6qkK7qG9w6Y0TePcuXO0Wi3q9fqBvtyWlpZoNptcuHCBgYEBwuEwGxsbhz5PWZYJhUKEw+Fji4S7fRHeT7rtVHeru6UkSQfazPB6vUQiEebm5rYJVkVResnu7Xa71xa62+vtVn8nJyd7TlYODreLVqvF4uIiQ0NDBIPB/R9wSCRJ6rUmdqvee+EIDgcHh0PTDTU7yK6dMekn/O2jrP3+RUZ/9mGkPcLqWq0WqqreccHRJRb10SzXaAoTgjoYMvKwiTeiYq2WKaXqtARg2WiqxNCDURS3hvEnKTyDLt7yE+8k/Vct/uJTn+K9/+QfoGgK5rCfpU9d4uyHzt/pl3dH0CNualvlfQVHF0VRDjT3kMvlelkXHo8Hv99/aLGgKAqRSIRAIECxWGRubu7YWVRut3vPdpx7iWAweOBAxZNGCNFLku9WHUzTZHZ2dt/HNptNhBC3VMdarRatVutQwuEoqesODv0kmUyeiOAAOHv27IHv6wgOBweHQ5HJZNjY2DhU21PgLYNU5wpsfmyWxAdO73q/er2Oy+Xqy5BuP7Bx032ZhrsjlGp1C71u0w64kE75EYUG1XwS85yPGjZSuQ6tNnZLxppb4t0jU3wqU+DPfu2jWJLAF1Gw5ldozSeQPEYn+E9TQdM6Q+33OK6Im9oBB8cPQ7eC4PP5SCQSrKysHHhhqGka0WgUr9dLLpdjZmambwPFrVar13pzLy88FUXBNM2eW92dxrZtXC4XtVqNSqWCEIKtra0DCb9arUaz2cTr9fblWqRp2j3tTOZwd9NsNmk0Gnfcdfbe/3ZzcHA4NpZlsbGxwcsvv8za2tqhZyyEEAx84DS1+QK5r+ze4lIoFE580O0wtKwphJAAG6+p4DcVFr6Rpdlq0x5yI9wKFZ/ORtkiEdeg2sLSJNqNGuULQVLPVrDMQb7/Iz/OJ77x9xQ0BcnjRov7yL64Dtk81vI61sVZrGdeoP21F2g/d5H2hRmsmUWspTWsjS3sTB67VMFuNF/xNpt61KSe6m9rST6f730mo9Eoa2trBxIbLpeLkZERJicne8PxGxsbfXUvqtfrJJNJhoeH7+m5SCEE1WqV06dP43IdLPPlpFlbW8PtdpPL5chkMocSfJlMhlAo1JfzsCzrVVHhcrh7OUprab9xKhwODg57ksvl+mLtKOkyg//kPpZ+/QVcwyaukVsH2boe+XfLbnClFsVUH0K1LiDVvLz3vJ+Pfy6F95SH05pCqdTm459Yw+tVeMMbI6BJYFvgkqgqj1B8eoHSFxaYEODZEnzmqc8yND1G+O0P8OJvPM2b3vco0g0Bf7Ta0GhCo4ndaHT+XK5iZwvYjSY0GtC2QFVAUxGadq06oiL065USNBVxlzoMuiJuCjP9dS3a3NzE4/EQj8exLGvfXWlN04jH43g8HrLZLJcvXz5RIZfJZPB4PMRiMTY3N0/see4k3UyKcDh8V/zuut1uQqEQiqLgcrkO7aiTz+eJx+O9KslxqFQqDA4O3jXVH4dXH4VC4Y5XORzB4eDgsCv5fL6vPvL6gEn8e6ZY/f2LjP/LR5BN9Zb7dKscd4Ory9raGuPD341b/0Vqa2Xe8x1x1FE3n/yrJJvJZUy3zJnTHv63//k0mtZZ4MtSAct2Y557jPb5c7TyNZTZEt/xP97ER7/4B+TLMpm/uYiWq7H+6Ssk3nUaIURn91tVOjfTYLe9cNuyeqKkI0w6QsQuV679+dpNlq6LkRuESFuWaGDj8nqQrjns3E70iJv6V/u38Mrn85imSSwWI5fL4Xa7d72vLMvEYjH8fj+pVIparYaiKLelarS6usrU1BRCCNLp9D3XYtMNvevawt5Jum11qVSK9fX1I1UXbNtma2uLWCzG0tLSsc5nfX2dyclJAoHAXTPj4vDqY2FhgdOnd29pPmnEXhfa8+fP288888xtPB0HB4e7hWKxuGfS9HFIfnyWRrLK0I/df8uC1+VyMT4+zurq6h2d5VBkmZDfS+OpGdyDHyfw1m9Sa3hptXdfoMsij43GavoXmJx6M7Ozs9fbc1oWCAGpGugytlumvVJGLbTx6iah+4Ywz0YRfcjduF4t6VRJGpUqa5kUNcuiLQkky8aSBErbQrEsVCRcikLY40Vy6dsESr+rJaWFLC/98v/H6//D+/pyvEuXLvXe43g8jmmaLC0tbWuLkiSJcDhMOBwml8v1evk1TWNiYoLLly/35Vz2Q1EUwuEwwWCQcrlMKpU69M773Yosy5w+fZorV67c0fYhRVGYmppicXHx2O+tEIKxsTFKpRLpdPrQwlSSJHRdp16vE41GabfbpFKpY52Tg8NxiMfjRKPREzu+EOJZ27Z3dERxKhwODg47cpLl/+h3TrD0my+Q/uwykXeObvu3Wq3W27W+U4LDNFwEdIP0R5+hdCEFH/kASvMUpvZnUG/QtrzYdKszNpIoIYkGrXaI9ew/p9mOI8vy9oVXV0hEXIi5IlzM0rqSR/q2IfKjgnx+FfFfL+EVLgJnE3geGED2HK38fWO1ZKO4QSqbAkGn6gFYckc0tWQJS0DThhJt6tUyw5LUmxfZuVqi3VQ5uSZOFPlA1RI94qZ+wPC//bAsi1arxcjICJIkYRgGpVKJ6elpqtUquVwOIQSxWIxyuczs7Oy2ykKj0aDVauF2u4+dtXEQWq0Wm5ubbG1tEQwGGRkZodFosLi4+IqfzWm32xQKBYLB4B1dVMfjcTKZTF+EnG3brK6uMjg4SCAQYH19/VAOVaZpMjIygm3bCCFeFdbIDnc3m5ub+Hw+dF2/7c/tCA4HB4dbaLVaJ9oWIRSJwQ/ex+KvfJP4YyP4p8JomoaqqmiaRqvVuiNfzpIkCPt9SKUmG7/4BSqNFsrPPYLs1VjZfAeJ+NvwmV+kWf04llW69iiLenOCXPmdVOoP4zYDjCUSlEqlnReRssCe9sG0j9JfzKN8fpXQ81nwKlivjVCIuyglNzD+9Yvoo37M1wzgfmgA7Qi5HbOzs3svvITAuiG1u2C3uVIroSgKQ6dGMAzjWrWkdVMLVxNKZawbRUnb2lGIXP9z56aYGtjQLDdQzeP1ExcKBWRZ7s1iAKysrCCEwOv1EggEEEKwuLi4ax9+sVgkEomQTqepVqu3pR3IsqxeEODw8DADAwP3RBp1JpNhZGTkjgoOIQT1er1vx2s2mywuLhKLxZiYmODq1asHPn6lUsG2bS5duoSqqvdcG53DK5OZmRnOnDlzILvxfuIIDgcHh1u4HfMTWtDFG3/zO3BJKjWatFotKpVKL0zrdveBG7pGyO+jcDlJ6deeoTLgxvUzDyCu5YZYlsXqukTOfC8jwx/i6tVnkESTtuXGsjsD8N3e8bW1tQNVZwJvG2L23z6D50NnUaptpJdy8NkVrH80hft7pvAYHioXtsj99d8hGQrmQwO4Hx7AdSq0bzL5UXd5u1kD3bwCIQSyLON2uxkdHd19tqRtQbPZa+Oy602oN7CL5esD8M0WyBJTT/hovXgVOerdsXJy0GpJMpnE6/HQLBSpF0uoaqfqZNs2hUKBQqFwy2OEEBiGgWmamKbZs2GOxWIYhkG9XqdSqZDP529L1WNtbY3p6WkKhcIrPhiuWq0iy/KBA/ZOAtu2+76QikajhEIhlpeXDyVmuuGARxlad3A4KWzb5urVq5w5c2bfsL5+4ggOBweHW8hk+usidCPRaBSXy4VhGFQqFZ77r39P4dkkIz/9MJJ6+52VhBAEfR4MXSP5t1dp/bfLVB6N4PqHp3Zc9JbLZSxbQVETvcWHLMtEo1H8fv+eu+k3o3g1vA+GyX1lg8g7RrHeZsCb45CukxYt7E8t4noozsCPPoqtSlRfSJL6oxdp5aq4H4hjPjyA+/4YkuvWS3m/3JBs26bValEoFFhYWMDtdmPbdu8myzKBQKDjfiLr4OqU6neSC7ZtQ7NF7rObmJaGaujUK1XaxSK6ZaO02tBodZy+uhUSVbnuvNUVJLpKqVan0Wjgc5u4ggGipQr1Wh1sG4RAkdJ4XV/Gwk2Ld+E2Q5imiWEYNBoNyuUy6XS68/O8tjgWQuByuTBNk+HhYZrNJltbW71AwZPAsizW1tZIJBLMzMyc2PPcLhqNBrqun/gCW5Ik/H4/uq7jcrmwbRvLsjAMo68VlvHxcWzbPnI2S7lcxuPxOILD4a6i3W6zsLDA5OTkbXtOR3A4ODhsI5fLnVg/ebeffnl5mWQySb1eJ/DWQSpXcyT/bJaB750+kefdDU1ViAT81OsN1v7LN7E/t0rt3aMYbx3a83HlcrmXIO33+0kkEuTzeWZmZg49MBv6liGW/+NLhN823BkYVySIG9hA9YOTiJUm9T+7ALUW7seHSXzkMWyg8sImhS8vkvxP38R1KtQRHw/FUcMdlyZN0/q6yBkYGOhlStxMMpnsVQ4CgQCBQGDHnTMhBJYiUz9rsmRUkTI37RYroLldnJqYgEYTqdW+bgdcb2AXS72Wri27iSoJApKM3W6jhAK0v3mBkWKRraiL2ND/iSpnUBUZyZUlU/npWwTGzdi2TbVapVqtkkql8Pv9xONxBgYG2NraIp/P9+W9vJl2u33HnZ36RbFYZHx8nEajQaVSYWNjo2/XE0VReraewWAQTdMoFoukUimEEOi6zurqal/fS8MwuHz58pGPWSwWGR4epl6v71hxc3C4U9zuFj9HcDg4OGxjpwVlv5AkqTdc2kUIwcAPnmHxV75B/mub+B+Ln9jz34jfY+J1G6SzBaq//wLtCzlaP3QG1/37h31VKhVM0ySbzWKaJul0+shtaK5hD1rUoPBcCv/52PbnadaoxIH3hhBNm+JmEe13n8YwTTyPjzDw468DGyoXkpSf2yDzyUsoAQPz4QG80yZV+iM4vF4vPp9vzx1427apVCpUKhXW1tZQVRW/308kEkFRFFqtFhsbG51B7pBK/ktrBN8+fMtxGo0GM3NzNJtNJEnC7XYTCARwhV1omkatWr0W6BakmkpTzBcQyQzq9Dg0G6gtC299E0XK02xHaFlt3PLXD5TPcTP5fJ58Po/H4yEajRKPx1ldXe1765Pb7b5ndsCTySRbW1u4XC4GBwdxu919eb9cLhdjY2O9jA/btllZWdm2aDoJk4nuwPdRKZfLLC8vMzQ0hN/vZ319va/Bkg4OrxQcweHg4LCNk8plUBSFYDC4YwVAdisM/pNzLH/0RfQhE9fQ4QekD3weskwk6MOybNaWNrF/+2Ua6RriZx5ET5gHOka5XO5ZC1arVUzzYI/bjdBbh0j9zfItguNGbFVQH9apD8Uptmwya2tov3UZfyyM5/UjxH7kEbChNpuh8vwG+b+8iv2OCNZfryKmfIhxL+KILWvdOYfD7PI2m01SqRSpVOqWnv7qbJ7m2u6L0O4i0rIsSqXSLS1NQggmJiYol8uUM3mMbBn1gdNs+tyUw16QghhWCEVKIoRNpvBGfFFfL1vhsHTPwePxMDw8TC6XI5lM9nXnPhQK0W63T1Tw3y5urBRpmnZswaHrOmNjY6yvr9/WKoGu6wghjv1zrlQqzMzMEI1GmZqaIplMks1mX/HOZA6vbOQbDENuB47gcHBw2IZpmn1zeZFlGb/fj8/nwzAMCoXCrkGCriEPse+aZO3/ucjYv3gE2ej/5cnjNgh4TXLFMqWFDNLvXKAsC/Sfe82hLGgbjQaSJPVctY6brOx5MMzGn81RmS/gnvDtfWchQBW0xty0RgwqTQv9Kxfx/FED8/wI7seGsN8ap37WhmITEdSxvroFf76IGPcgpv2IaR/Cc2vo4m4UCoXegu8o3CxUlIBOM3v0z5ht2+RyOQKBAFu1GnIsjKjXKendz4zGavbn8OhfwbLdlGpPkCrNMzExARzdFKFUKjEzM8PQ0BCTk5MsLy/3JVV7Y2OjN/twr9BtcTpuSjfA0NAQyWTytooNTdMYHx9nbW2tLy1atm2TTCZ7CebRaJStrS1HeDjcEXw+H4ODg7f1OR3B4eDgsA2v19uXoXFJkpicnKRWq5FOp3e3ib0B/2NxqnMFNv7gCoMfuq9v1RZZkggHfEiSYCOVpXUxjfRfrlAYdGP+03NHCturVCqMjo6iKMqxAxKFJAi9dZDMF1b3Fxw3IgnQZeqPBKg/bFNcL9D6Ugpr2IDNKmLQRLw+hvT6GHa1hT1TwL5awPrbNQjpiNN+pGkfxFx7vtdut7svC8cuSlCnnTueqM1ms4yPj5NMJjEDgVsWo20rQL76rt7/d4ffg8HgsVzY2u02S0tLhEIhJicn2dzc7FnyHod2u43b7b6jDk/9QgjB6OgozWazL9cSWZZvq4NXNxByc3Oz73M79XqdpaUlDMMgGo0SiURIpVKUy2VisU6FM5vNnqhRgcOrG03TGB0d3f+OfcYRHA4ODts4bnsQdBYcQ0NDlMvlQ+dpxP7BKZZ+/Xmyn1sltEOP/2Fxu3RCfi/FcpV8qQxPbyCeWqDwaBTzuyePLGqKxSLBYJArV670ZYcy8PgAqU8v0czWUYNH2OmWBI0hHdoqzBWRXsohPrWCPe3DPheAYTfiwRA8GMJuW9hLZewredofmwdAnPZ1qh9jJkLeLsBCoRAbGxvHfo1dlKBOK9s4Vn98vV6n2Wzi8Xjwer17OhNJktRLer569epRT3sbmUyGcrnM8PAwHo+HtbW1QxsGCCEIBAK0223q9TrVapXx8XEWFhZesaKjKzba7fau1czDIknSbasCqKraE7K5XO7EnqdarfaEx9jYGJZlkclkaLfbxGIxhoaGSKVSpNPpEzsHh1cnjUaD1dVVEomEY4vr4OBw5zhqi4iiKBiGgd/vx+v1Ui6Xj9SCI6kSQx+8j8Vf/SauUQ/u6cCRzkcIQcjvRVMVkpkcjXoT8dQC7ac3qb13FM+bj1dOzufzDAwM9KXHGzpzLP7HYmS/tEbsOyeOcSAJpv1Y034oNxEX80h/uwZtG/tcAOtcAOHXEBNemPBiv8OGrRrWlQLWF9chXUdMejttV1M+hKH0hr77haTLCFVglVvIh2jtuplcLkckEunlHdxMLBbD7/ejqiq1Wo3l5eW+Llzr9Tpzc3PE43GmpqZYWVk51E784OAgmqbRbreRZZn5+Xni8TiGYRCPxxFC9AajTdM8kaHoftO1kV1dXT32sXRdx+fzIcvyocXcURkZGSGdTvelarUfiqIQj8ep1+vbBuCz2Sy6rpNIJPD7/ayurvY1zNDBIZvNks1mmZiY6Msm40FwBIeDg0OPWq124CwA0zQJBALouo6u69i2Ta1WI5/Ps7GxcawFqhp2kfjBM6z9p0uM/8tHUPyH2/HXNZVIwEdho8iz//qLDP6zh3B9Zon6lTztHzmD+77gkc+tS3eg2e/3921xEnrLEPO/+hyRd40iaX0Y6DNV7PMR2o+GYbOG9HIW+Q9mIerCOhfAnvYjNAliBnLMgCfj2KVmp/XqYg7rM6swYJD9AS+BoIfNPi56lIBOK1c/tuAYGBjYcRfY5/Ph9/tZWlo60cWabdtsbGxQKpUONVAeCAQwDIO5ublt1Qyv10s4HO7tPE5PX7eKXlpauuutVbtZGGfPnqVcLlMsFikUCrcIBk3TaLVaWJaFx+PB5XLRbHYCQD0eDz6fDyEEhUKB+fn521LxCYVC2LZ926oKw8PDVKvVHTNz6vU6CwsLBINBJiYmyGQypFKpV2zlC64bkjgzK3cP/TA9OShirx/8+fPn7Weeeea2nIiDg8Od5aBio2t1KkkS6XSaarVKo9E4kR3I1KcXKV/KMvpTDx14ziLg9WAaLtL5Agv/4XnyT80zkfDQDGqoP/0Q2oC7b+fn8/kIBoPHnuG4keXfeQnP/WGCTyb6dsxttCzEXBHxcg6xWum1XNnD7s5A+g3YTQt7oYiWsZj8rke58L/8ZafqMe1HDJsI+egzNmv/4SX8TyYwHwof6+V4vV5CoRC1Wq2XUu92uwmHwywuLt5Wu1lZlhkaGkJVVVZWVmg0GjsurlwuF+Pj48zPz98ihiYnJ3G7d/6MWpbFhQsXTuTc+8nIyAjQMRvwer14vV7q9TqtVgtd11FVlVarhSzLtFotJEkin8+jqiqKovSS3vs5N7QfiqIwNTW148/kJNB1nfHx8QO1ZCqKQiKRwOPxUK/X2drauqurXYZhoKoqpVKpJ5B8Pl8vy6ef10uH43H69Oletk0/EEI8a9v2+Z3+zalwODi8yrEsi1QqtacdpyRJBAIBIpEIzWaTZDJ5W77wwu8cpTpfYOupeWLfdWrP+6qKQiTgo9Vus76VpllqUP/iKqfibpKbFZpRndGwq6/nV6/X+3qxBgh9yzAbH5sh8MaBk7EoViTs037s034oNRGXbm25wt95TUKVENN+WgCmguv7TlN/Pon1N6uQb1wXH6e8CP1wFRk11KlwHJdSqdRzROpmdrTb7SMnQx+H7kB5d1dakqRO2KFlbbtpmka9XicYDNJsNikUCr12mq5g2glJknpDxnczKysrvde/srKCEKI3EN8Vhd1Ftsvlot1u3/YQsptJJBJkMpnb1roUCoUO7FDVarVYXl5GCIHH42FoaIjZ2dk7/p7djKZpvZbAer3O0NBQTzTKsszq6iqxWKzn0OVw5+n399deOILDweFVTK1Wu6Wl42Z0Xe9lHiwvL9/WHWMhBIM/dJaFX/4GxoQP7yPRHe/nNd34PW6yhRLlaucLrv7xWYZkmZXNKjVDxr6co/xCGs+jOx/jKBw3FGwn3NN+kATlyzk8Z4/f+rUnnptarl66oeXq/iD2lA+065UlEXUhvyUBb0lgFxrYVwpYz6fhU0swZCJ1B88D+3+JyQGd1jGscbvYtn3XtRl1+6O7SJK07SbLMrIso6oqhmHg9XpZWFgAYHNzk0Bg97mlWCxGJpO5q1trujMcExMTlEolms3mrrMtt7OKsRvRaBRd1/s25L4fXbOAwz6fbdsUi0W2trYYHx8nl8tRLpepVqt3tE1JluXevFQqlWJlZaV3bTRNE0VRegP4y8vLTE9PUygUnLmUO4yi3F4J4AgOB4dXKcVi8UClbU3TqFQqLC8v34azuhXZVBn84DlWfvsl9EETLX5991eWJSJ+HwjBeiqDoX6ZAf/XaM0m2Pz6AIuVJq53jhB6TQTjdAAl1N+cA8Mw+i7AhBCEv2WIzOdXT15wXH9SGDCwBgx46wBittOVaG69AAAgAElEQVRyJX1uvdNydX8ATt/0EJ+GOB9BOh/Brrex54sdAfLlTfAoiGk/0mkfDLp3FGVKQKd66eQHc+8GupWN3ZienmZ4eLgXmFer1XC5dq7GSZLE0NDQHft9PCj1ep1kMsmpU6fI5/Ok0+m+ZJb0m2g0it/vZ2Fh4bYt2rsBlIlEglgsRjabJZfLHVhEptNp6vU6pmmSSCRQVZWtrS0ymcxtFx6maTIyMkI+n+fq1avbWmtt277F3tfv9/eqXA53lr02Nk4CR3A4OLzKsCyLdDq946Di3Yox5iX6vnFWf+8CY//iESRdxjRcBH0eCqUKhXIFl3qJmO//ReRBGn6Gxkc/gGS/68SS0+FkBAeA73yU5FPz1Dcr6PH+zZwcCEXCPuPHPnOt5epiHul/rMHrHkD6ZhpGXL2Wqy5ClxFnA3A2gG3ZsFrBupqn/cllqLU6rVen/YiJ62nnSp9aqu4FlpaWME0Ty7JoNBqsra0xOTm56/39fj+5XO6u7uOHjnVwoVDoZZaUSiVWV1fvmqHhG8XG7W6/S6VSpFIpTNMkGAwSi8VIp9Ok0+kDCY9SqUSpVGJzcxNd14nH44TDYba2tnpVpcPSbUmsVqs7DvrfTDgcJhKJsLS0RKVSOdBz+Hw+dF1namqKRqNBrVZD0zRUVSWVSt111cp7mUgkclufzxEcDg73OJZlsbKyQrFYPNIX/Um0DR0F/xMDVOcKbP3pLOc+ch5NUdhM52heWyho1hpSvk67HsKKyri0NQqFkz1vXddPJJBMUmUCTwyQ+eIaie+Z6vvxD4xHxX5dhPb5MBgyVNp7tlxBJ8SQERN5xIS3DWJn6thX81hf24JPLCLGPIjTfpSAeuyWqn5ZEt9p6vX6Le0lrVZrz5aHkZERLl26dFe3VkHndSSTSVKpFFNTU735lduJ2+3G7XbTbrdpt9tYloXb7cbv9zM/P3/bxcaNlMtlyuUymqYRi8WYnp4mlUodqlrRDRN0u91EIhFisRhCCKrVKtVqtef+1Wq1aLfbSJKE3+/HNE0WFhZ62SmKopDNZjFNk4GBgZ4ZSHdurytiJEkikUj0XNYOI27m5+cRQqCqam/mo1QqUSgUSCQS2wbNHU4GSZLwev9/9t48yLX0LPN8vrPrHElH+77kXnnvLVeVy4XLu8sb2NjY3cBAQ3tYGpqAJmKaGGbMP8xMdwQQAXR3GBiImTY2zTQ0TbMYGDzgxsYbtjGUXa5y1b238uaeKaWU2nfp6Czzh+45lbqpzJQyJWXmLf0iblRlpnTOkXT0fd/7ve/7PI5ZSdWMGTPGh6Io2NzcvNCEyjDMlQg4CCGY++GbEA401O4U0A2zMKdjqtQB+aoD+vdIIIEmAAq19psmfk2Kokys6c79tgg2f/HrCHxgDrR4yUM1IQBDQX9zANqTMshGDdRLJeB+yZX+qAuIHFe5AgDi4UGeDoB6+r7b+WYNxloF5F4V9q0GtC8egHrEdabbOYA+PxC73Q6fzwdFUVAqlabaWzQN9vf3kUgkTjTmoigK8/Pz2NjYmPKVnQ9d16Fp2tTHEofDgWg0inK5DI7jrP4ZwzAuPdg4iqIo2N/fB8/zVmN1qVRCsVgcekHfbDaxu7sL4BVfJJvNBlEUQdM0GIYBy7KgKArFYhE0TVt+H41Goy/rTQiBIAigKAqSJGFxcdFSFqMoCrVa7cz+v5MwDAOKolhqVs1mE7VaDQ6HA6FQCAcHBw/FRsJVZHFxETab7VLOPQs4Zsx4iNnY2LiwXG0oFLr0xRwB4HLaIQo8MrUcXv6FZxH9iVuwzTvB7NUhfCmD5tMraHR+EYKxDkWNQlHjE7+uSWZ/WJmH/ZYH5a9m4B2D4/rYuF9ypVklV2XQf3Nf5erWfZUrZy8Io/7LZq8863U96VtiY0BuuYFbblCajubPfhXOUgfGH28ButFrOF9xgiTsA2WQeZ4HwzCgKKpvMe5yua7Fbv8o1Ot13LlzB5FIBG734F4e0+/C7AG46k24uq5P1dlYlmWEQiFsb29fieb0Yeh0Otjb2wPLsvB6vVhcXESz2UShUECz2Rx6Ia6qKmq12rGyO6/XC47jrFKsSCSCdrt9rMTW7CcCelmYcrmMZDKJRqMxtub6QCCAVCplXePBwQEikQhWVlawvb195e/n64bH47m0YAOYBRwzZjy0ZLPZCwUbhBBrJ9D0NZiWIdZROJaBzyWj0+0inSvCkCgEf2AF6Y/fxso/WYBwr4rWu6LQgjZAB+rt6dWliqKITCYzseN7noli/xO34XkmAkJPb6E2NHYWxrf5oT3lAzItUC+VQf/e/ZKruATqdgm4U4YmUDBu9S+aCU0BIRu0x73gP5gE8vdLr76YBfI7vX4P0+38foan0WhgdXX1WCkARVFYWFgY2rTyumCqPcmyfOJCnWEY+P1++P1+6LqOg4ODqbhkn4dWq4VEIoFKpYKDg4OJnsvsi7iuC9dut4tMJoPDw0MrcDINVs3yKFNSeZS+h6NliOZ/h3GFVxQFGxsbuHHjxrn7cAghcLvdsNlsaDab0HW97ziapmFvbw/RaBSiKF7Lz+2qQtM0QqHQpV7DLOCYMeMhRFXVM3XOWZaFKIpWw56qqqhWqzAMA263Gx6PxwpYms0mHA4HZFlGKpWa2kTgtItwSiKKlRqa7VfO6bjlgRBzQP3ULuo/89ixJuZpwXHcRNVWbEkHWJlH7VtFOJ+YboPfSBAChEXoYdFSuaL/cg8k34ZhZ0H/3ga0f7EMY1kGS2fA0Hl0ugtW47gw5wD8AohfAPWmIIyGCmO9AuPlCvRPp4CAAGpFBvU6L1KpFJLJ5LFLEAQBoVBoogHgZXH37l3E43E4HI5TH2cqWNnt9iupYpXJZFAoFDA3NwdBECaWdXC73fD7/dja2rr2aki6rvfJLFMUZRkksiyLUCgEjuOG9mZptVoIBAIAelm0QCBgSS2b5WVm2ZXZ82IGBQzD9P08Ci6XC4FAAO12G7VaDZIkgabpgRliXdevRBnvw4Tpi3OZzAKOGTMeQkxN/9NYWFhAs9mEoihotVrgeR6xWK90p91u4+WXX4amaZBlGQ6HA/v7+5ahWbFYRC6Xm1idLUPT8Lmc0A0DB7kitKOlMooG8W/TMOYcuNdWwX8xBf93zU/kOs5CURQrWJsUnmeiKH4+dbUDjqMwFIxlJ6DqMNw80NFBih0wv3YbzC9QCD/y2wAMqJoX+cCHBzaOE4kBedwLPO7tuZ3v1GGsVaD+8TaqH0zg8GtVOJ4IQ1j09GV+fD4fqtXq0Io51wVd17GzswOn04lEInHm42VZhiiK2NjYOPPeZFkWHo8HsiyD4zi0Wq2J9oXwfE+aepIBB9BbmIuieO0DjgfRdb1PZKBeryOZTEIURatB3FR/GlRi2Ol0rM+gVCqh2WzC4/FgaWnJUowihEDTNKvv4+i5RxXJcDgcCAaD0DQN+/v71nfztCzctEvvHnbcbveJMtvTZBZwzJjxEFGpVJBKpc6sZXc6nVAUZeRd0FKphFqthnA4jKWlJaRSqbEv7uyiAJfDjkqtgVqzv3eEVBWIn0lBjYjovD6A0JtD2PmV52Cbc8L+Gu9Yr2NYWJadaI+L43Evsp/cRGu3Blvi9B3uK4OqQ09IwLIT8PAwnCygGfAlfgcGaGi6EwxdgGtxH8V70qmHIiwFsuQElpy9npmOjqpTRee/vQi10IJ4KwDpiRBsNwOgRRZzc3MPXT+HySilMyzLYnV1FfV6HcViEY1Go6/Ekud5q3QF6C1Ei8UiPB4PJEkaq/qazWaDy+WyPBgKhcJE5U9NEYFYLAabzTbx8q3LRFVVbG1twel0guM42O12cBwHQRDQ7XYtXxezYZ/nebRaLcuQzyxvy2azkCQJnU7nWJB2XjU4URQRiUSQTqdHknB+WNTnrgKmothVYBZwzJjxkLC7uzvUJE5R1IX6MVRVxd7eHpxOJ+LxOKrVKrLZ7IUXeBRFwSs7QNM0soUSump//wmdacL2uTQ6T3jRvdHrB2AcHCI/uorUx24j8bNPgPNNryEuEolYzr+ThNAU3G+LoPj5FKI/tDrRc40Njob+A4vHfq0YUYi4A4M0ABjQOf9IXhyEEECg0Y7RmH/PW2FUFDS+lUHtK3s4/N1vQlhwQ3wshNCSF+na6SWF1xVz91fXdVSrVTidzlN3g+12O+x2u/XccrkMURT7djxVVcX6+joMw4AkSQgEAtja2rrwtdI0bfmJlMtlbG5uTi3j0G63sbu7i7m5uYc64ABe+VwfhOd52Gw2CIIAjuNgGAYMw8Dh4SHi8Th0XYfP50Mmk0Gj0ThxLDvv4p8Qgk6nM/IYad7fMy5OPB6/MtmiWcAxY8ZDgGnUdBY2mw3z8/NQVRWSJEEURWsSAjDw/09StahWq6jX6wiFQlheXh55F6vvungOHtmJRquFXKly7O/segX8P+TQelsYWqx/R9y2IMP7HQmkf/sOEj/7OCiWPtc1jIKpY7+7uzuVnTjXm0LY+Lf/CLWqgHFeTr/KOCjWvxsUUcAzuyg334kuvQy1eL6F7fb2NhYXFyG/fR7y2+ehd1Q0XzpE84UsGp9aA94qQ2d7GZKT3M6vG4QQazF2584dGIYBhmGwsrIy1KKCoih4PJ6+36mqiu3tbQQCAWSzWbAsC57nx7LL7HQ60W63L62fRFEUS9b71bhjPsjfBeipFXU6HatMLxKJgBCCbreLg4ODsZW6EULO9b1jGGYWcIwBm812Zt/XNJkFHDNmPASY2utnYcprFgoFS9L16KRgLmjM/yeEQNd11Ov1gcfTdR3pdBqSJCESiUCWZRwcHAytjkUIgdtph8BxyJcq6DyoN28Y4L+RB7tZRfM749Bd/MDjuN4eQWuriux/XUfowysTX1yaZoqxWGyoOvmLwkgsnE/6UfxSGoH3z030XJPEMGzIVX/U+plxt8/tNt5qtVAqlax7muIZ2J+MwP5kBIZuoPzyAfabOejfKMD4b1s9xasVGWTODsJNPiidBKZC0VGfAtNY7zwKNKqqYm1tzVKiM30XgF7t/UXLnmRZRrFYvNAxLoqiKLDb7VfelX2auN1ua0w3Va5M40FJksYScBBCEAqFcHh4ONLzzCb4k+acGcMzSFzjMpkFHDNmPAQMYwxFCIEsywAwkovtMDQaDayvr1tOuZlMZmCK/yg8y8LrcqKtKDjID7geVYftiwcgTRWNDyRh2E4ergghCP3gCnZ+9TlUvpqB602Tr1mt1WooFotIJBLY3Nyc+Pk8z0Sw82svwPft8alkcaYBI3PQal0Ymn4u2d90Oj1QMpZQBO4bEXANGVs8DeNRF4w7D7idLzt7vh8OdlwvZyrcu3fvWEB/HvlrRVGwvr5u7SRvbW317YbGYjFUq1W0220oigJFUSw51mGgaRo2m+3SF/rpdBqJRAIHBweoVI5nT1+N7O3tIRaLIZFIIJVKQdM0SzyEZcfzffD7/eh0OkMHrYQQxGIxMAyDra2tC/tHvdqJRCInOolP0rD2NGYBx4wZrxKcTieazSZEUZxIiYFhGMhms6hUKohGo5BlGel0emAw5HJIkGw2FCtVtDrHa7pJU4X4mX1oMo/W++LAEItRiqcR+fGb2P3o8xBidghTaLDO5XJwu93geX7iUsF8SIIQs6P69Rxcb7hcPfVxQRgKtJ2FWlHAekZXUTEMA+l02lJXexBJkuB2u1FCCeT1flCv98NoazA2qjDuVaF/7gBw8yDLTlDLTiBou/KlV4MWYqOWnzQajYE9Gkd3timKgsvlGvj8drttlVSagciDOBwO1Ov1c/s1UBQFmqbBsix0XT+3MEOz2cTW1hbm5uagqupYm+GvK4qiWCWJ8XjcUjVst9sIBoNwOp1W8/hRiVrDMNBoNNBoNE79XHmeh8fjGdoXh6IoJJNJq7zv1Vj+Nk5kWT5WOmmSSqVQKpXAsj2BDVOxbBrMAo4ZM645Z2USTNxuN4rFohVwjJNwOAy73d5XmmWz2bC0tITDw0OrQZ1laHhdMjRNw0G+OHChRBXaED+TgrLqgvKYp+fxMCR8SETw+5aQ+vhtzH3kSdDS5Hevzd2iaXiTeN4RxeFfbEF+OnjlF8bDwrg5qOXzBRxA7/53u92QpMFqV36/v0+Ckwi05XZuaDqMvQaMe1Vof7IDaHov67HsBJkb7HZ+FTnJiXwQxWIR6XTa+pmiKMRiMRBCkMvlhpIkFQQBgiBYfg7AK5KpjUYDrVYLrVYLiqJAEASwLAuO46x/5nnN/5rlm6b/wyD29vbOnaHodDooFApwOByzgAO92v54PI5Wq9XnW9NoNHD79m3rc3qwl4eiKAQCAfA8j7t3754YGIiiiFqtNnQ2zOFwwDCMK+kdc91gWRbRaHTg344Ky3S7XWxubuLGjRtTu7ZZwDFjxjVnGKOzQCAAjuNQq9UmsnvEsiwKhYJVPnHUKCocDkOWZZQLeYgCh3KtjnpzcI0ws1OD8OUM2m8MQZ0/X4bC+aQf7a0qDv6flxH9yVsTX5gXi0UEg0HU63XwPD9S2cmoSDfcMP5kE831CqTlwbvP1w3GxUMttoEF57mPsb29jUceeWRgCcFpi2dCUyBzDmDOAePdkVfczv8uC3xyB2Te3gtAlpwg0tWZLgVBsO65YrFoqVCdRaFQOKbYZCoYZTIZdDodpFIpxOPxka+Joig4HI6JNanG43EQQobeYHmQZrN56U7LVwFCCOLxODKZzInlTmYJ3aA+Cl3XIUnSqfMIx3FDlfmasCw7UU+WVwuEECwuLg4c87a3t499nuMqnxuWqzOCzpgxYyQajQZ2dnZOLaegaRqxWAwURWFjY8OaJMa9CO92u5bKyVFUVcXuzg6ikTBCkSgKxSIarQGZAMMA92IJ3EtFNN8Tg+6/mLyt/0Pz2P31F1D461343jfZxrlqtQqXy4WVlRUYhgGKolAoFJDP58ce3BFC4H4mguLnUg9PwOHmoZYvJpVqGAbW19cHqjUxDAOXy3XmQpUQMsDtvNoLQP57CvALoFZ6fR/w8ZeaYWq326jX65ZJ29Hm+ZPI5/MDNyc4jrOOB/S8fLxer+XPcZWIxWJoNBoDF7M8z8Plch37XI7uzttstletYpWJzWYDwzCw2WyWUeCw0DRtObifBEVRcLvdI/W1MQwz0nXMGEwymRy46ZLL5QYGj2ZP57SYBRwzZlxDOp3OmTr5Ztq8Uqkgm81av5/EZNvtdgfulogCD4/sQLlcwkH2EOFwGIuLi0ilUq/UZGsGhK9mQBc6aHxXEsYYyqAIQyH6Yzewfd8UULoxfMnJeUilUhAEAY1GAyzLWlLBe3t7YzcFdL0+iNxfbkPJt6bqOzIpGDcPtXjxcjRVVbGzs4P5+eOu85FIBLVabaRG1J7buQd43POK2/m9KvQ/2ABoCuR+8EHi4rka3i+KWabodrtRKpVQqVTQbret7NrR8kbTOXoQLMvC5XL1qcttbm4iGAzC7/dP4ZWMRjAYxP7+ft/veJ7H3NwcyuVy38L1aPChaVqfuterlWaziXv37sHn82FxcRF379498zkMw1iGkNVqta981JQIbzQaUBQFfr8f1Wp1JL8V0zyVoijwPG9l42fSuMPBcRzm5uYGNoLrut43/x/F652uWe4s4Jgx45phmnSdhtvtRjAYRDqdHpg2n0SG46hfB0UI3LIDPMvisFiG0u0tgnZ3dyHLMhKJBCqVCg53DyB8Zg8GR6HxnQmAHd/CjZF5RH5kFenfuYPk//Lac/cIDIOmaVZteLfbtYwRE4kE1tfXx6q4QvE0XG8KofiFNELfc9xc77rBuHi01sfjOm32EDzYz0FRFG7cuIFGo4F0Oj1yv02f2/l7o0C2Bf1eFfpnU0BZAVl09vo+Fp0gwnQVxBiGgSAIx0qljvrpnITb7YbH48Hh4eGxezSbzSKfz0MQBMsp/KhZ4GXhcrmQSqWs12UGGwcHBxN1L3+Y6Ha7aDQaQysVRSIR6LqOUql07D222WwIBoMwDAO6roOm6aGbxU1omkYkEgHQ20yjaRoURfX1Xs0YTCAQ6OulepCTJPOPSmBPi1nAMWPGNWNnZ+fURYTT6YTP5zvR1XdSGQ4zlctzLHwuJ5rtDg5yBTx4tkqlgnq9jrA3iOW5BWRfo6IcZQBq/CUq4rILnnfGkPr4HSR+5nFQYwxozqJarUIURUQikbE3Q3reGsHmL38D/u9Mgj5FLvg6wLh5aJXxNNyzLHuiUSXQU61aXl62lFrOAyEECImgQyLw1hCMqtIrvXqxBP1Te0BEBLVyv/HcPXkFmHK5jMXFRWQymZG/2xzHWeV/gzAD6UajgXw+b0lrn6QKNi0eeeQR5HI5VCoViKI4CzbOgSRJQzXQm/4s9+7dQyAQQDwe71MfJISg1WphZ2fHWsSO2sNmZqzM57lcLtjt9lnAcQosy2J+fv7UoLHVap3oZ3IZ2cvrPVPNmPEqw9RKPw2Hw4FCoWAFGyzLQpZlMAwDlmVP1Oa+CGZJldtphygIKFSqaA+Qu7XYq6L8n19G/f3LCLzrFqRGAwcHBxNJobvfFUNrs4rDP91A6PuXx378kzB36RwOB1ZXV1Gv11Gv10+sQT8KIQRutxtutxvVahWFQqHvvWE9AqRH3Kh8LQvPM4MVSa4LjJuHWhpPwGG+52cRjUbRbDbHoixGnBzIkz7gSR8MRYOxXYexVoH+5SwgMj3J3RW553Y+gaC62+2i0+mMbNRHCIHT6RxKdMLEMAyUy2XQNI1wePJeNydhilGEw2E0Gg1L1nXG8LRaLbhcrhODTROO42AYBliWhcfjQa1Wg9vttgz9KIqyxqbzNn4/GKA0Go2JN/jbbDbIsoxcLnftPD/OymqYnLRWOOrJNU2uh+bfjBkzAOBY7fIgRFHs27mKRCIQBAHdbhfVahXb29vjb9C7PyHRFIWDXOHUYIN9uQzb5w/QeiaMsmxY5mPLy8twOs+vVHQShBCEPvwImndLqPzD4FrWcZ/P5/NheXkZhmHg5ZdfxsbGBur1Oux2OxYXF7G0tIRQKDQw+JNlGcvLy3A4HMhms+B5HisrKwgEAqDpV8p1PM9EUPxC6trXpNNODlpThdG9eLDZ7XaHDlonsUtPOBrUigz6AwnQP3ML9AfiAAG0/28P2q+9BO3/3YX+cgWGMt4FTqlUgsfjGcnMKxAIoNVqncuY76gi3WUjSRJu3LhxamZrxnEqlQp4nj+zTK5cLqNUKmFxcRHtdhuFQqFvnKYoauxjULfbhaqqiMfjA409LwJFUQiHw0gkEqBpGouLi5Ak6VrIjIuiiNXV1aGCDQAnSoVPSknuLGYZjhkzrhFnNeIxDAOapq2dW1Mvf21tbWILU6ckwmkXoWkayvUm9JPOoxvgn82B2a2j+f4EdLm3ONJ13XIBNg0DDw4OxiotS4sMIj9+E3u/8S3wUQlCdDgZ0VGRZRnBYBDtdruvpE3TNJTLZUspSRAEuN1uzM/PY2trC6qqwm63IxwOQ9M0pFIpK2is1+tgWRZ+vx/Ly8sol8vI5/OwzTtBiyzqLxbheM10m//GCaEIGCcHtdIBe8EmeE3TcOfOHSwsLJy5ALXZbBAEYWJynIQQICqBjkrAOyIwyh0Ya1Xoz+aAP98BSZhu504Q58VcfyuVCux2O5LJJFiWhaIoaLfb6HQ61n8fHDt4nr9QycrOzg5WVlYuxbH4QSiKwuLi4olKXDOOYxgGCoUCvF4vUqnUqY/N5/NQVdUyYDSbuzudDrxeryVgME62trbgdDrh9/shCMKJjc+DOBpEmf4u5j9ZllGr1azeOofDgVAoZL2eVquFbDZ7pbIeNE0jkUicGECcxEmmfsFgcByXNTKzgGPGjGvEWUGDKIpoNpvWzzzPo9lsTiTYoGkKPpcMGAYOckUkJSdYlh0cKHR12D6fBlF1ND+QhDGgsbbZbGJ9fR2BQABLS0vIZDLn1twfhBC1I/DdC0h/vNdETovjG/5EUUQoFAIhpC9YOIl2u42DgwP4fD7Mz89DVVUwDGO5tT/4/G63i3Q6jcPDQ/h8PiwtLfXUYj5QRfZvdq51wAEAtKtXVnXRgAPofUc2NjYQCoXg8/lOfWw8Hse9e/cufM5hIC5+sNv55w8AmQNZkXtu56HR3c4Nw7Cyn4QQa+ea53m43W4IggCGYdDpdKzgQ5IkdDqdC2Uq1tbWYLfbMTc3d+5jjBOfzwe73T5y0/KrlVqtdqKbPNAb1wzDgKqqfWNxtVqFLMuoVCpgGGas47SJpmlW5u6kPoSj0DRtiSDout4353W7XSiKgm63i93d3b5So1qthlqtBkIIBEHA/Pw88vn8pQYchBDQNA2apuF0Oi8UIJiBlAnLslN1Fz/KLOCYMeOaMEytqcPh6As4TBfscSPZBLiddlTqTdQavfOpqmrJGx6F1LsQP5OC5uPRemMUoE9eTJkLbjPbYSrSjKsETH59EK2tKjK//zIiP37zwml0juMQDAZhs9ms6x6FfD5veZiUy2VEIhFwHHdiwKKqKjKZDHK5HLxeL574p08j5QugVm4Arus7nLNj7OMwyWQyqNfrSCQSJ5ZkXNbE2+92bsDYb8BYq0D70/tu50tOkBUZJGkHGVHowDAMtNvtY5mbBwORdDqNcDiMUqk0koTpgwyzGJwmmqa96r02hsWcH056v7xeL2RZhq7rWFtbszaTzPG5WCyCYZi+Po5xwnEcGIY5dQOHYRgkEgnru5xKpc4lIGCqbKmqeqHvw0WIRCLweDxjPWYymcTa2pr182UKPsx6OGbMuAZkMpkzU8oejweiKPaVSSiKMlY3UYoQ+N0ynJKIbKFsBRvAYC8OKteC9Jc76C460X5z6NRg4yjtdtvqe1hcXByrXnjguxfRLSsoffbsfpiToGkaoVAICwsLaLVauHfv3sjBhkmlUrF2CDudzlCLYE3TcHh4iLW1NWiMjuXHVxGPx6+EbOl5YFmjp90AACAASURBVNzchc3/BlGv10+UhbwqEJqAStpBvycK+l+tgv7BRRA3D/3LWWgffQnaH21Bf74Io3GxEkMzECmXy1ZwfHh4iGj0YqIDV6GkykRVVWxtbc2CjSExDMMq2XwQQohV609RFBYWFqy/tVot0DSN5eVlFIvFib3fpqP5aSaUFEWBZVncvXsX2WwWfr//3BtJpnHrtBqq5+fnkUwmIQgCVlZWxh5sAL3vp5np5Xl+5LKscXJ9t8RmzHiVUKlUzlQSEQQBfr8fm5ubfVkQc7fvvDtQDklEo9WCrhsQeA5e2YlGq41c6fji+sGAg9mqQvhqFu23hKAmztekls/nUa1Wrd6OVCp1YWUhiu2ZAu78u+cgJBwQV4Z37CaEwOPxwO/3o1Kp4N69e2NNvXc6Hdjtw/eX6LqOKtPGCz/0+3jqP3w7kskk2u02crlcX6ZrXHi93jPLlM7Fo4+O/5j3OTw8hK7rU9ecPw+EEMAngPgEUG8MwGiabudV6H+TAnzjdTtvNpsX/jyTyeSFnj9OGIYZWu51Ro/d3V2Ioohut2stuHVdRyQS6fvOcBzX1/OkqioODw8nKh5QKpVgGAZisRgURUEul0Oj0YDNZoPb7QZN09jb2wNN0zAMA8ViEZIkIRQKHfOlGQZFUbC1tYVkMgmn02kpC45bZEWSJESjUStYn3QTdygUQrvdnrjy11nMAo4ZM644zWYTNpsNDMNYwQNFUdb/E0IgSRJKpdLAgdFMm4/aHCtwHIIeF2pNHt2uCpvAIV+uoKMMHnwt8z/DAPd8AdzLFTS/Iw7de7Fdd3MSMJusTd+Ai+yqsR4B4f9xFenfvYu5j7wWjHx2VsGcJNrtNra2tsYiqfogw2Y4jsI4OIirbqz/6bdQeW8VLpcLsVgM3W4XuVxurCUvhUJhIk25jefzqH41i/BP3hr7sYHeQv4k3flJlYOMAyIyII95gMc8MNQH3c5Jr+xq2QkSl87ldu50Oi/kXyHL8qWVpZ3E/Pw89vb2zp1xfDVgzhtm9sDswTED85NKcT0eD9LpNGRZBiFkrMIeJ2GKbbhcLoTDYTAMA13XUalULLUsVVXBcRwURUEqlcLy8jJKpdK5BCE6nQ42NjbgdDohSRICgQBUVcXGxsaFxgpBEODz+eB0Oi9l8+Mq9FmdGnCYqgTXYWdoxoyHlW63i3g8fqJ/hrnw5jgObrf72N9pmj6X94bX7YRhGHA77KjUG0jnTk+dd7tdsAwD2xcPQFUUNL4rCWOMjdmlUgm1Wg2RSASLi4tIpVJnepKchnTDDddbwj1TwP/pMRBm8DhHCEEoFILT6UQqlZpozXq32wVN07Db7SOdx/NMBLu/9SK874qhVCqhVCpBlmWEQiHouo5cLndlZEwHQbt5qOXxB3AmpVLpxICDZdmJBI/jhjAUyKITWHTC+I4ocNiGvlaB/rcHQKkDsuDoBSALDpAhzSBlWR5KansQFEVduBxrUpjj5STUk64jHMchEAjAbrefOheYa72TyuREUQTLslYfwDQbq83Ag+M4aJpmXYPH47F8QhRFga7ryOfzCAQC5y6nNBvWzfJkURSxtLRklax2Oh1rPho0dtA0bTVnS5IEl8s1W0fjjICj2+3i9u3bCIfDY62hnjFjxvDQNI1ut4uNjY0TH3NWacVwO1EGgN5xJJsAUeBBEYKuqsLGc6ApCuopE4xaa4HzUYBmoPGdCeCEBfxFUFUVu7u7kGUZiUQClUoF2Wz23NkO73sTaG1VkfvzLQS+Z/HY3202G2KxGFqtliWjOGl2d3cRjUZxeHg4tPqLELWDD4qofjMP+ameRnulUkGlUoHD4UAgEEAwGLTcma8ak2gaP8ppTaChUAg7OzsTO/ckIIQAQRvooK3ndl7rHnc7X+6VXhHP4AwEz/OWS/SoCIKAhYWFK72ICofDoGnaMqg7CUEQoKrqVHbrLwuWZU9VoxoWjuOgqioMw8CdO3cupVeGpmnMzc2hWq2iVCrB4XCg3W73fX7FYhE+n28ssteDGrl5nkcoFIKiKMcCDkEQsLS0dKFzPqwMtQ1iTnwsyyIUCl2pJrEZMx527HY7tre3Jza4U6QBv+//hmR7DrouIVf4MYR9HwJFCFRVg6ppULrqqUENVeqA+9sU6P/tBlrviAATNlGqVCqo1+sIh8NYXl4eSop2EIQQRH54Fdu/8g0I8044n/Rbvw8EAnC5XDg4OLhQ2cmoNBoNqxZ5FLlJzzNR5D+9C+fr+psmTdlHu90Ov9+PQCCAfD6Pcrl8ZZprKTsLXdGgKxoo7rhk8kU5rVHS4XBcuLTosiEOFuS1XuC1XhhdHcZWred2/pVDwMaArDhBLctA9BW3c1mWz/WaCSFXPtgwCQQCYBgG6XS67/eEELhcLgSDQTAMg/39/YlIu14VxrVRQlHUwCz6tJAkCfF4HOl02rp3B93DhmEgn88jkUhYmw3mWFcoFIbKHouiiGQy2We2+iCD/jbbnD+ZoQIOTdPQarXQarVQrVZht9sRi8XOVaYxY8aM0TDrpDc2NiayQPR7fxt227Poal4Q0kHQ/+vIFaNotuPoqmdPVPR+HbYvZtB5vR+qpoHluPE7mQ9A0zTs7+/DbrcjHo9je3v7XLtZtMQi+mM3sfdbL4KPSJDnPIjFYuh0OlPLajxIpVLB3NwcQqHQ0D0T9kc9yH5yA62tKsSF4yorZgOkKIp9gcckVWaGhRAC5r4XBxc8WZHmvJylzBKLxXD37t0r28sxCoSlQFZkYEXufa7pJvS1KrS/2gMaKsiiE2TFCefS0pmGb4MIhULXItgw8Xg88Hg8UFUV9XodhJBjKkQOh+OhDjjGqX4UCoUmNhedBsMwCIfDSKVSQ5WHFgoFtFotEEKsDRiO4xAKhc70aUkkEn1u6icRDAaPmWdOS+HqOnKuUaNer+Pll18e97XMmDHjBARBmFjTl2j7JrqaBwAFw7ABRIeBO0MFG+ztEmxfyqD1rii6SzK63e7UNyLq9TpyuRwCgcC5VXuEhAOBD83DXuYwl0wil8thb2/v0syfut0udnZ24PF4Tt1hOwqhCNxvi6L4+fSpj2s2m9jZ2cHOzg5EUcTKygp8Pt+lLyLNgGMSnBWIUhSF+fn5iZz7MiGEgEQl0O8Ig/mJVdA/ugISsoFLdUHVVNQ+8SL0Z/MwqqdLElMUBbvdDlmWr+0OLsMwcLlcAxeElykVOmn8fv9YAw6KoqaqTMbzPBKJhFWmNMqY2Gw20Wg0rM0Wc3PlNCXAeDw+VLAB9O6po8qMZnnejMGce2Vgs73iCNtqtXB4eGg1ykiSZOkmmxbxplay1+u99IltxozriCRJYBhm7AOapsmg6Dp0XQJgAAbAGk54WAYGDNCEgAJBW9dRNYMQ3YDwtUPQB0003p+A4eyVWZrSuBdp5j4PxWIRdrsdKysryOfzKJVKI+1W8zyPJz/8ZjR2KvjyL/01PN89d2HJ0YvidrtRKpVGCnpcbwgi/1c76BbbYD2nq4O1223s7e2B53n4/X6srKygWCyiUCiAYRhEo9G+92DSgSQzwcbxYZrCbTYbbt68iVwuh1wuN5HruGxojwD7u33wer2o1BqgHvfCuFeB/oX7bufLTlAr8jG382Qy+VAvyh9WPB7PhVyqT4LjOMzPz2Nra2vsxz6K2+1GMBjE4eEh9vf3oes6YrEY/H7/udXyzP6OQWVVwWBwqAyFpmkoFouoVqt92fx2u421tbW+BvMZr3DqDEJRlDXJmEo3oijC4XBYb6amadjc3OxLr5mDtfncowukbDYLSZKsfpBZWdaMGcMziR33XPFfIhT4VTB0AYCBVvsW9M5TCAgsDMOAavSayRXl/gJe0SB+rreL3vhAAjhScz/I/G8aGIaBnZ0dS3owEAigXq9jf3//1NQ/RVHweDzw+XzIZrMotPKo3SuC+gIH9zOXq8Bjt9uP1Z6fBW1jID8dRPFLaQQ/tHD2E9BbjO/v71sGUcvLy2i32zAMo+/8hmFMtFSOcfNQS5Nx+B3WOZiiKASDQdjt9okvpqbF0eyE3W5Hs9m0FH+omy7gpusVt/N7FWh/tgMoek9u9zVuUHH7LNi4ZsiybEnITgpJkhCLxZBKpcZWXsVxnNVXY2YxNjc3+76/tVrtXL4VLMvC7/ef2LvkdrtPVLI7imlKe9pr3t3dxcrKysjX+LBz6t3I8zxWV1dPPYBhGKBpeuCuq9frtSQZj2I2d3a7XQQCAdA0PYsGZ8wYgknUzbbat7Cf/iXw/AZ0XUSz9TgAAtLpws0yICCgSU+/iqkq4D+TghYW0X46AFD9WYDLCjhM2u029vf3QVEUlpeXLanEo9A0DafTCYfDYZmEbWxsoNvtgmJpRH7sJnb/wzchJB2wzQ+XWh83hBDwPH+unhTP2yPY+tXn4H9vEhQ/fAO2oihIp9M4PDy06vQvqvAyCoyLR2dvMtK9hmGc6C0wCEmSprKDOykGBRnVahXpdHrgpgWhCUjSDiTtwLujMArtnt/HcwUQicXBb34N0uMhiI8FwTgfvrn6snuYxoFpShoMBqdWReJyueByuZDL5ZDNZi98PL/fD1VVUSgUoOs6Op3Osc+m2+3C6XRiaWkJmqYhnU6fmcGkKMpStrp3796x9SohZCiJ51ardapapMko5q2vJi4c/jIMg9XVVei6fkwm7SzX3EajYQ3oj07QaXbGjIeFSZRUAUBXjaCrRvp+V+yqYCkCO02jomowsi14PrsP7QkfaqsyoB+fpLvdrlVOeZnoug5d1yGKIgRBAMMwlguxIAio1+uoVCpWmv4onN+G0A+uIP2JO0h+5LVgHNNX5eN5HoqinGshxPlsEBdlVP4hC/dbI2c/4QFUVUW1Wp168yPj5tB4YTIZDqDnWh+JDP9+SJIEj8eDYrE4sWsaJ4OCjEqlcmKQcRrEK4B4BVDoLcaF13rR/NYhCn/0EtiQvRd8PB4CF3FceunhOLjur8FutyORSFxaufqwPRVnHcPpdGJtbe3U+7XZbGJtbQ0MwyCZTA712Zl9H7VabeD8Oeyclc/nhzrXKOPMq4mx5dsoigLHcX2R5iiujC+++CJYlsX8/PxMdnfGjBMQRXGq8p2HnS7AA9U7BdB/f4j620IQkjK8DA0dBuqqhob2ynf8sjMcR2k0GnC73ZbGviAI6HQ6Q0kM21/jRWu7ivTv3EX8px89l4vzRbiofrznmSgyf7gO11vC51pMGYYx9UUY4xagliaXUalWqyMvBPx+/5UKOAgh4DjO+seybN/PZrnUeYKM085pezIE95vmYKg6Wmt5NJ7PIPMbXwMIrODDtuw90TzzqnOd+0qPOoVfFh6PB/l8fujSxUG43W5Uq9Wh7lvTC2TYLGyhULDMAhVFweHhIZrN5sjXeNaYSFHULNg4hXMFHJubm9B1HTzPQxRFiKIInuexuLiItbU1a3L3+/04ODgY+rjdbhdra2tIJpN9NXqKolg3oTngXucBYsaM8zLtYNwwDJS/kga7UUXzfXHobh51TUNd0yBQFBwMDZll0FA1/NZ/+k/4+6/9Az74wQ/iPe95T99xPvnJT+Kzn/0sbt26hZ/6qZ/Cpz71KTz33HP4+Z//+YHn/ehHP4pIJILv+77vO/e1P9j/EAqF0O12h84a+N4/h/3f/Bbyn9qB/4PTVTC6aMAhLssgDEHjTgn2m+NTqJkkjJuDWp5chkNVVbTb7ZHKd1mWnVhW8Sw4jrMksc3AgqZpKIqCbrcLRVGgKAoajQYURUEwGES9Xh+bvKssyxAEwfoH9NzOxZsBiDcDMP6ZASVVRfP5LIqfvINutg7brQCkx4IQHw2Ctl+fjUOzX/W6KQxNUr1wVObn58+tXspxHDweD/b29oZ+jiiKQ4uTGIZhOYe73W5L9nx3dxeGYaDRaKBcLp9pjnhWJucyPUrOQtM0KwFA0/SlrKFHDjgURbEiw3a7faJrLU3T53YxPRrhlstl7O/vH3sMIQSRSORKf8AzZowbnh/sGjwRVB22Lx6ANFU0visJw9Y/XLR1HW1FB0MI7AwFB00j4HHjK1/5Mt72trdZ16ppGv7xH//R+q7SdAWETK834LwQiiD8I6vY+ZXnIMw54XhsenKgNpvtTIfk0yCEwPOOKIqfT50r4LiMDAdlYwDDgNZUQYuTaXZdX18fueQhFAoNnIMmhakaZrfbUS6XUa/XreDitAVxLpdDPB6/cEaGoigsLS2dublBCAEfk8HHZLjfvwK13EbzW1nUn00j9/svgE/IkJ4IQXwsBC549WvabTbbUP4OVwWO466UASPLsgiHwyNtMgOAz+eDz+ezfDOGRRTFU7MUhBCIoghN0/qc5M3AIxaLIRQKWddrejqd1mh/2vwrSdJEFMHGgaqquHv3rvUzIcSaj0ulElZXV8dSFncW5xrVCSFn7hI2Gg3UajU4nU4UCgUAvQ/LLLniOM6qm6Np2pKx9Pv9fVHmSY6QpoLKLOCY8WriqBz1JCFNFeJn9qHLHJrvjQOnlEqohoFyV0NV1RCNRKEC2Ln9El771FNoaDpeeuklMAyDGzdEGMankUx8EX5/GZLEg+O2oShzU3lN54FxcIj8ixtI/ceXwIefAOefzvt/0QwHADhf58fhX2yhk2mCD43eVzPtgMMy/yt3JhZwALDkLOfm5obKdrhcLuTz+ak00EciETgcDhQKBaTT6ZGknVutFhRFgcvlulCWw+l0niuTyrgEON+ahPOtSegdFa27vdKr8qe/DEpk7jedhyAseiy386uELMvXJuBgWRZLS0tXJtgw8Xq9KBaLQ8lQm7TbbWiaNrIUNUVRfeex2+0ghFifYSAQgNPphGEYYBgGiqJge3vb+k6l02ksLS2hXq9bz9nY2MAjjzxy4jk9Hg8EQUA2m7XEj3ieRzwev9LCRw9uXhmG0bcxUavVzszujIORR3WO43Djxg1kMhlUKhU4nU64XC50Oh0oigJBEEDTNCqVCnK5nPXhiqKIhYUFtFotK019lHA4DF3Xj32BRFE8cfAcRlVgxoyHiWk4IVOFNsTPpKA8IkN53AsMufA0AHR0He9617vwmU9/Gm9++mnILIPf/drX8MzbI2h3/gTVKoGqRaHrKmg6h2jk/8B+6pfQ7V7d77Jt3gnvexNIf/w2Ev/zE6C4ye4EsSwLXdcvXINPsTRcbw6j+IUUwt+/PNJzL0u1h3Hz0ModIDJZGVafz4eDgwMkk8mhFm1zc3N9O4STwOVyQRRFrK2tnfv9z+VyCIfDFwo4xmHsR/G9AEN6PATDMNDZKaPxzQzyf/AtqOUWxEeDvezHzQAo4WpI4w9r9nbZSJI09H17Gfj9/pEygvV6Hd1ud2SBBjMLy/M8QqEQOI6DruuIRCLWZsn6+rqV2QiHw0gmk1YPn67r2N/fRzwex/r6OjRNQ7fbRTqdPjUDKooi5ufnLWGS62DtcNZ4MC1VrXO9U2ZjzNEP5UGdbofDgWw2a0WtiUQCwOk7tIO+QB6PB5IkWT4gM2a8mpm0oR6zW4Pwdxm03xiEek5J2Keffhof+9jH8NJ+CpIg4Fu3X8LP/GvgD/6YBQwaPYFdwDB4EKLA5fpz5HL/aoyvYvy43hZBa7OK7B+uI/ThlYnu/p8kM34e3G8JY/MXv47Ad82BFkdr5r8M5R7GzaNbnIz5n4nP54MkSTg8PEQ+n0cgEDj7uhgGkUhkoC8KRVFwOp0XWuSbvlTDCBqcRqPRgK7rcDgcQ+/WS5IEnudhGAY8Hs/Ys6iEEAhzbghzbnj/yQ10C000X8ii+sUdHH7iOQhLHktyl/VensIdRVEjCd1cBl6vF+Fw+LIv41TOE7hlMhkkk0mUy+Wh33/zfvX7/Tg8PLSCFXPDRtf1vu/SwcEBYrEY4vE4dnd3AcASWYhGo9bvisUiZFk+03vGvF+uOu12+8z3dFqvY6Ir+GAwCEEQrJTWeZlq3fqMGVeYiQUchgHuxRK4l4povicG/QKlQzzP46mnnsJXv/pV2Gw2zC/F4Q4+C13nQAwVTEOF0ewtqFXNCUl6Flfd2JkQgtAPrmDnV59D5SsZuN48uUl/nIseVuZhf9SD8lcy8L47PvTzLi3D4ZqM27jd3jOvE0URLMtawie5XA4+n2+oCdfc/NrY2Oj7fAKBAFwuF7xeLzRNA8uyIIRY/zRNQ6VSQbfbRbfbhaqqoGkamqZZZVrRaBSFQmEsZVv5fB5+v3+ogMPcrZ0mrFeE/I55yO+Yh97qonk7h8Y3Myj+xV0wbtt91asg+KRr6kEvz/MT39Q5D4QQxOPxa5GFoShqqLL7o5j9wIlEAtvb20M9p9lsghCCXC7Xlw0+zZx0f38fyWQSfr/f2gw/PDzEwsJCX4Zle3sbN27cuBYBxVmYpV+nkU6nEYvFJn4tE08ZTFvLfcaMh5mJTIaaAeGrWdD5FhofSMKwX0zWttvt4p3vfCc++tGPgjJofNvqa1HLfwGlTBPNtoFOpQ2mpQEGQIgOw7gaMrpnQfE0Ij9+E7sffR58zA5bcnS322EYdbI+C88zUex/7DY874gOLe97GU3jAMB4eLTXBwuRnJdwOAxJkqwy32azaQUMhmEMneUAegtSn89n1UQzDAOXy4X19XWrJ9F0aTePz3Ec7HY7bDYbnE4nGIaxVB7T6TQcDgcoihq5hv0kqtUqAoGAZWp51uu5TCgbC/vrIrC/LgJD09HeKKH5QgaHH/8G9LYK8TW90ivbqn/ipYxAL9tz1QKOy/bYOA/nGcMymQwSiQSi0ShSqdSZj6/VaufqualWq32+G4ZhYG9vDwsLC2g0GpbZ4Pb2NhYWFkY+/lXjtADMpFwuPxwBx4wZM8aDORiOE9LWYPtcCgZDofH+JMBebFLTujoO1vNI+hex/0IOitLBu5c+hFbzJlzBb4Cqc2ADIggpAm0VNFVFufLBMb2a06FpeqjB9zT4kIjQ9y8h/YnbmPvIk6Cl8QdL4y7rsCUcYD08as8X4HzSP7bjTgLGxaNbGt897nA4IIqildEYRC6XGzrgAHqZjlwu17egMs0SB6Gq6kA1HVmW4ff7Ua1Wkclkhj7/MOTzefh8vmMBhyn9SghBKBQaS7/GuCA0BduKF7YVL7zfewtKpo7mCxmUP72O7Me+Dtuqr5f9eE0QjDyZBl1Zlocyd5sWD1oEXAdUVT33+LW/v4/5+Xn4fL6JfQ6aph0L3hRFQTabRSwWw+bmJgzDQLPZRLFYhMdzPWTFT2KY8txpbS7NAo4ZM64J5qKEpmmrPlWWZTidTmtHKZfLDV2WQVUU2P5mH2rCjs5TfuAcyjG6piO/U8HB3Tzufn4bpXwF9xZ38O4ffjN++dd+Ec5Qr4xFoX0g1E+CIi0YjAYi6ND1Fu7dFpEtvRaa1tNf5zhuItKCdrsddrv9QlKzJo7X+tHaqiL9u3cR+6lHxz5Y2+32sZm2mXieiaL4udTQAcelZTjMpvExYbrKn7YAMnX4z6rZNmEYBsvLy1hbWwPP86AoyiqRGoVKpXKirPxFqVQqEEXRGhdkWUYkEpmK9OW44EJ2cKEluL59CVpdQfPFLBrPZ15xO3+sV3rFRZ1ju1enpQI4LNct2AB6MqvDclS5FOiJouzu7mJxcRHVavVCRoInoWnawO9BqVSC3W5HOBy2erXS6TTa7fa1NvMbZlya1n0/CzhmzLgmmOUb4XDYWki0222USiWrdjyZTKJWq6FQKJyaDaHTDdg+f4DO63zoPjKaHF4t30T6Th4Hd/PIrBVg99gQXvUhfNOPiODF4x9aguxzILYStnZXFCWJcuX9UNVvgFBd6AyN9JYL//rDXRih37QWDPF4HD/3cz93/jdpABzHIRaLYXd398IZDhP/B+ex+xsvoPDXu/C9LzmWYzIMg1gsBkLISAZYw+B4zIvsJzfR2qlNrBRsHDBuHmpJGVvAY7pvn0U+nx864DCPa7PZEI1GsbOzM/YA8aKYgdDDUodO2zk43hCH4w1xy+28+UIWmf/zHwDgvt9HELYV34Xdzs8TPE6CaSkHjZthg2ifz4dQKISNjY2+MrZut4tcLodIJDJ0P8comGqqDwY7AJBKpZBMJhGLxZBKpSz52Gq1ivn5+UsvQRwFRVGwubk51Pd/WplOclqd3VNPPWU8++yzU7mQGTNmnE46nbbUdRRFGahmRNM0vF4v3G43FEXBwcHBsYwH+3IZ/NfzaD0ThjaE/KjS7CKzVkD6bi/IUBUdkVUvwjd8CD/ig815fBBOJBJotVon1qXbcw3wpRa0Z3M4vOUH97hvhHdiNOLxOJrNpuUHNC7USgfbv/Icwv98BdIF3bwlSUIsFkOpVBpLFmYQhc/uo52qI/pDq2c+1tSWX19fn8i1nMbWR76CxP/+baAv2EsEACsrK9jZ2TmzFJGiKNy8eXOkY29vb6PRaFxag/1JLC0tXWlPgHFiGAaUdA3Nb2bQeCGDbqYO201/L/vxmvO5nW9vb5/o/zUN7HY7IpHIubxQrgIvvfTSqd8JhmGQTCatXXVFUbC2ttb3GEIIbty4gXv37o1tk+gosiwjFAphc3Pz2PHNBn1CiOVEbhKPx69NX3Kj0cDW1taZj+M4bqyeLoSQrxuG8dSgv80yHDNmXBPK5XKfTvmg2kxN03B4eIjDw0O43W4kk0lsbGz0Hqsb4J/Ngd2to/n+BHR58IRmlUndyePg5TxK+zX4F9wI3/Dhkbcm4Io4ztx9Zln21BrcjsTCVm4Bi04wn0vBWHGB2CYzHHEcN7aG3KMwMo/Ij6wi/Tt3kPzZ14L1nm+RFwgE4Ha7sb+/P5SiyHlxvTGI9X+zi26lA1Y+HiQSQsCy7KXv7jLu++Z/Fww4zN3IYfqeTE3+URonVVW9csEGTdOvmmADuO92HnWCjzp7bufVNpovZFH/Rhq5/3Lf7fy+4SAXGi5j4PV6px5wMAwDn88Hj8dz7TNSsiyfKBHt9/uPlcxyHHesb81uRdwLJQAAIABJREFUt6Pdbk8k2AB6WRiapjE3N4etra2+udQwDOzu7h5zIgeAvb09S+nuqjOMMmwsFpuK4Z/JLOCYMeMacNREc1hKpRJomkYikcDW2gaEz6dAFB2NDyQBGwP2fgOpYRio5hr3A4wCMmsFrL5hHo+8aQFPve8x2L020A+oG50UcJhSoCzLnlrK0rWxYFQdpWUPfIctpP5mH7YPzo30+gZh1tOzLAue563U+SRqgQFAXHbB8644Up+4g8TPPA5qxKZ7WZbhcDgs46lJQossnK/zo/SlAwQ+MHfs77FYDKIoWvry03DWHgTj4qEWO+BjFyspGcWLAugF9IqiYG5ubqhF36TuqYtwHRZCk4RxCnC+JQnnW5LQFQ2tuzk0n88i/e+/DEpgID7WMyMUFt0nKraZQgPDlOJdFIfDgWRyPCWZV4VYLIZIJIJqtYpqtYp2uw2appFMJk9cBLMs27cxMKoJ4HkoFotgGAbxeHxgJiCbzWJxcRGZTKZvY2FjYwMrKytXPjA8q19LkqSpBhvALOCYMePKYyponIdMOov6fgsx1oWcLYPWO6IATbAwNw+KUIBB8M3P3cFLX9jBzbcs4JnvfiMYgYFkF4/tUp20m/vg7w3DONtplhAoNhagATLvBP+ZA6h7dTDx0RaZkUjEMgY1m+l1XUe320Wn00G73cbW1tZEzbzc74yitVXF4Z9sIPTPRnP0lmUZhUJhalkFzzNR7Hz0efi+Iw6KfWVCstvtEAShz+X6MprGgVcyHBfF4XCMrHTTbDZx9+5dzM/Pn9pIedlZoEE4nc5r3dw6biiOhvRYCNJjIfiMx9DZKaP5fBb5P/wW1OJ9t/PHgxBvBUDZ+gO1ubk53LlzZ+IZrFAoNNHjXxYURcHlcg29oD3aT+F2u2Gz2SwjvklSLpdPvEZzDrHb7X0bF6qq4uDgANFodOLXdxHOCohG6VkbF7OAY8aMK4yu60PVYQ6i01Dwd7/893ikqEL+v/4HiO99FF/7r3+PZlFB8iNz+I8//4dYfn0Cr3n7I3ji3atotVq9hr82kC/kJq5H35FYcC0VtYSMwBMtbP3ZNuw/fQuE6mVI3G43JEmCIAiW+paZQaFpGk6nE4ZhWE27l7UItEwB/91zqHwtC/np4VS2KIqCJElnB2djhA+KEOJ2VJ/NwfXG3mKHEIJIJGI1SZpcmvmfm4d6QWlciqIshaoHf2+z2U4tXdN1HRsbG/B4PCcu4DVNuxKO1DRNw+fzwev1Xvkd18vkqNu550OrPbfzb2VR/fIuDn/3mxAW3PcNB0Ngvb0sXzQaneh3k6Koa9WEPEkEQUC1WoXH44HP58P29vZUxh+Kok6dN9rt9sBemkqlci0CDlMGexCXce/NAo4ZM64o6XR66LQyx+7C5fpz6JqIUvl7Uclx+Pt/+yWstgm+nCvjj973m/g3f/3TeOrdj0EOOKCgg3f/9LcBAKrNMqrrg2tuJ4kicZAPaqgG7TDCIpw7LdCbbYTfsQJJklAul3F4eAhVVS0jM47joKoqOp0Oms0m8vn8laijp0UG0R+/id1ffwF8TIIQPTtTY7fb+0zopoXnHTEc/tkm5DcEQQiB2+1Gu92eaP/IKDAuHs07w0trDkIUxT4DPhOv14tAIIBSqYSDgwPQNA1ZltFoNI6VkJnqNAsLC8cWHRzHTaXsYxA8z0OWZXg8nqHqtGcch/WKkJ+Zh/zMPPS2iubtQzSfz6D4ly+DkYVe6dUTIdhstoltvFyFgPWqYO62m6aVk+rdeBAzK34SZiD0IGYm/aoH+cFg8EQTxUqlMvUG+NloNWPGFWXYkhZC2oiEfgEU1QCIDo7bw3//wddhjjD4q0IZLRsNhqOQOUzjsdc/imazOXajsfOg2FgwigqiG6hFnFj4iRUQpxOFYhmpVKpvIjBlYufm5pDL5a7M4vgofERC4HsWkP7t20j+r0+CFk8fXmVZPtEsbpJIqy4YmoHmvQqkFRc8Ho+lO38VoMdQUtXpdKweHtM5GOiVa2xtbcHj8Vh12LVaDX6/33qcpmkoFotoNBpQVRVra2uIRqNwu9195wiFQlMLOCRJgs/ngyRJV36Rc92gBAb2JyOwPxmBoRtob5bQfP4Ah7/zHEhLgfG9IRiFNkhYBLmgMeqDXIdF6zQwyxdVVUWlUkE4HB5rdsnMJjEMA0VRoCg96W2/399XLhWJRMCyLIrFImq1GgRBOLGXrVwuX3lTQLfbjVarNXCcenAOnca9OAs4Zsy4ooTDYdjtduzs7Jz6OJqugKIbUFUPYKiwtdfwnvf9ADYTNjy6V0H6dh7FVBXFdK+Br1arXY0a9Pt9HHyzC2kuAtbhwsZvfw7lrALpny8NfIphGFfavEz+tiBam1Uc/N7LiP7Lm6cGjSzLXor0JSGkZwT4+RRct/zgOG7sDvYXgR1DSZWqqqBpGrFYDBzHQVEUqKpquX43m03YbDZ0Oh3oug6WZcGy7P/P3puHSZLe9Z3fuDMjMiLv+6rKquprWtMzI2mkkYRGIEu2BEhggXZB5pAQXnsPzGKzfpbH+3jtfxZz7cN6ba85BCysVrIMyAaBQLDilIw0Uk/P1d11n1l532dEZMT+kRPRlVWZWZlVmVVZPfl5nnlmpvOKzuN939/1/YIgCLAsi2AwCF3XkcvlUC6XcXBwAIIgevq9T2tZmBQXrSTzRoYgCViXXbAuu+D+yBNQMnVsvraGdklG5zObIOI2ENfsIJYlEOL5B/Tr9fqVNPebNCRJgmEYKIqCVCqFxcVFeL3eM6sLkiQJv99vioYQBGGuASzLmmp8uq6bviGiKEIQBGSzWXi9XoRCIWiaNnCvLJfLMx9wAN0gSpblE+2lnU4Hr776ao+8Ps/zCIVCU1O6mwccc+bMMKIowu/3Dxwat1gsIIgo2u0ELMw6iKqM+va7oP1XK1igSSy8fj/DSK3T6cxUGwYR8iC2EodCAnvrW3B5WRS+WYTysASmjyFhtVqdWGWAYRiQJDnxw7bv7y5h7xfvofAn+3C/Lzrwfru7u4jH49A0bSqyvcOwP+tD5ve30UzVoC6qcDgcE/cpOSuUg4VaPp/5nzGEur6+3pVOfb3acTRbedxszGjjqNfrKBaLEEURPp8PHMchk8lgf38fBEH0tCFIkjS1KgdJklhaWpr3+V8ijE+Aiwgj7aFBrEjQN6rQ18rQ/jQJuDgQ1ySQK3bAZznTd3UecDxCkiTk83lTljaRSKDdbp9prQ+Hw9B1HZlMBu12u29SgOM4OBwOLC0toVarQRAE7O3todFooFQqwWq1mop1/dqupj3jOEkcDkdfqWdd13vem0ajgfX1dTAMg2AwCEmSJnods3PymDNnTl+MTA9FUaBp2hycFkURdrsdmqZBbf1faH/jPwAhH4S3fCfY3f0e2U5jM6zX67Db7ZfSe34cp9MJt8eD+r117PM6QAEWnoHnfQFk/9MO6P9ROtHCYJSx3W732AdkQRDg8/nAsqzpJqzrOnRdR6lUQqlUmkjvMMmQCH3iJnZ+7i6scRH8td7AiSRJEAQBVVWRzWYvxUiKZCk4nwvAbemW3Gcl2AAAkqFAWml0KjLoPn4ho3A0uNB1Ha1Wa2yZ32q1imaziaWlJaiqikKhgL29PZAkaR4S/X7/xH5Lhnu5ruuwWq3zQfAZwel0Ip1Og7DSIG47gdtO6B0N+l4d+moFnc9tAboOYsUO4poEImYb2e18liqLl43L5TLXIVVVsbu7i8XFxbEDDrfbDYZhsLW1NXS+r91uI51OI5vNwuVyodVq9UghN5tNMyDs555+VeY4gNE8OY6iKAp2d3fhdDonOhw/DzjmzLkCOBwOcBwHnuehaVpPr7mNtoIsk6BvfgyqhYSuEwgEAn1lBavVqtmnelGDeQaiKEIURdTrdbAsC7fbje3NLTh3UiCueaFTJCohEa6NAophHu0vJ2F5f68Rm6Zp2NnZQSKRgCzLI/sssCyLaDSKZDKJZrPZ83e3Wq1mpqvRaGBvb69noxr3vRIEAaQogv6xN2Pz372I+E/cMQ/OdrsdwWAQBEGYw3w0TcNisaDT6VzoZ+J8dwil17KwLMxehpV2sFCLZw84BEGYSAZSVVVsbW0hGo2aGdCdnR0sLi6acswEQZxbuKCfIdqc2aDfYY2gSBALIrAgQn9fCMi1oa+Wof1FGsjtgFgUu8HHsjTU0HTa7XhXCY7jzEQQANP4b9gcxXGsViu8Xi82NjZG/k1qmjZQPrtarQ4MOICrMcdRLBaRTqd7BuQFQQDP8wCATCYz8LGTlkafBxxz5lwBms0mCIIwB1utVivsdjsYGah/eQ22912HIHWVPsrl8sBFRNM0ZDIZJBIJs3x8EdhsNoRCIeTzedjtdnQ6HWxubnYH+KwM2IaCtshBEVgoAgvPO7w4/M1NME+5Qfl6/RAURcH+/j5CodDIAYfNZjONqI7TbDbRbDaRSqUQCoWwsLBgbkButxtWqxWKoqBQKKBUKp0or7tcLvh8PnODMwIH/7v8uP6OJ3Dw15voeBm4vW7wPI/t7W2QJIloNGoGheFwGFarFffv37+w+RrGyUFYtEFON4EZS9I98uIYPxgiSRKSJE1MGEGWZWxubiIej5vVxq2tLaysrIDjuLGCDaO6RZKkqXQliuKVyJK+kRmWdCAIAvBaQHgtIN/ph15Xoa+XoT8oQ/viAeC3gDSqH+7e3viZmKWbIRKJBNbW1sz/b7VaJwIOY76gXxBiqBtOMnEzTMXqKgSM/ebMFEWBx+Mxh+kNUZbjTFpJbR5wzJlzRTCGWgmCgKqo2P3MV4CNEhp/K4z03vbIz2MYzfl8Pmxvj/648yBJErLZbN/2E5lnwdVltMVuNrsSFOFZz6P0bUE0P78N4UdvnMi0tFot0DQ9cvVhWJbKQNd1HBwcwOfzwel0giAIlMtlbG9vQxAEM7AolUqoVqvd4WuXyyzfdzodkCTZ08rGMAwopYOQO4qWLmN9fd08oNZqNdjtdmxtbUEQBEQikQs9gLAsi8hzi/jSP/wcoj/+JhDk5Rj99eM8XhxOp3PiwgiGmeXy8jJqtRqazSbW1tbMAcvTMrAkSeLGjRvzwOKKYrFYRj7EEgIN4o4buOOGrmjQd2rd6sdvbQAM2Q08VuwgosJMSHrPEsZcxXHTWQOSJLG8vIxms4mNjY0Tt7daLXg8noldD8MwQ4OKyxD9GBejs+Bocq7dbkOWZVgsFtjt9p6g5GjwUSqVYLFYJvaezgOOOXOuACzLmhlbRifB/WUSQtyLzscT4CjCnEXo90+z2TyRqajVahfqcmu1WlEs9vdWaAsspPQRJ1eeQdvGwullkPpmHsrdPNhnehe8TqeDWq2GRCIBgiDQarVM+b/jBwO73Q6WZU8NOAz6VYfq9Trq9ToYhjEDD03T0Gw2T7RgHUVRFLTcCr709/8DvB9ehPSM17wtlUpheXkZsizD6+3++UWoHhlIkgRVU+F+wo/aKwWIT7ov5HVHgXacPeBwuVwDtefPg6qqODg4QCwWw+7uLprNJmq12qmHRq/XC6/XOw82rjDHD2yjQjAkiGUJWO6alCLVhLZagfalA1AfioFON1GrHsB6yweKP7/q1ePA0b1K07QeVULjvwd9Fs1m05TYnQQMwwztAmCYq/GZRaNRPHjwoOe9PapEddR1nCRJ7O3tmfdVFMVMsBmGqmddy6YWcBgtE7qum+6Rc+bMORtG24XX7QHVAYjr11BrNSDLsln1OPqPMROg6zosFgvq9Tqq1aqpOtHpdE492PI8j06nc+7BRkmSQNP0wCywbGXAtFUQHQ061V3IqkERntU8Kh+Oo/5b66BvOEAe87UwMjHGDITP54MsyycCG6/Xi2QyOZFsoqIoAxXDBkEJDMKfvIm9f/MKuBAPLtBd3DudDtLpNILBIJrNJhqNBoLB4MDy9qRRFAXNZhPP/Hfvxp//L78/WwGHk0N776SqyjAMd2hFUabWKlitVlGpVLCwsGDOUe3s7JjVR2OTNkz5SJKcS9o+BjgcDhweHp5rDSEIAgjyoII88HwA0HS4SKHH7dwwHGTc/ASv/mpxtDJZLBYRiUTMYXLjoMvz/OsKjd39zlCZ63Q6psz1JNqqTnueq6IgR5IkFhYWsLm5CQBDZW9FUcSNGzeQTCZRKpWQz+d7REVYlsW1a9fOdB1TCThUVcXa2pr5xUmlUtA0DT6fz7x9Z2cHoVBootHonDmPK5IkIZfNIfXlF9BiNcg3HcCQga5r164hnU6jXq+bPe02m82cV7BYLHA4HGZLSCqVMg9poiiaSh8kSSKdTg8scZ+GMbuxvb09eLMmCSiWR3McAKBaGbQlDnYWkG870frDPfAfWez7cFVVUavV4HA4IEkSAoEANE1DMplEtVodGuxcFJaoCO+HF5H8lfuI/+TTILlupq5UKqHRaJiD/Fardaruxkcpl8tdky1/AME7UTT3a7BETndIvwi6LVUyOI5DIpEwZ2gGKULRNI14PI5WqzVRw7Dj8DwPu91uDqUaBxye55FIJKb2uscxBmqtVutMyVw/rpAkiWAwOFGDTLvTAeeTUTjfk4DWVtF4NYPGS2kUv7AK2s51g487fnCLzokP784yRxNhzWYTnU4HNpsNtVrNbGGy2WxYXu71aqrX69jf30e5XAZFUWcOOAzpa4/HY3YIDOIq/fZ4nkckEsH+/v6pg+4kSSISiSASiWBzc7MngSPLMjKZjHmeH4eJv1ulUtcl2DhcGD8Uo69Z0zQ8fPgQuq5jb2/vzJHSnDlvJJRXUrD8zQFKz7oAavjmQxAEKIoyF0pN00zZV4NqtWr2p+ZyOcRiMVSrVXOILJfLoVQqgWVZJBIJVCqVsQfIjLmEnZ2dUw/8bYEF13g0xwG8XuV4mEPtvSFUfvFVqNtV0EMUlYxs09raWnc+IRIxlYRmYTjT8VwAzc0KUv/PKoIfv9GzNmazWUQiEdRqNXAcd6Ea70pHhXjNiYPfeRGhv3f9wl53GJE7i3jzdzwHTdeQz+dNQ75BGAICwxRXzouxCR8cHPTM6QAX18utaRq2t7fNA8BFBzpvZFwuFzKZzMRaHo+2tJJcH7fzl1LI/MaL0Goy+Cf9EO4EYL3pBcldnUPuWTgeXBUKBbhcLtRqtaGHXEEQcP36dSSTyTMlmEiSNCXX2+02Dg8PT7hxX3UcDgd4ngfLsiiVSiiXywiHw0MDp4WFBTx8+LBnDy0UCpcbcCiKgu3tbbP9wmazwe3uqrIcHBwgFAoB6EavRjAiyzLq9XpP/9icOXMeoes6Wl/egHwvieD3P4N2LdP3MGqYm/E8D6fTOVJwcDRb12w2YbPZQNM0Dg4OzMfLsoxyuYxYLIadnZ2xWgqO9rqfxvE5DgBQLTRadg5ipQX5O2Jofn4btv/+iR6Ne5IkYbfbzTXEaONUVRUbGxsIh8MzEWwY+D+6hN2fv4fSnyfhfM8jfXOe51Eul6Hr+oVnzTRNg+OaF7XXilCrMmjx8gchy40KnBUHdtN7kFUF4XB4YJuUIAhDlVYmRTAYRLVaPdE/7nK5pjoP1Wq1kMvl0Gg0TgQ6s/TdfiMQDoexs7Mzkec6OptwlB638797C0qmjvq9FEp/uon0r34T1mvu16sfAdCO6ThCXyaRSATr6+vm/wuCAFmWQZLkSB0xgUBgLG8cgiBMoZBarTZSgsx43FXESI4YsvIPHjwAz/Pm9zEYDPYkUFRVxdLSElZXV3v+7CweJGfa2YzeY4ZhwHEcWq1WT2bJyAQdHh5ib28PPM+bbo3H3Q63trbM/xZFEfF4/CyXNGfOY4eudFD/3VegVVoQ//7bQQosFr0CVldXe7JsBEFgYWEBNE1DlmWkUim0Wq2xKhKKogwc6j48PEQ0GkU4HB6rXYUkyZF76RVjjkPToB9ZxKpBEd4HWVRv+SC/kIX8lTS4dwfN2wOBAFiWRbVaRSqV6gmIjHUqGh3s9n3RkAyF0CdvYvfnX4QlZoM1YTeTMzs7O7DZbBc+XFwqlWCz2fD8z38nXvr8C/B+4PLXYFVTkX8pCc7PQoZiZuT6EQwGkU6np674Q5LkiYyn1WpFp9PB/v4+IpHIuT+7UqmEdDqNTqcDnudRr9eH/r2uSg/544JhtjqqAMUkYHwCHO9bguN9S+g0FDReSaNxL4XC774GxiuAvxOA8GQAbFS6sofgo1gsFrOt1Gq1wmazYW1tDU6nc6THG5WKUYMOiqLgcrmwv78/ljBAMBg8/U6XRDqdNhW/BuF2u81z+9F92mq1mtWLQWpgAExTxHEYOeDodDrY29uDqqrmcM4gfD4farUayuUyQqEQNE3D6urqiezMcarVKtbW1rC0tDRX9JjzhkartlH7zF1QTh7iD70FBNPNPhjymkA3EMjn84hEIlAUpSd4nzQsyw4MSPrh8XhOPSwBR3wJGBKaW4RNp6BYOBAE0R1sJ0nQTy0hzFAofeIOav9xE5YODQjdQXFJknrmxY7T6XRMd/ZZkaBkPVYEPnYNyV97gDv/6tsQiUTMSpAkSReetbZYLGi323AuuFH8y0N43hcd2Sl5mrQqTVgD3Q1TUZS+ijDG4Oi4bsRnup5WC5IkmVUoTdPg8XiQSqXMdq5xKx31eh2ZTKavklwwGMTOzs7QfXPY8Oec6RAOh1GtVifuUTAKFM9AfDYC8dkIdFVDcz2Pxr00Uv/+69BVDYLRenXdY+4ZVxGjU8ZIJmiaZir5jcI4VQ5VVZFMJuH3+0dSnSMIAolEYmbnj40W3dMCjkHBqVFhz+VyQ72MSqXSdAKOVqs1knMjQRCIRqOgado0tBp3yKrdbmN9fX1isx1G6eeoTChBEKjVaiiVSpBlGQzDYGVlZSKvN2fOeVFTVdQ/fRfsM2FYnk8MXBiCwSBsNhuy2exUDfyMUna73UaxWBzp4G64vQ6D53ksLi6aalqIdmDXNHRel/k1fDaqpRLowzKiNxfR/FE3oOqwhCW0223s7+8PPaCrqmoe5C8yK3katttuOOwO+L1+bG5sQla6h0qSJC/O+I9hEIvFAHRlkkEAzjf5UP5mFo5nL9f12mKxIPKeCNa/ch8IM2i32yey+RRFmcmti8AYWhVFEZ1OB6IootFomFnRfD5vii0cR1VVtFottFotyLKMdruNRqNx7iB4UFvOnOlhZNAHuVNfFARNgr/hBX/DC/dHn4ByWEP9XgqFL6xC/qUXwN/0dqsfb/KDEq9OJaxWq0HTNNjtdgDdgy3DMGO1mhpD/oeHh31v5zgOHo8HFosFFEWBoiiQJAmbzTa0ymGIWMzy787oQjgtwT9IfTKZTJpVVqBXqYskScRiMWSz2TMFXKd+grIs9/TTDSMcDkPTNFN666zIsoytrS3zoGVIeBqKIBaLBYlE4kQVpF6vD1fDGcB5ZT/nzJkU8sMMGp9/Ffy33wR7+/RsqSiKEISTbVaTxFB88vv9oGm6r/oHQRAQBME8/BlB/jAoikK1WjWTE1ytDTFbR27xpIKG87CG4LUoDippFH7mLp763z+EdCE92nxIuw2LxTJTAQdJklh530381b/4AjQLAe+HuwpcpVIJsVgMhUJhqhlUq9WKWCyGXC5nSh5SFIXbn3wWX/1f/xj2t/ourT3DYrFgYWEB9z/3DZTSRTjDEdTrdUSjUdRqNdTrdXAch8XFRZRKpakOih+l2Wya/h4cx0GSpJ4Dja7rWF1dxcLCgqnfXywW+1Yv5lxtvF7vpQccRyEIAmxIBBsS4fzACjrVNuovd1uvcp95GWxYgvB66xUTtM1065Xxvno8HlOC/Cy2Cm63G7VarSeAMOTTrVarKffa6XTMs+UgSJJEKBSaeYnrVqtlJh+NWcZBgdrx87Mx9gA8mg0jCAKLi4vY3d3tadNeXOyvGHkapwYco8phWq1W8DzfY0t/HoapA7RaLdy/fx8LCwvmsKiiKKdq7ZMkCafTCUEQzEPOnDmzgK7raH91B62v7MD2sadBR0Zf2EiSNFs7poWhFGK0Sh1tYYlEIrDb7dA0zdSqJwjC3DAGLeQkSfb8XmWeAdNUQGg69GOu12W3FfYX17FwawH0BzIgZR0WmkMTwwMOgiDgcDhOrbZcNA6HA9VaFfYPRrDzM3dhWZQgPuk2zeS8Xu/Yfh+jQpIkotGoKRtscHh4iIWFBdz63mdQ2CqDT9h7Hme40losFrAsi/39/TOraYmiaLrdHr+2WCyGZDKJcq6ETqmbDGo0GuacRCaTMVv8pvUenYamaaYa3NGKlK7rU21tPM6ofe1zJgtFUeA4bmaTlZTIQXpHDNI7YtDkDlqrOdTvpZD8xa+CoEkIr/t9WJZcM9E+eRSKomCzdeW5jQTWWb/n0WgUxWIR9XodrVbLTHINM2s9zlUx7tQ0rUfQgCTJoddseAdxHIdwOIzt7e0T9yFJEizLwmazmYP0mUzG/HzG5dSAY9QhGovF0rf/LRAITOUgdHRhH6c/2263n6jAzHK0P+fxR+9oaHzhPjr7ZYiffBaUY/xSpcPhGPl35nQ6TRUKXddRLBZH0iyv1WrweDywWq0Ih8Nmi2Kn08H9+/chiiKi0ajZz87zPFZWVrC+vt63TUiW5R41DJ0ku8PjDRmyrbcFQGNI1B4cwO11IBJwIfnZ/4LwD70TBEMO7dU9Ls89KzidTqRSKdAii8T/8DRaXy8CixqEgGgaAJZKpakcaPx+v2kEeRRd17G7u4vYc3G0vvSg5zaCIBCLxVAul1EoFEDTNCKRCDY2NsbK3pMkaWbHGIZBJpPp+fwCgQBqtRoqlQpoB4vm2qOqVL1ex87ODuLxOFRVHdgucREoioJsNotwOHyhAcZRXC7XzB+CHme8Xu/Yni9GAuQ8bs3jQrIU+Nt+8Lf98Hy/DnmvgvpLKeQ/9yqUXL1725Pd22fB7dxisYDnebPSYYgOnQWSJOF2u+F2d01NDfXCUc6LNE3j2rVrV+Y3tru7a+66H2f8AAAgAElEQVTjLMtieXl56LWTJIknnngCAHpaqI5itLUZ+zTLsvD7z95ue2rAMeqGZwweHsXn88Hj8aDZbE61nWHUYON4u5fhAmu4L8+Zc9FoTQX1z74IgqEg/sizIM6osU7TNJaXl7G1tTVwBsDv90MURWiaZlYoWJZFLBYz5WSHIQgCNjY20Gw2QVFUT8ujrusol8totVrmOlAoFBAMBhEKhZBKpUxDQaMtq1wun+jLb/MMLNU2SE2HRpOQeRbQdAReToGrykChBjAUiEUrXv5nX8STP/PtUFV14NCwJEnQNG1q7WZnwZhNMaq4i89eg3ZLBcOy0DkdaqeDer0+lT5hQRDMQft+dDodFGtlWAUe5XwTrLs7lOz1etFoNHoqChzHjSWXTFEUvF4vFEXB7u6u6ZUiSRIKhQJ4nofNZjNbeGkHZ1Y4DFqtlunJMc25pVHI5/MQRRE+n+/C2rqOcpp515zpcpZzQzgcNttyNjc34fF4LvT8QRAEuJgdXMwO13dch1psov5SGrW/2Uf2N++BW3B0W6/uBMB4L8eugKIo05QUwETbmGiaxvXr17G9vT109uuqBRuHh4fm30cQBMTj8ZGvvVqtIpvNnvhzl8tl2lkY52SappHNZkHT9JkU8k493YyavRJF8USbklFun1U3Rk3TUCgU5kofcy6FTr6O2qfvglnxwPr+6yDI82XhLRYLbt68if39/ROtkA6HAzabDQcHByfaYKLRKLxe76mHJlmWIQiC6f7aj+NJh3Q6DZ/Ph+XlZciyjP39fchy10Ha6XRC13VwHAe52YR0WIUt3wDXUNChSZQDYjfgIAlU/TYwjSJ0kgDR0UBYKBBPOZD8wn3Y3hPpG3BwHGe6nM9SD73RWwx0r9FiseD+1n0c/sZDEBSBwN+7NpWKDEVRCIfDSCaTQ98P1spCcTIo/tkG/N/VNZVzOBwn1vdUKoVoNIpYLIZ6vW5m3A3582w2awZ6xsxIrVYzK3GyLGNzcxNerxcOhwPNZrPns6JdHNTSyYQXTdMXoko1Cnt7e1heXkaz2RxLUnMSzPety4UkSVgslpFN5hiGMQ/PzWYTjUYDu7u7cLvdlyaxSjutsD+/APvzC9DaKpr3s6jfS6H4B2ugRBbCU925D27Ree79aVRKpVJPMmEayaJhz0lR1JUKNg4ODkwFSZqmxwo2gP5jE8bMytH/N54znU4jnU5DkqSxpcCHRgKj9uc6HA7Isnzih1etVtHpdGZqWLMfyWQSFEWZ5aM5c6aNslVA/XP3YP22ZXBvmaxPRCQSQafTMQ9ADMPA6/Xi8PCw7286lUphaWkJuVxu6EE0nU4jkUggn8+PVVVMpVInfBIajQYajYa5acvNFvhyC5TSAXQNGkWhbXvUblUPiJBFDjECoEkSlNIB+6wX8tdq4JSTlQCWZRGPx01PklnBarXCbrebMyWKokBVVfj9fujfp2Hn5+6i/NcpON41uQMIRVHweDxwOp0oFAqnHowdDgfylixKX03B+4E4LKIVBEH0fR/39/fhcrlM4z3DoMvlcp1Q/tvf3+8bKPTLrgEAJbLoNFToigaCebSp1Wq1malYdTod7O7umt+1UWceT8NQzxkU2M/9N2YDj8czcluVoihoNBrged4UagC6lbJWq3XmQdxJQXI0hKeCEJ4KdmcKt4qo30sh+5v3oFbajyR3b03X7fz4HlUqlaCqKiwWy0SqeoZiXD8Yhjm1FWlW0DQNW1tbPe9XPzGl0zBMVY+2VQ+T9zZGGCqVCu7fv4+lpaWRkx8T+dYYA+MrKysndMPv378/iZeYOpVKZR5wzLkQ2t/cR/NP1iB85EkwS+6pvEY0GsXq6qopfZrP5weWkBVFgaZppnHgIAw5z6NqVKMyKEBptVpdBSmSQGbJjeDDLHRVA6npkI/1EysCi6Kdg8vKgmyswmIpoLngBWoq7BYR5dajg3QkEkEul5vYAXBSiKKIcrlsHiSNTWNxcRFknIT23yjY+rm74KI2WOPjaZzzPG+2rBmqK7qum6+5sbEx0qwORVGAQIJftqP0tTRWvutNA4MUXdd7Dk/AI8PF8w50EyQB2s5CLbfBeB7NNZXL5ZnSwG82m9ja2jIrhaVSCeVy+VRZykEYQ/2Hh4cDA45ZV8t5ozBuO5Qsy+B5/sT6Wa/XTVnlWYAgCFgSLlgSLri/+xaUXB31e2mUv7yF9Ke+CeuKG/wdP4QnA6Cdk/st9vNukmXZnPNiGGZs74dRcTqdCIfDU3nuabC+vm6uMYaa1NGZyFEhSRIrKyt4+PChaTh6PLCTZRmZTOaE+qQxAzpqhW4iAcfh4SFSqRQCgQDsdvvAjNUsc9n9wHMef3RdR/NLa1DupyF+/FlQU+yRJUkSiUQCyWQSBwcHpwYIsizDZrOdapZUqVQgSdLEvA+azaYpedjhaGSW3Ai9lgZ0HZ0+xlVyR4EWvg9n+J/DCQ0t9w00d34anf0asNi9P03TYFl2ZOOni0QUxRPDzp1OB1tbWwiFQnjTtzwNySrh5Z/5Syz8T8+AEkYf4jQOP+l0ukdbPp1Oj1URKJVKiMfjwPeoEDoWeL3eS1P1ox0c1GJvwGGooM0Shn+U1WqFw+FAIpFAu902e9HH8VYJhUJoNBpDOwNm5WD6RockSfA8P/T8IIoiPB6Pqag5aKbs8PAQdrt9JlvQGY8Ax3sTcLw3gU5DQfPVTNfz4/MPQLutr899BM/tdn5aN4wxC3geaJqGJElmtdUQxJhWIDMNDg8PzWCD53ksLCycqypjBB3FYhF2ux3lcrknAW/I4vZjHKXCiX2zjaHRaDSKUqk0UiZtllAUBa+88gqAbqQbDAavRFltztVAl1XUf/tl6C0V4o++DSQ/fiZiXIzB2lHmFwzZ23a7bUqWHncWZ1kWPM9PtHfcqHAYyAKLfNQOvlIFCB0A0ef+v45Wi4OqWmGxPICysIfKNyxQNQ30kgRRFC/MDG5UKIpCNBpFp9PpezjpdDrY29uDxWJB/JlFbD/1AMnfeIDIP7g9Uu80TdOmcMd5kyeHh4fweDy4/s4nkHvlEC9+4euwLF3OZmwEHED3YGAc8GZ1f2k2m2g2mzg8PIQoinA4HKYqWKlUQrVaHdqO6PV6wbLsUOUrURTne9MMsbCwgLW1tb7fyX5Z82FV152dHSwtLU38GicJxTOwvTUM21vD0DsaWhsF1F9MPXI7f5O/K7l7zQOSHU/44rTDqyGlfZZM/lEikQju378PhmGQSCRmMsgbRLPZNKvKoVBoYuIRxnuwuroK4JHhby6XG9qWPI6S4kTfZcPoyOfzmQZJVw2e5yFJEu7fv49gMDhXAplzbrRyC7X/9y6ogAjho3dAUBd3WGBZdqQZBk3TwPM8gsEgarUa/H4/Go1Gz2ISDofRbDYnKnNtZPpomjb/m7r2/0Fw/DYWNQsOsz+BVvtmz/2bTQkcp6DTef0gTjrAvMmKxr/7BsQfvz3QnPCyIAgCS0tLI5nUtVotqKqKxe+7jfs//VXkv7gLzwfjQx9js9kQiUSQz+cnVl3O5XKoVCpwSw7cfMdtZOuDW/KmCe1koZZkMAxjHsRUVb00KdpxqFarqFarIEkSkiSZqi+VSuXEYCwA8z6nyXYeHeacc/kY2eF+QUe/VpNhAUez2ZzIgfqiICgS1mseWK954P7eJ6Ckaqi/lEbxD1bR/qUXuk7oT43udj7Kun14eNitwJ4DkiRx8+bNKxm453I5MAxz5haqfhQKBWQymZ7K21FPj2GMU72deFhXrVavVB/cUTweD9xuNw4ODqDrOpLJJLLZLFZWVq7kF3PO5aMelFH7zIuwvC0G7p0LF94KctSwZxgul8s0RAK6WQvDZ8FAURS02+2JHuaNBdNUJqIzcDl+G6pqB0m24HP/MnaTv9DzmHr9x0CSvwBd30I2+/2w2xdAhqqgvBa0//wQ2ke9U5GUPSuCIEBRlJGlU/P5PLwBH8ofv4Htn7kLy4II263+iQ8jg76zs3NmE75ByLKMg3oKlU/t49mfei/K1cqFG+1RDg5KuolgMDjRgOoi0TQNpVIJpVIJDMPAbrcjFAqBJEnzM6MoCizLYmdnZ2j7G8dxYJjL90qY04sRdBztqzc+4+Oc1t54cHBw6QPkZ4EgCLBBEWxQhPNvL6NTbaPxSrf1Kv/ZV8CExK7h4J3Bbuc2mw2lUmmoYMKk2t+v6pkuGp2syMyDBw/OLcIxzNH8KBMPODiOO/Ow3GUSCoXAcRw2NjZ63nxFUbC6unqlZNLmzAbya2k0fu818B+6Bfbm2c1yzoPP5zMNlAYRCoVAEERPn36xWEQgEABFUWAYBpLUbVWa9BC2z+dDPp/vbfvSgW4rFQHgZDuY1bqAbPZfmD24DkdXNcP6oTiq//pVdD4gg3XPTobQbrePJZlaLpfh9/sh+CSEfvgG2v+liPC33kahUkS73YbNZoMkSbDZbJBlGdvb21NzPCYZEoqg4Su/8Cd4y489f+GeE4yTA1nWIUnd3vBAIGAOL15FFEVBLpdDLpeDxWIBx3GgadrsCjgtOXBVk3lvBEiSxPLyMlKpFDwez8DsM8uyQ89I9Xp95APcLEOJHMTnohCfi0JXOmg+zKP+0utu5xQJ4U4A/B0/rMtu0+3c5/OhVCphYWEB+Xy+734zTkZ9znDy+fxEFP/q9fpIoksTP0FzHAdVVWduqO80JEnC3t5e3zdfVVWsra1d2U1uzsWi6zpaf7mJ5hcfwPYDb760YAPoboKxWGzg7S6XCzzPm5WNo48jCAIEQSASiZiVkkmKK7AsC5vN1qNypKo+lCofAk2VQEBHNv+jJx7H87xpmgc8kukjnRy454NQXyuNLNs7bTiOgyiKYw2wG++93+/HtW+9jbf98/cj+5V9xONxXL9+HU6nE41GAxsbG9jc3JxasGHg/JYQ8n91gEImD57nL3Rtp5wcyvczWF9fR6FQAEVRWFxcnKkK1llptVqmaEIymTzVW8SYoZozuxj+BcNaXUaRND6u/HbVIRgK/G0fvN//JOI//T4E/uFbQQoMCr/9Grb/yReR/uUXUP3aPigFuHnzJqxWKyKRyMBB7qPr/5yzMyh5xHHcWAn2UfegiYfQpVIJoVAI0Wi0J2NKkqRZJpvFg7ssy3C5XAM/AEVRUCqV5jMdc4aiqxoav/cqOukaxE++DaR0+eZckiQhGo2eCCqA7pBqP2M8TdOQy+Vw7do10zPD+PNJ4XA4UCwWTzxnofy9KFa+E7pO4/gSZQRBR7NcRsABANw7/SA3dajp2VCdczqdJys4p+DxeNBut81MZ66dw9aXHyB1fx+eDy1c+PpJSyxsb3Jj5w9W4fjBt2FxcRG7u7sX4oXBOLtD461WC61WC9VqFX6/H4uLi6fOOsw6NE1jYWEBmUxmJK+q+ezG48EoAcdV/l6fBkEQ4KJ2cNHX3c5LLTReSvW6nb/eehWPx7GxsXGiXXR7exsrKytXZtZlFjF88gwoijK/mwsLCwC6thajfBcvLeBot9vY3t5GIpHAysqKKc+oaRo6nQ5omka73UahUDihgnOZ5HI5xGIxlEqlgeXORqNh2rvPmXMcrS6j/pkXQdhYiJ94Kwh2dr4nhtzi0SqeKIpdg6cBi0UmkzEDcEmSJq79z/P8wHYvXe8fqOm6DlVVe9oSjmbcCZoE+yYH5Ls56IsAYZ3+Z2Cz2RCNRkGSJKrVKg4ODkw9c0mSxhLQoCgKTqfzhGdG4GPXsPNzd0F5WNjfPtiUaVq43hPC/i+9hp13+eEN+LC0tISdnZ2pmyqSNgaa3IEmd0zFm3Q6bRoozprPyqhQFIWFhYWR90GGYWCz2S7gyuZMm1GqVG+kShbtsEB69wKkdx9xO38pjdIX10AKLISnvGgsd+9rKPbpuo61tTXEYjEIgvCGaHdvNBo4PDyErusIBALnXg+OVolFUTT3MINsNjty4Huhxn/H0XUdW1tbYBgGnU4HnU7HvHCCIGC1WhGNRqGq6li9zdMgGo3CZrNBURTs7u4O7a00Bv8mKUU25/Ggk62h9um7YJ8IwPLe5ZlsKRQEATdu3EChUEAqlQLDMH2rHv3gOG7ivbNWq/VMLVq1Wg2SJJnBipHIMKCdFsgOBq0vbcP6ofOpmZyGKIoIh8PY3t5Gq9WCz+fD8vIy2u02WJZFNpsdq/zvdrtRrVZPDOZTVhrhH7mF3f/jJXARGyyRiz18WqMiGLcF1ZfyIGgS7XYb8Xh8qvMjQHe/MKRxWf+jQ1g2m0U0GoXFYrlyMx0kSWJhYQGVSuXU+SqDeXXj8WGUrPwbKeA4Sn+38zSIrRI0TYOlAiAioOUkAJYylZQYhnmsxX00TevpRNje3kY8Hj+Xd4hhFGuxWOB0Ok/cPmxvDoVCyGaz5j41qi/Q1D4dTdPQbrehquoJZ8JGo4Hd3V2Ew+GRyovTgiAISJKEtbU1rK+vn9pDa5BMJi90cHLObKNs5FH9ta/D8u4ErH9rZSaDjaO4XC7cunULPM+PrGzkcrkmWpG0Wq2mw/m4GJ4hBpVKpWdgjSAIUNfskF/KQ92bjpSrzWZDLBYzg41mswld15FOp7G/v49isYjV1dWx3jOGYYa2dXIhAb6PJJD81dfQaUy/nek4rveEkf9yt1pTrVaRSqWGzgdNiqNeHAb1eh3r6+ugafpKHcYJgkA8Hkej0Rh5D2FZ9kqZks0ZjuElM4x5F8Ujt3P3d9/EjW9/K+glB8LffQfxt1xHVHWC+uMUtBdy0CsyFEXBw4cPr1TiYRySyeSJv9sklAmDwWDfYAMA/P7Bs6e1Ws3cg61W68iB3qWFg4aefywWQyAQwMLCgrmBRyIRrKys4MaNG/B6vVO7BpZlzRaNcclkMqe2Sqiq+tj+AOZ0aX9tD/XfeRnCR++Ae/pqKcg4HI6RJfZyuRwikQj8fv9ENsPzqNm1Wi0oimK2eFWr1Z5Fr16vo9VpQ/qpp0GF+Kn0Qxt+JRsbGyfaiur1+kg9+UcxnOEzmcxQ2WH7W/0Qbrpw+FsPL7zPW3zSDbXSRnO7m5gpl8vQNG3qrT60k4NaOllFUVUVBwcHEAQBVqu1zyNnC8PRWJblE27zwziv58Cc2WNYoB6JRC7wSq4GNE3j2q3r2Nzdxtr+JpohGiv/7fNwuJ3o/PJDqJ9ahVWhsX5/9bEbuDdMQ/sx7j4zDhaLZaA4R6VSgdvtBkmS8Pl8Iz/npYbRpVKpm42kKGSzWZAkCZqmoes6stmsaZhVKBSmIoUWj8fPpStvRNVA9wDF8zyq1eqJqNNwbLTb7XA4HI9t2e+NhN7R0PyjVSgbOYg/8iwo19UsgdvtdpAkid3d3aEH2Hw+j2azCUmSkEgksLW1dS4/jmq1ikAgAIZhzvQ8h4eHCAaDKJW6pfadnR3Y7XZYrVbwPG+uI9s//VeQ3hyC9++sAOiWos+rtOVwOKCq6ljKU6dhtJ+O8pze705g7xfvofClfbjfP1lN9mEQJAHXu8Mo/FkS4R+WAHS/F36/H6qqTm2eg3ZyUIv9g1Nd15HJZOD3+7G9vT2V158UkUgEmqaNNdMjSdKldgHMmQ6GFLJR5WIYBqIowufzzasbA6BpGjzPo9FoIF8qQNFUOJ5fRCVOgW+QiCzHsfG7LyB5rYXqn27BezMK6/Xx3c5niXK5PLTt2QiufD7fVM6VkUgE+/v7fc/fqqri1q1bYz3fpX+zh7UciKKIRqMxNd3lQqEwUClnFPx+P5LJJJrNJhRFGejEq2ka6vU6OI7D1tYWVFWF3W6Hx+OZLy5XEL2lovYf7wGaDvFH3wbScrWNuERRxM2bN7G7uzvUTdpQq1IUBfF4HOvr62d+zU6ng2KxCK/Xi2QyOfbjZVlGsVjE8vLy0IG16MffjI1/+WW4nouBcVqRSCSwu7s7cvtkP856zcNgGGbkSivJkAj9yC3s/GzXFFC4Ntlh/mE4ngtg/Y++BqXUBuPgUCqVQJIk4vE46vU60un0xF3eaQeH9t7gWb9isQi32w2bzXYpbuijEA6HzcB+VAxJ6jmPJz6fD5IkjTxwO6fXNNHwJLp1+1bXpDR9COWOBJRlVFdYdP56FcQvvwDrDS+EJ/3gn/SDngHVyFHJ5/OnVkJ1XTd9faxWK3w+30TbL42zQalUwuHhoXkWt1qtZ1IIm+nTrtfrnWgW8TiGRXwsFjOHj8ZpU+A4buSBSYZh4PP5TPUZ40vCsiwSicQ88LgidEpN1D99F1TUAf6DN0BQj0e1yhhkrdfr2N7ePrXaEQicXykpl8thZWUFmUxm5MM2z/NdUzxBGOn+logE13sTSP7fLyL+j54D0G1n2NraOpOWuyRJUFV14jrww5x1+8E4OQR/8DoOf+MB4j/5NBjHxWTBKZ6G4+1+VL+ehet93cOwobTk9XrPHYj2g3ayqL80vP2u3W4jGAyi3W4jl8tN1C/mvASDQbAse+rv6jiBQGBeDX/MeSMEG2traz3nJIqiQNM0OI4Dy7KwWq0QBGGkM9DxgGN9fR2KovT8rgh79yDcfJcTie99Cp3VEuovpZD/3KtgArbXDQcDYEPiTM5bGlXQcRPtzWYTOzs7IAhi4pLBDocDDocD5XIZ2Wz2zG2eM3vKlSQJuq5PXfbw8PAQ0WgUN27cAEmSaDabfX0JjsPz/FhDr8FgELlc7kT2T5ZlPHjwAAsLC3PZwxlH3Suh9tl7sLxrAdzbYjO5WJ0XQRBw/fp1rK+vDwwCjO/+eTEU7CiKGhpwUBQFn88Hp9N5pgOY/7tv4eFP/hEqLx5CeioIoJtxXl1dHfu5jIropGm322O3zgg3nHC+O4Tkp+4j9mNPmm69wHjJkGEYLWqlUgmdTgeRSAQ3f+omNLkDgiUhy7IpDEIQBDiOg8fjGVl9aRRopwVqcXC7VigUAk3T2NragsvlgtfrNRNIl4Fh3EiSJJxOJ3iex9bW1ljBBsMwIyu/zJkzyxxfs411//j6tLi4eGoiiSTJnjPXaXOAe7kkrj93vet2rmporuZQv5dC6l//DUDADD6sK+6e9fOyqFQq2NvbA8/z8Hq9Z6rYGmvxNLDb7SM5ig9iZgMOjuMuzE0yk8lAFEW8+uqrWFhYgCRJAwMdi8UCv98Pq9U68vyHIAjgOG5oL9729jZ8Pt9YAzhzLg75pUM0/vABhO+6Deb69IQMZgGapnHt2rWB8w4cx526EFIUBYZhwHEcLBYLaJoGQRBotVqoVCrmRpHJZIZuGh6P59zVFJKlEP740zj4tbuw/awPJEuBZVlYLJax5g4oioIgCNjf3z/X9fRDVdUzVTld74+iuVVB5vNb8H/PEqxWK0KhkNmiVSgUzDmXcZAkCW63GwzDoNFowOv1miIYD1cfYvvfvgTnWwPwvStqfrYAzOxXtVqdmFwu7WShlvp/R8LhMFiWxc7ODjRNQ6PRuJQBcpfLhUAgYJpQapoGXdchy/JICazjLC0tTelK58y5WGw220hqSltbW1hZWRmaeInFYtjc3Bz5tRVFQT6fh9vdDSj4Wz7wt3zQ/2sd8kEFjXtpFH73PpR0DdYnfN0A5LYPlNBbHdB1HfJuGVx8eu2rR1t9aZo+s7GqsffOIjMbcDAMM3VTKaCrVBWNRpHNZgGcrp4jSVJ30304ukoMSXYzgafdP5PJoNFomC6Pcy4fXdfR+vIG5HtJ2H74LaD9bwx5SkM1KZ1Om78Ng0GLIcuy8Pl8pxoEHg0gNE2DIAgoFArm791qtcLtdkOSpIm1lEhPBVFMbCPz+fsIfPQ2gO7mNU6VwxhOn4bynDHkPu5GQxAEgj94Hdv/6i4i71lC7J0xpFIplMtlCIIAl8sFn8+HXC6HfD4/cA3y+XzweDxotVpme1culzM3QIZhQNM0Wq0WdF2H6z1hpH9nE7Zn3CeyaalUCtFotK8TOMdxsNvtKBaLI1fJSCsN6Do6DRUU/2jLikQioGm6p1Wp0WggGAxCEIQLSVgRBGHKu6+vr59Zee0o8Xh83mI757HB6/WiUqmMlIBYX1/H9evXB37/eZ4fe1bLUFQ6CkEQ4CJ2cBE7nN9+ret2/nIatRcOkP2te+DiDgh3/OCfDID129B8mMPu//wl+D75Zri+/frIrz0qx1t8zxJwkCQ59hD3RfOGXNVYljVLQxRFIZ/Pmy0ApVIJsVgM+/v7fb/UNE2bmvujoijKyBFnrVZDq9UCy7Lz/t1LRlc6qH/+FWilVnc43PbGU4vx+/3wer3IZrPI5XLQdd3M3ALdhdtut8Pn852pZ5QkSbhcrgsx0gz94FNY/ad/DMc7Y7CEJbAsi3g8fmr7DUmSsNvt4DgOqVRqKtfWarVQKBQQj8extbU1VlBD8QyWfvwZLDy5hLVvPoAmdAOAer2Oer0OlmURCATgdDpRLBYhyzJkWUa73Yau66b/x9raGliWhaZpJzKSiqL0BAjCdQeg6WisliBc79VxL5VKsNlsSCQSqNVq5jqrqipIkjTbx0Y1nTTN/0ptUDxtDlOTJImdnZ2etdjof47FYqako6IoODg4GDsAIUkSFEWdCIxYlgVFUaAoCn6/H+12G5ubmxORKXa5XHPPjTmPFSRJYmlpCWtra6cmGXRdx+rqqtni3g9RFMcKOEY5uNMOC6RviUP6lnjX7fxhDvUXUyj98V+DtNLo1BV0ajLS//4FaE0V7o/c6iZadB2AChBnrygcHByYCov1eh1OpxMWiwWVSgUWi+VEq73hcddsNnv2iatgwUAMWySfeOIJ/bOf/ewFXs4jJEmC0+kcuRd3YWHBDAZarRYajYa5aVIU1SOZSZIkKpUKyuVy35YRSZLg9XqxsbFx4rYbN26Yg9+jQpIkrl+/jo2NjVMzYA6HA9VqFbquD/3RzZkuWrWN2mdeBOW0gv/wEyCYqyutN0mKxSJarRY6nQ6cTufIw9uzQu6Layh//QCJf/a8mZk3nNeB7oZHkiRCoRAEQYCmaT2BVLVanep8QFQQFlQAACAASURBVDgchqqqY8t1R6NR5F9N4ZVf/CoWfvIpkJaTuSRBEGCz2cCyLDiOA8MwaDabIAgC9Xp9bDPT4l8fovpyHrF/cLvv7YIgmJWGZrMJhmHQbrfNocZCoTDyrEfy/3wZjm8Lw37Hj1gsBpqmsbGxMdJhwmazIRwOo1KpIJVKnRoY0DQNt9ttGmKlUimzxdZutyMYDJoV63K5PDFhE47jsLKyMpHnmjNn1tA0DaurqyP9ZkmSxPLyct8kVrvdxtra2sivyzAMrl8/W1VC13W0tovY/kd/CLXQhN7RAIKA6zuuIfKPw0DqfwM6VcD+YcD1/cCYsxOG7C1N00gkEiBJEoVCAZqmoVKpIBwOm3NyBiRJwmKxwGKxoFwuI5lMwuFwIBAIzERllCCIb+i6/pZ+t13+1Q2gVqshHA6PrNNPEITZk80wDMLhMCiKQrVahc1mQ6PRQL1eRz6fP7VVq9VqgeO4EwNKQDdatlgsYwUcmqYhk8kgHA5ja2tr4P2sViv8fj+q1So0TUMul5vPdFwCarqK+qfvgn06DMvzicdyOPysDHIlvSq437+M4l/soPiXO3C9ewEAxqqwiKJ4rv7a0yiVSggEAkMDDqPt8+jBmeM4dLwkrAkJh59eQ+jjN058b42KhwFJkhAEATzPn2nI2/5WHzK/t412pgnOd3Ju4vjrGS0Vuq5ja2sL0WgUPM+biix2ux2tVsu8n3F9FosF/EfugHFZEFyKIZPJmA7jo8jM1mo1rK2tIRgMYnl5GQcHBwNVrPx+P5xOJ8rlMjY2NkxncMPNXJZlbG1tTWw+xcDIAs+Z87hCkiSuXbuGhw8fnqrApGka1tbWsLi4eMKVfVxxjfMogREEAcrCQO/oYAI2aG0VUDXU76Wgp34fhNYCKCdQ/s+A7V0AN7p6U6vVMqu8qqpiZ2cHkiSZLcwURcFisQxVt6NpGrdu3boyiemZDTiMQ/rCwgI2NjZOLRdtbW3B6/WCpmkzW8myLERRRLVaRbU6WMf9OJFIBKlUqu9rHh4eIhwOo16vj1XCyufzcDgc5vUcx+gFPqp1PA84Lh7lYRb1z78C/oM3wL4peNmXM2fCECSB8I88g62f/StITwdBi+O3yS0vLyObzaJQKEzc7dtYVwYpPYXDYYhiV87RqOaqqgqWZaEoCvwfXcLuz99D8c+ScH1reOhraZo29tp4FJKl4HxHAMW/OEDge5bHeqyiKNja2oLf78fS0pIZwNE0DU3ToKoqrFYrms0mGo0GKIGB1upge3sbrVYLBEEgkUjA4XCMpGRotFqJoohoNGoGbJqmoVQqQZZlWK1WiKKItbW1ngPR2tqamYFMp9MTDzYIgsDy8vKVOTTMmXNWSJLEysoKNjc3T+320HUdm5ubCIVCJxJChiHdKJxXHpYSOYR+4h1g/TawYRGUw9JN5uy/AGgEACOxM16b/fEOmna73TMvabSODdtjDH+fq8JMX6kx5DiO6sjRjUKWZeTz+bE2VKNcNahMbmTtYrHYWOo5BEGYLQX98Hq9kGW5x5DM6NWbM310XUfrqzuo/95rsH3s6Xmw8RjDL7ngeHsUqc+8fKbH0zSNYDA4NVO2/f19eDweSJJk/plhrkdRFB4+fIiHDx+aMtsMw0DTNGiaBpKhEPrkTRT+eBfNzfJUru8ozm8Jofy1DDqN8Ss+uq4jlUqhWq1CURRsbm5idXUVyWQS+XweDx8+xPb2NjKZDA5e3cHGf37JrE4bDuPjSjRWq1Wsra0hk8kgm82iVqvB4XAgHA7D6/UOdNWNRCIol8tnDs6Gsbi4OFHN/DlzZhlDBXFU2edkMnlCrMPhcMDj8Yz0+PP+ZikbC8d7E+Bv+0A7rY8qx55PAgQNdPKA9LcBdrTqRqfTwdra2qnJqkHJaQOe56/cvNdMBxzBYLDvAOMgSJI8d8ZxFKnMg4MDZLPZsXwBrFYrqtVq36ieJEm43e6+rpLHFYLmTB69o6Hx+/ch3z2A+MlnQUcuzrl5zuUQ+N4nULl7iPrDs/tFGIPkk0ZRFOzs7MDv95utPIFAAJ1OB7u7u2ZmvlarIZ/Po1Ao9LR4sR4rAh+7hoNP3YdaOb9q0jAYJwfhphOlvzn7MH2n0+lZcxuNhtlWakA7OCjF3uRLo9E40W4xCpqmmYmjQqGA3d1dbGxsYHV1te/ab1SZx52rGYVIJHKmv8OcOVedYDCIaDQ60n2r1eqJdvRAIDCSGM+02l9huQ7EfwVY+A3A84mB8xtG4nt3dxcPHz7E/fv3T+2OEUURgiAMDThmVfp2GDMbcLjdbtjt9rFkKFut1rmdO0fV5q/X62i1WiNvFoIgDPziOxwO1Gq1vnMh08iozXmE1lRQ+61vQq+0IH7iWVCOi9fwn3PxUAKL0A88hYNPfROaenZ1j2kt+s1mExsbG6bYhSRJSCaTfe/L8/yJRIbtthv2tweQ/PUH3UHHKeJ6TxiFPzuArp0t2UNR1KlrPO3k0Cn1BhxGoDLNLB/P83A6nSMrao2D1+s9VUJ6zpzHGWN9G4Vms3liZmuU376maRORq+4LQQNk/zNgPp/Ha6+9htXVVRweHqJSqYw0+2uz2RAKhbC9vT101qVcLk/dGHvSzGzAUalU0Gw2EY/HRx7abTabpva8KIpnCj4URRn5B1AsFk2zJ6DbNuXz+SBJkqka4HA4QFEUnE7nwNkNt9uNfD7f9zU6nc5EXJ3nnKRTaKD6K38Dym+D8H1Pg+ij7DPn8cX+9ghouwX5L46ueHKcaXoFGbMMgUAAmUym76HcWHP6VUI9H4yDIIHc70/XdZtflECLLKov91/DToMkyVOHSGknB7V40suoVCpNVcjAarWiXC6fen3j4vV64ff7J/qcc+ZcReLx0QetK5VKT6XR4/GM1GWyuro6cqfMJNA0DYeHh2eSqnW73UilUiPtLfv7+9MLpqbAzAYcRluBoigjz0rIsoxMJgOO4+B0OpFIJE5oGJ+GERSMEjmXSiW0221z45AkyQw2RFFEp9OBJElYWVmBpmmmHOSNGzfAcRwIgkAsFjMHIwdxFgWZOcNRtguo/urXYHl7HPzfuQGCnCtRvdEgCALhTzyDzH96ADk3+Pc3DI7jEIvFEI1GEYlEEIlEEA6HEYlEEIvFsLy8jFgsBq/XC4/Hg2g0ikQigVAohGAwiEAgYJru9Ut0NBoNsCw7cKbM5XL1SID3/P1IAsEfuoHKNzKo3pvuGmJUOc4CQRCn+k+QHAWCIaDVe6vEhsGh4blxFYjH4/NgY86c16FpeqzfgyHYAXQHwm/cuNEz7zaIg4OzrU9n4egs7jjQNA2e58d6/DDl01ljplO6Ho8H9Xodfr9/JP10oFt1cLlcEAQBsiyfKTNlGFcNa2eiaRqCICCfzyMajZpqMRRFYW9vr+daaZqGy+VCOBxGNpsFRVFIJLpyq+Vy+dQfQqlUgt/vv1JqBLNM++4Bml9ahfCRJ8EsjTa4NufxhAvY4PnACg5+/S4W/8k7x3psvV6HLMtmWftopdPpdKLZbCKTyYBlWfA8D4IgUKlU4Pf7oaoqVFUFQRAgSRI0TZtS3pVKBZVKBY1GA4qioFgsDryGozKK/aBFFqGP38TBL70KLiSA9U6nZVB6yoPM5zfR2q/BEhkvyZNMJpFIJCBJ0vA11/m6+Z/tURuboVfvcDgGVonPy6RksSmKwtLS0nxAfM6cY3i9XvA8P3ILfTKZ7GkxJQgCfr8f2Wz2xOOZFANmn4HqViHH5In+/nK5HJrNJvx+f8/zlstnE+yw2+2oVCpjzSJfpXPhpQUcNE33lMKNN9j4N8uyEAQBNE2DoigIgjCSu6TD4YDdbkcymRxaNRhGu92G0+kERVF9AxZRFBEKhUwzK6DrT2C1WqEoyokvi6qqyGQyPcZa5XIZqqqO9MXqdDp47bXXYLVa51rt50DXdbT+ZA3ya2mIH38WlPdqmdbNmQ7e77yO1X/6JZRfOID9LcOlZI9iqET1a3nkeR7tdhutVgutVqsnYxUMBk0p1uOwLAu73Q6/3w+O46Bp2sBhZUOn/TQHbeuiBPcH4zj4ldcQ/8dPgWQnXw0gaBLOd4dQ+PIBQj8wusmW4aehqurAGRXzvg4OaqEN7lhAI8vyVIb3AUxM9thmsyEWi12pw8GcOReJIAi4ceMGdv9/9t48PLK7vPf8nrXOqX2vUpVUpV3d6rbd3bR3Y2y8YIzZDTg3OAHsMJMZIJdJTDK5k8mTYfKQADcQwjAhgQDJvQ4Oi8mQmbAFDGEP7m677W51a5dKJak21b6cOsv8UV2nVa0qqVZtfT7Po8dWqerUkVr6/X7v+37f77u01NIkcQBQRAnra2twOJ0QBEFNXBh+boDnUx4ohAJCIpB5IQPH/9adJGMikUA2m4XT6cTly5fBcRwoitoyAbwVbDbbjuvgtezWsD9ZllvqW67HngUcer1ejeY2Zwar/1UUBQsLCzAajejv74fZbN7xl5DjONhsNiQSibaDDaAyKCqTyWBkZATLy8tqb4jVaoXBYIAkSVhZWal7P81mw9rpy9hNDeJhQxFE5L7+EpS8ANOTt4I0aFlGjQokQ6H/iVNY+swvYTzuAdVkL89OB/1GbGxswOl0Yn19HTRNgyAIVa8rCAKi0ahaCTUajQ3XvarBRTOHYutdfSjMpbH+zAy87xzvyTBL6519mP2T/4CYFkCbd/77qlZ6k8kkotHozhPAr1Q4NlN1+NuvsoKqbPag2VdqaOwFJElicHAQ09PTLY0EIF5Ognk+hvg7JPBlCn3DHqytReH+v9yQ9BIUTgEkgH+GB34NQId520wmg3A4DJIkwfN8zRreCJPJBL1eD5qmkc1mkc1m1YQ2QRAwm80gSbLls2sul8PMzIw6qbwX5HI5dQBhMBhsez3bs4BDURS152I7qplBk8lUt+LAcRwsFgtMJhNIksTGxkbb5azNrK+vI5/PIxgMQlEUkCSJSCSy46Tybg8CuxZZlrUsWYvI6SKyT58F5THB8OiNIGjt56dRi/GYG8ZJN9a/+jJ877xpx+cLgtB2FisajWJsbAwWiwXlchkURSGZTG6pZEiStO1axrJs0w2DBEHA+9gYFj9+FqmfrMF6V/fnzNAGBuZTLmz8eBWuh3duBPX7/UilUjvuAer1bTqI11jj2u12ZLPZfTmvqDpkUFuvNTRaw+fzNZ9EkBQsv7gG+79HQE0lgP/lJpT/4ifgYAYhDkGxXDmTUVc+Yug44Ki61lXHNni93rpjDar4/X7VgKJQKMBiscDn86kJI57nUSwWt73GdhSLRUxNTWF0dLSuZEyWZSwsLKhW4h6PBwZDcwqP1dXVGrlqJ86AexZwiKIIg8GA8fFx5HK5hn0MVUmBTqfD8PAw5ufnVXtZi8UCr9eLZDKJlZWVrlcAMpkMpqamVNmU5hZ18BDDKeS+fA66mwPQ3TXYk8yuxuHA9/iNuPTUd2C7Owg+0Jxd6fj4eI01brU6SxBEQytVWZZx6dIl9XOz2bxlkm4zsCzb0kGb1FHwPzmJxU+8AN2AEXyw+1l3+6t8WPyr83A8MACSaXzQtlgsYBimJbtZ2qpD/uLVfhadTgen04m5ubmO7rnbaFUNDY3OMBgMYBimcuaSFBCZ8tWPtAAiXa58ZMog8iJ8BREAgVKkAOGvL0D+z8fx00+cw7sHX43yahmKXQFZIEHpKWCo8/vbnGxaWlpCIBBAMBhEKBQCz/MwmUwgCALlchkGgwGyLGN2dlZNSCcSCRAEoR768/l82wmszfd0+fJlDA0N1QQTsixjenpaPb/m83nMz8/X9A8yDAOWZdVZdpIkQVEUtY+wil6vh8vlavse9yzgKJVKCIfDcDgcsNls2zZOV5sinU4nRkZGUC6X1d6OhYWFnkuN9kug0cqgQQ1AuLCO/DcvQP/6SbCTmiuMxvbQZg7etx3DyufOYORP7t02OK0uznNzcx0PlrJarW35qdM03bIlIuvRw/vYGMJ/dwGDHzoFytDdOSK6PgN0Pj3SZ6Kw3tr4b87lcjVtBFKF2iSpIkkSAwMDWFtb21e2kBzH9VTaoKFx2FBECVKyCClRgLxRgJQoQNooQC/kkR5ioPvyPBQDDcXMQjEzUEwM5AEDspKE8GoaSwtpRObieKhMARSBcxfC8L/sxq1/chsUTgH7uywQAmAE8DEA7s7u99rAoFo98Hq9OHLkCAqFAtLpNGRZBsMwyGazdZ1GFUVpuVdlO6oBxOb9SBAEzMzM1A1mqoGFJElNJa4oisLg4GBH97gnAQdJkpiYmEA+n0cul2tasxaLxVTdtCRJEEWx46jwoGA0GuH3N9/Qej2jKApKP15A6T+WYHz8FGifZa9vSeOAYL9vGBs/WkTi+/Nw3Dfc8HnVtafT9adqiBEKhVp+bdUVr1VMJ5wozKcR/uIU+n/7eNctoe339iP6zQVYbnHXDdpYlgVFUS1vtswmSVVfXx8KhcK+Gnxls9m0NVpD4xoUUYK0UYS0UYB8JZiQNv1XyQkgLRwoOw/KxoO082DHnXBZdEgVVlH87SMASUAolLE2nUD44jrCF2MQiiL8R10I3OTFrW8/hpU/fx4/vRDG8FvGMXxbPxRFwVRpCgN/PwATaQL06MogiEaS+rW1Nayvr/dcVr8ZnucxNDTUMMExNzfXtTPy6Ohox4mUbQMOnU7Xkk64WUiShCzLWFxsfSDV9dg4zTBMx5Hl9YIiysh/8wKk9UylOdzc2eR5jesLgiDgf/IU5v70R7Dc7APd4PdnO6vaVrBarWo2rFWqGa12cL1hEMufPo/4vy7C+brBtq7RCOOkDetfn0VhNg396NZgn6KotqrGlJWFmBLU5svZ2dlu3O6ONCPD9Pv9PR1AqKGxX1HKVwMKKZGHvFGElMhXPt8oVgIKKwfKxoOy8yBtPNgjzqufm7m6SQ9JkiGeXUViNYnnn51CIpSGa8gG31En7nnyFGx+U83fJv/rYzgV9uL4/cPq47IsY3Fp8erBvAsRx3Zr7m4GGwC27RGrOqFuhqIokCQJkiRBEIS6h1SHr5ZKpZo+aYIgoNPp0NfXVyMdbpdtAw5JkjA8PKw2LuZyubYHmmymqnPWaI5yuYzp6WlVa1fV27EsC51Ot2u2aPsdOScg98w5EDwD03tuBsFqPxeN1uEDVtheGUT4v72IwP90S93ndCvg4Hm+rYQOQRCwWq1t9y8QFAnfu45g4aNnwQ2ZYZxsvYdku3uzv6oyCLBRwNHOfCSSoUDyNCxGc8PJ692mmX0qEAg0NXhMQ+MgcjWgyFdkT9dUKZR8GaTtSkBxJYhgj7pA2fWgbFzDgKIeyUgGs2eWMHs2hIUXV2AfMOPEW4ZxxztvhMHGgWYaV3T7j7nRf6y+XqpQKEAQBHBc5wnI/TJHh6bpbe9lsxnHkSNHWjonFgoFkCTZdbvxbe9AFEVMT08jEAigXC7D4/HAZDK1PbK9iiRJ6nTZRhN0NWoplUoNdXYjIyN1pxRfT0jRHLJPnwE76QF3/5jWHK7REZ5Hj+Hy730b2ZcjMF6zicmy3LWq7/r6OoaHh5HL5Vqy2aVpuuP7oC06+N59FOHPX0Dw906CcXSvGmi91YPo/7sAIV4Ee8119Xp92/dNW1nIgrxvElY+n08LNjQONJWA4moAsSWgKJSvVCj0quyJnXRflUCZdG3LMot5AYvnVzB7NoS5s8so5gQMn+zHxK2DeO3/cBdMdgMKhULH1UyWZbsSbABQqwN7vQZt9/6yLKvnRYqiWk5K9+o8ueNdSJKETCYDmqYxOzsLr9eL4eHhmo77VpFlGXNzcwgGgyBJsm5DjUbzCIIAhmGwsLAAiqJgs9lUT+frgfJsHLmvvQj+gXHoTmoaao3OoTgavnedQOjzZzD+5w+A3JRZ287golXK5TJCoRD6+/tx+fLlptdUjuO6YmahH7XA/sAAVj5/AYEP3lTzfXYCqaNgvc2LjR+F4Xnz1V4YhmFgt9sxMzPT1nVpmw6KIAH7IJ/gcrnachfT0NhNFOFKQFE3qMhDKYogrVerE5SNh27SDbIaUJh1XUvgybKM8HQUs2eXMXc2hLW5GPqPeDBycgCP/sGD8Aw6trwXz/MYHR3t6MzZ7d6qVh0Ce8F2P4tre9t2GqcgyzIymQxyuRxKpRIGBgZ6opxp6orFYhFOp7PyyxIOw+/37+g7vBPlchkrKyvw+/1awNEhxWIRoVBI/QWsZkoZhoHZbIbL5Tq0sqvSfyyj8NwsDG+/CcygtvlrdA/LaT8Szy0g+s1L8LxlEsDOszHaIZfLQZKkpjcxjuPg9XpV975Osd3rR2EujcjX5uB9bKwr1wQA290+zH/0DFwPB0HqKoEMwzAolUpNOXtdqzEmCAL2416QBLmrFcx672W1WuHxaM53GnuPXBIhX3F5qtdHoZSkmh4KysaDOe4Gaet+QFGPa2VSJocBIycH8Mp3nELwWB8Y3c69ARzHYWxsDJcvX27rHqLRKHie71oS1u/37zs77s1snpshSRJmZmZqmr4TiQQymQyKxSJEUdwSvPRKrtrUKZRl2RrN7erqKkZHR0FRFNbX19vOtBUKBTAMA5qmO7aWvJ5pdPAol8uIx+OIx+NgGAZOp/PQWOsqsoLCdy6hPB2D6YlbQNn1e31LGocQ/2+ewPQffg/WOwLQeY07TpNtF0EQmgo47HY73G43VldXuxb4EAQB76+PV4YC/nwNltu8Xbku6+BgGLMi+Yt12O/2qe+lfp1l4XK5YDKZ1ISIoijqHJPq/8uyrP63/AYXFBnwuir32O3g71qy2Sw8Ho861R2omKn09/f39H01NKrIJbHGLlatUlypWqgBhb1apdCD8ZtB2fUgbTxIE7urAXozMql2YFm2bRl+NpvFhQsX1Enmen1n5wW9Xg+9Xt/yVPBuQRBEwzVos5yqStUed3R0FDMzMztKWnvVp9JUwOF0OmsGNMmyjJmZGXUuxvT0dFtNgEClT+QwHID3O+VyGaurq1hdXQXP83C73Qd2MJVSFJH72otQRLniRMV3d5aAhkYV1mWA6w1HsPJ3ZzD0v76yZ9rWasCxHS6XCxaLBXNzc113DqR4Gv4nJ7H0ly9C128E12/synXt9/gRfvoybK/sA0EQaoLJ7/fDZDJBkiRsbGzUTFnfTh+d+VUEuRfjGH7fK+D1euFwOLC2ttazjb+6bvb396uSDi3Y0OgmclFUg4fNQYUaUAiSahdbbcxmBiyVx/YgoNhy/9vJpH7/QXiGtsqk2sXr9WJjY6MjOX80GkUwGOz4XgKBAKampjq+TqtwHIfBwcGGqpVGVuGCIODChQsNr+tyueBwOHoqFdsx4HC73RAEYYsdrSzLiEQioChKHeLUDu06lmi0T6FQwOJixSpuZGRkr2+nJaRkAbmnz4IasMLw8BEQlBasavQW52vHkPzxIlK/CMF62wA8Hk/NAbkbMAyzreW31WqFzWbryqDBRuj6DPA8OlJpIn/qFCh95zJMfsQMUkch+3ICrtMVKW4ikYCiKJiengZJkhgZGUEqlVIrCNsdJmibDmKihHw+j7m5OVgsFvT396NQKGB9fb0nQwBTqRSMRiPcbjeSyeR1b9Ch0RpyUbzaN5HIX51JUZ1DUZZUu1hV8hTYFFAY9zagqEcyklEDjPkXQm3JpNqBJEl4PJ62z5tA90Yr0DSNoaEhLC8v75pCx+l0wuvdvgKdyWRavi7P86pEtJfy+22vXO0BmJ+fb/icSCSCsbExJBKJlhd7iqJAEIQWcOwRhUJB7aM5CIihJLJffgHcnYPQ3RbYd4uwxuGEpEn433MKi3/5M5hu8MDlciEWi7W8bul0uoosqI4Elef5hkEMRVHo6+vD7Oxszzc282k3CvNprP63S/D/1mTHf2MEQcB+T8UiN3j3GFKpVI1dY7UnxmAwNCVXo61Xp40DlWAgnU7D6XRieHgYyWSyJ5a5q6ur4DjuwCVoNHqPXCxD2ihCTuTryJ6KUESpZgYFZefBBC3qY4Rh/wUU19JIJjV2cwAPvffOtmVS7eB0Ojv6GxdFEcVisSuuVQaDAUeOHMHLL7+8K65VzZhUtCL7ZRgGXq8XFsvuDEfeNuAgSRLz8/PbbqySJCEWi8Hr9WJpaenqhWkaNpsN2WxW7dUgCKImKNHpdHve6X+9s7GxAbPZvO/lVcL5VeT/vykY3nQczIRrr29H4zrDMOGE+WQf1r7yMvzvOolAILBtIqYeXq8XHMdhcXGxZlMwGCqbdaOEjd1uRyqV6kn2vh7uNw9j6ZMvIPHdEBwPDnR8PfMpFyL/PA+iqEBmth4SKIpqOpCiLSykbBmKJKvVTUVREI1GsbGxAbfbjfHxcUQika5ZrpMkiYGBgX2/Rmr0BrlQrqlIXNtHoYgKKBun9kxUAgrblWoFdyACimuRZRmrM1E1wFidjaF/woPhk/1dl0m1g9/vr5H5t8ri4iImJia6dj+trGGdvs92NEpoNbrW2NjYrrY0bBtwCILQVBYvHo/DarViYmJCnVRoMBiQTqdVe61qr0Y6ncb6+jokSdICjn0CSZJIJBKqrIFhGFgsFthstj13t1IUBcUfzkE4uwLju06D9mibvsbe4H3sBlx66tuwvTIIw4gdJpNpx/I1RVEwGo3gOA56vR6RSASDg4NIJpOQZRmyLMNutyMcDtd9PUEQcDgcLQc3nUDQJHxPTGLxY2fBDZpgGLd2dD2SIeG6fwBOnxtLK0sgCEK1RJdlGTzPN+24RdAkKAMDMSWAsddmKEVRRDgcRjweR19fn9rf0Y7EQL13ksSRI0e0PsNDjFwob7WL3dRTAUnZ1JBdqVIwg7arFQo9c+ACino0kknd9bZTCB7vnUyqHSwWC2KxWNvyqHK5jJdeegkkSYJl2W17Ippht4yPdvo9a8U5VpIkrKysYGCg86RSsxDblYGOHTumPPPMM01fjGEY6HQ6MAyDdDqtBivVJkCS7c9N1wAAIABJREFUJOF2u2G1WhEOh6HX61UnJY39CUmS0Ov1sNlsMJlMu7rxKmUJ+X9+GdJGAcbHToA0dXfqpYZGqyR+tID4t2Yw+n/eBwWVPoRGGSWj0Qi/3498Po9isYh8Po9cLgeO42AwGECSJCiKgiAIDbPxVqsVFosFi4uLvfy26pK7tIHVL11C8EMnwVg7+9vTKQzstBXL6TA8AS+MRiMikQj8fj/W19dbCgpCHz8Hx1uGwQ9vP3DPaDTC6/VCFEWsra217DBGEAQCgYBW2TjAKIoCpSDW2sVurlRsXAkoHLUBxeap2YcloLiWUkHAwosrmDsXwuzZEIrZEoZP9GP4ZD+GT/TD7OiOcUSvEEWxa03bDMN0VPFYXFzsKLHRLMePH2/4tVKphOnp6ZavOTAw0FVJFUEQzyuKcrre17qavi6Xy3U332pQI8sy1tbWQNM09Ho9dDodstlsN29Bo8vIsoxsNqv+O5Ekqf57bg5WWZZFIBDo2jRPOVtC9h/PgbRyML3rNIguDSTT0OgE2yuD2HhuAfHvzMD50BhGRkZw6dKluvpdh8OBjY2Nmp4FoKKxbfbwy3FcSxPIu4lhwgbbq3wIf/4iAr9zIwi6/WSDzsLD6nWAS+vB2fSYm5tDqVRCJpOBzWZrabOuNI4XgR0Cjmw2i5mZGdjtdgSDQWSzWayvrzeViez0AKKxOyiKAiVfrmMXe3UOBRRUKhR2vSp9YoZsatXisAYU17KtTOpDD+y5TKpVaJqGz+drWB1uhc0DWNuhVzaym9mpArOThLRaUb6W5eVlGAyGXVGz7LpeRq/Xw2AwYHp6GmNjY5qk6oDRqFGr6vNsMBg6nlIprmeQe/os2Jt84O4dOVCLoMbhhiAI+N9zCrP/xw9gubUfjI3H0NBQ3SFQ6+vrCAaDiMVibTc4yrK8p7//9gcHUJhPI/KNeXgebb9hOpPJQHJLmHr6eZhf40OpXOlHiUQiGB0drZlzsRO0lYWYbL6fJZFIIJlMwuVyqQHiTnTq06/RHdSAYlNF4tpeChC4EkzwamDBjNjVxwievm73kGQkg7lzlQBj/oUVGG16DJ/s35cyqXaw2+0oFotd6ddKJpNtBxxOpxOiKKJUKqFcLtes290ysKj2+jXC5XI1VAtVZwfNzs7W/frCwgJGR0dbup/l5WVkMhl1XhJQcbXdjl0NOAiCgN/vV3VmJEm2PTRQY3+Sy+UwNTUFu90Or9fbsgSrfDmK3Ddegv6hI2Bv7OvRXWpotA/Xb4b9vmGE//4cgr9zO/R6PYaGhrb0WRSLRQiCAIfD0fZUcFmWd2wU7CUEQaDvNyaw+NGzSA+aYD69/YbSCEVRkEhuwHGDDys/C8Fy5Tosy4KiqJYcXmg7BzHemjxKlmWsr6/Dbrc3zPRtxmrtrG9lL0mlUnj66afxq1/9ColEAgaDAcFgEG9961vxla98BRzH4Y//+I9rXvPd734Xf/M3f4NPfepT6Ovrw/nz5/Hss89iamoKpVIJLpcLJ0+exJvf/OYdDxWtUBNQJBoEFBRxtYeiOthu1HFVAqXNYVIpFQQsnA9j7uxyjUxq9HQADz55x76XSbWDz+dT3e46oZN1lmGYur0Qsizj8uXLNVVVnudhtVqRSCRaSrjvtCbRNA2e5+v2tciyvK3pSDsJ4uow1s1cW83f8j4tv0sHOJ1OkCSJYrEInU63a64rGrtPIpHAxsYGBgcHd4zMgcovb+kXSyj+eB7Gx06ADth24S41NNrD8+ZJXHrq20ifW4X5RB8MBgOGh4fVSgdFUfD7/SAIouEgpp0gCAIWi2XPe9woPQPfk5NY/vR56PoN0Hnbs8AURRGGQTMSX1qB5bQbFEVhcHAQa2trLW28tJVFYbq9w4UgCLBYLNjY2Gj4nGq/2kHlIx/5CEqlEj7wgQ+gr68PqVQKL730ErLZLD74wQ/ife97H7797W/jNa95DQAgGo3ic5/7HJ544gn09fXhW9/6Fj7zmc/g3nvvxR/8wR/A6/UiHo/jueeew5e//GV84AMfaPpeFEWBkhOuSJyuGWp3ZSYFQRNX+ybsPCinHuy4Q31MCygaU5VJVfswVmei8I+7D6xMql0GBgYgimJH8tNuycE3Q5IkhoeHEY1GYbVaa85CDocDqVQK2WwWoigim81um3hp5hw1MDCAlZUVFAqFmmBAluWu99/6fD6k0+max3YK2nY14Mjn8+qwlI2NjZab+DQOFoqiYH5+Hv39/dtG54oko/CvUxAXN2B68lZQVm2wlsb+hmQp+N99EitfOAvjx9wgWQp6vR4jIyOYnZ3F0NAQMpkMlpeX2/JnpygKAwMDKJVKbQcs3YTrN8L9piGs/O1FDD51AiTX+tYhSRJYuwlipoz8fBpH77kByWSy5e+PtuogJduT4lZdWQwGA8LhcN1Kx0GZS1SPXC6Hl19+GR/+8Idx0003AajIHMbGxtTn/NZv/Rb+9m8+i5P9AlzUPP7y0/+GydERPPTQQ4jFYvjsZz+LRx55BO9973vV17jdbhw9enTLga42oMhfE1BUAgyCpkDaODWgoF16UBMOkHY9KCunBRQt0lAm9ehJBI71geWuz59nMBjEpUuX2p7r1syBvh1Ylm24plgsFrVhO5PJbDEH2Sw1bSZgYFlWHUa4ueKjKApMJhNcLlfdans2m0UsFoPT6Wz6+6JpGpOTk0gmk0ilUqrJxravafrqHUKSJIxGIyRJQj6fh9vt7mhapMbBIRQKQRCEuqV4uVhG7p9eAEgCpiduBdHGQUZDYy8wn+jDxvACIt+4CO/bK+4hPM9jZGRkx/lF28GyLILBIDKZzL5aIy23eVGYS2P16Wn43n2k5cxpVR5mv8eHPqcHJEm2NbGdttcO/2uFYrGImZkZeL1ejI6OYmVlpeYQfdCniHMcB47j8Mtf/hKTk5N1m1kfuP9+/PxfPolPfux/xx039WNuegqffsoJJC/gJz+ZhiiKePTRRwFckU1khSuN2AUgUUB6c1BxJaDY7O5EuwygJlwgr8yhIK/TA3C3uFYmVcgUD71Mqh2q1YR2nJoAwGze3oSi15hMJpjNZmSzWVitVrjdbtA0jWQy2fJaq9frawKOamLF4/FAr9fXdT1cW1uDwWBoaQ0kSRJ2u72pgYRAjwMOnU4Ho9EIg8EAvV6PbDaLUqkEQRDUCbEa1weRSASCINQ0ZUmJPLL//QyYESf414yrg7w0NA4Kvt84gcu//x1Y7wyA81c2LJ7n4fF4atxTaJqG2+1WnfqAinSH5/lKf8MVPW81QxWJRLaV/ewV7reNYOkvXsDGc2HY722tEiDLMnQ6HW5+z93IL6Qx88JlUObWD6OUiYWUF6GUZRBM62uGoihYXV1FJpNBf38/UqkU1tfXoSgKHA5Hy9fbT1AUhQ9+8IP4q7/6K3zrW9/C8PAwJicnceedd1513crO4v1v9OJ//vgCXvrnS3jq8Vth1fOQzv8D5n+gB5Mog/j6HOKJiiU5wVIVaVO1QuE2QnfEpT7WTrVLozGyLGN1NqYGGNerTKoddDodBgYGEAqFWq4s90JS1Sr1KgTt9JNtZ3phMpnUURXXMjc3h6NHj/Zs/EFPVgqKouDxeGAymZBOp5FKpRAOh3dlMIrG/iWZTKJUKmFgYABEOIvcV14E/6oR6G7ZvcEzGhrdhLHx8LxlEiufP4PhP3qVehCw2+3IZDLIZDJgGAZDQ0NIpVLgeR7BYBD5fB5WqxWxWAxGoxEulwvr6+sYHBzct8EGAJAMBd+Tk1j6+FnwQSP44eb92wVBqFQ1IuuYf/Y8QBJwv2Go5XsgSAK0hYWYKoFxtl+RqNrm+nw+8DwPm812oJvFq9xxxx04ffo0Lly4gKmpKTz//PN49tln8fjjj+Ptb387UFyD1cTiwVuG8OMfTuNmnoMYkUByIcilIVA8A/0dAbVqQeq0gKLXpKIZ1a5Wk0l1hsVigclkwtLS0nU7dqHdZL6iKAiFQjtKo9ql6yuJ3W6H2+1GMpnE9PR01yzBNA4HhUIBly9eArOSg/nBfsgDBhRTKdVhQZvoq3HQcDw4io0fLWLj3xdhv3tQfXxgYACXL1/GwMAA4vE4SqUSbDYbcrkcDAYDFhYWUC6Xkc1m4ff7MT4+jrW1tX0bbFRhHRy875zAyt9dxOCHToE2N+dBL0kSJElCuVyG5Y4+LPzFOTgfCoBkW3eHoa06iBudBRzVe1peXobZbIbNdniMKliWxYkTJ3DixAk89thj+NSnPoV//Md/xFve8hbQnAdyoQxiIw+aZ8D2m0EaZID1YOShk/hB6CxyXhp2+8FtnN/vCMWyKpOaObOsyaS6DEmSGBwcRC6Xw+Li4nV3Dt2pL25kZASLi4swGAxQFKVGftWuFLgZuhZwkCSJoaEhyLKM+fl5bb6GxlYUBbrnY6BXcsg/4EecKgKbZCcsy2J0dFQLOjQOFARJwP/EKcx/7Mcwn+wDbapM5a5qimdnZyFJEiYmJrC0tIR8Pl/z+nK5jIWFBVAU1dPFvpsYj9lhvd2L8BcuYuB9NzQthywWi+A4DoJbAD9oQuqXEdjuat3+uhpwdAuv19u1a+1HAoEAJElCqVhC6ScyyIQDpHUWBKtAKScBhQcG3oY7+zz44he/iK9+9as1TeNVqsGyRmtsJ5N661P3wzvs1GRSPcBgMODIkSMIhULXjYRfluUdx01wHIeJiQlIkoSLFy/WfK2Xv4ddCzh4nleDDQ2NLZRl8P++CqIgIv9gPxR+66+eIAiYm5treQCNhsZeox+xw3rbAFb/8TwG3ntafZxlWRAEofqcXxtsbOagBBtVHK8NovCZ84j9yyJcb2xOGiUIgtrI7LjXj7WvzMJ6p7flTa7SON4dW3WapndlUvBukMlk8Gd/9me4//77MTQ0BJ7nMT09ja997Wu4cfI4xH+6CEWQYP5PfwQy9THgpe9AKkyAuu0xwBCEExUXq7/+679GLpfD/fffD4/Hg0QigR/+8IcQBAHvf//79/rbPBCkohU3qdkzFZmUwcpj5NSAJpPaZUiSRCAQwMrKyr6vHneDVqo51b1pc7tDL5vnuxZwGAwGzeZWoy5EXoT+eyFIVh0KDw0A22RDtd8hjYOK923HcOmpbyN3KQbDxFV7QZvNBpqma6q+er2+5pB7bQPftZ+XSqV9VzUmSAJ97zqKxY+eATdogummnS0VdTqd6gqlH7cCJIHcpSSMR1qTM9FWHYS1xsFbKzTrsHIQqGYuv/nNbyIcDqNcLsPhcOCuE7fiNbkRUA49DK87AoImAcsEYA5DWL0brCGoXuPhhx+G3+/Hs88+i4985CMoFotwu904efIk3vGOd+zhd7e/2SyTmj27jHz6ikzqFQE88MQdsDg1mdReUrWmbRR0JBIJkCQJiqJA0zQYhmlrIN5eQ9M0xsfHMT8/D1EUwbJswyCCJEmMj49jYWEBQKUS2svvmdiuk//YsWPKM888s+NFdDodhoaGMDs7q00O16iBjBWh/7cVCEesEG60A01kMoeGhrSyvcaBJPnzZUSevYjRP70fJF0JrGVZxtzcHNxut/p7LQgCisVi3cz+tY8RBAG9Xo+pqanefwNtUFhIY+WzLyPwwRNg3dv3VFStaKvTcDd+uorMC3EEfvt4S++ZezGO9E/X0Pc/Hmv7vqtMTk4eahln6fwaMl9/GcbXTYA73V/zNaVYRuZTP4LpqVdrkp4W2U4mNXJyQJNJ7VNWV1fVngWCIEAQBMrlcl3XJoIg4HK51KHVGjtDEMTziqKcrve1roQyOp0O+XxeCzY0aqAXM+B+sobi7V6IQ803IG5sbGgBh8aBxHJrPxI/mEf8W9NwPVKxISVJEsViEel0GisrK5XZBi02MY6MjMBgMHQ0SbdX8INmOB4OYuXzFxD83RPbNoFnMhmYTCY14LDc7Eb0mwsoreeh8zS2crwW2tb+LI5rEQRhX1hidhtFUZD/zjSKz6/A8p7TYAa2OooRHAOCJqHkyyAMh0NW1ktSsWwlwLhGJnXnW08geNynyaQOAH19fejru9o3Fg6HkUgk6j5XURREIhFEo1EYjUZYLJYdnex6MdX7sNCVgOOwLtgabaIoYM8nwF7YQP6Bfsiu1pxkrlcrO42DD0EQ8L/7FGb+6N9guW0ArLNyiOY4rqOJ4alUCmazeV8GHABgvasPxfk01r88De/jEw0zu6lUCsFgEIlEAqIogmQoWO/wIvHDMPre3nzvFm1lu9Y0vrCwgEAgsK13/UFDLpSR+fKLUIoibO+/A+QVI4N6EFYecjIPUgs4tqDJpA43uVyuYbCxGUVRVJtzgiDU6eDXsra2hlgsBoIgwHGcGqAcRGlWL+jop0CSJNxuN6xWa0ebqcYhQlLA/XQNVKKE3OuDUAytZ3xEUdSyBBoHFp3XCOdrx7DyxbMY+r07AQDDw8OYmppq254xlUphZGQE6+vrLV2DoijodDooiqJWFXoBQRDwvGMMi//1HFI/WYO1gfNUsVhELBbD8PAw5ufnUS6XYbvbh7k/fR7uRwZB6ZvbkkgjA0WQIQtSW7a6mxFFEXNzc7DZbKrO+yAjrmeR/tIZMONOGB+50q+xDaRND3mjAPgP/gySTlEUBeGZaF2Z1Jt/9z70jbg0mdQhot7E7Z1YXl5GKBRS5VgEQYAkSbWSDUBdbwuFAtbW1kCSJHieh91ubxisXA90FHCYTCbo9Xqtd0MDAEAUJfDfX4HCksg9HADamAJcJZ1OH4ohXBrXJ67XT+Dy738XqV+twHLar1rkzszMtHW9crmMTCYDh8OBaDS67XNJkoTVagVFUbDZbBBFUXUrEoTuODvVfV8dBf8TR7H0yRegGzCCD9aXUcbjcSiKovb9waKDcdKO5M/W4Livv+5rroUgCFBXqhxsC1Ks7UilUgc+4Ci9tI7M116C8eEJcDc397MkbTyUje404B9EVJnU2RDmz4VgsPIYPqnJpK4HbDYbCoUCRFFUE53NoChKS5PMZVlGLpdDLpcDSZIwma7PGTcdBRw6nQ6lUkkLNjRApgTovxtCOWhE6bSrqebw7Ugmk1rAoXFgIRkK/U+cwtJnfgnjcQ8ojgbHcR3N2ohGoxgeHkYymdx2zXW73eA4Dvl8HtFoFKlUCpOTkxgcHFSfQxAEotFoU3KCVmA9engeG0P48xcQ/NAp0Mb6h7VEIqFO947FYrDf40PoCxdhv8fX9EwP2qbrasCh0zWWHe13FEVB/rszKP4qBMu7XwEm0PzaSVr1kJYPv11olS0yqVTxSqN3Px54z+2aTOo6YnMvhyiKu2LMEQqFcPTo0Z6/z36k7YDDYDDAbrdrczc0QIVz4J9bRem0E+Xx7gQJmuZR46BjPOaGcdKN9a++DN87bwJQ8Thv1wteEATEYjH09/c3XHer1Y1rq85TU1MgSVLNylmt1p4dsE03OVGYT2P1S1Po/+3jIMj6yYd4PI5AIIBYLAZ+0AzarEPmfALmEzvb6wLdbRwHAJ/P17Vr7Sat9GvUg7TxKL8Y3vmJB5SqTGr+XAizZ5cRno7CN+bCyMkBTSaloULTNHw+HxKJBEqlUksVjFaQJAlTU1NgGAYsy0Kn04HjOOj1+kN/7mn7u6sOsOrVP4rGwYCZSkJ3JobCvT5Ifd1ruryedY4ahwff4zfi0lPfge3uIPiAFU6ns6PhU7FYDEajEW63G5FIBAzDwGAwwGw2o1gsgqIo5HK5LRWQzYOdqp/3ctid6/WDWP70ecT/dRHO1w3WfU6xWES5XIbJZKrIxe71I/HcSvMBh1UHcaM7EjGCIMDzrZlb7AfE9SzSf38GzFhz/Rr1IK085GTv+nv2gkYyqTveosmkNBpjt9vVuTyiKCKdTiOdTqNQKECSJJAkCZ1Op0qw2j3/Vl9/bV8dwzDo6+vr6fC9vaTtgENRFCQSCTidToTDhzc7otEAWYHuP6KgQ1nkXxeAbOnu4UWzxdU4DNBmDt63H8fK585g5E/uhU6nA0mSbTePA5WS/MjICJxOJyRJQqFQQDqdBsuyYBgGq6urO16jUCjA7XaDIIieJI0IioTv3Uex8NEz4IbMME7WDtcjCAIsyyKXy8HhcFTscm90YP3ZORSWM+AHdtY40zYdSkuZrtzvQUyclV5eR+arL8Hw8AT4Jvs16kGYOCh5AUpZAsF01oC/VwjFMhZfCmP2bAhzZ5eRSxYwdEKTSWm0D03TNQFIPURRRCwWQzKZ3JLUaYdyuYylpSXQNA2v17utrFyWZUxPT8NoNMLv90OWZciyXLdKIooistkszGbzFjMeWZaRSCQQj8dht9vhcrnavneG2T6Q76h+E4/HMT4+jmg0qvVxXE+UZfDPhUGIMvKvC0LhurtJ0TStOVRpHBrsrx7Cxg8XkPj+PBz3DcNgMCCTaf+gLIoiLl++3NEhuVgsolQqwWQyIZ1Ot32d7aDNLHzvPoq1v78E/5/dB7PbqsoISJKEIAggCAI6nQ4ulwvRaBS2V/qQeC4M/+MTO1/fpkPuhXhX7vUgSWo66deoB0ESIC085FQB1AE5mCuKgtXZKObObpVJvfGDr0bfiDaoTaP3VAMDr9cLURSRSCSQzWZRKpXa7tUDKmt8KBRCLBbD6GitXfj6+jpKpRIKhQLK5TI2NjZqqubBYFBtSl9cXEQul6tJcFksFpjNZpRKJeTz+ZoxBM3sKbIsI5lMIpPJoFwuQ5blphvuOwo4JElCJBJBMBjE3NxcR1k7jYMBkS1D/70QJBePwm0egOr+Rn0QpQ0aGo0gCAL+J09h7k9/BMvNPuh0uo4CDqA7GXmGYVAqda8Hoh76EQtu+fCDoAQKqY0kypKIcrlckw3U6XTwer0YGxuD1WjB2T/4AcS0ANq8fdW0IqkqduU+FUWBKIr7XkMtF8rIPPMi5HwZtvfdAdLcnT4cwsZD3tjfAUcqllX7MObOhaA3cxg5OYDb33wCgzdoMimNvYWmabjdbrjdbvUxUaysd9WPqiyrGgxvbGw0tCuvJmI2E4/Hd3Qp3NyUXm+fSaVS6qT1a9mumlMqlTA3N9dRINXx6hqPx8EwDILBIBYWFg5kaVqjOahIAfz3VyAct0M4ZuvYiaoRmjuVxmGDD1hhe2UQS0+fQ/6uvT/U0TQNiqJ6HnDQNA3nqBc/+uN/gUwo8D42tuU5pVIJi4uLqhHJQ194DMV0AQWihHg83nCDqzSNd8/md3l5GUNDQ127XrcRI1fma4w6YH7nybb6NRqxH/s4tpNJ3f9uTSalsf+haRo0TTdMotrt9hpJE0mScDgcsFqtdaVPO8llSZJseQh3tS/FYrHUTbhUKxqxWAwMwzRcj/V6PQKBwLbv1ZV0ztraGiYmJsDzvNpMrnG4oOfS4H6+juJdfRADvV3or1ePao3DjefRY3jpsz8EkdWBbGAXu1vsVmLIZrMhnU7D8aZBLH78LFI/X4PlNm/d51Z96kvreWS+tYobfv8ujI2NYWNjA5lMBsVisaaKTvIUoCiQ8mLTAwO3I5fLQRCEnjbTt0vp5cp8DcNrO+vXaMR+mMXRSCY1fKJfk0lpHFpIkoTT6YTTub1ZRqlUqum5YxgGHMfBYDDAZDLVdR08fvw4yuUyisUiBEGAIAgQRREcx8FkMm0bnIiiiHA4jEwmA0VRYDKZ4HQ6axwSSZKEzWaDx+Np6m+zKwGHwWAARVGqz/x2coGqI4nGAUFRwL4QB3s5hfxDA5DtrUXPrRIMBrVNReNQQnE07LcMIFFKQ+GormaoW6Va2u9V03iVUqkEs9kMiqfhf3ISS3/5InT9RnD9jZMWOo8e69k8Ln7jLNx3BxAIBGCz2UAQBCRJQjKZRCQSAUEQqjVuNwIOAFhdXUUwGOzKtbpBTb/Guzrv12gEadWjvLD7szg0mZSGRnPwPI9jx45t+xxBEBCPx9XkiSzLsFqt8Pl8LSVyZVnGzMxMjfS1WCyqk9T1ej1cLlfLyeGurNJVf3idTgeHwwGWZRGP1zbzMQyD/v5+GAwGXLx4sSMdGEEQavOhoijI5XKdfgsa9RBl8D9eA5kWkHskCKVLm3ojHA6HVt3QONT4bx3Fxk/PofxiHOyp9txAukUul4PH48Ha2lrP3iOdTsPr9VYyaX2A59ERhD9XGQq4XZBgv9ePyP+zAMutHszOziIQCKBcLiMej2NgYADFYhHpdBq0TQcpWQJ83XG1y2QykGV5XyQ95GIZmS+fh5wXutqvUQ/SxkNO9r7CUVcmdZMfI6cGcP+7boPFpa3/GhrtEg6Ha5rAgcoQ5VQqhaGhIej1zY0uWF1d3eK6VS6XUSqVMDk52fb62JUTZLlcRiQSAVAJLEZGRtTGQFmWodPp0NfXVxnwxPNtNZcbDAa43W6wLAuKotTueIIgMDMz041vQ2MTREEE/28rUAw0cg8HgB5nY00mU83UTw2NwwhJkjA5zEiu5iDFiqCcva0Ybsfy8jKGh4d7XnUmCELdvMyn3SgspLH6D1Pwv/dYQ3cow1Eb5K/NIj+TgmHMiuXlZUxMTGB1dVXttSgWi6CtOpQT3e1DicfjbVtDdovafo0TPa+GVXo4ilAUpauOXYqiYG0uVqlgnA1h5XIEfaMujJzUZFIaGt1mcHAQsVgM6+vrNZVrRVEwNzeHkZGRHU15BEGoOyvKaDR2PBy16ynrcrmMlZUVOBwOtWQvyzIWFxdRKBTg8XhaKuETBAG32w2r1YrV1VXVCgyoTO3VGoy7D7lRgv67IZRHLSiddPSsObyKyWTaVzIGDY1e0j8aRLaYR/7r89C/fXjPLFllWVaHBfaKqiPL5myZ+03DWPrkC0h8NwTHgwN1X0cQBOz3+JH4wQoMY1bIsoxCoQCj0YhMJoNIJAKfz4c123RXp40DFdvJcrm8Z5PH1fkarx0Hf0v9n0+3IVgaBEtByQogWpxUfi2NZFK3vekmBI/3Qcfvvx4ZDY3DgtPphN1uRzQa3eJoJQi+BoY0AAAgAElEQVTCjgFHMpnc8hjLsjs2hDdDTzQymUymbsaMJMmmgw2KouBwOGC325HNZjEzM7NFhsWybM9dVq43qFAW/I/WULrVhfJI76d9m83mrvwia2gcFBiGAW/UQ3yFE+XzCbA3OvbsXkiS7EjeuhMsy0IQap2kCJqE74lJLH7sLLhBEwzj9ZNG1ls8iP7LAoRYAayTrwwHvFKNSSaT8Hq9YBwcCpe3bpDtQpIkfD4fRFFU32+3UBQF+e/NovjL5a7M12iVqqyKbDHgEIplLL28itmzy5g9o8mkNDT2GpIk4fF44HK5EIlEkM/nQdN0U+uZwWAAQRAgSRJ6vR5WqxUmk6krlchdNR1vdsKu3W6H2+1GOp3G3Nzclg2riiRJLVuAaTRAUcBeTIJ9IY7CfX5Int7PwrBYLBgY2J0MnobGfmJwaBBTmTyK/74KpSCC4Pdm/kO9JBBFUZBluSvN5Dqdru76zdh06PvNCax+cQrBp06CsW095JI6CtbbvUj8MAzvW0fAcZxaKZFlGYIgwBS0If2L9Y7vE6g0Zfb39yOXy2F9fR08z+9awLG5X8P6/ttBmXd/XyNsesgbBWDAtu3zNJmUhsbBgCRJeL31XQEbYTAYdmxOb5ddDzgIgoDZbIaiKLBYLNDpdFuGolitVszOzu44vTybzdYMWdFoE1kB9/N1UGsF5B4JQDH1vuRttVrR3999e0cNjYMATdNw+txYP1ZE8Tsh8G8c3JP7qPq+WywWEAQBvV4PiqJU96pyuYzl5eW2K8n1KhxVDBM22O7xIfx3FxH4nRvr9inYXunD/J+fgef1QzCbzbh06ZL6tUKhAJPfVmkabxOSJGE2m2GxWMDzPMLhsDp5faf9p1uI0VylX2PYviv9Go0grTzkBta46XgWc+dCmD1TkUnxJg6jpzSZlIaGRvPsasAhCAIikYhqcZjJZMDzPMrlMgRBAEmSKJfLWFhYaGqxpyiqp3KA6wJBgv4HYYAAco8EALZ3eu4qRqNRCzY0rntYlgXl5iGcT4A55QQ9sPuDzNLpNBRFUSvP0WhUDS6Gh4chSRL8fj9EUYQkSSiVSsjlcg2n414Ly7LbzmayPzCAwnwakW/MwfPo6NbXOzgYJqzAsoDiRO0cjkKhAKPTDHFDaLrZ2WKxQK/XQ1EUMAwDo9GIXC6HjY0NLC0t1VR1diNLX7oQQear52F4zTj4W/e22kva9JDmK+6SmkxKQ0Oj2+x6HT8ej9dY5pbLZbhcrh0nKNaDYZhdy0IdRoi0AP33ViD16VG81Q2Qu9O8qsmoNDSuDN8jCfCvDaDw7AKM7zsGYpf+BqvEYrGGXyNJEpFIRJVY0TQNlmURDAYxPz+/perBMAxkWa5JAu20RhMEgb7HJ7D40bNID0ZgPr21Ym2/1w9WZLbYnxeLRdjtdtz5iTfAOGoHSZHI5/PI5/PI5XIoFovgOA4cx4EgCPA8D4PBgHg8DoIgUCqVEA6HGyatehlwKIqC/L/NoviLZVh+8xSY4PYypl6jKArimQLSv1jAL345r8mkNDQ0us7eCIc3kU6n4XQ6YbFYkEqlWnptqVQCx3FwOp3bbpwaW6HW8+C/H0bphAPlo7u32Tmdzp664mhoHBSqVQLmlAPC81EIP1uH7s7W9La9giAI6HQ65HK5Lb0cpVIJgUAAiUQCpVIJoijCbrfDarUilUphZWVFfW41CNkOSs/A9+Qklj99Hrp+A3Te2pka/JAZXIJDdjEFbGot0+l0EEURM//8Igyv9ID16tWgwmazgWVZiKKIfD6vBkJzc3NNV8V75R4mF8vIPHMecra0Z/0aQK1Mav6FFZj1LF7FMLjtXbdoMikNDY2us+cBB1CxIfT5fGp5v1kEQVCHQnEch5WVlZ5OzT0sMDMp6H4ZReHuPkj93RmY1QwkSWo9NxoaV6hObSUIAvybBpH964tgbrCDNO/9QU9RFBSLRRgMhrqDpBRFUZuqWZZFMpnEzMwMRkZGEI/H1e8tHo8jEAggHo8jFos1XJ+5fiPcbxrCyt9exOBTJ0ByV7cmgiAgUCJ4iUMeV6sqVqsVsVgM6dUkEOIAOw1BENTEVbMmJY24dvBVN1D7NYZsMP/6TSDoxsmXqp281+vd0cqyGTbLpObOhpDdyGPoJj+GTw7gvt+8DRaXEZmPfh+mm/wg2H1xNNDQ0DhE7ItVpTqG3WazIZFItPRaURQxPz8Pv9+PoaEhLC0t9WSjOBQoCnRnYmDm0sg/PADZ2rvJtfXw+XxaWV5DA0AqlVIP5QBAuXnobnOj8M0lGH59ay/DXpDNZqHX67cEHEDl/utVpCORCAYGBsAwDIrFIlZXVzE7Owuv14vx8XHk83lwHIfp6ektr7Xc5kVhPo3Vp6fhe/eRmgqD4iBhszmw9sI6OL8RNE1Dp9Mhm82CtrJ1Z3F0EmwA3Q84ShcjyHzlPAwPjoG/bWcr8MXFReRyOczNzWFiYgI03dp2rSgK1ufjmDmztMVN6g3/+d66MinSykFOFkC5tR4NDQ2N7rIvAg6gUuUYHBxsOeAAKgtrKBSC0+nE+Pi4OoJdEAQUi0WkUimt8iHK4H+0CiIvIvdIEMou23BarVZtSKOGBiqV2eXl5S2P6+71IfOJ8yhfSoKZ2Pu/FbPZjFAo1NJrqj16JEnCZDIhEAhgfn4ey8vL4HkeRqNxW6tZ96MjWPqLF7Dx3Ars9141lmA4FqyVR+JHYfh+bRyyLKtOWrRNB3Gj+/OYOg1YqiiKgvz3Z1H82TIsv3EKzODOEtZisaj2rCiKgoWFBYyO7hyIVmVSc2dDmDsXAmfUYeRkP259440YvMG3o0yKtOq1gENDQ6Mn7JuAg+f5hvaJzRKLxRCPx8GyLFiWhU6ng81mg9lsxvLy8nUbdBB5EfrvhSBZdCi8dgCgdrfKUPW319C43hFFsW52HwAIhgT/xiAK/7wI+oNmEExv/05Zlq2ZY1RvHke7a6Ysy0ilUqAoCoFAALOzsygUCigUCnC5XGqwcC0kQ8H35CSWPn4WXMAE/YgFNE1jYGAAC5fmkDkbg/jIIGhTpT+D4zjQVh3yFzfaus9eI5dEZJ55EXK6BOsHmu/XuLYhv1gsIplMbknalEtlLL5UXyb16t+4FdYWAwfSxldmcWhoaGh0mX0TcFitVkQikY6voygKSqUSSqUSMpkMYrEY+vv7MTY2hnQ6jUwms8Xt5DBDxovQf28FwhErhBvtQI8aIRtB0zSGhoZ29T01NPYjsixjZmZm20M8M2GF4I+h9IMwuAd7G6R7PB7VReraBmmCIFAoFDpO0iQSCfA8D5/PpzaTS5IEmqYbulexDg7exycQ/sJFDH7oFOyDdmQyGRQVAaYbHUj+dA3O1wSQz+fB8zwom66upGqvqenX+E/b92tseW0dOdfa2hosFktjmdTv3IO+UVdHslXCykNONLYx1tDQ0GiXfRNwUBTVM4vbUCgEjuNgMpng9XohSVKNHeJhneVBL2XA/XgNxdu9EId2v0TucrngcnW2AWpoHBbW19eb6gvgXx9A5pMvgbnJAcrTebPwdsRiMXXQXa8Ih8MYHh7GsWPH1HkZOzlAGSftsN7uRfgLFzH2iXHErlip2+/xY+n/fgmO+/pRKBSg1+vB9EhSBVSCxHbWr1b7NTYjiiLW1tbUz/OpItYuxxG4yYtPPvkPYBimJZlUK5BWPcS5+M5P1NDQ0GiRfRVw9PLgXywWUSwWEY1G4XK5MDw8DKCSySsWi4hEIoen8qEoYF/aAPtyAvkH+iG7entoqQdBEPB4PLv+vhoa+xFZlmvmD20HaWbB3edD4RsLMLz3SM/sWRvJmrqNoiiYnZ2tbQJv4n0drw1C+u8zYClWbVzn+o3QefRIn4uBv0sPj8eDsdNHkR9ea3r4Xyu0GnBU+jXmUPzZUtP9GlWi0Sg4jkNoOYRcsoCXvjeH8MUYCukS+iaccA3Z8Mjv3YGxo70zFSBtPBRNUqWhodED9k3A0amFYStEo1FEo1H1c4vFAr/fj0gkgmQyuSv30DMkBdzP1kDFSsi9PgjFwOzJbZjN5j15Xw2N/UizwUYV9nYPhDMxlM/Ewb7C2ZN76lUg04hWgxuCJOD/9SNQRBkunR0bUhrlchn2e/yIfXsJ5le4sLS0BJqmcfoP70d4LYyc1N3Dcit7klwSkfmn85BTxZb6NapuUivREGiWRCqSw6++PgXPmB13vvNGOAIWkNWBkHRvA0TSykNOFaDIyq4PodTQ0Dh45HI5xONx5HI5MMz25819E3DsVratHqlUCgzDQKfbXZvYbkMUJfA/WIHCkMi9LgD0uOl0O1q1cNTQOMy06r5HkAT4Nw8h98VLoI9aQep78/e0n400qq5WoiLBEXDBKtsRXluFclzB+tdnUVjIgBiqHIqX//ZF3PxfHsD07ExXE1fNXkuM5ZD+4hkwgzaYf+3GHfs1Momc2uhddZO64fVBUDoCJoceD77/lvrv02PLd4KhQPAMlGwJxB4NJNTQ0Njf5PN50DSN6enpmj1kJ5XSvjkV7mXAAVR+UN0YrrRXkCkB/HdDEANGlE67gD3OTu1WtUpDY78jimJb/Wl0vwHsjQ4U/3UZ+rd233hhr9fca2EYBkajUf0QBAG5XA6RRBQr35mBsiLg1v/yANKmNFwffg1m/uUl6IcqldRcMovEYgxut7um/6FTstlsjZNXPYSpKNL/9CIMD4yBu22gbuWo6iY1dy6E2bPLyMRzGLqpH8Mn+/Hq37gVeqsOly9f3vF+dqPfkLTykDfyILWAQ0NDow5zc3NtvW5fBBx2u71mCNZekE6n4Xa7wfM8CoWDpWGlwjnwz62i9AonyvvAvx84vI34Ghqt0klTNveAH5m/OA9xIQN6sLvGD7stqboWkiRhNBphMBhgMplAEASy2SzS6TRWV1drsvnm2z1Y+4dL+PnHv4sjv3UzFBOBm997N1ZWwsjLBdA2HeZ/OIXT774b8Xi8awYk8XgcTmd9Sdt2/RpVmVS1ihG6tI6+ESeGTw7gDR+odZMql8uYmZlp+p7abWRvFtKmr1jjBnv2FhoaGgeQUChUd+Brs2wbcOzGhsRxHNxud9sRU7eQJAmZTAYcxx2ogIO5lITu+RgK9/RB8hn2+nZU9lPmVENjL+kkmULwNLjXB1D4xgKM7zsGgu7uQXMv/07HxsZU+/LFxcUtsyc2QxAEPI+NYfG/nsPUV8/C9kofkueisPityDMAbdWhuJpFsVgEy7I9czysopREpKv9Gu+/HZSFQyaRUysYc2crMqnhE/245fXH8bY/fA04/VY3qVQqVXcI5HYkEomGQVA3IG085KRmjauhoXGVRCLRcY/ztgEHx3EwGo2qQ0gvYFkWgiB0PPSvU9xuN6xWK/L5A7LQygp0v4qCXsoi/7oAZEv3rBG7gSap0tCo0ElGCACYG+wQfhWD8NN16O7u69Jd7b2kSpIkrK2tNR2QkSwF/xOTWPrEOXADRvRN9KO8WIRsk0DbdCgtZyFJEiiq+XkXO+FyubbedyyH1JfOgPSZEL+1D//x1TNbZVKP7zx0LxQKtbWBr6+vw26396zKQVh5SDOxnlxbQ0Pj4JHL5RAOhzu+zo6SqsHBQUQika4M5atHNptFf39/z21xd0IURWQymYPhUlWWwT8XBiHKyD8ShMJ1b4PtFlrAoaFRqW50uq4RBAH+DUFkP3MBzA12kLaDbW4BVORUkiSBYZiWKkCsm4fnsTGEvzSFG//hFTjzzX+HqFf+//buPDiS/LoP/PeXmZVZWfd9AXXg6O7pnns45HBIyaQ8JE0ORYoidXmlkJaSLZOSrLH+WDt2tRvyKqSwg3Z4bDlMa1eilzIlUV6ePiStKA5pDSkPj5nR3NMX7hsF1F2VVXnuH9WobjSqgALqBPA+EYhuAIXMLPTML/P9fr/3HuxxB/RcA6Zp9i3gYIzt6+xtWRY2vnETxc+/jHnRwivPXUV8NoyphybxoX/4biQudN9zaGlpCeVy+UTXNeggkfM5YBZOzyo/IWRwCoUCVldX+3KsrnI49mb/j1r2PolwOIxisTjyPf97ORyjnvU7CqtqcPzlGoyQBOXxCYAfz9KFFHAQ0pyN7gc+ZIf0ziiU/7IE589d7Msxhz3WMcYQiUTg9XpbE0wOh+PYD97uB0NQ16sQOB4sJSH3hTkkP3kv9EKjryscgUAA1YLS3Cb14jLUv15GUgXqP5jG7A/N4In7J9puk+pEURQoioJisdhTzyfG2IBzOGRYFHAQQoC+BRvAMZLGRVHEhQsXUCgUsLa21rcblaqqY1EdStd1NBoNOJ3OgW4h6wWXVeB4Zg3qvQGo9/mBESd9HuaoesyEnAf9bCYqvSuOyr95DdobediudN9QrpNhBhySJGFychKqqmJxcRGqqsLn8yEej8Pn84ExBtM0kc/n8fTTT+M73/kOHn/8cfz0T//0vuN85StfwTPPPIN7r1zBO833QV2poAEVX/r8F/Dia9/D//Xxr0KSJKRSKTz55JOIxWIAmsnfv/Ebv9Hx+gKBAH7zN38TumqgvFODTRLw7d99FqXdKqbvS+BKHfC/fQaRf/AYeF/39yvTNFEqlbC9vd3ztmG73Y56vQ6Xy9XTcY7CnCIszYDV0MGksagrQwgZgX7nwh17NPH5fPB4PFhdXe2p+sqefD6PcDgMh8Mx8vyJUqmEUCgEm80Gy7IOfJimObJrFBZKsD+3hfoPxKCn+lutZhAcDseoL4GQkevnSh8TOMgfyaD2hXkIMx4wqbeZfMMw4HQ6+75q3c7k5CTy+fy+fiSFQgHVarU1vtpsNgSDQYRCIQQCAbzwwgv4sR/7sVZ/JMMw8P3vfx9+f3OyRTcN1Der+NzNL0L2lvB/fPYS4nEeSytRfPGLO/jUpz6Fp556Cul0Gn6/H7/927994LqWl5fx737n05jyXcLX/u33oDd0PPHJR1FeVvHD//DdiPqdKP/hS7Bd9ML1kStgtqN/57quY2FhAbqu93XlXpIkCIKAZDLZt2O2wxhrlcblY9TAlZDzZq+QR7/7qZ3oaBzHIZVKoV6vY2lpqecoaHt7G5FIBIuLiz0dp1eFQgE2mw2yLIMxduDD7XbjzTffHO72L8uC+PIuxGtF1P5OEmbwdNRGp07j5LwbRCEMYcYDYdqN+tfXIH8w1dOx1tbWMD09jUaj0deVmDt5PB4EAgHwPN+2+eGd9w7DMLC2tgZFUXD//fcjn89jcXERly9fhmmaeP311yEIAmZnZ1GtVrGV3cL1yetA4AX86/87Ar/7ReiMIRo38eijEn75l6P43Oc+h1//9V8Hx3Hwer0AgFqxjvWrO5h7aRn/8aufQSwwgcuTDyHzcAzR2QBCoRDij8WhXs2i+LvfPbS/Rjv5fH4gQVytVsOlS5f6ftx2mpWqFAo4CDknCoUCNjY2cOnSJSwvLwPof6PRnsIXu92OS5cutS70pA/io64Hv2evako7kiRBFMXhBhu6CfmvN8EVVVQ/lIY1oG7Dg3BUsyxCzrpBrYban0yh/PSrEB8JgY+ffCVRVVWsrKxgcnIS8/PzfV8+DwSaD+8bGxvHCmgqlQoqlQruv/9+PPvss/jwhz+M+fl5PPfcc3j88cexs9OsoFQqFfFXz34a7/uQC7HkNLIvrsEWl2HZJHBcFT/1UzfxqU+Fsby0AkGRsX51B+tv7qBWqCM868O3rn0Nl98+g3/yv/0vrS2goVAI0WgUtW/OQ/nrJXh+5mGI04Fjve9BbckdZN7GgXNR4jgh50a9Xm/laiwvLw9sq21fRjCfz4fLly+3qk0dB8/ziEaj2NjY6MelDMze/tlhYYoOx/+3AhgWqk+mTlWwMcwbIyHjShTFfX8PBoNIp9OYmppCOp1GLBY70f8rnMsG+9+ZhPKVxZ5vDNVqFdlsFplMpq/L56FQCMFgEAsLCyiXyyfaWvbII4/gjTfewMLCAhqNBt544w089thjre9r2guoVouIRD2obJWgFeuwGgYAC42ahEhAhZJfxuf/zz/DK39+E6JdwDv+7n34yX/2BLLumzCkBn75Vz8Jm80GnueRSCQQ9YdQ/qOX0XhtE75fefuxg41Bbrt1u4e3lXZvSxUh5GzTdR1zc3OtzyuVysDyqvv6FOvz+eDz+ZDL5bC5udnVTSYSiaBYLA5lH3EvFEVBLBaDIAh9X2a6G5dvwPH1VWjTHjQeCY11cng7dz5oEXJe2e12OBwOxGIx2Gw2lMtl5HI5GIbR2uIzPT2NtbW11s/srfYe9Sfe40GDOSDkeNhmPCiVSifOF8nlcuA4DtPT01hYWICmaeB5Hk6nExzHQdd1aJrW9RgdiUTg8XhaeQwn5XA48MADD+Ab3/gGLMvChQsXEAjcDgAk6ToAwDQtwMkBAget2EBFUWGaFjRFgDtYxQ/95CN47B1va/3ct771LXznO9/BU089hUQigVgsBqfTCWOnivy/+w6ESS98n3isq3yNuw1qdnDvv6NhYX4Z5o3s0M5HCBmN+fn5A2PWoJpfD2TaPBAIIBAIIJfLYWNjo+MALEkSvF4vbty4MYjL6CtVVZHP5zE7O4tCodBx61Wv+NUK5Gc30XhbGNqsdyDnGDTaTkUIWg/r29vbbbfZVCoV+Hw+ZDIZqKraSp4GcOSfAGC+3wntZhGSw4VoNIrV1dUT52Lk83nIsozp6WlomgZJklCr1aDrOgRBgN1uR61Ww/r6+qHbSgOBQCvY6Mf208cffxxf/vKXwRjD+973vtbXGYCQT4bLyWFzTYXNAgyZg91lgyfiAM8zzK3XIdp4PJCMIQATNQBvzM3jS1/8In7h538eT37gAxBubaVSr2VR+k+vwPmeWdgfT514m++gtlPd2Q9kGGhLFSHnwzCbbg90n04gEEC5XO5YZ31iYgKmaY5134s7bW9vI5fLIZ1Ow+12n7hxUye2N/KQXt6F8kQCRvT0VnmiClWENGmaduiAXigUemo2qvyPZVhf0xD++QcwOTmJSqWCRqPZAM8wjNafd/7dNE1IkgSHw9H6EAQBiqK0xutKpQLLsiAIAnieh9frRSQSgcPhgKIoUFUVuq5D13XUajWoqgq3241wOIz5+fm+5bpdunQJPM+jVCrhrQ89BLdNgFvgwYsCBP1B/MA7nXjmmzn87UdsiE25IAZl6AA0y8KX/+sOQtFZuCcnUQRDsVDEH372s/jo+96Ln3rXDwIbazB4HvXvZ6G8sA33T1yGOBsGdB2WIIxNbiEw/DLjnNcOq1SHZZhgPG2RJYT0buCJAbFYDLVa7cANyOVyQRAEVKtVxGKxvrRNHwZd15HL5eD3+/sXcJgW7N/dBr9RQ/WDKVie070ladB14gk5LfY6ag+K/T0TKD/9KoqvbEBRFPj9fgiC0MpL4HkeHMcd+FNVVSiKAl3XUa1WIYoiZFmG3W6HZVmoVquIRqPw+XwwDAPVahU3b95EKBQCz/PQNA02mw12ux3RaLRVyW9xcbFvyec2xmAXePzbp5+GWiqCmQbqhgnFMFFUdWyUp/EjH3kAz3/3f+Dp38/i5/6+hAwE5HIavvrVNWxsmPjFX/xH0BkH0zTx+S98AfFUGj/xC38PRZ6HqaiofPV1GLka3D9xEUJchlUuAbrWDDp4HhBsYIIACDZg70+bAMb1p7lgt/ZKAw8Ls/HNfhzlBtgx+o4QQk6PYTdoHnjAIUkSLl++jGw2i+3tbTDGMDExAYfDgbW1NdRqNczMzMDlco1tw727lUolxOPx/hxMNeD4ZjPYqv5wChCHeyPrt0gkQjkchNzidrt7WsE4CpN4yB9Oo/aVRfD/6D7s7u52fK3P50MgEADHceA4Dm63G4qioFaroVQqtZKdp6amcOnSJZRKJdy4cWNfwLS5uYnZ2Vmsrq7u+7ogCDAMo6fVap4x2HkOTp4HZxMQlEQ0TANunw83d3ag3coH0fe2l5nA937vR/GPfzmPZ19ZxWc/u4BczoTDwXDvvW782q/9cwQC98Nms6HRaGB+fh4A8PGPfxyWakBfLYLZBQgxN/Bdhs985jOIRJp5EpZlAbp+66MZgKBWhXXrc4sxQBDA7gxEBAE8x8EwDTQ3ffUHY2yoY6plWbBqGsAzqM+vALIA8YEJcO7hBj2EkMEaVGpAJ+ywG8Sjjz5qPf/88307mWmamJubgyzLKBaLrZtTKBSCIAhDf/MntZfAt3cDOylWUuH4+hqMuAP1xyIANz5L+CfBGMO999476ssgZKzcuHFj4EUxqn9wHfykE/YnJjq+JpFIwDAMFAoFmKbZcSWC53mIotgxcTCRSMCyrJ4rC3IAJJ6Dnedh5zkwAHXDRMMwUTcNGBYgyzISicS+KipA86H46hevo7JexVt+6T64vK/D4fgeOE6DotyLSuUxWJYDkiRhZmZmXzUw9foOSn/yMpxPzML+juPna1iWBZjm7UBE1wBNh6VrWM3nAcOAA4De+mB3/B04bjDicrmQyWSO9TO9qP/VTSj/+TVYlTog8mAcB8///j7wkfFvOEsIOZppmlhaWhpI/6X777//BcuyHm33vaHWWt2rzLK9vb3v6/V6HaFQaJiX0pN+dEXntxTI31hD48EgtCv+Pl3ZaB23JDIh58HMzAyuXr060OVr+UfSKP/O67A9GAQf6ly0QVXVI4MfwzAOrVKytbWFTCaDYDB46IrK3RgAieNuBRkcBMbQME3UDRMVTYfWZvKr01i7+JdLyN8s4K1PPQLOZkOt9jBqtYf3vUaWZUxNTbWCDcuyoPzVApRvn6y/Rut9MAbwfPPjjkl/BkDmbdja2oICCwKaN1gbLMi3/s7DgnlHAKLdFYxYbYKRcDh8ous8KfGhCdT/4ios3QaYFviEF1yYtskSclasr68PrNnrYYaeDeZ0Og98TVEUyLJ8apKNPR5PT/9YtptFyM+sQfnB2JkJNoDhJzYSchpwHIfZ2dnBnsMnwf7uOJT/3FTTsyUAACAASURBVLk3R7+SoA3DwMrKCsLh8JGTDCLH4LEJCEsiJhx2eEQBFoC8qmFNaWCnoaGiG22DDaA5iXF3ad31721g5dtreOSTD8LmODjmcByHqampfSsbVkNH+Y9fRuPVk/XX6FYwGATQDCQUMJTBkAeHLDhsgMMqOGyBoQiGBhg4WHDAQgAWJmBiAiaiMBGECQdM8Axw8BwsXR9acRXOK0P+8YcA3YSlaBAfS49VAj0h5ORM0xzoNt/DDL2bXLuGIoZhYHl5GalUCltbW8jn80O9JsYYJEmC3W6HJElgjLUGd03TkM/nW5/7/c0A4UQJ45YF6cUd2OZKqH0gCdN/tvbEUu4GIe2JoohIJHJgdbev53hHFOqLO9BezUF8INj2Nf16aFVVFaVSCbFYbF8fEeFWHoad5yBxHAzLQt0wUdZ17DRMHPfsPM/vq/K1ezWHa1+5ibc+9QjsvoMrORzH4eLFi/uaGBq7NRT/44sQJjwn7q/RLY7jIMvyIStEDAYAA0Dj1ue3WeCA1sqIBsAjirAK+ebWLdNsVs+6I3n9zmT2fgYF4kMTUK9EoX5vGbb7+5SvSAgZqb20hlEZesDRqbNutVrF6uoqYrHYwAMOURTh9/tbQYYgCFBVFfV6vVVScq/qisvlQigUwvb2NgqFAlwuF3K53PFPqpuQv7UBVtVR/VAalnx6Ood3i/pvENLZ3jgyKEzgIH8kg9of3YTtghdswGPM5uYmMpkMUhMTqGS3Yb9VPrVumKjpBnKGhl43kem63qrQVFot45U/eB0P/cJ9cMUOrpS3CzbUGzsoff5lOP72DOR3DmemPhqNYnFx8QQ/yWACUG99AEAwmQJ3a1y1THN/ErumwVKUW58bsHiufVUtQQA7ZCXK3M0CFsACQbBb92fGGBx/90EwZwG8rz9Vxwgho1OtVrG0tDT0ylR3GslTL8/zbUtFOhyOvve2aGdychKKoqBQKKBerx/Z+GQvSTwYDKLRaBx7Jp/VdDi+vgrTK6L2/iQgnM265nurP4SQgziOgyiKA220JGTcEO7xof61Vcg/ktn3vX48bDPcSvTmmqsYjc11OOMJsEgUa2trrQpS/ZLP53HhwgXcfHUOf/PvX8aVn7wE/+zBcUaWZaTT6VawYVkWlGcXUHt2sad8jZPo178vx3H7JnEYxwGi2PzY+9qtPy3LAgwd0DpU1QJrlvO9KxCBYAOqFUBVYdUqQDQOJtkBPQ9e+S243r0KrPwh4H4/EPw4QFurCBlriqKg0WiA53nU63UUi0XU6/VRXxaAEQUcnW58Xq8Xq6urAz23x+MBY+xYFVZqtRrm5+eRSqXg9XqPtcLB7dbh+Poa1EteqA8Gz+yAfefNnhDSXjwex9LS0kDPYf9AEpWnX4XtkRCE5P5k35Nsqboz0VvkuGYVKcNATtWgmhbY/ALS6TRiExN9H79tNhsaSgMvfvolTL0vjehDkQOvEQQBMzMzrc+tho7yl16DsVOD/1ceB+8fbh+JfpV3P053ccbYrSDCBuD2+2XoUFWrXoela4CmAdVqs0KiosNamofl9oLj/gjQVgA+CMAEyn8GyPcCzsf68t4IIf03jIqIvRjJE2K7bVWiKILjuEOro/RDNBo9cZNBTdOgaVrXwYqwXIb925uoPx6FPuU50TlPg0AgALebSiYSchS32w2O4wa6rM05BNg/kITylUW4fuVesGOW27Yx1gowJI6DfisPo6jqUM2DeRiWZWFpaQmpVAqpVAq5XA7VarUv+SIBfwBL319B5IEwUu9Ktn3NvnyNXA3FP3gRQsID3ycHm6/Rzl5uSz9EIgeDq5M4rKqWZeiwFm7t6bas5hcNA5Z2E4xz35ogu/U7VJco4CBkjOi6jvX1dVQqlZFulerW2AQchmGAMQZBEA5UJekXl8vV6qx7Epubm3C73UeXxbUsiK/lIb6eQ+29kzDDZ7dTq91uRyKRGPVlEHJqhMNhbG1tDfQctoeDUJ/PQn1uC9I7m83s7iyGcSeeodkL49ZKhoVmHkb1GHkYlmVheXkZoVAI0WgUtVqt5z4ddskOTuPx+jdfx6Ufv9DxdXvbc9UbOyj9yStw/ND00PI17nay3I2DBEEYzoqxaTVXRRwOMLcHsMvN39tmGlBeATip2WERFmDr3OOFEDJYtVoNu7u7qNfrEEURpmmOpLRtL8Yq4CgUCgiFQgNrACgIQsdmV92wLAv5fB4ej6dzwGFYsD+3BX5HQfWH07BcZ7dULGMM09PTo74MQk6VYDA48ICDMQb5IxlUfvdN2O4PgPPs3/e/V0nKzvFgDLea7ZkoaDqME65MWJaFbDYLTdPgcvXWt8GyLLA8w83X5nDxo7OHBg+apmHzm29C+PYGPP/TgxBn2lfoGrRyudy3/I3jbKfqBbPZwDJtxvDgLwKb/xTQdwGYgPNdgPPxoVwTIeS2SqWC9fX1fWPLOG+bOszYBBwAsLOzg9nZWWSz2bZJ5b0SBKEvx+1Y575uQP7mGiyBQ/WDacB2NpPD98Tj8Y7/loSQ9jiOQygUws7OTl+P6+A51Izb6xF8RIb09gjqf7oC/09fgI3j4LUJcMsSVNNC3TCwo6kde2CcVKVSQSwW61gcpBvr397Au37mb6Fur8PiDrk+zQT/Rh67GTcu/tJjsAUPVq8aBsMwTla9sIORN8K1hYGJfwVoqwCzA7bEmc0/JGQcDbIb+KiM5Gmx00OqrusolUqt5kn95na7e66CxXFc25soV1Th+G9LMIJ2KE9MnPlgA0DPs5iEnFd7D+T9EpJsiMlSqzStyDG4BR7JD05h6p0TcFeaY1ZVN7CmNJBtqCgf0nCvF7quo1wud9UYsJ3tv9nGo08+it3c7qHBBiupkL68CC5bh+URkW0Ue7nsE9N1HW+++WbfKiwObTvVUTgJkGYAcYKCDUKGSNd13Lx580wFG8CIAo7DcjR2dnYGUl5VEARIktTzP+Bewie/rYCVm0tc/HoVjj9dhnp/AI23RZoVP84BavRHyMmlUqlj/wzPFeCSvgdJmAfQ3B4VtYvwCAIYGEKSDROyhIAogmcMZdPAWqOBhX//KgzTgjakxMLt7W3Y7XZcvHgRly5dQiKR6Go1NHctjytvvYIG6siXO/dj4lYqkL60COMeL7QnEgADisXRBBz97hvl9Xr7ejxCyPi6MxejVCrhxo0buHr16kDLp4/KSKZRDvtFqqoK0zRht9sP1A7meb5VfrVer0NRFNTrddTr9X25GU6nEzzPw7IsmKYJ0zQhyzLK5XLPlVM4joNpGHD8tyWAY6g/GoL0Sh7Ku+MwEqNZzh8F2kpFSG+cTif8fn/XD6w8K2HS91vguWYVpGz5FxAS3g2R42DCgmlZ4MGwUq/DtJp5AFPxOLh7OOBH3gFTM7CtZwf5llo0TWslUIuiiGAwiNnZWayurnbMfyutlJGZygAOhlypw/Yky4LwUg7CS7tQ3zsBc/L2mGsYBkzTHPrY1K+qVHtGvp2KEDI0KysrKJfLCAQCfd2WOY5GEnActa+3UqnA5XLtCzgYY0in06jVasjlcrDb7ZBlGYFAALIsY3d3F9lsFpIkIZlMolqtgjHWap4kCEJf6t9bloVYJArtf34c2kIO2noR3K/+AJJhP8rlMnK53OEVrM6IWCw26ksg5NSbmJiApmld9W6w226C58rQzQA4VoHb/i1U6z+IOmdC5Bg4MHCMYa9urc1mQy6Xw9bWFsySivK/fg2uf3AZfHS4VfNUVcXm5iZsNhsymQwYY9A0DcViEaZpwuFwoFqowlV3wx6SsF3q0I1dMyF+cwMs30DjYxlYnoMrrFevXsWVK1cG/I726+dMJM/zsNnObqERQshtjUajtRXzrAcbwIgCjqNWGfb2/+4lVTLGkEql0Gg0WhWs7qx3zvM8ZmZm0Gg04PF4sLOzcyAhM51OIxAIoFqt9lSveH19HdVnNuHQONimApAfTaG+VMBcKQe3242JiQlUq9UT9/oYd36/n5LFCemjVCqFN95448jXaUYEAAPPSuCYirqWQa5x+2FXYAwCx/aVsd0bazmPCPt7JqB8dRHOX7xnaCVjGWPw+/0Ih8Oo1WqYm5uDqqoQRRFerxeCIGB7fRtb383iLT/+CBaXF9ofp6RC/PNVWEEJjY9lAGF8xp9+FSMBaDsVIefJ8vLyqC9hqIYecHQzG1StVpFMJiFJEiRJgs/ng2VZWFtba/t6wzCwvLyMTCYDAG0f9peWlpBIJDA1NYWlpaVj9/rgWR6MmbDW7OCfXUFd5FG7ugUzIEG9xwf1bRHs7u4in8/jwoULbbeEnXaJRAKBQGDUl0HImcJxXFfNAFVjEpulT8JjfxaqPol87YP7vq9bFnSj82SO+PYI1Bey0F7chfiWwW/b8fl8iEQiaDQaWFpa2jceNhoNbG9vQ28YeP53XkToShC1ehVut/vATB+3WoX4l2vQHw5CfzBwaALzKHpviKLYtzKVgyqYQggZP4PqOTeuhh5wdLPdyLIsVCoVZDIZKIoCURSPLCFZr9extrYGnuc73rjX19cRDocxPT2NxcXFrpfCvdIzCDq+BMBCqfou1B5+O9SHgzCiDlj2/VVY9hKAJEk6cwHHsGrDE3LedNt9vKY+iJr64InOwTgG+UenUP3sNQiXfeAcgxn+OY7D5OQkBEE4NGfD1E288h9ehSvuxMyTUygWiwiHw7cDDsuC8HIOwt8czNfoZBQBRz+qHwLNa5ck6egXEkLOBFEUoSjKqC9jaIYecHT7y11ZWWn9PZlMdnUj6WbQ32tMNTU1heXl5S6ux0TQ8WXophsAgyfxV8j96IdgWp1vfrqun9p9uBzHtVaW7uT1emkbFSGnnDDphPhAEPU/X4HjY1N9P77NZkM6nUa1Wj10u4BlWXjjP12DZQFXfqq5xatarWJychI2mw1arQHxv2+A5Trna7QzinKyPp8PGxsbPRcksdvtfboiQshpcN6eqYY+Oh931p8xBpfL1deciEKhAF3XkU6nsba2dkSgwmCaMjjWAMDBsmywrMODCU3TTk3AwXEcZFmGx+Np7akmhAzXMGfm7e+dQPlfvQp9sQwh4+7bcR0OB5LJJLLZ7JEJkHN/toDKegWP/uoj4G7lY1iWhVKpBK/kRPkPr8EKSGh8NHOsnkaDKKl+FI7j4PP5ei6PSyvIhJwv52l1AxhBH47jVvRwu91QFKXvnccrlQoWFxe7yEtg2Kx+AqbphGXZsFX9e7Bw+Gybqqr7ZqvGceaKMYZEIoErV65gamoKwWCQgg1CzgEmC7B/KAXlq4uw9P705WCMIZlMYm1t7chgY+Xba9h4fhOPfOJBCNL+LanluS34OCeMS16o70kcu4Hq1tbWsa+9H/pRtW8UwRIhZDQ2NjZ6KmB0Gg39CfM4STI8zyMQCAysoVO9Xsf8/DxSqRSi0SgajQbq9Tpyudy+lZi6Povl0m93fdxKpYLJyUmk0+lWsKHrOpaXl/f1CxmFvRWjZDJ57pbzCBlXPM8PdWyw3R+A+vwOGn+9Bfu74j0fz+/3Q1GUI8v7br+axdyfzeNtv/YWiO47Jm5u5WtoL+2C/60Z8I8loJ8gEXtUY1qvXeMFQaDxmJBz5DyUwb3bUAMO0zS72ucqSRKCwSC8Xi8KhcJAO8hqmoa5ublWvw6Hw4F0Oo1SqdSsX3+CCNSyLNy8eROSJEHTNDQaDaTTaciyPJKAw263w+PxIBAI0CoGIWPI6XQOtcgEYwzyh9OofPoNiA8EwPlPnqzM8zzC4fCRfY4KC0W8/sdX8cgnHoQj7Lj9Dc1EK1/joxkUykX4fL4TrVac1ipPp/W6CSHH1+2z8Fkz1KfPbrZTTUxMwO12Y3d3F9evX+/7VqpOTNNErVZDrVZDPp9HJBLBhQsXsLW1hUKhcOzjaZq2L7gYxdIZx3FIp9NwOs9PB3RCTiOPx4Pd3d2hnpMP2SH9QAzKf1mC8+cuHvvnGWMQRRHxeBzFYvHQgKm6VcVLv/cK7vuZy/CmPbePsddfw387X6NWq53oATwSiSAcDh/75/ql20pj7VDAQcj5cd62Uu0ZasBRrVaPfI3H4xlqoNGOYRjY2NhAoVBAPB5HIBDA7u4uSqXSiaNSm8021JrLHo8Hk5OTtExPyCkgy4Pp/i3L8qEPwtLfiqHyb16D9kYetivd5xA4HA5kMhmoqopardZqyNpOo9TAC59+GbMfmkH43tv9Pzr11zhuXwtZlhGLxUY+seLz+U60TcLhcNA4Tcg5IggCAoHAudtWNdSAo5seHONEURTMz8+3tiPtzeTl8/ljbX9gjMFutw+lIgFjDOl0Gi6Xa+DnIoT0B8dx4Hm+rxMtjDHYbDYkk8mO252YwEH+SAa1L8xDmPGASd3lIgQCAWxubh55w9TrOl789MuYeHsck48nml88or9GNz2MGGMIBAKIRCI950/0SywWQz6fP/akVDzeew4NIeR0icVi5y7gGOq0SjezVuO4r61UKmFxcRFzc3PQdR1TU1PHmpFyOp1QFGUo721mZoaCDUJOoX6vcuyVmbXZbPB4PB1fJ8x4IEy7oT+XRTQaRSqVQiAQ6DjGMcbgdruPzK0zdRMvf+ZVeDMeTL8/0/yibkJ8Zh38tSIaH8u0beYnSVLHewXP80gkErj33nsRj8fHJtgAmkHjzMwMHA7Hka8VRRHhcBj33HPPwFa3CCHji+O4Q8fls2jscjgsyxpJt9huaJqGbDYLWZa7uuHu8Xq9sCwL8Xj8xIno3Ugmk2NZgpcQcjSPx3NklaeTWFtbQyqVQqVS6Tj2BH7iHqQzGRRzBRTrRXg8HoTDYWxvb7fKkluWBZfLBb/fj2q1euhqjGVZeP2P3wQncLjnxy+CMQZW1iD++Qosn9i2v4YkSTBNs9n4767iGjzPY3JyEm53//qGDILdbsf09DR0XcfGxsaBe4TP5xu7QIkQMnzZbHOCp1wuj+VE+yAMvUrVUcY54ADQqmZ1nARPl8sFRVEgCMKh2xt6EYlE4PV6+35cQshw+Hy+vjY43aMoCkqlEqLRKDY2Ntq+Jj41ibUX5rD5J6/B+cnLKBaLkGUZ4XAYgUAAPM+D45oJ3bu7u0c0SwVu/td51LZrzcZ+PAdurQrxa2vQHwpCf+h2vsaeiYkJOJ3O1qqK3W5vTVBJkoSZmZlTleewN9ZPTExgZ2cHhmEgGo2eqvdACBmc7e1tbG1twW63D7VC4SiNXY3UcQ84otEoqtVqVwnwQDNZ3LIsLC8vAwDS6TTi8XjHG/9JSJKESCTSt+MRQoZvbzJjEDefUqnUdozgeR6xWAw8z6PsNwAGqN/LQnosAkVRWuPWcSw/u4qtl7fxtl97C3gbB+HlXQgv7kJ9TwJm8uB2T0EQWsVCTNNEJBKB2+1GqVRqvcY0zVP5sM5xHI3NhJB96vU6GGOwLOvcBBvAEHM4uqnQJIpi3xMn+8nhcMDj8RxakeVusizv+w9qY2Oj79sCRl2dhRDSHz6fbyDHbVf5SZZlzM7OwjAMzM/PN3tzfCSD+tdWYVZO1i9o6+VtLPzFIh75pYcg2oVmvsbVW/kabYINoLkVdG8VwLIs7O7u7tvb3Gg0ThT4EELIOGo0GueyNO7QAo5uEsZ9Ph8qlcpYBhyMMSQSCWxsbBzr+hwOx4EItt/79cZ9XzMhpDuDCjj2qmABzbHM4/EgnU5jfX0dm5ubrZsfH3dAfEsI9T89/gN+fq6AN/7kGh7+xANwigKkLy8CpoXGRzOwPGLbn2GMQZZlZLPZ1td0XYdhGHA6nbDZbBAEAaLY/ucJIeS0Oa/b38cq4MjlcnA6nWM5Yx8Oh9FoNPYt8x8lGo3C7XYjn8+3vsbzfN8DjvO0JEfIWSYIwkC2lOZyOciyjEuXLuHy5cuIRCJYWlpqm4thf2IC+kIZ+lxzrDNrR69OVzareOn3X8X9P3sFPo6H9MUFGBe8UN87cSA5/E6WZcEwjAOBlmmamJiYwNTUFGKxGFXeI4ScKdFodNSXMHRDy+HopkKVy+UCY2zslpr2ShhubGx01U2WMYZkMgme5zE/P99aEfF4PIjH433vKFwoFEbaYZcQ0j/HbXzXDcuyMDc3B47jDlSAuhuTeMgfTqP6/86Dj8vQXtyF7188dqBHx9J/X0boniB4O48XP/0SLn1kBjGNQfiLNajvbZ+v0c7CwgIymQwEQUC5XG4FF9evX2+95sqVK8d8x4QQMr7C4TCKxeK5mjAeWsBx1E0uFAohEAhgYWGh7zfbXmmahs3NTbjdbkSjUTQaDdRqNaiq2vowDAN2ux2yLMPr9aJer2NlZQWWZUEQBCQSCYiiiOXl5b43ABy3AI0QcnKRSAQrKyt9P65hGF1tB7UsC2ZJhfY3O9BeBji3CLOigb8j4DBUAy/93qu4YpfQ8IlIvTeJTNkCt1BA42MZWN7ut0Cpqor5+XmkUin4/X7U6/V91brsdvupTBgnhJDDTE9P480336SyuP122AqH3++Hz+fD/Px8V8nlw7aXyLi7uwvGGBwOB2RZhiRJ8Hg8rWT3er0ORVGQzWZbW6+CwSDC4TByuVwrAOk36r1ByNnh9Xqxubl55CTNoBhLFVR//xqYQ4BV0gDLglXRgODtcSZ/swA7gKTBg+UMiK+XgPuCqH8sc+gWqk50Xcf8/Hzb7/n9/hO+E0IIGV8cx8HpdA6k/9I4GkrAYZpmx1l9URQRjUaxsLAwlsHG3SzL6qosrs1mQyqValWA6WZL2Ul109mWEHJ6TE5OYmFhYSTnFjJueP7Xh1D5f65Bv1mCka3DLO8PfrZfzWKyAfASg4PnoFwrovazFyCcINg4yjjm9BFCSD84HI5zE3AMZZ36sGZWk5OT2N7eHrttVL2QZRnT09PI5/NYXFwcaLABYF8JSULI6ed0Og/0bwiFQpiZmRnKiqYw44H3n74Fzp+9AIBBv1GEwOXAswIAYPGrc7jH7YTDxsPy2OCJOOB4Lnv4QU+IKlQRQs6q8zShMvAVDtM0USgU2n4vHA7DMAzkcrlBX8bQeDweJBIJrK6uDiVqZYxBkqSBn4cQMlyRSASWZSGbzSIYDMLv92N3dxeZTAZLS0tH5oIJgtBTiXEmcJCfTMHxKBBPfQ52eRUAoOgX8dYL98FdlGDNeGBc8EBNumAk+3/jZIxR/gYh5MxyOp1wu91tKwaeNQMPODo1yWOMIRgMYm5ubtCXMDR7ie+Li4tDqzwQDAaHch5CyPBFo1FYlgXGGBYXF6FpGjiOQygUwsbGRtttqJIkIR6PQxCEPiSfW5i88B9g47ehm83StbJwDQ/8SxMbO08Bjs63EEEQEAgEIIoiNjc3T7Rl9jyWjiSEnC/pdBoLCwtHbtU/7QYecHRa3fB4PFAUZWSJkf0Wi8XgdDqHmvhut9sPbLsghJwtsVgM165da42V+XweLpcLs7OzsCwL5XIZlUoFPM/D4XDA7XZje3u7LyvHIr8CG7cN3fQCaPYH0S0/ZOkmeFcJhhlo+3N7xTKKxSJUVcXs7OyxV30lSUIoFOr5PRBCyLjzer0UcPSqUxOrQCDQ934UoxKNRuF0OrGwsDC0ErXBYBDxeHwo5yKEjFYymWxVcTIMA4uLiwCa+Q1utxs+nw+6rqNer2Nzc7OnrVR3YjBaf7vrG3d87zaO41o9iObm5lpBUqVSQTKZxNbWVsdJqDsFAgEkEoleL58QQk6FQCCAra2tvo3d42jgAQfP8wd+gRzHQZblM7FnLRKJwOVyYXFxcWjBxuTk5IHOvISQs2uvFPfdeRuqqrZKdg9Cw0jBsNzgWAWm1WzIx7MSVH0Cunlw9SGZTELXdSwtLe37eq1WQ7VaPTLfjDGGVCoFt9vdvzdBCCGnQDqd7lge/CwYeDaezWY78DXTNMEYO/XNTsLhMDweDxYXF4cWlcqyTMEGIedQMpkcwVl5bJZ/CZZlh8CKEFgBuhnAVuXv4+5Vj1gsBsYY1tbWDhzF4XDA4XAgm+1cyYoxhosXL1KwQQg5l856i4OBr3AIQvtT6LoOQRBORe+NdkKhEHw+H5aXl4e6BJZOp4d2LkLI+BBFER6Pp9VUdFgaRhpLhX8GSVgELA4NI42756p4nkcwGGzbO0QQBMRiMWxtbR26CpzJZNpOUBFCCDn9Br7C0ekGsxdwnEY+nw+RSAQ2mw3T09OIxWJDOW80Gj21vzNCSO8mJyc75sUNFo+GPoOGMYV2tw3DMLC6uopkMtnqmyGKImZmZnDhwgU0Gg0Ui8WOR/f5fOeqHj0hhJw3A396bVeVhOd52Gy2oeU89JvP58P6+jqKxSI4jsPk5CSmpqawsrIysBUbm82GcDg8kGMTQk4HjuMQi8WwsbEx6ks5oFgsgjGGqakprK+vIxQKoVQqHbqNag8liBNCSLP66LDaKgzbQFc4yuVy2zyNaDTaKpd42vA8D1mWUSwWYVkWDMPA0tISKpUKZmZm4PF44HK5+t6sirZSEUKAZoW6cV3pLBQK2NraQjgcRq1Ww87OzpE/k0wmqbkfIYQAZ7oU+EDvWvl8/sDX7HY73G43bty4MchTD4zL5UK1Wj0QSGWzWdRqtVZfjL1mV4dtI+iWz+eD3W7v+TiEkLMhk8ng5s2bo76MtgqFQlelb4FmKUiv1zvgKyKEkNPB5/NhY2PjTJbHHei00t5e3jslEokjkwfHmcvl6ljOt1qtYmFhAQsLC1heXkYoFEI6nW77e+iWLMu03YAQso/dbj/1WyxpbCOEkIPO6rg40IDj7iRAxhjsdntfZv1HZW+F4yiKomBubg6VSgXT09MIBoPHPpfH48HMzAxtNyCEHBCNRnuazBglh8OBqampUV8GIYSMHa/XO7bbZnsx1IDDsiwoinJqq5GIogjLso6Ve7K7u4u5uTl4vV5kMpmu/yMKBoNIpVInvVRCyDkwPT096ks4Nq/Xi+npaZpIIYSQDva2558lAx3x291QKpXKqQ04lfk8OAAABpFJREFUnE5nV6sbd9M0DfPz86hWq5idnYUsy4e+PpFIIB6Pn/QyCSHnxGmbBQsGgyNqYEgIIaeHx+MZ9SX03cCnmHie3/d5pVKBy+Ua9GkHguf5nsreZrNZrK6uIpVKtW1wJUkS7rnnHgQCgV4ukxBCxk40GqWJFEII6cJpm0zqxtDfkaIoEEURPM+fuix8y7J6brpVqVSQzWaRTqcxPz/fSp5njOHChQv9uExCyDlgmiauX78+6svoSiqVOpMzdoQQMgiapo36Eg7ldrsxMTEBjuOg6zpUVT0ySBpowGEYRtugolqtwuVynerk8V7k83mEQiF4PJ5W+cjTXnGGEDJ8g2o02i+MMczMzFBZb0IIOYZO1VBHzev1Ih6P7wsuRFHsqoDJ0PtwAM1Zfr/fj1Kp1LYx4Liy2+19ucEnk0nUarVWsMEYO9PNXggh/cdxHPx+f8dxdtRcLhdSqRQlhxNCyDGNyw4gxhjcbjf8fj+cTmdP4/lA7wSdmj/l83kYhnGq9vM6HA44nc6uOucehud5uFwubGxstL4WiUTopkwIObZxHEMFQcD09DQymQyNa4QQckymaaJer4/6MgA0m8ymUim43e6ex/OBrnB0+oVZloVisXiqOsxKkoRqtdpz1GkYBorFIgKBALLZLOLx+Il6dBBCyDg90LvdbkSjUdo+RQghJ7S8vIxSqTTqywDQnCDvZ1XZgQUctVptUIceCZ7nj9V/4zDZbBaSJCGdTsPtdvflmIQQMkw2mw0ulwsul+tUTR4RQsi4Gpfcjb38u34aWMCxubl56Pd7rfY0bL1upbqTqqoIhUIUbBBCeiYIQk+5ZaIowu12Q9M0CIIAt9sNSZJQqVRQrVahKAoMw4DX64Xf70exWEStVkMymWxb3psQQsjoMcYgCAJ4nocgCJBlGQ6HA/V6HdVqFfV6HYZhQBCEVvVYxhg4jkMwGOwqEfw4BhJwGIZx5AqH1+s9URO9UTpp47+7ybJMvTYIIX0xOzuLbDaL3d3drn+G4zh4vV5Eo9GOpQwDgUDbceqoxqWEEEJOxuv1dsx/Pg5BEDA7O9t2fHe73SOpjDqQgOOo1Q2XywVJkrCysjKI0w9MtVqFJEmtCJDjOFSr1WNV2nI6nUin0wO8SkLIeSIIAuLxOOx2O3K5HBRFOfAaxhgCgQA8Hg9kWR6r3A9CCCFNk5OTSCQSyOfz2NzcPHYlV0EQYLPZMDU1NXbjfN8DDtM0D43OGGOIx+PY2Ng4VSVx9zQaDTDGWln7ALC7u4vt7e1WQjnHca2GfntcLhcmJyfPZPdIQsjo+f1++P1+qKqKubm51njkdruRTCbH7uZDCCHkoL0tTX6/H6urq10lkTscDqRSqbF+xuz7lRUKhUMDib0bYqVS6feph8ayLCwtLcHj8SCVSiEYDCIYDELX9dY/9l7gVa/XEYlExvo/AkLI2SGKIi5fvjzqyyCEENIDjuOQSqVQr9exvLy8L1fPsixYlgWO45BMJk9FTnDfn4K3t7cPP6EgnJkKVqVSCaZptmYO7wwqOI6jPA1CCCGEEHJidrsdFy9eHPVl9Kyva+z1ev3IaimWZZ26ClWHoW0KhBBCCCGEdNbXp+Wtra2uXndWAo52uRqEEEIIIYSQ2/oWcJimeWTDEo/Hg2AwODaNTXplmiauXr3atioMIYQQQgghpI8Bx1FZ9OFwGLFYDAsLC2cmhwNoBh1zc3OjvgxCCCGEEELGUt+Sxg9LFne73fD5fJifn++pIy4hhBBCCCHkdOk54NA0DYqiQFXVjq/hOA6KopzZYIPn+VFfAiGEEEIIIWOp54Dj+vXrp7KBXz8lk8lRXwIhhBBCCCFjiWq69igYDMLlco36MgghhBBCCBlLPQcc3fShUFUVdru911ONHUmSEI/HR30ZhBBCCCGEjK2hBByKooDneYii2OvpxgZjDFNTU6O+DEIIIYQQQsZazwFHtwnT5XIZbre719ONjXQ6DUHoW5EvQgghhBBCzqSen5hdLhfq9fqRr9M0DW63G7u7u72ecmQEQUAgEEAoFOpqZYcQQgghhJDzrueAIxAIYGdnp/MJBAGJRAKSJGFtba3X0w0dx3Hwer2IRqO0okEIIYQQQsgxscNK2jLGnh/itRBCCCGEEEJOpx3Lst7f7huHBhyEEEIIIYQQ0gtKRCCEEEIIIYQMDAUchBBCCCGEkIGhgIMQQgghhBAyMBRwEEIIIYQQQgaGAg5CCCGEEELIwPz/9gCWurzu658AAAAASUVORK5CYII=\n",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"# Map projection\n",
"crs = ccrs.PlateCarree()\n",
"fig, ax = plt.subplots(1, 1, figsize=(20, 8), subplot_kw=dict(projection=crs))\n",
"ax.coastlines(color='lightgray')\n",
"ax.add_feature(cfeature.LAND, facecolor='lightgray')\n",
"ax.add_feature(cfeature.BORDERS, edgecolor='white')\n",
"# Uncomment for the map to span the whole world\n",
"# ax.set_extent([-160, 180, -60, 90], crs=ccrs.PlateCarree())\n",
"\n",
"# Overlay network graph\n",
"nx.draw_networkx(graph, ax=ax,\n",
" pos=geo_pos,\n",
" font_size=14,\n",
" alpha=0.7,\n",
" node_color=col, cmap=plt.cm.spring_r,\n",
" edge_color=edge_col, edge_cmap=plt.cm.get_cmap('RdPu'),\n",
" node_size=sizes,\n",
" labels=labels)"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"### Directed graph for trade"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"source": [
"Now, let's create a directed graph for the flow data restricted to the top origins of illicit outflows relative to trade value, and applying the standard thresholding described above."
]
},
{
"cell_type": "code",
"execution_count": 109,
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"outputs": [],
"source": [
"# Graph data for conduits relative to trade\n",
"flow_data_trade = create_graph_data('2016', threshold_var='trade')\n",
"flow_data_trade = threshold_partner_IFF(flow_data_trade)"
]
},
{
"cell_type": "code",
"execution_count": 110,
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"outputs": [],
"source": [
"# Create directed graph\n",
"graph = nx.from_pandas_edgelist(flow_data_trade,\n",
" 'reporter.ISO',\n",
" 'partner.ISO', \n",
" 'Imp_IFF_hi',\n",
" create_using = nx.DiGraph())"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"source": [
"This graph contains 70 vertices and 99 edges."
]
},
{
"cell_type": "code",
"execution_count": 111,
"metadata": {
"slideshow": {
"slide_type": "skip"
},
"tags": [
"hide-input"
]
},
"outputs": [
{
"data": {
"text/plain": [
"(70, 99)"
]
},
"execution_count": 111,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# Check the number of nodes and edges in the graph\n",
"len(graph.nodes()), len(graph.edges())"
]
},
{
"cell_type": "code",
"execution_count": 112,
"metadata": {
"slideshow": {
"slide_type": "-"
}
},
"outputs": [],
"source": [
"# Generate graph attributes and auxiliary variables\n",
"col, edge_col, outdeg, deg, sizes, labels = set_graph_attributes(graph)"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"source": [
"The network of illicit flows from the top origins of illicit outflows relative to trade value is displayed below."
]
},
{
"cell_type": "code",
"execution_count": 113,
"metadata": {
"slideshow": {
"slide_type": "slide"
},
"tags": [
"hide-input"
]
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAi4AAAHRCAYAAABNZjKOAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4yLjEsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy+j8jraAAAgAElEQVR4nOydd3hUVf6H3zN90kijpAChSC+hiCCCrKKiIjbsumLvXXetP7GuvfeKawPEhshiL1Slhd4hQBLS2ySZTLvn98edNDJJZpIBDJ73eeYhc+9pNxnmfu63HSGlRKFQKBQKhaI9YDjUC1AoFAqFQqEIFiVcFAqFQqFQtBuUcFEoFAqFQtFuUMJFoVAoFApFu0EJF4VCoVAoFO0GJVwUCoVCoVC0G5RwUSgUCoVC0SxCiA1CiAmHeh2ghItCoVAo/sYIIc4XQvwhhKgUQuT7f75eCCH852cIIdxCCIf/tV4I8R8hRId6Y0wTQviEEBVCiHIhRIYQYvKhu6rwI6UcKKX8FUAIMV0I8dGhWosSLgqFQqH4WyKEuAN4EXga6AJ0Bq4FxgKWek2fklJGAx2By4DRwGIhRGS9NkullFFALPAuMFsIEX+A1286kOP/VVHCRaFQKBR/O/wWk4eB66WUc6SUDqmzWkp5kZTStX8fKWW1lHI5MAVIQBcx+7fRgPcAO9AzwLzThBCLhRAvCyHKhBCbhRDH11+XEOJdIcQ+IUS2EOJRIYRxv77PCyGKgekBxjcKIe4VQuzwW4hWCiG6+s+9KITY67cKrRRCjKvXb7oQYo4QYpa/3yohxNB65zOFEBOFEJOAe4Hz/BamNf7zlwkhNvn77hRCXBPcXyJ0lHBRKBQKxd+RMYAV+DrUjlJKB/ADMG7/c34ryJVABbCtiSGOAnYCicCDwBf1rDMfAF6gNzAMONE/3v59OwGPBRj7duAC4BQgBrgcqPKfWw6kA/HAJ8BnQghbvb6nA5/VO/+VEMK837UvAB4HZkkpo6SUNeImH5jsn/My4HkhxPAmrr9NKOGiUCgUir8jiUChlNJbc0AIsUQIUSqEcAohxrfQPwf9Bl/DaCFEKZCLLhzOlFKWNdE3H3hBSumRUs4CtgCnCiE6AycDt0opK6WU+cDzwPn155VSviyl9EopnQHGvhK4X0q5xW9BWiOlLAKQUn4kpSzy930WXbj1rdd3pd/65AGeA2zobrEWkVJ+K6Xc4Z/zN+B7Agi7cPC39I8pFAqF4m9PEZAohDDViBcp5dEAQogsWn6wTwGK671fJqU8Jsi5s2XDHY53A8lAd8AM7PPHBuNfx956bev/HIiuwI5AJ/wxPVf655Lo1pHEQGNLKTX/7yG5pYvxj30yuvWoj3/NEcC6YPqGirK4KBQKheLvyFLAhe4eCQkhRBQwEVjYyrlTRD1lAnRDt+Ds9a8pUUoZ63/FSCkH1mtbX/AEYi/QK8CaxwH/Bs4F4qSUsUAZUH8dXeu1NwCp/nXtT4M1CCGswOfAM0Bn/9jz9xs7bCjholAoFIq/HVLKUuAh4DUhxFQhRJQQwiCESAciA/URQliFECOAr4AS4P1WTt8JuFkIYRZCnAP0B+ZLKfehu1ieFULE+NfTSwhxbAhjvwM8IoQ4QugMEUIkANHosTMFgEkI8X/oFpf6jBBCnOWP07kVXUQtCzBHHpDmFzegZ2BZ/WN7/daXE0NYc0go4aJQKBSKvyVSyqfQg1n/hR53kge8iW6ZWFKv6b+EEA5019B/gZXA0VLKylZO/QdwBFCIHmA7tSYOBfgnuhDYiC6O5gBJIYz9HDAbXQCVo6dm24HvgP8BW9FdU9U0djt9DZznn/cS4Cx/vMv+fOb/t0gIscofrHyzf94S4EJgbghrDgnR0M2mUCgUCoXiQCGEmAZcGUI8zEFBCDEd6C2lvPhQr6UllMVFoVAoFApFu0EJF4VCoVAoFO0G5SpSKBQKhULRblAWF4VCoVAoFO0GJVwUCoVCoVC0G5qtnJuYmCjT0tIO0lIUCoVCoTj0rFy5slBK2fFgzTdJTJKFFIZ1zJWs/E5KOSmsg/5FaFa4pKWlsWLFioO1FoVCoVAoDjlCiN0Hc75CCllBeO+1ApHYcqv2idqrSKFQKBSKQ40Ic6LMYZx3o2JcFAqFQqFQtBuUxUWhUCgUikONsrgEjbK4KBQKhUKhaDcoi4tCoVAoFIeacFtcDmOUcFEoFAqF4pAilXAJAeUqUigUCoVC0W5QFheFQqFQKA4lAmVxCQFlcVEoFAqFQtFuUBYXhUKhUCgONcriEjRKuCgUCoVCcahRwiVolKtIoVAoFApFu0EJF4VCoVAoDjVChvfV0nRCvCeEyBdCrK93LF4I8YMQYpv/37h65+4RQmwXQmwRQpzUxJg9hBB/+PvPEkJY/MeFEOIlf/+1Qojh9fpM8o+5XQhxdzC/KiVcFAqFQqH4+zEDmLTfsbuBn6SURwA/+d8jhBgAnA8M9Pd5TQhhDDDmk8Dz/v4lwBX+4ycDR/hfVwOv+8c1Aq/6zw8ALvDP1SxKuCgUCoVCcUgJs7UlCIuLlPJ3oHi/w6cDH/h//gA4o97xmVJKl5RyF7AdGFW/oxBCAMcBc5ro/1+pswyIFUIk+cfYLqXcKaV0AzP9bZtFCReFQqFQKA4lNXVcDqJwaYLOUsp9AP5/O/mPpwB767XL8h+rTwJQKqX0BmjTVP9gxm2EyipSKBQKheLwI1EIsaLe+7eklG+1ciwR4Nj+6qi5Nk2dC2bcRijholAoFArFoSb86dCFUsqRIfbJE0IkSSn3+V05+f7jWUDXeu1SgZz950N3AZn8Vpf6bZrqbwli3EYoV5FCoVAoFAqAucCl/p8vBb6ud/x8IYRVCNEDPcj2TwAhxH+FEKOklBL4BZjaRP9/+rOLRgNlflfUcuAIfzaSBT0AeG5Li1QWF4VCoVAoDjUHuQCdEOJTYAK6SykLeBB4ApgthLgC2AOcAyCl3CCEmA1sBLzADVJKn3+oIcA+/8//BmYKIR4FVgPv+o/PB05BD+qtAi7zj+sVQtwIfAcYgfeklBtaWrsSLgqFQqFQ/M2QUl7QxKnjm2j/GPBY/WNCiBhgm5Ryr7/NTvbLNvIfl8ANTYw7H13YBI0SLgqFQqFQHGraYcl/KWU5fqvMwUQJF4VCoVAoDiltSmH+26GCcxUKhUKhULQblMVFoVAoFIpDSU0BOkVQKIuLQqFQKBSKdoOyuCgOT4qzYd9WcDnBYAR7NHQfAraoQ70yhUKhaIyyuASNEi6KwwefF3atgozvoCyv7pgQYDTDoo+hezoMOQE6pR3SpYYVz26o+gG8BYAPjPFgHwfWwYd6ZQqFIliUcAkaJVwUhwdV5fDtc+AoBq+r4Tkp647tWgl71kK/cTBmKoh26i2VGjh/gdI3wL1ef4/Hf9IIpa+CKRk6XAtRk0FYD+VqFQqFImwo4aJo/1RXwJeP6+KltphjE0gJXjdsXgjuKjj2Ut0ic6DQnFD1DTg+AV8h4AURDfbxED0NzF1bGiHAmC7IvwGql4GsCtDAB9IJnh1Q9H9Q9g4kfQTGhDZejEKhODCodOhQUMJF0b6REua/CM4gREt9vG7YuRISUmHwxPCvSyuHkqehcg4g9hMYueDIhIqPwJIOcfeCdWhw40oP5F4K7rUgq4No7wTPTsg5A5LngbFDKy5GoVAo/joo4aJotxiNRgb364OnNB+TAS4d3Ydbjx+MwSD4dUsOp7/2HT0SY2rbPzP1KHp37MDkVxew/sFzdPGy8lumz/mdqOgY7rzzzvAszJsLeefq/+JuopFH37zd9QfknQ8Jz0HkyS2PXfRo8KKl/lzefMi7GpJnhdBPoVAcNJTFJWiUcFG0W+x2OxnP3gB71pFf7uTCd3+mzOnmoSn6Tu7jjkhi3o2TGvTJLHQ0HET6oDQPomMIC1oZ5J4NvlwgSAuQdELRbWCI0oNqm8JXTu6uT7j14X0sX+vCahGkpZh44YEEzro+j/ULUmubTn+hhKhIA3de1YFpdxUw+R8RTD11Hbg2gbV/265RoVCEF1XHJSTaaWSiQuEnexMAnWLsvHXxOF75dQP6fl5B4nFB3o7wrafofvDlE7RoqUFWQ8G1oFU23cTxGWdek82Eo2zs+LUrG79P5fG74sgrDFYgeaD8ndDWpVAoFH8xlHBRtF+k1NOc/fTsGIMmJfkOJwALt+0j/ZHPa187CsoDj+N0BD4eAlFRUeArhqrvAQ8zPqvgxv8rBmDaHYXMmd9QkEQN2ANA5l4vIm03L88oByRUfsWNN97IjBkzGs3xy/+ex2zSuPaiOutQ+gArXZONQa7SB5XzQasI/QIVCsWBRcjwvg5jlKtI0Y6Runipf6Te20Cuot1FAUSK5kOEI7OoYpaeoRTid0anRAMvvu/gmgujsZS/AXJI40bSx/rNuYwYFDitecduL+mnZte+zy3wcedVgQJxzeDNBkvf0BapUCgUfxGUcFG0b+oJjp0F5RgNgk7RdjbtKw3YPCHSRklVwzovxVVueiQmtn0tjo9CDJrV6RhvZOwIKx98XsFVFxaBVtK4kVZJcwbSXt1NZHybUvt++gsBxgBAhNfiIkvA+yFonwE1c8aD8TwwXgxCZTEpFEFxmFtJwokSLor2ixCg6fEdBQ4n1368kBsnDGzWehJlM5MUE8FPm7I5vn8KxZXVLNiYxS3HHNOmpTidTtJPWukvBAfFZRpTJkYE3f/u62M4+dJ8Lj8vKXBtFoOdgUeYmPO/JtxdQSNBBL+upofZC54HQPsKMAL117wDvBvAez8YzgbzwyCS2z6nQnHYcvi7d8KJEi6KdovTWU36w5/hcbsxGQWXHHUEt0+sc7PUxLjUcP8pw5g6oif/vewf3PDpIu6YswwEPHjT1fTq1atNa7Hb7WTM7wJ4AZjxWQUr1ump0IF01P7HenQ1MyrdyidflwauRyPMHHdMR+59ppi3Z5Zz1fl6nMvyNS6qqrXgFyrdYOocfPtAaGvAfTJQTtNByH4ho80C1wKwfAeGgW2bV6FQKFDCRdGO8fl8sGUJLJ7ZqMz/hL7JlL14WcB+A5Lj+OWO0/Q3RjNcdH/dSekGbS74ZoLMAzQQiWA4C4znNG+tEDaQjd0wCXFGSsrqxEVxqY/EuMZun3uv78DU6wsZf2zg/5Yi5iK+fOMtbn0klyfeKMNmrUuHbolr7i/k1keLQFjp2v1Uli5d2mKfgGjbwX0iumgJBi9QBO7jwfIHGLq3bl6F4nBHWVyCRgkXRfum10hYOrt1fQ0mSEvXd4yWZeB9BnxvARpQT4BIQFsM3tv1uA3T3SCSGo9nGagXlNuPCaOtvPCeg0vPjsJiEcyYU8k/xtgatevX28yAI8zMW7CcUUef3nj8mItJ7vwes1/p1OhU/RouANNvjav9ecbTHfUfRCR0fgPsYwP9NlpGSvCcTYPfTdA4wHMOWP9s3dzhRlaC50vwbdDjdEQMGPuA+WwQcS33VygUhwyVDq1o35gsMOlG/d9QEAaIioNxF+nxGu7R4HsZ3ZIQ6MZcCVSB731wHQnahsZNYq7RxcF+TD4+gnFHWhlx2j7ST85h8QoXT94d6OYouO+OE8jKygm8ZlOyX3SYA59vFqHvGm07OuSeRUVFpKenkz6sL126ryOlZxXpR7mI7VLNgGENLV3TH/XwzPO6u2zaVW5SelbjcklAo7BgG2lphzjWxbcDnLeCoxdU/ws8r4H3U/C8CdX3g6MvVF0JvnWHdp2Kvxc1BehUOnRQKIvL4Yq3AsrWgcehB1SYOkDsEDA2ftJv93TpDSdcCz+8oZfxbwmjCaIS4LQ7wFwJrglAHsEVjfMAxX7Xx1Iw9ACgoqJCj00RVpCVTDsnimnn1PV68NZYHrw1ttFoaV1NrP/efzMXdoaOuQdN+6Lp6Ts+B9mngi/Y9aJbjPb0hTXTIOcDcHvAZITYKDhuCIzoBZamxVBCQgIZGRngPo/pD+8iKhLuvM1E5m6NyWd5muwHYDTCex/4uO5qE/r2B823b4TPA9VVoGlgjQBLG3a59nwLziv96/AGaKDX/8H7BXjngfU/YA3sblQoFIcOJVwONyp2wN7PoOAXECbdvC9A3+jPB11OgtSpENGKXYnDgc+riwuzDQxhNPh1HQhn3A1/fumvpiv0m159TFZdxA04Foafoq/BdSpQQGiVbiW66+N0sKypi7QVRoi9C0oe1sv4h4QZzH3AOrL5ZsYOkPw57LsAfDl6TE5zrB0Ki8aCNwZcRXXHXV6odMHsRTBrIYztD2eMBnMTXwmyCrQF6NcefM2bW2808fzLPq663Ii+a7Vbf4lmLGRSQtZWWP0jZG0Bg1H/Hfu80CERhp8AvUeAOQQrm+dbcF5BrThpFp/eznWv/rP1yuDnUShay2FuJQknSrgcLmhe2PI0FPwGmgc9TiPATS3nW8hdAMmnQ69rdZfJgaa8CNb9CpuWgNulCxZNg+g4SJ8IfUeBxd72eeJTdLdRVRls/A32rgdXFRhMVFUaqe42ivgJx+sWFwBtF1EJ86kotJG5W6N/upt+fQXV1RAdBTdca+LSi/WqtDM+9HL5NV4y/rAwZLAB0Bg0fCPzvvmctJ5T69YQfQF4NkPF7BDEixmMnaDTB4FTkPbH1BlS5kLpW+D4ry5I5f5bBUTAj+Ng/SDwGGhSmLn84m7RRti+D26ZAhGBrBoFtObroltXwTFHG/jwEx+nnVJT4bcEaCKzKXcXLHgX3E59OwYAX72sqdJ8WDgHfv8MRp8GQ//R8iK0HX5LS6hisgpc94NxCJhGhdhXoQgRJVyCRgmXwwHpg3X3Qtla0FwtNPbptU9yvgFPKfS7J7ibZWtwVsCP70POdv0p2l9zpfZfRzEs/QqWfAmDxsOYM8JjhYnoACOn6C8/s00PUMVCphWOJyLW/7H3vd6gW6+egtXL9Jv2zl0aZ53vQdMkl/1Tb5+aAo896WXWRzVP+hp43wWmNhiHuOlgiIPyN/T9gZqz5ogIMKVB5491a0qwGKIg/naIuwmqfkIWzgZTKQKfHsvy+3jY4AFPkJYkjw9yiuGVeXDbGWDebxsB6WT/kDjRhOVl/4/Tvf8yMmWqh1MnGdEtf87ARpvMDfDdO+BtwZ1UI2iWfQNlhTBuapOfYaPRyOCB8ehiSXL+WWbuvt2KxyN54FEXn8/1YrVChB0eutfKySeYiUoupyKnZluFama8ez0r1o3mlVdeaX5dCoXioKCCcw8Htr0cpGiph1YNBQth94cHZk2OYpj9OGRv0038WhM3UK9bd+lsWAjfvqa3DTOVWWUIDSI0+O9Rr6D5NF1I+d5vsk/PHgaee9LES6/VrXvyKUY2bJJs2VrPAiAX6xlJ9RECYm+FLt9A5Dl6mrSIBKyAGYRdj4WxDIfEFyBpLhhbmckizGie8VROPxbP2och5WtwPQmLveAOcaNHnwbZRfBjRoB5YthfgCUkQElJw6fE4mJITGwoInr3MpA+RDD7cx96oa0AO3Hn7Q5OtNTH64ZNS2HV9002sdvtZCwykrEokoxFUdx9uy5MH3jUxb48yfplkaxfFsU3syJwBNyySoK2NYBFS6EIJ2EOzD3MrTdKuLR3XMUY+99G+uWLSL9yOelXLueJT3YDMG9pIcOuWsHQK5YzYNqfvDlXz1aZPmMXKecsIf3yhQw67gbmfvVZmNdUBV89D1WOpgXL/njdsG87/PhBo/2H2squLzYgkRgQ2LaVMefiT9ELpDVfnn94uoHNW+rWYhDwr9tNPP5UfXFlBrkv8ACWIyDxCUhdAQlPoXW4B+euSyD+IUhaAElfQMSJeixSK5FSUv36byAl3jV79YM/ZoDXR9TbtwGgSY2bF81m0MxHGDzrUY6c8wS7ygsBSPvofgqd9bKoPD74Za3uymtAJ3ThVUdUlCApSfDTL/rfuLhYsuAHjWOObmz9uO/fJp55wYv+ldM4SJmfP8J43Yuk/2dm7SuzqJxft2Yz+fV5AMxYtgnDTa+yNruwttughz4gc8EsqGyqrkzNnHVUVUne/sDDy0/ZsFr1tXbuZODcs5rJ1vJtbvqcQqE4qChXUXsnZy52q5GMd45scNjj1bj62a38+fpwUjvacLk1MnPrbtS3TU3lzvO6sWmPj3GXX0H+lLMxtNFNExUVpWfXrJgPleXMWLKRFXvyeeW88Uz/9k+irGbunDiMao+X096YzzE9k3jw1CPJK6/its8Xs2xXHnGRNiyJL/Ov+x/kzDPPbNN6atj+UQYGv29CAGWzNpJ110BSBzT/8Q+kny48z8BjT3rZlVlzYxfoqdLNYIiCyFOpmLeZ4sdcdHn7WGyD2li91o/nly1ou/Qbuba9AFnoQKzJbLD4WdtXklNZxtrz7sMgDGRVlBBpbiY7x+OD9XtgSFrdMWEC4zXAE9S3vPz3HTM33Orljrt1MffgvSZ69Wz8ORo4wMDwdDOr1kQ2jqsq2AvlRdjNRjLuOb/Bqcz9NsVMjY3ise9WMuvykxqOsWERjDql0bxOp5v0Y/Jq399zm5X+fQ10SxXExATrIvUAhS22UijaxGFuJQknSri0ZzQfZH8R8A7rqPLh9UkSYvSnSKvFQN9ujau+9u9mxCQ8FBYW0qlT48JmIeP1wMYlerBwANxeH2e/vYARXTvy4KlHIqXkjLf+x6VH9eWTy04AYLe1M3Ozstq+Fj+VmaV4/RYXT9coRt51LMlD+4Cn+Yyc1Ws0+vdreHMzmQR33GLkyWdrbt4aEMD1sR9SSso/WA1A8bOLSHrvrDbvSK2VVOH++M+64FWDAd/81ZiMokG2776qcpIiYjD4BUNqVAtuKZcHFm9sKFwATFcx/f4XgDqX5ID+Bn75LnB2z4y3Gx7/YlYEWLc0bpjxc9AuwsmD0vh9ew5b8kro29l/HT4vrPsNRp6kZyDVw243krGo4ed+7foQXWiACBTorlCEi5o6LoqgUK6i9oyrADQ3TrdW6yZKv3I5s37OJz7GzJSjE+h+/jIueGQjH/+Qh6Y1/o/xx8ZyDEKjY3zLN9+g2LG6yVNeTXL+e99zRKdYnjhjDAA/b8nGYjRy7bhBte26e4u46bKLw7Me4Pycf3OZ7xFij0xGxtkYduMYDMYIoGOTfTJ3a9x5j5ebrjM2OjftEiM//qxRUKgXVkOkNh5gP6qXZ+Mr0vfv8WSWUv1H24WZsBgxTxqI6BoHVhMgkdnF4G4oAs7tNZxvdq8jffbj3LHkc1YX7G158JIAViSRom99QGsywOxgvBBEAHG8ax1IDafHV+smOvOt+QFHMQjBvyYO4/HvVjY84fNCYXaAHo3FYe+eBvZkSRyOwDcKu03gdtedKy6RJCZENXllCoXi4KIsLu0ZbwUII3aLoZGrCOCdu/qxbmcFP64s4ZnZe/lhZTEz7u4PwPNzsvjohzyiI0zMejAd4asEU9uK0zmdTtJPPgvcukuquMrFlMFpteef+mE1E/um8sLUup2YN+wrZnjXxIYDCQGZ6/RMozBgNOniI/nYHux8aTGaT8NgNIDxRuCu2nY7dkqGjXbVpkPfdJ2xNqOoPhaL4ObrjdxypxcMU/Rg2xYoeXM50qkLClntpei5xaTOPr+FXs0jIq1YzxmBMBuRXg3r1OHIuX/A3oYxN6lRcWy54EF+ztrKz9lbOP6bF/nsxCs5PrVf04N7m7BKmN8A9w6Qa2kpRqgOO4jhYHqx8Skpa/eZCuQqCsSFI/vw2Hcr2VVYL65FGKA6kMvOoM9fLxU6IkJwxSVmbv53NW++YMNiEezL1fjpNy8Xn2fh2LFGPprl4fJLLDidktlf+njqPyOCvFaFopUoi0vQKOHSnjG0XPp9cM8oBveM4pITO9Pjgj+Ycbd+vCbGBQBhDmqslrDb7WQ8fh0U60HAM5ZuZsWe/Nrzx/RKYumuXLbmldKnc4AATeCGWb+zaMc+LDHzWb5xa5vXVJ/k8T2Iem0ZuRtySR6SDKZpVBQ+CrhI627AWdK0cJt2iYlpl9S9v/kGEzffEA2We4Oa25beBXNqDJU/bidqSn9MSdFtvJo6tHwHxv5dABCRNjAaGtY+AaxGMyd3H8jJ3QfSOSKar3ataV64RDRR3E1YwLIAPBeAtogW43uIBMNxYP5Q/5wFIsTva5PRwB3HpfPkD6v2G6TxQE6nh/RjitBdejDpeBNPPGTj0Qes3P+IiwGjKrDZBJER8PC9+t//xSdtXHNrNS+96UZK+Of5EYw/bnpoi1QoFAcMJVzaM5Y40AL73iucXlZscTAhXY8DyNheQffOTQVkSjA13mOnVTSTETS+dxKXHtWXk1+bx8LbziQ5NpKBSfF8nrGzts2r542nsMLJyBe+Dc966hE/IhmbD3Ys2qULF5Gouy98Mwm9OJkVxBgwNHPzrz/3TbprrGrxHuKuPwpjdBtK1++Hll+O+dgj9DdpnRsJl1UFe+gSEUNyZCya1FhblM2QhJSmBzQZoW8z7i9hB/MXoP0C3udALkG3bNR8Fq2AF8R4MN0OhmObrhUkhF4B1xNCKj8wbXQ/nvpxFY6aAnoSsDb+DPt8Pn3vIe/n1IgX0K1mTz1i46lHGovVlGQD82bXi4sxjgZDz5DWp1CEjLK4BI0SLu0ZcwzE9Mfp/pH0K5fXHp40Kp77Lu7OUzP3cs1zW7FbDETajMy4O9BNVkDiOL1cfTiwNQ4Ars/Zw3pRUOFk0qvf8PttZ3Jc3xTunbuM139fz3Xj9TiXKh8HpCheRFI0RpuJzB+3M+56/w7JphdA2wQyg+BdHxY93sPyachrEBYDePZPNW4bMt+B6OSPUerZGWIioJ4bJd/p4KpfP8blD4Ad1TmNGwdNqD0/ZPZjGPy/73N7Dee5Y8+D8QNbuBADUk7APVfDU30JURc4gWL/yQQwnqD/joKhW3/YuSa4tn4sJiM3TxjCLXMW+dcjILEJsWW9Rd97KGRxChAB1rtabqZQtInDv/ZKOFHCpb3T9QJ8v24HX+Mv5flPDAnYZfq0HnVvDFboem741tMzXU9vbWazw2vHDSK3vIopb8zn+5tO46trTua2zxfz1I+r6RhlJ9Jq4cmHp4dvTfWIH5bExiV76g4IC1jmg+c80JYQlOtD9Nb7BCqk1gLCZEQGW802CKTTg+CUpQQAACAASURBVKz2ImL9cTZCwInpMGcJFVc9D8CkbgOZ1C2wEMm8+NHGB/ulQIfmLXDS68XzzUIMZomWGQGmNsTrpE+E3RupeO6aRqcm9ElhQh9dAE0b3Z9po/vXnrt5wlBunjAUDCYYNE7f0TEQxsFgfdy/91Ao4iUCLNeDaWIIfRQKxYFGCZf2TsIoMNgCCpeWEWDrBDHBuTtaoqKiQi8+t2wuANPG9GPaGH3s6ac23Otl+qmjmH6q/nNSBxMzLz+x7mRcNBy1FLbOA6mBKQai/wHxU8GU0KY1Jo1PY/OyTMr2ldMhyS88hB3MX4E2z+/6WEPDvZ5M6FaWHmC6AwxnN79JYDMIsyGswkXLL8fQKaphavWRfWDBKiithACZZM1iMcGUo5ptIr1ePPMWIqQHYRBtD4/q3B2iYvV9iFqDAAa3EMhtvRzwgesBghMvftFivb91a1IoQkVZXIJGpUO3d4QRBj2qW05CxWiDgQ+Hdz3WCOg1rPWuHoMPkjKgahW4d4NnLzg3QMHbsOVE2H0LuHa1enmJR6YSG2Ujc+nuhieEAYxTwPorWJaDaToYb0Pz3kDpwn9S8PObYF0BxgtaLVqA2gygcNHATVSD1Qy3nQ52i17uN1jMJrh8IqQmNtvM88Ofumgx6mMbowxIVxu2ahAC/nEhmFqhgEwWGHqcLnxawJ1/Drlv3w3G49HjcPb/P2MGbHpMS8SHYHvgwO3jpVAoWo0SLocDHQbAoId1y0tQCDBGwJBnILJ7+Ndz1GQwtyK1WmgQUQXxOY3PSRdINzh+gR3nQ+Xyxm2CIGFEMqZKLzsXNSN+DL3BdBuYHyfv9TPYe0s/Nl+5C+fOklbN2QCzARnqHkLNoOU7MHQKkKGUEAP3nAPx0bqQaQ6LSW9z3ckwpEfzbQFDn554HEaklEivhjHahHdvaSuvwE9ybzj+ktDEi8mii+TRpzXbTPo0CmesZuspH1H4vgkiv4CoDLDcCqZJYBwDxpPAch1ELYXI75R7SHFwqSlAp/YqCgrlKjpciB8Fw16CbS9BxVbdxSL3ewoWZhCCatmb757sxqSZvRo9c4aF6AQ47UaY+1Lw2SLCB1YXDF4Hhub+00nQqiDzeug5A+wtBJHuh71LNOZIC3t+3dlyY8Dxyy6QkugoM2vPmcnI36/AGNk2i0s4g3O1vHKMaU24z+Kj4cELYN1u+GE1ZBXqcSCapltiJBBhhYnpMLoP2IP7NJh6dUEYvFTPW4VxZD98uwuxJYQhK633cLBFwnfv6QXlmvrsmMx69trwiTDy5GatItVbCtl75wLc2Q7wSYyxfkFtSAZbcKnsYUP6wLEICt8H13bQnLr1ztwZ4i+C2FP1BwqFQtEsSrgcTkQfAcNfhqosyPocihaDtwoQerpzp39AypmsfjiDvPm/81bsIxz59EmMumVsm/cpakTnNDj7TvjmVXA7mxEwEgwaxJTDgI1gCtIaIat18dLvp5A3Kex4VCrbf9iEp9qD2db0E75rTxme7HKEEBiNBiipZtN13zDwg9aX6xfmMAfn5jsQo5qxkhgNkN4DOaAbxbd9Qex5QzAaJFjMEBcFaZ1a5Q7xbdmDt8pI5Jg+MKZPG65gP1L7UsLZWKPziTBv1gO9jf6/r+bThc2widDvKN0t2QKFH6zGlVkKPl0MG+NbU/W3jUgJxTMh/3XdcqhV1TvnBlcF5D4NuU9B3BnQ5c7WuX4V7ZvD3EoSTpRwORyJSIU+twC3BDzd7cTerH3iNywaZNzxHaue/J0z5k8jeXiQ6avBEp8M/3wE9m6C1T9A7q66m5AENC/7jDu4bdZSlm92YLUYSEs2c9LYKN7/qs714PVJNmx3sfHr3uQVeTn95j30SLEABrD045nn3mDixOBN+4lHppK4ci97V2TR85imb/qlczc3iEeJsBop/m47VVuLiOzbfBxIU4Q/ONeBoXPLxexKnvkV17ZS3D4z9qPbVpNEejwIZyXG3i1vdRDSuF4fxc8tpuLrTdiP60nEI3dSvX4Ppa8vossj/9CFSkRMSEIr5bGJGGJtFH+QAQaB6WALF6lB9nQoWwCymaDgmnMlX0JVBvR4B4wdDsoSFX8RlHAJGiVc/oZEpXYAhO5WBQz5Tta8tozkd84O/2TCAN0G6i+nAypL9c0NrXZk5Secdeo7XHpGLDOfTwYgY7MTR6XGLRfXCYN7X8wlva+N/j1t5BVVMG54JPNe9cfm2AdDr9DiERJGphBtNrFrSWazwkVWezF2isJbWIlmNWPuEcvoVydj6dT6fWt0i0t4XEXS7UWWOxHxzbtpKudtpHqxHozsWpmNfVzbhIuWnY87uxrb2S3HwwSLr7iK/Dv/h3unXgvGGGdHSknBf/7AvaUcd6kVS8/Qb+TS7aPi512kPn0iFUuysKSEr2JxUOQ+DWX/0y2EwSBdUL0Ddl0DPf8Lhta7JRWKwxUlXP6GRHSJAiSdenvonOal05hO9Jpig02LoEc62A7QhnL2aP3l55evZ2A2w7XnxtceS+/X8In49xWVzP6unFWzewUes3oLeHLB3CXoZSSMSIbianYtyWy2XZc7x9LlzrFkT/8Fj9NDZV5lm0QLoAfnhsniIgsrEAlRCGPTbj73pnzK3lgG/jmrlwexwWILaNv24CnSiEwK08acQO51X+PNLq+t2i9dXip/y8S9S7e8lc1eT8e7Q9+7qvC9VVh7xxN7Sl9iT+kbtvUGg9FoZPARVmou6vxJHbj7yo7M+62cB17JR9PA45XcclEChaVePvteLxq4bls1g4/YDKZeXH71Xdx8880Hdd2KQ8HhH1AbTpRw+bvhqca8exkXPlaKLVrDYJAYjZnIFZkIkwUWz4S0oTDkBOiUduDWITXWby1mxICmTfel5T4ueyCL/z6eSkxUXXGxhasqSZ+63f/OwOdzVtJr0KlBT23vHIU5xsr2RZlIKVuMV7EkRyP3luHI2Ndsu2AIZ3Culteym8i9Plf/wSDAKNAKKvEVVWFMaF0QqHS7oaICQ4/wuhUTp0+k+NmFuDcVgACt0kPBo7+BPwPL8e1WEm47GoM1+K8sd1YZRR+uoddn54V1rcFitxnJmNOb+nsoeTySqx/K4c9PepHaxYzLrZGZ7aFvDyv3Xa3vnB01aiMZc3qBMQ763XBI1q5Q/JVRwuXvRFkBzH0W3FVExzd86hdQV+125yrYvQ4GHw9HTjkwtSyku2bWJrnu0RwunhzL2GENXSENXEWGKOjWMeTpO45KZc+iHRRuL6TjEc33NydH49xcgK/KgzuvAkvntriKwmdx0fLLMXRsXrhEnTOEiLMGkXf+R0Sdl45WUAGm1gdiazn5uPe5sZ8UPjcRgLV/R4xxdjpcMQLP7lI0t4ZWVg0WI0iJdPmo+i2TqBN7N7M4H2Svgk3zoCwHs6uavjeYMKzeClWTIG1s69L0W4O3SM8i2m/jR0eVD69PkhCrC3GrxUDfHk0E4koXVCyG6PDskq74i6MsLkGjhMvfhfJC+PI/eoZPMxshAvp5rxvW/QSeahh7AJ5YhZWBvazM+T5w/Y8Pvi4hM9vNh4+3FAAqwRi6kEgYkULHLfnsWrK7ReFiSYnBk+MgemgXyjNySTypmZtnC4Q1xiXfgejcsrtGFlUhEESdPbjV2VA1aDuycO+pJqJnfMuNQ8C9owj3lkI6PnoCwmpC+jTib6ig6OVlGKIt2AZ3wTqwU+DOUsLm/8GGr3Tx4tXjSYQBBG4oz4HVH8Oqj6DnsTD8QjAe4NiR8p9wurR6lkG458qOnDepA1MmxND9pC0cf1QUk8dHc8EpHTAEKhSoVUHxHCVc/g7U1HFRBIUqQPdXwpcF1TPB+QY43wbXl6CVhWFcH3zzXHCipT5eN2xeDFuWtH0N+yMEx40fiMsjeXtOce3h5eur+G15Jfe9lMfHT3TFZGrhRiu9YOkW8vQJI5Kx+2DX4swW25qTo/FkO4gelkRFG91F4UyHbrL43H64txRg7texzaJFutzgqMCQltTmsfan/OM1RJ87GOF3BQmjAXNqDMJowD4yhZjT+2FOCSDSNA2WvAZr54C7sla0NMLrAp8bdv4K3z+ktz2QeAqwWw1kzOld+zpvkh5c/M5DKfz0dg9GDbLzzAeFXP5AdjPj5B3YdSoU7RBlcTnUSA08v0LVK+D9E/1P4kGX4GbAC9bJYL8OTIE3TWyJ3OU/cuuLc1i+Kw+ryUBaQjQvnHs0fTrH8vyPa7nnqz/Je/oSOvgLkP26JYd/PP8Nc68/idOGpMHyuUy+43HuvPNOJkyYEI6rBkB0vIIvX8ri1v/s5Il3C7BZ9XToarek0qlx1m17GrR/+Z4kYL8YF2MM9z+0gKlTp4Y0d/yIZLy5FexZ0vL2AaaOkfgcLqIGdiR35vqQ5mlEuF1FQQgXz5Z8LH2bsFaEgMzJw5PrxjZmQJvHqo93nwPn0j3E3z620TlfibOuaFyjBUlY8T5krdBFSTD4PFCWBb88CRP/ry49P9zI5tczuI+NwX1sXHJaLD0mbWXGY02N4wn/2hR/TZTFJWiUcDmUaBVQfiF411K3K3H9Qm3+n11fgutbsF0EkY/pNvAgkVJy5qVXcenINGZecRwAGXsLySt30qdzLJ8u386RaR35cnUm046uy7pIjYvksf+t1oWLywnVFW261IB0mERyp8eZ/WxoFpOypf4bp7BBzw/BHvomkfZOUVhibVRmllFV6iQitukgYWEQmDtHYUuKxpGxL6iA3ibHClNwrvRpyKJKRAsxLqBbXKLOG9rmObXMHKq3VBB3VfAZXMFQ/ukaoqb0xxDVONbDV+Jssmic0WRicNdYXfwDX90+nsyCSk5/7nd6dorC6fYxeVgyz1w0vLZPQXk1yTd+ySuXjeaarqNgwOSwXkvd4gKnbldU+VixwcmEI3X3ZsbmaronN7PNgTF8mVsKxeGCEi6HClkJZSeDbxcNxUogfIATqj8GrRii3wg6YPaXuZ9jlj6uHV/3lJzeVa+RsqOgjAqXh6fPHs3jC1Y3EC5DUxPw+DR+2JjFCQNS9RiZcGOwQeJlUPB+88W5AiEsEDGkVaKlhoQRKaRuNZK5dDcDTm5+HHNKNLh9CKMB195ybN1aVxwsXMG5sqgS0cGuC6Hm2vk0PNsKsfQJPYC5wTjOamSZA5Haqdn061DxlTip/H47SR+d0+R5Y1xg4WK3mMh4fFKDY5kFlYzr25F5d03A6fYy7N4FnDmyK2P76tf/2R97GN07kU8X7+Cak+dD/1NCehAImsjhjWJcJo2N4r6rO/LUe4Vc83AOdquBSLuBGY82EcclrBB1dPjXpvhroiwuQaOEy6Gi/KogRUt9nOBeAM7nIeL2oHqsX/kHI9ICuwk+Xb6DC47szbjeSWzJ/YX8ciedYupuEvefPJz75y7XhYs7RGERLB2vhept4FgYfJEuzGBOgm4vtmnqhBHJxOeWk7kks2XhkhyDZ58e5+JYs68NwiU8wbnBuom8e0sxxNoxxLQtm0bm5OMp8GIb0/rA5EA45qwn4riemBIbF9GTmsRX6grsKqoqqbW0NIXdYiK9eyzZJXUl9j9duptnLxrGha8uITu/mJR96yG5dS7Y5icfim/jJPBkNTo1//W0ZrtW/FnzkCEhPjQXqKK9ouq4hIIKzj0EGI1G0sfOYdC4XE67qIzSMv0L+NfFbiZf2DAYd9qNDubM1cXNvO/dDPtHNkNH3c2AAf158803W57M69k/I7OWmSu2c/7I3hgMgrOG9eCzVTsanB93hD+mZNu+Fm8SrUYI6Pq0vsGcsCNlC5YkQ4RuZen1SauyieqTMCIFU5WXXUt3t9jWUhOgm94Fx+rcVs8ZruBcme9AdGrZjeDZXIClb9usLQDann0415RgHR6+Mv9alQfHVxuJuTCwG0tzuDBEmAJblfb+idPtI/2e+aTfM58zn/+9UZOSSjfbch2M76cL971FleSWOhnVK5Fzj+rGrEVbYccvYbueBggBiZeDaO0WAwKix4EpvNlbCsXhgLK4HALsdiMZvyYAXi69wcGr71Zz3+3NFwTzeCRX317Bn993IDU5Bpf5PjJzj2xxroF9j2DOnM8aHV+bVcS2/DJOeHEeAG6fRs/EGG6YMKhBu/tOHsZj/1uFyXwA00eFEVKmQ9wZyJz3kI7fERYLQnrQn0TMgERa+yI6XQ7Rx4a8sWIgEkYkU51Zyp6d1fi8Poympt0u5pRoKhbvJXpSb/a+8kfrJw2Tq0jLCzajKB9zv7YF5kpnNbK8AtEpEYMtfF8ZFXM3YRuejDk1sPWqOTcRzhLsFiMZ/zml0amFWwoYcvd8tuwr5+7TBtDFH780c+luzh2t1/85f0x3rnj7D26/pLhR/7ARdyoUvu3fYDRE4S9s0OnGA7IsxV8UZXEJGmVxOdjISj2FFy8AY440kZ3b8peao0LqhaviDEAlVu11+vZtuYT5cSeehMvr4+2Fm2qPLc/M55bZS5g+eSSZj19E5uMXkfPkJWSXVrK7yNGg/4kDulJS5WZNVlFIl9kqItIx9H6Jgq8exLn3n9D5Zuh8IyTdBb3nUDx9Eo4PLUiaj+sIFlvHSCyxNhK7RJOztvk0Z0tyDJ6ccqKHdsGxJhepte5LJlzBucFnFBVg6dfG+JbsPDxFGrYx3ds0ToMxPT7KZ60l5qL0Jtv4SqqbFi4+b5P9xvXtyNonTmHdE6fw+k/byMgsAXQ30Yzfd5J2y9dMefZ31uwuZdve/DZdR7MYItCS30YaYyCUz6ywQbfnwBZet5xCcbighMvBxreztmCszyf56XcPU05q2ZoRH2dgykkWug8v5oKry/l41no0X8tP7qJLL7689Sx+2JRFr/s/ZeBDs5k+byW/bs3hzPS0Bm3PTE9j5oodjca459QjySoKQz2ZIIk+9UgK3+uITJwGHa+E+HPBmgZuL+5ft1P5+mKkLzyuq4SRKaR0jSdzSfPuInNyNO4cB+aECMxxdpw7W/ekHlZXUQvF56TLi3dvKeZeCW2aS8vaR9WKQmxHhV4vpykqv9+OuXsc1mZEla/YiTGuidgcW8uirU9SDPdMGciT8zayJaecSpeX7FfOJPPF08l88XTumTKAmYu3tzhOqEgpcW/Mo+SJn8k79wfKf/8XWFJ0N2dzCDsYIiHtDYg+JuzrUvyFqSlAF87XYYxyFR1sZDlOpyR9QgmZezVGDDVxwgQ9HVI0UQK/JoHonReiWbfRy4+/e3jm1Sp+WHYpM2Z81Px8QpB87FnMjjTVlfRvgufOqctgmNA3ufbnU/p1w+eqxmBpojR5mLGPTEFWe3Gtz8c2uDOgP6EjAU3iWrgDraSK6LuOQ1ja9hFOGJ6MY+Eudi7JZNyNjeuI1GDuHIWvqArN7auNc4noHbogCEdWkdQkWoGjxXL/nu1FmLrFtel3JCudyPIqiIxuc4Bv7ZiapOzjjIB1W+rTrKsosU9Qc117fG+e+XYTj8/dwJkjuzY4d/bonpz/5moeCGqk4HD+tpPyt5YhK93Iai8IsJ94NKSdopfvL3gPnOtr3Z8g9K0BzImQcJnuXmpJ4CgUf3OUcDno2LDbBRm/xlFWrjH5wnJefbeam6+2kxAvKCltqJSLSyWJ8XWGscEDTAweYOKSc2z0GPk1M2YEMWW/MbDim1at1qcZ2PRnJE65gtE3NX+jCRfCIIg5awBlX2ysFS5aqRPMRnB5wePDsyoL9/I9WMf2bNNc8SOS2T13E5mbmqleCgiTAVNiJN68CqLTk3Bk7KPzOQNDnk8XLm2zFsmyKoTNjLA3U/8Df3xLGwNzZU4unlKJ7ei0No1TH+eiTAx2M7YRzW/U6CutxtCUcOnUD8en14GzoQtzwoDOTBjQufa93WIi+5UzAw4xpFscGzdtCniutUjNv8eSV/8biygr5rR4/ekjerz+cmdD9XbQHGCwgzkZbP0OzJ5givbDYW4lCSfKVXSwMSTVZvl0iDHw0uNRPPOaE49HckRPIzl5Gpu26v773Xt9rNngJX2wkYoKya+L6ywmGRvMdO8eZMyBNRJOvAaMzd/oGmE0IRJTWfdTHAsf+IGSXQcwkHE/ok/rS+VPO/E59IwqWVYNbq8uXqKtdHj+zDaLFtADdB2bC3FXuinNCrxvUg3mFN1dFJXeBcfqVpb+D4OrSOaFkFHUxsBcLSsP55+F2MamtWmcGqSUlH2YQczF6S0W8fMVN118DiEo29MXTWvls5cQ0HUkWBqnYbcF+4ReWAZ3qXUH247q1vg6LSkQcyzEToaY48HeX4kWhXIVhYASLgcbY3KDglfDhpgYOtDIzC9dWK2Cj16L5rKbK0ifUMLUyx2883wUHWIMSCRPveyk7+gS0ieU8uBTJmYEZW7x03UATLwCTEFmBxnNkNgdw+m3Meb50+hkt/LllZ8jQ9nrqA2YEiKwj06lYsE2fTldY4m+5wTiZlyIwWzS96gJA7bESCxxdnoMTWZXC3Euekq0HqBbsbEA6Q19DeEIztXyHRg6B5tR1HqLi6yoRFY60TQLpk5tSz2vwZWxD83hImJ8WotttWbK/Ts35JP3lQkREdO6m77RAoPPDr1fCzg+WIGscBP74AlgMWIb33ZxrVAoGqJcRYeAiqIvwXEzoJfR/+bjunTQsUeZWbYgtlGf6CgD82fWtLNB3CIwhpjlkZYOp98Fy+dC9iZA6Hu31MdsBZMFd8pY/rxpN/077KPnOYPYMmMVe9btY+W7yxl55ajQ5m0lHc4aQOGLy4iZOhBhNWEZoccoWI87AtdP2zBd0bag0xoSRiZjMcOuJZkMO7fp0vjmlBjcOQ5M0VZsKdFUbi4kalBoFo1wxLgEk1HkK6tGK6vGlNr4sxQsMjsPb7nAdnT4sonKPsog5sKhQVXf9TYR4yJ9GjkP/0Knm8YhTjwLFtwPnqrgaw0ZLTD+DohJCnX5zVLx+TqqF2eS8PRkjLF2rJ9ciIg8wLtQKw4TDn8rSThRFpdDgWWSXrK+VZjAPDJ00VJDYlc4+Qa48DFIPxG69IK4ZEjsBmlDYeLVcMmTMOxE3LlVrD3vM1ZP+YTht43FWuHhp38voCzr4GQY2UelolW4cG0qaHDcetwRuBbuQLqaTokNhYThydg1QWYLhejMydF4cvR08Zo4l1AJR+XcYIrPebYUYO7TEWFovQtCy86lanlB2NxE7m1FeLYXETUpuMBaraQ6oKuoZM5GhMlI7Bn9Iaoj3gnT0awJYGoheNhkA3MEHH8vdAk9Pqk5qr7fStXXG0h4/GSM/roxhihr2HfRboDU9K0yDpIVVKH4q6AsLocCYYaYT6DsTCCUUvoCRKy+V1FbiegAI0/TXwGwxEdgsJnQqr2ULtlD2Z9ZpB2ThnlzPl9f8zmXzLvswH4p4w/SPaM/5Z9vxDagzrJh7BSNqWci7j93Yx3Xq83zJIxMIWvBNnI35OKucmOJCCwqLUnRlOVsAaiNc0m6OLTNC8ORDq3lOTC3YHHRd4Rug5uovALpdOMt0TClxbV6nPqUfZxB9LmDEZbgaproWUUNxYi32Eney8tIe+d0ELD55aWsu3UBHkMMF2ZeChvnQfEOMJj0G7oQulsxMkHfULHbmODdpUFSvTgTx/vLSXjqVIwdw+NSaxKZDZ63wfcuUEzts6foCabbwXgOCJWV1C5RFpegURaXQ4V5BMR8CAT7JWNCio7smXEf7qID/OXox5bqf6qXYIq2MvTf47HazFSsL2DNxxkHZQ0xU/pR8eMOtMqGqdzWiX2o/nFrWOaIH55MaUYuSYO7sGf53ibb1biKwG9xWdOK0v9tdBVJKXVXUQsxLu7NBW3KKNJy8vBWGrAd3T0sAtWTXU71n1lEnzGg5cb49ykqa7xPUe5zS4id3BdHQSVfJT3F2lv+B1KixdshZRic8ABMfhrG3ghHXQlHXw8nPaQf63ls2EWLKyOHspcWEf/wSZi6tt4t1yKyGFxnQ/Ug8L0IFKFH+fv0l9wGnruguht4Hj5wW3QoDgyqjktIKOFyKLEcC7ELwHwcYPW/9icCsIF1Kl7Td2Q/n8vKEW+w6bIvKVuy54AGy9p7x4NBYE2JpuPkPsQf053xb51BpNPHd7fPoyLP0fIgbcTUMRL7yBQcCxoWCrMc2Q3fnhJ8+8rbPIctIQJrgp1u/bqwa3Fmk+3MSdF48yqQPo2oQZ2o2laEVh2au0pY2hicW+HSrQiRTdfUkVLqFpdWZhRJKZHZeVStKg5bGnT5zDVETemHIciYD63chSHSjKi3DUPV6n1ULNpN5On9+P3Y9/HlV2FAIIHovol1nSM7QnI6dB8DKcMhtmvjCcKAe0sBpf/5mdh7j8N8RGLLHVqLzILq0aD9hL4pa1Mbs1YAVeB9Cdzn+St0KxSHH0q4HGpM/aHDLIhbDvbrwNgPDMlgSAXjUIj8P4jfCNEvY+6Qiq13PGiS0h92sPmfX7D2xP8eMPHS9bpRDPrgTEYtvIKin3ZR/MsuOo/pRs+zBtItNY55N809IPPuT8xZAyj/YmODY8JsxHpsL1w/h8fqkjAyhYTYiGY3XDRYjBjj7HjyKzHazUT0iqdiQ2gl44WpbRYXLV/fo6g5K4gv1wEWE8YAOy4HRXkFuD14djiw9G9bOjXoLp+qH3YQc+7gkPrUt7ZIr0bOw7/S5a5jiOnfke73HYMGSH9tgZi+B1A4BMCzp4SS6d/T4dZxWIcmt9yhtcgycJ0I7AOaLyBZRxVoP4PnOhX/0p5QFpegUcLlr4IxCSLvg7iFEL8G4ldD3I9gvwIMdW6BhFP7gFG/aUlN0uWyYQcs1iR+XHc6ndoXc6yd/i+fwqabvsVT6mTUf07Em1tBwZ9ZrJ+z7oDMXZ+I0an4Spz/z95Zh0d1Z2/8c8czycQmnhAhBJfgXtxatFSgAm1pu3Vvt91ulbpuu3WnhrQ4LU6hWPHgkEASIO4ySUbv/f0xgdgkmZkk7O6PeZ9nHsid+5WZZPx5bAAAIABJREFUTOaee8573hdjfZLumI4Y/0hpFfn/wD4RKCutpO8+h9hEq7WyuiUaqnkuLhJ0W0rOFXOb7yhqqSO0mJmL1ahEMzjGqe6f5lD2y1G0Y+KRBzrPvbAV19VwKVx4BLm/Br+rEwAI6xOJJANR74UMAb/uoY1N1eqw5RkoenYdunkDWtW/ySEsr+MTdBKwcfyEyOhJJjr2NJLQw8j81y2Xblq++8FKcHQViQONdE408v6/y8G2AsQdbbs/Dzz4D8ATuPyPwX9kHIJchqCWI6jl6Pq24d1eLQSOjCN4ckeSn9yAOsCLwe9djV6h4PeHVlJZWNGmawtyGb4zulC2vG7WRdEuAHmIDsvBjBavoe8XieF0IV5+GvJO5zd6nirSt15nkWs8F0EpR7K2gOPiREdRSxRzJUlCysqhKqmoVbqJxAozhhUn8Z3d06Vxdp8ie+Biya8g/7N9hP9zBIIgYC6uYu/c5ahHxXBj/jP0Wz2bbnf0bfFendpXSRWFz6zF59oeaMcmtO1ikgls3wJQVSUx9XozTz+uIPmIhsN71Oz6S+STz2s+SzfOlJO0R8POzWpefcvChQwDWP/Vtnv0oPXgybg4DU/g8j8Gn8QwfAdE0n35bNrPH8PJOUsx5xguy9rxz4+i/EgOuctOEH9jD/w76ImJD+b3R9e0+dq+0zpj2HAWsbKu7oydpHu6xfPr+4RTdCib2CExTRouKsN1NQTd3m60RCtlSOYWZFycEJ+znG5BxqW0HGwSxsMFqHu3PCg2rDqJpn8kyii/5k+uBVtJjTN0zls7CJjZDU18IAC7b12KwWZl/MIbAYi9pjNqXdv7aIkVZor+uQ6vq+LwntG9zdfDtpyLMts/L7YxdLCM8WPtnB+tVuCj95W88W5DHoteL9ChvUB2tgTiHyC5QSL34DKjlYMWT+DiwX8TZEo5XRfdgE/PMIKv60bYrYmcnLMUa3ljhL3Wg1yrpOunU0h+ZiPmbAPDPp6C8UQBF7alcXpN63q+1IcixAev3uEYNtQl6aoHx2E9mYuthVkfdaAWdbCWyPZBpO1Kb/Q8VYQOS5a9VOTdOQjjhTKsBuffe7tybks4Lk2XiiSriOVsIcqO7gUuYmYONosKdd+oFhtYSmYbZYuO4HdzostjL7ZCG/ZkUHkwm5B7+gOQsew4OZvO0uff16B1l8PjBiSTleIXN6DqHILPnMuT3cH2AxdFKo+fFOnbu+7XdXx7GYYKibKyuhep8xdEjEbo2UMAZGD77fLs1wMPLhM8gcv/OCLuH4CubwTJd69CNLdMH8QZ+PaJIOqOPpx86Dd07QPp+cQwosP9WHXvcqpKXNGkcWPtauPF2hC8lKiGxGHaeqaRUc5D3zcCX7WqycCldku0TCnHu0swhiO5Tq9xUTnXXUJ1c6Uia3oR8lAfp7t36sx9sZvoaEmrdBMZ1qegjA9E1dF14qytqArBV032/K2EPzMcmVaJqbCSvbevgN6hdL/9MgUP2JV6i1/fgixQi+99Q9pcv6hm4ZrP1UVJGke4eHzxUhvd+hpp39XEw/cr0GgEwAhSQdvv1YOWw5NxcRqewOV/HIIgEDd/DDKNgtSn1l8WL6GYx4ZgKa4i85uD9Hx8KGKFhZguYax/8vc2XVc7pB22/ApMyXW/iDVjO2LanIwktuy16/tEIOZVUJZdjqHAcQbHTs6taQPXJYa5xHMR5DKQCWBzfa9SlQXJaEHwb8R4kIv6LW52AhWXgiBg3JONZmDLWoglm0jZz4fdyraAvVRUdTQXZaQvujF2v589ty2j1GJl4uJZly14kGwiZZ+sRu6Tif/DUQji5TMatWu02NGti4z9B+uWGFPTRHy8BXQ6+3tx40w5xw9o2L5JxePPWMjJkbCXmjxt0R78/4IncKkNsRKs58B8GqxZIFmaH1MfVQY4sQcObIZ9G+DIDihs2xqzoJCR8PE1VJ0p4sI7O9t0LaguV306lbTXt2M6X8rwz6ZhOp7PmXWnObsppc3WFeQydNO6ULasbllKHh+EoFFgPe6mY3M19P0iKTqYTczAdpz7yzHPRRWhw5JTfilIckf6X1C4p557sUzU1EW7JYq5YmYuNkmDqnMIMp+WcUaqtqcj81Gh7uMeT8aaY6Bsazrhz9oJuRm/HiNnSyrdXhmDX3QbCr1dhFiBVLIQ8fhwfMc9je+MDxCyb4D0q+DcJChbAWIbl2eFGsXim2fJ2bFLZNMW++emqkriocctPPVYw3Le4IFybp0t54NPrIC6zjwe/JfCI0DnEjyBiySB6SAU/A0ye0LOBMibATmjILMXFL8CVie6VnLS4fdv4JsXYNuvsGsN7P4dtq+Axe/Aoncg5RDY2qacI9eq6PzdDApWnCL3x8NtskZteHfUE/vUME7cs5qQge2IuaYTnROjWHH3MkwucD5che+0zpSvS0GsqgkqBUFAPbZTi5V0A/tEUJSUTczAGFIbEaKTeSmReauwFlYCoOsdRvkhFwNTpcytlmjnOorcU8y1dxPlYjxR1uIykSRJlP50GL9bEt3OjJjOFuF3TUfU0X6Y8ivYd+cqzPH+9Ht4SIv25hRKf4a0wZD7KnJtHoLCiiBVgFQBmMFyBvJfgLSBUN6G/BHZFKxWDWo1eHkJrFyi4pU3rXTqZaRHfxP9+8p44B7H9gl/f0zJt99bKS8HZCPbbo8eePAfwJUduFjPQ85YyL8JqtYDZpAqQTJUm5cZwPAdZI+CgntANDacQxLhj19g2cdw9gjYrGAxV0tuS3b3ZasF8i7App9h8bv2rEwbQBnkTZcfZ3LhvV0UbzrbJmvURtSdfZHr1Jx7fxcD3hhP8YEsorqGsukf69tsTWW4Dk3PMAwb674+9fB4LAczEMsd/I6chDrAC69QHyJiAps0XFTVMlvUdtBjKazEUuQ8v0dQysGNluiL4nONPl9pxpZdjjIu0OW5KSoBpYLK7RloBke7Pr4WTAezEA1mvIbHujW+fPs5pCoL+nl9ANh7xwpKLBYmLroRWSvoyjSJwneh4A2QqhDkTQTgUqU9kMl7Gkq+bZu9KOZw/ISV+Dh78Neju4yt69WcPqzhzDENLzyrvBQY3nargo/er+E1RUQI5KR7ofPtDDLnbBY8+A/Dk3FxGldu4GI+DTlXg/Ws/UuIxu6AzYAJqjZD3nQQa3EfJAnW/wAn94DV3LxKpcUMRTmw6F0wVrbSC6kLr7gAOn01nTOPrcPghnuxKxBkAl0+uoaMLw9gPl/K4HcmIZwr4/ivR0jfntZm6/rN7NJASVemU6PsG4Xpz5YFbIF9I9DY4MKBDGyNlHOUEb6XOosEmYBPz1CXfIsEpQzJDSJ1c+JzlpQCFPGB9sDI1bkzcxFlWhQRvi02Ciz9MQm/m3u55Uwtmqxkz9+KIAgoQ3w4v+goOdvSiH9sCEFd21hkrvRnKPnOftPiLCQjFL4H5WtbfTufff4Ls2+T8coL7voreYPi8VbdkwdtCE/g4jSuzMDFlgP5N4BURuMBS32YwHIWCm4Hqfqic2ATpB6zZ1SchWiDilJY/XmbyXHr+oQT/84ETs1bgTG9pE3WuAhNpC8Jr43lxN9WEzu9C97hOhLHd2bFnUuxVLnBEXIC2qExWLINmM4U1t3LmE6YNiW3iKCs7xtJ+Yl8guL1ZBzKdHiOMkKHuQ5B1zWei7vquc2Visyn81G5Qcy9VCY6Xd7iMpE5uQBLWjHe490TZyv46gDq+ABkOhWmggoO3LOa8mANQ58b1aJ9NQuxgldffpRuE5PpOfk8iVPOM2leFn9/q4YIfi7TQvtR6ZSU2dh72MhVszPoNP4cncef5s47b6WyorRVt3TPPfdwdNufjBvrmgaOHSoQOoB8aqvuyYP/XxAE4VFBEI4LgnBMEISFgiBoBEEIFARhoyAIKdX/OiRJCYIwt/qcFEEQ5tY6HicIwp7q44sFQVBVHxcEQfhQEIQzgiAcEQShj7v7viIDF7kqgsTxp+g+Npvr7ymgssp+EcnItjJtXj4JV2UTPyyLh18oxmy2XwS37jYy+bYMMB8B42awWln+1ScI97/DqVx7p8HWlAwmf17Xv+e2nzbya1IKM75aQ+JbP9Nh/gL8nvyYxEdfJ7FHN3bt2tUmrzFwfAeiHh7MyVuXYilqm+zORYTO7IpPtxDSXvmTYZ9MJfu3ZEI7BrHlhY1tsp6gkOE7rTNly+uSdBXdwpDMVqxn3G//1PeNoOBAJnFDYklrRIhOFVlTKgLXeS6Cmw7RzYnPWdx0hJYKikGjpnLbBTRDY1weXxulPybhe2MPu5mkizCdL6XwpyMEze2DzE/DvnkrKbFZmfDTDchbqCnTHHZveoc1W8o5uKIdR9ZEs2lBJF+9GsLKzRWcPGP3CHr4lQLmP6LHZJa4/qEc3nxKz+kNMZxcF83E4T6U57Y862LLKMa0/gQVb2+kdN4PGB49gDXlE8AVzRoVCBGgXgOCssV78uBy4PIL0AmCEAk8BPSTJKk7IAdmAU8DmyVJSgA2V/9cf2wg8AIwEBgAvFArwHkTeL96fDEwr/r4JCCh+nE38Km779aVF7iIBrw0kLQulGObwlGpBD77sQJJkrj27kKmT/Ai5c9wkreFY6iUePbtendRUiWUfQpnD7Nw30mGtY9g0cHmSaHL75xM0lM38dWsMQxvH0HS328i6a0nGTKk7ciGYXMSCbw6gVO3LcfWRtkPsJNjO707gbyVp7BlldPjkSHoTBKHFhwgY++FNlnTd3pnyn9PruPOLMgENGM6YmqBkq6+TzjFh3OIHRRN+u50h+coI3wxZ9a4Ul+OjItktiKVVSEENn4Bc7ejSMrKQVT5IGgUKNq537FjySjFuD8Tn6ldXN+DJJH92jaC7uiDTCmjuNhI3u7zRM7tReSglnFunFicrJQlBAUIqNX28lZQoJzIMAXvPRPEfS/ms3ZbBeUVIjdP0/Hxj6XMnaFjcG97W7ogCFw3UUmo8pcWbkOiYv5ajD/txZqUAUYrgq8GRfdrQb0JCAGaKuPJAS+Q9Qf1LhD0LdqPB1cEFICXIAgKQAtkAdOABdXPLwCmOxg3AdgoSVKRJEnFwEZgomAnXY0GfnUwfhrwvWTHX4C/IAjh7mz6ygtcKpbX+XF4fzVn0i1s2WlCoxa4/Qb7F4NcLvD+8/58s7jiUkbmEszHMOxfyM6zGXw9ewyLDrrRAixJkHYMjG3r8xP99+FoYvxJeeC3VjEjbAzKAC86fzCJkw/8Rte7+1OZWcbAm3qzfN6vWE2tryOhjPBF0y0EQz0SsnpkAubd6UhuBmoqfy+8wnwICvElbWe6w7JT/YyLJtoP0WzDlFPe4FzHm3e9HVoqMCDofRo1PbQVViIarcgjmu46ajCvKCJl5WFKMeA1JKZF+ihlC4/gM72LW+J35ZtTsWSUoZ+TSMWZQtL/ukChRmDkGxPd3o+zsGalMn6glQvZVjqOO8d9L+SxbY+d53L1SG8C/WTMeTKXT160B4XHks307e6gXdx0zO4v5CYEQcDrgREXVf5BJUd9XR87V0jWCzRnQPU1CAMBDeBb66EB+XX2AEe9EYTL0DLuQeui9TMuQYIg7K/1uLv2cpIkZQLvAOex24+XSpK0AQiVJCm7+pxs7BFzfUQCte9KM6qP6YESSZKs9Y43NcZlXHmBS9XqS/+1WiXWbq2iR2cVx5Mt9O1RN63qq5MRHSnnTHrDC++KQ1uY2DmGjiEBBGrVHLyQ5/pe5AoodmOcCxBkAvHvTsRmMJP2/JY2FajTj40naHw8qc9vYfinU8n69QQB0X5se+2PNlnP99quDUm6gVoUXcMw7XKfHKzvG4EttwJJlCg+35AjZCfnll96LwVBQNfLeSE6QSlzWfZfzG26o8hcnW1xNfCQCopB60XVjowWmSraCiup3HwW3+t7uDxWrLSQ/fp2wp8biaCUcfSNHSh1KsZ8MxNVC/VkmoOtsILSD37DR6fmwIp2fPFKMMGBcm58JIfvltqzavff4kf/nho6tW8mIBOUYCtr+pwmIJYbMa08ghDhB0o5yGSohsfbnywtg4074Kti+Hw2LP4nbH0UCt4H1e+gSQPVtyDr7fb6HvwH0TY6LgWSJPWr9fiizpL20s40IA6IALwFQbjFhR3Xh9TE8abGuIwrL3CxFVNllEicmEO/yblERyqYd6N3o5Lajo+bWLj9PLP6dARgVp+OLDyY3Lgkt8Pf18Wp2lYmH0CmktPpy2mU78kg67N9bbpWh5dGU7o/E3mJiagJCUSG+bPvs7/IPpzV6mt5D4/BklGGObW4znHNGLuSrrvQ942k6GAWsUNiHMr/y31UoJRhK6lpvdb1DnO6XOROqag5jyLL6XyUnd0g5mbmgI8fYrnRfcVdoOyXo3iP63DJGNEV5H22D22fcHwGRnFuQRLl6cUEJIYSP7Gj2/txBmK5kaJn1+E1JA5BIUMuFxg5UMtLD+v56Plglq63yxbIqsWOL6JbgooDxxrLrLiXsbJdKKbi+TUoOgSje30aypEJqKf1RMjLg28Xwnufwo49cD4D8gogxQg7bPBNJryzE3Yng9h2GVUP/l9iLJAmSVK+JEkWYBkwBMi9WMKp/tfR3XUGUFteOwp7makAewlIUe94U2NcxpUXuABeGoGkdWEkrQvj3y8HoFIJdOuoZP+RuuWFsnKRC1k24mPqEgMLi0W2JBVz56LNxL70LW9vOcjig8kEajUUV9X9QiuqNBLko2l8Mwp3Wx1dg8JXTefvZ5Lz7SEKVrSdIaLcW0XXT6aQ/NQGej8+jIzfkxn6t0Esv+PXRtuL3YWglOM7pROly+tmXZR9orDllWM9X9zIyKah7xtB4YEs4gbHktaIEF1tLReo5rk4SdB1h5wr5ZUjhDbRUXTKdUdoSRSRsvMxplahGRzjVvsygGgwYVh1Ct3sni6PNaUWUbz0OGFPDaMyo5Skx9eh9leRMMv1uVyBaLRQ9PwG1H0i8bpmEKdTDaSkmy89n3TSREykY2LrA7f6sWB5OXuSagLXH1eWk5NXBXLXSnUAlgPnqXh1LeqZvdHM6ocgk6G9bTCaGDl89SOcSbPr/jgSrzSboawcNvwBCxaDue24bB60MS5/O/R5YJAgCNpqbsoY4CSwCrjYJTQXWAl2Mq8gCJurj68HxguCEFCduRkPrJfsaeg/gOvqj6+ed051d9Eg7KUptzQ7rrzARe6YsDZmmJrKKpHvf7VzTmw2icfnl3Db9Vq0XnXfpl9/szBnbAznXryd9Bdu58JLdxCn96Wo0khWaQUnc+xdRueKyjicWUBiZCMXFNEGPk7WoksqYMV+eHYRPPo9PLIAnlkIS3ZDgXPpaXWEjs4LriXthS2U7jzv3LpuwK9/JBG39iLtxT8Y+OYE8tacRqvXsuOdP1t9Ld8ZXSn/LRmxFo9GkMvQjEpwO+sS2CfCTtAdGN2oEJ29Jbo2QTeM8sM5TpXi3Mu4NF4qkkQJS3K+y47QUl4h6LRU7bzQojbo8pUn0QyIQukqv0aSyJq/jeB7+qMI0rL/jhWUqwTiBkfjFeVOC7CT61psFL+8CUWUH7q7BiIogzGYgpn7VB5dJ56j5+TznDhj5sUHHQv5hQYpWPSvUJ54s4BO48/RZcI5tu+rwjeoLwjO34hIkoRx5RGqvt2N9olxqIbF1zx5IhmW/wYWJ/lhFiukn4cflkAbctk8+P8DSZL2YCfRHgSOYo8HvgDeAMYJgpACjKv+GSCcauMrSZKKgPnAvurHy9XHAP4OPCYIwhnsnJevq4//DqQCZ4Avgfvc3Xvb9hj+N0I7HVjS4LAgCCz/Moj7ni1m/odliKLE1aO9eO2pmsBi804TUQOyyC+yofPy4bbOeQyOsafXZ/bqwKKDKfx463hu/3kjRqsNpUzGV7PG4OfVSJ3ePwT8m3HOzS+DhTvhVDYggbXWl1KlGf44AdtOQlwwzBoKUU2rpnp3CabjJ1NIvm813RbfgLaze742zSH2qWEcGP89epuEOlBL1MB2bHlvO12mdyOki/slifpQRvmi7hxExZZUdJNqSgvqMR0pfWYN2lv6uSzIpvLT4BWhQ6dVk5ecj8lgQl2Pa6GK9K2TcVGH6ZCp5BjPl+IV00ww6kbGpalSkS2zFJmPyuUyjZSZC/6BWM+fRN3LPU8hyWSlfPFRQt692uWxpWtTsJUY0c/uSdpXByg+kYe6dxjePmpkbpScnIFkEyl5eyuCRoHfI8MvcYL6XvUEu355uVqMsi5GDtQycqC2zrHBvb3YvjCq5oDgDWH3Or8Ps5WqL3ci5pTh8/JkZLW7xcoNsGSl80HLRVhtcCET/twNo4a6NtaD/zz+A6JxkiS9gL2tuTZM2LMv9TEI+LjW2G+AbxzMmYq9Rbr+cQm4vyX7vYgrL+OinYbhtGNxrHYRClZ/G0zKn+Gc3RHBv18OuNQeOXKwhqqUKDL2RmC6cB0FmZkMbl/zZf/QiEQ+vWEUQ9tH8NdjN5L01E3se2IW4zrXbeUcmRDFmr9NBaUa+o1teq/p+fDKMjieYf9Ssjq4k7KJdqJncg68uRJOOhZNqw2/odHEvjiak3OWYcp2shPGRdiNGKeQ9tqf9PvHCE59to9hDw9jxbxfEVv5jtDv2q6U1jdeDPNFHhOAeW/j0v1NQd8vgtKjuUQmRnBuT8PslLJeqQicb4sWlHJwIeMi2USkwgqEYMeBi9kNfotksyHl5mM6b0LTr51buisAhvUpKBP0qBJca721GczkvLWDiOdHUplZxtGnN3Kh0siEz6ZjKzG6xZVpDpIkUfbxLsRSIwFPj6rboeVzTcsml6lBe5VTp4pFFVTMXwuShPdzk+oELXK5nMTeven2yTv0+urfvLdnB6Jk/6xsPZeK8NqzrE6p+axPXvI9W8+lAjDyx6/Yfz4ddu0l/WwqCQkJrF/fdvYbHrQmLr+Oi8s7lKSPJEla1fyZbY8rL3CReYH2OsBNYSZBC7p7wdsXYrqAzL0vfGRyiG+ijp9TAu/9BlUW53nXJit8vMEe8DSD4BldCJubyKk5y7CWtY0ponfnIGIfG0LmWzvp/uAgKvZmIlPK+OvD1nWw9h4RiyW9GPO5uh1ALSHp6vtEUrD/ohBdeoPn65eKwHkhOsHFdmipsALBz6vRzJH5lOv6LVJeIfjqMO6+gGZIjEtjL81hEyn7KQm/WxNdHpv30R58hsXg1SuU/XesoNJPyaCXx+IX7Y+tqAp5QBO8MDdRvmA/lpQCAp4fh1Bf0E6mgeD5ILixrqCBkLdBaP67wHo2H8Pza1D0i8br/hEN9uHl5UXSbfdy/K6H2Tj7dn4/m8xL27dcej5K58erO7c1uUZGUSETxo7h3XffZcKECa6/Hg88+C/HlRe4APg9BjJ/XO4AEDSIiv5sjPqLrQn/4vCPGiwWFZKr8yiUpB3rzP6R33H+g92UbD/XMHj4dCOY3CDama3w8XoQm492Iu4bgG5AJMl3r0R0wzvHGUT9rT8yjYIALyWlKYUMuDGRba/9QdHZwuYHOwlBKUc3uVOD1mjVwBisqYXYcl3PKun7RlB0MIu4ITGkOeC51C8VAfaWaCc8i1wl57ZFR5GUmYsQHIT5WA7q/u2aH+AAlX+mI/PToO7lmoaU8XQBJWtOE/bYEFI/209ZWhGWcG/63jcQySYilpuR+7Vu4GJYehTjznQC5k9wqDMj2WzYDH0Rlbe7FrwIGgh+Ebybz7aYd56l8p1NeN02CM20Xo5b1yXpUndQiLcPX0yazkcH/rrEneoVGoafWs3GtDMO18gxGBi/4AtemTiFqVM9cv//U/gvz7j8N+HKDFzkegj5pTp4cTZjogFlV2QhX+LbJxJzbgW5v59j17taqgoFJCfutkAApQqm3IWyaxeqkgs59/qfnLh9Gbs7f0DqS9V6J+n5UGjA55sH7T+WF+D1zf0kLn2Zrr+8wJw/vsEi2uvfW7NOM3ndv+suY7Tay0vN7UYQiHt5NDJvFWefWN8mGi8XjRgzvzxIv6eu4ugbfzL00eGsuGspYiu2b/rO6EL5mtN1zAsFlQL18HhMW1wXCAysVtCN7h/Nub/ON9irMkKHOatexiUxHMORHKRmgkZXyblNeRRJZhvW9CKU8c6XaiSrDSm3AHOWGVXXULcE4yRJouyHQ/jd2tsl7RhJlMiav5XQBwdhLKni2HObOVdSwdVfXosgkyGWmZD5qBAUrffVVLkhmcqVx9G/Ngm5f00JShJFpOIibCmnEI8chJxMJHE6hLwOMp2dt9IYBG+QBULYR+A7s8n1JVHCuGg/xl8O4v3MBJT9mshw1QpcANoHBCJKEnkVNUKV/xw6ild2ONZGmrP6Vx7oN4jr4zs3uScPPPhfxpUZuAAo20PoelD1qL7Daizw0AAq0E6FkCUg09Dji6nINPYUr6lcTmrmEIRew+28FaUDIq5cYX+07wY3PA7tOhF5Vz+UQVqQwFZuRqaUE3pdN/v5G480ECiL9w0maebzHJ35AhkVxSxJPdD4azNZYP1hp94GQS4j4aNrMKYVc+GtHU6NcRWaKD86zB9NwZcHiBjVHnluBZYqC/u/2Ntqa6ii/VF10GP4o67wnHpMR0xbkl1WDVb5atBG+SIWVuIT7E3uibpSBnI/DdgkbLUyZcpAL5SBWirPNJNNcjXj0oT4nCW1EHmkHzIv50ufUl4BQoAvxr/cF50zHshEMlnxctHbqGTlKSSLDf9ru7D/jhWYw7xJfKTG+bm1y0TGXemUf7uPwFcnNnC9lvJyENPOQHnZJcEmWVg46CZD3B4IfR3U3QEZCGr7Axlo+kHYexC3C7xHNLm+VGWh8v3NWFPy8Hl5CvLopsnzQINsaf37ieHRsQBsP5/eYOjY2Hh+OJZEZUXbKnJ70MpoGwG6/7e4cgMXAEUYhK6CkNXVvBc1doMyL0AJsgDwfQAidoP+nUutjtq4ACJu7glyAVWoD/l/ZJCy1R+yCDpvAAAgAElEQVRx7ssw6nqI7AABIeAXBCHtoN84uP0FmHwX6MMAEBQyop8YisxLYVdSVcgwF1TY77YOpjfqHC2XyRgQEkdmRTMaJam5UGFs+pyLc3op6fzdDApXnybnhyTn3jsXEXZDd7QJekKCvEldfJSRjw5n83MbKHGgTOsuHCnpKmIDkem1WJKaJy3Xh75fJIUHHAvRCYLgOOviBM/FVXJuU6UiixuO0FJmDoSFYNx3Ac1g9/gtZT8k4XtTokvaL9YSI7nv7SLiuZGc/XQfFTkGSgQbg5+uufjbiquQB7YOMdd0OIvSD3YQ+PIEhx5MQkgYaGtlVZRKBE312oISfCZBu+XQ/gjEbIGYrRB/BKIWgvfoZjktYl45hhfXIPPX4v3MBGS+TgZktUjDqcVFyGUCId51sz/PDh3Jq7u2Nhj61ODhDIxox/WLF2C1tr7Vhgce/Dfgyg5cLkLVCfRvQ9RJiNgLYVsg8hBEJIHfQyBvSHzs8M8RaGP96btiNkN23UX5sTz2TPgRA7Ew80G49VmY+xzMegIGTgRtw1R/2OyeyFRyQmf1oNv3M0l+8Hcy39+J1MS1wGi1sCcvlYlR3Zt+TXI5lDkXuAAo9Vq6/HgdGe/vpmjj2eYHuAhBEOj03kSK152h+539Of7WDgY9OISVf1vWaiUqn1FxmM8UYj5f1xhTPaaTWyRdfZ8ICvdXC9E5IOg2xnMxNMNzcZmc24T4nPlUHkoXWtolqxUprwhLvg1FtD/yQG3zg+rBdCofy/kSvMd3cGlc3ge78R0fj1Ul58TLW0kvKufqr2bWcX62FVfVKee4C3NyPiWvbcH/H6NRJjQiOWA22R9e1esFNFJuk6lBEQKKoOqsS/OwnsjG8OJvqMZ0RnPHYASFkyVpQbhExs+vqOCedSt5oO+gBuW48e0TKDZWcTi34Wft/XHX4OsfwLx589rU4sODVoYn4+I0PIFLbQgKkAeCIhJkvjSq4Q+o9FqGHboPXdcQ1KE+9F58A+3m9WXfpB8598neZnkOADKNgj5/zqPDG+PxHxpN4rpbKf4jzSH/4WxZPolLX0b/w6NE++jpqY9yMGPt14K9hdoFaGL96fT1dM4+vo7yQ24JGjYJlV5L5/cnUbnqNAqtkkAfDYbccg4taKLs5QIEVTVJt54ysHpYeyzHshGLG2p0NAV9v0gKD2YRNzSWtF0NCboOW6J7h1PWzHvnCjlXEiXE/HJkTbRCq1wg5ko5+QiBfhj3ZLgtOlf2UxK+N/Z0SR+n8mguZZtTCbl/APvvWIEY70/Hmxo6P9uKjcgDW1Yqsl4oofiFDfg9MrxRfRrJaERMOYUQ2Q5Z524QEoYsqHX0hUybTlH5761o77sK9fguLnGAqoxGEr/8kG5ffMDYhd8wPq4DLwwf7fDcZ4eMJKO8tMFxQalkwY8/kJ2dzVNPPeXcwp4A5z8PT+DiNK48Abo2giAIRN3Wm8DhMRz92yry16XQ/ZMpaKKaVhNVh9VckNQRvnRdeAPC4z80OO8ixyW7soSRa95l1bkkpsY00YYqSqB1nXSp6x1O/LsTOT1vBd2WzsIrLsDlOZpC0PgOFIxJQZ1rIOn1P5n0w0yWzF1CwoSO6MJdl0uvD98ZXci8ayX6e/tfurAKXkpUA2MwbTuD13TnpeQDe4dTciSH4AQ9FQUVlOeWowut+X05aon26RlKxcl8RIsNWSMXdlfIuVJpJYJGieCAwyKWmxALK1FEO+8ELGXmQkQoxl1bCXrHde0Sy4VSjAez0D8z0vk1bSLZ87cS+tgQUr89hKncRHapgTtfub3BubbiqhZpuNjyDBQ9uw7dHf0bLYNJpuqgJTwKmd6erZJHRTs81xVIVhHjD3uwnsjG+4VrkIe5/nm22Wyw/zD8tqGBfP/ImPaMjGl/6eepHbsg/ePVSz9vveVO+3/8dKjax7Jhw4bGFxKNULkayj4H6znADChBHgK6ueB9I8g9DtMe/HfCk3FpZWjjA+m/bg6BV8Wy+6qvyV5yzKV0rUynQdD7NPp8uNafN/pfy+tJ65qeSCED/ya6IppA4Lh42j02hFO3LsVS6FqWwhl0mD8Gy+kC4sZ34MwX++l390BW3beiVdLaqtgAlLEBVGxLr3NcPbYTxk3JLq2h1Knxjvaj/FQhsYMbtkWrInyx1BPwU/io0bTzpeJUQRMTO18qaqqjyJycj7KDvq6QWlNzWSxIBUXYymXIdCoUUa5fmMoWHkY3oysyrfNk4OJfjiOo5Mg66jn1xnbSiwxM/HyGQ+fnlpSKbCVVFD6zFu30bmjHOTZolEwme9ASFoEsqPVUo8VyIxVvrkcsMODz0mSXghZJlLDmG6j68yxln+2k4JNjSHI37ymVShg/sqnFoOQdyOwNxc+DNQV70AJgAVsmlL4PmQOg4DEQW//v3wNHaOVsy//zjIsncGkDyBQy2j8xlL7LZpH69k6O3L4cS5ELLtATekJ9gaxamB6bSKXVzPZse5vv5qxTRP381KXH7oI0GNWtDsnPVYTe0gv9lE6cum05tqrWNW5T+NiNGNmfTdHRXOJ6RVCYUsCxJUdaZX6/a7tQWp+k2zEYQS7DeiLXpbkC+0bYhegGx5Bej+diz7g01IjRJYZjaEJBV1DKGnSNNQYxtxxZaOPEXFccnaXsfISgAIx73PMmshZUULklFd11zfCrao8prCT3oz2E/eMq9t+xAnnPECJHt6f9BMeBhbulIrHCTNE/1+E1PA6fa3s4PEcyVwctIWHIglvPdsKWYXd2lscFoX18DIILmU5LaiEFM7+h+K7FGN7bimndSaSiKixXTwG1ixlTpRKG9IdujbRCSxbIvwPKv7JbGziwN7CfVwWYoHIN5EwFm3tmpR540FbwBC5tCN/EcAb9eQfqMB27hnxJweZU5wYOSgBJwnC7XZ8lVhfEsetevPS0IAgcnvk8w8MTGBnRiao7PibjprcuPQaHdYARXVu8/3ZPDUPTPoCU+9e43E7cHPwGRhF5Sy8iowP46/G1TPlwKr8/spqKfEOL5/Ye3R7TqQIsGTVlHEEQUI/tiHHzaZfm0veJpOhAFrEOFHTt5NyGBpe6xDDKkxon6No5Ls69n812FLlCzM3KRYgIw7gz3a3ApXzJUbwnJLiUEcl5dxf+UzpxftVpRFHi7PFsxrzXeInKnVKRZLJS/OIGVJ2C8Znb1/E5ZrM9aAkOQRYS5tL8TcFy8AIVr65DfW0iXjf1R5C59pUqjw4ApQKQLlHqZF3CUfXpAPfMBW9t9fNNQBDs54waCuMaac+WJCh8FEy7qwMTZ2ACazrk3QyS80R/D9yEJ+PiNDyBSxtD7qWk8xvj6P7ZFE48+Bsnn1iPrbKZDIZG1WzWpVGo5DA4Afxd7xapD0EQiH97AmKlhbTnNrd6h0Lc34ejtkoExPiTsyaZXjf35reHV7d4Xplage7qjg1JuiM6YNl3AbHCeYsDfb8ICg9mETOgHZlJWVhruVDL9V6IlRbEer9PXWJ4k+RmlzgujZSKJEmq7ihyLnMgmS1IhSXYrCpEo7XxTptGIBpMGFafwneW8xyhioNZGHafRzM6juT3dnG+rIIx709Gq2/8s2krds2nSLKJFL++BVmgFt/7hjgkwkqW6qBFH4ws1DWV30bXlSRMq49Q9c0utI+NQTXctQ6rixCzSuv5RAn4P11Nxg0JhsfusQcjOh9QKaF2YKRUgkIBvbrB3XNhxJBGGwqWL56PEPwxp1LsGcL0C1a8Ol4gcVI2XcdkMefRAiyWmr/vvUkmRt6YS8KIc/QZt4VrJvbj6NGjbr1GD5yAR8fFJXgCl8sE/cg4Bu+8E0txFbuHf03pgaymB0zpCz2iXQtelHLEqCD2vbiPY8O+JPvdHVSdzHOqw6kxyFRyOn4xjfJ9WWR90nqCcRfn7vrpFLwyykn5IYle13Ync38GJ1Ycb/Hcftd2oWzVqTpcEpmvBmViJObtTma+qCboHs1FqVYQ0jmECwdrFIkFQUAZrsNcr7PIp1sIlWeLGi2xudIO3Zj4nC3fLjAmD3aOxyRl5yEEB1aXiWJc0l8BKF9+Aq/B0SjCG7ceqLOetYaQe+DeNXgNiUKXoKdrM4GPrbjKaWdoSZQofX87WEX8nxjhkOsjWSz2oCVQjyzMPQfsBnOarVR9uh3zX+n4vDQZRYLrZSdJkqj4+QDFjyxH8NeiHN0JAOXwDsj9ar1+jQaGDoS/Pwi3XG/nrwwfBGOvgsnj4emH4PqpEBHa5HoLf/6SYf3VLFpdI0wXH6MgaW04RzeEk5FtY8kae+koN9/GDfcX8NqT/qRsi+Dg76E88zczZ8+4rkDtgQdtAU/gchmhDPCi59fT6fCPqzh0wxLOvrEd0ZHjM9jvnO4aDcM6gVIOTV1oBMEe4CTGIj08EckmUXmhjAsf7uHopB9I6vIBVcdd43bUhsJXTefvryXn+yTy63FHWgqfrsHEPzaU0HBfdj/8G9M/n8GaB1ZS5WLrcn2o2geijPKlYntdQq16bEeMm5zXdFH6qPGO8afkRJ5dz2Vnet11HJSLZBoF2gQ9Fcfrqu3WTOpcO7QkSfZSkQOOi+VUHspOwU632kqZuQiRoRh3ncPLxTKRZLJS/ssxfG/u5fSYwp+PIA/Ukp2Ug+Cl5PjOVCZ8PK3J/db4FDWvlSJJEuVf7sGaVUrAP8c6bM2WrNVBi38gsvBIp/feFMTiSipeWQs2EZ/nr0amd50AbyuqpPjBZVT+chiv63sT+O8Z+D80HM2NffF9YIjjQYIA8bH2oGXiaBg1DPr1Aq/m+UCGkpPs3JvN128Fsmh1w78ruVxgQKKazFz7Z/KjBeXMnenNkH41v4dh/RVMn9i6HYYe1IMn4+I0PIHLfwBhM7syaPsdlPyVwd5xC6hIaUQiXibArCHw7HQY0tEewGiUSCoFNglsIkhyGfRvD09OhrtGI/dSoZ9ai5wngSiToW7vhNR4E1CH6+iy4FrSX/qD0p3nWzRXfbS7bwBB0f7YSoxUHMun6/RurH38txbP60hJV9kjAslgwpraRNdPPej7VgvRDY0lvV5nkV091wFBt1fjPBenlXMN1SUt74YXcvPpfKcdoSWTGam4FFGpxZpZiqqna+USw9pkVJ2CUDnph2TJM5D/2T68r+3CmX/vIctkYviLdufnpmArNSHTqZzqkjIsTMJ0KJPAlyYgaBpmJSWrFTHlNIKfP0IrBS3W1AIMz69G0bsdXg+MQFC7Xsqt2nia4rsXYys14f+vGfjMrvF68pmViEztpmt9E1jxy9tMHKGlY3slgX4yDh4113neaJTYc8jExBH2IOh4soU+3esRg6UKMPzS6nvzwAN34Alc/kPQRPjSZ/ksImb3YO+4BVz46kDjHJKIQJhzFbx7C9w5CuGmocjmXkVxfCz7d1VR3LE9xNRcxCKfGEptw2q/XqFNZ2ychLZzMB0/mULyfaupOJnf4vkuQpAJdP10CgFmkQMvbGbIg0NI++MsKetdV7utDZ+x8RhP5NfJiAgyAfUY17Iu+r526f+4aun/2r8nuwidA4Ju78Z5Ls6WisS8cmShvg6zFK50FEnZeQihekx7MtD0b+eSgaFkEyn7+TC+tzShGVQPOW/twP/arhz+5xZ8J8YjqWT0uXdgs+PsPkXNl4kq1pygamMKga9OQqZrGNRJVivimVMIOl+EiCiXBOAag3lXKpVvbcBrziA0MxJdnlOsNFPy3O8YPtmBYkh7gr6bhTLm8mQwFv6yg1lT7UHJrKneLFxlLxedPWclcVI2+sQMoiMV9OziuItp4LQcuozO4uF/NKEL40HL4cm4OA1P4FIbFWbIKIOzxZBtALNryrOuQhAEou/ux4ANc8j84TCHrluMKafh3fslaFTQMwaGdEQY1omgZ8aR8PEUTt+/hgv//uvSBVUT7Y8m2h8EiHpyKCUHs0mZsRBrK2iy+A2NJvbF0ZyauwyTg0yDu/Bq50e318fj76Nm/zMbmPbFTFb+bRlGF2wL6kOmUaCbmEDZylN1jqtHdcC8MxXJ5JyXS2DfCAoPZOLfzh+ZQk5hak2GTBXhi6WRlujyRqT/nVXOFXMddxRJNhFLSoHzGZfMHISIUIy70l02VazcmoZcr0XTy7ksjWH3BSqTcigsqkQZ5EXS2pOXnJ+bg1jSvMFi1R9nMSxKIvC1icgdkHwlmw3xzGkEbx1CZLsWBy2SKGFccgDjkgN4/2Miyv6ORe2agulQBkXzFmE+lY/uuYn4P+aYj9MWKCwsZMv2NO78exGxQzN5+/MyFq+pRJJqOC5ntkXw1yETqzbavx+6dVRy8FhNVmbPyjDmP+5PaZnzpHYPXIVHx8UVeAIXSYJjefDqDpj3Gzz9B7z4Jzy5GW5fDV8dguzWu0A7gnfHIAZsmotvn3B2D/2anHrdME3Bf1gMvdfNofC3ZE7OW4G13P7lkrBgBt1W3UzEA4PovORGDOklnL7mB0zNORc7geAZXQi7rTcnb12KtRW/zMJm9yBmaAy5f6ajNNroMLYDG59uRmivGfjO6ELZilNItbhE8iAfFB1DMO9Oc2qOwMQwSo/nIVnFBvL/ykjHpSLvzkEYM8qwGhq+P852FUn5jjuKrOdLkOm1DrMNDeYwmpBKypG8dZhP5qHu14xVRO2xkkTZj0lOc1tEs43sV7fhPbMbaV8fJA8b/R4aSlAX5zJDzWVcjPsuUPb5bgLnT0ThQGX5UtCi9UaIim550FJlofJfW7CeynXe2bn2eIuNsn9to2z+BoRoPUHfzUbTp3XKVs7i119/Zc6sAZzb1Y70nZFc+CuSuHYKMnJqgvbwUDlv/N2f1z+2Zw7vn6Pju18r2LW/5rNbaRRx1qfJAw/aGld24JJZDg+shzd2QVIuWEUwWqHKav/XZIONafDYJnh9l/1YG0GmlNPh2REkLrqeMy9t5ejdq7CUOpdtUEf60nPlTSgDvUia9D2VKYV4xQXi3dOuV+GTGE63tbditoqcnrkIw86GvjuuIuLe/vgOiuL0XSsRWykzJQgCXT+8hmCtmu13r2D0i+M4tfoEaVvdN31UJ+hRhvtQudN9kq7SR413rD8lx/OIG1zXKVoV0dBoEUBQyPDpGozhsANStJM6Lo2Jz5lP5TmfbcnKRQgLwnQwC1WPcGQOrAMag3FvBpLFhtcQ57IMhQsOoYjQceKTPQRd35WyXAOD/36V0+vZxeccBy7m4zmUvrONgOfHoYxrGEBINhvi2WQEjRdCu5gWBy0XnZ0FnQbvf7jg7FwNy9kCiu5ajHHbWbTzBqN/8xpk3q5bcLQUCxcuZMaMG0Co2f/MSVpe+6hueXP6BC8qjRLb9xoJC5Gz+KMgnnmrhA5XZTFkRg6//m7mgXtvvdzbv7Lgybg4jSs3cEkthqe3QF4FGG2XHFkbwCbZiZRHcuGZP6A5DZYWwr9/JIN2zEPurWT3kC8p+jPdqXEytYKEdyYSde8ADk/7iYI1dYXWNDH+dF83F0Gv5czfVlG8qGUqtYIgEPfyaOQ+Ks4+vq7VNF5Uwd70/XwaSrONY29tZ/LH01lx1zLMFebmBzcC32u7Urq0bhZL1TcaW3YZtsyGJnWOYCfoZhJXT4hOEazFVlKF6KDs1BjPxU7OdYbj4rhUZOe3OBe4iJm5CJEXRedcK3OU/ZSE782JTrVOmzPLKPj2EGVqBV4x/uxbepRJX15bx/m5OdhKqpD7NwwQLKmFFM/fhP+TI1F1bdj2K4k2xNQUBJUaITq2xUGL9WSO3dl5dCe87hzivLMz9jKe4Yf9lDy1ClGhIODT6/G+pkuL9tMSbN26lYlTHgJZTbD30O061n4fwrGNNeU/QRA4vC6c4QPs7/+gPmq2LQnlzJ8R7FoexqpvIug3/PHLvn8PPHCEKzNwya+El7bbMyvOXm8tIuQY4LWd9mCmDaHwVtH1/Ul0eX8SR+9ayel/bMLmZLYn7OZedP/5elJf2ELa/K11SiTKIC1dV9+MulsI6a/8Sc7r21qkiCvIZSR8dA3GcyVceHOH2/PUR/CkBDpP78bpr/cTHB1A1MB2bH7OfWKgz7h4jEdzsOTUqPIKChnqkR0wbnYu63KRoBuZGEFRWjFVpXb1UUEuQxHmgyW7oeJvYzwXZ8m5jYnP2TuKmi+/SFVGKDeAnx+mA5loBjkfuJhO5mHJKMN7XLxT52e/sR3lsGjO/3qCYm85XWf1InJgO6fXA8elImtWGUXPrcf33sEOy1ySKCKeTUFQKhFi4loctJi3nKbywz/wunc46gldXZrPlldO8UPLqFx2BPXEbgR9fh3KMOd0b1oTp17eyoE5S9kzcxE7xy9gQ/y/yD80AQR3zSvloJ0GssY91DxoITwCdC7higpcBEHg8ccfh0XHocrCO8krefHE4kvPf5G6kc7rH6Lz+ocYsOVpdhTU3KWP3PY8ndY8QK+Pb6d/j94kJSW1+X6Dx3dg8K67qLpQyl8jvqHsSOMy8rWhSwyn94a5GA7ncGzWEswFNaRcubeKTj9eh++YOLJ/PsqF+1cjVrqfzZB7Ken83QwKf0sm5/vWe0+6vT+JYL0Pf8xazMR3r+HIosOc3+1eiUvmpUQ3vgPlK+tmXTRjOmLamuJUEKHvG0HhgSzkSjlRfSNJ/6umJdxeLnLUWRTWSMal+VKRVGVBMloQ6snri0YrtoxSlPHN8y3sZaIQzEdzUMYFuqRIW/ZjEr6zezqVbSjflk7VqXzOrj5NxB2JZOzL4Kr5Y51e6yLql4pshRUUPbsWn5t64zWiYQAliaI906JQIMS0b1HQIllFqhb8hen343g/fzXKHs5zUSRJomrtSYrv/xVLQRV+r03G966Bl42AWx+5vyeT8fNRclaeomBLGlUZZchDZ4MsGHA+e3QJghb8Hmr1fXrggbu4ogIXtVrNsqXLKPjjBNS7bqzJ3s/naRvZMfIVTk34kM96381Nez8gx1hjMPbTgIc4POYd7osbz5NPPnlZ9qzSa+n1/bXEPTKYA9MXkvbeLqeyJEq9lu6LbsCnVxhJExbUuYDKlHLa/+tqgm7pRcGO86TO+gVLrvseQcpALV1+mEnGB7sp2nDG7XlqQ+GrZujCGzBeKCX1u0Nc88EUVty5FIvRvVKd78yulK04Wee9k0f4IY/0x3zgQrPjAxLDKTmeh81sJW5wbB3Dxca0XLzaB2IprmrgsC2oms+4iHllyIJ1DS7GljMFKGIDEJwowYgXRed2nnOpTGQ5V4IxKRufyY2Y9dVew2gl67VtGIK90XUNZs/CJCZ+Nt2h83NzsDtD20sVYrmRomfXoZ3QyWGpRRJFxLQzIJMhxLYsaBENJire2oCYU4bPy5ORh/s5P7a0itJnf8Pw5W5kPdsR/N0s1E6SkdsCkigSenXCJTkEmUZBz4+uIbB/AoQuAVkA4IL+jKCFkB9B4Typ2wM34cm4OI0rKnBRKBTcPWIm7yc39MN58/QK3u5xK0Fqe2q+T0B75saM4OOzDbtaBgvtyDzX/MWutSAIAhGzezBo2x0UbE5l36QfqExr3rFVUMiIe24k7V8ezbGbfyHnp8N15mz39+FEPjWc0rNFpF6/GGMLtFk0sf50/no6Z59YT/nBxn16XEHA0Gh6zu3DgRe3EDM4muAuwWydv8WtudQdg5AHe1O5q+7vTTOmIyYnSLpKbxW69gGUHMuzdxbVyv6oInSOCboywS5EV79cpGi+HdpeJmpcMbc5SJVVUFEJgf4Y/zrnkqli2c+H0c3s5hSRN/+rA1j9NeRsTccQ5EW7q2JpPz7B6bVqw1ZchTzQC9Fooej5Daj7ROJ9Y8OOJkkSEdPshG1ZbDyC4P7XmC2zhIrnVyOPCUT75FiXnJ1Ne85RdM8STKcK8H5oJIHPjXWJ/NyakCSJvPVn2Nr/c/I2nCWgfyTIBPRDo4m9q9p4UhEO4WtBGW8PSGgi2BO8QRYEoctA7byGjwctgCdwcRpXVOACcH/IKH5K+5NSS0Wd48fLMugb0L7OsX4B8RwvaxigrMs6xPTeo9p0n47g1c6PfqtvJmRqZ/aM/o6M75OcIsUGXdOJXituIuPTvaQ8vq4OkTR0TiLt35uIobCS1LlLMWx1rkXYEXwSw+nw3kRO37mCKicCK2fQ4/1JBAZ7s/X6RUz+aDoHvt5H1sFMt+byc6CkqxocizUlH1tB8xmnwOpyUeygaM7tOY9Ynb1RRvhizmxYKoJqnks9Bd2LyrlN/e4uis/Vh7OKuVJmLkJ4CJbkAmT+XigiGs7lCNb8Ciq3paGb2b3Zc03nSij4IYnz+7OJfnggp1afZMy7jTs/NwdbsRGZTkXxy5tQRPmhu2tgg0yKJElIaakgicjiOrjsxlwblqQLVLyyFvW0XnjdPMDpucQqM2Vvb6Hs7S0Q5EvQF9ejHdm++YFthOJ9mewa/z1HH1tLp+dGMnz7PHp/OwNdl2D6/jiz7nsoD4Gw9RD8DWhGAioQdLUealD1Av27ELkHVP85YrEHHjSGKy5w8bUomRM9gg/P/N7suZIEQq27kpv3fkjU73fz5snlPDhmdltus1EIMoHYBwbS77ebufD5PpJm/4Ipv6LZcdqOQSSum4OlpIrDU3/GVOtCGzAhgY7fXYvRZOP8UxsocjIgcoSAsfG0e2wIp25d2qBE4g5kagUjlt1EwYEsctalMOGtSSy74xesZtdb033Gd6DqUDbWvFokXbUC1bA4TFuaN5DT942kcH8m3npv/CL9yDpqzywpIx1nXKCa55JUNwMlyASQy+zt942gMfE5ZxVzxcycmjKRC6Jz5YuP4D0xAblf0+2/kiSR/eo2ynw1BAyIZO9Phxj73tVNOj83OZ9VRDSYKf9iD4JGgd8jwx0HLempSDYrsvYJbgctkiRhWnOUqi93on10NKoRzmeIzCdyKL7nF4y7zqGZ2Rv9B9ORB7nuV9QaMJwpZN/sX9g7cxGRN3Zn1OH7iJjeBfXsL2sAACAASURBVEEQ0HUKYvTh+1A7MuEUBNAMhpDvIHIXBH8LQR9C8FcQvhnCVoF2EghuuNN74CY8AnSu4IoLXAAeSbiGr9O3UGGtEVjq6hvFgeK6rsEHS1Lp6ltT2/1pwEOkTfyEm9oN5/6v51+2/TqCrmsIA7fcjk/nYHYP+ZK835svdyh81HT5ajpBUzpxaOL3lNQyINT1j6TLr7MwC5D9+T5y5m912sG4PkJv6YV+amdOzV3WqEOyKwjoF0nPO/ux8/7VdJ3eDd9IP7a/uc3leWRaJT7j4ilbVa9VfEwnTJuTm+UO6ftGUHTQ7urdfkgs6dVCdKoIHZbGMi69wik/5KizqGmCriPxOVtJFWK5CUVU0xwMyVAJRpO9TLQrHc1g5/gttjIThjWn8W3GwRmgbNNZio/lUXgyH3OsL36xAXS5sflxjcFaUoXKT45YZiTg6VENiK2SJCGdS0OyWpDFd3Q/aDFbqfpsO+bdqfi8PBlFx6ZdlS+Ns9gwfPMXZS+sxSrKCHhnKrrZzrWKtzaM/8feeYdHUXBd/DfbN71XCKEFElqA0EJv0kXAAiiICvbeK2J9X8unWFGwASJIR7o0QXrvJARCSCW97G6ydeb7YwNJyO4mgYD6mvM8eYDdqUt25sy9556TrefYE2v5s+d3eLcPZmDCE0RO7YysDmPbVyAPBE0X0A4ATXdQ1G0SrAEN+Cvw7yMu3mr8VJ7c2Sie71Mq9BIvRo3mpZM/k2+yPzkfLbrATxf/4NFmQ6usrpQpeDf2bvaeO86ZM7V3uL0RkKkVtJzRnw7zxpH48iZOPb7minOuMwiCQOPHu9Hqq5EkPLKa9K/3XamuaFv6E/Pb3YhuSvI3nyftsTXYatieMzR+oSfaFn4kPbqmykj2taLTFyPx8NGw4/ZFjP5mDHu/2E32ydpNWVWG19gYSlZUFekqmvkjeGmwnHCtzfGLDaHodC42k5XI+CZc2JMCgDLYA2t+qUOip27shWS1YbrKfbmmkWhH5nOWxFyUUYE13iylTHubyJZWDFYRZYvahSPqV5xC27MJihpGeMVSCxnv7iAzrZgWr/Tm8PcHGPLVrdclkNXPO4RMIeA7fXA14bEkSUipKUhm03VVWsTCUgzvbQCLDY83hiPzr914rzW10D7mvDYBeffmBH13B8paBk7WJyw6EwlvbWNru6+Qq+QMOPU4Ua/0QVEHXU4D/sZoqLjUGv8+4tK3CWjkPNdyFHnmiqfkW8O6cH+TAcT/8RqtNz7JtMPf8HOXJwnVVg9C08pVPPfU03z88cc388idwrdHY3rsmgrAnp7fUbinFlMyfSKJ3TCZ3FUJJDy46oo1vSrYg+hlE5CHelGSlM/Fe5ZiTndcTXAFQRBo9uEQRKOVC9O3XLdBnSCXMWDl3aRuPU/JoUwGvXsLKx5Yis1at6qQJjoQuY+G0r3pVV8fGIVpc6KTtexQuKnwbO5L0clsuxHdrhT7sSnlKPzdsORUb9kJguBQ54KLvCLJbEUqKUPwq1rmNyfmompds75FzLiELDz4iulcbQiFaLJSsvRkrez9c77ZT57OROCAZuxfeITeMwbh1dh18rMr6JedwHw4A8L8qrnLSpKElHYRyVhmr7TIr6GqANgu5KF/cw2KDo3QPtEPQVOziFYSJUpXHKfohVWYc0vxfKE/vs/1uaZU6OuBaLaS/NU+trT+HENyIf32P0jb/xuK+i9qUTXgBqDBx6VO+FcRF71eDz0bgQTBGh9Kb/uFGTF3XXn/keZDSBzyOQlDPufAgA/oExhz5b0/+r5NnG8LAKRWfjx11xRmz/gQW3oBYkYhYi3EnTcSCk81bb4cSav/DOLY5GUkzdhWoxW/ppEXHVbdjcJTzdFh8yktzzFSeKlpNW8smjZB6IuMpExaQpmTwEBXkKnkRM2+Fd2BTDK/2n9N51UZfl0aETO5I9vvXUbHSR1Re6rZ82ndje+8HIl0ezfDciwTsdxYzhn84+xGdEGtAjHpTBRn2p13leGuBLoOdC4qu0DXEaQ8PYK/R7V2SW0miiSdAUxm8Pe16zBqOU1kWJeIOjoIVTPX/jDGcwWk/XCYkhwDtA1AEAQ6Pdy1VvtwhNLfz1K66hSa29ohD6iqj5EkCSk9FanMgKxFq2smLeY9yRg++B3tPV3RjK1dsrMtV0/Ry6sxLDwCEYEEzrkTbR0M/OoDkiiSsfgkW9t9Rfa6JHqsvYfOc8fiFnmDUqUlCUQDWPNAvPZw0wY04EbjX0VcAFAroF8TUFxjWVstpyS/hIz7fyN9/FLS71pC2p2LybjjFyTxr2e5QSNa0WP3NPQJuewb8CO60zkul5dpFLT8ZBjhD8Zx7NYF5JVrZWRqBc0/H4H3wOaUmWykPraGkvU1C1ivhsJTTet5Y7k0/yi5y07XvEIN6DZnNHK1nF3jFzN69lj+/HA7eWfrNsbtObQFZQczsFYSNcvc1ai6RmDa7joXyb9TGPkHMxEEgcgeTUgpH4tWOhmJBvu01dVGdIKLkWgxW1dNmCtJUq0cc6VyUa6Ya8CWrUPVLsTl8mAXxpb8cgyvSa7HXiVJIn36FrJzSol+fyC7P9rB8Dljrrl1Y9ydgu7HA/i9NxSsUhWDPEmSkDLSkAx6ZM2vjbRIooRxyWGMiw7h/vIQlF0ja15HkjBuS6LwyWWYkwrQTIzD/8PhdTLvqw/kbklme485nPtkNx1mjaLH2nvwjq1dQnedYUmF3PcgORaS4+BiP0juABe6Q8G3YCu4MfttQFU0VFxqjX8fcQG4Kwa81C5tDBxCJYcOwXh8OASZpuqFVN3M5y8R6jmCOtCd2IV30PjBOA6OWEDKl/tqJFWhk2Jp+/PtJL+xhZT37FEAgkygyfR+BN3XiVKjlawPdpA/+2Cd2z7qUE+i543j4jt/ULzz+gIeZXI5A5ZM5Ny6RMxn8uj3xkBWTl2GKNZeRyNzV+ExqDklq6u2htQDo+wiXRfn5985jPxygW5kj0iSy9tFrgS6XrEh6I5eqrJduwmd42N2lFFky9IhqBXIXUztSJKEmJGNLDwE456LqLtF1Mq9tXRbMvJAdzQ1kJzitWdJ25tO8KhWHFpynC5PxuPf+trM1kzHMin+bCd+bw9B0dgHW5HxCjmQJAkpMx1JV2KvtCjq3pqRjBZKP9uK9XSW3VQusmZNilhipOT9Tei/3Y2o1eI3czSet7W57hiBuqDoSBa7h83n2KOrafl8T/rsmUbggBs0am0rhIwpkDociheAVApYQTIBItjyofBLSOkDOa+CdO0O2w1oQH3i30lcvNTwdl/7n7UlG2o5tPSDZ7oi16oInjW6yqdnSS1G/9k2JP3fo8QqCAKNJsfSbesUcn5L4OCtCyhLcx0o6NkpjNgNkyk5lMnJCUuujDOHTosj4o2+GIpNFKw6w6XXt9Q5EdqtVQAtvx7J2cfWYDh97UZ3AMF9I2k+pg3bJy0lbkpnJEli/9d767QNu0j3dBVCp4gORhJFrInOq1S+HUIoPmMX6DbrGVlRcQn3cuieC3bdkNxNifFixecvKJyLcx2Zz5kTc1DVRBJ0erDZwNebst0ptWoTSZJE8c9H8brHdbXFpjOR9OpmDEYr6vhGlFwsovuLtU9+rgzz2VyK3t+Kz6sDULYMsG+/oAy5r30EW8rKQCouQtby2kiLmKtD/9ZaBHc17q8OReZdc7XEfCiNwseWYjychaJPFIHfjEPZ5Aa1ZBzAcKGQQ5OXsXfUAkJvbcWAk48TfkfbG0eaLFmQOgrK9pcTFSfTf5LR/r5uNaTfDaLrVmoDrgMNFZda499JXABCPODjQdDKD1QykDu5QKjloJRB/0iY3guU9kqLKioQ3/s7AeAWG4jXw90p2pBC1h0LMHy9429DYNya+tJl/SQCBjRjb58fyFx0wmVFQRXoTrvFd+HRNogjQ+ZecX31Hx1Niy9HosvUYUjKJ/2hVVgL63YR846PoOnbA0m4dzkmB9k+dUGvn8ZiEkUOTFnBbd/dzra3NlN4ofYlbXVMIDIPNWX7K0S6giBcGY12BoWbCs8WfhSeyKZxXCOyTmRhLrM4dc+9DLtAt1K7yIU415H5nCUhF2UNwlwxIxshLBhJZ8KSmIu6c8027cZ9aSBKaHtEuFwu86OdZF0sov0Xw/njjU0M/65uyc+XYU0rovDN3/F+ujfqDmFXXrcV2gMWxawMpKJCZC1bIyjq7kJrTShPdu7TEu20nnazPxeQjBZ0X/9JycfbsJokvF8bhM+jPewapJsAU56BE8+uZ3u32bi38GdQwhM0faQrshqO+7pg00HG3WDLwylhuRqSEcxnIOtRkK5/SrABV6PBx6Uu+PcSFwBfDbzTz05gBjW1kxS5YCcyMsH+/l1tYM4ImBprNw2rBM8pcfhM7oDfjMF4jmtH+OrJeNzTiYKV57g0fgGls3f+LQiMIJfR9Nl4Oq+cwIVPdnP83uWYXZjDCQoZTaf3p+n0/pycsJhLC48D4NUzgtYLbkd3sQizCKmTlmJOqZtDbsDo1oQ+0Ikzk5ZhLb72z0bhpqLPD2NJXJuA7Ww+PZ/vw8oHl9e6jSUIAt5joym+SqSr7tcC896LLoMn/TuHU3AoE5WbipA2IaQdTLO757ogY1cHLl52z3UER60ic2KOS8dcuyYk2z5NtD8NdWwYMk3NxOJytcXVk33ZmVwSZx8ibFwbjv12mpjx7QnrWne/D1uOnoLXNuB5f5dq3jK2wjIEyYBUkG+vtCjrTlrM285S+tk2tA/1Rj2s5haPJTGHwieWUbbjArQIIWDOHWg61T5c8XpgNZhJfH8HW9t8iWSTGHDiMVpP74fiGjKe6ozC2Xi0+QOwE+du49KIHZVKRJ8UArsmEzsqldhRqaSkW/DoUEnzJZn4acFmHn/4tht/jA1ogAv8u4nLZYR5wrSO8PNo+GkUfD3M/vc5I+DWluDh2CdBEAS8H+qOPNB+kxEUcrzu7kj46sm4jW1P/uJEsif+QtkPu/8WBMarQwjddzyAppE3e+LnkLfJtRA18NbWtF8xkfQv9pH0wkZEkxW3mCBilo6nNK0IW6A7F6csp3R/usvtXI3Qh+Lwjo8gceqqKvEDdUXk2DaE9Ilk1/3L6TolDmNRGYe+P1Dr9T2GtqRsbzrWSiRO5qNF2S4U885kp+v5dw4j76A9dqBpfCQXdl9EGeqB9ZLeqYmdR4eQKiPRgpOKi2QTkfINCIEVxEWyiljPF1xpqzhEsc4+FeLjZTedq0WbyHQyG2uWDveB1ZOXr+xblDjzyGqMkoTXyJak/ZlCn3cG17jtq2ErKiP/1fW43dYGt8FR1d/P0yPDYK+0KOvmSyLZypOd157A/Y3hKNu7Jh+SVcSw4CDFMzZgzjPhfm83/N8eXKNbcH1AtNpImX2QLdFfoDuZTe9dU2n/2XA0wbXzlLluSBYoWVDlpX3LGnN0dQRvP+XHXSM8Obo6gqOrI4hs5IA8SmYwXb/IvgFXoWEcuk5oIC6VIQigVYKPxi7EvUbI1Aq87+9C+KpJqIdGk7vgNDn3/IJx7p6/nMDINQpavT+ItrNHc/rpdZx+Zj1Wg/PqgnurAGI3TsaSa+D4bb9gyixB3dib6GUTsBQZEcO9yXhxI8Ura2/GJwgCkTP6o/DWcO7ZDdc1jdV3/u2UlFo49uBvjPn+dja9upHidNdansuQe6pxH9gM3dUi3UFRGF20i/zjKhx0m8Y34cLuFGRqBXJvDdZcx5Usz9hQ9CeyrxAbuwFddZIj5RsQvLVVWhyWCwXIQzyRuTAau5wEjdmG6XAGmu6uWz8AxQuO4jWhA4LC+WUgd95R0g5k0PH729j83Fp78rN73YiFaDBT8PoGtL2a4jG2XfX3cy5hKzSi7BCDoKojaTGYKP1wE2JWMR5vjUQe5tpV2JpWRNHzKylbn4Do7UHAF7fhPqzVDRfgSpJE5orTbG3/NRlLTtF1+XjifrkDj1qaA9YbDJuvv9VjKwTzhfo5ngY04BrQQFwcwXoSjD9A2Uwo+wpMS0F0rl9wBpm7Ct9HexC+4h6UfVqSM/cUufcuxLhg/19OYPz7RtJj1zRsejN7e31P0QHnwYUKTzXRP4zBf2hLjgyZR9GuVJS+Wlr9cgeCVoHF343cb/eT+9meWpMQQS6jxRfDMaWXkPrfP6/5PNxCPOny31tI2nYe6XQe3R7rwepHV9S6ZeQ9JtrupFvpuJUdwpEKy7Cm5Dtcx7d9CMUJediMFiLjI0nZnYIkSeUCXcftIqWPBlWgO6Xn7DocZxUXR20iS2KOS32LfQrnErLwEEyHM1C2DEDm5bp6YEkpxHQiG4+RrZwuYy0ycuyl3wkbE83pzUk07tu0zsnPktlK4VubULUKxOPeztXeF3OzETMzEY025AG1C4K8DFtmEfrpa5A19sXthcEI7s7bLJIoUbbmFEUv/YY5TYdyQCsCv7ytxviE+kDejhT+7PkdZ9/bQfuZw4j/fTK+cTenJVUNut9AqjnbzDUkOwFqQP2ioeJSazQQl8uQTGBaDEW9oHgYGKZD6X+g9F3QPweF0aB7Aqx1L5PKvTT4Pdub8CUTkXduSs73x8m7bxGmRQf+UgKj9NHQbs5oWkzvx9HxSzj33nZEJ4JRQSbQ+KketPpyBAkP/Ub6rP12D5hvbkXbKoAyEfR708h8YSNiLfOJ5FolrX+8jYINSVz66cg1n0ebx7qhbebDgafW0m1SJ4ouFnH8l6O1WlfdLhhBLafsYAVxE+Qy1ANaYtri2LdGoVXiFeVP4YlsfMK9UXmoyU3KKx+JdiHQraRzcTYObZ8oqnoDr9G/pagEBBl4edR6mqj4l2N4jmuDzIWD7JmHf8Nkkwie2okzi0/UOflZsokUvr8Vma8Wr0fjq1U1xLwcpOwspKBI5N6aOtkJWI6mY3hnPepR7dDe09Xl2Lctz0Dxm+sxLDmKVZTj8+YteN/fxWWlqT5QciKbvbcu4Mj9K2n2RDf67n+QoFta3NTx6mqwXt9EH4AglI9KN6ABfxEaiAuAmAVFvUH/AtgSgDLAiF28ZgEM9n+bl0DxLVD6sV1PUEfI/d3wf7UfYb/chRDTiJw5x8h/YBGmxQeRDNeWCVQfCBkTTfedD1B8MJP9g+ZiSHJ+UfLt25TY9ZPIXX6ahAd/QzRZiXxvEH4jWlGcWozNZCXtgZVY82r3VKf0cyN6/jjSv9hLwYa6G9wBCDIZ/effQX6pmVOPrmHMd7ez/rm16LNrrpIJglDupFu11aUe0BLTn+eRnGhwLhvRQXm7aFcKynBPlwLdKjoXJ+PQjsznLAk5Lq3+LydBI0qY9qaiiXft8GrN0VO2IwXPcW2cLlO0/QLnVybQ+acx/P7kagZ9OqJOyc+SKFH86Z9gFfF5vm81YiHm5yJlZSBr0RrRICHzqZ2+RJIkTGtPUjZnJ25PD0DVr7pepvKyxh3nKXp6OeZzBQhRIQR9dwfq9jfIyK0cpalFHH5gJbuHzCNwUHMGnHqcRhPaX7NRX/2ibtctrVrAbK5Yp6DYRoCvvGGy6EagoeJSa/wdvkl/LcRLUDQAxFTsBMUVrIARyj6H0unXvEtFiCcBbw0i5IfbESNDyJlzjIJpizAvPfSXERhNqCedlo8nfFIH9g+eS+q3B5y2WzSNvWn/293I3ZQcHTafsuRCwp/sTviT3cnfm468uR8XJy3D5IIAVdleEx9a/zCG8y/+ju5Q5jUdv1+7EKIf7srF41mIh7LoNKUza574rVbreo6IonR3KrZK493yIE8UzQIw73dsmOfXOYz88mNt2iOSC7tTUIZ5uR6J7hiK7tjliosMatEqEg1mbJf0KCIdW/FXTBOFYD6VjTzQHUWw65DEkl9P4D48CrmTdpJkEzk4aTmhQ1pw/nC6Pfn5zuraFGeQJAndnH1YM4vxeX1gtZFkMT8PKTPdLsTVaOyj0H41e61IFhtls3di3nkej7dGomjlPNlZ1JnQfbwNw/d7MZeKeDzQHf/XBiJzIrSvD5gLSjn14u/8Efct2nAvBp55guZPdkd+k7ONXEJeN2+avl21/LzK/jtdZhRZvE5P/27uoLj5IZP/82ggLrXGv5u4SDYoHgtSIXZSUluUgvEnMC66rt0rm/gQ9MFQgr8ajTXIj+w5xyh86FfMy/8aAiMIAo2ndqbrpnvJXHiCw2MWYXRSQZBrlbScOYywqZ05Nupn8tcnEXhXO5p+cAs5axPR9mtK2rRV6GvplOvRIYQWnw4jcepKypKvzWK884wBmBUCJ9/ZRtcJsWSfuMTJpSdqXE/uqca9f9PqTrqDojBudizSDYgLJ/9w+WRRuRFdjV4ubYMxnMlDNNvKDeictYoqiIclKQ9Fc3/nbY2CYlAqELw8ykMVI12eq63EiGFtIl7j2ztdJuG5DZQVG2kyvS8Hv9zDkK9H16m9oV90FNORDPzeGlKtFSUW5CNlpiFr0RpBYycrdvM518RFLCrF8N56pDILHm8ORxbgfArHfCTdbtl/KhvRy4PAr8fiNqhFrY+/rrCVWUj6aCdbYr7Eqjcx4NijRL89AOVNmFJyBdPxTAxLj2PcexFrRrE9pd1jKAhulJZJNOp14crPJz84tjX47PVAlv+uJ3ZUKt3vSOeOYR706eYNbr1v8tk0oAEV+Bs9CtxcXLp0iaefHM+BAwdQqyQiI2TMfNedsVN0nNxZkXQ744NSPNwFnn9cy5TH9Wz6w0zyIV/U6jLy0mYQN/hlUlJSrutYVFEBBM8chenkJQq/2kvOnOO4rzyF+9i2KAe3cSk6vBFwb+lP1033cuHjXezt/QOtP7qFkLEx1ZYTBIHQybG4xwRyZtoqdEezaPJiL6J+GEPS1FUE3dmGS29uxX9qZ3wnOL9RXobvwGY0fr4XZyYto92qiSjrmH6rdFfR+9vb2DFlGYlPrmP0N2P4dcJCmvVvhpu/6215jYkm561t+EzqcOUmreoSgWHOHmxZJchDq+pOfNsHU5KYj81oIbRdCIVpRVjdlS5bRXIPFZoIbwwJuQ7FuZIoIebqkFXSuNTk33I5CVqSJIy7U/B76xaX56lbdgptn0gUQY5v/IaEXBJnHaDrvHH8/tRq+rw1CK86CFgNa05T9vtZ/D8ehcyz6u+tVFiAlJ5q92nRVhCVynb/jmBLycfwyRZUfVuiHhPrVAsjmawY5u7HtDMZi17EbWxbPCfE1ir24Fog2URS5x0l4a0/8O0aTq/t9+PZysXI+k2G7tu9lB7LtT+eSvYfhbdI2OcS4lnHRG7KuKr/Dg9RsGZOWNUXlY1BXf16UAWSGdgEpGFvu3sDnUGo+Trw78T/fpWkPvGvrLhIksSYMWPo16OA8we9Ob3bh/dfcyM7t+a+rVwu8MOC8mqIpAfqrzKibhtCyKzb8H9nMEa5G7nfn6D48SWYVx256RUYmVJO81f60HHxnZx7dzsnpq7CUuRYSOwVF07HjfdSsj+dU3cvRR3hQ/SSu8hbnYiqbySFv54g+787nHqcVEbw3e0JuC2aM/euwObCBM4ZIoZFEdKvKbm5BsRd6bS7sz3rnllT43qaDiEIchnGw1VN4tR9m2PaWr3qItco8WrlT+HxbOQKORFdGpOZWoglU+dyoskzNgTdkUsOx6Gl4lIEjRJBW1GlsCTmOrX6t08TZSOEhWBNLgCZgKKp83Rn0WhBt+wU3hM7ON3evjELCY6PIDNXhyAT6PhQ7ZOfy7adR7/oKH7vD6uWqSQVFSKmpSBrEYWgrfqeWFhh9381LPsuYPjvRrR3d0EzrqNT0mI5m0vhMyswHUjDIirwe28oXvd0uiGkRZIkslYnsK3jLNLmHqXLojvouviuvxVpAdD0Lc84ErETFwG8748Hr3Fc8zOr4Aa+Dzl/X0oD6RUgGLgbeA54GXgSiAepPUgLymMGGtCAa8O/krhs27YNpULk4ckVLYnYdgoah9f8cTz9kIZPvynDapWAUpCuz7reEbRxjQj5YRy+L/Wl1KQk76cTlDy5BMtvR286gfHuHEaPnVNReKvZEz+H/D8c+zeogtxpt2Q8bq0COHLLXKw6EzHLJ1CyLx2a+WE6X0DGU+sQXXjGXEbj53viFuVP0qNr7OXtOiJ+5gjyc3QkzzlIl3HtSN19kcS1CS7XuSzSreakOzAK47Ykh6TLv1N4FSO6lEPpyNyU2PKdRyF4xpbrXBxVXBxNFLmw+pfyC0GtQvB0v2I656qlo1+TiLpdMMpIxzqHc+/vwJBWQsuZQ9j51haGz6598rPxQBol3+7B752hKK6qTknFRYipF5A1j0Jwq175ctQqkkQJ49IjlC04YE927tbU4X4lq4hh0WFK3tmApdCELCqEoNljUUVfW/hjTSjYncrOfj9y5o2txPxnMD233Ydf97q7CN8oiEYLunkHuXTHfAq/2l9xhRfA/6nuuI/rAL6PgszT/mKdoARlJHgMc/y2NB9oDcwEioES7IMOZuz6wVLgJPAI0AqklDru/38YDQZ0dcK/kricPHmSzh1DgeqjoOdTbMT2K7ry883cqlWGiEYyenVXMn/x5arLjUlMFQQBt16RhP58J96PxaMvkZE3/yS6p5fedAIjd1MS/X9Difl8OCcfXk3CS79jczDyLChkNHtrAE1f78uJ8Ysp2JpM9K93YckrxWiVkPlpSZ2yHEuW62kfQRBo9uEtiGYbya9trnMatVuoJ3FvD6LYTU7SM+sZ9fmt/PbICow1RAx4joii9M+L2CpVlhSNfZEHeWI5XN0d2D8ujIJDVY3olGFemJ2kREO5QLe84nK1OFfM1iGrJKy15RnAbEUe4lhse1mUC1C2+6LLaSLJaqNk4TG873YcpliaWsSpd7bT/r2BbH1tE12eqn3ys/nUJYo/3o7v9MEor6r4SCXFiBeT7aTF3XF76upWkWS0UPr5NqwnM/B4Z5TTZGdrRhFFr6zG+Mc5zAbwejge3xf6ujTqu1bozuSy+1MdqwAAIABJREFUb9wiDt69lCYPdKL/oYcJGRH11442V4LpcDp5T60iY+iP6JeewC2+MeEr7sZzqL0l5HN3W9xvL6+0KQIhfAHIPKj9LUAFilAI/wkEB5+vNAs7ISmj5iq0HkgH4kBqMLK7ggbiUmv8K4mLHWbsNdSqaB4p5+gfPld+Hr63egn71ae1fPSlEVGEuo4X1hWCTMB9UAvCFo7HY3IcJTki+QtPo3v25hOYgEHN6bFrKqZLevb2+YGSyqGBlRB4WzTtl08gbeYeLrzzB81njULuq6HweDbuA5qROmkZZSezXe5LppQT9e2t6I9eIuPLfXU+1uiHuiD3UlPmoUTcdpFWw1uz8YV1LteRe2tw7xOJbo0jkW5iteX9O4eRf8hecWnSvQlpB9NRhnq4FOh6xARSllyAJFGtVXT1RJE5MRdlqyCHN0dJFJGychDCg7FmlSDmGVDFOJ+yMWxJRhHqibpt9WUkSWLfbQsJiA5AH6ilJK241snPluR8Ct/ZjM8L/artXyopRkw5j6xZS6ekBaomQ4u5evRvrUPQKnF/bZjDZGdJkihbd5ril1ZjzTciubsR9O0YtJdbI/WIsowSjj70Gzv7/4h/fGMGnnmCiMk3TjdTF9iKyyj+YieZo34i9/l1CJJI0Ae3ELJqCl7P9EPm5473kz0JfKknXg/3rLqyuiU0XgXKJvb2j9PqixwEDWjjIGKl46kkaSvwPPaKSm0hAkVAf3uAYwMaUAf89d+++oQeuAicBwpxyinatGnDocMXudbTb9FMTmxbOYtXmah7ufXaIChkeI5qTfjiCbiNbUdxhpWCJWfQP78My+qjSNegB7kWqPzdaP/TGJo935NDYxeR/PEuRAftHPfWgcRuvBdTlo6Td/5K+PM98YpvTNbik/g82JmMx9eg2+w6K0nhqSZ67lhyFhwnd+mpOh2nTC6j9zejyTidw6U1icQNjyZpYyLnN7v2ivEqD16sXOVR92iK9Uw2tvyq4/K+7YIpSSrAWmbBzUeLX6QvJqUMswviIlMrcIsKoCxHX2OryJKYi9KJMFfKKwStBsHdDeOei2h6NHF6M5UkiZIFR/G+x3G15cJX+9GfzSdm1ki2PLeO4XPG1Cr52ZpZQsEbG/F6pAfquKpJ1JKuxE5amrZA8HA9nn15HNqamI1+xhpUvZujfbCXw2RnW76Bkrc3UvbbScylEpqh0fh/NAJ5YP1m/ViKyjj92ma2dZyF0k/LwDNP0OK5nshdGPbdDEiiROmWc+RMW0LmrfMx7kjGa0xrwlbfi//nY1B3q9oulHlo0I5q63hjysYQsRHCvge3AYAKBHcQPOxkRtCA1+3QeDmEzy1vL1UgPz+f2NhYYjuOJCS0lPBGErEdJTrESsS0sf/98o9MLrF+fcV36tNPJTRaG8XF+cDiG/BJ/QPRUHGpNf75U0U2YD3wAbAPUGHnEmagMfAido1Ypdb6gAEDePUVgTnzSpg22f4lP3DYSmlZ7f+zX3tWy4gJOhy1m24kBLUCrzva4TGyNbolJylaeAz18kTcNpxBPTQaxcAYhBtQKq9yDIJA6F1t8e0ZwclHVpO7IYl2s0fj1qzq05jCS03MT2NJ+2wPx4bOp9U3o1AFeZD68W4i3+hLzgd/Yk4rxm9KR6cld1WIB63njeX0nYtRBrnj0yey1sfp3yGUqHs7UXT8Ehde2czwj0ew8sHlPH78adROUng1He3mZMajl9CW/13QKlHFN8X0xzncxlUIW+UaJd6tAyg8donA7o2J7NGEwpIyPFxMFoFdoFuWXoIqvOqNQMzWoaxSccnBY5zjKQwp054EDWDcfRGP2537rBj3pIEgoOlWXYtRllHC8Zd+p90jXdj59V5iJnSoVfKzLd9AwWvr8ZjYEW3fqiGNkl6HeOGcnbR41mzjbysyYjuViXHNcbQP90bZoZHD5Uw7k9HP2QMeGqxG8P9gOCpXwZPXAJvJyoWv95P04U5CRrai/6GH0Ta+8bEANcGSUYz+xwMYdlxEkETc4kLxfbYXyujrNNMTBHs1RRsHNh3YskEss7eRFCEgcz7t5e/vz9EjC4E4ZswADw94/vnq3+PZsyUW/AJDhlS8tnARdOkCK1bomTLlQ2Dy9Z1HA/5V+GdXXLYCYcBEYCcVJrd67MTlPHZRexDwacVqgiCwYsVGNm230jyukDY9i5jxYSlhIbX/ONq0VtCpvRqLScPLvT7hhW4fMTXiDSZ4PMfDLd6qrzN0CplWiffkjoQvnoCyR1MKzxkp+i0Jw4vLsKw+dlMqMJpGXnReNZGQMTHsG/Aj6T8dqaZHEWQCEc/EE/XZMBKmrcJqtBIxox8X3tyKz5Pd0a1PIvutbQ5dZC/DLSqAqG9GkfTEWgync+p0jJ1nDKDgbB7y9kGIG5KJ7NOUza9udLp8hZNuVZGuZlAUpi1nq2Ux+XWqZEQXH0lWRpHLVhHYdS6lqcVVWkWSJNlbReUaF0mUsJzNc1hxudImCgvGVmzEci4PdUfn2TfFPx/B+57YauRQkiT23fErfiEeSL0jSN95sVbJz6LOSMFrG3Ab0gr3EdFVt2nQIyYnIYtsXivSIpqsiHoTli1ncH9jmEPSIupN6D7ZhmHufiwmCXlUMIHfjK1X0iLZRNJ+PsaWmC/I33GRnpun0HHO6L+UtEhmG/rlJ7g0cSGXJv6KNTEHvwc7E7r2Pnz/M/L6ScvVkHuCqgVo2oGqqUvSUoHPsF94HePsWYm334H580BWPhF2/ryEXg/vvmMnMJAC0uF6OIF/OBoqLrXGP7fisgS4F7sWzBX05X++DqRgF7wLEBYezuKFH0Dp+1TuzVb2cAGY8VLF6OZPX1YtRy+f688rI6dxblcKEhICAhISXEfacV0h81Tj+2BXvO5oR/G8IxSuS0QrnkO76TSqwTEoBkbf0AqMIBNo8lhX/Ac05cSDq8hZd5Y2X4xAHVz1s/Lt34zYdZM4ff8K3Fr40+zTYSQ/u4HGL/bCtCuV9EdWE/bJUKdurl7dG9P03YEkTF5O21UTUYfXLpBP6a6i5xcj2fPMOiJ83Oj8WFcWv7aeNne0I7K340kVrxFRXJx9EFuxEXm5iZi8eQCCRoH1VBbKdhW+FgFx4eTuswt3m/aMZNeMTbRRuPbd8ewQwsUP/oQOlTQhepP96bfcs8eaXoTMS31l/5Uh5RaAuxuCmxbTxkTUnRohOHFnNZ64hC3XgFv/6vqPC3MOoT+VQ9f541j61G8M/XZMjcnPotFCwfTfUXcKx/2uqmPVkkGPeP4ssibNELxqvuFLBhP6DzcjU8rxfGeUQ78i87EM9F/8CV4aTIUWfJ7tg7aGSIO6QJIkcjac4/Rrm5G7Ken801j8e9ff9q8FpjPZ6H86ROmBDBQaGW49Iwj8YAjyxs5H3f867MSZeafFIjHxbvj4I4iIqCDNCxfChPHQuzckToGcHImgoENAp5tyxH9P/O+TjfrEP7PisoPakZbKKAW+Az6q9Jp6wnUchBrUd/H+7jdo1DaEyloXQ1EZyz7cRNlNDFCU+2rxeyqe0Hl3IEQGUnDWSMmmZEpfWY5lzTGkshtbgfGIDqTblvvwbBvEnp7fkb26+vixpokPHdbcg6CSc376Vpp+eAsZn+1BFhOIKsqf1EnLMKcWOd1HwKjWhD4Yx5lJy7A68ZRxhCYjW+MfG4oYG0La+38y5O1bWDl1GRYnYZByXy1uvSLQravwbxEEAfWgVtWcdP0qCXQDmvtTUmbGnFHichLKvVUAloIyrIaK/Ys59oyiy1URS4LzYEWp3HQO7G0iV9NEJT8fxWtCh2rOu6WpRZx4fiPNh7Xk2JYkIvo1qzH5WbLYKHx7M4pG3nhO61algiOVGuykJaIpgrePi63YYcssRv/mGvB2Q97IqxppkUxW9N/tQTdzO1ZJhqhSEzR7XL2SlsIDGeweNJeTL2yk9Zv96P3nA38ZaRH1Jkq+30/WmHnkProKqVBP4Cu9CPntPrxfG/w3JS0AzquLb7wBbdrA+PFVK32LfoXx4+0VmLFjYMkSI3ahbgMaUDv844iLh4cH3McV0pJCCm2pKj6bwQw+5mMAbuVW5jPf/kYpTHt1Gh/NKGcvMm/w/AGoqzW3AuRNwf1tBEHgo8Mv4R/hY/d4ksloHd+UJW+sY7LvS7zS51MObTyNKN6cUDJFsAf+L/Yh5LuxSP5eFCQZ0W1NoezVG09gZCo5Laf3J3bB7Zx9bQsnH12NtaTq1JNcqyTq8+GETulI4hPrCH2yB/nLz2A0WvGe0J7UKcspPew8ryh0Wme8ezchcepKRCcBiI4QP3MEyatO43NrK6R15wmNDWXrjM1Ol7/cLqoi0u3dHMvhdERdBWnybReM7lwB1lIzgiAQ3qMJoihhK3Y+7SUoZLg19aUsW3/lNTHb0USRgzaRTUS6lIsQFoxYZsF0LBNNtwiH+zEnF2A6nYP7iFZVtyFJHJi0HF9fDdqJbTmz5CQDPh7u9Hgv77fooz8QNAq8n+59FWkpRTx3FlnjSASfmrNwLMczMLyzDvWIdih6tkThV9WQzno+j6LnVmJJyMFcZMVtZAz+/xmK3K/2IY+uoE/K58D4xey/fRGNJraj/9FHCB0dfdNHmyVJomxvKrmPrSRj5FxKfzuFR78IQpdMIGD2nWgGR9/wBOvrh+Pq4h9/SCxbDl9+UfX148clkpJg8C0Q2VRi0a+X20W1aUv9D6PBx6VO+Lt/K6pDBFxP0lbB53zOdKZTRBG72c0+cR9PK56uWEA1CDy+pvZfHDXIo8BrVfkYISiUcj47/RpeQR50vyOW19Y8zPySD3nw67vQ5xj4YMS33O3zIl89tJCs89cfK18bKBt5E/DmQIK/vBWrWkPBOTP6HRftBGbt8RtKYHy6NaLHrqkIChm7e86hYFdqlfcFQSDsvk7EzB1Lyn934N4rgtIT2RT8mULw9P5kPruB4jXVx48vrxs5vR8KPy3nnt1QTXPiDO7hXnSaPoAL+9OwFJXRqVskR+cdIv1AmsPltZ3DkCwixuMVv2wyTzXKzo0w7aiYhpKrFXhHB1J4zJ763Cw+ErNShqUGga57lD9l2RVTSlLu1RNFOQ6N56ScPPDyQNBqMB1KR9kqqJq1/mWU/HIMr9vbIruqjXRh9kEMCbm0eDaeTa/9XmPysyRJlHy1G7HYiO/L/atML0llpYjnEhEaRSD4uq4KSJKEaf0pyr79E7en+qPqH2WfKCpPhpZsIqWLj1D81gZsciXmIisBn4zEY0zbeiEVxks6jj2+hj97fYd3bCgDzzxBkwc6I1NUn166kbDk6Cn6ZAeZw3+k4PWNyBUSwR8MJnjFFDyf6oc8wPUU1l8F29ksbGezEE2VK5XVhdyFhRL33Q/z5oKnZ9X/t4ULYcabkHJBIOWCQGaGQEaGxMWL/1zVQgNuPv55vy2O7VecIpJIHuRBXuRF9rOfL6UvUX6hhFeAy9cr9a0gbwSGd8C6H/sc9dU3dg8QZKC+H9yeA6Eq0dG4q/n+0ntX/q1UKxk8LZ7B0+LJScln+X9+Z+cvh/njh734R/ox4sm+DLy3G25eN/ZJQ9XMj6D/DMF0Ooei2QcwpNrw2JWKastplANjUAxojaCtfw2MwlNNm89HkLP+LMenLCdsQntavNanyk3Uq0s4HX+/lzMP/oZMLUduspE+6wBNZg7l0iubsaQW4f9I12o3LUEuo8VnwzkzcSmp7++gyet9a3VMMY90JWn+EdTDo7g06wADXuzHivuX8sjBJ1BcdXMXBAGvMdGULD+NtkPIldc1A1th+GEvmuExV47Lv1ygG9gjgsj4JqTMO44lU4c2xrmBm3vrAHIqJWGL2Trk0fb9SGYr1otFqFpUF59KmdnIwuzLGXdfRNvTcWvDeklH2c6L+C6u2g41XCjkxEubaNoumHP5enya+dWY/KybexBLUh5+/x2OUGlMWjKWlZOWxsj8XKcFSxYbZT/uwXYhD48ZI5GVjy9fHoW2ZRaj+2w7klXEYhLQtArCf2qXKvu7Vlh0Js7/326Sv95PxORYBp5+ApULonYjIFlslG5OQr/4OOYLRaiDNPjcGYN2XAdkN/gaUF+wzPkDysqrnDIBBJCN6o1q4EHsLrl2fPMN5OTAI49CZU+KV162t4nWX2WnNOY2BYsW5fHSyzf6DP7m+B+vktQn/nkVFxt19nx7nufZwAba0IY+9LHrXU5ftZCiE3ivAJ+9oHkQ5O1A1gRkLUHRGzxmgm8CuL9ejbRchiAIDp8MgyL9efjbCcwt+oCXlk/FL9CTn59byb0BrzD9li85vOkMtlrk+FwP1DFBBM8cQcDr/TEWWCnMlCjdl07Zaze2AhM0LIr4PdMoPZfP3v4/orvKeE4V5EG7JXfhFhVA0dEslEFunH9pEyGfDMWwO42sVzY5bAnJtUpa/XAbBZvOk/VD7SYSLnu7HJu5m7BHu8KaJHwjfdn+/jaHy3uOaoVh2wVsuoq2j6JNiJ1YnMu78pp/XMVkUePOjcgvKqX0guO03cvwiAnEWFAh0qpsPmc5n4+isXc1wa1ksyFdykMIC0Kyihj3paLp4Zi4lCw6jsfIVsi9Kqoxkihy8P6V+Ae54/1QZw5/s48hX7lOftYvO4FxVwq+7wxBVkm4KxmNiEkJCGGNkPm5nu4Ri8swvL8ByWDC480RV0gLgLWgDKHEQNHLqxHlCoypenxe6IvPoz2um7SIZivJX+5jS+vPMaQU0u/AQ7T9eMhNJS3m5HwKZmwiY9iPFH+2E3WoGyFfjSTw10m439f9H0NaAITQSoJrUQKbhEw2GpAzY4ZwZRT6lVcEDHqBo0eq/tx1l8CFZIHWrSv/vin55JPHeOnl12/qufwt0dAqqjX+WRUXB1pKwYkBXOXXj3McCYkEEhARkcllUOBwNZA3BvcZ13+sjjYtlxE3qh1xo9pRnKNj46ydbJy1kw9HzUHQyOk/pRvDH+1NoyjnDqjXC02nMIJnjca4J42iOQeQbHI8D2civ4EVGFWAOx0W3E7mguMcHPULTZ/pQZPHul5pOciUcpq/MxDPjqGcf3UT/gOacfaBlbScPZriuUdJm7aK8JnDUfhVvcgrfbVEzx/LyTGLUIV64j/MtbgUIKBjGC3ujiX1aCa+PlpiW/uzetZeYsa2IbRD1RRchZ8bbj0ao1uXhM9ddh2VIBPQDIzCtDkRZUt7K8e/cxgJX+61H5NGiTzIncKjWYTgHNpIX0SLiDmvFFWAWxXzOXOCE31Ldh6CjxeCRo3pSAaKMC+Hxmu2YiOGDUmEzr+jyuvnZx3AeLGIqBFRbJ+1t8bk59Lfz1K66hT+/zcSuU8lS35TOWkJDUfm7zy5GiolO/dpgXps1ZBEsaAUaX8yICEq1cjlCoK+u93hJFVdIIkiGYtPcWb6Vjyi/OmxbhLeHVz9b9QvxFIzhlWn0a84hS3XgKaRO/6PdEYzvM0NqW7eSIgpuVi3nkJMuATGShdgART390bRMRKkJ4CPqdu0xGUogCfq5Vgb8O/BP6/ichX88aeQqk+3BRQQgP0pUETkUR5lPvNpSUtmMeuvOMxq8A7y5M43h/Fd1rvM2PI4sf1asu2bXTzb/r88Gv0Oa2btQF9UFwvt2kMQBLTxEYR8PxbvKZ0oOVNMSYkK07EsjK+vwLKu/iswgiAQfk8Hum27j5y1Zzk4agFlqcVVlgkaG0P75RMpPpyFMsKHxHuX43F7G9y7NiL1nqWYzldnm5oIH1r/eBvJL/2OrjzwsCbEvTWArO0X8BnflsKlp+nzaA9W3L8UmwMvGa+xMZQsO1VVpNuvJeY9KUjlU0k+bYPRnS/EWu6d49U6EH1SvstjkKnkqL1U6I5lIZVZkIwWhHJyYEl0PFEkZWQj1GKaSLfsJG59m6IIrHBd1J/L59T0rQR7q8kJcUOQu05+Nu5OQffjAfzeG1qFHEkmk520hIQiC3CdZWTZn4LhvxvRTOyC5vZOVUiLafcFCp9dga3USlm2Efex7fB7e/B1k5aczefZ3n0O52fuIfbbW+mx5p6bQlokScJ4JIPc59aQMWIuhgWHcI8NJPSHsQTMvxvtuI7/GNIipudj/mkHxpd+xfzJRqRcHYoRHVD93wRQye2k5b5edtICwKtAW+zun3WBG/AJCPUf1fDPQz1XW/7HKy7/LOLiwKTWAw9CCWULWwA7adnABnrRC4Bv+ZaWtKQf/fiET/iQD8m15iL5SkjFBsSkDKx/nsSyeAdi+s0RzlaGIAi07tmMl1Y+yPc57/PAp2OR2+CX51ZxX8irvDVqFgc3nLohrSRBJuA+oDlh8+7AY0wbig7nU2LSYj6ZfcMIjFukD13W3UPALS3Y2/cHMhYcr0IK3GMC6bhxMihkCB4qzj20CllzP/wf6ULaAysx7K0upvVoH0KLmcNInLaKMgfk5mooPdTEfz6Sfa9vovmMAcjWnUfrq2XnxzuqLavtEo5ktGI6WWF8J/NzQxETgmn3BcAu0PWJCaTgqF2gG9g9AluOvtq2KkNQylG7q9AduXSlTXS5ZWNOzKlWcZGsNqScfITQIPtNsjwN+mqIZRZ0y07hNbHCY0USRQ7cv5LgKH98JrZnz8xdLpOfTccyKf5sJ35vD0HRuGK0WTKXk5agEGSBzquCkihhXHaEsp/34/7SLai6V/jliAYzus+2Y5h3AMnXk7JcMz7P9MJ9ROvrEuAWHc5k99B5HH98LS1f7EWfPdMI7O/Yp6c+YcsvpfibvWTeOpf8F9Yh0xkIeqUnwcvvxevVW5A3rV9n3xsF8VIR5p93YnxlMeYP1yNlFaG4pQ2qj8ejfmkUir7RyJQK5LfHoZjaB0WnSp+toAZ+B2Kp/ZCDFngLhIfq/Vwa8L+Pf1arCCillEZUuGs+y7PMYx6P8RjP8RwAb/ImzWlODjl8wAfsxV7GDyOMp3iKF20v8u3O22G7FeQysIl2sZmTC/nNgpuXliGP9GbII71JOZbBhq92sPOXQ8zckYwoh/739WDIAz2IiKlfx0xBIcNjRCvcB7dAv/oMhfOOoGrhh/vpHKxbE1AMiEbRv1W9PTEKchlNn+5BwMBmnJi2itz1Z4n5bPgV7YHCW0PMvHGkzdxN1veHSXllE+HPxhP2f0PJfH4DAY91w+f2NlW26TugGY1f7M2Zyctou3IiqkrVBkeIvDWas3OPkJmYg2f7YDooZWz8dCfRt7UhKLqikiDIykW6K06jaVdxs9YMjKJsxXE0A6MA8O8cTv6hTILiI4i4pQXJXx1AFEVkzn6nVHJUbgp0R7OQ+oZfaROJJUbEwjIUEVW9UKTsXAQ/bwS1CvPZXFDJqy0DoF+TgKZDKMomFe+d+3wftkIjvk282Lc1iS5P93Sa/Gw+m0vR+1vxeXUAykrOtJLZbCctgUHIgpxXMCSjhdJvdyIVGPB4eyQynwo9iflEJvovdiBr5Isp34zbkEjkKXrUTvKYagNDcgEJb24jd9sFWr3elyYPdELmIOOoPiFZRcr+vIB+4VFMSfmofJR4D26K9o5Y5KE1e9j8XSDmFGPdcgrxZAbojAjBXij6t0bWpzUyjePvujI+yvHGBG+QtgPvAF9hFyNeTd7l2KsyLYD/gjCsns7kfwT/41WS+oTgyigrLi5OOnjw4E08nFpgFzAEu7X/tUALvAG28ZewrT9gJy3lEGIikDcJRmgUgODki3uzYSozs3/FcdZ9vp3U45nYZODf1I9hj/Sm7/jOePq5vkFfC0Sj/am95JdjaGJDcA9QIGTk2wnMgNYI9Rg0ZzNaOffudi4tPknM58MJHFpVp1Kw5TxnH1+LSqMgcEI7gu5sS8YTa/Ho15TAp3tUCxZM+79dFG5Nps2Su5DX4BisTy9mWcevGL5mEmcfWIV5cCRJ+1OZuuNhuw6qHNa8UlLHLSRy7SRkHvZtSjaRwod+xWv6UBQRvpydc5CcXRfp9dM4JEniWMwXBM0fS1ic49wda66BtImLuZRloNN/+4DehHp8F4wH09H/epSAj0ZW/Zz2H0MIDkDWJJySnw4iWWx4T+tWZRnJaiPjzkUEvjsYdflEk+5sHtviv6NJCz9sI1tyeMkJ7jv4GHIHN3drWhH5L67F+8leVUS/ksWMeDYBwT8AWUhYtfUuQ8zTY/hkC/IIX7T3x18R10pmK4afD2LedQEi/DEn5OP7Ul/UsWFc6P8DESsn1rlFZMo1cPb9HaQtOE7zJ7rR/JkeKJzkT9UXLKlF6BcexbDlPDJBQhvth/udHVB2bfoP8FuxQyzQYdt8CtvxNCgxIgR6Iu/UBFm/GGQOnIuvCZIZWAl8CaQDRsAL6A48A0IHFyv/PSAIwiFJkuJu1v7iAiKlg6On1+s2hR8euKnncDPxj6u4EA8EA8nXuL4ETAN5QAiy8X2xLNsFRjNCsA8yfy9spy8ibT6C4OeBEBGErHEQQojvXxZjr9aq6D0xjt4T47h0Ppct3+1l8+xdLJ2+jrnPr6D9kNbc8kA8cUNjkNeTH4VMo8T77lg8R0dT8usJ8peeRNujMe7nc7FuPYNiYDSK/vVDYOQaBa3eHUjgkBZXAhuj3h2Eopwg+A1sTof1kzl97zJyFhzHnFFCkx/HkPnS72Q+t4HQ9wcjc6s4jkbPxmPK1HH2kTW0/v42lzcUj0bedH6jP3tf3kiPz4aR8NR6BB85e7/YTfzTva4spwhwQ9u1EboNSXiXV3oEuQxN/5aYtpxFcV83u0D38z329wQBi1ZB2qYkp8RFUMmRCfa2ijWlAFWMvYphSchBdXWbyGJFyi1AFhsD2PUnPk/3rrZNw+bzKMK9rpAWySZy4L6VNOrdBPfGnqz7ag+3/zbZIWmx5egpeG0Dnvd3uYq0WBCTEhH8/F2SFuvZbEo/24Z6eBtUwyt8V6zJeehmbkfm64ZFlKOUyQmaPRaZpxrJYkMstTr1oXG4H4OZ8zP3kPz5XsIntGPgycdQB9W8jZGjAAAgAElEQVRvMnRliGUWSjeeRbfkBLYsHeoAFX4T2qAZ3Q7ZDXhouBEQiwzYtpzCdiwNikrB3x151+bI+8cg87w+TZFDCCrgzvKfBtQKlw3oGlAr/POIiwD8CAyl7iJ2N2A6lOt2Efy8UE7oh2X5LmRtIpG3aYI8trl97DSrADE1F9vOE0hFBoTwAGSNA5FFBIGP+0132QQIaR7I3f8Zxfh3hnN0wxk2ztrJqd/Pcn53CiaLlf5TujH4vh40bec8cK8ukHmo8XkgDs9xbSj5+Sh5axNx7xeJW3Ie1i0r6pXA+PVuQo9dU0l48Xf29vqOtrNH49PVfh7aSB9i108m6dn15G88jylTR9Sc0eT+325S719B+GfDUZZnIwmCQLP/DiZhygqSX91Msw8Gu/y/inmsG2fnHyE/rZjA4S1RpBax7b2ttB4VjV/zCm8S77Ex5H2+F69xFf4t6oFRFL+yBrd74vBpG4QuuRCLwYzSXYUi2J30/Y7N7cDensMq4hkbgvViAep+9hK8OTEXt1uqluOlS7kI/j4IKiXWjGLEEiPKq1o9kihR8vNRfJ/oceW1s5/sRvh/9s47PKoy/+Kf905PmdRJJwmB9NB771WUqiCogGt3XVddV11d6+ru2ttawS5iBUSRLkjvLaTQ0ntPZiaTKff+/rihSYCAiODP8zzzJHPnvrdMufe833KOR8ZY1kC6ViF1emciepxKpDy1jVT94we8JqTiNeL4vhW3S00P+QcghZ/+O+VcexDH/O2Ybu2PrrMqSKZ4ZBoX7qPx23S0aRHYNxbgd3tvTCPij71/nloHGn/jSUW7p4Ps8pD33k6y/7WW4AExDNx4M97tfh0ZfEVRaNpfhnXebho3F6A1SXh1CsH77/3QdIg8bW3QpQS5oRHP6v14duVDlQ0CvdB0iUYzNBXJ7+Jq2PyBVuIP4tJqXH7EBWAgKnk5Qfr/rPACbgT+fvJi4WNCd/2wk5dpNIgoC1KUBUhBaWxCLqhAya/AtfMgCIHUJgQp2oJoY7noaSWNVkO3cWl0G5dGTUkdaz7cyvI317P54x2seW8LAdH+jLypL4On98Av+JfPRjX+JgL+3AffqR2p+3AnFd8dxmdUe0w5zQRmeDLawb+cwOj8jHR4+yrKFmWx+9oviZrVmbgHByDpNGi8dCS+eSXFc7ZT+J/17B8/j+SvptHwbRb5N3xN5MtjMSarkQpJpyHx7avYP2U+Ra9tIeovvU+7z6PaLkuv+IhJW++gZsp8uoxLYeHNXzNr5U3HalRMvaKQG5poyqzA2BzR0ISZ0cQE4Nyah6FfHP6pIdTsLiGkXww+CcE0LDvVr+kohF6D4pLx7RwOB3KQQn1RFEXtKLqr30nrKkWlJ3cT9Y455WbfuDEPodNg7KkSk/qMcrKfXU/8gBgc7QMo+XofYz+YcspxyDYn1Y8sxdS/LT6TjgvRKW63Gmnx80echrQosoxj3nbcO/PxfmQMmki1vsNTUk/Dq2vVdQLNOPPrsfxvAtqIk40xPdWNaALOPONXFIWSbzLIeGQVpjZ+9F44Hf9up4/8/BJ4ahqxfZuBdWEGirUJY7gRyx1dMYxMQVwGeiuyrQn5xww8O3NRKq3gZ0LTqQ2aYalIAb9eVOoP/IGLjcuTuABMRY2cTAOaOL3Xlzdqeugp4N6WVzlb9ESYDGgSoiAhSu2AqbEi55fjySpAWbUbEdCcVoq2IMICL2paKSDcj4kPjmDCA8PJWHuIlXM2sW3hXpa88COfPLSYDiMSGTG7N93HpKL7hYJeWos3QX8bgHl6J+re20HFpnx8xyUg5VbheOTCEZjQ8Un494pk/53fs3X4B6S9Mx6fxGC1pfrmHnh3DCP7hm/YN+x9UhZOR9/Gj8LbvyXs8aH4DFa7HTQ+epI+nET6hHnow30IuTrttPuzdIuk3bWd2Pb4Srq+eSW7r/2CJl+J7e9spedtKuk5VqT7TeYx4gJqkW7TqgMY+sUR1E0VogvpF4NfaijaBfuwVtrwCW4hpdAccfFJC0HafwgR6K12IkkgnVBYrDhdKFU1SN1UUuHYmIvPtV1O2Vz9p3swz+iEEALZ7WHb7IXEXZ0GhXVs/HIvY9+ddIrzs+J0U/PECvSJFnxmdju+3O1GPpSF8DUjIqJa/H0otibsr69F8ch4P3klko9BjVSsyMb26Q503dpgW5uH9/gUfGd0afE3cVQ193SoXJvL/gdXoLg9dHz1CkJGtDvtuucLxSPTuLkA6/zdNKWXo/eV8O0dhWlKJzTxob9JZPVcIDc6kddm4tmeg1LeAGYjmrQoNHekIgW3zkH9gqOxHJx1oHhA5wteYSAurq3CZYk/Ii6txuVLXACGAaXAEuBZYAtq0bpAVeyPAh4ApgMXaMIhhIBAXzSBvieklWpUIrN+P0qtFRERhBQdgtTGAgE+F+XiJ4QgdXA8qYPjsdbYWT9vOyve3kjOhlze213EKzd+wpDrezF8Zi/iOrd8M2otdBFmgh8Zgiu3hto527HuK8V3fBJSXnUzgUlBOzjxFxEYQ5gvXb6aSuF7O9k26iPiHhhA9K3dEZLAv1cbuvz0J9InfUb6qI+If38ika9eQfG9S3EW1hMwoyNCCPShPiR9NJmMqz9HH+qD/8DY0+6v+5PD+DL1FRJu6ELU7K6w5gir/rmchLFJ+Dd375ivSiJ/ynyC7+lzTEVW3ysG29zNeMoaCOoWQdm6XHV5lBmLxZfcjbmkXZV6yv6EEKCV8An3wubwgCSO6becZGBYWoEIDkTotHhq7LhyazB0Pjni4NhTgqfKjtdgVQ8j+9kNaL11aNLLyInyIWZIHG2Htz9pjOKRqXlmNVKACfMdfY/tU/F4VBl/b19EZJsWvyeekjrsL6xC2yEC44yeCK2EXGOn4Y31yJU2RPtQ7FuLCXxyJIbU07dNq6miU4lL3d5SMh9eRUNWBclPDiVyatoFT8+4iuqwfp2O7YcDSIqMMdobvwf6oB+YgDhLUfdvDbnJhfxTFp5tOSil9eCjR0qNRHfzYKTQ36irydMEpWsh50toLAOp+daiyCDpIWYiRI0Bw+XTdfUHLl1c3sQF1A67K5sfVqAKcAMBzY9fmTOoaaVgpCi1cEZNK1WiFJTj2nkIoDmlFILUJhhh+nU7HwB8ArwYfedARt85kCM7C1g1ZxPr521n7/cZrJu3HXOoL8Nn92bIjB4EhJ7/rEwXG4DlXyNoyq6g9p1tNOTW4DcpBSm/6oIQGCEEbf7UjcBBbUm/ZREVSw+S9sY4jJFm9KE+dF5zI9k3LeTA9V8T/dgQoj+aROFd3+PKqyXkgQGqC3N8EAnvXEX2zYtImXc13qkttwHrfQ30e3Uc627/lknbbqdq5WFSB8ax6NZvuGHJbIQQaC3emLpH0rDsEH6T1EJZoddiGNCOptUHCeoeScbLG9XtRZrxM+nJ2ZjXInFRx2qQmpw4XeDIqcWZdaqxolJUimijEhXH5nwM3aMQ+pNnr/Wf7MY8vRNCK1G3r4yDL2+iw8zO1FXbOPRDNjen333yNmWFupfWgVvG/+FBx6Ihx0iLl7dqmtgCaXHtK6LxjZ8wXt0V/VDVdbppcy7Wtzei6xKFM7sGXaiWkLcnnWQR0BI81Y1oAo+niuz5tWQ9/iPlSw8R/9AAenw1FY3hwl2iZIcL++ojWL/ciyu/FoOfloAxsZjGd0SKObPX0m8N2eVGXp+NZ8sRlOI68NIhpUSgm9kfKfLXqfVpNco2wL7nAAGe5ty9fIL+k8cBRz6DI/MgZhLEz4JLPJJ18fH7F427kLj8icuJ8OGCRVbOF2paKRISIo+nlQoqkLML8KxuTis1F/mK8F8/rRTXtQ1xb7ThhucnsPmr3aycs5GC9FLWvreZzx5fQuqg9gyf1Zte49LQGc6PYBgSLYS+MBbHnhJq39lGfXUjflNOIDAjUtAOOn8C490+kB7LZ5LzwgY2DZhL0n9HEn51KpJOQ/KHk8l/YQN5j6/GllFO7IeTKfn7Mgr//B0Rz41C42vA3DOKuKeHkzXzG9IWTccQ2TJZi52QQvaHu9j74gZS3rwK+9iPyDco7P5oJ12aUynmSclUv7ntGHEBtUi34enl+E3sgC23Fpe1CV2EL3qnTM6m3NOel9BKKKX1KGYTDbtLkLIq8L2u67HXFacTpboOqUdHQE0TeQ09uV3cebgKZ3Ylln+NQHZ52DZrAYl39ca29ABbqxsY8fIVmAKPF2MqikLDu1twF9cR+MwYRHOHkeLxIB8+gDCaEG1iTiEtiqLgXJZJ0+K9eP1lCNrkMGSbE9vczbgyS9F2jca2Jge/P/fFa0jrUjqqM7QJZ5WdA/9ZR/6Hu2l7ew+GZd2Fznxhul0URcGZXYn1y73Y1+SgNQpM7f0JemwQ2l5xp/hBXUqQ3R7kTQfxbD6EUlgLRi1ScgS66X2Qoi8RYbv87yH77ZOJSks4+nr+QjUi0/GBP8jLz/EHcWk1Lt1f7S+FYgd3Lij1qrKjFAaaCyvcdjaclFbqFIfikVFKm7uVNuxHqbEiIoOOdyv9imklg5eeQTf0ZNANPSnKLuPH9zaz5oMtVB2oZN4j3/HaLfMYdG13hs/sTXz3lmfbZ4OxUzihr1+JY2shtW9vRZEV/KakIedV/GICI2kl2j0wgOAR7Ui/5Vsqlhwg+cXR6AJMRN/XD5+0EA7dvhh7ViXJ86+m6uVN5M/8hqjXrkAXaSZoXCLOUiuZ139N2jfXovVv+cbY79Ur+LrrG7Sb1pG4+/vj/mAny/6+hPYj4/ENN+PVuw0VT/+EI7PiWDGwNjYQKcgLz/5S/FJDqN5dSkjfaITLQ0lWEW6nG20L9UVCr0Eub0AT5U/DrhK8DlWiSzhB9K24HBEShNBqke1OnPtKCXhw6EnbqP90D75XpyEMWjKfXIMh1BvN/jLyIn0ICDaQdPXJzs/W+btp2lVE0HPjkJo/B0X2IB85iNAbENGxp5IWd7Oz8+FK1SQxxBdXegkNr/2ENjEUj8GIJ6cWyxsT0Ya2fubgrrBRX9zA5odXEjEllaF77sAY7tvq8WeCp86B7YdsrF+nI9c5MAZoCZ6RgmFMKlL46f2ZfmvIHhl562E8Gw+i5FeDXouUFIpuck+kuDNbLFx0VGxpHWk5EZ4mqNgEB96DxD/9esf2B37XuPwE6M4G90GwvwONXzUXhEmAoooiaZPB+89gGAXiwomonS+URidKYQVyfgVyQTkoiqobE21BamP51dNKbpeHHd+ls3ruZrLWHyY0wUJZcS1Gs4Hhs/ow9LoeBEWcX05aURQaf8ql9p1tSL56zJOT0eaU4jlQphKYwYmI84zweOwuDj62mrLvskn73ziChqq1HfaDVewf/ynCqCVt8Qwa1+RS9f5OIl8cg6mjqpOS+8SPWPeWkTJvCtJpZtt7X9pA/vfZjF02iz1TPueI1Y7DR8f0b65HCEH1u9txV9gI+cegY2McK7Jx7Spkf64dc0IQKX/ty4ExH7OiuIIr3plCbK/oU/ZTMPFTAnsE4oq2UDA/k9AQAyHvHde+8GzYgWgbhRQRSuNPR7AvzSbomeNqo+7SBkpmf03kF9dSd6ia9aM/pvtTQyhZmMlP2/O5ceddJ5ko2r7LwPZ1OkHPj0PTrFKsyLIaadHqELFxp5AWua4R+ys/InwMeN0+EDQC+7ydNP10GF3/dli/z8ZnSgd8runY6uih7PZQ8NEeal/aiBLtT/uXRuOT8MsjCIpHxrGjCOsXe3HsLEbvo8GUFoxpYge0XaIRF0jn6EJDlmXk7Tl4NhxAyasGrYQUH4JmaAqa+Is72WotfHx8sH43HpqqWLK1grvfymLVf7ojCcGd/8sgI9+GrCiM62nhuZsS0esk1uypZvwTu4gLN9HYJDNu8kyef/l/v/WptIiLLkAXEqNsn/zQBd2meOv2360A3e+HuCh2qL0dnGtRi1zcLa8nfAA9+H8M+m4tr/MbQFEUqLU2k5gKlKJKhL+3WhsTbWlOK/16F96qwhrWfLCVVXM3IWklvC3eHNlfTHK/OIbN7E2f8R3Rn0ekRPHI2FYeom7ODrSRZswTk9BkF+I5WHa8BuY8CUzV6iOk3/kdoeMSiX9iKBovHe46B+lXfExTqZWE9yeik6H0sVWEPDgQ8+h4FFnh4B2LQRLEvz6uRQ0R2e1hQa+36PDXvkQPaceWIe+xS3Ey7OlRdJjaCXeZlfypXxD7w/VIpuaoRaOLmls/p7JHO8q3FdH/oynk3LSQzAY7Xr2jGHzPwFP2Uzh1PgGRGnS3DSLz6s+Jnp5GwAND1O05mvCs2ohm9ECERkPNv1ej7xCO97jkY+OrX9qAMGjwu6k7q3q8Q7vbu+P4ZA9bbA463dqTrrcdV9ZtXHOY+jlbCHpuHNpwNVWmyLIaadFoELHtTiEtnrxq1dm5XxyGKV3x5FWrYnKhvrg9Eu5DVQT8Y8gpgnmng6IolC7OJuPhlRiCvYkK9iL04YGYOv+ym7O7pAHrtxnYFmciZBljkA6vccnohyUhXQA5gF8Dsiwj78nHsy4bJacSJIFoH4J2UBKalJZFCy8l+Ph4YV04klXbi7jl1f0sf7o7ceEmet29mdvHRTN7ZCQej8Itr+wn0FfHczcnsmZPNc9/nct3T3al0SXR5S+7mfvxl/Tr1+/sO7zI+IO4XNq49JWUWgPFBtVXNpMWB6clLQCKFZRqqJkCTWsv1hGeFUIIRICaUtKN64XupjFo+ncASeDZmIHr3aW4vt2EZ/dhlOp6zkQ4zwdBUQFMfmQUrx9+lFvfmkp4TBBeQoO7rokFz67kuoh/8Nptn5G1Oeec9i00Ej6jEoj47Bq8Brel6qVN1OY4EJN6ouSpNTCu5ftRmlznfsxD4+i74WaclXY2D5xL3c5itH5GOq6+Ed+uERy44Rtq95US9dZVVLy0kap3t4OA9i+PxVlqJe/plj9/Sath4NsT2PL3ZWDSkvjMcJJMJr6/ezG2CivaUB+MncOwLjt0/DxNOvS9YvB1u6jaUQyAPsKX8Ch/cjbmtvzeaCWUukZ0bYMwBRhQAk6oRSkpR4QFIzQaFJcHx/bCkxRtPTWN2JYdxPeaDmQ8tRavWH/0xQ2UBBjQmQ10uaXHsXUd2wuof2sTgU+NPpm05BwCSaKlSItrWx62fy/FOK0bhsldaFy4l7rHl6LrEUPj/kokbz2Wtya2mrRUbchn/aD3yHpsNWn/HUm/1bOQ3B40Aeenj6I0ubGtOEjZrQsoue5znEv349cnlND/jiTgwxkYp3a/5EiLoii49+XT9PpynH+bj/vjDSAJtLMHoH9uGobbh18WpAUA2c26PSXc/Mp+vn+yK+0ivFi9uxqjXsPskaruj0YjeOnWJN5bXoTdcbLzukkn0zlGQ1FB/m9x9Jcm/nCHbjUu/xoXRYGaWeA+hCro0lo0Qt1sCPgedMlnX/0iQ2gktf4lMgh6J6M4nCiFlcj55bh2HwZZUSMxzW3XFyqtJEkSHYYl0mFYIg1VNn76ZBur5mwi2OxNdU4Vz07/AI1OYvis3gy7vifBUQGtOx+tBt8JKXiPScC6IIOKp3/C1CMS32m9UXbk4FixH+2IVLSDEs4pAqMLNNHx/YmUfLmfnVM+J/rW7rS9rx/J868h56EVFL+8iYadJcS9O4GSB5bhzKsl9NEhJM6dwP6Jn1ESYSb8T11P2a6leyRxV6ex5e9LGThnIlFLDlKTqeH7uxdzzbxr8ZuUQvWcHZgnHP/uGIYn0vTyWqx5tbgamtBFmPEvqSdnQy6KopxCDiSdAG8DQqfB5KOjqem4b5ZcVIrUTiUqTXtK0Eb5HUvvADR8nY7XkLbU59aS8+4O+n0ymdyHV7LvcDnXb7jtWPuwM6OMuufWEvDYCHRt1e4TRZGRcw+rxxDbDiGOz18URaFp4R6cq7Px+vtIhLeBun8uASHQ9o6jYWEm/n/tj6l/bKs+n/qMcjIfWUXd7lKSnhhCm+nHU0qeGsc5ExfnwUqsC/ZjW3EIrUnCGGok4J6e6AbEI/zOZVt24DPgTVRNBSfgCwwC7gE6nH7oOcKTWYRnTSbyoXKQFURsMNrr+iB1jjm9Cecljianm/GP72TNsz1JaqMSxP15VrrFn1z4bvbWEh1i5FCx/aTlNQ0uDhY1MLBb3EU75ksev3OycSFxef5qmiGE4PoZo8G9E2jC7VawpJQz7roa9me5SehbSWPj8S/DFTNqmL/QQVmFh3HX1dBpSAEpab0ZO3bsb3cSrYQw6pHaR6Ad2hndzBHoJvVDhPgjHyjC9dFKXPPX4N6wX00zeTxn32Ar4BvkzRV3D+aFvQ9yz+ezCI0JRq5xEBriR+aag9ze4WkeHvkaP366FYe9dQV6kkGLeVpHIj+fhjban/J//khDDWiu64ecU6lGYFacewQm/OpU+qz7EzUb8tk28kPsR2qI++9Iov7WH+uGfNKv/QLLY0ORrU4Kb/sWSQiSPp5M8ZtbqVpyoMVt9vjXcAqXH6J0XS6JL4wios5FwbpcMhftx6tvNJ4KG00HKo+tr02woNFr8G8fSPXuEvQRvmht6nlU59Wcsn2NBoSfCbnRheTxYM2vB0BpdEC9FRGi1n04NuZi7Hs82iLbXTQsyMB7chrbZy2g0wujqHpzKxkeFz3u6U9QcxTEdaSKmidX4H//YPQpqp6KoigouUdAlpHatj9JH0VpctP42hrcuwrwfmIc7iNV1P79W7RJobjqXLhyagh5a2KrSEtjYR27blnEhmEfENQ/hmEZfyb6+s7HW6+dHuRGN5Lv2TVT5Pom6r9Kp2T6fMr/vAjP1iMEjY0l5Lkx+L8zDf24judAWhqAOwEL8FdgB1AEVKAaoH0M9AK6AKtbuc1T4TlYgvOd1Tj+9hmut9egOFxop/ZC/8K1GO4ehbZr28uCtLjtTsrW5yG7TrimyG50WkHflADmLis8tlihZfUJRTneQLQuvYaOt20gbPqPjOsdTljQr+CV9AdaDSGEvxDiKyFElhAiUwjRRwgRKIRYIYQ42Py3xdmpEGJm8zoHhRAzT1jeVgixpXn550IIffNyIYR4VQhxSAixVwhx6oyxlbj0fzlngLe3N+npW2m0q/bpK9Y6iQxX60BSk7RMGmvg6VdUG+mFPzhwuWHaBCOPPmtjxCADe1YHkfGTP/95+jSSupcohBAIfx80HU9IKw3sABoJz6ZMXO/+gGvRJjy7DiNX/fK0khCC+F6x3PbONN4seJKhs3vhanDibzTi62Vg6dsbuCHqYV6+6VP2rz/Uqv1J3nr8Z3cjYv5UJLORsgdXYHPo0M4egHzkBALjPEPa72cwRprptnA6YVensXX4BxS8t5PwW7sT9/wolOpG9o3/FOMVCZg6hJJ3/VdIHoXE9ydy5MEV1G8rOmV7erORvq9cwbrbvkXy1pP26jgS9HoW37EQR4NDNaH8JvOk98kwPAGzWUfV9mJ0Eb44ixto2y+WnA25p74HkgJmE65DlWjCzDTsLQOau4nCLAiNhCIrODblYeoXe2yc9dtMjF0iODhnJ75JwXgBBeVWHG6Z3n9Xa2ncxfVU/3MZ5tv7YGg2ejxKWhS3Gyku/iTSIldZsT65BLQaTHcNxvbWRhq/z8AwOoWGhVmYhrQj6D9j0LSkAnwCXLWN7H9oBT92fQtDsDfDM++i/b190fysPspTq8r9n657TZEVHDuKqHh4GUUTP6bx0214BWsIub8PwR9Ox+ueYWgSw86x+60M6A7MRY24WFtYx43qI7IbGAe83eqtyznlOOeuwfH3+bheX4XS4EA7uRv656/FcM8YtD3bXRZk5URU7Shm2aA5fBbwND9OnEful+m4rE4kIfjiH53YdqCeZ+arjrep0T5sP1h/0vh6m5uCCgftwtVo4YC0APa+1Y99b/bjzcU57N7X8qTh/x8ucJqo9dGbV4CliqIkAZ2ATOBBYJWiKPHAqubnJ0EIEQg8hsryewKPnUBw/gu81Dy+BjjaPjYGiG9+3IIa7jwvXF6/olOgMGaIzPcr1RTRZwscXDvhOIN/9F4fvlzsYHe6iweftvK/f6utliVlHqLCj596x/ZbLu5hX2AIjYQUEYS2dzK6awaimzUSTWoMSk0D7u+24Hp/Oe4VO/FkF6LYzyWddipMPgaG3tiHpzfey6Or7iS8nYXKrArik8Jx25y8ctM8bop/nHlP/UBZXtVZt6cxGwm4vRcRn1wDskLpfcuwCxO6mwYhH6nA8fACXCsyWk1ghCSIub0HPZbdQOEHu9h19ef49Igk4b2J6AwaDv1lCY2KQuDMLuTP/gbJ4ab9K2M5cMsiGg9Xn7K92IkpmOOD2PPcOoJGtCNhQiphgd4sve97zOOTaFh2ELnxeHTIMKg9vm43lVsL0EWacRU3ENsnhtwW6lwkSQEfI67sCgydw7FlVyI7PcjFx72JXAcqkLz1aKPU7i7F5aH+87140sLI/XA3HZ8aRuErm9iXXcbYdyeh0WnwVNmpfvgHfKZ3wTRI1VRRFAUlLwfF7UJql3ASaXEfLMf62Pfoe7dF0y2G2gcWI4X6Ivv7Ylt5mODnxuIzucMZzRA9DheHXtzIyuTXcFbZGbLzNlKeGY6uBWVcAE91y2kid5mV2ve2UzzxY6ofW450pATLtESCX7oS8ytT0A9PQXifT1q0AdXk7AitTyk3ovqEzD/tGnJBFc73f8LxwOc4X16OUm1FO64T+hemYbhvLNo+CUhncCi/lOGyNuG2uRAaCY/dRcGiTH6a+jlfhD0HgJdRw3dPduHT1cXMXVrIsC6B2Js8fLRSnQR4PAr3vZvFrBEReBlPbixIiPLmoWnx/Pf1jy/6ef0BFUIIM+qPYi6AoihORVFqgfHAh82rfQhMaGH4KGCFoijViqLUACuA0UKdSQwFvmph/HjgI0XFZsBfCHFelfmXeY2Lh2kTAnjyhUrGjTCwN9PNjdeaWLdFTVt4eWgm4eQAACAASURBVAmef8yXgRNquPdWL+Lj1NO9c7YXU2+t4/X37AwfqGf2jEVEpD38W57IBYUw6hHtI5DaR6jRjzqb2q10qAjPmj0Is/fxluuIoPNuE22TEs7MFyYy/ZlxbP82nVVzNuGqsJM2LIGC9BLu7vZfYjtGMmJWb/pO6oTJ5/RhYU2QF4H39MN8bUdq399Byb1LMU/tiPetqXhW7cexfD/akc01MK3wXPJJDKbXylkc+e86NvWfS/ILo0n+YirZ139NxRfpNMQH0+afgym+fxmWe/oQ/cAAVeNl4XT0IcejCkII+r16Bd90f5N2UzvQ/smhlK8+wqYl2eRO7YR3h1CsKw9jvjIJAMlsJLhPNDlfZqEL8cZT00hsjzZs/2TnKccoKTJ4G3FmV2DsFY0pxh/7viKMVjvCoiq5OjbkYuwbe2yMbfkhpAgze55YQ5dXx1Lz4S6y3W7Sru9KRA/VCLL64R/wGpWI9xVq/Y2iKCj5uSjOplNIi3PdIRzztmG8oTdNOwpxfZ+JcUJHGj7bh7FfDIEPDj6jSJvikSn4dC9Zj/+IX+cw+q2ahTnl7HojRyMuoKaNGtfn0vBNOs6sCgx+WszJ/hjHpaDt3vaCuI/DfUAeZyzcbxF2VHfWIYBKJuXiGtwr05EzisHuQkSY0Y5OQ+qXiPQL/cB+CzTVNFKXWUFdRjl1mRXUNv/vqLDjGx+o5noASa/BK8rMsMXXQbdnAIlAXz1Ln+7GwL9tI9hPz4JHO3PH65k8Ne8IsqIwtoeFZ2YltLjf2yak8PyN68nJyaFt27YX8YwvUVz8Gpc41Bzp+0KITqh507uBUEVRSgAURSkRQrT0g44ECk54Xti8LAioVRTF/bPlZxpTcq4Hfvn9yn6Gjikacgs8fLbAwdhhp+bLrxxpwN9PcMes44WNo4YYOLIlmKU/NvHDaiddhuwiPaMCi0WtDWjKrqB+SRZBd/VFukS1H1oLIQT4+6Dx90HTsa0qgldWg1xQgWdLFkpVPSI86JgtgQjyPWfxOZ1BR5+ru9Dn6i5U5FWz+r3N/Pj+FqJjgoluZ+HHT7fx9t1f0ntCJ4bP7EXawPanDZlrw3wJfmgwrrxaaudup+GrdMzXd8b79lTcy1UCoxuVimbg2QmMpNfQ/p+DCR7Znn23fIt/7ygSPp7M4Tu/w1NuJeuhFST8azhVL2/Ed3Q8lskpZM36htQvp6I5Qa7eNyaALg8OZP2dixm7bBYd3xlP1aRPWXjTV9z09mTqv8w4RlwAgqd3xv7adlw2J9oQH0LD/ag4WImjwYHR9zh5k2QPipcBV1Y55pnd8O0ShutAAaYkyzFy4diYh//9ql6MIivUz9tNidDg1zmMgLb+bP/Xj1RbG5n45HBkh4vqR5dh6BqJ99RO6hhFQSnIQ3E0IrVPPNZSr8gyjvk7cG/PwzCtO9YPt6FLDUPq3Ib6T/YQcN9AjL3anPa9VRSF8h8OkvHwSrQ+Brp9PJmgfqdq1ZwOnppGhF6i+uUN2JdmozFpMPgI/Gd1QDckASmydUXfrUMDGs27dOig3oM1Gnj9dejbF3JzITkZkpLA4QBfX7jzTpjZnLH/4APYvt3Jq/9+DffiMcjpRWB1IsJ80Q5LQRqQiHSR3eHPB4qi4KiwUZdRoZKTZpJSl1mBq6EJv2QL/ikh+CUFkzi4Lf4pIXjH+iNpJBalvUb9gUoS7+hJ1/+MRKPXYi1Jh61/A7mJNhYTOR8eb/df/ETLpQuDOwUyuFOzPYFkwBQ/jaKizy/G6f9/RbAQ4kQ9k3cURXnnhOdaoCtwl6IoW4QQr9BCWug0aLGc6QzLzzTmnHHZExcQXDXKwN+ebGDNNwFUVZ/6PkgCfn6fDAyQmD7JxPRJJsZd38iyt79kcEEoDdtLaLK6QQG/q1LQt7u0PUzOFUIjqSaQEUHQKwmlyYVSoGrHePZuAY9HFcFrY1HJjNe5Fc9ZYgKZ+sRYpjw6mr0rslg1ZxMFWwroPSoVLy89b/z5C5psTobN7MWwG3oRHtey8Jguxh/Lk8NxHqikds426j/bi9/sbniNTsO9NB3XstYTGP9eUfTZcBMHHlnJjimfk/z8KCrm7MDbpCPzL9/R9uFBNK44ghRswishmAO3LSbp/YmIE0L8aXf34eAnuzk0bw/xMzrT4bZeVL23lXWL99Oh2ErToSoM7dXviqFLFOZAAxXfZ6GP9EWusBPVJZK8LfkkDldnn4qsIDweZFlBtjnRRPjh2ykcnbscEamSIFd+LXKjC12CSqgbN+TRUNtEye4yhm+/jSN/WsDesjrGfTIVnV5DzeMr0Eb54XtzL4QQKmkpzEex25Dik46TFrsT+//WIjtciJRIrB9uwzSlM9bF2WgCvQh5e9IZu32qtxSS8dAKmipspDwznLBxia0mu7K1CdvKw9S9tx25vgltUQX+fUMxjklB0zn6mAXBhcUnmEywe7f6bNkyeOghWNvcDd+uHezapf5/5AhMmgSyDLNnHx3vQYhXUHK6oB2QgDQoBekSNWJUFAV7UX2LBEWRFfxSLPgnh+CXbCFqXCL+KSF4RZnP+Pl1emIohgAT4UNP6ADyiwdTKNjOt51ZgcgR5zn2dwjBrxFxqTyLjkshUKgoytFaia9QiUuZECK8OdoSDpSfZuzgE55HAWuAStQUkLY56hIFFJ8wps3PxhRzHrjMiYsAoeXGa034mSU6JOtYs+Hs3S2r1zvp3VWHl5egwSpzOMeFyDpEpfGEsQLsG/PA6UYXF3RJe5r8EgiD7lhaCUCpsyHnlyMfLsGzdi/C7HVcBO8c0koajUSX0Sl0GZ1CXXkDP32stlXrZeg5viNVRbXc0+s5olPCGD6zF/2v7oqX76kkSZ8QTMizY2hKL6Xm7W3Uf7ob/5u6YxzTAfeSfbiW70c38uwERuujJ+XlsVQsPUjGX5YQOikFqcqGrxxM/subCRrVDpNbRltch1NWOPLQCuKeHXnsgi5pNQx4ewLLJnxCmzEJtL2/P6U/HGDdF/tIvak39QsysdzfX31PJUFgl3DKF+zH0j4EZ3E9sX1iyNmYd5y41NlVjZ4yK/oEC0ISmNMC0RwqQwSr0QbHplyMfWIQkkpCqt/bzuG95XR5fRzWpQfJyK+h7ZhEYofEUfvsGjBo8PvrgOOkpagAxWY9KdLiKa3H/sJKpDYBuIsakLRWDGPTqJuzA99Z3fC+Mvm0N7GG7Eoy/7mKmi2FJD02hDY3dGpVRFJRFJp2l2BdlEHj+jz0/jokjwtD1zCCHhqMZLkwMv+nxxsnPauvh4DTBHTi4uDFF+G++04kLoC3wPBwEND5VzvKc4Eiy1hza6nLaE7tZJYfIysaLx3+KRb8kkMI6BhG22kd8EsJwRjifV5WHrGTWzYJpcP9x6Iu5wTJAEm3gu7S0tn5zXGRU0WKopQKIQqEEImKomQDw4CM5sdM4D/NfxcBCCEiUWtUhgHLgGdOKMgdCTykKIoihPgRmIJaHHZsPPAt8GchxHzUot66oympc8VlfjfWgOImKkLD3Td7nX31ZuzY4+LPD9Wj1QpkWfCn2eMZbR9G0TeHkD2KWuAtQfGLG3A1epC0Ap23Dr3FC2PbAIxJFkydI9AnWZACvX41f6HfAsLPG02Htmg6tEWRZZSyWpT8cjxbs1Eq6xBhgapBZLQFEXTmmdpR+IX4cuV9Qxl37xCyN+awas4mdi7YS9ch7YlMC2fTor28e+839LwyjRGzetNxSMIpqSRDWhhhr11J4/ZCat/eRp3Tjf9NPTBc0QH3960nMJbR8fTZeBMZd/+A/VAVlm4RKI0ubFmVWN0yYQNjcS07SEO5naJXNhP11z7Hxob0jKLtpFS2PrCMge9OpPOciZQOncPyr3YzKtpC0F29kYzqvi1XJJH/4noi+sXhKm4grl8s697YeGxbSlkDil6Hu7geQ3P7ssnHTcnOWsLHe9B4STg25uF7g6ru3LSnhNyNhQQNjCWkTxu2jHif4gorNz0/hvo3NiLXNhL41Ci1E0lRUIoLURrq1UiLVj0md3oxttfXILULxbGjGNOUzti3FNK04hDBL41DF9Py3dxR0kD2v9ZS/NV+2t3bl64fTETbioiDu9KGbUk21kUZ4HRj9IbgMW3QD0+matEhDGmhF4G0AJTS2AidO6vpoJISWH2GTueuXSEr6+Rl6tf8vK6xvwiyy0PD4epToif12ZXog7yOERRLn2ji/9QNv2QLhsDWXwt/Efziocs/YddTrScvkgHiroE2l74Exf8T3AV82tyyfASYjdq084UQ4k9APnB187rhNBeJKYpSLYR4CtjW/NqTiqIc7W54AJgvhPgXsIvm4l9gCTAWOIRaPHbi1OCccFkTF6vVCnV3geMbQNUZGNxPz+B+J19Uc7efrO55/53e3H/n0QJMI1jmgOSHz6QC8v+8GFulE+9wL+I+uQZ3bhVNe4pp3FtKU14tjbuLqdtUiNO2DUkCrVGDPtCEvo0fxvggTB1DMSSHoI30v+yjNEKSEOGBEB6I5mhaqbASuaAcz5JccLnVAt+jInjeZ04rCSFI6hdHUr84Zr8yiQ3zd7JqziZqS+oZ96d+aLx1zL1/IfWVVobe0IvhM3sRGX9yXZipexTGbpE0rs+j9t1tCIMW/1tVAuP6fq9KYEaloRkQf1oCow/2ptMnkymet48DD68kpG8bXHm1+AyIIfeTPcTe2BXl83RKP9yFPsKXkGvSjo3t+fQIvkx7ldL1uYT1j6XHI0P54elVNEhgW3UE3yvUiIplUFvSn/gRYW/CWeckdloan9wwH9kjI2kk5PIGFIMeuawB/VWq07RSVoGtEqz7yvBpH4C7sA5DR7XoPu/fP1FT7WDUa2MpfOxH9lU2MOK1K3EvzsB1oJLA/4w9dr5KSRFKXS1SgkpaFEXBuSITx1e7kX1MKLWNmK7vQd072/Aa1h7zo8MR+lMjJ656B4ee30jOW9uIntmZYRl3oQ86801RcXto3JCPdVEGTXtLMQTp8A3XYxzTEW2/9kj+6njPh/vRBJ6fau65w3lSqmjTJrjhBkhPP805tDjxlVG7jH4deBwu6g9UHSuMPUpQGg5X4xVpxi/Fgl+ShYgR7Um+uw9+SRZ0vr+ul1mrENwdej4He/8DTdWqiWJLZQsak+odl3w7RAy76Id5WeA3EKBTFGU3qkbAz9HSh9QbOGYupSjKe8B7LWzzCGqL9M+XK6giSr8Yl/edFcDrNnB8x/ldVLRgvAIk1YjO0LUN7ZfdSNk9CzH0ikGK8Ecf4Y++bzuOzgvl+kbk/Bo8+VU4M8pozCjHWWzFmVeNLbMC5yf7QFHQ6iV0Zj36cF+McQGYUkMxpIWijfJHCro8ozTCoEO0C0dqp95MlTobckEF8pESPD/tQ/iY1G6l6JCzppW8zCZG3NKPEbf0I3dPEavnbmLtG1tp2zWKodO6U1ZYw/39XyS8vYURs3oz4JqueDeLjAkh8BoQi6lfDPZVh6l+bh2aEB8Cbu2B4QqdSmCWpZ+RwAghiJzRkcD+0aTfthjFo1C/7BBRN3cn5/UtRMzoiPzDQXIfXY0+xBv/wWrXg97PSJ+XxrLutm+ZtPMO2tzWg47fZrF7byE+H+46Rlz8ki047C5cB8txujX4WHzwDfWhNKOMiA7hyOX1yEYdnkN16BItKFYbOJqQLIE07C5BW1GPsUcbhE6DfXcJB74/SLePJ9OUWcnuJVkEd4+ijQbsG3JVp+fmYmK5pAiltqY50qJTicQHm3BuL8TTKGMa0Zamcjv1c7YT8OBgjF0jT3lvPE1uct/ZzsH/rCNkVHsGb7sVr5gzm226cmuwfpeF7fsstdDWpGCe1A7dkESkxLBTWqk9NY1Ip3HovvDwAY7ri/TpA5WVUFHR8tq7dqkFuydDA5yf4eiJcNmc1GdVUJuhEpTaZoJiy6/DNy7gGEGJnpiC38MWzAnBaE2/vSHsGeGXAP3nQl0m5HwNFZubXxCgeMAcr0ZZLH1AurybHf4/Q1GU13/rYziKy5+46FLBNAMaP+XcyIsAKQB8Hj95qa+RsDnTTjtKMpuQ0kxo0yIwjO2AL6A43cjFdcj51SqhOVCB40AlLoeC0+qgdmMB5UsOIbtktAYNOr2EPtQbQ4wfxkQLxrRQdNEBaCL9LqsojfDzRuPnjSYtVk0rldei5Ff8LK3U3K0UfPq0UmynSG58dQrXPTuerQv2smrOJvL2FjF8endC4i3sWJbB3PsX0H1sKsNn9qLz8CQ0GgkhCbxHtMdrSFusSw5Q8egq9O0D8b+5JwYDuL7bi2t5M4Hp3zKBMcX40/27GeT9byv5L25Efn0zsQ8OoGjuTnySgzEfriH75kWkfjUNn06qw3Tbyalkf7CTvc+vp8s/BtNlzngKe75J44FK7FnleCWFIGk1BHQKx1pQC251v0eF6CI6hKOUN6BIGoRWgybQCzn7CCIiFN8uTmrW5mHK0+I1OhGA3bcsIqhbBGFXJLJz2PvkVtuYed0w7IsyCHphHJpmrRS5tBilukqNtOh0yPUObM+vwFXcgPAy4H1dL+o+2Ik2yg/L25PQ+J1MHBRZpujzdDIfXY1vkoW+S2/A3CH0tJ+/bHdiX3UY66JM3AW1GAK1+KWZMY5OQdurLeIM7e+emsZfJ+Licqh/hQRCQna6oSGFE2sAs7LA44GgILCfrERPbi787W9w110/37ATtQGjdXDWNjand5ojKM1kxVFuw5wQpBbJJllod31n/FIsmNsHIf0qhckXCUKAfwp0SVFDVh6HSlq0Xupn8QfOgt+/v9CFxOVzlzwTfJ9UjRMdP9A68qIFYYaABaBpnUncmSD0WjSxQWhig9ARjxHwVRSUSityQY1KaAqqcR2upKnUhlunx+lQaMiupmpjMR67C62XFq0EOj8DhjZmNe2UEoo2ViU0UvD5FdZdLAhJQoQFQlggmp6JalqpSPVW8izdBk3uZhLTHJFpIa2kN+rof203+l/bjdLDFfz4/ha+/fdKgqMDmPn4FTg9Hj56ZDEv/+lThl7Xg2EzexOdHKb6IF2VjM+oeBq+zaT8viUYOofjf1N3dHhUArPs9ARGaCRi/9KboKFt2TdrAflPriXiL72wZlRgB/zaBZIxeT4dllyHKSEYIQT9X7+Sb3qo2i7mdkH0e2Es6Y+swPHQCrovmAFAYLcI7BX16NKrUdwybfvEcnj9Efrd1ge5rAHZKRDNN2+5qBRNp2R8dW7yX96Mf7iegEeGUfT5PirTyxl58K+Uz9nBzoPljLyrN66F+wl69go0FrXAUS4rQamqQIpPRuj0ePKrafjXUjwNLgyjklB8TNS8uB7zzT3xGp1wynepfMVhMv6xAqHV0OXd8QQPbllXQ1EUnPvKsC7OxL7mCPpAAwajjP+1iegGJiC1DW7V91Q+D5+iVkGWUVxuPAfKkPcUIWeUIqWOoLFxJZ07Hz0H+PBDtS0a4PBh6NLleDv0XXf9rDAXUKPksafszlFhU2tPMpprULIqqMs4tcU49Gctxr9rCAHai5UG/B3hD+LSaogzybN3795d2b59+2lfv6SgKGB7BeyvNT+3tbCSDpBA1wX83gJN2MU8QkBtRZULavAUVCPnVyMXVOPOr8Gl0eHS6XE1yjRVOWgqt+OudaD10qHVCbQ6gSHMB0NcAMbkEHRtA9FE+aGN9LtAAl2/Lo6llQoqUAoqED7G5m6lEEREIELXMof2uD3sXprJqjmbyFh7iF6TO5E6NJ4Duwr48ZNtWKIDGDGrNwOndce32V1Ztrto+Cqd+s/3Yuofg//sbkhOJ67v9iDnVTWnkBJabL2Vm9xkP7CCugUZBIyNx7tTGIWvbcE30hd7Ti1p383A1FxMu+e5dRStOsyYH1TRjx0T52E8UkPAu1cR2Suawx/uonBhBpacWtp9O4PqBgdzJ3zAwwcewHbHPOySF+i1WJ4YgmfTTjQjB4CssL7tSyROSyLgkWEsa/sSSdM7EP3AAJYPeBcl0puekb4E/ms0uni1lVwuL0UpL1MjLXoDzo2Hsb6+DkWnw/u2flgXZSI3NBH4jyFoI/1OOt/aHcVk/GMl9vxaUp4eTvjElruKPFV2bEsPYP02E6XRidFHYIz3xzA8CU2PcxOJU5wejgycS9ymmy8YGZedbuQdh5EzipGzyxEWH6ROkWg6RCKFBYFIRK0JPHcoig9NVR9QvavT8Tbj5i6en7cY+6VYWtVifMlD8QBLQFmAapUAEA5iCjDydx9FEULsOEsr8QVF99A2yvYZF9Z6Rrx070U9h4uJ3w9xOQqlERzfgu118BxGLZD2gPAG4zTwugm0sb/xQZ4MxSOjlNbjaSYycn7zwyXjMXvh0uppsntoKm+kqageV7kdjUmL1iihRUHnb8AY448x0YK+XSCaSH80UX5IQd5nlGn/raDICkp5DUp+M5GpqEWEBhzvVgr2a/GiX1NSx9qPtrJqzmZ0Bi2DZ/XEL8qPjQv2sGNpBl1HJTNiVm+6jkxGo9UgNzRR99kerAsy8B4Zj98NXRDWRlzfn53AlC85wJE7v0MfZSbm0cEcum8ZBl897nIbKV9OxatzOLLLwzfd36DzgwNpf20nnFV20gfO5bDsZuKeu2g4UMWayZ+RGuKN5aYu+F3flYeDH+cf2/+CeH451jrQtrMQMD0O3G40aWpqaFvn/xF1XUcK91VgX32E/rvvIPueJWxdkc2ofm0I/OdwDJ3U9nW5ohylrBgpPhn0euzvbqRxeTb6LlFo+7Wj7n+b8B6bhO/1XU/SpbEdribz0dVU/pRL4iODiLmx6ympCsUt07g5H9viLBw7izCEGDGYFIzD4tENSEBqpTP4z+Eus1I46xtif7jhvMYfhex2I+/MQd5TgHyoAmE2IiWGoukbhxTopdZT6IzNLUELgRmozQznsA+nhvoDwSwfeTf+yaH4JVnwSwlRu3l+QYvxJQulHpTXUC1snKhWCSfCB/AG7gFxh3pd/R3iohOXsDbK9hn3XNBtihfv+4O4XJZQFFDsIAwgLr+smFxrP5Zqkguq8eRXo1RYESG+eMzeOIUWV6MHR4mNppwamgrrkQwadN46tJKCViPQR/piSghC3y4YTaSfGqWJ8ENcQgV/ivNot1IFcn45NLlUEbyjtgQ+J4edFUUh46dDrJqziR2L99NpVBJ9p3alsrSO1R9vpSy36lgqKTYtAk9NI3Uf7cL2wwF8xidjntEJUWNTIzD51ehGN6eQfnbjbiptYN+4T3DVOGj73ChK3t2Op7Ae4fQQ//o4zCPaUbYpn+WT53HN/rsxBJgofn49BXN3YJ2cxJDHhzM/4Bn6XJWEwQgRc6/m7SvmMnhSKlF55dRtr0A/oB3+PXVouqQhAv1QnB729nwDukZR8G02Pe7uhbFfDEtnfkHfzqFY/jEUYx/VKVquLEcpKUZKSELxCOof/g53YT1eN/bGeaAKx9YCAh4cgqHD8chiU7mV7Gd+ouizfcT9pTft7u6N1ufk7hRXfi2277OxLslCY9BgMMkYUy3ohySi6Rrzi0XimrIqKH9yDW3mXX32lX8G2e1B3pOLvCcf+WAFwkuPlBiCpnscUlzzeTbZVbJyjLQcxX+Ap2gteVE8WmR3MG77ZgwBMWcfcLlDKQBlMFAKOM6ysgmIAbEKxMWPXP/a+IO4XNq4/O7m5wIhLusZgeTvpbaPdjje+aE43ciFtcgF1Riaa2d8sSJSvRCjIvGYvXErGpw2N46iBhqyK6n86gBCHERn1qPVCTQeD/oAA4a2Aejjg9FG+aNtJjVSsM9Fj9IIvQ4RF44U19ytVG9XIzG5ZbjWpyO8jM0kJgQRGYTQaUkdFE/qoHhstXbWz9vB108txVbTyJAbe5E4oB07V2Tyz9H/IyDMzPCZvRg0ozvh0zpS98EOiqd9ju81HTDP6g+VDbi+24NrafopBMYQ5kvXTbeQed1X5Nz7AwFT05CSg6lemM2Re34g+m99CZnZhbYTUtj60HIGvDWe8Lv7YP1iP5tf20TatE4EdApDDvbClVGCp9JK2z4x1OwqJDLCB8nPiGRQVJnWADMATbuLMUb5kvnFftqnBhMwvSMbJ82je0IgAXf2OU5aqipQSoqQ4pNxHaim4ZkVCB893n8bSv1bW9HFBxPy9mQkH7XbyG1t4vBLmzjy+haiZnRkaPqfMViO/zbkRhf2H49gW5yJK6cGY4gBv2g9hmGJaPu3RwoxX7DP23OO9S2yx4O8Lx95V55KVgxapIQQdLP7o0mI+D/2zjs+jup6+987s31XWvUu2Zbc5N6xccOFYpsQiumYFmpCTyUhlORHCCGQkPAGSCB00zuEZjC4gW3ci9wkW5Zk2eplpa1z7/vHrMracgMDNuj5fEY75c7sndHs3GfOec45++5gc4IQGMEITVtqTIFsUTWNRT1JHDSLAb94HaEpdLtxgG/1IPSe6PrH6PaD11465qGqQI3FLF1zoOvSBj+wDdQ4YCWII1mi4QeKbo3LIePYsbio9SAfBPUepvlSAF4Q54L2UxA9v8vefadQMioEjhKZNleTagmi5SQichNRXjfhiEawKUSwtIFAUTWB7fWooIE10Y7VrqMjsaCw53mx90nGkpNgWmmi03eR5tx0KzWgyqqQOzu5laL5Y0Rqh1upZGUZHz/2OYtfWEnfsT2ZcvlxWJxW5s9dzvJ3NzB0al+mXzqWYYNzaH5qFYEVFXgvHEbcGQNQlQ2E31mLLNvXAqOUovSu+VTNXYeR7CTjtH7sfng57jQ3aT/qT8JPR/PK8P/H9JfOJ+P4PKruW8SWx1ewWoUZfXJ/3K0RPI2tpJ0zgIoUD7se+Jhho3oQagjjKHTiGt8DfWAfABr+vpD1LxbRtKmG0dePoUUTBD/ZQvxZg8m80czMK+tqUBVliIJ+tL6wlsC7G7CP7YHMTaH1pXV4fzoO1/TeZtuwQeljK9h89wJSp/Si/11TcOcn8xafgQAAIABJREFUtZ9XaEMVvnc30fpJMbZkBzZLBMfILKyT+6IPyolxLx0pNP9vC61LdpL+f9P320YaBrKoHLmyFLmlyixV0TcVbWQv9L5ZMYUi20KM26N4iqraQ4w9vTpCjBMGpJkRPP18WBz/Bh7FfI4Y0ckKhDGjh34FzOL7/m7XDjkes8Ze+GAt94INmAza+0e+T98hvhOLy5wbj+gxxV9/+b21uBz9xEUtBeM6YDOmz3XvtwEbpo5lDOgPg+i6EukPEaolGCsE3lmPrGxAJLnR85LQ8pKQXjfhMASrWggU1xHYUktgay1GUxBbkgOr24qugR4OY0t0YM9PwpJnEhpLtvmppX17VhoVCqMqas2yBDurIRCKkphotJLHSbA1xBevrObjxz9n16YqJl08mnHnDKd4TTnznvyCXVurOeGCUUw/cQCehWWENlXjvWQEnlP7ocrr90tg9jy9mrJ7F9LiC5F2xgAaXtuIJyuOhMFpBMbnsvqBJZy14qdEKpspu+hV3llVSu8T+5IYkmTEOUj0gvMvp7Hix/+m3/AeaJkJuPNC2E4+DpEQjzIkRSf8mx1lrbj9YQY/NIPqfywmkO1l6AsXACDra1FlO1GJOTTftwC5uwnX+SNoWVyOChsk3joFS0YcSil2vbqRots+xtUrkQF/mk7CcNOiZdT7aflgqym09QVxJFmwJ1qwT+uHPr43WuI3a6VseHYNkT0+Un4+PvZ/qxTGpgrkiu2oLVUopdD6pqGN6IHWP4dIc6hT9eIOguLfExti7I0SlLiCJPQD1rEKAvMwXSNBzDwto4E+39SpH51Qa7n77lHMfT6Mrpt13R59WPDrWxWVleCMGsd6F8ArL2vceZfkL/fBjhJBWpoAHHjiwefrKiDi2EQ3cTm6cXS/Tsi3QF7EgUOc2+oLLQRjLOjvghh3gPY/HAi3Hb1/Bnr/Dh+0ikjk7sYOq0xRJWJnHU4E7rxEtBl5aFcPQyV5CLcaBHbUEyyuI7C1Dt+WGsLri7EmO7HG2bDYNCyRCLqU2HskYMlL6LDS5HwzVhphsyJ6ZaD1Ms9JNbealpjSKsKLN4LThp6XxsRJPZh0/gh2ldQy/79fcO+P/k1mn1ROvXICecOyWfTKKu66di5xiS5OO20YAz/cStPcNXh/MhL3tSegyuoIv7OGyAfrsZwyCH18H9IvHoYt3U3Jrz6kaWkZWq8EfKWNSEPiqWzGlexi7f2LGPabyTgKU5mWE887r65hQFYiKX1TETletO21pKe6CJY3ET8qC1QQvGZ6w5alZWxbVc2w2yazZ+5a6h9ZSk1rmFGPnWWea30dcmcp4d02Wv70LrrTgv28UTQ8uwbPmQPxnDcUoWtUz9/Oxls/QknFkIdmkTa9AGVI/J/vxPdOEYFl5diz3LjtIeyT80yhbf/Mb418Gg2xriJj6y6M5SUmWQkbiN6p+Efls6c8SOPyWhqe/sSsYtxkhhh7C1NJKEwlffKYrxlibMe0qvyw8fmS3/LOuxFWfimw2wU1NYpQ9LH63DOCUaP2vS9SUuD+BxT3/rnNYiW/1T5//9Cdx+VwcPQSF7XgEEhLzA5AMxgzQV8CYp/Ul90AhEVDz0lEz0mE4wsA801XNfjbI5qM1WWmELiuBWemF3deEtrsPuh5x0FqHME9LSaZKa4jsK0O37ZaQp9VYEmsw5boMKOdlETzh0yrTTS5Xrs4ONuLlupBHIF8FiLOhT6wBwzsYbqVqqNJ8FZuRb2/nLS0RM4/u5BzbpjAqmXlfPL4Fzx58+scf85wbnv5CnzNAT55ehn/eXMt08f1Zspjy3E/vYrEq8bg/NlUVGmtSWDeNwlMwtQ+9H3sdLZe8xaOAWlUlzZCTSsRf4hcl5VV9y4k/5zBxJ9ZCK9upEe2l4adDYS9TuxTRhGct4UEp4XAniDWRAhuU9ijrq7Vt7xPxvG56Kt3kZrjorGqhaw/nozdY0c11BPZvI3WeXVENlZh65mI4Y3D98ZGkv/vJGyFaTSu2c3G387Dt7WWwj9OJfvsgUQqm2n49zJa3t2MZtewewRJoxOxTemHZWwBoovClt80jDo/uk0RfG4RbKtGBcIYmV4qWzVWPL0ZFdqCd2Bau3sne1ZfvIWpuHO7jjbrxteAClBZOY+UZIXdbv4eU1LarvH+B9LLL4Mnn4Jf/0qRlBQGpBlCLY7hJHrdOGZw1LmKduzYwamnzmL96hrArNl05x8MPB7B+vWKU2cJZp+lUVenmHaSwQ3XaUw5QVA42KBfXwiFYdSIBB5/ogqr9eiJnDkWoYLhdiGw0eZqKq9DuO1oUVeTnpeElpuE8joJlzURKK4lsK2N1NQS3F6PJc5uWmncZpI9PRRGj0Sw5kZdTjltOpqo68l9ZKw0KhQxk+C1RSv5TbdSnc3Bgvk7+OTZL3F5nUy7YhyjThvE6k82M++JpThLGzizdw5xqR7SbxqPc0wOaodJYFRFPZYZgwmlJbHlijfwTunFrteK0PxhNKtOcyBMa5qLUxdfRenMZ/DeOpHXT36KUYMy6P/G+bTc/i4YEXbVGfS7roCGxa2k3jOL8tc2svqy1zn+wZMJvLmRxj0+dtWEmLblJlRjA8F5q2h5uwJNCCwD0mhZU4t9aCbe644nsMdH0Z3zqf6omL6/nUTenKEEP9+J751NhLfW4shxYRMh7OPzsUzog1aQ+q0RACUlvtJGGjdWESnZQ6IK4PugAle6BeuAZKpqw1Q3C7yF6dGCgak40j3dBOXbgtqBr3kwEyb5aG2F6dPg3HMEkycLTpgqY1xFJ06H+/5iuoo8HkFrKxiG4q47NTzxEl9zLYik/X+XlLBpO2zeDr5W0DXT2jisELKPLgH0t+8qylFfXnLDET2m+Muvu11F3y6aOZBIrLFRcfJMg6uu0LjsUo0dOxQFBbB6hQXDUJx4SjMvvXgvF15027fX5e8hhN2KXpCKXpBKGwU0rRrN0fIGdYQXbEWW1aP8IbTcRJy5SbgHJaHNKEDLSQBdI1TRFENm/MV1BHY0o1WGsKW3YI2rwWLVsBgRhC+AJc7WyeXUpqeJamkOw0ojbJa93Ep+ZFkVSTurOS1P59S7JrCpNsL8Dzbywm3vMGLWQObcOZOkvETmP7OUypfWMvXGWmxpHtJuGk/a9dOQ22sIv7MGrWIdfX85huKHV5N1en8aVlXSur4Kt9fGnqJq1lz7Fjmz+iE31pA5MhtfdQv16/fgGZSBf00ZDF6Flrsex6h6Ig2bqXixiD5jRxN4p4hwKMJnG2sYnJmAUVVDy38WE97ajK6DyE/F98UeEm4cjz4wnY23fczOZ9aQf+1o+r91AcH5JVSe8zzWVCcOm0H88SlYT+iHPronwvnNiatlJFrFeK8EbU5LhKE/zidFRqApCHmJNFgsaHPG45mSjwfI/8Z61Y2Dw4fHo7NiuWDhQpj/qeLc8xV//pO5dX+uIoAbrodhI+Dnt7S9/DYDXRCX1gAsWQWLVkLEgGCoY5sQsHgVJCfAlDEwrL8psulGNw6Ao5S41LA/4uLzwYxTDS44T+Paa/a9wXVdMGa0pKL8NaCbuBxpCE0g0uPR0uOxjO7Zvl75gu0iYGPLHsLzipB7mhApHvS8JJPQjM1EO3sAWoILpRThPT6T0GyrJVhch29bHYHyIMgAtnqJrbwV65oqNCXRW4OIQAhLZjx6dkInK01US+M5eKVcEedEH9ADBvQw3WPVjQzeWcXAnnE0TU5j8cYG/nvlXEIGTL3yeC798Foqt1ax+aElhH/9PltcFiznDGTElZOwRqOQ8gc6KV1ZgTs3AVuCk4YlO0nPjGfNs6uJP28oenUdI/9Sje5/BS3jIVyTIrgtNSQZFjRN4OltoCKvM+pfFoR8k+Y3J/PGPT2ZcP85hP7fUhp+9T/0zHgsNkFYd0B9mKS/zaJ07nqKz36J7DMLGXvPVIILdtDwh49xZDhIyLdjn9DLtK7kHeAN+Ctg3xBjk6C0VzEuTCVrZBrDT0jFOsCOqmtFS3agDcxGG90bzW6Fj+bi6p18RPvVja+KOECi64ITToATThAMHqR46umD6y0SEgQXnK/418Nta7oIma+uh0deMMlLpIswa6UgHIHdNfDqR/DlBrj0dLD9wKzlgm6Ny2Hg6CMuqhoz+VHXvtJbfim54nLBzTd1zcoDAcXSZYoHH9ho/iiEQBmS8PJSwu9vwHHlBPTsr1/ltRuxEB47lsJMKMxsX6cihll8ssx0M4X/tx5jZx1CF+2uJmduEp4T8xFzhiF0DaUUkTp/O5kJbKujtbiOQGkr0hfCHrBg9SmsZT4sWjl6KIxoaEU4rGYumk7CYEt2Alp611YaIQQiLQHSEtBH9SUpHOHUilpm7NzDtk+3Mv/9Nfzing/pPyqHaddMoM+0fmy67zNcczfwwSPLqBudwdhrxtN71mB6vbmGna9tA4cd7+hsbGWN+OQe5Oi/0+uSVWDR0GyxWi1dRcwZqSE0CTZz2XPWB1xwhk5kaS+a8pyE3E5cTUH8dQauswqo80VYMeG/ZIzIYPgFgwhv2EMkFMRpDWIfn4p1Ul8zSdwBo2kOjpgqxlGC0rCxmtayRjw9E8zIncJUcn9cyOBbJ+NJtiFWlSA37UFV1aGFktHGF6CN6Y3miCWVRoMfLfHb19Z0oytksHmzgaYp+vSJaq3WKHr0gPUbDr73LTcLRh+niEQAYstJUN8I/3zOLAJ1KGNyKAzby+HfL8O153YUk/qhoJu4HDKOOuIiRA1mePPe683PqVMEb76t+MUtKhqKZ6K4GIaNjLB1G8w+UzBkiIYKNRBeUEnozbWoYAQMiWo+WEbIbhwpCIuOHtXBEI18VUqh6lvbo5qMlTsJvbEaVd+Klu1FyzUJjSs3Cc/phYhOUUmRpkA7mQkU19G6rY5gSTPh6hbsuV5sWgBri8S6owEtYqA1+VFNAfT0uHbLTOeop85WGmG1IHqmo/VMp3DSEPrf4ueSonKWPP8lr//uLf59jZ/Js/oz5fbxjNjciP/1IjZe8zqPB1sYffEYpv7lJBrvW0TT5j14BjYw63//QXP40Oz7ibZou3U1aU4RCyDQHRF0IljG/5a6ZdfQNK8HWu8kjJMLWfWnhSQlORkwJAWLXWALtOApdGKbmG8micvwdv1dB0B7FeOuQoz7JJnp7QtTyb9wKN4BacT17ggxlnVNGEu2IOetRO5uQuuZjD66J9pxfdBcXVvAZDCCChlHTMfUja8JYcfnm8H1N75GQ4PEYjHDnv/9qGD2OYoL5yicTnNATUmBeR/GPptTUgRnnK7xt78bsfWLpIJHX4ZA8NBISxsiBuyqgrc/hdOnff3z68b3EkedONfX/Bn9+k+horSDbd9wk8HIEYL5n5ri3PJyeHauZP48nbg4wY4dilNPN1i/2kJlpeKE6Qb3/dnO1JX/QpV2+jEJINFtPjStupmfIzoJqw4Wbd91XbXb3zqLZq6zddqua91Cw0OACoSR5fXt2hlZVo8srzfrz+QloUcJjZabiEiJFW8arWGCJR1RTm0RT6GKJmxZcdiz47AmOLA49Gi0UxC1uxlsenvG4Lb6Tnq2Fz09LsZKo5SibPFWPnlkEQvfLiI7w8XU6X0YmJREy+eV7HAInl22hcwROcweJBh4663ocf5Dr0PX9hOMkpc2SL+N9RfeQrg5A7chcbmtOHt7sRsBbIMysEzsgz4k95CSxLVXMY4SlIYoQQk3BtuLA5pRPGYeFE+vxC5DjGWDD+PzLcii3aiKRkTPJPTCTLSxfdA8B8+GG9nto/zy1+n5vzmHeHG68Y1DbQI1ikOP4NwbDhBFIPLa19x98y+Y++xz6IAmBI+eNJuR6dncvvhDXt68Fnc0cOLsfkP53ViToOj3/4rBKRlEpKQwNYOnFn+KK+m7sY5/6+LczBz15WU/O6LHFPf8tluc+23B48kiM0Pj408k06aa0UPvf6i48XqN+Z+aT/ibbtSo3K04Y7bkf2/HPlwzMwV/vlvjnntDnPrJeYTe2kD4o03mG4AucF58HCLFA2EDFTYgOqmYT9kxHzKQLSHzTaBzu1B038je+5r7t89LCZa9SY/WNRFqa2frYl1Me+3QCZVFB10c9eRJOKzovdPQe6d1EgJL1J7mdu1M+NMtyLI6VDCClpvYHtGk5SXh7JuMa1B6zDFlKEJwR0MHmdlWS2NxHcHSBqypbux5bmxhHWtVAEvtbrRlO1HVPmSDfy8rjZfMbC8XP3whFz6usfy1NXzyyCKeWr2GSWOymBSXwO2DexPsGU/yz25BuAMIDXR7hMGDTBe+RYdL5mjcdKNA0wS/+73Bu//reGlobYXikgiNux14POb/6ow5PiqL7+fVAf/Ek+XA7hZYJ/Uxk8Ql7ZskTimFf1dzlwRFRWS7eyehMJXsmX3xDkjFnRMfk4W2K8imVowvtiA3VqLKGhB5iWiDstCvOAEt3nVY/2ej3o+e0O0mOqog+kfT/S+mIy/WocKBWS26g7R8/vnnvPPmW6y86EbsFgs1rS2EZITbFn3A7pYm1l16Cw6LleZQgPuXL2jfz2mxsvoSs0Lyhe+9wCN3/pFb/nH/1z69bnz/cNQRF+jF00/E8bMbGvn5L02//x23aRQUxA68996jc9lPDOZcKrnn/2IfvKf/WHDnH2wsXrGCiedNxDajkMgX/0LLewK9z/UIEcA89TQQ14C4HETKN3I2SkqTCEW6ID1hAxXZm/QYqM7EKWxAIIxsDnRNtiKySwLWmXgBHWTGdpiWJcteJMumIyyHa5XSDjo4dgWhaYhML1qmF8b06rimzQGTzJTWYWzaTfjDjciqJrS0OJPItFln8hJx9k3B2Tf2f6sikmBZYzuZCRTX01hcS7CkHt1jw56fhM3lxmZo6JU+LOWNUNuCUdEINp3CbC+DZ4+k/oIxLPqylPve3cCjlXdzWdMYHkupR7Mo/vqARNfNSDeAfz1s8OtbJX/+C2RmwuhRgk8/1klIMO/rs86OUFwCz70Q4eorrDQ0KFaukXhcPur6+cmaMw1tQCZC01BS0ry9nsYoQemc5l53WNrdOwmD0uhxziASBhx+iLFs9mMs3YrcuAtVWm8mz+ufiX7JRLREz2H/L9tg1PvRkw69TlE3vnnIiEHZu38gd8YFaJbdHHrafxuyKZ2qn56C95IiHCf1RwhBZXEJKZoVu8W891NcblrDIf6zdik7rroVh8V8NYmzObhz/EldHnliZg/WLlt5BM7uWEF3ArrDwdFHXISFAQNvYP68+zHTcHfgyf/GirWeeLxjef3qjlMRIo41q/8B2kSQj6J5bsc2fe8S7RFgJ6g/gvoDcBpoD4M4fJ3AAU9H08Cugd3Cd2XzUIZJnAjtZR2KyEO3IrWGkF2Ro7ZjhPYmVLHt0MS+BMfSBemxmVairogQVi2GFIkkN5b0eBibj9IENLQia33I8noiK0qRuxoQNgtaTiJaj468MyIjHkevRBy9EvFOL+i4TlIRrmxuJzOBbbUE1pvWGnQNR0Ei9iwvVq8dawTiI2FmZidy4ozB/PcJCx+WraKmSZLmjP1Pv/+B5PEnFB+8p/Gj0yUrlmk8/Qzs2QMJCfDsc5IVq2DcWHj+ZYOrr7Dy6hsGP5qpkZpk4aXKx3EtEzQ910zt8gg1XwSxJTnbCUrq2Bx6Xz7CzIGSfHgWkM6QrUHk0q3IDRXIHXWIzHi0/hnoFx2PlnRkiiweboHFbnwzCDUGKH9/KyUvrqP8va0YwQgnPP8YBWffDOzg4BW0XUAhzU/cSrC0iqr/W4D1oS9IuGo0Jw4dyR98jfR9/F6m5/Xh3P5DSXQ4yYtPIM52cGtbRBq8t30TpxT8wJKIdhOXQ8bRR1wAtKvB+DomQgXMjtY4epoD/wjb/LpvglwG2mcgsg/Q/tiD0DUz2ZPd+p2QJ6UUGDLGmrSve66LdZFYy5Hyh/axMu3f3WeApiH9YWRRJazbZWq+RfT5oEctSXYLOG0Itw1ht4JVxxqd4nu7oX8cytILI2AQqg8SqvETLK6leXcLwd0+VFhiz47HatH56c8MHnxIcvcfYwn23fdI/voXjePHaUgpqa0VXH6Z+Z/YsUPxm99JMjPggft0LrjYoKJC8vzLBnfcJkjPCjL77OXc9fBGMxrLEkapIWj6b4DTQBz6T1gpZf402nRtSiEDIeSXxaiNu5AldYh0D6JPGtbTRqAlx5ttFagmf/s8qGiGd2UeqvNxu2jTeVtkew2aDnJHzV7bzM92zZ3s6OM+xz6cNsrso5ISDGXuoxTKiN6TbfOyY1LRNm3tlZTmuci29nSsUxIlid1fSTMLvup8vOj+ko7jt/VFRvsZs37vdnQcp+24ivZjoKL/X9lxHZQkdluna125uYFw0MALJPT0oukC1/PlVL5yHa6pi3Cf8QFanA9hD7ZrtZQEFbQh6700v3QyLfPGIluro/8LCNeFqP7zYuIKbaz4yS9ZuG0T88u2ce7bz/LbsbFC2yfWLefBlQupDbSy5PzryI1PwB8JM+ypBwCYmJPPTwaOMq9Zd16XbuyFo5O4iCwQl4J6hoMz/73hAnE78CcOTlo6IwiUg5wK2nIQR+YNsxtm6DGWqCXlO3rZVlK1EyHZHDCjmsobkBUNyMoG1M46cNlM/VOSG+GxIeKcSF2AP4IwwOa1YrULXMk2VL4HFUom0hwiXB8AFNdeZmP4hFZ+9YvYN6cNG2HEcJOodNbCG4bioksMbr5B8Mh/FGPGCM45S/DY0yG2lSgmTDbz5lisik3FLQwaZB5D8CUqcBEqYqH14ZswtvaNHaigY2CLIQVt3ywg0QkIVIMf4bSC3YJqiUBFLWplLbxY1HHt2v9El5WIroh+RpdVp1UgzO/svK+CcFMYBOxZUx7bJ9XxRUrF7tNOZtrWq07n1t6mi3PtvC7aJYQwyWv0s31ZO5TljnXt27Wofixmmeiy6LS9837R9hqxy0KYLxlCIPTo8XSt/fuFppnH0aLH0TodX48eR+/cTmtv195e1xAapFc0s+KvnyPDBkoIcqf1In7O0Oj3Tia07ndoiSvRU+cj7NUgNFQ4Ddl4CviH4zpBxzVN4HtxNb4F5e3X1zU6k/gL+6G/8SEn5BVwQl4Bg1MyeXTtF+xsaqA5FCDO5uCywaO5bPBoBj3xVwxlRt511rhA9Nx/KKSlO4/LYeHoJC4A2oNglGAKxg6VfLhAXABiOp74ofgadXbsUPTqLfnH3wXXX2f+CK67QTJqJFx6icall0s+W6CIjwe/32DsccXcc/ctZOc99k2dWTe+ApQhMfwRDH8YGYhgBCJIf9j8DLStNzD2WhdpCRFuCRPxBQm3hIi0hqNTiEggQsRvTkYogiYNdKFMPbMFdKuGVBD0GwSDBsGIos3DpgQoIVDRgVZKicsluPgiwT8eUu1p0jujpMRse/JMg2afSWYyMwVSCc6ZbbY571zBqadLGhuhVwGAoqkJXngB/u//Oo4lHAEE4L7xLzQ8/StCm8bGDGa0+CEUQWQkRrMLCKhvRtW3QlMAUR9CJLoQA3IgzhkdGDsNhu3zmjkQtw2g0U9zUDQ/OwbJjmWhae0Db+f9G19Yh60gCdf4Hh3t9t6/feDuGJC77lvs/N77tROGtgG8G+0oe3gZDVIR8UdQSjHx91Nx7yVuh/7ABbGrcmIXg4u2gyjHPT6bxF9NRU9ysfnLlWhVlfSJN5Mfrq7eRb/EVIanZXHdvDd49KSzcFisGFISkl0kpWtDtPhoN7qxN45e4iJ00N8CeTWolzHV7vu7yW2YT8GbQbsD5JUxW9PS4MF/Kq6+SmGz7fsAu+9ejdlnCZRS/P1ByZTpT7B+3f3Y7EdW7/J9gFIKGTRM0uCPIIMmQTD8UbIQCCP9ESJtpKEpSNgXItwSIuwLEmkJm5O/0xSIYAQjRAIRZMggEowgQxIjYmCEDWRYIpUCXZhaFk2YpEFECQRt1nPT3C6lQkqJjEgUoFt0dKuGZtXRbdHJbsFit6A7LFgSbVicbixOC5rTinLbwGVFc9uwauD0h9BaQ+i+IKLZj9YSxJrswpHqwRbnwOqwcPO9Olab4KYbNEaMMbjsko43xYED4JP5iocfVdx0g+CuO3Rmn2sw/1PF1iKdaScZ7KmC5543xejl5fDC83DOOea9un274sSTYolLG4QtRMIl9xF8958IRiFSPRBsheIylLSgDctBra9AbqtBpNjRju+JPqY3Wo/Ub+Fu2ReNrxbhGJGNc0zOwRt34xvBmj8vYPN/vuS0L66mcUsNmx5dTtI+pOXQ4LlyHGJ6P7DphCISiy9IszK44aNXaGhsxKJp9E5M4d8nzsZrd/D7xR8w6Mn7ibPZcVqsXDJwFFmeLqzbVgtMHPk1z/QYQ7fF5ZBx9BIXMP33+uOgbgH5D1DPA1Y6zNSY8+JK0K4F0RNUE/BizGFSU2H88YKnnlZcecX+37yEENx8k+D1N+C9/93Oj894EDBV95/f+C6lHxdzwaabj/hpflXIiOywOvhN0mD4IxitYULNASJNQULNIcLNUWuDL0TYFzKtDW2WB3+ESKCDPBjBCJGggQxFMMISI2RgRAzzuwyFNKTpGWgjD5jkQUZN+p3Jg9AEmq6hWTR0i4Zu1dGsGrpNx2K3oNl0LA4LFocVi9eF7rBid1mxRCer22ZOHpu5zmk1CYcjSjgcltjlNiLisKLbzWNrlq+XfVP6ghgVjdGpof1TVvkQwQgCP7ImAhKEMEhKEpwzW/D4E5Jw2EyKWFcPF86R3HKz4I7fm4Tmiy8UoRCMm2CwfYdpMOjXD159SWPYKMnDj8DOnYpf/ELw+usmmendW+H2wLSpcO+9YLVGM52uDzDizCt567f/5MTsvggbiLAFVd6IrNoIqXHQOx2VFI9K8SBbIlDVjEhyH1IOmCMJo86P3p019zuBUoovf/sRO9/axKwFV+DOjic+P4ncU/p+5WNqNp3Xxz6KEQiDEMhrmNEsAAAgAElEQVSQgZKKp2+7l95yJwRjI5T+PGkmf540s8tj+W68u1NngZEDv3K/jkl0E5dDxtFNXNogBoL+KKi/gvoCqMe0AaeAGAeiU5ZO9R5dndZvfiWYcark8ssOfnOMGCHZtOktTlN/Z919C/n0to8IdVVno+0rlUJG3RNhX4hQo59wc4hQYyBqcQgSaQ4R8oWItIQ63BedrQ7+DquDEYyYhCHUZnEwiYMRkUgjSiCkKWRsd1koFdXlme4IoZn5QjTdJA2aRTOtDpZOVgdbp8HfbUVPcWJzRkmDy4rFFSUNUfJgjbNjjbNhcVpjSYPdEiUVukkaHBYsdv0rhUB/F1CGRFb7YgnKriaMigZUMNJetVrP9sLIXCqzE9i8Zhebl+ygYm0lOUMzMYSgdutUkgs/4uc3Kx76l8EdvxfcebtJnJ56WvLXBySvvWGQ4IWZMwR33aHx6H8ke/bAwsWK1St0EIrFi2DadJg1Ex55RPHhR7C70qwNEwopHngA/H5oK37+/PMwYbzg5SUvcOK4G8GmQ1YcoiAe4XWhDeiDrPEha3wYRbsJV5vzqtGP8DrRUjxoKW5Eiic670FL9ZjExnpk064bDd3h0N8FlJR8fv27VC8rZ9ZnP8GRsm8eoK+KnmcNYMtTq0wxs4C4giR63joL/vYkhCKxwq5DgdUCIwaA8+D1x7rxw8SxQVzaIOJAnHiQRnvoKolSr16CMaMFc58/+I/I1PM186DlNiJ7/ej+5brDJA1SRslD1EVBJw2gwCQNmtZOHrR28qCj2zR0m2Uvl4WOJcGBy2WSAovLisVtkoR20uCOfsbbsXntWFydSUQHadBt+lGfcO67gPKHOxGTxg6isrsJLd7RTlAsvZKxT8hHz06g0R9i66LtbFu4na3/XU7N9jp6HZdHn4n5nHH3TDLT42n+cBszrA9R949Kkv7ffNLTJa1NsT+tSy7WuOTifYncnbebOqyFi6PEWCiGDBH87Kfm3XT3n2DBZ7Tne7HZBL/5TadzUopXXoUP3xNMmvgloUvjcCgJukIYAiIR9H5pWAZm7v3VqIhE1bdESU0LqtqHsaWK8JISk9jUtyLiHGgpHkSKu4PUpHgQqR60ZPdh10Qy6gPoCd3E5duEjBgs/MnrNO9oYMa8y7B5j4zFq2FzNev/toQdr25o12Q7kl38aNFVWJw2uOocePAZM+3/ocKiQ3oynD71iPTx2IHqtrgcBo4t4nJICBONw9wHv/2NYPa5kkkTDzyor1qlmDpVp7SLbXHJ7mhwQTTCo+0X2znMMhoCqYy2T4kKKpQ/gjJCpgZDCCK6KS4UuoamR8WGuhZdZxIeovOH1q5je+d92+Y7bxN7tdP0jgiEzu3FfvZt60/ndvtf19F+v/P7XXeA+fZ9OtYBiOYgqsaHqmo2p93NyD1NqJYQWkZ8u/XEelwPnNkJ6FnxCIcVpRTVxbVsXVjCtpfWsHVhCS11rfSZmE/vCb0Ye/E55A3PRjYGqXtnM7UPLqO4oonkH/Uj7+ZxVL1VRNXSTFLHlKPbDiA63C9U54z/+P1mNfRevfZ/vy5eDL16Qe++ihOmwEfUcuZ5s1E1DajqelR1PZHXP0EkxCFSExEpCean3YawaIjUOLTUrkWQSkpUvd8kNtU+VI0Po6SG8LIdqBofsq4F4bJFic1epCYlSmwcHVV+ZSCCChsI9w+s8u93CCMYYf75L2EEIpzy3sVYXF+vRpRSit0LdrDugcVULS2j8OoxzN50M4uuep2y97ZyygeX4kqPJihMSYDrzoeHX4RgqOvq0J1htUBOOlx+Fli+h0NTN44Yvod3RwKmDmbfYor9+wsGFAreeVcxZvS+g4FSin8+pKjcDTNOzsAS/ANbnljJZze+iy8QQgEXltyCZv36l01JGUNsZBvhMWQ76ZGGBKmQhrnenI9d19a2bVsMWeo8v991B5jvap/O/YuYy5FDOaY6zO85YN8kQikcusBlAadNw2XTcNk1XHadiCFp8Ru0tETwtUbw+cL4msO0tkZirquSqj28VUH7sohqcvraLeg2D2JZNbVf1lDzly9YHDCLBOouK5Z4O5pFY8s/luD3h2kNRkhZOoeZbz6EM6MJfX8FFvdC+52oxb5xSQmdDWcffKD49W+goQHmPgfHHy94/nk471xz+7nnKp7+w8OcFk5HK8xBK8xBDO+PikRQtY2omgbktjLU0nXgtCNSEtFSExEpieBx7mOlE5qGSHajJbuh377iTSUVqqHVtNa0uaJ21iFX7owutyAc1nZrjbTb0F1WIqvLO0iOs5vEfFMIt4SYd8ZcbAkOpr9xQXtxzK8CGTbY/sp61j2wmHBziEE3H8/UF87FEv3/Hf/PH+Hb2UDK8KzYHdNT4BeXwoKV8PlqMxlMZ92LECZhiXPDlDEwauAPryp0G7otLoeM7x9xERMO6FP93a2C4aNit//y15I/3m3Wixl7nGD+PAc22wzQdfpfOZq+l45g02Nfsu2FdUeEtEB0UDg2JCDfGZRSqAZ/F+LYRmRjtJ5QVrQwYrRIopbp3W/lYSNsULqinK0LS9i6sITiRdvxpLjoPT6f3uN7kj+uJ8m5CWZeEENiBA2avyin7r0tNC4sxTUojYRpBXjG5hDauIfmNzYSqPezqVLHqhSTZvVh59x1vDbhYk77+GXiCxrQ9IMUrlOQnAz19cRYW+rqYORIcLvNqKJevQQnnyw4+WQ49UemsNcwFK++Bm+9DXf/SaFUmNra1bSOK8Bd1kD46fmIOGc7idEGmlmClVTQ2IysrkdWVqPWbgGlECmJpjUmNdG00BxEoyQ0gUhym3WT+qbte2pSoZr87cQmsKYSzaYRnrep3T0lbHrUWuPex3KjpbgR7m6dw1dBsMHPh6c+i7dvChP+fdpXFqmHGgNs+s+XbPjn58QXJDH89qnkzeq7z73hyUvAk7efgogeN8ycCCcdD+u3wubt4Gs1CYrXA8MHQI/MWJbejW4cAEdddegjAmMcsPxrHMAB2gYQPY5Uj7pxAKiwgbG7qYOU7OogKVj0dteOnu2NEpUEtDRPTAXnrhBqDVHyRSlbF5SwdVEJO5aVkVqQTO8Jveg7qYDeE3rhzYwNxVRK0bq+ito3iqh7ezO2TA/JpxeSdGo/LIlOWueX0PTsKrDqNPdNYdGDS+h35gDS6nysea+EUJwdV1YcaQM9jPxDNTbXQ+CoAhFE6OZvTUndzLgatoLfBbqbMSft5N4/K6ZNE9TVKcaOg/f+Bx98YBKTF543dS5KmaHRt/0OgkF44G/wwfvmA1+F0rj00ilMnzmTOXPmmMRhZzWyqBy5qcIU6rZZYhLcMedMa8B0LdXUI6vrocWPSPJ2EJnkBMTXJO0ti3fS+MI6sv45q/17VdSt1+aOkjW+juUan+l27OyG6iQe1lI84LZ167n2gr/Kx/unPEXGxJ6M/duMrySSby6tZ8ODn7P16VXknNKHwTePJ2Xk9yuj+IHwrVeHzs5SX1595cEbHgbEHX/org59TEH7FcjLAN9XPMC4btLyDUA2BaKEpCnWelLbgpbqNq0mWV4sAzKwn9gPPduLFnfoQsKW+laKF+9g64Jiti7a3h7x02diPifePJmC8b1w7UcYGixrpPaNImrf3IQKGySfXkj/F87BkZ+IChm0vL+F6rmr0VPcxF05mlWvbqD4oc+ZcOVIal7dwMpyH0knFlC7qhJ7dSsj7jgDa0oioT/1YEfrRnpMXo+e2cr7C8uZdNxofEv6Y1mVgRYK485SPPXkT7nu+lZ+Hs26e8ftUFAguPZaRWsrHDcW7HaFxwPjj4fhw+HGm+CM083+K2WD4OmcPqQXjz78CBfOnIVISkTrmYbWMw118jBUqUliwk98jEhwoxXmohVmI7xucDsRbif0zEIHVCjcrpORG4pR9U0Q5466lqI6GefhiTzlXpWhhRCIeAfEO9Dz9y1yqpSCltA+pCa8aXf7OpTaL6kRKR5EnP0HRWx8ZY28f9KT9Dp7ECPumnrY5161rJx1Dyxi17xi+l42kjNW/QxP7n4sKd04suh2FR0yvp8WFxUBOQbYxOGXaXeB9imIEUe+Xz8AKEMi9zTvFVpszmOoWOtJdgJathc9Pe4rhd027Go0hbQLt7N1YUlMxE+fifn0Oi4P2wHEiJF6P3XvbqH2zSICJfUkzepL8umFuIdnIoRA+sP43i6i+cV1WPOTiL9oGK1WnQ8vfJG4zDj6eW1sXFiGPT+JrHMGseKOT+iZEUfaT4bQ57LhaLt9+OcuY+VH1Yw53oP1orGcNe5BfnHZRIb2sxIs08CmY6uswn3nJ2g9XkSIQ63MuzfswCaUykVV7kZuLwWrFS2/JyIlOWYAU1KidkQtMVsqEImeDktMfNdFGpUhUfWNqOoGVI0p+sVqQaQmokVdTMS7DzhQNjyzmkh1Kym3HP8Vz7GLfrUEkTUt7RaaDmuN6Z5SIaPDDZW6t+XGjfDuq+05VtG0rZb3TnySAdeNZfDPxx/yftKQ7Hx7E+seWExLWSODbjyevpePwBb/w823851YXK654ogeU9z+x26LyzEFYQHtwyh52c2hkxcnaM92k5ZDgGwJ7uXaiU57mtESnR2hxX1SsZ/QGz07AeF1fOVBIibiJ6pR6SriRz8IAZKBMA0fb6f2jSKal5bhndyLzGvGED+pB1p0X9kcpOm1DTS/uh77sExS7zkZa59kNjy6jC9+P4/hZ/RHrtzFl0saGXLnVBKGZ/DerGcoHJKJP9NN30uHYEmII/DySrYvqGTEnRPg3TWIIT1wex0UzdvOqIH9MNKcYLUSbIzD9uRw7He8ghkVd5jXRgpUYCSau4cZ8ZadhcjKRO2pQm4thm0lJoFJSzWtHJqGyE9Hy09HnTIcVVqF3FhOePE8RJIHbUAuWv/sGBIjdM0U8aYkAr1Ma0hTS7trSW3aDqFwhzUmJdF0NXVy5xn1gSOew0W47ehuO3qPpK6vjT+8D6kJl9REl1tQgfC+OWw6E5sE1zFRLqBu3W4+mPE0w2+fQv+rRh/SPuGWEFufWsX6vy/BnuRk8C3j6XnmgK+dtLEbXxHdFpdDxveTuACIFNC+BDkTKMKsd7S/G8MNaKC9CuKHlj9g/1BSmYnZdu0rjlWBcIww1jYh35zPiEfYv/5tJaVk1/rd7ULabQu3IwT0mZRP7wn5TL9lMpkD0tEOwX+vDEnz0nJq3yii/oNtuAenk3xGIfkPnIIe1yH+NOpaaX5pHb53NuEc34P0f56GtUcC/poWPjrzOZq31TJhUi6ln5USsls5ZfGVKAGvjX6EfqNziDu1H73HpKJ7XNGq1LtwnVSItaQcFe9Es+g4PXaaq30oqx1LopVI2IJtXE/87/uwrD4bfcjLCH3fiLgDXqtWO7uuOhnvlM+J+8lxJskQApGRjkhPQ1XXIEu2dxCY9LR23YPQNUR+Blp+hmlV2RElMYuKEMlxaANy0PrnIOJiCYcQArwehNeDVpBrXmd/oMO9tLII1dzSKQw7kUhNC868b7eMhnBa0XMT0XMTu9yuAmFkrWmxUVF3VLg9KsqHag2hJcUSG9HZHZXo/M4TLVYvK+fD055l7N9mUnD+kIO2b61sZsNDX7D5P8tJn9CDSf89g/TxPb43lqdufP/x/SUuACIJtM+BRSDvBz4CHHSUDAgDmSB+BeI8EEcum+SxBOUPY1RGyUl5Y5SoNGBUNqHFOUytSZYXPTcR29ie6DkJaEmuI/qg2yfiZ/F2PClu+kzIZ/CMQs740yxSeiUd8ncqpfAX1VD7xkZq396MNdlF8umFZP98PLa2PBNRRHY30/T8GlrnFeM6sTcZj52JJcPMbVL2cTHzLn2FHkPSyfXaWPtZOQVXjmLYXVPxVzTxytCHyD8ulyGP/pgVv/+QAVcOQljtVP9zPka9QY85uchVpYh0M2zUKjS8g1MxQhp6vMIQOrrDghzXm9DjGo47Q5DwJsJyKORFAG4i1c8TLK+k+rE1NH9QTOq9p2DrbWpGhBCmpSU1BVVbhyzZYRKYXj0QWZkxg67QNURBBlpBlMRs32NqYhZsRKR6TXdS/+x9SEz7/k4HIjcDcjPM/0G4LQy7HrmllMjmClRiEGO5bLfM4P5uXTXCYY1aB7vWcahQBFnb0k5qZI0PY205KuqeUs0BRKJr3+R8be6pJPdBReRfB7vmlzD/vJeY+PgZ5J3a74Bt69btZt3fFrPzzU0UnD+EHy2+Cm+ffbVFRxzKB5F1oBpMa7hIAX0o3WGVndGdgO5w8P0mLhANsZsI+kRQVcB6oBFwAtnAoB9EGJ5SClnXilHeEOvaqWhENgfQM+PbxbG2MXno2YPRM73fWJ6NA0X8jJszijmPnr1PxM+hILirmbq3iqh9owjDFyb5x/3p99SZOPvu+4AOlzbQNHc1/sWleE7tT+YzZ6Mnme4RIxRh6e/nsemplYwcnk79bh9bawNMfv0C0if2pGVbHW+O/hcZQzOZ/NGlfHzmXCY9fBK6x4O/rAm1ppS4s0civ9yKyMmEBjMsWgtJ4vqlEK4PY3VJhM2DChl4LxlF7RXb0B45H8usePRhc1ERiWbdN5xaGgIVtCBDeVgT3sKeX0jPt/2UXf8ugZ2NlF/4KvGn9iHp15PQork7hBCIlGS0lGRUXT1y+w5kyXa0nj1M19JeuTOEriF6Z6L1zkRFjE4kZgMizWsKe/tnIzz710EIqwWRkQwZyQCoJ3diG9MPvDpyVzVqzRYzb05UI6OlJMAhhGF/mxA2C3qmFzK7thSpsIGqa2kXD8saH3LDLsJtxKbBj0hwsk9yvjZik+xGfEXXzM53NrPw8teY8uK5ZE3J77p/SlHx0TbWPbCY+nV7GPCz4zh76804krrWMh1RGJsg8AiEXqZjqBGYhb0cYP8p2OeAlvzN9+VYQDdxOWR8/4lLZ4g04PvtClKhCEZlU5fiWPPtssO9Yx2Zi57lNX353+BbIXy9iJ+DIdIUoP5/W6l9o4jWzTUkzehDjz9MwzMqu0t9QmhzDY3PrSK4upK4swaR9fx5aJ1cRvVbavjwghexG5Ix/ZLYsr6W9Om9+dGDM7HFO/Ct3c170/6Lq1ciJ336E0qeX0vW5BxsiW6UplN03Vv07+fElmIFPQUVkohk08ojfSFcvRIJVzQjUm0Ip0AFImjxduw/HoKxpAh98xxk5BrEsJUES3+PLW8PRCxmgjqpUMaZbP/TCHY/qZH/Jz9Zl4AlwUnP/57BnvsW0/xJCS3zt+P7ZDvJv5yIZ0afGKuGSEpET0pENTYhS7YjS3ag9chD5GYjushYKiw6ok8WWp8sk8SUREnMp+sRGQkdlhj3gcWcRn0AS49U9Jx46NsWNeRvD8OObCuDVr8Zet0ehu3tsk9HC4RVR6THo6V3TbJVRJrEplOIt7FpN+E2AXFDtKxC6l6RUW1lFvZTVqH4hbV8cdP/OPHti0g7Lnef7UYwQvHcNaz72xIQMPjm8RS8OQT9CLhxDwoVgpbrIPwOEIlOe7fxQeA+CPwFnPeA45Jvvl/d+N7g6H0idGO/UEqhGgMxmpP2qsX10cRsbWnth2bjmDnAdPd8i8m8DhTxc8bdMw8a8XMwyGCExk9NkW3T4p3Ej+9B+uUj8E7uibafh3Ng7W6anllFuKSOuHMHk/ybE9BcHRYlpRRFT6xgyS/fo7BfMprDwcaNtRz3rx/R40yzUm3Dgh0sOO9FjAQHpy+8kmCdn7V/XcjpC+Yg7E5KH1uJ12FgGdUHuWY71vMmEX51BdrQPEJNAfCFsaQ4MVZWwtR8tFCESMjMsBs3ezBVb27Au7wcFU7GOvpyfItG4VtaTO7dI2i8ZyHBSh0jNYn8e09Cs35K8W/mEakLkHfz8QirTsZvJ2Hvm0zVP74gflAStfd8RuMzq0n53WQcg2Kz3wpvPPrwoajmZtMCs7AULS8XkZeDsHZtaRMWHdE3C61vlmltKNltkpj56xGZiR0kxrXvvWbUx1aGFkKAx4XwuKBXthmGHQx16GTWbUU1NCPi3R3J8VISEcdQ8T1h0RBpcWhp+ymrYEhUfWuHgLjah7GtmvAX283luhaExx5DarYt3cXa59Zz8tzZJA+LrUEVqG2l6JFlFP1rKUlDMjju/hlkTy/49txxKgy+MyGyiq6yl8ciak30/xZUHThv/qZ7d/RC0G1xOQwc28QlEgYZBqvje+kvVWEDY0+zSUgqYt07aAI9pyMhm3VQpklO0uO+cevJPv08QhE/B/0eqfAtr6D2zSLq3tuKq38KyT8upOe9J2HZT+imUorAsnKanlmFUdNC/IXDcN99EsIW25dAvZ/5V7xG7dIyRg9OpawqiKOnh1NX/QxXpjnoVL+8gVW/fp8GFGd9dgVWt43FV7/JpEdmojkctO5sYvOd85l0dQHCqSFSshAJHlSND5HiofLzMuLT42ht9EPYQMtNQdtSjQpFayzZLbgvG03ozZXYKnyoPfUknj2Qmv+uJLjTRvzVk2h8aC2tm3fT8OoG8u+cirNnIttu/YjAzkb63H8KQhMkzh6IrWcCFb/4AO/MPhjLSqn82Ts4x+WSfP1YrNmx1gERF4c+ZDCqpQW5vRS5aAkiJ9u0wtj2Ty6FVUf0y0brl22SmOLdyKIywp+sQ2Qlmu6kflkIlx0ZCIOhEK4Dux6F3YbIToNsMxOvMgxUXZNJZLZXoJZvAJsVkZJg5pRJTYS4A4dhH80wo7WiyfS6gJIS1eBvrxW1/vGVbH57K1MvHYjj/XU0P/c5wmnDJ3S2rKmldNUecifkMv3BU0gem2cSnm/z2rRcHyUtB8kYHQM/BP4KWk+wn/ENdawb3ycce8SlvhzWfwQly0BGTH2KlJCQBUNmQM9RYDm26p/I5sA+lhNjVyOyugUt2d1uPbEUZmCf3tfMf/Id5lg4aMTPzZPJHHhoET+HAv+WGmrf3ETtG0XocTaSTy9k4DsXYc/evwZGSYV/wXYan10NYYP4i4bjmpKPsOzbp4oF2/novBfITLBTOCqLTYsrGHrXVPpdOwYhzGy1u/7fMor/vZyKpgCnffIT3Fnx7Hx3MzIYInlwKkq3sebql+j/sxEI4UNWVGGbM83sS60PkRxH5cLVJOUn4atsMjUOWclo68tQwQ5y4D6pD3teWIO1ogW5shjLzNGkXjOa6v+uIueXQ0n44ynIX79Dy3+W4hycQealw7EmO9l0zdv4S+oY+MxsLPF23KOy6fncbMqufxdH/0wSnZLWtVWUX/gKcacXknj5CPT4WMuFcLvRBw1AtfqRO0oxFn2OyM5E69ED4TiwlUNYdUT/bLT+2aYod1vUEvPxGkR2MjItGS3h8MPhhf7/2Tvv8Kjq9It/vvdOyWQmmfTeSSWE3jsqRTqIgIrYRcW+q67dLbquda0/y9oVEVFAKSKC9F4CBEJPCCQhvU3qzL3398cNCSEJBAUXV87z5HmSmVuTm7nnvu95z5F1cuKvTwXpY9gOPa4gvwRt7xFwufRKjJ83wt8L4W3/zcn7hYKQJF3g6+3O9i/SyFifzejtM7GF2xsDD19cQ/7GY8SPiWfsbV0wKwpqRj7VW/SUb2Ey1Kd5n2rO15j2LX5B5dN1qAC5nV/D31OWZVJS4tFch5BljTf/5U7fXvrtZfM2Fw8/U012roqHTRAcKHj+aXdS2ss883w1739Wi79vOXXOqTz51Idcc+115/V3+LvBpYpLm/H7IS7l+fDzO1CaA6qih3VB44RzaTas/xzWfwZdx0Py0ItKdKspKmq+o7G9c4pAFpfSmLcTascwJK5xtPhXVinOB873xE9bUJfnoPg7naw4i6vxHZtI3H/G457kf8b1NJdK5bJDlH+RimQ1Yr+xK5a+kS1qXRSnwuYnlrH33c106uBPsSZzIqeKEWtvxZ6g70dTVDKeXEHhukyO5Fdw2aeT8O0YRF1FLRvuWciETTchzBYy39+GUuUkON6GVqQgJYcgbBa06jpwqWAzk7Mmk4CkQCrzKpDDAxBBPlBb21BxAf0J3H5Hb6rfWY1YfRh5RDe8JyRR9MVONKeCbDHi8/woCu+ZT9GfFxI8+1r8xiSSZDaw7/bv2D7kQ5K/mIQ10R9TqCfRn19F9qM/UXK8moDrOlH9zU6c+/LIuupLvG/sgv3qDs2qT8Ldgtw+ES0mCvVoFsr6jYigQH0SyXJ2HZIwGhD1hnZanQv1UC61yw8gOWtxzl6rt5PiQxCWc79h6mPYHsh2D4iN0P9GVTUNpnjK1hxwVCG8PRtbS35eCNPv62HmVGiqysYHlnBiTSajVt+K2cfC4a92k/bKWmpLa+hwf18umzO1xeRnTdPQymuaGPMpOWVou7IbYxVkqYHQNPO08beBe9NYBbWokqq/LkKK9cd95iAkPxsWi4XU9aOh9lOWLq/i0b9Xs2qhB3n5KpNvrmTWe9YGIrN2o4vDGQop7fXr7oE73PjzPW4cPGym22W3M+nqyRhbaVX+T+MScWkzfh/EpegoLH4RnDW07sUCuOp7qtvnQVku9J3+m5MXtbJOr5ac5nui5FcgeVka8nYMMX6YB7RDDrUjvC4u984LNfFzNigVtZQsPUTR/HQq0/LwHh5L+BOD8OgZdtYnaLXWReWi/ZTP3okhxBOfB/ph7hrS6u+17HARSyd8jlRcRbcr4zjw81Hib+9BxycHNxjRKdVODt2ziNrSag7nVdD9ySFEjtRHTrc9toyuT/TH5GGmMsvB/r+tpN+yG1Bnr4JAC3L3OOBktcWGWqdQsD2HiMnxpM3fhdw1WhddupmRtKbiRbfe4ZR/4YlaUY6yKh3DkGT8buoKaKiqiuRuwu+N8eTf+BX5d80j6OMp+A6LJfHt0Ry4fwm7xs4i9sVh+I9LQnI3EfbqlRS8vZmct7cT8tRADAt3Y+7iR9X6LMrm7MH3nl5YL49png7t5oacEI8WFYWalYWycTPC3x8pOgphbdtUijAZkJNIp44AACAASURBVNuHI4pVDPurkVIiUdOPoSxLRYT76e2k+BCE2y+/UQl3N0REMEQE6zoZp0vXyRSWoO7LQCsuA6ulIQlb+Hvr8Qa/A6iKytrbFlB2oJAr5l/Hoc93suf19dgivej82GAixiSccQpLCIGwW8BuQW7XnPRrmobmqG3qOJzvwLn3lFgFaFKpQdXAJKMeLsTxyDzMU+vNWWu/BJyUV2h4e+nX0pvv13LDVFMDaQHo37vl205cu1rcLQolJSUEBDQP7byESziJi5+4VBTCkpfAeQ49U1cdHN4Ibh7QbeJ5PyRN1fTpgFPbO/XeJ1q1Ezm40dbe1C9a/z7Yfl6M2S4ELuTEz9mg1imUr86kaME+ylZl4NE7HP9rOhJ3eTRSG25mamUdjgV7KZ+zG3NSAH5PX445ObDV5TVNY99/trL2wUUkxPtAtzAytp5gyLxr8e8T0bCcs7iK/TfPxxTmSUZxFeEj4ukwszcAeeuzyP7pEL2fH4hmMLNzxlxiH+qPRa3FZTZg6BWPcNOffk/qW/K2HMcr0Q/PIE8qi6uQA+o1DXYPpNzCJscohMBrZm9Kn1iMfdFu5AGJeI1OQDmaSfWmY9j6ROrk5e2J5N/4FYWPLMLvhVH4joynXbWTjGd+5sgzP1OxI5foJwYjDBIBd/fCHOvD8ceWE/T4INyKy2H5AWyTEin5cDuls3bhd38f3DoGNfudCbMJOS4WLSoSLes4yuatCF9vncB4tCw6PR1KaQ2yjztycjhycjharRP1YC5q+nGUH3cgIvwbKzHmX/e0LYwGRLAfBOsj8JqqopVU6ETmeB7ajn1Q7wQs/L2Q/LzB7nHROeQqdS5WTptL1YkKfLsFM7/rW4QOi+Xyr6/Bv0fYedmHEALh4QYebsjRreRFVTXNi3LtytariJoGdQq1n26iuqqKzgPrqKlVyD2hsmKBfl3s2a9ww9S2Vda273QRF6P+QUnLJR+Xc8HFeSethxCCBycO5uXR7QB46YfdOGqdPDOuK8NfWUpeeSOZyS+vJtzHyqYnxnLjB6sZ3SmcSZoGcf3As/FGptU4qV2fgXlw3Fk/qLQaJ0pOefP2Tk4Zks2si2FDvZDDvTD1jtR/9rFedB+Ap+NCT/ycDZqmUbkjl6J56RQvPoBbjDe+45OI/NtlGLzbRpCUshoq5qbhmL8Htx5hBLw8ElO7M/tB1JbVsGLyLAo2HafnhCQOrz1OcDdPRn8xGaOtUcNRc7SUfTd8i/fwWI4cKsToYabvy1fq+611sfa2+Qz9ZhLCaCTj3e1oToWYe3vhfP9ncJOQOjd6apysuOSsOUpI/yisdgtVZTXI/vXExceOwZjf7FjNSQFICcEopQW4ftqLcUQKSBKFH23H2jsCIQQGPyve/xxJ8UMLKX3+Z7z+MoSAq5JRq10ce3U9jtQT7L76KxLfG4vJ34p9RBymCDvH71uCfXwiXg8OpvLNNXgNDEEL9OHEo8tw6xCI7z29MIY19y0RRiOiXTQiMhztWDbKtlSE3RMpJhphP3MFTik+baLIbETuEIHcIUInMQdydBKzdAciMkAnMXHBv5rEQL1OxNcOvnZIiNJvxo4qXfBbWIrrQBbU1OotpZMVGR/7L/ZXOR9wVdWxZOjHOI6V4qpy4t8jjPHb7sIjsmUH4AsFIQQ0xCrU+/FUO1H25IJRRgqxY+zfDss8M6mrA4FyNmx2Mf3OStLWN78mel1RTnmFxrAhRl57Xq/avfpODe9/VsuRTJUfvvYATQHx32+RX8LFi4uauJjNZr5dvY1HB4bgd1pK8NIHhzd8X1nrpNvfvuMfE7o13YCqwt7l0PtaAFxHCql4fjlqUSXG5GDkQI8GYza1ie5EJypqeQ1ykGdj9aR7BPI4vdVzoYzZzjc0TaPwSBEHVl/YiZ+2oPpwMcUL9ARmYZTxHZ9E+/nXYg5vuw28q7CSitm7qFxyAMvgaAL/b3yLN9nTkb30AD9e+xVBAe7ET2jPgaWH6f3OWMLHJjVZzrErj/03zyP03t7k5JRRmJrL+FW3ItW3qnY+t4qQy6LwjLJTeayaA8+uot/Km6GmDi0jH/nq7ghj47+VVliBCPQk96O9tL+lO4rdQqWjBtlfd2kWAV7IZg1N1ZoRXq+7elNw+9f4/LAbQ592egVKg4pVmXgOjgbAkhKE+409qf58K9Jb6/Cc2Y+gaZ1Qq53kfLwD78tiSB3+CYnvjcOzeyiW9gFEf3k1x+5bTO2hYoL/PorqL7airEgn5MWhVG7M4fgN8/AYGYf3Ld2apDmfhDAYENGRiIgwtOwclJ27EFarHifg3fKNVS2pRm6FlAqzETklEjklEq2mDvVALuqeLJQftiOiAvR2Ulxwi34mvwRCCH0SycOKFKNXLrSaOl0nU1iCunM/WqkD4WVrOobtduHI/EloqsqRr9JYe+cCNJdKl6eHkHR7T0z2iyfwUI4LwDypC8a+7ZB8T7qNC32kV4M+PQ0UFmsUFGokJ8hs36kwbqS+1KafPJm7oI6FPzZmcp3UuHz7fR3T73JweHgdbm3QUv3P4VLFpc24qImLQRLcPiiRV5el8ezE1kMu7/tyEyNTwhiaHNr0DU2BA2vRul5F9bw9VM/bBU4VjBKOt9fqAWw5ZWA2nJK7Y8fYOVSvnvjbfnfTCadO/Bxam8HB1Ud+ccbP+YCzoJKihfspnp9OXa4Dn7EJtHtzNO4dAs5J1+PMLqdiVipVKzOwXhlP0EdXYQhoeYT0VChOF5tmzGfv7F10Gp9EXnoxVUU1jN4xE8tp1v+lKzM49MASYv45lJKKWtLe3sTEDXc0VGOK0/JI/7/NTD04Ewwmdt7+DXGPDMAW74tz4TawmZC7tGuyTa3IgUgMJnd9Fpd/dBUlpZVUV9U1EherG4oTtMIyREBT23ljmB1zt1DqSsqQ5m3HcGU7/G7oyIlXN+ExMKqB6HhNSaFqWw7VqzMQBgmPGX0Iua07SqWTwgX7iHxsEHunf0vkXwYQdH0nDH7uRH40gdy//czRGd8T/sZITEcKcby4AsuYZMK+nETph9vJmjRbF/BObi7ghfqJn4hwRFgoWk4uSlq6rtmJjkL4NhVrKyXVGKPOXi0QbibkjpHIHSPRquv0SszuoyhLtiGiA/VKTOz5IzGn7leEBUKYXp3VXApacZlelTl8DG3TbnAzIfy8G8ewbecv9sJVVcfBT1PZ9fJaqnMrCOwbybDvr0M+DxWn8w1jhxDoENL8jXqt1r4DCooCvj6Cmbea6TW0guGXGRt0LlXVLd+gJ44x8clslU8+/ZQZM2ZcsOO/hN8/Lmrigqowc0gCHZ+ez8MjWg4Pm7c9k62ZhWx6fEzL2xCCqjfnULPulNRdRUPY3XC/rpvuHGv7/RhanY4zTfx0GJHI+GdHnveJn7MeU5WT0h91ka1jey5eV8QQ+qd+ePaNaHEc+UyoO1JM+Rep1Gw+hm1ce4K/mIzcRr1N6c5clo79FElR6XJrTw7N3k2XZ4cSd2u3Zr+P/K/TOPb8GhLeH0elS2X19K8Z8+NN2OpHrnWR5HwGfTIe2SRx5L1U0DSi7+6pV+02H0EamNCM6GpFDsqKa3APsuEeYKNGVaiqdTW0ioTZgKtcwZRTBAHN83Lsd/XlxPVzMLllo6b44d49EgSU/3QY+7BYfRtCEPTMZWRO+QppYxZCEthu603Yfb1Rqpzk/mcbybOv5sDdi6jYlkO754ciW4yE/P1yij/bSea1cwl7ZQT2F8bieGM1danZ+NwzEPvUFIpe30TZ12n43NUL27CWjcyEJCHCQhsTqfcfANmgV2D89ZHZX5IMLSwm5E5RyJ2iGknMzkyUxduQYoKQksIQsUFNKlznC8IgIwJ8IEBPndbUU8awTxShpR0CRa2vxtQ7/Xp7nnNcQVWeg/S3NpL+7hZ8OwejuVTa392bHv8cdlEJ9s+G6upaOg8sApxoGnzythVZFgQFCr76wMojf9XHoQP8BH6+Ek891FIFychTj4/m2ptf4bbbbvvNHq4uClwyoDsnXNzEBfC0mJjeN5bXl+/Fclo7I7ukkntnbWLpg8Mwt9bq0MByZTSGfuHUrT1M3bbj4FIQJhlj/O9PBNYw8VNPVH6riZ+zQXOplK87SuG8dMpWZGDrHoLvxPa0e3sM8llMx1pC7d58yj/fQe3efDwmpeDzYH8ka9tK9ZqmseeJH9nwyjoShsVSU+kib0s2V66/Hc9Y32bL5ry5ifzZu2n/1WScBoml/d5jyIcT8TvFlXTvm5sweZoJHRRGVV4dB59bTf/VtyBkCWXLQahTkAcnN922qqEVV5K9q4CQ/lEAuEsS1U6lwYhNmGWcpU7UnCLkzk2rNQCGYDvWnoFUV9bhvmgfUmI4gff05sRL6/C8PKaBKMlWE6EvjSBrxgIkSza8vwnbbb2IfHQAapWTjCeWk/LNFA4/vpxdY78g6cMJuIXb8Z3eGXM7b47dv4SAe3vj9fQIahbspuzh77De3IvgV0ZQvTWbotc2UjZrF77398HSJbjZcUI9gQkOQgQFouUXoB5uTKQ+3TX3XNGExFTVoh7IQUnNQFu0DaldIFJSOKJd0AWzDxCSAC8PZC8PiKsfw66srh/DLkXJrB/D9rE3HcNuhVSV7Mlj9yvrODo/nZgpKQyZNZl1ty8gaUZPOv1l4AU5hwsJRVGg5n2o/itQ1eS93j0MrFrYsoj7mb+cSmZluvV+mv37m/8f/CFwibi0GRc5cdH/kPdfkUzXvy3gpn5xje9oGjd8sJq/jEyhfciZStAakkHC3CsSc69INJeKa++JX2S69N/Af3Pi52zQNI3KXXkUzU+neOF+zKGe+E5IIuKJwRj9zj3ETdM0anfkUv75DpzHyvCc2hHfpy5Hcmv7ZVqdUcSKCZ9TeLSMbnf34dBnO0mc2YsOjw5EOk1sqblUMp5cjiM1l+Rvr0Ezyyzu/z5dHhlI1OjEhuUqMktI/cdKJu2aAZLMjhu/Jv6xgVhjfdBUDdfPe5E6hDXbPuXV4GYkZ30WUaP07ckVdQgBdTVOzBYTwijjLKxDyylG07QWn7I9ru3EiT//hKWHN+qmDGxDkpHe3ULZkoN4nZII7Jboj/9dvSj5Og377lwcH2zCdksvov92GYf+vJQDMxeR9MlETnySSuqVn5Hw1ii8B0Vj6xdJ1CcTOXbPImoPFhH4UH+MnUKp+Pcq6rYfx3prH0I/mYhj6UHyn1yOOckfn7t7YYpsOVFZCIEIDEAE+KMVFqEeycSVW4qoq0BT/X91iKJwNyN3jkbuHK2TmP3ZKNsPoy3cihRbX4lpF3TBxbXCatHHqiND9DHsOmfjGPbew2gl5WBzb2wt+XqRsz6btFfXUZSaS/u7enH1/vupzq/kh+Gf0OnRgbS/q9cFPeYLCvMUqH7mF64sgZwC8h+UtFzCOeEiJy76h7iPzczkHtF8sPYAN/fXyctLS9NwMxqYeVn7s2xCArO18UeDhLFjfX+2MhdqCkCpA4MVPMLBeHbdxIVEWW65Xk1ZfYRDa49QcOS3nfhpC2qySimer5vDaZqG7/gkkuZMwS36l008aJpG9fosyj/fgVpei+e0zliviD2np2dN08j69zpWPPUTQV2CiRweSNb3+7ns+2n4tTA6qlQ7OTRzIWqtQvs5UxBuBhaP+pTQITF0vLdPk+2uu+M7uj49GDe7kaOf7UEYJKLu6qlvZ+9RKK1BmpbcbB8NE0WfpNL3eV1MrhQ4sLgZqSqr1omL2YBS7gJZgtJK8G5+/ckJodg6elJRqOCxeA9y73gC7+lNzt9WYh8R16T95jW5A5VbsqmzGmFXLo4PNmO7pSexLw7jwN2L2D/jOxL/Mx5rSiD77/yekFu6EnZvb8zR3kTPuprjDy0l647vCXt5OF4vjqXyky2U/Xk+tnsH4nFlPNYhMZTN3k32zfPxGBGL923dWm3dCSH0VpGfL2rVDqSqEpS1G3Qju9CQ85ICLdzNyF1ikLvEoFXWoO7PQdl6qJ7EBOskJibwN5kQEiYjIsQfQhrNC7WSclw5hRx5dyN7Zu1D0yD5uiSGvDgAU6g/hYdKWTbmc3q+OJzYaZ0v+DFeUAhPcH8Tqu7m3Cz/AWxgfedCHNXvB5cqLm3GxU1cJEknHprKn4Z14M0VexveemLeNsK8rXR+Zn7Da97uJn5+WJevz/h0PffP3gQIwuO3sGHjJn0hxQkn1sHhuVCZA5KRBlM71QmBvSBmAtjjL7h53cU08XM2OIurKVm0n8L56dQeLcVnVALRL4/A2jnoF/fiNUWlauURyj9PBUlgn9YFy8CocxZE1x0vZdO0Oezbkk3HGT05/m063h1CGLXtLowttJecRbpHi1uMN3H/GoYwSqyasQDJJNPv1SubLHvo851U5zlIuqUjtSW17Ht6Jf3X3oqQBJpLQVmRBnZ35BaqflqRA5fZiJAlPOqFqUpBJe7uJirLavAOsoNJBqeCCPbR20UtEBdhNGC9IpqC99LRov1wLdyJ9eruGAOtlH63D++JjeRdCEHw00PImPIV7jO6U/fTfhwfbcZ2U0/iXh/J/tu+48A9i0h4azSdf7ie9FsXULEjl/g3RmHwNBPx1mjyXl1PxjVfE/7GKGwz+lK3JYuKl37G7fJ4LJO74H1jFzzHJVL8/jayJn2F1/WdsE9NaTXcUqvRRZuGft2hrAz1SKaeSB0VgQgNPW+kQljdkLvGIHeNQXPU6JWYzQfRvt+CFFdPYqJ/GxID+vj9vvd3svetjXgnB9Dz/64itE8wFJahFpaQ/c5uVj2/kz4PdSGyqwdqfrGehi3/9//ffzHME/TAxOqnaBt5kUDYwDYf5OgLfXSX8D+Ci5q4OHIzYf4zoKgE2i1U/V9j9Hntuze2ut7Ht9T3iIWAqB4wpF6hXpwOW/+qRwYo9f9Ual3TlXPXQf4W8IyBHk+f1wqMqqrk7snjwOrDF8XEz9mgVDspXX6EonnpOLZkYx8SRcjdvfDsH9ngLvtLoNUpVP54kPIvUpF9LHjN6Ilbr/BzJkCaqpH/0WZWPrYMyc9K+2ldyJqzh77vjyf0yvgW16k5Wsq+6d/iMyqe8If6IYRgx4tryN9ynPGrb2vS7qnOd7D5oR8Y9fONoKlsvX4BCU8OxhqjkxB1VwbUqsi941rcl1ZYQXmZk5ABUQ3nphRU4u7hRmWZfv0JIcAoIwK80XKKIDmyxW3JCeF4DHdQtuYEXvnlyP3jCLinN8f/sgz76ASkU6Z+ZA8zoS8O59hd3xPxzlgq31qLQ2zBdmMPEt4ZQ/qN33Lozz8Q+8qVdJx3DUeeWkHqiE9J+nAC1gQ/gh7qT2msD5k3zSPkH5fjMTAKr1g/HG+toezxhXjcNwg5xI7/w/2xT+5A8ZsbOTZ3Dz4ze2EbFttsrFupH4UWQoCXF3LXzmjl5TqBychEiojQE6kN5+/jSNjckLu1Q+7WTicx+46jbDyA9t0WpPiQRhJzAaYGyw8XkfbvDRyetZOIsYkMX3wDvqca+9k9yD5QxepX9jJo1tWEpHjr7aXU/WhlDoS3xylj2F4I8++jrd0At1tAjoCqh0AtQte8nF5NMAIyGLqC+xuXSMslA7pzwkVNXLAHgXcYFGb8svVlI6TU+70UbIetz4Jae5aVNFBqofQgrLkP+v8bTG1zBz0dZ5r4SR6e8F+Z+DkbNEWlfMMxihfso+THQ1g7BeE7Pol2r41Etv26D1C12olj4T4qZu/CGO2NzyODcOvcstDzbHAdLyXtrvlsWZFJ/JQUSrfk4CysYkzqTNz8rC2u0+DRcl9vgq7Xy/KHv9nD7jc2MHH9DEweTafLNt6/mPgbuuAVZSN3cQaSQSZyhj6Wr9U6cW0+AKU1yF2iWj7fIgeFR8sJ6d9IRpQCB1a7m54QXQ9hlhG+dpTdR1o9XxHmj1tMJpUbJNSYQFxzNuN+31DM0V6UfrsXn6kpTZa3JAfid3sPcp/5mfC3RlP2zFIcQmC7oTuJH05g73VzOfL4T8Q8dwWx/xpG3uzd7Jowi9jnh+E/NhGvCe0xRXlz/MEl1F7fGd+buuDx+DBqlqRT9thC3Kd1x3x5PKYoL4JeGkH1jlyKXl2vC3jv64OlW+O4rG4+17SdJDw9kTt3RHM49ETqNesR4WFIEeHnPVdI2NyQu8cid49Fq6hG3ZeNsn6fTmLiQpDahyGiAn4VidE0jbz1Wex+ZR15azJJuLU7E3ffgzWkuVA+4+s01t+9kCvmX0dg33q35nCd2GguF1pR/Rj2waNoG3eBxdx0DNt6EUSEaApoB0ErQfdw8QER11ilNg4Fzx2gbIKa18G5Dp3AyHpLyTQJzDNAbpmo/yFxibi0GRc3cQHocx0sfkHXoZwLZBOEpoBfFFRkwra2kJZToLmgpgg2PQH9XgGp8Yl269epZGw8ytUvj2uyysU68XM2aJpGdXoBhfPSKf5+H8YAG77jEgl9qB+mNnilnA1qRS0V8/ZQ8c0ezCmB+D83DFPCmcMSWz1WRaV01g7WP7OcwiqF5Ju7c2z2brq9MJx2N3Rp9QO9dGUGh+5fQsy/huIzXK+Q5G0+zuo7FzD6hxuxnWZil7VwPwWbjzPwP6NxVdWx654fGLDu1oZqgrL9EMLNgoi2IDxb1nhohQ6yd+XT/d5BDa8pBZVYvd0bKi6g5/lo7m5Q50RzVCNszbcnZAnh44nnVe0o+Sgdvw4eqKnHCLi7F1n3LcZrQlKzVo33tR2p3JJN4X+2EfDsSEoeW0SlAOv07iR9OpE9U+aQ+fdVRD05iMCpKVjb+7P35vl6VMDjg3DvEkz0rHqzuoNFBD8zBMvI9hg7BON4bRV1245hu7M/kqcbli7BhH48Eceyw+T/9WdMsb743tsLU5S3bvffykSRsNmQU5LRqqpQM46irFuPCA1BioxAmM+/TYHwsCD3iEXuEYtWXq1XYtamoy3Y3FiJOQcSo7oUMuels/uVtdQWVtHh/r4M/nRSiy1KgAMfbWfbEz8xYukN+LZA2oXBgAj0hcB6l1pVhbL6MeycArRdB/SHc3+vBjKDl8d50Qu1CVoh1H0CzrdoICIAuEB4gfE+MF6rfy8EGHqDrfdvc2yX8IfBxU9c/KP1Vs/P7+j6lLZANoFfJAy+Xf85/WNQ6rBN+oENL/Xl+pd3ApBVUI3dasDubsTP08hPz/Zmx+Eyut63lh/+2pPh3fyhMhvyN0FQXzRN4/tnlvLjSyvRNI3hf7mMzE3HGiZ+cnbnEtrx4pj4aQtqj5dTVJ/ArFY78R2XRMLnk7DEntk6v61QSqqp+Ho3ju/SsfSJIPC10W0yIWsNzoxiMh5dwoafjuDfO5KAijrKduQyctMdeJxBGJw/J41j/1pDwn/G4dFdNymsOFrCDxO+YPB/JuDftamZVl15Detnfs/gTyci4WL73UtJfGYI7vX70KpqUXdmgGZC6h3b6n7V/AqKcx34JjeO3SsFDqz+NqrKahpeE2YZ6hREsC9qTjFyfGhLm0Py98YsaxhjfKkL9IS5W7E8PRZL+wCK56Thd31TcacQgpC/XUbG5K9w7xGK93MjKXl0MUgC67RutP9iEmmTZnPMaiTiT/2wdQyiy483sO/O79g9+SsS3x2LKdiDqE8mkvPEco7eNI+w10ZijPDG/vwYqmZto+xP87HOHICpcyhCEngMj8U6OIryOWlk37oA29B2GCPtSGeJchDu7sjJSWgx0aiZR1HWbUSEBCFFRSLcLoxrrPC0IPeMQ+4Zh1ZepUcOrNmrk5iE0HoS0/IUVF1FLQc+2Eba6+uxhtnp9PBAIsYmNjgst4S01zaQ9uo6rlxxE15tJO5CksDbE9nbE+Ij9biCymp9eqmgBNeR41BZjfD1avST8W19DPsXQ9Og7mVw/gt9aKIF/YpWBXV/hbqnwfQcmG47v8fwv4xLPi7nhIufuABEdIZhD8DyN3V9iquVyokk1+tausGAG0Ey6FWTop2c7LGmRHmS+sYAAG58dSejewQwqX/jk8+Xq3Lo396bL1fn6MRFqYHDc3F69eCdqz5m34qDuGoVhCR4LOpZ2vWNuqgmfs4GV1kNxYsOUDQ/nZpDRXiPjCfquSuwdWs9Sfmc95HnoHz2Tqp+PIT75e0Ien8ihuBf1m4D0JwKjtmp7Hh5LQeOlpFwbWdy5+4l6YG+JD/Uv9WbhaZpZL++kYI5e2g/ZwqWdrqZWG1ZDYtGf0bnhwYQfZrlP8DWR5cRekU7gnoHU7I1B2dJHRG3NcZJKFsOICIDUNdnInVoOexOcyrgqMHeObThxqepGkphFbYYj9MqLjJanYIU4qvrXFohLvh4QnExXtelkP/4cvyvDEdZtpeAe3px9Pbv8LkqGek0zxzZ043QF4Zz7J5FRM26Gu/nRlL82GIQAtu0biTPnkzaxNnI7kZC7+yJ0cdCh1lXc/Rfa0kd/glJ/xmPR9cQQl8aTuF7W8mY+jXhr12JpUMg1ht6YuoShuPNNTh7R+I+rTvCZEAyG/C6vjMeYxIp+WAbxW9uxpToh1rjOutou7C4IScloMVEoR7NQtmwCREQoE8iuZ/7iH1bITzdkXvFI/eKRyurRE3PRlmVhragCimhvhIT6U9VTgVpr2/gwEfbCbk8hstmTyWg55kDDzVNI/UfKzn0WSqjVt2KRytj5G06TiF0x16bO0TVj2HX1qEV6URGTTuMVlqO8LDqJOakTsbyK8ifpkHtA+D6Eqg5y8L1Hi51T4B2AsxP/vL9XsIltILfB3EBCE6Aa16Foztg92Ioza1v39QHZADED4T2l4PHKSmnR5e0eReapjF3XS7L/tGLAY9soKZOwc0kQ3kmn17zCmlL8k9OaCMkwZhnhjH8ocvO2yleKKi1LkpXHKFowT4q1mfhOSCKoFu7YR8c3UTU+WvhPFZK+RepVK85inV0AsGfXo3s++tuNs6DhZz4x3I2rc1C9bIQNSCa4pWZXP7DdHy7tGA7JN8xvQAAIABJREFUXg/NpZLx+E84dueRPO8aTAG67kVxKiybMpuQgdF0vK9Ps/Xy1h3l6Px0rtozE7W2ju03L6TPjzc0kDr9yTwLKSYcKSW81SdbrbiSWk0QXG88B6CWVSO5G7H6uDfVuJgMaHUKIsQHdd+xVs9JyBKa1Q25pBJLv0hqXAbMK/bi1icG924hFH25C/9bujVbz9IxCN+bu5L98FKiPp6Iz3MjKX50EUgC27VdSf5qMrsnfonkbiT4hi4IWSLqsYF4dAlmz7RviHx0AMHXd8Z/Rg/M7XzIumshQX8ZgH1kPMaOIdhfHk/lu+soe+R7bPcPwhCpE0TZyw2/P/VDqXJSm5bHsatm43NnD2wj488aRCrMZuT4OLSoKNSsYyibtiL8fHUCY7uwlgXCbkXuHY/cOx6ttBI1/Tj5H29gz6IMsg+UE3d1MuM23YFnjM9Zt6VpGpsfWkr2jwcZtfpW3IN+OYFv9XjNJkRIAITolT1NUdCKy3XBb0Y22pY9YDQg/Ot1Mn7e4Glt9qCi5BZCZRVSu9OE8s5X60lLU2O5M6MKnG+AiADTDWdf/BIuVVzOAb8f4gIgGyCmh/5VWQLV5Xr7yOQOnv66GPd05G/Wx5zbgHV7S4gOdKddsJXBKb4s3prPxL7BIATTX2hPv3sncmhtBnuX7idr+3Gy006c5xM8f9BUjYrNxyman07JDwdxbx+A7/gkol8YjsHz/GoH6g4WUv55KjU7cvCYmEzwl1OQPX9deV+rc+GYtYPDH25l255CokYnUrwiA8/+0Qz+aiqGM4RcKlVODs5ciOZUSJ4zpUFUrGkaa+9ZiJAl+r82stkHt6vGyZrb5tP7tZEYzRoH/rWZ2IcH4H7KE7KycR8iJQp1QyaGCa3nZ2lFDspLawm+Lqpx3fxKZH8r7nYLBVklDa8Ls4xW60L4+6KVV6LVOltORZYkhJsR5fBRPG/uTt5N3+A2vT3Ob7YRMLMXGTd+i8+UlBZF1D7Xd6Zqy3HyX9tA4J/7622jxxYDYLu2Kx2+mszuibORLUYCJncAwPfKOCzxvqTf9C0V23OJ/edQPK9ohynczrF7dbM6/3t6I3mYsf1pCLU/H6L8mR+wXNUJt5HtG8mJS8Xruk4YI+wU/XsDpV/uxvf+Prj3aKWydAqEyYgcG4MWGYF27DjK1u0ILy89kdrz/JOAU6GpKsfWHmP3K+soP1RE8m3d6NPTH+PxfLTv1uFKDNMrMeF+LRIxVVFZf+f3FO86waiVt2D2uXAVo1MhZFkX8fp7Q5J+3VNeqVdkCkrQ9h4Bp6uxteTvjfC2o+3PQMsrQisqQ+6RrFcKtTJky59ISZZwuSApQfDJu264uwtku6Ph9ehIwWfvu/HCv+tQFPjX381ANUcPPcSQ0c+wffsOvLx+eaXpD4FLxKXN+H0Rl1Nh9da/zgZnZZs3+eXqHKYO1J/ipw4M4bMVx3XiorgwSrUkDokjcUgco58chqqqaMrFd6FV7S/UnWy/24fsacZ3fBIdlkzH9CtaNa2hdvcJyj7bgfNgER5TOuLzyKBmrYpfgrr0PIpeXMmuvUXk5jqIvjyO4p8z6ffhREKGtq4pgaYeLTEvDGsytr3zlXWc2JDFhDW3NXe5BXY+uwqvRH+ixsVTe6yI0q159Hz6iob31aJy1IwTyMN64Ko9hIhuPTLCebyE0vxqkk+drilwIPvbsHpZOLo7p3FhY33FRZYQgfpYtIgOar5RIYEkQNMwSAq2MUk4DjuwVpZgHFiHrV8ERZ+lEnBnzxZWFQT/44oGvYvHoOhGzYsQ2K7pQvLsq0mb/BWSxYjfGN2R172dD52XTOfA/YvZOe4Lkj6YgFuCH9FfTub4g0s4du8iQv81DNlqwu2yOIztA3G8tgrn9mPY7h6I5OOuJ0P7WLB0Dib0owlULj9CwT9WYYr2wvfe3pjaULkQRgMiJgoREY6WnY2yYyfCw6YTGK+2p4u3Ba5qJ4c+S2X3v9djcDeS8mA/Yq7u0ORa0kocuiZm2U40Rw1SUmgjiREC1amwcvpcavIrGbHsxmYTa78lhBBgtyHsNqTYcP34q2vQCnSXX2VbOpQ7QFVBA+1oDq7SCgyDuyPEl1gsgtT1Oum67pYa3vnAyYP3mLBYaHj9httreOt9J08+YqJLvypuvM5IUqLEfQ+X8/enp14iLZdwXvH7JS5thWhbK0RRNL5Zd4LvNuXx7JxDaBoUVdRRUeXCw2rQbxqnQJIkuDjsVqjLrdBFtgv24SqtxndcEnEfjMc98ZdN7pwJmqZRsyWb8s934Mpz4HltJ/z/PhTRivnYOW27xkXFp1s5MX8Pm/cV45ngj72sDlkSjEmdedYn1prMUvbd8C2+o+MJ+3O/JhWVjPl72fXqOiasn4GphWpQ8e4T7Ht3C+N3zESrriZ15o90em9804Tj9enI3ePQdmchd4s6Y7ujMi0Hze6OfEqKsVJQieRvxWq3NNW4mGW0Ot2kTYT4ouYUIbVEXCQBqobULgT1cA6e0zqTc81sbDO74ZqzGf87+pNx3Tf4XtsR2d78HA1eFkKfH8bxB5fgNnsyxiCPevKyCATYpnYh+fNJ7LnmaySLAZ8rdPt12Woi8b1xZL+zhdQRn5Lw1mi8B0UR+f44cp9bTeZ1cwl/YxSmcDtykCee/xhF9Tc7KX1oAdbb++hTRV768QghsF3RDuvAKMq+TiN7xnfYhsTgPaM7hja0FYVBRkRGNCZS70pDuFt0UuPt/at0WtX5Dva+tYn0dzcT0Cucfm+PIXhQdMvBkt425L6JyH0T0YordBKzNFUXbscEs+q1VITFxLCF15+xOvjfgrC4ISKCICIIGVBLylGWbdD1LKoGJeW4Fq7COOLfnOrBMqCvzK40pdn2+vTSX7dYBK/808xdD9by8P1GKhwurrt68293Yr9bXPJxORf87xMXsxdU5Zx1sZ9SC+kU7cHSvzdmhdzwSirzN57g+qFxYLq4nhhc5bWULD1I0fx0qvbk4z08joinBuPRM+ys+oFfAk3VqF6TSfnnO9BqFTyndcb9snbnnPbcGup25VL66mqOFNWQtuUEkUNiKF6ZSY9XRxJ9bcez3pAcO0+w/5b5hN3Xh8DrOzV5L39rNitvn8+oxTfgEdH876gnPy+g2z+uwN3XSN6i/YRM7oglvPFJXs0tRssrRQzrimvh9xjvuqLZdpqcT1YJbjF+TV7TKy5WrHa304iLAWr1m4EU4ouyaV/LG613kRYxISg/bMbQKwnPaV0o//kY9mA35KP5eF4eQ+HHOwhsQb8D4N41BJ9pnch+5Eci/zMe2ccd73+OouTRRQghsE7pTNInE0mf/i3xb4/Ga4DusyGEIOzOnthSAtl35/eE3tadsHt6EfzUYEpm7yZj2jeEvTgMa88whCzhPrkLxk6hevXlaHmzSpwwyXhd1wmP0QmUfLidY5O/wuuajtindURyO/uNXsgyIjwMERqClpuHunc/GI16IrWf7zkRmJL0fNJeWUfmt3uJvroDo1fd2uapHwDh44HcLwm5XxJ1RwtZPvFL3Awa/UYFwNo9qEnhiNCLy6+pGRxVOmGp18IQ6IvkWw1aUcMiLpfGkh9djBja9LahKBrLV7q4Zbr+dxs53MAHnzqZfnsNa390B3UfaNUgLt4Jy0v4feF/n7iED4PyI/p00Bnw5eocJvRp+pR7Vb9g/m/xUa6/IgYCm5fff2uodQplqzIpmp9O+ZpMPPqEEzCtE16XxbRqt/5roblUqpYfouzzVCSLEc/pXbH0izxv5EitqsPx0RZKVxxm+4kqaqqcBEb7oBZWM2rrndhaIBqno2TFEQ4/+AMxLwzDZ1jTVlJFVik/jP+cwe+NJ6B7y5qKva9vRLYYSLi5C2pZOdnzDtL1s0kN72uahrJuL3LvBLQj+QgfK5L/mf14pPJqPEY0ddRVCioxxvrh7mFsOg5tOqXiEuSNVlCG5lKaWdMLIdAQCG8bmI1oucV4TEymYu5u1BE9UBel4nf7EI5Mn4/v9Z0x+LR8o/C9uRtVW7MpeHszAff1aSQvf1kEQuAxuRMJ749l/23fkfjBODxPmZrx6h9Jl6XTSb95PhWpucS/NhKfazpiivbm+J+X4n9XzwYzPGNCAPaXxlE85CMcLy7H48HBGOOaEgLZ7obfA32xX51M0VubyZqoC3g9Rsa3yUtFSBIiNBgREoSWl4968HBDIrUI8G+VLGiaRs6KI+x+ZR1F23NIurMnk/bdj8W/ZfPCtqCmqIqlk+fi2y2Cvv83BnGynbR4G1qtEympXhMTcvGRGBHij2HMIHB3azw2JR2qjVRXQ+e+ujB3QF+ZW6brnzUnX8/MUunWWWboZY3X68zbjVTXQEK8BJhAK71EXM6GSxWXNuN/n7iEDIA9eniXY+6IJm99/ECnFr8/ibG9AhnbKxgCe//Xwhc1TcOxLUcX2S45iFs7H3zHJxH17OUYLqBHjFbrwrHkAOWzdmIItuFzX1/M3ULP6wdu7bbjlL2+lkKzkY0bsgnqHkbNgWPEPDKQ9g/2bZOpVv5Xuzn2wloSPhiPR7fmfiyLx3xGxwf6ET2+5TDOiowSUp9bxZh1t+EqqeDI61to//zwJuepZRWgVdYgtY/ANWsDcreYMx6Tq8aJm6zhNqhp0m1DxcUsUVnaOKFxchwa6rUcvh5oeSWI0KYVG6BB4yLFhqIdzkYK8cXr1h6UfrUH3yGRsOUw9pFxFH6wjaCH+rd4fEIShDw7VM8z6h6CrV9kPXkZqZMXCeyTOhH3xkj23bKA9l9MwtYxsGF9c4gnHRdcy+EnlpN65ae0/3ACtt7hRH8+SU+YPlBE0KMD6kMyBcIgY53enYp/LsNtZHssEzo2IyXGMDtB/xxKza4TFP17A2WzduN7X2/ce4ef8XfdcE5CIIICEYEBaAWFqEcyGwlMYEDDtaTUuTjy1W7SXl2PUqeQ8kBfrvjmGgxtqPKcCVW5Ffww/GPChsfR44X668fPE3lAe+QB7VELylDTj+P6fis4FaT2YUiJYYiQX9feOl8QsgzW0z5PhARoTbQsp+Lk62VlGqOvruat95zce6cuDJfq5Vg6NP4It5pL+O3wv381yWYIvwKO/qC74Z7z+kY9dPE3RvXhYl1ku2AfwizjOz6J9guuxRx2foWIp0OtqsOxIJ2KObsxJvjh9+QQzCkt6C1+zT4ctVS8v4mqbcfZr0pkrDhEYLw/rqNlDF9+M94dz74/TdPIfm0jBV/vof3XU7CcJvBUXQo/Tv2KoD4RdHqwX6vbWHvHAlL+1A+PCA9qMvJxjw/EEubZZBll3R4MfZOg1oW6LwfDxNaniQAK1mXiYZAwBTQVROtTRTbchUZlk4qLAa228doUJ/1cWiIuQgJVRWoXgmveWqR+HXAfFkf57F04fbyRlqXiN60vh+9Ygu+NXTC2UkEw+LoT8s+hZD/yI9GzJ2MMsCH7WhvaRgiB91UdaffiMPZO/4bk2VdjPUUzJZkNxL04nBNf7mLn+FnEvTAcv9EJRH0xiexHfuTo7d8R9soItConso8b5j7RGOIDcLyxGueO49juHYQc2Fww7tYxiJAPxlO5IoOC59dgjLDje28fzLFnF/BCPYEJ8Ef4+6EVFzcQGKd3EPsXHmPvW5vwSvSj+7NDCRsee14cZysyS/hh2MfETu9C58cHtUhEJH87kr8dbUB7tIJyncR8txkUtbESE3xxkJgGCF/g7I7ldrvg9RfNjJtaw523GjEaTz8HJ4gL+7n1u8clA7pzwv8+cQGInwZ5W6CmADS17evJZggbBl4th+idbzgLKin6fj9F89Nx5jnwGZNIu/8bg3v71kve5wtKeQ0Vc9NwzNuLW7cQ/F+8EtN5ctA9FTUbj1L+5jpqonxYt6sQs90Nd0UjsHsYXf5xOXIbnnxPerRUnubR0vC+prH2vsWgwYA3R7f6uzv0aSo1BZWkPNgXV0ExWbP2kfC3ptoV9WAOIBCxIaibjyDFBSHczzwhUrQmA7PBgO3Uqo2iopZWI/tZsboUqsqq0TRNv9GaDQ0VF6jXuezOoEVZuSR0nYuHO8JuRTtegBQRiNedvSj59zoCZnRGWZaG17gECt7bSsjjg1raCgDWHmF4T+5Azl9+JOL98QhZQvazntI2At+JHVGrXey9di4d5k7FEtN0ki/omo5Y2weQfss8KnbkEvXoQMJfH0n+6xvJuOZrAu/r3ZBTJPta8XxqBDXfp1H2l++x3tgT08B2zf4+Qghsl8dgHRhJ2Td7ybnzO6yDovC5oweGVnKoTocQAuHri6NMkPavnzn01TLC+/gz9L2h+A3reN4SmEv3FfDD8E9I+VM/ku9tWVfU7LgC7EgBdrSB7dHy6ysx8zfrlbSTJCbI679PYoQfSInA+rMu2qWTTKcOErPnurj+mtP+h+WBIC5uY86LApeIS5vxxyAuRhv0eR7WPwy1JW2rvMhmCOoLyRfWtlqprKNk6SGK5qdTufMEXkPbEfZwfzz7hF+Q5Npm+y+sonzOLioX78cyIIrAt8diDD//QmS1rIbydzZQty+fnCg/tr67haCUIGoOFzPoi8kEDTlz+6XheKucHLxrIZqi0v4Uj5ZTseu1DeSuyWTC2pbHngGq8xxsfngpw5dMpy63lPKdJ4i6s3fTFpGioqzfi2FIJ4QQKNsykAcmnPUYHXtyEMmnVYCKqpDsbgiDhMkggRDU1TgxW0xNWkUAItgX7cftaKravCIgJH3yAxDtQlAP5SBFBOLWMww5wEZ1iYKp1oVvnwAOP74Gv5u6YgppfRTe77buZG3NofCdLfjP1IXpOnlpHJX2n5CCWu1kz5Q5dJg3FbfTqn4enYLosvQG9t3xHbunzCHx3bEEPtAXtzhfTvx9ZZNqmJAElnEpGDuG4Pi3nndkndEXydqcDAqjjNfUFDxGxVP64XaOTZmDfUoKXtM6nXXsPm+DHniYuzKDxFu7c9WeB3C3gXokA2XNeqQofTLp1yRSF+7I4cdRn9H92aHE39T1nNcXQiACvZACvdAGJaPllaGmH8P17UYQ1JOYcESg/b9HYowP4DhxBHA0e8txomn7/PuvG1tNgwcYGDzAANjAeP8FPshL+KPhIhno/Q1g8YcBr0NAd5CMILXyBCC7gcEd4q6FTg82G4M+H1CdCqU/H+HwfYvY2ed9ihcdwG9yBzptvJ2Yl0Zg7x95wUmLK6ec4pfXkHvD1+BSCfrgKnwfGXRBSEvNmiMU3vkNdSaJzYW17PlmD3ZPN+yhnozdeXebSYuzsIq9U+Zg9LWQ8OH4FklLxoJ0dr60hpHfT2tx7PkkNty/iLgbuuCT7I9s0lAUA26n3eDVvVkIDwsiwh+tyIGWV4aU2LpbL+gTSq7sMtxim4pQlQK9TXQSpyZEnyrOBRAWE8LDglZQ1nwHkt4qApBiQtCy8nQhrxB439mL8o+3I4/virosDe+rkih4d8sZj1fIEqHPD6X02z1Ubmx07ZX9bXg/N5LqhXupnJ9G4LUdCZnRnT2T51CX1/wmZvR1p8PsyXh2DSZ1+CdU7MjFPjoB32mdqTlcTMF7W3UjtHoYon2xvzAWydONsgfn49yT2+oxyh5mfO/rQ9inV+E8WkrWVV9SPj8dTWlaPVUVlYy5aXzX911WXv81wYOimZrxJ3r8cxjWUE+E3RO5Syfkbl3QyitQ1qxHPZyB5mxjBtopyFt3lKUjPqXP66N+EWk5HUIIpCAvDENSMN41AsOE3qCB65sNON9ZimtlGmpeaZPf4W8Cw1h+1W1CeIA8+Hwdzf82hHZ+v/6H8ceouJyEyQO6PwE1JZC1RP+qK9PbR5IRbOHQbhIE9dF/Po/QNI3KnSd03crCA5gj7PiOTyLiqSEYf6Ut/rnAmVlC2ec7qNl4DNu4JII/n9xQyj/fUEqqKH9rPa6sEhxXxLPq6RV4R3ljKKqh+xujiZ6S0uZt1WSWsG/6t/iOSyTswb4tPoEWbMtm5W3zGLVoOh6RrZsTZn2/j8KtOQz8YAKO3cdxHCwheGqXJstoLgVl0z4Mo3shhMC1PQOpU0SzSZ/TUbTrBN4B7hjDmu7/pDD3JNztFirLavAOsuutotqm3hi6zqUYAk87DyEaKy7uZoS/F9rRPES7EEyJ/pg7B1O5ORdLXCDeVjNHXkvH/9ZumMJb1xgY/KyEPDuUnMeXET1naoOfihxga2gbCQlCbu2GWu0kbcocUr6Z2uy6FbJE1OODsHUJZs91c4l6bCBmdyP2sQlUrDhC7cEiQv52GVK9r4kwG7De2gdjlzAqXl2JeVAs7lO71ot6m8MY6kngs1dQk5ZH0WsbKat34DWmBLD/w+3seW09lmAPUv7cn8hxSa1mWAkPG3LHDmiVlagZR1HXbkCE1SdSm87e0shedoiV133NoE8nETbi/LeRhRCIYG+kYG+0IR3Qckv0dtLX68EgN7aT/D0vfCVGmMDtfai5kRaDFc8IC7h9eEEe/i7hj40/FnE5CTdviL9W/wKduFygf66azBKKFugJzAC+E5JImjsFt1+RkvxLULuvgPLPdlCblofH1R3wub8/UgsVi/MBTdOo+fkQFe9vwnRZHAdK69j/+E/YfdxxdzMydPtdWM9BZNzg0XJ/HwKnNZ/+AnAcK2XJ+C8Y9M44Anq0HnpXV6YnPw/85CqqM4sxepnxGRzb7Aagph5BBHkj/T97Zx0exbm28d87K3F3gyR4ggR3LVJcilNKKXU/H7TU3dtzyqE99ZYKLa6laKEt7gR3Eghx92R3Z97vj00gIZtkQ4H2cLivay/Yd0fe2Z3M3PM893M/gV5IKdH2xaGf2KXWuSZticc/2AXhUzmMrqZVJi6VTOiuiLgA1r5FZ5LRta5cmVQx4gKgNAxBO5uI0sAaCfK8vwMp9y3F5ZNhWD7agO8dTUn7dDehb/Wrcd4uncLwGBFF0rMbCPt06KWIn87fFa93BpH9zGpAEPpYJ9RCM0cnLKL5onHobRjd+Q5qjHNjH45NXYaDk4Hgcc0J/7YryS9vIn7KUsJmD8YQePn7MbYNw/OfIyj4z1Zyn1uF2xM90YVWH/lzbB5A8BfDyFp6jIsz15GfWUxhQy96/zgWfzurkACEiwu65lHI4mK0uPOoW3cgQoJQ6tdHONrWMcUvO8a2B1dy25IJBHYPt3tfVwshBCLYGyXYG9mnBTIp25pOWrAVjHqUZqHomoUhainP/1PQDwLjB2CaTu1NFsvhBA5fgs52ZdstXImbP0pyLfG/RYWlZjVUkuesnUtlmWL+GpMWc2YRqd8d4NjInzg+egGWnBIiPxxIi01TCXm88w0jLVJKSmKTSJu+mozn1+PYOpjgBRPwuLP1dSMtanohOa+sp3DxYcTUDqz7fC8XN57FySyJur8D/dZNqRNpyd54jhNTlhLxVt9qSYspv5TVQ+fS4vHORI6KrnF7e57dQEj/RgR0DgNTCcVJxTgGVb7oyxIT6r7T6LtYS6jlhUwQCiKsdrFy0tbzuDrrEL5XEJcrUkXOlVJFejBVjrgowT7I5MyqqYEyE7pLb8MDkYmZyFJrukMf4m6tMlp2DH2/KNwNpeT/EU/puaxa5+73UAc0k0rm1/sqjev83fB6exCFyw9TtOoY9WZ2w71TGMfuXIJaaLvqxLmhDzFrJmPJLyXui72YM4sIfqcf7rc3Im7iIooOVu7zpXg44fZsXxz7NiH3xdWUrDtRbVokMzaZP6YsZvX9y8mMCST0kQ7UK1Zh3RksaVXTWLVBODmhi2qKrotV46Nu34l67ASyuHKE4fQPsWx/+GcGrJ58Q0hLlXkKgRLijb5vKwyPDkI/pB2UWjDP24L5i/WoW44hM/Kuz86Nd4HjPBBBQHUCaWH9TNQHp+VgGH595nKz4laqyG78b0RcZBqoX4P6MVaRmR7QrC9lJOieBCXmT+1CLTaT8+tZMpcfp2BPEh59Igh+ojPuXetV6nFyIyClpGRnArk/HEDLLsZ9UgwuAxpVG4K/VvssXneS/Dl7cR7ajKRgL3ZMXIhnqAdGIejxxzQ8owNq31AFpM0/TML7W2nyzQjc2tjWlmgWlQ0TFuDfIZSYGTU/3aVsiefCyuOMOvwY6b8cxznCHa9uEVWWU/efQYkIRHhbNS/q3jiUdrat3ytCSknylnj0Y+tVjbikF2CsUFZeMeJS3mSxIoSbM+h1kF0A3pe1N0IRSE2WNylHOBgQIT7I+BREE2u0wWNKG5LvXIjryKGw7QwBIxqR9sluwj6o7GN0JYReIeTd/sSNX4hzm2CcKxj26QLc8H5rsLWrNBDxam/OPrWe43cvo9n3o9BVsbXPR++aRVA/PcWaFwdu/56mnwzF9542OER6kfDYLwRM74rn8KaX9y8EjgOaYogOJP/ff2Dan4Drw91QPJyQmsbFtac5/K9t5JzMIPqxznSePQSHMi8j9a4Ycr6NJWHCIjzGNMdzcisUl7qRc+HoiK5JY2REONr5BNSduxF+figR4Rz/7jCH3tnMwI1T8YqqvkfVjYIQAhHigxLig+zbEpmYiXbsIuYfNyOcHS6nk3yuYY8yfV/QnQT1DzDPAnUz1utomU+Lrh8YHwelszWleQu3cJ1wcxMXaQbL46D9hDW4VP4EVXp5GW0RaCtANALDIuvTgq1NlZWuVhpTNfK2J5C5/Dg5G87i0joQnxHNaDB7MLo6XjSvBaSqUfRHHHlzY0FK3O9sjXOviOsv9E3NJ2/WFrRCE87P9GbrW3+Qvi8JF0VH5MAmtHq1T6WePbVBSsnFD3eQsfSYTY+Witj2jzVoZpXu/xlaI7GwlJjZet9yOs8eTElcFl7t/RFOLlWqdmRhCdqhOAwTe1vfW1S0gxcw/qPmmz5A7plMXNwMCBejNYpSAVXFuU6X3HOFsXI5dDmUsr5FugrExerjUpnkKA1C0E5cQCkjLjovJ9zGtCDvm314jWmP86I9pO3OouROCLOHAAAgAElEQVRkBo5NbHjDVIAhwJXg124j8dkNRCwYV8l9V3ept9FqUAQN3u3HqcdXc/L+lTT9egSKUQWWAu8CRwAH/J+zIBxUwmY25dyr+8k/PI3Qh7oQPmckFx61dpj2/0fnSueoLtQTj7eGULTgAJlPLCU11I8Ty46jc9TT4v+6EjGmeZXzSefqgM+jHXG/I4qsT8oceB9oh9uwpnVuSyGMRnSNGiDD6yEvXCT2yUWcWpvMwF/uxONvQFquhBACEeqLEuqL7NcKebGMxMz9w0piospIjPc1IDFCgL6X9QVWK38EiD/XDf5/Hrd8XOqEm5e4yBIwDwa5n0pEpQpUoBjkUTB1BMMmUC67rGqlFk5NWYp7j3CCH+6AlJKio2llHZhPYghyxWdEM8Ke6V6t2df1hjSrFK4/Td6PB1E8HPG8rz2OncKuu3BPapKiVcco+HE/LqNbkuPjyqrhc3H2dMJFg25LJhBQx5C6tGice24DRUfTrR4tNXynh2bvIPG3c4zcdj+6WqJJsa//jme0P2GDmpC8YD/69iG41Kt6IVd3n0RpVg/hbhWeaseTEEEeCK/af9ukLfHU7xxi8ylXTS9E53+lOLdiVVFV4nLJiK55+OVBRYC5cjWNqB+A3HIIWVSCcLbeQNzGtSB5wnzM41ui+LsTdLsLqR/vov5Hg2s9Dtfu9fEY1JikF34l7OMhldo76IPcK5RKQ6NZAzn5wEqS5zxD8P1fIoQG5JctbUEpu5/p3Y7Q6L141KIFXPz0YYLueoOIeaO5OH0dFx5ZRej7A9BV6KBcklPCybN5HPslHk/ni7QeE0XEG7fX2sfIEORGwOu3UXIsjcxZO8iZfxifxzvh3LVe3f8e9Hr2fXmaC9tzGbRwGE5ZcagHMq0dqT2uo6bkT0AIgQjzRQkrJzEZVhLz/e8IV6fLJMbrGjmBX2njbzoLpvOgFYLiDMb6YKy5o/st3EJdcXMSFynBMrGMtNirhFeBXDD3B+MeEEFoZpVT9yynYH8SxWezkKpG1soTyFIVnxFNaTJvDE4N7HP0vB7QSiwUrjpB3vyDGOp54v1Udxxigm6I54MlMZfcWVtA0/B8ZxD7v9rH0S9X4WLQE9IulPazBtVYjmwLVo+Wn0FC1MKxNUat4led4MC7mxm57X4cbAhEKyLzYDInv9zLiNhHOP/pLsLGN0YfUFWvInML0U4mYrjrtktj2t44dG2rppNsIWnreRo29UH4Vq62kSYVraAUpUKLhkrl0DZSRQBKsDfmfacrD1bwcbk0pNch6gWgnUtG19w6V8XJgMfUtuR+uhvf53vg8P5aTMcKKT6ahlN07VEDv0c7cv6eZWR9ewCfeyqX+14mL1aH3SZfnAF1NkLU7LIqlAL0rhBy72wufnIR38EfU/+zoaS+v424iYsI+3gIxcVmjny4jbjFRwm/I5rBm+/DI8yDwi+2kzfzZ1yf7Ik+onatkWOUP8GfD6Noy3kyP9xB7k+HrA68TWuOOJVDahrbH/2FjD0XGfzHNBx9XZCqikxMQj14COHiYm0n4HVjRfZ1gVAEop4fSj0/ZP8YZEK6lcR89xvCzfkyifH8kw9c0gQF6yH7SzDFgdBbz1EhrJ5ZhvrgdT+4DqjehuIWbkVc6oCbkrjo9HpaNBdY868wfozCM0/psVgkL72qsmiphkvZ3+qYUQrt2yq8/IaF7b8bECIHtfQl2nbaw8zgMTQ644I0a1gyiig6lk74O/1xbXNjyEF10ApM5C8/Sv7iIzhEB+D7ej8cmt2YELZUNYqWH6Fg4UFcJ7bG1DSAFeMXYM4uwRWFzrOHUP+OmgWytmDOKOLE1GU4N/Eh4u1+NeqC0g8k8ds9Sxn082TcaxE6axaVrfetoN1b/TAl5OHZ2gccHG1avas7jqOLibzkjCsLS9DOpqKfULsjKkDylng6dO+E8Kl8I1AzCtH5OFdKhzh7OJF+IRuoPlWElxuYLMiCYoRrGekRlauKyqE0DEY7cAaaXyZZLoObkrfgMKa4XPRdGxLomkTq7J2Efz6s1mMRBh0h7w0gbsJCnNoE4RwTVOlzfZA7Xm8Nomj5CwjxFcKhdmv4S3M1mgh7dBmnpzvh3X8mAc92J/fV3/ilzX8oBKIf78zo40/g5H85KuD6j16YNp8l77V1OI1ogePQ5rU2+hRC4NIjHOcuYeQtP0HyE7/g1CkMn4c6oA+sPuKgmVU237OUwoQ8Bm6ceomAC50OUS8MERqCTEpBPXIcHB2sBMb779c4sSKEIhD1/VHq+yMHxCAvlEVi5mxCeDhf1sTUlcSUnoHEu0ArBlloHSu//5b/azoJaS9BxpsQ8h041G7i+D+Jv4i4CCF0wF4gUUo5RAjhDSwAwoF4YKyUMtvGelOAF8reviGl/K5sPAKYD3gD+4HJUkqTsP6B/BsYBBQBd0sp91/NnG/KqiInJ0Hsbj2xu43E7jbyzFNWfvbCKypJyZLD+wzE7jayZaMBsxn691OoX0/w9RwNsPDRx3NpYvam4XEnpFp2MgkweDni1jb4L7tAqTnF5Hy5h6QJ8zDHZ+P/4WD83ux/w0iL+Xw2WdN/pnRPAt4fDuNCjonFXT7HklqIfwMfhh189KpIS0l8NkdGzsOzVziR7w+okbQUJOaxZvhcenwyjICOtZe+Hv33TgyuRhpMbEnivFjcmvpisBEm19Jz0S6ko7S5XH6sHTiP0iwYYUcbgsLkPEqyi3HUSZvCXN0VKS+rxsW2AV05ykthtaTMy4OKqBJxARChfsjcQmR+heaNegXPBzqQ89kudAOaYygpQV7MouhA9WZvFWEIciPo5T4kzlyPWrG3khBMnjwZfbAjbg9+hypL8PODIUMur7t8ObRsCU2bQosW1vcAqgoxMdC6XSljf/+OLqP74Kl3Zeq/ptPgoQ60iwqgfqQPjld8X0IIHHo2xOPdoZh2nyfvtbWomYV2HYfQ6/AYHU29JRPQ+7uQMGkRmf/ZhVZQlWxZSsxsHDuf0sxiBqyebDNqKBQFJTQYXddOKKEhaCdOoe7ai5aWfuMN4q4CQlFQwv3RD2qD4YnB6Ho3R2YVYJ6zEfOcjag7TyFzL59H6v5zmL//HWm+4hwtPQYJY0DNvExaqoMsBDULEsZByZHrcFS38CfwBHC8wvtngI1SykbAxrL3lVBGbl4GOgIdgJeFEOVPke8CH5atnw1MKxsfCDQqe90PfHq1E775iIu8iDXtUxlFRZIvv1H56EM9jo5W4uHmJnjlRSup+fA9PW+/b+HoMY2PPzUxe+ltRM4eTL2XexMwrQ0ePcPRedTco+Z6wZJWQPbs7SRPWoiWW0Lg5yPxfaEPxogbk6aSFo2CeQfIevoXnPo3xvnp3myavoadz67HWUKbp3vQd/VdOAfVXfxXEJvM0TsWEPxge8Kmd62RFJoLSlkz7AeaP9yRBqOb17rtvHNZHHxnM92+GM7pt7fQeHp7DH6eNise1O3H0LVvjDBeJinqvnh07exME205T1DX+sjMQhvEpbIwF6zl0Jd8XGwY0JVDKde5lOOKcujLwwpKRCDa2aRK4049whHOBoo2x2MY2Qb/aFdSZ++w65gA3HpH4H5bJEkvbrx0U3ZxceHIkSMUF89DKJINGyDkcgESBw/CjBmwYgWcOAErV1rfHzoEOh3Exlpfe7bp+fihPjgaHJjRaSJR/+hKg/ljyVl2jOSXf0OzEYXS+bvh/togDM2DyH1qBaXb4+w+FsXViM8jHQn7cQxqeiEX7phH7uKjSIv1+zQXlLJh6Fx0Rh19l09E71xzWkMoCkpQILounVAi6qOdjUPdsRstJfW/gsBA+XkTgH5wWwyPD0HXszkyMx/z179i/nYT6q5TqLtOIRMzscz94zJ5sWTAxbvLCEsdjlUWQeLdYEm9Dkfz34xrXAptZ/RGCBEKDAa+qjA8HPiu7P/fASNsrDoA2CClzCqLxmwAbi+LqvQBFttYfzjwvbRiJ+AphAi6csP24OYjLto6ioshpoPp0mvBIpUzZyX1wgRubrZvjEFBgicf09O5p5kXnlEIiNiAz9AmBNwVQ70XetF4zijCZva4oYdivphL5nubSZm6BHQKgd+NxntGd/TBN04YaD6bSeYTKzAdS8X3oxHkejgzv/XHZOxIwDfYnSHbH6Dpwx2vKgqV/etZTkxdRuQ7/QiY1LLGZTVVY8OkRfi2Dqa1Hb+DlJJtD66k5VPdsKQX4eChQ+fhDLqq2VEtMROZkYfSIvzyWFouMrcI0dC+zthJW+IJ7haOzCxAqeLhUoDOv/KYyxXiXGxEXKCCQLccirCZKgIQDULQziRWHhMCr4c6kfvlXkSreuh9nDHmFVCw66JdxwXg/48uWDIKyZp78NLYwIED+eWXl4EC5s2DCRMuL//BB/DccxBRxvkiIuDZZ+H99ytvV+9i4oMjK3ju7Zdp3b09BwZ8R2l6IRFz70DNLeH8tOVYMou4EkKn4Dw6Brdn+1H04z4KPt6CLLbftl8f6Ir/K30I+vdgCjeeI2H8QnJWn2Jt/29xredJr5/G1qkKTgiBEuCPrlN7lEYNrKXU23aiJSYjq/mt/o4QOgUlsozEPDEEXfcotMQsyCoATSJTcrB8Z428xB/6kOYDD1Va/5XZmXzwdTZ3z0whok8cMcPO02roeTZuL+Lo6VIa94+nuESzppWy5zB48GDmz5//Fx3tLZRhFvA05boKKwKklMkAZf/aCumHAAkV3l8sG/MBcqS81BCwfLymdeqMm4+4yCycnLiUJordbWTcmKqphznfqcR0MBHWoJSEBCs7feRBBVWFu+/SAZlV1rlRMJ3NJOPVjaQ+tAKdrzNBP43D65FOdnfGvRaQJpX87/eS/fwaXEZE4/FSX/Z+sotVQ79Hl2ci+q42DN7xAB5N/WrfmA2k/nSIczM30OSbkXj1a1Dr8tunr8FSZKLHp8PsIkmnvz1AaWYRzR7swMmXNhJ+bww616rfn5QSddtRdJ2bVbLz1/bFo2sdbncpefLWeIK7hEFBCXhWFude6ZoLVo3LpXLoGiIuws8DmVeMLKlglljN07wI8oZSMzIrv9K4Q8tAjE18KVh2DMP4DniHGkj/aIfdUQGr3uV2Mr/aR/Fh65Py+PGDmD8/gZISaySlY8fLyx89Cm3bVt5Gu3bW8Yr48EPQ6wt4/MmpRLzYi8hX+3B04mLSlp8g9MOBuHQMJW78IkpOpNucl6GRH54fDAedIGf6cswn0+w6nnI4NPUl6JMhuN3dmsQXN9LQyUj7/+tSbauA2iCEQPHzRdehLUpUE2RyMurWHWgJF/+rCAyUkZgGgYhgLytZBpASmZqD+bsNkL+CmiIt7z/tS+zK+sx63o8HX04jupEDo/q58uanWYCZ5Ys/x2wqZfz48TfkeP4rcO0jLr5CiL0VXvdX2p0QQ4A0KeU+m/OpZbY2xmQN4zWtU2fchOJc299DwwaCCwmS/HyJm5tg6hQdU6foaN7GhFp2z1AUcTmL8BdEekuPpJI79wCmE+m4j2uJ91PdUWoJV18PmE6kkffhZnQhHvh8MorCvFJW9fiSogu5eHk40fOnsfh1rndV25ZScvFf28lYfoKoxeNwiqi9KuPwxzu5uOGMXWXPAEUp+ex5Zj0D1t7Fqdd/p9kr3VBcnKx2+VfOJz4VSswoTS/rZaQmUffFYZjWy65jKs0pJvdsFr713VE9q3rDqOmFOHao/H25el5RDm1WbXoFCUVBBHohk7MQEYGXLP9tLisESoNgtLOJ6LybVvrM8/4OpD62EtchTdG1rY/rujMUbLuAWzfbvkVXwhjqTuALPUl8eh0ALVsGER8vmDdPMmhQ5WXLC0pqGjt4EGbNgj17nBAiG3DHd3ATnBv7cmzqUvL3J9Hgzb44NPTm/H0rCHqpF+79qpbVCicDrg91o3RXPPnvbcSxfxOcRsfYTTgLE3LZOGMNkWOa0yAmiJT/W4dThxC8H+mAIfDqfE+EEAhvb/D2Rubkop2LQzsXf7kjte7GGlL+KagaIsjb2hfJ3x3cnRFuO+GUfUSsc2tHElOtD98vPepN6xEXGD3AjWc+SOXnxU9fz5nfAmRIKdvV8HlXYJgQYhDgCLgLIeYCqUKIICllclkqx9YTwUWgV4X3ocDvQAbWFJC+LOoSCiRVWCfsinUq57btxM0XcRG2dR/OzoJpd+t49EkLJSVWVqKqElN1xRDiBtry771I6hOryHhtI06d6hGyYALuE1rdcNIiSy3kfbWLnNc24DKxNZ4v9uXsutMsaPMxxaezaDiwCcMPP3bVpEUzq5x7ej05v8URvXS8XaTl/C8n2f/W7wxaNfmSS2pt2PnELzSe2gZRaKbkYg4erfxBX/W7tEZbjqHrGlWpQkWeS0M4G1GC7OuUnbz9Av7tQxG5xVWs/qFc42Ir4lJGXHSK9VnEYvtmUG5EB9QabVIaBKOdSaoSTTFEeOHUPZzcuQcwjGiNq4+erI+310mL4d6vIa7d6yNNKlJqDBumZ8aMymkigOho2Lu38tj+/RBVZo9UXAyTJsEnn0BAQOXjcW7kQ8zauzBnF3No+E84tgig3ufDSH1vG2n/2YXUbM/XoWM4nu8Px3IyjbwXfkFNqd36Pvd0Jr/0/Jom97enzet98bgjmnpLx2MIcefipMVkfrQTtaAmD6jaITw90LWJQde6FTI7x9qROi4eabGdGvy7Qd+1GYa7e6Mf3BZd+0bomoSg6A6WGc/VjrWbixjR13ruOzspfDDTlx6TLjJ+kAuNgs5fz6n/d6HcgO4GalyklM9KKUOllOHAeGCTlPJOYCUwpWyxKcAKACFEiBBiY9n4OqC/EMKrTJTbH1gnrReU34DRV65ftt27hBWdgNzylFRdcfMRF6VfFY3LMy9YLxJvvqojKEjQvI2J1h1NdL/NzJQ7FYKruMk7gzLuuk5TapKiLfGkPricrFnbcRnYmOCfxuM2IgrhcOMDYaYjKWQ8shQtvRDfT0ahaxPKhrsWseWxn3HR6ej9zSi6fjUSg+vVCZTVQhOn7l2BOa2QqAVjazSWK0fGwWQ2TV3CgCUTcbdTiHx+xXEyDyTTYkZXDj20ilb/7otwdLIpyNVOXgS9DhFZWcei7o1DsdO7Bcr1LfWRmQVVhLlg1bgofrY0LhUqdRyqKYkGRLD3FToX2yXRAPh6gCKQ6TlVPvKY1o7CVSdQiyzoh8Xg4WQhf9M5O47wMvyndwVNkrM0lalTNV56yVo1VBEzZsDbb0N8vPV9fDy89RZMn3758549y6uQTFirJi9D7+pAs69G4DOkCQdu/57SrGIi5o2hcHsCF6evRSuyrWdRvJ1xe2EAxq6R5D67ipJNp6slZlmHUljd+2tinu9Ji//renkbLka8H2xP2LwxqNklJIyaT+6CI0iL7d/GXgh3N3QxLdG1a40sKETdsh31zDmkyX5tzt8Gama1jv7lw0+9l0FknzjufCqF5x68/PsO7eOKp7vCw5M8rFVGt3AZf59eRe8A/YQQp4F+Ze8BggALgJQyC3gd2FP2eq1sDGAm8H9CiDNYNS9fl42vBs4BZ4AvgYevdoI3X6pI1Ect7g/yjyofGQyCd97Q884b1R92QaYDoIHuzusyPWnRKNp0lrwfYxFGHe53tsape3itnhTXC1qxmYJv91CyLR73h7rg2DWclF0JrB0zD4rN1O9Qj65zRuEUcPVOm6b0Qk5OXYZzMz8i3uprV++mwqQ81gybS/ePhxJoZ4THlFvC9kdX0euH0Zx5awuNZnRE7+5oU5ArVQ11x3H0fVtXimJIkwXtaALGQbYbOtpC8tbzdHi5DzIjt0rERSs2g1lFca9M+IxlJdamEjNGRwPCUFYSbcN0TwR4ITPykGYLwqC3kjCpAVW/x/J0kTyTBP6VI1p6Xxdch0eR+81evGf2xLj+GFlf7sCtd6Td55/QKwiDjpS3DxO5KIAnnkisskxMDLz7LgwdCmYzGAzw3nvW8aQka6SlaVPre+slqDvR0dH8+OOPlY4j7NGOuLYM4MRDPxP6UHvqfTOClNd/J27yEsI+GoTRhkhdKAKnIdEYWgRRMOsPzPsTcHmgK0oFV960XQlsGP4jnf89mMhxLapsA0Dv74r/S70oPZVB5r93krugzIG3Z/ifskMQrq7oWkQji4qsHam3bUeEBKPUr4dw+GuqFusMYcTHU0d2bmUyl5WrEhFqPa/ff9qXUf1dmf19DlNmprJv2eW/YUUBRQgQ/yXH+z8AKeXvWFM9SCkzgdtsLNYJ+E+Fdb4BvrGxrXNYS6SvHJfAI9divjdfxAVAP53qO5jWBh0od4Cwv4OxPZAmlYKVx0m+cwEFP5/A85HOBHwxEueeEX8ZaSk9kEjmQ0vQisz4fjoKY6d67HljEyv6fYOSW0qXN/tz2y+T/xRpKY7L5ujIeXj2iSTyvf52kRZzoYnVw+YS9UB7Go61fWOxhT0z1xM2sDFGRZDxRxwhoxuD0dF2tOVIPMLTFSXM74rxiyj1fRHu9qWlLCVmMmKTCegUZjPioqYXoPi62LzZuXg4UphjrZqpUaBr0CN83ZGpZR5QigLVpEwAlIYhaOeSbKZV3Ce1onhHAub4bBzu7oKnm0bempM1HqNWYiH/9ziSXtzIqd5zODT4a1y71ydrwSCktB5vr16watXldUaNgsOHreXQhw9b3wMEB1v1LsePQ2ysG7Gxc4iNja1EWirCq0c4MWvuIn3FCU49ugr/md3wHN6U+ImLKdpffXpcX98bj3eHovi4kDt9OeZD1mWTfjvHhqFz6f71yGpJS0U4NPYl+D9D8H2qG1mf7iHp/pWUHPnzpbzC2RlddDN0nTuCpqFu24l64iSypKT2lf9qGEJxdTEQ5K9n43br+ZuVo7J2SxHd2l32vVEUwRNTPNE0WLflSp8XAQbbjVP/Z/H3ibjYhJTyYynlymu+4avAzRdxARB9QXQGuRWo64XAA/SvXrOpaEVmCn4+Tv6CQxga+uD9XG8cW9pXYnu9oBWayP9qF6X7LuLxWDcc2oeRn5DDuv7fknsqg6CGvvRaOB73hrVbq9eE/APJnLp3BWEzuuA/oeZy50tzUzV+nbQQn5YBtHm2p937Sv4jjgurTjB854Ps7PsdnVeNQRiMoFQlStJsQd19Cv3wTlU+U/fF2e3dApC6+yJeUX4YXR0ozSyo0qdITavq4VIO57J0kVegR7UmdOWwlkVnQagf1Xm5XFrW0xWcHJDJmYiQyhb3iqsD7pNjyPlsN/7vD0QJ96Vw7h7cb29cSdCq5paQ/0c8+ZvOUbjzIo7N/HDrE4nvg+0xhlgjHclv6pClc6+6v55arCG1wehrecZwDHWn1YpJnH1uAwcHzSVqzkiCG3iR8OQa/B/vhNdo26aHwqjHZWpHDK1Dyf9oMxmuzuz56Sh9Fo4nqJf9vzGAc+cwnDqEkP/zSVKeWodTm2CrgPdPWhMIR0d0TZuUdaS+gLpjF8LfHyWiPsLZudb1/xK4DYOc7/j+vQAeeTWd6e9Yq75eftSbBvUqRwyFELzwsBfvfZnNgO4VfmhhBPfhN3LWt3AT4SYlLgoYFoJ5AMgj2NevSAFcwbAWROifnoKWX0r+kiPkLz2KY+tg/N65HWNj+/qkXE+U7L5A3kfbcOgQhu+nd6C4GDmz+Aib7luKwSJpO707LV/oiaL/c5UP2b+e5exT62jwwe143RZp93o7nlqLKb+U/gvH2x2StxSb2Xr/Cjp/NISz728jZEIUTsEuYLAditYOnEMJ8UHxryy+lblFyAuZKHd3t3u+yWX+LQAyM98u19xyVPRyqcmEDqwCXfXgOWtySIgaIy5QFnU5m4gSUvWccxsRTf6iI5TsT8Lxge7w/DJyFx/GpUck+ZvOkbcpjpIjqbh0DMPttgiCXu6N3qtqBCpg+m2kfzYV/0e/Qejr9oCgFhu48Nk0Er/7nuhPh+LVuWYXZMVRT6N/DST5h1gODfuJhh8MIPz7USSUdZgOeKpbtV2gjTEhZHVuxO4nf6HL0Ab4Rdonur4SQqfgPqIZrv0bkjP3IBcnL8FtWFO8prZB5/7n0h7CwQFd40bI8HC0Cwmou/YifH2sBMb1GjVEvFZwaATGSKIaHuO3H6peK799t/KD2R0D3LhjwGVCH/9bBBgjwSHqylX/h3F9oiQ3K27OVBGAcAbDr6CMABzKXjYXBFxANATjDlDsiwxUBzWziOxPd5E0YT6WlHwCPh6G76t9/3LSouWXkPPB7+R/ugOP6T3xeKwbFinZMGURm+5Zgoe7E0M3TiPmlT5/mrSk/mj1aGk6Z2SdSMuRT3dxYc0pbl88sU4GYLGv/453ywBcvZxIXXWCRtM7gNHBZopIlphQD5xB17lZlc/UA+dRWoRZdSR2ImnreYK7hyOLSq0l9FdoVGy55pbDuWKjRaMOqhHnAoggb2RKttUPRKk54gLW6iIZl4JUbbjsGnV43teenE93UppZQomzK5bFezk3ZgHFx9PxmdSSxr/fQ9jsQXgOb2aTtICVTHgOf4OMrwchNftSawDS7EDWNyPI/L4J9R/tyKEpSzn57AbUakS3FRE0OYbouXdw7sWNJP94iPAf7qA0PocLD/5cqS1BRZz4Yg97XtrIoG33Ezy1HXkvr6F49bGrdrdVnA1439+OsAVj0fJLuXDHPHLmHUKa/5yAF0AYDegaRqLr1gXh4oK6dz9q7CFkXn7tK99IeN1Plc7Q9kI4Wde/hcv4C6qK/ptx8xIXsIq/DHPAeAyUJwEPwAlwA5wBIyjDwbAaDAdB1G6EVh0sKflk/WsryXctQpZaCPz6Dnye6YWh3tU93V1LlGyLI+PBpSiuDvh8MgqHmGDS9iXyU9QsLiw9RvTYVow69gS+Hf5cpElKScI/t5H02R6il4zDNcZ+N+cLa0+x7/XfrGXP1dwobSEzNpmTX++jw9v9OXj/z7RfNBpFL0Bnu7+Quuc0SvHV6R4AACAASURBVINgxBX9iqSUaHvPoWsbbve+NVUjZccFgrrVR2ZY9S1XRok0OyMutaaKHI0Idydkei7VNVqstLyrE8LLDXmxsnmbVDUK9yWRF5tCyckMkh76GZO/D46eBvwnRxHyRl/c+kSiONXenwnAIcILY/CbpM26CyldL2lebMMNqbmS/9k0RO5DeHg4kPrpbtosGUdpaiE7un5Fjh2Ovm5tgolZN4W8/ckcf2AlQa/3waGJD3ETFlF6tnKlyqH3t3Lwnc0M/n0a3i0CcezbBI83B1P6xxny39yAll3Vmdde6H1d8H+hF8GfDqN4RwIJYxdQsPHcNbH7FwY9SmQ4um5dEV6eqAcOou6PRebk/ultXxO4DgTnbtQ5TygcwKkTuA2pfdlbuIVqcHMTl3KIEDC8CsZEMB4FwxYwHgBjChjmg9LR5tO5PTCfzyHzrd9JuXcpiouRoB/G4P1kV/R/QtB6raDmFJPz1kby5+zF89k+uD/YGeGgY+9bv7O0x5foCswMWDCBrl+NwGCjmqUu0Mwq555aR87v8TRfNgHHWro2V0Tm4RQ2TllC/0UT8Ghgv65Gs6hsuXc57d7qR/ysnfgPaIBHM08w2BbkyoJitKPx6DpV7U4rk3KQpRZEhP0NKzMOJuMS4o6Tr0u1pdCWtMIqdv/lcKninluzt8cl+/9qGi1WWb5BMNqZxCri2tS3N6N3dcD7ia44+TsR8FQ3lAEt0e08jVoH6/xyeAxtipo9muSX5yNL/oU0N0ZKA1K6YBXJG4CWwGcIJQOnQa8ijybh2SccDzcHTt+3giZv3kajV3sTe+diTj7/a63zMPo602LBWFxbBBA76Adc+jfE9/52xE9dRv7meKSU7HvxV07N2ceQzfdW0mvpgj3weHMI+kgfcmaswLTnQp2PuSIcGnoTNHswvjO7k/3VPpKmLafk8LXpxSP0OpT69dB164zw80U9dAR17360rKy/th+SEBD4ITh1sD/yIpzAsS0EzbaS71uojFsRF7txc2pcbCHTBGvS4HwRFEhwN0HjHOhvBLe6fw2mk+nkzo2l9FAKbndEEzxvfKWSy78SUkpKfj9L/hc7cerbGI/pPREOegoSc1k7+ieyD6cS0T2cnj+MqdKF92qgFpo49dDPCEUQtWAsOmf7ntYBCpPzWT30B7rNGkRQ1/p12u/RWTswejriVd+TQ29vofeBe61iXBvlzwDqzpMo0eEI16oXWm2fNdpSlwqv5C3nL+tbMgpsms/VFHFxrhJxqTnVIIJ90E4noov0RWqaTf/scqi5JeSfKCB37kGKn99rU1wLULI1noIVx3G9oxV5G45R8J8teMzoU/OB20Dgsz2Jm7gQ89FuGBuNQZpTEG4aODhg9Wm5TGQNDRzwfHUAOS+vxbNHGHJzAkfHLKDFiol02XEfx2esY0e3r2n+6VA8O1TfykToFSJe7IVrTCBHJiwk4sVehP17EAn/WE2iXiE3q4jBv0/DyQZxFHoF54ltMbQOoWD2Zkz7E3CZ0sGuTuDVwblTGE7tQ8hffYqUmetxbBWIzyMdMYT++d5iQqdDhIUiQoKRyalox06C0YASEY7w9flrOtYrRgj+HLI+gZw5VjJtq0u0cLESHY+7wOcxEP9FzsG38LfEzU9cDufBDxdhb5khl6kCE92owH/OQ28fmBQKkVVV/AVrTiIc9Lj0saaRSg4mk/fDAcxx2biNa4nPc73sDqvfCKiZheR9vA01OR+vVwZgaGIt9z27/CgbpyxGr0LPWUNoNK3tNbnYmdILOXn3Mlyi/Yl4q2+1AklbMBeaWDN8LlH3tqPRBPt9UwDyzmZx8N0tDPr1bg6MWUjrOcPR6aRV22IDMrsA7WwShil9q36maqgHzmN4uOpnNSFpazyRw60CQ5lZgAiqXEIvpaxR4+JSSeNSvQFdOZRgH9Q/Dlvz4TZSRebk/CriWtc2/gQNboaxjW2tkedDHUmbsRqXgY0xTuyI9sNW1MxCdD51I7SKs4GQ9wegFKVgSrdgcHEFfSDVXWIMDX3xfOV2sl9Zi2eXENieyNExC2i+dAKtvh1FyrLjxE5cRPDEljR4rgc6x+ovVX5Dm+LSxJdjU5fh3imMZH8XMn+Lo/2dMTh41JzKMDQLxOODERR+tYOcp1bi9mRP9A2uXo8mdAruQ5vi2rcBuT8e4uKUJbgNaYLXPW3Q1TIXu7avKIiQIERwIDI1De30WThzDiUyHOHvd+MJjNBZyYj3A1CwAbK/BnMCyJKyVH0YeE0Dl/5WonML1eMmj5JcS9y88TopYe5FePIo7Mi2EhbTFSdGiQYmDTakw30HYVNlPUDpkVSyPthK9j+3UrQ1ntRHV5L1zh8494okeN543Me2+NuQFiklRetPkfnIMvSRPvjMHoGhiR/mIhMbJi9kw8SF+IV7M+bQYzS+t901ucAVn8vi6Mh5ePWNJOLdfnUiLVLT2HjXYryj/WnzfK867VdKydYHVtBqZncufr4P39si8WnvDwZjtSFodcdxdK0bIByrXjy1UykIbxcUP/ufjKWUJG2JJ6i7NUokM/IRvpVLoWV+KegESjVpOOcK7rnCQVd7qsjVCYx6yCuxNryTkpJTGaR/todzYxfYFNd6jWuFklZ9w1BjY18c24WQN+8QTj0bUGp0omj2b3Z/DxXhEOSA1HQkPferlVjZKEWvCEMjX7xeGQDn0/HoEISzpnF04iIsBSYCRzaj8477KIrLZmf3r8ndW9XoriKcG/vSYsVEktecgj1J3P7bPegVwfmpyzCn24gCVIDiYsTtiZ44j2tN3hvrKV560KaouS5QnAx43duWsAXjkMUWLoyeT87cg7WSU3shhEAJDEDXuQNKgwirmd32XWjJKX9NQ0dhBLfBUG8pNNgDDQ9Dg71Qb5lVz3KLtNSOW6kiu3HzRlzmJsJ3CVBqxx+xhnW5N89Y3/fxQ80qIn3mWjCraBaVrH9uweuRzjj3iqzTDfpGQE3NJ3f2VrTcErzeGogh0prPzziYzKrB32POLKLj091p9VKfq+58eyXy9ydx6r6VhD3VFf/x9pvElWPHzPWUZhXRb97YOpOo03P2Y8opwb95AEc+30fPffdZq2xs9CMC0NJy0BIzMfRrbfvzfXHo2tpf/QSQcyoDnYMe9/rWFIht87nqoy1g1bicz7Uao9mTKgIQgd6U7Esg92A2BdtTQErc+kQS8FQ3nFsHVTk3RXgActsRZInJJmkD8Ly3PSn3LsVtRBTOD3RD/WgDllOp6BsH1DqfipAF+egjAnBuH4glx4QxpPbf1dDID6+XB5D96jrc2wYi96ZwfPISon4cjYOfC62+H0Xq0uMcGL+IkDtb0eDZ7ig2WmJYikz8Nnkx+qY+NOoewbGJi2n8yRAsR9OIG7+IsH8PxKl5zcfj0C0SfRN/Cj7ajOlAIq6P96jx97MHel9n/J7rgcf45mTO3knuoiP4PNoRl74NrsnDgxDCGmnx80VmZqHFxVsjMBHhiODAKg0/b+EWbgbcnGf1/hz4NsEaUakLysiLdq6AlIdWoOWXNViTAALn3n8v0iI1SdGqY2Q8vgJjyyB8Zg3HEOmD1DT2vv07izp9ihEYufV+Wr/a95qRlqz1Zzh5z3Ii3+9/VaTl6Oe7if/5BAOW1K3sGaAoOZ89z26g86yBHH70F1p+NgS9Qa3WIRewNlLs0NhmmbMsNqGdSEKJqVvjyKQt8QR3D7duQ9OQ2YUI78rplZo8XMBaDn3Jx8Wor7aqqKK4Nv2n45TuvoDO2UDYrEE0XHsXgTO749I+xOa5KYwGRKgvMj6l2nnog91xub0xuXP24dgqmCJnd0q+2FIn8afUNCgsQLi643tfG0wXC8hdVbMjbzkMjf3weqk/SnI27jH+GLOKODFtOVqpBSEEgXdE0Xn7vRSezmRH96/J3VfZMdeUW8La27/HKcCVPgvHU/8fXWj80WBOPvgzpZok4JluXHh4FbmrT9U6F52fK+4v346xTSi5T6+kdMtZu7+DmmCM9CZo1iD8XuhF9rexJN6znJKD1f8mdYUQAsXXB337tuiimyFTU1G3bke7kIBUr02U5xauJ65xtOVWxOW/DykfHeDJQ2+yp+A4DsJIuGMgsyIeZ9SJ5znS+odLy71y4WtcdU7MCJnI3aff5I/cWDz0LsjOOgwmC8t7vITQKUhVIhSBmlmEvpoKkRsNS1IuubO2gFnD5/3B6OtZn/yLUgv4Zej3ZB1KIXp8K7p8Ogz9NUxnpc49yMVZO2j63ShcW9XdAfjCutPseWUTI7fch6N33Z1Bdzy+iibT2pIy9zD+Axrh1yMUNLVaQa6WkI7MKUBpHm7780MJKI0CEc51E1aX+7cAkFsMzg6IK0iYPRGXS+LcKwzoqnOudZsUBTsOoR/cDMXfPi2G0jAE7Wg8StPqyZn7Xa1JnrQQt7EtcHu8B6Wv/4xl6xkM3RvZtQ+KCsHBAaHXo+jBobE/cXevxjHaHwc7uoAbmvjj9VJ/sl9bj1u0L3lH0jn54M80/XI4Qq/g4O9Kq7l3kLL4GAfGLiRkSisazOxOaV4p6wZ+j3+nMDrPHnQpwuDVM5yYNZM5Pm05+fU9qffvQSQ9s57S05n4PdapRhG20Ck4jWyJoWUw+bP+wLT/Ii73dq425VcXOLcPwemHOyhYc5rU537FIdofn8c6Ygi7di1GhLcXOm8vZG4e2rk4tHPxKOH1EKEhCP1Necm/hf8x3HRnsUwsZuTSx5jiO5D5TazW/bEFp0k1Zde67vvhDzPatzc4KvBzB3D6+6nfpapRtPIoBfNjcR0Xg/Pw6EtW7WeXHeXXyYsw6hQGL72T0EGNr91+peTiP7eTufIE0YvH4xhed3+azCOpbLxrMbcvmYDHVbQTiF92jKxDqUTdGcOxp9bTc98DYDaBo+2ohpTSGm3p3KySnX1FqPvi0PWoWh5dG5K3xNP26R7W/WTariiyEpeaIi4VyqGNOsxJeWT9eLBG51opJeYtschCe9ygrRBh/sg/DiELSxAutgWiOk8n3Ma3JOeL3fi90Z8cfz8MC/eg7xCOcKid+MqCfISrVSMkLSp6X1f8HulE4lNrCZ87BqUGcW05DE398XypPzmvrce9mQ95RzM49dgvNP54MEKnIIQgaEw03j3qc+zJNWzv8hVpuUXUG9eCtm/0rZJ6cQzzoNXKSZx5Zj0nnlhN4w8HkvnRThIe/4WQd/ujq4WI6Bv44vnBcAq/3U3ujOW4PtYDQ9Sfb9chFIHb4Ma43BZJ7rxDXLx7GW6DGuE1rS06zz8v4L20Hw93dK1bIfPz0eLi0bacR6kXhqgXijD8PbR5t1CGcgO6W7ALf5+8xzXCb+8twyD0PBg04tJYjGsjwhzs9+cAYFPGNZ7Zn4flQjZZM1ZRsv08Pv8ahsuoFgidgqXEzPqJC1g/bj6hHUKZGDfjmpIWzaxybsY6cjbHE71swlWRlqKUfNYM/YGu/xpIUFkJcV1QmlPMjsd/ofOHgzj6f+to9dlQ9EYN9Aark6wNyHMpYFFRmtg21pOZBcjUXJSmdWv2VpCYiymvFK9m1ootLcO2h4uaXlCthwuAs7sjBRkFpH+2h5SvY0n76WitzrVCCESQFzLNfidVodchwgPQzlXflBDAbUxzTEfTKD2Sitdj3ShKK8W0PLbW7ZeniSi3plctoNfjOSYaY7gXqe9vtXuuxqb+eL7YD31+IW6NvdEOpXDm6fWV0lYOAa5EvtGH9JQ83AsseDoakGbbaWHFUU+jDwcSfG9bjk5eguvoaPR+LsRPWowpoXYzN+Ggx/WBLrjc04n8f/5G0U/7kJZrI35VHPV4TW1D2KJxSItmFfD+EItWi0i7rhBubuhatkDXoS2yuBh16w7U02eQJtM13c8t3MKNwk1HXI4cOkxbZ9tP0GdLEomJvfvS67OUFZU+fyr+E+tnO+9i0it/H0tqqWoULIgl86lVON3WEO93B6MPsYaW0w8m80PkB8QvPUqfj4YyaOM0HK4iBVMd1AITJ+9ZjjmzmKj5YzH41H3b5iJr2XOTu9vQeFLMVc1jz9PrqTe4CRnLjhMwqDG+PetZU0TV9COSWlm0pWtUtSJIdX8cSqt6iDq2OEjacp6gbvUvbbc68zlbEZdy59qU97eS9tAqCpLyUHNL8B7amIAJ0XY514pgH2R63SzglQbByDM1ExfF0YDHPW3J+WwXxjB3zI1CUf84iVbbvoqLwOiA0JfN2WIlLkIIgl7uTeHOBPLWnbZ7rsZmAXi+0BdDcTFuDT0xb7/AuZc2XSIv2UdTWd3rG5q+2IvusQ+RfySNnb2+Ia8azYgQgqC7Yoj64Q7OvbQRk1GH55ho4u5cQuHu2p16AYzt6+H5wXAs5zLJfX4VatK1c7DVezvhN7M7IV8Np/hACgljFpC/7sw1N5gTLi7omkeh69QezBYrgTl5CllSek33cwtXiVsaF7tx0xEXTNU/DTVwDCE25ttLrwcDK3cnfT/84Uuf/Tjqg+s9U7tgjssk88kVmA4m4zN7BM5DohCKQErJntc2saj9J7i4OzLhxD9o8kCHa+rjYEor5NjYBTgEu9Hkq+F1MpYrh9Q0Nk1ZgmcTX9q91Puq5pH8exwJa05R/7ZIsjafp9nbt4GppFqHXADtRAI4GhHhtitJpJRo++Lr1An60nwqNFYE26XQAGqaVZxry7lW52Kk4YeDKREQOLM7Ts18wWKfiFIE+yAzCuo0ZxHiiywoQubVXBrsMrAJak4xJdsv4PNwJ3ISTZh/2lXjOjI/H+FqPX4ppTXiUqY50rk5EPL+AFLe+sOuCEc5jFGBeL7QF6OpFLdID0rWn+H8u1tI35vImr7f0v6d/jR7sAMOgW7EzB9D+KMd2TdyHmfe2oxWTXWWe9uyVgG7E0n++SQBz/fg4ox1ZM0/bNecFC9n3J7vh2OvhuQ+/wslG05eU3JhDPci6F+34/9SL3LnHiTx7mUUH0i+Ztsvh3ByQhfVFF2XjgCo23eiHjuBLLY//VgF8hzIJSC/AfkTyM0gb4mC64RbxMVu3HTEJTqoMfsK7atmqBEef638R5pV8ufuI/vZNTgPicLrzdvRB1hvDkVpBSxs8x/2vfEb7Z7sxuijT+BWB4t9e1B8tsyjpX9DIt6pm0dLRex8dgPFaQX0+nLkVZEqa+fn5XR4pz8nZm6g5RfD0DsIK2GpRpArLarVt6WGaIu8kAlCIMLqrrVJ2hpPcPfLLr8yswDlioiLJbuY4vO5JL27jVO9viHzu1gcGvsSMW8MkYvH4/dwB9xbBYKUmErMdpdDAwg/Dyg2oRXZ/6QsFAUlIgitlqiL0Ct4PtiRnM92YQhwgXaRWE6noR617aMipYTCfCgjLmia9XutkL5zivLH9/72JM5YWy2psAVjdCCez/fFQTPjHu5O9rzDrO3zDV0/H0bDSZcNC4UQBE9sSeet08jbn8SuPnPIr8Zy3+jnQotF43Bu5sep537F/4WeZM87TPJrv9vVJFEIgePAKNxfG0jJ2uPkv7cRLa9unbFrg1O7EEK+G4XHhBakvbiRlBlrMZ3Puab7ABCOjuiaNEbXrTMYDKg7d6MeOYYsvNy/SRYXo6Wl296AVEH+DFoPkC1A3gvySZAPgxwGMhS0d0D+/dLut/DfjZuOuPTp3ZtSaebLlJWXxvbkH+d8aR1KDx0VqHft0i11hflUOpmPL8dyOgOfj0fiPKDJpRvwmUWH+T78fUoS87hj+wN0eG/ANStzLkf+viSOjV1AyOMdCX2y81VHcY59uYe4Zce4fekkdDa8N+zBgVd/w6d1EHkb4wgc1hTfHvXBXFpj+bN2OB7h644SUj0pUffGobSLqPOxlWQXkxeXjW/ry7qYcrt/c3I+WT8eJH7acs7c/j3mUol730garplM+JyR+ExuVcluXwiBi6e1skjUUA59JRSdDuHtgkyq2w1BNAxBO5tYa5TAqWt9FDcHCtecwu/B9qSfKsI8bxfSVkSoqBCMxstiT4vFJqH0mtgSQ7Abaf/aVqc5G5sH4vn8bRgspRgUjej6XuhTbUeNHIPdab1oHPUeas/e4T9x9p0taDbIiNArRL7cm4iXenHiydU4j2qGObWA8/evxJJtX9RBH+aFxztD0QW6kzN9OabYmg3y6gqhCNxub0TYkvE4tAgg8Z7lpL+3FdXO+dVpX0YjukYNrB2pnZxQd+9FPXQYmV+AdvwkWuwhZPYVxEmmgGwFcjKwDSgB8oBCIL/slQa8ATIC5LJrPu+bDrciLnbjpiMuYkQQy1q8xYacPTTYN5bo/XfySsI3BBtrLx29pHHZNYWY5wZgusHiNWmykP/NbrJfXofL/7N33uFVVWnb/619anrvhYQktNB7kw4ioihI7zqWcXTsOjr2MpZRZ3TGroigAygiSFUERIr03ktISCEhvee0vb4/dkIS0s4Jmff9Xs19XVzGc/bea522172e537uZ3I33B4eglKpKXFY7GyY9B9+nL6MhBs7MOviYwT1vrZuzvUh78dznL5jJW3fHEvwVNc9WqqQ9tM59jzzE+PWzMbcDF0MQM6BDM58foC48R3I/zWVDq+MBFsF6PUNurJKqw3H3jPoBnZq8LrS7kA9fBFdzxiX53RpRwoh/aLQGXSac+2JLGRxBRfuXk3SlGrn2phPbsa3Z3Adce3V0CqLyuuUQzcFEeiFzMhr+sCa54T4gc0BeY1rVoQQ+P6xH4UL9qHzNmEa2R5rsR3Hz3UjmVo1UY00WaUwt75rhr0wgpKfL1C0yTVvlPSTuew/nENgnDcBcb7kvr+HzK8ONzj3iJndGLDtDgr2pGnRl+OX6z026OYOdF0xnfSP9mHxMGBODOLC9G+oONuw03CtsQw6POb2xevPQyh9fzulC3Y5TT6dhWLS4ze3B9HLpyIEXLxtGfkLD6JWtOw4AMJgQImLRXfdQISXN459B5A52nvhOHQYaam8H8oMkL2As2gEpTGUA2UawVEXtficW/H7xG+uHJoIN8K7xfK1eKnOUzU9XACej77jyt8LE/6q/aEDxgXDE076V7gCVYWKYrCWa9UwZq8rbq/WE1kU/uMX9DH+BLw/Ebte4TP/V4i5PoE+L41i9fWf4yi1Me6bGcTc2vCifC3IXHyI9Hd2NdujpQp5Jy6zceY3XP/NNHzbNa/vi2p3sP3OlfR4ehhnnt1Cz0UT0bvpoMICbg2XGKsHzqNEB6EENeyLoZ7MQIT5IPxcbzB56ZcLRLYPIvPv2ynelIReLwmONxLy2HW1nGvLt19wynXVo9L2P9Dd5NqiF+SFPOmagZkQAiUuHPV8OrqAxtsbmLqEYuwQRMk3xwi6szfJE78iUjmCrk8swqe6NJvSEvCPqT6xgYgLgM7bTMQb15N6/1rMHYJqRZ8awpkF+9n/zCbGrJuNl5AU/G0TMtKTy3/fjs7dSNCtHes9zxzhTc9vp5Hx5WH2jf+KNvf2IeahgShXpTw9OgTRfcMczty/lsxjl4mc2ZWU278j/IUReI1wzk3Z0CUcn7duofSjHRQ+sRrPB4eib+Pv1LnOQufnRuBjg/Ge0pm8f+8m9bal+P+pL57XJ7jUGNQZCL0eEdsGtbAQqtJENjuOffvRDeiJYCSQA7hCnsqBe0G2BTG4Ref728BvP0rSkvjNRVwAmB+tpXuaA70C0xruSNsslBbA/lXw5UOw7ElY9TIsfxYWPYD88X1KP1xFwcsb8ZrTG7+/jkTn587Wu1aiOlSS1p1mWe/38Iv1Z3bq4/8V0iKl5OIb28n8ZD+Jy6ddE2kpyyph3U2LGfjmWMKHuC58rcKxt3diCnCnfG864RM7ETA4ulKQa6KhfkSyzILj0Hl0A+pfzKqg7ruArpfzc6sprvVcfx7Ps3noPIxE/XMcUa+NxBAfVMe51pFdiuJE5213HzOlBWUIgw5c0H+IQC9kXgnS5trOWyMuGU6JSn3v6UfR0sMIncDr1kTKMWJfdaD6gPIy0BtqeYJIh71RkzO3rqEE3N6T9Md+aFJTcuyfOznw4hbGbbmdgG5hGLuG4/vkSNw9BF5hHmQ8v5ncDQ1XKwkhiJjdnQHb7iB/Ryp7Rn5O8Ym60Re9t4mOn9+K/5h4zv99B3539+HSK1vJ/nif0+JbxcuE5yPDMd/cmaLnN1C++hhSbfmFyNjGl9C/X0/wSyMpXHKU9LkrKG+ij1NzIKWEHE0HVpWSzUxNY9rEQcQlnKZTZyvjblQ5c0YidCrPPFtdFJGTIzGYVO67X3vs+RdUIqJUuvcspVPiGJYsWdLi8/0/jyofl9ZUkVP4bRKXPr4wI8J18mJS4C9x0KaF9C0OO2xdoJGVIxvAWgYOm6bRsFtBtUPyQdx16wmacApzV22hK7tczJmvqysdBIIb1s9pltNsU1BtDs4/vIGiHReb7dFSBXu5jfW3fEm7Wd1pP7v+vkDOoPBsLkf+vp12kxIp3HeJDi+N0N5LKbVIVQNw7D2D0j4S4dMwYZClFajns1C6Nm7x7yisoOD7U6Q+uE4T1y46hKGtH/tT84j7bjpB9/bF3CEQcksb9nBxgrhUuee6nCoy6BH+nsjMpo0VayHAG3Q6ZFbT5xmifXEfGkvRooMEzutB1t5cHEfSUC9o2pqa1URXYK8/VVQT/nO6o/d34/I7v9b7vJSSAy9s5uQHexj/yx/wqRG1M3bTyIuHjw7vUHdSH/+R/J8vNDqeOdKbnt9NI3J+T/bd+BVJb+1AvcqLRSiC6AcH0O7dcSS9tg3zDQkUbTpP+uM/opbbGr3+lWsIgXl4Aj6vjse68wLFL/+AmlfW9InNgFuPMCIWTsRnVjcuv/gzlx7egDXZxe9CIxBCoBs2BN3wIehGDEUZOYzJ77zN8DHZnD8rOHFM4W+vCLKyoG1bWLO2+txvvoHExNrXe+hBwaEDCqu+k9x9953YbM69p61oRX34bRIXgPlRMCvSOfIi0EjLj9oGjgAAIABJREFUY3Ew2kWjuoZgt8Lav0PSPo2gOOrfGQsFhHAgii/Dypch9yKrRiyo7I+kQUrJz7evaJl51YCjxMrp+d/hKKyg49LJzfJoqYJUVTbNXY5PnD99nh/R/OtIyY67V9H5/v4kvbqN7p/ejM5Nr2lbGhHkyqIy1JMX0fVt3AVXPXQRpWM4wlyXANUU1569fhHFm5LwGt6W+A2ziVlwK5ZYXzw7BmNwr3ZclbkNlEI3YfdfBY9K91ytqsiF6ImiIEJ8kRnO6TGqIIRAiQ9Hnm+8uqgKPvN7Ubr+NLLchv/MbhQ5zNiW7UF1qLWriargaDhVVHMOYS+PpOjHcxRvrU06pJTseXQDKd+dYPwvf8Azui6RNnYLx+eJEXj46vEJdiPl/nUU7kptcszIeT3ov/V28n5JYc+ohZScqlst4zcslu7rZpP7wzmsXiakQyV57gpsmc6Xn+tCvfF++Ub0HUIoeGwVlt3JTp/rCoQi8Lo+nujl03DrGUb6H1aR/dov2POqBbyOEkvTgt7yQji3BY59D0e/g9M/QkGaZlyo1yN0On7euhWDwcY991R/37p3F0RFgZsbdOwA+/ZpN61l30imTK7/d5qQIHF3l+TntxzJ+s2gNeLiNH57GpcqCAHzoqCbNyxOg0OFGhmw1fhATYq2ix8cALMjIcF1zUO9kBI2fQi5qVqExbmTwFYO697CnuOJXq/gFxdAQNdQgnpH1Cr/bAlYL5dyat4KPLuGEvvyyGtuHrn7rz9RdqmYmzbOvyYvmTOf7cdWYsVxOpeIKZ3xH1iZIlJ0jS6Ijt2nULrENmhpf+W4fRfQj9VEx1JKLGdyKd6cRPHmC9gyi/EaGkvArG549I+sYwKn+be0qfWYzC1BiQmqO46TERd3n5pVRS74XgiBCPFBPZWBq40plLgI7N/vRBnQqcnuwbpADzxvTaTgk70EPDSYM2OP4D06GHXbSZS27ghjDRInJTgcoGt6RnpfNyJeG0Paw+sxL52CIdQL1aGy457vyT9+mXFb7sDUiKjZ1CMCn78Mh9e3IFWVpDu/J37RRLx6hDU6rlu0D71WTift84PsveFLYv7cjzb396+lfTFH+9D1+5mc/8uPXN6fQdiN7bgw4xsi/3ED7k6mUYVOwX1KDwzdIih5Zyu2/Wl4zO+HaMG+YVfGMurwndUNr/Htyf9sP6mTl+E7sys+M7qQ9cRGbOlFRH89FWGs8blICdln4ORayDiq7aAcNkAFxaDdP73DIXE8RPXm2LFj9OrpR0N73WlTBUuXSUJDtY8/PAwy6uHGBw5YSUhwIzi4hTaIrfhd4rdLXKrQw0f7d9kCa7MguRxK7eBlgHYemhDXpwWbEGZl8dDdt7Nr53b83AwY9Toev74rfh5GJry3kdgAL1QpCfZ24z9/GE6wtxsLd5zhseV7iPB1p8Lu4O6J1/PQ+8tabE5Xo/x8HqfmrCBoamci7u93zaZ1Jxfs5/zyY0z89W709UQynEVpRhH7ntpI7yeHkvHZQbp/OkETNNttDfYjApB5xahJmRjmjmr0+urlQmRBKeVFKsWV4lqkxGtkW0KeGIx797BGCVzG9hS6/ql/7bFzGuhTdNnZiIu5sqpIh3TF6l1REEHeyK3HkQ61wV5M9UH4eCA8zciMXERkXdJ1NbxndCNj+lIcl4oJnN+DvCPp+K85ivHhYbUPrBTmOvt9cu8Zjv+sbqQ/8SOR74/nlz+spCK7jBt+nIvBs+mml6Yekfg8rpEXVDg3dwXtlkzGI7HxRVEIQdTtPQkc2Zbj963l8urTdP7wJjxqpKR0bgYS/jmOzEWHSHl9O5F39CT1/rWEPDII3wkdnHp9oDWP9H3rFko/20XBo6vwfHAohoSm3/PmQOdrJvCRQfhM6Uzuv3eTctNXqCVWhCLIfW83gQ8N1A5UVdizAJJ/BYeVWuFdALVys5WfDLs+geOrwe4DWIH6N2Jjx8Izz0FICEytJ9ryj39KPvlUkpQEG9a10Abxt4bfeJSkJfHbTRVdjWCTJtp9oT28mQjPtYPpES1KWqSU3HLLLQyJdCfpb1PY/8ytLL1rOGn5mu/EdfGhHHpuIkeen0SfmCDe23LiyrlT+7Tl0HMT2fHETbyy+HtSz51psXnVRPG+dM2j5YH+RP65/zWTlrRN59n91I+MWzMbt8BruyHt+vNa4md24+I/d1WmiAxaishgbLAfEYB95wl0vRIQ5vqb5qkVdoq3XKDwrZ8pPFNM1hs7NHHtO+OI3zCH0Mevw6N3RKOkRbU7yNyVSuigGsZzUtZr9y8dKmpBOTon3g/3yqqiZkVcjDqEtwcy23X7eREX0aQZXRUUDyM+c3pS8MEuAqZ3pehQNqKND47tKbUPbKAUujEE3N4LadCxvu9HOMrtjFkzyynSUgVTT428eIaY8PYzcmbmN5Q5Wc7s1saXXqtmEDa9C3vGLCL53V1IR7X2RQhB2NwedFo0kfQvD6MfEMXlD/aQ9eaOWsc1BeFmwPO+63Cf1YviVzdStvyQS+e7CkOUDyGvjtYaW9pUpMVB4dfHqDicqUVatv8LkneCw0Id0nI17BYoTCexZDf796fR0JJhNAp69YS33pZMmlT3+YceFJw+qbBsiWDOvDwqKlrWtO//Plo4TfQbJ0G/H+LyP4DNmzdj1Cnc06t659YmwIv7R9ZWqkkpKa6w4edR9wYd4GkmPtiHS3t+aPH55f1wltN/WKV5tEzpfM3Xyz95mY0zvmb00qn4tb+2XWTyiuPkH7+MklFCxIwu+PWP0hZC1XGlZLw+qJn5yMx8lO61S1cdhRUUrDpF6gOV4trFBzErVnweH0nbb6Zq4tr2gU4Tt+xDl/CK9sGtpg6ozKrpo9xrz8+RW4bibXYq/eZR6eOCQQGH6vSCJoSCVCUi3N9lnQuAEheGTMms31SuHnhO6Ig9rQjriSxCH+qN7BSEY08yamYN0tRIKXRDsJVYOH4qG5lXTr+HBjYrYmfqFYnPY8PwCjXh7WXg9JSvqXDSaVYogug7e9Nvy3yyfzjHnusXUXoV8fHuHUGPH+ZSeiYHi6eRksOZXPzTGhzFrvX4MQ2IxefvE7Adu0TRs+twZLnWb8oVlO9Jw36pBOFpQJh0YFPJ+ONq5JHvIONIZaTFSah2RsR7Yiko4JNPqhfEvXslKTW46yMPC15/VRAQ0PBvauJEQe9ePnzxxRfNeVmtaAXQSlxaDLLCzvHjx+kZH4FsoFx327lMur+wgugnlvLTyXRuH1S3g/PF3BIqrDa6GlxfjBpD5qJDXPjrJjp8MRG/4c0vU65C2eUS1o5fzIA3ridimHN+Fw3Bkq91fu4woyulJ3No/9xwbWfYRD8iQGuk2K8DQq/DmlFE7peHSb79O01cuzkJrxGauDb6qUHogjwwdWuead+lbSm1+hNBZZoowLMO+XFW3wKV5dCF5VrXZxds/1EUkCoiPAC1GcRFeLgh/L2QqfWbs9U53qDD564+FHywG68+QRQdzEPtFoP96z1XSoabKoW+GhW5ZawfvRC/LiGMWDmDzBe2YLvsWg+mKph6R+Hz6HC8wsx4e+g4edtSLBnOEwP3WD96r55J2ORE9oz+guR/765FIo3BHnT5ZhoeicHknspGmg1cmPENFhet+HUBHng/OxZjvzYU/mU1lp9bvpkigFuvcMI/nUDo30YT/NJIgp4ZhvfUDnBqLZ7zNCM4VZX8edE+Ov9lDV3+soY+z6znQuX7H/PgSrr8ZQ1dn1zL0Jc3cjG7kO/uG87Gn6zEJagkdlF5/gVJeI3G6omJgrlzm9oIePLssw/x9ttvo6r/vajT/0m0Rlycxm9f49IcOHKhZB3YL4FaCroAMHUG96Eg6goP1TIr2fOXYfHJ1Dqt2mwg4E9f7WD7uSyMOoW/T+7LdfGhrPnz9QC8vv4wjy/fw4ezNTOmZXuT2HIqg9NZhXwy5zrMasu49kopSX1jO3nrzpL47TTMbZpf7lwFe4WNDbd+RcL0rnSY2/Oar7fn8R+IHB3PpU8O0Hv5VHRmvVYy3kg/IgBHShYVSXmUZ+opeXF3tbh2dvc64lrbhsMoLni3XI2M7cnETaodpWqoK7R6uRRdcNP6FqguhwagKl3kjIBTCFBVlPAAHFuPIqV0Oe2nxEegns9AiW1c0FoF9xFxFC05TPnWJIxxYVxef56wcIF6JA1dtygt4uLuXJqn7FIx68csJGpcO/q8NgYhBH5TOpPxlx+J/uQWlzQ7VTD1icLn0WHw5s+QXs7JSUvo9P1MjE6SSKEIou/uQ+DoeI7du5rL358i8f2b8IjXzOSEXqHtCyPw6hHGuac2EnJje5Jnf0vEa6PxHNh4ef3V47jd3AVDl3BK/rkV64FUPO4aiOJpwp6cCyro27reQ6vWGAYdbt2v+lyTsmFv9Xdk2a4UMvLLOPK3G1EUQVpuGR7m6vvblr+OItDLzHPfHuHllcf45M4BfP3PQRC2m5pal2NH6n7v5s0TzJunPf78czU/S0GvXo9x+vTT1/T6WvH7RmvEpSYqDkLmvZByHeS+DgUfQ9FXkP8vyHoIkgdA/vvgqG21XrJ4P7LMRsxRK/t2HNHSB8B7Mwex6eFxZJfUzefe3D2aX85WO59O7dOW4y/exrbHx/PI17vJLGjezrMmVKuD8w9toGhnKonftQxpkarKlvkr8Ir2pe+LI6/5ehlbkkj/4SzGQguRs7vh1zcSpAo2a73lz9KhUrovnczXt3F+5koy12ejlloJeWIw7bbcTvjLI/EaHluLtEirHfV4KroeMc2ao5SSS9tTajVWhMpS6ID6SqFdibho5dAAwqQHZwW6ilYRJzzdwKiHfNfTDiI2DJma7XQZtlAEvnd0p3B5El5j2mO5UIi9R1vs3+zVzOScKIUGKE7OZ82QT4mb3vUKaQEIvLM3KAo5H+51+bVUwdQ3Gp9Hh+EV4YanUDk5aQk2F/v7uLf1o8+62YTc2ok9oxaS8v6eWmZyQbd0pOuK6eRtT0GN9yf9yY3kLj7scuREHxuAzxs3o3ibKXxkJda9Fyl6bgPFr/3UcMqwIg0yv4TUd+DiW3Dpcyg5qkUom8KJNWCvvhddKignzNcNpdJ5NzLAvd709YD4QNLzy7UxDgaCdLWOrQpm4C4QzmuYfjdoNaBzCa3EBbQfZO4/IGM2lG4EaQVZk2xIkKWg5kH+e3BxDFg0Ya09o5CytafArjLYpz0VqsoHv1T3dClrYFHYfjaLuKC6i96AuBBmD4jnnY3192JxFvZiC6fnrcBRbNE8WlrIvG7Ps5sovljA8M8nNllK2+Qcy6xsv2sV7ad3pTypgHbPDNOesFo0o7nKfkRV4tqMpzdxZtgCsl7fjmKzEn5bNHE/zWtSXKseS0NpE4jwbri8tjEUnM5B727AK6o28atKFV0NZz1coHbERRh1TnUo1g5WtOoQQAkPQHWxbxGAMBsRYf7IFOdbB5gSPNFHelO27jTBf+zD5e/OIiL8sG887pT5XMGpbNYO/YzODwyg+1NDa0WJhE4h4rXRFKw4TmkTviyNzrFvND6PDMU70h0Pu52Tty3F7qIeRSiCNn/sQ9+f5pG18iR7xy2m7Hz1e+zRIYjuP8xFtauUGXXkLj3Cpee2uNT9GjSy6vGHAbjfNYDitzYjyyyoJRYsm2s4AksJBb/AqT/A8amQ/j5kfQmXl0L6h3DmXjg2CbJXgtqI6LWo9uc8pV8bVh9Mp/tT63jkq/0cTK7/O7ThSAa39KpMsZb5Q/kDgKv3EwMQB+J5F8/7HaGVuDiNVuICkPsaFC6oJCtNfODSAmoBpE8Dy2nyn9+oNa4DFDcDn3e9h19OpRP7l6X0fWUVcz/fyuuT+gDVGpduL6xg8a5zvDW5f71DPHFjbz7/+SjFxc0T71mzSjgxZRmmNr60+6iyOqcFcGrhAc4tPcINK2ddU9lzFQ68sAX/xGCy/3NMqyIy6zUfEIcde5l6lbj2EKYOgcQum0Lsssn4Rkncb+2F4gR5cuy/cG1pom3JhF8XU+dxmdtAKbQLEZeqcmioJC5OR1zElV22CA9olkAXKlsAOFldJKWEkmJ87+lH4aKDeI9siy2rFGt8BI5NJ5BFlkbJbM7BDNaNWECvl0bS6b76v/v6QA/CXxlNxtM/Yc9tvuusqV8bvB8aileEO+5lFk5NWYajzPX0q0e8P33WzyZkfHt2j/qCix/uvRJ90Xub6LRwIgHj2pGfWkjp2VxS7ljZrHnLyqgbKmCxU7Zoj/ZdUK1w/nFIehpKDlduqmqWJKsaWbGkQupbcGI22OrpGu6wa5HMGogMcOf032/i1andUIRg5Kub2HSsmtwMf+Ungu9dzk/HM5kxMKb6xOLpwCM4T17MQAKITSBa3v27Fb8/tGpcitdo6SDpYnmeLENmzALlzxj7RmFoH4Q+2AvfYA+WpJkRGSfqnFL47tx6LzVvUDvm1RDqhvu6k5mRBkbXf+Tl53I5NXcFwdO6EH7ftXu0VCH95yR2/eUHJmy5AzcnF+XGkHMgg7NfHCS2dxT+83vg2zsCa0YRwlFB4fokchYcwaNfJF4j2hL2wnD0vtXREsexZISHGRHddCWTLCxDXsxFmXdds+easT2ZsKuM56BhjYsrEZeqcmjANdt/oVxZiJRwf2x763ZuduoyMaHI7ceQFdYGy8mvwFIBQsHYMRS3wf5Yjj5H3LIVIDJRhqlgNYEcjLaoDamV5svakcJPk5Yw6P2biJmY2NAIAHj0j8Lnlo5kPLmRqA9uapbeBcA8oA08PATe3gqppZyasZyOS6doZcI1IctALgX5DpAGVKAtyh1AeQShjKfNff0IvD6e4/euIev7UyS+Nx73WD9NF/PQQLy6h3L6vrX49gwjaerXRP/7RswdnK+0c6TmayXxqg0UBVlmo+TT7XiN+hpKjmgbpqagVoAlDU7MgU7/AUONCGED3dRNBh03dIvghm4RhPiYWbk/lZGdNZO9LX8dhYdJz7yPfuXZ5Ud4e1Yv7SS9CZTnQe0MPAFkA2XU3fR5VD42B8QbIFr9WxrFbzxK0pL43UZc0tLSmDBhAgldpxA37DQPvJSD1Sr5eVc5Iv48n31ddOXYg8ctiPjzvPmpVkEw7/HLRAxKxlpRTtDretT7e9HlqYm4jUrA1DUc0X2s9uNuDoQCsb2aRVqK96ZzYurXRDw4gIj7r92jpQr5p7PZOG0Zo/4zBb+O1+54qdocbPvDd8Td0gk1rQi/IHeSJi8j95PdSIsdU0II7bbMJ+qdcfhO6FCLtEi7A8eu0+gGdXLq9TkOpqB0iUIYms/RM7al1Im4SFVF5jfUp6gUXbBzN2mj2QBSYq2wIQwupIoUcSVVhK8n2FVkses7fWHQI6KCUZMuNXmsLC4GLwXB3fg/NhVzz3fReZ1H51mK0Jcj3AuQci1wExADUjNRTPvxHD9NXMLQRbc1SVqqEHRPX1Srg9zP9rv8mmrCPCAGn4eG4hXljjGzkNNzV6BWvcfSAo6HQQ0F+TBwHCgELEA+8Cuo80ENA/UfWvRlw2yCbkhg9/DPufjxvivRF7/hbem+bjZlGcVYPAwk37GSoo3nnJ6nx9x++C+ahf8Xs/B55Ubc5/bBrdfPUHrUOdJSBWkHWwGce7D240KAqXZq+sCFPDLyte+MqkqOpBbQ5irvITejnn/O6s2i7RfIK7Fo7UvcKztfK7eBOAdiHXAzEA54A0FAF+AtEJmgvNdKWlrRovhdEhcpJRMnTuSWG3twdlMcZ36KpqRU5a9va+H2Lu2NLFtbLY5duraEbh1r70Z1imDBN1magPdqYVxYBwjvALpmpFOMbtDnVpdPy9twltN3rSLu7RsInnztHi1VKM8uZd34xfR/dQyRI+Ku+XrSoXLg4fWIIgtuP18gyM+ELLcR8uRgQh/rjzE2uI64tibUw0mIEF+UMP+mx5ISdV8Sul4xzZ5vSVohthILflfvngvKwcOkdXWuOabVgVpiQfF1Tk8jhKi2/XfFPVco1akiIRDh/s0qiwYqexc13mFYSgllyQi/scBihChHcau7oAohgRIgFbiDgpP3sHXOckatmE7kmHin5yT0ChGvjyFvyVHKrrH7sXlgDD4PDsE70h19ci5n/7AK6SgAdRjwCVq0oCExfDGQD/I5UGciFEnM/f3p++McLi09yr6bv6K8siTa3MaXbmtmYWzjS4kqSX9pK5ff2+1Sl2jhZkAfF8jbh5fTbeYbdJ26n+4zjnPDn8/w5L/Tah176HQZHScfAyDm5iNMeryKKNlYvno382beUvviCSNAqSbwl4squOmtrXT+yxq6PrUWvSK4b3TdXl9hfm5MH9CG9zaeAd8o8Kj2qdK6Rw8GZQUoqaDkg5IJyiFQ7mwlLE6j1YDOFfwuU0WbN2/GbDYz/+ZcKK1ApxP846+BxA5PYXh/N6LD9RSVqGTl2AkO0LHhlzLGDa0dAXlwng//+LyQO6flgO5o7QGEgJF3w7q3Ieeic2ZPQmieJeMeBY+mF+WayFx4kPR/76bDF5Pw7Bri0rmNoarsOW5yZzrM79Xs66gVdkp/TaV4UxKXN5zh+LEsOnQLwzQwmnZvj9UiJ9YKbSFupCpFWmw49p1Ff9tgp8aVGQVIix0R2/woUUZlf6KrozuavqWeiqKcUnQB7i6lN6p0Lm5GvQvERdO4VJVBK+EByIw8aB/l9LhXLhUVhNx6GFlSrlUp1QdLHiJ0JogUwNnWBGV4Rn/OhH1P4BlZN9XWFAwhnoS/OJL0JzcSu2wqev/miasBzINitazFP36h6GwG5ecG4xZ/AYGz0YwyYA2o94LyIR7tAum7cS7J/9rNrmGfE//0ECJv74nOzUC7d8Zx6YtDpLy+DbnqFJZzeUS8MgrF3bmNzK+//sqaVUs48FVPTHoLOQU2jp+vYP6LF3j1vmofoqU/5jHj+up7xb6TZRw/X05inJumg6k4X/vCCSPhxBpKPpsKwNhu4YztFk59SP5nbdLzr7l9QG+GTuOdeg2taMV/E7/LiMvx48fp1atXZWWQxky9vRSiw/ScS9GEb7eN9eCbdaXsPFBBz0QTJmPthSs6XM/g3mYWr8wHW1LdQXQGuPERiO+rLcYNRV+E0JxhfcPh1mcgwHmDNKlKLr76C5kLD5K4YnqLkhYpJVvu+A6PCG/6vdx4D6D6YC8oryOuNbYLIM2oI+62RCoc0O71ylJY1aH1IzI2nl5zHDiHEhuKEuDt1BzU/Vq0RSjNT5llbEsm7CrjOQA1p7iBNJHzwtwqXLH9Nzlv+y+EuEJe4NoEukKnQ8SEoiY1ItJVnwZDGsJp0qJB727DM+ItkM1rYeF5XRt8xrUj4+mfXIpc1Afz4Fh8HryOkNt38fZ/TtO5axldezjo3svB8JHaf+PbO/Dx1/7u3svBzp2SYSMctO/koFvPYgZd9xmnT2uur0KnEPvgAPqsn0X64sPsv2UJ5RcLEUIQPq8HiYsmUXy5lIJT2STNWo41o6iJGWq4dOkSgR5FmPQaqQr0NTC0lxe+Xnp2H6uODH39Ux7TxlQTl0dnhfC3z6tSfhKsWWCvMaa7H4R3rRV1cQk6A0Reu29TKxpAa8TFafwuicsVsy5ZWxMg4crOeso4T75ZX8KS1SVMH1+/0PKpe/z4+8fZqPYGwsyKHq6bC1Nfh+7jwOSpPaY3aTcBRQ+xfeDGx2DS8+DlvJhP82hZT9HuNBJXTMMc7eP0uc5g73ObKL6Qz4iFk5wue67pXHtu7OJazrUxC24lp8KGrdxG6ZZkun82AcWoq+GQa9TSHw1AllagHk5C19+5BnfSoWr6lmuoJgKtsWKDFUX1EZfLJU4Lc6twxfbfqANXymmV6pJoEeiNLClHljfPuFCJC0c2UF0kZTmYFqPoKpg9p/qGaLdLgoIl42/SHlu4UHLffXVvmDGxZeTkvN6seQEE3dcPtdhC3sKDzb5GFcyDYzkW9wNrf7BzYK/CkYM6fvpB4avFCof26/j0I4XrBsOh/ToO7dcxcKB2P/hqkcLhAzrmzlF57LHHa13Ts0MQfX+aR8DQGHYNXUDa5weQUuLdJ4IeP85BNeoozi0jaerXlB1ouoJrzOjRpF4qpt2ko9z7Wgpb92vVhdOv92fpj1rJ8q6jJQT46EmIru6GPmWUPwdOl3EutarQQAHLVWm2/neD2afR31q90Blh+OPNJz2taBytPi4u4XdJXBITE9m3bx+I6h99UbFK6iU7cdHaDzM0SI/BINi4o5yRA+sPUcfHGOjeyY2vVzXhueLuDT3Gw6y3YMYbMPFZmPo3mPsujLgTgmJcmv8Vj5ZSKx2XtJxHSxVOLzrIma8OM3blTPSNlFJLKak4nUP2B3tImryMC1O/xnIqh4DZ3euIa0szitj/9E/4+7oR+8e++HTTKhdQ7Rp5aaQfEYBj7xmUDlEIb+deq3omE+HvgRLkXHSmPlTklVGcUkBQj7rOsjK3BKVBYa5rxOWKxsWoc9oMDqhVWSQUBRHqh7zUzKhLeCCytAJZn/GhfQkAHh5w7BiUl2s3xY0bISLC2RGW1dkoOD03g46IN64nd9FByg41LSJuHJvJzC0jMBBMpkrju0BBeLhzUbkh1wnOnc8BWVtvougVYh8eSJ91s0hbeJADtyyhPLUQY7AnXZZPw3tIDIWFFSTds5r85ccbHcPTw8D+xYl8/FQbgvz0TH3qPAtX5zBttD/LN+WjqpKlP+Yx/fraKWWdDh6bHcqrC2v4tThKa1/c5AHXP6vpVJwiIUJLEQ1/HAKuvVVIK1rREvhdEpeRI0dSVlbGopVaWsjhkDzyag7zJnrhbq5+S1580J/XHw9Ap2v4pvbXe0N4818bnBtYKGD2Au9gcPdtlnjXmlnCicnLMMf6tahHSxUytl5g52MbGLd6Nu71LMDSXulc+8Y2zt2wmNQH1uEotjTuXCslv963hvAB0YhSO/FPDK56Qou21OOQW2tkOzx0AAAgAElEQVTMwlLUU6no+tYVDjYEdf8FdL2urYfSpR0phPaLRNHXLSVtCQ+XKnj6VolzXSiHBu09q5E+UZrZtwhAKAIlLgz1fD0RAfkRQtFIxw1jYe1a7eElS2H6NKdHAJz8ndQDQ5gXYc+NIP2JH3EUXkNnYfVzxoyuIDUN2nV0cO99Klu3Or87Xb1G0qWzAnJ5vc97dgyi76b5+F3Xhl1DFpC26BBCrxD30khinx9BcWEFqW/uIPPVX5D2BtxxhRGdDob18uaFuyP49+PRfLs5n6hQIzHhJrYeKObbzflMGVVXCzd7nD+/HCzmYmZlA1Clnk2XewDc8DK0H62REr257jE6AygGiOoDN7wEIc5FOltxDWiNuDiN3yVxEULw3Xff8c0PDhJGptJu1EXMJsHfHqndH2RgTzO3jG58EUps703PXvWbabU0ys/mcmziEgLGtyfm5ZHN9rdoCAVncvhx6lJGfzUZ/07VgtZazrXDF5D1xnZ03mai3h1H/PrZTTrXJn97nPxjWVj3ZdD905tRqipx7FbNX6IJm3jHrlMo3doinOyDI8utqKcyULo73z+mPmRsS6lX3wIt45pbhSrbf5cjLkp1xAWuTecCIOIiUM+l17Ku1/6ujnJMmwZLl0FFheTIEejXz9mr2wHnHXrrg9fwWLxHtSXjmU3X0JgwFU9Pwf49Ch9/oBAUCFNnqCz8ovGGfzPnqHTv5WDHTsmbb0iQDad8FL1C20cH0XvNTFI/3c+BSUupSC8ieGInun43A4squbTqFCl3fV8vCTt95ixn06uJ/6Ez5bQJ0yKS08f489DbqcRFmogMqRulNOgVHpoewj+XXNa+G6YGdG9Gd+g5E277APrOh5BO4BMBXmEQEA+db4Vb34UhfwZv53pZtaIV/1P43SYso6KiWL12u9Z/SK22uh7W341h/evuUp5/oHp3s/CNykVdmMB3PitW3Ptfn2/RnjTO3rOa6CeHEDTZOS8MV1Ceo5U99315NJGj4rEXlFOyNYXizUmU7k7DnBiM94hYAu/tgzHc+fSLJb+cXx9YR2gbP6Lmt8e7a1WKqLIfkblxYqjmFKGmXMYw13mBsHokFSUh1Gmi0xAyticz4JUxdR6XVjuUWcCnbtpKIy6uRVw8qjpEB/s63x0aqGq0eOV/Q/yQucVIm71ZvjUi2FeL4OQWQWClZspqBaXaqbVrV0FysmTJEhh3gytXV8HpCp6GEfzgQJLnfkvel4cJmN29GVfQNEA6nWDYMBg2TNCli+SLRSrz6veHBDSNS+/eNaOCTae9vBKD6bdpHhfe3smvgz+j3UsjCJ/ZlR4b53Lq3jVkH8zAMmkpMR/djCmu+v5SUlLC/S9lUpB3Cb0O4iNNfPxXrSpr8ig/HngrlX891nD12B0TAnl5wSXQ+4EhsMHjtDfCALGDtH+t+N/FbzxK0pL43RIXAIQOfO+E/HdButaITYMOvKa2+LSuRt76syQ9uZH4d8fhOySmxa/vsNjZMPE/RI+OI8RsIPn276g4kY1H/0i8RrYl/MUR6HzqCSc7gT2PbiCgQyCGUgdxj9a4Odqq+hE1HjVy7DyBrncCwuR8Ssyx/wK6Ic6nleqDrcxK7pFMQvrVrfKSeaUIf896q5Uc2SUozYi45KTmI0x6VFd66ijVXi4AQq9DBPkgM/MRUc4Lva+cL0RlC4B0rXLL4UDm5yL8vYCsK8fdfBM8+hj8vAVynQzwSKuC5Wg5ikcO+jb+DUbnmpyjQUfEG2NJnvkN7t3DcOviaiVdAKdPSxQFEhK0z+/QIUmbNq5UngkQzo2rGHTEPXEdwePaceyPq8laeZJO744jcfEkUv+5k/QP92Gd+jUxb4/Fq/K33atXL3b+uhuOTNAs/msgyM+AbVdda4Lk77te+dtkVMj4YQDE/c2F19SK/1389tM7LYnfN3EB8L0DKnZB+S7XHCqFGUL+Bfpraz/fFDIXHiT9vT10XDwJD5dv0o2jSly7ee63yIwiAqXA4u9BwJzuePSPqmuN7iIyNp0n7Yez+DkE3X6aW50ictg1Ua658QVezchFZheijOvj9JgytwSZVYjSoX5/CmeRtTuNgK6hGNzrhuNlA6XQarkNbA4Ub9ciPR4+bqQczahMFbkScVFqRVwARJhmRKe4SFykww5WKyLaD5mVi7xUKT4tLwfvIUh9ClXRittvBx8f6NJF8PPPTt5sFYn1QCSWPVtRs4rRx/ijjw/E0C4IQ0Iguggfp1OfxkhvQp8eSvrjPxC7bCo6V95vMYaSki3c/0AZBYVaT8j4OPj4Q1eIlAeIgS4cD15dQui3ZT4X3txRGX0ZSdRDA/HsFsrpe9dw/v61RDzQn8D5PbXKRkMg+AyCwh11yEvTEKDzAu8BLp7Xilb830ArcREKhLwPWX+G8p1ORF6ERlqC3wKPoS06FSkljkILel+z5tHy2jbyN54j8duWK3eWdpWyg5co3pxE8eYkkpLyKLbauWHpVLz7R7WYbsZeZmX73asIDPUmZnIi3omV6bUr5c9NCHKlxLHjBLr+HRD1iGMbguPABZRu0S6dUx8047mY+ufWYI+iEpRAD5dbLbhXpYqMzvu4ALUaLV55KDwAx6HzDZygQTocWgdumxVptWrpIKRWku5mRM0pRRcUBAFekJEGbo8D/7lyfmSk4IEH6r/2wi9g5arqOe36tXLM/Ei85s3Ba55G8Oznc7CdzcGyL5XSJQdRC8rRxwdgiA/C0C4QfUIQulCvBt9L79HxlO1N59Lzm4l4a6zz77mYQ69eT7Fze/3fj2HDBMOG1X7u581XH+sDjHBuvBpQDDrinhxC0I3tOHbParJWnaTTO+Po/sNcTsxeTsrbv1JxMoeIl0eimPQQ+6zWNNGSifOmf2iC3Hb/dr3kuRX/u2iNuDiNVuICoJgg9AMoWg4FH4Ajp26naGHW/t99CPj9GUwdW3wa+RvOce7BdXT6ZiqXPt2PJbWQxBXTMfg13zEUtIWi9NdUijYnUbI1GUOYF14j2mIdE0f2e9lM3H0P7qF1XWCvBQee24x7gDtmnZ64R2qkiBw2jbA0IciVyZeR5VaUjs47wUopUfcno59x7TvNS9uT6Xp//deROQ1UFF12XZgLWsSltLAcXLH8B4RQkFKl5pItwgOQP+xDOlSETqkkKVawWTSSYrNqOhajEYxGhLsH+PqDTndl8Zf+vsikTBSTQHp6QYEbUsRTUnyszhy0hV77e948wbx5ded5IckT+7JbcZCBrlM4ipsBY+cwjJ2rRZ9qcQW2cznYz+ZQ8UsSts+07siGhEAM8YHo2wVhSAhCCXC/Ms/gRwaRPPtb8pcdxX9a17oD1/um+QKTgKWACyTxCtxBPNQo6W4K3l1D6f/z7SS9sZ1dgz+j3Ssj6bZhDuce3UDG96eoOJtLzCcTMAR5QodP4fQfwZLhRERYBzoPaPceuMU0e36taMX/72glLlUQCvhMAe/JYDkIhUvAnqYRGMUH3PpqepbmpIYsFVBWBHY7mMzg4aOZLlyFjA/2oJbbOX7LErwHRtFpyWQUc/PKnTVxbTLFmy5QuqdaXBt0b1+M4d5kbEtmz21LmLD59hYnLdn70jmz8CABOh3dt8xHqdIzSKnt9M3uTUdbdp5AP7Cj0+Z3APJiLgiBiLq29J1qd5C5O43rl9ZvUy9zS1Da1k3FNKcUGmpWFeldN6CzVRMd6XBoTfY8zahnLyB8TFoqyWgCQyVJMfqBTt9ohEKJC8e+cgci0h1ZWIGano3S40Wkz0wErmnBVJsOoYtE6fRH7F/vRXmm/m7PipcZU49ITD2qNUWOvDLs53Kwnc2mfMNpiv61HaEI9AlaesnQLojw54Zx8d7VuHUNxa2Tk60dlGdAXUXD/Ynqh5QKQviCmO/SefVOwagj/umhBN9YqX1ZdYqO/xhLbq8IUv62lYobvyR+wS24dQ6Bjl9A1leQtVSz8levEgYrboAE/3EQfjsYWzal3Ir/AVQZ0LXCKbQSl6shBJh7av+uBVJC2jnYvxkuntUiDFVVIIoCXQdCt8Hg5QdARXIBpSeytVMdKuXn81ErHC4RF2t6EcWbL1C8OYmKk5Xi2lFtCX+ptri24GwOP05ZyqgvJ+Of2LI3OdXmYPudKwkI9SJhbg+8OtZY4G0WTVSgNJ7GUc+kg6Ig4lwrw3Tsu4DSO/aau2JnH7yEVxtfzA0Y+zXs4XJtERdXyqGl6kDabWC1oOZma4RQVbUoSrAPstCCEh/dJEmpF55uiAAzsqwChA7dqEEIowHkR8Dd4CR5kXYdssyHvFVvEzAnFrE1CceWU+hHdXLqfJ2/O7q+0Zj6amXtUkrU7FJsZ7Oxnc2hbMVRbOdy8AkzkfvYGnxmdMfUORR9fCCKRyOGhiIelJWg3owz1UEAUlXA7oE0/oQQLedS7d0jjP5bb+f869vZNegz2r86isQlkzk59ztOTllG2zeux3d8ewj/A4TNh8LtkLMWbLkgHaD3Ad+hEHAD6K4tMtuK/2W0Ehen0Upc/hvIvQSrPoXyEi00D1o/npo4+Iv2L6EbjJ5G2ju/avoGRaC46bHnlVN64jI+Axv2IpFSYjmde0WvYrtcitfQGALmNiyurcgt08qeXxhJ1Gjnu/U6i6NvbgerA08/d9o+WCPVUtWPyK3xiIR0qDh2nkQ/qrtLC660O1APX8T40NjmTv0Kqhor1juOlA1qXNTsEgwdXSeCVU0WGzKgk6paV5OiOjQyLFWEmzt4+4JeIykyxoF6Jg2hdz1ap2bnoh4+BQEeUO5A16tG6b2YBdILmImWRm2YwEjVA1uqD7a05WR/fBS/W63op/TB+uYGdH1jEd6uL7JCCHTBnuiCPbWmiWj9uhyXish+fSslP5zBdigd+4U8FH93DAmaVsbQLhBD2wBEzU2AGAbKRlBvRNOPNBx9UctM2PM9kL++g+JehH68vGZyXBOKSU/Cs8MIHq9pXzwSAkhcMZVzD6znzEPriTqWRejj1yEUnUZSfFtWW9eKVvxfQytxaWlcSoEVH2jRhcbgqNxZnzsCBTkUbtNjDPcieFoXfIfF4NElhKLNSVhTCzFGVe/wrhbXIgReI9sS8uQQ3LuHNiqudVjsbJj0H2Ju7kinu5yv1HEWBaezOfLmdvx1enp8O+OqFFEFGExNCgbV4ykIH3eXq2LUkxmIMB+En+upmqtxaXsy8ZO71P9kqUVLR9XjEWO/XIp5SPNSRaWVBnSgIi0VYLUiK8kKDocmnDUaEWa3KyQFSwWyuFBLAdWAEu6PY+vh6p5cTkCWlaMePYMsKETp0h6spTgOpKB0c9QWOosJIC8CC4C3kbIEEAgh0fwsLcBAhPIY5at1VBxKxmtYLDlfHCTk/v7o+sdhX3kQwxzXqnIaglAE+ggfQt4YR/LMbzD3iyXotRtxpBZgO6ulmSq2nseeko8+zKtWmkkf0xuhTwX5Ncg3gFTAgOY5I9CqqHpgPT6V/FcM5F/Op+28PMTW4+iHdW6R+deET89wBmy7g/OvbWP/TUto/+ooSvakkfzRPkqPXSb2o5vRNRZJasX/bbRGXJxGK3FpSRTmwHcfNk1aasJug+wMej0dDxPuvKL9yPn8AJff2onflM6EPDaoXnFt1L9uxJQQ4NTiJKXk57tWYg5wZ8DrdU3VrhVSVdlx1yr8gjzpcFcfPDvUML5yVPUjajwCIG12HLtPo7/ZaTvWK1D3XUB3jQ0VQXufMranMOTdm+p/voFoC2gRF1c0LrLShM9gs4CUOHQl+N3XBVlYoGlSzG7g7QN6Q72fsVSUWpb/VRCebmA0IPOKEU100pYOB/JsMur5iyhx0Si9O2v+LWlFCJMb8mIWou1VpeXCH3gU5MPIkh8QhstgBvAFuoPQolVed9somfwlPmO8SXv3MAGzuqG/sSuW51ehu5CDEtuEOZoLUMx6It4cS8q8b3HrGoq5XSD6GH/cRrfTXqfNgT05vzLNlE35+lPYM4rQR/tiSIjHkLACfWI2+tBchCgH4QV0BNEWc3/wvuMofLybC18l0XaKHeHlhq5XXIvN/8rrMOlJeG64pn25ZzUeHYOIfnoIyS9upXzMF7RfOqXWRqYVrfg9opW4tBCEEDw8YQxvDddC629u2U+JxcrzYwfw/IZf8TQZeXR4beMo3cPv0CUsAJtDRa/XMffABR58/hVyPtxL7mcHAMj/7gQFa0/j1jkE7xGxBP+pH4Yw18W0+1/+mfyT2Uz4+Q6XBK/O4vQn+ylLLSQs0pe2D9RogSAl2CrA6NZkJYZ6KAkl3B8lxM+lsWVpBer5LPTTr72aKP9UNgZPE56R9S8ODelbpJSNalyqSApWK7LyvzjsGpkzGnH3NlNaoqfoX78SssBJU8MaTRavhlJl/98AcZFSIjMuox47jfDzQTe8P8JdS9/IwgLw9EKJM6Gey0C5mrjUHN/aC4xeIOqmfhSzAd+7+lD0+T58b2xLzoIDhD4yCP2EHti+3oPxsRvqNfFrLkyxfoQ8Opj0RzcQu3QKSg0PHmHQaZGWhEBAqwiUFXZsSbnYz2ZjPXKJ0m+zUXNK0bcNwJAQgD5BxdCuEF2YNx63dEE6JHy6h5SV6bSxO8DTjK69010mXYJP7wj6b/8D5//2C2df3U7sI4PI/GgvR0Z/QYcFt+A5MBrV7sByLg+3Dq6bDbbi/ze0GtC5glbi0kIwmUys2LaLJ3vHEujpXP7ezaDn0GOzALhcXMaM5Su5+EMKd5VWh9EFEP3v8Xj0af4N8uySw5z8bB8Tf72nXkO1a0VpehH7ntqIr6LQ/ZMJtdNVNotT/YhkhRXHgXMYJl/n8vjqoYsoHcNraxiaiYxtyYRfV7++BRruUSSLLaATKB5GpFTBaqsuQb6KpAiTCTy9wVAdSfHwdaPM4sBY7opfh6g34gKVZdFp2dClbhRKFpWgHjmFtFhRenZGCardrE+WFCMCg8DHgPz1BNJq08S59cFub/SzdR+fSNGyo3i4WUlfnkTAnO7o+8fh+OUM6u4kdANaNmrhc1MHSvekkfnKVsJfGd3oscKsx9gpBGOnal2SWmq9Uslk2ZVCyeJ9yBKrVpKdEIh5eFvYkkTqT5eJkvsR7iaUqJaLHNWEzqyn3YsjCB7fnmN/XI1n91DILuPYjG+IeeI60hcdwpJaSN9Df0If2LId4lvRiv+f0epQ1ELQK4K7BnbjH1sPNOv8YC93Pr5lMIuOrsEQ54cuwA10AumQlB9ufnO6SztS2P7gOsatno1HMyI1TUFKyc57V+PlY6bT08PwbF/jJq6qWirM0HS7AMe+syhxYZX28q7Bse8Cut7XniYCuLQ9pUHjOaibKpJSIq0W1NwCfO7ojJqVgcxIQxbkIW02hNGE8A9AhEehhISh+AUgPLwQRmOt9I+7jxvl5TbXnXMbibioGbm1GyZabTiOnMKxbS8iLBjd8P51SYvNWimidkeYjBoBSq7/+yelrCRkDRMXIQS+Dw+heEsmoTNiyfl0P0IRGKb2xbbyALLcVVfYphH65FDKT2RTsOqky+cqHkaM3cLxuK0bvk+OJGjBNAI/mYz7xC4IswFRYUdx1+PhUMnZnoN18S9YNp3CkedcdVJz4Ns3ggHb78At1p+CpDw8B0Zz9vktlJ7Pw2FTSXt9W92TZCnYvoDyO6D8ViifDpYnwXH8vzbPVlwjWrtDO43WiEtLQVX506DOdH3jSx4f0btZl2gb7I80gPfHowgJCUG12LEmF6APaZ7gtPB8Lj9OXsLILyYR0CW0WddoCsnLj5OzJ43IdkHE3tdXe7C8RNuFq5Wi0iZSU7KkHPVYMoaZrruRqpcLkYVliPiWeX0Z25Lp/dSwep/TynGL0LcLRM3P1Sp97NrCLa02HEV2hF+Apk9xserEw8eN0jIr3q50hxaac269IlxfD3BIKC5HerkhU9JRT5zTCMuoQQhTA5G3kmLw8LxyPSUuHPVMGkq7eowAHQ5QdE2+VreeERgSAhFZhZQdLMKW2RNDbCC6xHDs645gmNS830tDUNwNRP79elLu+A63ziG1Ghg263o+bph6R2HqXf0eFH6yi9Jvj5J3tBg/+3HyPt8Liq6yhUEQ+sq0lOLVvB5fV0PnZqD9yyMJuak9h2d8g6j8zKWUXFp2lOiXRmpVhGoKWP8B9iVo8drS6os4dGD7DJQ4MDwK+onXZKTXihZEq4+LS2glLi0GibfZxJw+nXh32yHcmtGdF4dD00JUQjHpMbdvXhjakl/OuvGL6fXMcKLHtmvWNZocI6+Mnfetwcsh6fFpZYpISi0KYK/cSesM2mON3CAdu0+jJLZBeLleIqvuT0bXI6ZFWhUUpxZgL7Ph2z5QiyZcrUmx25DZReClRxiM4O4JRgNCKJTvOYHjshZhaQ7cfdwoK7MirQ6nq4GEEMhK8nL1+yuEQIT7o55JRRbnw/9j77zD4yivt32/M7vaJmlVbRUXuRtXudtgOwZTjQHTbUILocYh1ARIIYSEhACBQDCkQcJHwAUDwZhiHGPj3i3cu2XLlqxmdW2deb8/ZtVX0q60ivmRva9rL6PZmXdGy2rn7DnPeY6ioJ47GpHQjli3ugqR1KCZEL27I9fuQro8CFuz362dbEtjEn54LkX3LyH92gyK/7KZjF9egGnWaDy/WoJ63gCUtMgKTi39k+n2wLmcevRzst69HsXW+TJiY5x3TURYTFS/u4PyEx6SJndHvWws/hPl+A4WU7Poa/xHSlDirQHX3xQjoOmX3ER7E/Z5x2Yg3EZwW/c+8Xs08n69kt5P28F1HeAm+IgADXCBvhs8PwD/ErD+DUS0UynK/y2igUvEMG4cD04dxeg/vMP3xg9tZ/+WHC0tR1VVunUL0QG0FTSv0fbc67KBDLsv/A6dUNn0yOdYzSrDfj6V2AF1brXNvjX43Ma/5uAfjrK8Gv1QPubbLgz7/FKXaNuOYf7+tLCPbbKOlODzUX2ogOkvX4AsOm2US1SToUmJMYIUqapQ5UHp0xNhbmqiZwhzO96K7XBaqa1yg0kBnwYxIf5p1peLmgZu0u0BzYu25yim80cieqa3GwxJn88I0OwNeglhNiF6dUM/WoA6NKvpAf7QA5eYfslYz8vCfaQCk6cC78kKYno4MV02HP+iLZjvnx5RbxQA59XnULPlJKefXUPGr8LP5rVH/K1jkZpOzYKvqbQpOG07sXx3CtYpfYHA+/NUhdHJdLAYz7pc/LlnUFJj64dLmgakYu6bZLgmh0DVniLc1V5MNhNIUDQdRRHUnlwJrjcI1VAPakH7DNy3gvXd6FyjbwLRjEvIRAOXCJPksHJD9kDe2LSHOyaE5hAKUFxdy72LVvDDm27o1Ae4lJKv7v2ImHgLk57vvBlba5z6zxFOLNlP72Fp9Jk7vvEFNN3RFNNmG7S2YT/qqH4IW/jf+uTRIoQ9BiU9IfRjpDSCksY+Kb5AkOJ2ozpsiIREo9zTvMR1phpirS2CFjDs/i2jOi6grrf9NxsTokO9kdULdAOXJHUdeeQE+sFjiJQkZLkbpVeIk7KrqyC25WBDpV8mes5haBa4SL8f0Y7oujEJd47j9O2LSb6mG2Vvbab7zy5CnTYIbe0h9F0nUUeEPpcqFIQQpP18GrmzF1HxyQGclw+K6PoAzu+NB59Ozfu7qLYoxP17M6ZrJxoZL0Vg6pmAqWcCtgsGAIYPk/+E0ZbtP1iCa/lB/CfLMWUmGIFMXUDTOwlhChJMrD/K1JW3ocXbcZ8op+ZQKWXr9zJ43quEHrTU4QJtJfj+BDGtTM2MEuUbSDRwiRSKYtyk/V4eOX80r679usnTv/liE3/8akf9zyefuhOXz0/28/8y2qFVhVvGDeXh517o1GVs/91XlO4sZNZXd6JEaNJzc3y126g5/iAXvlNC6uRUhPwU9Mkgbgs4q2KULiz2Nu399aJy9LxizNOzO3Qd2tZjKG14tzQJUurKPT6vMSfKHGOUdeyO+iBl5WPvMf0f1yIswXUJeisdRRCJjEvA9r/OPTfUyQGNBLp6YQn6zv0Ihx116nhw2NF3fhq8zBMEo0zUcs6T6JGKXJWDrHYZHjF1aH6whl7eM3WPxXHFYGqOnSEuy4PnSAmWfimYbhiHf/4mozMsSFDYGVRHDJkvXMqJu/+NdWg3LFnhtdqHgvPuiUhNp/ajPahmgT0uB9PFwZ2fhUnB3DcZc99kuMTYJr1+/MfOGIZ5ewupXbIH7XQV5qzEgPOvEcwoKQ5cn+7DtewAsbeMIenq4ayu+Jpf5fwczi3EMM6Dnbt1Plls5bKLTbz0qpcnnvJSeMSB02lcz6o1fq6a7aZPbwWoJSX5cf7z5Q9BRPa1jxIm0YxLyEQDlwhRfeYM/O1JALrHOah97of1zz116SSeurSlx4j2YuNvOQL6DYPYjtf6Dy/cxd6/buGa9fdgjrTDppQg3wP5OxRxgP43+1BMEjgUeP4LkD8HZoH6CMRktyv809bvQx0/KPTsQuPL8frR9+QRM2Nk4PKkUbrweloPUuLtRukniFjYVVpL1YkKUrNbn4/UlvmcVlyN2i38OUV12J1WSk+WhzWvCABFIKtq0A/uRVbVoIwYhJLWSKOSloTML0X0azvrUjf3CHvL4EuoCqJPOvrhU6jZjcZEtNMKHQznzaPIv2kB5rTu+D7bhuWHl6AOyUDLSEBbsRfTpa04FncC66AUUudO5NSPl5H1r+tQLJH/2Eu471zD1fqz/ajmI4g4G6ZzB4d0rIgxYR7UDfOghhKx7vLhP1JqtGVvzaNmwQ60khqjEuvVqH5rK57tJ7nqpzO4+uKfgywH4K9v+nhnkY9LLjSCkPmL/YwbrfDhx35uv7kh8zllksrSxXVBZyxoy8A0IyKvRZSO8O3vBIok0cJmpLDajLlDHa0Vm8wwZlqHT396/QnW/GgpM5bcgiOjbQFm2Egf6LeDvAvYhRrjDQQtjanFEAUuAtN3gIUK54EAACAASURBVKVtLqmfLEGeqUIZnhX+5UiJ9vVxRI9EpO5CLzqNzM9DlhQh3S6EqiLinYj0HihpmSjJqYi4eITV2qr53ul1x0mb2BPF1Pq3ztYCF6lLtJIa1JQIZFxiTCG3REu/H/14IfqGHERyAur0c5sELWDY/+v5Z9pfrFk3UXOU/hnoR/KbbgxDnFu/TryF+Juy8RzXiLH48Ww9AoDpurH4l+9BltW0s0LHSLh+KDFZCRQ+t7ZL1gdIvH8ylgsHUr29DM/y3Wg7j3d4LcVmJmZYGo6rh5Pw2AWk/O0GHLNH1UnpQNPx7cin6u+vgSwF4OAhnad/7+Xtv1lRFMGRozrV1ZLfPGlh/uK2guFq8L3a4WuNEuW/TTRwiSSTZ4KlAxNaTWYj25LeMS+SyqNnWHbdu1zwj2tIHhHhtmcpQb8N+JAmrZWtogO1oN9kZGGCLinR1u1FnTS43W4gKSXS70PW1qCXl6EXG0GKvukgypDuCKUuSMlESa8LUpwIqy0sh+BTq1sfrFh/LSVVKEFcc/VyF4o9BtGJb/KOOo2LRUV62s64SCnRTxag/WcdeLwok0aiDOwT9LUUdQ667SCrqxCxrXvoiLRkcHmQZVXG/rpuvDc64MIcd+1QfLnlVJdaYP8hpNuLkhqHOnUQvg865oPUHkII0p88n5qNeVQuO9Ql5wBIengqMVMHUL2jHM+/t6If6bgHU3O0gkqQYOqfguPmMSS9dBXx96QBAp9PctP33bzwTAy9ehr/T+Yv9jPnejNTzlU4cEinqLihY3HNBo3sc2vJPreWZ573gn4kYtcZpYNEfVxCJhq4RJLYBLhurhG8hCqwNcVARl+4+KYOeSp4ylx8MvNtxvxsGr1nRF58iPwbRvakA8I//QaQRU2X83qRJ06C148yqKkYs2WQUmhkUooLkbU1CEVBxDnBnoQsrEGdeI4RtFhtxuTcTlCwNpf0KVlt7iNLa4JmXDqrb4G6QYsuaCfjIiuq0NZsQT+Yizp2BMqQvq17sgCieyLyTFWb5Sfp94MneJmofh1FGJ4udVkXzSgTdURILiwmnHeOQztaRcWuKnwrtyOlxHTpMPTDheiHC8NeMxTUOAuZz1/C6d+uxptX0SXnAEj6yTRM4/pQvbMCz7vr0AvKIrJu3D2T6PbebSS/PIvY2aMwD0xFKLWAxi9+7WXoYIXZ1zWUgxYs9jP7WhOKIrjmChPvfdjwHpgySSVnvZ2c9XZ+9uMYkF1noBclSqSJBi6RJiUdbnoUUjKMTEprpSOT2dAHDJsIs+42tBghcmrVUUp3nUbz+ll2/Xx6XtyfYXMntn9gmAghuOXWh6gLWvx+SWqaxswrjRvrP9/SSU3TyB6jMXioxkt/1Fm2TJI9xtgW66xg0OChZGdnc+utt6LXVCOLTiOFhnreINA1I0ipqAtSTjYKUgQiNh6RlomS3gMlpVt9kKJ/nYcyvCeiI145QfDVeCndXUjahLa7WmRJFSKlZVZCK65udUZRqDgSbNRWuFrNuEiPFy1nL9q6bSg9043ZQimJRsZDD+6eCyBMKiLViTzdRrmorkzUTvZE9MtEP3yqQU/URlmtPRwX90d6/MjYZLSCMmRuPsJixnztGHwLNzfxM4oktiHdSLlnLKd+/Dl6OC7FYZL8s+kow3tSs7cSzxsr8Rw6TdmD83G9t6nDayo2M8La/D0fy6o1ft5f4ufVPzQIsHfu1jh0ROeiq1xkDa1hwft+5r/XRiZPdH6qepROUGdAF824hERUnNsVOJPgu49C8SnY/hUcDHQTCWG4jdpjYfT5MHQ8WMOfMbL6viVU5ZaRNrk3JkcM5/7hsgj/AgYOh5Xde9y4XGCzCZYvh8xmHb833iB49RWF0lLJoCE6O7YKcrYZN7RpF2i88JzG6LFboLwcyhqVLCya4ZdS55MSGwcxFkQ7AZyUEn3rUUxXR85t9fTGPFKy0zG1YVImvX5weSG+ZSlQK65B6WTGxdC4uBExKjS6oUopkcdOou87jOiRZrjeNpobJISClDpt5T1EwP5f6RXcH0hWVxkt4O0gUg3huCypQFiVsIW5TdZSFRLunUDZK+s5neOlh3MfolsSypgs+Oog2trDmKZ2jXFi4pwR1G45RdGL60h7fGqXnAMg5ZcXUfzzz6k9XIj93TXYkkzoe/OAyHkrlVV043v3VfDuG1bi4hreBfPf8/PUEzE88WhDNq7PsBqOn2glIFQGROyaonSQb3mwEUmigUtXkpoJl9wEF80Gr8vwC7HajPJQB71avJVuKo+eQffpnPryKBN+e1GXtT2Dj8sukXzyqeC6a2H+QsmcGwVr1rb8A0tOFvTvBwUF0LNn0zWoeh9cDV1VQhHgiEVJCN+KXeaXIz1+RJ/OmfQ1Jn9NbpvziaBBmBtsmrGRcels4GI1Mi4xpvqyjiw5g7bzAJhNqJPHIpxBNChCGNb+baBkJKNtPxz0OaNM5G6zTNRwKoHSLxN5OB/OSUOEKcxtjnViT9T5DuwJKVTsdZOQuAt12jjMN47D+/J/UMf0Rjg65kTcFkII0n91AcduWEjluEzip0d20GNj4m8bg//NFQgRKLdpEnmmGpEUJEMnNUAJ67Phz3/dQFGx5L6HPE22V1RKPnu/aZB99UwTCxb7mTCu+edFLJjvD/mcUaKcbaKBy38DRQGrA9obWyIleHaAL8+oOSuxEDMQYhq0KwXrTqCYVHSfDhI2PbGc7uN7knl+3y64cJ3ZNwqe/o3OzMsVdu6S3HG7EjRwOXFC4vbAiBHNn9Eg7gzY0pC5+YAf4YgxSg0duaJtR1HHZAUNIDpKwdpcsh86r819WpsKDUbGxdy/cxOC7fU+LirS5UHbshNZWo4ybCAis3vrWhKl9UGLdYj0JGRRGVLTWwp4a6rB7ghZyKz0z8D/yUbUASnQit9NqAghSPjBREoe/5xyl0b8SCfKwVyUwX1QR/fG/3EO5tld4/ysxlvJfO4S8u7/BOvgVGIyI9yJF6Dsp5/gHGJvMJRWwLPtGNaLhhuBSuVaKPon1O41uvcQoMZC4hWQOgcsbZsaPvHTn/LEoxngfZz2xPMvPtsQBE6b0uijX9hADd+5OkqEiWZcQiaqcfkmoFdB+T/hxBQouA1KfgGlz0Dxz+DUtZB3GVT9G3QPB9/egd/lQ7GopE3uzYylt5Dxnawuu7QRIwS5x2H+AsmMS1vePBcukgwdodF3gM4D9wus1ub7+FFENUKoaF/tRySmIjJ6BjU6aw+p6Wg7jrdpOhcumk+jcPNJ0s9rp6OoPQ+XTmZcYqxmpC7B6cfsygeHHfXCc1F6pLUtgBWiTY0LgLCYEU4Hsqi8xXOyurLNbqIWayXGgc1iiHk7mXEBsAxOxTIyHWd2GgVLi9H3H0OWV2K6YiTatuPopyIjbA2GbUQayXeM5tRPliF9XaN3iX/kfMqOaFQfqMZX7gNAW7MfSj+C3RfC8Z9CTQ5IL0Z0o4NWCSWLYP81cOhO8LbTmWS+HuhoZsoO5h9HLf+j/J8i+m4927g2wfHJUPYCaAVGpkXWgHQ1/Os7CCVPQt40FCWPXjMGcuPO+7l69V30njEorLbfjnDlTMGjP5HMmd3yBnrjDYI9O1XWrFJ45MeS06ebf2swAfHoO46g9ExF6ZZgdAd1oAtIP3gakeRASY3ct+Pi7fnE903CktB2G7ssrWo9cCmq6ZT5nJQSeboYu92ER3rxymTUIf1DK8UoSssxC0EI1hYtNT+43eAI79qVfhmGeLYTGpfGOO8ah3/XaTx51XgdKWibdoEtBtPMkfgXbjbEwF1E0q3ZmBJtFL28oUvWt0/sTca/5pD89m1o5w2nbEclDPgKTj4LWjnorXXz+IxgpiYHDswGV/BSH2AIa21LgHCDZzuYLgPzvWEeFyXyRFiY+y3P3kQDl7NJ7Wo4fQfIaiNAaQtZA1ox03/9Npd/MJGEAZ0rTbSHu7QW6RfomuCO7wme/Llg+PDWv/lPmiS45WbBy680/4NRkN7+aDuOoE4KzUm0NfRtx1DHRLYkZuhb2s62QBvmc5qOXu5CTe5YxkVW1aBv2I6++yD2RAcVpTHonjDKYKL9UhE0CHSbUB1emah+rT7djUGQEfpsNPdwYr+oP/GDkil4Yz/E2tF3H0KdMgBZ60Xf1nEjt/YQQpD+m+lUfnGYqq+Odd15VAXn1cNIf92MY+Q2kO4Qj9RAq4DDd4K3jTZxdSTYlgJOIBTXbAeYrgHL3zust4sS5WwRDVzOFt4jUDg3jA8wAGkEMPnfNb6tdSFr7/gQ3acghI0ePQQP/Kj9t8pjPxb84y1JVVXjO1os2pbuKAMzEQmdyEq4vOj781Gye3V4jWAUrM0lox3/FghoXIK0QuultShOa/CBeG2t5/Oj7TqAtnozIjUZdfq5OJIc1Pq0sC3/0duPIJSMZGTBmSbZi/ZM51pDWM3g05CnisM+tjWct4/Bf6gYvdpLrScOeaIASsox3zge3/tbkR5fxM7VHFOCjczfX0LBUyvxna7qsvPgPY2acRvZ1+cw7Lr9XP/jY9S6jKBTHZND9o37GXbdfq544CjlVX4m3HKQ7Bv30+uyPaROXUd29jCys7PJzc0Nvr46FuxbwHwfEEfLgVdmwArKRLC+CZbXQERljt8YohmXkIkGLmeLsleIHban/sd/Lq5izgNNv1GVnNFIHZeLx2O8Ca+65zSTrjtplJMqF3TZpeV9eoBTyw6x97X1CKXp7J5p0wRLlxhlnttvU3j1lYa3UEaG4PQptb4tc9WXcYwZ8Qj6nhOoEzpnjqfvzEMZkIawR67LROo6+WuPt2k851uxF//qA8jiSqQuW2gh/GF6uEgp0Y+fMlxvvT7Dpn9AFkJRcDhtuPxayJb/QOgZF4cVrDHI0oDzraaB2xV2mQgwhNVmM/rhU+Ef2wpqoo2464cT2yOWonlbUUYPQdu8C9E7CaVfN/zL9rS/SCewj0on6eaRnHrsC6S/azxkKFmIzaKQs3AwuxcPJsas8OfFJQBNtifFq8xbWMKmtweSs3AwT9+Xxo2XJJAzvy85W/5DVlZW6+dQ0sHyG3AcA8srYLoT1FlgugnMj4J9I9iXG3OJopmWbw5RH5ewiAYuZwOtHGqXN9l0zSUOlq9z1X8DA1j8eQ1XTndgsQjKKzW27/ZQXqlz7EQVVLwZ0g0rXHw1Xr66eTE9RmWQdfdYEE8B4XvNGJjRNo1HGZZl3Dg7gbbtmOHxEUHO7CvGkmAjto3ZTtp/9uB/fyv4dHwvfY732aYzmPSi0F1zZVkF2leb0Y/loU4YiTpmGMLaEIjZnTZcXj+ElXFp24Cuya4ZSQ06l5oqsNk7pI+Smh/hjEOeKEL6IydqjbthBFpBFcLvp2pPJSItBT1nP+ZrxqB9tR+9pAuzIUDy90aj2MwUz+u4SVyr6D4oWdxk05RRDg7neVrsOmmEg1NFrWSYmq3RKsJiiHatL4HtbbD+BSw/BaXrWr+jRPlvEQ1czgZV70Ezy7D4OIWp46x8vKJBrLdgaTVzrjBuiu9/XsMV0x3MnhnLgqXVRonJtTril7bh3iWoHo1zF882ulmUOcAdhB+82JHVi9EP1KCO7Zy5lSytRhZWoAxue8JxuBSsySVjStv6FnVC3wbxqyJQLx7W5PlQOoqkx4O2fQ/ahh0ofXqgfmcCIimhxX4OpxWXV0N6wsm4CJAyJAFrY4GurOpYmQgAvx9htSC6JSKPR86eX7GbcX5vDDanhaI/bUQMH4AsKUfWVmOaPgT/4m0RO1cwhCLIeOZCKj7eT/W6COtqanbQWBTk90s+W1fJ8P5NReGaJlmxuYorvxNkSrz0QtnHkb2uKN8cohmXkIkGLmcD14ag2pY5VwSCEiC/0M/BYz7On2h8sM3/uIY5VziYc4WD+R/XGFoXd05EL6tw3XGOLtzFhBcuxdbY10J5CZiLEby0l16OAeJBWYZ/rQN1dH+ENRSxYOto24+hjOyF6ITFfDDy1x5v13hOHd+3PqUu+qQaPze+tuKaVktFUtfRDx9H+896MJlQLzoPpXdmq+3NdqeNWo8vrFKREKI+eGkPJSDQ1f3+jpeJoH4qtNIvI6LlIoDYmYPAp6GaBJXLj6FOGI6+fS/K5P7Ik2fQ9ua3v0gnMCXbyXj2YvJ/sQJfUXXkFvYbIxdcHp3sG/cz9rsH6JUWw/evTmqyPXnaLs5Ualw0sZWg0l8ZuWuKEuX/KNHA5WygBxfWzrzAztptbiqrdBZ9WsN1lzpQVUFhiZ/Dx31MHmtlYJ8YTCbYfcALWvtTf9uj9nQV/7Q+xZqb3mPFNe+SMTKdPveOa7qTEKD+DpSPgUswnPSaa03igHik9wdIfQd60WBk/hmU7M51AUkp0bfloo6NnHdLHflr2h+sqGQkQowKqiDmtsktgo7WMi56USnalxuQp4tRp4xDHTEIYW59pAAYtv8uty88cS6EHLjgdBj7FZYYZaIw5mM1wa+ByYTok4bML42ocFaYVBLuHY/FJCh6dRM44xF9eiC/3od63Vj8i7YgtS7SoARwjM0k8YZh5D+xPHLnkhog67UsOQsH86fHexBjNj6C67Yf/3QoXp9k3sKSVhbquvlKUc4y/+WMixCipxBipRBinxBijxDigcD2JCHEciHEocC/QeeBCCFuC+xzSAhxW6PtfYQQmwLbFwohYgLbhRDiFSHEYSHETiHE6I6+VNHA5WwgggtMbVaFS6fa+fCLmkCZyPhGvHBpDWUVGn2+k0fW1BPknvQbmRmlo9qTBioOlKB5NQ4u2Im7uJbBj09p3fBMfAfUpaAcBPE0cA/wXeBBEH8B5TS+xTPw/X03/s+3oowb2OlBiPJEKQiB6Bm+YV1bVB4vQ/P4SRjQyrr+WqjeD+XbUM83o17ZG9HKnKLGGRdZ40LblIO+Yw/KkAEo541BxIeW2bA7rdS6feGViiBknYsQwsi6nCjscJlI6jroGigqIsaMyExBHivo0FqtYZvaBzXJRozdRPmS/ShD+yHdXkQsiCQ72qr9ET1fMFLuGgtCUPLnLZFZUI2n/WwlOONUXvlJJi+8XYTPF+TmE4G/+SjfRM6Kj4sfeERKeQ4wEZgrhBgCPA6skFIOAFYEfm6CECIJ+CXG4K3xwC8bBTi/B14KHF8GfD+w/TJgQOBxN/B6x16raOBydjBl0tqH2JyZsbz4ZgWFJRoTRxkBzvyl1Xz+j3RyV/cid3Uvtn2UyYJPasCU1ulLKf/6dP2VSGD59QvI/7idG4PIAOURUOeB+haoL4ByA4gY8PnB44OyGvTNB9ByO6eB0LYeQxnbp2332A5QsOY4GVOyWq5bcxgO/ga2zITdD8D+n2JO+itm2y/h6zuhZBXoDRkRrbgGtZsD6dfQ9h1GW7kR4YxDvfA8lIxuYV23w2nDVevtQMYltM4iANISkYXlnSgTBbItgd9L6Z+BfiSy5Zu6UQAmv5+i1zYj/RJ1wnDknsOoM4bh/2wXsrId36POXoOqkPnsRZR/sIeaTSc7v6BjeMDSv31GDbYzcqCNBcuauwarEBf5KfBR/jeRUhZIKbcH/rsK2AdkAlcBbwV2ewuYFeTwS4DlUsozUsoyYDlwqTA+GC4AFgc5/irg/0mDjUCCECK9+cKhEA1czgZxN4KwUeuS9DjveP3jxTfKuXiKjfwiPzde7kAIQe5JHyfy/fVBDECfnmbiYxU27Y5A4LK3uF4yKIDM7HSSJvTo+IKNv/m7vciSig4vJf0a+tcnUEdndfx6WqHFYEV/Lex+EHbeA8XLQfeCVtPwkF4jA3PoGdgyC6r2I70aeo0H4apCW7EOqmpQL5iIMrhfh8owDqeN2lpveO3QYJSKQvByAVASbcgyVyfKRP4mjrmiV3dkcQWyNhw/ovaxjkzHck43LM4Yyj/Yi4iPRRnSD3n8OOqEvvg/2hHR8wXDlOIg45mLyP/ZcvylrTnchrpYAji/Q/X67KBPV69vOuTr45f7cstMQ/9y+5XJvPp4DxBmSL2lc9cR5ZtL5DMuKUKIrY0ed7d6aiGygFHAJqC7lLIAjOAGCDbRNhPIa/TzycC2ZKBcSulvtr2tY8Im6j50NrCOBTUR/XBw/Ufxlqz6/87qYebU+uadL4Lty78L6Ze1fR7pAc9ScM0D7TDgBmJA6QbWO8F6E6eWG1bisQlWvrPgRtIu7t/hXwtoaOW1mjFdPh6lZ2qHl9L35SPSExCJnZsDFIz8tbkMvSeg5fFXw867wX06MDOmrYtyGY/dP0R3Pk7ilWnoB46ijB6Gkhr+tOvG2OsCF0+YGZcQBi3WIc06ePzIWk/HPHECwtw6hElF9O6GfrQAdVhkdUgJ907Afd+/KfrLFhKuPgfRvxcivxjRPw7f/J2ouSUoWV3rIO2Y2BPnrHPIf2I5Gc9dTNEf1pF8xxgsfYKW/dsm9VZjqKLewWyRpQfYO+eHFOV/ihIp5dj2dhJCxALvAw9KKStDzBIH20m2sb2tY8ImmnE5GwgBzntBtD0fp/XjrZDQavBsCDBrX4Qz50D1o6DtAlwY7xEP6HlQ+yycGc4F/1jH8DvP4YaSn4YWtGhVcOb/wfEb4OhFxiP3Oij9G2hloOnQLQHz7Rd1KmgB0LceQ42wdwuAq6SGmlOVpIxMN0STex4Bd0H7QUuTi3OjlP4WzVeCev7ETgctYLRD11Z7OpZxCSFwkbqOcLuMadHN7f9DRPr9iGYzipR+mcgIdxcBmPskYp/WF1uChTOLdhsanXHDkCfyMV00CN/CzcZgyi4m9d7x+MtdHL7kLSqWHuh4q7RjGMSOa1Xj1ibCCj1aSA2ifFs4SwZ0QggzRtDyjpTyg8DmwroSTuDfoiCHngR6Nvq5B5APlGCUgEzNtrd1TNhEA5ezRfyNYB0T/oeYsBmlJtuE4M9LP1TdAbUvg6wCWmvpdAFukoZsYvzv5yE40/Z5/YVQ8BgcmQwlL4F7J/jyjIdnN5TOgyPfwXzFF5iv63wLtKxxox8pRBkRWYt/gIK1x0mb1AtFVeDMBk7n7WP2k7vpd8M2hty8nRmP7kVMXsfp0oZA5gcvHOHZt0+yansFzks2Mup7OQy5ZSPPrXs5YkMu7U4btdUeCDdwUZTQSkU11WC1oWSmoBd0sCOtWcYFQPRIQVbWIitrOrZmGzjvGINS66X0r1vRa30IuxVl1GCkrwJ0ib75aMTP2ZwzC3fhPVqGdPlBk7h3B/scD5Gs58DaP7y/e2GBnj+D2DEdP2+Ubz7//a4iAbwB7JNSvtjoqSVAXZfQbcBHgf0zhRArAtuXARcLIRIDotyLgWXSMJRaCVzX/PjAurcGuosmAhV1JalwiQYuZwuhQvc/g2WU8W0qpGNsEHsFJP8s+PNSQvUj4F0BhFqT94B2DCqubX3Qo+cQ5M6CyqVG+SnYftIN0ovwfIk4fjW4doV4/uDoO46jnJNhzMWJMI0HK8qT/+Lqx3OYNiqeI4vGsPdfo/ntPb14+s5ePDovF4DtB6pZu6uSR+YYBnhTRsaz4x/ZbP37SOav2c+2jStaO1VYOJw2aqrc4ZeKQhTn1s0mCjYpOmT8QQIXRUHpkx5xkS6AqVsscVcPwZZspXT+TgCUXukoSfEoo7rh+3A7/i2H8by4DP1UczFrZPAcLAl8IzZ+du1qJjiXLtBOgH8/aKfaFuEqFhjwBsSfFwhe2tAaKTbjkfU8JM3s7K8RJUpzzgNuAS4QQuQEHjOAZ4GLhBCHgIsCPwOkY3QiIaU8A/wa2BJ4PB3YBvAY8LAQ4jCG5uWNwPZPgaPAYeBvwA86euHRwOVsotgg/S1w3gVKHIhWtBzCDmo3I2BJ+a1xo2qGqqpkZw9k5KTXGX1BPus3Gx+euSc0bD1LyJ5WxpDzyrh1blWTNku/X5Iy6DRPPLUdXK+1PLfvFJy4OTDUMZRMgA56FeTdDp6OfxvWusi7BQx9S/qULHCdZOXqTZhNgntnNYjbswfE8rNbe3DklJuV28v54UtHefWhvpibDVJ02FTGDIrlyPYQbdjbwe60UVvpDrtUJBTRbslE6jrU1kBsLKJ7ArKsGukNz39FSmlkXNSW0jjRPwP9cNeYw8V/Nxvh9VP6j+1o1UYWTBk9BKorQfPjf3M98nARsqBrBo9m/Go6fRbcSOzULFAEvpMVxuvt/xoq74bSAVA2Bcovg7JzjZ+rfw5abvAFFQv0+QMMegeSrjQCGMUBSqzxEFaI6QmZj8LQFeCc0iW/V5RvGP/ljIuUcq2UUkgpR0gpswOPT6WUpVLK6VLKAYF/6wKSicC8Rse/KaXsH3j8o9H2o1LK8YHt10spPYHtUko5V0rZT0o5XEq5taMvVTRwOdsIEyQ9CL03Q+rvjAyMmgpKPKjdwTYZur8OvdZB/BxaG4xms9nIWT2ar1c5+d3PHTzxm4a0fb8slZxViexancDJfJ1FHzXMR/lipY9B/VQWLalB1v4lYJTViFP3G4FIuBoqWQun7gnNGK0ZelEFsqIW0b/zXVPN8VZ7KNtbTPfxPaBiB7uP1jJmUMuAUVEErz/al2t/doCBPW1MzW5pwV5a4WPj3kqGdo+Mj4nFZkbXdLzuMLQ2EFrGpbYGLFaEakKoKiI1AXk6zAyFroMQQUtjIi0JvD7kmcg7uypxFpy3jcaeaKH0bcMtWhaVoa3Mh2pfvSRQ1ob5uoWBpV8SPf80kz7zryd2mhUqLoDyK8D7EeDByHBWB/6tAfebUDYZKm42XK6DYe0HvZ6EYV9Cvz8bZaS+L8Ggd+GcjyD5GlA7qIOLEiXCSClflVIuOdvXAdHA5ZuDiIHYyyFzMfTeCFk7oPd6IyNjnxw0y9IUCb51AFRWSRITgmVlBONHmThV0HCTm/+hhwfuttErU2Xjlirw/qfhAPd+nnl5A0NnHmHElcfInpXLZXed5Ik/FDdZN2efm3NmHAMg64IjlJT5Acm2nDz69Mlkx47wWlf1bbmoo7IQ4J/dMQAAIABJREFUauTfnoUb80jJTsdkNYO/qmWg1ojsAbEM62vnB1c3DaDWfF3JqO/lcPFDe3j85kyG9o5MOUsIERi0qIXn2KqIdg3oZFUlIq7BdE5kJKGHWy7yB8+2gHHtxgiArsm6xF09FMWkUPavHLQKN/rug4gBcaAGAnlNImtaDiyMNNaBVfR88nmEtg9DJ9ba6+4DPOD7CsovBr0NWwDVbgh34ydB7Fiw9mn1C0qUbysRzraEKM79v0q0HfpbgsvlInuaD7dHp6BQ58sPW2YI3G7Jpu1+Xn7GEThGsmK1j7+8EEt5pWT+B+VMOu8dsFwCwIblz7B0ZQXbP+iNJUahpMzPnkNevvfT0/zukYaOoQWfVnHTzKZOrDsPuLnuR/ksfP1yRo0aFfLvIXWJtu0Y5u9P68Cr0D75a3JJD+hbEApD+zpYvKq41f0VYWhfGzNlZDxLnxvSsKHdoDJ0HE4bbgHS40fYQxQ4C6XNzFZ9mSi1e/02JSMZbduh8C4uiDC3MUr/TPzLt6GMGxRxw0ARo5J473j0l9dT/I/tdP/hRETPXPTUw2i7y6DMh55bZ5O/DUMHWNfplAbMxDD57MR16SVQfiXIMkLPQLqNklHlDeBcCiLymq0oUf7XiGZcviXYbGZyVjnZvyGRzxfGc+vcqvqJwUdyNbKnlZE8qJRemQojhho3n6VfeDl/shm7XXDtzBg+/NSL5guUPaSfguOrSUlUsMQYb5OURBPfGW8nIV5h09cNAt1Fn1Uxe0bDUMZ9R7zMmpvP28+lMX7QYdBDH1YnjxYh7DEo6S2nJ0eC/LWGYy4A5gQuGJuKx6vztyWn6/fZsq+Kr3aEYZxnjty1OhJsuIUMT+fSnuV/XZmosf9KehKyqByphXGeNjIuACTHgyKQxV2jNbFfNABTko3KhbvRKn2oQ/tjuvZ81BkDEQOsqFM2AEOAqcBvMDSBbwC/BS4EBgJ/x/AzCg8hBLd89/z6oMXvl6QOLmXmTcb75J/z3aQOLiV7Wln9Y+8BP1tzfAybUoi3dh94P+bIkSP07duXysrosMQozYhmXEImGrh8a2h4o04aZ6bkjE5xibGtTuNyeFMSG7f5WfK5kVKf/6GH/6z2kjX6DGMuLKe0TGfl6kCrp1bFxefFknfaz8BLjvKDXxXy1WajU2nO5fEs+LQKgI05LpITVAZkNWQHrpp7ild/0Y3JY+yAGfyhlyS0rcdQxnSNKFfz+inacpL0c40Wa5kwAaTGh78bzPIt5fS7YRtDb97OU2/mkZESYrZDsUG3yHV8OJw2XJLwApd2hizWdRM1OSTGjEiIRRaFHqBJzd8k+Gl5GQKlf9d4uoAhQk780blY40wU/83Q9QmrBfOUfsQ8/CKmYb/DcC2vpWkJRwI1GM0MD2JoDFsbYhgch8PB7t0HcLkMHc3yVT4y05p+fN54lYWcVYn1jyGDTIzNNjN1kpkX5pVC7SvMnTuXZ555hvj4+GCnifK/ylnycfm/SjRw+dYgqKv87T/kR9MgOalpWjw9TeHZX9j53csuKqt01m7ycWJHErnbjce8Z2OZ/0Hg27J0E+sws+393vz16TRSE1VufDiff35QwewZcSxeVoWuSxZ8WsWcy5veFC+c5ODviyvQNGncVPXQvuFKrx99Tx7qqKzOvhhBKd6ej7NfEpYEG7K8Em3jIaR2DukpVhb9ejBHFo1hz79G88nzQxjQ0xBFrnp1OGMHN/x+00Y7m5aJkJB6YcSu0e604UJCOC3RbWRcpK4b/i1BhiqG3RYdpBW6xaX0y0A/UtBlxnC28T2J6Z9M9Uf78BXXYAQk5yFETuC/26MGI7iZAIQzjsLPZdPtfLLcCFzmf+hhzjWhebH89md2/v6Om+f+mIPPW86cOXPCOG+UKFGaEw1cviW4XH6ypxmp6hvvquKtP8Whqi3r+bNmxFDrkrz8VzcXTDZjsTTsc9Vl8Sz5/Awej8doz5Z+VFUwbYKdX/0ohVd/3p33v6iiZ7qZrEwzX2128f4XVdxwWdOb4qu/MEZb/OBXhUa3ixraJGJ990mU3ilBpzBHgvw1x+k5LQstZy/a+u0oPTMQ2XMRSgecTAGpq9Dt0oh2fjicVly6HmbGpY2uotpaiLEEzZQoGcnhCXRbaYVucikJseCwIjtqcBcCST86F4tNpei1zRj+VkcxOntCxYuhf7khjGM0Zl8tWPChB7dbsnOPnwljmr4WCz/yNCkVuVxG8JbgVHjsfhtP/KaC116cHsY5o/xPEc24hExUnPstQfP7oWwC6MeabM/qpbJ7TcNcFSEEX68KPmclKVGhuPCk4TMhYzhw3IIia+vLQDn73fTOMMSFcy6P46Fni+jX00yPtKaCQ0WB+X9I55Lvn+TJVwp5+k+hWf9r2451mXeL1HXU4kLGTkkAoaBeeB4ixgz0gG6XQNGykDNDAFIKpBaH6NXG6IUOYHfacGll4U2IbmPIoqxu2k3U5LCMJOSXOUgp2xXTGh4uGoQwnNHoLjqFktk1c4SqUhVm7P4t+lYXZ14vQFUhNfAWW7YMHnoINm6ExESIiYGf/ASuvtp4fu1aePhhqKz0AMt5+OFfc/fdvwjhrJIRQ03k5unM/8DDjAtblhJvvMrCq78PPnX7sxU+uqcq7N17kEHB5yxGiRIlRKIZl28LQoDtfsDewQUUsFwOirN+vWp1Brc9UciQy48x4spj7D3i5an7kwG4/tI49hz2MPvy4LV6S4zCR6/1YckqmPfaX9s9u6yoRZ4oRRnWicnUra1dcgZt5UaSEkEbOQx15OBA0BKg78OQOAmUEB2MMSF9sbhdj4E5sloFh9OGS9ORnjDFuVKvF2PXIaVstUwEIOxWsMUgS0MQigaEuaF0Cyn9MpC5p8MT/oZBcnIyOTt2sOG1bO65S+GhhyAnB3bsgFmzYOpUOHoUtm2DBQvg5EnjuNOn4aab4M9/hv37Ye1alb/85U988sknIZ/7yktjePSpmpDLRGCI4CsqJcsWxfPjX6ygtraTk6ajfDuJZlxCJhq4fJuwXmtMfu5QIs0O9p802TJm2sOsX9CfvZ/0YeeSPnzwp0xSEo21U5NM+HYP4t7ZTTtqcr/sV7+PM14lZ8dW5s6d2+7ZtR3HUYb3RJgjlwSUtW60zTvRtu6mxp7MqjePY+8XxNROqDDoaci8ucFmPRjCDCIGnKMoX3kHSkpWxK61DrvTisuvhZVxaQgmmn1Y1dYEykStt+Aqoepc2mmFbnI9sTZEYhwyr/U2885iyogl7trVCLWhRPbll0aG5d57G/br3Rvuv9/473nz4PbbYfRo4+eUFD/PPVfFs8/+NoQzGq/xHTdZePIRO8OHhPZauFySR56sYd7vHQwfYuWqy7N55plnQjo2yv8SUR+XcIgGLt8mhB2cS0AkAuH4RdjA+S6ofZtuVhPBeR0hz1Jqci1WiL0QzBnt7iqlRN96FDVC3URS09APHEVbuQHi7KgXnseJnHLD5r/V6xXQ63YYvxT6PQy2LIw/DwUQYIqHjOthzLsw7CX8JyVqaisjGjqBw2nD5dNC1rjo5WfQC40WdlmQj15wCr20GL2kCFlRDo7gpYs6DIFuOwM2of1W6Obr9s/sMjM6g3KEpWlwt2dPQ1ASjD17YEyzOYVjxwr27NkTwvlMQCw9MlQeuCd4YNtc47J+s49f/6GWWTNiGDLIBJh46lfPs2DBAg4dCtNDJ0qUKPVENS7fNtR0SFwJFdcbg9+opXWzrNhABmERmEYG36XbE+A9Cq4dxiDFUBAWsAyAtGfb3K2utCHzyw3DtT6haWHaWk8WFKPvPoBwxqFOm4BwGKWz/LW59Jzer/1FVAt0u8x4SAm6FxQzjU3mpJRoxTWoqW0HBR3BCFz8oZeKdB18Aat7XQOzGVwucAXKEW4XutQRSSlByzxKRjK+Dfva1bm01wrdYt2+6fg37UP6/BHNojVQiRAm2hLlzp1raFpiYmDLFuN/Z8tfUQ3JpLa6qhzOnNPkT2naeTFMO8/Qutw+x8rtc1oG+OeOb/QFwjSIuIQxHDlypP0TRvnf41ueJYkk0YzLtxGlOyR8BfH/AvMFgAVEPBAX+NcG6nCIexGSdrUetAAIE/T4C8SeD8IG7TmPCjvYxkHPt0Fp2wvF/+FWvL/6AN/iTSjnpCOUjruayqoa9PXb0fceQskegjohuz5okVJSsKaR8VyoCGEEMs2ccWWVB1SB4gjR6yUMDMt/f8ilIuFMbLgbC4GITwBLI/2FpoHL1XpQEm8HJFS2o7sIoRW6yXVZYxBpicjjhe3v3CFiCQyqrWfoUNi+veHnefNgxQooLm54fmuzsW7btvkZMmRg+6cTFrDeBnT0/7kDbD/q4LFRokRpTDTj8m1FCIiZbDz0QvAfBlllBBZqJqghZB/q14qB9BfBtQXOvAm16wETyMA3fWEGdLCNgaTvg31Si5t9UKxmqPZAtQe9oBzv8VLMP7wYYW6/c6UO6fOj7z+CPJGPMqgvSt+eLYYAVh0vR/dpOPsnh/47t0FXZVvAaIeu9fiRIfq4CFVFxjmhMuC/Y7UhvN6GxIDVhshoXfAshEBJN9qiVWcbpa8QWqGbo/TLNLqL+meGdVxoJGJ8fDVkXC64AH76U3j9dbjvPmNbYx3s3LkwYQJccw1kZ0NpKTz2mIcnn2yq7WoV2wPg+QD007Q+oygYFuPLQcyMMI6J8j9FnQFdlJCIBi7/CyjdIaZ7+/u1hRBgH288/MVQsxq0wM1ScYLjPDCnh3dZSbHoqgJaYOpwajyYQksCSimRJ/LR9x5GdE9BnX4uwhq80yN/TS7pU7IiNj9HK65G7dY1gYvdacPl9kEYPi4iLh5ZWQ42O0IIdHOgPGGxIDJbBnItjq8T6J7TK+jzUsqwMy4AIisNuW430u1FWCOdnVKB24HXqQsihIB//9toh37uOaNF2uGA3//eOCI9Hf71L7jrLqiqMkpHDz44jiuuuC60UyoJhoas/LKA9X8owaUV1P7gfMfIXkaJ0hrRwCVkon9JUcLHlArOazu/jtNu3D1UBWVsH0xXjwspuJBlFWhf7wdAnZiNSGw5ULIx+WtyyagbrBgBjIxL5IW5YGhcat2+0A3o/IcQrvlgPwa4oTwR1LFgmYDo0bvdoAWMwEXbebT1HQKuvKGs1WTdGBOiZyryWAHinMi9/g38iKeeeoPGs4fS040W6NaYOtXQuxjYgb+Ed0q1NySugsrvgX8nRvASLIAJBNGWGRD7cscE7lGiRAlKNHCJ8t9Dahg26xJIgFgL6BJl8kBMV41uEbRITQNFqd8u3R70vYeRhSUoQ/ojemWEFOgUrD3O8PsmROzX6MrAxe604XL52i4VSQmez6HmZfDvB/yIRjdPhc/BokPV1eC4H0x9W18LEMnx4PIia92Gt0tzwmiFbo7SLwN9dy7KOb1DMroLj4HAJKRchxDeMI81A0OBDrjBKd0g4RPwHwDXX8DzHsZ7WgX8RjnW+n2w3g5qkPb7KFGCEc24hExUnBula5E66J+DfzpodtB6gdYbNDtK+nWY7qjFfFV2y6BF19FWbkTfuR+p6+iHj6OtWA9mE+qF56L0zgzpJugqrqGmoIrkEZG7gWjF1V2mcbHYzOi6xFvTyo1YalD5CFTMBX8ORraheZBTa2x3L4IzF4JnZZvnFIpApCW13hYdZit0E9KTkcXl+D5ej//Nz5C14U9mbpv3kO5EpD+cjzIFQyOzpHOnNg0yBO7JxyDpa0hcC0l7IOkAOB6PBi1RonQR0cAlStehfw5aT9DnAKsxtAiewENHsBZ14I8D+3za9NCDuVDrQuaeRFu+DllYgjp1POrwQQhz6B41+WtzSZvUE0WN3Fu9KzMuQgjs9hhqKl0tn5QSKh8A94cYwUl7aCBrofwO8K5tc08lI6n1uUUdzLhoB/LQ3vmPoWEqOGP8GxOOv1AoJKPYtqK7M9E9oVyjBcgENgIRCiyECZRkUHsaOphQhOlRojQhakAXDtG/sChdg/YP0G8AioDqNnasBopBnw3a3wGjtVkeOGrc6HRDAyMmjULEhR8s5K85TsbkrA78Ai0588svKLp7Md4DRdSuOETNZ/u7ZAqyPdZCbWWQzITrXXB/CgQJatrEBeW3gV7S6h5tTYqW/vA8XOpQUhNAVYyAC8BsQphC7xgLnR6osXuQnsfQKmPRa4KItH1W8MVC0W2gbQO6ZiZWlChRup5o4BIl8uifgnyA8G6wLpAPg/4x2tqt9YJQFAWqaqC0vEOXUrA2N3z/ltawmvDnloFHw/XFIar+sbX9YzqA3WGhprqhzVcIwS233AI1LwK1+P2S1CFFzLy5DICnnq/mhddqmqyRNbaYklLjNXzmj9UMnZLHiBEjyM7OZtOmTS3OKbonIMurkV5fywvqQCs0gEiKwzRrckOWJeKdRY2JQ43/DUpsGTX/fhD98CQ41gdy+8CuofDhFfDsg/BGb3j+77D8C6gMYUZTlCj/LaIZl5CJinOjRIzCwkIeeuhBNm5cRGKCbkzmfVQhMRFeeFGy9KOGb9u336Ex83LBddcasXNxsSSjVxV/enkOdw5bBt1TEA6bMQzRbEYkhD/M0FvtoWxfMd3GRcZHxHH5OXg2HEe6/WBRSXhsWqdM81rDHmehtqoh4+JwONi9axOuWh82Kyz/yktmemiZiw1bvSxd7mX78kQs1iRKxDK8vpYdS0JVEakJyIIyRO9uTZ/sQCt0/boJsZiunox/8VegBl4rKTFErBEuG0mJWL2GuONxcPji4Pt4A9qhTZuMKYw33QS9uqLjKUqUMIj6uIRFNOMSJSJIKZk1axZTJzs5ejCebZtNLHhHrZ/M2x7vLZZMnAALFroxTS7ANHoo6qC+KH16ovRIC8s2vnDLSd7q8zxLZ/4/7OlxVJ+sbDE5uSPEDEur95mxTsrCOibyk6wB7PFWaqubWtlfdoGVT5YbWaf5H7qZMyu09tqCQp2UJIHFIgA3KfH7ycgIPj9KZCTX61yklPUPNK3j4lxAOB2oV/bDNGklnMqGk33gZH/I6wenL4Gaf4Ns3bo/ZFasgPXrwRcka9QcTQOPxzB2yTvR+XNHiRLlv0Y0cIkSEb788ktiYmK49+5d1GlaevcW3P/D0N5i8xfq/OE5lZOnNE7ldW56ri3FTvWpSvJX51J1vIx/DXqRnfM2dmpNMLpvLNkZoAoS7j+v0+u1hiPeiqtZV9HsqxQW/NuF2y3Zuc/PhNGhZSsunhZDXr7OwHNL+MFPCvlq1WdB95MVNeDX0Hfn4n3jc/wfbUDm5yHz84znS4vQq6vC/2W0Uii+FcU9E8G7oJ/BEGlLwAe+fVD2BJwaBZWvN+hhwmX/Pti8KbSgpTE+H7zzjjFJO0qUs0m0VBQy0cAlSkTYs2cPo0cNB7YHfX7NWkn2GH/9Y8nShj+svDzJ6UIYP15ww3WChYt2g6zo8LXEZSVijjX0FLpfJ65XAufcOqrD6+HaD0XzIP8pEm5eSbffF6Ko+zp+k20FXdc5veMkvlovx0+VsWHeakpzTgEwYoggN09j/oduZkxvqhVprStcCIh1KGz7Iom/Ph9ParLgxltf45///GeT/aSm43v3S/Rdx8DthVoPwulommXxeMAfZlDgP2FkVNxrMTrJWmvxrgFZDZV/hDMPGS30YfDMM88w9PwLGPHyK2S//md+tWoVs+Y3uND9bs0a+r/8Sv3PHx84wJXvzgcg66U/MvyPfyR7ZDbZ2dn86EfReUJRonzTiWpcokQQN8YQOj9z79dYu04SEwPP/15hymTRQuNSx4JFkhuuM+6+s29Q+P7dkocfLQXadsRtDSEEaRN6cGLZYcxxFq7+8vvExIfpXCp9UPE5lLwB3pOBuUw6CqCoAnL/DeZUSP4eJFwJSvBxA+GwbN5qXvvReyhCIIAVP1zIXZcHBmAKB1deYuHRp6tY9UEipWcagqbkRIWCoqY3+6oaSYLTeE1VVQQmGcczfPRM3lrwPrfffnv9vkJVUKePQluRY2wwqSg9U8ER2zADSVERzoTQfxmtHIquD3QyhRiISBe4PoPyBEh8KqRDNmzYwNIPP2T7ffdikZKSmlpqfF5e2/L3hn3yThJvsVBUXUO3WAfr8/I4r1fP+udX3nobKd1S4ZFHoq3MUc4e3/IsSSSJ/pVGiQhDhw5l+45d9T/P+5PKii9UilvvwK1n/gKdf/4/SVZ/P1deo/H1To1Dh9qwoA+BxHMMgekVS28lvk9SeAdr1XDsDsh/GjyHQbppevOVxk3WewJOPwdHZ4O/FfO2MJh66wSsFhOalPilJEZV+M5PphtPmgZzxxw7Tz4cy/BzmpaJpk4ys2SZh6pq4xo/+MTNyCEmVFVw4LCfQ0cDBnVCJWd3Fb17txSjqgN7oPz/9u48PKryeuD49713JrNkI8mEAAm7iIQaI6CACCIgqAjITlBZKgJqlU3b6k8Upf4qKNiita1LBVSCLCrWVqwLW4tFSQuKIAgYQAhLQgjZM8vtHzckGbLNxECIz/k8z/1jmDt3GcfMmfOe97zJ7cw0jdeHah6NcjrLnlcxLlSAX+phYWGQ8wx4zaBl6ep8fjG3dAbU4hzirzlG8s3HSeyXQeo6c4imba9j7D3gNt/X/FQo+ZqZM2eycOHCGs+VkZGBS6lzDfZxhTpp3aQJkTYb+7PM/yZHc3MZmdiJrUfMYa+tR37gupYt/Q/kdsPBH/eZE6LupI9LMCRwEfWiX79+FBV5+eOfyhujFQTQI23vXoP8Ajh6yEL6fnN75FcWVq78NPCTGyVQ+C5kT4OsUZA1lu6z32fIu61o0avqhQOr5SuC7ydC0Tfml2it5y6E4u/hYAp4f9z02tBIBxPmD8FSmnHp3SGOiN6l7fqdU0mID2PGPc5Kr0tKtPKLnzu4fmg2yf2z+NPyQl5dbM7Cyss3mPjgWRJ7Z5LU9xi7955l3rx5VZ5f79EJFRsJmkKF2lG6xZyObrejQoLMKBW8A1Q9tDRrShg71jdj3Wsupj2SjdttMG6Ik5Xvl35gjBJ8Oa+wZs0axo4dW+NpBg4cyJHjx7n890u474O/sSk9HYDrWrZk65Ej7M3MpEN0ND0SEth65Ager4+vTpzgmhblM81uXLaM5CUvkHzLrTz//PPB3acQ4qKToSJRL5RSvPfeX5k1sxMLF+UQ64LQUMWC/685Nk5928fwYf5FGiOHt2LcneuY+/hvaz6pNwvyX4KCNzCzIOUFliE6tO7+GZx8CUKnQuhkcw2Z2hydCyXppUNDgfKA+xQcnglt/xLE6yq7dXY/Vs7/kJzcIm5/dBBKKfLy8sx6GuUCw5wBYw79lNe6TJvgZNqEyvfX9SorWz+IBhwQ9jCE3lftuZVS6Lc7UXmvQuHTQB6qiRPUFeC9D7Tu1RfU+PEQyG+iDm2tOB2K7BwfKcOcjL0/iydmRQJeNm9YS5s2rarMDlUUFhZG2pzZbNmxkw3p3zN29RqeGTCAXq3MwMVr+OjZMoFr4+N5atNm/ns8g44xMdgrzFLbMHEirlAn9L0RbrghgPsT4gL4iWdJ6pMELqLeNG/enJWpL4LvAc7vltv3vO+DpX8x611GVVpkOoyk5Lns3j2p5pN59kPWSPDlUHPRZz7kLoLCtRC9GvSYag954odvmDX9Nf79VR5RETohVsUvJ7uIitAZ9uBh2iWEUFjs47Y+4Tz3sNkuPq/Ay5xnT/DJ53nYbXuIabaLZxe9QPfudVvUUdc1pi4ewcdPv0/rEZ1KAxZlbqEPQe6vCL5zLmZbekdK9c973gP3fDTjMDiKygpkFYCx21zUUTUFy6/BckeNAUxhYTHJg8qHXU6f8TH0Jkel/f7zdQkd2lho6tJp6tLRFOzcXcJViSGs/GsBKSOSAro13Wajb9s29G3bhiubxrFs506eGdCfF7Z9gdfwcU+XroTbbBR5PGxMT/erbyk/iA4hF7JBnhCivkjgIuqXGgU88CMOYIAaU/Munh8gcwgYZ839a1VUGugMBddHoFVeINHsQ3MbEweHsWKh2efk0LES3t+QS1SETu8uTj54qTWFRT6uHn2A4f0j6NXFyZTHj9E2PoTv/t4BTbNw8GxP9mQGUNhT6Z5K4GAa7FjPDb4T3PCYDqm/NJ9r2wWSbgLXaPB8CYVrCC54cUCTt0CLqvyUYYD7/8DzCtWvf2QA+WB8D+5Z4NsCIS+BqroJnsOusWN9+TpAS1fns/2r8uDy+VfzeCU1n4OHPaxfHlv27ynDzOGizpdbWfdRLk892anWO9u7dy+a202H0sc7jh+ndWQkibGxHMvNZcuhw7w0eDAAyc3i+NP2NBbeNKDygXQdoqp4f4S4GKQBXVAkcBH1S9lBLQZjJoEtBFiRE9RzNQ/pGAacHm9Onw0oaDnHA96jcGYGRL9W6dnPPv2UEHWa6WPKf423bhHCA3fEsPGL8iEoh10juaOdoyfdHDhcwravC3lrQQKapgAv7SL/RbvuCwK/LMOArz6GtA9KL7O0EZu3worPB7fDoZ0QHgP9Z4LDZq5bVOv7awUVAk3ehJBrq97F/VQtQcv5CsD7DpRYIOTFAIeO/M2aEsZD0yJ458MCJsw6zYEtzbHbFSlDQxl450lu6GEjqVMITV21D+3l5eXxwLLlnDlyBItSXBYdzctDhqCUontCAjlFRVh1M8DqmdCSl9P+U6kw98Zly9B1Hd5eRVJSEsuXLw/6noT40SRwCZgELqL+6ZPBewSMRQT+hegENQP0KdXukZWVRf9+PcF7iOMnPeg6xEZrpP/gpUWczu5N5b/e5z2XS1io4qF7w5g08wybPi8hMlxh8AaLn7+Z/gNH+x37m13/pUun2ocKsnO8fHe4hD7dnHzxdSHJHe3oesUvbw08JyEkgKJgw4Atb8H+bWbGpab9PCWQnQHrFsCtM6DJAMh/AdzbMWc8VSiEVaWLUdrHm/U9ehVDIwDef4LMth2NAAALo0lEQVTnRYIPMAvAuwq8g8AytIrnAwtmRtziZNmafJatyWfanWG0b2MhJkrn18/kMPPuGNBqnw7ftWtXtm7fDkt+D2f817P62x3j/R5PujqZSVcn+/1b+qyZZralZ0/oX0UmRghxyZFZReLC0B8HtQhwADWt6hxq7qMWgv5UjYeMiYlhx4ae7PjYxfS7nMy6J5Qdn8Sy42MXWi2f5GfnhrPjk1h+92Q00++9t/IORgkV/3e4/zfHuGrEfq4ZewCALf8pIGn4fpr13cttfcJp5qqmc63SwBtgF9a0v9YetJzPXQx/XwKFnSB6Lbi2QOgssI8B223gmAjhv4XYXRAxv8qgRSnFnDlzwL0IKOS537mZ97T/NVzVvZCUif5t+CdNLcbpKiA31wAKwP0sM2bMQClFZsXhMaVj9vOp3eMzIln8ai6+0lW2U4Y5+faAm+GDHGDvEdh7ohT06QPWOq59pGlwzTV1e60Q9UWmQwdMMi7iwtGngDEOfCvAeA7IoPwLzQ3EgXoItPGgwms/nu8MFG8iuCEifz27Ko4eq9xzpXPnJNauyAfMrM0fHmtBZraHbmPNItNzNS770ou5fsL3DB8QTuf2dnbuK8LnM0qHigB8oNU+xKHrOlfGR2EYBrpSvJjSi+vaNyM9M5dO81bRMa682dvsAVcyoefltHl0BdsfHYErTMGWN2HIHNBbQdjsoN4Dm83GO++s5pEZZ3G5Kr+Xe7714fPB5n/5yM83CA0tz6Bc1k6x7gMvd6ZY8Hl3s2HDSeLj/RexzDtzCDJ6lz2eNDqUSaPN4HXebP8sStekEPZubF72eNaUcGZNCQdbF7AEsfhh8tWQng579gTX9t9ihZEjIaJuzQ6FEBefZFzEhaXCQJ8K+l7Qd4P+aem2C/R9oE8LLGgB8GaYNRs/wvoNxdx+s93sjFtBvwGDKSqGP64sD2oKiip3fL28jY1HprhY8Fom7VuF0K2zgyf+cLJsEcfv0vNY9/dttV6Hw2Zlx+Nj2Dl3FL8dfi2PvPtl2XPtYyPYMXdk2Tah5+XnvdqAkwchtw5FwIDFYmHq3Uk8/2LVCxuuWOXhrhQLA/trvP83/5WkU0ZbeHutWX+zcXMRvXo4sZy/crSlWeDZkqooJ4RXkRWr8TUKhg2DxMTAMi9KmfsNvx06XlG36xSi3kgDumBI4CIuDqVAtQSVXLq1Cr6w08inqvqJmtbqOefh+bm063GSOx84w6MPNikt7q2wr6bx3vIZbNpeSNtB+7h23EEmPnqUBbPiKh13+phoNqcV8P0PJbz6ZAuOZ3q47JbvuHL4fu55KpcWCW1rvg+PG3w+8JlBwdkiN1HOIAMyw4BdG4J7TQX3T0vgrbeLycmp/Afu7bVexo7SSRltIXW1f+DS4TLFqUzIzjZIXV3MuNHVZCoiHwusb04lIWC9Aux9g3+ppsOw280AJi4OLJbKHw6LxaxpuaIT3H03JHauwzUKIRqSDBWJxkOFUdUwUUyURnaOf3bk9BkfbVuV//J+dm44I261s+S1AibOyCRtZ+Up0c0Tp7Ny0XowKmci+l5bXqfjsGsc/axj2eNXniwdKlEOaPs6OH5W832cOEBhiYfk+WspcnvIyCngs9m3lT194NRZkuevLXv8wrjr6N2huf8xfF44sB16+hcZByoiopgJ43WW/NGDo8IyTl+meYl1KVq30kiIN/j5vT6ysw2iosoDgBFDdVau8bDtSx9//kPl/iwAhHQE18uQeU9gHYgBsIElHmKXVzvVulZKQeefmduJ45CWBqdPQ4kbnA5ISIAuXcBZU92VEA3gJ54lqU8SuIjGQ0+oNMQD5grIzZvqfLqlmP69bZzO9rF+YzEzpvh/OWmaYsYUJ8tWl/DRPz5j0KBB/gcKaQnOrpD/JdW1q6/h4syZRLUFLQBFeThCLOyYa3bf+/zACSa8vpFdT4wCyoeKauWuQyO6c1QMM++30qVXEZPvKv8zkLrKy7f7fLTpZB77bK7B2nVepkwq32fcaJ0uvYqYON6CptWwDpS9D8SugFOTAI9fZ2N/ujkEGNIFXK9U2WenTuKawa2D6+dYQlxI0sclKDJUJBoPLQzst1DVx3b5kkh+8/s8kgecot/oLJ6YHU77NpXjcqUcPPbrO6pfvC/hWbDEAMH84tdAj4DWLwW2u+H/B6pn+zgy84o4lVsUxDkrHycoWleio8MZM0LntWVmzYrPZ7D6XS9fbbOTvsdB+h4H6962kbrK4/fSVi01nn7Cyn1Tw0Gvpj/MObauEJ8G0QvA2rm0z094+YYNnLdD03egaWr9BS1CiJ8sybiIxiVsOhR9xLyH/At6Ey+3smFN1e38l/6uSYVHBiNTFjLyjmoyBZZIaLcC0ieD+3iVw0Z+VAjoTaDNUrBWroepkt0/E/Tt8TN4fT5iwmwUnPZU86IqWO2171MdfTgwkzkPWnnxz+Y5N//TR3wLRXyL8sCwz/Uauyf7yMjwD5Km3W0FFFgmALUsTKhCwDnU3DyHwXvcXHFbRYK1LWgRdb8PIX4qJOMSMAlcRONiTTKLN927CH44xw6OYVDT8AaAtSm0WwWn34CsN83hKd95wxyaE9AgehzETAJLk6qOVLWm7cpqXAAMDJZNvhG9tBnN+TUuP+/VkQf7mUNQSU+tQSstOB1z0/Usvivw056Tl1damGyZRFzcyxRkltev/Hujf6ZJ1xUZB80i26UvV1whWgN9CKgo0ktXZA6IpZW5CSFEHSmjhnRzt27djO3bt1/EyxEiAN4syBwAvizMlYgDYQPLFeB6D5St9t3PMbyQtwXOfAjeTHPxQUsMRAyA8P6g1bHp2ablsO/zssUMg6ZbYfijEN2ibq8H8B2Bom6cvyBmYBxg3wxaYt3PL8QlSimVZhhGt4t1vm7JVmP7J0H8+AmAis28qPdwMUnGRTQ+egy4PoSsUWZvl9oWHFROsF4NUUuDC1rAnN0S3tfc6tOV/WH/F+CtY+DSpPmPC1oAtJZgWw3FIwh60caQ1yVoEaLe/PR7r9QnKc4VjZPeDGL/ARFzQUuoomeIDjjAkgiRCyE6FbRLaApsdDy07waWOjTUs1ih9/ja9wuE3gds64BwoLaaGRvgBNubYBlSP+cXQoggScZFNF7KCaGTwDkRSrZB8QbwnQR0M7Cx3wrWSzgr0OcuKMiB4/sDX69It0K/KdC0liZ3wdB7geNrcC8tXXSxCLN+qASwYgYsOlimgeUe0JrXcDAhRJ1IxiVgEriIxk8psPUwt8ZE0+HmB+BfqbBvq9lbz1dNzY7VBpoFBk6H5ucvAVAPVCyEPAzW2eD7FHzfAWeBMFDtQB8Iqo71PEIIUY8kcBGiIWka9L4DugyG3Zvhmw1mV9xzrep9HohOgORB0PoqM9i5kJRuBin6wAt7HiFEOWlAFxQJXIS4FIQ2gWuGQtfBkJsFJQVmhsURAU7pcyLET54ELgGTwEWIS4mmQ2TThr4KIYS4ZEngIoQQQjQ0ybgETKZDCyGEEKLRkIyLEEII0aCkAV0wJOMihBBCiEZDMi5CCCFEQ5Lp0EGRwEUIIYRoaBK4BEyGioQQQgjRaEjGRQghhGhoknEJmGRchBBCCNFoSMZFCCGEaGiScQmYBC5CCCFEg5I+LsGQoSIhhBBCNBqScRFCCCEakvRxCYpkXIQQQgjRaEjGRQghhGhoknEJmAQuQgghREOTwCVgMlQkhBBCiEZDMi5CCCFEQ5OMS8Ak4yKEEEKIRkMyLkIIIUSDkgZ0wZCMixBCCCEaDcm4CCGEEA1JGtAFRQIXIYQQoqFJ4BIwGSoSQgghRKMhGRchhBCioUnGJWCScRFCCCFEoyEZFyGEEKKhScYlYMowqn+zlFKngEMX73KEEEKIBtfaMIzYi3UypdR6wFXPh800DOPmej7mJaHGwEUIIYQQ4lIiNS5CCCGEaDQkcBFCCCFEoyGBixBCCCEaDQlchBBCCNFoSOAihBBCiEbjf6vghWtHvNkOAAAAAElFTkSuQmCC\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"# Draw directed graph and color nodes by GDP per capita\n",
"plt.figure(figsize = (10,8))\n",
"\n",
"pos = nx.spring_layout(graph)\n",
"nodes = nx.draw_networkx_nodes(graph, pos,\n",
" node_color=col, cmap=plt.cm.spring_r)\n",
"edges = nx.draw_networkx_edges(graph, pos,\n",
" edge_color=edge_col, \n",
" edge_cmap=plt.cm.get_cmap('RdPu'))\n",
"thous_fmt = FuncFormatter(lambda x, p: format(int(x), ','))\n",
"nx.draw_networkx_labels(graph, pos, font_size=10)\n",
"clb = plt.colorbar(nodes, format=thous_fmt)\n",
"clb.ax.set_title('GDP per capita');"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"source": [
"Finally, the figure below visualizes the directed graph on a map."
]
},
{
"cell_type": "code",
"execution_count": 114,
"metadata": {
"slideshow": {
"slide_type": "slide"
},
"tags": [
"hide-input"
]
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAABAIAAAHBCAYAAADzZBkIAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4yLjEsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy+j8jraAAAgAElEQVR4nOy9W3ArW3rf9+97N+53AuD9svfm2fvMeGY045F1iRwrsmfKsaTITuJUIr+kVJWqVF6cPDoveUzlIa5yLlVREqfykEgVV5yLFSexLI1GtqOjM9LM6Mw++8Y7SAIg7g2g79154Fl9ABIEARAgQHL9qlCbmwC7Fwn06rX+3/f9P8bzPFAoFAqFQqFQKBQKhUJ5GrDzHgCFQqFQKBQKhUKhUCiU+4MKARQKhUKhUCgUCoVCoTwhqBBAoVAoFAqFQqFQKBTKE4IKARQKhUKhUCgUCoVCoTwhqBBAoVAoFAqFQqFQKBTKE4IKARQKhUKhUCgUCoVCoTwh+GFPfuc73/Eqlcp9jYUyZXRdx7zaQ0qSBMMw5nLu+4DjOAiCAIZh+r5vmiYcx5nTqCiU67As6//L8/y1zyxltnieB8/z4LouXNcFz/P+e3L1dZZlDZyzyTHmiSAI4PmhS4ZHh+u6t97HOI4DwzD+g2VZeo1R+jAM496uYYZhwPP8k7tWKRTKzfzgBz/4vz3P+86g54bOFJVKBZ9++ulsRkWZOaqq4vj4eG4LyFAohHa7PZdzz4poNIpcLnfjTdYwDDQaDRiGAcMwYNs2FQYoc4FhGCwvLyMWi817KE8CXddRrVZhGAYsy4Jt2zfOvYFAAIqi+P93XReNRmPum/1hrK+vIxwOz3sYc0HXdTQaDXS7XbAsC1mWEQgEEAgE6IaLMhau66LT6eDo6Gim52EYBjs7O5AkaabnoVAoiw/DMKmbnqN3sHvC8zxomgZBEMBx3MCI0LQJh8PY3d3F8fExOp3OzM93lYcoArAsC5ZlwXGcH/XneR6iKCIej9/6vkmShKWlJf//ruvCsix0Oh202220Wq1Z/woUCsLhMFZXV+9lnqFcUqvVUK/XR3ptt9tFt9u98zkZhoEoimAYBrqu3/l4vbAsi0gkgkwmA1EUp3rsh4Ysy8hms/MeBuURwLIswuEwdnZ2sLe3NzPxz/M8cBzn/991XWiaBk3T/HlDlmUIgjCT81MolIcBFQLuiXK5jIuLi2vfJ6mEPM9DkiRIkgRFUaYWaeA4DpubmwCATqeDSqXSt2C0LOvO5xiVQCAATdPmHvUiC2ey6WdZFoFAAMlkcqKNk23b/g1W13WYpgnLsmgmAOXeYVkWm5ubfdFmyv2Qz+eh6/pUNvij4nnetdR1ci8RRREcx8F1XTiO4z8A+GI0wzD+10T8JBFvWZbv7fegUJ4asizj2bNnKBQK0HUdrutO9fhkXWnbNg4PD4cKhaIoIhAIIBqNIhgMUgGZQnlCUCFgAN1uF9VqFZ1Ox59MSSpgKBSaaIN+U3qW53n+Am1QLSKp91IUBSsrK9cmaNu28e7dO/+15EEWg/F4HMFgEAAQDAb9rwmfffbZ2L/LqJCxktq4+1wg30QqlRo7skOU9G6366f8k43+vEUNCoUgyzK2trboIm6ObG1tYX9/f65znW3bsG0bnU4HsVgMKysrcxsLhUK5GVEUsbW1BeByndFqtdBsNqFp2p3XF4FAYOTyUNM0YZomGo0GgMu1m6IoiEajSCQSE4+BQqEsPlQI6KHT6eDg4ODa903TRLfbRa1WA3C54X716tVYx47FYuA4DmdnZ2NF4YmBlGVZ+Pzzz5HL5fomZoZhBirJlmVB0zR/YpdlGalU6lq98LRN/RiG8W8601a4p0GlUvFvcFexbRulUqlvo7+IvwOFchVZlrGzszPvYVBwKQYUi0VUq9V7FQpJKRMRrYPBIHieR6fTgWEYME0TLMsilUpRsYhCWTBYlkUsFru2RnNdF6ZpQtd1/zoma8LejNLerB6O46Bp2sQ+BMTHgIiJdL6gUB4vVAjoYVjqFMdxkCQJgUBgYsMkMoFPiud5ODs7Q6fTwerqqj8uQRBuPa6u6zg/P792k3n27BlM00SxWISqqhMvXCORCARBQLVanejn7wtSfjGIk5OTuXgpUCh3pbcWlDJ/stksstksGo0GSqXSzEqwVldX/Q0/YW9vzxeAB9FqtbC2tvbk6/4plIfAuKU6hmFgf39/KqWJmUyGigAUyiPnyQsBruuiXC6jVqsNjf46juMbPImieC3FfhSSySSSyeSNz9u2jVarhXa7DU3TbnSdbjabkGUZ6XQawOVm/uDgAJqmDT1/IBDA2dmZ39pIkiTEYjGIooi1tTUAl38P27Z9xZmkmZKbylXVmeM4BINBdDodnJ6e+sfuLVMgbbPmAcuyEAQB0Wj01kiYaZr3ODIKZXrQzJXFhET4dF3H2dnZVEsGVlZWBmY2xWKxofcCXdevlZPF43HkcrmpjY1Codw/mqZhb29v6Gt621ySbAKyluN5HoIgQBCEoUETCoXyeHiQQoDruqjX6zBN89rG07KsPrM2SZL8GqxBnJ2dDY2eXEUQhJm14+J5HolEoi/1n6SFXd2Y9woRLMtie3sbjuOgVquh1Wr5KnJvhF5V1WvnPDs7gyiKeP78uX8sURQnihbZtu1/Pa/aeYZhkEqlEAqFoCjKWGr2ixcvoOs6Wq0Wut0udF3v+50olEXFMAzouk4N3hYU4t9AUm5VVUWj0ZhIwCEb90H3Idu2cX5+PvKxiH8LFUEplIePIAhIpVJ+pih5kNKBXoj3UbvdRrfb9YNPwOU6sDcDNhAI0MwACuWRwgzbsH3zm9/0Pv3003sczs3Yto1KpYJmszlWmiXP89jd3R36Gk3T0Gw20W63YZqmvzjrdfNXFAXBYHDszeU8IbWhlUrFX/CRB8HzPCSTyTu3RnJdd6SshFkiSRI2Nzen3tfZcZy+LA1Sp0e7AlAWjUAggLW1NdrbfMF5//792N4skUgE+Xz+1vdWVdUbO5iQ+1kwGEQ4HIYkSQ/mfkahUO5Gs9n0S5XGDdasr69PXBZLoVDmC8MwP/A875uDnlvo1aJlWbi4uECz2Zx40zVKapOiKH3ttlzXffCLo9PT01t7WguCgEgkMpEr7NnZGVRVXQhDPdIGy7IsvHv3Duvr6xOVbtxEqVRCvV6nHQIoC0+328WbN2+Qz+ep2/MCs76+jmq1ilarNZKwzTDMwK4xgwiHw3TBTpkKpFTQNE2/ZJBkJXqeh0wmQ7OQHgDlchmVSuVOa7WTkxO/nGB1dZW2qKVQHgkLKQR0Oh2cn58PNe8blUkWwzctttrtNkqlUl/Um+M4hMPhmbdo6m0t4zgOOI7z67w6nQ5kWcbq6ipYloWu67eKAMCl0FKtVm81+AsEAlhaWurbXE+a1joLro6j2+1OVQiIRCJ+dgWFsiiQNqGCIPhzASmRoovzxUYUReRyOeRyOX9ur9fr6Ha7AwXHXC734MVpyuJjWRYajQba7TZ0Xb81ANNqtRAKhbC2tkY/nwtKqVTCxcXFnY/T6/V0fHyMdDqNRqMBXdf75ixSrnsV0pIwHA4jGo1Sg1sKZUFYqNKAWq2Gcrl857pshmF8c7hWq4VGo+HXQDIM45uiiKIISZIgyzIURRlaF39wcDDUUX5aEbhCoQDLsvqi3IZhjLTpZhgGy8vLiMViqNVqaDQa0DRtapHseDyO5eVlAMDR0dFAz4F5QQwcI5HIzKJhruuiUqmgVqtR7wDKXOF5HtFoFMlkkrq/PzJs2/az0siDQhkX13WhqqofzXccx3+4ruv3qXdd91rJ4LjQtPH7h/iNNBoNdLvdmXUmmRUMw/jrtmg0OtXgDYVC6WdYacDCCAE/+clPxr4RcRwHRVEQiUQQiUT6aicvLi5QKpXGHgfLsgiHw0in031RtXa7jaOjo6FjXF1dhSAIUFUVuq77iziO45BKpUaq2/3ss8/GHnMvDMPg1atXfd+zLAudTqevAwB5kJr3UZBlGYlEApFIBCzL+sciSjF5kPP0phEC6Pt79LrVkn9ZlvXNHsmDLIp7hRBihEiU5XlshEzTRKVSQavVoqIAZa6wLIsXL17QCAuF8kSxbRvtdtv3h5ikBnwSAoEAlpeXqbv8hJDAwlUPJ/LekX95nkcoFEIgEECr1YKmaY/Oo4jjOCwtLdGStjEwTRPVahWGYcAwjIGlur0ZGuRrjuMgiqIfBA0GgxAE4V7HTrlfHoQQoKoqms3mNSM2kvJKNoySJCESiSAYDA6MlDiOg4ODg6mUFVwVBVzXxcnJyUSR8FAohI2NjVtfN4kgcpWPP/74xudM00S73e4TTlzXRbFYHKsOnmEYRCIRxGKxvo38sAiWaZq+Oy0xZex99N4Ar7a4EQQB6XR6Ic2tSGpvu932Mzl6/xa9j97fq7fFYu/vNChy4zgONE3zF3kUSi/ZbBapVGrew6BQKDOGtBkmAYdZ3w+IAz3ZOAQCAeoifwuWZflBgqv38t5sDBpEuE40GsXq6uq8h7Hw2LaNt2/fTlXwI+WGJFOaXOvUfPjh8yDMAqdhcKSqKo6Pj6d2Ybiui2aziWazeedjDSsr6IXjuDvdHK6qeqqq4uLiwlcLCWdnZ5AkCUtLS74btSzLODs7G+k8nueN9LchCuRd3xNN0/y2iGS8i7IQYVnW7xc+DUaZdA3DQLPZhKqqI5eOUB4vzWaTCgEUyiPEMAzU63W0220YhjGTSD9pG9y7AXhIHZLmjW3bqNfraLVa12rmKeMxq/bcj439/f2pf848z/Nblbfbbf/7u7u74Hkerutib2/PL18mAVriVUTmEDp3PCwWRgi4K7Zt4+joaN7DuJFR052eP39+7QI6Pj5Gq9Ua6efX19f9r28ziTEMA8fHxwiHw1hfX0csFhtZCBiVaU9Uruui0WjAsixsbm5O9dgPCUmSkMlkkMlkAFz+XV6/fj3nUVHmBe0DT6E8Hmq1GiqVylSva+KP1LvZDwaDNNo3BqqqolQq9aXwkw4KlLtDSj4pw+l2u/d2z08kEv4cUSwW/VJiUgZ8W2kxKQPmeR7pdJq+vwvIo7kD8DyPzc1NdLvdvv7Jnuf5Uemradiu6878YmIYBmtrayN/+AepaKFQCO12+9aobyKR8H0NNE0b2SlWVVVYlgVBELC0tDSRt8J9M2qGxVOBZVkEAgF0u915D4Vyj5C2cvTmSqE8HprN5lTWJsTXJxaL0QjdHTBNE0dHR7Rz0JQhHW4ikQji8TgVpUYkEAhge3sb5XIZnU5nZhmh6XQaS0tL/v+TySQcxxnLnJLss4hnGGXxmJtHAKkLJ4Z1g1xtOY7zVetZ3MTev38/1sROOg0oigKO4/oevcZ3s7zh2rYNTdP8uvlh51NVFaqqotPpwDTNG1XrlZWVvnSsUqnkK46DzEfmjSRJyGazdPNzA6qqolqt9qV2UR43yWQSuVxu3sOgUCh3pNlsolwuT7TpZBgGwWAQyWSS3h+nRKFQQKPRmPcwHgWCICAQCCAcDvum05S7o+s6yuXytYAh2SdIkgRBEK6ZUF79t/frcDiMeDw+9LyWZaHZbKLdbvf5fpFsGTIfpdNp2hViziyMWeDZ2RlqtdrEP99rsAagz2yNPBRFQSqVGslJvtlsolAo9H2PHIds+IPB4KNKnyPqXK1W87MAeg3+SMYEcRPtzZ4wDAOapvmGjr3iDWlDRI5xlasmeURAIXVGvV0DSMcBx3H8VEbyXiyiWeCiYts23r9//+jchSmDSSQSyOfz8x4GhUIZE13XUSqV0G63J+qeFA6HkUql+jodUabDuAEjypcIgoBoNIpEIkHb3N4TpmnOPCBJeXgsjBBgmiYODw/vpbaFYRiEQiHkcrlHMQE5joOLiwuwLItQKARZlq9d6KRmB8C135l0PJgkjYhs1kVRxMrKylhtRhzHga7rMAwDoVBopPeCZIpcPQ8RMTzP6+tUQLkZ13Xx4cMHWkP+CBFFEalUyr8OZpU5RaFQpo9t2yiXy2g0GhNl3UmShPX19UexvpklV4MYlmX5wYqr3XsYhoHneX3ZqWQNQ7kbJDotyzIkSfLLeF3Xxc7OzsDPMVnzkTrzWd3fyPX3mO+fuq6j2+36Gdi2bfulQ48l0Em5mYURAgiVSgXFYnHqx70JnueRyWTutT/pxcUFGo2GHy0nf+dehXSUi6/T6aBYLELTtGvPDXPk7zWSMwwDe3t7d07xZxgGOzs713oGm6bpdyYgkfxB57pab+S6LjqdDjqdjn+TJn8v4LK+cWNjAzzPo9FoXMveGAQRStLpNBRFudPv+1hwXRfHx8e0VOAR8vLly0e9eKFQHivlchnlcnmin83lckgmk1Me0ePiw4cPdAP/QOA4DisrKygWi7631yiZMVczTWOxWN8ac1Sutu0mWbIkW3VQlispweE4buzz3Reu66JaraJSqQzNDGVZFoqiIJlMIhKJ3OMIKffFQrUP7Ha7925GZ9s2zs7OUCqVIIqiX6M0rV64RHFut9vQdR2CIKBSqQx8rWEYKJfLqNVq2N3dHXrc22rThk2UjUbDFwKOjo7uLAJEIhGsrKz0/b1qtRouLi5GMg1JJBL+BD1qiYiu63jz5o1vUDIKruui1Wqh1WrR+qQvYFkWGxsbdy7NoSwOxISUigAUysPDdV1/AzPOvblXHKcMh2bBPRwcx5mo6xcRDMg1dHFxgVgs5pe8jnOcXkit+zBzu06ng3K5DJ7nEYvFkEqlFu66fPv27Uhr596g3Pb2Ng2iPTHu9VNbr9dxenp6n6fsw3EcaJoGTdNQrVaRz+cRi8WgaZqfpmTbNhKJBKLR6LWfJ3V8gUAAyWTSn2hGvdgILMve2PqO1N0LgoB0Oj1Rm5BkMnkt8j4poihifX39WhbAwcHByM79HMchk8nAdV0cHR2N7fhfrVZ934Zx/hae56HdbqPdblMzNQD5fB6SJOH8/HzeQ6GMSCQSgSAI4DgOsixDlmWaCkyhPFAsy8L5+fnI7YAJDMMgn8/fat41L2zbRqVSQavV6usxLgiC319cFEV//rppk2aaJgzDAM/zd96McBy3cEbHlNnz/v37G5+7yWPsLpDPfqVS8VtxLwrr6+toNpswDKPPxK/X1A/o9/Wi18zT495KA5rNJk5OTqZyrPsiFAphaWkJtm3j/Pz82iZUlmWsr6+jUqmgWq2OdMxgMIj19fUbb4Rv374duS3HMEg7uUwm47uJjgq5gadSqb5uAoRJIssMw4Dn+Tv/bolEAoZhjC0mBIPBG8WXp4aqqjg+Pqa9jx8I9LNLoTx8XNfF69evx/65cDiM1dXVhc3+cV0Xn3/++Vj3k0gkgrW1tWvff/36tb8RuWv5w97e3sCSSgplluTz+XstQx6E67pQVRWVSmXoNUCykohw19v9rFfEIx3KKA+XuZcGqKo6ExGA53kwDDOVjfMgSDT5JnRdx4cPH/DixQtfCb+N21zvp3Wzd10X7XYbhmHg2bNnePPmzVClT5IkbGxs3GoEWKvVJkov9zxvKu8TwzDY3NyEruuo1+uwLAumad5aC2iaJgqFAuLx+JMuEwAuF5YrKysPTph7qowrelEolIcPz/NYX19f+DTdg4ODsUXlVqsF13WvrXcURfHnu/Pzc/A835ed6bouNE3zTY+vRjc9z4Msy377RCoEUO6bs7MzxGKxuQl3pmni3bt3I7221xhznPV5b/cvYgLZKyCQVuu0y9fDYOZCgKqqE9X+DENRFKysrODw8HBmIsCoOI6Dg4MDbG5ujnTx1Wo1JJPJa6n2hO3tbTSbTdRqtancxMiFuL6+joODg4Gv6TUWvI1JzY2mRbVaHTn7ohfLstBoNNBoNHzvgEwmg0AgMINRLjalUgkXFxfzHgZlCESht23bX+zSGyqF8rCwLAvHx8d+au443OYhtAjcFnEcxtU5rdPpXKvJbrVa8DwPzWYTmqYNrdkmqKqKi4sL3+iNts+l3CeRSGSu92rSXWGWKf7k2OTauikQR7yMwuHwzMZCuTszFwJGcXofFZ7nsbq6CkmS8O7du4WpZdE0DXt7eyO//vDwEC9evBj4HMuyiMfjfi1gu91GtVqdqO0fcFneAMBX7q4eg+M4WJYF27ZHSv0JBoNoNptjj2OR6PUOYFkWW1tbT6b/8tHREVRVnfcwKLdAolzBYBDLy8tUBKBQHiCmaU68UTYM48aAwbxRVRVnZ2cTB2JWVlbA8zxs20apVEKz2Ry4vul0OhOvN6gAQJkHowSXSFtn27YRCAQQj8cRDocHtgTXdR2dTgeiKCIUCg3sUkBKAYgXx87OzshZAbPE8zwcHR0tfHnTU2fmHgG2baPZbEJVVWiadqfJ+eOPPwYwnlHdorK+vj62Skba9NXr9ZFez7IsdnZ2/BvtbQQCAeTz+aGbYlIO8ZiQJAmyLMMwDN+skVwX2WwWqVRqziOcHp9//jldID1AEokE8vn8vIdBoVDG5LPPPpvo54jJbjweX5gF9F0FAADY3NxEMBjE/v4+ut3uja/jeR7pdJqa21IeHIIgYGNjY6CQ57ou9vb2YBjGwJ8TRfFaK+2rEB8vsm59KCUwPM8jEokMzYqmTA/btnFxcYFms4mPPvroRo+AezMLJJA2Fc1mE51OZ6QbCsuykGUZW1tb/jFInRjpP//QWsWIoojnz59P9LOu66JQKKDdbvep6BzHQVEURKNRRKNRsCyLN2/ejJRO18vy8vJQd+JeQ5+ngCAIWF9ffzRZA6ZpolqtQtd1SJIERVHAcRwuLi4ezA3lKbK7u0sNeyhTR1VVmKbZ14+bGEgRF3fTNGGaJmzbhuu6EAQBoVAI8Xj80cyLs0JVVdTrdRiGAcuyxr53MgyDaDSKbDY7t+tfVVWcnp6OvZYYBFnLFYtF2s6W8qgRRRHhcLhvnrxNAHsqMAzjZ0PcVk7R287RcRz/X3IvkiRpaDeSp0az2cTZ2Vlf0O8rX/nK4ggBV6nVajg7O/P/z3EcJElCIBBAOByGoihD39xyuTz3uvW7IMsyYrEYEonETD7Ek0YjhkUgSZZHsVh8Us7zDMP4KqyiKAiFQg/eDEXTNBQKBd9oCYA/wVJmTyAQ8NX/24hGo1hdXb2HUVGeAp1OB4VCYSo+O4IgIBAIIBaLIRgMPug58T6wbRvHx8djbwgURcHy8vK9iy+TBBSGQdYXmqbh6OhoqsemUBYVUg5DuQ7Hcf469K77CiIyLC8vP8l2y8ViEZVKpe97w4SAO8vLruvi7OwMHMf5m/dxFgGJRMKvY5/kDUskEmg0Gg8uI4Cg6zqKxSKKxSJ4nvejLNNwtr/LZo6YFW5ubl57P0m3hqckAgCX9U4kMtZqtVAqlQB8KRBks1lEIpE5j3J0XNfFwcEB3fTPEUVRsLW1NVLKLY0iUKaBaZo4Pj6+tdPKOFiWhWaz6Zegkew0UgtO6Yd0BNjf3/dTgEdZBGuahnq9jlwud4+jvVybTXMDU6/Xkc1moSgKdnd3qYEt5UlARYCbmWbJqud56HQ6ePfuHUKhEDY2NqZ27IdAJpOBrutwHMf3hxvGrRkBn3zyCTqdDjqdDnRdhyiKyGaz/oHPz8/7XNwZhkEmk0E6nR54TMuyUK1Wkclkpho1qNVq0HXdv5FaluWn4fW2liFjZBhm4TdAg9KKBuG6LqrVKgRB6EuxsSwLb9++vdMYeJ6/0b3YdV1UKhVUq1Vad/4FHMchl8shFovNeyi3UigU0Gg05j2MJ4sgCP5cxDAMgMuFAlkssCzri4OZTIZuqChDIWV3qqqi2+364njvZ4xhmIlEc57n/ew8VVVHundyHIetrS1aCzoFyN97XpkWtm3jzZs3Uz3mzs6Ov6758OHDVIUpCoVCIbx8+XLuWWq2baPdbkOSpLlkEjMMM1lGgKZpeP369bXv1+t1JBIJv7awF8/zfHU3n8/7GyLbtv26duCyl3lv1LvT6aBarfptsziOgyzLCIVCI/3BEokEAODt27e3pjpOI/XkPiC13NVq9UZzwU6ng6Ojo76FGdk8TGMzKgjCjc+xLHut9aDjODAMA7quwzAM/zHLdPNZt0oZB8dxUCgUYBgGlpaW5j2coTyEa+Axc9s85bqu7zpORQDKVWzbRrlcRrfbhWEYU72eOY5DLBaDoigIBAJgWRaapsHzPD+lu9VqodVqXYtySZKEzc1NPw22WCyi3W4jGo0imUzOfUH2EBn3b3ZxcQHLsvxSNlmWh97Lb4PneeTz+b4yzrtCMkDPzs6oCEChUGbGvO85pmni/fv3A+/RDMP4UXue5yEIAnie99tGX/2XYRgoioJgMDi1MryJVpee593ay50Y2hWLRciy7AsAhFarBcdxoGkaNE279nwvgiAgHA4jkUjcWhsXj8cftGfATSiK4n9t2zYqlQoajcbAVCPbttFoNNBoNPx2hO12e6BL6W3Yto29vT2IoghJkpBKpYZ+8EiJyKAWKtNQ/YmJFblolpaWEAwG0el0UCwW/QXxvDe5JM1xkcWAcUtxnmI5yLwQBAHRaBSpVIqKAE8FywVYANzwG7uu6zg9PZ2psefq6iocx4GqqiiXy32CP8MwCIVCSKfTCIfDODo66vtZx3Fwfn5+rS+8rusolUpQFAWZTIb2lp4Bpmlif39/aApy7/2TtCSLxWK3Liin2XaWGFJqmkYNAykUykx5/fq17+slyzI0TfOz5mzb7lvX9n5NAtOCIPgdHQRB8AObxDyXHCOVSg0sD97b27tx7ex5nj9fj5qt1+l0+jwAeJ73jb8nEQhmvsIk6RBXIZHuUbAsC7Vazb9hcBwHURQhyzICgQCCwaC/qSHtdg4PDyfa+C4KgiD4KlEgEOjbDLx7927kCDgpGwgGg9jc3ESxWBwrHZyUWJBFp6Io/gLu4uLC//CP8qGbJGpPIlNLS0tDzxEMBrG9vd13rvPz85FbLc6CRRcD0um0PyHe9N6QcpNUKuWXgVBmgyiKiMViI19PlEeC6QC//Rr4cRlgGeAXN4F/ZQP4olyEMGrrNkVR/Mh7pVIZ21siHo+D4zgcHh4OfJ7UX+bzeZRKJd/cNxgM+tkD3W73RnGfGMQRbxUSBeldbEmSBJ7n6XUwJqQF7seSQqMAACAASURBVDB6Hbh1XUer1cLZ2RkYhoEkSTdmbkzTo4SsZ6jISaFQZg0pmxu37TyZK0c11D0+PoYgCMjn831CdyqV8j3FZgEpKe0VCDiOQzgcRiqVujWAPtQj4NWrV95v/dZvTXXAs4SoN2QhYdu2r2ITFdx13XuvZ58kkhoIBPx2iVcxTRPlchmtVmuszXU4HMb6+josy8Lx8fFEEaX19XUAwMnJiX9uhmGQy+X88oybuIvz8NUShFEwTRNHR0dzFYQURekTKBYVx3FQr9eh67q/qO+t7R2W2kSZHEmSEI/HZ9Y1hPIA+N/fAd8/AeIS4HpA0wR+/WPgq0twXRf1eh3lcnnofSsUCmF5eRkcxwG43LR1u13EYjFYluWnipP7IMMw/kaQwPM8kskk4vE4Dg4Ohs6buVwOyWSyr3yl2+2i0+lM3biX9J5OpVKPygGaLE4B+JGmcecAIuISw2Vg8o4EV+F5HtFoFOl0um/Dbts2TNPEwcHBxPcDnuexs7MDnuepPwCFQnl0CIKAlZUVBINBv0RuXp5cDMPg448/nl3XgEWiV725qvw4juMvpEjkjZjd3RWmJ3LDsqx/cyQbZc/zIEkSQqEQBEGAruvQdd03M7x6M2UYBisrKzeeTxRF/3nTNFGpVGCapr8I9DzP7/1Mjh2NRrG8vAzgyyjvJELAoIiU53k4OztDqVTCxsZGXxkDodcEbRImWShomjaXbhLBYBDRaHSkdMtFgeM4pFKpvu/Zto16vY5WqzXTNOSnBMuyCAaDSCQSNDWacsmHOhDgLzMAuMuHu1dHKe2iVqv13R+IOEf6KBMikYifZUfub/F4HJZlwTRN35y3t9aQROA1TYNt2wiFQmg0Gtjb27s1AiJJEo6Pj9FqtWbzN+nBtm0/I5BhGASDQSSTyTtdP67rotlsQhTFW1sUTwvHcdBqtdBsNqFp2jVhZ5T2oGRObjabfffE3kUny7KQZfnOQoBt2/5n6mp0ied5vHjxAqenpxOVDBDzwUQiga2tLXQ6HViWhXK5TJ3VKRTKg8eyLBwcHCxESe1t539UQsCokIg6AKysrODs7Mw3YSC1a+RBjAvJg+d5P5WRZdlrPXBvitoQ0zzSVWHQRp8Y7YmiOHLKnCiKaLfbAze8PM9DlmVEIpFr0fpJW/UMWyA6joNut3tNCHBdFx8+fJjofIR4PD72z0SjUUSjUWia5i++iGu2ZVkzuzhJVMwwDCQSiQfnmn1ycoJWqzX3yeuxIIqiH9GkqbCUa8RloNwBZP5SyNYMlLtVNKv9GyJZlrG5uQnLssDzPDiOg+M4sG0bgiD4EVrDMFAqlVAqlfx2tKIootFooFar9d0rSJs/URRxfn4+cracoihz6RTjeR7a7bZfdiDL8kQmhKZp4vT0tO97xLSJ3N9J/fykgoPjOGg0Gr6QOix7LxKJYHl5Gbquo1AojC18k0WnJEl9AYBpQX4X4jsUDAaRSqWwurqKw8PDiUWHWq2GRqOBly9fotlsUhGAQqE8Kh7COvrJrkoZhkE4HEYkEhnJXd91XWiahk6ng1AoBJ7nYZrm2HXvvV0VJEnyTSc8z/MXNbfVc1zlps058Wdot9sIhUI4PDyE4zgzbZ04aMN+eHg48Q2eZVk8f/58og1UpVJBsVi89n1RFPHs2TO4rouLi4uR22GNA2mTWa1WwTCMX64iy7Jv6LGI2QKnp6d+L3DK6BChkLzP5L2WZXkh32fKAvHXnsE5asAqN+E6HoyUiNZHl5vPeDzuf37C4TDK5XKfTwfZuLIsO3DzSOZ/QRD86Gu32/W9AxzHGWrUexPlchkrKyt+Z5v7yAwYBMmuK5VKY5UQyLKMtbU1HB8f+98jpk29JRPVahXJZBK5XO7WsViWhXq9DlVV/VbGo9JqtfD555/fedF4H2VwrutCVdWpmQeSTEYKhUKh3D+PyiNgHHpdc0nKZO+jt2XDIBf6RCKBbDYLlmVxcXExdSMIYhIoy7Jv2EcWKWQspCRhlE2sIAgjG15MCsMw2N7e9oUMUkd41/MGAgFsbGyMtaHSNA17e3s3Pn91cWeaJs7Pz6fqjHwbpAQkGo3e2zmHUa1WcX5+Pu9hLBy9rdQIJP32MdUsU+4f13Wxv78Ps6Ii8OMGnNUg9JwCj7/0XVEUxY+2klK2u4iWDMMgFoshl8tNZePZm+lycXExV3PWXnrvz8M4Pz8fyQA1lUohm832fa/b7aLRaPgZYA8h8rOIPH/+3J9Ha7XaVFsUUigUCgX4yle+8jQ8AsaBmBxNWkNeq9VQr9fBcdxM0tlc1+1LgRzEOAuPWYsAwOV4Pnz44JsLTWtT2e12Ua1WkU6nR/6ZQZkAvVxdIIqiiPX1dZyent7bYtbzPJycnKBSqWB9fX2uaeOqqlIR4AqBQAD5fH7sDB0KZRQMw7gUK9sGkr/5GfQ9Hfp//DV4/GX5WCAQwMHBwVSzlTzPQ71eHynCPQqtVgvdbhebm5sIBAILIwTUajU0m0189NFHN76G3FeGQUoFe98Dy7Lw9u3bqY31KZPL5SCKIlzXRbFYpK0EKRQK5Z55skLANOjt/0j5kkn9B4Yxbp1mJpPBwcHBwOcikciNooKiKPe+mNU0DW/evPGduOdBb4osBXN9LyiPn2aziZOTE/ANA+l/+B7a4WUqOv+TBsK7y4hGo9jf359ZCZfneVMxMSIp9vV6fSbz/l1wHAeWZUEQhIHPD6trFwQBL168GPjcLNtAPRVYlsXW1pYvsh4fH09UokKhUCiUu0GFAMrCEw6Hx47KEmdpTdPAcRxYloUgCL579lVc1537YuT8/LwvKk/MK7PZ7K2tGe9KJpNBuVx+8umtVxeoFMq0OTs7Q61Wg1DTkPnHB9AONHgAwAExMYhEKo39g/2ZmvERIeCubGxsoFqtLpwIQNB1/UYhIJVKQRAEnJycXHuORP3T6TRYloWmadB13TeapUxOOBzG6uoqWJaFYRio1+tUBKBQKJQ5QYUAykIiSRKSyeSdWvCNmv5qGAb292e78J4E4k1xH2ZK6XQasizj6Oho5udaVBRFwebm5sKY+7mu63cbkSRpYFvOcbAsC5VKxffBuNoZJZfLUeOuGUL8AIgRHde1YTgM3Oal74v89WWk/ubXcfjJ57Bis/0MTksIOD09xfLyMtrt9kQtRknng1nA8zwURYFt27i4uPC7LfA8j2g0CkmSEI1GYZrmwCi/ZVm0Xn3KrKysIBKJ4ODggLakpVAolAWACgGUe0OSpGv9r3vheR6JRAKpVOreNmOmaeL9+/f3cq5JYFn23swEn+Kil+M4RKPRkZzG74PT01M0Go2BmRk8zyOTyVzLDiEmcrVaDa7rQpZlhMNh/3NTqVTQbDZv3XCFQqGROqhQxsc0TXz48KEv1V9fCcP81W0kmX3YiShS/97P4+wf/gmMJQ6IBWc6HsuyEI1GRzLKG4aqqigUClhfX8fx8fHYbeQcx0EsFkMmk0G32/Ufk3TkIQiCgHw+D47jcHR0NHDDWS6XwXEcIpHIwvgaPHYYhkG5XPbbNVMoFApl/lAhgHIvsCyLzc1N8DwP27bRarUgCAIkSZrrBuwmH4G7EI/HkUwm/Y4UzWYThUJhorT7aZl6jcJT8bsgEUFiarkonJycDG3daNs2zs7OcH5+jng8DlmWUa1Wr7UMI5upcWuZI5HIROOmDIf4AQxCqmlgfnEbSz/zEqd/to/WN+7nPTg5OcHS0tJUjtVut3FycuK34xtXDCD96ePxOJaXl/uesywLqqqi2+36qflXN5Gk+4+iKIhGo+h0OigUCrcKX47jUBHgHvE8b2JzZgqFQqHMhsVZBVMeLRzHwXVdvHnzBsClG/vW1tacR3UZSZ1FvadlWb4IAADRaBThcBinp6dDN3q9CIKAzc3NexVJdnd3cXh4+GhSNjmOgyiKCAQCEAQBPM8jFAot1OafcHZ2NvJnw/O8G921GccF3zbgKAJccbzf8+DgYO7dKx4bhUIBjUbjxufjgTAiP7OL8//hE6jPZCA0O28KhmHA8zwkSUIgEPDbYrZarTtHaDudDrrdLqLR6NhCAKHZbF4TAgRBQCKRuJYFY5omeJ7351jXdVEoFLC/vz/ZL0ChUCgUyhOErvgoM0UUReRyub7a8263i7dv38K2bYRCIeTz+RsNncbBdV0cHR35NbgEEoknNfezpt1u4/Xr10ilUr45IcuyWF1dRTqdxtHR0VABIp1OTy1aNw4cx2F7exuNRgOnp6cPxjiQZVmIoghJkhAMBhEKhRYizX8cotEobNuGaZp++cy4f3/WtJH/vfcQVR0uz+HsLz6DGRvdV4B0r+j93FImw7Zt7O3tDb3Ok7E4omuJy6ykz4rwvrEzk7HIsoyNjY2BAg/pxmIYBs7Pz33TNs7UwFs6LCkAl5duPUc8HocoijdmPozCMDHCtm1/HgVw7frWdR2tVmvic1MoFAqF8hShQgBlZhDztcPDw2vPkQWyqqp4+/YteJ5HJBK5U6324eHhxNGoWVCpVFCpVBAIBJBOp/3uBy9evICmaSiXy2i32/6Gbx5ZAIOIxWIIh8PY29tb6FROlmWxsbGBQCAw76HcmWAwCFEUUalUYBgGLMuCbdtwXXdkQSBw3oLY0mEHRPBdE7G3JZS/vTH2WCqVCsLhMILB2dapP1ZUVcXx8fHQ921paQlRJYiLf/Qp9J0IZACQpm/UmMlkkMlkhr7GsiyUy2V/7gxf7CN98kMADDyWQXHrZ6BFbj6GLMtYWlrC/v7+1MVDx3FQKBT6DC4DgQBisRgikYgvDJA5dlG7F1AoFAqFsohQIYAyExiG8R3YR0k1t20btVoNtVoNLMtCURTEYjFEo9GRIpOFQmGhRIBeut2unxERCoWwuroKRVGwvr4O4DKDwLIsxOPxeQ6zD47jEI/HF7ZntiRJ2N7eflRR6263i1qtNvFmyhU4MLgsD2A8D86YpQHA5XW7vLxMRYAJOT8/v9WALxwOI5lMovQP/hm6YQ5My4IXFoApuPj3Qswlb8IwDJyenvbNm7zRRvrkh3A4ER7LgXUsLO3/Cxx+9V8F2JuFCs/zEAqFbixZGRXXdfuu6atipOu6aLfbX2YucBwCgQCi0SgcxwHDMA8mk4lCoVAolFlzW7knFQIoU0eWZaytrYFl2bEimgTXddHpdNDpdHB6eopnz55Bkoanp04iAsxj0dhut/H5559je3vbbwcXCoXudQyjssibwVEFoodENBr1SwQajQZUVYWu6yO3V+vmImg8SyN8VEMnEUL9xfBI8FUSiQSy2eyj+7veB61WC6enpyO9V6qqotPpILa7jrpZA3OmXQoBU+Ym809N03B6enqthAoABONyHvW+2PS7nADe0sDZJhxxcJmJruvY39/H+vo6ZFnG+fn5xPPq3t4ewuEwYrEYZFnGysoKDg8PbywbcBwHqqr6GQMUCoVCoTxVyL6GdMRKp9O3ll5TIYAyNTiOw8rKil93CmCoUdaonJyc+D2vc7ncwFTw58+fQ1VVlEol6LoOhmH8B6kt7e2ZznEcMpkMPM9DpVJBo9GYWT/rQRweHuLFixcLvemS5dkZl92Vx9zvnud5pFIphEKhkdzPfRgG1a+toPq1FYT+658g8OEDOv/OM3ihm28CJKK6vLxMTQIngDjU32Y6GolEfMHP8zwokoz6+1O4z8PgSEbAFGEYBul0uu97qqri/Px8aLmPJV2Kf4xrw2N5sLYJlxPg8MPLlSzLwv7+PnZ2dhCNRiee9w3DgGEYqFQqAC7noGw2+yRbm1IoFAqFMi69gcZRoCs/ythwHAdFUfo21qIo9jk7G4aBo6OjsWrMZVkeGKXq/d7+/j5EUcTOzs61TXQ4HO4TIUYll8shl8vBNM2Re67fFcdxUCwWkc/nZ3qeu8CyrN8SbJFgWXahyihmRavVutYacFTcqAi2aUH4cRXWN9Lw5EvhRBAEv8Y6GAwutBC1yGiahpOTk5HmN0mSkM/nUS6X/e9VPv0xNO5yjmFVE154er4gV80eTdPE4eHhSGO1pSBK8a9iqfFjeI4Fj+VR3P4LQ8sCCIFAAJ7njdz9YhR0XaciAIVCoVAoI+B5Hg4ODrC7uzvy+o4KAZSxyOfz11o5XcV1Xbx//37kY4qi6NfNG4aBg4ODoT3tZ7V5EUUR+Xwe+Xweqqr2dTqYBbVaDclk8tayh3kSiUSQTCZvrXu+T7a2tp7EBrbX6M1xHOi6Dk3TYJqmbyjoOM5A0ar7r2+DK2vgSzpCv19E9NtbiP38s/v+FR4VruuiXq+jVquNLNAwDIOVlRWUSqUve9Z7HjI/OYf+s5et8hjVhpvtz3JiHAfRwgnEdgd6JILW8jJwy2c+mUxiaWmp79qoVqs4Pz8fbayqBfH/PAY+reLwP/kupN89hPEyCzc0muiWTqdhWRYEQVhok1EKhUKhUB4rpIPa5ubmSK+nQgBlZGRZvlUEAC436iTtnaRwG4bRJw4wDINQKISlpaW+FHRJkrC7uwvgssaV9KfWdR2hUAjJZPJeNoGkR/Vd+2vfhm3bCy0EAJcZE4qioFAozHUcgiBgeXl5oUsWZgXHcQgGg0N9G2zbhqZpl+LAf/dDOG8qcGpd8GtxSOz0a9CfAsTEtF6v35r+PwiyOfZFAABCXYcrcnCCl+8J0zLh9pYGuC6yP/ohAvU6XIZFuHgOqdXCxatX147PsizS6fTAefHo6Gi02nnbBf9pBcL3zsGWdXghAa4gwv2eCv5zG+Z/FAO4240Mj4+PkUwmsbW1hU6ng0qlMpJRLIVCoVAolOnR6XSwt7eHtbU16hFAmR7jbMCufvAkSUIymUS320U6nUYkEvGfc10XJycnAxet+XweuVxu8kFPiKIoePnyJdrtNorF4sCShdvgeR6yLKPb7Q4UFHieX2hDvl5IKvn+/v5EG6K7IAgC8vn8RGUfTwme5/2/UYPj4MVkcPkIgt/dhfzttTmP7uFgWZZfIjQsM2kUZFnuEwEAQC52oee+vO4Z1YIX+XK+lNptKI0GLEkGGAaO5yFcLKL27BmcL1qLCoKAbDaLaDQ68LylUmlkAz3hn55D+IMiIDDwRA7ukgL2QwtgGDAXOrj/7wLOz95uPOk4DsrlMi4uLhCPx7G6uuqXUFAoFAqFQrk/NE3D/v4+Xrx4MfR1VAig3AhxbpYkCYqi3NlMbNCGvtPp4PDw8EaX6UFKluu66Ha7EEURothfW9vtdnFxcQFN0yAIAmRZ9iOpNx2r0Wj4DptXCYVC2NnZgeM4qNVqaDabMAxjJFds27bRbrcRiUSQzWZ9d2sStZ2HwHEXBEHAixcvcHZ2duc2YaPAMAw2NjYejFiySIT/1jfBBkXYhQY6/8drSN9aBcNOtz3dY8N1XRwcHEw1in21HR48D3KxjfpPZS//b7mA7QEy1/caAP3tBJnL70uShNXV1VtF2YuLi5HHaP38EpimAeGfl+FFRXgxEdwPqvAEFowHcL97Bnc3Ci85WuaS53mo1WoIhUK0RIBCmRISfwCerUK3nsPxIrf/AIVCefKMErijQgDlGqIoYnNz89Z0kmnQ6XQGbqpDoRCWl5evjUHXdezt7fk/E41Gsbq6CuAyCta7ACap0r0ROYZhfINDz/P6FqonJycIhULIZrPXFtocxyGdTvtO3Lquo1arQVXVWy+0VqsFVVXx0UcfIZlMjvJnWWjy+Tyi0ehQAWcaeF9sfCjjw8UvHWP5zQQYRYD5ugTp4+ycR7W4qKqK4+PjqX+erwoBfNsCXMCOXAqYjGrBC/N9m34zFIIVCEDodOFyHFjHhpZIwBFFPN/aGqljBs/zo2czyBzAszD/yjL4dy24YR7sH9fgAYDhAAIL9o8rcL6zPNLhBEFALpcDx3F9BokUCmUyQuIfIRP67wEAjhvFSfPvwPVohhyFMm1kWQbP89B1/c4ZgfcBy7JQFAWu68K2bTiO05eBPEomLRUCHgGC3oKoN2EEErDFu0VPl5aWrrWdmiWZTAamaULX9cu2WoqCbDZ7Y/bB0dFR32K92+36X48iXHieB9u2b7zA2+02Pnz44BsHkpZfV5Fl2Xf8d10XhmGg2+2i2+32Gbn1nrdSqfjmbw+dYDCIzc1N7O/vz/Q8hUIBGxsbMz3HY4ZhGCi/sA3tn7yH+GrJb8NJ+ZJZGoNeFQKkYgd6Nuhv/JnW9Y4BHsfh7PlXkfj8LUTBhh6Loba1hVg8PnLbzNXVVRwcHIz0Wu4nDTCOB/Mvr8D6RQ/QbLDZIBjTBfujGqx/axOIjNbVIJVKIZVKoVqtolKpzFQopFCeChH5+3A9Ea4XAs/WoQh76Jhfm/ewKJRHRSqVQjabhW3bePPmzbyHMxCGYSDLMqLRKOJD1gREGLiaNT0IKgQ8cOT2BfJ7vw/Ag8fyKDz/JVjSZErxzs7OXIzYVlZWRn5tPp/vW7T3umJGIpGptZoiLbd4nsfKysqNggDwpSKnKMq1iL/rutA0Dd1u98Z63odKIBBAPB6/VgM9Te4jK+WxIzxPQfsn72G9q0B8cX8i30Nhloag3W4XuVwO3W4XmqZBLnagfvSl4eplRsCVz3jDhPOfvkanY6P53RWYf/4y42mcVqOkFOq2bCWmbUH4ozKMf20DYJnLhyDC/VbqUhD4UQ2I356VEwwGkcvlYFkW9vf3aUkAhTIhXsuE2zSBrgNPt+Ecquj+Ugby6lsw7qWwZjl0HqdQpokkSchmL7Mm522MfRVRFBEOh5FMJkfa2AOX+5JRX0uFgAdOqH4IwIMtBMAbbShqEYajwK3qcCs6nJIGsAyUvzx8s729vf0g3NjD4TB2d3fRbrchy3LfB53neTAMM9UolG3bODw8xObmJiRJAsuyY3UtYFn2Vrf3h0wul4OqqjNLoXpoPgqLCMMwkH9hC9r39iA8T9GsgCvM8tpstVrwPA/r6+s43TsC17VgJhT/+atGgTjvAr/5DkJZByuz4I7bAC7nvXG7pdwqcHgehN87h/3VBLzEgM2+zIFxvMvyAGlw1IHneWSzWQQCARSLRbRarbHGSKFQ+tH/3mu4px14DIC6CU93UF3+RbCpECSugKb+CzCd0cp0KJTHDsdxEAQBoihClmU/KOc4zshtzMPhsB+Q1HUd7XZ7lkMeCsMwSCQSiEQiUBTlfrqkzfwMlJliylHAc8HaBsAwUP95C9Xf/F0wAR5MgINnuBC/kRoqBGxubkJRlBufXzR4nkcsFhv4nCiKI/f4Hoeb0mxXV1cfXaR/HFiWxfPnz1EoFKa+CchkMvcyCT4FxJdL0H73Pez9GoTth+9TMU3uaoJ6G8QkNGgAWiZwGXX/ArZlwdn6QoA9aAH/7XuwHQuiyAIewNQMQHegQkWj0bhx3ruK67p9pUmD4N41wbRt2N9IDX4Bw8ALC2DaFrwrQgDDMEgmk0ilUqjVajg9PaVlABTKFOB/MQ/jv/wcnuWAETmI31kB981l1Lq/Nu+hUSgLAcdx2NzcHBq85HkeqVQKlUpl4PMsy/qlbCzLwjAMHB8fo9PpzGrYQ+E4DplMBvF4/N7XvVQIeOC0UjtgHRtKu4x2bAXOyw1In38G89PKZXqZ6QEiC7vQAbccuBYNXF9ff1TR6mAwOBMh4CZoCuzlhLq2tgbTNHF8fDxRq8WrMAyDVOqGDQplbBiWgfIvbUH7g30qBAxg2plEVwmFQqi9/gx6rr/EiGn3lAa0LIBnIHUdoGcdwO014bxKoFAowLKskTxcbu180LUh/GEZxl9bBbibM0S8sACoNtDzkQkGg8jn8zBNk5YBUChTwvM8uG+bsP9ZCUyIB0wWbFKG+Nc3b/9hCuWJEI/HkcvlRtosZ7NZNBqNvoxVURSRzWb9FuaqquL8/Hxu9zFirtvbUv2+oULAQ4dh0ci+RAMvAVyuH8P/4VfR/m/ewPr0Ap7jgV8Novs/fQAcD8JXEhC+mgC3EoQsy4+uN3smk7mX1naEUc27BlGr1eB53qPoJABcTrA7Ozs3Pu+6Lk5PT9FsNm89VjabpdkAU0b8ag7aP/0A67gOYS0+7+EsFDzPj9RmZxJkWYbrOGBP6jA+2uh7jlEtuEQI+HNJIC3D/rs/AQeAa9tgXA/cUQfOq0tfgVKphGq1itXV1aECrqIoSCQSaDabAzMDxD8own4Zg5cZnglm/5U8IPbPcdFoFMViEaqq3v7LUyiUW3ErOqz/6wRew4T4K+tgJA7af/ZjiP/2NpgAXaZTKBzHYWNjY+zs5c3NTezt7SEQCCCfz/vlxI1GA+fn57dmzs2KUCiEXC63EJ2x6AzzCGF4FqHf2EWHZeB1bQR+dfNSbT7XYH1WQ/d/PUT4N3Yh/qiFjltB4Hny0dQN8zyPQCDQ101glkwyiVztV85x3Mgpvw8ZlmWxurqKbDaL4+PjG6OWLMs+GnFkkWA4FvLPb0L/3j6EX/+peQ9noRBFcWZCQDKZhFasw0gpANcjbtkuoDtAsOc2/KYF67ur8GIinLoB6+eut3y0bRsHBwdIJpM3emiwLIt8Pu9H7o+OjvxMKeagBc91Yf/5wRk3giBAURQEg0HYn5yDBYvwv7wFnufBsiw6nc69Zl1RKI8Vz3Bgf+8c9p9Uwf98FvxPp8F8MUcof+frYJLz3yRQKPNmnCyAq0iShJcvX/r/J0bgs8gAkGUZiUQCsVgMtm2jUChc24ukUqmFK3ulQsAjheFZBH9jF7AuDaMYhgGXD4DLByD90jIYF5BkAYXf/AGcroXot5YR/fYKgi9SYNiHLQpEo9F7EwJUVR2r3aLrunjz5k2fkVehUIAgCI+qRGMYgiBge3sbmqb5fcZZlgXHcWBZFvE4jVbPCunry9B+fx/2eQt8bn6paIuGJElTrw1kWRYrKyvgOA7Nf/FjGNn+65tRLXghwW8lCNsFPqsDf2sbzJ9W4aUVQLh5sTBqJEEURWxvb+Pw8BDdTgfeSgjWagicK2nEswAAIABJREFUKIDneYiiiGAwiEgk4mdGeJ4HWZbRjXVhHtT7ajFFUbxTJhSF8tTxPA/On9Vh/T8FcJthyP/+R2CutBFlU4tv3kyhzBKWZafmYTZORupNRKNR6LruC+HEDDyZTF7rLCaKIra2tmCaJk5PT9HpdJBIJPzOBIsEFQIeMQzLDHR7ZhgG4IDs33iF7N94Bb3QQvOTAs7+/p/CbhmIfGsZsZ9eQXA3/eBEgYuLC5RKpXs73621uD24rov3798PdPM+ODiYW/vGeaEoCtbX1+c9jCcFI3CQf3YD2vf2Ef6btA81IRQKTbWkiOd5bGxsoNvt4uTwCJlCE/UX/Z/1a60D3zSBrALEJLA1E9bzm01I4/E4EonEjc9fhWVZbG1tofbbPwIncAj/yktomoZms4lOp4NOp4NisXjt5xjRBRvXUXr71vdQEEVxrHmPQqF8iVvswvqdk0sj539jC9zaza2JKZSHzl38d1zXhWVZdxYCGo3GyIa2LMtifX0dhmHAMAxYlgVZln1TQXK8QCAwUns+URT72pwvIlQIeKL0lgLIKxHIKy+x9GsvYZypl6LA//gjWDXNzxQIvfwyZW1ROTs7u1d/AOBS2bcsa6R+90dHR0PTjz98+PDkxADK/SN/awWN7x/AKbfBZegiFMA1NX8SBEHwr+/V1VW0Wi2Uy2VI5S6sqATvSq39tdaBP6wC304Dnge2bsAd1NIPl+mHy8vjtw8z31Xg7tWh/psbOHn9+trzHNqI4Q8AuGjg5+AgBk+3gCMV1moAwGU7z0AggL29vbHPT6E8ZbyuDev3zuB8Vofwl/LgfurhZ19Sng7jbOhZlkUikehLgSeb+v39/bFKao+Pj5HNZicyj75ahjsK2Wz21pbfj62UlwoBTxTP8/DZZ5/5KdmCICCdTiOcDyPzqx8h86sfwSi20fykgOL//GcwLzqIfHMZsW+vIPgqA5ZfLFHg5OTkTik/d+Ht27dgWRaiKCKXy12bQFzXRaFQGCn1+MOHD9je3n5Q7RwpDwtG5CH/9Bq07x8g9Ne/Mu/hLAQsy0JRlIki3RzHYW1tDcFgEKVSCbquw3Vdv+xFLnag564vKvoyAsraZdeA7QjQdQAGgHL99kwi++PiGTZa/+AzhH/tFZre4DafOfx9iDgFAwYBvMEJ/jYg8+D+tAb355awurYGjuNweHg49vkplKeK53pw/qQC63fPwL2MQ/4PXlEDQMpCQNb/PM+D53kIggBBECBJEiRJgiAIN9ayk429bduwLAuO48C2bYRCoYGbaJZlIUnSSGICwzBgWdYvXQsEAmP/bqqq4vj4eKxshFgsNlam3WOBzkZPHNd1/Qv6+PgYr1698p+TsiFkfnkXmV/ehXnRQfOTUxT/l5/A/Ht/hMg3coj+9CpCX1laCFFg3jWrrutC13UcHBwgl8shmUz6EcFx2+nt7e1ha2trosmPQhkF6dtraP7n34dT64JLzO9zpus69vb24HkeGIbxow7k5i3L8tBOFNMklUrh5ORkrJ9ZWlrq8whZWlrC6ekpjo6OLr/hepBKHbSfX/e9YFQL7uoXC6Yf1oA/lwBY5lo2APEPiUajCAaDE5kMtf/xO4hbCUgv0lDOrAGChwMJp7BwOU4BNbDQ4UoBeByDAC9DkiR8+PBhpm0WKZTHhHvShvk7JwDHQvr1Z2Dz9J5OWQyu3rvGhWzsx3W9J3X2PM/3iRCSJEFRFPD83balk3oB5PP5JykCAFQIoPTgeR6q1epAx3YxHUT6rz5H+q8+h1ntovnJKcr/2xsc/xd/hMjX84h+exnhr2bBivPZkOfzecTjcRwdHfX1DJ0H5+fnKBaLd1ow7+/vUzGAMjNYRYD0rVXof3iA4C+/uv0HZoBhGL4IAKBPACDc5Io/C6LRKGzbRqVSubWDQDgcxurq6sBNeS6XQ71eBwCIdR2OwsMJXC8dYlpfZASYDvC6Afy7zwEAbM2AG/9ycfXs2bM7OQxbh3UYPy4h8bd/FsBl6qPrumg0Gj2v4tDBRwjicwCAhg24+CIrKSRAK7XAP7vsGjCvdksUykPBa1uw/t9TOHstCL+0DO6riUfTmYnysAkGg1j7IrtrHkxS1jYqJBg3zj2KYRhsbW096SxcKgRQ+iiVSre2bhOTAaS/+wzp7z6DVdfQ/KSAyu+8x8l/9ceIfC13KQp8LXfvooCiKNjd3UW5XPbTcufFNKJm+/v7ePbs2UL0GaU8PuS/sI7m3/1DKH9xG2zkfn0pTNO8Nbq8ubl57500kskkkskkbNtGqVRCs9mE53l9LfXC4fBQTxCWZZHJZFAulyEWO9e6BfivI6UBrxvAWhD4okyAqRvwvsgIYFn2TiKAZzlo/fafIfgrL/xSA9LNIPv/s/em0ZGd533n7651a19QKKCwFLZGryRFipQoUxKp1Vos2/Ii24qdiY89iSZjx86ZMzNnMjmZJccf4nzIJGdmMrbHY+fYsU9keVNiy5YX2bQkUiIpcWdvABpLASigUPt+1/lQXbcbjbXRQDeAvr9z+pCourfqraq7vO//eZ7/MzhINpt1yyL8/I/Y5W/SFDust6bo1ieAE5ZxKh3q9TrhcPgOAcHDw6OHY9mYL+Uxn88hP9GH9vOXEDSvw4bHg+f2ErbTQLFYpFKpoOs6pmkeeM4diUQeeEbxg8YTAjw20attTaVS+9peiftJfmKa5CemMcotqi+vsPGXsyz96iuEHxsg+vQI4cfTSNr9O9RSqRR+v/9Weu4JZmZmhrNnz+7LjNDD424QgyrqE0O0vjlP8FPn7+t7r6ys7HrjFgSBGzdubHn87Nmz+3LqvVdkWWZ4eHhf0Qtd11lbW6NWq+E4DpcuXSKZTLKRz4Mo0N5OCLAcaJk4QRm+W4CP3Mp8EEs6xmQY4J6NQzf+6jLlS35WxSK8UySTyRCJRNzPaJomyWQSvVCn+ftXESdHCXz6HNOKQrFYpF6vI00mkGNRNE2jXq/f03g8PE4r1lwN4yuLCGEV38+eRex/eCOMHseLVCq17zn9SWF1dfVQAm6VSsUtI1AUhXPnzt3za540PCHAYwvr6+vEYjE6nQ7NZpN2u+228IjFYvj9/m2jVErMT9/Hp+j7+BRmtU3l5RWKX7tB9te+Q+jRFNGnR4g8kUbyH/2iNhwO09/fTz6fP/L3Okocx+H69eucPXv2nmunPDzuxP/+cSr/1wv4n51EDB79ArvHXsaZO93gj8M5YNu2a5BUq9XY2NjYso0oigwG4uQmTWx167VSqBsQkGGtDYYNY7e6FgjFDs7N0oBwOHzgcc69cY1m0gT5VkbR4uIiIyMjrutxp9Nh/a1vMbD4RYSYRfX151i9oKJpGn19fUSjUYRPDCD6ZARRfOBlVx4exw27rGN8NYuz3ED55AjihZhXBuBxLAgEAmQymWNx3zxMSqXSkXjV7FUSeFo5XUeHx6Fx7dq1LY+122239lWWZfx+P9FolEgkskUYkCMafR+dpO+jk5i1DtVXVij93QLLv/5dQpf6b4kCR7j4GBgYcFOHTjK2bTMzM8P58/c3autx+hEjGuojA7RfXCDwsen78p69yPnd4vP57ilN/jBot9vMzMzs+Pzt2QqRfJuq7lD3bV0UCDUDO6J0swGe6IPewqFtIlh2N1OAg7cpWs+t0ew0EbMN7Onopuey2awbTXEsk5Hmv0MarYMDifECZec9tNttlpeXARDfKSMuNvB/7jzpdJparXagMXl4nCYcw8Z8YQ3zxXXk9/Yj/9A4wjain4fH/ea0lQH0sG2b+fl5ms3mgx7KqcITAjwOhGma1Go1d1IYDAYZHBzc1nBDDvtIfHiCxIcnMOs61e+uUH5hieX/77sEL/QTfd8I0SeHjkQU0DTtxAsBHh5HifbBCaq/8i20948j3odsnYPWmN+Lw/FhYNs2s7Ozmx90HAL5Ir5KDTOgEX7ycWzbRhRF7LkNRj5whquVrSmMQs3A8Ulwrbq5LKCod40CBQFVVQ9cErS+nEN+rYj5vu2/s56ZklSoIEWb2BsBEAXkSAVB13F8t0oSnJAMtW72w8jIiFtS4OHxMOI4Dva1CsafZREG/Pi+cB4x7vn4eBwP+vv7GRgYeNDDOBKuX79+pFH7hzWTZ1chQFEUAoGAp7547Emj0WB2dhafz8fExMSOqUhySCXx7DiJZ8exGjrVV1epfDvLyn94jcDZPmJPjxB5agg5fDg31k6ncyiv86AZHR190EPwOKVI8QDKdJLOS4v4n5s68vfrRZVt2973Pv39/QeOjh8W22UyxGYX6JtZwKFrrdfI5bn85KNczExBo4M0FGcioTE3N7dpP6Fm4JR1OBPulgj0Hi91sDLdMoHx8fEDjVPPVUERMS/FkGSZYDCIz+dzW8U6juP+V4pGMe0P4It8B8swaMxcgNHN124nrCDUupOvUqlEf38/q6urBxqbh8dJxi60Mf4si1PsoHzfKNId2TYeHg8Kv9/P2NjYqSsD6NErxztKHlbTwF2PGMdxGBoaQhAEyuUy5XL5oa2h8NgfnU6HK1eukEgkiMViu7a/k4Iq8Q+MEf/AGFbLuCUK/PbrBKbiRN83SvQ9Q8gHdDRfXl4+NULAjRs30DSNdDp96tK9PB48/mcnqf7Gy2jfM4agHu1EQpZlzp49y5UrV/a1fSAQIBAIYJrmsZrkCKZFYnYRw6eCKHazAzZKRNo65uw6rfEoa8tZms0mkiRtamkkVHXslSZ8aHLTa9rjYRxVJB6PH8gU0bEdan/4NtHPjJCcTqKqKo1Gg06ngyRJiKKIIAjIzgqStYDphCle/ntovIvEUxl8UxdJNTtsbGzcGm9IQWiYbo/nSCSCpmk0Gg2azSaNRuNI6jU9PI4Ljm5h/l0O85UN5A8MIH9+EkHyygA8HjyCIDA6OuqawJ5W7kcnsOM0v7if7PqpTdNkZmYGv99PPB5nfHyc69ev36+xeZxgisUixWIR6J5cgUCAwcHBHSe3kl8h/kyG+DMZrLZJ7bWuKLD6O2/gn4wTfXqY6HtHUKJ7iwK2bZPNZqlWq4f6mR40vR6pp7X+y+PBIaVCyGNx2q9k8T8zfuTvJ8sygiDsawHZbDbdDiD3q2vAdtzpTyDYNuC49f2yoqA4DkarxbVQBZLg3HQjvhNhuYntk2AoiKZpTExMoOs65S+9gfRYimQ6ve1+e9F6YQEcAd3QWV1dpdVqbfmOg+JrDMi/0x1H02DjK2FmX/woj/zaYyhKnlgsxvT0NKVSiWazSTAYJPJLk9ghmUq1wuzsLIqiEAwGGRgYwLIsV2joiQOnRYD1eLhxHAfrrRLGXywjjYfQfu4CQvjBXH88PO4kHo+TTqcfuHfO/aCyw730XkkmkwSDQSRJuucuPSeVfckfrVYLXdc5e/bsUY/H4xRimibVapVqtYqiKPT19bknXq9P9u0XMkmTib1vlNj7RrE7JrXXc1S+vUzuP72Ffyx2SxSIb/UjKJfLLC8vn+oIlWVZ3Lhxg1AoRCaTeShuAh5Hj/9Dk9R++7to7xlFUI4+Ra4nBNwZLd+N2dlZzp0790CO+TujBbYi045F0UoVhIAfv+3gBIO0g0Eib6xTeXzndk12SsP5+DCCIDA+Po4kSfj9fprZJrHPDBzo81mlFo2/miX+c+9jfWNxh+/UJiV/EcsJYJQdmrMdhr9nhfxGEdM0MU2TVqvFxsYGg4ODRKNRSqUSK7/3Co0LQZzB7jW30+lQr9dZX19ncHAQwzBot9sEAgH6+/sxTXNLOYTH6UQURcLhMJZlYRgGhmHcVdnPccXONTG+soTTtlB/ZBxp/OAdPDw8DhNVVRkbG8Pnezi8KXRd3/cc4W6QJInBwcFDf92Txr7zICKRyJH8EB4PF4ZhkMvldt1GFEVkWebMmTOIPpnoe0eIvncEW7eovXFTFPi9t9FGo0SfHiH05CB1odvR4GEyBqzX67zzzjvIsozP58Pv9xMMBgkGg5444HHXyOkIcjpM59UVtPcejidFrVYjn8+j6zqO46AoCplMBlVV3Tak7XZ73/cWy7JYXFw8cP38veD3+1EU5VZ5nCCQe+ISyXdmiDSaMJBCeO4ZonMrlN+VgjtSh/v6+rpRDcOGqIpvNEp6dNgVGOy2gd00ELcROPfCcRwqX3oT4dlhVttFbNsmnU7jOA7tdtv9J2AgoGNUZBozVQQbBEREu77p9XqCgN/vJ5/PI1ebCHUVB/+W973dL6DXVebChQt3JfB4nDwkSaKvr49EIkGr1QJwDS5t28YwDOr1Omtraw94pHeH0zYxvraK9WYR5cNDSE8mEaSH00TM43ghCALpdJpEIvGgh3JfOaoMsweVXXjc2FUIUFUVQRCIxWIkk0nm5+fv07A8HmZs2952QS+qEtGnhok+NUyz1mD17UVWqyWExQZ2xcBpm4hRFTH2cKikPXqRvEaj4fY01zSN4eHhbbs4eHjshPbcJI0vvYHvyeF7qoE1TZPFxUWazSbnzp3jxo0brqp/7do1IpEIY2NjAFy+fHn7sTTy+JoFLFmjER3FEbtZCvV6nWKx+EAmQ1NTU2SzWYaHh2m32ziGTfDcRZbfnGH08bMImkIqt0BsLEZWabmiQTKZZHBwkHQ6TekP3qL5rQrD/+ijm17bWm8g9wc3ORfbtk2lUqFcLqPrOqqqEggECIfDrv+KbdvMfPtN9Cd9oJpwM4WyVquhaRqhUIhkMokoijd9UzKo2jx6VMGu1XAQKV0LkjIsRKW7uOvv76fVarGysgJ0DQOp7c8fKBgMumaEHicbQRBQFAWfz4eqqpv+K4oi5XKZubm5LfdrSZJQFIXx8XEKhcKJ6DLhOA7WqwWMv1pBOh9F+/lLCMGHs2bY4/ihaRrj4+MPZR37UZXBtlot1tbWTm2Xhf2y6xElSRIXLlzgypUrVKtVT933uG8IgrBrVHtu4QaEQAwFcEwbu9zBeKuE8XYJMeFDeSSO8mgCqe/hrPlpt9vMzs4yNjZGOOylNHrsDyUTR4wH0N9YxffE8F3vb9s2a2trFAoF97FqtUokEnFFqt5jly9f5vz580xMTLC8vLwppThUmiOV/TaC4+AI0CoNsDrxYRC614SVlRXW1tYIBAKMjo7etwwYWZZpNpvMzc3hExX831ij/naO2k9MMPudtwlkkkTWSgQ/doFzPoVarUalUulG7CsVIuEI9b9bxD/dt+W1rfU6UipEu91mY2ODer2+ZQFlGAaNRoN8Pk8ikUAURTrVJnLABx0DUxLd77Ber1Ov34r0T01NIXYsWi98L877/orI+BzVt1QW8p/DdyYMdveen0qlmJ2d3bS4u71zwF7Yto0gCGia5nUcOoEIgkA8Hqevr8/NgNF1nU6nQ7vdplKpoOv6rsbRlmVhWRb1ep1wOOxmioiieKCyAUEQ6Ovro1qtHknWn51toP/pIogCvp+aQhzy/Hc8jhftdts12BUEgenp6UOJaFuWdezd8ntZwocpKAqCgN/vP/Umi/thT2lJFEW33ZCHx/1ir/7ZExMTzM/P4zgOgiyinIuhnIvhfHYcc66K8WaR+r9/BzGiojyW6IoCyYdPFFhZWeHcuXMPehgeJwj/c5M0/vQy6ruGEMT9p8RWKhWWl5e33CsCgQCFQmHLjbznYB8IBJiennYft0wT/Q9/H1Py4YgyOA7+xjr+eo5WeOjWdpZFrVZjeXn5vrbXVFWVdrOF/PtX6Vwto+oG0f+o0368n7IKxacSjLabtMtt1zwP6Iojuo3yriC+QMh9Pdu2qVarFCrrtCdFnJmZfY3DNWMtGWQuTCFHNGRZxnEcNxp/e3aBgMBI/yDm2cdZ/Zc6l/ueo10yGPifn2TqGYFwOEwikdh+sRWSEfLtfY2r1WqxtLREJpMhm81uEiM8HhySJCHLMrIsoyiK+/93/pMkiVqtRjabdVP+D0q1WqW/vx+/308gEEBVVRzHoV6v02g0qNfruy7se0bVveyfwz6WnIaB8ZfLWDNVlI8OIz2eeGh7iXucHBzH2dYvJ5fLUSqV3EBaT9jdLhik6zozMzPYtk0qlSKV2tnT5jgQDAbv2TBQlmU3Q+5hNQbcjn3lmGQyGZaWljwxwOO+sVebymAwyPnz57l27drmtlySgDIdRZmO4nx2HOtGDf3NIo1fvYwQlFEevSkKpB6OlHnDMKjVap5vgMe+kScTCJqM/s4avkf2Z6Rz/fr1TXV8vkITtdrBDKpI0yKpVIrBwUF38Z7L5boR6m2OSUkU0BSJpiNj2T1XfgHR2v6aUKlUSKfTR5oyads2lmWhKAp+v78rBMyUUQwTQQB1sY5oOPiLTcof6d4vt+WbOcyxEOujCvW5OWRZdrubiI02giXj3EU6sjRTRXopz1xEglz3u+wJLNCdMEa+u0ZgtoxoWgiiivzcRQb/t48jX1lHPRdDTYcIh8O0Wi0qlcq2k627KQ0AaDQaZLNZRkZGaLfbXlnhA8Ln8zEyMoLP58O2bbeM7PZ/7XYbwzDcvw8z87NerxMKdbNcisUi7XYbWZYJBoOEQiFSqRS5XI5yuezuI8sysViMeDwOdH0ncrkcyWSSSCRCp9O557ITx3KwXs5jPL+K9FgC7ecvImgPX8q1x8nFsiwuX76M3+8nHA5TrVa3Fe4WFhZIJBIMDQ1terwX5IWuSH3chYBYLHZPQoCmaZw5c+YQR3R62NeVLxwOc/78+S0pnx4eR4XjODQajV1rg3pmRTv1FxVEAXkqgjwVwfmBMayFOsabRRr/7xUEv4zyaLd8QBzwn+ooQK/1miiKTExMeL4BHrsiCAL+Zydp/fUM6qWBfZ0bt0f1olfy9L12y0BuY6VK8fFuOzxN0/D5fGiatimtsddZpFdb7EudQVm5jO0oiLaBI0p0Askd339paYmJiYmDfNxN2LZNqVTCsixEUaRSqWyaXLmpzS2TzkeG8P3ZYvcJBwTLRr5R65oBytuIbmUd3ighWw6WYSO8O7xJvFC/uU7nM3eR2dA2Ub6eQ//UyCZjwjsFez0kE+wY2LkWzdUywkyDwf/nh6j9/ptEnoqh1+vkcrld0y7vpjSgR71eZ35+nsnJSc6dO0e1WiWXy3neAfcJVVWZmpoil8u52SP3G9u2XZ+JHqZpuoJTJpPB5/MRjUaRJIlwOIzf76darW7JSCiXy6TTaaanp1ldXaVWqx1oTNaNGsZXlhCCMr6fOYvY790PH0Z6gmnvH+wdgDpuOI5Ds9ncswSrWCzSaDSYnJx0ywBarRaiKLplPD1z2OPKvfoEPGwGi3fDviVQURRJp9P09/dz9epV72buceRsbGzsefLvJgTcjiAKyBNh5Ikw2vdnuqLAW0Uav3kNQRW7mQKPJBDTp1cUsG2b2dlZzpw546VFeeyKcq6f1l9fx7i2gXquf8/t+/v7WV9fR+yY9L2+iumTu4tT2yF2JU9tKoER9rnu9XdmAiwtLdFoNNy/xdA5ksEagfoquhpiY+S9mOrO14JGo3HgiYyu6xQKBSqVypbF8OjoKGtra67Q4S6ygwrGhQTNmTr6hwbwv7xO5+kU4etlHP8Ot9XXi/BIHKFugCZjGAajo6OUSiUcw0JomjjR/dd8Kl9fw5qOYA8Gdt2uOR4lcLWE9XoNx7CxCk0c0wZDp3RbJHZXQgpC0wTbgbsoF3Ech5mZGWRZZmRkBEEQtiwMPY4GXdepVqtEo1HK5fKxzOjsdDpomuZ2GiiXyywuLm47vzRNk6WlJUKhEOl0mkAgcFcdCeyKjvEXWeylBsonRpAuxk7tvd5jM7IsE4/HXbNLVVU3+VX0yqlkWabdbtNqtTb99zTQ6XS4cuUK4+PjLC8vbynJWVtbeyDdePbLvfoExGKxQx7R6eGuc6F6rcpOy8nhcXyp1Wp0Op1de6X2Ioh3o+QKgoA8HkYeD6N9XwZrqdHNFPitayAJKI8kUB5LIA0FTuVEoVqtekKAx64IgoD27CSt5+dQzib3PA+SyST5fB5Rv5lW3ItQiwKOKCB2TAjfOo/vnOjfGdGwJZX1zDM0b1R55Ye/wmO/ZhF7z+5jvnHjBslkkmAw6LYm3IuNjY1d25mapkk0GiWfz295TlpuYA0HAAEn6kMrtGkPhba+CIBlwxtF+MkphK8s4YQVIpEIpml2fU5KOk5E2fciW5yvIa426Xx+avcNHYfoG3mMwQD1X7hE8I9uYK91WPvl55n4p88wU9ihhGHLhxVwNAkaJoR392/pkU6n6evro9PpuG0ivYzC+8vKygoTExOMj48zNzf3oIezhYO0FqzX68zNzTE5OYlhGHtmOzimjfnCOuYLa8jv6Uf9wXEE1SuTe1hIJBKkUikqlYrrSdHpdLYtgRFFEU3T0DSNQCBAf38/tm1TKBQol8snPgDqOA43btzY9rnbhfjjSigU2lRGtF/C4bBXGrsLByqKCofDnhDgcV+Yn5/f0+wuFottO1HfD4IgIGdCyJkQ2qdHsZabGG8Waf7uDNi45QPSSPDUiAInoZWTx4NHvTRI62szmDeKKJNbXe5vp6fWGwEFM6AgNQ0sTUbqWDiyiBHZLDxlMplNf+80waq8uIpjObzz332Dd//+J9EGds4KsG17U3aQKIpcvHhx1+1zuRzB4gp9C28h2ia1vhGKmUtuq0JN03a8tsjLTczxEILl4EgCvlyD4vcMbbst16qQ1CCuItRNnHBXvJQkCVVVsUoV7MQ+257qFurf5tA/OohfuwbYtKxzwFbnZ/9CFbnaofiBERxZpDMWpT3hoKhB+mMa3M26/GZ5gLNPIaBSqRCJRJiZmTnxE+iTyPj4OH6/n1ar5fpQnBYsy3LLTno+ONtud7WC8edLCEkN3z88h/iQdhF6WBkZGSESibCwsLCvha5t21tS7YPBIH19faRSKWZmZk5t9zTHcajVase6y1RfX9+eQkCvw0gwGPS8sfbJrkLATguG/v5+RFGkVCodSSsXD48ehmHs2eeYIEdKAAAgAElEQVRzrw4D+0UQBOSRIPJIEO2TI9irTfQ3izS/OAem3c0UeDSOlAmdaFHAEwI89oMg3vQKeH5uTyGg1/4PSWT1Q5MMvLCIr9hCDyisfSCDrd5apA4MDGyZbIyOjm5rsFd+MQcimA2Dt//b53nXb30cObi/832vVOjFxUV89SIDMy9jizKOKBLLzYEgUBh71I0ObTuBtB2klQadZ1IouSaiaePIIlZoh9T+Vwvw7j5oWqCIoHT9BxRFYWBggNzXs9jx/QkBygvrWJkgfWf+hLD8IiDQMB9jrfMzwK3rklJqE7pSpPjBrghAy0Rcb3Hhlz5DLVtmOXd3KfpOWEGoG+x3Sd9sNmm1Wm5qeigUwjTNTe7025VjeNw7qqri8/lYX18/tVkYhmGwsLDA+Pg4CwsLm/wE7EIb48+zOBttlE+PIk1HH+BIPR4Ua2trWJbFyMgIV69ePdBrNBoNGo0G6XSagYGBU13adNxFDr+/W7q7m7AcCoUYHNyfybFHl12FgF5f5zsVFVEU6e/vd9NmstnsqVOcPY4PvYjcTmLAbqm9B0UQBKShIP6hINr3jmDnWhhvFmn9wQ2ctnVTFEggjZ88UcCLznnsF/WxdDcrYKmMPLp9jV25XHb7hAMYYR/ZT0yD49D5xReRLT/SZwMgdvuT9/ff8hyoVqusra1t6jjQw3Ecau+UEGUR23Jo3Kgx8y9f4vwvv39fY9+ti0Cr1aJerxOr5MFxsOWuuGAqKqHiCoWxR4nH4zQajW3PF3GjjR2QcYIKgmkjNQw6Oy02NtpQ7MB0BCHf3hRRLxQKnDt3DsWS6KT2FjjE5QbSfJ3258cIyy9iOjFAICi/gdhpYtPNmBA6FrGXc1QfT2HdFE7k2RrmgJ8bX3yD5KcmaBRu82S4rdPATpNBJ7S/zgGiKLo96BVFIZlMkkgkXJdqy7IwDMON3MzPz3sBhUNClmVXaCsUCpvOy9NIu90mm82SyWS4ceMGnXoL8+9ymK9sIL9/APnHJxG2M+48ZUiSRCwWo16vb3stfVgxDINcLud2oLgX1tbWmJ6edrNsTiM9I8HjjKZpu37/yeTOpsIe27OrELCfOsvbDTc8PI6KfD5PqVRifHx8U317Pp8/8uNPEASkdAApHUD73hGstRbGW0VaX57HaZgoj8RRHkkgTYTvqu/6g0DTNBKJxLYCn4fHnQiSiPbBCVrPzxH+qXdvu83y8vIOOwuov/QU1gtrCL9+jTP/08fxDUU2bVIqlXacuBprLczmzYWnA/Gn+un78Mi+xi2KIqOjOzvwLy523f5tSUG4baEv2Db+vhTnz58HYHZ2dtv9peUm1vDNMgXDJmhlcYQFfEshygMXMNXbvAJeK8JjCZBExJrR9QK4SU9kEIpt7LN7uCIbNsrXVtGfGwSfguEkUYQCDgKWE8bm5nXRdoi9kqM1GqYzeOs1pesVak2D4otvMvkP3s16tUAkEiGZTG5qJSVJkttqrmeY1Ww2MZIaTllnr6vt5OQk7Xbb7RPfExi2a/0Uj8eZnJxkdnb2xDl274amaW70qvf5BUHANE1qtdqRRd78fj/RaNT97h+GuVm9XmdtbY2x9Cjv/PM/w4kr+P7xBcS7MN48yUiSxPj4OKZpkkwmMU2TUqlEvV7HMIyHWvj3+/2k0+k9XfX3Q6+UbHh4mNnZ2RP7vUYikRMduI3H4zsKAaIo3nN3gYeRQ2mcensbKA+Po8I0TWZmZojFYgwMDLC6uvpALmjSgB9pYBjto8NY+RbGmyVaf7KIXdXd8gF5IoIgHR9RoCfYtdttFhYWGBgY2BSZ9fDYCd8Tw7T+dg5ztYqcjmx5fnx83DVhMgzDjfbGIjGW/8GXMIptLFVm5o0vMfUrP4B2/tZxNzo6ypUrV7ZdsChJjfP/6hm00RCXf/HrTPwPTxA6u7/IjiiKWzoI9FoDVioVbNtGliSk4THE0iL+Zh3TNLFFEfuJ51hcWKDT6ey4kJKWGxiPdtsRRWrXCcVm0Y0QWnGNYHWZ7NlPYCn+bivBt0vw09MACFUD+44a+3arTfjsII347tcL+aU8dkrDnghjrja49rWPMf4zlxEwKRo/QM8jIHS5AKJA/fytdklC3UAsdCheL+J/qh9BEJiamqLRaLCwsLDF80cURRRFcRe0g4OD+H44013YyiKtVgtBEFAUhbW1NQRBcMUERVGYmZnZ+0e6iWEYxz4ldb+oqkoqlSIYDFKr1Vw3cuiKPr2FSbvdplqtUq1WD1UAqdVqXLlyhXg8zsjIiGt0VqlUTuzCZS/stRZr/+Ea4kfPc/Z//zjzK92uAz6fD0EQTrWfVU8E6Ikh0K1pj8fjJJNJZFnGsqxNgl6r1To159tu+P1+xsbGyOVyBzKY245KpUIoFGJ0dNQVk08Sfr+fTCbDtWvXts3CKpVKx9ojALqeYNuVZ4RCoS3eQx7741CEgMHBwWPbnsbj9FEulw/twn6vSP1+pI/40T4yhLXRxnirSPvPs9jFDsqlrtGgPBl+IOmJkiQhSRK6rm86N3upux4e+0FQJLRnxmj93RzhH398y/M9U547MQpNli0QFRHbtGivNSh++QpDtwkBPUM/XdeZnZ3dNEEVZJHEc8MA+Pr8VL+T37cQYJomjUaDdrtNvd5d5Pc6kIyMjKBIIsKrX4Glt7AsG7Qg0vkPsv58mb5gH5JR3Pl+ZtpI+RbtdFdoiBpzmKIPS+5G5GW9QaC2Si0xCZfLMByAm9FJoW64XgCiKBKLxaiuFhj8zCWq2cUdI1fCWgv5aoXmZ0Zp/u4M9S/NIcgCaz/5s5u2863U0VbqFJ4bhdtKlqSZKsagRu2rVZL/7N1sbGygqirZbHbb97Ntm06nQ6fTcSP5wkoT+fkcxucnCYfD3W4HgkA0GsWyrK64IsvbRv53ovebTE9PY1kW6+vrJzJaJcsyqVSKSCRCoVBgZWVlx+NHEARCoRCRSIT+/n4Mw3BFgZ2yYwKBgJu2e3spWrPZ3OKx0Fv8FwoFt142EAicutpmp21i/M0q1htFlOfSFIYs/JiMjo5SLBZdIcQ0TYrF4hYxRJZlNE1zDeJOGtuJAHCrpr1HT9ALBAIkk0n8fj+Li4snwiX+oCiKQiaTYXl5eUcjyYPS68QRj8dPVOmNIAhMTEwAMDY2xvXr17dsU61Wj322qCiKJBIJt1tIL/vvuAsYx5l7FgIKhQK2bTM0NLTjpMLD42FASmpIHxpC+9AQdqmD8WaR9l9msQsdlAuxrihwJnJkooCmaQSDQaLRKIFAgGw2u61gMjU1dawv9B7HD+29o5T/zTxWvo7Uv0OLvDswy22wHURFRtAExn/5e4l9cnrLduVyec97R+hcjOrrGwx9/uye79ubKCwsLADdSeHU1BT5fJ5Wq8Xs7CzhjRlSy9/BUAJgCYg3sujtd0j/2E8g+/348mXqO7y+lGthJzS4aYAoGDa2f4f6/lcL8P5b3iZCzST0dIbgUL/bfUf2CzTmN8hMZigWi7RaLQzDuBXJtBzUr61SkaH6L17Bqes4HQv1idTmcdV0Im/kKb0vjaNurvWUZqpUym2CUxHkmI98Ps/Zs2cJBAL7XgQ54VseAbdPru9lot1sNrl8+TKSJOHz+RgdHUXX9RMTxZUkif7+fmKxGKVSievXr+8Zbe25c/e+t0AgQCQSYWxsDNu2qVarbquyeDxOPB7HNE03c8AtJxEEhoeHqdfrFItFGo0GiUQCTdPcTATbtpEk6dgI54eB4zhYrxYw/noF6WwU7ecvItz0wVhZWWFsbIzR0VEWFhZoNpuEw2ESiQSDg4PUajV3YQxdj4FeC+KjWDTeiaIohEIhDMOgXt/pCrM/ei3R9mrB2MvS6n22/v7utee0CgGiKDI2NsbGxsaR/J6O47C6ukomk3Gzy04CgUDAnff5fD5CodC2x2C5XCaRSGx5/DjRO5cDgQDDw8PefPYeuSchwLZtVldXD2ssHh6nBjHuw/dsGt+zaexyB+PNEp2/WaH5xdmuKPBIAnk6iqDc+wWsFxm4PRW6WCxuO/kbGxvD59tnmzIPj5sIqoz2dIbW128Q+uFH97WPbzTKxL/9NKF3DzHzj76McaO8KZpp2zaLi4v7mhCn//45zJbpRqFFUUSSpC0OwvF4nFQqtSna0TOM0jSNZDJJPp9HXCphCyIIAnauhdMRsOducP2nv0Tmf/0YcrYMUg3ObjUAlLINzOEAAGLbpF0awBdaRzI7CLaFLftohtOQa3a7BEyGEQSBYDDI4E++DzuiUGnWKBQKdDod5JfzCJYDzjB9fX3E43FCoRDz8/PYto1/sY0xEcNYKuO0TKyKjhhXUSZuRUAE0yb+8ir1C32Ysc0t0oSKjlA1KLy+QeTTt1Ine62i9h0NDcoIbQssBw6x7MlxHEzTxDRNyuUymUyGtbU16vX6pkW1JEkPPKU5GAzSbDbdEoipqSkqlQozMzMH7n7Qa1eWy+XcGv+JiQlEUaRcLm9butGjl1UyODjopoEXCgXXm6C3UDyJEe/tsJcb6F9ZAgd8f28KcXhzJpLjOCwsLKAoipv63BNdVFUlFApRqVRot9ubfq9eGvn8/Pyhi1CaphEOh4lEIiiKQr1eR1EURkZGNpWGOI6zpXXdbvQWbLdHR/dDvV5ndHSUWq22pxjQK/8RBME1Dz/upNNpGo3GkXbL6JVZxGKxu/ruHyR3GgHuVNKdy+WIxWLHenEtiuKebcU99s89CQG9ydiDvjl7eBxnxJgP3wcH8X1wECwHR7dwdBu7qiMoIoJPQlCl2zt/7ZtepOP2i7ZlWdumgaqququTuofHbvjel6Hyb7+OVWohxf17bi+qErGPTAIQ/76zVP70Gn1//11IYR+GYXD9+vVdJ5aqqjI+Ps7GxgaNtszlX/42T/8vH2PgkeFd37eX0n47PVGsUCgwNjaGNTyJWJzFrHRwqjqyalNfUwhYabRf70PP1hGFWeyfn4bxzSmH0nKDzs0ov2+tQdMYZbUVIRGp44RClFKXuv4Ar2bhXQmSqW6HnXarReWPL5O/oILv1qRMLHUQpzoEjP9CMxcjx1OMjIx36x0daLfWUd8/Tbhe5/Jijc7LeTAcpN4iyHGIvrqG3uenNbbVw0G6XsXoU2mtN0l/aJhkMkl/fz+6rm/bsnFHRAEnIEPdcEsdDpt8Po+u60SjUYaGhtB1Hcuy0DQNURQpFousra09kHr3SCTC8PAwlmW5Y2g2m4caDGm1WrRaLXK53J5tsqArphWLRYrFIpqmnSq/hdtxGgbGX61gXa2gfGwI6Ym+Hbv1OI6zbf2zrus7LtparRYrKyuMj49Tq9Wo1+t3VeJyJ4IgEIvF6OvrQxRFqtUqq6urmxb5iqIQiURcQVMQBEZHR6lUKvs6xnttk+/0QtmLVqtFsVhkYGAAn89HvV6nVqthmiZ+vx9N0/D5fK4AYJomtm2jqqpbMlQoFI6khEdVVbdssd1uHyji7vP59sySOAyKxSKDg4MnRgi4s832Tt+rbdtsbGyQSqW2fd7j9HHPq4KJiYm7Mgby8HgYiUaj+Hw+ZFl2L8hGpcXKwjJWRcfOtVA0BXkghNLvxxYc9wbsOA6iKCKKoru/oihuGuid9FKi76RXhy0IAtPT057Jp8ddIfoVfE+O0P7GDYLff/Gu9o1+eILSl69Q/+YC0U+e3bJYCQaD7sKv1WohSZI7IRwaGsLqS/HWyt9SejPPwKNbhQBd19368t0mjoZhMDs7y8DgOeLVFZQbVxHOhWkVZIp/MczFykegKBEtTWA8rrIxdEfErG0i1gzs/u7kW8s1qNYN/vxfZUm2RM795nvw+0LQtuBqBf7rsxiGQafT4cblGbSXF+HxzZEMuV4mNfoHiLQRcFDIk81+P4okE3qpRNVnIqo1psYm+Z5f+XEsx2L+S6/RTHQ/Z2C2jNgyKb97+97J8vUKhUKT0CN9DE2MEAqFuH79+oEi2E5YQagZOEckBFiW5S5s4VZtfKvVwnEchoeHmZycpNPp4DgO7XabZrNJu90+UnFAURSGhoaYn59HEISueaLPd6RRx7v9PCelnOJucCwH65U8xt+uIj2WQPuFiwja0YjZ1WqVVqtFOBymr6+PcDhMNpvddN/tGe/thCRJbpS+3W6zurq6Y9TdMIwtx08+n2doaIjz589j27b7r9Pp0G633f8GAgHS6TT5fP5Ax+DGxgYbGxvIskw4HCYcDrvnWaVSodPpYJrmluu0LMv4/X76+/tJpVLk8/l7Ekx6aJpGf38/wWDQLTcOhUKkUinW1tbcEpfe3Kk3xh63Cy+O49yXFoqNRgNJktA07USce3cGgXa7T66vr7vdZDxOP/d8RdU0jbNnz1KpVFxzpp0mGIIg4PP5TsRJ4+FxWIyNjW1rZGIHg6yU15FQEJMadllHx8Co2zirbWKRKOknp1EC+590VyqVfaUW9roIbGxs4DgOfX19XraAx55o7x+n8u++gf+5ScTIVhFqx/0yMXwTccp/co3Ix86gaRoXL16k2Wwiy7IrSvl8vm3PFcknM/SLl2gOmiwuLjI0NIRt2/ta/N+J4zjk1jcop55CuRLjzbdXeOZHPsT5s8OI/0Kh7WuiiApaIwHq5nuVtNzEGvSDJCAYNtZMmYXvrKNWLeyOTfkvl/B/4VK3U8B4CEIKlUqFoaEhfKa4qXUgALaDYucRZAOTBAIdAlynADivrNFYqmP9YAY9X+fFf/67RL9wgeBkH5Off7Jb4lBpI5XyrD81uCVdXxRFxLIOukXxrSLv+Y0fwu/3Mzc3d/AU354QsI9NJamAgI1pHbw7yZ3XssXFRXfRIggCmqYRi8XceUWpVDoSA6+RkRE2NjbctlVzc3NEIhFvLnOEWPM1jK8sIfhlfD99FnHg7iLfB8EwDIrFIqVSiUwmw8WLF93HTdPE5/OxuLjV1NPn85FIJIjFYlQqFebn5w+0GLUsi6WlJSRJQhTFbuvim/4ZvffQNA3Lsg6ljKHXanC/50yv/WWtVuuWOg0OEg6HWV5evivhqiesqKpKLBZD0zQ2NjZYXl52r02FQoFgMOgu7i3LIhAIYNs2sVjM9dqwbZt4PL6n8HIUbGxsMDk56Xq69Loz7LYOelDE45uNdvf6vZaWlhgbGzvKIXkcEw6tfWB/fzf90bZtZmdnt70I9hT8XsrRdulbHkfL6OgogUCAxcXFHXtxehwOkiQxMTGBLMuuc3lvQuE4DqlUikceeYRisUgul8NOdGv3Hd3CCUqUpSalF1/Hd63DwGMZIk+kkQI7mJLRVXj3Y9jpOA5XrlzZ9Fg+n0eSJFKplNdRwGNHxKCK+vgQrW/OE/zU+bvaN/aJMxR+53Var+cIPDkEdCO++0W2RfS1FtV45VDSUvXlMm/+ytv8xzcX0fMij//3z5GJZ/BtBMAB54NtNE3b1HVDXm5g3UzJr/7NIquvrWM2THw6oAhUvr5C6vNnkF4twseH3PdaX19n4skLNAJxlsWa+3pCzcAwkjiiH4VuFLzEkwgVHfk7G3Q+N4EDNP7TLNoHB9HGYvT393fFu0QfdnUW+XND0ArjD3RNQtvtNoIgoKoqjmHRTA5ijM2SODO4Y6vG/eKEZKjvPcGNRv4LffEvAlAs/xDlyo8c+D3vZDsDsF6t/FE4ecfjcVRV3RJ5PYndDU4CTlXH+Ooy1mId5RMjSJdiO5YBHNkYbnoN9ATzHr0WZaVSCU3T3MVsz9/i2rVrh1KaYVnWptc5jnO1RqPB3Nycm6VzuzhimuamdrI9c7pgMIjP58O2bff5arXK4uLitgvT2zsghEIhQqEQs7OzOI6DpmluacVBhZd7pZe95PP50DTN9aHRNI16vU4ulzsWgkAvq+V29goY1Wo1dF33MkcfAg49BCiKItPT0+i6ztra2rZpQz1zlF6qT7vddk8gj6MlFApRq9WIx+PH8uZy0hFFkXA4TH9/P7Vajfn5+R1vBMVikVgsxtDQEIlEgkajQblcpl6vY/RcvyPgyCrlby6y/OvfIXixn+jTI0SfHEIK3rpAdzod5ubm7ik91rIsyuWyJwR47Ir2/nGq//cL+J+dRAzuf5IQfnqE9d96jepfz7pCwHaYpkm9XkfXdfx+P8FgsLvQS8QoUae5UCMwvrUW/q6wHbSvLvHqaglsh+e/Pc+48Tj6P7tC/AWJ9ohC9KzM8PCwOxHSdZ1WTmJV7U6gzNfWWSl38Ge7fzuOg9OxqXx5gYTtQOaWkVmhUKD29TlSl8aYmpoim83SarUQix0ELYLd+KdImRu0dD+V+hTK1xYwn0riRFU638jhOBD/9BQjoyM0m02uX7lG8rUXiTzyRxjLIiE1w3rjF1hoWvh8vq7o3mrh/715nLE+xn70UXexfC81rU5YQSjtJeCb9MW/iGlFAYFE7A+pVD+N4xxdRLfnsH8U2QC1Wo10Ou3eOz2OBse0MV9cx/zmGvJTSbQfvNj1znmA3Cma9f5WVZVAIMDCwoJbtvIw4jgO2WyWaDS6yYyuV3KgqiqKotDpdGg0GqysrByojEeSJIaHh8lms+6+vQj8cWBLq1VBIJVKcebMmQOXbxwmd7b33a7sQxAEZFl212fQzcA6c+bMfRmjx4PjyHKBVVVldHSUWCy2Y82yZVkEg0FGRkZYXFz0brL3gWq1SrvdZnJy0s3KMAwDXdfpdDqn0mjofjEyMoKmaeRyuX37ZpTLZWq1GhcuXNjSj13XddcbQHxOxGroVL+7SvnbWVZ+81WC55NEnx7BmNTIVw/vRjM7O8vU1NShvZ7H6UKKaqiXBmi/uEDgY1vbAe6EHNUIPTVE++08+kIZdSzmPlcul1ldXd39+tPvoClBCt9YuWchQHm7xMa1AoWmjiqKNGodvvPHV/jBdw8QTDbJPz5G7Y8WYHYR3pVAlmUmxyewWwbOgAqWw7nHklQvJjB/5Qo4Dk7bRgopNL+1RuKnz8MdUUxno0Xu1VlGx+NkMhnarTaduTli/82j6O+skjfShCNhzqbDmF8YQ4prVPMVQj8+hfIFze2Hns/nCb+Zxz/yEpYmYdlh5PYNLPtVFPVJN01eXG/j6CZLfzbD2E89xfz8/L27x4cVhMU9Um8dAcfWEMU2OCKOo4JztGVH8Xjc9Rc4bJLJpGuo5nE0WNcr3TKApIbvH55D7Nt/2dH9QBRFIpEIg4ODLC0t0Wg0GB0dRdO0U9OR4V44DJ+A3RgaGnLLj08CjuOwtrZGqVRiaGiIWCx2z4Gae+HOdoDbfY+pVIr+/m4ZV0/U8MpFHw6O/FcOh8NcvHiRcrlMuVzectGsVqtkMhlSqdS+0po9Dofr168Ti8WQZZlgMEg8Hsfn8yEIAo1Gg2q1Sq1Ww7IsJEly099uVwt7iKJIMBik3W5v+/zDQCKR2HshswO9i++d3JmSJQVV4h8cI/7BMaymQfW1VcrfylJTNeyagbXSQLkYRwzuXD6wF70skVarddduxB4PD9oHJ6j+6rfQ3j+O6N//8Rb5wBjrVwvUn58n8V897j7ebDb37r8uwfrvzdAstej7wM4ZBXviOPheyPH6QpGmYWHbDugWb/znq/xgyg9+BV+9Q+fJPoSvreI8Fqevr49OsU5pPgcTQ6iFJmZYpTJT4clPZah9bIT1P54n808eg1+7Co/Gt7ytqqjEPngOSZK48cIb9K87hKYGqP7aCzTbDao/Pk1tpUDpy0vYP3oGc0NgkDjVRpnc8i2hT1us4ss3aT6aJswSkmggIhKJDBNJjdNoNOjv70dKj1KLpUgGNNpGh2azeVdlAb063kQi4XYcqQYLVK+8iZvj5Dioqw2UYhtlo4261kTZaFL8/BeIPvbbCFis5X8eh4Nfk/ZDs9k8kozCYDBILBbj2rVrh/7aHmAXOxh/nsXJt1A+OYp0bmu7zgfJwMCAu4jSdX1TXf7GxgZjY2Ooqsr6+vqJaK13Eul5gJzE9UHvmBkfHycajW7b0vl2el4QvTIDTdNYWVnZV4vd3bgzI2C7FtK3Z4L6fD6va8BDxH2Re0RRdJ1U33nnnS0XzGvXrjE6Orqvdjkeh0Ov3/CdSJJEKBQiEomQTqfdvt2dTsd1bO21OHIch0Ag4IoAPp+PVqtFqVSiVqs9FL9lz7DqIJEoWZaZnJw8UA2WFFCIP5Mh9J40N2bn6IR0jNeL1P71G0gjQZRH4yiXEojhg03AC4UCIyMjB9rX4/QjJQIo00k6Ly/hf3Zy3/sF3zWII0DjlWWinz2PdNNwcLvuF3ciiAKdhRq12TKO7SCIB6wbFgQaP3GGkUGFH/hmiJcur/HoBzI89a4EWkDGBgKlFp1exsJig9j5GNnfetH1B9ByDVr9ATa+PIv2yAAVAyS/DG8UYToC2zibx84PIYd8zM/P47+8irRwndZfGuhWCns6CY6D8rer6GfDmD6b5n9eQDmTZuj7LqAtd4145UqH8DsFOh+eJJW4iCzIiNYiduBzSOIj3Lhxo+u94ziE/mQVMxVBGggQT2eYnp5mY2MDv99Pp9NB13XXhKsXIep1JOnr63Mnj47jkMvl6HQ6xENRxv/JhzEkm3a7zVouR/TFVZRiGweQWiZ6v59K7F1Usu852O9zADqdDpIkIcvyodbkdjodDMNgaGjorg3RPHbG0W3Mb+QwX8ojP5NC/twEgnL8HMr9fj/ZbHbbbJBWq8X169cZHBzkzJkzFItF6vX6sUlXPy2k02nm5+e3Pfd6XRoMw6BSqRzb87NQKJBKpbYVAnrX23g8jmmabslDp9MhEAjcc8bJ0NDQFvf/O+ec4XDY6xDwEHPf8z76+vrI5/ObHtN1ncXFRa+jwDHAsiwqlQqVSsV1rL19YqUoCn6/H7/fjyAIVCoVstkstm0jCAKRSIREIsHQ0BDlcplisXhqTSF7389BvRYOKgLczvz8PLppIIgC/k+Pon1sCPNaBf2tIu2vZpEyIZTHEijnooih/b9XuVze9p2tT2kAACAASURBVAbi4dHD/+wk1d94Ge19GQR1f7cSUZGIPJOh/dYajW8uEflUt7QgEomwurq650QuOB2lMlOmvVzHP7q1u8B+caIqY+8bxicoLGy0GMiESMc1JMPGkgWCxSalTAznySTS5SrCJwTkjTbmUyOkR4fxiTFurJdInutDEgVsw0LUJHitCD+Qcd9H0zT8fj+O42DPl3FEAVPXiYev4hsqIwR0VMMgrw0gXasi1EzMTyVxsi0Gp0eJfjiDZVmMjY1h6gbiagXpZ88ihQLoL10h2/8ROkYLozIALN/6nleaGNUm7/zOW0z/+48QuZnZFY1GKZVKqKpKOBx2O/nYto0sy265WKvV4urVq27t/eDgILOzs6zmcxR/6evwc5eIJGKcmZ5m/v01En9wFSSxmyXxgWE4qEizT2RZJpVKEQqFXIf1SqVy6MZcpmkyNzfH0NAQk5OTVKtVRFGk0+nsGd3z2IrjOFjvlDG+mkUcDeL7xxcQj6gV5WEgiuKux5RlWSwvLxMIBIhGo4yMjCDLMo1Gg1qt5h0jh0CtVmNwcNAtk+zV44uiSDQapVqtEggEGBwcpFwus7a2duwEgd5nGB8f3zS2XiCpVCoxMzOzKaN2cnKyayJ9D5kmIyMjxGKxLY/fOa+LRo9XJo7H/eW+CwEDAwNun9DbMQxjk9mIx4PHcZwtN8GeC+x2jsmO47gigqqqxONxJiYm0HW9a5Z1irIERFF0MyJs26Zer28yFdsPhUKBdDp9T+NIpVIsLS25fwuqhPJIAuWRbjqjYzvQtrAbJo5odifoIptMmO50Rr59fDuVLXh4SKkQ8lic9itZ/M+M73u/yPsz1F7KUv/GPOGPTyHIXUfjS5cuoeu6G1nr9Yq/Hd9YGEkVacxU7kkIABBbFrYm4bOhmNBYu5AieX2DZsyPZNsk+/pI/tgFjOUqdsdg4GefwdEkmuUKnbUy4f4EP/bLP4pg2/SbNqvJWUY/fBZHFty+14Zh0Gq1EByIfaZr9CeZbeROE7utYEsiUsJA7wugfGONzmdGsXWLzleXefT/+KzrndBptxmfqSP4FTqvtxAKNcypl0nJ3wAJKub7KRg/euu3manS0i2CU3Gmv+cSxWKRmZmZHa9N4XAY0zS3FTVLpRKyLDM6Osr8/Dy2KmBs1MlbRrfLiK7QOBNDW6phJP10RkL39LvshSRJnDlzhlKp5JqxHmVatuM4LC8vE4vFUFUVy7K6pReS9MBNwE4Sdr6F8adLOA0T9bPjSJP3dv4eBqqqYhjGtvOSnnnafo6tZrPpRm5lWSYUCpFMJlEUZUvgy+PuWF1dJRqN0m63sSwLVVVdQ9SZmRl3jqooCgMDA0xNTbG4uHjsAlDz8/PbpuRvV7I1MDAAcE9CUiaTIRLZn5dONptFUZQtJQQeDwcPxAmiF5W4Ey8b4PTQ6xqxvr5OOBwmkUiQTqfdnrUn2Uugl34aj8e31FEJgkCpVGJtbW3P16lWq6TTadcUcD/GLLZtu9E76J5L+1FzbcOi+kaO5YUl7DNBrNUmYp+PkBYknIqRy+W27OOpxB574X92gtrvvor23gyCvL/sEd94DCnsw5FFWq+tEnhq2H1OVVUGBwfdv4vFIisrK7f2HQsj6jb1a2WSH7630hWhZWILApom09ZtOgEVS5MpTiZQVJWxRIJavUb1nSWaX5ujvxknWPbhk0zyz1r88b9+nh/9P7+fpBrkykszjJ4ZIfutqzQHuhHqXpq9JEmUrq1Q+nYR/bNjWLKG3VFR5BqCDLWhcZhrYZ6P4gz4af7uDKFL3XTXXjp68GqJ5nodTQX5/2fvzYMjzc/7vs979ttv3zcaaNzAHDu7O3vvitQuT1EUxVCkSF22DlOWIsmWUqWK5VQlKldciitRUkmciu0SncQlKUpk2WRRikguLZJLrZZL7sW9d3YGg/sGGn3f/V75o6ffHQyAwTEHsDP9qULN1ADd/U5349e/3/d5nu+3ZWKqIp6BZ2k5IUAkpDxPwfgkNn6wHKSZCvnpPA/94acpFov7Hkb2M8LLZrNomsbg4CCroXmEUhvffIn8hSrBzzxI/nQQ5+lL1M7Gdpgk3my6h7eDrLE3k6s35aVSidHRUWzbviVJBXcSTtPE+O4a1pt5lA+lkR5NIEi3Nw5wN7xeL6Ojo0Cn86PVarkt2YZhkEqlaDQah46l60YJVqtVxsbGaLVavajJG+BaE9BWq7XremUYBsvLy0SjUcbGxlhZWTlRBp/dItp+xGIx/H4/8/PzR36s4eFhAoG9hbbdulzm5uYYHx/veUPdhRyLEJBMJnsfnncJjuNQLpcpl8t4PB6i0Sjj4+NsbW2xtbV13Jd3JLoiQCKRYG5uzjVUbLfbSJLE5OQk+Xx+30XfMAzW1tbI5XKIosiZM2f2bcWfnZ2l1Wpx7ty5Q12zqEjU0wKOxw+OgxjT8L5Zp/78PJUnozhDXhBBinZmtb1eby8/tse+yAMhpFSA1msraI8OHug2giAQ/OAQtdfWqD47v00IuJZoNEowGGRmZgbDMJAjHpSASu1iwfUvOSpCw8JyQAtrVKttlJaJ4ZHxBwJkMpn3Yp/CFv63m/h0GSMpoK3YSC87hIaDWJaBqKuc+fHzGNka8fER6s0G0WjUnfdUVRU141Cdqneqj7Nlcn8bQ/5IGiyRsjSCvLmF9fEBzAslxJrN+C88Qq1Ww3EcPOs19MUy+R9Jk5jN40gComlhEkCiiYOI4yg4dH5fxZUatkck+dEzaJkgc4vzR36OrmZ5eZnBwUHSP32e0p+9CKeCrJ/zYhQLpPpSLH28fcszs0VRpNFoMDs7e0sfZz8Mw2B9ff2WRRbeCTiOg/V6HuM7K0gTQbTfvgfhBoxsbzbRaJSNjQ1yuZxbZdY0Db/fj8fjoVQq3dAexTRNFhcXGR0dpV6vn4g8+TsJQRBQFAVZlt2v7j6sUCgQi8VOlBBwUCKRCCsrK0dO8BodHd23sr/XOOvMzAz33HNPbyT0LuNYhABFUXrGgHchrVbLPfieOnXKNRe8FZFPtxJVVUmlUszOzrrtZ91F27KsQ7WpdltLbdvm0qVL+Hy+92aKbRtVVV3X4qsdi49CX18fgUAAwzAIBAIoDynYv2iz8tosxVIBwipOywIBEsGdc2U9euyG98Nj1L78Fp6HBhCkg20ggh8YJP+NKeSwRnu+gDqy02W/iyzLTE5OcvnyZQzDwHc2QuONLZqrNbwDR29DFxomtuWgRTW2qq1Opd0j09/fz8bGxnubSF1GVEQcy0EwbQQcylsNRr4wjNU0WP+T77FRsLnnt36UWrOBKIosLCy4rcKKopDWovT/zMPIfo22J0/9iwlIaRitVYarX0H9oow4MIY1/gj8lECj1SQQCBD2+FDemKf4cJLwWoVKyk89qBF+ZZ32336G8Me/i4DJVvsLrhAgXy6j3ZMm/mNnWVxZummfs45tk33uHcZ+/DGyYQ3nyWHiV5ywg8Eg4+PjXLp06aY81rUEg0H6+/u5ePFi51pOwN5BVVUkScLr9e7YWPt8Pvr6+vB6ve5oXLPZRBRFJEm642fH7dU67a8vgu3g+bkxxMFbOy5yWCRJIhgMup1w7Xabdrt90w+O3WJAL5b55uH1el2B2DTNbV+2bRMIBPB4PO+7fSW8t6Yc1XcqGAweqL3/et2npmn2ikB3GccWEinL8vu6PbzH0Wm32ywvL5NIJIhEIti2Ta1We9+8H7pVoJs9g2ZZlts90UWWZaLR6I4ImbW1NVKp1KGUW1EUd7SLibLI4KMTDAJm26BycZPqy+ssvfw8Slgj9FiG0OMZtIEby23vceeiDEUQQxrtt9bxPHCwWD857EUbiyBoSidK8DpCAHTeu10xIPbZMcrzZWqXSzcoBFjYho036qVZLiM3O0KAIAj09fWRTCaZmZnBWS7ROqtSm64TKgUwwwov51b5+Z/+JRzDQv2dCdKmTWEuS1Yo7ep/s/LVl2k9v4HTMomNR0n8/o9h5Cv4rS8jRVcxmjLt5/4Z82u/wfjPP4Wu69SqVZL+MPznH0W8MINh1mi+XUZ9ZZbmSgPzkRhrH/pvCAQCaF4BxbLQVA/+TyaREn4ufPlFlA/cHI8PoWUReHUTqWXhCAKGT6Xvyvodi8WQZXnb4TyTyeD3+/cckxIEgXg8TqvVolqtbnvOfD4f6XR61ySJTCZzYmLEisUigiCg6zqmaaLrOsFgcIcDt6qqO7xg3k+fd4fBqZkY31nBulhC+Xg/0oOxG+rauVWEw2E3HvlWEgwGqVarJ0K4uhNIJBJEo1G2trZYX1+/4wSWQCBwQ2JUf//BPn+vbv9XVZVYLMba2hpAz6vtLuTYhABFUe7ID8IeB6NYLFIsFvH5fCQSCTKZDO++++6JX9hFUSQcDjM3N3fT7/vaLhlRFPH5fMzOzu6IkMnlchQKhQONExwUWVWI3D9A5P4BnC8+RO3iFqWXlpn9F88i+VRCT2QIP57BMxA8kZu7HseH98Pj1L7+Lur59IHfG8EPDlP67iz2fAGr1EQKXT9CsCsGXCi+Rfyjg1Smi8Q/vPdYwX4IDRO7baMlvDRXt1BaJjWfzuzsrDsjPDIyQn7lMtaHh5F/VEN6fAgxoPKLyhNU61XWXr6E9uwKcy9tof3COIFHds9edhaqGLkGYa/I5psb9Oky2X/7JvFH52n1+bByNpJgkf7xDKZpMj83R/DVDUqAen6A2NlxDH8Cj7FGq99CemAQ/z84jxbxU61WsSyrk0Etq2y9cIEf/vJzDP7vHzzyc3M1SrZB8OV1WgN+jA+P0qrU8fp0AoEAU1NTOwTRSCTiOlUnEgkCgQDVapV6ve7OXweDQbxeL7quMzAwgGEYbG5u4vP5tuVZ73jNTtC6Y5om2WyWaDTK6dOnj/tyjhXHdrBe2cL47irSfVG037kHwXts28t9iUQi27xHbhXBYLA3OnKT6O/vx+v1Mj09feL3iUdBFEVisdiRhc7BwcED+Ux16RphTkxMIIoiXq+XtbW1E7XG9rg9HNtKrWnaDedj9nj/U6vVaLVanDp1iuHhYba2tk60sU5/fz/VavW63QC2bePz+Q7d/nlt1cC2bUql0p4/fytNXQRRwH9PAv89Cfp/5QHqUzlKLy4z+98/h6TJhB7PEHoigzYY6n1w9EAeiyKoEsaFTdRzqQPdxv9gms0/e53wg2lqzy8S/NSpfW8jiiLesA8sm9p06YZ8AoSGiW04eAf8NKvtzmiAJmNeEagbjQbBYJDIRD+O49B+cZXFf/RVXhiRid+bJP1oCtm0cTaamEGlEx+4B/KwH9+H+2iNBlHbFmWjRvhn7qNa+SQR+bsYQh1x7HGU2Dgrq2uE1l9F9y1RTD+CdnGFaatFYB38XgXfrz+G3TLxhDuGUle3kcaXbOIfP4PvK28h6jc4j207+N7No82XqTyUpJ32IZkGqk8j/en7d63I+f1+Bga2izOapqFpGs1mk5WVFWzbdoVg6BzuuwLA2tqaW1E3DAPLstB13Y0HvDoh5SSg6/qBq3BXc6NFEI/Hg67rCIJAsVi8pakJ+2EtVDG+voigSXh+ZRKxTz+2azkI3a6427H/1HWdzc3NW/44dyJdF3ufz4ff76fVajE3N3es7/VbSX9/P5VK5dDvS0EQGBsbO9R+0LZtgsEg8XjcLSTpus74+PihHrvHncGxCQE9M4oeXUzT5MKFCwQCAeLxuJtZfVJUX6/XSzgcdufr93NzXV5eZmhoCFmWb4khoqZpZDKZXVtnbwWCIOA7Hcd3Ok76l85Tn85TenGZ+f/peQRZ7IgCj2fwjoR7osBdiiAIeD80TuO70yj3JA/0PhBVicDDA9iKSO35xU6UoLJ/W6ItOgiWA5ZDa6OO1ne0yKPOaICDJ6VjNE2clol5VaxmpVIhlUhSf2aG8tOXEEotjJZNpdTmzM+d6dxHoQV1E9svI3r2vvb2xwdQX98iWFIxBYF6s4EvGkBL/hyFi6fxn/Uhxs+ytLyGr/a3xPr+GHtMIWj9gFzynyPZXqqXF6jPlBD//DXsPi+e33uMoaEhFhYWOt4hhk3tm1PYkodH/+fPUDQqR65GijWD4MvrOJJI4WOD2Fpnq2BZFuViiUgqRrQukU6nsW2bhYUFPB4Pg4N7G0ZOT0/v+u+O41CtVt3Rp6mpqW3fVxTl0N4rt5L+/n6CweCBqm9bW1uucWxX6D1M1Q5wxw+u/jJNk3q9jiiKrvlyLpe7rYZ0TqWN8TcrWPNVlE8MIN0bOZHrvyzLeL1evF4vPp8PRVFuSzcAdEb4BgcHyeVyrg9Bu93ujQrsgSiKxONxwuEwoihSq9WoVqtks9kTFwd4VLxeL5FIBMdxaLVatNttFEVxux0OQ9ec+rBrSrlcJp/PUywWOXXq1KFv3+PO4the/V5UYI9rqVQqVCoVhoaG8Pv9162G3wjdg/3Vs1DX28Douk6hUGBxcfFA79tms8ns7Kzb4to1iJKkTqxYu300d21N00in08ea9SoIAr7JGL7JGOm/fz+N2QKlF5dZ+Jc/ACDcFQXGTuamsMetQzmToPHMZYzLW6inDjabHvzgEBt//Bq+Pj+N19bQH9s/EtCyLARNQg2q1C6XjiYEmDaC7eDUDMSQileTqZrOtui7YDCI0LJpPrcAgKiI2DYM6xrKlWq7cKmMk9axV6uIe7VCmzbSTBnvhTrJXz1D9dsXWdrM05yaw+rXMfQgYkGGwixiy2R04BICCRACWMYmPm+WsHQG5bfGMJ3OdVstk2Kz4madA0hzFQxV5O1/+g3Of+WnSPWncRzn0J1JnuUK/tez1E9FaEyGd8QBrqyvUviXLyB+8Sy1VgNVVTFNk4mJievebzKZpFgsHmpD3+0MOCkcxJH7ajY3N3cIGAdd+8PhMLFYDFVVaTab1Ot18vk8y8vL20RyRVGIx+NMTExQLpfZ2tq6pYcmx7Ixf7CJ+b0N5IfjnTEA9eTMFauqSigUcg//giDQaDRoNptsbW3dVif5breGruv4/X5UVUVRFGzbxjAMTNPEMAx373OnI0kSIyMjiKJIq9Wi0Wi4EY3dCnW1WmVhYeHQsY0nHV3XSafTiKJIodBJvfF4PK6ouLy8fCiBSNM0xsbGjlRU7XapdE2qx8fHb1thqcfJ49iEgDtF3etx86nVaui6ftOFAFnuOIJrmkY+n9/RgrXXIlwoFLYZ9R0E0zTZ2NhAkiTOnj0LdOb6NzY2DlzZUhSFQCBANBo9kYu0IAjo41H08Sh9v3AfzYUixReXWfxXL+KYtms0qE9Ge6LAXYAgCGhPjtF4dhZlMn6g11ybiOJYNspklOqz83gfHdj3dpZlIQVVJFmkdrlI7MnDt2YLDQvbI+JUDISgiu6VqZg21x5njEKNRkpBztcQbAfbsYmLKtQM8EgIcxWcR2PYs6U9hQBxvY7Qtkn8Fz9K86/exvjyG/jHg9Q+2o//Ty6T+l8+y+WVWbAdYjNVGL8Pa+slbKeEKYusv1LF+f63MH52DCngATqHnXg87oqLANLlMsW1GsHzcaqNOuqVCC3DMFBV1e1Q2nOzadoE3siiZBuUPtCPGd1jzREEjJaBUauCJGJZ1oHa45PJJMlkEtu2uXDhwq4/I8syuq7j9XrdGDfbtm84MeVmMDw8fCARoLvJVlX1hiq/wWCQYrFIPp+/7v10Y2g3NzeJxWKMjY1Rq9XY2to6svv4XliXSxhPLyNEVDy/dhoxfvI+l3w+H9FolLW1NdbW1o5dSLrWABhw4+4URUFRFJLJJIlEgs3NzUPvNd5PDA4OUq1WKRaLeDwevF4v8XjcHRWen5+/4wSALpqmYRgGi4uLN3xfwWCQoaGhI93Wtu1t5y/HcZienmZ4eHiHmXSPu4NjEwJ6mao99qJer7tmUzeLbvxUPp9naenmRWpdj1Ao5LpFz8/PH+gD3u/3E4vF8Pl876vxGUEQ8I5E8I5E6PvZe2kulSi9sMzyl17GapqEHusYDeqnT6aLdI+bg3pvH41npjHnCyij0X1/XhAEgh8corVZx2kYGAvF60YJQmfjoia80LSO7BMgNExsWURQOl+6R6Zi2Fy96lQqFQbG+rB/fAgn18SZ9PPW3yxy9mMjsNUEScSJqhBUsRvW7h4BtoM0XcZK+9BGIlR+uAxRH+qrOeS38ngfG8QT0QlVQ5RKJaxKjfbFB1BO/SblwuuUZ8/hPCvS/ulBHE3EvnKo6baa67reWVeaJuJKjey7eVK/ez8A+Xwe27bp7+/H4+kICKVSaVcRXi62CL64jhH1UPjYEI5y/bXHjntAEI6UOb3bZ3931n43wVMURSYmJsjlcqyvrx9bW/VBZ3Bv1ky44zjbRgr2w7IsNjc3yWazRCIRBgcHabfbLC0t3fCYnV1oYXxzGWejgfITGcRTJ9cbplgskkgkMAzj2EWAvejG3XXFrXw+TzAYJJ1OY5ompVLJ7QK5U4hGo8iy7KaItFqtE+0HdbOpVCokk7ubyR6GrqB6VPbahy4sLLgJJ1cLAsVikUKhwOjo6JEfs8fJ5tiEgJMy79fj5NFsNlFVFVEUb/h9Ioqi6za7sLBw0yskuz1eNBolmUxu2yBfT/iSJIlkMkkkEnlfHf73QhAEvENhvEPhjiiwXKb44hLL/+6HWNV2p1PgsQy+M3EE8WRuJnscDUEU8D51pSvgAEIAQPBHhlj4598l+ZnTVP92jug/2FsI6K4HSsqLXW6DLtHebOBJHc6gTGiYWA4IoU5esk+TqF0jBDjFJqXvzzL+5P1Y4yO8+h+fJ/GrZxHPxZEulLAiEu1fmkQqtdDGg7t6BCgvrCM9s4zxXz3I7JuX8L+9gfehfuoLZVS/gve+NI5hEpstUYqB3e/DeXWercGn8Md+kuIffYf2p/pxIp4d991oNKhWq4yMjLD49Ou0RbAF8JyPuz/TNeULBAJkMhl0Xd8uBDgO3ukivosFKucTtIY6G8CuUZemaXi9XlRVpVQqsbW1hWmaOBkdsWEfab1SVZV77rmHQqGAYRg71sq9iMVixGIx2u32jjjV28HU1NSB5mlVVT3WjkfHccjn8+TzeZLJJGNjY8zPzx/pUOy0bczvrWO+lEX+kSTyF0YR9hGJjhvHcchms6RSqX39fE4S3c6BUCjkmmcWCoVb4jN0HJRKJeLxOMFg8K4SALp0R0G8Xu+R96GDg4OEQqEbuo7rPfftdpuFhQXXl6TdbrvrhmEYKMoNGtD2OJEcixDQEwF6XA/HcWg2m+9Vu/ZBEARUVd31e6lUCtu2mZ6evmWVJEmSCAQCJJPJPa9jr41uKpUikbg5Wd8nFS0TpC9zjr7Pn6O5Uqb00gqrf/oaRrFJ6NEBwk8MdkQB6WRvMHscDPV8mtoz06y8M0NTwz1M+nw+tzINVx3q4zqewRCOptB8d+u6UYIzMzMAiIqEp9+HIAnUpkuHFgLEhtURAoKdjY1flai2t1dNpZUaW2tblDby9H/qfoT7EkT8Hk6dOU3uaz+gNbdK6GcmyHtVIp8YRJCvef82TTzPrtEYDyPNlGnG2jR+Mo7+egHLEen7H34SyefB/NZrCD+YZ/BslNXTMUxVojq/jlcxyPz+j7G4sbLrwdJxHJaXlzl79izqUo2NlQqhx1K7Vmp9Ph+lUol0Ok1/fz+2bdOsN3Dmczj9XhoPj+NXBPQr88zdyL9ms8nm5iaGYRCLxZiYmKBer1NXg1SXcod6zrc9/1eiso6CqqqMjIwAnSrW7Zqttm2by5cvc/r06esKF6dOnaJSqbCwsHBDj3cjiRhdNjc3sSyL0dFR5ufnabfbCILgtqSLorjjq16vU61Wsd8tYnxzGWHAh+c3zyKGd/9sO4kUCgXi8Tg+n49arXbcl3MoSqUSpVIJj8fDyMgIuVzujjAXtCyLjY0NUqnUXSkEQOd3+iiv5VGSAfbiIF0mjuPs+L0pl8tHXrN7nGyORQi4UxTOHreOdru956H6aroH6b3mR7uRVTf7g1RVVSKRCJFI5ECOq7qub1uAPR4Po6Ojd51bqzYQRPtckNTnztJaq1B6aYW1/+dN2rk6oUf6CT2ewXdPEvHaQ1WP9wW2bbOxuUH+I2EoFHHCHhqNxr7u9cKTfiqrqygfjjL9wwsw0JnFFgTB/bJte9vvsWcogJ1rUJsuEv1g+nAX2jCxfTLioB8ch2gmyIa1fY0QV+sY5yK0Qiorr19i9fkNPvVPP4mqqgia0vFEMEVSpp+Vr1xG+yfBbbf3fG2BpkdETHkQFmoIUyXkoEzlbBT1ixMoA2Gclom93kQcCuEt1hmaEViYjCFuNFmy1ohkFMbGxtja2trxuRkOh0mlUrQaDezZEtmLBTK/tHuefblcZnBwkKWlJWq1Gp58m+h6GybjmCOduD5ZFBEEgXa7zdTU1A7Bfm1tjWw2i67rSJqIP3v8h5Ph4WHq9Tpzc3Nomsbg4CDNZtM1IOu2h9+sUUTLsqjVavvO0gYCAcLh8KGNGq/lZrTf53I5bNtmbGwMx3GQJMk1qeumMXS/HMehv6+f2qUsS6/OoXx2GGksuP+D3AQEQbipn9Obm5ukUilmZ2dv2n3eTlqtFvV6nWg0Si53dNHtJCDLMn19ffj9/vf9/+VGUFX10J053dGog+yHd8OyLAqFApZlYVnWkbuVqtVqTwi4QzmWU8jdvBD02B9ZlgkEAu4s2X7UajXm5uZu8VW9h6Zp+zpkX0tfXx99fX3Yto1pmkde1O8kPOkAyZ86Q/KnztDerFF6aZn1//AO7Y0XCV4RBfz3pnqiwPuE7nyy4zggC+jfWKT5yUHsvUznrsL2iljZGtZ9UcS3CzgxGa7pEPH5fGQyGRYXF2k0GniGA7Q261SP4BNg3BfFmQihtB0kUSL21Ahx//bfSfPBGHgV4v9pjeZAiIA3iEf3YLdM2isl5ISP5kYZIRNF8WwfZRLXangXFwn+9GXUapnK/BB17RFKF4o4mpNl1gAAIABJREFURRPzp4bJ5/MEXlhB6AvCVgshFkZpm8S/U6R+X4j6qEo+n6dSqTA8PIzjOO5nZ19fHz6fj62tLeKhKPFffIR4C+IPZFwvFPe1oFMF2tjYYGhoiOX/7wWUqRzZR1IYcgOyDXT1TRKBPwFE8uV/iG2f2fV5M02TSqXCoBPByJ8Mnx9d1zl37hzLy8ssLi6iqiper5dQKORWviVJcg/xxWLxhsYKDlqV6+/vvyEh4GYeiguFArVazfUd2PXxmhbms2vY7xQZ+O3HOffffYpsNnvL92uJRMIV1BuNhuug3zWNk2XZraR2n5ODPDeGYaBp2vuyK6DL5uYmo6OjNBqN961fgN/vZ2BggEKhsKvAeLcgXhFaD+PXcTMKRtPT0zfFK+Ok+m30uHFuuxBQq9VOTD58j5NJOp2mWCzuW8Xpbryvbje+1ciyzNjY2JFvL4piTwTYBTXpI/Hp0yQ+fZp2tkbp5RU2v/oui//qRYIP9RN+IoP/vhTiAXLme9x+bNvebpImiRj3RlFfz9H86MC+txdkEWeriXWhgLTWgHdLKBM2wdJFACqhU9SA9fV1BgcHEUWRSrKfFXGK1ddXaOea+NNBfD4f5XJ5z81m18ND/btVqheKhH5sgkDMz7s/eIO31pp89vc+0ml9Xy/izBUJBjSElsWblwtMfvoeAGovrSCdjVI+66Hgl0istJF1xXV5x3HQ/nIe/UdmkVQDqyATGFui8VaGihQk1qdjr9fZYAlvqY4kthEHEwg/eo7yv/4+aipA4hPn3er8wsICCwsLDA8PE4lEyOVyhMNhZmZmMAyDxp+9BdEgH/jSF9y0kkAgwNjYGKurqzQajU7efDxB9eUZhI0q+Y8N4VzxNBBokwr+EY6jADbp0L9hbut/A3YXVjKZDHpDolA8WRHAmUyGcrnM5uYmlUplx2Gxm8KSSCTIZDKUSiUKhQLNZhNFUdzq+H6Uy2Wi0f39L0RRJJPJsLGxccs20V6vl1ardaDr3qsS6DgO1pt5jG+tII0HUX/9NFtqjfLsLMPDw7Tb7Rsav9A0DV3X8Xg8tNttNzLOcRw3yndxcZFWq4XP5yMQCDA8PAxsH6nrdgZ1/27btlvltCzLHWOxbZvh4WEURWFzc/OW+wLdSlqtFsvLywwNDbG2ttaJTr3yHFiW5XZ2nLTRAVEU8fl8rt/B0tLS+1bIOCqqqjI+Ps7GxoY7Gnd1IkIymXTHcK7F5/NtM3k9Ktls9shrjyRJqKrqRl8eZ2x1j1vLbRcCeqpSj+uRSqXcTNW98Pl8hMNhgsEg1WqVpaWl23Z90Wj0jjD0O8moCR+JT50i8alTtHN1yi+vsPnXl1j81y8RfDBN6PEMgfN9iCcou/puRxRFhoeHt81FG2fCqP9hFqHYwgnvv6GRHohhPr2M/YkBtFem6fe8BXQ2uMHyZVYzP0GJzgytLMv4fD786RAf+Ml78IS8CHInLzydTlMul8nn87TbbTemy3EcNE2jr6+PcmURu2kiR71QbaIng9Snimia1vE0eKuIFYnSfHkZT9rH2nPLfPThTMeI7aV5Kh+PAg7iep1KQ0TWFfr7+zvZ2MUqluPAqB+hWgMHBMumsNbA/4sPIX1/AzEgIagCi+Ma/Rvge/Jeal+7BB4PoV+4393sq6rK5OQkxWLRdXUeGBjAsiwMw0Aot0n9xH347k1jtNpsbmUpFAoUCgUikQjj4+NcvnyZiKnCZpXs2gaND6Th6u4JwUIQTCzbBzjIQgWw2G17IEkSoVAI22NiFRo3ZY79ZhIMBgkGO63s6+vr28YpDMNwTfQURSEcDjMyMuIeokRRxDAM6vX6dTfQq6uryLLsPs71CIfDhMNhbNumWCyyvr5+4Iro9Z5bSZIYGBhA0zQkSXLf74c99NprddpfXwLLRv25MaRBv/u9drtNu92+oUOmrusMDQ1RLpdptVqoqkooFELTNPe+y+WyO9pXrVapVqusra3h8Xjcw+5uiKKILMtIkuS+L8fHx8lms8iyzPr6+h0RxVetVlleXiYe75iAdjsjJElCURRkWca2bXcExjRN93vdbphuZFyr1aJWq1EqlW6oMi9JErquu6bOV49weTwedF13uzu6AsbdhCRJZDIZ8vk8sVgMSZJYXl52E7H6+/vdfWQul6NYLCKKIpqmkUqlbtoe86BdtdcyOjraO/jfRdx2ISAcDt+Sme0e73+6CvLMzIz7/pAkiUgk4n7oqKpKq9VyN1W3+wOm+0EqSdKuUVc9bi5qTCf+yUnin5zEKDQovbzC1jcvs/RHLxM430f48QyBB/oQPXeX18JJJBAIuBvBaDSKYRiUzhVQ38zTemr/GX5h2I/TsrB1iVBgAdompt45bElmnVDhbZreFIAbsbXy1TeZ+rsLyD4P6c+PY1mWu2ZkMhlkWXbnxKvVqttiaVdbmHUDJeLFWSvj7wtRK753iDJm88gTMai1yEteBh/KIHtkWnMFasMKiIAgIuWbNJsgeTvGa6OZIea/+h1qv3aW1ZyfseJXkXxt8vMDGB+4Fy2uIW418TkGgmhhNtssjETwf+8CvstFYr/9BIK8U+DqHijb7Tbr6+vugS/uCSGFvVz6P37AwC/cRygUolaroWkawWAQ0zAZTWeQ/V7q5SrN0RDey0Wkchup0kbdaiIXmhR/45OE498EIFf5AldvDVRVxePx0Gq13MOhqqmdLo66geC7OR1O7ljFTdoE9/X10Wq1dq1mG4ZBNpulVCoB71XLNU0jHA4zNDTE7OzsnvuUxcXFQ22Wu50ohUKBVqtFIBBwRSePx0Oz2SSfz+97cBUEgVAoRCqVolgssrS0hCiK7vvdcRxWVlb2FQScuonxzCrWOwWUj/UjPbR7gkt3pOKwSJJEMBgkkUjQaDRYXV3d8f/o5sjv9X/eL0/+2jz0arVKIBAgFAqhquod5b/TFUj24uqDvyzLbqdAVxgQRRGPx4PH4yEQCJBKpSiVSuTz+X2fZ+isAYFAAK/X2/EIkSTq9brbjeI4jvtnvV5naWnprhsB6FbO/X4/Ho+HYrHIxsYGW1tbjI+PIwjCrqkj3TSU20kgEMBxnF3fU4ODgz0R4C7jWFbKYDDofgD36NElFotRLBaxLAtFUYjFYoTDYSqVCsVi0d2IHqeIVCqVKJfLOI7TU01vM0rES/wTE8Q/MYFRalJ+eYXct2dY+tIr+O9PEX4iQ+CBNJJ252wA328Eg0H6+vrcSkjj8UE8zywTjadwrlTs91r7BUFAOh/FfiMPaQ1qFrhhAAKCs/NAog0HMOom+dc2SH52BOi0zO5mrge4Ld1WpYVVayNHvdiXG/iG+6iXO1VJx7AwFosIfQFkTWBqpsjk588DUHluAXlQp32lUuuEVMzFIrLaqaSW/vRVhEsVNvwanoEw075fxv/XM2wkgvg/nYSGibpWwz7fR7DeYnUsjLBQpRZUqf14hM3ZKQDi8TipVGrH9auqytDQkJuE4kmEWfzrC+Q2tjAXFhgZGeHUqVOUy2Uam0VaP3yHpmRTPxsl2d/H6PgYtT//BkLTQjBtxKZJczhI3v4cpdyHARHLDrvrbyDQMRLsRroqisL8/DxjY2OIYQ2r0EQ8oBBQq9XcWfXrdQaqqkoqlbrhmCzodJhdr6392nb5ZrPJ+vo6/f39nD59mmaz6bq4X3uwmZ+fZ3x8/FCCsOM4TExMuIaG3YOYz+cjlUoRiUTcDrerOwIkSSIejxOJRGg2m9tara9+v3eft72EAMd2sH64hfHMKtK9EbTfOYeg771eiqLI4OAg5XKZ9fX1ff9/oigSj8eJRqPuIcPv9+8wAuwmA+1l8ntYBEHA7/cTCoUIBAJu1ftu4erxiN2wbdsdySgWi8iyTCQSYWRkhHa7veN2xWKRRqOB1+slkUig6zqlUolqtcrm5uaxxmOeBDRNc58zRVEYHx93xeaNjQ3q9br7fhcEgUKhQCgUuu3i1F4GnN3xOtu22djYIJ/P4zgOyWTypqy7Pd5fHMuOWdO0u2qR7nEwcrkcAwMDhEIhJEmiUCgwPT190xyfbxbdhfWkXdfdhBLSiH18nNjHxzHLLUqvrJD/7hzLX3oF/30pQo9nCD6YRtJ7ube3k1qtxszMjFuJSmbSiJ9PUF/K0U5rbpV2rw2rdD5G+/+6RPGxe/FfmEdq1UEWEbAoh87u+HnPSIDW99ex2xbtfBN1H2PCcDiMY1jYdQPRq3Qy0asNtFQQo2ViGhbOYhE55cd4ZwM5pLL6+gYfebAfq9am8cY6iR97lJXcGgBmn478jQ1sDxirJd75i9d4sd5m82tvE9EkPvcHT1H79fP4vBKCIBB8aR3BJxFsG2yNRTHLFuq312h9dqjTZXBlbclmsyQSiT2r46IoMhJKs/TN16mf8uI716kGi6LI1tYW5Wcv4L1cpPRgktZAEGyTlZUVzp49y+ZkmNAL61i6jHM2hfj5c3iMBq3We3PvqVTK9Ty4uprb3Vhubm52hIBiAyVz/Rb5fD5/qJb4drvN0tISy8vLhEIh+vr6jryBLpfLhMNhJElyn8tisbjviOLq6irtdpu+vj4EQSAajbKwsOCu+ZFIhEQiwfT0NGNjYwcWA0RRdDs6BgcHEQSBSqVCu92mWCwyPDxMOp1mbW1t2+263XKzs7PXPYQ1Gg3C4fCu37MWqxhfX0JQRTy/MonYt3/k5tzcHKqqMjw8fF0hQBAEYrEY8XiccrnM0tIS/f39VCoV1tfXb2l0b19fH4FAwO0UvBtb0Q+LaZpks1my2SyBQGBbPnx3zMswDCRJYmtri6WlpV4X7xX6+vqIRqNUKhX3AC2KInNzczvWOE3TOqLpMY2TdjviriYSibjXI4oi6XSadDqNaZp3VBdNj4NzLK+6JPVme3vspFarMTU1hcfjwTCME9dadvXcbigU6imnJwQ56CH20TFiHx3DrLQov7pG8XsLrPyfP8R3Lkn48QzBh9JIN6mFucfeSJLktpp2Z9WFhon+5VmaXxjH7/cTi8VYWVnZ9fZC1IMQ81DfDLBmf4BQZRYrrLCy2Y8yObjj57XhANl/P41vPERtuoT62O4HMk3TGBkZQZZlrGIDWxRRYh5otkESET0qelCjXm4gTeeQMiFafzNFZTLE0KNDyKpM+blZvPcmiaRjFJvlTgzfRhN7KEr1hWV+8Lt/yX96cxUtHcRuGDxxNon41RUCnx2n9pCG0DSwvDLCvREKg0Fqsor61wsYPz4A8Z3XfenSJfdwtdtG0nhzg1apibFi472v01oqixLmty+i5uoUPjqIrb+XFe9TPGDa9H3kPM4TZ1GiAQiolNsNRoN91Go1Go0GiqKg6zrFYnGHQ373MLC5uQmPqHgLG+hrtuvDoCgKqqoiSRK1Wo3l5eUjH8ocx6FYLFIsFlGUjhljJBLZ99Bt27ZbIbdtm76+PvffRVFkfHyccrlMNpvFNE33uhVFcat2hUKBYrGI3++n1WphmiZjY2Osra3h9/vRdZ2FhQW3M+PUqVMHMoHVdZ2trS1isRi6rqNpGvl8HtM0cRzHHTnIZDLurLXP53Pn4fcTMJrNJj6fj0Qi4baEC4ZD/YVVck/PovxYBum+yIF9HSzLotFoYFmWe9jutoF3X1dJkhgfH6fRaLhCRTAYdA8Vuq4TCATw+/3UajVyudwNV5S7rfD9/f00Go0TWTB4v7Bbx0z3d/9GTCLvRFKpFD6fj6mpKaLRKMlk0jV1lWV5x/t6aGjoWD2lEomEu750I0ILhQLxeHyHEWFPBLh7OZZXvqcs9rgeB5lZu13ouk5/f3/PD+B9ghzwEP3QCNEPjWDV2h1R4MVlVv7dq/jOxAk9MUjwoTRy4PYlTdxNDAwM7Mjtdrwy5kSIwdQA1pVWxL0QHJPg4zWcxddpPXw/m3+hMr1Uovr0DMn/MUbqE8Pbfl4OexBEAS2lU7tcJPLY9nb6bkt1IpF473pqbRwE5IgXp9oEf+ew6wtp1EtNtJkc8mAY2SsyPV9k8ucfxnEcKs8tYH52gMbSknvoMAIyYsiBlknGdPjwP/kIT/+Lb/HwWBTFAM9gmMTZDEosQPZ7b9GIajQHA7RSOvKz65g/msQe3H28yLIsNjc32dzcxOfzMTAw4B42Hceh9cYaVcVG1jrCurpWo9VYIviRc6xV8+iShM/nIxqN4hgWNAy2XpumkfQgKeD527fZOO0HVWJ9fZ1IJIKiKLTbbTY3N4nFYmSz2b1fbEmgERFp3IY4YMMwyOVy5HI5d768G8V6tWC8WyvstZXsbDZLPB5nYmICQRDceWrDMNB1nXw+j67rbjeA3+/nnXfeod1uE4vFEARhR/VvdnaWU6dO7bvpTyaTrlkhdCpyp06dYnZ2lmaziW3bLCwsEIlEqNVqbtxYNzpyv71Tu91mdnaWaDSKIiuYqzXMuRJ9T00S+dgYK2ur1739XhQKBVKpFIIguMJSuVxmZWXFHb/odjF0jTlzuZxbsa9UKqysrLhpFl1DxsOYG0ajURKJREfMu2IiWKlUjmyI1mNvus9tjw5er5dkMomiKMzNzblr834cd2dKOBxmY2Njx3Wsr6+7yRw9ehyLEFAul4/jYXv0ODQ+n68nArxPkXwqkSeHiTw5jFU3KL+2RunFZVb/+DX0UzFCj2cIPTKAHOyJAjcLWZaRnAoSVQwiOELnd6d9XxRFENlY3cS0dq/cCY5Bf/Uv8KRXsYUmCG+wNvwU8tsGkg3rv/8yZs1k4HPj227nGQ4gqxLVrc6hIpPJ4Pf796xw2NU2lgNyzAvVBsIVIUAPeamsl1G3apiyiKiJrEyX+PCD/bSmcgiyQEVuQ+m9qo+81aQ2oiDWGoiTKZSmyVOPDDHmV1hYqHF2PIqoK1jffJuYT6D63Drazz5K4flFCh9MgXqwalG3W6rrOG2vVWlna9gTMsqwH//rWTxrNVYfk4iIQYaHh2k0GrRrDTb+3+dwcnUqDycxIxrUrjz/973X0SSKIqVSyRU4fD4f9Xp922e1JElum70kSZQvrlGTTfDd3m1Ed758r+/th2VZbGxsYJommqZt607xer0MDw+Ty+W4cOECkiS5Lu1dr4DdME2TxcVFEokEXq/3uiMdiqKwvr7O+vq6KwhcXenvtm0flVarxfL3LmF8YwkhrKL8xCCF3DKnT5/Gk88dSWi/1nNDFEUmJyfp7+8nEAgwOzvL6Ogomqa5DvaapnHp0qVth5Cuk3y3O+da0bCLIAioqoppmq5nUDKZZG5u7kQVCnrc2ei6TjKZRFVVstksxWLxUIXM466y7zUmU6lU3A6pHj2O5V36fs517XFnoqoqgiDg9XoJBAKuSVaPOwNJV4h8cIjIB4ewmiaV1zuiwNqfvYk+HumIAo8NIAd7os+RsWq05/9Xhq3XAAEHkYLwoxTFj+D4FdAV5NeLMOrd9eaB1lto5jKGGMaRFKRag9iDbzH9pSSWBILpsPWHr2PWTIZ/8bR7O20kgIPD0K+cxStpe85Id7GrLWzLRgt7cSoNhEC3I8BL6eImyUyI9htr1DM6w48NI8kS+ecWCDw5jBEQ36uU2Q7eF9epfWgA8bEEZklg7itv8pnPnSM7V+FH/tknsZ+ewn59EckrIjTr2KEQje8vERiKkLzvFLlcjkKhcODKUbFYpFQq0b8gUM7XUZQI+nwFsWmS/9ggakAnEomQz+cp/2AK34U8zYkw9Y8Owh6u8JOTkzs2rBcvXtwxp27bNrmrq/8BB/GFPPYHkge69pPIteNn3Tb4bizfYSp6XWd3WZaZmJjY8xBw9UH2Zscp28UWxjeXcdYaKD+RQTwdcrskcrkc8Xh8z7GcQz2ObbO4uOh2UMRiMVqtljsu0U25kCTJ7bqQJMn1nugalF1LKBQiHA6j6/q2meXu9fdEgB5HJRKJkEqlsG2bqampfX8+mUwSiUTY2NigWCwe6rESicR1PV5uF9fzYisWi655bo+7m2PzCDhp89897m4mJiaOfdHucXuQNJnwE4OEnxjEappU31in+OIya3/+Ft6RcEcUeHQAJbL7gbXHHqz9G6TGqxgEQBDBMYk6z2A5PpzAx0BXcF5ag4FhUHf6xEhOFQcJBAEhqGDn28iZBmaljSgKOKaDY0Ht2VWcv3/KnXPWxoOofTqNN0poZ6Kw01NwG061hW04yDEvTrWKkO5shvSQl+rlLYQHhhAlmF2tMPFLZzCLTZrvZon9vfsxmpX3hADLQbAcnFwT5Xyad7/0Bj8ykaS+1ST0n91D7HyazX/7IkJGBpoIH7qf9rf+Du9TYQKfPYsgifT19RGPx7l48eKe1xuPx6nVajSbzU512rbJFUusvr7K0Gmd+oMxGpNhEATC4TDlbJ72l3+IBhQ/lMEKvje73nWK7mJZFtPT05w5c2bbY46MjDA9Pb2t1X5HJazcRrpYet8KAd0Dq6qqFAoFt/thZmaG8fFxEonEgZzyr6U7Vx8IBHZ872a55F+LY9iYz29gvrCJ/EQS+fOjHSPMq8jlcpw6dQqv13tTijFdF3pFUQiHwywvLzMwMECr1cIwDBRFYWJiwq08Oo5DoVBgampqx/4vFAqRTCbdBISr4+e6XRQ9EaDHUfD7/e6sfnf05np0kzJEUWR6evrQ7f3Dw8O7/u4fB7v5FnTJZrM9IaAHcExCwMTEBFNTU8c+P9OjB4DH4+mJAHcpkiZ3Dv6PZ7DbFpU31im9uMz6X7yNNhTqGA0+OoAa299h+66mvYldfQ3DCULXiEyQsRydGM/RDn6Oar2GmdJQ3i1inN+Zm9yUMwj8AMExcbwSktyg1LwXU7RRdZmW4xD44imGf/WebWZn2nCAyvc2SA30k397g4GnRq97qXa1jdW2kCNeWMoi+DtdIL6QRmE+jz2RQlAcVlbqPHV/muq3ZtEfSiPqCpLxnoAhmDbiWh3hoxrZVwpIKihlg/qoxqnPncV4awWh0UKkifTQONUX1js58L/0AIL03nojyzJnzpwhm81ur7jT2cRebXY3MzNDq9lEfnGTZs1g6Fc+SN3jsLS0RDgUIqwHyP/xczSHAjTHQu+9Flfodj51D1Uej4dkcudBXtM0UqnU9eev/QpC1egkHRzQfO4kUSgUKJVKBAIBkskksViMUqlEpVJBVdVDG9oFAoF9524lScLr9br56zeK4zjYl0oYTy8jpL14fvMMYnj3USfbtllZWWFoaMidrb/RPVjXYX5zcxNdf2+N7OaULy4uUq1WXW+B3R6vO/u/vLxMrVbb9bp7IkCPwyJJEkNDQ9sinqempg5kKtn1sDgogUCAcDh84jpJr7eO3exupB7vX46tI2B8fPxA7Tk9etxqdsvr7nH3IaoSoUcHCD06gG1YVN/aoPjCMutffgdtIHhlfCCDGu+JAtditjZoNw0Qth9CHFR0uY7s9bC6tkH7fAzvNxYxzkVA3r5haihjbHk/RrT5LIJjUaiNsLlwltE/T6H8+3mWc3WKbxd2OJ4Lsogw20S7V2fpW9P7Xqtda2M1TGS/DJYNWqdirokitUoTYypLw6cy/MQIoihS+d4Cid94FGDbJk+aLkHNQIxqXP6ri3zmoxNsvZEn9egAVJq0v3kBMSAiDidpVSWar67i/dAIomfnx64sy6TTabfy36VarXLhwgVGRkbQdZ0xPUHu//4e2bkyA585i5wIEAQSip+mYZL92ssUH41j74jNtInxdYLNH+J4JvGf/q9B2rtqlc/n9zdhk0UcVYK6dcM+AaJQJen9EzzSMqXWUxTbnwRuvbhg2zY+nw9FUZBlmf7+fmq1GtVq1Y0IXF1dpVKpIIqim7Nt2zbz8/PbNtMHqQJ2M8cvX758w4dbe6uJ8fQSTrGN8pkhpPHrxzhCZzb48uXLpFIpJicn2djYoFAoHOpxE4kEyWTSFTKKxSL5fJ6BgQH8fr/7PDiOQyqVwu/3U61WaTQabqKELMvunz6fj2azuasI0KPHUVBVddcuz73m+1VVxefzuekWhUJhR/fUXkxOTu5w4D8peL1eqtXqrt87aHJIjzufY3OyOEjUTo8et5p0Ok0wuP8GqsfdhahIBB/qJ/hQP7ZpU317g9KLy2x+9V3UlJ/wE1dEgeTuju93G8Waho4Njt0ZC7iCSJOGHUVTPLTbbeyIByvlRblUxDi3sy2xpD1CyfMwzZUyr/zaN0kPXSLzx/0o90aJzIjkv5WntlzFl/Fvu11gKIrTMGgVGrRKTTyhvb0e7EoLq2EgqwKO3+tuiDyVNk1ZgFqbubrJ+Gfup/HOJlLQg2eoY6znRt/aDo4iUvzdB0CER0+naBTaxL74MM3X12gZVRzHRAprWIkUta9cwPt4BmkfD4qRkZEdYwK2bXdasF9fx3hzGaEhsrpa47E/OI9jWBg/mCVwYY3CI+GOwLILOpcI8X1MAiitt6gt/ym+4X+853V4vd5dHfh3EJARKgbOIYQAq2UhquK2jWjM81fo8jtYToCo9jWa1jhN69SB7/OoCFfGKaanp1EUhaGhIer1OuFwmGw2iyAI7udDV6iZm5sjlUoRj8e3+SgcJk72RuLznJaF+ewa5qs55Cf7kJ9IbOsw2Q/btllbW6NQKDAwMEAgEGBlZeVA3QGyLJNIJFhaWqJarSKKolthXVtbc7sMuu8br9eL3+8nkUigaZrr9n/1n16vl/n5+SM9Fz16XEt3JOVaEaCbynE1Pp+P4eHhHT8bi8WIxWJUKpV9RwlKpdKuXVUngesZs/eEgB5djtXS8rBmPD163Ey67aA9elwPURYJPpAm+EAa+x/a1C5sUnpxmcu//23UuM8dLfD0+fe/szuUhqFhCQ8SdF7BdAI4gozotJBosW5/hGSrha7rlMvlTlfAt1cwzoRhtwOMIGDVbAQgu1Am+2vPMPlfPki8ZuOVJbJ/t4Lv753efptzXioX80TOJsm/vUH6g3u3aJv5OqKuIrTabnQggJqrU6+1EWSblVyLJ+9Ls/XaD2LyAAAgAElEQVSlVwg8+d59aZqGruvUqzWEpoX07VUufWeBx+5L0xpKkPiZe9h4fpbWXBssE+FUhvJ/fIfwrz5M/e/mkCav/x6RZblz//X6e//oOOjfnsWWJKQPTNJ69xWkkIY/4qH5py8i9gXRfvkJxhSBqampziHMccCm0/Fg2YhyHUEBkHCQ8CjXbwv1er2cOXOGixcvXlcMcAKd8QCHg/lpmDWDN3/rbwHwpHTUhIYoiSR/L4ejKjgogIAk1K97PzcLx3Go1Wpomka5XHbn3JvNJv39/RQKBXw+H7qus7KyQq1Ww+Px4PP5mJmZce8nGo2+JxIdgDNnzrC+vn6oarzjOFhv5jG+tYI0FkT7x2cRAkcvqDSbTWZnZ0kmk0xMTJDNZikUCtd9vW3bZmtri1QqRSqV2ub6380pv5quj8D12qxFUXS7Anr0OCyqqpJKpZBl2e3s2a09f2ZmBsdxEEURXddJJBLbxgZ241rD1N3Y3NykWCwyPj5+qDXgVlOr1a7bdRSPx2/j1fQ4yRyrEDA8PLxnfEyPHrcSn893YlXcHicXURYJ3N9H4P4+Bn71IWoXtyi+uMz0f/sMSthL6PEM4cczePpPhlnQ7UKWZbLip7FsHyHnBQSnhkmQ/PMPUX+6jfrnEsVXVxBGfdgJL3bEg3K53BEDdsEstRE8InbDQpyv8tofvMSpx9IER4OsPrOC/TMTiMpV8/oRhfLUKvGPjJLbTwjINVCSPpzqe4kBjuOgbtWp52rUvTJDHxjFLjZpzRWI/9rD7m1FUWQkMcDqH/4lPDTE3N+9jbbWpDgJp/7RYzhvraDH/n/23js40vy+z3ze/HbOiI08g8kzm2czl/RyRXK1DBJNyRRp0ZIVfNbZJcvlsstn18mWy7ZUZdeV5ZMtWaKCFU+UKFEURVLkLpfLzXHizgwGGWiggc7xzfdHAz3ADDCDybPLfqq60Ojw9tvp7d83fT4itfNFfPcPY7yRIfYz96MMRXGWq8hdl08EWJa1KQkQtiTCb64gHx5Evm+I6pdOkl8o07Mrivk3p1Cf3Is02lrQKcDY2Bjnj7+L9p0M6skC2C5izcLerWF8vg+VJVx0pouHScebl7VGrdVqV+wI8IIKVHY+ayoHFJSYRmOmQnOpjl020Xv8rPzUkwSCU8hCCdNNU7f3XnljN4hqtUowGKRcLlOpVJicnGzbT67bKmaz2U2vhed5hEIh8vk8kUiEvr6+q3pMSZLawnqbkj7b4C7Vsf56Ds9wUT8zijR4Y5KOnuexvLxMuVxuK53n83ny+fyWRRrXdclms2SzWQYGBgiFQtsqqiuKgs/no1KpXPZzVK1W6e3tJRKJUKlUKBQKO5rj7tABWl1UO+kwHh4evqy158XUarUdd+7IsszMzAzDw8N3jEbA5dxB4vF4Z/3boc1tTQT4/X6Ghoau2HrTocON5nb7u3Z47yNIIsEDXQQPdNH/hbupvbtK6dV5zv/Sc0hBlejRASJH0+jp9//oSXd3N4VCgbzwYfLehxAxSb6RJzqZw3dvEq9owP86S92ykB/vQXwghf78EtZ4ZEtbO6tkgCTi4iA5Hr6KjXZPitA7BXTHo3A8R+Ke1kLG5/MxND7IC0sniO6OM//s9sllz3GxywbKeBQqDRhqJWycTAVfQKNWajBdarL7sVEq35sl8EA/4kUOB/n/+RKE/Jx67jxjySDvTjVI/9xDSPUm1vfOoqdlKqtBat+dI/zDB9EOdFMtV6gKJpLmoDWbKIqCZVk0m02azSamaWKa5oWZc9dDrVh0nWmifuwIYm8Ez3apvzDFwjsZHvrFD6L/8BGEi/QGdF2nz59g8XFQzpcQsyZuUKH2zB6q7EehgE0Iz9WZmJggmUy2xQgvZn5+/orvuxdSEHaQCLArJqW3Vym9tYK52sSuWcghheDuCHv/3YN4YZ3Zyi8iCSUst2etM+DW0Gg0iMUujFSYptkOhrfCMAwmJycZGhoiGo2SzWav+bGvJNjl1W14NYeStxGP9uDtCyNs8X25XhqNBrOzs2iaRjKZZHx8nEajQblcplwubxmYVyqVbRMBgUCAgYEBDMOgr6+P2dnZbRMelUoFSZIwTZNYLNZ2rOjQYSecP3+ePXv2XDEAv1L1fyNXchcIhUIkEom2zoUoiszNzTE9Pc3o6OiOH+dmkc/nt01ihMPhq05cdnh/c9ujoVAoRDqd3tGio0OHG8F6NaZDhxuFIAoE96cI7k/R9+N3UT+To/jKPJP/8Xkk3wVnAn0g8r6czRNFkf3791MsFpmfn8fFB4KAElbwVlawp/OkP3uExV/+HsbZEs7Hh/ACMvJkGXvXpbPVdmFtEaOJqGGNgU+O0v3MMCwZ6GcKrDy/SOKeLkRRZGxsDIDgUAzBg8ZKDbNioIYuFXDyaiauB0rCh1dtIK6NBljnc2ghHddzWaxYPDKeZPH3jtHz8w9vur9xdgXjzQVyj40gvTGH2hVE6g4R3pvA/IOXETQHYe8A4slZbLOK/4mWg8Hs1AzeA1HKizv4nXM8BMeltyyjfe4BBFXGqxnU/uAN6tN5AmMJop+9d+u7FhvI7xZQzDLWWBi16VB/eghvTUneIrXp9qVSadtEgKZpV7aZCykIK1u3dNsVk9I7q5TeXKExXyW0L07iA/30/tAoJ37+BbRuP3t/8ShqQl972mEc79YnzSKRyLaCWtthWRbnz59HVdW2A8C1VAK3CrDXHRu8soWHQeAn92M6NuqaqGU+nyeXy92UsUrDMFhYWGBxcZFgMNi29atUKpdUGGVZ3rbS39vby8LCApVKhV27dpFIJLZNBKzbCkIrAOsEKR2uBsdxOHXqFIIg4PP5LgnE17tYdF0nGt26A+1iPM/bUigwFAohSRI9PT0sLCxgWRa2bW/6Hudyuds2cuo4DtPT09setwVBYHBw8BbvVYc7ndueCACIRqNomrZp5q5DhxuJruvtGcSxsbE7pn2rw/sPQRAI7E0S2Juk7+8foT6Rp/TKPNO/8j0ERSJytJ/o0TT6UPR9lxTYKLwprI2qa/f0o97VS+V3X0P2izg/OoYgCJh3JdFeXsYeC19iPxf7QB/790QRRcj8xims11ZwTBf5gRThpRpSXMe1XSKJC0mE8HiC6vkCsT1J8ieX6Xnw0gWPW20lAuSIjmeUwd8KQq2JHF6piaorJO7qp3k8i9ITRNmg++B5HoX/8RL2oV5e/a1XefpAF9WaQ+hAF9bXjiFgIPTGqJ1toh/qonJuFc/zsG0bV/CQJyvY915eXTpWFZCmCgQPDhL86FDr/iczWM+fwypYFByB9Kf2X/q86ibN56cw3lpAu38AX1Knpq8gOGDv2bmI3UbGxsZYXl6+7Hy3F5I3jQa0g/+3VmnMVQjtjZF4vI/QgfimUY70j+0h8VhfOwlwO1lvTc9ms1dl6ed5XnsGd3p6mng8Tjgcvqrflost9SKRCL3dPcz/2THMYgP1wS4Wpgrt/VJVlUQiwfj4OKVSiVKptLmT5AbheR6BQIB6vU4ul6O3t3fT9ZIkkUwmN412BgKBtmCiJElUKhWg1aK8VZVUEAQ0TdsUSBmG0ba4vKJQZYcOG/A8j3q9vikpV6lUmJuba39/FhYWiMfjBAKBth7LVkiSxN69e9udLKIoIooi4XAYWZaZm5vb1uUik8kQDAZvuZNAqVRifn7+st+b99t6o8ON4Y5IBECrvbMjHtjhZrGeBOjt7e04VnS4ZQiCQGB3gsDuBL0/dpjGZKGVFPivLwEQXesU8I3G3hc/0hvbESXTwXXB95kHaf7RS3hGA/O+JOafTaP/xB6cfj8oIvJMFXt4s6aC1u1H6/a3ZpgjGnLFYemrU/R/fJTY7jDqyQL2jEH/4QudPeHdCVZfnSdxsJvcie0SAQaO4yH7RARFQxAFPMvBnC7gZivYokDXgW4qz08TeGywvYAURZHKX7+LnatzrNTkgdE4tT4/1sM96FWTrG4QTPkQGzqe0SD86YM0vzdD7aV5ws+ME1h1qW+jhwCAYYMkEj/fRHv6XsSoH7fUwPzbd6Fuoj5ziPJ/e4Wl2SIHP3OofTfPtGm+NEPzxRnUgz1E/vHDiGEd2TQ5KzSxB4OXJFmgFbRdHNxtRXd3N4qisLi4uOX1XkiBgkH+xQylN1eoz1QI7YuReKyX0P4Dl4xVrNP7yVvXPitJEqqq4vP5CIVCKIqCbdtYloVlWRSLRWq1Gj09Pds+zytRr9fbFW9FURgdHUVRrjze4Pe3PuPBYBC/5kOyBd79pW9i7wkgPRLHFMyW6OMapmmSyWTIZrMkEgm6urpQVRVRFMlkMtvO6++U9arqelBvGAbd3d0IgsDY2BimaVKtVvH7/RSLRURRpL+/H9M0SSQS7aTR6upqe5sXV0yhlZgfGBjA87x2e/X68c/zPMLhMKVS6bqeS4edo8nnUaQVLKcLw779re3Xw+nTpwmFQti2fUkXiud55HI5crkc0BKM3m5WXpZlhoeHaTQaBAIBXNfl3LlzO0q6zczMMD5+c1xPbNtmdnaWvr4+dF1vjzHsxH6zk1zrsBV3TCIAYGBgoGMj0+Gm4fP5Oi4BHW4bgiDgH4vjH4vT8/cO0ZwpUnx5ntn/9gqe47bHB/y74u/ZpMBGu6J60oflQWN1lcLBONaeMNJEBSVTo/nFs+g/OY5xJIH21ir20NYBqyAIxB7uof6dReSCgScJJKc9Vn/tLLn9Ce7++H3t24bHk0z+73fo+/heTvyPV7fcP69m4lguguJh+VUalQrWXBFUEdexiR1MYQfqrH4oxKpUhFOtwEpEQH9zisITvYQLNaSHdmGYLsJEEedUHvOZITKKijZZof5ImFgmgzaepPriLOGP7iax5NG7N4UxEGRlZWWTQrpUaBJ5MUPhqUGaH9mFHvZhvTmH9fIUyn2DyPcOYpxYpp6vEzvYjRrz4zkuxpsLNJ49jzwUJfzTR5ESF2ZgVVXFFwxs2SI6NDREIBDYceU6Ho+zsrKyaQFs1yzKx1YpvZGl91iFquIQf6SXwZ86gKTdXOVsTdMQBOESlXlJkgiHw4TDYXw+X1sh3PM8HMdBkiQymQzNNY0GRVFQVZXR0dH29YVC4crjEFfAsizOnDlDd3c3oVCoHaiv47ouzWaTarWKYRiEQiGMySKr33iLZshD+ng/sn7519BxnE3aBJqmMTAwgN/vJ5PJXNOCXxRFxsfHMU2Ter3O7Oxsy7ZSUZAkCUEQUFWVUChEIBBoB+z5fB6/3082m91SV2FdSV2W5bZPeyAQIJPJtIP9je+d3++nu7sbSZK21WnocPVkpwqsTJfYdbQfzX8hSRX1fYW4/yuACHjka5+k2PzobdvP68XzvMva5m2kUChcVjRv3dHCqhhIPpmxsTHOnDnT/n4Jno3slLDFIJ54oQPANE1s274pWlTrXQoTExNEo1FKpdKOv+/v1XVFh5vLHZUICAaD+Hy+6/4h7tBhK250+2SHDteKIAj4hmP4hmP0/MhBmnMlSq/MM/8/XsNp2u1OAf944j314y0IAqIoomkatV1J7N2QWMjRhUJlskz1YBzFJ+GKAs3fPof+hd1oroe4UMNNb62EHnuiHzmkEj6cwDjRIPXhA8z+6ls0SgYrx5foOtyqbPv6Qth1Ey3hw1Qtps5N4ghuqzV/3dpMdPH+2ThzmAh4eDMzCA0b7yNJhEaU+xoWpeMrdEkKPNJ94Xm9s0L9cAzNH2T3o+Oc+fUXie8O4z43T6NqYNfSOIMy9cMhEMCpmij9Ybywj/qr89jLVXyPjxCJRIhEIriuS7VcoXR8mooqUXhqCE8RCbkKxh+9DpKA/qP3IsZbwb1xbImVmSLpn7gX4+QSjb89hxjWCf3Y3cj9W7f+9/f3bym61mg0CIWuztViaGiIc+fO0czUMLMN7KqFHFSIP54mKK+if2YUQjde4G89OC0WiyiKQiAQwHEcBEHAdV1M02x/5nRdb6vOLywsIAgCjuOgaVpblHh9bbHRVqtQKCBJEpqm0dPTw9TU1A3Z9+XlZZaXlzc9F8/zNi3a3ZJJ5YsnwQblY2nk1M5sGC9mXcCwv7+f0dFR5ufnMU3zqhICfr+fZrN5STFmvXMCWp+dUqmEIAjour6jtVqz2aRQKLB3715c18UwDBqNBolEom375routVqt/d5JkkRfXx/RaJSZmZlOp+gNIHMmx9/8t1cIxHzsfWyIQx8epW/MJe7/KrYbBSTAJh74CyrGQzjezubp36usd7/shHd+8dtUzDrxz40h6hKCKCC6DfoLf4zilHFEncXop7HkePs+q6ur2+qvXCu1Wm1Tl8PVdgDF4/Er36jD9x13VCIAWguOd99993bvRof3IR1Log53IoIg4BuM4huM0vN3D9KcL1F8ZZ7533wDp2oSeSBN5IE0gb3Jm6IYfiNZtyDbiLtcxHlrCiUYJlJRmd0bQZusYIwEaf7uBNIPDuAl9PbM5sXBkhASaCpFmn8wzeJclYNPHybxQD/mySxT35yg63BvWxAq8KMDTGamiH64j8Ji/pIZdOWNFap/Ok33z+zCiPtpxHzoX5tDXKozr7kcMwwS52p0/d8PXXj8TA3fl6d42bP5yL94iuJfnUX7gTShb8xQkcAI6/DsMnxcg3jLYz6x7OLFREL3psn/yXEUw0RObVCtLjdR//osXX6Fvif3sVRYQZ4pYT7/Fsojo8iH+9sJILdh0XhzkdxihbFsheZ3agR+cD/K2OW7m3RdZ3x8nPn5+U2Lx3w+v2PrKLNqsPzyHIsvzFAulwnfkyQ6GMffH8Z2bQzDwBFEqFrtRIAgCASDwXbyZSfBot/vJxKJUCwW2+J70GqzX99OuVwmk8m0j+M+n69dcXNdl3q9vulzI4oiAwMD6LrO4uLitvuxPs7SaDRIJpOEQqH2fPuNZKP+gFs0sb4+j7dQQ/lIGnHf9euFuK7L3NwciUSCkZGRdhfCxMTEjmzQQqHQjtqLoVV1vZqCzfrjN5tNGo0GzWYTwzDaYmsXJyxs22Zqaop0Ok0sFts0atBhezzPwzYdmhWTRsXAqFnt829+6TTNxTrmSpPvvZvn+d94g8c+G+Kn/4NAKwkArZBARBJrOM77LxEQj8fbHS1X6ojyPA/XdLCqJlbVwshVcUom7/695/CNR9j/TxUUtYAthZGdCuHGO+RCH2zf/2r0RnbK7Ozsdd2/YxnYYSvuuESALMukUqnLChR16HCtWJa1o9nNDh1uF3o6Qk86Qs8PH6C5UKb0yjyLv/sWVrFJ5IE00aNrSQHpvSF4KXRFwHbR70lT/f9OEP7UMOUP96FOV7FHQjgxjfibZbqeGkQZ3Lpioe52mXh2hd6Yn1NfOsH4544w9/kvsfrSDKWVQyysLOK6LlbVpP7teUzbw23a9H5qbPO+5EzQJFTHpabLYDiI2SZSyWDWbBLr89MMiBBZ0xHxPLQ/n2LeJyKcKiPZLvbhOPGpRVRcGoqEO93A/lwfxFutoSMjI1TePIHcG0bbkwDLxXO8ttWffTqD9dw5lAdHkO5K4y6ViX97ATGso3z+AcTQ5uRF47tTlM6sEO3yEXxiDPVQz46DxvXW92azSblcbo2nbCOQtY5VM1l6eY7MC9PkT2VJHukl/aFRuh9II+ubj521Wo3ZTBOn60JbbG9v76bKk2maTE9PbxuMJhKJtl5BIpHAMAzOnTuHJEn09vZSrVa3tOi7UiCqaRqqqnL27NkdV8aXlpbo6emhWq3elHlaz3KxX1zGfimLfDSF/KlhBPXGfo83zkAPDg6iadq2r72iKO2ROUmSrjvQ2Iqenh6CwSDnzp3b1ImxE3K5HOl0+vs2EeB5Hrbh0KgYNKtm61QxN5+vmTQrRvu8IAjoQbV1Cqnt89F0iLk3lvBsFxwPRRIxaglcN4AklHG8UOuvG8Rykrf7qd8QPM/Ds10ESaRbSaDkRJozBSrVZeyqiVU1sasmdm3D+aqJVTOwaxaCKCAHVUrvrlCbLZH8wji+XRHMuRqOkQAV8BwEXFzx5gqfrqysXFdnzHrnVIcOF3PHJQKgJVB0cQtMhw43glqttmMLmQ4dbjd6fxj9h/bT/UP7MTIVSq8ukPn9Y5i5OpH7+4kcTRPYl0KU79wfeEEQEEe7IFdCvaef5OkatTEVZ1+0VX+abmCdrVKXJ4j85ANbbqPrwQFO/urLRJE5/+Y0/vuDRP/VIaL9fmYWZxHXkiKCINA4Wyb8VJqlL09euqGCgRBRkUwHW5ORZqoggi16+A4nEY4XKCcuBLXi2zm85RrvzhX5wFCMcrFObDSM9NZ5LEWiPt/EOxDDTV+o9k9MTJDMN1D3t0TW/AdS1L8zhWfaWN86g7tcRvvhuxGiPqzvnMN5dwnliXGkPd2bAnwnX6fxrQkqXzvDSq7G7l98Eu3wlQX+tkLXdXT9wkK1VqthGEY7YLdqJsuvtCr/+ZPLJA/30P/BUe75F48j+7ZPnAYCAfprAZycTOSJrd1YVFVtq9w7joOiKGia1vbfbjab5PP59r5omkY8HkdVVRqNxqb2+qvBNE0kSbqqgL5arVKv19mzZw/5fJ6VlZUbkhDwPA/3bAnra/MI3T60n9mLGLv5quK2bW+Z+JZluW272Wg0KBaLbQu/G40gCO3P29XSaDRwHIfx8XFqtVr79F4d8/M8D6tpbxnQN6oGRtWiWTVoVEyMtesEcWNgr6EHFfSghi+sEesLtYN9X1BFC6oo2oVlfXW1TubUKounVqks1sAFNaDgj+o88KMHOPq5g2TK++kO/TqqlMF0+lmq/DQet1bx/nJ4rofbsHHrNs7aX7du46z9dRut08b/HcMheDhB5AP9GNMVrFcL1N0ZlKCKHFCRg2rrfFAlMBBBDijIwfXLtdb5gIKktl7Ls7/+Gid/5QVq31sm/S/vQYlrWKJHuVog2DxLTR2j6Ltn835fw3FjXYxzvWNG0zRCoRA+n++aj4Mb9+dm6RZ0eG9zx34iRkdHOX/+fEcvoMMNZSctkh063IlovSG6PrGXrk/sxViuUnp1gaU/PoG5XCV8Xx+Ro2mCB7vvyKSAONyF/TdvoT11Fyu/8xLOcBKqFsJbedyHu6g83YXzrUWqx8/jRlviauvCYqIoIqky3R8ewQyYjIyGyJ5cJlA2qXxpkmxEYv8vtBZh2lAQ439X8A0FMZbqOE0bSb/wM+eVDMSwgiuLeKKAPF9DrFnMGxa9QzGKbxdoamvq5ZaD7+uzvGXaHI76qQsC/h6ZoKDQDCnUzzawEhrCyOZ5+2aziV1sIMVb86dK0o9TNqj92guo+7vRPns/bqaM8ZVjiL0R9B9/EMF3wcnErZk0njuPeSyDelc/nq5SQyD11O4b9n7Mzs5i2zZzJ2donCnRLDTw9QUJPp4k/eN76OpvJSXWhd4uhxTVodC4YrUpEolgFU9RWpqkqo1hEdgk6rWxi6Ber98QobhrqYAtLi6yurrKwMBAu5PienBzTay/nsMrmChPDyDtvjY7x2tBFEV6enoIhUIUi0Wq1Wo70VIqlVhaWrrp+5DNZhkfH2dpaemagqPJyUk0rTVyEwwG2y4GG8UGbxee52E1bBprQft68N4oG61K/caAf+2vKAlrwbvWCuDXAvlAVCeRDqMHNbSggm8t8Je3cd7YCtt0WDy5QubUKpnTq1gNi979KYbv6+WBz+7ny//6OQrzFR79ybs49PSulo2rk2au+O8AD7g5o2ee7V4arK8H8fUtLt8Q4LtNB1GXEH1y6+SXkfwb/vpk5LiG6Fu/XEHt9SOpMr19vcQficOPXd/+Rw91s+f/eIDkp8fIli50p6yGnmQ19OSW99mJO1WxWGR5eXnL8RhoJWxvlGCmqqqdJECHLbmjPxUjIyNMTk5eog7cocO1sO593KHDex2tO0jXM3voemYP5kqN0msLZP/sNHP//VXC9/S2kgKHujd5t99OBL+GkAzDSonCfXGUiRLWeBQSGsLvTeB9fozGEz00J5bwxsIgCu0KZVuA8PE4hb+aQH9tmTNncxz52cOYx/K4u4PUF6r4+4PIEQ1BE3FLFr7BIPXJMqH9FwJMr2whDQWx16pm0kwFyhYLgsu+5SbNI0maE63gSP3aLKtVE2exQmQgRuOZIWI1F09ssLLsIgdlbE1A9l36GnuFJlJUx/M8zLfmkVVoiiqBx3ZhPnsWdyaP+uRepNELxyPPsGm8OI3x8izq4V4i/+RRjGNLVAoNeh4fviFtnVbdJPPyLGbYAA+kmELwwSQB12tZKQL5SoH8u63X/uDBg1fcphjVMacuX03O5/MYmW8Tr/0FEVECJUw28o/w+Xyoqkp/f/+m29+IhG0oFKJarV7TfdeV86/HatYzHezvLGG/sYr8aDfyZ7tu6TjPulbDuXPn8Pv9xGIx+vr6MAyDZrN5y8YvHcfBcZwdiwtuhWEYGIZBPp+nt7e3nRAQRfGGdjK0A/uKQbNmtVrut2rHr5o0qwbNqoUki+2qvBZQ8YUvDezbLfohFfkGHpM9z6O8XGsF/qdWWZ0sEBuM0Lc/ySP/4AjRdGhTl9HDXziCbTiMPZzeYmuXTwK4lrMWoDtrwbp1IYhvOBf+b1wa1HuWe0kQ3w7cfTJSUEHt8rUu33idX0bU5avWxhEEgX379t2wVviuhwbpemhwx65msixf0aEqm81uOfJ0sxgdfW/bQna4edzRiQBRFBkdHeXUqVO3e1c6vMcRBIHdu3d3ZqQ6vO9QUwFSHxsn9bFxzFyd8msLZL9yhtn//irhe/qIHO0ndLhnW0/3W4U42k3u7Ax2SiVwqoAXULAPxhAX60hfW8B5qg/9t85Q6fEjf2F3O2jyPA9N00in05w78SpCzqT/ni7mX1wkvjdKyvNYeWmJoU/vAkAfCtGcqRDYFaV2rnghEeB6eDUbJShhaTJCxULIG7iSh7YviXCmjP6pNM23ZxFyTZQ3VziVKfFQf5Ty/hgDxTrarvxsWrEAACAASURBVG5yz5/FUmXkEY8Yb6KNhfCkx7DX5mpFTwBVAsvB/MoxnJkC0Z99kNUvvkX9f30PZV8P+hceRFhrO/UcF+O1ORrPT6KMJgj/7INIsdYcf/PtRZYmcxz+hceu+XW3GxbLr86z+N1pcieWie/voufRQcKHEhhuqxV1qwAtGNzaxeFipKgPp3D5ZH2lUiFUexVP0HCkALJdIRmosFhN0d/ff8lxWZKk6xbbCoVC11zNT6VSRCKRa5qZ9zwP50QB6xsLSMNB9H+8DyF07QmFayUQCGCaJpZlUSqVbkv1XBAEBgYGsCzriqMBgUAAy7K2TQKtb0sURc6fP48sy4yMjGDb9rbijp7nYTbsSwL6Rvt8qx2/JaxntgJ7RbzQir9hzj4Q85EYjGyq4mvBGxvY7wSrYbN8NsfiqVUyp1rJnN79KXY9OsAjP3EE1b/1KI/neQwc7MKt2xgLtQ2Bu7NWmbc2VOMvCvYbditx6L+oKr92XvTLyDENsT/QCuI3XC75ZQRNuqXuN1frirJTdlKUVBSF4eHtE7eu67K0tHTLrDEVRaG/v7/TDdBhW+74T4Yoisiy3FF873DNqKrKwMBA50DY4X2PmvCT/Mhukh/ZjVVoUHptgdWvnWPu114jdKSH6NE0obt6ELVb/12wUkFWlkVE08a4K4n+epZq7zDuh3oR/3AS8UQR52MD6N9epPYnU2ifGUWQWovHer1OvV7n4D96kFP//jm6o37efHaa5NE++PMZ8q8vM/DJUURZRBsKYUxXCByKs/xX0+3HFxo2juOh6yK2LiMt1JBshyXbpjfkg2ENvTtAs2qi/tkUp4pN9gd91P0KqdEgke4oRAKUzuZwPxEgpf57IkIOKayC9jcsZP8Nlp0mKQcRRWj+/qtIB/vwgj6EuRyK6GJ1xQn8nb3AWpByfInGt84hJgKEPn8vcm+4vb9OqUntrQyWrhC9t++qXmu7YbH82jyZ706zemyJ+IFu+h4d4q6ffwQlsDko7e7uptlstn9rrzZZKkV1nOLlF8jpdJrsah8+cw7XMXHxKFYl0un0to+3Z88eDMNgZmbmqlvK16vhi4uLV3U/aLkRxGIxJiYmrnrd4S7VW2MATQf10yNIQztLptwMwuHwbW+dDwQCKIrC5OTktu+hKIoMDg62P3uyLLc7ANY1JVRVRVVVisUiUxMzrdb7qsnSRIEHPngXZ1+aZeZ0plWl31C9N6omsiajBRT0kIpvrR1fD6mEEj6SQ5G1oH599l5FukO6qNbxPI/ifIXM6VUWT62QnyoRT4fpHopy9CO7CfhVvIaDs2pRmZ3fHMg3NlftBUnYMohfD9yVlO+SIH69Qi8o4nvGyrZcLnP69GlSqRTJZPKGFYAURdnymBCJROjq6kLTLq+tsLq6yvLy8k0RIt2IKIpEo1G6uro6694OV+Q98QkZGRlhdnb2qn1xO3z/omka3d3d7RnjDh2+31BiPpJP7SL51C6sUpPyawus/u155v7n64SOdBM5miZ0V++mGfqbheu6zMzMIFkuvlyd8lAE71QeZbKMtSuC+/FBpN8/j/XRNIGUTqNuYX5pCvXTI+220GKxSGJPN/WqiXM8T/8TabKzFcKWS1KRKZ7IEb8rhT4UIveVaeIfH6axUMMxHCRNQmg6OK6Hqoo0NRlpLo9bsliUXcZm6/DhfmRNgpJJ5cwqZqFOsDcKH+qheyCF8sg+Fn79RYwf6CcR+xNEp4S5HEHRA6i+CvHIl/AH/yven56iuVJG+QcfwJkv4S4UEX9wN9FfeJz8b79N+Icc7KkCjW+eBUkk8MmDKCOXuiUYx5Yo5+r0f3jXjhbgdrNV+c+8MMPqOxni+7vofXSYw//0YdTg5ReoG4UErxYxrOHVzZY690X6FJ7t4M3lcV6aIJ7djfCpXsTmPFrfD+APbT12sLKygmVZTExMMDQ0dFUBrSiKxGIxkslkW5zwagmFQpRKpatKAngNG+vZDM7xPMoH+5Duu71Wn4IgEA6HOX/+/G3bB2i1SDuOs+26zfM8ulLd1CtNjr9ykkbVwmrYaJqGP9Cyh8wtFsnO5FmazFFerSJr8oVKfUClnKnx4c8+ypezXyc1HMEX0tAC69crd15g77gbKu4XzcmvVeYbRYPsTImVhTIrSxUkD+IBnZhPYSjuR62KiJN1nIxJzS9vaqlXo9qlwf5aq/3F38/3M57nkc1mMU2TdHqrUYirJxqN0mi09FBEUcTn8+2o2m6aJhMTE1fV5STLMrIsb9uFIIoi6XQaRVGQJKm9T531boer5T2RCNA0jd27LwglmabJ5ORkp0ugw5aEQiGGhoZu92506HDHoER0Ek+OkXhyDLvcpPT6Ivlnp5j/9TcIHuoicjRN+O5epMsoxF8rxWKRxcWWvZ8oCfhW6pQHIjTv78L/7ALWcAgiKs5H00hfX8A6HCVkupSmq5hfnkb91DCCILSsPzWFwF1JaufK9I4O8cbzC4R3hQhXHZa+t0j8rhTaYBBzoYYgCvjSAepTZUJ7YwgNG9dy0RSoqBK+c2XAQxuOIzSAwQC4Hv5ck7cbFR5NR6nfm2I0V0P7ySPM/KdvUvtACvwyklgGU8TzAEnA9RQksYz51RN4xQbqg0PYr0xjzZVQ702jPtpSaBckgdx/+g5KSMH/5DjK/q5tg/zm6/Nkpgo8+Csf2fa1tZsW2dcWWFwL/mN7U/Q9OsTh//Mh1NCtUf4WRAExpOGUmsiJ1kiD1zCxn3sX9/QiXsOCfBXxwTHUoacvuy3TNFleXkYQBLq7u9vV4SshSRKJRIJ4PE61WmVmZuaatYWCweCO5+c9z8N5M4f1rUWkvRH0nzuAELj9y6pQKESz2bzl6vqCIDC+e7z1utgusiLx3F+8zNLUars136iZ7Yq+Wbd4/O/ex/Chfl7/y7Nb2N5p+FIqe0bSHHlmFC2gIl0UzMqyjKSIHPjQyC17np7lbjkLvzmg3xzcrwf/nukg6psr7oJPotK0yOVqrGRrVKsGqaEI/U+kuXdfkkg6tDYvL71nbGPvFEql0g1LBCQSiSvO/l+M67pXnQQALqvwr+s6o6OjnaC/ww3h9v9iXQOqqrJ3b6u9cm5u7ra3v3W4/az7Y4fD4as+UHfo8P2EHNZJfGiUxIdGsSsG5TcWKX53hoXfeIPAgS6iR9OE7+lFClzfXHM+nyebzW5K2Lo+BdsnoxcaNFN+7C4f2sk8xpEkjIRwD8Xwpir4XBf944M0/3wG8y9nUT8+iGmayLJM6kODzJ94m+jpIgMfHqT47AJa3cY9V8EoNNFiOnJCx8zUWzoBE0VCe2NQt3FNFzEgI5Qs5JpFznPoEiW4OwqCgPy3c1gNh/64TD3uY9DnIeoSTtXAeKwbL9r6yaxV7yGqfhtBNBElC9mqUlk8RH7cB6M6vX+5gO8TB3FTUSg0cVZr1L91DrHSwJQkkv/qicsu6J3VGtVjSyg9QQKjm49ndtMi+/oCmRdmWHk7Q2xPslX5/7kHb1nwfzFSVMcpXEgE4Hh4k1m8ugkNE+JB5PuvLFa13sq/bh94pQW0oigkk0kikQjlcpnJycnrFhosFot0dXVRrVYv24HoztcwvzoLooD2uTHEvsC2t73VhMNhBEFA07Rrsu1bx3W9tdn5iwXz1n3trU3t+EbN4if+o05xpcyx599FUkU8PPSgSqQrQPdobFOgrwVUFFVmz54x5IRzTR0ciqJc9XvueR6e6V42iN943abL6zae611Sdd/YUi9HVMRe/6Xz9D4Z0deal2+UDDKnW+r+S6ez+KI6vYeSHN2/h+RoDEnpBHk3As/zKBaLt9w22nVdisUi2Wx20zFsfWwJuGKybivXlng8Tl/f1Y2KdehwOd6TiYCNDAwMkEqlyGQy1Gq12707HW4Dqqqya9euTna0Q4erRA5pxJ8YIf7ECE7NpPxmhuLLcyz81psE9qVanQL39iEHd54UyOVyl7UKq3cF8K/UaSb8NO9NEfyrGczxKJ5PxnuoCyFTx254aO+W8D63i+bvnMP86hzq0wNUKhV67xlkVj1G4/Us3f/yCPNfnyFQM+npDpN7dZm+HxhqCQZOVwjsipD9xprgW8FA1EScgIo0X8WtmGQlj/4VE34oBhUTvrOA4HogS6QOhNAVWJm3SdkW4XCQ2rPnUY7nEcsS5ad/EG/311HqTRoTH6LCB4mcWaQ6FGb16TT+Q93Yf3oaZ6VK+fQS+iPDpH7pAJn/8B2shQrq4PY2cs13liiu1uh/eg8AjmGTfb1V+V95a5Ho7gR9j49w6B/fvuB/I2LMh1u8IDgoBDWkDx/E/Z0XwKci+BSEdOyy23Bdl2q1SiwWIx6PMz8/v20SQJblti1ePp+/pnn+7cjn821V+q3s9byahfXNBZyJMsqT/UhH4nfc7PTS0hJjY2OEw+FN3Q3twL6ydqpdsLtrX75ugVdpVexVn3zB7m6tHV8PqUS6g3SPXVS9D2kke0LsuX+YyKi6o1FO13Upl8vE4/GrcjLwPA+v6VAvVxC6e7HnGjRztUst6bZSsm/YLTcSfyswF/3KRZZ0EnJCR01f+H/jbQT16uflXdtldarYEvk7vUotV6dnT5Le/Unu/uQe/LFrH8/pcHmWl5dvaSJgenp6W8cSz/Oo1+t0d3dvK3IJrQTXemfr/Pw81WqVvr6+W57Q6PD+5z2fCIBWm8zIyAiLi4u3TImzw53D5RRaO3TosDOkgErssSFijw3h1C3Kb2UovTLP4u+8jX880eoUuLcPObx94LkTS6Rm3Edkuoho2LghFWssgvb2Ks2HekAUcD82gP075/C9vYp5VwL9861kgPX1eUqfDrUU3R/tpfrCEoGJCoNPj5D/zXdJVB0yL2TofWqwJRg4UyFxf4rmXBXXcpDyJlJQwdJlpDdzYLuoXQEYCYNPRvniuxyfK5EO+zCHfMRkl8KKR2M8Sun/fYnkzzxMaK9D8fklmvclEd66F2/yPtxdMeqSQmgqR+1AAvGdAu4PRikWChTiBmpEI/HAfuR4mHKthu+xASrPTZH4+3dt+xrVX5llea7EntE4b/zn5y8E/48Nc+gfPYAavnLQYNs2rutelwXeTrlYMNBdKuG8NIHy+Ydxnj2NMJBAkC8/qz0/P8/IyAiyLKMoypZOBqIokkwmicfjlMtlXNdleXn5hj+fhYUFxsbGcByHXC6H67p4jofz6grW8xmkIwn0n9uPcAv0NS6H67jtqryx9rdRMRk7MMyKmudLv/oNmmWjZYdXMTEbdjuw94U0tA3q+JGeID271E12d1pAQdxhK7qiKIyOjtJoNJibm9tREsBzPdyGzeKZOcbv2cf8y5NYpeYlXvLb+cwLitiqwH/aYvjBEV77f761oTKvoHT7LgjerQfyPqn1/y3QDqjlGy1rv9OrLJ/NEUoF6N2X5L7P7CMxFNnxa9vh+rAsi2w2S1dX1y15vCslJR3HuSTppSgKu3btIpfLUS6XN7X+Dw4O3rR97dDhfZEIWKevr49arYbruq25MUlqn9b/9/l8rKysXDYT1+G9ga7rDA4O3pKFbocO309IfoXYI4PEHhnEaVhU3l6i+Mo8i7/3Dv6xGJGjaSIP9CNvCEjXRwGuhCeJNBJ+/Ct1qukwxpEEwT+bxNwXw41q4JdxPjWE88WzKC9nMT/Uh/73d9P87bMUvnKOvp/pY8+P3M3Lf/0XJN7K0f25XSz+4VmKpkVUlKlMlNCHQ5SeX0TSZbReP/WpCpGCgRSUsRURdapMCYeoJcLdCYSJEsuvZhgJ6ZR9An7RoVqBylgM+8EUta/P4/zzvyT2Mw+R/KWPkHn+HbQFB//uGB4OZtmj8OQgrizg/9MZ9BdXifxQH+XjeRo/kGZ+JQMrmdYL0OdBwGXlxCliqdbM6fosqGPaLH9zguJzUzRNh8UXZ+l9dOfBv2mazM7OXjIfLwgCsizj9/u3tOu7XqSojp1tdeS5yyXsrx9H/tA+xIEE4mDyivdfrwrXajU0TWNwcBCfz9dOBgiCQCwWI5VKUa1WOX/+PJZlMTY2ht/vp16v39Dn4zgO09PTdHV1MT4+TmF2hcwX38RpGGg/MY6Y8t3Qx2s/ru1eaMXf2I6//rdmtgL7NUV8s2Gj+pW2nd16271yt0y1Umf4rp52BV8PqWj+nQf2O8WzWy32Q3sHWT63yOKJmUvn5LcI4p26jdd0WoG5T0b/cYG+3j7OvfEOtm23Be7kuLbJc35jq72iq/h8PkzTJDQco/enD9zQ53a1OJZDdqLQDv6NiknP/iTpI93c/6MH0G+DjWSHFtlslmg0ekvWi4ODg5w9e/ayt0mlUuTz+faxOp1OI0kSXV1dtyxh0aEDvM8SAdAS8xBFEU3TcJzWzJlt2ziOg2EYRCIRhoaGWF1dpVwu3/AFRIebz7paajgcvvKNO3TocF1IPoXoQwNEHxrAadpU32klBTJ/eBzfSIzI0X4i9/eTyWR2vM16V4DY2RzV/hCeJmEcSqC/vkL9yTVRpx4/xgd78X9jAfP+FEJIQf/x3dh/PE3+2ALB3XG03RGqJ3PEa8P0/+g4uV9+h9FDSTLfyzDyuT3YuSZu027rBISLBkpAwqk6ULEoCBCPanjdGuIvn6ZaMUl0B0nHRCp1h0LUj/1gCgwHwXBwVJHCb75M369+muiufiSried4iGGF5ngccbaG79Xl1u1/YARLF5GWGiBd1EIsCHCygN3jYwWXbDaLV3FoHi9TeG6RnoCKUbc48M8eZfQf3r/j13R5eXnb1mrP89p+8p7n3fAKkxTzYZzN4WbL2H9zHPmJVhIAQPBfeeFdqVTQNI1du3bRbDapVqvthEW5XCYcDmMYBtPT05tm3svlMpFI5Kb8jpumyezJSXhpldT+NPv/r6dYWlmmWCzueBvtwH7jfH3VbPnWb5ivb6xdbjXsltVde47+gq1drD90iZieFlARt3AnUBSB0bEBLLm+s/Z8y9naP/5iZfvGpe32nuXS8+gwbs8QJ375u+3Afj1Yl4IKapevrV6/yZZOl9vuCk1BIJTy8fC//RgrKyvkcrkr7ncgEKCvrw/XdW+LeLTneVRX6u12/5WJAtH+IL37Uzz4+UPEB8N33NjI9zOTk5OMj4/f9A5SVVVJpVLbHo8FQSAejxOPx7Esi0qlQiBw52iMdPj+4n2XCIhGo5w+fXrbH798Po+maYTDYfr6+pAkiXK5TKVSoVardewJ73B8Ph8jIyOdUYAOHW4Dki63ugGOpnFNh8o7S5RemSfz5yfhHw5jvr6CciCOGLl88GcFFDxZRC0ZmFEdc18U9d0CUqaO09sSnHOPdsF0nSE9iTKWRFFVuPcQ5eNLLPzVCWKP9FL4owkix/J0P9rH8q+dpOS5eG+u4vzIbtT+AMZslcCuCKvfnsereyh9GvZCDQwHKarD3XHk7y4xcXKF3YkAkSMRSqsVZopNdv2dfoSSie8b89gjYdxDMaJfnWbpD75H6qNHEMe7qD/7Oi4C8deXKBU8jPu76f+xYbTBFItvTeDGtVbgfxHuWAjnN86Q6ddoLNZIPNZH/MEeDj01hvSbJzn2+gL3/NiRHb8vKysrO56vLpfLnDhxAlmWCYfDaJqGruv4fL5rPq5KUR1vpYz9tWPIH9iLOHR1gq2FfJ6Y6lJYnieS6mNqagrXddF1nXA4zMLCwiUaQOtdFOFwGFmWqdfr1Ot1ms3mdf+Oe7aL/eIy9otZ5AdSrPbYVGamGB0dJbdcoJittNTvK2YrmL9ETG8tsG9uEdivBfGx/hC+UGLtupa/vepXtgzsr7i/nodnOO1AvlG3qIaSyEsOKycXL69s37DBY7Og3cZg3S8jxzTEvsAloniST0bQJYLBIHKXTvqfbz/uspPnsLq6iq7rJJNJ8vn8Fd/Her2V6Dhz5sw1P+7VYhs2y2fz7eDftVx69ycZfbCfh3/8MKr/xjuvdLgx2LbN1NQUY2NjN/2xuru7SSQSnDt37hIRzFAo1D6vKArx+KX2sR063Cred4mAdR/hy2kFGIbRXjipqko4HKarqwtN06hWq+3EwE7tPlRV3VapPpfLXbeKcYcW4XC4MyvVocMdgqhKRO5vdQNMT05RzhRw5ms0v7mA1OVDORhHORRDjG6hKSAIa6KBNcyoDpKIcU8K/fUs9WeG8QcCaJpG6t/sofrlk2TnljB2BXBdF7dh0vz2HPo9cQzbwXx5Gd+j3aSeHmLlK9MMDUTIv7GMPhyiOVMh/Egvc188jaupSLv9eCeKND2XgCTjDYco/tsTpIMactpPOKZgZhWqgyJStoH+7QWMu5PoTQvtdJ7moThSvkbp1beJf+QR5JCOVzdQezXsD/SRTvTirtY5d+4c0mQOIXbhubuWQ/V0gdJbK5RP5ul3JaJjIXr/yS6UcCtxUijl0c/nid7bh+zbWQvrtc7J27a96XdSlmXGx8c3bXenvtSCZ6NkV5F/5AnE4SuPAmzENJoEzn6FuJ3FE0WEu//ehX1w3qVZO4dtDSPL+wgEAu2TJEnUajUWFhaQJAm/3080GkVRFAqFAqurq1dUoXdsd0Pg3gro3bMl9DcKNBXI9KlU3p6h8fxZjJrFw8/cxaHHx/nK776wQSSvFeQnBsKtgD6gtP6uteLvtCLseR5uw8Fqt9Rb21fpGxdb1DkIkrDJM74QTCA5InbeaLXRJ32bgvuNrfaCcnXid+tdl7quY9s2oVDoupMv66N+tVqNc+fO7Wh7lmXhuu51uyNcDs/zKGWqZE6vsnhyhfx0ifhwhL79KR7/qbuJ9AU7Vf/3EOsaFgMDAzf9sWRZ3vIY1NPTc9Mfu0OHnfK+SwRA60t2uUSALMvtNjLTNFldXWV1dRVJkgiHw0QiEfr6+mg0GpTL5UtEiy4+6AeDQXw+3yUtg7IsMzIywuzs7JbCRx12jqqqnSRAhw53IK7rUq3XECMq/s+Mtaqp58tYx/I0n11ETGioh+IoB+OI8QuBcT3pp3uuhGA5eIqENRJCPVUgZqik9qSpVCrMLy7gTGfwThZwP78bev2IYRX9H+ym+ZtnCfQFKGdq6PM1uj81Sv6PJqgLLvVvL9LziSTewnGiqQlGPnYGfdFG2b0f+12JqqfguzuB8OVJqvkmsd4gveMBcnkP72PDmL93DP1bC1j3JwnPlPGElrCZHdWp7A+iv7SE1rOIrYdZTosk+nsZSyYpnl4g970JvEe7EfIGTlihfDzXCv5P5PD1B4jc00XPp8ZQVg2E55fwQhsqiIZNccxH70O7bul7KAgCiURiy246SZIIBAIkEokt21fdXBXruVNkj6SYr2dxTyy3tynLMqlU6rIVr6Wzb5GqzCAmesFuYp/6Gm7qw2jqJP1dv4Qg2GiaH1f6L9QavdRqNXK53CWBX6lUwrEcPFsg1ZVibHQX85MZTr1yltxiqd2O39hgd+eYTlswLyTLpLM2uiVQuTuKOBZicK1Svx7s+0M6A3t6+OS/fmzL5+I57oXAfcWgUa9e+H/NT349cN8c7K8F85p0IVj3yZvOi34ZNapdake3Xpm/yG5OjgRJ9/SQONpPtVq9bptlURSRJKmtZm4YBoZhoCgKlmUxOzt7XdtPJBIUCoWrcg4AqFarpFIpFhYWblhHp1m3WDqTa836n1pFlAV696fY+8FhusfjyNr7cun8fUO5XL4lj7OVk5miKB1dqw53FO/Lo5koiiQSiW1nzEZGRlqtdJ7H0tJS+8vqOA6FQoFCodD2+gyHw1vadVz8g1MsFrdMPjQaDQYHBymVSiwvL3dGD66R0dEre1B36NDh1nPxwl2QRZQ9UZQ90VZSYLKCdTxP81dPIsY1lIMxlINxpKROM6rjX61T6w2BINC8L0V42aBcLJFZblm3iQ9145urYv/lLM7nd4FfRoxq6D8xjv+/HGM1Wyf+dg71mSHCD6Qw1VPc9bFjxJ7IYq+aaFGd2DMNKFpo8ZeIHjTwnxum6vsU53+vwlAsQPc9USpFj8rTI4SPr2DNlvF+JEr4dB5XFUESqRxJIU5X8Z2YxxkKUs4UiO1L4nk1kt3dLXGoF+ZwfDLlEzm05zMsFht4gwHCd6Xo+cQISmRDd0RIgW+7MF+DgSB4HtJXZ/GOxCkMuhRPnEBVVSKRyCZBwYsRRbEdjF0r3d3dqOrWdm+O41Aul9uLZ13XicfjRKNRnHyF3AsnyR+O4M3X8SoGrAmiresSLC4ukslkEAQBv9/fHkeQEFlaWETV/Ig1C0csAyZIfrr/8gT2F86BZ9FsJpDFGkbj2zz/lTK1YnPbdnzHdtGDClpAJd4b5oGPHubJv/sYc+cznHrtLLImXpivD7Yq9lgu9vNL2K+vIn+iG+m+JK7lbha4K9Qx6mX0nhjVYJHs/8/emwc3ep93np/f7z1wXwQBXiCbV9+yTku+YjuyY1s+ctpOUrE9TmaT1JzJ7k7tTM3u7M78sbs1M1ubmZrZTSqZbK2TzTGZeGyn7CSOb0nxLUuyLLVa3ewm2TxB3DfwXr/9AwSabJJNdkvdaqnxqUKBAF6AL0DifX/P93me7/PHF3Abe4N71XH3ltbvum2g9zLze/rlNcQraORXqVTodDoEg0HGx8dpNps3/T8SCoWYmprqZzez2ewrPqFJKXVTff7ZbJaxsTGOHz++bwvJUX938UqVjRfzbJzLUV6rk5qLM3YmxemfmCGSDg6y/gNuGMPoVgT1jqtCCDKZzKu8VwMG7OZ1KQRAd2FTKpX2Le/P5/NMTEwAHDh2UClFrVZ72dMFarUaCwsLjI2NMTc3x8rKyi0rYXu90sssDRgw4M7jegtkoUuMEzGMEzHUz0zjLtWwnitS/51zyKgJZ2IMR9s0RsMIKQkeHyFkRqlvVmD7Zb0hH+5cFK1oof5yBe/D0yAFMuEj9pv3kPu1x2n8zSr+D0S5/59+DZ/8DtLTaeXieFUDmY7hOhbWZhVDD+GWdUJn1gi5v0Xkv5uBQdyfQAAAIABJREFUZ38az5UU35nB93wRfatNWygCl8uAoD0Wxmm7mI9vYJ9O0PjoLMZWi/oLOdKPHsddq2HbNo2FCu6T6+TyLeypEPO6ZPKf3Ic+Hj7og0M9NAxPFWAyjFxv4jxboL5Sw386AXQr1nptbFJKwuEwo6OjuzJKnue9ImXZRw3s2u026+vrrK+uIRwPkQni6RLtqTzeG5MIKZBtF9lxEG0XOx1Aa7no+RadiMlmuIDSJcqUiAsVxt52L7XSKSKVFxHpEdr+hzm/cY5zv1/kA79eQ6kWbZ+H5Wa4/y338NX/8i0Mv04kGdx2w79ajm8GuucJZXnb/e9NXvj6M0yemuJ9H/0xXvric1TOF7BbDu2GDatN9Es1HFPQjhm4n7mE+vTCnqx7f8Z8ZpjwWIzjH32AtXPLe7PzAe2OChjb7TbtdptYLHbTYlEwGGRycpLl5eVbZq4spSQQCNxUEO+6Lqurq4TDYSYmJmg2m2xtbR3aktmuWWyez/cd/n1hk7HTw9zz/nnS8wm02zBecMCrw+3ymDJNk5MnT7K4uIhpmkxOTg78rQbccbxuoyspJRMTE6ysrOx57NrRSn7/4WOZXg69E1U8HmdmZobLly8PfANugMGBc8CAO5dYLHaksYFCE+hzUfS5KOqnj+Eu1Wg9V0DVPMYaYWL3Z2i3WpSKZezP/AjxwUnU9px26/4kgS+v4SiB+PYW6m0jAGjDAZKfOI79pe8zYX4KPWNR/2GUjqfw6Q4ybOA1HXRd0vI8vLqN6wmEFcXeahB7YAn54P/L0sJ/j+/5IpqnCPsEmuXSNjWcZBD9hTJiOkLz52ZQoe0yftejtVpGC/rp/KCCnBes/cVFjvl0Jv7BPWiZEP4/XECNHeIEfTaOeDKLKnfQLlbIb9SJ/OK9+27aG7FXrVYJBAJMTEyglGJpaenQXvjDaDabBIPB/UtmXa8b2Led7QDfRau0CW416fh07KaDaliI83XUYpFOXKfhebQcj4bt0rAc6i2batPGsj3e3PBhINGBgANbFRPj7e+n+Nthkv/bT7P49EuIX7+Ph4wHadmnCQWeo7o1R2klw/G3avzUx9/Bj/70u3hrFl6zidtyqDUdKq2r/fNC9PrlNWTQoBhcZuThKU5/+AHWn1lm9YkLmKsthAvaJ4+jzcf6wb4wD+6Xd4FsbovgsShh88a8EF4tAoEAPp/vyJ5H15JKpdjc3LxlIoAQgmPHjtFsNl9W+0K9XmdhYYFkMsns7Cy1Wo1cLodlWWiahvIU2UsFNl7oBv61XIORE0nGTg9z74eOE0rempGQA+4sekbhtwtd1zl+/Pht+30DBtwor1shALoL1Gw2uyfovlYVHxoaYmNj45aX7ZfL5b5Asbi4eEt/1+sJ13X7xlUDBgy4s/D59jEDPAQhBfpsFGMuxtDEFO3VAj/6vcdpfWcD4deIx02MJzbovCeDEAIvFcBLmMjxEOrbObzRAGquOz40+ViY1Ds+j6hbOP5RtFgbrWFDx9s2YHPQTQ1NSty2C7rEyrUI+nSkl8CJdpg48e8oXf5HGIUAnhQYUT/V9SahgI/mh6ZQ24aHnuPRuFBGPbmO82KRdrbMPR9+iCuLK8z8xn34f/8l2hMhZNE6cGLALkwNdW8Cnsojns7TEJB4w+GO+61Wi4WFhRv+3Ps4HrJzNbiPH5sl99QF/Is5VNXCq9vQtBFNB2W7dJSi5Xo0HQ/bcjhmarxQabPYsFB+HRXUybgawtMpDfkJhH34QgY+QyOiaQxpAkNIpKvwPV0g9GwZHA8vIFl/fpUHP/4gPwiFSJgGV377h3hNB2FINoM6WvARZNAgOF4n+jMx1p9e7laajOw0vzO2M/Na9/YB2dxLly4xMTVC8iNvYmV+AfdUBHHteMcjfPbpdJpKpXLHjx8OBAIcO3aMtbW1PQmQoyKlvGWJi54IYFnWDY0fPQjP8/qjB5PJJDMzM5SyFSLxMCgIuBE0x2T0VJLhmThSH6wp7jYCgcCgwnTAgB287r8NU1NTexZMjuOQz+cZHr6q6KdSqSNltV4uxWKRRCJBJBLZt+2gVwbf6yt6OX2ftxohBPPz8xiGgZQSz/NotVp0Oh18Pl9/HJVlWWxubr4sg5ZyuTwYsTJgwB1K7/t/VHqj6+LxOB3Lwv7+S5jvHEN/dAT3Sp3GMwXiT2zQfKaAvD+J+YYhOvcl8f/tJs0PZtA+v4L7MT/EDMYm/wi94mBtBNGcJjJsYNgerZaDr+ngCQEIdEPi2B5Cl/h1gR7WsaWEih89XCXx4J9T+Mav4FjgN3RKDw2jPTTaDf7PFbuGf88V8KUDZKbC+E/Faa1k0WMmTbcJlguuAr+GKHVQiSMKJA8m0X7nPO1ci9AjIzdfWu54V7P226X5Xt3Cq1h4NQsa3eBeth0826PtKZqOh4oHmH7b/Xztt56k7Xl4vm5gT8hABA2MqI7P1PFpGmEBJ2sWhaBBaD7FG+yuOZ7XcvBttNCLDr7n6rjNMqrtogIaVkDHCRuo2SheoY2R7eDpAqFpqIiBd3+CWqnKiX/2TmrNOlP/00PIgI7YDtKGhoYIBoMEg0FK5TK1hMXQ+2/MOFYphftMgdZX11k4GWPsY/dz4sOPsLGxcaQstJSS2dlZTNPEsixWVlbIZDIsLCwQiURethHfrcDv9/dFgJttcfT5fBiGcdPVBIeRyWRwHIe1tbVX5PVc2yN/ucT6uTy1bIsP/r1H8UdMvvPFp4hMBBjJpHnjY28AYG1tbdCmeRfS87eYmZkZmPYNGMBdIAT4/f59g+7NzU2klP3gsje39mbMam6UfD5PKpWi0WjsOsEKIZidnUXXdZRSSClpNptsbm7eka0ESqld2UApZX+00056jv/lcpnV1dX+/fF4vD/h4TARJp/PD4SAAQPuQHoz369HJBIhHA7j8/nw+XxIKalWq+RyOer1OomID3+xRSsVQj8WQT8WwZsJM3S5RtmDxv+3ABKSPskffeoP+c5Lz8CXHIxpl+TQEmPDYR6a7PD+D4wi6zZPfLPI734uB7ZCaAJNlyjbxXMVUhP8xJtj/MO/M4GwPSSgamH+zee+zbcfv8jf+9V/jnZ2iPx6jfb5CtXnCpipAPGHUqQ/MI2Z8OF7vkD9uxvUV7bIvPk0mqbhVdvdCQBCIEudbkXAUYiaSENQXK0R/Udnrt6vFMJRiLaD7LiIloOqW7iVDl61g6o73ax9y0HrOLi2R91VNLfL8Rsdp9sOYWgoXYLZdZbXTA2paZiGhhGQ6I7CbtnMv+0ElYt5VMvpGuHlbJTd6Zva+UM6c0FBwdSpmRJpgIyYmCPd/nijYuNbbuD/UGbb/E5HyN2ihv75KzAVx3l7GuNTC/BQksib0tTcBplMhpWVFbTI1cX58PAw0WiUYrFIPp+/qay2t9bA+qtui6Dvl+aQEyEKtRKNpRaTk5NEIhHW19ev+z88MTFBo9Hg0qVL6LqObdsUi0VmZ2fx+/2Mj49j2za6rnP+/Pkb3sdbQSQSQdM0RkdHCYVCVKvVPRUMPd8AXdeJRCL9cXyRSIRoNIqUsm86eCv2z+fzcenSpZf1OvV8k41zedbP5cktFImOhpm4J83f/T8+RLlSIpfPkjrVNXyuVCpUKhWGhoaYmZmhUCiQz+fveBPnnYZzA14+ve/vYIzfgAF3gRAAMDk5ycWLF/dk19fX13Ech3Q63Vf8L1y4cMv3p1KpEA6HOX78OLlcjnK5jOd5TExM0G63++p4b6TT7Ows6+vrr+jIk56DcyKR6J/we6MUm80mpmkSCASoVCrXXXwVi8UjB+jxeBy/30+z2SQej/dL/dPpNMB1xQDLsnAcZ1DSNWDAHcTi4uKBBl9CCOLxOMPDw3ieR7lcplar0el09hyLm+kQoY0ardRVEdE6O0TkpQrhtw7jPJbBXW/S+uYm4tslplWa/+aNH2LsV/4z7ZTiuR95/PkfrvCd5xv8z//qBG85E+L+hxM0NhsYhiQUNpEdl899vcCXf1DnJ94cR7gKCbhCUKh7/PCiywd/3uQLn/4yU1unMC43OPvBeeYfO4aZ3O0jIxyFYHt0Yr1OJBKheqncHwUoix3szD7+AEp1xYftwN6rWTiFFmqtTqftwLdWsb/mItoOWsfFcRQN26HZdqk3bTqOiyclniZQUiK0qxdNCDQEmieQro7f0/C1XWjTLZuXOtLQkbq+e558QKewvMXMz97DyguLu+4X/q75nWzZJL+7QWM6hm86Rmq/v3eujb7SguF9eq3XGzAewnnnaHdaghDYv34S9K5QUKvVKJfLJBIJQqEQnU4Hv99PLBbj8uXLN1UZpxo29lfWcS9UMH5iAu3+oV3VFu12u2/kOz8/z/r6ej8Q7l2UUiSTSQzDYHV1dVeV3vDwcP98pGkamtZtR0gkEpRKpRve31eaXC7XH/3oeR5jY2MYhkG73cYwDAzDwHVdpJQopWg2mwgh0DSNRqPB6urqLRt7LKVkbGzspkb+OZbL1sVi3+TPbtmMnUkx/cYx3vyJe/CFupM2HNcmn8/v+xrFYpFarcbY2BinTp2i1Wqxvr7+qidcDMMgFovRbDZpNpt9Iaf3PbjZ9o4Be9lvFOqAAXcjd0VUJaXk5MmTNBoNlpeXdyn/W1tbCCFIpVKYpkk0Gr0tM0bX1tYIBAIMDw8zMjJCp9NBCMHly5f72yilyOfz1Ot1pqenabVar0irQCAQYGZmZk/PvWmae0xUUqkUuVyObDbbv08I0S+RNAyDG8Hv9+9rzphOp3Ec57rO1VeuXBmMERww4A6gVquxtra2bwVVb3zr0NBQ32H+MDfwdtxPbLGE3rJxAtvHFF3SfnAY//e3aHxwCn0iBB+dRXsqRNjvJ/p2P+Ojq1i1KJk3+jk1PM2/+NeLfP6LeX7u0QTmRhP/iB/qDiEDLq7a/OW3q/z9j4xwZiaA8hSOJrH8Gl/8WpHTmQAfeHuTz376PA++91GSk0lS757cd3+F43WFAF3S6XQwNR1to4lyXJwf5TDPl2g5Fu7316DhQNNCNlxoOdhth0bbodlysRyPgJCkmgKpC5a/vkFLFwghEAiEAukoNJ+GHvETTZh7gvg9Y+iumUEvjIPN73o4QUFyJE7A3jsqV7Yckt/boHksSnM6duBrqIgB9WvOT0ohnyuhfSeH/XfmILqjFPeaufe5XI5QKIRpmoRCIZRSLCws3LARonIV7lM57G9soN07hP8fn0H491/qKKVYX18nEomQTqfRNA0pu59X77oX/E9NTVGv1/tjiVutFpFIZM9rjo2NUS6X74gM7ubmJlNT3TaKS5cuYRgGfr8fy7KwLKtfeWgYxm0tk0+n0zQajSNNCVBKUc02uoH/uTz5yyUSUzHGzwzztl+5j3gmsuf/e2ho6MDx0T1s2+bKlSv941Umk2FxcfFV+btJKUmn08TjcWq1Wn/KA3TbIjc2NpicnOTSpUu3rE3jbmMgBAwY0OWuEAJ6hEIhTpw4wcWLF3ctLrLZLJqmMTQ0RDKZvC1CAHQXEisrK0gpiUQiNBqNfU9C7XabXC7H5OTkLqHgZhgaGrphx9RUKkUqtV8O6JVlfHycarV6YHtGs9mkVqvtu/gaMGDA7WG/cas7GR8fR0rJ0tLS0YMLKWgOBwluNageuxqM2nNRzHMl9KUazkwUhMCdCGNczhF9n4OKhtE6Oq5SHBsyOHvMx3e+keejP5nG0QR+TdJwPbLZNr/1J5u855EoP/5gBNtRNKXA7tgI2+WJ71f4xMczTJyF0w+nWapeIlQK4mYbOKU2TrmDV2njFjp4lQ7xfAfbc2l+pY1PT9Jar5L7g+exXI+S4zAbCHDxmQ2UEqAABSKgISMmetTETAfxx32EwyaJtSb572cJv/8YyZqL897xq+Poepl549UxNZNth+T31mlORmnM7BUJduGTCE9BxwWfBq5C+/oGcr2J/QszELj+csNxnJfda+8u1bD/agUR1PH98gnkyNGc4K83KrgXKBuG0a/as22bbDa777lISsnIyAibm5sv6728UqyvrzM/P49t2/2qnJ14nndbRYBUKkUkErnuWsZuOWQvFFjfzvrjKcbOppj/sUne9nfvwwwenICQUhIMBvt+RYe9t57BoM/n49SpUzQaDer1OqVS6baIAkNDQ6TTaarVKgsLC/31T88ramcFSjQapVwu3/J9er3TE/wGDBhwlwkB0D24njx5khdffHHXQX59fR0pJfF4nMnJyX3HDt4qPM87dAFUKBSIRqM3XXZomiZjY2N3fBAdj8cPLOeDbiXFqVOnbuMeDRgwALrHqStXrlCv16+7nZSSUql0w8FFMx1i+IUc1ckY9HrLhaD9cIrAN7PUp8KgSbyECZ7CX7+ESCpI+9GKHeRclMljQV58ooS71QZHgU/guIr/80+yTI6ZfPKDw1QbNhKQPoluSl642KResjgb8rCWazzYCfEn//UrxP0Q+5MlXKXwPFCKrhFgQMMcDqAlDWqGTuaBCdZzZUL3p/FlQkQSPvwXqsy/P3M1S+/XENo+C0/bw/hfn0FMh4n88knE776EORyA9Ks/ykx2tisBMhEas4eIAABCoCIGom6jHIX+hRUIaNi/OAPmrZ3JrqoW9t+s4V6pY7wvg3Y2fvOmi9fQC5Q7nQ7ZbJZMJoNSqu/ds5/hWM9z6NUuNYeuwLK8vEw6nSadTlMoFCgUCq9K5nt4eJh4PM7i4uKuZIxSivJqjY0Xu73+pSsVhmcTjJ0Z5uSjx4iOhI789/Q8j4sXL5JIJJiensayrL4XyfVYXV3tt1L0Wpq2trZuKvAOhUK02+3rVrMIIZiYmMA0TRYXF/ccL3cmRJLJJKZpYprbbQ+Og2EYOI5z6PsasJc7fR08YMDt5K4TAq5HPp8nHo8Ti3XLH2+nGHAUNjY2mJ6eptFoHHmBEQqF+ieb1wKHuRsPyuIGDLh99DxMHMe5oRLtmwnC3ICB49fx5xq0Qz5wPLAVLgIPML+xgTURgs0WjqFhXFyHpAsdDzwQizWkJgCFLkGEDNy6zR//TRnHr/ObvzxOp26hPIXedKAFSggef6LII6dDaJoAqfPIj4/wn76xSGlGMPXfvh0ZNdGCBjKg9d9X6PE16otF4u89RuzYEOG3pzDWqlhvG0GWLTQH/McOX2xqSzXqhRah902AJlH3D8HTBXgsc8Of3yuJ7Lgkv7tBazxMYy5x5OepsIFYaqA/U8A7E8d9S+rwEYovA+V4ON/ewvlmFv2Nw/h/+gziFooO5XJ5V2Doui4zMzP7bjs7O3vHGAe2Wi2Wl5f7xoau695yH4NQqBu8u66L67rEYrG+COA4Dp2GxeaLBTZe7Gb9dZ/G+JkUZ94zQ3o+ge67+eWpZVlks1my2SyxWIyxsTEcxyGbzV535KPrulSrVarVKoFAgNHRUcbGxmi1Wv2Lbdu4rtsP1KPRKKZpsrW1RSQSYXR0FKVU34+h1WrheR6lUqmf3TcMg6mpKTqdzpHaESqVCq7r9ttXA4EAzWaTcDjM5cuX7wjB6bXE7ahwHTDgtcJdJQQUi8V+ud5BJfi90XexWAxd11laWrojev2gu3/ZbJaZmRkWFxcPPfiPjIy85g54h70nz/MGpoEDBtxiPM9jcXFxt1mYp7aD897l2tseOAqZnICFKmIh283K73p8+3n9n7evLQ/hKNo+CAUlnSbdHnJDgi7pKEXwUg67aiFKFkoCTYlwXZQGxE1EqcNG3iaVMPDaLlKXfPbxIs9ebvG//7NpRo+HUZaidLlKJGwgpaDecHnmQhvb9njy6TroNlauCrkYz29+l8qVBEITCJ/WHWnn717rAQlJSevLazhv6mB/ZR3tYgV7zI8v38aJGKhyp1si79P2uOf3kE8XKBXbpN+1Hfjfn0T8p5dQ7xiF4KtzjBOWy9D31mmNhqjPH10EAKDloH95HefDx/COR4/0FE3TiMfj2LZ9Q2157sVKtw1g2I/v104ik3u9Z241jUaDdru9r++NrutkMpldk3JebdrtNs1m85aXRY+MjBCLxeh0On0jRddx+cHjP2T52XU2zuWpbtZJzQ8xfmaYs4/NEUkFb8m+9CYFxOPx/rjCQqFAtVq97tqu1WqxuLiIpmkEAgECgUC/d1/XdTStKwzW63XC4TDNZpPx8XFWV1dpNBoIIQiFQv0RjHNzc9i23W812draum71404cx+kLUENDQ/1JF71Wz5WVlRv20rjb6I273jnpasCAAXeZENBzAr4eFy9e5NSpU+i6TigU4uzZs3iex7lz527TXl6fXt/azMwMFy5cOPBElkgkXnMiANBXuq/H5uYmmcyrmzEbMOBOQnkKZbndi+2iOg7erttXf+7ff53HKimFlfHDX68gKjbC9rpCgC5RhugH6FeD9e59ZipMaCRO+flV8BTKJyGkX91ux7b952/fVoakiSLyzCbi3hG8HRlBF7C/tYnPkKh6HFXXaU/PEeZ7EPeBp1hea/HDH9X4ybfHsBs2L27afPrxMr/xqxNk7hvCc1ycgIaeDtAxNXw+jSefyRGP6fyLX8+gABGuUXnqMZ76ZpT/66t/QeYnx9FDARxNdPfBUzi2h7bRwDUUnYaDsj3aP8hhXKlT/H9KJJSg0XHo/O6LSCm64wRNiQjoyKC2fd29RC7VUAEN+/ENZNRERA20IR98fQPenOoKCX4Nod+eflZhuSS/t0FnJET9+A2IAJ5C++YWcqWB+2DySCJANBql1Wpx7NixfiB9rTHtvr+q0Mb+4ioq38Z4bBLt5MEGhreDhYUFQqHQvpUB8Xgcn89HoVCgVqvdEcGa53k3bPJ7I4yNjREMBrl06RL1YrOf8d98MU8g5mPszDD3/eRxhmcTaLfR+6JXzRGJREgmk/3Rxc1mE9u2cRxn3/Wh67rU6/U9JfiBQICxsTGuXLnCqVOnyGQyLC8v98VTpdSu5xWLRY4dO0ar1eLixYs3/T5GRka4fPkynudRKBQwDIPjx4/v214w4CqTk5MDEWDAgH24q4SA3hirw2bWX758mfn5+b5qLqUkEAjcslE6N8rOMUsH9YeNjY3d5r16ZZiYmDj0JFmpVA4UAjzPw7btwQF/wB3DniDdcvE6zo7bHqrjHDlI33OxXZTjIUzt6sXQkL6rP+98TJp69zpgIKJ+xPZ2cnu7jnTIdfJQteFnjqG2g3Q0savMW0rZXzj3RgWapgkCxt51BnFm6IbLjxXQSgYJ5prUM7uDyc79w4T/YhHR6ZblbujjyKxF4VyBH71Q57NfLzJzPMRP/fgQa5tt/uMfZXnXO4aYnw5SqDiYjoMrXSxXQK5N5kycLz1T540/PszYAwm0toMmHFpPzzM6k+I/ep/j++WLvGX+TWg+HSkFvoaDrFmYGw2EXyN+KoUeNBh60zAyqDH2kRmMv17BeH8G16+jWg5e3carWqiyhVe18Go2qmajbbWpldpoYY3qF5ZRLRfVdtAURIRG9U8vIqRAAMKQXZ+B3iSAoIEM68iIgYiYiIiBjBqIgI7YFg/wa1d/Ng+fHCAUXRFgOEDteGJPSb9SCvv3ziMfGkZ7cPhqlUPHRf/rZfA8nPeOI/JHC0aazeYev5dUKkW1Wt33XKssD+fJTZzv59DfOoL+C7O3TSA5jEajQblcJh7f66UQCAT656tGo/GqVxnW63XGx8c5fvw4CwsLr+i+jI+NI5XG53/7yyw/s0mj0GT05DBjZ4Z54GdOEkzc/qqNa+kZQ/p8vr5Rn67rfXO+nonzQabFPXoTF6Cbsa/VatddI1qWxZUrV5ic3H8SyUFomkYqlSIej/fHB/b+ZkopNjY20HUdn883EAIOIBwOE40erUJpwIC7jbtKCAD6B/1sNnugOm9ZFufPn2d+fr7fW5/JZF7xk+bLoVqtEovFDhQCXquOqL22jOuZJyqlqFQqxGIxXNftzztWSqGUwvM8TNNkenr6NeONMODVQXnqasBtXw2uve3AXFne9n3O0YP0ax67kSC9+5h+NUg3JcKn94N0YXaDu53Pk6YG+uGB3lFZfPHFrllffO93JxaLkUqlMAwDIQSWZdHpdAgEAv3Wqk6nQz6fZ2hoiFgsdsPzuZvpEIkLBeoTkV3BqArqWKfi6H9W5aWl5/gfvvgUoWNbhCKQmYvx4Z8f510nA4Q0xV98JU+t6fLVH9T40uNFtLDRDahRuEqQMOGf/0sfy8stfv2TGZSp4fosbDXC6qPvxCx2GP/zY/ztwtN84NhZXA+8tocV9WGNBLG3fMiEwDqTxBMK0XaRrsL/nSzyYhVDruDFfHhRAy9q4kVMvPEQXtREBTQQAv1TF1hZKDH6f78dYXT72pVSqI6L+NPLJGYjeGMBvKbTFQ8qFl7VxqtZqJqNl2+hlmt4TQfVdFCW121j0ERXQBB0RxACQtJtbQjoiJCODBmIkIEWNRARA3c2if6mGO2mS0VJxFK9KyT4tX57A66Hd66Md76C9/gG+kdmkBGT6LNfZvgTfwYxSeHCR2j89b1H+jv3gqdrjbtmZmY4f/58X2RSSuGeK2P/zSpyMoTv759Gxu684/rq6ir5fJ7p6ekDW9dCoRCnTp3i8uXLRwraNE3D5/P1z2+vBM1mk4WFBebn5/H7/S87wdEottg4lyceT3BiPsIf/I+fJpTy88afP03yWAy5n0nmHUCn02FjY2PXfUIIhoeHmZ2dZXV1lU6nc+A6sd1uYxgGUkpyuRwjIyOEQiGKxWJ/coEQYlelgWmahwoMPXpjDZPJJJVKhcuXL+Pz+QgGg3teQyn1ih3/X28IIfojNAcMGLCXu04IgG6P1dDQELVajeXl5X238TyPS5cucfr0aaAboJ48eZJLly71DV9eTcrlMsePHz9QBfY87zUrBkxMTBzav9c7OfdGCl6LZVlcuHCBubk5AoFX34F7wI3TD9KvyYB71wbbvWB8V5b9anC/J0jf8dgNB+k7M+mm3JVh3+/ySgctTrYVAAAgAElEQVTpt5J2u31or+nIyAgbGxs0Gg08zyMQCGAYBoVCod/SEwgEsG2by5cvk0wmmZ2dJZ/PH7kf1g4ZKF1iVjtYse0MYtWCc2U6zxX5tdDb+Ngnfxb3TWki408yKn6PlpXEK1sE4xpYHj//oTQ/9+4k/nuGsDabaDETLe7DZzvYukbtYoXAuJ///McPoCuFpjyU1iBb+lmUrtNJ6/zYIx/gPf/wYTYjPnzFFma+hX+9TnCrRiPbQI+H4BtX0N96H0KBMx3GelMKX8Ol83PTiJqFrNnIqoW20cS4YCGrNsL18Pw6nafz+MaDmJdrXbEgakBQ7868/7FRjG9vdb0Cjvi/oxwP1Xb7woDXdLoVCQ0Hr2mjKl0RwavZqLqFt9lENR1o26QfdXHOHmPpM1e6IoK2LSBsX1AgNAErDURAQ2SbqKcLBFJBkp/6HG4wBK5Ocu6/0LaOcbRQpzut5+TJk7vuk1IyMzPTnZle7mB/bhnVcDB/dhpt5s52+2632ywtLTE/P3/gNpqmcfz4cbLZLMVicd/vWyKR6Ff1OY6DlPIVMR70+Xx9Q+Seid+N4touWwslNrZH+3VqFqNnhjHO6hQKBX7533yElZWVQ1v87kSUUuRyOWzbZmxsrJ9IaLfbfeO/TqezqxpA13UajQYXLlwgEomQSCT67QSe5/X9BJRSNBqNIwkvhmEwOztLo9HYZQZoWda+652BEHAwmUzmNbsWHjDgdnBXCgE9IpEIZ86cwXEclpaW9mStXNfdZQTUGz1YqVRe9YkCruv2jQPL5fKecV2v5fJ4KSWZTOa6n7GmdTNooVCoPxPWNE38fj/xeJxLly4B3NJeyLsZpdTe8vTOjiDduiYrvivLfk1Qf22Q3rs4XjcY9+0OxK/NiO8K0v36riB9T6C+4/VeS0H6rSabzZLL5a67TW9s1c6FaM9J+yB6plwTExPEYjHW1tb65a0HIgTNdIjgeh1ruQkvlGGrBSdj8IFJ2k0b/6UqjYRJJfcWou5/xRcrIYfiqLaLivnQhoN0ns2jsi20qIlbsdDiPhxNorsuWlDHbdhIv4YtBEpWkXYaf+2ttKSHLST+sEm7ZuGlQrTGI7TGI1TekEJr2JiXGwQjBvH33Y+9WsC3WEG5Ct9KDc8BXijipAO440Gc2WtKUi0X/btblKsdou+cQttqYSxUuiKB5eFFDdyIgX2ljvjbLGou0q0kCOnXFQWELhFhiQwf/ZgnHI+h760jplOoiTDx/+XBbQHB7YoHTQev5eI1bLzNFs5yDVV1CegaekAnV24yttVAIUEZqEgb56UitT9bQISMq60MgR3Xoe7PmBLbtmk0GoRCoV37ZSoN38U2rZCLdiqO9nCqK0S8BuglCnqBXzAY3DcQGRkZYWRkBM/zKJfLVCoVAoEA6XS6v/2FCxewLKvvW3TUbPK1+Hw+MpkMmqZRqVRYXl4+chm5Uop6rsn6duCfWygRnwgzdibFmz/xBoamov1jaKGUx8MlmUy+JoWAHjunQ2iaht/vx+/3Ew6HSSaTQPdzKRQKTE1NYRgGxWKRXC536OSjo2AYBpZlHdlocmeb1oCr+P3+/hSwAQMG7M9dLQQA/QDyxIkT+xoVZbNZjh07tuu+O8WxvlQqUa/X+/NyXdelVqthWRabm5t79vu1RCwWI5fLHRg09JR6KWW/amM/7pS/1e3kSEH6zqx4PyB3djzPw9t5+6AgfUdgLg/Iiu8O0n37lsLvysD7BkH67cRxnENFgEwmQzQapdlsMjEx0W/DAfb8fG07jm3bLC0tEY/HmZ6eplQqsbW1tX/Fj6dgsUbz+RIj9QbCH0A9mIS5SNdckK5hn+9cCfWNdQpf3yD0oY+TefN/QNlNVCyKEzYRgBzyYefaGMN+7IYDrsLVJIbroQd17IaNkfQjRBuEx0rxH6CLACnXpiG0rhBQv6alQQjcsIktBTIVxndmkis/PA9REz2kYeRaeAGJUW7hZRtQtvACOm46gJPqXry4CT8qUReK0M/O0N4ZJNoesmYhKzaibCOezmPWLGTVQnQ8vIjRvWxXEPSuVcjotnPcAMLxGHpqAyfqw56LE9EF+njowO29bAtrrUkg5kNLBXB+cYahoE5RCzI68jvgOWxd+gUwE+jpIJ7joeo2drbVrUzYUaGgWg7KVYQ+MMWFqSrmdxsYYRMtZODmGrSez+GbTcAvjqHGPZwrtb6IIAL6HeMNsB898fnChQvYto2u65w4ceLArKSUsl+l2MPzPJaXl0kmk2xubva3Oczf6CCSySS1Wu3Iz3c6DtkLxX7w79kuY2dSzL5pgrd+8l7M4MFiU6vV6gfLrwdc16XRaNBoNPY81qusWF5eJp1Oc/LkSWzbZmtr64YmYFyLlDd27jMMYyAE7MNreQ08YMDt4u6Lkq5DKpXqj5bpUavV7uhxdb2TztbWFoFAoD9j9uWchO4Ujh07xsWLF/c9wR1W7dAbE3SnceQg/drHdrjBK8u7bpZ9V5B+ULn7NVl26dO6pmMHBvdXs+rSNwjSX09cuXLluo9LKfsO770smRCi//e/9udSqbSvgFcul6nVaoyPjzM/P8/6+np3ca0UZNvwQgnOlSFmou5J0PYHCSb8NMZ2l4N7lke+0CH8VI7ZX5pGbtQpffajJH7hM3jRDnhdIcJIB7FqFcyNFjKo49a2qwKkxBfQaG+1kLKOFDabhd+g48zSkdASkrjnkA5KvOo+QqSnUK6H0+z2GI+enmUteoXmg0PozxYQKR9mVMNXaKGZCjtgIIVCW63je76AqDk0XigRmI5gZFs4w4Hu9AQAQ+IN+fGG/DAeRPzuS9g/NgpRExyv22pQ6bYcaMUOxlINWbMRLQcvbHS9CKIGKmribgsFKmR0jR53IByPoR9s4oQMKmeHCR7huyz8kvDZJCrtx3n3WPcYALTUm1jafBCEh4r4MCYvETw7hEpf3xhOOR5e00EGdAKTScJrisIXXsLruMTePYsIGnjPNeD+EM0vr9J5odQXEYQhEQFt2zjxmqqDoN71QwhtX++4LfzaLT9uWZZFsVjsVwY4jkO1Wt3XSHA/do7uDIfDBAIBpJQMDw/ftBAQjUb7VXL7oZSislHvOvy/kKewVGZoOsb4mRTv+LUHiI2Hj/y5dTodDMMgFArtGzy/ngiHw31forW1NTY3N/vj/W52DSaEYHR09FBxtrdtJpNBKfWarsC4FQwPDw8qQgcMOAJ3ZnT7KhKPx3cJAQDLy8vMzc31b4dCIYaHh4/c83q72Fmm+3pQQg3D4NSpU7z00ku7ehn9fv++2ZXe+4/H40dedO1EKYWytx3cjxKkWy7eNeXv18+ybwfp+nbZuk/vB97y2nJ333WC9B3952KfQF0YgyB9wNE5zMgvGo3S6XSwLKsvBNwsruuysrJCJBIhMz5BbTHH5h/8AK9mwdk4fGwOhroiX7PSJrZUpjEa7pfEW4tVqn+0gP94hPh9cdo/yGMLEPe+g9xnh4h+4gvovjyuF0GPmnR0iWu7aELrtwe4UuAzLPzxKk4rQ67xT+lYV3u6PSEoagZeNICsNkm6NmWp4/a+U44HUuAJQaVUwu/3k3r0FCteCVm26DySojPsp0Z3HJ+v2MJXaOF3WoiETtv2KJVbJN4ziv/ZAlqxjRc1cXpVA+lAtw3Ap6HOxuGZIrxzFHSJl/DhJfYRQR0PWe/6EciqjSx30K/UkTUL0XRQoR2VBGGd6GYNJ+qjcnr4SB4EYrWB8VeruG8cxntgaO9EAYzuyAdAhXWo23CIECB0iRY1US2HhmhjP77K2MfvI/b2Y7uOX4VCgY2f0gn/1HT39bcNFbs+CO7VaoPm1Wu72Nl122vtMFQMaFcFgp3CQXB3+4Lwa11TxcD29RFH3Xmex/r6+q77jtqL73keCwsL/e9kNpvti95SSs6cOYNlWf2e9V7f+vVePxQKYdv2Hm8jp+NQ3qhTWa9T2ayj6ZLkdIzJj91DKOG/OhXiBlFK9d3x19bWXpFS+TuV9fV1RkZGmJub48qVK7TbbZrNJvF4nGg0imVZuz73nmhwPVKpFJZlXdcwGbotC1NTU/3W1jvFyPpOwDRNRkdH99zfM4d8rU7VGjDgVjAQAq5hv4N0q9Xa4248OjpKOp1mc3OTYrF4O3fxUDRN2+PE/FpFSsnIyEh3YaUUIEgHEtibtT195pe9HJiS8g9XGbYCe3vQ9+tN72fZrwnSdwTX+5a8b2fZDwrS98/C64MgfcAdx2FBSiKRoNFo9H05Xg4mOjHPj1hoU11YIvHOOSL/8jGyuSzlaxa+VtSH8BRGw8by6zT+ZpXWd7IMfXSGsbig+MQm4bU24kOTlM6mMFv30P7L4/jf/UPikb9C08uEjrXxih560AeNDrrogKbhKZPsM+8m334/ibfsnf8OoEf8bJZa2AhGXIuq1KgLDeEolARv+2tcLpaYGB1CFauIqoXaMW1BmRrt0TDt0TAAWtNG+3c/wjIEqaiOZwg6kwlcXUNZHsaVGoGntkCIrjAQ1nCe2MJ7JAWB63z+usSL+/Di+4gErroqEpQ7xC8WUY6HU3aJnL+ICugYp9LIdw1hPl+82nIQ7lYSyOdKaN/J4Tw2gToWPvRvrCIGomZzWFiiXIX7VA77Gxv4PjaP+NV54qen92yXTCbJZrO7RlUKvw5+HW1oz+bX/53XGiq2dhsruuUOar1xjeFi1y9BCIHYr/IgqO2+HdbxnUzgddxuq0fIOFJm0rIsFhYW+u8zGAximuYuDw4pZb9f/Vra7XZ/hF273e671QshKBQK3SDUVVh1i3qhRadm4Qv7GD2eZPaRDGbAQNM0DMPANE18Pl9fhFhcXLyhz7nRaPTFgJdeeumGnvtao2ccaBhGX5jpTXXy+XwYhtEP0nuTVgqFwoGi6vDwMBcuXDj0905OTtJqtdjc3HxF389rHSHErsRdjytXrvSrNGq1GidOnLjduzZgwB3JQAi4hoPU2oPcjcfHx4lEIgdOH3jFqFqQ78Ds4QH+zWTDXw79TPquYNvZ3+HdviYY38dYbm+W3SHmeCi/REqNurlJ45r+8k4IuMcP38/RPJPArdlopoEePiBIP8h0bhCkD7iLqFQq180k9RazpVKJcPjwIHBftvv+eaFMeHqU6KNj1PQKTsIkV+hWVaVHRohEo2xsbFxt6dk2DfRfKpH9ShYR1hn7zTMM11qsfG2TSEhHm49Sb3e3te9JEPzMIpV7H6Ncfwy/7wKy+hL2M98k8UCY9nNNipv3wOk3YjfncHMr1NdaJN6y/277IyaFlQpVTaepJAnXIYRHyfGwJKjtqiSrUEc/kyFYNGA4iDT1A88jXsfDzbXRH50g++gUes3qVgsUWxilDm7IoHNfAjtg4HY89EIHYbvov3sOcSrWrxpwU36U/4inb03gxbqB/dBmDWs2SvnedNdTwFWIhk1ImqALRMPG2Gh2PQmqFl7OQnU81JuHu7eXan2hgIP69LeFgOvhLtWw/2oF4dfwffI4cjSI5dqsra0xMTGx9y1o2ivSA30zhoqwPbfd9vYVCPqGipst7O3HZchg7MwUxS8tYmV0Fv7tl9FCBnrYhx7uXmthEz1sooVMVFhSiLfxLBevZiNDOpnjJ2i2mnQ6Hcrl8qHn9f0EgkalxaUfLHPluXUuPbVCMBpg9sEMsw9Nkzk7hmEe7X9ofn6ehYWFG/rMms0mQggMw7gjJi3dCiYmJpBSsrCw0D9ueZ63x2tqJ1NTU/sKOdD1NPI870htjX6//1U3rb4TmZmZ2SNaLy4u7mpTeb3+Pw4YcDMMhIBr6I1/KZVKu+7vGWolEok9fgGRSIRkMrmnpeBGCRrPEg98BcsZo9D6OZQKQNtFfCuL+PoGKm6i/skbDn2dnQsGpRQ4Xjfo7uzOgu8JxA8K0vcted9dJr87k67tKHnvlb/LPVl2PWQeaCx3o0F6uVymvLoKD6cAcN6SIpFKvay/x4ABr2fW19cPrGYSQjAyMkI0GmVpaenGJ5AoBdkWPF+GF7t9/9yTwH44gR0SbBWqsONwmc/nSafTzM/Ps7m5Sblc7rpyL9QYWSgSeCRF8r44kXydS3+9QXIiQOhEjOJknPAXlrFOJ1AhA2c2ivF8EevhNO3OGfCd4fIXxkh83cQ8O0Tn968w9O+PQ9ggeDxO+2svHTh6qzc1AMARkpxmEFQeSatNTnRbCABUqUPuq+eYev89iNPzKF2wtbW172crXyiRL7SIPDbVzfpHfThRH42ZOHgKs9zGLLQIrdcw6hZWzE/rnSO0nynBPQmMfAff+RL637a7JoQpf18c8GLmwWX+riLxzCaeLq+KAACaQEVNvGAQL6DTedNI9/6Gg/75FZj1o96YRLYcZM3GyDa7rQc1G+WTu00LIyZezEAFNGRxf0d6VbOwv7SGu1THeN8E2tnErs++VCoRCoX2BL3j4+O3Xmy/DkIIMDU0U4P9qi72e45PY+oX7+PKlSuM/tt3EsSH27Bw6hZuvXvt1C3atSa1lMC6UKX15GbXSLHjor/5fp75+KfxvzFN7R1jGF8pYYR86DsEBD1sokVM9JCJFjaRAYPcZoXl81kWf7hKab3K1BvGmH1okrf/0sPE0jdXKej3+5mbm9vXZyAWix0Y2HqeRzAYPLTM/bWIlJJYLEaxWDxyAsE0TYLBIGtra/s+3htrfRhCCKSUNzX+8fXMyMgIwWBw132bm5t7vCoGI6UHDLjKQAjYh4mJCUZHR1laWuqX5Sml+iO2Tp06tadHvTdztteDdKMY2jqjkd/DUzp+/SUELrnPPIp4fBPaHhgSsdWGJze7Pap2N0PR/dkDR6EMCY9lKP3rb1HcEbwfFKTvW/a+nWXXQ+aBxnJ3YiY9Ho/v6s0cGOcMGHAwvRnm+6HrOpOTk7iu2y9VNk3zaN/xqtUd9/dCCRy1p+/fFu6+ZdK942ulUumOGgxFefHfP0F7pQrvSDGZMBD5Buc/vcrY2Rih6TDFk8MoTWKdjON/Ok/r7WNY9yYJfm4R6w1J8HezQvH3TVL91EtkPnGC8ucW4bPL8Etz2BMxDNfFyrXwpYN79skf8e2eGiAETaFhezpKgF8qlOdiVS2qGxXcvz1Pa72MeOs4Y2NjJBIJlpaWri7WlYInNnCSfvSRvb8PKbCGAlhDAerHQdguZqmNmW8iKm3831pHnYjTORWjHh9B2R56ro2ebeH7URFpeTjDXWHATQVwhv1dE0JPkXg2C1JQvi996HQBkW2hf2EF70wc982p7qSEazfyFKLpXPUkqFkYuWq3kmC9hZfvYHrutlBg4oZ0rItVrGcK6I+k8P/jMwhz/1aH1dXVPdntSCRCOBymXq9fd9/vJHK5HLlcjnQ6TaFSIus43f8FHYhvXwDwIQF/fBj/fcNAN1CRhsbMf3g3lc0SwpSoj4wStkKYbYlT64oJ7c061R/WWLmYZWWpwMZ6mYCukw4FGEtFuG88hpH30L+1Qe65AsVt8aBbkbC7MkEPd8UELWjs+10PBAJ7svvDw8P7Jk56FIvF1+252PM8Lly4wMjICJlM5rrtE5qmMTo6SjAYpFAo9I8JPcG12WzSbrcZGhq6rqljj17lQDAYxOfzYZom+Xz+rhUGhBBMTU3taYl1HGdfL6/h4eHbtWsDBtzxDISAA9A0jbm5Ocrl8q5Zrp7ncfHiRY4fP75HDEgmkwSDQS5fvnzDxi26LAIKT4UBgamtIr+Tg4rddXzWRLfEVhMov9Fd4BmyW55pSDBEd+Hr10j/xlt2B/03afrzWqM3XulOnBYwYMCdQrlcPtCROhAIMDU11Z+JfSQ6LrxU6QoAWy04GYPHMjAR3JOhdhznuv3S7Xabc5/9PnEnyAP/7L3kC1toP7iIudHg2a/mmHjrMJGxAPltEQCgc88Qkc8uIgttvKQf51gE81wJ68HuYi/2cJqt338R57kCvkfStLJNgk9uYr9zlOhsFPt8YX8hIGzQru/NbCtX4WmStqET81w61TaNsE7zuXXcqTBuu83i4iKjo6OMj4/3y3dFoYO93sT/rr0mVvuhDI1OOkQnHQJHo/1CCV86iFloEb5UAiHoJAN05iK0H06hXNBzLbRcC/+zebRiGzdqElAuKqhTeGTsUBFAnq+gfWMT991jeMej19lQoMIGbtjAHb/msWIb49PLeA+lkFUL73yF9jez6IYkORlEbrXwvrTaryDoVhNstxv4uuJALpdjcnJy18tOT0/jOA4rKyuvKTd6TdOIRqNH/z7Rfa+bm5s02y206FXPiaLZghDYAYeK1WT5mU1KqzVm7p/grZ+4n+kHMkSGQl0/gLbTFQwaV6sP3HoHp27jNiw6W/Ud91s4je6113HQgl1RQA8Z6BHf1eqDmMA6rqNsj0Q0TjwcY+G753A01fVJOKKh4s2iOl1/B20fw0zDWCPgP4fnhWg0H+hWVN5ibNveYwi4H6lUCikl2Wx2l+eDYRjE43F8Ph+hUIhCoXDksnWlFKOjo3Q6Hfx+f7+F5G4jHA4zNTW1r4H0flVEQgii0esc2wYMuMsYCAGHEI/H8fv9XLp0qR/c27bNysrKvs78gUCA06dPc+HChRsKSDvOHLaXxJBd9bLSeTfev3oQ1hqIJzYRL5S6i6+3jlz3dYQQ6Ml9sk13CRMTE+RyuYHiO2DAAVzraL6T0dFRstlsf0GpaRq6ruPz+XZnCXf0/XO5BpMheDAJc5GDe8fpCgG9GdnXiqVey6H22SXsy1XEx45zZfkyk6NjqHc8SPH3nmTq7SlCw/6uCLDzd5ganfuS+J/K0XxvBuveIYJfuIJ1T6Jbzh00CL8pTfmra4R/fpbGMwXCF6p440HMU0PYLxbhHZNciz9s0q7be1oHhKNAgmtobGoGkbpDfEyntdSmcd9V97qtrS1OnDjB5OQkxWKRztfWyZfbxN+z93f1kFISiURoNBq7zx9n/n/23js8kvy+03srdlfnDDQyMIPJm7iRXJKSSC6TKN1JFJMSyTtKOmX7JPru0aN7nrPPZ5+zZVmSz5ZsPUoWzxQpieKKorgMIkXuLrmBuzsZMwAGoYHOubor/fxHAz2DQRhgJy3Jfp8Hz/Q0Go3qKlTV75s+nxjiH9YwfRrmPWEQArVlo5dMjFyT6Jkirl/FShp0J0O07k8hPEHimRw0PExZIfy5KyBLPY2BTa2BuK+fZJbqNsrX8zjvnUSk91b835OIjtRxsXUZ+7kSIm+i/bOjSEejtIVAMl3khoVc2+gkWGz0ugrqFm5Apf1Dk8SerWDOdZETAZRkADkeQApoqKrK9PQ0uVzupkfx7hSVSoWJiYl9JwIURUGW5S2VzGaxTe5Mkdz5Et1Gl+zxFKP3ZHjgJw4TCAY5fHirOJokSSiGhmJoQPBA2ytcD6dl4za6/eSA07JwGhZa00J70aIldWhMSTSqdSqfmsNZau1fUDGg7Wj9uJ+CRedbBar/8QyhfzpF8N2TyJtdP9G/JhH/c0CAkHG9MKtr/wbb3q43cavZFAncDUVRSCQSzM3NMT093dcUsG0bWZaxbZvFxcUdr4m7Ydv2FhHGeDxOKBS65YkAXddv6Cpzt9itC2AT13W3JF02+W4R0h4w4FYxSATsA7/fz9GjRzl37lz/ub1aFGVZ5vDhw1y4cGHfAkeeMFip/QZ+9SKOF8dyJ3rfGA0iPnQIUenC4o3bIu92i/7NsGm90263+/tXluX+wkiSJAzD6GfXdyIcDg8u9AMG7EKpVNr1miRJEn6/v6+sHI/HGR4exrZtHMehVq3CWnvb3D9PjICx/1vJZlfAtQtM63Kd+p9cRD8SI/Hx+/ALj+hinoUz63jrKrO/8gTW6QXmte7WJMDmz8/G0M9UUFdaOGMh3JEA2rkq9r3J3md52zi5Z54jGdapXq5j/9IptM8uo751mNLfLTLkOFjXab8omoKqydimgx64povB9ZBk8DSlV5VvupgRP8FKgVREpio8/NEYw8PDtNttbNsmk8ng/5kxMm88QTerUK/Xt1X+EokE6XSabrdLNpulVqtRLBZ7r1NlxP1JeK4Ebx/t6QuEdJyQTnsyCp5Aq3fxlUyCC1XiL3aQTRfPp1B6JIud8IMEcsNGKZioeZPAxRpy08aJamhKAOm9sV4SIKpzMwgPOusm3d89i/rmYdQfm75aKZYkREDFDai41+e0hYCOC5qMOhODShfnYpHuM228Uq+9XE4GUBIBYgmDSrg3+oYmI/zKvmwQ7wadTgfP8wgGg/vqZBgdHSW/nmf1dKEX/J8tYps22RNpJh8YZvh4El/w6jHqdExyudwts0STFBkt4kOL7K2FsDmK533sOLCXoKKDaNtXBRXNBqJ1nWNDx+2NHF6XILje5rH+7Dp2tUvjP12m9XfLRD58hPAbBYn4J3CcGJtLWkWpkE7+36yu/Ztbsk/2olwuMz4+vmtiynVdKpUKk5OTCCGo1WpEo1GKxeKW4P9m7P+azSZDQ0OEw2GazeZNWwn6/X5GRkbw+/2USqU9xQ/vBtFotC/UuBu7rYV3shUcMOB7mUEiYJ+oqko4HO4LuWQymRu+fjMZsF88EaBt37fzN+O+3tcN2OvC+FrEcRxyuRz1en1fN69ms0mhUMDn85HNZl+9kvmAAd+D7FUxMgyDbrfbTxSk0+meTsp6bc+5/4Ni23Y/ESAcj9bnljCfLRB53wy+exIYzQ6xSpu1msfan15i/Ecnqf7N04QfO85MOsLK6sr2So8i0Xkojf9bBZojQaz7kxifW8I+EQdVJnA0hghpmE+v4zsUoVPsoLxxCOMbBboOqKt1rIntXnT+kI7Z6G5JBEhOz5KNjeBWath4kkQ3oCHFo0xnswhJZnV5mebGfLS81sb5H1/G/4v3k5qaZmZmhsXFRTqdDpFIhOHhYSzL6j+nKAqpVIpDhw7RaDQoFApY9yeQ/uAC4s1DcL1jgCxhx/zYMT/MxIi9mEerdekMBZLi/SMAACAASURBVIheKKGYDlbcj5Uw6GYMzJlIL3Beb6N/chHtngiSLhH57CJeQL2qM5Dx91r29xFkCyHwzlaxP7eM6nn4338Y6Uh0/38YktRPKF3W60w9OkUweLWa7bUtvHIbt9zGK5skV12KIzKBv1xAdryrwoXhawQMIzrCuPtJgmKxyMTEBJ7n0el06Ha7dLvd/mPXdamvt8idKXL8F0/wWz/+h4SHQ2SPp3j8o/cRGwvvmeQvlUoEg8E72vIsyzJjY2NEo1GuXLnSe/KAgoqbCCEQprvFyvHahILXtPHyJstfuEIj18KnKwQlmfq/LnP892yYgGuXs64bw/CfBhxu9zLXNE1s2yYSifSTqNeTy+X6a8ZWq8XQ0BDFYpFIJEK3u7Ow5kGwbZv19XVSqRSjo6Nbila7sdnttYmm9WwuDcMgEomwtrZGo9FgbGyM48eP960RDzK+sCOmg1S1EMPGlvNSM+skcqcRkkx55BSOb3sni67rTE5O7ku8dqfOM1VV0fWbS3QOGPDdxiARcABGR0dZXV0lHo/vq+qs6zrT09MH9uC9Gb6TLnKVSmVX9dwb0e12WVhYIJVKIYToVxdHR0e3uToMGDCgx17JtmAw2Bf2Ul0J2ZMw/+AVKHT2nPs/KJuJAGetTe2PL6JEdRIfvxclpBGptjCaXZYKDqVPLjD+oRnirkP+UBTrG68g3TvJxOEJarUa6+vrWz6PMx5CnK6gzdWwj8Rw0wbahRr2iZ4yffTt49Q+e4X4Tx+h/XyRwM8cQ15t4z+jYF6ooIxGca+znfKHdbqtrYteyRFICgif2mupbzloqsbQP3sM/2SK9bU1KBcJCw9PVmlLMjydp7LeJDGqsrq6SjgcZmpqCtu2+wrgCwsL/d/hui7r6+sUi0USiQQzMzO0hloUXt+i81IFHtnFEUUIoi8XkC2XwpvGQJFpALLlopdNfCWTwJUakivo2BL26TrW92exHh/DjfmoffAwSrWLUuigrrXxv1QC2+u5E6SNXoIg5d82/uEVOthPLiEaNto/ncL3SgVPkni1hn9CCObn58lkMv0ASg7oyAEddaynsmcApTNnaH3oMHTdnnBhozdioKybaBdqyHUbyfX6GgRb/o3qiIB6R5IE1WqVarWKpmn4fL6eGKLPIOQPEwgHMOsmBbtM5o1DeK7Hj/2Ht+NyMK2bK1euYBjGjh7qt5NwOMzRo0cP1AF5PZsjBQRUdpaQBLfron52Hne1Sct2acoeeA6pnML1Q5qSZOF6Idj13W4tjUaDQCCwYyLA5/PheR75fL7/nK7raJpGPB6/ZevDSqWC4zg3HIs0DINkMkk4HN4S0Nu23f+6ePFiX3hwcXERRVH6XQKbXU6vFvlSA/XPLiNSftyHk3gn4xBTGZn7BxS7N2LhM6ssnXhH7/UbXaHpdJpEYnuydi+CweCW7t3ByOiAAdsZREwHQFVVJiYmDvQzwWBwT1XdW813ymiAaZo7zionk0my2SyLi4v7stG5XhH23LlzjI+PE40eoBI1YMD3ALVabddZ1k0BpfxLC/DUFZzLDeTfO4b0SAYxFdxz7v+g2LaNWDap/PZpgj84jvH6IWQB8WIDxfVYvNKl9uQy4z91iLjZpXgig+tTaWeCGKeXmMMim80yOzvLysrK1XZrSaLzcJrAUyvY0xGs+5IYX1zBPhoDRSL25hEu/6c50kh0L1bxuh68bYTQN3KsP1tm9vVZasGt+iq+kA+zfl3FzvGQZQnPp6B2PJLvv5/wo1NUXrrClQsXeskJRaMtPOKuQ8BzqDyTRzoa6yvlNxoNrly5gqIoNBoNTpw4gSzL2wIp13UpFAqUSiXi8TiTP/EInQtF8v425vXHUgiirxRRTYfyg8OgXD1mnq7QGQ7RGQ6BEGhfW0d9qYR2X5RIpYHy7XXUNyXxF9p0E37chB/raC/gltoO6sY4gfF8AaXSxY35cNMGdkzHPFfDOVvtjQE8kkZSZMRCE5o379Wdz+dptVpMT0/v+H1N03oVVZ+Clzbw0jsIxFluP0Eg122UvIl2acPhoLuZJNC2WiFGNpIEt1BoVwhB/nKJ3Nkiq2eKVK7USE7HGDmRZuqhUVKjcQI+P8VSgalDk/tSj7+enWai7wTdbvem29E3EUJg1y3M5SbmSov2chNzpYlV7tIum7hi47B4AkOSyX8mjv2RNJpawHFiSJKNqtQpln8cuDPrIdM0d+0SnZ2dBbZ62dfr9X4Ro/83fAuIxWJ7dn0dPXoU1+05t8zPz++pbXAtruvSarXQNO3Vu0A4HtRtaNjgip47yScX4RPzuB+bQvE6OFrv/PVZTU4cP4as3FyIMjExwZkzZ4BeQmGQCBgwYDuDRMAdIJvN3rFEQLvdxvO81/SIwMrKypb9IUkSuq4zMjLSbwUdHx+nWCxSq9VwNm2X9snS0hK1Wo2xsbHX9H4YMOBOsau4mhCwbjI+PUX3pTyNT52Hk725f8u10U+mbtkiFcCtWdTOLBFIh4n/Z6dQ0way45Es1HE0hYUzTVr/sMbYRw+TqJoUT6RxN9rgOwmD6GIN0e6yvLxMKBRidHSUZrPJ2toanufhpgyc4QC+V8p0H0jhRXXUuRrO0Rh60o//WJzmV1bxzUTovFIm8FAa44OHWPq338S3VEc+4se75prREwzcKpYlOR6SLhOdypIcHqb18iqLf/yPWFEFcSLef50lyawrGsGVGp2CSfJHjvSCpY1k7bUL6m63i8/n2zWQ8zyPUqlEuVwmftlh/G1HsYRDoVDoBRdCED1dRG1alB/O7qij0NsoD/XvVxF1C/OfH8EMadSFIIxGQJYILNeJvZzHCeo9R4KkgRXzYU+GsSc3uuAcD7loIr6Rx/rEZXxBlfjRCJ7t4lyo4WYMREhFatx8IgB6rdT5fH7HQGtfFWhdwUsqeMkdBBBtrydcuCFWqBS7aPM98UKp4+KF1H5ioJ8kCGuIkLavJEG3ZbF2rtSf9Vd9CiMn0px4YprM4Tiq7+oSrNls9quXkUiEaDRKrVa78ee7hmtHKe4ka2trryoR4Dke3bzZD/bNlSbt5SZIEoHRIMZoiOg9SbLvnMSXMag+l+f5X/gyEhLRiI4xGmLm3z7Oau5+Uok/IRD4Fp4Xolj6aWqNd96GT7ozpmnuGIBfW5CYnJzsB6XNZpORkZGr5+8tZDPBcO32BINBTNPsCxXG43Gy2eyBuxFqtRoTExMsLy9vFxHsukh1G+oWUt3eeNz7V2pY0PUQYQ1UCSwPMWLg3ZvAfSSFFNTQ60fxrc8jPIF65CG4ySQA9IL/kZERVldXb5mGxoAB320MEgF3AFmW8fl8t3RBvRtCCNbW1hgZud7T6fZhmiamafZF/TbVWkOh0I4jFJqm9X1w/X4/Y2Nj20YaZFne0ha6yWa77I0WHfV6nfPnzzMzM7OvebIBA76b2Uy8bc5Nym0X+XITabGFfyiC78Egc6vL8FOH+z9j2za6rt+y61bnxRKNT17G/5F7Cb1uiPJSF81ySObrNEM+cl8r0vl2idGPzpIstigeS+EYV2fzhSJjJgwChTbNsQjNZpO5uTmGhoaYnZ1ldXWVRqNB58E0oc8sYB2NYd2XxPe1NZzZKMgS8XdNUP6tl8l85FhvPOChNP7jcZy0n9LfrBH4aIhm8qruiBHZnggIDMVJv+shuqrH4ldewnmliFyzEFM7OLpIEu2vFmi4LocfSKC7NhVZpXtdgvJGiYD+PhCCstOk8t98nujPv46RkZFete65SziNGyQB6hbaZ5bwUn7c901d7fKQJNyAjhzyM/LhJ/b8/Vt42x7f+779v81+2MkLHHpdejc1r6zJeAk/XmKHJIHj9ToJNhwOlHIXbbHZ6yQwHbyghohouBEdEdFxIxpuUKNYbpM73wv+62tN0ocTjJxIcfKdhwind3D0sVwkj57g4TWf69WcdwftWLxVTE9Pc/HixT2PhdN2tgT75kqLzlobPeHDGA0RGAuRecs4xmgQLaJv6W60K12Kf71A7RtrRMfCqB5oEZ1D/9Wj6HE/rutnvfCrd+Kj7ojneZimSTabpV6vYxgGzWaT0dGrrgWbjiCbyZ5Op3PLnS+WlpYIBoP9tVOj0SASiaAoCisrK1iWhaZpFItFgsEg6XR6f24WQkDLYfVbF0llM0xPT4Ln0VosU1jM0Y3KSF0Xip1eAtDyEIaCGDIg0jtPCG6M4Tge0g9kEQkdzZLInBgnHo8jixOwPg+SDEM7dwC9GhKJBIFAAL//JpxQBgz4LmaQCLhDTE9P70vA5VZQLpcZHh6+bdVwy7J6Hsft9p4WiaVSicnJyW3JgJ0C/P0yNDTE0NBQ/ya6uXDeqcXNdV0uXrxIPB5H0zQSicRAP2DA9yTRaLSXHBQgPA88gbgHkEBIvXN6/L7DW37G5/OhadrOb3gAPNOh8al57IUGsY8dQzkWRdM1/O0u8VKTSjzI+pMr2AsNsh89QjJXp3Q0hRPcrnfSzgSJXyzRHA2DJOF5HrlcjlqtxujoKLFYjFwuh3U4iu+FIp03DCEMFXW+gXMoQviBFDlFQqpZvfGAjovsVwjel6IqSQSfXIYfP9Jvq/cFdZql3jVms7oUGNMo/+3zlE5EkVfqEFKRFxp4O4m5ugLpxRLSvUnKmg+/55LwbLpCpiqreBvBTrfbJRgM7s/+azYCX8pRPbtKtVJhqCETOz6J+9Bh7EJhxzllabmF+uQy7kMpvAcSO87F27a9o7itZLvolQ7aShPrK2tYV1r4H0sjPZbBSgVwje1z9vJ8A/WpHPKDiZ5LQbGDF1S3WBd6Ee1A8/mxWGzb9dswjNvXDq/KeHHfLsd1I0lQt+muNsl9Y5ncxTKri1UCqsLoeJRHZhOkH51EivvwojqepuC53paRDQDftwr4XirTfucYzlQEv9+PJEn7btveZGhoCEW5MzPx1yPLMrOzs1y6dKknhFg2aS81MZdbvcB/pYnTtImeSpF+PIsxFkJSZIyRIIpv923uLDepfHGF1itlIo8NMfUbD+JUu1z6jacZ/dmTGDN33g9elmUMw8AwDILBIIqiIITAMAxkWSaZTO76s4FAAFVVGR0d3VVY8GZptVrMz89jGAahUIhcLsfw8DChUAjP89B1nU6nQy6XY2ZmpuckY7vQsJEaNlLd6j2+tqrfsMEnI8I65UiJUmQO7VSK4KEUqhwlmYjjqb2RJ9M093Sm0QJ+DEViaHoaPXOt2LMMI7O3ZZ8MkgADBuzOICq6Q9zp2f1Go3HL5+Q9z7th1v96Op3ObbHz8/v9W7Ltp0+f3rVLYLMams/nCQaDu86bDhjw3YZwPTpnCwRHAuT//hydUgMmQpA1tgUkO7H7PKjA8L+ColSxrAks+3q5rh7WXI36n82hH4uR+PX7kH1Kr9NAVYmVWxSSYYp/sYBb7jL8kVlSSzXKR5LYoZ1FT+2ghlBk9HoXK3p1cddut5mbmyOTyXD48GHW/AHc338eqxrHuj+J79k8zkwYWVOIvGmY2j+s4jsW648HBGej1HNtso7A/9VVOt8/BoAR9lFcrPbHEOr1OvN/9DRhYeKdiqE07F6ruCaDf3tAIy80aJU6BH/2GAAdWWFNkol4LsOuRU1WaUkylUqF8fFxRkdHbyygKkuI1yXhuSLhQ0HcsskFwyEYj5LJZBgaGqJQKPSSCkIgv1RBebqA885RxOTBXVY8Raa12Mb+4hrKqTi+Dx9Fatv4Sibhy9WeheLmGEHSwNMVvKQPAXQe2JjJ9QRKpdtLCqy28H97Q4QwY+BsCBHuJEJ4LeVyeVsCOZlMUi6XD/yZbgbP8SjOV/uz/q1Sm+GjKbI/fIiTx1MEIj7kZm/UYDOw0ldbSHUbuWUjDHWLw4F2uY7csAh+egHr3iSRD9xPvbrCsPb7+KRlau7rqbpvZ69590wmQzq9i4DkbcS1HOpXatTmy9TmK1Qvl/GyEpH7EjQvVpH9KolHhhifnkWP9hIqqqruWUAQQtA+X6Xy1DLd1Tax7xsh82OHUAK95aoW93H4v38D/vG74xi02Vb/agiHwxQKhf440+3ENE00TWNkZIRSvkjQCCBZAnGxhnwhj1u3ab3dIL0iKP/V2Z4mxkb1XkQ0xHAA78hGNT+s9V1SNrEkiUw4zMjYWP+5VCqF4zjbil7xeHzLeo0jt/WjDxgw4AAMEgF3iDvtw1qpVG55ImBlZeXAbZiBwA6tkLeBsbExlpaWbvi6VqvF2bNnUVV1YD844LsSIQTWlRqtZ5dpfWsVNRmg9ViETlaCkQDgQftm5lIF6dT/QTj0VXrBicR64edptR6/+grbo/m3S3S+VSDygRl8JxObG0d4vYp8RKGQjlD8o4sIx2P4pw6TnK9QPpzACu8xyiNJtDNBAvnWlkTA5udeX1/vdwd4v/R98Ncv0Hh9Gr4loVxp4k6Gib9jgqUvrDDyltH+eEBwNkbpazmsXz6F9sdzSGMRxOEIwbjBm/7Jw4yMjLC8vEyr1UJudCG2YR1Yt5FCKmIXa1fx1AqmJpE4Erv6nCRRU1TaQibuOgRxKSNYWVlhenoaRVFurIlyT4zI7+fQg1B6fBShKf0Z882W30wmQ/lrl6ifrmF9YBpiB3eUca80sT+7hOST8X14Fnk4gADMuB9zNAxCoLZs9JKJkWsSPVPE9at04n6cShfHchG6ArKEm/TjJv1Yx3o6ClLLRi10UAvXiBDGeyKEmw4FInB1ibLT/czn8+2/vfkmaJXN/pz/+oUSoVSA7IkUD73vOMmpKPJ1STUvquNFd9jfrkBq9ToJNrUJ1NU2UtdF8hyML60Q/+AbqJb+IwH1DK4IkVA+T9ebwRQ7V0tjsdir7rA7CN1ah9p8merlXtBfu1ymtd4klA0TnUkQnU4w8tg40ekEa5V1fKmrwo2yLBOPxxkaGsJxnB07T4Tr0XihSPkLywjHI/HWMUZ+NoOsbU8O3a0kALBnEuNG+P3+vijothn7V4sQ0HG3zuTXLaJTGVKPJ1n+H75Md75MJaz1Av2wBhEdMR0i3ygz885TRJ642g3mOA4LCwt7jl+GQiEmJiZ27Drd6bm7kaQaMGDA/hgkAu4AnU7njlctms0m1WqVWCx24xfvk4OqxSYSiTsmXhSNRjEMg2q1SrfbpV6v73ojc10X13VZWFjA5/MxOTn5HWW7OGDATjhlsxf8P7uCcFyCD48x/GtvQNtov1xdXb0l1yGf7yLh0FdxnAQgI0ldMqn/k/nWY4CCk9uwBUz4SH78PuRwb7xAdj0ShQaeLGHZNo2/XAZVIvP+QyTnylRm4tuC+51opwIMLdWQbBehba/CdzodLl26xPDQMKnHj9FeWcK6P4XvxRLtiRD+8RDyUABnqUV3sYHXcfGPBHEaFi1JJvvEENbnltB/8QEef/vDnHtmnrm5uX67q9R18LxeO7zUsJFsH15ih0SA7cGZKsrDOytV25JMXtEICo+Ma9MyPWrVKocOHeLSpUu7JwOEILzUQE/qlGStF2hfQ6vVopWvEXqxQfIHjpD8L9/ZFxrcr72baFjYn1/BnW+gvX0M5Z74zl1tkoQT0nFCOu3JKHgCrd7FVzJRHZfI5+dxM4Fex0DCwI76+iJ7IqhhBzXsqasihEqxlxjQL9Uwnl4HTcaaDNG9J4la6SLSGtJ1QffQ0BC1Wu3WBVaAa7sULlVYPVMkd6ZIt2ExfCLF2H1DPPzBk/jDr/J+oUgbegI6LkHwBP5n1hG6DLKE/GAWz1CBCkKoCHSghSy1YZe47FbrAQnPo7na2Aj6K71q/0IFt+sQm04QnUmQuT/L7I+cJDweRdnhHJwI97QKHMfBtm0M42pS4Pp7rdd1qX19jcqXV1ATflLvmSR4MvGadUAaGtpBC+QApNPpHRMhu+L15vOlDRG+7W37Vq9LKKIjIhpSwkfkgXGGHjnEypkFmm9NgTG04xhOF7hw8UJ/pESSJIaHh4nH47veK3Ya97yW6zWxZFkerK8GDHgNM0gE3AHu1kVweXkZTdNuWTB+EOX+QCBwRwULobefM5nMNn/xvdhMGqRSKTzPw3EcVFXdktXuBwCS9JpdnAz43sQzbdov5Gg+s4y92iDwQJbET9yLb2Z74DYyMkKtVjvQebwTitxEIAO9c0QIHUlqINGh9eUarS+sEPnhSYxHMn0fedV2SOYbmAGdqqYRWKwSmI4RPhEgdb5IdTpON76D9dsOCFWmE/MTKLZpZXdfkK7n1zlyaJZstUVu1IbnCiirbdzRIPF3j1P/80sEHspcHQ+YidK6VMc8FWPkF2bwjw9x+dIif/E/f54P/LdvvfrGttf7XEIgNW3ouIjM9m2XLlRpVjoE33Pv7h9GkmhJCqYkE/Mc1HIBORbbM2APzVXwrbcov2UcPrkIjw9taamX1k3Uv1nCPB5jsZvHt1AnnU5z5MgRyuUypVIJ13UJhUL9mftNQVXhejhPF3C+uob6YAr/L59E2mOGexuyhB3zY8f8qFMV2vdl0PwyetkkeraIYjpYcX9/jMAJXqMToMq4wwHc4QDdjf0r122UoolQZVqffhnqXZSRCMpYDGU8hjoWRfJrzMzMcPny5VedDBBC0Cy0e4H/2SKFuQqx0RDZE2ke+6l7SExEbtu1v3tfEjcbwJmKkJ0ao9ZtUvXeiqFcQqWGJbK0vaNbfsbn85HJZPoV5leLbdrUFyq9Cv9G4N9YquKPGUSn40Sn48y86yjRmThGKnjgfaCq6o66PJIkYTctKl9cofaPOQKzMbIfOYYxfedn/g/CzMzMTa/ndF1namqKhYWF3hOOdzW4b2yt6lO3kVoO+JV+yz4RHZH2482Er7btb5yjmyNMpmlSrlUZOTWNtbCwp97EZmFkk0KhwOjo6I6JgLGxsRuOejqOg9/v7ycChOh1O20ZDRgwYMBrhkEi4A6w2RZ3pywEr2VhYYGTJ0/e9Pt4nrfvahL0bhh3g3a7ve82UVVVMQyDRCKxo/7BpsL6tTdJWZb7nQ63Q/tgwIAbIRwP82yB1rPLdM4U8M0miXz/NMapDNIO1blrUVX1phMBXWsShIost/C8AKpaotsa51BkBPHOIaR/cgwhg/AEuWYLr9khUWxSiwdouDLl3z5N9l9nSHz/GNrXLlCbjNFJ7C8JsEk7EyS6UKU1HNpVcE4IweWFy2QNgyOz07Q+lqH+1DmqoxB94wiF/+c8sbB2zXhAFLUjM3LyJKJWY+EPvorlOHRbFkKIq0GQ4/VE/toO+BTkqo19bHvnlfjCClZEI5i9cSLWkyTKioaRSNMt5kk4FpVrxAQ3Cc1VMHItSo9m8Xwq0pABZ6twT2/0Qj5XQ/nyGu5bs3izvaCq2+3ZLeq6TjqdZnZ2lkqlQiqV2iJOWJlbo/u7Z5FiOr6PHUVO3aTAVlgD06U7HqKbDtAAZMtFL5n4SiahhRp4AmtDX6CbNPD81yxJJGlLi738U/cRkHXclRrucpXu1xdor9aQYwbqWIyp8Rh2xs98aXVfm+d0HdYvllk93Qv+PdsleyLNzKOjvOHD96IHbl4o80ZIioz2nqOkolHC4TCdTofl5WVsMcWi9RuoUg1bZBBs3Zbh4eED3X+EEJildr+lf/Nfs9ImMh7rBf0zCcZ/YIboVBwtcPuKF62VOlbBZO0TF9FTBhO/dj96+mDn/53GMAxGR0dfleicZ9q4FRO3fM1XtUOk26b+YAhprY2UM5GX24jwxnz+WAAvEkVEdAipe2pnxONxVFXF5/MRCARYWlrqd2/KskwgENi38KSmaYTDYXRdR9f1LYm1TCazZ4epZVk7djIJIahUKsRisbtmbzlgwIDdGSQC7hDZbJZms3lzVkevAiEEtVrtpvUC9qVmfQ03G2y8WgKBAEeOHNlW1Yerlf2dKii2bW87Np7nkU6nEUL07as8z6NYLFIsFkkmk0Qikb5a8IABt4v+3P8zG3P/qQChR8dIfPAelB3U9XfjZuZbN3HdJLn1/4Kh9O+gqUWaqxNc+l/ezev+nR8toSE8r9+Ro+ZKBEtNSukw7ZZL+XdeJvBoBimlEl3rsD4WxUwdXEfEiviQPIHWsncVFgSwHYeVSp7Q/3Qa/0cfJPHGo9Tn51GHAwTvT9K5WEPPhEnFk0x/eApFyL2OovU8xsNh7L/MoZouVtvGt7mfHQ9PlpAbNiKkIle620cDLBfm6qiPH6yNWA8EyK83UJAYdi3qskJTUkCSCF6qYKw2KD06grfhPy8eSiF9eQ1xIoby9QLyxTrOeycR6e0Bi2VZrKysoGlavwNqZWUFr9rF/twyImeivWsM+Wj0llS/RViDxnXXVF2hkw3RyYZACBTTwVcy8RXaRM6X8DTlqvBgwr9l9KNcLhOamECeTaPN9maOhevhrjdwl2s4c0XcL1fJ4rH+WLRn6aj0tAlQ5d69MNckd7ZI7nSR0kKVxFSUkRNp3vwzDxAdCd2Rji9JkgiFQkSvCf5rtRpra2tbzk+PEJbYeRZ+L0tcz3GpL9Wob4j31eYr1BbKyIpMdDpBdDrOyBsmOP4T9xEaiWzTN7hdVM/mmf+LM9TOF4j93CGyHzmGGrz9yZabIRQKMTIysmsXgBACr2Hhltu4lU4vyK+YVwP/SgfheahxAzluoCYMlISBNh4lGDdIBmXWEyXaU232X2a5SiQSIZVKUavVME2TXC63Ze1l2zapVIpgMEiz2dyzGKXrOjMzM1SrVS5evLglCbDZgbIb3W6Xubm5PTsxb8W9Z8CAAbeeQSLgDiHLMocOHeL8+fP7blu/VaysrBAOh191sFoqlcjlcgf6mbvZQr/bTXuvz69pGqdOnaJarbK8vNx/3nGcXQUPS6USpVKJYDDI+Pj4wJpwwC1nx7n/X786939QdF2/JXZrnc4J5i/8Fo2/uIR9pU30J2dZrlQYzyRRNjtpWiYpXaMwnqC91qb8u6cJvm2M8KNpfFcquKMJ2trBLNL6XCMaWNsjEQDgDhlYqxjp5wAAIABJREFUIQXp5RyRR4+Qng8iMmky/+4dGLKOFvFRXauwbq7zrV99iiP/5mH0gM6w2aH+Q+ME/u4MnYU6vpMbs/5uLxEg1W2EX+0Fu9c5BkjfLlOvdQm862C+7n6/n063i3uNmGAAj85iE99yc0sSAICpENge6h9fgrCO/aFpMPa+Dtm2TS6XI5lMYn9pFeeZAupjGdT3TiPtIMz2ahEhrdfqvBuShBvQaAc02uORnvBgw8JXMgku1Ym/nMcO6VhJg/ZwiKbc3P4Wiow6EkUdicIjvX3t1TuIuRXWEw3Uv12kcKHMlbrJUqkFAY3sA0Mc+f5Jho8+gOq7M9dsWZYJBoM3DP73y+Y4m9Xo9hX7N1X7m6t1AplQv7X/yHtPEp1O4N/n6M2tRHge+WeWWfzUGbrVDlM/coJ7P/5Gzs3d+XXQQfD5fD3hTmTcWoduubFRyb8a4G/+X/KpKPFegK/E/ajpAL4jSZREACXuRwpou66HdCBcsA6sv7RJIpFgfX19VyvCcrmMaZrEYjEMw9gzEZDJZHAch0qlsm3EZi9LRIBisbjn8RweHr7l4tUDBgy4NQwilzuIqqocP36ctbW1Oyoe6HkeFy5cIJlM9tvIboRpmpTLZRqNxoEXKrIsf8f4tnqetyVBEAr1qkKbNzVN027Y3dBqtTh37hypVIrh4eHbur0Dvvs5yNz/QQkGg7ckEWBd3LAFPBEn8Wv3IvsU2l2LSrNNIhRAFuDYDu1EGH+pRbrqEfrYCf7gi5/kud//Gt/3trfwy7/5r+CaRqNPf/rTPPXUU5w8eZKf//mf57Of/SwvvPACv/mbv7njNvz7P/8DjrpB3vVrH0PcoKrZfTCN76s5Oq+bxBcO0G3ZBIZiLP7pK5SevoQb1kj9zHGMyTCtuSrq/WnaPp2QBL7DUazPLMKhOPgVJAFCVZAaNkKm5zN/3XERX1jGzRgo0T0cEK5D0zQ8z+tfbxxJpqBoJOYrJK7UqD2SRVw3ry+VLdSGjSdLuD99uC/EtxdCCLxzNcQJD6/QwfcvjiHH9r+d+yasIuUOEOBIEk7EhxPx0ZqOgeuhV7v4yiaRc0WqDwzT+ewLaKNJpLE4UnJ7BV8IwXq+weWLNbQRj68vFFEDMmNHhnkiHiDhCLRiFzHXxKm5OBkDN+3Hjfn2te/2QtO0fkv1tY91Xe8rxefz+VcV/Ash8CwPWZWQFJnzf/QS33yljN2yiE722vqTJzLM/OBRIpMxFP3uLu1cyyH3xXkWPn0GNagz/d4TZF4/jrRxr1VV9Y53R+6ItTmfb0HTRkyEUFsesTN1SpUlvKaFHNJ7QX7CQIkbaBMx/Pf3HitxP/JNJpPS6TSlUunAfxM+nw+fz0ej0dj1NZ7n0Wq1iMfjtFp7O8Wsrq6SSCSYnp6m1WqRz+f7c/43Gi3Y676k6zqp1M6CqQMGDLj7DBIBdxhZlhkZGWF4eJjl5eVdM7m3GsdxWF9fZ319HUmSGB0d7c97NRoNms0mnU4Hy7IOfIOWJGmLyuzdsuQrl8vUajU8z+vfJKPR6K4dAoVCoW/rKMtyf/EWCARotVoEAgFSqRSXL1/e1+8vFovIstxvocvlcjSbzb7IoK7rd9RJYcB3Djcz938QbjZBJ2yP5pNX6DxXJPLBQ/hOxLd8v1KqEkOmWWuw6jkEOwp6ycMaChBIaSSQSY1m+Porz/ML1yTYXNflm9/8JvF4HFlu4/edR1F2X+ACCEXC0VT8ZRMzvfc55UV0Oimdzqeeww3rKN8wUT/8CERl2heqEFTxOi7Bw1FaczWi96dp+H1k6k38kxHaig/5ySW8H5lEEgJPk3uCXkJsHwswHcSVJtoPHawbwDCMbUmawJU6ypUmy4+OEfbBsGtRlVVMSUaab6L+/SruEyOIr6xBzYJdbAz7+6HYwX5yCVG3ED8K/g8cum2VWRG+QUfAjVBkrA1Rwd4bCpZHNMYbbeSncoiOjTwax4wYLOZbzJ8vMP/CMkbEz8zrxgioId7yq48gXxPgtzfeR65ZqIUOSsHEd7aC3HZw0v6r1oVpP+g3Pu9isRjJZBKfz4fruliW1f9qNBr9x0IIjhw5QrPZvGHA51ku5mqL9koTc7mF7JMZfmKC6jMFtJZCdCLO1GOHiH7oIYLD4deUgK3V6LL02fMsPXmB6OEkJ375MeInM9u2MRgMHnjc8MDsZKvXsGFDfV+q2+B4/bl8983DKJ7EWHQI7T2BXuAf8SPtMZ9/q5iZmTmQk0A4HO7Zg5bL+zp/g8Eg+Xx+z9dsjj2WSqV+QmB5eZlms0m5XCYaje66dtmr2/JmXRZuFs/zuHLlSr/oMzw8jKqqVCqVga3hgAEMEgF3DVmWmZiYIJfLUSqV7ujvFkKwvLxMsVjct4jMXqTTaYLBYD8RcDcurpZlsbp6VSRqc0G9vr6+q0XgtRlyz/Podrv9DPjme3Q6nV677j72kyRJJBI90S7HcbYdV9M0qdVqTE9PD5IBA3pz/4u1Xuv/t1bR0gGCjxx87v8g3EwiwF5tUf+TiyhJ/xZbwE30jk2i2GC1bdEM6nROV8j92RyZf3GS4akswbqF2XUZnpog3GzwzWef5fDEBG3X5fTp02iaxwMPrNDtfJ3syAskkyUCgQCyXMfzdlYTt8I6gXzrhokAgO79KUKfuoz19nH0F0tIlkvgniSNfJvkw0N0XikTnI2x+omLALiKQldVifhlzIkQrLpIT+dBEghNRm7a4AhEbOuxkp7J02jZBN9yMMHU668zgcUaofkqpUdHcA2NCuDzPGKuje+5Cu2X69g/PI7IBqBiwfMleOvOTi2i6+J8JYfzfAn1zcOoj6bhNsePO2kE3BSSREeDi3EHPZRi7fl1Lv3J81SulBlLBpiZSfCG950ifmoMaSSGo0qcP39+x/fxYj6smA9me+3KUsfpWRfmTfyvlFBKXbyQhpP2b3QNGHjhqw4HsViMTCaDZVmsra3RbrdvGJCVy2VSqdSW+5Rdt2gvNzGXm5grTdrLTaxyF/+QgTEawhgLkXgwQywR5/5feeDW7ctbjLneZPEvz5L7yjzpR8d56N8/QWh891bwaDR684mAvq2eDY2rwf1VWz0bZDYCfR02VPdF1th4rENA6R9TRVE4evToXdH72RTy3K/QcSaTodls7uv1siyjKEq/3V9RlF6HieehKAqTk5NAb81SLpdpNpuUSiU6nQ5jY2PMzc317ZaPHz++4/5JJBLUarUtRSRVVRkbG7trhaFN8vk8zebVsaK5ubn+470KRQMGfK8wSATcZbLZLIFAgGKxeEtadg/CfpMAkiQRCAS2ZPWFEKiqSiaTwefzce7cOQDGx8e3eAbfKVRV3aZyu0m322VxcZHZ2dktz09MTPS7MjY/o23bCCHQNA3Lssjn8/1W3USi521s2zbJZLIfzDuOQ6FQIJFI9McudltMSJKEpr22BZIG3F6cstkT/Xt2GeF6BB8ZY/jjj6PtI5i9WV6NjoUQgvaXc7S/sELohyfxP5LeVuEzmh1ilTblVIiuoWM+V6D+F/PEf/Y48qiB+49zNEZiqOkwal3wwMlH+cJTT3Hfz/0MMUnjD599mh989wrF0hqmaeC6MTyvg6bmyQ7/d6ys/tfsFLk6hobacVBMG9fY+7wSPoXuPUn8LxaxTiWQy13UiI7vUATRtGm/UCTx0aNYBROnbaMGNJp+H3GfRKNt4/3QFMofbywiNQWp0QaJbR0B3pdzeFMhZP/BOjn8fn8/OAos1QldvpoE2KTrQOnzefS6ReJ9o7QiOg0h4IEE0h/OId441LcSg96xc18qY//9CspMBP8vnkDaSOBsOiHctlntgIrUccEVoNxc1qFd7ZDbsPZTdYV3/MKbEDGZt/76Wxk9NtQTvKu08VYreHNreF89jxT2kxk2yIc8EOypvC78Ks5YCGdsI2hxBUqli1ow0ZZbGM8XQQjctIF2KsvQ4QxLi1dod/d3DxWux8rZJU49di+FL6xQPV+ivdwET2CMhgiMhYicSDD09gn8QwHk67Y1Obz3jPbdoj5XYuFTZyh9O8fY22d5w//+HnyJG4t/7isRvmmr17B3ruo3r7HVC2u94D7Vs9Vjo8rPPq0vNU3j8OHDd1X0d2ho6Iaz9pvk83mGhob6HY17sfl+kiSRSqVIJpM9FwnTRNd1Wq0W1WoVXdcZGxtjaWmJVqvVf350dJQrV64ghGBhYYGZmZltv0PXdY4ePYplWZRKJfx+P/F4fNvr7gZ7JZwGIs8DBgwSAa8JotFoX0hl8wJcr9dvSbX+VnCtN+0mkiShKAqKorCwsIDjOCiKctcEYWRZ5siRI5RKpS3Bu8/n61vo7PQzExN7t++urKzQbDb7LWU73ThUVSWbzW5775GREVzX7Qf+nucRiUQGooLfg+w49/+T992Suf+DcNBko1vpUv+zOYTjEf/P70G93lJOCMI1k0CzQ2EogqOrtP9xjcbfLpH4xZPowwbJ80WcgEY1rlFvtXFdl/e84wl+5V9+nIu5dXRF5sy5p/m1f2nxJ/9vEInNkQEJT/jx+S7j95+l0zmxfQNliXYqQDDfoj65u7XVJtaxGPrZCt5sFKnlIGmC+LsnqPxf59A7DjiCwHSE9lyNyL0pLE3FF/JRqbQhrOG9LYv6uUs4rugFJIqEuCYRIDUsvNUW+k/P7rEVO7M5N20s1QnNVSg9MoJ7rYVd3UL7zBJeyk/7/dNYikTMtQngUQmrWJMheLkCD/Xmcb21dm8MwPLQ3z+DMnGHK3OyhAiq0LQherCqm2t7FC9XWN0I/s1qh+FjSUZOpnn03fcTjARJHasxdvyaa3IiiJIIwqkxhOshCg2SqxVa5SKdoELwQgnPp9JNGsiZKJqubakUbkGRcFN+3JQfjsdBCKSWg16xGHt4lvJfvYj24jKhhL83UpDpjRQIQ8VpO5irTcyVVq/av9qkk2ujRXWiUpjpxw+zMuzHGA2ixXy7nv+GYSCEIB6Pv6asaoUQlJ5fZeFTZ2jnGkz88DFO/NKjqAewHJRlGUXqCfFJxe5GJd/qV/Klug0dFxFSIaJvtdXbDPLD2p7Jnf0SDAaZnJx8TQSFPp9vX+u+RqNBKpXaly21EAJZlpmdncU0TS5duoQsy/1xls1uFtM0sW2biYkJFhcXMU2TfD7PzMwMsViMarVKu92mVCrtKh6o6/q2tdDdxLKsPUdxXgvHfMCAu80gInmNEQwGCQaDZDIZVldX76io4G7bE4lEaLVaLC0tbfleKBQimUz2F1OvBRXgZDJJMpnEdV0kSbrpC/3o6GhfN+Cg77U5JjDge5M7Nfd/EA6SCOg8X6TxqXkCb84SeNso0nViapIniJcaKK5HIRvDU2SaX1im/bU1kr96CjXpJ3G+iKOrVKdjIEkIoGPZNEyLhx9+mFdeehHXFRw5FiCWbOHZAtkVGC2Hnp+WBLj4fJd3TgQA7UyQ1OkC9fHojQXfVJnug2n83y7h/dgU6pUykTdkyf3eaYIBrTcesKETELl3Q+AqGcBbqPWCwWwAyVCQX6z0/u/RC3Y3EF/O0bJdQm84+FysLMvoaw18FyuUHsniXmOtJi23UJ9cxn0ohfdAoiesBxQVDUN4JF2b1uuiNJ7M4R2LYn85h3u6gvbWEZTXpbYdO7jaEXA72XQOEPtIBDSL7X7VP3+xTGQ4RPZ4ikc+dJKpU2PE4jECgQCu6zI/P48Qglwux+jo6Lb3khQZaTgKw1GmmSK3vELJrxK6UCZ6pkjq6CxSyI+bcFCDfti4Vwgh6Ha7/aBoM8HdaDToSB1SR6doWCaFkwHE7CG8S3U6Z8t0v7SMeaVBs2HTFQJjLITvUJTgoSip1w9jjARR/Cq2Jjh0aBIzZO0pQjs2NranZ/vdwHNc1r6ywMKnzyJJMPmjJxh+0ySyuv1aJoTAa1o9Zf3ytXZ6V1X3lVkdL6SgnK/1gvyIhsj4Iaz3Av2getMCjjdiaGjoNTUnHgwG910AWl1dZXp6mk6nc8PreqlUolarbXEnuHYMcpN2u83Kygrj4+NcuHChP0Y6PT1Nu93GsixyuRzhcPg7oqX+Rm4M+Xx+IPA84HueQSLgNczIyAiZTIYrV668anuZm8UwDOLx+I72gde3lb6WKt2KcusCrdfSQmHAa5u7Mfd/EGq12g1f47UdGp+8jLPcIvZzx9HGt1eSZccjWajjaAqFTBQhQfMzi3ReKpH81XtQojqJiyU8RaZ6KL5NVd/1PB5/4xv57f/1f8OPyvvecwIr/3dYlQ6WDaJro5iblRwZz9u9ldg1NBxDxV/t0EnceCzJng6jny6DJiGXOigBmcijQ9hzddovFAn+wAi5T13qv16KBeg2LXTHxXU8JJ/SC1BKHbyj0S2fTXx9HY5E++roB0HxwLhYpvBIFnfTElEI5JcqKE8XcN45ipi87lhIEqak0JFkwkOglE26/+FFeDSD/5dPIgXu8jV5QzBwpxSxY7nkL5b7wb9t2gwfTzH5YJZHf/IUvo3zJRqNMjw8TD6fp1AobAlgKpUK2Wz2hkna7NgopWqF5rEkIhjECemsfP3bhGUdaS6PsB2smJ9u0kCZSqOFDDRNw+/3I4RgcnISs95GlVW+9jtfojFfxVxpImsKxmiQwJEYxltGSUd8BF2BVuqgFDrIq20cS+A2bJy0gZ3y02g0SCQSu853b46pvVZw2hbLfzfHlb8+R2A0wpF//joS9wzh1bvYC9WrdnrXBvsVE0lXrtrqJQyUVAB9Nom6+f92jfX1dZyTdz7hsWkP+Fpas0Cva3C/dLtdlpeXmZiYYH5+fsexyE0OYv/cbDa37Jdut0s+n2dsbKwvnHz58mWOHTu27/e8W9xI+LpSqQwSAQO+53ltXQUHbENVVWZmZnAch1wuR71ev6OV92KxiOd5fY/ZawOJTUukTW5l8D1gwHcSTqlN69mVuzL3v19arda2KpDP5+uPrrRaLboXqtT/9CK+exIkfv1epB2U0zXLIZmv0wr7aUQMBFD//y5jLzRI/Mo9KCGV+Fyvk6lyOLElUPYsD2u9zfon5hi7fwqvbLOSX2fqYz9JMPs0/iHo1Dw8Q0PxPCTPARTa7b2F0tqZIIF8a1+JACQJ67FhAsEgzZCM/nKZ+A9NsfyvvgGnZWI/fpjuehu37aAEVPxhH7WOS7jTperISKqEOBqHMw1E95qFe6WDmzfx/fipG2/DdfhzTZRDMpVTKVz/RlDrCpQv5ZBXTewPTENs90SSs9wi/+QSiiQRGQ8SfleWiiKzlz79HekICGvQdPq/r7He6rf7Fy9ViE9EyR5P8fhH7yM2trMCfjKZZHl5eVf7s/1W9bLZLLlcDtd1UVQVcyiACZDKopgOvpKJr9BG+vYr1Os2la5HreXQrHRJHx1Bi+hUCxV8QwGy75jstfaHtx8Te+MLNkQICx3Ugon/pRJKuUvraI2h9z9K6dIKXkhDVhXi8TjdbhdVVRkZGbnrLcvCcmldLrP6V+cofX2RyGj0/2fvzYMkve8yz8/vPTLzzfuurMqsu++WW7cPyULyfR/4GDAMh2FjdhmWweMZYJjdHZhdgtmAdTATO4TBxHItGFjA2MYY+cBgy0i2ZMmSLXVVd3XdR9aZ9/0ev/0jK7O7uuvqVrXUkvIT0SF1dVXmW1WZ7/t+j+d5OHF7Ck0I7M9OsvYn32vH6l1R6OuDITznUtsxewfH6oX00KE07keNqqrX+AXdKuwXBbgbHcPAwcFBpqenD/6CQ3Clp0Dn/3O5HIFAoOtLYFkWc3NzDA0Nveiv1f04KPr5pbDV0KPHzabXCHiJoGkag4ODOI5DsVikWCzSaDSuO3v2RsjlctRqNUZHR7FtuysFUFV1x4n2Vltl7NHjZuLUTGpPZ6l8awkz++Lp/g9Ls9lE13XS6XTXMdrlctFoNFAVBXwxpj6zQuCHxnGf3t3oyVNrEtmqUIj6qfvcSMuh+OlL2Pkm0Z+7DcWjEp7Jo1gOWyfjSClpzJapTuSpTRbYenQeMyDRH/DgOR3i//70J1leXkYxDLLrP4oQn0DXJIrPBE8du9nkySffS6VaBto3yS6X65pIqkbUIDRfRGlaOIfI9e6/+wT1+QLV9QL6pSLe20cRMQ8KgtZEAWMoQHW2SPBsDI/fTaVu47Is1KbSznKXwJAP5iuw0YCEB+fhJWoKBF91fcZuvq0m6ZPj1FtNmp0mQNVC+8IiGBrmD4/sGWUnyybmV5exp0vob0mjng3T/N2LKFstkjFJRaiUFPWajYwON/t12tRh/fvrLF1aIzuxCY6k/2yCY/cPcv9Hb8flPdg4tfMa3YtisXioRkAsFiOXyzE0NEShUGjLANbrbbf+5Sr1pQq15QpOw8af8BAIuUj6NE5GdFwpid2nkbhniFbYc+iVdenRsAb9WJ2tGglISePZKfwFB/ezeYyqRMuYqJkQ6qAf4QA3sbaSUiJrZnuKn6th5+tYnal+rk5zqUh1rkC91MA7HuXYu07iGQ6jhq+Y7oeef6zei1WE3arFn+M4B97PCSEYHBxkYWGh+7FcLkcwGCQWix1ZApVt23g8nh2Sg6WlJcbGxnAch42NDSqVCpOTk4yMjNxSGywdstnsgZKJvbwOevR4JdFrBLzEUBSFSCTSdWS1LIuVlRVKpdKRP1c4HN6RANC5OOzWCDAMY8+TquM4rK+v43K5CAaD5PN5PB7PLWWA1KPHYejq/r+9RP38Op4TcYJveHF1/4fFMAzi8TiVSoVms4kQglKphLncjgVMvnGcEx9/PYqmsLm5udOESkr8pQb+cp3NZBDTrSNNh8IfXkDakujPnEHoCqHZAvZajXlLofLPE9QuFtAjbrynIsTeOUQ8Oky1XiP6pgxNzWQwNUy5XMY0TYqlt5EvPIdlPYtNGkSE7PQav/Lxr+H4H+keyuDgIL/0S7+043uTqkI9auDdqFHJ7B412CEUCqFpGnOlDXwXC7SG/LieyxN5c4bK5+epPbVx2SfgbAyPX6dZMynrOkalgtQVqNkIVWC/NoHy+QWcfzmOeHIT5dz1+YJEWiqpu8+Sz+dYXWxPR8VqHe0Lizhnw9ivTexaxEvbwXp8A+vrq2h3xdoygG2HdHlXjNpTBZpvTxN2LFK2SV7RaF41ubsZm2VSSgrLZbLnN1k5v0n+/BYJt4vU+8c5+YZhgn2+62o+uFyudvLBPpM90zS7GeF7YTVMSvMF6vMVJpaeY+qPvk89W0Xz63jTfoy0n/h9/RgZH66oZ8cx1mwHq9DEvVUncDGHXmnRinhoRg2aMQMr4Nqz0XI1uktnfHy8u3otpUQWG1hLBezFAuazWeytGmpfAG0wjJoJow6GUa5DViSlxCk2d6zpX6nPt/J1hKKgRjzdib4S8dCwHbLn1yltVkh/5DbOvPMkroD74Cd8Hui6fuD69lGhqip9fX23rHfPQfdwV5oa+ny+HRsyq6urjIyMHFkjIJvNXiM56HhzDA8Po2ka2WwWx3GYmZkhmUySTCaP5LmPilwut+85TlEUgsH9rxU9erwS6DUCXuJomsbQ0FA3wq5cLu+pFVNVlXg8TjAYxLIsNjc3qVQqu54sPR5PV5fZodFoXLO6Fo1GWV9fx7IsLly40L2oCyHQNA0p5Y4u95UZynBrOfb26LEbe+r+P3Jr6P4Py9ra2g6XdOlIav+0Qu0fVvC/bxjrHj/Ts9MYhkEmk2kXdYUCSEk4V8HVstlIhbA1Fadhk/+9CRS/TvCHR6lM5HEeXWFlskDdq+M9HcV/Lkbfh8fRQpeLiR8/9ROXn387y/rKQuAjH/k4ANNz8O5zDT74hxHkeo3loKB1VZ/lYx/72I6/15I+IlNbVNKBfQszj6et03ZCLsyRAMJ00CYLhN+eYePPptCf2SJwXx/rD7enboqqoHs0tmxBptjAdiuIsgVNB+fuOMKSKH85S3Orgfvf7G5ouBsDvgihkRjLcwuUaJ+zlYkC6tfXsN/Uj3N895tUe6aE+cVFRNCF+6dPoiSuSnK4PYr4vQvYD6bY8up4HJuoY9KUClWPF93t7p6Tj2IjoFltsTq5dTnez60ycCbBmbeMkvzgGYxvrGG+aeSGHtvv9+/t7H8FMzMzjI2NIYSgkatTnM1RmMlRnM1Tms1T26wSyITwvTaCmtBJv28MI+1HO4yHgqrQihm0Yu2muDBt3LkGrq06kWfWUUyHZtRDK9ZuDNj7bDn09fXt0F8LIRBhA1fYgNvabuuyaWEvF7GWCrSeWsL+22cRhgt1MIyWCaP0B5CailNoXJ7qX6nTLzRQDP3y9D7sQUv5cZ9JbK/tGyjbkZSO7bD+2CJznzmPXTMZ/sHTvOoNo6iuF+bWMBQKsbm5edMeXwiBYRj09/e/KLHG14Pb7UbTtGu2AjrpRn7/ZX+QeDy+oxHg9XoP9T45LKVSCVVVGRkZYWZmpntMlmUxOzvLyMjIjsSC9fX1rtH1rcJ+0aiRSORQ3iI9erwS6DUCXiZ0Iuz6+/txHIdSqcTGxgaWZeFyuUgmkzsm8G63G5/Ph+M4rK6uXpNO0N/fz9ra2r7RNBsbG2xsbOD1ehkcHGRpaal7Uy+lPFSnv1qtMjExQTqd7kkLetxSvBR0/4el0WjsuFG0cw1Kf3oJKSH68Vehxi4Xk/V6nfn5ecbGxlj/yiwBWUMZCZAbiBKKhGmVGkz9xjewTAccD/XfvUD63jSZf/0gJLwoxs7Lyl7FpqZp+07BarZFeWOTaFPQr8YoB1UK5SrOHjd3pk9HqgquUhMZD6DrOqqqtqPKtmUQHo8HwzC6CSjNO+L4PzuLlTTwLtXwno3irDVQKhbNbBW7aaO6VTwBF/W6Tc0ENwKRb4Ej27Fmb+zH+V+eoKmCf+hwE6ZQQxAaDDP73CQNnwaORP3ndZSpEtYHh5FXF/eAU2hhfmkJuVxFf8cgyqnQ7j9br4Y8EYKnc3BfkoaisioUQkjGR0fbPhHbTdor3MX8AAAgAElEQVSDNLS7IR3J1nyR7MQm2fObFLMVksci9J9NcPbt4wQSV6wJ1ywo37h8LRAI7HkNciyHxlqNxloN30iQx7//GFufXQZbEhqNEhqN0P/qDKd++ByBdBBFU7l48SKtVgtP342vMktdpdHno9HXPg8ojW1/ga06/kt5pCq6TYFG1Ngh6zjMCrWUID0uiAVA0ZA+A3OpiPXYMtbaBZx8A6EJ1LgXbSCIPhxGH4ti3JPuTvkP2k6yGiYrX51h/rMTuKMGYz90G4lXZ15wSVMymSSfz9/Q6/AgUqkU8Xj8yB/3ZmEYBqdOnaLZbJLL5Wg0Grjd7l1ji68uuGOxGMvLy0d6PPl8Hl3X6e/v35EY1ZEGxOPxHe/Nubk5Tp48ecsYMO71WhZC7Jo00qPHK5Vb4x3b40hRFIVwOHyowrqTdx8IBJifnwfaEzOPx3NgPq2iKKRSKQKBAMvLy3uaOR2ElJLV1VXy+XxvO6DHi8o1uv+7bm3d/2FwHIfZ2Vmg/V5rfGeTymfn8L5hAO8bB3aNlmtU6zzz249w5iP38uwn/5HyqEaf5cNTVlFzKg/8zr+gtFYgOp4A20YRCivZFex6CVnbvVDfbTqzn4az6dLxNFoUFYnrHyYRbzjGQF+UYrVGtdHE5/Ohqmp7awFACGpJHwlvkMD4GM1mE8dxsG0b27YxTZPNzc0d3irS0GidiaKsVNCfyxN9xxCr/9czNJ7ZwpPxU5spEjgdxeN30yg1adoKbttB5Eyc+LZWXAA1C8Wnw2IVBvdvFLk3asSCMfLFYrsJ0LDR/n4JHDA/MgpXNVKk6WA9uob12DraaxJoHxhB6AecI++OIf5qDvmaOKgKUgg8qX5KlQqthTkkkFc1bHG4c2292GR1sr3uvzqxiRFy038mzrn3HCcxFkHd63gMFWE6YDpw0DFfhaIoeL1eFhcXsWoW9eVKV8dfX6rQWKvjirox0n5auSbRe5IM/bvTDKQH9pSp7eesfqM4Ho16OkA9HQApUSsmermJsCVaw8JxJP6WoG8ghSYU7HLz8rr+Lo770nK6k/v2Hw/GawbR3nGiPc0PeZB1E3tbTmAtFrD+eRoZ8+JkwjjbmwMi5LnmnNUqNlj4wgWWHr5I+HSSV/37+wmfevFScRRFYXR0lEuXLh35Y9+qEoCDcLvd9Pf37/s5nXukjneUZVk3JVmqXq/j8VzblKxUKmQymR3yUCkly8vLDA8PH/lx3Ai6ru/aYOqY4/bo0aNNrxHQA2hPXkZHR5mdne3eJF+dCnA1kUgEl8vF1NTUdcXedBoNpVIJn8+H1+slGo1SKpVoNBq3pPFMj5cvu+r+3ziKcfbW1/0fRKlUYmVlBdu2caom5b+cwcrWCP/MGfRMu2BV1S1CwS8hpUax9A7MioelX3+S8pMbNGfK3PEf3sC3f+OrnPzl03z3f/0SYshDPHYcX8DHyreewbNQYPNMAmcPQ7sbpenSCJVqbEQD9GXq1D5/keYPn6GvP4XbMGjU6yAEfX19SClRFAXljIKsNJi5MEVTHm7K2DwbIXChgBXUiQZcLLsUGk+s433XINVL242AgItGpYVt2jgOqA0LM96WPMiZEma5hevnb0P9u0XsfzkO/t1vNl2bNcLfW0f/H28nv7iA2Gqi/e0izqgf+4G+HSZ0UkqcC0XMh5cQKQP3/3QKJXxIzXbSgJgbJotwtn2eDofDTE1NYas6PumQtE2q22aC8qqC0bEcNmcLZCfaxX91q0bqZJz+M3HufP9JvJFri4NdEQLp16BiQuTgY5dS0tpqUFuu4Pf4yKkbPPO/PYpVMTEG/Aw/NMarf+R+Zp6dQfrB5XUhhNixTp3NZikUCoyMjFyTZONyuW5KM+AyAtunYxsaeh38ZfDONXCWCuSzl7ALdYTXhZb0o6ZDbR+AmBfXsShqxECLGgiffmDTUfhcKCeT6CfbumxpOdirpXZjYGKdxpcvgBBdn4GmprL42CLrjy3Sd/8w9/6fb8OXvjX00R6PZ8ea+VGgKMrLfqCgKEpX+nDhwoWb8hyqqu56b9dJHLn63250GHQziMfjLC0tXfPx67lX7dHjlUCvEdCji8/nY3x8nGw2S6VS2feEKYTA7XbTarWu68TqcrkYHR3FcRwGBgao1Wo0Gg2mp6dptVrcdtv1R2/16HG9vFx0/wexurqKZVm05sqU/vAC7nMxoj96/IqJss1A//+BS2/nTBvGs3ztI6+ncrGIEtCZ+/sLqEE3D33i/WT/4SL6nSF8D/RjmibmhSX8K2U2bkITAMDWtgtUIagl/aTuPYcaD7JVLlBbzRLyeTEti0qjhT8QwOVysbKyQujiJprfRbP/kGakmkLjrjiuZzZxnc8Tfn2KxmPruKWgNNXeNvD4240A0bSREjQhaW4Xts4XFrAibtx3JnDqEuULizgfHgV1ZzHX0ZTXHhglKKA1sYn2lRXsB/pwzuzc3nI2G5h/v4gstNDfM4Q6fv1Fm7w7jnh0HXkm3HXMt20bhKAqVOpCIexY9NktCorOVqHZXvef2GTtwhb+uJf+M3Hu+fBpYiMhFPXGCisZ0BFlE3lVI8AxbeorVeorVWpLFerLVerLFRS3ijfjx/fgGK6wh1P/5k60aLvgHxkZwTRNztx/lnq9jtfrRUpJsVhsv6dbLfL5PPV6ncnJSYaGhnZI4sbGxpicnLyh7wMAy4GSidj+Q7kFTRvnXBQhQZ+u4sk5GC43Wida72wI9fWjbVM+v47YKuOs5JHLBWQ5h+J3EKqOEtDgEE2A3RCagpZpbwLAtglhoc7WI7PM/84T5Cc2SI2GuP3BEbwnoqiVBk7Vc10mhDeT/v5+SqXSkUkEXgnFntvtpl6vUywWSSQSrK6uPq/HE0J0p+WdZlkwGOxubRmG0W3YdLxdrt7ychznQOPOF4pwOEw+n7+mOWFZ1i1zjD163Ar0GgE9dmAYBgMDA8zMzOz5OUIIxsfHcbvd2LZNqVQ6lFGN2J7e1et15ubmdt04sCzrltGY9Xj58XLS/R+GsaFRJr/4FGrKTeBHjuE+sbPgVJUKur6GabXXg/3aBOd++idZa6lUZ8vULhSY/atnufdX38Ly8jK+B9orq8ZGFf9yub0JcIi4vhul6dLwWDa+M8cRps3Kb/w95bcNIQMuqvUGQa9BLOgDXcOREikltaSP0FyBasp/aDd3cyyI67k80oK+OxJM/v0i3oUKjeUqTstuNwLKTYSp4EiBKkELqFhSIi4WUR7aNnp7XQKRrSEeWUU+dHm915WrE/nuGvk7+/AmgsiaieuxTVrvHUT2X96Aki0b6+urWE9uoj2QQnttAnGDBTjjAfhaFlZqBE8Fr5mOmZbD+ekiG89usHl+nWrFJHYmQeZcH/f+0Fk8gSMqEv061nqdarV1OaZvqUJrq4E7aWCkfXgzfsLn4njTfrTtbQqXy4U/HuDc6+/Atm2azSZut5v5+Xl0Xe/KBtxuN4ZhIITA5/ORTCbJ5XJsbm4yPz/P6OhoV1Otado1sbddpISmgyi1oHxFsd8p/MstaDrIgA5BHRnUcQa8yJMhDEdncHAQ/QHvwbF6fjfKcFu7Lmst5EoeZzmP9b1FpCNR0hFEJoIyEEH4rt+1X0rJxuNLzH3mPM3NGsMfvI073jKOKkTbhHCxQOs7i9ifexbhd1/eTBgMo8SvL9XhqFAUhVgstsOc+PnSarVu2ajAoyAcDlOv11ldXWVsbIxGo3FZJnVIIpEIwWAQl8vVTXDoGD1bloUQgtXVVYQQZDIZqtUqmUwGRVH2lCKUSqVbxu9peHiYqampa/yqJiYmUFUVy7JQFIV4PE48Hu81B3q8IulVXD2uwePxcOrUKWZnZ6/R8KqqyvDwMKZpMjc3h8vlIpPJYNs2rVaLRqPBxsZG9/N1XScSiRAKhVAUhUql0r0hvboJoOt6rwnQ48h5Oer+D0N1Js/Mbz2GMRyidSKAGtx5U+x2u/H7R7Ct4+jaJKrlYJbuxHxwhIiqEAGal4rkfm8C27QIvHYAy7IwNmsEF4tsnU5ge27u+1VP95FKpynVqmzOzKOdDGJ8a53am9MgBKVanUqjQTwSJp5MUS4WKEuJcCR61cT0718IqKqKruvouo7r/WdwvjSNWKniGvLTeGId97kItbkSnoCL4moFobhAAUsKfF6oP7NFq2rifvdQ+wGFwHlnBvX/ncbpbxeJer5B5Kk18nckaQXcOJ9+Du/9xxn45YeYXWj7skgpsZ/NY355GXXEj+dnTyOebyEuBPLuGOLpHOYDJn6/n9XZdVa23f03LuUJp/30n45z7sdvZyTjI4BDSdGoHNI74GqkI2mu17cn/G09f+O7mzi2xLg9hpH2EzwVoe/Ng3j6vCj7+Aa43W6q1SoLCwtdo0fbtruT/87Usl6vd69TW1tbXXPcoaEh5ubmmJ2dZXR0FK/Xi1NqYrRUKrUGykQBUTZ3Fv2A3C7yCejIoAuZMtqFf0AHn3ZNcymRSNDX13dDPy/hdSGO9aEca8tbKNVxlvPIuU3MR6cQhvtyU6A/jNin6Wa3LLL/NMf835xH9WiMfOAMyfuGdmxyaGMxtLFY93flbFSwlgpYC3maj84i6yZqOtxNKFDTQcQLlCDQSSA6KiqVykvWJ+AwRCIRstkstm2zsLDA6OgorVbr0F4BgUCARCJBNpul2WzumPB3Nj5DoRBjY2OYpkmj0eimPsVisW6E9dUUCoVbphGgKMquyRRXpll14q3X19cJhUL09/f37kN7vKLovdp77IqiKIyPj9Nqtdjc3OyabVmWRaFQ6KYMWJbFzMwM8Xicer1OKpWiVqtRrVaJx+MkEgmazSZbW1tIKffVAR5kkNOjx2F5Oev+D0I6kuxnJ1j93CRDH72T2IMjVCoV1tbWiETazQ8hBIFAYHu9+g9wKp9FuAw8A+9Gry+1m3rP5ih++hLRnz5FtVFrf/70CqH5Apun41jG0ZsudY7NcZy24WkiQeWZ51g2NFSvTl9Yw5ypos1XsEbaK9+OI1nfyqO5DfoH0vhyGzT7a3jXqxT3aQQMDAwQCoVotVpYloUVtAj8qwew83WUu2f5/q98A92tUZ0qYvS7WZvKgU9FqGBL0L0K8k/nsVOX49gAMDTs9w6i/vU8ilsQnc6RvyOJZbjo29CoH0uwGTUZ8WxLC1ZrmF9cRDYdXB8eRR3y73HE1491IoBcatEoNvn9j/01ZsOk/0yCsdekue8nzuG6IuquDNSlQ8S28GKTVzXMfRoCdsNqr/YvVy6v9q9U0YMujIwfb9pH4vUD+M4lcddtnLdcn1O3YRg0Gg2AHYX/3gckoWxilqqsPL3G0OvOMOJPsfzkFLOFC4S/uIEmVLwxD5U3BsF0kFE3csQPQVe7+HcffG7w+XwEAgEURcHv9x/Z1FkIASEvasgLZ9JIRyI3y8iVPPZzS8h/PI+I+NobA+kooi+IUBXMSpPFL15k8e8uEBiNcvpnXk3kVX0H+wwoArUvgNoXgLsHAXAqTeylAtZikcY/XcJeK6PGfKiDYdRMe3NABK81ITwKNE3bN/Ltemk2m0fyOLcqnTSUzrbM6uoqiUSia/q8Hy6Xi3Q6zfz8/K6GrVJKGo1Gd7ATDocpFovdf9/a2iKRSOzqubGfAewLjeM412UOWCwWu9sPPXq8Uug1Anrsi8vlYmBgoPt3x3FYXl7esdZvWVZXn+bxeLoXBp/PRy6XY21t7VDPdWVObo8e18srRfe/H831KjP/7TEQgrO/+TbcyfZKdGd12rZtHMfB4/FgmiZew0ARCnh/BMtx0NBwuVwUH1um9JlZIv/qNK6RAIVCgXSqn8pTC6yfjGN5j/7nqWkaIyMj3ZtLRVFYXFwkVK6g6UEsXaXmd6PdHsZ4fJ1y2rfDiX5lZaW9nm34UI+n0B6ZpirB2i1hz+vF6/Vy4cKFHZtJSq5BbKJO7PXj3P/pH+Y7v/ZlqtMFRh66i7ETo/gms3Ahiwy5qBpuxGwZ7UMjBINB3G43UkqCwSCMgT02jPz6FOtnE2geHyPHRqgVK0SGYiwuLqJpGkO+PuoyR/ZVVdS747smOFwPUkqK2Upb6//cJltzBcYH45z2ebj/p24nNODft4izhMLGtplgwjapCZWCUGgVW91ivzPtN4stPP1evGk/RsZP7NUpjAEf6tXxkTNllGdyXK9qOxgMks1mL3+g5UCptb2mf8XK/vbHaNhIn9ad3i8UvkfivnFG3nYH0xemKP5ImuMnTuByuVh/9lmc+69viq/rOn19fS/YtFMoApEMQjKIescw0rKRayXkcg7725eoLRRYnq2weqFA4vXD3PWf30RgZPcp7WFR/G6UU33op9o/G2na2Ktl7KUC5vk1Gl+6AKqCNhhCzbQ3B9S+wI3LV65C1/UjM3O80kDy5UpfX193Sl+pVEilUof6ulQqxebm5qGKdsdxromXhnbBv1sj4GZEQd4ohUJhxzlEVVXGxsYQQnDp0qVdvSR2S0no0ePlTK8R0OO6UBSFwcHt6YHjsLW1xdbWVvei2yn6U6kUhmEc6apfjx67sUP370h896Zf1rr/3ZBSsvWPsyz80dP0/+BpUu89taOorFQqxONxfL62Btg0Tarrm9QvLlDqC+GKtTcFisUipa8vUXl4kejPnkUfaP8MW8ub1OdLBN9xL8vPx2xtH6LRKLVajenpaTweT/cm1ePScbdMLF2lFDRIVZsU0wae727SeHVyx2Nsbm7S39/PbKVMKuhmwFIpht2UqjWunDP6fD7K5fI1N4JO1ENF5qh/6puoD5zkTX/yozi2Q63R4Fuff4YfePNZtHfdQf7JBTYmNiHmZfwnXovH56VUKqGqalsaVagRWWuiPXSS0WQQaUtWLsxTMkwiaxYJb4TJX/sKoQeGid43zMbsTg3r9dCqmaxd3GLluXa0H4pg4GyCEw8N03fiTkYGM1QfXySc8B7omeBYDo3VGltLFRrLFeylEvWlCqaq4h4MYGT8RO5IMPDuETwJ43AFYEBHlA8oyqSEur1twGfidXsQaZvGn02gddb2rSv1+e0Jvhz143RW+f36jtQFgDVKaGaA1GiGlZUVpqamGB0dPfCQ3W430WgUTdPQNA3DMF50/bDQVEQ6Qqkpmf9Gls3vbNF/Vx+vfvMY7mod+Y3nsKYjiPS2lCBoPP/n1FW0wTDaYBj367aTLPL1bnRh6+kVnHwNtT/Y9RlQ0yGUG2wUGoZxZI2AW6kgvVl00pYqlQqWZV2TknHixIldo507karPh46PwK1MOBxmdXW1e563bZu1tTWGhoY4ceIE09PTBINBtra2ul+zurpKOBzuyQN6vGLovdJ73DCKopBIJEgkLucQd7RW1WqVXC53XRf1VqvV68b2OBSvVN3/bljlJnOffIL6UolTv/oGvKPXTgX9fn/XLV1TVfyVJkGPQfV4Bk1VsCyrvZI7WUVftxn6T6/DMtpTNVe5SfRSjtXjUYZtG7fbfVPWbg3DIJfLIaXcMalqujQ8LYuqDxxVoepzox/XUL62Tms8iBO7fM4wTRNd1zl58hTN/ipyNY/hceH3esiXqtSaTXRdJxaLMTc3t+txNO5KEpgoUPvqBH/zbx9GuTtO7MOjfP3Pn2H0uWVC8Qju95/jxP3HcN5zDy2ryvT0dHelWSs1iT2RZe10HOszT+E+X6b1QALrnhjOYoXspyYIffxNxH70NhKj/ddd+EgpyS+WyJ5vR/sVlsskxsP0n0lw+s2jBJLe7ntACEEoESXbzMJzBbgz1n0cq2pu6/i3DfyWKzTX6rhiHrxpH0baj/8tIwwPeOnzK5hCUFA07Ot8f8mA3nbXL7UQ5SsM+Lr/3/44qtIu7gM60Q/dSX4qi3M6vK3V18FQD23+eCXZbJbx8XESiQQbGxusra3tu4Iei8Xo6+t70Qv/K5FSsvV0lvnPnKe6VGLoPSc59TOvRr9i00lWGm1/geU85uMzCJd2uSmQDiM8z3+LRwiBGvWiRr1wrr0pKBsm1nKx3Rj49gL2chERcF/2GciEDm1CGAgEdqygPx86BpEvd66UpnRiVB3HQQixZ1xmvV5/3vdaHXPBq7mVrr+KojAyMrLD/LojFdA0jZMnTwLta8/y8nL3nFAoFHC73SiKgsfjuabB0qPHy4leI6DHkZJMJnEc5xpzlsNwq3XwLcvq3uAnk8mXtfHQS4FrdP8nXzm6/70ofjfL7G8/TvS+QcY+9jqUPWL8NE3D7XYzNDSEJhQEUK5V8WznQQPYaw38oylC77qdZqvt0G7WG8j5TdQPncbt2Lhcrj2juUKhEJZl3VCWtNfrxTCMXY2umm6dULnenhoLQTlo0JctkLsrjvHoKtV3DXcnwZZlceHChfYU1+MhFfDREpJCpUwo4CPg86C4DfL5fFd/fjXSq9G8O4Hn0VV8QZ3aag4vWxy/cwL/yUWUnMbG1BpzP1ZE/g8nGTzphXCwndteahJ9IktxLIL9yAbC0Kj9yDDiz2doPZfD3qijvzlN1txifHycRqOBlJJoNLrr+m2HRrnF6uQm2W2jP5dPZ+BMgtvePk7yeAR1j9e/oiiUSiXiDx0n/1uPsLI00y78l6vYdQtjwIeR8eMbC5L4gQGMft81ryEJrEpJwLHps1uUFZWyuKoo78TqXVnodwr8kolysYT+pzOow0EsBRyfikx4cMYC7SI/qMP28yaTSYxwmOVLeeTx55917zgOS0tLDA8PE4/HsW2b2dnZbrHkOA5+vx9d1zEM45YxOgNwLJu1by4w95nzSEcy8oOnST04gqJd+/sWfg/qyX442d+OD8xV24kEU6s435hEBA1EOoqSiSBSIcQuj3EjCI+OPh5HH99OQnAkzvq2CeFcjuY3Z5BNqy0lyIS2TQhDu56zg8HgkfgECCGIxWIHf+LLgCun8uVymXA4TC6X6zay/H4/1Wq1+1rvGP89n9e5rusoirLrPdut1ECD9rUlHo9370nj8fg1nxMOhwkGgywsLFCtVndEMQohOH369C33ffXocVSI/U6499xzj/zOd77zAh5Oj5cLhULhmriq/dA0jRMnTtwyJ1vLsrh48eKOoqcTQ1Uul1lcXGRwcHBHRnWPo+ca3X/Sh+/Vabx3D7xidP+74bRsFv/4afLfXmLs515D8NzB2tCZqSlU00bZyFOM+LvFs5SS0v83g7lQZuQ/3kf/SJqpqSm0ukl/UWKfSFGhvTHQ39+PoigoisLKygqFQoFIJEIikehO49fW1q5rqmcYBsPDwywuLu7eRJCS1FqBzXgQa7t4CRaqKLbEfDyHORqgdWp3bXTGFcSfSSJ1FSEEuc0NwqEQ1VqN7Ooazl7XP9Mh8tlHEelvop99DDWpUrNMEl4VmgqWW6ExEaR04idxr99GS/XSsBSiT6xQ7gtgPbaFczaMdW8M+4ktzL9bQLcl6i+eQ0TaJoGqqjIwMNCdOl24cKH79I7tsDVfbBf+5zcpb1RJHo8ycCZB/+k4vtjua99Oy6a+Ur1s3rdcob5S5eT7byM1EmfiK9/HuDOOkfbjjl+H6VuzvbavFlsECnUom1SrDk7Jahf+Tbs9+Q+0J/qd4r6zwh+eaKA+lKFvvG3CtbS0RKlUuvb3lcmg6zoLCwtH1hgWQjA2NkY+n6dQKLSLZCnp6+vbsc12lGxtbVGpVAgEAjfUQLbqJstfvsT85ybx9vsZ+cAZYncN3PC0VdoOcqOEXG5HFcqtCiIRbBsPDoQRiQDiJl57nXLHhLDQlhWsV1ATvssJBYNhlGB7Qp3L5bq69xslEomQTl+fOeVLlZmZmW4D1ev1kk63z98ej4djx45d8/m1Wo3l5WWCweCOhKfD4Ha7icfjBAIBtra2dv369kbWyRv7Zm4i8/PzNBqNA4/NcRwmJyd33PsFg0GGhoZu9iH26HHTEEI8KaW8Z7d/620E9LgphMNhXC7XjpWs/fB6vbdEE8BxHNbW1rqaMa/Xi8/nY2trC7e7fQPfceVdXl7m1KlTL9qxvpzp6P4r314C+crU/e9FdTrHzG89hnc0wm2/9Q60AyLyAGSlRmarzqwhMKP+7jRXWg7FP53CLrZIfuwOfNEApmmi1U1iExtsDoeply5Pqjs6VNM0GRwcZGBggGazyeLiIvV6HcMwGBwcpFKpHKqQc7vdDA8Ps7S0tPcmgRC03DruptltBFQC7a2A6r0JPF9ZwhwKIL07L2eKoqCnIljrRS6V1vF4je7NnGNbDMSjFKs1yrWrDbMkodjfEf2f/xSRb1Jc1Gkuuaj5vNi2jmhIrJaNa7BKX+JTOJEg5vd+Bu8zASqGG+uRTew39WOqAvN3LiACOu6fP4s6UUR8dQXngyOgtI0b6/U6brcbVVWpF5usPLdBdmKTtQtbeKMG/afj3PmDJ4mPhlGuyKeXUmKWWu1ivxPVt1ShlWvi6TMwtg38IncmMNI+YgNxgtJD+jEP8o6ril8poWrtNOArm5eN+UomyMuxeqWAjh7QCSYVzJCbUsiD9Ot7ru1rmsbAT95OvVRlaWmJSCSy68Q3EAjg8Xh2yCyOglQqRbPZvGbj4qibuI7jUC6X2djY6G6b1Gq162oENHM1Fv72AktfniJ6LsXtv/wDhI4//8m2UBVEKgypMOrdo8iWhcwWcFbyOI9cQFaaKANhxEAEJROBkPdIV7yVgBvldB/66StMCLOltgnhs1kaD0+CpqBlwvgGw2husIS8xvPhsNxKWx03G4/H020E1Ot1NK1t+LpXk8vr9XL8+PEdjceD8Pl8xONxPB4PW1tbZLPZPTfDbtU1+uHhYaCdDLC4uEgwGOw2YoEd/x0fH2dqaqr7tZVK5YU/4B49XiB6jYAeNw2v10tfX9+hUgP2uqjcbCzLwnEcXC4XtVqN+fn5bgGTSqUIBAKUSiUMw0DTtB3H2VlD7sRI9eIPnx9OzaT63SzVb1/W/cd+7JWp+98N6UiynznP2hcuMvRTdxL7gcbU/DIAACAASURBVJFDfZ2zVcC5OI92bIgBj9ZtZEnLIf/7k0RO9jH+0Xu774Gt5VViE5uUBkPUY94dj3Wldv/SpUs70kM6/14sFhkZGemuX++H3+/vml3tR+MKnwDY9goIePBbNrUTYTxPrFN/8HK6yfDwMF6vl3K5TOnx83hSfhpK2yn6+PHjFCs1Ws0m0aCfgNdDrlSl0WoBkmj4z4mEP49pRtAaLTx6E7NuonqV9toyEloSJxRF2i5UigSG/wsbk/8ac6KP1lv7aX1nE7lURX97BuV0uP11MQ/ir+YQ/7yOfKAPIQU+j5+nv/Ycdzx4lm9+6hm8MRcDZxPc/aFTGKH2hFTaDo31+uWYvqW2rh9HYqT9eDN+gmei9L11CE+fd0fDAABb0tgo0382RTgVp/iVZYRkh1Yft4IMuC5P8iMu5LCvO+HHs1MKYANNKQk7FinpUJAOdZRdmwGWZbH5rWn0/gClRqlbmF+JEIJUKkU2mz3SJgC0DdWuLHo0TeuuNt8onVhdy7K68W27Gacd9rxVWSwy/zfnWf/WIv0PjvKaT7wDb+rmbZsJl4YYjqMMb6/z15rIlQLOUh7rmQUkbMcUbnsM+NxH+/y6ijYUQRuK4GbbhDBXw14qYi8VSGQLrN7hx/P0FtKtYCUM7ISBPES8I9xaOvWbTSqVIp/PdyVGtVoN0zQJhUL7ft3AwMChogYjkQipVIrV1VUWFhYOfH/eCulP5XJ5z0ZfxzuiVCp1t5I0TesOdTpJV1dKVBzHwXGcW2JY1aPHUdNrBPS4qSQSCdxuNwsLC6RSKRRFIZfLdfNvO5OTF3KNrzP1N02Tcrm864XN5XIRDoeZmprC7/fj9/uZmpq65ga2Y5bTbDap1+uMjIz0LhbXgbQc6ufXqT6+3NP970NzrcL0f30MRVc585tvxX2IzQgpJXJpDWd5HfW2Y4iAjwAwPj5OfiPHxmyW5AdOcuz1Z1leXqbRaGBX6iTOb1BOB6gf4jl2K/SLxSLRaBRVVQ/VCDioCSCEwDLcuBsmmqoitpsPlaDBoNRx+uMoX15A5i3spEEgEEDXdSYmJgAwEl6861UaUQPHcbAsiz/4gz/gkUce4d3vfjfvf+97iQZ9WLbBM899kl/8hf/Op373HMGgCyeu8NS3C3zuH3JMb5loKIR9Csczbt7xUYNjHg0tr2MpDcIP/i5Z8xf4jz//C9hhlV/777+BJ3TFTbEiKL02ztonv0/h/Brv+PdvY/LRGZamsrzmXXfxtl98La1qi/pKhfJ3N1nbXu1vZGvoEXfbwC/jJ/lQBiPtQw+72wVPy4Hytib/ucLOqX7ZRNQsRL+fYtVF/IO3Ufzfv4S8L4lzItQu/AP6jhjGwyKFIK/quKRDxLbwY5NXdaxdirBGuYZvLAEN9twGsCzrpkzeGo0GgUCAVquFqqrEYjGKxSIXL17kzJkzhzpfO45DoVAgn8/TarW6zeJIJIJhGHtus1xp5HY1UkoK59eZ++vzFC9tMfjOE9z/u+/DFTjaovswCK8bcawP5Vhf+/dTquMs5ZFzm5iPTiEMNyITaTcH+sMI19HeOgohUGM+1JgPbh/AABrzi+TvFrify+M+n0fbzOL4tHZTIGlgJQyc4N6bKK8UFKXdoFRVlUQiwczMzKGK8c55cjfDvysplUokk0lM0zywCXAz5TaHpbOxcOzYsV0NEXdLA+h8X7lcbkfKwJUUCoWeT1SPlyW9RkCPm04wGERRFIrFIn6/n6GhoW53tRPhtbi4yNjY2E0/llartWd+bAe/308mk2FtbQ3btikWi4fSPNdqNWZnZxkfH7/u4+pMljobCh0dq23bmKZJqVTCNM2uo/VLmb10/9GPvOoVrfvfDSklm1+bZfGPn6b/A2dIvffkoaZd0nFwLi1ApY565ymE+/LPVbMUcv/t+/iOReAt4a42X2nZxCc2qaT81PpufKoTCARQVRVN0/a9yTQMo9sk3A0hBKdOnbrsgm07BMVlZ2xFUWgUSqTcLvjpQUTDQgTcNFutHRrjRtQgNFdAaVo4bq274aPrOl/5yle4//77abRaBLwqscjDgI6g3YT69Oc3+PxfrPOWu3y8800hTp8OsjRV5eKmxZ/88Qq//rP92A2JpfrRXJvMFv+CxL0jeCN+nnzmKe5/3f2sXcyRnWhr/c26ybFXDfDhn38bG9l1moUcMaGhCMHkbz5FdaV82cBvyE/8dX0YUQOt6Vwu8DdNmFm/vLbfidXb1ubLoGtHrF7q+CDhSIRqtYru94EDzvEgGEdz+W8JhTVVJyBtknaLslApK5c3CIQQRO8cprVWBq3dNPV4PF03806Kw26eAUdBqVQiFAohhOhGnnVkAouLi92V4Q4dw8tms9n9s5expBBi30bCrkWH47D+rSXmPnMes9xk5AfPcO4/PIB6xMX1jSKEgJAXNeSFs2mkI5GbZeRyHvvZJeTXziOiPpR0FDEQQfQFDxcjeZ30D6bJl4s074jTBHAkaqGJul5HW6nieWYLTGe7KeBpNwjiHtCUV9RGQLVaxXGc7mZAq9U6tJ49k8kwOzt7zcd1XScej2MYBqqqdpsMezXqhBCMjIy86EkNjuN0jf4KhQKp1LXeObvd+9m2zbPPPrvrY3bOTb0BT4+XK7fGlafHy56Ok229Xu8azKiqSl9fH5qm0Wg0aDQaNz0+cGpqat+utsvlIpPJsLCwsKuD+UHU6/VuTJuUslvUQ1sqcfXGwJVGP4ehUqm8ZBsB1+j+X53p6f73wSw1mfvk4zSzFU795zfiHTmc7lWaFs75adA0lNtPIK7QbLZyNSb+09eI3Jtm8MfvQAjB4uIiQkriExvUEl6q/c9vJblTeAUCgR1SAmgX/16vl1Kp1F233Ov92Nko6Ez2o/kKDZdGzdc+RwghUFoWY4EwittN8xvPoL/nAZbXlnds7khVoR7z4t2oUckEu5Ph48ePUygUePjhh/nwhz+Mw6PYdhWBgselMzNd428+u85HfyrNO0Y0iuUWiahGcMTD2beF+KFiE7tqY0qQtkCGYjxZeIJz536O6prkL3/nc6x9rkU4HSDZF+C2OwZQmg6n33QbM1+c4PufeATP/X34Uz62LmZ5/ccfYOPxGZTKdoE/XUc8XQKFruke2/F6csCAoKvdAPDuHavXKXKnpqawbZvh4WGSP3k3q8/MwmuTu37NYaaE1yAEZaFREyoRx8Jnm+QVjaaiMDQ0hFVqsvb5Z+EDQ91zWGeyPj4+Ti6X2zc14fmwsbHBxsZGt7F0ZeOpXC4zMzOD1+ul0WhQq9WOVKZ2ZUFqtyxWvjrD/Gcn0INuRj54huRrMjfVpO8oEIpAJIOQDKLeOYy0bORqEbmSx/72JWShhkiF2hKCTBQRPVxU4EEoioJhGJfPIYrAjnqwo56uOaiomWjrDbSNOsZTG6j5JqUPjtH8xgzaYAw1c9mE8OVKLpdD0zSCwSBTU1Ooqnro+yifz0cymWR9fb37sUwmg9/vJ5fLkc1msW27+2c3IpFI10T2xWZzc7N7Pdnrvuqg49Q0jf7+fhYXF4F2Y/BWND/s0eOo6DUCerwg7HYRsW17x+RudnaWEydO3DSzmWazeeBqWyfG60aaAB1204pC+8I0OTlJMBjs6pf3e57OevWVzry3qhHPXuym+4//+O24Rnu6//0oPLXC3G8/TvSBYcb/7X17xgJejaw1sJ+9hBIPI0bTO37GjdUyk7/yjyTfOs7AB892P94XjVPM5anGvVTTzz+urdlssra2xvDwMD6fj3w+j+M4GIZBNBql1WoRCARQFKVtJDcw0N2+uZru8UuJpQgC5Tq+WoumS6Xp1unLFrBlDv3Be1DPDmOvlUmEoiytZ3c8Ti3pI3Jxi0o6QDgcpl6vI4Tgfe97H5/61Kd46KGHSL/qC6yv6ThS0jRN/vnRIl5D423v6kPMlfA0bZpFE6kKPPkmVtXClEDMTUsXzMxU+e5TRT50agrP8l1UCzmi6Tp98258hTLesEkg6WPwnmEu/dMUd51IILI20uVQ+txzjH7sDVTOr9DwqDhjge6En0Pqoq8mFouhKMqOid/S0hKjZ4ZJrFTYsB1QLxtkDQ4O4vW2PSHy+fyOCK2DCAaDhMNhNjc32axWMaRD1DHREv0oQrBwaR6t1N4AyOVy2LbNyMgIW1tblMvlHYXIzUJKSaPRwO/372gU1Wq153W+34++vj5apQaLf3eRxS9eIHQywdmPvY7w6cRL9vwnNBWRiUImigrIhtk2HlzK4XzlWWTL2vYXiLb/G7jxQjyVSu06se4gvTrmiI45st28lBIkaD43re9lsb84gXBpqJlQO50gE0ZJ+m/KBsOLRWejplAoYNv2dccmJpNJgsEgpVKJWq1GoVBgZWXlwIaY1+ttx9HusvXyYtBoNHacR3aLCezg8Xjwer24XK5rznOqqhIKhbqNgJt1bujR41bh1ngH93jZ4/F4Dlyvt22bixcvcvz48ZtycTnMer/H4+nmzUK7EMlkMt2LwvOlozUtFAoHfm7HAOhKXuzVu8PQ0/3fOHbTYvEPn6b45ApjH3sdwVcdfvtD5kvYk7Moo2mU1M6boNpCgclf/UfSHzpL3ztPXP4a00J57CLBoKC0RxPA6/USCoV26CPX19f3jZ4SQmCaZjdCrUPHEX5gYICNjQ1qtRqpVIqBgQEWFxdxuVxdaUGlUmmvcwtB3/IWumWjWTa2otCK+DF1jaZbR6m3MM9Po42mmfvmJAP3niadTrO8vNx9XtOnIzUFV6ldAHamQmfPnmVsbIwvfOFveM090zhOuxB2JCwt10gkdQyPjjMaQi+1ePifCvzZV/IAWAh+9d8NEK400RWFR7+a544Tbt76uk1WPxdkPnaC/NYl3va6d0LYjQzoBO/KUMuVsO+JEv4XZ4lHojRbTfS4D+HSiL799HXFru5FxzX86tQW27aZW1rgxDtPs/XFJ3COtX83iUSie/4FOHbsWNf48SD8fj+pVIqtrS0GBwcpFAqsr69T9gcYjCcoX5zA41ewy2a7UBOCYrGIz+cjFAq9IE2ADsvLy4yNjVGpVK7xezlqVFth+v95mtVH5ki+boh7/8tb8WX2N3B7KSI8OmI0gTLa1obLcqMdUbicw3x8um1MmN72FxiIIDz6oR/b5/PtMG07iNGxMQzDoFKp4L9vDCFE24RwO7aw9p1FZKmJOhBEzWxHF2ZC13VMtxoejwePx9M1/rsRjX7nMaDdyJ2ent7385PJJMnk7htFLwaWZXWPuRMXahi7R6xC+/zWaDS4dOnSNf/W8avy+Xzouv6S3cDs0eOw9BoBPV4QEolEV5u530Vd0zQWFhZIp9PduL7dqFQqZLPZ7kpcJBI5cOXroM6uEAKPx7NDD2oYBqFQiNXV1etfl32eXP1z8vv9193tf6Fo6/4LVL+9TPXJnu7/RqhMbTHzX7+F71iUs7/1drTr+Lk52Q2cuSzq6TFEeOdqf2Vqiwu/9nWGP3on8YdGux+Xlo39yAQi7Gfw7jGKxeI1RajP5yOTyVAsFpmcnMS2bTRNY3x8nGq1uud7StO0HTKgq7nSrTqbzTI8PMzx48dRVZVisYjjOAwMDKCqKobfT81bJliqIQFHbccJOqrCWn+YUKFGUgiEA63xIOt/8Tjpn3sTLperq0NHCGpxLwlfCE3Tdhz3+9//fj7xiV/n0iUL2DmllVLSqjbQbFDdCm94TYC7TniZXWnyiU+vEzIhHnEhXQrfPt/kx340SvSESjl+gteuufj9P/8j3veTY+h6u9AIDA22DUqH/CTHB8heXED91gb1VwWQEdee20TXSzqdZn19/fL3fwWWZSGFQPleHudYoK3hj0a78gGAubk5RkfbrxVN0/B6vW2Dxkql2xzoOP2Hw2GWl5cplUoUCgUGBgY4c+YMrVaLpZUVGg5EVEldkTh1C8vb/lnYto3L5do7NvIm0Gq1WF1dZWhoiOnp6ZuSVlOfK6PoCtVHNug/meG+334P7sjeRcnLDRHwoJ7qh1P9ba+bXBW5kse5sIrz9UlEyHu5MZAKIbT9m8M+n+9QJpKhUAifz0ez2WRhYQFN0zh27Bhax4TwjnaB59Ra2MvtdILWY3PUlosoYQNtuzGgZkIo0aONT7yZ1Gq1Heft5ztEcbvdpFKpHduaV3KrNQFM0+TSpUvd+6Xjx4/va9LZYbfhzujoaHcrqnP+O3/+PEIIBgcHb4lEhB49jppeI6DHC0Z/fz+RSIS1tTVCoVBXf9ZBVVXGx8dZX1/vxnxdfUKv1+vtaVO5DLS719VqlWw2ixCCWCx2jUFMp1t8UCEfiUSo1Wo7bsY7f3+hmwC7Uan8/+y9d5Ss6V3f+XneUDl3V8fqfPPciZqskUZpQCAJlmSEEctZ2yD/YbB3AbPLYU0yYLwcERfDYjBeEcQajJGQCMpCGkkz0gTNzJ0bOudYOb7hefaPt6tu1+3qe7tvmLkzU99z+lRXvVVd1RXeen/f5xvKXLx4sVVzczug6/u/cShXsvbfX2bj4xcZ/Rf30fPY2LVv1LytUqjZZVS2iH7PCUSwXYZbfGGDS//XF5n8Vw+RfDDTdp/uF19GRAJob/JWzhKJBKZptqS4mqa1Kt32Brk5jsP6+jr9/f0HynZzuRzpdHofsdYJUkrm5uYIhUI4jtMaXjc2NshkMvj9frYTYUzHJVqqoUlFoxmsJgSFZBjNF6BfBzM4j3xbBXdzE79uYuH9LaNkkazpxI6PMD0710ayjY2Oct+dZ/njD/8V3/0tATRb4t+uMBqAi/NV9IUSmg66CfGQj6DpUrUUmibQNYHuKJ57qcT2ZoPf/O11fr1SoDE/h9IEUlM895N/wQNTd5N46yRmSpL7/15E+jRkZgKfpbGVz6P9zhzyO0Yh7gef5tkBfEcPPYvH46TTaSzLOtBzH4lEaNgN3M0qrFYJn+ijXq+37feaw1RfXx+u61IsFhFCtPzASimEENTrdS5cuNAaqF3X9TIn9q7iCo1N3SQU89FTqFLzhylqukdI7AaivpLI5/MEAgEmJiZYWFi4IfIlGAy20tQrL2XJfnoFt9Bg/KfexOmfeDuh+Bt7PyiEQPREoCcCd46gXInaLHrBg1+fR2XLiHSsVVUoeqMIrf09f7WQur1ovo7N932z3vfK1WEt5EM7nsY8vqtgcCVyo4yznMeZ2ab+uWlwJHomjjGS8JQDg7HbVs12Zcjm6upqyy5wvb79gwjcdDp9W5EAzYDm5r5mZGTkUCQAePWJe7+/fD7fgYpL13WZn58nEokwPj5+w4+7iy5uJ3SJgC5eUQQCgVaAVSKRoFQqtbppm2ng5XIZpRTT09MYhsH4+Di2bbO8vHzVgVwpxfb2NrVajbGxMTRNw7KsawYE7n1szR39/Px86/Jm+N/tgGarwKsZzLPP9/+moa7v/zpRXysx+xtfQfPp3PGr34yvN3To2yrHRZ6fAynR7jmJMNt357mnV5j9ra9w7MffTPyuy+SYkhL55HmE30R74FjbaxYOh1uy/fHxccrlcsc093K5zODg4MGPTSny+TyxWOyaREATndQF5XLZOzgTgq2eKP66heFK5BUe36qwoOfnyYQ+jcroUP09hoJ/yIV5RWiuQOp8lviPvJvyn36RUAQC6xVktsjgJ2YwShY/LM7yb1/6E15I50Eq7LrkvjNB/vozOT76xQLv+7Y+3LgfdmqokInrMyGoo6UD6HGDz3w0y0OPJnj/9/ipzN1B/ZPvolZTfO7C03x1/hs8qk2S+EAv+T9+Dv9nVxDAylc/xvAvvRvf8RF2nt7B+b9fRqWD3r7QVSipkAEdFdS9hH+/jvDr4Ncw0xGGnziDLxHCtR1cx8Uf84iUtXML3uAU8K57pR9a13eH8Pt64OvbxO4/1iJWr3w99u4HwRui9644uq7bcd+67zIhsKI+tquCBIoB16KYzaJepaqx9fV10uk0x48fp1KpkM/nD6ySPQjNrJdnP/IkW3+7gDA0Uu/KEL23F83Q3/AkQCcIXUMMJmAwgX7/BMpyvHyBlRzy8+dRlYYXOrirGCAePLQ9oHlssHd/pZRibm6u1T5y0GPSh2LoQzF40Evbl8U67nIeZymP/ckLuFsV9L4IeibRIge0V6Hm8Uo0m4b2okmE2LbN0NDQdf3dK59rIQSjo6NtNq9XG/V6vc361N/fTzx+eOtNU+22vLzc+v/2olmpu1c1dCvqTbvo4tVGlwjo4lVFNBolEom0agSVUgSDwdYO2LKslm/1SgghCIVC+6SllUqFmZmZlgT4sAd3q6urrK6ucvLkSfx+/y33kF4v1tbW8Pl8N8T4HxVX+v6Dp9LE3jnp+f6N10/w0isFpRTbn5pl6cPPM/Tdd9D/vhNHIlFUvYF8aQZiYbSpkX3J49ufn2fhD5/h5E8/TuTE5bwAJRXyKxdBCLSHjne8z2Zg5sbGxoGVbs3E/1AoRLVa7XigXiwWWxL160W9Xm+FPilNY33IT0J7hkhollr9DK70DvwCvk+ia19CrQdxIn5ULIdm/CZDf/EW/Pk6xgOTuBfW0F5cI5nw4d+qUkdSHwxTP5WkvJ3kIWOUv/r0IrZrYAcN7ro3zne+x+K//m2edQwefihOfwhyCxU++VIDZWjIviBZDZ5+scyP/4shJvptsstvQTxxiupIlNrOGB/60IfY+qkTHHtohCUrizt1EgoWItdg/sNfpf/tJ5n8g+9h8Uc/RmMlj0j6EaYGQiCkQpQcqLqogI4KGihTw58QBHuiLP6XL6MFTLSAgVOxKM95lWpYEiwX6i7oAny6pzII6BQSAdIffAsjbz6Nz+9DSJONz51H2jYioF9WJOySDleqE653BV1FDFTZYUc3CUgvTFAToCmFfBUIxK2tLXZ2dojFYqRSKYaGhlr2hmvZyAypM9Dbz5d/6u+oVav0ffcUoZOJ1nOUTCZfiX/hNQ/hMxBjvWhju5/xSgO5mkOt5HCe8+xDYjhJMmGQ1a2O7Ri9vb309vZiGAZSyn2LBVJK1tbWWt7vw0CLBdDODGCe8QhUZTm4a0XcpQLW86u4Hz+H8BttOQNa3341w61GJwKviVwux8DAwHUdIwwPD7fsWz6fj8nJydsmFBC817Tp79c0jcnJyetqnEokEui63gqubrY6lUolcrlcx9u8Eu1WXXTxSuL2+WR38YZFU8olhMB13UOzriMjI8RisVbFWHMQCYfDDAwMXDPw5iDs7OyQyWSu+/a3Gs0vqGKxSDKZbAtxu5no+v5vDexCnfnfeYrGZpVTv/AOQmOHqwVsQhXLuOdm0UYGEEP708c3PnGRlb94idM/3/63lVLIpy+hbBf9sdNXrS0LhUJXrXNTSlGtVhkeHkYpha7rTE9Pt2Tefr+f0dHRG7bUNBoNfD6fVxUo8gwO/wyGsUUUcN04K+s/iyyniBfPofolWjKBXqigdBORnMXMP4j0G4jj/dhzW7h+g8ZojNJOguxqnnPfyFN+KYt/OMJb3/oBnr70K0g0glIiwwHe/8OjTNyT4O//YZsvfCFHo+6S9AuOnwzzsz8zRU+Pj7/5+BZG0ODOt0WwNUHJfBPB5SqxZxe4czBCfzjJpelLTExN4qZ9kPY+OwqwgWXK9FXyRH/hMWo//3nko/0QM6FsQ8mGogV5G1FoIHIWgdEEg99xD5UX1nDObyN0AQiEUoSl8gL5QgYq6UcFdZRfR5kaShcoQ4AmmPubrzP4tjOY6TDrH30Be6MEDRfVkKi665EIDRca0ju1ZTsx0CQHAs3f9ZYCoaVc8GneZbskhIoYiJKNruvE+vow/H4alSoDrkVBM6gI7cAaxFuFveGthmGQSCQYGhpC07TW5XtzFuxcg/JXt7jv+x/l4ke/QfiJfnoy+33DnfrLu7g2RNiPfnwAjg943+eFGnIlR99KDlUvURgKEVopYcX8WL1BUldYAQ8ajHO5XKuq+Loel8/AGEthjKXws7sv3fFCCJ3lPNZTi6hyA30ofrmhYPjWhxBeLV9DKUUul7uuXKFoNEosFsM0zasqv14tNJVKkUiE0dHR614QcV2XXC7XIrynp6fRdX1f7e1eFIvFLhHQxesK4mqrpffff7/62te+9go+nC7eqGgmTYdCIQqFwlVX8QOBAKOjo21esPX19VbavxCCkydPHioX4CCcOHGChYWF21IVYBgGmUwGpRQLCwst+8TN+nLq5PsPPzjc9f3fBOS/tsL8f3qansfHGf6+O9GO6DuVm1nkzBLayXG01H4Z5OpfvsTG309z+ufeQWDwsoxTKYX82gyqXEN/y5lrBnQVCoVrNmWMjY1hmiYrKyvE43FM02zdJh6Pk0wm90nLj4pm9/ulS5eIRT5MIv5RHNfzqBr6DpXigwR+/wl8I89gfsdfgn8EdzWPHKyj+7+dxd94DGckQvrtZ3CWdqh9/Bz5qoOzWWVdN4nd10vk7l6MqElgMcvIyR9DBsAJxVCdVveUwp+vU8vbaOPRtsHV0DfJ5t5PvvjtoBR92QKVgmLkXQ+S/chXqWXL2CMRrEwEGW8n0kzTZGpqiouffgbx1wu4H5iC2H6yLRqNMjw0zNqlRQqzGx5RULKh5EDJ8k6LFtRcREBHBDRvKDc0hC4QwotDFFKBqwjEI/T+T3eBX2Ptr571LANBw7MjhLxTFTSQfh10vOfEUbskgYvaSxZc8buypKdIaOwSC1sNRN1h9Be/CXRBZWGHwoUNZL1ByATh16kGTVx/0waxV5nQWZ1wqxAIBEgkEsTjcWzbZmdxi/yzG9jrNaa++yx1bLYK2x1vGw6HW0FjXdw8KClZOj9DqVHDKFugCSa2QR9OefkCfTGWV1cObLqIxWL75N83E60QwiXPUuCuFdGSIYxMvKUc0JLBm/re3djYuGp7i9/v5/jx4zft/m4X5PN5pJQ3tAiysLBwVUXFQYhGoy17axddvFYghPi6Uur+Ttu6ioAubgskEgkSHhLsmgAAIABJREFUiQTZbLbla6tUKm3p4k00k8v3oskIa5pGNBrFcRwCgcBtEfJ3M+H3+xkfHyebzbYOABzHYXp6mmPHjl03GdD1/d9auHWHpT96lsKza0z+b48Su+NogUtKKdTCGnJjB/3O44hIaN/2pQ8/T+6pZe745Sfw9YTatsln51DFKvpb77gmCQDewc7VfLlNyWmzDrBer3Pq1CkMwyAQCBCNRm9KCFwymaRSqeA4Doaxg+LycCyVH92XY/PRDL5siv6KwjA+jgjXqdt34zf+NdX7l5B/dJ7SwCC5l7dZXaqRuCfF1GQE/0PDKF3DyNWJfm4ZBGyM/HN6+/8TynXp+PUoBDKgoxsOsuIgIt6Kn67lcZw+iuV3tK5XjoSIp3xIIXFPmtRqvfiWykQ/s4wyRIsUcHu8/VSlUiF51wjZlQqRF6sE3jvITi6LaZqtFTqfz8fC4gI1WYPxq/h1HYkq26iiDWVnD2Gw56fq0Cg6FH7670j/4H2M/Mu3MvOfv4CyXIQrERUboUA0XETNRVQdb7A3tFZuQZMoUCEd1RNoIw9UaHeAb+4/FsuEFywSD4yytbRO3TZxjRg0XMp1h0DdIVa3qRcdahYo6xrqhKbi4CB1wu72TuoEAvuzE/aiXq+ztrbGzBdeRl926T0xQN89GZKTvVRrVbaW1w687fX6sru4OoSmMXrmOEtLSzSiDcYyI+jbFS9f4MvTqEIVXyaMntAQjsSJ+NqIumKxeEvzdTqFELobJY8YmN6i/tlpcOWulWC3oWAgekMhhD09PWxtbZFKpTrWDXdqDXk9IJE4moruShQKhesiAYDbcnGoiy5uBF0ioIvbCnsZ3mg0ysDAAFtbW21DhW3bbG5utkkCe3t72dzcJBaL0dfXR6VSue4dvaZpGIZxpOCoVwrxeJxCodBxFWBmZubQ1TnQ9f2/Uihf3GH2179M5EQPd3zoaLWAsJtqfXEeGhb6vacQvna5qVKK+d99msp0ljO/9C7MWKBtm3xhAbVdRH/b2UMfdGqaRiaT6agKSCQSRKPRFgnQvB9N0wgEAmQyGYQQ+6oIjwohBOl0ukUGVmt3E418CRcb0NBFlUrtPmpDUWpDUXp6/h0bi9+Ds7RK0epn8h4/l/7jM4QNjQEhSD0xgv6Yp6Jwzm8TXK+gb9Twr1co39FDfTQKYgSRK9Kb/GMcGUep/YFg0tAxwgaNbAMRMdG1HFKFWNv435HSG841KdEdh8TkBPbCImHLYmegB2cgBPen0bMNfMtlwl/ZQFgudiaCPphhcHCQ4HcGifhCWLkK6VOnkFJSLBbZ2tqiUqkcbr9kaJDwez8HQSqoOPBynq2/fpH44xMET/RRen4V8hYUbc+eYGoQNSFiwkAQggbCtztIG8JTGLgSLddArFah5iCqLqLmeFkFQR0VMFAaqJU666fPYSRDjN19nLUX5igWChAKYQUNHEOQkA4pJclpBnVt//tVuWqXHNirRHChSRw0z5fslmpBWbvXbRILdRc0sU9tIPw6yqdR36hSuZhHKkXkvjSFXo3YmRSNUpXlF2dQPtFRnRAIBK5ae9vFjWNkZOTymYwfLeMdM6i6jX92BVXNk3puE82RNFJBGj1BGj0BZNAkm822MkduNYSuYQzFMYbi8JC3giyLdZzFHO5yAfvvz+NuV9D7o7shhJ5yQIsc/v1jGAYTExMEg0F6enq4dOlS23al1C6J2j3U34v19fV9lzU/x9fav96sitcuurhd0N07dHFboxkENDMz0/JtxePxfRU2mqYxNDREtVplbW3tukkA8HyjW1tbTE5OtqTNuq63vkxrtdqrxrTX63UGBgbY3t7e94WklGJjY6P9QOkKdPT9P5Tp+v5vAZQrWf2Lc2z+7SXGfuhNpN58dFmqaljIc7MQ9KPdeWLfKqZ0XGZ/4ytYOzVO/cI7MELtr6E8t4xazaG//SzCd7TdfTweRym1b6Dv7e1lZWVlXwf7xsYGQ0NDLZLuRhOWw+EwlmW1WgfKlccwjC2S8b9GCEm++K0Uit8CgLRdsBXLH8+y/uk1+t/sgwcEEz99P0bIICT8OJUGaIBSuLak5+tr5MaT7LxrFOW7PHAWiu/BdSOke/4QoZVwZRilLtePSV3DNBS6r4Amqzgyw+b2/4HPPwLCwrZtIvUGadtFhMO4q2uovauQQuD2BKj1BKjd3YtWtAjnHIKhEIXPnMNSLsvCofbRWYwnxmiM3SI/qia8Af+BXsQLOdYuLJL5pjvYedNAy2aFUlBz96kJVM5ClXaJguKu6ipietkGERNGAt5pWAdTR5gCYUvE7Bz5pU24JCm/tEbm2+6DP3ua+qUVRNUFAZWgTj2gEwoIAiGDasiHDBmXlQdN60LUhET7+/2w2iWllGdx2KM4kCWb0te3qDy5hRE2idzbiz8dRFiSoakR/FJn9kOfR5as/eqEhA/t+4/h+4dV1owt9JCJCJhoQQMt6IU5akETLWSg+Q20kOmFPO5u7xKvNw4RMAkdG0JeLLP1lhH0mo1vp45/p0bsUpbsff2QXUWOKMRg4pb79ztBiwXwnR2Es57vXlkO7koRZyWP9ewK7sfOIYJ7QwgTaOnIVUMIm5V3fr+fqampfdlGFy9e5MSJE10yYBeNRqNNKRoKeeq5/v5+TNM8MJy6iSu/97ro4rWObkZAF68JOI5Do9EgEAig6wevauZyOVZWVm7KfaZSKdLpNI7j4LpuS5UQCoVoNBosLCy8oqqBYDBIJBKht7eX5eXljmSHpmmtru+98Hz/y5S/utL1/b8CqK+WmP2NL6MHTSZ+5KE2qf5hocpV3Jdm0AZ7ESMD+ywa0nK49CtfBOD4Tz6GdsWgL8+vIGc30N9xFhG4fpKnVquxuLiIbdstxc1eNUAnHD/uSXgPWx3YCf39/SilOrQOePcrbUnlXI7ys9uUz2V55BfeTSFfoBa0iQ0kGBgYaNVLjfYOUv/CLLleSfTFHaQuCPgE2/f04wQ7DwSaViQS/hLJ+N+g60XvbgWAwGg0KC0dZ/OZxzDe+l7Gx6da+6eNjQ1sy2KwN41WLuO+eI6GabDUe7CfdXh4GMuy2F5Yw7dcxlwuY6xUcNdqNN45jH1HEhW4hQfyz+3ATAnz/ccZGRmhXq+zurp6+Ns3V+CbxECTNGieLzvQcBHLVdQ9KejxQ8Qkdf8osWP9LL04g+sHAgai7u6qChzCFYtA1abWUDRq0rMo1HbVBnUXfNplG8Jeq0JQR4WMtsvwdw4jdIoWuc+vUvjSGqHjCZLvGCY4EWtt7+vrIxqNMjc3t28IaKkThMBvmIyE+1E1G1l3kNXd05rt/dTdPb+3bxea8IiCPcSBaJ7vRCg0Lw9d3i4CxhvexiWl5Ny5c/s3KAUKxu0g/s0Kar2ASITQhpOIoSRiIH4oy9SthlIKuV1pVRe6ywVUpRlCuFtdOBxH+A/eF1y8eHHfQoUQgnA43LJgvlZRqVSYm5sDPNvYUZogmtj7HhkdHSUWu/xZn5ub6xjAuNcmZ5omJ0+evJ6H30UXrxqulhHQJQK6eN1hfn7+lve9jo6O4jjO0Q6WbwCRSIRMJkM+n6dQKFw11RY8smK0b5jac+tUnlrGXisTetMQkQeHu77/WwilFFv/MMPyn3yD4X9yB33vOVotYBNyJ4+8uIB2bBQtvb+KzKlaXPz3X8BMBZn6Nw+jXXEQKy+tIS+uekqA0M2RKhcKBTY3NztWdO1FMBhkZGSES5cu3RBRNjExwdbWVttnWdoulXM5Ss9sU3k5S2A4QnQ38C+V6SWVSjE/P4+u65w4cYLz58+jlGIsM4L9Ny/hvLhC4fEMjUyE6GIBARSv2drg4vfPoGtFhHCQKoBvLYEo91C76DD+Lx9mfWOdQqGAz+djZGQEIQRbW1vYG5sM5Iu4msZCX+f07mY918WLF9sGTWG5mF9ax/fsDsZQELcngDUSwc5EkJGbvJppS8Tvnkd9YAqtJ8j4+DjlcvmGqh/3wZEY/3Ua594eCGhQtBE1yeCjx4mdGmTp956k8vwaBA2IGt6Kf9REixhEwxpG1KAYD2DH/J71QXkr+k1iQNRcqDre79U9lzVPHQkBjyBQQR3HUZTni1SXyvhOxAk/3I8xFPasDCEDDI2enh5SqRSzs7PXzLyYnJxsrS4eBUoplO0ia87uj0cWqPqe83V7zzbnMsGwh1BQlovm13eJgsvkQJs6oUUk7Dm/V50QMG7Is3474Ny5cweu2p45cwZN01CuRG0UUas55EoWla0g+mJoQ0kveLD3la8CPAiyauEuF1oNBe5aET0V8lQDmTjGSAKRuBxC2ByWM5kMmqaxsbHR5mtvVmW+1iCl5Pz5822vbSKRIJPJHPlvNRqNNpVnEysrKx1rA/v6+tja2kIpxeDg4HU1MXTRxauJLhHQxRsKxWKRxcXFW3ofze7aZgCREALHcdA0jWAwiGVZ7Ozs3JTANPDyEnp6eq6dwu5KWChDTwBtsUpPyU/0oZGu7/8VgJ2vM/c7T2FtV5n6Xx8hOLI/1f9aUEqhVjaRyxvoZ6YQsf2KDbtY58LPfY7wsRTjH7x/Xw2gnN1AvrSI/vY7EZGbLyu/FtEWDAYZGxtjc3OTQqFw3Z+BM2fOcP78eZyG3T78ZyJE791N+9+TrC+EaLV91Ot1xsbGyOdyVBY2GRjPkM/mqa/ncftCKFNDSEV4tUR5KOrJ5I8As2YzPpzBcjS2XliiOnbwCp3fskioS1R6ctTrx3Gc/tY2XdeZnJwkm82ys7PT8fbaJ1eg7KA/kMJcruBbqSCDRosUcBO+jivdR8YX1j1P/7uGMAyD48ePc+HChZsqhTU+uog8nUAej7VdHovFSKfTzFya9lQE5d32g7KzqzCwMEo2ZrGBU3aw/ZeJgo4/EXO/AsD1FAWNC3mKX1jFWakSO5UkMhFFV2KXOPBIBGoOsccmSX7zKZb/6Els22kRCCpotMgCFdRRCT+hSJjJqcmb9jxdD5QrPWKgfpkwuCF1QoskeG2pEw76/g8EAhw7dqzjbZTloNbyyJUcajmHqjU8UmAoiZZJQuzmpv3fCJQrcde9EMKmcgDwAgh3qwvrUZ2Nba+FKZ1OUyqVWkpJn8+HaZqMjIy8puwCBw3pTXLnZsBxHM6fP7/vcl3XiUQiFAqFm3p/XXTxSqFLBHTxhsKB8sCbDJ/Px+DgII1Go9WlrpSiVquRSqVu2opac8DZ2Nggn8/vv4JSsFaDl3LwcgFSPrgrhXF3GsNvopQiEAgQCATY2dlpyxYwTZNIJEIymbyu1awuPOSe9moBe98+4dUCXgfpoqRETi9CqYp29hjCv1/Ob+1UeflnPkPywQwjP3D3frvA4hbyuXkvGDAW3Hf7m4Xl5eXO78VdhEIhUqkUoVCIubm5I7d3SNtlPDPO/D+cZ+ZPnj9w+L8SiUSCcDjMysoKPt3AWK9g2BJjohctGkTO5lDLBYzHJxBCkF1YRQlwjyi7D/j9TAyPcOGLz1H6f6cJ/fhdBxJtwcALDA78B0ChlJ/llV/CdjzrTjQaJZVKdWxHacGRaB+ZRZ1MoB7oBakwtmqYy2V8S2UQAisTwR4J4/QGj0xqtFC0EH80jfrhkxDQyWQySClZX1+/aWSA/pk1VNKHvHf/itrExAS5XO6q7yuhFHHXxl+1yVcUjbLrVSaWO7QiQIsYUBGDer5B6UIe23KJvmWAyGODaPHOJEo8FmNgYJD5Fy5iZyteHWNTbdBsUKi5qLiJc38vvR/bRA+YiIgPLeJHi/i8n/Du6e5lYvdy4b89ZfxXqhNU3catXkWd0Hb5tdUJ+9QI1zh/veqE6enpli3JMAxSqdS+XKGrPg+VBnI1h1rJIVdyXiDmcAots2slCN0+eTpKKVSh7qkFdskBd6fK1t1RbEOhozH+1rtZWFxA0zTGxsZa++TXSnbA6uoq2Wy247ZQKMTQ0NBNq09eXFykWCzuu/zMmTNYlnXT7qeLLl5JdImALt5Q2NzcvLmS1uvAsWPHWFlZuaaE/7BoJrG3pbgXLG/4fzHvkQFnk3BHopUUnkqlCAQC17QvGIZBOp1mfX2dYDBIb29vm2+ui4Ph1h0W//AZis+vM/mvHyZ65mi1gE0o20GemwHDQDs1juiQg1FfL/Hyv/sM/d98jKHvumPfdrm8g3xmBv3xOxDxW5/9UCqVWFpauuqQmEqlSCaT+wKsOuFK2f/wE1Oc/V8e5uK5C1cd/vdCCEEsECJxsYi5UsJ8/Djasb7LidBSUf7Dr+J7Uwb/vRnq06ss5Daxg0c7GB4ZGUGt7pDb2GL7Y8sY9/Rg3ts5jTzd+7tEIv+I66YwjC22t/85xdITwOE/oxQs9D+ZwX3fKIzseW2VQs9bmEslfMsVtJqDNRzGHolg94c8Cf1R8LFFGAzB/b0YhkF/fz/RaJTNzc0DD8SPAu3pbUTNwX3rwL5toVCITCbDzMzMNVUkPiVJug4ukNdNnCuHaqWgIZH5OpUnNyl/ZQNDE0Sn4vjjfkSTOLClpx7YoySInOln+LFTzD9zgQa2t/0q5Epvby/96T5U1UaWLe+n0kCWLGTFap2qcqO1XbmyjSC4/OP3yIKwr+3y28G/fhQoqfYQBVdRJ9Tb7RA3S52g/Bo1LGKpOHrId0Oki1IKClXkcs6zEqzmERE/YjjpqQYGE0cOYj0MLMsLHjVNE8MwjrQKrSyHSy9dQG6W8b+co/+b7iJ4cgC7VCM7vcJOrYRK+tE0jZMnT141d+nVxsLCwqHCnw3DIJFIkE6nb/j/aTQaLC8vt47frqYm6aKL1wKuRgTc/lRgF10cETdr+L5eJBKJljLgZmFlZYWxsTGGB4Yov7yOcz5H5allOJ2A947AYHDfylYgEDhUWNvAwAC2baOUolqtsri42LI+dNnvg1G+sM3sr3+FyOlezv7at6CHrs+3rap13Ben0XoTiInhjget1YU853/uswx/9x30f+uJfdvlahb59Rn0t555RUgA8FazT506xfLycscVFPByBfbWfF6J5vBfOZ+nsVzCPxgmfCpO33dNesO/T5AYSl0z8yMYDJLuTRO6lMP5x3n0OzMY77xj3wG60ATB95yh8sdfxzzZh3+8n7EXFpk+Fj60vN40TcLhMAu5aUKlBuaj/VifXMG4p6fja9dojBGLfha0AiCw7ctBnpqmHW61Pe7D/ZYM+seXcD8w5Q2n4DUQJP24ST/1u3rRShbmSoXAuRzhJ9exB0IeKTAUbmtGOAjhd03gn6lhhSNYtsX6+jrZbJaxsTHq9TrVavVQz9GBiJqIzc77pOagc+LECYrF4lVDXy2hsaGbRJVLn2tREjolTW+9hm7VIf+Pa+S+sEpgNErqh04RPBbf//o4sk1FEI6EyTx6koU/forGhS1PbVBzvNyC2F7CwICJCFoiSFKEUa5Ci/rRoofL41CW65EEZQu5hyBwiw3UWglZbCCruyRC1UKY+hUKAx+iA4mgRXyIkPmqqw2EJtDDvhtqovHUCfIykdBRneDgFurY653VCYUr1Qm7hMKB6oQ9hEPb9nAA/WwGzmZQUqK2SqjVPO4Ly6jPnEP0RDxSIJNEpGP72l2uB50IsWa1sWma9PX1tRoDroTwGTh+gRwO4wyHmVc5xFc30NcrGFs1Ipt1RMOh8sQICzsvMJoZQR+6egjhK416vc7KysqhlYqO47C9vc3Ozg533LGfKD8Kmg0MluXtA1+LmQpddHFY3D6f+i66uEmIx+M3VB94o0gmk2xsbNy8P+hK1GyJxY8vc/yH34o50of//ilW3jlEudo54TYejxONRjt66vYiFAoRCoWYnp5uu1xKyfT0NJlM5jWdMnwrIB3J6n97ia2/n2bsg/eTeuTgusZrQeWKuOfn0CaG0QY6ryiXL25z4Re/wNg/u4/ex8f3P56NPPLpafTHTiOSket+LNcDTdMYHR1le3u7YzdzOBzeNzxK28XaqKFsiebXCZ9OEj6d9OwUV6y8Ngmqg5BOp0mn06ilHPb/eAk3FsD3vQ+gJQ8+eDQGY5h3DVL/5EVC334WcyRNzKpRPGSmYiKRoFAoUA+bJBYtjNN9ND6xhJwroU/uV9IUS9+E0ByCgZcplx+hVj/b2lar1Q4vWZ6IIu9OoX1sCflPJkAXxGKxlne1Uqkgoz4ap3w0TiURdQdzpYJvvkToqU2c3gD2SARrOIIKGQQCAXp6egiFQmSzWfx+v/d6sU40FMOXCKHrOpqmYVkWmUzmhgMgVdS4LNvfg2YY6uLiIpZlcfz48Wu3vwhBSRhUhU5SOoRdm42cw8bn1yg+tUnkrh5GfvQu/AOd3wuhUIhwOIw2rCGEQNM0YrEYS0tL1B5OwMO7+z1XQsVptx0IAQk/kScLbG08hVuoowUM9EQAIxlETwS83xMB9N3zRiKAtttQIXw6ui+Inry2fUcphao5u+qChqcu2FUZuJtl7FlrjxLBQtUdtLC5Sxr4W3aENgVC2IcW9U5vp+FvL4QQCJ+O5tPh6HErLVxVnVC7bHOwi4396oQ95w9UJ/jDiFULcWkRUb6AcBz0gRj6cAJtJOn9HvQdOTvBNM19RICUEsuysCyLubk5jh07diBZHwwGWwn4UimImbixBNYJ730t6g5atkG1z0f+yUuYSxX0nlBbdaGIBzo+XqUU7nIBPdOBXLsJaOYBRKNRwuHwgfkptxo+n4/R0aPX/nbRxWsJt+c3QBdd3ABebVm7aZr76nuOjA6+f/3hQQjpbOfLpGwfutn545vJZDAM41DWhFgsRi6XO3BVcnl5mUqlcl01Pa9H1FaKzP76lzGifu740Lvxpa7fhy/XtpDza+inJxGJaMfrFL6xzvSvfonJf/UQyQf3pyOr7SLyyxfQHj2F6On8N14J9Pb24vf793ndTdOk0WggbZfaXAmkIjAaBUsS9odInx4k3p/E57u8cug4DrlcjlqtRj6f36dqEUIQiUQYHh5GrzrYn3gRuVnCfPwE2mTvoQ5Mg287RvF3voQzn0Wb7CP95HmK44d/LXO5HErXsIMm/oqF/Wg/1pMbBDsQAaBTKLyPQuF9+7YYhnGkwVo9nEasVtGe3GTkAw9imiaFQqFVF7q9vd3y2KuAgTUVx5qKgy2JNwxS8RhyIYe/fwAzHWVna5tcLkcqlUIpxdzcHM78NuJ/ZFHf1x5+Nzw8zODgYEcbQzAYPJQCSkVNT5a/B9FolOHhYRYWFqjVagghqNVq+Hy+Q+1HXSFYXq5R+tQy1oUcyUf66fmpe9ETB6uZ0uk0qVSqte+TUqKUar3v2qBrEPN5P3vQ29vLwI/c7f1fSiHLFk6ujpur4ebrOIU69Us7uLk6Tr6Om6+BEG3kwF6ywNg9r0XapexCCETIRAuZcIi6V+VIT01QtlB7CAJZamBvVy+rEHYJBQSXsw32EARa1N9SILTIhJDvNRc6+0qqE2TNxinWsTbLuLMLyJ2XkQ0HZRpIXQdd957Tg9QJAaNld4iYklpUwnbdqy7167s/Wus1mJmZ4fjx4237zybGxsZ4+eWXD9y/qICBO+QdQ+Qe7OHY+x/EXSt6AYQvb1L/5EUAr7KwGUQ46KkdnMUcpV/7PP63ThH69rPtCghnAdwZ0AbAOH2kIFMpJfPz8y3y2DCMI4XNxuPxV/34r4suXmvoEgFdvO5wM1Ourwe6rl//Y7jC96/d20v0xx4gPthDOBxmY2ODcrlMKpWiv7+fWq2272BZ0zR2dnYOVaHY9CBeDU1mPhqNvuqS01cLSim2/n6a5T99geH3n6XvW45f93OhlELNLqOyRfR7TiCCnQeW3FPLzP72Vzn+E48Ru7N/33aVLeF+6TzawyfQ+m5gyewmIRqNcubMGdbX171BWUpUzaW8WcDJNvD3BdHrgtGxMeIP7q9EbKKZWbEXTXIgGo0SCARQjsR5ZoHGM4vo94zgf/cdR/JRC79B8JtPUf34y0Q++DCmaTIcSrBSPTioDjzJ6NbWVut8PeonUGpQv7cH69MryJ06Ws/h7TTlcpm+vj5SqdThPPhCIL81w3Ajhiw0mM57xMvW1hbhcJj+/v7W32o0GliWheu6aH6DwTtPsLOzg9k3RG4tT/2z38BcLGH4dHZGIliZCG7KDydi8Nk12KhB/2VyZG1tjampKYaGhrBtm2g0iuM4hEIhhBCsrq5SKBSu/vjDphe0JxVonqJhcHCQ+fn5FuGjlCKfzzM5OdkKmczn8/tWBZVSVF/Okf3UMtZWjeTbhxn8vuOk/IKwLshJl6rwmgOEEJimJ5nv7+/HMAxmZmbaglOPgkAg0GZ5EUKgR/3oUT+Mdv4sNlf2m6SAm6/j5OpYSwWcb2zg5uu4hTqq4bRIAj0exEgG9ikN9Jj/QPm5MDT0WAA9du33oVIKLPeyomCvTSFXw17M7+Yb7G6v2t7gekWGQZNEEFeQCCJ4e4YiHhU3ok5QxVoreNBdzoKmo3qikIyg4iGUo9rVCXUHu1hGqzlEtAblsyHkJ5dhqQINFxoSBODXEU8Mc3HlOZIvWp7q4IqsBF/QoS5t77jCr4NPg4De+r352riui9A1jIynBODh3fdr/nIIof2NVdxsFX0wRvbTs9Rmc8TzFnK9RPgHH/CIqspvQ+Nv8B4gYJ6F6M+DOJy8f2lpiVQq1dq/RCIRGo0GwWCwjexQSlGv1/cd+wwODr4mwg+76OJ2QjcssIvXHdbX19ne3n7V7n90dJRCoXDVg2IhBFNTU0gpqZWq1GZ3KH1mDnehSPBto8QeGSWUjhHYlfcVi8VWVWETfX19+Hw+lpeXW5c1+9MPW/sVjUbp6+u7aphbNBqlXq+jlOLUqVOHfBZeP7ByNeZ/5ynsXJ3Jf/MIwcz1rzgox0WenwMp0U5PIg5QdWx/bo6F//IsJ3/6cSLH9yesq3wF9/Mvod1/DG04dd2P52bDtRy2v7bKxpcWyG1lCZ5OEByN0Xd8kHSm76bULrlz29ifu4hFhqziAAAgAElEQVTWE8Z4/ARa/PpUGUopKn/2LMZoErPfj9ousTOZYHt7u7WKFgwGSSY90iKRSKBpGrVarfV5MWo2PQs5Nk6mafzDCtgS/3uPJiU1TZOpqSlmZmYO1a4QCAQYHR5h7qc+gf0do5Bq9zQ0V8V8Ph8+nw/btnEcB9d128NGvScBfaeOb7mMuVRGOAo7E8HKWTi2hPe0/y+maZJIJPD5fOTzeXRdp16vYxgGIyMjLC4uXlMZYP7+Rez3T9A3NUw8Hmd7e7ujhck0zZY1ob/fI8JWVlZoVOsUv75F7tPLICD5zgyx+9IIw5P29/b2EgwGqW5uUN3apGCYDI2OYRgGUkrK5TIbGxvXbXEQQnD69OlbViEmLbeNKHDznsrA2SUK3FwNt2KjR33oictKAj0ZwEjsIQviAW9wvYlQSu0JRWzsIRDawxCb+QfKdtFC7SoD0YlEaOYeXGdLwGsFSinUTtlrI1jNodYLiEQIbTiJGE4h+mP7CM2NjY028lEpBY7aJQVcRMhAaBrDKoneUG2tDgVRo5JQyM+uXSYRLBfqrheU6dPhZAz93jSpbzQOVCe01AuaQBVrrP2f/0Aj2wAhCERNoidSpH6hD8P/SyDSIDRP1ag2IPjPIPR913xudnZ2WFtbI51O09vbS6PRoFarUSgUGBsba7N7appGIBBA13VPxeQ4DAwMdG2MXXRxALqtAV28oVCr1Zidnb0hL+uNIJlMkkgkmJubO/A6QiomMuOEUlG2//48ZiZG5HgfDcfCNE2y2Sy1Wo1qtXrgQJ9MJkmlUm1DfLNqcGlp6dDBXuPj45TL5Y7kSXNImZ2dbfmE30hftrmnlpn/3a+RfuckQ9979rpqAZtQ9QbypRmIhdGmRhAHDBIbn7jIyl+8xKmffTuh0f3PtSpWcT/3Itq9k2gjnXMFXklcHv4X2X5mhdhkiv7Hxuh/dBRf/OaFTcp8Fefzl5DZCubbT6CP3/j/7uaqlH//q4R/8E2oL53DeM+bEP5rhz62KqaUou/8FtnJFFZdUv2tlwj/2J2II7YQZDIZarVaRy9sLBZDStnaFzTzP1Y+8Q3E13eQ3z/lrfQdgGAwSDgcplgsXl1qrxRa0cK3VMacL6E/v4P95gGsqRj2YPiaDQRNif/W1haFQoHe3l5qtRqlUgmfz9dSc2grVYxMDFdTZLNZBgYGmJ6eviZxmYgm6O/r4/yfPcPqM4v0vCuDfyra8vdPTk4ipWR7e5tKpUImkyEUCKBpGqVclsW19SPJlA/C1XzZrxSUI3GLDZxdG4Kbr+Pka7i55u/1Vm5BW2ZBMoCe2Hs+iHbE6syjPU63jSy4rC5oJxGa54WhtTIM9ochXkEahHyI663KvE2gXInaKKJWssiVHCpXQfTFLhMDPRGEJlhbWzuUT35iYqItQLBarTI7O9v5vqUCS4JS+A0fI/5eZLmBW7WQFdt7raqeBUJWLS+nYle1UPjMDNKWKADpqVBOfCRLYPAroO1Rc6kKaL2Q+H+u+rjL5TLz8/Ot8z09PRSLRWzbJhKJkE6nOx5P6breUkd20UUXB6NLBHTxhkK9Xt8XfvdKY3R0lEaj0R4a2PT9v5iD857vf/In3sHa5jo110IIQTgcptFoHGpl8PTp08zOztJoNNouj8Vi9PX1sby8fKjWgHA4zNDQEJcuXdq37UqSwOfzceLE/tT61xvcms3iHzxD8aVNJn/0YaKn09e+0VWgimXcc7NoIwOIofSBctmVv3iJrU/OcOrn3k5gYL/nX5VqHglw5xja+PVVFd4MdBr+B94yTt8jIzd1+AdvmHCeXsB9fgnjvjH0+0Zvqk+5/sU5nIUsgckIoieKfuJwCdGlUonFxUX8uSq6Lamkw9T/fAZtOIzvsYObEjrB5/MxOTnJ3Nxc2+d5cHCQcDiM4zgEg0Fc10UpRblcZm11Fe3vVsBVyPdkbsqQuxfiYwv4XIkZNTF26jj9QayRCPZwBOXvvHJrmiajo6P4/f62AELbtimVSlSrVbSvbSP7/BQT3rHH0NAQruseGLBq5xvkP7dC4csb9Lw5w90ffJRI0vtsNBoN6vU6Pp+Per3O2tpa221TqRSpZJLcpQuY0iWnmTRuYCV/bGyMaPTVy+I4CpRSyJLVTha0EQd7cguuEnCoJ4No4VvfRKCUQjWc9myDAwgDWd4NRQwal/MNmmRBuJ00aOYbCP/tbVNQUqGqFmo566kFlnOoqoVIRxG9UQpRjQ29hlaxMXINNKnAlQhXgVQ4iQB2b4C+HYg7hhdy6UiyRoOdfh+xZzbRqzZCKu82rndaPRaHkI/BRcsj+wwNdM2znpi6l5Fh7J43dNAFi//hizQKNpouCPb4id0/QOLH1tHkfwNtz/eSLIBxAuK/euD/fa3jtcHBQSzL6kiEGIbxhlQpdtHFUdGtD+ziDQMp5VVX4l/Jx9Hqss3v+v5f8nz/nE3C/zwFCT96xI+7A7i0DvAPA5/Ph+u6+0gAgGKxiM/nY3x8nLW1tWv6doPBYMfrxGIxdF1vUwpYloWU8pbJYm8HlF7eYu43v0r0jjRnP/Ru9OD11QI2ITezyJkltJPjaKmD/cNLH36e3FPLnPnld+FL7fdUqkrDswOcGXlVSIDW8P/FBbafXW0N/6d++P6bPvzD7iAzu2sDGIjh/6cPIQ7hez4q/I+MYT2/iksSbXYD7fjgoQaGaDTK6OgoC+48yaU8FcKYbx6g/mfTmI/0I/TDDx3Nmqrx8XFWV1cplUoMDw9jmiazs7NIKRFCYBgGAwMD3udeCOS7htD+dBbxbBZ1334LyY1APdKP9edzND44hnAV5moFc6lM6GtbuCm/RwpkIsjw5c+Hbdtsbm6SSqVaLRJCiDZ1lr6WRZUMeJOn6MjlcgwNDe0jAhqrFbKfXqbyQpbYg32M/dt7MXsCLK4twe68Hw6H8fl8NBqNfYNCMBikr6/PUzNpBgEEKWnTUBp5zUAecSgcHBx8zZAAsJtbEPOjx/ww1vk6Silk1b6CHKhjLeRxnr+cZaBsiR73X2FFaLcl6LHADa3QCyEQARMtYELvIUIRXbnHpmAhKw2vbrFiYS8Vd9UHe4gDV+5TFTTPi5YKwYfm9+oEhfBIyOZAjSN3zytwXNSey9vOu3uv2/xd7vk77ddV9u71FN7AvTuIY+jg8yE3SjC3Q6jSYNSvsfZwP0KAuV1F+g2UJkAXGMUGSMVGf4iaA8OxPtA10oZGrbBF8YF+tKoDukBpArXb0qJ0gdA0Au87fOVe4C9fJlioEH98gtB33oM2EAN3GQp/BbIIIgrUgRoEv2vf7aWULbXQ1ZQOuq4Ti8UOPKbrhhh30cWNo0sEdPG6gZSStbW1I6XM3goMDw9j6gbzf/ssPJ+FbANOxeG9IzAYbFu5c133uloGAoHAVb24TZ9zKBS6JhEQi8U6Vr/19PS0eRObyOfzpFK3jy/9ZkE6ktU/f5GtT80w/sH7ST58/bWAsLvCtbCG3NhBv/M4ItI5MElJydzvfo3qTJYzv/wEZocuclWzPCXAiSG0qaOtNt8I3IbD9tf3DP9TPQw8NsapDz5wS4b/JmSuiv25C6hSHfOJ0+ijt+79JnSN0HtOU/nv3yB0LIzKlRGpww180WgUTdcQSiFciZ4JI2I+3HM5jDuP9pjz+TyNRoPx8XGWlpYIh8NtdX1KKWzbRtf1y4ohU0N+2wj6n83iDgRh6HChXIdCb8D7OV9AnU1iTcSwJmL8+od+jZFcDz8Q/iaCL+zghk3skQhfWD/HRz7xV/zBH/wBrutSr9f51Kc+xXPPPeeFFJomPT093Bub4i3j9xLEIwLq9TqmafLCCy/we7/3e9w1dgffGn4LjeUyiceH6PuZ+9HDncm4SqXSqkjbC03TGBkZYWVlpbVvrWs660IjJl0GXIuCZlDZDRO8FlKpFD09N5douR0gxJ5E/eGDs09kw2knC3I1nI0y9QvbLaWBrNpeYGJLSbAn5DB+WW1wrRwApbyV7rYhujVItw/gzcFcc1w0V6J8CjQdgj5wDZQb8Lzwrtz1ztuoqo0qlHDXbZya4yX/Nxxk3UVZLspR3n3oGppf93zzAa/6TwvtBvGFTETI16ppFGHT8/b7dITh81bU24Z6b7AXrd81hK63rcCjiasSkEopyFfJLG4yFy8RWiuhlRpYPUEaPUGsZMAb7oGioTAiLkNDnmR+sB5menoaN975uVdKHYngH/jJtyJ0HW0sdfkx6xmI/iJUfgvcRRBJCP8Y+B4BvGOdtbW1fVlHB0HXdSYmJsjn8wceH62srHDixInX9cJEF13canSJgC5eF5ifnz/0avotgythtkRj0yD6wARBy6D6UC9MRr0v+g6oVqukUqnWwf1hKriauFY6bqlUYnJykp2dHSzLapPpBgIBbNum0Wi0ZLV7V+4CgQA+n8/zQV+BbDb7uiMCasu7tYDx3VrAQ/R7Xw3KlciL89Cw0O89hfB1HmSk4zLz61/BztU4/e/f2VF9oOq2RwJM9qMdUrZ+I3i1hn8AZTk4T8/jvrCC8cA4+j0jB6aj30wY4ynMqV6cSgVtdgMOSQRIKZFKoQT4Kxb1WADfY/1YX9w4MhEAXr6JbdsMDAx0DLQLBoP4/f72fV3Sj/ymYfSPLeL+wDEI3byvdXV/D+IfN1B3JC4PzJrATQaoPjJAVSqMzRrmcpng89uYaxUCq1VKSYdf/dVfpdHI8r3fG+XsHVv4AzaLC2U+99dlvvx8g3d8y5R3H0pRyOd56vNf4T7nBF/9zFO898e/mYkfOo12neFxoVCoZUdo+3+EoKAbVJRGynUI45LTDWxx8HssHo8zNHTrP3e3E5Ty5ObNAVw4Et0n0FN+fDETNRQG1728qu1I1C5Z4BTruIUG7loe60KDWsnCLTVwy57fXDM09ICOFtC9U5+O7tfQDYHm09FM77RtZVwXHoGg75GuG7vnzV3ZevO6hoYIGHuuIxCGjm5cKXHfc1tDA333urvfg6rmtGoXm1WLXghiA7epQtgse9vqTosUaCkMrsw1CO8SCWHPpnBUCCEgGSaUnCC6uEj2QQ2jUCewUyMyl8d8voEd89PoCVLvDZFVWUzTJJ1OEwgEMDQdWakjjV3J/xU4f/48J06cOFTqvjF1gCLNvAfi/xlPDRBoI9kWFhYOnVsEXgZSvV4/0DIEXpvM4uIi4+Pjh/67XXTRRTu6REAXr3nUarVXjwTY5/v3s33Wob5mMvJP7+fSpUtXZb93dnbo7e0lkUh4AWArK60e8KuhWCzS399POBzuuCIGntx4a2uLTCbD7Ows6XQa0zRb1TvNoaJerzM0NEQ8Hmd9fZ16vU4mk+moEgBvBe/1Yg9QSrH5t5dY+ciLDH/fnfS9+9gN+0iVZXuhgEE/2p0nDhxkpeVw6Ve+CEJw6mfehubbvztWDRv38y8hRnrRTmdu6HFdDW3D/zOrxI69csM/7K5IXdrE/sIltOEE/g88jIjsV0bcSgSeOEHpt/8RXdlo90wcqo6wXq+TTqeJZ0Y9n65PR42Noe6pYQ5F0Hw6tVoN13UJBoNomoZlWa0VOCkllUqFcrnc2k80P5udlDx9fX1sbm7uIwjUsRjy/2fvzcMkPcvz3t/7bbVvXd3V1XtP9/Sskka7hIQkhAXI2AEjx1iARXDISbBDOMYxPsfHSWxfdoyT4+DYgA+xHYcEbGxjjIMwwTEgoQVJIGmENPv0vlQvVb3VXvUt7/mjuqu7p6u3mZ6Zbql+1zXX9FR9tfVU1fc+93s/9zOZR/n6GM4/7obdClHrCcB3JmE8Dx017NqKwIp7seJecmYca6jiePrbx/8nxelBPvvZNA2tKpYSQqLS0pLjnjuS5F6BKSyckmDx+WkGzpxkaHyYf/WzHyHzvOSiNkar3nNFT32z/CNLKMyoOj7p0GSb5IRKWlGRl3z2W1parqsTQDoVG/ra3fHKLvg62/pyYb6qOF++7dpd9VW2ddsB01naZb/kWEGlmK7VJ76mqF4pzFVNQW3yQtxf81ipKjgFCztXEQXsbBk7U/lTzpQqAYiTRYSmVCYgRAxU79ppCFpkKbfAe/VyC4QQCK9eGYnXtI02BcvByZfX5hssiQhmKr+Sb7AkKCBYyTbwrZ2qsJxxUBUTvMa6TJT29nbO585jhd1kw26yvRGE5WAsFDFmC4RPJ7HdGjM3OojROYxYiNgcFAbmWLixEco2cnmihOPgTS2iZwvMZks0334CruTcLgSwXkjfTl7RasLhMIlEYsvjstksuVxuTUjitSSbzVaElvrYwjr7lPo7t86+53JnQV8Rm/T9+3w+WlpbkVLi9/tr7qovY5om5XKZUChELpfb0ckynU7j9XprCgGqqhKLxZBSoqoqbW1taJqGaZrrxg02NjaiKAqDg4N0dnZiWRZTU1ObthSMj48Tj8fXzPbdb5TnCgx99gWsdImjn3wIzybW2O0is3ns0wMoLY2IjviGC1UrX+bCbz2FEfXQ83/ejVKj6JSmhf3UGURzCOX4lbUp1OJ6F//LOLM5zCfPQ76M/vBx1PbIVX28xcVF/vzP/5wXX3yRubk5fD4fXV1d3H///fzB138XOZtB+ZMgwrdeiHjf+97HQw89xIc//GGgIkK6XC46W9t47J6HaHngdoSi0NrazOjjryLvaMDj8aCqKrlcrtoLv5x0r6oqkUiEtrY2crkcmUwGKWXNcXqKouD1etePAFxC3tuM+OthxLMzyPt2KUVbiEr2wEup2kLApccaCjM+k6dfeJIH3z1DuKEBOaujmRbSLXHcXkzdi6/7hyiv/g/6/+gYnp4gp7xD3Hz7LfS89Qh3ybt44okneOCBB3bnNWzyfHNCpSAUwo5F3C4zp2iUFBUhBN3d3fh8vqVxbasL7FUFeLXHW4JtrxTRq3vB11nZlwv3jXvMN+sbF6vt5Mu73qtD3rSVHW/h1tcU7NVd9DW76mL9/WrKhlNNrjbrcguWAg7LwwuVyQiLRez5ItJyqmMSV09D0JZaEtSwBzXouiaTBYSmoAYrOQnbeX2U7ZoBiPZ8AXN0YdV0hTJO3qy0JVwydrHdpzPrtckGHETGAikp+SuOgIwQKGUbLVdmxu0gJvNIx8Y5FsX/chKzJ0g56gYpaXnhDO75DMKRyNPDyJEZxHt+BC6zsM1kMiwuLmKaZnXdkclkttUOsIx7adrHdh0ELte1FY2XWR556Pf7666EOvuWuhBQZ1+TyWQYGRm5Ng9WtCq7/qcWCPXGaPngfZXgnaV1xvIOlKqqzM/P09jYSDAY3FQIEEIQi8UYGBjYcU5ALperFhDLJ0y3243P5yMajZLJZDBNk2w2i23bKIqyrri/NK37/Pnz23rsdDpNOp3myJEj+1IJn3tujJE/epGmtx+k9aeOX9FYwGWc2QWcCyMoBztRmjYuZs10kXO//iT+vga6P3JHTbFAWjb202cQDX6UE927tvO1XPxPPT3M7MnJ61b8A8iShfXCEPaZSbS7DqCeaLsmxccnP/lJSqUSH/vYx2hpaWFxcZFTp07hcrn4wt/+JbnPP4/uE3zbP8e3vvUtPvWpT1Vv6/F4qp/n3/iN36BUKpFOp/na177GJ//LZ/i/Wn+NcFszTnMzuZdnEF06pVAl0FPXK20f+Xx+TY7J7OwsqqoSCATw+/0EAoGaxb7P59t0nCiKwPnxDtQv9OO0epC9Vy5sAXBjpCIuLJYhtLnwp6oqTU1NZDJDtLRIbG8QvCBsyb/5f/oZHS6AJTl2QOUTv/gtSj//HrT2MC//+l/ysY99DMuyuOWWW/irv/orRkdH6ezsrNzxklVd2BLhrCSeVxLQnZXr7Mq/9QZQvCG8F+dXHbuSsC6stbd1bEm2yYN5MEJofIHopIXy3SQFq3L9SoGt1NwdX2tjv+RYXUV4dtg3vnzZFn3jr0cuK7dgvjI60VzOLZgvYC0U1+YWRC4JOFwOPgy5tswt2O3Xh0tDdWmo0a0zPaSUq0IR105RiE6DZ7RM8qCG/tQk6li+Iia5VaRXQ3pUVI8GHg3v10dwfBq5Dx9GHc4SvDiPjIN7Lo3lcVV28qXEGplAPzsIN+58OlChUGBkZITe3l4SiQQXLlzY9HiXy4VlWetyncLh8LackctMT0/venBgLpcjkUjQ0dGx4bjQZddkLpdjeHiYWCyG17uLOS116lwD9t8Kvk6dVRQKBbxeLx6Ph7m5uU3toJfFUt8/pxdgKAvdfrirEe3OLtKFbHV3b/VizXEcbNumoaGBcDjMxMTEuufl9XoJBoOEQqGt53tvQDabZWJigo6ODrLZLJqm4XK5yOVyjI2N7Shv4HKxLGtfCQF23mTkT14iezZF3/99H/7DVz6LXkqJnJjBGZ9GPX4QEdx457Q8m+fsr32HyJ3tdDx2orYIYDvYz5xF+D0ot/ZccSFwafEf6ovSfG8XRz9y5zUv/qHy+7LPTWE904/SFcX12F01d9+vBrlcjtOnT/Obv/mbnDhxAqjY7fv6+qrHBN//Zsp/+iRuTaIoCpHIWlFnWQjweDwYhkEgEOB973sfv/7iKwy88iq3tb2tMpLtaJji8zO43lFp6TBNk3Q6TXd3N1JW7nt6eppMJoNt2ywsLGy6+HW5XDWnhKzBq2H/o07Uvx3Bfr8bwrvg2DFU5I0ReHkWHmzZ8LBlx8LMzAyOk8KRq95bJZtffLSRQsbkb55IM5cy8RgF2p44yQ9HcpDMcnNDN9m/fRUvcLfRzg//+Gvcetc7EbZT2a1URDXlXCoKUhUrCejq8nWVyzXdg7AlStGuXi8NbeVndSUx3dEV7EClUG8NRwk2NkFfGhGNQkNDpXh/gxXj+wHFpaE0+9Gb/RseIy0He3El4HA57LA0vFARC+aL2JkSikdfCTiMeNBCK9MQlkcrKpfR178bCCEQvkrrADVeawAojoyQeVjDhEqmQ8GGgoXI24iChVgsU0qbKBkTz6deo/gzfWSDBl1zSRxNXenlFwJHUWBw/LKEgMHBQaDyPRsOhzdcg0QiEeLxeHX9UCwWyWQy1RHKHo+HgYGBbT/u/Pw8hUKBnp6emi2Lk5OTlEol4vH4hkX9pccvTzOYmJigt7d33THLLV6wMvGpVCpx+PDhbT/vOnX2AvtnBV+nzhKO47CwsMD09DS2bWMYBn6/vzqy6tKAqB1To++fG8LwcBu4Kx8ZB0kwGERRFGZnZ2ue8FKpFJFIhK6uLkZGRqo2/d7eXmzbJp1OMzQ0dFkiwDLZbJaBgQECgQCqqjI2NrYjC96Vcr0nNOyEzNkkg7//PMEbmzn+ew+juq/86086Dk7/KGTylVBA18aFV3Eyw9lf+w7N7zhI60/WHtUkHQfn2XMIl45yx+XnFdgli9SLE0w9M8LsK5OEDl7f4n8ZJ5nBfOI8mDbGj92I0hq+po/vdrtxu918//vf59ixYzVbW7R4ELMnjPXq10HOVb4Pavw/lMtl3G437e3tlRaBaIhQdxu9vb0YhoF2UwTzU8MYD7Yglvpxp6am8Pv9WJaF2+1e2j3f3veVYRjbE/davTh3N6F8bRTn/T2VneUr5dYo4r/3I++NbTixxOVyoWna0rQSjUTCrF6nFhxaGzTsHj++H+SYnTWxgTm3xj/MnKPkVXnvI+/FyZexqeivhqrzZm5D97hAX9pZN9RKwJuhIHSlktKuK2AoCF2AAcIQBKSCVwgWdK1y/PIxxqrb6ErVNu71eunq6qqOfJXlRmRyGqbGoakZtlE81Nl7CE1Bi3rRNtl5l47ETpcq7oLFlVYE81yyOk7RXqjkFlRzCpYzCyLLExKWxIKrmFuwGW1tbZw7d67yD1VB+hXw6yxvP0jTxvrjcyChkDOZ+q0Xaf7tu8gLhYhuUFj6HChCoEkHAjvvt7csq1oYp1Ipurq6aG9vJ5FIVDdrLMvC5XIRCASqLsjl4j8QCCClZHZ2llwut+N1TLFYXBd46DgOw8PDVcdkf38/iqJgGAa6rmMYRvUcsLyBc+nGzEZBobVE2+o0lzp19hF1IaDOvuP8+fNrCtByuczIyAh+v594PE57e/tlWe3X9P0DHA/DBw/W3FXL5/Nks9mq6l1rYTwzM8PMzAxtbW0cPHgQx3HQdZ2FhYUNg/guB8uyavYUX210XcfjubJ0/WuBYzkk/uI1kt8ZovsjtxO5c3dC96Rp4ZwZBE1Fuflwxda7AfmRBc79xhO0vfcGmh/uq3mMdCTOcxdAFSh39e14Qbmm+N8DO/+rkSUT67lB7PPTaG/qQb2h7Zr07l6Kqqp8/OMf59Of/jTf/OY36enp4dixY9x7770rOznSwv3u/4aW+XvkRBnkfwXxz9bdl9frpVwuMzY2xpe+9CVKpRI9RZ3E2DhSEZgeULv9WCdn0e+qpGw7jlN1FIRCoR2JlpqmbTsPRd4SRSQKKP+QwHm4bVsj8jYlZCA7fXBqgebmZk6fPo2Usvoe1XWdRCJBOBxGCMGtt97C0089wXveY9LUaCCkwHGpCJ+G0uBGzBRxvGEWf+wE53/493zosX9K0B9AnS+hT+bQJ/P8x//9BUZ6F7j1gXuxAgbSrvRWS9OBslP523QqI9/KSz/nLOS8g63nkb0W5e8nq7epHlO2wXTQ741j3NGE+MYU5YxkwLiI4lJRXBrCUCs/YyGscyh+H0okiOo1lq7TqscqhopwqSiGhuJe+nv5fnZDhKlzVRGKQFsabbgRa3ILltoO7Pki5aEF8guFqlhQzS0IrxUItPBKhsHVyC3QNA23210zY8jKmuTPzZGRNvMji5QkIATqN4YJfeggkRcX8SsquAwolkETcGLnu9qr+/kty2JwcJD29naOHj1KPp8nn8/j8XgQQjA4OFhdwy3vpu9W4HOxWMTv9+M4DhcvXlxXnDuOQ7FY3FYeU2tr64ZrnFpOyLpzqM5+pC4E1Nl3bGT/z2az9Pf309jYSEdHR3Uut8fjwXGcqtVrDav6/oT+Sk0AACAASURBVJkrwZEQ/HgHtHg2XDyrqkpPTw8LCwukUqkNU/uXmZiYwOv1VhXn14NqrKoqfX19e35yQGFskcH//Dx6g5sbPvUw+iaLvZ0g80Wc0/2IaBhxoG3TBUD2Qorz//4puj58K433d9e+Pylxvn8Baduo9x7ddq98zeL/zXuj+IelNoAzk1jPDqD0NOL64N2VfunryD333MPtt9/OmTNnOHfuHC+99BJf/epXeeyxx3jve98LjCKMc0AYWUginS8hlPVCwCc+8Qny+TymaRIMBnn/Bz5AUyRKLrlIcel3b9wTp/i3w2h3Nq15jwghCIVCO7K/2ra9/TYcIXDe3obyZwOI1+aRN+3CuM/bGhHfHOe+n3gzTz31FF/+8pe555570HWdkZERnnzyST74wQ8C8PDD/5KRkWf51V89z/sf7aRbt/A0GYyfn+PUqSwRv0n6wkNcGBnE5XKtzAJvB24EpORG5yJPXzjJ/c3HUHIW5TYfZocfs9O/pcvB5fOhNHnwfrC26Fb5FQm627twnTi+NEO+MkveKVs4JbsyW75s4xRM7NQcMjOHVfIh0XDKNrJkV64vrRwvy3bl56X7AlYEA1fF0aAYKopbWysiLP1cFRDWXLbyt3CtFSGEXm9buBbsNLdgObPAXihiTmUpnk0uXV7EKVRyC5YzC1aEgqXcgkglAHGnIlJDQwOJRAJpORQG0+TOzZM7N085WcB7MIRzcwN2qoDuVog90kvzew9iCsHQLb3E+xP48iVELAr33QrRnTu1Li2spZSMjY2hKMpVdSl2dXURCKwf9zoyMnJFa61IJLLpmORgMLhuqkH9s1hnP1IXAursK5ZH123G7Oxs1XobCAQwTRNd1wmFQpVesUIRp38RXpuH4ZW+f3oClZCmLRBC4DgOk5OT237eO5mfux9oadm4V3gvIKVk5u8uMPHl07S//yaa3t67aydpOZ/GPjeEcqANJb55xsDiq1P0/+6z9Pyru4ncUTvMSEqJ82I/smCi3n9sw3GDy2xY/P/cnRjbSK2+VjjT6UobAGC86wRKfJfC63YBwzC4+eabufnmm3n00Uf5gz/4A770pS/xyCOPoKlRwEBEJEK3sKea0GqYSD70oQ8RCoXwer3V0VXFZA53plQVApRuP8JQsM8voh1ZWVwHAgGKxeKOFqq6ru+sFcdQcN7VifoXg9gxD8Sv0L3T7gVdoTHt4hd+4Rd4/PHH+cxnPoNlWXR3d/PRj36Ujo7KdAuPp4Vf+IX/yAvP/wZf//ook0MWuFXaGuGOe9y87aYH0UffxfPPf3FFBFiNEJy45w4+/dLzXLzVTYuvAX0ii/vcPL7vTWHGvRVRoNWHdO086E3TNA4ePLgirGzcZl5FFgrI1DSoGqIphtC3FrSk5awICqsFg41EhKKFmSusiAklG7l8zCqhYllwkJazIi6sdjO4V4kIS26FNeKC+xJxYdXtl69fdj5cD+fOfmVbuQWmjb1YWmo7WJVbMDRfySxYWMot8OprXQWhtZkFy7kFUkpy44ssvjyJFS2R+vtRiqNZfEfCxN7Tg+dAEKEplKfzpH+QpOWxw0TftjKFphgNMRwNIYTg6NGjly3ubyRSXk0RQNf1miKAbdvVDRohBLqu43K5UFUVRVGqf4QQlMtl8vl81UHqcrkIh8M0Nm5+btc0DSHEmpDo7eQP1Kmz16gLAXX2FaOjo1seI6VkYSwJXxmGR7ogaICURBQfnd3tqIZKKZxlTLlA+UdX+v53gqIoO7Lqvt5YPYIQqJ5Y4/E44fC17fu+lPJcgaFPP4+dNzn2ybfhbl2/ULhcnMkkzvAk6tEeRHjz+517YZyhz75A3yfeTPDG2uPcpJQ4J4eQ6QLqA8c3FAH2S/EPIAsm1vcGsPtn0O49iHq8Zc/vlHR2dmLbNuVyGc0bAuX3EeJXQNPJf/VRfO/LoTau7Zt1uVw0NTWtuawUcOFP5aq5AkII9HuaMb83vUYIWO6V1XV9W2KAqqprJhZsm6gL56FW1K+NYj/WC54rOOULgby9EfHiLF0/fYCPfvSj1ataWlowTZNUKrVyuHUrj77lv/PuO7+MO/g0olFBGY+SMt9DevBGXIqL3/uP/4Gx0VEK9vpi4fDhw3zmM58BwAFKhyOUDkcQRRs9kcUYzeD9wQxW1I3Z4afc7kN69VVPt/Z7TlGU2uLDVi/f44H2LliYR46PQrgBwpFN39tCU1A1A/UqjTiXjlwjIqwRF5ZdC8tCxNL1VqaETOXXOh/WCBSrbl+2EZqyys2wtv1BrBIaFJe6TkTYsH1itcvhDdY+IXQVrdGL1rid3IJC1UlgLxQxzyax5ouYyRyF0QXK6RLFbAmpqXi6w/hORFF/ogeRMSvTLgJ6ZTwkYDR7OfLp+9BCVyeY1e/fhpq2y2xk21/t/rwScWMrXC4XxWIRXdd3HBLoOE41Z6ZOnetJXQios2+wLGt7ff95C/74PIxkodULPg1OLzAPyJ8sETgWJ6cU6HnnrUxMTOw4XNCyLFKpFL29vQwODr4urP5XiuM41RDHYDDI5OQkHo+HcDh8TdsH5r43ysgfvUTsR/to/cdb765vFyklcnAcOZdGvfkQwrP5yTv5xBCjnz/J4X/7Fvx90Q3v03l1BDmbqYgA2tqdTatoknoxwfSze7/4h6XF66kJrOcGUQ814/onb6rMMd9DZDIZfud3foeHHnqIAwcO4PF4uHjxIl/5ylc4ceLEyugncTMo/xyhfR3j9lsofOMsvsduqxZ9lmXV3OmyXCoI0IoWlqfy2rWbGij//Tj2VB41Xrn/fD7P7OwsnZ2d22oPMAzjsr9n5OEQTiKP8o1xnEe6riwv4EgInpyCVBEaK+9BTdMIhULVxHAAI1emZbaI0Rpn+JvvRLb9FNwSJXB+aYEe9mBNmJQdh4jLQC1bZLebf+BWKfeEKPeEKr3+kzmM8SyeV1PYfgOzw484ZkBs/W2FEJclAqy+PZEG8AeQqRkYS0NTc0UkuA4IRaB6dPDoENr9+5dSIk1nvVhwqcuhbCGX3Ap23sRZKK4/dkmIqLZPlCyckgWIteLCRiLCNtsnFLeKWCVY7Mf2iUtzCxzLZuFskvlXisyOL5BLpGk4FqPhWIz27giGoWIvVgIP8+eyzPWqcGYBnp0BW0JQB7+GFtTBry/9W68IBYHKz01NTVd0rq4VvHq12chtsN3MJMdxKJVKZDIZgsHgjovypqYmxsbGME2TXC5XdYZtRTabZXR0tPr8dV3H7/cTiUTq4wfrXHPqQkCdfUPtgD2JSxsBoGR1QdGBP1oSAco2fHUEfqKz2vdf9Og0BjyM9U9QKBTo6uqiv79/xzv7yWQSVVUJh8Mkk8ldeHWvD0zT5Ny5cziOw/z8PIlEAk3TCAaDNDY2XrXFgpUrM/onL5M9n6LvV3ZnLOAy0rJxzg2B41RCAfXNvzanv3GBib8+zdHffCvezo3dEc6ZMeTUPOpbbkAYlfvcb8X/Ms7kYqUNQFMwHrkFpWn3XBi7idvt5vDhwzz++OMkEglM0yQajfLAAw/w0z/90zVv47qzg/KrCcxTUxg3VlpiNkzvF4JiwIU7UyK7JAQIVUG/O4b5vWnURw5UD02lUkSj0S1dAaqq0tzcvHM3wCrk/XHEXw4ink8i31SjQt4umoK8pQFemoV3VFpdvF5v1VorgFAqT2Aqjft4J+WRJGKqiHhTM0JVsbsaCF6cx2wOYGRMJILpQokmt4GuCObLOxQ7dAWzM4DZGQBboiULGGNZvC8n0Roa8bySpNzux466QYi17QBXgNB1iLdCLoucnkR6vYho06aBofsRIUS19YCr8JGWUoItKyJBVVxYEhZqiAjL4kK1fWLV9fISYaLSVmEj7V1sn7j0Nkv3tdvtE1JK8hNpUicnmT2ZYP70DL62INFbWjj0T28jfKQRRav9XgsDkUKBAf8A3NlUWQdlzFV/LEiWKmORM1bFMfCBXhb+5ixW5gL66tyC1T9vI7fA5/NtmZm0m9QSAi7NYerv7+fgwYMoikI+n2dubo5isUi5XF5z+3K5THv7zoKEQ6EQyWSSYrHI6OgoR48erfkcp6enyeVy6x5zGdM0mZ+fZ35+HiEEfX1910VYqfPGRGw2d/3222+XL7744jV8OnXq1GZoaKjmCSYa+DNC3u8AsJh/K7O/dAz60xUXgF8DBPzrG6ClorIGAgGampqqu1eNjY00NDQwPT3N4uLijp6Tz+cjFosxNDR0ZS/uDYSmaTQ0NNDY2LhrToHMmRkGf/95Qje30PGzt+zKWMBlZLGEc3oAgj6U3o5NQ/yklCS+cobkPwxw5DcexB3feOXsnBvHGZpBffBGbKhZ/Mfe1LGni38AmS9jPtuPMzyL9uaDqEfi+273bTtY4wvk/uqHBH7uHhSPzqlTpzY81pUuEkjmSPWuOEFkziT3qdfwffxGhH/FJdHd3U0ymdxw8ezz+Whvb6+OS70isibqFwewH26D7iuo6nIm4k8uIP/5YfBURL5QKEQikaAj2ogv2gAIEFRaJKTAEbLigHEclGwJ01AgVURvD7G4uEhyZoaIXilsUsUyG69KtociBH29B0k9d57Sy+PkHmyjdUYlcLgFtTOya04hAOnYyLlZyGYQ0SbwB16Xn4H9irSdqsAgLxEKVosLq10PK2GQW7RPlCyk6Vxe+8QlgoNt2iwMzrFwYZaFczOgKjTe2krj7W1Eb23FCOzM0j8xMbH9aULWUnGqCPSsJJ7zLk1IKK6MUFzOLViVUbAsFiyHHUq/xoWh/h3+D10eiqJUXV2rWZ7WtBpd14lEIusuX017e/tltTValsXY2BiNjY018wqKxSL9/Tv7nQQCAbq6unb8XOrU2QghxEtSyttrXVd3BNTZF9QqGgUlQt5vYzmVZNeQ99vM/egDyGIc0hbMFmG+DNkVdbipqWlNH2sqlSKfz9Pe3o5t2zsaYeM4zp5Pzd9rWJZVPVG73W5aWlq2bae7FMe0mfiLU8w+OUT3z91B+PbaYXyXi0xnsc8MonTEEa1Nmy7upZSM/Y9XmH8xwbFPPoTRsLG9z7mQwDybYC4QYeb3n1sp/u/r3vM7/8tIx8F+dQLrhSHUI3FcH3wTwvX6PZ1o7WH0w00Uv30R748f23BUF0DZ70IfXUDYDnKp4BQ+He3GBszvz2C8deV9alnWhjvUHo+Hjo4OxsfHd2e0ll/H/rEO1MdHsX+mt5Kdcjn4dGRfEH44B3fH8Pv9eDwe+vr6KJeKlSyBTBqZL7L4zfMkxjLwSHf15oGzs0hNUHpmFueneoj1tXOwr49kMomTzdDscZEslrE32aTYCkdKxhITdLz5KP1xHc2SeEMeSk8N4Mzm0A42oh2KofVEq26cy0UoKqIxhvQHkclpSC9W2gXqO3p7AqEqqB6l0kJxFZBSVtwINZwLm7VPWLN5MiMLLA7OkR5ZoDhfwBv14mv00tjgRVMV5LlZZn84zex/Pbmz9gm3hq4ryCYLeyqPzFsIQwVdQRgKGEqlZWLpMjRRPb+ZQYHvzu5130vSdrAzpXUCgZmYWRN8aBxwU35ztDKNabqwtgUhoENAA5e6ZYuS/e0E4sIiyvt7IbTyWRKYRMIjxOMNKGorsFYIWFhYWHdfpmluKAIcOnQIuPzWBk3TOHDgwIbXu91uYrHYpiLEpbzewqXr7G1evyu3Oq8rfD7ful5+iY7jBFCVyuWO40fe2QLUtswtJ91farHN5/NMTk4Sj8d3pNy+kcMCd4NiscjQ0BB9fX24XDvb7SiMLjLwe8/hink5/qmH0Xd5VJ4zM4czMIZyuBulYfPmW+k4DH3uRfKD8xz77YfQN9i5sYomya+9xtQ3zjGfhdDR2L4q/pdxJhYqbQBuHeMf34oSvfYhUdcDz4/0kf7D72GNL9DZ2cmFCxdqHicVQdln4MqWq9MDAIx7min81/Po97dULbYul6vmWFNN0+js7Nw9EWCZDh/OHY0oXxvFebRnyzF8X/jCF3jhhReq//Z6vRw4cID33PejtDw1i/fBLh577DEKhQJSSjxuFy3xOIf6DvGOt9xPPCuhvSL0zc7O8mu/9mv8yj//GCdSHooBHWeuwOTkJHNzczQ3N+NqaCCdStEsBKliibJz+WLAsg3Y4/EQi8Vweb243nQAJ1PCujCDeXKC4tdPo3Y1oB1qQjvYhOK7/OJduN3Q3gmLC8iJMWQohAg3bHsUaJ39iRBiaddfg0127dfY/V+bYv7MDL7WING39XLoltYN7f5r2icuFRY2aZ9wsmVciyWKB9wUvzYCZQdZdsB0kKaz6t820pYIvSIQeH/2MOe/8SSujKjZPlHNYHCpKH4DNepBX2qrELqCkJDNZEgdFTheFTGRh7EyImtWNmXSJkjWCgMBY+nvFcHA+s4EWn8W+4dziPf2oLwljlBLdLX+J/zeUbAVsINg/H8gOqu/r+1mqQghaG9vvyYW/FgshqZp1ZHWW01/2c50mLm5Oaampta0Gng8HuLx+GVvrtR5Y1IXAursC2rvvCtMzn+cxuAXAUilf4aNRIC2tjYMw2B4eLjm9ZlMhsbGRiKRyBo7ndvtplQqUauFxuVyUSqVdvpS6lxCf3//tpN9pZRMf/0Cib8+TcfPnKDxoZ5dteFKKZEjkzjTs6g39iH8mwf3OJbNwO89h7lY4uhvvnXdrlO15/+ZEVLPDhH0KbQ8eivH39q7r4p/AJktYT7TjzM+j35/H0pf7A1lgRZuHc/bDpH/+hkC/8fdhMPhmrtPwFJOQLEqBLS0tKC0KQy0jWO9Ood+ayOapmEYRk1nQTQaJZ1O764IsIS8vRExkUd5cgrnodYtjz98+DAf/OAHgYqI+tWvfpU//uoX+HcHP4CWsrBtm0cffZTjx48TMAwcJN/+7nf5xL/7dX7MexsPffQn19yfFTRQUg5CF4ishQRKpRKjo6P4fD7i8ThISXx+lmQ6U3OiwHZZXFyks7NzTQiYEnBh3NaBcVsHsmhiDaSwzs9Q+tYFlOYA+qEmtMMxlNDOAwCFEBCOgN+PTCWRYyPQFEN46wvzNyLlTIm5H06SenmS2VcqM+ejN7fS+tYebvj4vduy+wshQBOofmOD1c3GtABnzpzB+4G+TY+TtgRrSRhQQL69mbg3Dqas0T5RESKsdAlZym8oRNg3ujFnC5jPTFXbJ9ArTgRUgZIuITJlhJQoDmBLhOUgLIkoO2gjuYpgMFeGz53D/osBIp9fxNAvAEuhpzIJ5u+D8Z+Aiktzs3bnZVpbW2loaNjhb/PKaGhoqD7m1NTUGmdqLTZyiy0uLpJIJGqKBYVCgaGhIRRFIRaLbTkCsU4dqAsBdfYJtXbNAEpWNxNz/2bT27a3t6NpGsPDw5ueJCYnJzlw4ACBQIBSqYTP50PTNBRFwbIsDMMgk8kwNTWFaZq4XK66hWsXkFJiWRaLi4uk0+lqCGMwGFwjDpRn8wx9+gXsgsmx33kb7pbdTa+StoNzYRhKZdRbjiCMza2kdsni4n94BqEIjvy7B1AuDfx7ZoTZVyYJHWokdiRMX/dBPO+8BRHcX6nA0nawXxnD+sEw6g1tuD549xXbqfcr+g1xyicnKH1/jNa7Okin0zXDn4oBF/5kFrfLhcfrJRAIYNs2h//1g8x+px81FCIcDjM3N7fuO0kIQSQSWZPCv6sIgfNwO8qfDSBOzyOPRzY9fHkqAFTCsd761rfyuc99jvIjQaItTTiOQzAIN9wQxUMLms9HW1c3pWyRr/23/8kJ5e00seo9LwTFZi/6YhYnvXb3LpfLMTAwQCQSoTkWpz0YIjkzw0KhdhvGZmxnsS/cOvrxFvTjLZX57iNzmOdnKD03jOJ3VZwCh2MoTf4diV5C0xHxVmQui0xOI92eSpjgLgQV1tm7OJbNwrkUsycTzJ6cJJdIEzkWI3pLKwceOYa3LXjNxdP29vYtxy4LVYBaaS9YZtRKohs6voiP1taOHT/uyMgImUwG90Ntle+41U6E1X+bDrJsVx0KztJl4vMXUCyASr6InTHRxCxIbVVbgQ9IVB/z0rHGG7G4uHjNhYDVxONxMpnMphtJ2Wx2XWbB8PDwtsRhx3GYmppienqaQCCA1+slGAxe9wDCQqGAy+Wqt9TuMepnpTr7ggMHDjA4OEi5XEZRlA3Hxiyj6zrBYJBwOIxpmoyMjGypFBeLRQYGBnC73bhcLpLJJJlMBl3XURSlmjDe29vL9PQ0LpeLubm53XyZb1gutVkvn+w0TSMQCKAMFJn601eJvbOP1p+sjAVcfg/sxklFls1KKKDHhXLjoS3DxKx8mQu/9RRGo5eej92FYznMPDOypvhvfnMXR3/+TrRsHucH/aj3n9h3IoA9Nof5xHmE343x07ejRN7YO5tCCDzvPEr2T7+PcayZnp6emu1EtkvDf8cxwi1RsvkcqVSK+fl5Ghoa8MSD6NK1Yd9qJBKpJkxfNdwqzrs6Uf9qCDvmgabtuVOKxSIvvfQSra2tGMcacbcIhHOalpZhfN7PIcodFIu/xfSM4EcO380/uL7Oq6dP8SPx5rX3E/fjfW2eUra2jXd+fp7FxUViTU20dh8guDDP+PTMlt/7y/h8vh0v9IWuoh2stAhIR2KPL2BdmKHw5VdAEWh9MbRDTajt4W2nxAufHzxe5PxsxR3QEIVg6A3lpHk9I6Ukn8iQejlRSfdftvtvI93/WhEMBi8rzX95tN5ysdraurV7aDWri04hBBiVbAO2eQop/+Ugtm1idwfQf+oAxk1RSspLCOUJkCYV9+cCKG8HKkXmdier5HI5ZmdniUZrj/bdKeVymVKphOM42LaNEIJAILBh/otlWXi9XizL2rANIJPJrBECZmZmduwQk1KSTqdJp9PMzMwQCAQwTZN4PH7NxxQmEonqermhoYF4PF4XBPYIdSGgzr5A0zQOHTrE7Owsi4uLG+7E+/1+YrEYhmGQTqeZnp7e0ZdnuVxetwBf3XOWTCZxuVzVP/XWgKtLOV9iZnAetcmD9vGDzKswf/bMmmNisRix2OWPRJPZPPbpAZSWRkTH1qn3ZrrIuV9/Es+BML6b47z2u8+uK/6Xbf/O1EJFBHjzUURk//TSy0wR86mLOFNp9Af6UHo3D0t8I6E2+jDu7KDw9+fwvfdm2tvb1+1EqaqKqz3G5EunmPetFAKzs7OYQzNY3zyN57Hadl3DMK6N06jJjfOWeCUv4AO94K5dsJw5c4Zf/MVfBCrfj+FwmJ//+Z9H0VSE+jsY7iyK0oG5oKK6hnD7P4HL9SmYBX9DsKYFthxxEwTU+RIbdcM6jsPU9DSzc3N0trRw+NAhpqammN+gHWOZy03/Xo1QBFpnBK0zgvyRQzgzWawLM5T+4TxOtoTW14R+qAm1qwGhb17oCUVBRJtWwgQz6UqY4FIuisznwe2uZwnsE3bD7n+t6erq4uzZs9uyzddibm6OQCBQMxV/I1a341wWP3cENeLC1bXymLnCbSjaR4DPAzYoD4L6EYBNpz7V2jyanJzE7/dvO5/IcRxM06wW736/H0VRNp0KIITA6/XS1NSE379y/l8eFbgZi4uLlEolOjs7Nw073C6aphGLxbh48SKDg4OoqkpDQwNNTU3XpCBf/d6bm5tjYWGBjo6OHb2n6lwd6kJAnX2FqqobLpJ1Xae9vZ2JiYl1wYK7hc/nw+v1MjIyQigU2vYOVZ2dU764SPrP+zGORfC/q6tiX6zBzMwMqVSKtra2qoV5uzizCzgXRlAOdqI0bW6RBihMpHnpY3+HrSnYE4uEkjni93Vx9F/etW4B6CQXcV64gHrPEUR0f5zspOVgnxzFemkE9aZ2XG8/tmWh80bEfe8BMp97DvNCkvChJorF4pqC17Zt5hNTNLS3MD+/dgGn3dJI+VsTOKkiSuP6xfK1nEYij0cQkwWUb47jvLuzZpJ3X18f73vf+4DKTtrTTz/NZz/7WX75l/8llv0POGWNYrqAWvZSMiIIO0kkMsr0WBHp2eC9owjK7T7UV7Ye2WqaJgOjo8QCflo6Oshls5Q3CWnd7YWlEAK1OYDaHMB1Xy/OfB7rYpLSc8M4XzuFdiBamUDQG0W4N24nEi4XtHVAehGZGEcGg+D1I0cHEQ1NiFjzhretc/1YZ/efSBM5fn3t/jtFURQOHjzIxYsXL/s+MpnMjj5boVAIKSXFYpFisYiUEk3Ttr02M25e398uhILq+jDIfwLYIFbOubFYrKboqGkaPp+vplAwOTlJd3f3tp7PpUKKruscPnyYRCKx4W2klORyOXK5HMeOHat+rzc1NaFpGolEYlNxplgsbhhKezmsfp/atk0ymSSZTOJ2u2loaCAcDl+1c09bWxstLS3V9ZrjOIyMjBAMBuns7Nz6DupcNepCQJ19w/T0NMViccNRLO3t7aRSqasmAgghaG1tZWpqCl3X626Aq4Q0HbLfGKX4Uorgo724jm1doDuOw9jYGNPT03R1dW2p8kspkRMzOOPTqMcPIoIb+xWXe/4n/tcFhv/iNaK3tdL3z26j6e6ODXd/5GwG53vnUe46hGgKbvn89wL28Czmk+dRIj6MR+9ACe+vNoZridBVPO88Sv7x0wS7I8TjFSdJMpmsXC8EwufGMDyI5BRyVTq/0BW0O5own5vG9Y/Wz4pWVXVbqdG7hfOWOMpfDCJeTCHvaFp3va7rNDVVLm9qaqKzs5Nf+qVf4plnnuX22+1KCFjOBClx2aCpGsXsItmJHDmnuGFgVak7iP6d7e9yzWSyhMom8YCfqcXFmhMFPB4Pqnp1hSsl4sW4swvjzi6cXBmrP4l5epLi/zqD2h6u5Ar0xVBqfDcIISAUBp8fJzUDg5VFvpxLVaYMuPZXgOjrkf1g978cXC4Xvb29DAwMXNbtdyqwKYpSsz1nenqaZDKJruuEQiEaGxspFouMjY1t+b1XdRkIjUvLF0VRCIVC6wr+Zbt+LXbymlwukwpQBwAAIABJREFU15pgV9M0KZfL1RwpKWVFNFRVpJQ4jrNmoyiZTNLcvCL2RSIRQqEQZ86sdTheLbYSHBKJBIlEAl3XCYfDRKPRDVsbLhdFUYjH4zQ0NDAwMIBt26TTacbGxujo2HkORZ3doS4E1NnzOI7D8PAw+XyexsbGmqNRlk84WyWxXgm6riOlJB6Pk06nN5wjXufyMRM50l+8iBp1E/3ECZTAzmY/l8tlLl68SHd39xor3mqk4+D0j0Imj3rzEYR7fYBONfDv6WFmfziFr9lP4VyKu//fh2l75Nimz0HOZ7GfOYtyx0GU+JVZlK8FTrqA9d2LOKks+gOHUHvqScPbQe+NonWEKT41iOehQzQ3NyOEIJVK0dPTQ7FYZOaZk7gCBsXw2gR6/a4Y+T84jfFQG8KzchqORCIEg8HLXqxfFppSyQv44gB2swc6N29hEaIyc7xUUikWj4MyAgWLctCNz+dgLViY3w3w7flnQRHcdNNNNe+nFPdhmDbGRBa9aFJoC+C4N1+SzM7NEWtuplVVmZ5foHDJAn+zed5XA8VnYJxowzjRhixZWIMprAtJSk/2o0R9FafAoSbU6NpzltA0hMeLRIBtg1PGSYyjdPfu+d3l1yPLdv/Zk5U/Elmx+z/Yww2/cM++m/CyER6Ph66uLkZGRnZ8290aSdfc3LymIIZKS+fRo0eByk712bNna942GNxcVO/o6KCjo4NTp05VL5NS0tTUVLNFdGpqinA4vC3xsLOzk4mJCQqFAo7j0NLSgmEYm+5mO47D5OQk8/Pz1RGpq7l09/1ai8C1ME1zjVPgwIEDuy6uGobB4cOHGR8fJ51Os7i4iGma9PT07Orj1NkedSGgzp4nlUqRz+erI1HGx8fXfWGGQqHqbtzVwuVykU6ncbvdNDY2MjExcVUf742ElJL8k5PkvzWB/11duO+8sp704eHhmqnh0rRwzgyCpqLcfBix6gR3afEfPlzp+e94Rx9D//k5bvjVB2i8v3vz15HOYz99BuW2HpTW65dKvB2kZWO9OIL9yhjqLZ24fvQ4Yh/udF1PPG8/TOZz38O4qQU1FqhmVUxOTpLL5fB5NNyZ0johQAkaaIdDmC8mMe5rASoL5GAwyNDQENYm1verQtDAfmc76jfGsX+mF/wrAtzyRA+oBHJ997vfpVwuc8MNNzA39zbgCYpGgWJxkYW0wasvvpfnvvQVnu9/lfd+6KdoquEIUIoW/sEFVCTBbw6hBDSmGjxbCgFzc3MUi0Xa29tp83qZmZomvZTp4vV6r2v4lHBp6Efj6EfjlUkbI/OVsME/fwlcGvqSKKC0VKzkMr0IigKqApYNiws4yTFU/VtQ7gf/28H3luv2el7PbGb3737P/rD7Xy6BQKDmzvlmCCGu2WdLVVVaW1tJJBIYhkEsFqt+L0YiW7sDYW0mgJQSn8/HoUOH6O/vX7NLL6VkYGCAQ4cObXmfhmHsWGhUFKVqid/oO72pqYlkMomiKPT29qKqKqOjozsOd7waFItFzp07R1dX14YbK5fDuXPnqr8PTdOwLIt8Pk+5XL7ukw3eiNSFgDp7nuVd/mWrVXNzc7XXbHx8HF3XcbvdV+WLczkgx+fzoSgK8/PzlMtlFhcXr1oLwhsNe75E+s/7kZZD5OM3otXom74cEokE5XK5MpcckPkizul+RDSMONCGEKJS/P9gopL2v6r4P/rRuzECLhZ/OEX/7z5Lz8fuJnJH26aPJzMF7O+eRjnRjdK+t3fV7cFUpQ0gFsB4/50owZ3PTK9TmUnvfstB8l8/i/9n70AIQSwWY2hoCIBCwEUoZxHs7MS2bRKJBB6Ph6amJuRH20h8/iSmLWltb8XtdjM4OHj9doS6AzgnGirhgT/dA0uZHOfPn+dXf/VXgYoY2tzczIc//GEOHTqEaRrArfyXL2b57B/msVw+gsEXOGAG+di/+Hnu7OjCOT/LYudKdodWMDHmC4ReS5IzFJyyjVB1LN/23D/5fJ7+/n5aWlpoO9CNNpFgLpvdUzOzhaqg9UTReqLIdxzBSaQxL8xQePwUmE6lfeBQDOVgGwIHLBtZKoL5Fcg8DooX5n4ftFZwbV2k1NmcZbv/cuE/d3q6Yve/uYVDP3sr4SNNKG+gLJS2tjYsy9r2mmm3LeJb0dDQsE7E7+3t3fbtVVVdl99kGAY+n2/duq1cLjMxMUFb2+bn9ytBUZQNC9zm5uZ1gX0HDhwgl8sxOjq6q+eDyxG3pJQbbqxcLqtf0+r/p0wms2uTHOpsH7FZ38jtt98uX3zxxWv4dOrUWUu5XK4ZliKEoKurC8dx8Hq9zMzM7OooP5fLRWtra7X4z+fz9VaAq0Dx5RSZvxnCe38L3ofatj2Waye43W5iHj/e0WmUA2044VDN4v/Snv+5F8YZ+uwL9P3ymwnesHmQl8wVsb9zCuV4B0rP3g39chbyWN+9gDOfR3/wMGpX/aR7pUhHkv3TFzBua8d1SztQWdycP3++EtLV3sX8wjzBpiiWZWEYBtPT0xiGgbekUyjk8baFGR4evv7ho1Ki/M0IssGFfLBly8OFEBw9epSB/n7KnzuFfGsLdPgQf3AW+XNHwKXgm8kRSGQoRD1kYn5aXpmiHDDI+Qw8Xx7CUCVKj5+Jn9h5wRsIBBBAg8vAF2ve88n7Ukqc2RzW+RmsC0mchQLawcZKC0FPFLHw21B8DdQw2EmI/mvwvvl6P+19yUZ2/8ZbWmg4EX/d2P2vhEwmw9jY2JbfO4ZhbGvXfK+wujUA4IYbbgAqwcIbpe8vH7PXyGQyFItFSqUS2Wz2st1iuq7T09PD+fPnL/u5XM6EJsuyUBSlKnTk83mGhoaqmQXLoo2iKPT19V1z0emNghDiJSnl7bWuq//G6+xpDMOoOfpFSsnY2BgtLS0MDw/vWpG+3H4QDod3XVyos4KTt8j89SDWeI7wvziK3nH1RutZi1nGszksxcE8OYA5V0SxBS23tVR3/i8l+cQQo58/yeF/+xb8fZsXyzJfwn7yNMqR1j0rAkjTxvrBMPar42i3daH/+E0IdW8XTfsFoQg8P3aM3BdfQj8cQ/EaVZtnIpFgPjGFy+upOonK5XJ1Jy5c9uCROiPWyPUXAQCEwHlnO+oXBnBavcjDm0/hkFJSKpVQVBV5WyO8NAu6AhGjOo4w1+yn0OAhMJGh7cUJVNNBNW2yMR/5ww1oZ1NV98FOyWQyuF0ufNEG5OI8BMNr2n32GkII1EY/aqMf1709OOki1oUZzJfGKD5+Cv34QYyeHyDcKYTeAK69WZzsRdbY/V+ZIje+SORYjOgtLXT9xFF87aHXrd3/cgkEAhw5coREIsHCJmM599PvbTOnZiwWQ1VVdF1nfHx8b3znbsGlYxtzuRyTk5M7XvNe7ujI1aRSqR0JAY7jcO7cuaqQVEuI8Xq9tLW1rRELYGUTcDedCHVqUxcC6ux54vF4zREttm2vm999pUSjUVwuFxcvXrzuoS2vV8oXF0n/2UVcNzbQ8Es3IYyrs3B3ihY8n2Du5SQzk0WCd7fgOx7BeziE4tbIqjYdNUSAqb+7QOJvznDst34ET8cWhVCxXBEBeuMofa1X5XVcCVJKnP4k5lMXUVpCuD5wFyJQ3wnbbbSWIPpNLRT+9wV8P1Ep3patoDPZRY72dnL23Ll1C895Lc/E772G+709qFdRDNsRHg37XZ2oXxnGbnRDdPMJHMViEY/HQ+F4GPH0FPLsArJ9bbCYo6vkYj5CowvgSJSSReP5FIkuP9m5Iu5WC02bwbKiwM6+D5piMYQ/AIV8RQwIhBD6zkJGrxdK0I1xeyfG7Z3IgonVn6J0IYqcHQL3EbTeNNohF0qo3rpzKTXt/i1L6f4fuuUNZ/e/XBRFob29nUAgwNjYWM1j9pMQkE6nN70+Go1SLpfXfBfvtdeXyWSYm5ujq2v9VBmfz8fBgwexLItEIrHl691NHMchmUwSjUbXZUZYlsXAwACapuHxeNB1vRrQWC6X6e/vryletLe31wwjXBYuEokELpdr18Iq66ynLgTU2fM0NDQwOTm5K4rmVng8HhYXF+siwFVAmg7ZvxuleHJpLODR7QX/7ASnZJM9NUf25STWq0n8nT7Ue9o4cHMj6iU9yLZtr5mNLKUk8denSX57kGO//RDu5s0LM1kysb97GtHViHLk6vUXXi7OfA7zO+chV0Z/+zHUjt3/fddZwfOWg6T/8Fms4Tm07soORiwWIyUUZMmEsoXQVbxe75qFp/unjiKnCuhH1i50ltOprwtxD859zZW8gA/0grGxe0RV1YpdVVOQNzXA80l49/okbW8yBwJsl4piOxg5k4bcIjz0TQL3PU8IQbncweTUr2Db25u2IYQgFKqIdcLjBVVFphfAH9h3o/iER0e/sQX9xpaKg2dotjKB4JlBlLBnJVeg0bfnCpdrRdXu/8oUsycTSEcSvbmF+APdHP/YmzBC++v/fC8RClUcE6OjozWvz2QyqKqKpmnVkXl7kebmZvL5fHW8c63efMMw6OjoYGxsDJfLtafm2DuOw+joKFJKpqamqhlHl6JpGp2dndVd92t1rpienmZ6errScrkU5AgwPz+PaZqYpkmhUFh3u0tFgOXQ7Y0mErhcrkqoqpQMDQ1x6NChepDgVaIuBNTZ80xNTV0TEcDv9+N2u3fdZVBnaSzgFy6iNnmI/vIJlG0Gg22H5eI/czJJ/vwC3i4/7d1efA+fINsegk0WzfPz8wQCAaSUjH7+JIsnJzn22w9hNHg3fUxZtrCfOo2IR1CO7a35t7JsYb0whH16Eu3ObtQT7fU2gGuAcGl43nGE/N+dJfCRNyFUBa/XS7FUpFQocvj4MVAExWJx7aLt3ij2aBY14kNolf8nVVUpl8sb7tBdC+SNEUQij/K/J3B+rH3Dz5Gu6yt9qycaEH85hIytL8jSnSEybUEUy0GxHNSShUd5gWj3E5TtFkDBMEZpbPwTpqd/aVvP0eNZu1MuDBeEwpVEftsGj3dfFs1CV9EPxdAPxSoTCMYWKhMI/uokKALtcAztUAy17fVtd3csm8XzKVJLff5r7P7vPlK3++8ywWCQzs7OdWugYrG4buSgpmnE43HC4b01IlfTNPr6+rAsa9N+81AoVBUR9xKpVKq63t2O/X95MsFW5wop5a5+VorFIqOjowghaGlpIRQKsbCwUBVgNqOzs3PLUZBQcT8suwoGBwc5dOjQnhWg9jN1IaDOnudaiABQUYmz2ey+6BvbL0gpyT+RIP/tBP53d+G+48rGAi7jlGyyr82SeSVF/vwCngNBArc00v5IN835Itmgh2zAvakIAJV+O+k4DP3hD8gPL3D03z+EXqNdYM1rsmzsp88gokGUm7r2zEJUSolzYRrz6X6Ujgiux+5C+DZ/LXV2F/1ojPIrE5S+N4z7/2fvzYPsOs/zzt/Z7r7fvrc39L6hAYIkJFIkRYqmtVqrHScaO5LlxONUeYk9dnky4yo7S6UySrlcmcxEVbIzVpyJJUvWyKrIiizLsSWTkk1RCimSooSlFwC9L3fft7N888dFX6DR6+0FaDTOrwpVwO17zzno7vOd73u/532etzUzkS3LIp1MIr96lVyPf9vxpf4XC6BIOH+sWVSSZZmJiYlt/VHuGpKE9c4e5M9dR3otjXjT9q78pVIJv99PpVKBmtn0B5gpwFtiW44nVAlTlTEB3efA7U8hTAFCaaoFLD8u5+y+L3E75ZakahAKIwp5JNNE+Pwn5h49CJIiow5GUAcjiHdNYK0XMaYS1L52BVFtoI01lQLKQKRVSLpf2UnuH3m0i7F/dJHwpC33P24CgQDnzp0DbvV4b4dhGCwtLbWSUPr7+7fd3a1Wq1QqFUKh0JHn0e/G/Wo6d3uSg7bPFqdgMMja2hq6rh/XZe2IEILV1VUmJycZGxujVquxtrbWnFvdNneXZZmOjg46Ojr2vZjv7+/nypUrCCEwDIOpqSmGhoZwuWzlz1Fyf94pNg8U3d3dhMNhFhYWaNzMjD5qZFnG6XTidNoLp6PCzNYpfHYGYUHkNy6gRA83eO+0+O/6h2MoXg13uU4oUyYb9VHz7E9CZhoG0//uRcxCg8l/83YU9+4PXmFamH97BSngQb44dGIWGFaqhP7CFNQNHO97CLnnZO3SPChIkoT7vWcpfeq7aOe7UCIe4vE4K8vLdJSqWKZn2+KU9lQnld+/jOPtPUiOpotypVIhEAjsauJ17Kgy1of6UT53DbPLAz1blTK5XI6hoSGKxSKVpVRTSfBqGvFYB+yRAqJbPSADlgmKgiKXqFbP7/vy6vU6U1NTDAwMbJocSrICwTAU881WAX/wxCcK7AdJklC6AihdAZw/MoqVraBPJ6i/eAPryz9AHe5AnYihDncgOe+P6V2jWCfzxtpNd39b7n+SWFhY2LMQaVkW5XKZubk5AoEAmqa1Wgg0TWNubg7TNFldXUWWmyqpjd14e3d3Kw6Hg3K5jCzLdHfvndyyQSAQIJ1OH+OV7YwQgnK5jN/vx+VyMTg4CDSLGhvKjIP0+MuyTF9fX6tdxTRNFhYWkGUZwzAYHR29bws+Jwk7PtDmvmJlZeXInfwVRWFsbIxisUgymTy2YsODghCC2vdSlP5sDs9zPXje3nPgWMBtF/9v6sB3IXqr518I/PkqnlKNdDyA4djfg0E0TKySjvJamXO/9DTyHp8TpoX54hUkh4b8xNiJKAKIuo7xnRuYV9dQnxxGuXA8EYw27VH7uxsY8xm8H3kTkiSxuLhIeT2NZFnoOxSpqp+bRRny43iqmTzh8/no6upidnb3HXJN03A6na0s6vX19Zac8qiQrhWQv76C+bFR8Gy9T3w+H2fOnGHxT16m7DCQXssgHu+APVIHwKR7/f/A89hlhKphGCFWVv8FhtFe+oYsy61dzNsRQkClhGg0kAJBJOX0ThqtUh1jJokxncBczKH0h1HHYqjjMeQTpAzaTe4fvdhty/1PEJcuXTpWRabP52stGm2a5HI5lpaWGBsba2tjqlar7fqs2Jjn7qTwOAiKohCJRHC5XPj9/mMr7Gx8TwD6+vo2qR/222bwoGPHB9qcGnp6enC73SwvLx/ZMTVNwzTNIz3mg4pV1il+8QbGSpnQL55DO9N+FXinxf/Gzv/mNwsi6RKKYZLsDmHtsxfeqhpk/+AK3nefwf+Bvr2LAJaF9Z0pJEVBfsu9LwIIITCvrGG8OIs82IHzY08i7VMFYXP8OJ8aoPH9FfQrCRznOunt7eVKJos7W9+xEOB4aye1/3oD7ck4kiRRKpUQQhAMBsnn89t+JhqNEovFMAyDUqmE1+slFou1+naFEKysrBx6Mi9GAlgrVeQ/X8T6B4NbdvpLpRJLS0v0vOchZmZmELKE9L3UnvGDoJB86R8jiyrSgEqjcQYhjm4HWJIk8PpBriLyOfAHkLTTeZ/IPieOi2dwXDyDqBsYsymMmQT152eQO3yoEzG08ThyeHf/k6NGCEFltdja8c/8cB1Pl5/oxW5b7n/COX/+PJZl0Wg0uH79+pG3KZVKJcrlsu0IfxuhUKhl3HjUHPUxLctqFaCPk1AohM/na0UM+v1+ZmZm0HWdhYUFOjs7iUajLC0t4Xa7icViex/UpoVdCLC57wiHwxSLxSOLTenv7yebzR7JsR5k6lM5in8yi/PhKJF/9giStv+HQ1uL/5vIpkU0UcBQFZKdwT1lyBuYRZ3s719CG/LjPBtCsPsiSQiB9d0ZMAXyMxP3fMfdShTRn58Cy8LxwYeRu06e4dGDjqTIeN4/SflLP0AbiSI7VRyKym6/OfKAD8mlYk7lUc82F/IrKysMDAxQqVS27f+MRqPMzc21TKU8Hg8Oh6O18O/q6kLTtCNROYmn40hfnEN6cR3xtq1O1qWFNNZgAF9vhJJPhRfWYK0KXbtH3wmfhrHux+o6eFZ0R8f2/gUbSG43KDKiWACv775LFGgXyamine9CO9+FMCzM+Qz6VILyp19G9jpQx+NNpUDn8fgn6KU66e9vI/d/dpDzv2rL/e8nZFnG5XLR09PD6urqkScqzc3N4XK5cDgcOJ1OXC4XHo/ngZZ8t3tPXrt2bVun/ts5DmWHEIKrV68yPDx87H37t/8+yLLM2NgYqVSKZDIJNCMKC4UChUKBZDJJT0/PiTOyPKk8uHeazX1Nd3f3kRUCKpXKXTMkPI0I3aL0lXlq308T+Mgozon9Db6txf9rKSrT+1v8b6A1DKKJAmWfi2LQvacp4AZmtk7m9y7heiSK7/39SJK0q6xMCIH18iyirqO87dw97TMWNR3j29cwZxKoT4+gnO+558oEm51RByNow1GqL8ziec9Zgh0RspUasmFiqVt3QCVJQnu6E/3FtVYhoFqtkkqlOHPmDGtrazgcDgKBQCuyT9f1Tc7SlUqladp3k3aMmfZElrA+0IfymVmsbg9i9I77ZrFMurBE9EeGmmqGixH4Xgrev0eqRkBDKh7O5GqvQgDcTBQI3IwXvI8TBdpFUmXUkQ7UkQ6EJTBX8hhTCapfegMs0SwKTNxMIDhguohlmOSn0y2Tv9JintBkjI6LPba7/ykhFAoRCoWwLItqtUo+n6dcLreKjE6nE8MwME2zrfmUEIJqtbplIev1eunt7d0zMs6yrEONcYf9/L0ml8vtWQQ4KE6nk0ajsevP07IsZmdn6ezsvKs78bIsE4/Hicfjrdc2IiEty2JpaYn19XUGBwdt7689sAsBNvclmqYRCASOpBiQSqUYGBggnU7bBYE20ZfKFD4zjdrt2Vcs4I6L/4/svfjfwFVpEE6XyEW8VNvofTUSVTK/dwnP27rxvaO39Xo4HN72/UIIrFevI0pVlGfP37MIPiEE5qUVjBevoYzFcf7sU0h7mBranAxc7xqn+MkXMR7uIRqPkVxP4CzWqYW23yVXHwrT+MslzJUKyk1jvlQqhcvloru7G13XW5Nvj8dDIpHY9fzlcplwOMzq6urR/Ic8KuYH+1H+bB4z6kSOunE4HGiahqNLwdHrx+fz4XQ6qT8SQfqDKURJB9/Ov6/CpyHPH87TwDCMfWVMS6p6qhIF2kWSJdQzIdQzIcTbx7CSZYzpBPWvT2EVaqijTU8BdSiKtItcf1u5f6ef6Ju6Gf1ZW+5/mpFlGa/Xu6ucv1qtkkgkWu1NB6FcLjM9PY3b7aavr2/b+3txcZF8Pk84HG4t5m832KtWq2QyGer1OvF4HJ/PB9xMckmnSafTGIbBuXPn9lUM2GiTSKVSeDweQqHQPS8irKysHOnxHA4HXV1dmzZIisUiqVRqU6LBnayvr+N2u1vf43tBMBjE7XYzNzdHo9FA13VmZ2eZnJyk0WiQy+UIBAJ4PHe3PeqkYxcCbO5b+vv7mZ2d3VfW6m7UajVqtRqxWGzPibVNE2HdjAV8fgXfjw/ieqxjxwm1VTMo/TBzqMV/86QCX7GGr1AlFfejO/f/WX25TOb3L+N/Xx+et96SNUuStK0EUQiB9f05RKaE8tx5pG12cO8G1loB/fmrIEk4/t6jyHHbFOd+QvY4cL1znOqfX8b380+gCQnZ3LnPVlJktCfj6C+to/z9odbrd+Z6A/syBCwWi5t2TI6EHg/imS4GY2dwj3Wg63pz0qU0MBzNcw4NDbG+vk7ufBJez8AzO5v/Cb8GJeNQl9SOjPhWokDhVCUKtIskSShxH0rch/OZYax8FWM6if7yArWvXEIdiqCOxVFHO5DcWkvun3l9ldSrKwjTIvpojy33t9mC2+1mYGAAaEq2N9QD9Xq9pRjYb4GgWq2yurraOp5hGExPT2/yK7i9tVNRFOLx+Ja54dzcXGvRfvtnJUnacTFfLBZJp9NUKpUt/gi5XA7DMI5+fG2DRqOxrW9Df39/yzemWCzu+3vt9/tb3+c7X/f7/eTzeRYXF3f8/MLCAmfPnr2nxRGHw8H4+DiZTIa1tbVW0adWq5HP50mn00xOTt7zAs5Jwi4E2NzXDAwMMDU1dejjLC0tMTw8jK7rtl/ANgjdavX8m5kahc823Wkjv3EBJbJ1Arj94j9G10fHUDwH2M0WglCmhKNukuwKYraxMG/MFcn+wRUC/2AI95s2S9d2koxZlxYR6/lmEUC7+8OkqDbQX7yGdT2F+swIymT3A7VzeZpwPNpD4/VlCv/jOg0v+Ap1KpHtYwQBtMdjlP/9D7CKOrL/cMoPj8ezqVXgqAg9N4KoSEz/h69jvqsHijrSn8wifmUSKjlcLhednZ10/vJzlF5fpRSQyBcL205Ihf/wrQHLy8v09e3RgnAbkiQh/AGkShmRz8IpTxTYD3LQjePxfhyP92NVGuhTCYp/e536p16iVDbIFXTUiRiRx/vo/5At97fZHw6Hg1gstqdsvFartRJPhBBIkoTP5yMWi23awd0r0jCXyxGPxzGMrcXF7T63Ux95Npvd1Wg1GAzuqyXpOHE4HDz00EM7fj0SiWCaJjMzM1iWtef9upeXTDAYJJFIUK/Xt/26ZVmsr6+3FXt4XEQiEUKhENlsdlMhQwhBJpO55z+7k8SD/eSzue/RNO1IJrumaTI/P8/Y2Bi5XM5uEbiN6ssJCp+dpePfPEbjSo7Sl+fxvKMHz3ObYwGPfPF/E8m0iCaLWLJEsiuIaMOsr341R+6Ppgj+zBiu81vNyILBrUZ71pUlxGIK5UcvILWhOjgKhCUwf7CM8Z3rKBNdOP/Rk3f9GmyOFkmS8Lz/HDf+9g0Y9qHoJlpFR/duL2WXPCrqhTD6dxM439m77Xv2i6qqO07aDkM0GmW5uIhYriD9IItQZUSft1XcqNVqzM/Po2kavpUqgZ4+Ose7SKfTFIvFzdfkU5FKOgixb6+PO8nn83R3d7enDJAk8PpAUU59osB+2JD7b+z4Zy8lcMd9RB/tJ9rppVfXMW9kkLMF1EUXlkdDidpu7zZHg8vl2rTrv9O9fPtcb0PRt2EwuJFjD80iLaGOAAAgAElEQVR+8Xw+j67r6LreMjl0Op14vV6CweCWdgPDMFhdXaVQKCBJEuPj40xPT7fmgxueQu2ONfcSRVEYHx/fl6Hgfgp7AwMDTE9P7/j1jZYLVVU5e/Zs29d7lJim2VJ8bLSw6bpOIpEgEonYqoCb3B+/yTY2u3DmzJldB6b94vF4ME2TaDRKqVTatuXA5/NRq9W2rTafRoRuUfj0DPpKmYV/8k28D0UI//I5tN7mBHDL4n84gP/i4Rf/G6i6STRRoOpxUAjtvIu6HbU30uQ/f43Qz5/FObp1wb+xU3E71vQK1vV1lLdfQHLd3QW4tZJrpgE4VBw/eRE55r+r57c5PpS4DyXiQUnXqPuduIr1HQsB0IwSrH7qKo4f6W4rfeNOdF3fV+98u5imiep2YP14P8qfXMeMu2Bo6++rrutk5Sq5//tbOH/hIfr6+4nFYkiSRK1WY2lpiQYNhFOBigneg09J1tbWOHPmTNufk1xukJVmooDHh3TM7tcnCb1UJ/PGOunXVvYl9xemhbmYxZhKUv3c98ChoI7Hm7GEPQFbIWBzJOy2yD537lxLMXDnQq5YLLK2tka1WsU0TRwOBwMDA/syi7Msi5mZmVbBQAhBqVRClmVUVSUajZ4IT4CDIMsyIyMjZDIZotEolmVhmiaVSqVVdOnq6tqXy77D4WBkZIRr167t+j7DMCgUCq3Yv3vB2toa+XyelZUVZFmmu7ublZUVLMvixo0bjIyM3JPrOmnYhQCb+x6Hw4HL5Tq0V0ClUiGZTKJpGgMDA1y7dq214N8YRMLhMEtLS+RyuX0fV1EUHA5H64+iKKyvr98XqoPKCyvoK2VKyQrlko7rbV0oUSeFVxIUX01RmTn6xf8GzmqDSKpEPuyh4mtvcl59OUHhy3NEfvEcWv9W8xpJkrY8BKxra1jTK00lgPvu7QyKch3972axFjJoz44hj3faE+pTSNfjY1ybnqWxquNvNCh27VzokWNu5F4vxvfTaI8d3Im5VCoxODhILpc79Ph4O5lMhmAwSCFSwHpnD8qnpjAf3+E6h3zwNxa12TTXdJ2BgQHK5TKmaRKPx1leXgZfsz1AHKIQkM/nD1QIAJAcDgiEmp4BlgFu76m8B7e4+y/kCJ2L03Gxh/4PnsXbt7vcX1Jk1MEo6mAU8e4JrNUCxnSS6lcvQd1AHYs1Ewj6w/fMXNXmdLPbojKZTG5SDDQaDWZmZuju7iYaje563OXl5S3RiMlkkomJifty8X8nsiwfmRze7XYzOjrKtWvXdp3HLiwsADA6Onrs8YLbcfvP07KsVgvZ4uIi1Wq1VVB60LELATangt7e3j0rlHvRaDRIp9NAc9AYHBykVqshhMDr9VIqlSiVSvvO0ZUkqVVlrdfrLRfTaDTK+vr6oa71eDDxOl5HlbPUjT7KqUGyn7xEab1MWbdAhtXPzlCaK+Ieubn4/5mjXfxv4CnWCOQqpGN+Gm3uzJe/uUL5G8tEf+Uh1K6t7rCSJDE6Ooqi3PIZsOYSWJcXUZ57CKmNJILDICwL8/tLGN+dQznfjfMfPYXksIfk04rb50UTMlbBQMFA1k2sXZzVtac7aXxtEfXNOxtx7kWtViORSBCLxXY1eWoXVVXR9WZfv+jzIpwK8itJrAHvVtWOJCHe3AGvpLH6fKytrdHb28vs7Cx9fX10dnaS8s83CwFd26cp7AchBGtra3R1de395m1oJgpEbiYKFBC++3+HWwhBda3U2vFvyf1vuvuHznagHHDMkSQJpSeI0hPE+dwoZvpmAsG3rmGly6ijHc1owuGoPa7Z3BWGh4fJ5XKtXd8NVldXCQaDOyoNLMsin89vek1RFEZHR09FEeA4cLlcTExMcO3atdazYCfm5+eJxWJ3XVHR39/P0tISlUqlZVKpaRo9PT3A/lohHgTs0dnmVOB2N2Os9jI72S+JRIJqtYosy8iyTC6Xo1wuMzg4uOdOviRJBINBYrEY1WqVqamp1kNJ0zSCweAJVAMIOn1/iM/xPcBCILO6/G6KdRdlywKHhOJ1IDlk+n7jYVw9xxQRIwTBbAVXtdE0BWwjgkoIQfmvlqh8N0Hk1y+gbmNiKEkSY2Njm+TS1mIK6435pjGg/+ALkXYwl7IYz0+Bx4Hjf3ozcsTutX0Q6BzpY1lY6N9fw1msU43sHGOkjATAAvNaAXWb1pb90m6u935wOp23dt6WyoiHw0i6QPpOEvHUNi7a50NIf7uOyNWp0iwkaJrGysoKExMTpEJOKB3OMHCD+fn5bZ2v94MkyxAMNRMF8rmmieB9thDQyw0y319rLv5fW0UYZlPu/7bjdfdXol6Up4ZwPjWEVaxjTCfQX1um9ueXUAYizVjC0RjyLi0xNjaHJRQKEQqFSKVSLeXlbskAwJaFrKZpjIyM2EWAPVBVlbGxMZaWlloqr+3QdZ2VlRXS6TRjY2N37fpkWaa/v3/Ta5Zlcf36dSRJolQq0dXVdSztc/cTdiHA5tTQ29vLjRs3jux4xWJxy2uyLO/qWBsMBunq6qJer7OysrIld1WW5RNYBACnOofX8Sq6FQEkwKB78uu4n/kY3PBg1U0s3QLDonq9cCyFAMkSRFJFJCFIdAURbUhLhRAUvzxH/UqO6K9dQAluHdi3LQIsZ7BevY7yI+eRAsefLStKdfRvzWCt5tCeHUcejdlV6QeIUCjEunuVwpkg/mRl10KAJEloT3eifztxqELAXmPWQXA4HLfao5bKiAEf4qEwyh9fw+xyb/ULcCiIC2F4NQ1v72n1725Eijn7w9QWMge+Hk3T6OvrwzRNstkslmUdeBK/JVHAH2yqBU4olmGSn0mTfvVgcv/jQPY7cby5D8eb+xA1HeNaCmMqQf3r08idfrTxZguBHLw7hVebB4+Ojo59S+GdTid9fX3IsozX631gCgD5fJ5MJsPQ0NDeb96BOxfblmVRrVapVCpUKpVN82i3+97f77Is4/P5KJVKFAoFCoUC4+PjD3Qx4OQ+3Wxs2sTr9eJ0Oo/FJXsDSZLwer2oqtoyVtlwpJVlmWAwyPz8/I79uPV6HUVRUFX1RBkOylIVkGkWAQAUQDD8zy9gCT9CCKyKQSNRxRE/+sFcMZqmgA2nRi6yjbx4F4QlyH9+FmOtQvR/eQjZu7WVYNsiwFoO65VZlLdNIoWOd0demBbma4sYr8yhXDiD851nbbnsA8ro2XGumJdxvZCEsQjsMulUH4nS+KslrGQNOXawnVxFUYhEIgghkGUZj8eDw+HAMAwMw2BlZWVPN+k7cTgcrXFWWqwg3tENPg3z/X0oX1nA/OgI3FmMe1MU6Y9m8b53FNM0W0XSarWK60yI+qVE2/83r9dLKBTC7/eTTCZbrV26ru/LIGwnNiUKFHLgCzR9BE4Am+T+r62S/eF6U+5/sZvRjz1KaDJ2YLn/cSC5NLTz3WjnuxG6iTmfQZ9KUH9pDtnnbCoFJuLIMZ9dFLW5Z2yXIHScGIaBruv3bHFcLBZb7WLJZHLPeMf9slFM8Xq9rfOYponL5bonPgHb0d/fz9TUVEvBUCwW9/SQOM2cnKeFjc0R0NfXx+zs7LEdP5FIEAqF8Hg8VKtVYrEY6+vryLLciiDcy5TrOHboDkvd6McSLhSpgCk8qHKBujGAJZo7/5IkoXg13ENH7weg1XWiySKlgJuS39VeEcCwyH1mGqtkEPmnDyE7t28l2FIESOSxvjuN8vRZpMjxuvOb82n0F6abOd0//Thy6PiVBzYnF0VRQJYwVAXPVJbK5M4TEEmTUd8SR39pHeeHDiZ3r1QqpFIpGo0GQojW37u6uvB4PK2ddF3XqdfrJJPJXccnSZJQFKVZyKybkKnDRm9/nxfr8RjyVxawfnoY1NuKHEEHYsCLt6ZQKpVaL1erVbyxAIVqUyWg6/qOqqloNIrP50MIgdvtxjAMcrkc6+vrmwqrt/t/HIZWokCpAB5v89/3gB3l/s8McP5Xnjw2uf9RI2kK6mizRUBYAnMphzGdoPqnr4MsoY7FUcdjKGdCm6JpbWxOE1NTU612BEmSCIVCdHd331UlQiqV2vT3oyoE3Inff/LSj2RZZnJy8l5fxonBLgTYnCo28mRvd449SorF4iapk8PhQJIkEon97WZtDPQnrRhgCR8rhd8g5vs0mpygol8gWfoYtxQCx4O7XCeUKZON+qh52ttxEw2T7B9eRVJlIr94bseYtWg0uqkIINJFrJemkJ8cR+oIHOr6d72+Qg39W9NYiSLac+PIQwc3fbM5PWzc99UeH75LGSrDIdihgAWgvSVG5T/8EMc7e5E87T+yNySadyLLMtlsllqthmVZOByO1oR0eXm59b4NpVUm05Tub2QxA7BSaRYBblvwi8eiSCsV5OdXsd7Vu/mkb+7A6/WyXiq0XqrX63R0Rxn77R/DECaqqlKr1ahUKtRqNbxeL4qioGkaQgiSySSSJLG2trajJ8xRTqhbiQLFPJhmsyBwzPexZVrkp1NNuf/ra5Tms4Qm40QvdnPxAxP4+kP3/VgiyRJqfxi1P4x4xzhWotQ0G/zrKaxSHXUshjYeQxmIILXhFWNjc9LZ8DAQQiCEIJvNUigUGBkZuWsS9dtVYPs1wLY5nUi79Ss/9thj4pVXXrmLl2Njc3h0XWdqauqunMvhcDA8PLwpf3YvOjo6iEajLCwstC3JPTUIgT9fxVOqkY4HMNqUslpVg+z/cxkl6iL4kTEkZftJsSRJTE5OthYGIlvC/NZl5LeMIXeHD/3f2A5hWBivzmO+uoDyaB/qYwNIqj2RtWlSr9eZmZlBKzfo+N4qWc1J7andne5rX7yOHHPj+JHuI7uO/v5+8vn8JrdsSZIYHh5G0zRqtRqSJKGqKoqitNyhnU4nQ0NDLC8vU/zqTLNW+LY7rr9mIn/2GuLJGOL8bfeZEAw6O0ln0xS9zfEyHo8jSxKZ336exq9MIikybrcbr9eL2+2mXC7TaDSwLItKpbIvj5Vz584d+e6asKxmooAsg/9WokCj0WhljR+GympxW7l/9GL3iZP7HzdWtoIxk0SfSmAlS6hD0WYCwUgUqc0UGRubk8rtyoANVFUlEAig6zoej4doNIplWS3laS6XIxaLHSoKsFqtbknZ8vl8DA4OHviYNicbSZK+J4R4bLuvPThPFpsHBk3T8Pv925r9HTWNRoN8Pk8sFmNtbW1fn0mlUtTrdQYGBlhdXd0SW3PqsQSRdAnFMEl2h7DazJs2izrZ37uENhIg8PeHdt0Z6+npuVUEyFcw//Yy8ptHjq0IYM6l0J+fRo56cfzDt9hmWDZbWFlZAUD3aIiwE8eVEvpoFTO28++K9tYuan88g/ZM55HlsxcKBQKBwKbxRwjBtWvXUFUVl8uFJEkUi0U6OzsZGhpqmUAtLS3R1dVF9N0eCrUSSsxDMpm8dXCXgvWhfpQv3MCMu2HD30CSKNereBtqqxAQCoWYn59HuFUoGwi/tqOKYb9Uq9VWj+pR0UoUKN1KFDAti+npaWRZ5uzZs20VH1py/9dXSb+2gqWbRB7ppvPpfs790ydwhh7csUMOe3C8ZQDHWwawyg2M2ST6pVVqX7uMcibU9BUYiyP7707Uq43NYclkMqyvr6NpWkv1tJ1PlGEYLfVVsVgkkUhsKX6ura1t8qlql41n0O3c3q5l82BhFwJsTiVnzpzhypUrd+VciUSCsbExUqnUvg0Ai8UiN27cYGBggGg0Sr1eb/25GwWMe4VsWkQTBQxVIdkZhDb7QM1sncwnL+G6GMX3vv5diwAej4dwuLngF4Uq5jcvIT86hHzm6E1hrFwF41szWJky2o+OowwevFpvc3rJZDK3kkQkiXrAiTiv4vr2OuUPDux4Pyg9HuSIE+NSFu3ho/n9dTqdO0rrDcPYNDFcX18nl8vhcrmIRCLUajVmr04TeaNB6CcnkVVlcyEAIObC+tFulC8vYP7MCLiaqhgrouEWGiTzEHOhqiq6riP7VKSijvAffse3UqkceSEAbiYK+G4mCuSyzGeyQLPd48aNG4yMjOz42Zbc/7XVprv/bXL/vvc/dyrk/seB7HXgeKQXxyO9iLqBcT2FMZ2k/sIsctTbVAqMx1CidgSrzcnDsixmZ2dbY227MvydFFDJZPLAhYCdlKiZTIZIJHKgY9rcv9iFAJtTiaIo9PT0bFv5PI5zwc4D9k7U63VmZ2dxuVw4nU4cDgednZ34/f67ct13G61hEE0UKPtcFIPutkwBAYxElczvXcLzbDe+t/fu+l5N01oyN1GqYX7zh8gX+pH7j9YQRxgmxsvzmN9fRH3TANr7LiCpD0b0kE17FIvFLfd1LeDEJWrUXQqOK1ka53eehGlPd9J4fhX1QmTfC8YNI6qN998+Rnm93rbUSLcXKoeHhwmrPrI/fIP8494ds6HFuRBipYL8tSWsn+jH6XIR64xz49uvwHwOfuwM1WoVt9tN3a81CwH7vqKd2anAcRTcnihAIoEqSxiWoFqtks/nN7mPb8j906+vkvnBTbn/o12MfvQRQuceLLn/USA5VbTJLrTJrmYSy3y2aTb4ue+BU0W7WRSQuwN2UcXmRDA3N3cs41FnZ+eBP6soyrYFiZWVFUKh0AMTn2jTxH4K2ZxaIpEI6XT6WOMEoemKms/nD2S4stH3uiGDTSaT9PX1cfbsWYrFItls9tiMD+8mrkqDcLpELuKl6m1fzqkvl8n8/mX87+vD89bd+6llWWZkZARZlhGVOuYLP0SePIM8dPAH550IIbCup5ppAF0BnB99Asl/fzh329x9Go0G8/PzW16v+5wEV4rkn4jj/doC+qAfsU38JYAyEUJ8bRFroYQysD8nZqfTSWdnZ2vBf/viqF6v75lwsh2WZbGwsMDwyCDW28uYbveuLv3Wc13In7+B9HKK0AcfIpPJUB9wIf1VHvFsV6sQUPNrUNJ3PE6713jcCIeTumkRcqjUTYuyYbK6tELtcv7mrv8KZsMk+mg38bf2M/nLD7bc/6iRFBl1OIo6HEW85yzWSgF9OkH1Kz8E3Wq2D4zHUfpCR9ZOY2PTDsVi8Vjmb06nk0DgYEbHtVpt17lquVw+kU7/NseHXQiwOdUMDQ1x9erVYz1HK0rrCLAsi/n5+ZbPQV9fH6VSCcMwsCyLbDZ7ZOe6KwiBr1jDV6iSivvRne3Lfhs3CmQ/dZXAh4dxX9xdcu/xeBgcHGwWAWoNzBcuIY92I48encmala2gvzCFKNbQ3jWJ0m9L6Wx2Z2FhYdvXLU3BdCioKjQmw7i/m6Cyg9pFkiW0JzvRv72+70KAJEk0Gg1WV1cPfO3b0Wg0WPmvrxN+5xiSV9u9nUmVsX68H+UzswR/2s/CyhJ4VMRYEL6fodIVIRKJUOkPU5/PHsn1tavOOghzc3NYlsXa1TTytSKZG3miHx1n8a9W6Hikm773PYdvwJb73w0kSULpDaL0BhHPjWKlyxhTCerPz2DlqqijHc0WguGonUBgc1ewLItCobD3G9vE4XDs2oK0F3u1ntZqNbsQ8IBhFwJsTjUbjtfHGY+iKMqRS790XSeTyZDP5wmHwy337tHRUZLJJOl0+kjPdywIQShTwlE3SXYFMQ/gnF+/miP3R1OEPjaO89zeBn9dXV3NIkBdx3zhEtJADPns7m0E+0U0DIyX5zB/sIz6+CDKo332TpPNnjQajV133mt+J65incJDEXxfnkNdLGH0+bZ9r/bmDsrPr2Bl68jhvZU1kiQdz6LYEhSfv0Fh3AHufUwj/BrKh8dQNQ2pajWTBh6LIn1xjvJbu4hGo/S98yHyry6yRvsqhTs5zkLApdd/iFFugCox/3++juyQ8Z4N0/eOfkyPSs8vXSAWjx/b+W12R5IklA4fSocP59PDWIUaxnQC/XuL1L7yQ5TBSLOFYCyG5LYTCGzaQ9d10uk0mqYRje7s17K8vHzkRtCSJDE+Pn6oY+yVVGW3BTx42IUAm1PPcctEJUk6tnOYpkkqlWr9O5vN0t/ff+ILAZJpEU0WsWSJZFcQ0aYpIEDt+2ny/981wj9/FsdocO8P0FQEiIaB+c1LSD1h5HNn2j7vnQghsGYS6N+aQe4N4fyZJ5F8tlu1zf7YYqJ3B7WAk/BSnkJ3gOpTnbhfXKPU5QFt64RMcipob+pA/04C53v79jz3se1Gr1choO2vCHDzOhxDIYyazsiFcQr5AovSIoSdmJcy3BAWaqrB0OQo1Ub+0BPooywE6OUGmTfWWnJ/7dkwatSJnqvT/+uPoAaaud91wCnLmJUSwooiyfbO80lADrhwPNaP47F+RFXHmE2hTyeo/fUUSpe/ZTZoJ7zY7IRhGFSrVRYXFzfN9VKpFAMDA7hcm9sC6/X6saRB3Xmeg+BwOHb9ei6XIxqNUi6XUVUVp9Oe65x27EKAzaknFouRSCSO7fjHtuu2DY1GA0VR7uo520XVTaKJAlWPg0LI07YpIEDlu+sUvzJP5JfOoe2wO7odQjcxv3UJKRZAvjBw6IWQlS6jvzAFlQbae8+j9B5P7KDN6WWvCaHu1pANC7lhYvZ4MeNunG+kqb95e2NL7ck4ld+7jOPtPUjOvRebxzJOLJURZ3Z3aXe5XPh8Pnw+X9MDoFYjW8xR+dPrRJ4ZbsYR/nyU0t9cpygEhkti/XOv0v0rT1MoFA513YdRaFmmRWEmTfq1FVKvrVKayxI6GyN6sYee97yNpWozJtbVv1U+W7csNN1E5LIQCCGp9hTrJCG5NbQL3WgXuhG6iXEj3Uwg+LvryCF3y1dA7vDaLR02QHMjaaf2Ul3XmZ2dpa+vb5NJ6HZ+MEfBwMDAoY/h9Xo3bS7dSbVaZXZ2llqthiRJnD17dlcPGJv7H/spZXPq6ejoIJlMHsuEeKOX/27t0FuWRalUIhqN7jqY3yuc1QaRVIl82EPFd7DqdfmbK5S/sUz0Vx9C7fTs/4NCYP7dZaSQF/nRoUNN5ETDwPjODczLq6hPDKE80tvMEbexaQPLsvZWC0kSdV+zPaAS9VB7PI7vyzfQhwNY28j/5bATdTiA/r0UjrfuboB5bAXDpQqc3azSkWWZQCDQWvxvRBCm02nK5fKt78MFD7VPvkjoHz+K3O2j++89grqWIOspUbuSoFIqt4xeD0qj0cCyrH3LXCtrxdaOf+YH67hiXjoudjP6kVvu/oZhcO3atT2PVTUMJI8PUciBL4C0xw6czb1B0hS08TjaeLyZQLCUw5hKUP3CayBLqBPxptlgb9AuCjygLC0tkcvl9nzf4uIisizj9XqRZflYWlF7enpQj6CwuB+D2I33CCGYnp5mbGzsSM59mpiZmcHtdtPT03Pft1PYP1mbU48sy/T39x9Llba3t5dkMnkg9+2DIEkSuq6fSLmWp1gjkKuQjvlpuNrvvRRCUPrvS1T/R4LIr19AjbRRSLAESCDcGsqbRw48cRNCYF5dw/i7WeSBKM6PPYF0gJQDGxtoOjDvh5rfiTtfoxL1IDwq9YsduF9ao/ze/m0VNdpb49S+eAPtyTjSAdpuDoUQSItlxDs2G3D6/X7i8TiJRIL19XV0fYcEALeK+aF+cn/wKuZPD6HLXnyRIFm5jPCqVLJFtMDxyrT1coPsD9ZJvbZC+rVVzJpO9NEe4k/1M/lLT+AMbz5/sVjc9/PDNM1mm4A/gCgWwONFctmy85OMpMioAxHUgQjiXRNY60WMqQS1r11BVBtoYzcTCAYidjzsA0KpVNpXEWCD41IBbODxtLEpsgvBYJD19fV9v980TaamppicnLzvF7xHyUacbqVSObRvw73GLgTYPBD4/X4mJiaYnZ090mpto9G4q4Ojy+UiEomwvLx81865J0IQzFZwVRtNU8ADuDILISj+2Rz1qRzRX7+AEmhjF80SRGbSZMaiiIvDBy4CWMki+vNToJs4PvAwcvf+fAlsbHZiL3+ADep+J6GVfLOgJUs0xkNoswW0mTz6eGjL++V+H5JHxZzKoU7u3K5yLIqAdB1cCtxxj+q6jmEY+5s8d7qxnu1E/m+LuP/3Z2i8nIBIA+HTMEsNXOH9twNth9/v3zQu7yb37/ut8V3d/ROJRNutZcvLy01n72AIUciDaTYLAvbO8olHkiSUrgBKVwDnj4w2U2KmE9RfvIH15R+gDnegTsRQhzuQnPYU+jRSKBR2THq5V8zOztLR0UFX1+7xyXtxED+rk9qGei/ZeLYetVH4vcAexWweGDRNY2Ji4kjdXF0u154urEdJtVrFNM27es7dkCxBJFVEEoJEVxBxABd9YQnyn5/FWKsQ/dWHkHfIUd/+w4LwtczNi5GwxAEecnUd46XrmFPrqE8NozzUe/d3WW1OHZZl7TtD2lJldKeKo9Kg4XOCLFF9qhPvXy9h9PkQd5jySZKE9nQn+ovrd78QsFhGnLm1O+Xz+QgEArjdbjRt//euuBBBWq4QCgSZXb8M8zr4NaxC/dA9qd3d3VTWS6Rv7vhn3ljD1eEleofcfzcMwyCTyRzIX2ZDRispKgTDiGIeqVhA+AN2MeA+Qw57cD4xiPOJQaxSHWMmif7GCrWvXkbpD6OOxZpmg7Zy7FRQrVZPXBFgg1QqRTabpaOjg2g0eqBNqLW1tQOd21YDbOb22PBqtYrbff+qvuxCgM0DhSzL9PX1EYvFmJ+f31m+uk9UVaVerx/R1e2PQqFAMBjc927jcaEYTVPAhlMjF/EeyBRQ6Ba5z0xjVQwi//Qh5H2Yn936sCB0PYtsWKQnOkCirT42IQTm5VWMF68hD3fg/Nmn7DgpmyOj3WJj/WaMYONmIoUVdaEPB3C9kqT6tu4t71fPh2n85RLmSgWl52hko/tiqQwDPiRJoru7G5/PRyqVIpfL0d/fz9BQ05/jE5/4BF//+td5/PHH+ehHP7rpEF/60pf4xje+wfnJc/xf1bchO1Wq377B36h/ww9fXiBfF1iWj/HxCd73vve1dsHS6TT/6l/9q20vS1W0VesAACAASURBVJiCcCjMv/zZ3+S7n/iLW3L/J/uY/MW3bJH7b4dpmq141sMUUCKRSOvvkixDIASlIiKfhUDQThS4T5F9ThwXz+C4eAZRNzBmUxgzCerPzyB3+FAnYmjjceTwXbwfbY6U43D7P0pM02R9fZ319XU6OzuJxbY3ld2JUql0oPM2Go09EwceJPr7+1lfX6dcLlMqlU50IWAvFYhdCLB5IHG5XExMTJBOp1ldXT3wcZLJJPF4nLm5uaO7uD0oFAr09vYCzcXs7X8sy7orDzKtrhNNFikF3JT8rgMVAay6Se4PryJpMpFfOIe0TVzajghBcC6HWjeaRYCbO/j7LQRY64VmGwDg+NAjyF2Btq/fxmY39usPsEHN7yS8mKdw25q/drED/5duoKxVMLs2Ly4kRUZ7Io7+4hrKh4e3PaZpmrhcLmRZPpqI0w1/gKc76ejoQNM0ZmdnW8e+ceMGiqIghKBardLd3c3ly5e3XNPLL79MOBwGWUJXLFTtB/zH8r9A9Ql++ddjnOmXSSZLfPrTbn73d3+XX/u1X2NgYIBwOMzHP/7x5oEsQW2pRGU6z+wrU3xx5qs8+95nCKp+xn7r7K5y/9uxLIvZ2VkMwzj098jr9aKqKn7/5kQBSZIQPj9StWInCpwSJKeKdr4L7XwXwrAw5zPoUwnKn34Z2eu4FUvY6bdVICeYDVPRUqnE3NzcffWzWl9fJ5fLMTIysq8d+8PI2DOZzKHbEk4THo+HgYEBLl++zPr6Og6HY1NyxEnAsizW19f3NN61n0Q2DzTRaJRwOMzCwsKBKqXZbJZ4PI7L5bprhoHlcplUKoWqqsiyjCRJSJKELMuEw2FKpdKxuNZu4C7XCWXKZKM+ap6DVYitqkH2P15G6XAR/MgYktLGw1cIAgt5tLJOerKj1Y6wHzmxqOoY376GeS2J+vQIyrnu++rBb3P/0O54oLs1ZNNCaRiYG7J1Tab6ljjul9YpfWgQ7rhPtLfEKP+7N7AKDeRtfDXK5TLlcpkzZ84cjdw1r6NFvZx5bBKn08mNGzc2LZ5vV0fVajWCwSBer5eFhQXe+c53srKywre//W1UVWV0dJRyuUym8Hf8Rep3yJYM/uATj+EqFLCCbsLhMh//+FV++Zf7+cxnPsNv//ZvY2QbiCsVylezVKZzqGEnYkDjef1/8NYPPMsv/Nov4fXuHmt4J6VS6cj6PE3TZGhoaNuvSZIEHi8oSlMZ4A8gOWw5+WlAUmXUkQ7UkQ6EJTBX8s0Egi+9AZZoFgUmbiYQHKB9zuZ4MAyD6elpvF5vq3B7v/XD1+t1rl69ysjIyJ4m0odRkRYKBbsQcAeyLLfm/ouLi61C8L0mlUqRTCb3vQ6491dsY3OPkWWZwcFB6vU6S0tLbfXfu1yulpP/3SSTyWx7LR6P5/iKAELgz1fxlGokOwMYe/TY7oRZ1Mn+3iUcIwH8f7/9mD//UgFnoU5qMrbJk2C3h6CwBOYPlzFeuo4y3onzZ59EOkCygY3Nfrn9PpQkqSUdtCxr+yKBJFG7GSNYjt66t4wBH9ZsHselDI2Ho5s/4lbRHomifzeB811ntr2O1dVVBgcH6ezsbMstejucBYvB/+1HSeay245BdyKE4OGHH+aLX/wi586do7e3l1deeYWnnnqqFX/q8fwnvvnNPD/67h4Cpk6j2uy7tCwvsmTwE+9O8bv/Osl3fvMviKkRvGfD+B6O0vnhEfAqfOITnyAUj/Bbv/1bbRcB4GilwPvxSJCcLpAVRDEPbhPJbcvITxOSLKGeCaGeCSHePoaVLGNMJ6h/fQqrUEMdbXoKqENRpAMY69ocDZZlce3aNSzLolgs3uvLORSWZTEzM4OiKEQiEWKx2LYKgXZSEO6k0WiQSCSIx+OHudRTx/DwMHNzc/j9/hNRBICtPhB7qUVOxlXb2JwAnE4nIyMj1Go1lpaW9rWj193dTSKRONYd+BOBJYikSyiGSbI7hHXAXQ0zWyfzyUu4Lnbge19f20UA33IBd6ZK6lwMcUeM007xOtZqHv2FKVBkHD95ETnm3/Z9NjZHiaZpOJ1OwuEwPp+vlW2vqiq6rrO0tNQyG9qgHnDizlYpR285zEuyTP2tXfj+aglrLITpUTftWmlPdVL91BUcz/Vs214jhGBhYYGhoSGEEC3zO0mSNhke7YXL5WLg2VHWX7tBLrz/8e6xxx7jS1/6EtevX0eWZS5dusRP/MRP8NWvfhVZrlOvX6ZYlInFZeqpIlLFRE9VMQoNrJrBUF8axRVDekeIkXc/uWnM+PznP08+n+eTn/xks9WgTQzDONJCwH4nyZKmbU4U8PpsZdIpRJIklLgPJe7D+cwwVr6KMZ1Ef3mB2lcuoQ5FUMfiqKMdtj/NXWZxcXHTBs6xGKveZTY8TrLZLGfPnt30tVwud+j/XyKRoKOjwzYOvA1Zlhke3r41717h9XqpVCp4PB46Ojq2tKrdiV0IsLG5A5fLxejo6J4FgUAggCzL+9oZuxvUajVM02R4eJi1tbV9O5bvhWxaRBMFDFUh2Rls9eO3i7FeJfP7l/A8243v7b1tf967WsSTrJA6F8PaZiflzt1AUWmgvziLNZdGfWYU5WyXPdm2uWu4XC7cbjelUomVlZVNxcJ4PM74+DhCiFsL/pstPgDdNz0/NhBCwKMPgWmBQ2F9fb017sgxF/IZH8b302iPbW8cZZomc3NzDA8P43Q6kSQJr9eLEAJFUajX66ytre3YHuVwOBgYGGD1069QGFKB/RsjeTweHn74YV566SWWl5eZmJi4zUzPQEJGQkKRQA46kR0GXr8DKewCVSI3r+Pu0PDH3KiShEmzyPLGG29w6dIl/u2//bcHlqwuLi4e6HPbEYlE2jKM2pwokEf4g/b4dMqRg24cj/fjeLwfq9LAnE2hT61T++9XUHqDt3wF/K57famnnjtVAPd7EeB2DMNgamqKcDhMR0cHuVzuUF5Yt5PL5TaZodrce4rFIgsLC63CvsPhYHJyct8FG7sQYGOzAxsFgampqS3Sf0mS6OrqatsQ7Li5fv06wWCQ/v5+pqamDv1w0xoG0USBss9FMeg+kCkggL5cJvP7l/G/vx/PU51tf967XsK3ViJ5Lobl2F5OuVEIEJaF+cYyxndvoJztaqYB2HnPNncZTdNYXl7e9muJRIJcLodpmq0e+417tWM2TbHTR91/R6uLKfD9tzmsZ87Q9cQEgUCAcrmMaZroP/UQ9ZdWUT0eLMtqFR022oU8Hg8ulwtd15FlmWw2y/LyMrIso2kavb29DA4OUiqVqNfr6LqOYRiUy2Usy2JgYIDE4irF7yzAW861/b146qmn+MxnPsP169d574+9B4+q4FEVZNVHNOTE65WYmy1TH1FQBvxITgUJkDBYXDKwLI1gLIbf4SDmdTMzM8Nn/9//zC/+zz/H2Z4uRKkIqgqKCqq67wX1kRgo3uQgstAtiQL+INIhoxNt7g9kjwP54R60h3sQDQPjehpjOkn9W9eQw+5bvgLR9ttdbGx0XSeRSBwo/nQ3stmsXQg4QdTrdebn5wFa6r5Go8Hq6mrLVHwv7Nmxjc0edHd3s7i42JqoS5JEPB6n0Wjg8/nw+XwHjmQ5DvL5PKFQiEAgcCjZq6vSIJwukov4qB4iI7lxvUD2P10l8OFh3Bc72v68O1nGt1xsKgF2WNDLstx0Rl/ONdMAXBqOf/Am5KjvwNdtY3MY9uoX38mgrhZw4izWtxYCFInqU514np/nelAm3NmBw+FAVVU8Ix7QPKgBH6rP2TIRbTQarWKDYRhomoaqquTzeTo6OgiHwzQaDfL5PJVKhb6+PkqlEoqi4HK56OrqQlGUptz01QU4035MqAQ8cm6SL2oa5VKRtz/5BPV6HdMSlHRI59/J00/9EX/zFxk+/JMxIjcjRAUgyxm+8EU/sa5ennjyScLhMKlUit/5T/+Z97z/A7znAx8EwwDTQNRrYJjNv8tysyBwszBwq0iggCS3CgVH2dN50GitTYkCG/GCqi0Tf5CQHCra2U60s50I08JczGJMJal+7nvgUFDH481Ywp6ArRo5AvbbDmVjc9LZaTzYqx3gduxCgI3NHgQCASYnJ1ldXSWbzTI4OIhlWaysrKBpGj09PczMzNzry9xEtVrF5XIdrBAgBL5iDV+hSioeQHcefFJav5oj90dThD42jvNc+z287nSFwGKe9GQM07XzcDXUeYbGX17CWsqiPTuGPBa3J0w295RAIHCgvtO630l4IUdhm6+ZXR6MHi+u11Jkn9i8c6y/msT4TJa+//WtxOPxlh9Bo9GgUqlQqVSo1+s4nU6GhoYolUrMzMxsalkoFArIsry9qeBSBfr2tzvplGVcigyaSq/XTd20+Nf/8l/QMzTM4uIilmVRtywsIUhd+yAffOibvPHGFB//9zf4yEd6GRqSyOfzfOELMouL3fzO7/xmq2jx8Y9/nGg0yod/6qfIVW9r25JVcKgEAjFkIcA0WoUBqlWEaTSLBoC4WSRwIajSDGMwBBzG6SUQOHgE6eZEgVwrUcCqlJE0R9NTwOaBQFJk1MEo6mAU8e4JrNUCxnSS6lcvQd1AHYs1lQL9YTuB4ABsmATaHIyTYohn08ThcOB0Ojcl9jidzraeR/ZP1MZmH8iyTG9vLz6fj4WFhdbkudFooKoqiqKcKMNAt9t9MO8CIQhlSjjqBsmuIKZ6cJlq7fUU+S9cJ/xPJnGMtD9JdmWqBOdypCY7MHYyUrIEat1C+tPXkR7qaaYBHDDNwMbmKJFlmZGREWZnZ9v6nO5SmzGCdQNzGwVM7bEYvj+bozEaxIre6iVWH4nS+Otl5HrTEHDDlf9ONuKmtiOZTDI8PNyKHbwdaamMePf2UkNNlnApCi5FwaHIGJYFSNRMk6VyM4XF6w+gKMomOb7QLfKfWqDx9D/nn/3m63zjG3/Mf/kv82QyMorSx/Dw03ziE7/KxMQEANPT063v58/93M9tey1/+Id/2DTtU1W4TVQhcbP9QlitAoHfNEkVS4QlCU2RkGkWAwwBhhDogCkEuoDd9hCdTueRGGjdnigg5DLUqginGylsS3EfRCRJQukJovQEcT43ipm+mUDwrWtY6TLqaEezhWA4aj/39oFlWVy9evVIW4IeNIrFIpZl2YaBJ4ixsbGW6u8gyjRpt92Kxx57TLzyyiuHuT4bm1OFYRhbJtFDQ0NkMpkjdZ8+DJIkcfbsWaanp9sqTkimRTRZRMgSmQ4/4oCmgACV765T/Mo8kV84h9bXvjzfmasRvpYhPdGB7tt+YNOSFbRMDUIeBt80iRy2eyltTh75fL5tU7rQYg7drVHu2P53WpvJ47j6/7N3p0GSZddh3//3rbnvS2XtVd3V3TODJggMAGIIkgAIgpRFSiYpSpYthxQSKYUJissH0+EIO+xwhMMKR9gfbHGzTIZELRQlmKJIgAQNkARIYyMWDpbu6a2qq7v2ysqqzMo93+oPOZXd1ZW1L1ndfX8REzOdlZnvZk3ne/ede+45ZRo/PLGreKf1J8sMv+8qTIX3DQQcJhKJ9LKcevODtov41bv4P/cKqAqqEARUhYCqYqoKPtB2XNquR8d16TfNTiaThEKhXt0E3/ao/rM76BMRQj8ysef5pmkyNjZGIHC+hdNu3bq1688aoAnQhEADdNEtZKgBHm8HCfBxfLA9nzZQGBoimU6fWRaS12pCeROEAoqCyGS72xwk6W1erYNzv4hzfwN3uYI6keq2JbyaRQmfbJvKi25lZeXSFHd+ngUCAcbHx0+8HUq6eEKIr/u+/55+P5NXFkk6hn5pUevr64yNjaGq6rlfZDRNwzTN3grUzkS9Vqv19hzncjlqtdqxggCa7ZIuVmmFDKqJ0ImLAgI0PrdC40+XSf/sO9Dyx++RbVTfDgJcS/cNAihNm8i3S+jlDuXvHSE8lJJBAOnSisfjbG9vU632S/bvrx01CZdb+wYC7KsxjNltjPsVrBtPttxo35XDK7URIye/ed4pGJjJZNjY2ABAWW0SeFcGM2QSULuF/DquR9t1qVg27hG2PyiK0jsn+Z5P/d/OoiYMgj88vue5qVSK4eHhE3+G44hGo7sqiDt0b/bpfaYnn03l7SABAk2AoUDHg7jVxl9b6W05QFN7hQtRNVDVoxcwdCyolEFRwOtucfCbDUQ0fmafWXr+KVET4/UxjNfH8Ns2zlwJ516Rzh/fR8lH0a91txAo8aN3sniRNRoNGQQ4I+12m/v37xMMBhkZGTn3YK10vmQgQJKOSVGUXallzWaThYUFJiYmzvxCo+s62WwW0zQJBAL4vk+n06HdbuN5Xq/l2PT0NNvb2xSLRaLR6L7VyvsxWxapUp3tRIjmKdoW+b5P/Y8WaX9tg9Qv3ERLHf+99FqH1IMttmZS2M8WS/N8Qg/KhB5UaE3Hqb6eB03BNE9eyFCSLsLQ0NCxAgGdqElyabt7IyjYG5gTgtb784T/aAF7PIof6l7KlYiOShD7cQ2OX5KjZ2VlhempKQwhcGrbaDnohAO0PZ+63cH2jt+NxHVdIpEIvu/T/L1H+E2HyE/d2HODfJFBAICRkZF9t0o8ywVcHzr4vfhAMBhEKYzs2nKA44Bl4bea3f/2PPy3AwR7Chiqard7wI52B9ptCJjd5zg21Gt4gTqK9Unw62B+GPR3n/0vQ3ouiYCO/loB/bUCvu3iPt7Cvlek86VHKBGzmylwPYeSjbx0tXMcx2FjY4PNzc1BD+WF02q1mJ2dJR6PMzIyIrcLPKdkIECSjmmnANfTgsHgnr60Z2F4eBjLsigWi7Tb7X1X+YvFItlslpmZGXzfxzAMWq3Woe8fqrWJV5psZSN0AidP8/J9n9rvPqJzv0Lq52+ixo7/XnrdIn1/k/KVFFZsdxDBWG8S/dYGTkSn/KFR3KcyBTKZ43cikKSLZBjGseqICM/Hxyd/r4jWcdm4msaK7A54eUkT61qCwFeLtD745MZZGQ7h/Nkmfsw8VjExQ1Ewn0r3315dJl4YYdv3Wfn1L+N/Tx7skxetq1arDA8P0/7sKs58jehPv4rQdo+vUCiQTqdPfIyTaLfbhz/pANlstntzJVQwVODJuWnnlsv3/V53g+6/Xeh08Hc6Hjzd5aDT7r7QskDzIZECfx1R+0Xwa4AGnU9D5L8D8/tONXbpxSN0Fe1qd4uA7/m4SxWc+0VaH/8GKAJtJod2LYs6mkCcYvvfZdRsNtnY2MD3fXzfp9VqyXoAF2B7e5tarcbExESvjbP0/JCBAEk6pn5Rz3g8fuI9ufsJh8OYpsnCwsKhlcdd12Vtba3XM/zpCqJ9+T7xcpNAy6I4FMfVT14U0Hd9tn97Fme9RfrnbqKEjn9a0ZoW6XslKlNJOoknQQClYRP9dgmt2qF2M4tV2H2RmZiYkFVspedCLpdjdXX10OcFy02ys5sojgf4eJqKt8/3s/PONJHfnUddaeAOd78bSlhHhDWcb5fRv3P/m2pNdAv8mVr35t/1fNquS822KbU9fKDUesjU5BTed01THD5+FsDTAoEArXKDzpfXif3MayjB3d/bcDh84UEA4FQrhUKII1VnFkKArnf/efpx3g4SuO6TLgeNejcTBB/sJrRbkPkywt8GpdB9oVeH1r+SgQDpQEIRaONJtPEk/keu4RXr3WKDn7mHV++gzWTRr2VRJ1KIU8wBBsnzPBqNBrVaTab+D5DneczPzxOLxRgdHX2uswOerusTDAZf+Hnmi/vJJOmc9DvBPdu+4yzk83nW19eP1X6sWCwyPDx84FiE55Mq1RC+T3Eojn+KFkS+7VH5l/fx2w6pn3kNxTz+ZEJr2aTvltieTNBOvb2f0fUIP6gQnK3QvJpg+715eGacqVTqWL1SJWmQkskka2trh36f27EAnYiBWeug2h6+InCMfb5XmkL7/XmCX1qn/p9Owtsr7OpUDPv/foD2zlQvFVgR9Cr7B97+LrVdj5bjUu5Y9Mv2dxyH+c/fYuK9V0jmwhSLRcrl8ok+/3CuwNK//SbRn7yBEt+bMTSIiVar1TpVJtdZrH4JIZ5sFTDB3y6Dqnb/CYUhGALvK2A/tXorFA7uYyBJuwkhUPNR1HwU83uv4JWbOA826HzpEd7v30KbSnc7EFxJIwKXt11lu92mVqsRDoepVqtsbm4eu0WrdH52/p9ks9lBD+XEnp5Xtlot7t69y+joKIlEYoCjOj8yECBJx6Sqeyfl5XKZdDp9pBW/ozJN89iT1Hq9jmVZRKPRvnuSVadbFNAydSqp8KmKAnodl8pv3EUYCsl/9CpCP35AQW07pO+UqI7FaaW7hQWN1UZ3G0DCZOvDY3jhvZMS0zQvdB+xJJ2WoigkEolDb6R9VWFjJkv+ThG93cQxtH2/p6oQOGMR3NltzG9v0XlXd5uMyAWg7aItNoleTRBQVVRF0HFd2o5H1bJxjjh5duYqzN39Kqkff41wOHyiQIDZUHA329SGPPR8/y4i29vbDA8P9z2/npfHjx+f6vXnMtmNJxCaBob5ZD+3873Q/m3wtgAdaID5X579saWXhpIMYbxvAuN9E3gNC2d2A/v2Ku1PvYU6mujWFZjJoTxbq2dAyuUya2trl6pNs9TfabdbDZqiKAwPD7OystJ7bGlpiUajwchI/xa6zzMZCJCkY+qXEVAqlZiZmWFjYwPHOf1KzU4RwJPsb9vvQql3bNIbNeqxIPVo4HRBgJZD+dfeQs0Gif/nVxHq8d9L6Thk7mxQG4nSyoZR6xaRb5XQGja178xhHdBx4MqVKyceuyQNytDQ0JFupD1NYf16lrE3l3G1/t+tmK6RChgs1lu035cj8olHiOtJDFVBNzSGvn+Mxpc38K7E2epYWCfcKysWG/jvzVCv18nlcgghjrUC5261SRpZKuUy+tTBafSPHz9menr6ROM8rlqtdqpztRDiXPbDKuE+gRJtAuL/GzT/NfhNMD8K5l8582NLLyclbGC8cwTjnSP4HQfnYQnn/gadz82ipMPdTIFrWdT0xe//dhyH2dnZM5lXSRdje3sbXdcZGhoa9FBOLJVK4TgOxWKx91i5XKbdbjM1NfVcb314lgwESNIx9TsBuK5LpVIhnU6zvr5+6mNEo1GazeaJXrvT1SDQ7CA8n1YkQLDRIbFVp5yO0g6drverW7Uo/+pbGFdiRP/G1ImqECuWS+ZOifpQhGY6RPitTYIPt2leS7L9/sKu3uh7XqsoL9RJWHp5qKra2/JzGM9Q2XhPi3Dks6R1g2rzg9hONwsmZerEDR0hBElTB1Mn+BM38LdaCAQtx6X6apT6H8xjrzdQUidc1XM9WG3BSBjLsmg2mwwNDbG9vd3rXHLgZ2jYpCoBgu9PUCwtwyGxiGazieM4575NoFgs7prgncSFF8XSbkDsf77YY0ovHWFq6K8Mob8yhO96uI/L3WKDv/V1MDX0t4MCSiF27h0IKpUKy8vLMvX/OVQqlcjlcs/1XC2Xy+H7fq+NLjzZKjA1NUUw+GK05pSBAEk6pmc7BuzY2tpiamqq7yQ/Eongui7tdvtIF7VYLMb29vaJxqcoCp7rktqoodkutbiF0XHYyMe7acan4G512PrlWwTenSXyV8dOFgSwXTJ3NmhmgjieIP3HC9ipAFsfGccLHj4+Xb+8+xcl6TDZbJatrS1s2z7weQHjPkOZ/5Xu3bNPLPxZljb+R3LGFUK69qR9napSQ6GeDmKu2Jie0m3vZ6jor2ewv7SO+cPjJxvsehuSBgS66fpra2uk02mGhoYwTZNSqbRrkvQ033KJLkLmw5M8Ki4eObupVCqd+0pSpVI59XvIbiXSi06oCtp0Gm06jf9DN/BWqtj3i7Q+cQtsr7t94FoOdSxxrA4l+9na2sJxHHzfp1QqyQDAc24nGPA8y+fzBINBFhYWeo95nsfc3BzDw8OkUqkBju5syECAJB3TfoEAy7LwfX9P4cBMJkMqlcJ1XUzTxLZt2u02xWKRTqdDMpkkk8ngeR6e5+G6LrFY7MT1BhRFIR4IYUbCsFUjZUP9HVdRWw2cUxQ0dNZbbP3KbcIfGib84ZPtzxeOR/puiU5AR3tUx2g7VF/PYWf33wbwrEik/x5jSXpeTE1N8eDBgwMnusnoJ/B9BddLAqCpm6Qif4ruzuD5Pt7brxVCkBkqYFkW7ncGsO9t0Ih2z1H6G3mav3Qb4yMjiMAJ9t4vNvBHn6x8W5bVOy9pmsbY2BjRaJRGo0G73aZerxMMBrEtG+VOjeEfuMHDtcfH2td7EStJ+53Dj0oIIc9D0ktFCIE6EkcdieN/6CreZgPnXpHOZx/gVVpoVzPdLQTT6RN1IHBdl5WVlWNvPZIur50uDuFw+LluKxiLxbh27RqPHj3ade1YWVnBtm3y+fwAR3d6MhAgScd00KS2VqsRjUZ7gYBkMkkqleLhw4e9PW6maRKNRpmYmGB+fp58Ps/i4iKu6/YKijmOc6y+40/b2NggqxgYN6+hxCL4joMobpKYnMSyLBYWFo79vvZSna1fu0P0h8cJvXGyk55wPdK3i/gVC73WoHEjSWs6ceA2gF2vF4KhoaGBtBiTpLNkGAZXrlxhdnZ23+cIYeHz5GbYR8Gjw6Nad8uQoSgYqoImBBlgfX2dTqdD4NZa91VvDKHEDbQrMeyvb2B84ASr7EsNeG1vpeSd85RpmtTrdTzPIx6PMzIyQqvVQtRdjB+eYO7xwxOdwyzLIhAIHP7EAXlRUkIl6SSEEKiZCGomgvmBabxqG+fBBvbXF2l/4hbqZKq7hWAmiwgeLYNvp12bDAK8OJ7eY59MJolEIsTj8QGP6mQMw+DatWtsbW2xurra+3vaaDQGPLLTk4EASTqmg1Jc6/U6mUy3sFYkEiGdTjM/P7+r0E2n06HT6aCqKleuXKFer+86mTSbTZrNJlNTUywsLNBqtY4wKp+g8RaK0qBdugGzNdqqgm3qtEIG4zvLpwAAIABJREFUraBBc3uTwvAw+Xx+VzXUw1gPq5R//S6xvzlN8F0nS4cVjkv2S8uoay0aU3Hq3zWMFzj66ccwDK5evfpc7zeTpKcddqO73fgwQ6k7gEDgI/CoNb+n93PL83oFAJ/+VrZfzxL93Xnsqy3cbBD9A3na/+4h+ht5xBGDbgD4PmKpgf9DT6okCyFIpVJkMhkajQYPHz7cs7re+uNlrG9v8a7/869jBgPY9frRj/m28/6enzTIukMGIyXpCSUWwHh9DOP1MfyWjTNbwr5fpP2Ze6hD0V6xQSW+fwDtpDWRpOdDuVym2Ww+t4GAHalUikQiwebmJoqivBDXAhkIkKRjOKxybb1eZ3h4mNHRUVzXpdls7puGur6+jhCilz71tEqlguM4TExMsLy8fGgbwWTkd0lFfx8fgR0eodj8r2lGorja7hS9SqVyrLZ7nbtlKr95n8TfvYb5SvLIr3uaWmmT+2x3f1Xpw2PYmaNvA9iRz+dlEEB64ewU9uyn0Xo/61s+schnwFcp1/46bevG4W9qqLTfmyP4xTXqf20SdSyCiGi4d8porx1jP+NGG0IaRLorepqmMT4+juu6PH78uG+LqM5Xi3S+WiT2M6+xXa0Sj8epX8JAgGmap7rxeLrPtCRJT4igjn6zgH6zgG+7OPOb3Q4En3+IEg+gXc+hXcuhZMK7agwZhvHct52TDnZYXZznhaIo59M6dkBkIECSjuGwyaPv+9y7dw/oFgU7rPr12travj+r1+s8evSIiYkJNjY2+gYMdsTCn8NxY/gY6PoqnUwN19mb0mvb9pErcre/UWL73z8k+VOvYFw5uO1XP8JyCd/ZIvZWCXsswsZ3j8AhE3xVVQmFQpjmkyrnuq4/91FkSTqJeusN6q03jv06eyqK/mAb404Z67UUxgeGsL5YPF4g4Kn6AIFAgImJCba2tvYtDmjdKdP8w0ViH3sVJWZQrVbJZrMn2vN73oGAQqHA3NzciV6r67oMSkrSEQhdRb+WQ7+W63YgWKrg3CvS+vdvgiJ6QQF1RF7fXwYnaYctnT8ZCJCkYzjOKtJpCv7taLfbPHz4kMnJSTRN27flVceaJBT4Fr6v4WPguP1X73dqDxw2OW9+eZ3aJx+T+tir6KPHLIrl+wQWa0RulVAVaN9Ms/Vqdt9aANFolEQiQTQalRNs6aVybu23hKD9Rp7wHzzGnoyivprE/9Qi7nIDdeSIRZuWmnAlSjAYZGJigpWVFarVat+nOot1Gv/uIdG/fw01203/tW2bTqdDOBw+VlbAebckg+4ef13XT7RCJbMBJOn4hKqgTaTQJlL4H72Ot17Dub9B+1N3cNsWnTcSqDULN2XCGXQgkC6nhYUFxsdP2MVGOhcyECBJx3DU1DXTNNE07Uz2vdm2zcOHD5mYmCAUCu2q0L1zM1+s/CNS0d9BVatU6n8Vz9//5r3dbvdauoRCIUql0q6tB43PrtD43Arpn72Jlj9eUSyt0iH6zSJ4Pt5wCD+gsnUt0zcIsHODcd49wyXpsjrPm14vZmC9kiT4F0Wa3z+C/kYO+wvrqH9r+vAX79QH+OAQQ0NDrK2t7RsEcEttav/8HuG/OYU2sfsmeXt7m0QicaxAgO/7NJvNc6/KHwqFTtSi9UVoFyVJgySEQB2KoQ7FML/vCnNv3UNUGgTf3EDbtrALYayxCHYhBMYJup1Il1a1WmV2dpbp6Wm58HNJyBm4JB1D55D2e7quk06nSSQS+6bQnoTruszPzxONdlfo0uk0hUKhN0H3/Ail6t870nutra2RSCRwXZfNzU3Gx8e5ffs2vu9T/9Qi7a9vkP75m6gp8/A3e5uwXCJvbWIu16m/miLgeSgdl62Z9K4gwE7HhFQqhWEYx/49SNKLxDCMQ+uOnEbnHSkiv/cIbbGO/54sjf/923jbFkr8kO9e2QJFEBlJomkalUql79O8uk3t1+8S/MFRjD7bDra3t3v1PY6aFnpRrflOEoBUVfVSdzOQpOdRBxcvZlD/wXFEy8FYqmM+3Cb8F+s42UA3KDASwQ/KW5YXQbvd5t69e1y5ckXOAy8B+a2SpGM4aNI+NDREIpGgXC4zOzt75hN83/epVqu9lblQKMTw8DDJZJLV1dUj98be6UqwY2ebQO0/zGPNVkn9/E3U2BFPzr5P4HGVyFubdIYjbP7AOLHVOlrboXQj00vxS6VSDA0NyQiwJD0lEomcb7VsTaH1Rp7gF9ZwfnQK/Z0p7K8UMT86evDLSjbm94wzMjrK8vJy3+f4HZfab9zDeFeawPv7txR1XZdOp0MwGDxym6XJyckjPe+0TjIBTSZPVjBVkqT9Pb1N0Q9qdGYSdGYSYLnoq02MxTqhN0u4caMbFBiN4EXlDeTzzHVdHjx4wJUrV2RwdcBkIECSjuGgffXxeLxvO63z0mw2mZ2dJZ1OMz09Ta1W67VoOaqdfbLb/2YWp9gi9bPvQAkd7bSgldtEv7EBAirfPYwTN4ktVjFqHTZeyYKqoCgKU1NTsu+2JPWRSCT2rftxHEIIEokE6+vre37mDodxc0HMb23ivZGn9c/uYHywgNgn5TYYDDL5w9dpVxoUi8W+af2+41H7Vw9QC0GCP3hwUEHX9SOdE6PRKMPDw+j60fqOn9ZOAPU4drZUSZJ0dgqFQv+WxoaKPRHFnoiC66GttzAW6wQ+vYgfUHtBATdpwgXUFpHOlu/7zM3NMTMzIzMDBkgGAiTpiA7bFuD7/rGrY5+Fzc1NKpUKyWSS4eFhhBCsr6/vu6f3aUEzyPadIt52h9TPvIZiHr4fT3RcIrc3Mdca1F9L0x6PghBEl6oEKi2Kr2RBU4hGo4yNjcksAEnax1lOfmKxGJ1Op28af/u9OSK/N489HcN8LYN3q4L67v79j5PJJKX/9y4bsQ5k9q7U+L5P4z/MIwSEf3zqwDoHiqKgquq+RflUVSWTyZBOpy/8PKEoCplMhlKpdKTnx+NxeS6TpHOQSqVYXV09eP6kKjjDYZzhMLw3h7bZRl+sE/n8Kng+1mgEeyyCkw3uW5hYunx83+fBgwcyGDBAMhAgSUd0WGqr7/sXUvG6H9d1KZVKlEolIpEIIyMjhwYCvI5LoOXTqtXJfOwmnjgkiOH7BOe3Cd/Zoj0WZfMHxvHfXlWMrNQIbjbZeDULutorBChJ0sFOWr3+ab7vUywWKRQK1Go1XNfd/fOQhvP+AuOZAoFf/A6EB/VOk/X19V2r9YFAgFg0ysMvPoa/0//72/r0Eu5qi9h/9QpCO/jG2DTNvgFUwzAoFAoDr8A/NDREPB5neXm5byHYQCBAKpUikUjIIIAknaOhoaGjZ+goAicbxMkGab0rg7ptoS/WCf3lBkrDwRoJY49FsIdCcMg5Sho83/dZXFzkypUrgx7KS0kGAiTpiA5LuR9kIOBp7XYbVVUPLNDlNR3Kv3GX1/7pT+ArkPc8Hj58uG9dA32zRfSbG3iaQuV7RnDiTwoJhtfrhIt1iq9k8XUVTdOYmpo6l88mSS+aWCzG5ubmqd+n0+mwvb3N0NBQ3339ye++hr/c4OGnvkr1T1cZ/oevM31jGs/zcF0XRVEQQrBxexErLPqm2ra/vI715iaxf/wa4oDsoXg8Ti6Xw3XdPUX5JiYmBh4AeFowGOTq1avYts3Kygr1ep1gMMjIyAimefSCqZIkncy9e/d656Bj95oXAjdh4iZM2jfTKHUbfblO4G6Z8BfXsIdC3aDAcBj/CBmP0mC0Wi08z5MB1wGQgQBJOqKjrNpdhkBAoVCgVCrte0F1qxZbv3Kb9AcnsD2HuQdzZDIZJiYmePjw4a70PKXtELm9iVFsUntHhs5oZNcNQqjYILJco/RqFt/snk6uXr0qT+aSdETZbPZMAgEApVKJmZmZPYGAVCpFLB5j9u5jgl8tor0jwfI//zqVn2yiaVrv+9put+FPl2E0tOe9rdtbtD69ROxjr6FE9t/HL4Qgn8+zurqKEILh4WEMw8CyLHRdv7T1QnRdl1lMknTBPM/r/XMm7xfR6VxP0rmeRLRd9JU6xkKN0FeLOOkA9lgEazSMH7qYWiTS0VWrVRKJxKCH8dKRgQBJOqKDAgGapqFp2rm2AjuKWCxGIBBgaWmp78+drTblX75N4D1ZUv/JNK1WC9/32djYIJlMYhhGN5XX8wk+3CZ8b4v2eIzNH5jA13ff3AdLTaJL22y+ksUNdE8luq6fqC2XJL2sNE1DVdU96fwn8WxhPkVRGB8fRwjB/Pw8TlzHno4RaTpsrrewH29jtTyUhIEyW4WIjpit4v/o+K73tR/VaHx8nuhPXkftUzfgablcjlarRa1WAyAcDhONRtnc3MS2bZaWli6sM4AkSZffWZz7+vEDKtZ0HGs6DraHvtrAWKoT/FYJN6Jjj0WxRiN4h7VTlS5Eq9WSgYABkDN2STqigy5WoVAIx3EGGghQFIVCocDi4mLfojvOeoutX7lN+EPDRL5/hHg8vqciuOd56Bstot8s4gU0yt83itunTU9gq0X8cYXSK1mc4JPIukyllaTjCwaDfavzH5fv+2iaRjgcRtd1MpkMjUZj197b9rsyRD4+h9ayaf3Cl/BMDfPvXSPw7TKstaBsITY7NKMq5j+8gd90qP/mfcL/2TTaWOTQMYRCoV2dEFqtFqlUCgDLsmRBKEmSehRFOZM6KYfSFezxKPZ4FFwfbaPbgSD6p0v4mng7UyCCmw7IDgQDcl4BIelgMhAgSUd0UOparVajUCiQSCT6Vu2+CIVCgWq12reWgb1UZ+vX3iL6IxNEPzDM+Pg4juOwtbUFdG9EVFUl/PV11OVt6t+RoTMc6XtBNCttEvNlNm9kcJ5Jr+tXcEuSpIPFYrEzCQS0223K5TL5fB7LsiiVSnvOR2KrTemPlnDKHVzbQwlpiICKfzWGWG1CRMPdbFP7Ro3mcgMlpBH6kXGMV5JHGkOtVmN4eJhHjx5h2zamaeL7Prqu4/s+8Xj81J9TkqQXx+TkJA8ePLi4A6oCZyiEMxSC92RRtzoYS3XCX15HWC72aARrLIKTC4EqgwIXRWaTDob8rUvSEe3X2mYn/bbZbLK9vX3Bo3oiEAig6zqqqlKv12m321iWRftBhfJv3CX5X8yQ/K5RRkZGqFQqFItFhBAM5YdIRGNUf/8vsVWf7Y9O4O9TadfYbpOc22LzWho7vHdlb9BbIyTpeRSLxfr30T6BYrG4a0V+F98n8qfL6DmTSs3G98BvuQhTgStR+JNVEGANB2C7jX2ngpI0UQvhIx+/VCrh+z7T09M4joNhGMzNzWFZVq9mgCRJ0g7TNMnn86yvr1/8wYXATQdopQO03plBqVoYi3WC39pEra5iD4exxiLYhTDosvbRedJ1WbdhEGQgQJKOYL9sACEEU1NTNJvNo7e+OSdzc3Pouk4kEiESiZBOpzE0HW/MxfvIu9BDJu12m/X1dba3t4lGowznhrAflSj+4efZvp7AjfTvLQ5g1DqkZrfYmkljR/tvAZBFAiXp+DRNIxqN9vbVnxshqP/oFIFskMwXVyn95RZW3cFXBYyEoeXA9TidgMDb6iAiGr7tUv2l2yT/yXuPXAx1c3OTZrOJ7/t0Op1eEDUcPnpAQZKkl0c2m6VUKg08PdyLGbRfS9F+LYVoOhjLdczZbcJfXsfJBbtBgZEwfkDePp21jY0N0un956DS+ZB/kyXpCEqlUt/Hc7kctm0PPAiww7ZtyuUy5XKZ1pslqh9/SPZjNwleSfT6eSuKwvjwCEHFoPrJN9lMgPXu7IH74vS6Rer+JuUrKazY/nUAZERXkk5mZGSEu3fvnvtx/KBG6wdGUV9Lkv03Dyh+aQNFqWPmGjjv07B//Crtn/48uD5qLkjwo6MEPpA/dkeUVqu15zEZCJAkaT+6rg88EPA0P6TRmUnQmUkgLBd9pYG+WCf09Q3cpNkNCoxG8A7ooiId3c521Z2aMtLFkIEASTqE53lsbGzseTwUCpFIJJidnR3AqA7W/NI6tT9YIPWxV1FGg70ggKaoTA2P4T4qsTS3QONaAtSDV/G1pkX6XonKdJJO4uCK4Ze1NZgkXXaapjE2Nsbi4iLQTZednJykXq+zurp6Zu21driFMI2ff4WJX3yTWP638RGI/8GnWnsflVdeI/xjNzBuphD7bBM6iVBob1tCSZIk6AYKL2udId9QsSZjWJMxcDz09Sb6Yp3g7S28oNYLCrgJQxYbPIVisSgDARdMBgIk6RBbW1t96wOMjo6yvLx8qSLYAI3PrtD43Arpn30HWv7JjXm04TP66iS1txZZoYF3/fCTrdaySd8tUZlM0E4efpOfzWZPNXZJepntFNJbXl5mcnKSYrFIJBIhn8/vm3UUCoXQNG3fGiYHSaU+QSzyZzhuElABj3jsS1z/P3Q2tr9n39fpuo7jOMc+pgwUSpK0n3w+T6PRuLTBgB5NwR6JYI9EaHo+WqmFvlgn8mfLIATWaAR7LIyTCYIigwLS5SYDAZJ0iH6Ft6LRKI7jnEml77Pi+z71P1yk/WaJ9M/fRE11U/jVhk1myyP1wXewPrvAVtgCDk9lU9sO6TslqmNx2unDV/KCwaBsHyhJpxSPx3Fdl/n5eSzLol6vc/XqVVRVpdlsUqvVekX4crkcwWCQlZUVLMs61nEENvHwZ3DdON0gAICC7SaJBr/AZvVv4fm72wWapsnQ0BChUAjLslhaWuplGx0mnU7LGiKSJO1LURSuXr3KrVu3Bj2Uo1METi6EkwvRencWtWKhL9UJfW0DpeVgjYSxxyLY+RCcYXbVi0peIy6eDARI0iH6peQmk8le673LwPd9ar8zjzVXJfVz70CNGeB6hO+XibsG8R99nceLCzSVo03a1Y5D5s4GtZEorezh+3ojkQjj4+On/RiSJAGpVKq3Hcm2bR4+fEgwGCQcDpPL5VAUBcdxKJfLLC0tnSgbQFGaCGHjE33mJyogUNVtPOdJICCZTJLP5ykWiywsLJBIJJiammJpaenQgGgikaBQKBx7jJIkvXxCoVDfNsiXnhC4SRM3adK+mUapWejLDQJvlQl/cQ17KNQNCgyH8Q318Pd7Cck6UxdPBgIk6RBCiF0TbUVRiEQiLC0tDXBUT/iuz/ZvPcAttUn93DtQAirGap3oN0sorw4R++g7eby4SLNztHQ7xXJJ39mgPhShmY8c+vx8Pi+3BEjSGRsdHWV+fh6ATqdDp9OhUqmc2fu7XhjPCyNEB99/OpPHwUfBcZ9Ub04mk2QyGR4+fNjLPCiXyxiGQSqVOjAQMD4+TiwWO7NxS5L0YhsfH7+QwqnnzYsadG4YdG4kEW0HfbmB8ahG6CtFnEwAeyyCNRLBD8lbsR2ZTGbQQ3jpyL99knQIVVVxHKf3Z8/zEEKcefGuk/Btj8q/uIdveyQ/9hq67RL94jpK08H+/isMf8cMi4uLR46uK7ZL5s4GzVyYRuHZlcK9AoGADAJI0jkIh8MEAoFz3C+rsVX7MTLxf4nr+fh+ACE6aEqVzdqP4fuB3jhyuVxvq0Lv1ZpGMpnsBSueJYTg+vXraJqcZkiSdHSapmEYxrG3O11mfkDDuhLHuhIH20NfbWAs1gl+o4QbM7pBgdEIXswY9FAHKho9fN4pnS15hZakQzwbCABwXRdN0/Y8fpG8jkvl1+8gAhqpv3+d8GyZ4HyV5vUkyjtHGZsYp1wuH/liKmyX9J0SrVSQ+vDRVvAmJydP8QkkSTrI+Pg49+/fP7f3rzY/jO8rpGL/EU3dxPPClKp/m+3GD/WeE4vF6HQ6vfOIEIJQKEQmk6FSqexbI2BqakoGASRJOpHLsNBybnQFezyKPR4F10crNjEW60T/eBHfUHtBATdlvlQdCGQx2cGQV2lJOoRt23sec123b4DgonhNh61fu42WC5L7vgLRzy1iZ4JsfWQcL6hxfWwU27bRNI0rV64cuo9XOB6ZeyU6cZPa6NGCANlsVk70JekcGYZBIpE40y0BuwlqrQ9Ra30QRbTwfJMnhQO71tbWGBsb67U2HB0dxTAMqtUqm5ubfd81FovJVoGSJJ2YaZoDXWi5MKrAKYRxCmF4bw51s42xVCf8xVWE42OPRrDGIjjZIKgvdlAgmUwOeggvJTmLl6QDtFqtPZHpaDSK7/sDS1tzqxZbv3KbyHSUQiGA8qBM9T1D2NluNDUQCOB5HrOzs0C38M7Y2BjlcpmNjY09hcWE65G+V8IKG1TH40eKQGuaRj6fP/sPJ0nSLsPDw2xvb5+oIODRCTy//4277/ssLi4yPj7OjRs3cByHubm5fccjhGB0dPQcxypJ0osumUzSaDQGPYyLJQRuJkgrE6T1zgxK1Xp7+8AGat3GHo5gjYWxC+EXsgOB7Do1GDIQIEkHKJVKu/4shKBQKLC8vHzOE/P+nK022798i8LVGImQQmM4QmsqvqtXbSwWo1qt9v7cbDaZnZ1lbGyMV199Fdd12XrwGO9bj9m8liY1u4UT0NieTBw5DU1uCZCki6EoCiMjIwMtTur7PgsLCxiGcWi7wMnJSdkCSpKkU4nFYiiK8mJvETiIEHhxk3bcpP2ONKJhYyw3MO9vE/7SOk4+iDUWwR6J4JsvRgeCl/b/9YDJQIAkHUBVd59gs9kszWZzIJFqZ62B/X+9xZXxEO61OFuvpfECe7/CkUiEtbW1XY+5rsujR4+AbsbARC6H+O4Y4T+7RTUoqEwnjxwEyGazBAKBU38eSZKOJpFIsLW1NdCWWr7vHxoEyOVyhMOHtxuVJEk6iKIoDA0NsbKyMuihXAp+WKdzLUHnWgLRcdFXGuiLdUJf28BNmd2gwGgEL/z8tt+T147BkIEASTpAKBRia2ur9+dAIMD29vaFj8O/u0Xo/5nDnInS+KEJ7HT/oiqKomCaJq1Wa9/36tSbND/955ivjBP58e9GvPWYitvG1w4PBAwPD5NKpU78OSRJOpnJyUnu3LkzkEyko8jlcuRyuUEPQ5KkF0QqlWJ9fR3XdQc9lEvFN1WsqRjWVAwcD32tib5YJ/jtTbyw3gsKuHHjuSk2qKqqzCQbEBkIkKQDPFvwqtFoEA6HLywYICyXwJ8vo/7FOq3356l9ZOzAE3s4HKbZbB54sxCotNBaNu5fzlFbKBL66LuYCuksrq/2LYy4Y2JiQrZ2kaQBURSFXC7H+vr6oIeyx8jIiCz0JEnSmUskEvsWJb2MhBAEAgFCoRCapqGqKrqu9/57fX39bOePmoI92r3xb3o+2kYLfbFO5HPLoIheUMDJBC51UCCRSAx6CC8tGQiQpAMYxu6ervV6nXQ6ff4H9n0CCzWCX1yhfK+K/TeuoN88/LiBQGCfbAAXUyziYxCf9xAe1AsR6oUIreIymUKeqakp5ubm9kTfdV1nampqz+9CkqSL9exWpctABgglSTovkUjk0gcCNE0jFouRSqUO3TY5NjbG8PAwKysrNBoNfN8/u4wHReDkQzj5EK3Xs6jlDvpSndBX1hEdF3vk7Q4E+SCol2v1XRafHhwZCJCkQwgheivsnU4HIQS6rh+4en4aWrlN9JsbOMUW87erhP7BDYzpo7X0688nr/5rwsptwKd68yM89j+CG3yyl2xjYwMhBBMTE8zPz/c+bzgcZmpq6nQfSJKkU3McZ0/x0kESQjA9PS17P0uSdG4uy7YARVEIh8N4nofrugghSCaTJBKJY6e0q6rK2NhY78+e51EsFtnc3Dy7rV9C4KYCuKkA7e/IoNQs9KU6wVubqF+wsAvhbrZAIQTGYAPMyWRSbgsYIBkIkKQDWJa158Rcr9eJRCKUy+UzPZawXCK3NzFX62wKlbVvbZP66dfQR05XQEWjTFi5heMnAJdo9M8p2X9lz/OKxSLxeJxkMtmri/D0xUqSpMGxLGtgLUufpaoqMzMzaJqcQkiSdH4G3UJQVVUKhcK5pq7vFEbM5XLMzc0dWpT1JLyoQeeVFJ1XUoiWg7FUx3y4Tfgv1nGygScdCIIXe07XdZ1CoXChx5R2k1dxSTrA04UCdzQaDVKpFNVq9Wyi1b5P8FGV8FubtEejLOg69S+sk/7Zd6Dlj7faFggEaLfbux7zCOKjo9BEwcb2+xf0yufzuK7bC3CEw2E50ZekSyIUCp1rJtJRxWIxRkdH5QqOJEnnbhAZATup/slk8kIznhRFIZVKsbq6eq7H8YManZkEnZkEWC76ahNjsU7ozRJu3HjSgSB6vttBZYHZy0HO8iXpANVqdc9jlUqFaDRKJpM5deEubatN+M+XEXGD8geGqXxhnfabm6R/7iZqyjzWewUCAYLB4J5+4x5BVp1/QEb9JK4foOT+eN/XB4NBtra28H0fIQQjIyMn/lySJJ29bDY7sHZahmEwPj4uW4dKknTuPM+jUqkMJCPg2rVrAwt0ptNpwuEwc3NzR9omoGkajuOc/ICGij0RxZ6IguuhrbcwFusEPr2IH1CfdCBImmdabFAGAS4PGQiQpH14nrdvKm6z2UTXT96vVXQcIrc3MZbrPPr0EtaNFOqGhTNfI/XzN1Gjx39vwzBotVp9Lx5t/ypLzi8c+PqNjQ2y2SzVapWZmZlTfT5Jks7eRU9OFUUhkUiQy+VkdpAkSRdmYWGBer1+4cc9yZ7/sxYIBJiZmeH+/fsHPi8ej+O67tn9nlQFZziMMxyG9+bQNtvdDgSfXwXPxxqNYI9FcLJBUE4eFBBCkMlkzmbM0qnJK7sk7aNSqZz9m3o+wfltwne3aI9HWYwGqGzZuJ98jD4aZuiXvgc1dLIb8Ha7farIcKPRoNVqcePGjYFfCCVJ2ss0j5cl9LSdoqdCCAzDwHXdXeeLnY4EruuSSqUYGhqS5wFJkgbiVKvcfSiKgqIoB75vJBJhdHT0TI97UoZhMDU1xfz8fN+fp9NpAoEAy8vL5zMAReBkgzjZIK13ZVC3LfTFOqG/3EBpOFgjYeyxCPZQCLTjXScymYy8tlwiMhAL/109AAAXC0lEQVQgSfvY2NjY92ehUIhms3ms99NLLaLf3MAzFMrfO4IbM6n991/B3e4gDBW3YlH/w0XiPzF9ovFalnXq/cNTU1PyBC1Jl1QwGDz2uScUCpHP5wmH+xcddRwHz/Nke1BJki6NfvWOjiMUCjE+Pt4LADzNsiw6nQ7hcPhSz3f6nbM1TePq1atomsbdu3cvZiBC4CZM3IRJ+2YapW6jL9cJ3C0T/uIa9lCoGxQYDuObB3cg0HVdtgp8hud5VKtVbNsmm81e+PFlIECS+mi1WvveVIdCob578fejtBwit0voGy3qNzN0RiIgBNZineYX1hCagpLQ0UcjqMmTr/gB+L7fu/AJIXBdF8/zDn2dEIJ8Pi9bgUnSJTc9PU2tVmNlZaXvOSoQCBCJRIhGowSDwUMnujLlX5Kky2Z0dJRsNsva2hq1Wu3IrxNCEI/HD1zZNwzjuQl8Koqyaw43MjLSqwtw1lkTR+VFdDrXk3SuJxFtF32ljrFQI/TVIk46gD0WwRoN4/fJbh0eHh7AiC+3arXau5+o1+sX3rJbzgAkqY+DCnIVCgXW1tYOL+Ti+YTmKoTulWlNxqh9dAJdX2PU/FUU0WS5+r2YNxLE/vZVAjdTaKmzKcK1c9GYmJggHA5TLpdZX1/HcRwURcH3/d7Yd/ZqZbPZSx0ZlyTpiWg0yvXr1+l0Ojx8+BDP83q9qfdb+ZckSXqemKbJxMQE7Xabx48fH5jxGAgEGB8ff25u8I/qxo0bFItFSqUSmqYRjUbxPI8HDx70niOEQAhxpEWfs+YHVKzpONZ0HGwPfbWBsVQn+K0SbkTHHotijYbx4iZCCKLR6IWP8bKLxWK9gE+j0WB2dpZ8Pn9hvytx0M3Me97zHv9rX/vahQxEki4Lx3H2TbkKh8MMDQ0xNzd34HvoG02i39jAC2rU3pnFfbsNy1jwf0ETJXzfRBEdHjX/JzzO78teKBRIp9N7Hrcsi2az2TsBSZIkSZIkXVZbW1u92k2+7+N5Hp7nkc/nSSQSAx7d+dq5yVcUhYcPH/a2hymKwsTEBAsLCwNptbgv10fb6HYg0JbqND9QIKDqjF2dQhmOIc6wA8GLoFqtsrCwsOsxIQTT09NnkqkrhPi67/vv6fczmREgSc84qCWgEOLAdCylaRP5dgm93KH+HRk6hfCuliuqqOH5QXx0FNFCER08//wCAfvtsXueUuMkSZIkSXq5pVIpUqnUoIcxEE8v2BQKBVzXJRQKoSgK6+vrlysIAKAKnKEQzlAI3pNF8SBfNmn9wW3oOGgzWbTrOdTxJEKVi1GxWIx4PM729nbvMd/3WV9fZ3Jy8lyPLQMBkvSMp7+Iz9qpur2H6xGarRB6UKE1Haf6er5vJdVN66+RNT4O+NSd13H8vav1ZykSiZzr+0uSJEmSJEkX49kV4nA4TLPZxLKsI9eFulBCMHF1imA4DB+6hrvZwLlfpPPnc3ibDbSrGbRrObTpNMJ4eW9Lx8bGsCyLVqvVe6zRaJz7cV/e37gk9dFoNPY9iaqqSj6fp9loEP/iCo1X0zgJE2O9QfRbJZywTvlDo7iR/Vfaa85303JvIOhg+0PA+aZH7RQgicfj53ocSZIkSZIk6WJFIpFdiz7FYpFisTjAEe2mKMqu2jVqOoz6xhTmG1N4tQ7OgyL2m8u0P3kbdTyJdj2HdjWLEn75slanpqZ48OBBrx6G7/vUarVzrRcgAwGS9JS1tbW+jxuGweTkJJVKhfr/d5fEnU30rTZ22kSr2tS+I4tVOFqRLse/uNQ23/dZXFwkEon0+oRLkiRJkiRJL55cLker1TpWt4XzdFBmqhI1Md49hvHuMfy2jTNXwrlXpPPH91HyUfRr3S0ESvzl6GilKAozMzPMzc3R6XQAWFhYoFAoUK/XGR0dPfO6XjIQIElv8zxvV0rO0/L5POVyma1HK2S/to6vCILz29jxLJs/MA6XfI+TLMwiSZIkSZL04hsZGdm36PVFi8ViR3qeCOjorxXQXyvg2y7u4y3se0U6X3qEEjHRdoIC2cgLPafdCQbcunUL6C7o7XQyu3PnDq+88sqZBgNkIECS6LYL7F8bwMcQyyieoN0MkfyTBfStNp6p4kZ0AqsNqp6Pf4kX21VVlZ0BJEmSJEmSXgKapvVa0g3aSdLaha6iXc2iXc3iez7uUgXnfpHWx78BikCbyaFdy6KOJhDKixkUeLZ4IHSDAvV6/cjBlaOQgQBJolsgsF/V1Yz2cWLalzFqJlH7I1DMY+VCOHEDL6DhhDXYvwPnpTA1NTXoIUiSJEmSJEkXJBAI9NoMDtJBbeqPQigCbTyJNp7E/8g1vGK9W2zwM/fw6h20qxn06znUiRRCv8Srcsc0MjJCtVrd8/urVqt9AwGtVgtd19G0493ay0CAJNFNxXk2EKDQIKZ9GcePo2ESMT7N/Z/6J8Dzc6IZGhoiEAgMehiSJEmSJEnSBRkdHeXBgwenvhE/jUgkcuwb04MIIVDzUdR8FPN7r+BVWt2gwJcf4/3+LbSpdLcDwZU0IqCf2XEHQVEUTNPc0wa8UqlQrVZJpVJEo1FM0+Tx48e9rc2GYXDt2rUjH0cGAiSJbvr8TpXOHT4GHiYKLXy3jaqngOcnxT4UCpHJZAY9DEmSJEmSJOkCGYbBzMwMs7OzF7JFIBAIoCgKiqIghCCbzRIKhc71mEoiiPG+CYz3TeA1LJzZDezbq7Q/9RbqaKJbV2AmhxI1z3Uc52W/bb2e51EqlSiVSnt+dtzAjwwESBKg6/qeqJuPzpr1U2T038FxdKKF/xalal+KPVeH0TSNycnJQQ9DkiRJkiRJGoCd1eFisUi1WsVxnCO9TlEUdF3vVa7fjxCCdDpNLpcbeC0qJWxgvHME450j+B0HZ36z24Hgc7Mo6XA3U+BaFjV9tA5fl8GzC5RHcdz6ATIQIEl0vzj9Wq20vSssdf4bYrEYUX0E03y0b2eBQRNCEA6HyefzBIMvR6sVSZIkSZIkqT9N0xgeHmZ4eBjP86hWq7RaLZrNJu12e88KsmEYXL16lXK5zPr6+r6LX4FAgOnp6YEHAPoRpoZ+I49+I4/veriPy91ig7/1dTA19LeDAkohdmk7EHied6JAQCp1vBblMhAgSXSrcy4vL/f9WT6fJxqN7tqDcxkoioKqqui6TjqdJh6PD3pIkiRJkiRJ0iWkKAqJRIJEItF7rNVqsbGxQb1eJxKJMD4+DkA6nSadTuM4DouLizQajd5rUqkUw8PDFz7+kxCqgjadRptO4//QDbyVKvb9Iq1P3ALb624fuJZDHUsgLkErcM/zWFtbo1wuH/u1uq5jmsfbBiEDAZJE9+SoaVrftKlkMsnc3NyJInOnlc1mSSaTdDodhBAEAoEzLbwiSZIkSZIkvZyCwWDv5r8fTdOYmprCsixWV1fJZDKEw89Pev3ThBCoI3HUkTj+h67ibTa62wc++wCv0kK7muluIZhOD6wDwfr6OltbWyd67ejo6LFfI+8oJAmo1Wp9gwDBYBDHcQYSBABoNpvk83kMwxjI8SVJkiRJkqSXm2EYTExMDHoYZ0YIgZqJoGYimB+Yxqu2cR5sYH99kfYnbqFOprpbCGayiODFdSA4ah2HHa+88gqqevKghQwESC89z/NYWFjo+7NoNNq3dsBFOW7RD0mSJEmSJEmSjk6JBTBeH8N4fQy/ZePMlnAeFGl/5h7qULRXbFCJn28NrpGREUzTZGtr60hBgdMEAUAGAiSpb7GUHaFQqG97jouSTCYHdmxJkiRJkiRJepmIoI5+s4B+s4Bvu90OBPc36Hz+IUo8gHY9121LmA2febFBRVHI5XLkcjksy2Jubg7Xdfs+97j1APqRgQDppXfQin8wGKTZbF7gaHarVqu7irpIkiRJkiRJ0nnyPO9SdgS4aEJX0a/l0K/luh0Ilio494q0Pv4mKKKbKXA9hzoS3xMUcNeqKJkIQtv/99hut1lYWKBQKBCNRnf9zDAMRkdHefz48d5xCcHU1NSpP58MBEgvvf1u9AOBALZt79s65SI0m00ZCJAkSZIkSZIuhOd5vPXWW0D3hjMYDJLP53tFAtvtNuVymXq9juu6aJpGJpN54eerQlXQJlJoEyn8j17HW6/h3N+g/ak7+C0LfebtDgQTKfB96r/yebTpNKG/856+xQdXVlZ6hQGXl5e5ceMGnudRqVR6bQBXV1f7jmV0dPRMiofLQID00ut0Ovv+bL8tA2chGAxiWVbflB8hBPl8nkwmc27HlyRJkiRJkqSnPb0A5vs+zWaT+fl5hBB958WO41AsFl/4QMDThBCoQzHUoRjm913BKzex7xfpfGEe7/e+jYgF8Cot7G+v0vjNrxD+u+9FGG/fdvs+9UZjV3cAx3FYWFigWq0C3XsTRVGwLGvPsaPR6Jm1DJeBAOmlt18xDsuyzrVa/9TUFIqi0Ol0KBaLKIpCIBAgFAphmqZMyZIkSZIkSZIulKIofW/6D1ocG2T27GWgJEOY3zWJ+V2TePUOjX/xFfymhef7eF96hLdWJfKP349y6z/C5mO80BAi/z585cmt+E4QAGBzc7NvDQBN0xgbGzuzcctAgPRSO6gip+d5+L6Pqqr7Fuo4DcuyCAQCmKZ5pl9qSZIkSZIkSToJRVEY/f/bu5uvxLE8jONPQhIIICAvrVK+VDVldZ9e9Gb+iVnMZv7gWcx+zpnddC3GchStVosXad4ChDALD47WiCIGRfP97CQ3914XcE6e3Pu729uqVqtz3xP1IOAmI+VoUu/KzLmSaWgy8BVc9hX88+8yW/9RT47s2helExtqr1dm9rO/v68//vhDx8fHMgxDpVJJxWIx1BeFBAGItFarNfOaZVkKgkCO46jf74c+9tnZmXZ2djQcDnVycqLNzc3/KxQCAAAAPKdsNqtGo6FutztX+2VupX1tDMOQ+9dfJddWrJiSkXVlmIb0r7/Jb4zly5dtSEYw+2WkbduSro4R39/fl23bS1kpzNpjRNp9JwZMkzjP85YydqfT0W+//aaDgwMNBgNVq1USVQAAALy4d+/ezd02SvUB5mH/Wpa9X5K5nrwKASQFe39Sz0jIGvU1SOTVyd1d9d8wDFUq/1spsMztwqwIQKTdfNPvOI7evXunw8NDSVfbBprN5rOlnEEQyPM8JZPJZxkPAAAAuMu8dbJs235UaBBFvu/r39Uz+ft/UcwfaGzFJePuh/tKpRLKiQDzIAhApN3c+7+2tnZrhUC/35fruveeKhAGwzCUSqVUKpUIAQAAALAS0um0Op3OvW2WWVj7LZieujCZTCTD1Nh2Z7bd29tTIpF4trkRBCCyvj+SI5fL6eTk5PrvaRBweXm5tDkUCgVtbW0trX8AAABgEbu7u/r8+fOdW1enxbSf88H1NQmCQMfHxw8GKVPb29vPXiuMIACR5TiOtre31Wq1NB6P5brurXCg0+now4cP6na7t470CMve3h7FAQEAALCSTNPUhw8fdHBwcOtz27a1v7+vyWQiwzBeaHarKQgC1Wo1XVxczH1PNpt9kToLBAGItFwud/3FGwwGt+oBTAv4vX//Xp8/fw71CMFUKkUIAAAAgJXmuq4qlYo6nY7G47F831e5XF5aAbvXajAYqF6vL1RfrNVqaWtr69lqA0wRBCCyWq2WqtWqLMtSNpu980ubz+evf/jCxDIqAAAAvAau68p1Z+9tj7LxeKwvX748uqZYPB7X+vq6TNOUZVnPHgJIBAGIsFarJemqkme9Xr+zTbPZ1MbGhsrlsr5+/Rra2PyYAgAAAK/XrUKAczJNUx8/flyJIosEAYism0cHzjKtD5DP50MdO5PJhNofAAAAgOdRq9V0dnb26PtKpdJKhAASQQAibDQaPdhmWkOgWq2GNm4mk2FfFQAAAPAKnZ6eqtlsLnRvoVAIeTaLIwhAJPm+P1e7wWCg8XisXq+38Fjr6+sqlUqSdL0PCAAAAMDr0m63Fw4BNjY2VuplIE8kiKRGozFXuyAIFv7CGoahSqVCYUAAAADglRuPxzo+Pl7o3lgsdv1icFWsTiQBPJN6vT732Z7pdFrdbnehcYrFIiEAAAAA8AYMh8NHHw04tb29HfJsno4VAYiU8/Nzffv2be726XR65okCD0kmkwvdBwAAAGC1uK4rx3E0HA7nvsdxHO3u7q7ky0GCAERGo9F4VAhgGIZc1114RcDR0ZHy+bzK5fJC9wMAAABYHZ8+fZJ0tX3Y9321Wi1dXFz830oB0zRVLpeVy+VeYppzIQhAZGQyGfV6PfX7/bmW9mQyGfX7fQVBsPCYjUZD7XZb+Xxe2Wx2ZY4LAQAAALAY0zTlOI5KpZIKhYLa7bbG4/F1fbFcLrdShQHvQhCAyLAs63p/Tq/X0+Hh4cwwwDRNbW5uLlwQ5KbRaKTz83Odn59Lkn7++WdODgAAAADeANM0lc1mX3oaj8bTCCLn7OxMtVrt3jYbGxtqt9vq9/uhj7/q6SAAAACAt40nEkSK53kPhgCSlMvlHlVPYF6pVIogAAAAAMCL4okEkXJ6ejpXO8/zFI/HQx9/c3Mz9D4BAAAA4DEIAhAZvu/PtdTfMAw5jqPRaBTa2JZlaWdnR67rhtYnAAAvaTweq9frvfQ0AAALoEYAIuPy8nKudqVSSb1eT4PB4Mlj2ratcrmstbW1J/cFAMAqOTw8lOd5sixLhUJB6XRa8XicLXAA8AoQBCAyHqrU77quNjc3ZZqmqtVqKOP99NNPT+4HAIBVEwSBPM+TdLXi7ubpOI7jXJ+1DQBYTQQBiAzbtmdei8Viev/+vX7//fe5Vw48ZGdnJ5R+AABYNcPhcOa1MLfWAQCWg7VbiAzHcR5sE1YIkEgklEqlQukLAIBVc9/y/62trWecCQBgEawIQGTEYrGZ18bjsUzTlGEYmkwmTxrHMAzt7u4+qQ8AAFaZZVnK5XKaTCYyTVOmaSoWiykejyubzb709AAADyAIQGQ8VLzI933Ztn3vcsf7xGIxFYtFFQoFCiUBAN400zS1vb390tMAACyIIACRkkgkrosbfa/RaGh3d1etVkuWZanZbM5s+71MJsMqAAAAAACvAq8tESk//vijDMO489q3b99Ur9dlmqYSiYSSyeTc/a7CW5Fut6sgCF56GgAAAABWHCsCECnTh/x+v3/n9WazKUkql8uPqhVweXmpfD4fyhwf0u12dXp6qslkokwmo1wup5OTEw0GA0nSDz/8oGKxyPYEAAAAAHciCECk+L4/MwT4vl0ymbwOBh7SaDSWHgRMA4CbNQzq9brq9fqtdhcXF2q1Wtrf31/qfAAAAAC8TrwyBO5Qq9WUTCZVKBTkuq7i8bgsy5r5lt3zPDUajaXNp9Vq6fDwcO5ChplMZmlzAQAAAPC6sSIAkWJZllKplLrd7r3tgiBQtVrVxsaGstns9bFI0yOSgiBQEAQajUbyPE+e5+nr169qt9va29sLfd6u616PK10dUZhMJm/9H4ZhKB6PK5fLqVgshj4HAAAAAG8DQQAiZ2dnRwcHBxqNRve28zxPR0dHd16bBgO2bSuRSMiyrr5KnU4n9PlKkuM4+vTpk46OjrS2tnZdA6Ddbms0GimbzSoWiy1lbAAAAABvC0EAIseyLH38+FEHBwfyfX+hSvs3VwT0ej0Vi0VlMpmlnh5gWZYqlcqtz9bW1pY2HgAAAIC3iRoBiKzhcPjoECCdTt/5ueM4isVi+vLlSxhTAwAAAIClIQhAJMViMf3yyy9KJBKPum96RN8snuepVqs9ZWoAAAAAsFTGfWelG4bxj2ecCwAAAAAACEdtMpn8+a4L9wYBAAAAAADgbWFrAAAAAAAAEUIQAAAAAABAhBAEAAAAAAAQIQQBAAAAAABECEEAAAAAAAAR8l9KiikVShIOTgAAAABJRU5ErkJggg==\n",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"# Map projection\n",
"crs = ccrs.PlateCarree()\n",
"fig, ax = plt.subplots(1, 1, figsize=(20, 8), subplot_kw=dict(projection=crs))\n",
"ax.coastlines(color='lightgray')\n",
"ax.add_feature(cfeature.LAND, facecolor='lightgray')\n",
"ax.add_feature(cfeature.BORDERS, edgecolor='white')\n",
"# Uncomment for the map to span the whole world\n",
"# ax.set_extent([-160, 180, -60, 90], crs=ccrs.PlateCarree())\n",
"\n",
"# Overlay network graph\n",
"nx.draw_networkx(graph, ax=ax,\n",
" pos=geo_pos,\n",
" font_size=14,\n",
" alpha=0.7,\n",
" node_color=col, cmap=plt.cm.spring_r,\n",
" edge_color=edge_col, edge_cmap=plt.cm.get_cmap('RdPu'),\n",
" node_size=sizes,\n",
" labels=labels)"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"### Evolution of the network during 2000-2016"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"source": [
"The gif below displays the evolution of the network of illicit trade originating from Africa during 2000-2016 (i.e. the period for which we have data). The darkness of the edges (reflecting the logged dollar value of illicit trade) increased markedly during 2008-2009, perhaps reflecting the commodity supercycle at the time. If prices of internationally traded commodities increased, then it stands to reason that the dollar value of mis-invoiced trade increased as well.\n",
"\n",
"Europe is a destination hub for illicit outflows originating in Africa. The size of the nodes is proportional to their degree. The size of European nodes increased during 2008-2012 and decreased in 2015-2016."
]
},
{
"cell_type": "code",
"execution_count": 115,
"metadata": {
"slideshow": {
"slide_type": "skip"
},
"tags": [
"hide-cell",
"remove-output"
]
},
"outputs": [
{
"data": {
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"# Create network maps of illicit flows for 2000-2016\n",
"for y in range(2000, 2017, 1):\n",
"\n",
" # Entire network of illicit flows in 2016\n",
" flow_data_whole = create_graph_data(str(y), threshold=False, flow_threshold=1000000)\n",
"\n",
" # Create directed graph\n",
" graph = nx.from_pandas_edgelist(flow_data_whole,\n",
" 'reporter.ISO',\n",
" 'partner.ISO', \n",
" 'Imp_IFF_hi',\n",
" create_using = nx.DiGraph())\n",
"\n",
" # Set map attributes\n",
" col, edge_col, outdeg, deg, sizes, labels = set_graph_attributes(graph)\n",
"\n",
" # Map projection\n",
" crs = ccrs.PlateCarree()\n",
" fig, ax = plt.subplots(1, 1, figsize=(20, 8), subplot_kw=dict(projection=crs))\n",
" ax.coastlines(color='lightgray')\n",
" ax.add_feature(cfeature.LAND, facecolor='lightgray')\n",
" ax.add_feature(cfeature.BORDERS, edgecolor='white')\n",
" # Uncomment for the map to span the whole world\n",
" ax.set_extent([-160, 180, -60, 90], crs=ccrs.PlateCarree())\n",
"\n",
" # Overlay network graph\n",
" nx.draw_networkx(graph, ax=ax,\n",
" pos=geo_pos,\n",
" font_size=14,\n",
" alpha=0.7,\n",
" node_color=col, cmap=plt.cm.spring_r,\n",
" edge_color=edge_col, edge_cmap=plt.cm.get_cmap('RdPu'),\n",
" node_size=sizes,\n",
" labels=labels);\n",
" fig.suptitle('Network of illicit outflows originating in Africa in ' + str(y), fontsize=20)\n",
" plt.savefig('Images/Network_Maps/network_map_' + str(y) + '.png')\n",
" plt.clf();"
]
},
{
"cell_type": "code",
"execution_count": 116,
"metadata": {
"slideshow": {
"slide_type": "skip"
},
"tags": [
"hide-cell"
]
},
"outputs": [],
"source": [
"# Create gif from network map images\n",
"filenames = ['Images/Network_Maps/network_map_' + str(y) + '.png' for y in range(2000, 2017, 1)]\n",
"images = []\n",
"for filename in filenames:\n",
" images.append(imageio.imread(filename))\n",
"imageio.mimsave('Images/Network_Maps/Maps.gif', images, duration=2)"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
""
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"## Conclusion"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"source": [
"This project has utilized the newest estimates of trade mis-invoicing of the United Nations Economic Commission for Africa (). The data contains estimates of the dollar value of illicit trade in both imports and exports for all reporting jurisdictions in the UN COMTRADE database, for 21 commodity sectors during the period 2000-2016.\n",
"\n",
"Following the establishment of the High Level Panel on Illicit Financial Flows from Africa in 2015, the scale and severity of the problem has been well-recognized by policy-makers and NGOs. The next steps now are to move beyond scale estimates and to start understanding the nature, mechanisms, and directions of illicit trade on the continent. This project takes the first steps towards that goal.\n",
"\n",
"I have utilized unsupervised machine learning techniques such as dimension reduction, clustering, and network analysis to extract meaningful insights from the data. Given that the feature space is large, especially when analyzing the data in its dyadic form, dimension reduction techniques are necessary to project the data in a lower-dimensional space.\n",
"\n",
"Following that, I explored some clustering techniques to ascertain whether they were able to recover some of the ground truth labels of the observations such as regional groups or income classification. Cluster validation will require further work.\n",
"\n",
"Finally, I exploited the bilateral nature of the data and perfomed a preliminary network analysis for illicit trade originating from African countries. Given the methodology used to estimate mis-invoicing, an edge would be created between a reporter-partner pair for any discrepancy in mirrored trade statistics. Therefore, it is necessary to apply thresholding before conducting network analysis. Further work will need to examine network statistics such as centrality measures in order to yield further insights."
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"**Policy recommendations**\n",
"- Target 16.4 of the SDGs: \"By 2030, significantly reduce illicit financial and arms flows, strengthen the recovery and return of stolen assets and combat all forms of organized crime\"\n",
"- Estimates of the magnitude and severity of the problem have shed a spotlight on the need to combat illicit financial flows\n",
"- Deeper understanding of the origins and destinations is now crucial to guiding targeted interventions to combat illicit flows\n",
"- Strong subregional effects are apparent in illicit trade within the continent. Initiatives to combat illicit flows could be anchored within the [Regional Economic Communities](https://www.un.org/en/africa/osaa/peace/recs.shtml) of the African Union, such as ECOWAS."
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"**Next steps**\n",
"\n",
"I plan to take this project further. Notably, I plan to conduct analysis on the most disaggregated view of the data, that is, for a reporter-partner-year-commodity tuple. By filtering by commodity sector, I will be able to identify the relevant sinks and sources.\n",
"\n",
"Moreover, I am currently exploring spectral clustering. However, spectral clustering algorithms are currently implemented for *undirected* rather than directed graphs. There are several possible [approaches](https://arxiv.org/pdf/1308.0971.pdf) to dealing with clustering on directed graphs. One of them includes a naive approach where direction is ignored, and where the graph is treated as an undirected network.\n",
"\n",
"Finally, I am considering non-negative matrix factorization as an alternative form of dimension reduction."
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "skip"
},
"tags": [
"remove-cell"
]
},
"source": [
"**Export slide show**"
]
},
{
"cell_type": "code",
"execution_count": 117,
"metadata": {
"slideshow": {
"slide_type": "skip"
},
"tags": [
"remove-cell"
]
},
"outputs": [],
"source": [
"# Uncomment the line below to export key slides from this notebook\n",
"# ! jupyter nbconvert Unsupervised-learning-trade.ipynb --to slides --SlidesExporter.reveal_scroll=True"
]
}
],
"metadata": {
"celltoolbar": "Slideshow",
"hide_code_all_hidden": false,
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.7.6"
},
"toc": {
"base_numbering": 1,
"nav_menu": {
"height": "160px",
"width": "244px"
},
"number_sections": true,
"sideBar": true,
"skip_h1_title": true,
"title_cell": "Table of Contents",
"title_sidebar": "Contents",
"toc_cell": true,
"toc_position": {
"height": "440px",
"left": "95.9884px",
"top": "110.926px",
"width": "211.991px"
},
"toc_section_display": true,
"toc_window_display": true
},
"toc-autonumbering": true,
"toc-showmarkdowntxt": true,
"toc-showtags": false
},
"nbformat": 4,
"nbformat_minor": 4
}